Math Jams

rrusczyk 2010-02-10 19:02:18
Welcome to the 2010 AMC 10A/12A Math Jam!

rrusczyk 2010-02-10 19:02:23
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.

rrusczyk 2010-02-10 19:02:30
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.

rrusczyk 2010-02-10 19:02:52
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read

rrusczyk 2010-02-10 19:03:06
There are a lot of students here! As I said, only well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!

rrusczyk 2010-02-10 19:03:31
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go (and certainly not to 200 students)! Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!

rrusczyk 2010-02-10 19:03:57
We do have an assistant tonight who can help answer some of the questions. Her name is Wendy Hou (wobster109). She is a college sophomore majoring in computer programming. She has taken the USAMO four times and competed in a broad spectrum of high school competitions, and she had the honor of representing the U.S. in China as a member of the first U.S.A. CGMO team. She has extensive experience from summer programs and with Art of Problem Solving, both as a student and as a mentor. She spends her days frantically battling down a monstrous courseload. She haunts a bell tower. At night, she transforms into a velociraptress and howls at the moon.

rrusczyk 2010-02-10 19:04:08
She'll be joining us in about a half hour.

rrusczyk 2010-02-10 19:04:29
In her place, we have a super-sub, one of our instructors here at AoPS, Jeremy Copeland.

rrusczyk 2010-02-10 19:04:43
Before joining us at AoPS, he was working at MIT, teaching some pretty smart students there! He has a PhD from the University of Chicago, so he's very happy to now be living in San Diego.

rrusczyk 2010-02-10 19:04:56
He's smarter than all of us put together, but you wouldn't know it if you met him.

rrusczyk 2010-02-10 19:05:15
Assistants can answer questions by whispering to you or by opening a window with you to chat 1-on-1.

rrusczyk 2010-02-10 19:05:33
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the answer. That's not why we're here. We're going to work through the problems step-by-step, and people who post comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, are going to be ignored.

ksun48 2010-02-10 19:05:36
what about mr. sato

rrusczyk 2010-02-10 19:06:07
nsato helped prepare the Math Jam, but he has another class to teach this evening. Even Naoki cannot teach two classes at once!

rrusczyk 2010-02-10 19:06:20
The Math Jam will proceed as follows:

rrusczyk 2010-02-10 19:06:34
We will work the last 5 problems from the AMC 10A, then the last 5 problems from the AMC 12A. After that, time and my hands permitting, I will take requests for some other problems for discussion.

rrusczyk 2010-02-10 19:07:05
We'll get started with....

rrusczyk 2010-02-10 19:07:15

ritwik_anand 2010-02-10 19:07:32
vieta's equations

BOGTRO 2010-02-10 19:07:32
Vieta

nikeballa96 2010-02-10 19:07:32
vieta's!

MathTwo 2010-02-10 19:07:32
vieta's formulas

Just_Beginner 2010-02-10 19:07:32
Use vieta's formulas

Lord.of.AMC 2010-02-10 19:07:32
use vieta

MrBob 2010-02-10 19:07:32
use vietas formulas

rrusczyk 2010-02-10 19:07:40
Let's see how.

rrusczyk 2010-02-10 19:07:41
Let the zeros be r,s,t. What do we know about r,s,t?

darkdieuguerre 2010-02-10 19:08:02
r+s+t = a

simplyMathLete 2010-02-10 19:08:02
rst = 2010

BOGTRO 2010-02-10 19:08:02
rst=2010

mz94 2010-02-10 19:08:02
rst=2010

flare 2010-02-10 19:08:02
rst=2010

EricMathPath09 2010-02-10 19:08:02
rst=2010

Visitor03 2010-02-10 19:08:02
they're sum is a

Just_Beginner 2010-02-10 19:08:02
r+s+t=a

PhireKaLk6781 2010-02-10 19:08:02
r+s+t=a

fortenforge 2010-02-10 19:08:02
r + s + t = a and rst = 2010

Truffles 2010-02-10 19:08:02
rst = 2010 and r + s + t = a.

rrusczyk 2010-02-10 19:08:08
We have rst = 2010 and r+s+t = a.

rrusczyk 2010-02-10 19:08:18
This comes from some of you are calling "Vieta"

rrusczyk 2010-02-10 19:08:23

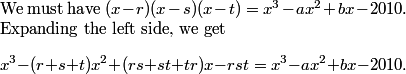
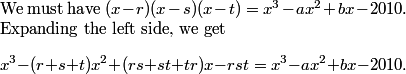
rrusczyk 2010-02-10 19:08:33
The constant terms give us rst = 2010, and the x^2 terms give us r+s+t = a.

rrusczyk 2010-02-10 19:08:47
This approach to relating roots and coefficients is what we call "Vieta"

ksun48 2010-02-10 19:08:54
we need to minimize r+s+t

rrusczyk 2010-02-10 19:08:58
We know that r,s,t are positive integers, so we must minimize r+s+t such that rst=2010.

prezcoin 2010-02-10 19:09:08
factorization of 2010= 2*3*5*67

nikeballa96 2010-02-10 19:09:08

abcak 2010-02-10 19:09:08
2010=2*3*5*67

Just_Beginner 2010-02-10 19:09:08
2010=67*3*2*5

PowerOfPi 2010-02-10 19:09:08
prime factorize 2010 to get 2*3*5*67

rrusczyk 2010-02-10 19:09:16

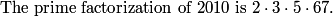
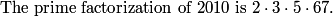
rrusczyk 2010-02-10 19:09:23
Now what?

Truffles 2010-02-10 19:09:48
2010 = (67)(3)(2)(5). In order to minimize r + s + t we use x,y,z as 67, 6, and 5. 67 + 6 + 5 = 78

sabretooth 2010-02-10 19:09:48
2*3 + 5 + 67

henrypickle 2010-02-10 19:09:48
67 is a zero because 67*another factor would be too large

nikeballa96 2010-02-10 19:09:48
we know r=67, so find s and t such that s+t is minimized.

EricMathPath09 2010-02-10 19:09:48
2010=2*3*5*67. The smallest possible sum is 6+5+67=11+67=78.

ksun48 2010-02-10 19:09:48
use 5, 6, and 67

flare 2010-02-10 19:09:48
smallest numbers possible are 6, 5, and 67... now sum them for the answer

megahertz 2010-02-10 19:09:48
to minimize, multiply the two smallest to get 6*5*67

rrusczyk 2010-02-10 19:09:53
To minimize r+s+t, we need 67 to be one of the roots (since multiplying 67 by anything will way increase r+s+t!) Then, we're left with two roots with product 2*3*5. A little intuition, or some trial and error, will tell us that we want one root to be 2*3 and the other to be 5, giving us a sum of 5+6+67 = 78.

rrusczyk 2010-02-10 19:10:02
This must be the right answer, since there are no smaller answers to check!!

rrusczyk 2010-02-10 19:10:47
A quick note: we have about 250 people in the room right now. So, those of you checking this out to see what our classes are like: this is not what our classes are like in general -- we won't be able to handle lots of questions tonight, for example.

MathSuperStar 2010-02-10 19:10:50
so it would be A

rrusczyk 2010-02-10 19:10:53
Exactly.

rrusczyk 2010-02-10 19:11:06
Also, I won't be able to answer general questions about our courses while doing the Math Jam.

rrusczyk 2010-02-10 19:11:21
You can email us at classes@artofproblemsolving.com to ask questions about specific courses.

rrusczyk 2010-02-10 19:11:35
You can learn about Vieta in our Intermediate Algebra text or Algebra 3 course.

rrusczyk 2010-02-10 19:11:45
Now, on to Problem 22!

rrusczyk 2010-02-10 19:11:48

rrusczyk 2010-02-10 19:12:09
One of my favorite counting strategies is what I call "constructive counting" -- we think about how to construct one instance of what we are trying to count.

rrusczyk 2010-02-10 19:12:26
How do we end up with a triangle entirely inside the circle?

sabretooth 2010-02-10 19:12:49
You need six points to make a single triangle under those conditions.

MathTwo 2010-02-10 19:12:49
three intersecting chords form a interior triangle

aleph0 2010-02-10 19:12:49
you need 6 points on the outside

fortenforge 2010-02-10 19:12:49
We need 3 lines that each intersect each other inside the circle.

straw1boy 2010-02-10 19:12:49
pick three chords

rrusczyk 2010-02-10 19:12:57
Such a triangle is formed by three lines:

rrusczyk 2010-02-10 19:13:02

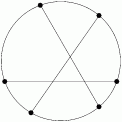
rrusczyk 2010-02-10 19:13:11
What's a natural question to ask ourselves about the triangle we've created with these three lines connecting these six points on the circle?

Just_Beginner 2010-02-10 19:13:34
is it unique?

pirox 2010-02-10 19:13:34
is there another?

ksun48 2010-02-10 19:13:34
what if they intersect?

aleph0 2010-02-10 19:13:34
does it always exist

agentcx 2010-02-10 19:13:34
when do the three lines intersect?

rrusczyk 2010-02-10 19:13:51
We should wonder both of these.

rrusczyk 2010-02-10 19:14:03
First, is this the only triangle we could make with these 6 points?

pirox 2010-02-10 19:14:24
ya

sparkle123 2010-02-10 19:14:24
yes

sabretooth 2010-02-10 19:14:24
yes

challenger 2010-02-10 19:14:24
yes

Wikipedian1337 2010-02-10 19:14:24
yes, each is paired w/ the opposite point

rrusczyk 2010-02-10 19:14:29
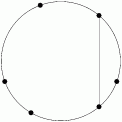
If we connect two adjacent points, neither of the other two lines can intersect the first edge we have drawn:

rrusczyk 2010-02-10 19:14:36

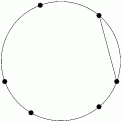
rrusczyk 2010-02-10 19:14:42
If we connect two points that have only one point between them, then there is only one more line that we can draw that will intersect the first line we have drawn:

rrusczyk 2010-02-10 19:14:48

Just_Beginner 2010-02-10 19:15:04
they have to be 3 vertices away

rrusczyk 2010-02-10 19:15:09
Therefore, to get a triangle from connecting 6 points, we must connect each pair of opposite points.

rrusczyk 2010-02-10 19:15:17
Will we always get a triangle when we take 6 points on the circle, and connect each pair of opposite points?

snowpaw 2010-02-10 19:15:48
the problems says that no 3 lines are collinear

darkdieuguerre 2010-02-10 19:15:48
yes because no three lines intersect at a single point

aleph0 2010-02-10 19:15:48
yes because no three lines are concurrent

MathTwo 2010-02-10 19:15:48
yeah we should

happyof 2010-02-10 19:15:48
yes

Lord.of.AMC 2010-02-10 19:15:48
yes

joshim5 2010-02-10 19:15:48
Yes, we will

ytrewq 2010-02-10 19:15:48
yes, no three chords intersect at a single point

rrusczyk 2010-02-10 19:15:53
Yes! If we do so, each pair of lines must intersect in the circle. These three intersections then form our triangle.

abcak 2010-02-10 19:15:59
yes. So that means for each set of 6 points, there is 1 possible triangle

rrusczyk 2010-02-10 19:16:03
Exactly!

megahertz 2010-02-10 19:16:16
so we count how many sets of 6 points there are

rrusczyk 2010-02-10 19:16:19
So, for every group of 6 points, we get exactly one triangle. Now our problem is simply counting how many groups of 6 points there are among the initial 8 points.

Just_Beginner 2010-02-10 19:16:39
how many ways to select 6 points from the 8 given is the new problem

nearsymmetric 2010-02-10 19:16:39
so 8 choose 6

fortenforge 2010-02-10 19:16:39
So we need to find the number of 6 points to be chosen from 8

MathTwo 2010-02-10 19:16:39
then 28 (A) is our answer

aleph0 2010-02-10 19:16:39
so we need 8 choose 6

simplyMathLete 2010-02-10 19:16:39
okay, so now 8C6?

mathrat 2010-02-10 19:16:39
8 choose 6?

megahertz 2010-02-10 19:16:39
so 8C6?

alex960531 2010-02-10 19:16:39
8C6 = 28 (A)

baldcypress 2010-02-10 19:16:39
8C2=28 A

challenger 2010-02-10 19:16:39
28

pumpkinpi 2010-02-10 19:16:41
So we have 8C6 = 8C2 = 56/2 = 28

rrusczyk 2010-02-10 19:16:46
This is simply C(8,6) = C(8,2) = 8*7/2 = 28, so there are 28 triangles.

LincolnMS nerd herd 2010-02-10 19:17:26
and so the answer is A and problem solved =)

rrusczyk 2010-02-10 19:17:29
Exactly.

ss5188 2010-02-10 19:17:37
but what about the triangles that have their vertices on the chords' ends?

rrusczyk 2010-02-10 19:17:45
The problem tells us not to count these.

megahertz 2010-02-10 19:18:06
what if the problem did?

rrusczyk 2010-02-10 19:18:22
Interesting question -- I challenge you all to think about that on your own :)

rrusczyk 2010-02-10 19:18:38
All right, let's take a look at the next problem

rrusczyk 2010-02-10 19:18:40

rrusczyk 2010-02-10 19:19:06
How can we get a feel for the problem?

AdithyaGanesh 2010-02-10 19:19:20
If you play around with it a bit, you'll notice that if you multiply the fractions through, many numbers get cancelled out.

megahertz 2010-02-10 19:19:20
try a small case of (n)

PowerOfPi 2010-02-10 19:19:20
Try small cases.

limac 2010-02-10 19:19:20
simple cases

sabretooth 2010-02-10 19:19:23
Try smaller examples first.

KingJames 2010-02-10 19:19:24
Try small values of n

rrusczyk 2010-02-10 19:19:33
We try small examples, since this will help us:

mathcountsloser 2010-02-10 19:19:36
Understand it??

LincolnMS nerd herd 2010-02-10 19:19:38
i would start small and work my way up

rrusczyk 2010-02-10 19:19:41
What is P(1)?

nsreenivas 2010-02-10 19:19:51
1/2

challenger 2010-02-10 19:19:51
1/2

PowerOfPi 2010-02-10 19:19:51
1/2

pirox 2010-02-10 19:19:51
1/2

ksun48 2010-02-10 19:19:51
1/2

darkdieuguerre 2010-02-10 19:19:51
1/2

Lord.of.AMC 2010-02-10 19:19:51
1/2

vcez 2010-02-10 19:19:51
1/2

xoangieexo 2010-02-10 19:19:51
1/2

xxrxxhxx 2010-02-10 19:19:51
1/2

Lord.of.AMC 2010-02-10 19:19:51
1/2

agentcx 2010-02-10 19:19:51
1/2

mathluver2.718 2010-02-10 19:19:51
1/2

rrusczyk 2010-02-10 19:19:57
We have P(1) = 1/2, since the first box has 1 red, 1 white.

rrusczyk 2010-02-10 19:20:01
What about P(2)?

Visitor03 2010-02-10 19:20:29
1/6

aerrowfinn72 2010-02-10 19:20:29
1/6

fortenforge 2010-02-10 19:20:29
1/2 * 1/3

megahertz 2010-02-10 19:20:29
1/2*1/3=1/6

mz94 2010-02-10 19:20:29
1/2*1/3=1/6

AdithyaGanesh 2010-02-10 19:20:29
1/6, or 1/2*1/3.

LincolnMS nerd herd 2010-02-10 19:20:29
1/2*1/3=1/6

simplyMathLete 2010-02-10 19:20:31
the second would be 1/2*1/3 = 1/6

rrusczyk 2010-02-10 19:20:34
We have P(2) = 1/2 * 1/3, since she must choose white, then red.

rrusczyk 2010-02-10 19:20:36
P(3)?

henrypickle 2010-02-10 19:20:59
1/2*2/3*1/4

Just_Beginner 2010-02-10 19:21:00
1/2*2/3*1/4

mgao 2010-02-10 19:21:00
1/2*2/3*1/4=1/12

ytrewq 2010-02-10 19:21:00
1/2*2/3*1/4=1/12

jxl28 2010-02-10 19:21:00
(1/2)(2/3)(1/4)=1/12

Visitor03 2010-02-10 19:21:00
1/2 * 2/3 * 1/4

rrusczyk 2010-02-10 19:21:03
We get P(3) = 1/2 * 2/3 * 1/4 = 1/3 * 1/4, since she must choose white-white-red.

rrusczyk 2010-02-10 19:21:10
P(4)?

challenger 2010-02-10 19:21:29
1/20

ksun48 2010-02-10 19:21:29
1/20

Just_Beginner 2010-02-10 19:21:29
1/2*2/3*3/4*1/5

lolFTW 2010-02-10 19:21:29
1/4*1/5=1/20

fortenforge 2010-02-10 19:21:29
1/2 * 2/3 * 3/4 * 1/5

The Archer 2010-02-10 19:21:29
(1/2)(2/3)(3/4)(1/5)=1/20

jxl28 2010-02-10 19:21:29
(1/2)(2/3)(3/4)(1/5)=1/20

wiiwilwin 2010-02-10 19:21:32
(1/2)(2/3)(3/4)(1/5)

rrusczyk 2010-02-10 19:21:36
We have P(4) = 1/2 * 2/3 * 3/4 * 1/5 = 1/4 * 1/5.

rrusczyk 2010-02-10 19:21:45
Aha! What do we guess P(n) will be?

megahertz 2010-02-10 19:22:15
numerators and denominators cancel out

prezcoin 2010-02-10 19:22:15

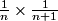
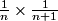
oxfz16 2010-02-10 19:22:15
the pattern is 1/[n(n+1)]

AdithyaGanesh 2010-02-10 19:22:15
So now, P(n) = 1/[n(n+1)].

PowerOfPi 2010-02-10 19:22:15
1/(n(n+1))

dolk 2010-02-10 19:22:15
1/(n(n+1))

Lord.of.AMC 2010-02-10 19:22:15
the product P(n) telescopes to 1/n(n + 1)

mathluver2.718 2010-02-10 19:22:15
1/(n)(n+1)

7thsamurai 2010-02-10 19:22:15
1/(n * (n+1))

rrusczyk 2010-02-10 19:22:25

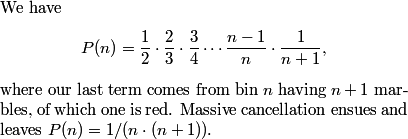
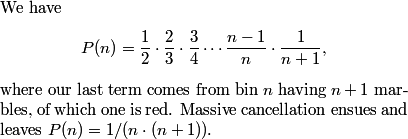
mgao 2010-02-10 19:22:47
so we need n(n+1)>2010

nikeballa96 2010-02-10 19:22:47
we need to find the smallest n such that n(n+1)>2010

flare 2010-02-10 19:23:00
so we have to find the smallest value such taht n^2+n is greater than 2010

ksun48 2010-02-10 19:23:03
now find 1/(n*(n+1)<1/2010

rrusczyk 2010-02-10 19:23:06
And that would be?

vcez 2010-02-10 19:23:27
n=45

aerrowfinn72 2010-02-10 19:23:27
45

fortenforge 2010-02-10 19:23:27
45

RobRoobiks 2010-02-10 19:23:27
45

henrypickle 2010-02-10 19:23:27
45

abcak 2010-02-10 19:23:27
we can easily see that is 45

steve123456 2010-02-10 19:23:27
45

gomath888 2010-02-10 19:23:27
45

simplyMathLete 2010-02-10 19:23:27
45*46 > 2010

msinghal 2010-02-10 19:23:27
45

rrusczyk 2010-02-10 19:23:35
So, we just need n^2 + n > 2010, and we'll get P(n) < 1/2010. Obviously 50^2 + 50 is way more than 2010, so (A) must be the answer. We can do a quick check and note that 44^2 + 44 = 1980, and 45^2 + 45 = 2070, so 45 is indeed correct.

challenger 2010-02-10 19:23:54
A

ksun48 2010-02-10 19:23:54
A again?

MathSuperStar 2010-02-10 19:23:54
its A

flare 2010-02-10 19:23:54
A is, once again, the answer

pirox 2010-02-10 19:23:54
so it's (A) 45 =P

rrusczyk 2010-02-10 19:23:57
The answer again is A.

rrusczyk 2010-02-10 19:24:22
(And again a reminder -- we won't get to every one of your questions tonight like we do in our regular classes. There are now nearly 300 of you here!)

rrusczyk 2010-02-10 19:24:29
Time for number 24

rrusczyk 2010-02-10 19:24:39

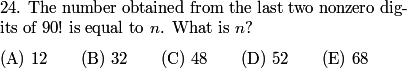
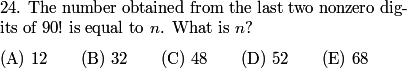
mathcountsloser 2010-02-10 19:24:46
#24 is very advanced for the amc 10

ksun48 2010-02-10 19:24:54
the hardest problem on the 10

rrusczyk 2010-02-10 19:25:02
I agree. This is the hardest problem on the test.

rrusczyk 2010-02-10 19:25:06
OK, before we get into the details of a solution, suppose you were given 6 minutes to get an answer. What would you do?

TheWorstPlayer 2010-02-10 19:25:34
bash?

rrusczyk 2010-02-10 19:25:43
That's what I'd try if I hadn't done this:

RobRoobiks 2010-02-10 19:25:47
skip it

aleph0 2010-02-10 19:25:47
break my pencil

rrusczyk 2010-02-10 19:25:56
Just start multiplying away, you only want the last two digits, and any time you hit a factor of 5, you pull a factor of 2 out of some other number. For example, when working through the 20s, you'd multiply by 23, then 6, then 26, where you pair two of the 2's from 24 with the 5's in 25, and just throw them away.

rrusczyk 2010-02-10 19:26:02
This isn't a terribly revealing way to do the problem, but it will work, and for most people (including me), it will be way faster than finding the "smart" way to do the problem.

rrusczyk 2010-02-10 19:26:14
OK. Moving on to trying to find the smart way to do it...

rrusczyk 2010-02-10 19:26:24
After we lop off all the trailing zeroes, we want the last two digits that remain. Let's let n be the number that's left after clipping off all the trailing zeroes. We want the remainder when n is divided by 100. We sometimes refer to this as "n mod 100".

rrusczyk 2010-02-10 19:26:33
(If you aren't familiar with mods, check out our Introduction to Number Theory book or class; we unfortunately don't have time tonight to teach all the fundamentals of mods. The rest of this solution will be pretty impossible to follow if you aren't proficient with mods.)

rrusczyk 2010-02-10 19:26:42
Now, might we attack something simpler than mod 100 for starters?

mathcountsloser 2010-02-10 19:26:53
I used mod 25

mgao 2010-02-10 19:26:54
mod 25

PhireKaLk6781 2010-02-10 19:26:54
mod 25

vjnmath 2010-02-10 19:26:54
mod 25

rrusczyk 2010-02-10 19:27:03
We might start with mod 25; since 100 = 25 * 4, and if we can find the remainder upon division by 25, we've at least narrowed down our choices considerably.

rrusczyk 2010-02-10 19:27:08
Why else does 25 seem like a convenient choice?

rrusczyk 2010-02-10 19:27:34
Why is convenient for this particular problem?

rrusczyk 2010-02-10 19:28:33
If we start cranking out the factorials, what do we see that's convenient?

aleph0 2010-02-10 19:28:55
a lot of stuff cancels

rrusczyk 2010-02-10 19:28:58
Why?

rrusczyk 2010-02-10 19:29:21
What I'm driving at is 4!

rrusczyk 2010-02-10 19:29:27
What is 4! in mod 25?

darkdieuguerre 2010-02-10 19:29:47
-1

prezcoin 2010-02-10 19:29:47
-1

simplyMathLete 2010-02-10 19:29:47
-1

EricMathPath09 2010-02-10 19:29:47
-1

abcak 2010-02-10 19:29:47
-1...holy cow

mathcountsloser 2010-02-10 19:29:47
or -1.

PhireKaLk6781 2010-02-10 19:29:47
or it can be -1 mod 25

rrusczyk 2010-02-10 19:29:49

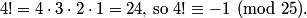
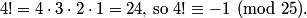
rrusczyk 2010-02-10 19:29:58
(Again, if you aren't familiar with mods, check out our Introduction to Number Theory book or class; we unfortunately don't have time tonight to teach all the fundamentals of mods. The rest of this solution will be pretty impossible to follow if you aren't proficient with mods.)

rrusczyk 2010-02-10 19:30:02
That's pretty nice, since multiplying by -1 is way easy.

rrusczyk 2010-02-10 19:30:09
Are there any other groups that have convenient products like this?

abcak 2010-02-10 19:30:40
6*7*8*9!

xxrxxhxx 2010-02-10 19:30:40
So then we have grouping, 1*2*3*4, 6*7*8*9, 11*12*13*14... and on and on

darkdieuguerre 2010-02-10 19:30:40
(5k+1)(5k+2)(5k+3)(5k+4) in general

ksun48 2010-02-10 19:30:40
6*7*8*9, 11*12*13*14

PowerOfPi 2010-02-10 19:30:42
9*8*7*6

rrusczyk 2010-02-10 19:30:48

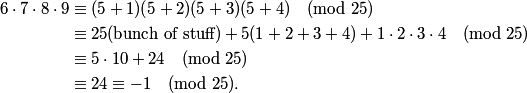
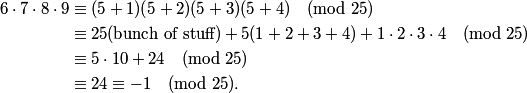
rrusczyk 2010-02-10 19:30:55
That's really nice. Similarly, we can group all the numbers that aren't divisible by 5 into groups of 4 whose products are congruent to -1 mod 25. So, we have

rrusczyk 2010-02-10 19:31:00

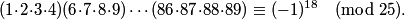
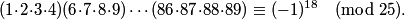
rrusczyk 2010-02-10 19:31:06

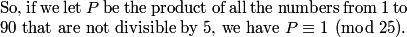
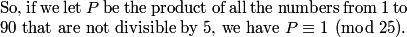
nmani2 2010-02-10 19:31:11
you leave out all the 5s!

ksun48 2010-02-10 19:31:31
then divide by 2's for the 5's

gopack25 2010-02-10 19:31:31
u can leave out all the 5

Jesse 2010-02-10 19:31:31
but they cancel with the 2s!

rrusczyk 2010-02-10 19:31:39
Of course, we're going to have to give up some of the factors of 2 in this product to combine with factors of 5 in the other numbers to make the 10s that give us the 0s we'll lop off at the end. How many 2's are we going to use doing this?

aleph0 2010-02-10 19:31:54
21

nikeballa96 2010-02-10 19:31:54
21.

33286 2010-02-10 19:31:54
21

challenger 2010-02-10 19:31:54
21

lxu1 2010-02-10 19:31:58
21

rrusczyk 2010-02-10 19:32:02
We have to count the factors of 5 in 5*10*15*...*90.

rrusczyk 2010-02-10 19:32:07
There are 3 multiples of 25, and 18 total multiples of 5, for a total of 18+3 = 21 factors of 5.

rrusczyk 2010-02-10 19:32:13
So, we have P = 2^{21} * Q, where Q is the number we really care about, since we'll use up the 21 2s making 10s. (We'll get some 2's back when we multiply out the multiples of 5 -- we'll get to that shortly.)

rrusczyk 2010-02-10 19:32:35

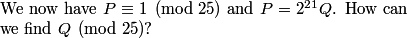
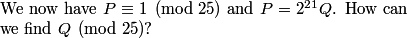
aleph0 2010-02-10 19:33:16
and nicely 2^21=2 mod 25

happyof 2010-02-10 19:33:16
2^10=-1 mod 25

rrusczyk 2010-02-10 19:33:34

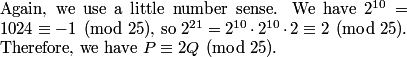
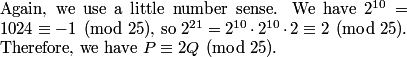
rrusczyk 2010-02-10 19:33:49
So, what is Q(mod 25)?

gomath888 2010-02-10 19:34:00
q=13

SuitcaseAsian 2010-02-10 19:34:00
13?

aleph0 2010-02-10 19:34:00
13

prezcoin 2010-02-10 19:34:00
13

simplyMathLete 2010-02-10 19:34:05
so Q = 13(mod25)

rrusczyk 2010-02-10 19:34:10

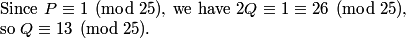
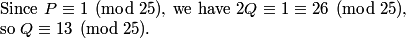
rrusczyk 2010-02-10 19:34:19
We've now learned that the product of all the numbers from 1 to 90 without factors of 5 is 2^{21} times Q, where Q is congruent to 13 mod 25.

rrusczyk 2010-02-10 19:34:36
(If you're totally lost on this problem, don't feel bad -- it's by far the hardest problem on this test, I think)

rrusczyk 2010-02-10 19:34:45
Now, we have to deal with 5*10*15*...*90. Of course, we have to strip out the factors of 5. We know there are 21 of these, and we'll pair them with the 21 2's we took out of P.

rrusczyk 2010-02-10 19:35:02

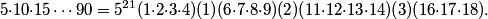
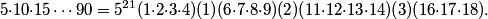
rrusczyk 2010-02-10 19:35:12
So, we want to know what

rrusczyk 2010-02-10 19:35:19

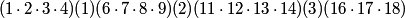
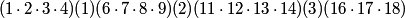
rrusczyk 2010-02-10 19:35:22
is mod 25

33286 2010-02-10 19:35:36
we have more -1s mod 25

agentcx 2010-02-10 19:35:36
doesnt that go back to the congruencies we discussed earlier?

rrusczyk 2010-02-10 19:35:56
Yep, we have already dealt with a lot of these already.

simplyMathLete 2010-02-10 19:36:01
24 = -1(mod25)

nmani2 2010-02-10 19:36:03
1*2*3*4 = -1 and doesn't this become a whole lot of -1s

2009 2010-02-10 19:36:16
many things cancel out!

rrusczyk 2010-02-10 19:36:21
Fortunately, we've already dealt with the first three long products, so we can simplify this as

aleph0 2010-02-10 19:36:25
so we can cancel out 1,2,3,4, 6,7,8,9, and 11,12,13,14 to make -1

rrusczyk 2010-02-10 19:36:30

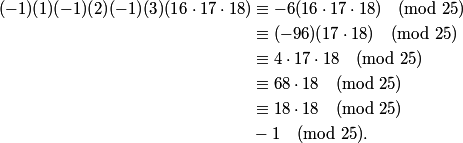
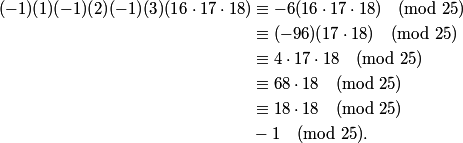
megahertz 2010-02-10 19:36:48
how do we get rid of 16*17*18?

rrusczyk 2010-02-10 19:36:54
Just chug it out like we did above.

rrusczyk 2010-02-10 19:37:14
And what do we do with this?

33286 2010-02-10 19:37:36
multiply it by 13

agentcx 2010-02-10 19:37:36
combine with the 13 (mod 25) to get 12 (mod 25) (A)

challenger 2010-02-10 19:37:36
multiple with Q

nikeballa96 2010-02-10 19:37:45
combine with 13.

rrusczyk 2010-02-10 19:37:50
So, we multiply this by Q and the resulting product is -13 mod 25, which is equivalent to 12 mod 25. From the 5 choices, it's obvious that the only one that fits is (A), but how else could we eliminate the other 2-digit numbers that are congruent to 12 mod 25?

aleph0 2010-02-10 19:38:21
must be divisible by 4

gomath888 2010-02-10 19:38:21
0 mod 4

rrusczyk 2010-02-10 19:38:26
We know that the last two digits form a multiple of 4, since there are many more factors of 2 in 90! than factors of 5. The only 2-digit multiple of 4 that is congruent to 12 mod 25 is 12 itself, so the answer is 12.

rrusczyk 2010-02-10 19:38:35
And, yes, it would almost certainly have been faster to gut it out than to find this solution.

rrusczyk 2010-02-10 19:38:53
This solution is pretty tough to find, and very tough to get through if you're not well-versed with mods.

sabretooth 2010-02-10 19:38:59
four A's!

flare 2010-02-10 19:38:59
A for 4 problems in a row??

rrusczyk 2010-02-10 19:39:02
Yep

PowerOfPi 2010-02-10 19:39:05
And is that the easiest way?

aopsaccount2131 2010-02-10 19:39:05
this was the "slick" solution?

rrusczyk 2010-02-10 19:39:20
As far as I know; the other solutions I've seen are essentially this.

bunnygirl 2010-02-10 19:39:53
is this really feasible in the time given?

rrusczyk 2010-02-10 19:40:02
It certainly will cut down on perfect scores...

rrusczyk 2010-02-10 19:40:07
Let's go to #25

rrusczyk 2010-02-10 19:40:12

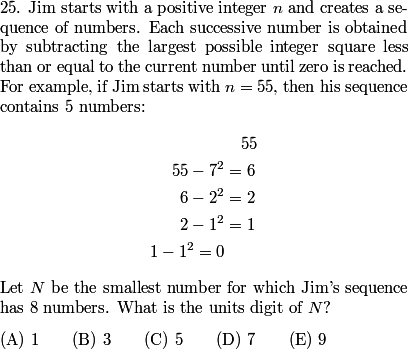
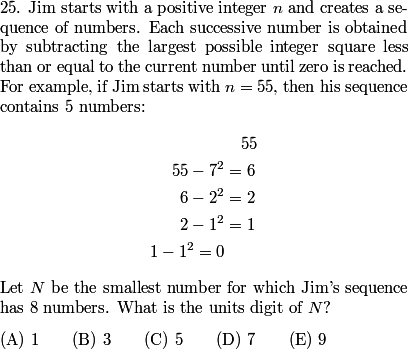
rrusczyk 2010-02-10 19:40:58
Before I get started -- if you are trying to attend a class tonight besides this math jam, click Classroom again on the sidebar.

rrusczyk 2010-02-10 19:41:09
Um, this problem is confusing. How can we make it easier?

SuitcaseAsian 2010-02-10 19:41:29
Work backwords from 0

bunnygirl 2010-02-10 19:41:29
work backwards!

PowerOfPi 2010-02-10 19:41:29
Try some simple cases.

PhireKaLk6781 2010-02-10 19:41:29
work backwards from 0

GoldenStar 2010-02-10 19:41:29
try an example?

nikeballa96 2010-02-10 19:41:29
instead of 8, try 1. and 2. and 3.

rrusczyk 2010-02-10 19:41:33
Let's try a smaller sequence length. The smallest number that starts a 1-term sequence is easy -- it's 0. 2-term sequences aren't much harder 1,0. Tada.

rrusczyk 2010-02-10 19:41:39
How about 3-term sequences? What's the smallest possible starting number?

pumpkinpi 2010-02-10 19:41:56
2

billy314 2010-02-10 19:41:56
2

natiator 2010-02-10 19:41:56
2

prezcoin 2010-02-10 19:41:56
2

aleph0 2010-02-10 19:41:56
2, 1, 0

ksun48 2010-02-10 19:41:56
0, 1, 2

sjiang 2010-02-10 19:41:56
Two

rrusczyk 2010-02-10 19:42:00
Oh, yeah, 2 works: 2,1,0.

rrusczyk 2010-02-10 19:42:04
4-term?

ritwik_anand 2010-02-10 19:42:21
3,2,1,0

nikeballa96 2010-02-10 19:42:21
4 term...3.

natiator 2010-02-10 19:42:21
3

Iggy Iguana 2010-02-10 19:42:21
3

nikeballa96 2010-02-10 19:42:21
3.

aleph0 2010-02-10 19:42:21
3,2,1,0

ksun48 2010-02-10 19:42:21
3, 2, 1, 0

jxl28 2010-02-10 19:42:21
3,2,1,0

happyof 2010-02-10 19:42:21
3,2,1,0

aerrowfinn72 2010-02-10 19:42:21
3,2,1,0

PhireKaLk6781 2010-02-10 19:42:24
nice countdown here...

rrusczyk 2010-02-10 19:42:27
4-term?

rrusczyk 2010-02-10 19:42:34
3,2,1,0.

rrusczyk 2010-02-10 19:42:37
5-term?

challenger 2010-02-10 19:42:55
7,3,2,1,0

c32r17qp181cd912 2010-02-10 19:42:55
then 7.

nikeballa96 2010-02-10 19:42:55
7, 3, 2, 1, 0

ksun48 2010-02-10 19:42:55
7, 3, 2, 1, 0

PhireKaLk6781 2010-02-10 19:42:55
7,3,2,1,0

TheWorstPlayer 2010-02-10 19:42:55
7

henrypickle 2010-02-10 19:42:55
7

darkdieuguerre 2010-02-10 19:42:55
7,3,2,1,0

EricMathPath09 2010-02-10 19:42:55
7,3,2,1,0

aleph0 2010-02-10 19:42:55
7,3,2,1,0

MrBob 2010-02-10 19:42:55
7,3,2,1,0

rrusczyk 2010-02-10 19:43:03
We have to go all the way up to 7: 7,3,2,1,0.

rrusczyk 2010-02-10 19:43:09
If we start with 4, 5, or 6, the next step is lower than 3 (subtract 4), and we'll get to 0 in less than 5 terms.

rrusczyk 2010-02-10 19:43:11
6-term?

nikeballa96 2010-02-10 19:43:21
23, 7, 3, 2, 1, 0

theprodigy 2010-02-10 19:43:21
23,7,3,2,1,0

nikeballa96 2010-02-10 19:43:21
23, 7, 3, 2, 1, 0

rrusczyk 2010-02-10 19:43:35
Yikes! How did we figure out that the next one is 23?

rrusczyk 2010-02-10 19:43:49
We know that the second term in the sequence is at least 7. Suppose it is 7. Then, let the first term be k. What could k be?

darkdieuguerre 2010-02-10 19:44:17
we add a minimal square

nsreenivas 2010-02-10 19:44:17
9+7=16 which is 4^2 so 7+16=23

EricMathPath09 2010-02-10 19:44:17
+9 gives 16, which doesn't work, so we have to do + 16 to get 23.

nikeballa96 2010-02-10 19:44:17
7+1 doesnt work, nor does 7+4, nor does 7+9. 7+16 does! =]

ss5188 2010-02-10 19:44:17
7+16=23 and 16 is the smallest square to add in the sequence

rrusczyk 2010-02-10 19:44:28
We get to 7 by subtracting a square from k. Moreover, the square we subtract from k is the largest square less than k. So, since k > 7, we already know that the square we subtract cannot be 1 or 4.

aerrowfinn72 2010-02-10 19:44:33
cuz adding 9 dusnt work..u get 16 which reduces to 0..so u go to the nxt square

rrusczyk 2010-02-10 19:44:48
It can't be 9. If we subtracted 9, then the previous number is 7+9 = 16. But we can subtract 16 from that! So, we couldn't have subtracted 9.

rrusczyk 2010-02-10 19:44:59
But we could have subtracted 16!

c32r17qp181cd912 2010-02-10 19:45:06
Hence, 7+16=23.

AAFlyer 2010-02-10 19:45:12
so it must have beel 16

rrusczyk 2010-02-10 19:45:20
That gives us:

rrusczyk 2010-02-10 19:45:25
23,7,3,2,1,0.

rrusczyk 2010-02-10 19:45:49
OK, time for 7-term sequences.

rrusczyk 2010-02-10 19:45:57
x,23,7,3,2,1,0

rrusczyk 2010-02-10 19:46:05
I see a lot of you jumping to the answer.

rrusczyk 2010-02-10 19:46:10
Some of you are even right:)

rrusczyk 2010-02-10 19:46:29
How can we begin to think about this?

pumpkinpi 2010-02-10 19:46:49
x - n^2 = 23 for some integer n

PowerOfPi 2010-02-10 19:46:49
x-a^2=23

ksun48 2010-02-10 19:46:49
x-y^2=23

rrusczyk 2010-02-10 19:46:55
We want x - n^2 = 23, but we also want n^2 to be the largest square less than x. How can we find that square quickly?

rrusczyk 2010-02-10 19:47:03
What else do we know about x?

aopsaccount2131 2010-02-10 19:47:33
less than (n+1) ^ 2

ytrewq 2010-02-10 19:47:33
(n+1)^2>x

LincolnMS nerd herd 2010-02-10 19:47:33
it is between n^2 and the next big square number

33286 2010-02-10 19:47:33
less than (n+1)^2

rrusczyk 2010-02-10 19:47:47
We must have x < (n+1)^2.

rrusczyk 2010-02-10 19:47:52
How does that help?

mgao 2010-02-10 19:48:28
2n+1 > 23

henrypickle 2010-02-10 19:48:29
n^2+23<(n+1)^2

aopsaccount2131 2010-02-10 19:48:29
(n+1)^2 - n^2 = 2n + !

aerrowfinn72 2010-02-10 19:48:50
nxt is 167....so its 167, 23, 6, 3, 2, 1, 0

mgao 2010-02-10 19:48:50
then x = 167.

rrusczyk 2010-02-10 19:48:57
So 23 + n^2 < (n+1)^2, which means 23 < (n+1)^ - n^2 = 2n + 1. Aha. That gives us n > 11, which means our next term is 23 + 12^2 = 167.

rrusczyk 2010-02-10 19:49:03
Finally, we're almost there:

rrusczyk 2010-02-10 19:49:08
x, 167, 23, 7, 3, 2, 1, 0.

rrusczyk 2010-02-10 19:49:19
How do we take that next step?

zheng 2010-02-10 19:49:52
Same procedure

henrypickle 2010-02-10 19:49:54
x=n^2+167

pumpkinpi 2010-02-10 19:49:54
We do it again: 2n + 1 > 167

darkdieuguerre 2010-02-10 19:49:54
repeat for 167

The Archer 2010-02-10 19:49:54
2n+1>167

Just_Beginner 2010-02-10 19:49:55
same thing

The Hobbit 2010-02-10 19:49:55
same thing?

y2ucc 2010-02-10 19:49:57
same way as before

rrusczyk 2010-02-10 19:50:06
Just as before, we want (n+1)^2 > x = 167 + n^2, so 167 < (n+1)^2 - n^2 = 2n + 1, which means n > 83.

karatemagic7 2010-02-10 19:50:24
then n=84, so 84^2+167 mod 10 = 3

dolk 2010-02-10 19:50:24
((167+1)/2)^2+167

basketball9 2010-02-10 19:50:24
2n+1>167 so n is 84

mgao 2010-02-10 19:50:24
then 84^2 + 167 will have units digit 3

TheWorstPlayer 2010-02-10 19:50:27
n = 84, 84^2 + 67 gives us 3 as the last digit

rrusczyk 2010-02-10 19:50:35
Therefore, x = 167 + 84^2, which has last digit 3.

bunnygirl 2010-02-10 19:50:43
can you solve this problem without working backwards?

rrusczyk 2010-02-10 19:50:50
I doubt it!

rrusczyk 2010-02-10 19:50:55
Yes, the answer is B

aopsaccount2131 2010-02-10 19:51:03
how do we know that it is good to minimize earlier on? could there exist a better solution with larger numbers earlier on?

rrusczyk 2010-02-10 19:51:35
This is a very good question, and for those of you preparing for the USAMO, you should definitely think about how you could prove that what we did is optimal.

rrusczyk 2010-02-10 19:51:59
I recommend you post your thoughts on this on the message board -- it's not trivial to write such a proof in a clear, rigorous way.

rrusczyk 2010-02-10 19:52:27
We'll take a 2-minute break, and then start with the AMC 12.

rrusczyk 2010-02-10 19:52:51
Again, I'll note that there are nearly 300 people here, so we won't be able to answer all your questions!

rrusczyk 2010-02-10 19:54:25
We'll do the last 5 problems of the AMC 12 now, and then I'll take requests.

rrusczyk 2010-02-10 19:54:49
I don't have any idea what the index will be this year -- we'll have to wait and see.

rrusczyk 2010-02-10 19:55:33
(No I can't guess :) )

rrusczyk 2010-02-10 19:55:48
On to AMC 12

rrusczyk 2010-02-10 19:55:49

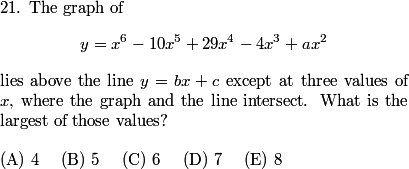
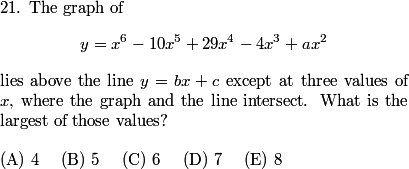
rrusczyk 2010-02-10 19:56:17

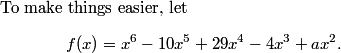
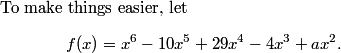
mgao 2010-02-10 19:56:25
it must be tangent to the line because if it werent it would go below, contradiction.

rrusczyk 2010-02-10 19:56:32
Let the three points of intersections be (p, f(p)), (q, f(q)), and (r, f(r)).

rrusczyk 2010-02-10 19:56:37

rrusczyk 2010-02-10 19:56:45
Now what?

33286 2010-02-10 19:56:56
The line is tangent at the three points. Subtract bx+c from the equation.

aleph0 2010-02-10 19:56:56
but f(x)-bx-c must have three multiple roots

darkdieuguerre 2010-02-10 19:57:02
We have that f(x) - y = [(x-p)(x-q)(x-r)]^2

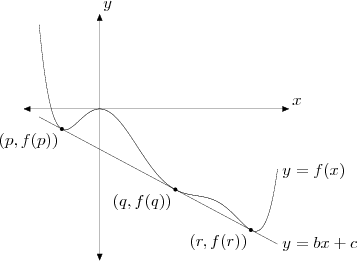
rrusczyk 2010-02-10 19:57:05
Consider the difference g(x) = f(x) - (bx + c).

rrusczyk 2010-02-10 19:57:18
How do we know that this difference is the product of three squares of binomials?

33286 2010-02-10 19:57:53
Otherwise it would change sign at the roots.

zserf 2010-02-10 19:57:54
If there were cubes, then it would cross the line

pumpkinpi 2010-02-10 19:57:56
for each root r there is a factor (x-r)

rrusczyk 2010-02-10 19:58:05
For each root, we have a factor (x-r).

33286 2010-02-10 19:58:37
Or rather, two factors (x-r).

rrusczyk 2010-02-10 19:58:41
True, why?

Infrared 2010-02-10 19:59:35
The graph has to stay positive, which implies a double root

flare 2010-02-10 19:59:38
because the multiplicity of the roots must be even so it does not cross the point... which the diagram proves?

rrusczyk 2010-02-10 19:59:41
But if we only had one such factor then when x goes from just above r to just below r, g(x) would change signs. So, there must be a second factor of x-r to keep the sign positive.

rrusczyk 2010-02-10 20:00:00
(To prove this rigorously, you'd use calculus, but intuitively, we can see why we must have a double root.)

megahertz 2010-02-10 20:00:04
how do you know they are double roots and not complex?

rrusczyk 2010-02-10 20:00:18
We know we have 3 roots that correspond to the three tangent points.

rrusczyk 2010-02-10 20:00:23
3 real roots, that is.

rrusczyk 2010-02-10 20:00:47
And now we know that each root is a double root (or a root 4 times or 6, or whatever)

rrusczyk 2010-02-10 20:01:13
Why do we not have a (x-r)^4 in the factorization of f(x)- (bx+c)?

SuitcaseAsian 2010-02-10 20:01:21
Well it has to be double since there are only 6 roots

LincolnMS nerd herd 2010-02-10 20:01:21
but since it's tangent at 2 points, it's 3 roots twice

aleph0 2010-02-10 20:01:21
but it can't be 4 or 6 because there are three of them

turak 2010-02-10 20:01:21
not 4,6,etc because highest exponent is 6

rrusczyk 2010-02-10 20:01:28
Exactly -- there are 6 total roots.

33286 2010-02-10 20:01:30
g(x) must be a square of the cubic function y=(x-p)(x-q)(x-r).

rrusczyk 2010-02-10 20:01:40
We conclude that the multiplicities of the roots x = p, q, and r are all 2.

rrusczyk 2010-02-10 20:01:47
Therefore:

rrusczyk 2010-02-10 20:01:56

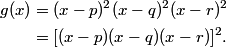
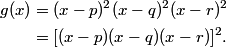
rrusczyk 2010-02-10 20:02:11
Now what?

Just_Beginner 2010-02-10 20:02:32
expand then set coefficents equal to each other?

mathrat 2010-02-10 20:02:32
expand!!!1

y2ucc 2010-02-10 20:02:36
expand

rrusczyk 2010-02-10 20:02:49
How might we go about expanding in a sensible way?

rrusczyk 2010-02-10 20:02:58
Do we really want to multiply that whole thing out?

gomath888 2010-02-10 20:03:13
expand cubic

rrusczyk 2010-02-10 20:03:22

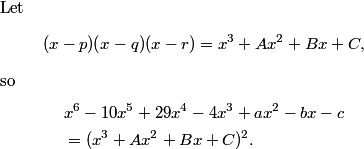
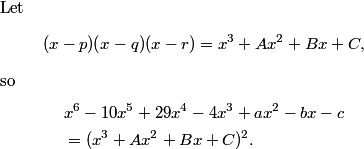
rrusczyk 2010-02-10 20:03:43
Expanding this square is a little easier. What do we get?

Infrared 2010-02-10 20:05:04
We don't need to expand it more, we just look at how the coefficients multiply for each case

rrusczyk 2010-02-10 20:05:13
True; what do we get for x^5 on the right?

aleph0 2010-02-10 20:05:22
2A

ksun48 2010-02-10 20:05:22
2A

nearsymmetric 2010-02-10 20:05:24
A=-5

aleph0 2010-02-10 20:05:28
so A=-5

rrusczyk 2010-02-10 20:05:29
We get 2A, so A = -5.

rrusczyk 2010-02-10 20:05:37
Next up, what about x^4 on the right?

aleph0 2010-02-10 20:06:02
A^2+2B

33286 2010-02-10 20:06:02
A^2+2B

megahertz 2010-02-10 20:06:02
A^2+2B?

Just_Beginner 2010-02-10 20:06:02
B+A^2+B

rrusczyk 2010-02-10 20:06:08
We get A^2 + 2B, and A=-5, so B = 2

rrusczyk 2010-02-10 20:06:20
And C?

rrusczyk 2010-02-10 20:06:34
How do we get that?

aggarwal 2010-02-10 20:06:49
8

sparkle123 2010-02-10 20:06:49
2C+2AB

ksun48 2010-02-10 20:06:49
do x^3

darkdieuguerre 2010-02-10 20:06:49
solving for the x^3 term

aleph0 2010-02-10 20:06:49
2AB+2C=-4?

33286 2010-02-10 20:06:49
-4=2AB+2C

rrusczyk 2010-02-10 20:07:06
The x^3 term gives -4 = 2AB + 2C, and using our values of A and B give C = 8.

rrusczyk 2010-02-10 20:07:11

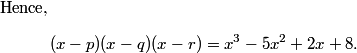
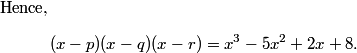
rrusczyk 2010-02-10 20:07:17
Now what?

mgao 2010-02-10 20:07:52
roots can only be factors of 8 and 8 doesnt work so 4 has to be the largest root

karatemagic7 2010-02-10 20:07:52
Yay, noq we get that the solutions are -1,2,4.

CountdownKing 2010-02-10 20:08:08
well -1 works, so factoring out x+1 we will get 2 and 4, so hopefully after coming this far we can realize that 4 is greatest

ytrewq 2010-02-10 20:08:10
factors as (x-4)(x-2)(x+1)

rrusczyk 2010-02-10 20:08:27
We can factor this cubic as (x+1)(x-2)(x+4) (-1 is obviously a root, and then you have a quadratic after you factor out x+1)

nikeballa96 2010-02-10 20:08:32
another A. good thing we're on another test. :)

33286 2010-02-10 20:08:34
Or we could just plug in all the answer choices XD

rrusczyk 2010-02-10 20:08:39
That works too :)

rrusczyk 2010-02-10 20:08:40
Therefore, the largest root is 4, and the answer is (A).

rrusczyk 2010-02-10 20:08:54
On to:

rrusczyk 2010-02-10 20:08:54

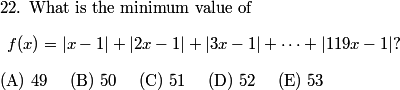
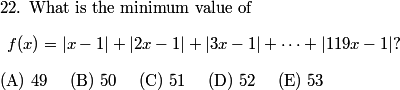
rrusczyk 2010-02-10 20:09:08
Any suggestions where to start?

Poincare 2010-02-10 20:09:16
OMG

rrusczyk 2010-02-10 20:09:22
Not a bad first thought.

rrusczyk 2010-02-10 20:09:42
What tool is helpful in dealing with funky functions?

THECHAMP 2010-02-10 20:10:00
graph

nearsymmetric 2010-02-10 20:10:05
graph it

rrusczyk 2010-02-10 20:10:15

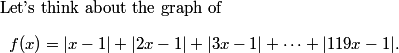
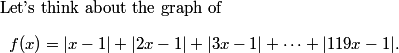
rrusczyk 2010-02-10 20:10:20
What does the graph look like when x is really large?

mgao 2010-02-10 20:10:52
slope is huge

joeislittle 2010-02-10 20:10:52
it is a line

happyof 2010-02-10 20:10:52
linear very steep

darkdieuguerre 2010-02-10 20:10:56
a straight line

Infrared 2010-02-10 20:10:56
7140X-119

zserf 2010-02-10 20:11:01
You can just ignore absolute values in that case.

rrusczyk 2010-02-10 20:11:11
Exactly. It's a line. With slope 1+2+3+...+119

rrusczyk 2010-02-10 20:11:16
What about when x is negative?

ytrewq 2010-02-10 20:12:02
-7140X+119

dragoneye776 2010-02-10 20:12:02
Slope is negatively steep

flare 2010-02-10 20:12:02
the graph goes the opposite way?/

PowerOfPi 2010-02-10 20:12:02
-7140x+119

natiator 2010-02-10 20:12:02
it's another line

nearsymmetric 2010-02-10 20:12:02
opposite slope

rrusczyk 2010-02-10 20:12:06
When x is negative, the graph is a line with slope -(1+2+3+4+ . . . + 119).

rrusczyk 2010-02-10 20:12:14
What happens in-between?

mgao 2010-02-10 20:12:53
the graph looks like a deformed approximation of a parabola and we want to find the "vertex"-ish point

joeislittle 2010-02-10 20:12:53
lots of lines

mgao 2010-02-10 20:12:53
slope slowly goes up til it reaches 7140

MrBob 2010-02-10 20:12:53
intermediate slope

prezcoin 2010-02-10 20:12:53
it curves down, then back up

Wikipedian1337 2010-02-10 20:12:53
signs start shifting

nikeballa96 2010-02-10 20:12:53
at some point...it turns around.

MeowmixOX;D 2010-02-10 20:12:53
less steep slope

nearsymmetric 2010-02-10 20:12:53
we lose some negative slopes, gain some positives

kthxbai 2010-02-10 20:12:53
shifts from negative to positive every time it hits 1, 1/2, 1/3, 1/4 ...

rrusczyk 2010-02-10 20:13:06
What is the smallest value of x at which the slope stops being -(1+2+3+4+ . . . + 119)?

mgao 2010-02-10 20:13:25
1/119

aleph0 2010-02-10 20:13:25
1/119

prezcoin 2010-02-10 20:13:25
1/119

bbgun34 2010-02-10 20:13:25
x=1/119

darkdieuguerre 2010-02-10 20:13:25
x = 1/119

rrusczyk 2010-02-10 20:13:31
When x = 1/119, the term |119x - 1| is 0. Then, when x > 1/119, we have |119x - 1| = 119x - 1, instead of -(119x - 1). So, when 1/118 > x > 1/119, the graph is a line with slope -(1+2+3+ . . . + 118) + 119.

rrusczyk 2010-02-10 20:13:39
Aha, the slope is a little less negative.

nikeballa96 2010-02-10 20:13:52
...still pretty dang negative.

rrusczyk 2010-02-10 20:13:58
Indeed. But...

mgao 2010-02-10 20:14:00
then 1/118, etc.

rrusczyk 2010-02-10 20:14:05
As x increases from 0 to 1, the graph is a series of line segments. As x passes each value of the form 1/n, where n is an integer, the corresponding n term in the slope expression switches from positive to negative. For example, the slope when 1/49 > x > 1/50 is -(1+2+3+4+...+49) + (50+51 +. . . 119).

aleph0 2010-02-10 20:14:25
so when the slope is 0 (or close to it) is when the graph will be at a minimum

nearsymmetric 2010-02-10 20:14:25
we need the place where the sum of the negatively sloped pieces is equal (or nearly equal) to the sum of the poisitives

rrusczyk 2010-02-10 20:14:34
Our problem now is to determine at what value of x the slope switches from negative to positive---when that happens, the graph stops going down and starts going up, and we can find our minimum.

rrusczyk 2010-02-10 20:14:44
How will we find where the sign switches?

rrusczyk 2010-02-10 20:15:20
What should we compute first?

dday25 2010-02-10 20:15:45
1+2+3+...+119?

sjiang 2010-02-10 20:15:45
1+2+...+119

darkdieuguerre 2010-02-10 20:15:45
a smaller triangular sum which is roughly half 119*120/2

aleph0 2010-02-10 20:15:45
the value 1+2+...+119

Wikipedian1337 2010-02-10 20:15:48
2a(a+1)/2 = 119*120/2

rrusczyk 2010-02-10 20:15:51
We start with the sum 1+2+3+. . . + 119 = 119(120)/2 = 119*60 = 7140.

rrusczyk 2010-02-10 20:16:05
Then what do want to find?

mgao 2010-02-10 20:16:15
let 1/k be where it switches then we need 1+2+...+k > (k+1) + ... + 119

zserf 2010-02-10 20:16:30
A triangular number that is close to half of it.

aleph0 2010-02-10 20:16:30
another number so that n(n+1) is approximately 7140

rrusczyk 2010-02-10 20:16:32
Then, we want the smallest value of n such that 1+2+...+ n >= 7140/2.

Just_Beginner 2010-02-10 20:16:34
a triangluar number about 1/2 that, or 3570

aleph0 2010-02-10 20:16:52
but this equals 84*85

CountdownKing 2010-02-10 20:16:52
looks like we can be exact with 84

nearsymmetric 2010-02-10 20:16:52
Find n such that 1+2+...+n<=(1/2)*S <=1+2+...+(n+1). where S = 1+2+...+119

aleph0 2010-02-10 20:16:52
we can find that 85*84=7140

karanbir 2010-02-10 20:16:56
halfway point is 3570, and it will switch when 1+2+3+...+n-1+n=3570

rrusczyk 2010-02-10 20:17:01
This gives us n(n+1)/2 >= 3570. From here we can do a little trial-and-error to solve n^2 + n >= 7140. We find that we get equality at n=84. What does that tell us?

darkdieuguerre 2010-02-10 20:17:19
If we evaluate at x = 1/84, we get our minimum

aleph0 2010-02-10 20:17:20
that the segment is flat when 1/85<x<1/84

rrusczyk 2010-02-10 20:17:29
That tells us that the graph for 1/84 > x > 1/85 is a horizontal line segment. The graph goes upward both to the left and the right of this segment, so the y-coordinate of points on this segment give us our desired minimum. And what is that minimum?

darkdieuguerre 2010-02-10 20:17:49
49

CountdownKing 2010-02-10 20:17:49
try x=1/84 you will see that we get 49, and we know that our method was optimal because we got the lowest choice

mathrat 2010-02-10 20:17:49
49

aleph0 2010-02-10 20:17:59
84-(119-84)

33286 2010-02-10 20:17:59
84-(119-84)=49

rrusczyk 2010-02-10 20:18:03

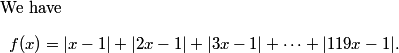
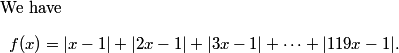
rrusczyk 2010-02-10 20:18:09
All terms of the form |nx - 1| for n >= 85 equal nx - 1 for x > 1/85, and all terms of the form |nx-1| for n <= 84 equal 1 - nx for x < 1/84.

rrusczyk 2010-02-10 20:18:14

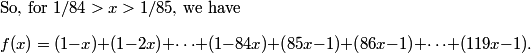
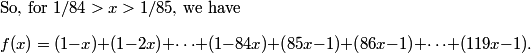
rrusczyk 2010-02-10 20:18:22
We just saw that 1+2+3+ . . . + 84 = 85 + 86 + . . . + 119, so all the nx terms cancel out when 1/84 > x > 1/85. We're left with 84 terms of +1 and (119-84) terms of (-1), so our minimum is 84 - 35 = 49.

EricMathPath09 2010-02-10 20:18:25
ANOTHER A?!

nikeballa96 2010-02-10 20:18:25
ANOTHER A?!

rrusczyk 2010-02-10 20:18:32
I hear an echo.

rrusczyk 2010-02-10 20:18:54
Fortunately, we've already taken care of #23; it was the same as #24 on the AMC 10

rrusczyk 2010-02-10 20:19:05
(And it was another A, for those of you keeping score at home)

megahertz 2010-02-10 20:19:18
Are they trying to mess with us? Next year they will switch it to E and millions of children will guess the last 5 wrong.

rrusczyk 2010-02-10 20:19:21
True

rrusczyk 2010-02-10 20:19:28

rrusczyk 2010-02-10 20:19:34
The domain of f(x) is the set of x for which f(x) is defined. For which x is f(x) defined?

darkdieuguerre 2010-02-10 20:19:57
when the product of the sine functions is strictly positive

aleph0 2010-02-10 20:19:57
when that product is positive

gomath888 2010-02-10 20:19:57
the product of sines is positive

Wikipedian1337 2010-02-10 20:19:57
whenever the thing in the log > 0

rrusczyk 2010-02-10 20:20:05

rrusczyk 2010-02-10 20:20:09

Wikipedian1337 2010-02-10 20:20:39
at a/n where a is an integer

33286 2010-02-10 20:20:39
k/n

GoldenFrog1618 2010-02-10 20:20:39
x is a multiple of 1/n

rrusczyk 2010-02-10 20:20:47

rrusczyk 2010-02-10 20:21:08
Now, how might we organize information about when each factor is positive or negative?

aleph0 2010-02-10 20:21:30
draw a diagram?

Just_Beginner 2010-02-10 20:21:30
make a chart

darkdieuguerre 2010-02-10 20:21:30
the sine function alternates between positive and negative after each zero

rrusczyk 2010-02-10 20:22:03
We can make a sign chart to keep track of where each switches sign.

rrusczyk 2010-02-10 20:22:13

rrusczyk 2010-02-10 20:22:17

rrusczyk 2010-02-10 20:22:26
In the same way, we can construct the sign chart for each of the functions sin(pi x), sin(2 pi x), ..., sin(8 pi x).

rrusczyk 2010-02-10 20:22:40

aleph0 2010-02-10 20:22:45
(or a sine chart :) )

Poincare 2010-02-10 20:22:54
the chart? how do you read it?

rrusczyk 2010-02-10 20:23:08
Each number line represents a single factor.

rrusczyk 2010-02-10 20:23:14
The first is sin(pi*x).

rrusczyk 2010-02-10 20:23:19
The number line goes from 0 to 1.

rrusczyk 2010-02-10 20:23:39
We put a + where the factor is positive, a 0 where it is 0, and a - where it is negative.

rrusczyk 2010-02-10 20:23:43
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/811a277df64c0aaa792f534aac1d18dc.png

rrusczyk 2010-02-10 20:23:49
There's a link for the image.

Poincare 2010-02-10 20:23:51
oh okay. so, at 1/3 sin (3pi x) is 0 right?

rrusczyk 2010-02-10 20:23:54
Right.

nikeballa96 2010-02-10 20:23:58
that's kinda awesome.

rrusczyk 2010-02-10 20:24:05
Ya, a nice way to track information.

mgao 2010-02-10 20:24:12
so somehow, we need to find the number of fragments that that splits it into.

darkdieuguerre 2010-02-10 20:24:17
so now the only problem is keeping track of numbers where multiple functions have zeroes

aleph0 2010-02-10 20:24:19
so at any value of x draw a vertical line at x, if 0 is on that line then it is zero, otherwise if there are an odd number of -s then it is negative and an even number makes it positive

rrusczyk 2010-02-10 20:24:34
Exactly. We'll have to be pretty organized about this.

rrusczyk 2010-02-10 20:24:54
How will we get organized? What should we do?

aleph0 2010-02-10 20:25:25
we can see that there are two lined up zeroes at 1/4, 1/3, 1/2, 2/3, and 3,4 (4 in the case of 1/2)

rrusczyk 2010-02-10 20:25:41
Yeah, we're going to have to worry about points at which two factors switch.

rrusczyk 2010-02-10 20:25:58
In order to count the intervals, what can we count?

darkdieuguerre 2010-02-10 20:26:11
number of distinct zeroes

yforman 2010-02-10 20:26:18
the total number of vertical lines excluding the ones aleph0 listed

rrusczyk 2010-02-10 20:26:23
We can count endpoints of our intervals.

aleph0 2010-02-10 20:26:40
but if two intervals share an endpoint?

rrusczyk 2010-02-10 20:26:47
Indeed -- we'll have to be careful about that.

rrusczyk 2010-02-10 20:26:53
Let's start dumb, and then fix it.

rrusczyk 2010-02-10 20:27:11
How many total 0's (endpoints) do we have if we don't care about the ones that share?

rrusczyk 2010-02-10 20:27:49
(I'm not looking for distinct 0's; I'm looking for a quick count of total 0s)

rrusczyk 2010-02-10 20:27:54

yforman 2010-02-10 20:28:03
2+3+...+9 = 44

c32r17qp181cd912 2010-02-10 20:28:10
44.

simplyMathLete 2010-02-10 20:28:10
44

Iggy Iguana 2010-02-10 20:28:18
44

briantix 2010-02-10 20:28:18
44

rrusczyk 2010-02-10 20:28:22
We have n + 1 endpoints (0s) for each n, 1 <= n <= 8, so we get 2 + 3 + 4 + ... + 9 = 44 endpoints.

rrusczyk 2010-02-10 20:28:29
But clearly, some endpoints are double counted, or more. Which endpoints are counted more than once?

darkdieuguerre 2010-02-10 20:29:08
x = 0 and x=1

c32r17qp181cd912 2010-02-10 20:29:08
The end zeroes.

ytrewq 2010-02-10 20:29:08
0, 1/4, 1/3, 1/2, 2/3, 3/4, 1

ksun48 2010-02-10 20:29:08
0, 1/4, 1/3, 1/4, 2/3, 3/4, 1

aleph0 2010-02-10 20:29:08
1/4,1/3,1/2,2/3,3/4

CountdownKing 2010-02-10 20:29:08
1/2,1/3,1/4,2/3,3/4

aleph0 2010-02-10 20:29:08
and also 0 and 1

rrusczyk 2010-02-10 20:29:17
The quarters, halves, thirds, and the ends.

rrusczyk 2010-02-10 20:29:28
How do we correct for these?

pirox 2010-02-10 20:29:56
subtract

gh625 2010-02-10 20:29:57
subtract

aleph0 2010-02-10 20:29:57
subtract them?

bbgun34 2010-02-10 20:29:57
subtract the repeats

zserf 2010-02-10 20:29:57
subtract the duplicates.

rrusczyk 2010-02-10 20:30:08
OK, let's deal with the ends first. What do we have to subtract for these?

aleph0 2010-02-10 20:30:34
7 for each end

bbgun34 2010-02-10 20:30:34
7 and 7; 14 in all

pirox 2010-02-10 20:30:34
44-14

yforman 2010-02-10 20:30:34
7 each = 14 total

tenniskidperson3 2010-02-10 20:30:34
7 each

ytrewq 2010-02-10 20:30:34
subtract 7 each

FantasyLover 2010-02-10 20:30:36
7*2

rrusczyk 2010-02-10 20:30:39
Each end is counted 8 times, so we have to subtract each 7 times.

rrusczyk 2010-02-10 20:30:59
OK, hou about the halves, quarters, and thirds?

ytrewq 2010-02-10 20:31:58
3 for the halves, 1 for all the others

pumpkinpi 2010-02-10 20:31:58
1/2 is counted four times, so we subtract 3: 30-3=27. 1/4, 1/3, 2/3, and 3/4 are each counted twice, so we subtract 4: 27-4=23

kthxbai 2010-02-10 20:31:58
1/2 is counted 4 times , so subtract 3. 1/4 and 3/4 are each counted twice, so subtract 1*2=2. 1/3 and 2/3 are each counted twice, so subtract 1*2=2.

rrusczyk 2010-02-10 20:32:05
The endpoint 1/2 is counted 4 times. The endpoints 1/4 and 3/4 are counted twice. The endpoints 1/3 and 2/3 are counted twice.

pumpkinpi 2010-02-10 20:32:07
thus we have 23 endpoints and 22 intervals -> D

rrusczyk 2010-02-10 20:32:14
Hence, the total number of endpoints is 44 - 2 x 7 - 3 - 2 x 1 - 2 x 1 = 23, which means there are 22 open sub-intervals.

rrusczyk 2010-02-10 20:32:19
As x increases from 0 to 1, x will hit these endpoints. At these values, does g(x) always change sign, from positive to negative or negative to positive?

ytrewq 2010-02-10 20:32:42
not at the double counted ones

33286 2010-02-10 20:32:42
No - at 1/3, 1/2, 1/4, 3/4 and 2/3 it doesn't

c32r17qp181cd912 2010-02-10 20:32:42
Not always.

rrusczyk 2010-02-10 20:32:49
No, because an even number of factors may change sign simultaneously. For example, as x passes through 1/4, both sin(4 pi x) and sin(8 pi x) change sign. As a result, g(x) is positive for x slightly less than 1/4, and x slightly greater than 1/4.

rrusczyk 2010-02-10 20:32:56
The values of x for which an even number of factors change simultaneously are the values of x which appear as an endpoint in an even number of sign charts. These are exactly the endpoints that were double counted above.

rrusczyk 2010-02-10 20:33:05
Now we know how the sign of g(x) behaves, we can construct the sign chart of g(x).

rrusczyk 2010-02-10 20:33:13

rrusczyk 2010-02-10 20:33:30
What do we do now?

rrusczyk 2010-02-10 20:33:46
The sign of g(x) alternates at each endpoint (that is, it goes from positive to negative or negative to positive), except at the endpoints we indicated above, namely 1/2, 1/4, 3/4, 1/3, and 2/3.

aleph0 2010-02-10 20:33:49
so then we can count the pluses to get 12, B

darkdieuguerre 2010-02-10 20:33:49
12 positive regions = B

bobma99 2010-02-10 20:33:49
count

yforman 2010-02-10 20:33:49
count the "+"s

mgao 2010-02-10 20:33:49
count the number of +s

tenniskidperson3 2010-02-10 20:33:49
The answer is 12

rrusczyk 2010-02-10 20:33:54
Now we can read off the sign chart the number of open sub-intervals where g(x) is positive, which is 12. The answer is (B).

rrusczyk 2010-02-10 20:34:03
Pretty tough problem -- that's why it's #24.

aleph0 2010-02-10 20:34:19
25 is harder

rrusczyk 2010-02-10 20:34:22
LEt's see!

rrusczyk 2010-02-10 20:34:36

rrusczyk 2010-02-10 20:34:50
Let a, b, c, and d be the sides of the quadrilateral, so a + b + c + d = 32. Is there anything else we can immediately say about these side lengths?

BarbieRocks 2010-02-10 20:35:12
a+b+c>d?

billy314 2010-02-10 20:35:12
a+b+c < d

rrusczyk 2010-02-10 20:35:16
By the triangle inequality, any side length must be less than the sum of the other three side lengths.

LincolnMS nerd herd 2010-02-10 20:35:18
a+b+c<d?

rrusczyk 2010-02-10 20:35:24

rrusczyk 2010-02-10 20:35:33
What do these tell us?

aleph0 2010-02-10 20:35:47
all <16

darkdieuguerre 2010-02-10 20:35:47
they cannot be greater than or equal to 16

mgao 2010-02-10 20:35:47
thus, none of them are larger than 15.

xpmath 2010-02-10 20:35:47
each of the sides is less than 16

rrusczyk 2010-02-10 20:35:52
Let's consider the first inequality, a < b + c + d.

rrusczyk 2010-02-10 20:35:59
Since a + b + c + d = 32, the inequality becomes a < 32 - a, so 2a < 32, or a < 16.

rrusczyk 2010-02-10 20:36:04
Since a is a positive integer, a <= 15. Similarly, b, c, d <= 15.

rrusczyk 2010-02-10 20:36:11
Conversely, suppose a <= 15. Then a < 16, which is equivalent to a < b + c + d. Similarly, the other inequalities are satisfied.

rrusczyk 2010-02-10 20:36:19
Therefore, as long as a, b, c, and d are all at most 15, there exists a convex quadrilateral whose side lengths are a, b, c, and d

mgao 2010-02-10 20:36:26
first of all a quadrangle has one degree of freedom so any quadrangle can be cyclic.

33286 2010-02-10 20:36:26
However, any sequence of side lengths that is a quadrilateral at all may form a cyclic quadrilateral.

tenniskidperson3 2010-02-10 20:36:41
There is exactly one cyclic quadrilateral per valid regular quadrilateral with ordered sides.

rrusczyk 2010-02-10 20:36:43
Exactly. Furthermore, this cyclic quadrilateral is unique, in the sense given in the problem.

rrusczyk 2010-02-10 20:36:52
The idea is as follows: Suppose that the quadrilateral is made of links and hinges. Then unlike the triangle, the quadrilateral can flex, and the angles can change, with the side lengths remaining the same.

rrusczyk 2010-02-10 20:37:05
(Cyclic means that we can inscribe the quadrilateral in a circle.

rrusczyk 2010-02-10 20:37:17
I really think they should have included that in the problem...)

rrusczyk 2010-02-10 20:37:22

rrusczyk 2010-02-10 20:37:31
Consider one pair of opposite vertices. The quadrilateral can be flexed so that at one extreme, the angle at one of these vertices is close to 180 degrees, so that the sum of the angles at both vertices is greater than 180 degrees.

rrusczyk 2010-02-10 20:37:38
But then at the other extreme, one of the angles at the other two opposite vertices can be made close to 180 degrees, and the sum of the angles at the other pair of opposite vertices is greater than 180 degrees.

rrusczyk 2010-02-10 20:37:46
At exactly one point in between, the sum of the angles of opposite vertices must have been 180 degrees. At this point, the quadrilateral is cyclic.

darkdieuguerre 2010-02-10 20:38:04
is this statement easily provable?

rrusczyk 2010-02-10 20:38:06
Not "easy" to be completely rigorous.

Wikipedian1337 2010-02-10 20:38:08
somebody should post a rigorous proof of this on the message board

rrusczyk 2010-02-10 20:38:12
That's a good idea.

simplyMathLete 2010-02-10 20:38:19
so there is exactly one for each set of sides

rrusczyk 2010-02-10 20:38:32
Hence, every quadruple (a,b,c,d) that satisfies a + b + c + d = 32 and a <= 15, b <= 15, c <= 15, and d <= 15 corresponds to a unique cyclic quadrilateral.

zserf 2010-02-10 20:38:34
So any 4 lengths that make a quadrilateral can be inscribed in a circle?

rrusczyk 2010-02-10 20:38:37
correct

tenniskidperson3 2010-02-10 20:38:46
No, the sides have to be ordered.

rrusczyk 2010-02-10 20:38:52
right; given the order.

aggarwal 2010-02-10 20:38:54
isnt it a combinatorics problem

rrusczyk 2010-02-10 20:38:57
It is now.

c32r17qp181cd912 2010-02-10 20:39:01
Now all we have to do is find the number of possible side groupings.

aleph0 2010-02-10 20:39:01
so now we consider how many ordered sets of sides there are

rrusczyk 2010-02-10 20:39:27
How will we go about this count

rrusczyk 2010-02-10 20:39:28
?

Iggy Iguana 2010-02-10 20:39:52
complementary counting?

tenniskidperson3 2010-02-10 20:39:52
Complementary Counting, I suppose

rrusczyk 2010-02-10 20:39:57
We can use complementary counting. We can count the number of quadruples a + b + c + d = 32, without the restriction that all variables are at most 15, and then discard the quadruples we don't want to count, i.e. those quadruples where some variable is at least 16.

rrusczyk 2010-02-10 20:40:04
How many quadruples of positive integers (a,b,c,d) satisfy a + b + c + d = 32?

xpmath 2010-02-10 20:40:38
31C3

aggarwal 2010-02-10 20:40:38
4495

mgao 2010-02-10 20:40:38
(31 choose 3)

Just_Beginner 2010-02-10 20:40:38
31C3

darkdieuguerre 2010-02-10 20:40:38
31C3

ytrewq 2010-02-10 20:40:38
31C3

briantix 2010-02-10 20:40:40
31 coose 3

rrusczyk 2010-02-10 20:40:45
There is a standard technique, sometimes called stars-and-bars, for counting the number of such quadruples.

rrusczyk 2010-02-10 20:40:49
Imagine a row of 32 stars. We are allowed to insert 3 bars between any two adjacent stars, and there is at most one bar between any two adjacent stars.

rrusczyk 2010-02-10 20:40:53
For example, if we had ten stars, the bars may be placed like this: *|***|**|****

rrusczyk 2010-02-10 20:40:58
This placement of bars then corresponds to the quadruple (1,3,2,4), where each number represents the number of stars in the groups determined by the bars. Note that there are 9 places to place 3 bars.

Just_Beginner 2010-02-10 20:41:01
that is 4495

nikeballa96 2010-02-10 20:41:01
which is 4495

rrusczyk 2010-02-10 20:41:08

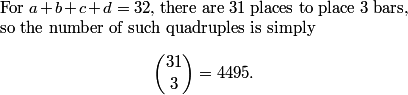
rrusczyk 2010-02-10 20:41:18
Now we must subtract the number of quadruples where some variable is at least 16. What makes our job easier?

Just_Beginner 2010-02-10 20:41:44
only one can be at ost 16

ytrewq 2010-02-10 20:41:44
only one can be greater than 16 at one time

rrusczyk 2010-02-10 20:41:52
If some variable is at least 16, then it is the only variable that is at least 16, because a, b, c, and d are positive integers satisfying a + b + c + d = 32. Hence, we can treat each variable separately.

rrusczyk 2010-02-10 20:41:57
What is the number of quadruples (a,b,c,d) such that a + b + c + d = 32 and a >= 16? How can we compute this?

mgao 2010-02-10 20:42:11
we just let a' = a-15, if a>15.

bbgun34 2010-02-10 20:42:12
take the variable at least 16 and subtract 15 from it

ksun48 2010-02-10 20:42:12
subtract 15 from a

rrusczyk 2010-02-10 20:42:20
To apply the stars-and-bars argument, let t = a - 15. Then t is a positive integer, and t + b + c + d = (a - 15) + b + c + d = 17. So how many such quadruples (t,b,c,d) are there?

mgao 2010-02-10 20:42:53
(16 choose 3)

darkdieuguerre 2010-02-10 20:42:53
16C3

bbgun34 2010-02-10 20:42:53
16C3

Just_Beginner 2010-02-10 20:42:53
16C3

aleph0 2010-02-10 20:42:53
16 choose 3

mz94 2010-02-10 20:42:53
16c3

karatemagic7 2010-02-10 20:42:53
16C3

tenniskidperson3 2010-02-10 20:42:53
16 c 3=560

gh625 2010-02-10 20:42:53
16C3

rrusczyk 2010-02-10 20:43:01

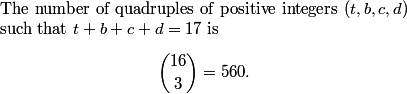
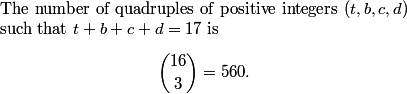
rrusczyk 2010-02-10 20:43:04
Therefore, there are 560 quadruples of positive integers (a,b,c,d) such that a + b + c + d = 32 and a >= 16.

mgao 2010-02-10 20:43:13
and any variable can be the big one so we have 4(16 choose 3).

FantasyLover 2010-02-10 20:43:13
*4 because of the symmetry

rrusczyk 2010-02-10 20:43:17
But we have the same number for the cases b >= 16, c >= 16, and d >= 16.

rrusczyk 2010-02-10 20:43:26
Therefore, the number of quadruples of positive integers (a,b,c,d) such that a + b + c + d = 32 and all variables are at most 15 is 4495 - 4 x 560 = 2255.

rrusczyk 2010-02-10 20:43:36
Now what?

aleph0 2010-02-10 20:43:54
but what about rotations

Wikipedian1337 2010-02-10 20:43:57
whats considered distinct?

rrusczyk 2010-02-10 20:44:02
Oh yeah....

rrusczyk 2010-02-10 20:44:10
We have to worry about rotations

33286 2010-02-10 20:44:14
we've counted most possibilites 4 times: abcd, bcda, cdab, dabc. But some we've only counted twice and one once.

rrusczyk 2010-02-10 20:44:19
Now, since we are allowed to rotate the quadrilateral, the four quadruples (a,b,c,d), (b,c,d,a), (c,d,a,b), and (d,a,b,c) all represent the same cyclic quadrilateral. (However, (d,c,b,a) does not necessarily represent the same cyclic quadrilateral, since we are not allowed to reflect the quadrilateral.)

rrusczyk 2010-02-10 20:44:24
So it seems that each cyclic quadrilateral we are interested in corresponds to four quadruples in our set, so we should be able to simply divide 2255 by 4 to get the answer. But 2255 is not divisible by 4. Have we made a mistake?

darkdieuguerre 2010-02-10 20:44:52
because we have quadruples like 8,8,8,8

aleph0 2010-02-10 20:44:52
some of them (like 8,8,8,8) will not be affected

karatemagic7 2010-02-10 20:44:52
No becasue 8888 is only counted once.

ksun48 2010-02-10 20:44:52
but what about (8,8,8,8)?

Visitor03 2010-02-10 20:45:07
rrusczyk, how do you type so fast?

rrusczyk 2010-02-10 20:45:09
25 fingers. Word's with z give me problems.

rrusczyk 2010-02-10 20:45:16
Not every cyclic quadrilateral corresponds to four quadruples in our set, because not every quadruple (a,b,c,d) generates four different quadruples. For example, for a = b = c = d = 8, we only get one distinct quadruple, namely (8,8,8,8), and for a = c = 1 and b = d = 15, we only get two distinct quadruples, namely (1,15,1,15) and (15,1,15,1). So we have to account for possible repetitions.

rrusczyk 2010-02-10 20:45:27
So we consider the four quadruples (a,b,c,d), (b,c,d,a), (c,d,a,b), and (d,a,b,c), and the ways they can be equal to each other.

rrusczyk 2010-02-10 20:45:36
Suppose the first two quadruples (a,b,c,d) and (b,c,d,a) are equal. What does this say?

tenniskidperson3 2010-02-10 20:46:00
a=b=c=d=8

darkdieuguerre 2010-02-10 20:46:00
a=b=c=d

aleph0 2010-02-10 20:46:00
a=b, b=c, c=d, d=a

yforman 2010-02-10 20:46:02
a=b=c=d=8, and all four quadruples are equal

rrusczyk 2010-02-10 20:46:04
If (a,b,c,d) and (b,c,d,a) are equal, then a = b, b = c, c = d, and d = a, which means a = b = c = d = 8. The only such quadruple then is (8,8,8,8).

rrusczyk 2010-02-10 20:46:10
Next, suppose the first and third quadruples (a,b,c,d) and (c,d,a,b) are equal. What does this say?

ksun48 2010-02-10 20:46:28
a=c, b=d

darkdieuguerre 2010-02-10 20:46:28
a=c and b=d

pumpkinpi 2010-02-10 20:46:28
a=c, b=d

nikeballa96 2010-02-10 20:46:28
a=c, b=d

tenniskidperson3 2010-02-10 20:46:28
a=c, b=d, a+b=16

BarbieRocks 2010-02-10 20:46:28
a=c, b=d,

KingJames 2010-02-10 20:46:31
a=c, b=d

rrusczyk 2010-02-10 20:46:54
OK, and how many pairs do we have here?

briantix 2010-02-10 20:47:24
7

33286 2010-02-10 20:47:24
7?

c32r17qp181cd912 2010-02-10 20:47:24
7.

Just_Beginner 2010-02-10 20:47:30
7?

rrusczyk 2010-02-10 20:47:32
If (a,b,c,d) and (c,d,a,b) are equal, then a = c and b = d. The 14 quadruples in this case are (1,15,1,15), (2,14,2,14), (3,13,3,14), ..., (15,1,15,1). (We do not include the quadruple (8,8,8,8), because we have already counted it.) These 14 quadruples correspond to 7 cyclic quadrilaterals.

rrusczyk 2010-02-10 20:47:56
Finally, suppose the first and fourth quadruples (a,b,c,d) and (d,a,b,c) are equal. What does this say?

darkdieuguerre 2010-02-10 20:48:17
a=b=c=d again

yforman 2010-02-10 20:48:17
a=b=c=d=8 again

pumpkinpi 2010-02-10 20:48:17
a=b=c=d=8 again

jxl28 2010-02-10 20:48:17
a=b=c=d again

nikeballa96 2010-02-10 20:48:17
a=b=c=d again?

Wikipedian1337 2010-02-10 20:48:17
again 8888

ksun48 2010-02-10 20:48:17
they are all 8, same as first one

trigfan 2010-02-10 20:48:17
8,8,8,8

rrusczyk 2010-02-10 20:48:19
Like the first case, the only possibility is (8,8,8,8).

rrusczyk 2010-02-10 20:48:28
Therefore, in all other quadruples, each quadruple (a,b,c,d) generates four different quadruples (a,b,c,d), (b,c,d,a), (c,d,a,b), and (d,a,b,c). How many such quadruples are there?

33286 2010-02-10 20:49:03
2240/4

7thsamurai 2010-02-10 20:49:03
(2255 - 15) / 4 = 560

rrusczyk 2010-02-10 20:49:09
The number of such quadruples is 2255 - 1 - 14 = 2240.

rrusczyk 2010-02-10 20:49:15
Now we can divide by 4. These 2240 quadruples correspond to 2240/4 = 560 cyclic quadrilaterals.

rrusczyk 2010-02-10 20:49:24
So, is the answer A AGAIN?!?

darkdieuguerre 2010-02-10 20:49:32
560 + 1 + 7 = 568 giving us C

yforman 2010-02-10 20:49:32
560+ the eight special ones = 568

Aeroalon 2010-02-10 20:49:43
Plus the 8 we counted

7thsamurai 2010-02-10 20:49:43
560 + 7 + 1 = 568

aleph0 2010-02-10 20:49:43
so then, with those 560, we add back 8,8,8,8 and the 7 rectangles to make 568 (C)

pirox 2010-02-10 20:49:45

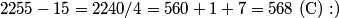
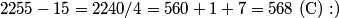
rrusczyk 2010-02-10 20:50:11
Ah, yeah. Gotta remember the special cases -- we add those back in. That gives us 1+7+560 = 568 cyclic quadrilaterals...

rrusczyk 2010-02-10 20:50:43
I'll take another short break, and then take requests.

pt90 2010-02-10 20:52:00
On number 24, sin(8x)=0 for 7 values, sin(7x)=0 for 6, sin(6x)=0 for 5, sin(5x)=0 for 4, then the rest are "repeats". 7+6+5+4=22. The answer should be roughly half so around 11. Only one choice is close. it seems like an efficient, though hardly rigorous, time saver (especially on a #24). is this legitamate?

rrusczyk 2010-02-10 20:52:09
Great approach for getting a sensible guess.

bunnygirl 2010-02-10 20:53:17
Can you please go over #18 on amc 10 A

rrusczyk 2010-02-10 20:54:03
This was also #16 on the AMC 12

rrusczyk 2010-02-10 20:54:09

rrusczyk 2010-02-10 20:54:21
First, we focus on the difference between the numbers that Bernardo can pick and the numbers that Silvia can pick. What is this difference?

Just_Beginner 2010-02-10 20:54:32
he has a 9

ksun48 2010-02-10 20:54:32
the 9

simplyMathLete 2010-02-10 20:54:32
B can pick 9

darkdieuguerre 2010-02-10 20:54:32
Bernarndo can pick a 9

rohbat 2010-02-10 20:54:32
9

infinity1 2010-02-10 20:54:32
he can pick 9

bunnygirl 2010-02-10 20:54:32
9

rrusczyk 2010-02-10 20:54:35
Bernardo has access to the digit 9, while Silvia does not.

rrusczyk 2010-02-10 20:54:40
What happens if Bernardo picks the digit 9?

pt90 2010-02-10 20:54:45
If he picks a 9, then he "wins". 1/3 of the time

Aeroalon 2010-02-10 20:54:45
The 9. Bernardo's number is automactially higher if he picks the 9.

7thsamurai 2010-02-10 20:54:45
He wins

rrusczyk 2010-02-10 20:54:49
If Bernardo picks the digit 9, then his 3-digit number will start with the digit 9, so no matter what his other digits are, his number will be greater than Silvia's number. What is the probability that Bernardo picks the digit 9?

darkdieuguerre 2010-02-10 20:55:02
1/3

ksun48 2010-02-10 20:55:02
the probability is 1/3

infinity1 2010-02-10 20:55:02
1/3

dday25 2010-02-10 20:55:02
1/3

happymath 2010-02-10 20:55:02
1/3

nikeballa96 2010-02-10 20:55:02
1/3

rrusczyk 2010-02-10 20:55:06
The probability that Bernardo picks the digit 9 is simply 3/9 = 1/3, because he picks 3 digits out of 9.

rrusczyk 2010-02-10 20:55:16
If Bernardo does not pick the digit 9, then Bernardo and Silvia have access to the same set of digits. Does that mean the probability that Bernardo's number is greater than Silvia's is 1/2?

challenger 2010-02-10 20:55:30
nope

nikeballa96 2010-02-10 20:55:30
no. they can be the same.

darkdieuguerre 2010-02-10 20:55:30
no, they could pick equal numbers

jxl28 2010-02-10 20:55:30
No, they can be equal

smokewisps 2010-02-10 20:55:30
no, not if they're equal

ksun48 2010-02-10 20:55:30
no equals is not counted for

rrusczyk 2010-02-10 20:55:35
No, because Bernardo's number could be equal to Silvia's. What is the probability that this occurs?

pt90 2010-02-10 20:55:48
1/56 chance it will be the same number

dday25 2010-02-10 20:55:48
1/56

megahertz 2010-02-10 20:55:48
1/56

ytrewq 2010-02-10 20:55:48
1/56

trigfan 2010-02-10 20:55:48
1/56

yforman 2010-02-10 20:55:53
1/(8c3) = 1/56

rrusczyk 2010-02-10 20:55:57

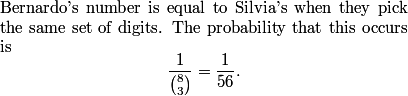
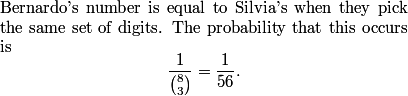
rrusczyk 2010-02-10 20:56:07
So given that Bernardo does not pick the digit 9, what is the probability that Bernardo's number is greater than Silvia's?

nikeballa96 2010-02-10 20:56:32
the rest of it will be split evenly between silvia and bernardo

darkdieuguerre 2010-02-10 20:56:32
1/2(1-1/56)

ytrewq 2010-02-10 20:56:32
1/2*55/56

simplyMathLete 2010-02-10 20:56:32
55/112

gh625 2010-02-10 20:56:32
55/112

megahertz 2010-02-10 20:56:32
1/2(1- 1/56)=55/112

dday25 2010-02-10 20:56:32
1/2(1-1/56)

rrusczyk 2010-02-10 20:56:36
The probability that Bernardo and Silvia do not pick the same set of digits is 1 - 1/56 = 55/56. Then by symmetry, the probability that Bernardo's number is greater than Silvia's is simply half of this, or 55/112.

rrusczyk 2010-02-10 20:56:40
And how do we finish?

rrusczyk 2010-02-10 20:57:05
Careful!! I see some of you adding this to 1/3

pt90 2010-02-10 20:57:21
so 1/2*55/56 for the case where he doesn't pick a 9, which happens two thirds of the time. so this times 2/3 plus 1/3 is the answer

ytrewq 2010-02-10 20:57:21
2/3 of that plus 1/3=37/56

challenger 2010-02-10 20:57:21
55/112*2/3 + 1/3

trigfan 2010-02-10 20:57:21
2/3*55/112+1/3=37/56

rrusczyk 2010-02-10 20:57:26

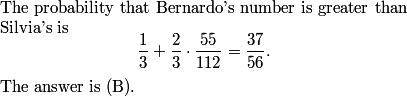
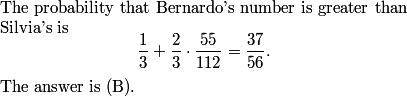
rrusczyk 2010-02-10 20:57:38
That 55/112 is only the probably 2/3 of the time.

rrusczyk 2010-02-10 20:58:02
I'll do #17 on the AMC 12, which is #19 on the AMC 10

rrusczyk 2010-02-10 20:58:22

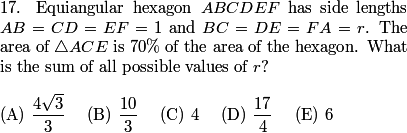
nikeballa96 2010-02-10 20:58:45
draw a picture.

rrusczyk 2010-02-10 20:58:49

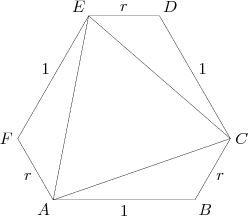
rrusczyk 2010-02-10 20:58:56
Since hexagon ABCDEF is equiangular, all of its angles are equal to 120 degrees. So what does this say about triangle ACE?

darkdieuguerre 2010-02-10 20:59:12
equilateral

mz94 2010-02-10 20:59:12
equilateral

PowerOfPi 2010-02-10 20:59:12
equilateral

professordad 2010-02-10 20:59:12
equilateral

ksun48 2010-02-10 20:59:12
equilateral

RunpengFAILS 2010-02-10 20:59:12
IT IS ALSO EQUILATERAL

pianoforte 2010-02-10 20:59:17
equilateral from symmetry

rrusczyk 2010-02-10 20:59:21
By SAS, triangles ABC, CDE, and EFA are all congruent. Therefore, AC = CE = EA, which means triangle ACE is equilateral.

rrusczyk 2010-02-10 20:59:29
How can we find the area of equilateral triangle ACE?

nikeballa96 2010-02-10 20:59:45
cosine law on DCE to find CE

joeislittle 2010-02-10 20:59:45
we can determine its area using cosines

kp54 2010-02-10 20:59:45
law of cosines

darkdieuguerre 2010-02-10 20:59:48
find the side length

yforman 2010-02-10 20:59:50
use law of cosines to find the length of each side

rrusczyk 2010-02-10 21:00:02
We can apply the law of cosines.

rrusczyk 2010-02-10 21:00:11

rrusczyk 2010-02-10 21:00:47
(For those of you who don't know the Law of Cosines, there is a clever solution that involves extending the long sides of the hexagon to form an equilateral triangle.)

mz94 2010-02-10 21:00:59
what if we drop a perpendicular from C to AB at X. since we know CXB is a 30 60 90 triangle we have BX=r/2 and CX=r(sqrt3)/2 adn then use pythag

rrusczyk 2010-02-10 21:01:11
It involves cleverly dropping an altitude like this.

rrusczyk 2010-02-10 21:01:20
So, we have AC^2

rrusczyk 2010-02-10 21:01:25
What do we do with that?

BarbieRocks 2010-02-10 21:01:39
i drew FC and found the total area using the two trapezoids, becasue FC=r+1

rrusczyk 2010-02-10 21:01:45
That's pretty clever, too.

joeislittle 2010-02-10 21:01:52
find the area of the triangle in terms of r

7thsamurai 2010-02-10 21:01:53
We can find the area of ACE with it: AC^2 sqrt(3) / 4

rrusczyk 2010-02-10 21:02:01

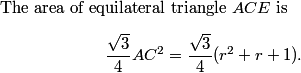
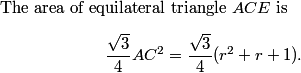
simplyMathLete 2010-02-10 21:02:28
and then we could use absinC/2 and complemetary counting

Aeroalon 2010-02-10 21:02:35
We have been told this is 70% of the hexagon

lxu1 2010-02-10 21:02:35
we can find the area of the rest using 1/2sine120xr

rrusczyk 2010-02-10 21:02:40
We are given that the area of triangle ACE is 70% of the area of the hexagon.

rrusczyk 2010-02-10 21:02:47
The areas of triangles ABC, CDE, and EFA then collectively make up the remaining 30% of the area of the hexagon.

rrusczyk 2010-02-10 21:02:51
Furthermore, these three triangles are congruent, so the area of each such triangle is 10% of the area of the hexagon. What is the area of triangle ABC in terms of r?

pumpkinpi 2010-02-10 21:03:39
r(sqrt3)(1/4)

PowerOfPi 2010-02-10 21:03:39
r*sqrt(3)/4

lxu1 2010-02-10 21:03:39
sqrt3/4 x r

7thsamurai 2010-02-10 21:03:39
1 * r * sin 120 / 2 = r sqrt(3) / 4. I think.

rrusczyk 2010-02-10 21:03:45

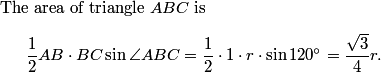
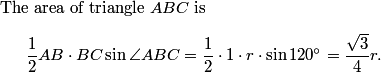
rrusczyk 2010-02-10 21:03:55
All right, what equation does this give us?

darkdieuguerre 2010-02-10 21:04:34
(r*sqrt(3)/4) / (r^2+r+1 * sqrt(3) / 4) = 1/7

33286 2010-02-10 21:04:38
r^2+r+1=7r

Aeroalon 2010-02-10 21:04:38
7r = r^2 + r + 1

rrusczyk 2010-02-10 21:04:42

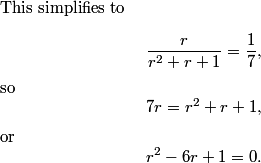
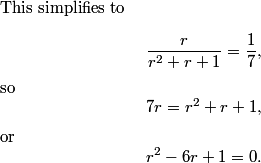
rrusczyk 2010-02-10 21:04:54
What is the sum of all possible values of r?

nikeballa96 2010-02-10 21:05:00
hence, the sum is 6, by vietas!

professordad 2010-02-10 21:05:00
so the sum is -(-6) is 6!

darkdieuguerre 2010-02-10 21:05:00
by vieta's, the sum of the roots is 6

pumpkinpi 2010-02-10 21:05:05
By Vieta, the sum of the roots is 6

7thsamurai 2010-02-10 21:05:05
6

jxl28 2010-02-10 21:05:09
6.

EricMathPath09 2010-02-10 21:05:11
6

gh625 2010-02-10 21:05:11
6

rrusczyk 2010-02-10 21:05:13
By Vieta's formulas for the sum and product of the roots of a quadratic, the sum of all possible values of r is 6. The answer is (E). (For good measure, we check that the roots of the quadratic, namely 3 +/- 2 sqrt(2), are real.)

mz94 2010-02-10 21:05:16
another way to find the area of the hexagon is to extend AB, CD, and EF to form a equilateral triangle with side length r+2

rrusczyk 2010-02-10 21:05:24
Yep, that would work, too.

rrusczyk 2010-02-10 21:05:50
#18 AMC 12

rrusczyk 2010-02-10 21:05:51

rrusczyk 2010-02-10 21:06:17
We'll take a look at a couple different ways to do this.

rrusczyk 2010-02-10 21:06:26
Any ideas?

yankeesrule007 2010-02-10 21:06:35
recursion?

rrusczyk 2010-02-10 21:06:44
Let's try something a little like this:

mathrat 2010-02-10 21:06:47
draw out the paths diagram- (like pascals triangle)

dday25 2010-02-10 21:06:49
Counting along gridlines.

rrusczyk 2010-02-10 21:07:03
If we just started at (-4,-4), how many ways can we get to (-4,-4)?

Aeroalon 2010-02-10 21:07:11
1

aerrowfinn72 2010-02-10 21:07:11
1

lasse 2010-02-10 21:07:11
1

pumpkinpi 2010-02-10 21:07:14
1: stay

Rocket95 2010-02-10 21:07:14
1

Canis Lupus 2010-02-10 21:07:14
1

yankeesrule007 2010-02-10 21:07:14
1

rrusczyk 2010-02-10 21:07:16
Um, 1.

rrusczyk 2010-02-10 21:07:30
How about from (-3,-4) or from (-4,-3)?

pt90 2010-02-10 21:07:41
divide the problem into halves since it's symmetric

yankeesrule007 2010-02-10 21:07:41
1

Aeroalon 2010-02-10 21:07:41
Also 1

Rocket95 2010-02-10 21:07:41
1

lasse 2010-02-10 21:07:45
1

darkdieuguerre 2010-02-10 21:07:45
1, going either up or right

rrusczyk 2010-02-10 21:07:52
There is only one way to reach the point (-3,-4). Similarly, there is only one way to reach the point (-4,-3), so we label these points with the number 1.

rrusczyk 2010-02-10 21:07:57

rrusczyk 2010-02-10 21:08:03
How many ways can we reach the point (-3,-3)?

rrusczyk 2010-02-10 21:08:17
That is, how many ways can we get to (-4,-4) from (-3,-3)

andrewnycpops 2010-02-10 21:08:21
2

Aeroalon 2010-02-10 21:08:21
2: 1 + 1

utsamagoots3 2010-02-10 21:08:21
2

pumpkinpi 2010-02-10 21:08:21
2

zigzag 2010-02-10 21:08:21
2

etude 2010-02-10 21:08:21
2

megahertz 2010-02-10 21:08:21
2

7thsamurai 2010-02-10 21:08:21
2; add the 1's

trigfan 2010-02-10 21:08:21
2

karanbir 2010-02-10 21:08:21
2

rrusczyk 2010-02-10 21:08:37
There are only two ways to reach (-4,-4) from the point (-3,-3), so we label this point with the number 2. This is the sum of labels at the points (-3,-4) and (-4,-3), because these are the only points through which to reach the point (-4,-4).

rrusczyk 2010-02-10 21:08:42

pirox 2010-02-10 21:08:46
keep going till you get to 4,4

simplyMathLete 2010-02-10 21:08:46
the entire bottom row is 1s, and all the left column is 1s

rrusczyk 2010-02-10 21:09:04
Exactly -- we just keep doing this reasoning all the way back to (4,4)

pumpkinpi 2010-02-10 21:09:08
it's looking a lot like pascal's triangle

Chaos 2010-02-10 21:09:08
rotated pascal's

aunch 2010-02-10 21:09:08
complete the square by adding the numbers to the left and bottom of the needed vertex

rrusczyk 2010-02-10 21:09:10
In general, the label at the point (x,y) will be the sum of the labels at (x - 1, y) and (x, y - 1). We just have to remember to stay outside or on the boundary of the square described by -2 <= x, y <= 2, and inside the square described by -4 <= x, y <= 4. (Without these restrictions, we would in fact generate Pascal's triangle.)

rrusczyk 2010-02-10 21:09:16
The rest of the diagram is completed as follows.

rrusczyk 2010-02-10 21:09:20

rrusczyk 2010-02-10 21:09:30
Hence, the answer is (D) 1698.

rrusczyk 2010-02-10 21:09:47
Now, if you didn't trust your repeated addition, there's a cleverer approach.

kp54 2010-02-10 21:10:05
paths must pass certain points namely (-4, 4), (-3, 3), (-2, 2), (4, -4), (3, -3), (2, -2),

rrusczyk 2010-02-10 21:10:09
The path from (-4,-4) must go through exactly one of (4,-4), (3,-3), (2,-2), (-2,2), (-3,3), and (-4,4).

rrusczyk 2010-02-10 21:10:13
There's only one path through (4,-4) and one through (-4,4). What about through (3,-3)?

yforman 2010-02-10 21:10:35
(8c1)^2 = 64

darkdieuguerre 2010-02-10 21:10:36
8^2 = 64

rrusczyk 2010-02-10 21:10:43
There are C(8,1) ways to get to (3,-3), since there are 8 steps from (-4,-4) to (3,-3), and only one is up. Similarly, to get from (3,-3) to (4,4), there are 8 steps, of which 1 is to the right. So, there are C(8,1) ways to finish the path. This gives us a total of C(8,1)*C(8,1) paths through (3,-3). Similarly, there are C(8,1)*C(8,1) paths through (-3,3).

rrusczyk 2010-02-10 21:10:53
What about through (2,-2)?

darkdieuguerre 2010-02-10 21:11:04
(8C2)^2 = 784

lasse 2010-02-10 21:11:04
C(8,2)*^2

dday25 2010-02-10 21:11:10
(8c2)^2

rrusczyk 2010-02-10 21:11:12
Similarly, there are C(8,2) paths to (2,-2), and C(8,2) paths from (2,-2) to (4,4), so there are C(8,2)*C(8,2) paths from (-4,-4) to (4,4) through (2,-2). Same goes for (-2,2).

rrusczyk 2010-02-10 21:11:17
This gives us our total count: 2(C(8,0)*C(8,0) + C(8,1)*C(8,1) + C(8,2)*C(8,2)).

rrusczyk 2010-02-10 21:11:22
I like to do counting problems two ways to make sure I haven't overlooked something!

rrusczyk 2010-02-10 21:11:41
So now we're sure that we're correct!

joeislittle 2010-02-10 21:12:02
what if we missed something twice?

rrusczyk 2010-02-10 21:12:12
Then we're sad :(

ksun48 2010-02-10 21:12:33
can we do #14 on the amc 10 please? pretty please with a :rose: on top?

rrusczyk 2010-02-10 21:12:47
I don't have a diagram handy, so you'll have to draw one on your own.

rrusczyk 2010-02-10 21:14:01

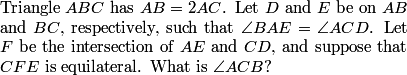
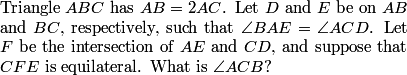
rrusczyk 2010-02-10 21:14:58
Now, hmmm. What do we do?

gh625 2010-02-10 21:15:30
You know that AFC = 120

rrusczyk 2010-02-10 21:15:44
OK, since CFE is equilateral, we have <AFC = <DFE = 120.

rrusczyk 2010-02-10 21:16:01
Then what?

mathwiz314 2010-02-10 21:16:08
BAC = 60

rrusczyk 2010-02-10 21:16:10
Why?

yankeesrule007 2010-02-10 21:16:44
do some angle chasing to get the angles of ABC in terms of angleBAE

yankeesrule007 2010-02-10 21:16:45
ACB=60+x and ABC=60-x also

rrusczyk 2010-02-10 21:17:06
We assign a variable to the equal angles: x = <BAE = <ACD

rrusczyk 2010-02-10 21:17:18
Then we can find other angles in terms of x.

rrusczyk 2010-02-10 21:17:35
We already have <BAF = x. What's <CAE in terms of x?

pumpkinpi 2010-02-10 21:18:13
60-x

jxl28 2010-02-10 21:18:13
60-x

happyof 2010-02-10 21:18:13
60-x

rrusczyk 2010-02-10 21:18:36
From triangle AFC, we have <CAE = 180 - <AFC - <ACF = 60 - x.

rrusczyk 2010-02-10 21:18:47
So, what does this give us?

lasse 2010-02-10 21:19:11
CAB=60-x+x=60

jxl28 2010-02-10 21:19:11
So <CAE+<BAE=60-x+x=<BAC=60

pumpkinpi 2010-02-10 21:19:11
since BAE = x, CAB = BAE + CAE = x + 60 - x = 60

rrusczyk 2010-02-10 21:19:25
That gives us <CAB = x + (60-x) = 60.

rrusczyk 2010-02-10 21:19:30
What does that give us?

lasse 2010-02-10 21:19:41
AC:AB = 1:2 so its a 30-60-90

jxl28 2010-02-10 21:19:41
ABC is a 30-60-90 triangle!

mathwiz314 2010-02-10 21:19:41
ABC= 30-60-90, then ACB=90

PowerOfPi 2010-02-10 21:19:45
30-60-90 triangle

rrusczyk 2010-02-10 21:20:11
Exactly; since AB = 2AC and the angle between them is 60, this triangle is similar to a 30-60-90 triangle.

yankeesrule007 2010-02-10 21:20:28
so the answer is 90

rrusczyk 2010-02-10 21:20:30
We conclude that <ACB is 90.

rrusczyk 2010-02-10 21:20:59
I have time for two more problems, I'll do one from each test.

rrusczyk 2010-02-10 21:21:07
Now, vote for the AMC 10 problem.

rrusczyk 2010-02-10 21:21:45

rrusczyk 2010-02-10 21:22:00
(I'll do #20, too -- it's quick :)

lasse 2010-02-10 21:22:11
Total vol = 3^3=27

joshim5 2010-02-10 21:22:21
total vllume is 27

rrusczyk 2010-02-10 21:22:29
Then what?

ss5188 2010-02-10 21:22:40
find the area of each hole and subtract overcounts

pumpkinpi 2010-02-10 21:22:41
try just making one hole and finding the volume that is taken out

henrypickle 2010-02-10 21:22:41
find empty space and subtract

bulutcocuk 2010-02-10 21:22:43
subtract the holes

rrusczyk 2010-02-10 21:22:45
We could start by trying to figure out what's left, but perhaps an easier strategy is to note that the initial cube has volume 3^3 = 27, and try to figure out what's cut out.

rrusczyk 2010-02-10 21:22:50
What's cut out?

joshim5 2010-02-10 21:23:00
the three holes are - (2*2*3)*3

aerrowfinn72 2010-02-10 21:23:00
take away three of 2*2*3..but ya needa add some back

rrusczyk 2010-02-10 21:23:18
Each hole has volume 2*2*3 = 12, for a total of 3*12 = 36 cut out.

rrusczyk 2010-02-10 21:23:27
That leaves us with 27 - 36 = -9.

rrusczyk 2010-02-10 21:23:28
Um.

stargroup 2010-02-10 21:23:40
It overlaps 3 times so you need to account for the overlap twice

aerrowfinn72 2010-02-10 21:23:40
add back 2 of 2*2*2

ksun48 2010-02-10 21:23:40
add 2 2*2*2's

ytrewq 2010-02-10 21:23:40
the center 2x2x2 is subtracted 3 times

MathTwo 2010-02-10 21:23:48
add some back you counted the 2x2x2 cube 3 times

jxl28 2010-02-10 21:23:50
You need to add back (2*2*2)*2

rrusczyk 2010-02-10 21:24:05
We subtracted the central overlap (a 2x2x2 cube) of the holes three times.

rrusczyk 2010-02-10 21:24:11
We add it back twice.

pirox 2010-02-10 21:24:19
-9+2*8=7

henrypickle 2010-02-10 21:24:19
which gives -9+16=7

myk 2010-02-10 21:24:19
the center cube overlaps 3 times, add 2(2^3) to -9 to get 7

rrusczyk 2010-02-10 21:24:32

rrusczyk 2010-02-10 21:24:43
We want to make the longest possible path. Let's start simple. What's the longest path the fly could take with the first step?

dolk 2010-02-10 21:25:30
sqrt(3)

7thsamurai 2010-02-10 21:25:30
sqrt(3)?

bobma99 2010-02-10 21:25:30
the opposite corner of the box

darkdieuguerre 2010-02-10 21:25:30
\sqrt{3} to the diagonally opposite corner

karanbir 2010-02-10 21:25:30
diagonagly opposite flying

GoldenFrog1618 2010-02-10 21:25:33
opposite corner

PowerOfPi 2010-02-10 21:25:33
space diagonal = sqrt(3)

rrusczyk 2010-02-10 21:25:40
The longest first step would be an interior diagonal, which has length sqrt(3).

rrusczyk 2010-02-10 21:25:44
So, there are 8 steps. Why wouldn't the answer just be 8*sqrt(3)?

bobma99 2010-02-10 21:26:05
you cant go back and forth 8 times

dday25 2010-02-10 21:26:05
Only 4 such diagonals.

dnkywin 2010-02-10 21:26:05
there are only4 diagonals

pumpkinpi 2010-02-10 21:26:05
there are only 4 interior diagonals

henrypickle 2010-02-10 21:26:08
8*sqrt 3 would be traveling back and forth between the two corners

rrusczyk 2010-02-10 21:26:14
The fly won't ever cover the same interior diagonal twice, and there are 4 interior diagonals. So, at most 4 of the steps could be along interior diagonals. These four together have length 4sqrt(3).

rrusczyk 2010-02-10 21:26:18
What is the longest the other 4 paths could be?

pirox 2010-02-10 21:26:27

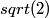
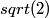
pumpkinpi 2010-02-10 21:26:27
sqrt2

moplam 2010-02-10 21:26:27
sqrt 2

jxl28 2010-02-10 21:26:27
sqrt(2)

ksun48 2010-02-10 21:26:27
\sqrt2

bulutcocuk 2010-02-10 21:26:27
root(2)

rpond 2010-02-10 21:26:27
sqrt(2)

megahertz 2010-02-10 21:26:27
sqrt{2}

gh625 2010-02-10 21:26:27
sqrt{2}

LincolnMS nerd herd 2010-02-10 21:26:27

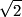
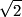
rrusczyk 2010-02-10 21:26:32
The longest the other 4 paths could be are face diagonals. This would add another 4sqrt(2) to the total length of the path.

rrusczyk 2010-02-10 21:26:36
What's left to check?

ksun48 2010-02-10 21:26:46
if it is possible

turak 2010-02-10 21:26:46
if its possible

joeislittle 2010-02-10 21:26:46
this is possible

moplam 2010-02-10 21:26:46
is it possible

pumpkinpi 2010-02-10 21:26:46
can this be accomplished?

darkdieuguerre 2010-02-10 21:26:49
that it's actually possible

7thsamurai 2010-02-10 21:26:49
That this is possible.

dday25 2010-02-10 21:26:49
If this is all possible in one path.

jenniferyin 2010-02-10 21:26:49
if its possible

rrusczyk 2010-02-10 21:26:54
We must check if such a path is possible -- can the fly visit all the vertices with four space diagonals and four face diagonals?

ksun48 2010-02-10 21:27:17
yes

vv123 2010-02-10 21:27:17
alternate rt3 and rt2 and get 4rt3+4rt2

happyof 2010-02-10 21:27:17
yes

challenger 2010-02-10 21:27:17
yep

soulspeedy 2010-02-10 21:27:17
yep

dday25 2010-02-10 21:27:21
Yes, it can if it alternates between the two types of diagonals.

rrusczyk 2010-02-10 21:27:25
Yes. It can do so with a sequence of face-space diagonal pairs.

rrusczyk 2010-02-10 21:27:30

rrusczyk 2010-02-10 21:27:38
That's the first pair.

rrusczyk 2010-02-10 21:27:40

rrusczyk 2010-02-10 21:27:48
There are the rest.

rrusczyk 2010-02-10 21:27:59
Start anywhere :)

pirox 2010-02-10 21:28:07
so it's (D)! :-D

yankeesrule007 2010-02-10 21:28:07
so the asnwer is D

ksun48 2010-02-10 21:28:07
red is plane, blue is space

Iggy Iguana 2010-02-10 21:28:07
so it is 4sqrt3 + 4 sqrt2

GoldenRatioOfPhi 2010-02-10 21:28:07
answer ia d

moplam 2010-02-10 21:28:09
Nice diagram

rrusczyk 2010-02-10 21:28:12
Thanks :)

rrusczyk 2010-02-10 21:28:19
OK, one more AMC 12 problem.

rrusczyk 2010-02-10 21:28:21
Vote time

rrusczyk 2010-02-10 21:28:46

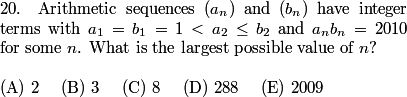
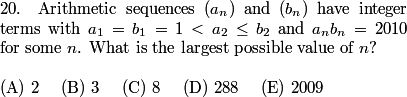
rrusczyk 2010-02-10 21:29:26
Let's look the first arithmetic sequence (a_n) first.

rrusczyk 2010-02-10 21:29:35
Let d_1 be its common difference. Then what is the nth term a_n?

crazypianist1116 2010-02-10 21:30:09
1 +(n-1)d

yankeesrule007 2010-02-10 21:30:09
1+ d_1(n-1)

stargroup 2010-02-10 21:30:09
1 + (n-1)d_1

yforman 2010-02-10 21:30:09
1+(n-1)d_1

mgao 2010-02-10 21:30:09
a_n = d_1(n-1)+1

tonypr 2010-02-10 21:30:09

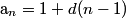
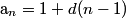
rrusczyk 2010-02-10 21:30:12

rrusczyk 2010-02-10 21:30:20

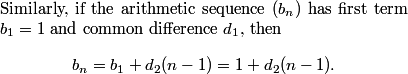
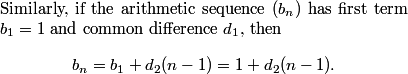
rrusczyk 2010-02-10 21:30:29

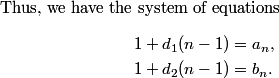
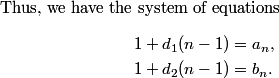
rrusczyk 2010-02-10 21:30:41
What can we do with these ?

rrusczyk 2010-02-10 21:31:09
I see some of you suggesting multiplying them.

rrusczyk 2010-02-10 21:31:19
That's gonna create an awful mess, no?

GoldenRatioOfPhi 2010-02-10 21:31:22
subtract

rrusczyk 2010-02-10 21:31:27
Subtract what?

crazypianist1116 2010-02-10 21:31:32
anbn=2010

MathTwo 2010-02-10 21:31:32
a_n and b_n are factors of 2010

karanbir 2010-02-10 21:31:36
an(bn)=2010

rrusczyk 2010-02-10 21:31:48
We do know that a_n and b_n multiply to 2010

rrusczyk 2010-02-10 21:31:55
Can we learn more from these equations?

moplam 2010-02-10 21:31:58
1 from both side

rrusczyk 2010-02-10 21:32:04
Let's try that.

rrusczyk 2010-02-10 21:32:05

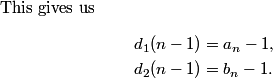
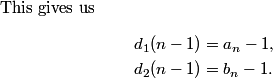
rrusczyk 2010-02-10 21:32:13
What does this tell us?

yankeesrule007 2010-02-10 21:32:38
Find to factors of 2010 which when you subtract them from 1, share a common factor

kthxbai 2010-02-10 21:32:38
a_n=b_n=1 (mod n-1)

karanbir 2010-02-10 21:32:45
devide by n-1

rrusczyk 2010-02-10 21:32:53

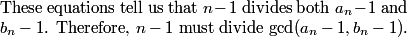
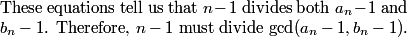
rrusczyk 2010-02-10 21:33:09
And what do we know about a_n and b_n that will help?

megahertz 2010-02-10 21:33:22
multiplies to 2010

rpond 2010-02-10 21:33:22
that they multiply to 2010, of course

BarbieRocks 2010-02-10 21:33:22
they multiply to 2010!!!

rrusczyk 2010-02-10 21:33:37
All right, we know all our possibilities for a_n and b_n.

rrusczyk 2010-02-10 21:33:44
We could go ahead and list them:

rrusczyk 2010-02-10 21:33:49

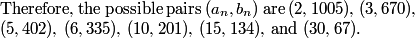
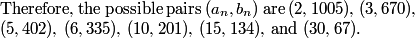
rrusczyk 2010-02-10 21:34:02
As we crank through these, what are we looking for?

rpond 2010-02-10 21:34:33
pairs that are both 1 (mod k) for some k

ShocK n AwE 2010-02-10 21:34:33
now we look for if we subtract 1, they should have a common factor besides 1

yforman 2010-02-10 21:34:33
the largest possible gcd of a_n-1 and b_n-1

BarbieRocks 2010-02-10 21:34:36
two numbers such that when you subtract 1 from each of them, they have a common factor

rrusczyk 2010-02-10 21:34:39
We're looking for the pair such that subtracting 1 from each gives a pair with a high GCD

rrusczyk 2010-02-10 21:35:10

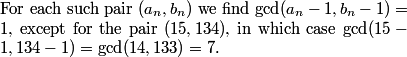
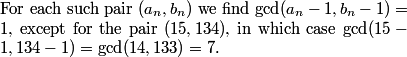
GoldenFrog1618 2010-02-10 21:35:12
(15,134) gives a n-1=7

ShocK n AwE 2010-02-10 21:35:13
15,134 is the only one

rpond 2010-02-10 21:35:18
but there's only one pair that does this: (15-1, 134-1) gives us a GCD of 7

MathTwo 2010-02-10 21:35:36
then n=8

MathTwo 2010-02-10 21:35:36
then n=8=>C

BarbieRocks 2010-02-10 21:35:36
so n=8.

ShocK n AwE 2010-02-10 21:35:39
n=8, yay

CubeX 2010-02-10 21:35:40
SO the answer is (C)=8

rrusczyk 2010-02-10 21:35:42

rrusczyk 2010-02-10 21:35:51
Therefore, the largest possible value of n is 8, and the answer is (C)

rrusczyk 2010-02-10 21:36:25
That's it for the Math Jam tonight. Thank you all for coming, and special thanks to our assistant, Wendy Hou (wobster109)

aunch 2010-02-10 21:36:37
just a side question... ive noticed many problems on not only the AMCs but also other math contests that they have a lot of problems regarding the year number.... for example this year there was a lot of problems with the number 2010.... is it a good idea to take a little time to memorize some proporties of 2010 like prime factorization, remainder when divided by 7, etc.?

rrusczyk 2010-02-10 21:36:39
Yes.

rrusczyk 2010-02-10 21:36:57
I see a lot of you asking about the index or average scores.

rrusczyk 2010-02-10 21:37:04
I really have no idea what it will be!

rrusczyk 2010-02-10 21:37:10
There's a lot of discussion on the forum about it

rrusczyk 2010-02-10 21:37:23
I also don't know how the AMC is handling the snow storms.

bobma99 2010-02-10 21:37:26
will this be saved somewhere so we can look over it again?

rrusczyk 2010-02-10 21:37:36
Yes, I will put the transcript up tonight in the Math Jam section

rrusczyk 2010-02-10 21:37:42
Under transcripts.

rrusczyk 2010-02-10 21:38:02
I think a lot of people found the test hard this year, so if you did, you're not alone.

henrypickle 2010-02-10 21:38:37
when does the amc website usually post things like the answer key, aime qualifying scores, etc.?

rrusczyk 2010-02-10 21:38:57
I'm not sure -- they usually post the qualifying scores on our site before posting anywhere else.

rrusczyk 2010-02-10 21:39:13
(I don't have a guess as to whether they will be lowered or not)

darkdieuguerre 2010-02-10 21:39:46
an answer key for both tests is already up in the forum :)

rrusczyk 2010-02-10 21:40:12
Again, I really don't have a guess for what the index will be!

rrusczyk 2010-02-10 21:40:25
Some of you have asked if you should take the B test if you passed the A

rrusczyk 2010-02-10 21:40:38
Yes -- the USAMO qualification is a combination of AMC and AIME scores.

rrusczyk 2010-02-10 21:41:39
For those of you asking about the snow, I suggest talking to the AMC

Visitor03 2010-02-10 21:41:46
If I passed the AMC 10A but didn't pass the B exam, would I still qualify for AIME?

rrusczyk 2010-02-10 21:41:48
Yes

mathwiz314 2010-02-10 21:41:50
My school doesn't offer the 10B, but offers the 12B, should I take the 12B if I passed the 10A?

rrusczyk 2010-02-10 21:42:03
I generally recommend students take both if they're strong enough to pass the 10

xpmath 2010-02-10 21:42:07
hm mr. rusczyk, did you take the tests for fun or did you just randomly look at the problems

rrusczyk 2010-02-10 21:42:14
I just did the last 5 problems for fun

dday25 2010-02-10 21:42:42
How well did you do? ;)

rrusczyk 2010-02-10 21:42:56
Pretty good :) But the 90! problem was easily the hardest for me.

westiepaw 2010-02-10 21:43:10
Which AoPS books would you especially reccomend to prep for the 10B?

rrusczyk 2010-02-10 21:43:18
The intro series and Volume 1

megahertz 2010-02-10 21:43:44
Which would you recommend for 12 and beginning AIME?

rrusczyk 2010-02-10 21:44:04
After mastering the earlier stuff, you're ready for Intermediate series and the AIME

aopsaccount2131 2010-02-10 21:44:52
i've noticed that a lot of the AIME problems can be solved without advanced topics (beyond second-year algebra, first-year geometry, etc.) is this generally true?

rrusczyk 2010-02-10 21:44:55
yes

LincolnMS nerd herd 2010-02-10 21:45:38
Is this AMC 10B easier than the A?

rrusczyk 2010-02-10 21:45:43
They try to make them the same.

pumpkinpi 2010-02-10 21:46:04
I like the comment in Volume 1 about most 3-D geometry problems being 2-D geometry problems in disguise!

rrusczyk 2010-02-10 21:46:11
:)

sparkle123 2010-02-10 21:47:09
Thanks SO MUCH for the math jam! this was amazing :)

rrusczyk 2010-02-10 21:47:22
Thanks for coming -- that's a wrap for tonight.

rrusczyk 2010-02-10 21:47:37
Feel free to write me at aops@artofproblemsolving.com if you want recommendations for books or classes!

twoplusthree 2010-02-10 21:47:44
thanks

RunpengFAILS 2010-02-10 21:47:44
THANK YOU

yankeesrule007 2010-02-10 21:47:44
thank you!

nearsymmetric 2010-02-10 21:47:44
Yes, thank you -- great session!

Visitor03 2010-02-10 21:47:44
Thank you, once again.

limac 2010-02-10 21:47:44
thank you for the math jam! :)

mathscience 2010-02-10 21:47:44
thanks a lot for the math jam!!!!:) it was amazing

xpmath 2010-02-10 21:48:07
thanks

pirox 2010-02-10 21:48:07
thanks!

turak 2010-02-10 21:48:07
thank you

Aeroalon 2010-02-10 21:48:07
Almost 3 hours :O

Ihatepie 2010-02-10 21:48:07
hard test

CubeX 2010-02-10 21:48:07
thanks

aggarwal 2010-02-10 21:48:24
see you in the B jam

westiepaw 2010-02-10 21:48:24
Thanks!

tonypr 2010-02-10 21:48:24
Thanks for the math jam!

2010 AMC 10/12 A Math Jam

Facilitator: Richard Rusczyk