Math Jams

DPatrick 2010-02-25 18:10:35
Welcome to the 2010 AMC 10B/12B Math Jam! We will start at 7 PM Eastern / 4 PM Pacific.

DPatrick 2010-02-25 18:11:16
The classroom is moderated, meaning that students can type into the classroom, but these comments will go only to the instructors, not directly into the room.

DPatrick 2010-02-25 18:59:43
Hello and welcome to the 2010 AMC 10B/12B Math Jam!

DPatrick 2010-02-25 18:59:57
My name is Dave Patrick, and I'll be leading the first part of tonight's discussion. Later, my colleague Naoki Sato will join us.

DPatrick 2010-02-25 19:00:09
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.

DPatrick 2010-02-25 19:00:26
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.

DPatrick 2010-02-25 19:00:39
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read. Only write comments that are relevant to the discussion.

DPatrick 2010-02-25 19:01:01
There are a lot of students here! As I said, only well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and definitely do not complain about it. This Math Jam will be much larger than one of our typical classes, so please be patient---there are quite a few of you here tonight!!

DPatrick 2010-02-25 19:01:21
Also, we won't be going through all of the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go.

DPatrick 2010-02-25 19:01:41
Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our regular classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!

DPatrick 2010-02-25 19:02:04
We will have an assistant tonight who can help answer some of the questions. He is Max Rosett (mrosett). Max is a sophomore at Yale who intends to double major in math and history. In high school, he qualified for the Math Olympiad Summer Program and was the captain of the ARML team for his home state of Utah. (He will be here a bit later.)

Orange-2728 2010-02-25 19:02:26
Is there audio for this class?

DPatrick 2010-02-25 19:02:47
There is no audio or video. What you are now seeing is everything there is to see.

DPatrick 2010-02-25 19:03:24
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a problem is posted, do not simply respond with the final answer. That's not why we're here.

DPatrick 2010-02-25 19:03:46
We're going to work through the problems step-by-step, and people who post comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, are going to be ignored.

DPatrick 2010-02-25 19:04:07
The Math Jam will proceed as follows:

DPatrick 2010-02-25 19:04:12
We will work the last 5 problems from the AMC 10B, then the last 5 problems from the AMC 12B. After that, time permitting, we will take requests for some other problems for discussion.

DPatrick 2010-02-25 19:04:33
One quick bit of news before we get started: we have a special weekend AIME seminar coming up! It's Saturday and Sunday, March 6 and 7, and will last from 3:30 - 6:30 Eastern (12:30 - 3:30 Pacific) each day. Each day consists of general approaches and important facts needed for problems within a given subject area, followed by a discussion of specific problems from past AIME competitions, or from other contests of a similar difficulty level. Day 1 is Counting & Algebra, Day 2 is Number Theory & Geometry. The cost is $65.

DPatrick 2010-02-25 19:04:59
If you are just beginning at the AIME level and only expect to get 1 or 2 (out of 15), then the AIME seminar is probably too advanced for you. The target audience for the seminar is students scoring in the 3-9 range trying to get up into the 10+ range. More information is available on the AoPS website by clicking the "Online Classes" link, and if you have further questions about this seminar, please email classes@artofproblemsolving.com, or post your question on the forum. (I will not take questions now.)

AIME15USAMO 2010-02-25 19:05:20
65 total or for each day?

DPatrick 2010-02-25 19:05:32
Total (for $65 you get both days).

DPatrick 2010-02-25 19:05:45
Finally, please do not ask about AIME qualifying, or what I think the qualifying score might be, or any other such contest-related administrative matters. Those questions are better posted on the forum or directed to AMC administrators or your teacher. I will not speculate on what I think the AIME qualifying scores might me. We are here tonight to talk about the math. :)

DPatrick 2010-02-25 19:06:23
Let's get started with #21 on the AMC 10B!

DPatrick 2010-02-25 19:06:35

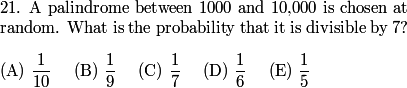
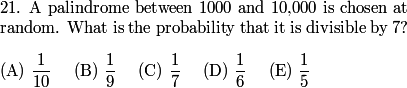
DPatrick 2010-02-25 19:06:48
(As you see, I will place each problem at the top of the screen as we discuss it. You can make the region at the top larger or smaller by dragging on the gray horizontal bar near the top.)

DPatrick 2010-02-25 19:06:59
(This problem was also #11 on the AMC 12B)

DPatrick 2010-02-25 19:07:28
Note: A palindrome is a number that reads the same forwards as backwards, so for example, 36763 and 182281 are palindromes.

DPatrick 2010-02-25 19:07:43
(I'm a little surprised that they didn't provide you with this information on the test. Oh, well.)

pi.guy3.14 2010-02-25 19:07:52
listing them out is probably not the best way?

DPatrick 2010-02-25 19:07:56
I agree. :)

DPatrick 2010-02-25 19:08:19
Also, trying to count them all is hopefully not what we need.

Jason27603 2010-02-25 19:08:38
write the number as 1000a+100b+10b+a=1001a+110b

ajl12504 2010-02-25 19:08:38
you could write this palindrome as 1000a + 100b + 10b +a

DPatrick 2010-02-25 19:08:55
That's a great way to approach it. We know that a palindrome that is between 1000 and 10000 is of the form XYYX, where X and Y are decimal digits.

DPatrick 2010-02-25 19:09:14
So we can write out XYYX in expanded form: 1000X + 100Y + 10Y + X = 1001X + 110Y.

DPatrick 2010-02-25 19:09:28
How does this help us out?

Infrared 2010-02-25 19:10:08
1001 is divisible by 7

DanielC 2010-02-25 19:10:08
1001 is divisable by 7 therefore so is 1001a

sparkle123 2010-02-25 19:10:08
1001 is divisible by 7 so Y must be divisible by 7

TheCopleyIndian 2010-02-25 19:10:08
1001 is always divisible by 7 so 110b has to also be divisible by 7

happymath 2010-02-25 19:10:08
we know 1001 is divisible by 7

DPatrick 2010-02-25 19:10:23
First, we note that 1001 is divisible by 7. Therefore, 1001X + 110Y is divisible by 7 if and only if 110Y is divisible by 7.

aerrowfinn72 2010-02-25 19:10:39
y must be a multiple of 7

HydraPyros 2010-02-25 19:10:39
The middle digits, or 110y must be divisible by 7

N1349 2010-02-25 19:10:39
for the whole number to be divisible by seven, y has to be 7

DPatrick 2010-02-25 19:10:52
Exactly. 110 is not divisible by 7. Since 7 is prime, this means 110Y is divisible by 7 if and only if Y is divisible by 7.

mathq 2010-02-25 19:11:15
So, Y=0 or 7

carmelninja 2010-02-25 19:11:15
we pick the digits that are divisble by 7

eat2thepieseye 2010-02-25 19:11:15
Y must be 0 or 7.

carmelninja 2010-02-25 19:11:15
y= 7 or 0

DPatrick 2010-02-25 19:11:21
Yes -- since Y is a decimal digit, Y is divisible by 7 if and only if Y = 0 or Y = 7.

DPatrick 2010-02-25 19:11:34
So how do we wrap this all up?

DanielC 2010-02-25 19:12:03
2/10=1/5

ajl12504 2010-02-25 19:12:03
=1/5

eat2thepieseye 2010-02-25 19:12:03
Two out of the ten digits work, so the probability is 1/5.

DPatrick 2010-02-25 19:12:21
The decimal digit Y can be any digit with equal probability, so the probability that XYYX is divisible by 7 is 2/10 = 1/5.

DPatrick 2010-02-25 19:12:29
The answer is (E).

DPatrick 2010-02-25 19:12:39
Note that we didn't have to count, nor did we have to worry about X.

DPatrick 2010-02-25 19:13:28
Writing a number in terms of its digits (like XYYX = 1001X + 110Y) is a common and useful algebraic / number-theory tool.

DPatrick 2010-02-25 19:13:42
Let's move on to #22 on the AMC 10B:

DPatrick 2010-02-25 19:13:50

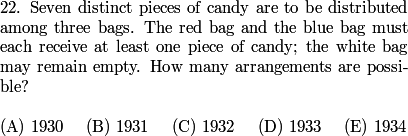
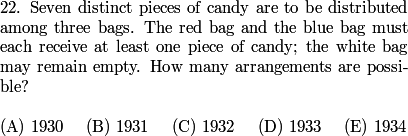
DPatrick 2010-02-25 19:14:21
(I should remind everyone that a full transcript of this Math Jam will be posted to the website at the conclusion, so if you come in late or miss something or something goes by too fast, you can always review it later.)

v_Enhance 2010-02-25 19:14:50
Start by counting the number of ways to divide the candy, then subtract for the cases where red and blue are empty?

auto123ml 2010-02-25 19:14:50
casework???? or maybe complementary counting...

DPatrick 2010-02-25 19:15:09
There are a number of ways to do this, but (I think) the easiest by far is to use complementary counting. This is the technique where we count all arrangements, and subtract the arrangements we don't want to count.

DPatrick 2010-02-25 19:15:26
We start by supposing there were no restrictions on how many candies can be in each bag. What is the number of arrangements in this case?

happymath 2010-02-25 19:15:54
without limits there are 3^7 ways

happyof 2010-02-25 19:15:54
total number of ways is 3^7

EricMathPath09 2010-02-25 19:15:54
There are 3^7 total ways that the candies can be distributed, disregarding the restrictions.

carmelninja 2010-02-25 19:15:54
each piece of candy can go to 3 places --> 3^7

DPatrick 2010-02-25 19:16:05
If no restrictions, then each of the seven pieces of candy can be in any of the three bags, so the number of arrangements is 3^7 = 2187.

DPatrick 2010-02-25 19:16:35
Now we have to subtract the cases that we DON'T want.

DPatrick 2010-02-25 19:16:53
The cases we're don't want are when EITHER the red bag or the blue bag is empty.

DPatrick 2010-02-25 19:16:59
How many arrangements are there where the red bag is empty?

RoFlLoLcOpT 2010-02-25 19:17:27
2^7 ways to have no candies in the red bag, and the same for the blue bag

v_Enhance 2010-02-25 19:17:28
2^ 7 = 128 by the same logic.

TheCopleyIndian 2010-02-25 19:17:28
2^7 for red to be empty and 2^7 for blue to be empty

DPatrick 2010-02-25 19:17:53
If the red bag is empty, then each of the seven pieces of candy can be in either the blue bag or the white bag. So each piece of candy has 2 possibilities, and (since there are 7 pieces) the number of such arrangements is 2^7 = 128.

DPatrick 2010-02-25 19:18:11
By exactly the same logic, the number of arrangements where the blue bag is empty is also 128.

v_Enhance 2010-02-25 19:18:26
Doesn't this overcount the case where BOTH red and blue are empty?

carmelninja 2010-02-25 19:18:26
but you overcounted

ajl12504 2010-02-25 19:18:32
then we have to add 1 because we counted one case twice - if both are empty

sparkle123 2010-02-25 19:18:32
1 case both blue and red bags are empty

DPatrick 2010-02-25 19:18:58
Right! This does not mean the number of arrangements where either the red bag or the blue bag is empty is equal to 128 + 128 = 256, because we have counted twice the arrangement where both bags are empty.

DPatrick 2010-02-25 19:19:04
If both the red bag and the blue bag is empty, then all the candies must be in the white bag, so there is only one such arrangement.

DPatrick 2010-02-25 19:19:28
Therefore, the number of arrangements where either the red bag or the blue bag is empty is equal to 128 + 128 - 1 = 255.

EricMathPath09 2010-02-25 19:19:33
This is a typical example of the Principle of Inclusion-Exclusion.

DPatrick 2010-02-25 19:19:51
Indeed, this problem was a classic example of the Principle of Inclusion-Exclusion, or PIE. (Look it up if you haven't heard of it before!)

v_Enhance 2010-02-25 19:20:00
So our answer is 2187 - 255 = 1932 (C).

sreyesh 2010-02-25 19:20:00
So the answer is 2187-255 = 1932, or C

RoFlLoLcOpT 2010-02-25 19:20:00
2187-255=1932 -> C

DPatrick 2010-02-25 19:20:27
Thus, we conclude that the number of possible arrangements is 2187 - 255 = 1932. (Again, recall that we counted ALL arrangements without restriction, then subtracted the bad ones.) The answer is (C).

DPatrick 2010-02-25 19:20:58
Of course, you don't have to subtract this last computation all the way out: once you realize the last digit is 2, you're set based on the answer choices.

DPatrick 2010-02-25 19:21:09
But it's a nice check of your work to compute it all the way and verify you get 1932.

Infrared 2010-02-25 19:21:14
Can we do this using balls and urns?

DPatrick 2010-02-25 19:21:33
It's hard: "balls and urns" (as the term is typically used) is for indistinguishable objects.

DPatrick 2010-02-25 19:21:45
Here we are told that the pieces of candy are distinguishable.

DPatrick 2010-02-25 19:22:27
(And if you don't know what "balls and urns" means, it's a common counting trick for arrangements of indistinguishable objects. Look it up afterwards, or get AoPS's Introduciton to Counting & Probability textbook :) )

DPatrick 2010-02-25 19:23:07
Note also could also solve this problem by just counting it directly: the easiest is probably to choose which marbles are in the red & blue bags.

DPatrick 2010-02-25 19:23:19

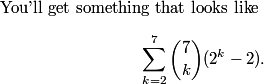
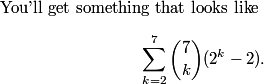
DPatrick 2010-02-25 19:23:27

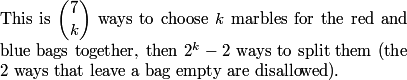
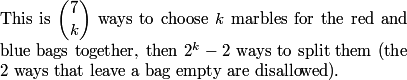
DPatrick 2010-02-25 19:23:39
But this method then leaves a lot of hand computation: (21)(2) + (35)(6) + (35)(14) + (21)(30) + (7)(62) + (1)(126).= 1932.

DPatrick 2010-02-25 19:23:55
There's also some interesting algebra relating these two solution methods (and involving the Binomial Theorem), but we'll leave that for you to explore on your own!

DPatrick 2010-02-25 19:24:04
Let

DPatrick 2010-02-25 19:24:16
Let's move on to #23 on the 10B, which is also #17 on the 12B.

DPatrick 2010-02-25 19:24:24

DPatrick 2010-02-25 19:25:08
(Again, let me reiterate that we cannot answer all of your questions directly because of the large size of this Math Jam. Rest assured that our regular classes are not like this.)

happyof 2010-02-25 19:25:35
1 and 9 are on opposite corners

GFParagon 2010-02-25 19:25:35
1 has to be in the top left corner and 9 in the bottom right corner

v_Enhance 2010-02-25 19:25:35
Well, we know that 1 must be in the upperleft corner, and 9 in the lowerright corner.

RoFlLoLcOpT 2010-02-25 19:25:35
the top left must be 1, bottom right must be 9

DPatrick 2010-02-25 19:25:51
A good first step is to notice that the 1 must go in the upper-left corner, and the 9 must in the lower right corner.

DPatrick 2010-02-25 19:25:55
So let's fill those in:

DPatrick 2010-02-25 19:25:59

DPatrick 2010-02-25 19:26:39
As is often the case, there are multiple ways to proceed from here. I'll present one that I think is the most natural.

spelljack825 2010-02-25 19:26:41
2 and 8 must be adjacent to 1 and 9 respectively

carmelninja 2010-02-25 19:26:42
2 must be next to 1 --> both cases are symmetric

PowerOfPi 2010-02-25 19:26:42
two choices for 2 and two choices for 8

maxkaplan 2010-02-25 19:26:42
2 can only be middle top row or middle left column

carmelninja 2010-02-25 19:26:42
2 must be next to 1 --> both cases symmetric

Infrared 2010-02-25 19:26:42
2 has to be adjacent to 1 and 8 must be adjacent to 9

DPatrick 2010-02-25 19:27:21
Right: the 2 (and the 8) are the most restrictive numbers to place, so let's worry about them next. Let's focus on the 2, and we'll remember that the 8 is essentially the same.

DPatrick 2010-02-25 19:27:27
The 2 must go either beside the 1 or below the 1.

DPatrick 2010-02-25 19:27:32

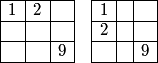
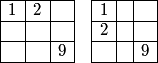
DPatrick 2010-02-25 19:27:45
Note that these cases are symmetric, so let's just focus on the first case (on the left above).

DPatrick 2010-02-25 19:27:58
Let's just continue in order...where must the 3 go?

mathsawesum 2010-02-25 19:28:43
Either next to the 2 or below the 1

erica539 2010-02-25 19:28:43
next to 2 or below 1

$LaTeX$ 2010-02-25 19:28:43
under 1, under 2, or next to 2

DPatrick 2010-02-25 19:28:53
The 3 must go beside the 1 or beside the 2:

DPatrick 2010-02-25 19:28:57

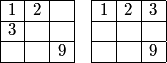
DPatrick 2010-02-25 19:29:19
In summary, the first three numbers 1, 2, and 3 either form an L-shape or lie straight.

2012 2010-02-25 19:29:43
So $Latex$ is wrong?

joshim5 2010-02-25 19:29:44
Why can't the 3 be in the middle box?

mathcountsloser 2010-02-25 19:29:44
what about the 3 under the two in the second diagram

DPatrick 2010-02-25 19:29:57
Yes, the 3 can't go under the 2, because then what would be put to the left of it?

DPatrick 2010-02-25 19:30:31
(Sorry $LaTeX$, I usually try not to post incorrect response, but with this many students it's easy for me to mess up.)

DPatrick 2010-02-25 19:30:49
Similarly, by symmetry, the last three numbers 7, 8, and 9 either form an L-shape or lie straight.

DPatrick 2010-02-25 19:31:11
So our tactic will be to count the number of arrays based on these cases, whether the 123 and/or the 789 form L-shapes or our straight.

DPatrick 2010-02-25 19:31:20
...are striaght.

DPatrick 2010-02-25 19:31:24
...straight!

DPatrick 2010-02-25 19:31:39
(As I said, there are other ways too, but this is the method I'll present.)

DPatrick 2010-02-25 19:31:52
First, let's look at the case where we have two L-shapes.

DPatrick 2010-02-25 19:31:55
For example:

DPatrick 2010-02-25 19:31:59

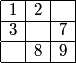
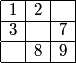
DPatrick 2010-02-25 19:32:03
Where can the 4, 5, and 6 go in this array?

rpond 2010-02-25 19:32:41
anywhere in any combination

v_Enhance 2010-02-25 19:32:41
Anywhere!

mbx24 2010-02-25 19:32:41
any way: 3!=6

mathcountsloser 2010-02-25 19:32:41
3! ways for them to go

dafjbomb 2010-02-25 19:32:41
there are 3! ways to arragne them

ajl12504 2010-02-25 19:32:41
there are 3! possibilities then = 6

DPatrick 2010-02-25 19:32:51
Yes -- the 4, 5, and 6 can be placed arbitrarily in the remaining three spaces, which gives us six possible arrays.

DPatrick 2010-02-25 19:32:59
And in how many ways can the numbers {1, 2, 3} and {7, 8, 9} both form an L-shape?

carmelninja 2010-02-25 19:33:28
so 2x2 = 4

v_Enhance 2010-02-25 19:33:28
2 cases for each so 2^2 = 4

happymath 2010-02-25 19:33:28
2*2=4 ways

ewcikewqikd 2010-02-25 19:33:28
2^2 = 4

mbx24 2010-02-25 19:33:28
2 each: 2*2=4

DPatrick 2010-02-25 19:33:48
The numbers {1, 2, 3} and {7, 8, 9} both form an L-shape in four different ways, since each of {1,2,3} and {7,8,9} form an L-shape in 2 ways, thus we get 2*2 = 4 total ways:

DPatrick 2010-02-25 19:33:56

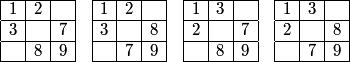
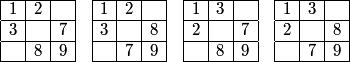
DPatrick 2010-02-25 19:34:14
So how many total arrangements in the "two L-shapes" case?

chengpeng123 2010-02-25 19:34:30
therefore, we get 4 * 6 for a total of 24 different ways

aerrowfinn72 2010-02-25 19:34:30
24...4*6

Thunder365 2010-02-25 19:34:30
6x4=24

DPatrick 2010-02-25 19:34:51
For each of these four L-shape arrangements, the numbers 4, 5, and 6 can be placed arbitrarily 3! = 6 ways in the remaining three spaces. Hence, there are 4 x 6 = 24 arrays in this case.

DPatrick 2010-02-25 19:35:01
We're not done!

DPatrick 2010-02-25 19:35:13
Next, we look at the case where one set of numbers form an L-shape, and another set of numbers lie straight. Let's look at one example:

DPatrick 2010-02-25 19:35:17

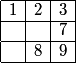
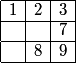
DPatrick 2010-02-25 19:35:21
Where can the 4, 5, and 6 go in this array?

dafjbomb 2010-02-25 19:35:56
there are only 2 choices

PowerOfPi 2010-02-25 19:35:56
4 must go below the 1, then there are 2 ways for the rest

RoFlLoLcOpT 2010-02-25 19:35:56
4 must go under 1, then the other two can go in either spot

mbx24 2010-02-25 19:35:56
two ways: 4 must be directly below 1.

kmao 2010-02-25 19:35:56
4 must be in the top left

GFParagon 2010-02-25 19:35:56
4 under the 1 and 5 and 6 can go anywhere= 2 options

DPatrick 2010-02-25 19:36:06
Right. The 4 must go below the 1. The 5 and 6 can then be placed arbitrarily, which gives us 2 possible arrays.

DPatrick 2010-02-25 19:36:32
Do we believe that all of the "1 L, 1 straight" combinations, by symmetry, have two ways to fill in {4,5,6}?

DPatrick 2010-02-25 19:36:52
It (pretty) clear that this is true; we can look at one more example to be (more) sure.

DPatrick 2010-02-25 19:36:56

DPatrick 2010-02-25 19:37:01
What about this one?

prezcoin 2010-02-25 19:37:26
the 6 must be above the 9, so there are 2 ways

carmelninja 2010-02-25 19:37:26
6 must go above 9

DanielC 2010-02-25 19:37:26
6 has to be above 9 so 2 possibilities

rpond 2010-02-25 19:37:26
the 6 must go in the bottom right, so there are 2 arrangements again

DPatrick 2010-02-25 19:37:31
The 6 must go above the 9. The 4 and 5 can then be placed arbitrarily, which gives us 2 possible arrays.

DPatrick 2010-02-25 19:37:58
We'll always leave and L-shaped "hole", and either the 4 or the 6 (depending on which way the hole points) will have to go in the middle of the hole.

DPatrick 2010-02-25 19:38:15
So once we have "1 L, 1 straight", there are 2 ways to finish.

DPatrick 2010-02-25 19:38:21
In how many ways can we have "1 L, 1 straight"?

DPatrick 2010-02-25 19:39:00
(before filling in 4,5,6 I mean)

carmelninja 2010-02-25 19:39:13
2x2x2x2 total ways

happymath 2010-02-25 19:39:13
2x4=8

ajl12504 2010-02-25 19:39:13
there are 8 possible ways

DPatrick 2010-02-25 19:39:25
We have 2 choices for which set {1,2,3} or {7,8,9} is the L and which is straight, times 2 choices for how the numbers are arranged in the L, times 2 choices for whether the straight line is horizontal or vertical.

DPatrick 2010-02-25 19:39:42
So 2*2*2 = 8 ways to arrange {1,2,3,7,8,9} in 1 L and 1 straight.

DPatrick 2010-02-25 19:39:59
I wouldn't do this on the actual contest (it'd take too long), but for clarity tonight, here are the 8 possibilities:

DPatrick 2010-02-25 19:40:04

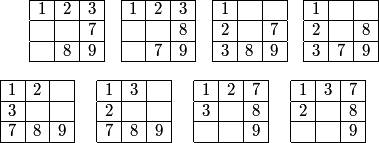
DPatrick 2010-02-25 19:40:35
And as we discussed a moment ago, for each of these eight arrays, the numbers 4, 5, and 6 can be placed two ways in the remaining three spaces. Hence, there are 8 x 2 = 16 arrays in the "1 L, 1 straight" case.

DPatrick 2010-02-25 19:40:53
Finally, we look at the case where the numbers {1, 2, 3} and {7, 8, 9} both lie straight. Let's look at an example:

DPatrick 2010-02-25 19:40:59

DPatrick 2010-02-25 19:41:03
Where can the 4, 5, and 6 go in this array?

prezcoin 2010-02-25 19:41:21
there is only one way: 456

v_Enhance 2010-02-25 19:41:22
There's only one way to fill this.. 4-5-6

PowerOfPi 2010-02-25 19:41:22
in order

aerrowfinn72 2010-02-25 19:41:22
just one way: 4,5,6

chengpeng123 2010-02-25 19:41:22
only 1 way, 4,5,6 in that order

DPatrick 2010-02-25 19:41:29
The numbers from left to right must be 4, 5, and 6, in that order. There is only one possible array.

DPatrick 2010-02-25 19:41:35
And how many arrays are there where the numbers {1, 2, 3} and {7, 8, 9} both lie straight?

stargroup 2010-02-25 19:42:03
there is also the rotation of this case, where we number by columns instead of rows

prezcoin 2010-02-25 19:42:03
there are two ways to arrange the 123 and 789, either horizontally or vertically

GFParagon 2010-02-25 19:42:03
2 straight line options

Lord.of.AMC 2010-02-25 19:42:03
2 for horizontal or vertical

DPatrick 2010-02-25 19:42:15
There are two arrays where the numbers {1, 2, 3} and {7, 8, 9} both lie straight: they are either both horizontal or both vertical.

DPatrick 2010-02-25 19:42:20

DPatrick 2010-02-25 19:42:30
For each of these two arrays, the numbers 4, 5, and 6 can be placed in only one way in the remaining three spaces. Hence, there are 2 x 1 = 2 arrays in the "2 straight" case.

gh625 2010-02-25 19:42:44
Therefore, the answer is 24+16+2=42.

atennis 2010-02-25 19:42:44
so the answer is 24+16+2=42 D

prezcoin 2010-02-25 19:42:44
so 24+16+2= 42 ways

DPatrick 2010-02-25 19:42:59
Yes: to finish, we add the counts from our three cases. The total number of arrays is 24 + 16 + 2 = 42. The answer is (D).

DPatrick 2010-02-25 19:43:20
The other main solution method that I know of is to start with the fact that the middle square must be a 4,5 or 6. (It's kind of the opposite of what we did.) The amount of work to do it this way is about the same. I'll leave it for you to work out on your own.

DPatrick 2010-02-25 19:43:43
(...when I say "start", I mean after putting the 1 and 9 in their corners.)

DPatrick 2010-02-25 19:44:14
Let's continue on with #24 on the AMC 10B, which was also #19 on the 12B:

DPatrick 2010-02-25 19:44:21

HydraPyros 2010-02-25 19:44:51
Brute force all the geometric sequences (with integer common ratios) that have the first four terms adding up to less than 100.

carmelninja 2010-02-25 19:44:51
trial - and - error?

DPatrick 2010-02-25 19:45:16
Certainly one viable approach is to brute force and/or "guess and check" some numbers, since the fact that the totals are less than 100 severely limits the possibilities.

DPatrick 2010-02-25 19:45:26
However, I will present a somewhat more systematic approach.

DPatrick 2010-02-25 19:45:47
We can set things up by defining variables.

mathcountsloser 2010-02-25 19:46:00
x,kx,k^2x, and k^3x as the geometric sequence

mathcountsloser 2010-02-25 19:46:00
x, x+y, x+2y, x+3y

RoFlLoLcOpT 2010-02-25 19:46:00

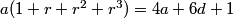
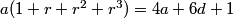
DPatrick 2010-02-25 19:46:27
That's the right idea. Let me use RoF...'s notation since it's a little more common with these sorts of sequences (r stands for "ratio" and d stands for "difference")

DPatrick 2010-02-25 19:46:39
We let the points scored by the Raiders in each quarter be a, ar, ar^2, and ar^3, and let the points scored by the Wildcats be a, a + d, a + 2d, and a + 3d.

DPatrick 2010-02-25 19:47:02

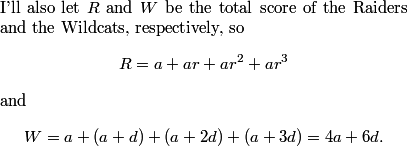
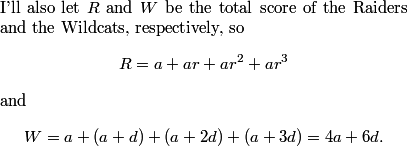
DPatrick 2010-02-25 19:47:15

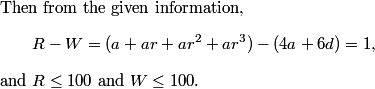
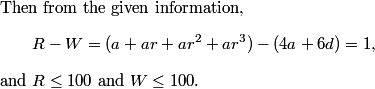
DPatrick 2010-02-25 19:47:40
What do we know about r and d?

PowerOfPi 2010-02-25 19:48:14
d is an integer and ar^3 is an integer

yunhua98 2010-02-25 19:48:14
they are greater than one

rpond 2010-02-25 19:48:14
d has to be an integer, r.............. at least rational

DPatrick 2010-02-25 19:48:19
Since the arithmetic sequence is increasing, d is a positive integer.

DPatrick 2010-02-25 19:48:25
Since the geometric sequence is increasing, r > 1.

DPatrick 2010-02-25 19:48:55
However, we don't immediately know that r is an integer! For example, the common ratio of the geometric sequence 8, 12, 18, 27 is 3/2, and this is a possibility we have to consider.

DPatrick 2010-02-25 19:49:38
We can let r = m/n, where m and n are relatively prime positive integers, and m > n.

PowerOfPi 2010-02-25 19:50:06
a is divisble by n^3

DPatrick 2010-02-25 19:50:28

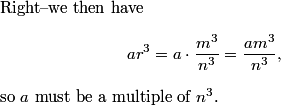
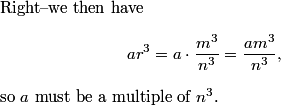
DPatrick 2010-02-25 19:51:05

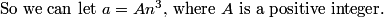
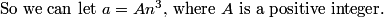
DPatrick 2010-02-25 19:51:27

DPatrick 2010-02-25 19:51:39

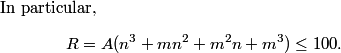
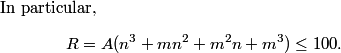
DPatrick 2010-02-25 19:52:10
Give the above inequality, what are the possible values of m and/or n? Can we find some bounds?

HydraPyros 2010-02-25 19:52:51
n must definitely be less than 5

ksun48 2010-02-25 19:53:03
n<=4

DPatrick 2010-02-25 19:53:20
Indeed, we must have both m and n less than 5 (since 5^3 is already too big).

chengpeng123 2010-02-25 19:53:25
n <= 3

DPatrick 2010-02-25 19:53:45
Since 5 > m > n, this already restricts n to 1, 2, or 3. But n=3 forces m=4, which is too big.

DPatrick 2010-02-25 19:54:10
The only possibilites are n=1, m=2, 3, or 4; and n=2, m=3.

DPatrick 2010-02-25 19:54:58
It's now relatively easy to check these cases individually. If you get lucky, you might first check the case that actually works, but for the purposes of this Math Jam, I will force us to be unlucky. :(

DPatrick 2010-02-25 19:55:19
Let me first recall the facts.

DPatrick 2010-02-25 19:55:29
\[R = A(n^3 + mn^2 + m^2 n + m^3) \le 100\]

DPatrick 2010-02-25 19:55:32
oops, my bad.

DPatrick 2010-02-25 19:55:45

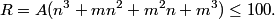
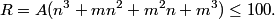
DPatrick 2010-02-25 19:56:11

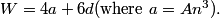
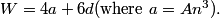
DPatrick 2010-02-25 19:56:27
And R,W are both at most 100 with R - W = 1.

DPatrick 2010-02-25 19:56:44
Now we'll run through the cases.

DPatrick 2010-02-25 19:56:53
Case 1: m = 4 and n = 1. Then R = 85A. What are the possible values of A?

mathcountsloser 2010-02-25 19:57:04
1.

Thunder365 2010-02-25 19:57:04
1

carmelninja 2010-02-25 19:57:04
1

DPatrick 2010-02-25 19:57:20
Clearly, since 85A <= 100 and A is a positive integer, we need A = 1, so R = 85.

DPatrick 2010-02-25 19:57:27
This makes W = R-1 = 84.

DPatrick 2010-02-25 19:57:31
Why is this impossible?

happymath 2010-02-25 19:57:52
80 isnt divisible by 6

DPatrick 2010-02-25 19:58:17
Right. W = 4a + 6d, and we know a = An^3 = (1)(1^3) = 1, so we need 6d = 80. But 80 isn't a multiple of 6.

DPatrick 2010-02-25 19:58:21
This case doesn't work.

DPatrick 2010-02-25 19:58:35
Case 2: m = 3 and n = 2. Then R = 65A. What are the possible values of A?

prezcoin 2010-02-25 19:58:47
A=1 again

Thunder365 2010-02-25 19:58:47
still 1

DPatrick 2010-02-25 19:59:12
Again, we have 65A <= 1, so A = 1.

DPatrick 2010-02-25 19:59:30
And a = An^3 = (1)(2^3) = 8.

DPatrick 2010-02-25 19:59:41
So W = 4a + 6d = 32 + 6d.

DPatrick 2010-02-25 19:59:47
...which must equal 65 - 1 = 64.

DPatrick 2010-02-25 20:00:16
(The most confusing part of this problem is just keeping track of all the different numbers. It's a bit hard to do "linearly" like in this transcript; it's actually much easier on a sheet of paper.)

chengpeng123 2010-02-25 20:00:24
which is impossible, 64 is not divisible by 6

pumpkinpi 2010-02-25 20:00:24
except that 64-32=32 isn't a multiple of 6

carmelninja 2010-02-25 20:00:24
which means 32 = 6d --> not possible

DPatrick 2010-02-25 20:00:43
Yep, we have the same problem as in the previous case: we need 32 = 6d, but 32 is not a multiple of 6. :(

DPatrick 2010-02-25 20:00:51
Case 3: m = 3 and n = 1. Then R = 40A.

sreyesh 2010-02-25 20:01:09
A = 1 or A=2

joshim5 2010-02-25 20:01:09
A=1,2

carmelninja 2010-02-25 20:01:09
A = 1,2

BarbieRocks 2010-02-25 20:01:09
A=1 or 2

letsruletheworldtogether 2010-02-25 20:01:09
A=1 or2

DPatrick 2010-02-25 20:01:28
We can have A = 1 or A = 2 now, but there's actually an easier way to quickly dispose of this case.

carmelninja 2010-02-25 20:01:42
not possible, since R must be odd

stargroup 2010-02-25 20:01:42
40A = 40a = 4a + 6d + 1

DPatrick 2010-02-25 20:02:05
Right. Since W = 4a + 6d in all the cases, we know W is even. And since R - W = 1, we know that R must be odd. But 40A is not odd. :(

letsruletheworldtogether 2010-02-25 20:02:22
last case!

DPatrick 2010-02-25 20:02:25
It had better work!

DPatrick 2010-02-25 20:02:30
Case 4: m = 2 and n = 1. Then R = 15A.

DPatrick 2010-02-25 20:02:52
Now it's essentially guess-and-check time.

rpond 2010-02-25 20:02:58
we can eliminate A = 2, 4, and 6 instantly

DPatrick 2010-02-25 20:03:14
Indeed, again we know that R must always be odd, so A = 1, 3, or 5 are the only possibilites.

DPatrick 2010-02-25 20:03:38
And using W = 4A + 6d = 15A - 1 should narrow it down.

DPatrick 2010-02-25 20:03:42
11A = 6d + 1

Infrared 2010-02-25 20:03:51
a=5 works!!!

Just_Beginner 2010-02-25 20:03:52
A should be 5

DPatrick 2010-02-25 20:04:10
Right: A=5 is the only one out of {1,3,5} where 11A is one more than a multiple of 6.

DPatrick 2010-02-25 20:04:49
Plugging in the numbers (getting d=9) and tidying up, we see that the points scored by the Raiders are 5, 10, 20, 40, for a total of 75, and the points scored by the Wildcats are 5, 14, 23, 32, for a total of 74.

Just_Beginner 2010-02-25 20:05:07
add 5+10+5+14=34

DPatrick 2010-02-25 20:05:12
In particular, the total number of points scored by the two teams in the first half is 5 + 10 + 5 + 14 = 34. The answer is (E).

DPatrick 2010-02-25 20:05:43
This took a lot longer that it would take on the real contest because I was trying so hard to be ultra-systematic.

DPatrick 2010-02-25 20:05:57
An educated guess-and-check on the contest is a bit faster.

DPatrick 2010-02-25 20:06:31
Let's finish the AMC 10B with #25:

DPatrick 2010-02-25 20:06:40

DPatrick 2010-02-25 20:06:54
This was also #21 on the AMC 12B.

DPatrick 2010-02-25 20:07:40
It's easiest to work with polynomials if we know their roots. The given information does not tell us about the roots of P(x). But can we construct a polynomial based on P(x) where we can work with the roots and factors?

stargroup 2010-02-25 20:08:03
P(x) - a has roots 1,3,5, and 7

mgao 2010-02-25 20:08:04
We know that P(x) -a = (x-1)(x-3)(x-5)(x-7)Q(x) for some polynomial w/integer coefficients Q(x).

Infrared 2010-02-25 20:08:04
consider P(x)+a and P(x)-a

rpond 2010-02-25 20:08:04
P(x)-a has zeroes at x = 1, 3, 5 and 7

DPatrick 2010-02-25 20:08:24
Right: we don't know the roots of P(x), but we do know many roots of P(x) - a, so let's consider the polynomial P(x) - a.

DPatrick 2010-02-25 20:08:43
(We could just as easily do P(x) + a, but the roots are slightly smaller in P(x) - a).

DPatrick 2010-02-25 20:08:55
For example, taking x = 1, we see P(1) - a = a - a = 0, so by the Factor Theorem, the polynomial P(x) - a has x - 1 as a factor.

DPatrick 2010-02-25 20:09:05
Similarly, taking x = 3, 5, and 7, we see that the polynomial P(x) - a has x - 3, x - 5, and x - 7 as factors.

DPatrick 2010-02-25 20:09:13

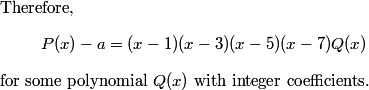
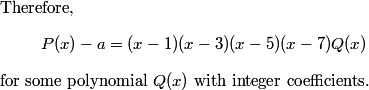
DPatrick 2010-02-25 20:09:24
Now what can we do?

Just_Beginner 2010-02-25 20:09:46
do the same with P(x)+a?

GoldenFrog1618 2010-02-25 20:09:46
make a similar one for P(x)+a

andre4177 2010-02-25 20:09:46
do the same with P(x) + a

DPatrick 2010-02-25 20:10:12
We can try that, but I'd rather continue to work with this one first and get as much out of it before we start with a new polynomial.

rpond 2010-02-25 20:10:22
see what P(2), P(4), etc equals

mgao 2010-02-25 20:10:22
substitute 2,4,6,8

cool 2010-02-25 20:10:22
plug in 2, 4, 6, 8

DPatrick 2010-02-25 20:10:42
Sure, let's plug in 2,4,6,8 to this polynomial that we have, and see what happens.

DPatrick 2010-02-25 20:11:12

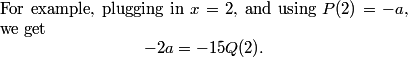
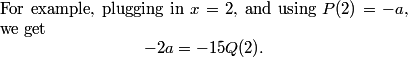
DPatrick 2010-02-25 20:11:42
(I popped P(x) - a up to the top of the window so we can keep track of it.)

stargroup 2010-02-25 20:11:51
-2a = -15Q(2) = 9Q(4) = -15Q(6) = 105Q(8)

cool 2010-02-25 20:11:51
-2a = -15Q(2) = 9Q(4) = -15Q(6) = 105Q(8)

DPatrick 2010-02-25 20:12:14
Right, we do the same thing for x=4,6,8. We always get -2a on the left side, and some multiple of some Q on the right side.

DPatrick 2010-02-25 20:12:35

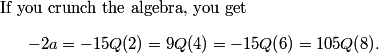
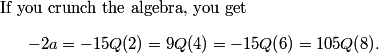
DPatrick 2010-02-25 20:12:44
What do these equations tell us about a?

Just_Beginner 2010-02-25 20:13:14
a has to be a multiple off 15, 9, 15, and 105 since there integers

BarbieRocks 2010-02-25 20:13:14
divisible by 15, 9, 105

aerrowfinn72 2010-02-25 20:13:14
multiple of 315

PhireKaLk6781 2010-02-25 20:13:14
divisible by 15,9,105

pumpkinpi 2010-02-25 20:13:14
multiple of 9, 15, 105

DPatrick 2010-02-25 20:13:26
Since everything in sight is an integer, the equations tell us that a is divisible by 9, 15, and 105.

DPatrick 2010-02-25 20:13:32
Therefore, a is divisible by lcm(9,15,105) = 315.

DPatrick 2010-02-25 20:13:43
Sadly, this only eliminates choice (A). All the other choices are divisible by 315.

DPatrick 2010-02-25 20:13:51
So we press on.

DPatrick 2010-02-25 20:14:43

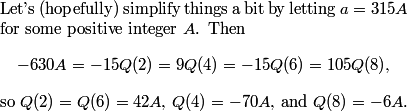
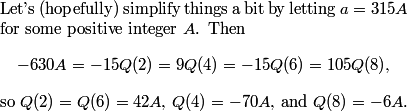
DPatrick 2010-02-25 20:15:17
What bit of data here lots most promising to work with next?

DPatrick 2010-02-25 20:15:23
...looks (not lots)...

prezcoin 2010-02-25 20:15:39
Q(2)=Q(6)

BarbieRocks 2010-02-25 20:15:39
Q(2) and Q(6)?

turak 2010-02-25 20:15:39
Q(2)=Q(6)

v_Enhance 2010-02-25 20:15:39

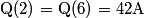
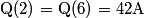
DPatrick 2010-02-25 20:15:44
Let's work with the equation Q(2) = Q(6) = 42A, since we have two equal Q-values.

DPatrick 2010-02-25 20:15:49
What should we do with it?

stargroup 2010-02-25 20:16:01
Q(x) - 42A = (x-2)(x-6)R(x)

rpond 2010-02-25 20:16:05
Q(x) - 42A = (x-2)(x-6)R(x)?

DPatrick 2010-02-25 20:16:20
Right, we can do the same thing we did at the start! We know two roots of Q(x) - 42A, so let's work with that.

DPatrick 2010-02-25 20:16:27

prezcoin 2010-02-25 20:17:00
plug in values?

rpond 2010-02-25 20:17:00
now plug in x = 4 and x = 8

v_Enhance 2010-02-25 20:17:00
Plug in Q(4) = -70A and Q(8) = -6A

DPatrick 2010-02-25 20:17:03
We've got x=4 and x=8 left over, so let's plug them in.

DPatrick 2010-02-25 20:17:10
Taking x = 4, we get -112A = -4R(4), so R(4) = 28A. Taking x = 8, we get -48A = 12R(8), so R(8) = -4A.

DPatrick 2010-02-25 20:17:36
Let's stop and recap. First, as long as R(x) satisfies R(4) = 28A and R(8) = -4A, then we can reverse all our steps, and all the given equations are satisfied. Second, we want A to be as small as possible.

DPatrick 2010-02-25 20:18:00
At this point, we can try to have A=1.

DPatrick 2010-02-25 20:18:06
Does there exist a polynomial R(x) with integer coefficients such that R(4) = 28 and R(8) = -4?

trigfan 2010-02-25 20:18:44
linear equation

BarbieRocks 2010-02-25 20:18:50
-8x+60

DPatrick 2010-02-25 20:18:54
Yes, namely R(x) = -8x + 60.

DPatrick 2010-02-25 20:19:10
(One way to see this is that the slope from (4,28) to (8,-4) is -8, and work from there.)

DPatrick 2010-02-25 20:19:29
So we're done! We can use A=1, R(x) = -8x +60, and work backwards to get our original P(x).

DPatrick 2010-02-25 20:19:48
Note you don't actually have to do this, you just need to know that it can be done.

EricMathPath09 2010-02-25 20:19:57
So the answer is 315?

Just_Beginner 2010-02-25 20:19:57
a would equal 315

DPatrick 2010-02-25 20:20:06
Therefore, since a = 315A, the smallest possible value of a is 315. The answer is (B).

DPatrick 2010-02-25 20:20:21
This was a hard problem, but an interesting one in my opinion.

DPatrick 2010-02-25 20:20:43
Let's take a 4-minute break so I can rest my fingers. :) We'll resume at 8:25 Eastern / 5:25 Pacific.

DPatrick 2010-02-25 20:24:38
Before we resume, let me say that I think a somewhat legitimate complaint that one could have about the AMC 10B is that 23 and 24 in particular (and 25 to a lesser extent) were very computational or casework-y problems that take some time to do.

DPatrick 2010-02-25 20:25:01
I actually think that 22-25 on the 12B (that we're about to do) by and large don't take as long, although they are harder for sure.

DPatrick 2010-02-25 20:25:41
Anyway, on to the AMC 12B! We already did #21 (which was #25 from the 10B that we just did), so let's continue with #22:

DPatrick 2010-02-25 20:25:48

DPatrick 2010-02-25 20:26:02

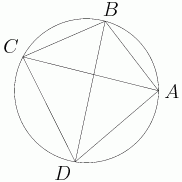
mgao 2010-02-25 20:26:16
we think of ptolemys

DPatrick 2010-02-25 20:26:28
Certainly. We have some information about the sides, and we want to know something about a diagonal. We do have a tool to relate the diagonals of a cyclic quadrilateral to its sides: Ptolemy's Theorem, which tells us that in cyclic quadrilateral ABCD, we have (AC)(BD) = (AD)(BC) + (AB)(CD)

DPatrick 2010-02-25 20:26:55
The only other information we have relates to the product of consecutive sides. Where in geometry have we seen the product of consecutive sides of a polygon?

Sasarai 2010-02-25 20:27:33
Cosine Law?

nikeballa96 2010-02-25 20:27:34
doesn't relate to what you said, but cosine law?

DPatrick 2010-02-25 20:28:01
True, but going down the trig road might get icky.

DPatrick 2010-02-25 20:28:12
Anything a bit simpler?

DPatrick 2010-02-25 20:28:34
Especially something that related to a circumcircle might help, since we happen to have a circumcircle available.

tenniskidperson3 2010-02-25 20:28:50
area maybe.

stargroup 2010-02-25 20:28:50
areas?

cool 2010-02-25 20:28:50
er this is what i did, but its still sort of complicated: AB*BC*AC/4R and likewise for the others are the areas

DPatrick 2010-02-25 20:29:15
It's is a bit complicated, but an uncomplicating factor is that all the R's are equal.

DPatrick 2010-02-25 20:29:32
First, let me explain for those who might not have seen this before: there are area formulas that involve the product of adjacent sides of a triangle. Specifically, for any triangle XYZ, we have [XYZ] = (1/2)(XY)(YZ)(sin Y), where [XYZ] denotes the area of XYZ. We also have [XYZ] = (XY)(YZ)(ZX) / 4R, where R is the circumradius of triangle XYZ.

DPatrick 2010-02-25 20:30:03
(The last step is just writing the sine in terms of the third side and the radius, using the Law of Sines.)

DPatrick 2010-02-25 20:30:23
The last area formula is particularly appealing because we might be able to make use of the fact that all four triangles with vertices among A,B,C, and D have the same circumcircle.

DPatrick 2010-02-25 20:30:44
Let me write them all out, repost the diagram, and we can stop and think about what to do next.

DPatrick 2010-02-25 20:30:51

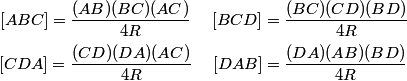
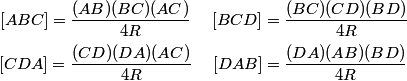
DPatrick 2010-02-25 20:30:55

DPatrick 2010-02-25 20:31:18
What can we do with these?

tenniskidperson3 2010-02-25 20:31:46
The sum of two of them is the sum of the other two.

bbgun34 2010-02-25 20:31:46
add them

tenniskidperson3 2010-02-25 20:31:46
So we add them.

DPatrick 2010-02-25 20:31:51
Aha!

DPatrick 2010-02-25 20:32:01
These four equations give us another equation that relates the sides and the diagonals of the quadrilateral. Since [ABC] + [CDA] = [BCD] + [DAB] (both equal [ABCD], we have:

DPatrick 2010-02-25 20:32:06

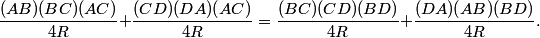
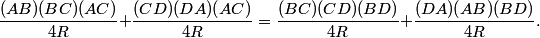
DPatrick 2010-02-25 20:32:29
We can clean this up a bit by multiplying by 4R and by letting a,b,c,d be the sides AB, BC, CD, DA, respectively. Then, we have AC(ab + cd) = BD(bc + ad)

DPatrick 2010-02-25 20:32:59
And rewriting Ptolemy's Equation in this notation gives (AC)(BD) = ac+bd as well.

DPatrick 2010-02-25 20:33:09
What now?

sparkle123 2010-02-25 20:33:24
given bc=ad

mgao 2010-02-25 20:33:24
use bc=ad

DPatrick 2010-02-25 20:33:46
We're given that, but I have a slight preference for doing something else first.

Sasarai 2010-02-25 20:34:02
Isolate for BD?

DPatrick 2010-02-25 20:34:37
That's what I would do next (though it probably doesn't make much difference). We want to solve for BD eventually, so let's use our area equation at Ptolemy's to eliminate AC in favor of BD.

DPatrick 2010-02-25 20:34:47

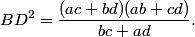
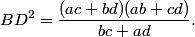
DPatrick 2010-02-25 20:35:06
(Convenient: now we have BD^2, and since all the answers are square roots, this is probably useful!)

DPatrick 2010-02-25 20:35:37
Now we can let ad = bc = t, and substitute into our expression for BD^2. When we multiply out the numerator, wonderful things happen: (I'll breeze through the algebra to save time.)

DPatrick 2010-02-25 20:35:48

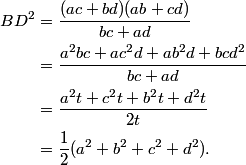
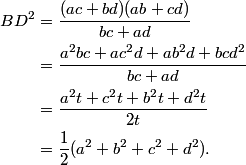
DPatrick 2010-02-25 20:36:09
(Of course, you don't really need "t", it just makes it clearer what's going on.)

DPatrick 2010-02-25 20:36:14
Cool, eh?

DPatrick 2010-02-25 20:36:24
Now our geometry problem is essentially a number game. We need to maximize the sum of the squares of the sides of the quadrilateral.

DPatrick 2010-02-25 20:36:52
Since each side is a distinct integer less than 15, is the maximum sum of squares simply 11^2 + 12^2 + 13^2 + 14^2?

Infrared 2010-02-25 20:37:02
14*6 and 12*7

carmelninja 2010-02-25 20:37:04
but products

DPatrick 2010-02-25 20:37:18
Right, we still have the ad = bc condition to satisfy.

DPatrick 2010-02-25 20:37:25
It tells us that we can't use 11 or 13; since we can't have a factor of either on both sides.

DPatrick 2010-02-25 20:37:38
However, we're fine with 14 and 12, though, since we can let the other two sides be 6 and 7, and we have (6)(14) = (12)(7). That's nice.

DPatrick 2010-02-25 20:38:16
It should also be clear we can't do any better: for example, having 10 forces us to have 5, and 10 and 5 are smaller than what we have.

DPatrick 2010-02-25 20:38:35
So, our maximal sum of squares is 14^2 + 12^2 + 7^2 + 6^2 = 425.

DPatrick 2010-02-25 20:39:15

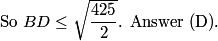
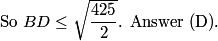
DPatrick 2010-02-25 20:39:38
This was a pretty problem, and quite challenging!

DPatrick 2010-02-25 20:39:59
Let's move on to #23 on the AMC 12B:

DPatrick 2010-02-25 20:40:05

toadsnfrogs 2010-02-25 20:40:20
what does monic mean?

DPatrick 2010-02-25 20:40:37
Good question: it means of the form x^2 + bx + c, where the coefficient of x^2 is 1.

DPatrick 2010-02-25 20:40:53
(You weren't the only one with that question!)

DPatrick 2010-02-25 20:41:16
But a big mistake would be writing P and Q in those forms and diving in to calculations.

DPatrick 2010-02-25 20:41:21
Instead, first stop and think for a moment.

DPatrick 2010-02-25 20:41:32
What does the fact that P(Q(x))'s zeros are -23, -21, -17, and -15 tell us about P or Q?

moplam 2010-02-25 20:42:05
Q(-23)=Q(-15), Q(-21)=Q(-17)??

DPatrick 2010-02-25 20:42:09
Exactly.

DPatrick 2010-02-25 20:42:21
P(x) only has two zeros. So Q(-23), Q(-21), Q(-17) and Q(-15) can only be two different values.

DPatrick 2010-02-25 20:43:01
Further, thinking about what the graph of a quadratic (a parabola) looks like, we must have Q(-23) = Q(-15) and Q(-21) = Q(-17). (Think about it some more on your own if you don't see what this must be the case. Maybe draw yourself a picture or two.)

DPatrick 2010-02-25 20:43:24
And most important, this means that the vertex of Q (the low point of the parabola) is at x = -19: the point halfway between the corresponding pairs of values.

DPatrick 2010-02-25 20:43:39
So what's the best way to write an expression for Q(x)?

rpond 2010-02-25 20:44:13
Q(x) = (x+19)^2-a

karatemagic7 2010-02-25 20:44:13
(x+19)^2+c

DPatrick 2010-02-25 20:44:30
Exactly. I would tweak it a little and write Q(x) = (x+19)^2 - q^2, where q > 0 is some unknown number.

DPatrick 2010-02-25 20:44:47
Note that I wrote it q^2 instead of q, so that the zeros of Q become q-19 and -q-19. No messy square roots to deal with.

DPatrick 2010-02-25 20:45:13
Using the same analysis on the other set of zeros, we can write P(x) = (x+54)^2 - p^2, where p > 0 is some unknown number, and its roots are p-54 and -p-54.

DPatrick 2010-02-25 20:45:34
Now what?

carmelninja 2010-02-25 20:46:17
find p^2 + q^2

DPatrick 2010-02-25 20:46:49
It's good to keep our eye on the goal: we want -(p^2 + q^2). This probably (but not necessarily) means trying to solve for p and q.

DPatrick 2010-02-25 20:47:08
What do we know about the roots of P and Q?

DPatrick 2010-02-25 20:47:16
Let's focus on P first. What are its roots?

Rocket95 2010-02-25 20:47:51
p-54, -p-54

Infrared 2010-02-25 20:47:51
Q(-23), -21

carmelninja 2010-02-25 20:47:51
p-54 and -p-54

bbgun34 2010-02-25 20:47:51
p-54 and -p-54

karatemagic7 2010-02-25 20:47:51
Q(-23) and Q(-21)

DPatrick 2010-02-25 20:48:09
You're all right, and the two different ways you wrote the roots of P are the key to finishing.

DPatrick 2010-02-25 20:48:17
On the one hand, the roots of P are p-54 and -p-54.

DPatrick 2010-02-25 20:48:43
On the other hand, so are Q(-21) and Q(-23), and we can compute: Q(-21) = (-21+19)^2 - q^2 = 4 - q^2 Q(-23) = (-23+19)^2 - q^2 = 16 - q^2

DPatrick 2010-02-25 20:49:03
How can we use this data to solve for p?

karatemagic7 2010-02-25 20:49:39
Subtracting the Two equations gives that 2p=12, p=6

DPatrick 2010-02-25 20:49:53
Bingo. The difference in the roots are 2p (on the one hand) and 12 (on the other hand).

DPatrick 2010-02-25 20:49:59
So 2p = 12, and p = 6.

theone142857 2010-02-25 20:50:15
Same for Q

DPatrick 2010-02-25 20:50:25
Right, we just repeat essentially the same process on the roots on Q.

DPatrick 2010-02-25 20:50:33
P(-51) is one root of Q, and P(-49) is the other root, and they differ by 2q.

DPatrick 2010-02-25 20:50:43
P(-51) = (-51+54)^2 - p^2 = 9 - p^2 P(-49) = (-49+54)^2 - p^2 = 25 - p^2

DPatrick 2010-02-25 20:51:03
So 16 = 2q, hence q = 8.

DPatrick 2010-02-25 20:51:12
And to finish, we get -(p^2 + q^2) = -(36 +64) = -100. Answer (A).

DPatrick 2010-02-25 20:51:48
This problem mainly required a good knowledge of how quadratics behave, and the different ways to think about them. Writing a quadratic in the form (x-h)^2 - k^2 is often very handy!

DPatrick 2010-02-25 20:51:59
Let's move on to #24:

DPatrick 2010-02-25 20:52:05

DPatrick 2010-02-25 20:52:45
Those numbers look ugly.

theone142857 2010-02-25 20:52:55
y=x-2010:whistle:?

GoldenFrog1618 2010-02-25 20:52:55
substitute x=a+2010

monkeythyme 2010-02-25 20:52:55
substitute k = x-2010?

theone142857 2010-02-25 20:52:55
Symmetry

DPatrick 2010-02-25 20:53:16
Right. Before doing anything else, we should note that we can add or subtract anything to x and it doesn't change the answer.

DPatrick 2010-02-25 20:53:43
To be more precise, let f(x) equal that function on the left side of the inequality. If, instead of finding where f(x) >= 1, we instead translate the function and find where f(x+c) >= 1 for any c we choose, does it change the answer? No!

DPatrick 2010-02-25 20:53:53
Think of the graph of f(x). We can slide this graph left and right as much as we want, as long as we don't slide it up or down and don't distort the scale. The size of the region where f >= 1 won't change: it'll just slide left and right too.

DPatrick 2010-02-25 20:54:21
I would use c = 2010. That will make our function nice and symmetric.

DPatrick 2010-02-25 20:54:32

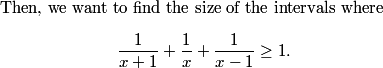
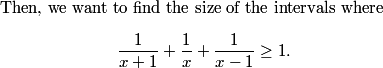
DPatrick 2010-02-25 20:54:47
It looks way, way nicer now!

rpond 2010-02-25 20:55:01
now multiply by (x+1)x(x-1)

toadsnfrogs 2010-02-25 20:55:01
common denomonator

DPatrick 2010-02-25 20:55:14
Yes, now I would write the left side as a single fraction.

DPatrick 2010-02-25 20:55:25

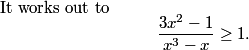
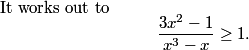
DPatrick 2010-02-25 20:56:13
A huge mistake at this point would be to multiply by x^3 - x to get 3x^2 - 1 >= x^3 - x.

DPatrick 2010-02-25 20:56:30
The denominator might be negative! (Of course, the numerator would have to be negative too for the fraction to be >= 1.)

DPatrick 2010-02-25 20:56:52
So we have two cases. One case is 3x^2 - 1 > x^3 - x > 0. The other case is 3x^2 - 1 < x^3 - x < 0. (Note it doesn't matter if we use < or <= since we only want the lengths of the intervals so the endpoints don't matter.)

DPatrick 2010-02-25 20:57:25
Now, at this stage, you can do a lot of algebra and make yourself unhappy, or you can do something that will make your life easier.

spelljack825 2010-02-25 20:57:41
draw a sketch!

DPatrick 2010-02-25 20:57:46
Absolutely.

DPatrick 2010-02-25 20:58:03
Let's sketch a quick graph of these two functions. They're both relatively easy to graph. Note that x^3 - x has roots at -1, 0, and 1, and that 3x^2 - 1 has roots at -1/sqrt(3) and 1/sqrt(3).

DPatrick 2010-02-25 20:58:09

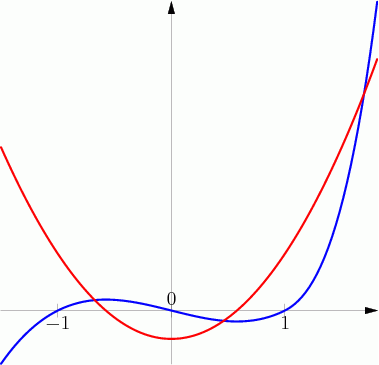
DPatrick 2010-02-25 20:58:30
The cubic x^3-x is blue and the parabola 3x^2 - 1 is red. I have distorted the cubic a bit when x>1 to make the picture scale nicer, but I haven't affected the general shape of the graphs. Your sketch doesn't need to be super-accurate to finish the problem.

DPatrick 2010-02-25 20:58:51
We need both the parabola and the cubic to be the same sign. If they are positive, we need the parabola above the cubic (that is, red above blue above the x-axis). If they are negative, we need the parabola below the cubic (that is, red below blue below the y-axis).

DPatrick 2010-02-25 20:59:19
So let me indicate the regions in the picture that we want:

DPatrick 2010-02-25 20:59:27

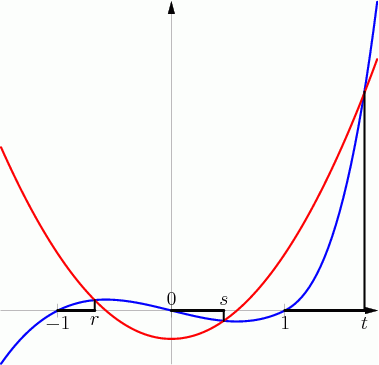
DPatrick 2010-02-25 20:59:50
I have labeled the points r,s,t where the graphs intersect.

theone142857 2010-02-25 20:59:55
:whistle:add them up

DPatrick 2010-02-25 21:00:12
Indeed, the intervals that work are (-1,r), (0,s), and (1,t). I add their lengths up, and the total length is (r+1) + s + (t-1) = r+s+t.

monkeythyme 2010-02-25 21:00:20
omg vietas

spelljack825 2010-02-25 21:00:20
vieta's!

DPatrick 2010-02-25 21:00:26
Ding ding ding!

DPatrick 2010-02-25 21:00:56
What are r, s, and t? They are where the graphs intersect, so they are where x^3 - x = 3x^2 - 1. Thus, they are the roots of the cubic x^3 - 3x^2 - x + 1.

DPatrick 2010-02-25 21:01:13
But by Vieta's Formulas, we know that the sum of the roots is r+s+t = 3.

MathTwo 2010-02-25 21:01:18
then 3 (c) is our answer

DPatrick 2010-02-25 21:01:24
So the answer is 3. Answer (C).

DPatrick 2010-02-25 21:01:35
They say that a picture is worth a thousand words. In this problem, a picture was worth a lot of messy algebra. :)

sparkle123 2010-02-25 21:01:45
how did they get the other answer choices?

DPatrick 2010-02-25 21:01:57
I think they may come up if you miss an interval...I'm not sure.

Thunder365 2010-02-25 21:02:02
And now #25....

DPatrick 2010-02-25 21:02:16

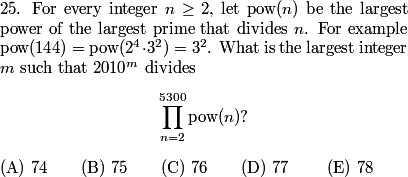
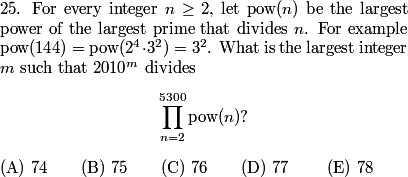
ProbaBillity 2010-02-25 21:02:53
what is that pi-shaped thing?

DPatrick 2010-02-25 21:03:05
It's a product. So the expression is pow(2) * pow(3) * pow(4) * ... * pow(5300).

DPatrick 2010-02-25 21:03:18
Where should we start?

v_Enhance 2010-02-25 21:03:28
Uh... start by factoring 2010 = 2*3*5*67?

stargroup 2010-02-25 21:03:28
2010 = 2*3*5*67

rpond 2010-02-25 21:03:31
we should start with factoring 2010

DPatrick 2010-02-25 21:03:39
The prime factorization of 2010 = 2 * 3 * 5 * 67 will almost certainly be necessary.

DPatrick 2010-02-25 21:03:52
We need to count the powers of 2, 3, 5, and 67 in the product of pow's, and whichever power appears the least will be our answer.

prezcoin 2010-02-25 21:04:03
focus on 67

Infrared 2010-02-25 21:04:04
we only need to worry about 67

DPatrick 2010-02-25 21:04:30
If you were pressed for time and wanted to gamble, you could assume that, but it is not at all obvious that this is the case, and I'm sure I could construct examples where it doesn't work.

DPatrick 2010-02-25 21:05:10
There is no reason to except that any one of 2, 3, 5, or 67 automatically has the smallest number of powers in the product of pow's. I'd check them all.

DPatrick 2010-02-25 21:05:29
Let's start with 2 because it's the easiest.

DPatrick 2010-02-25 21:05:46
We get pow(n) equal to a power of 2 if and only if n has no larger primes, so n must be a power of 2.

carmelninja 2010-02-25 21:06:04
1+...+12

mgao 2010-02-25 21:06:04
1+2+...+12 = 78

rpond 2010-02-25 21:06:09
the largest power of 2 below 5300 is 2^12 = 4096

DPatrick 2010-02-25 21:06:19
Since 2^12 < 5300 < 2^13, the first 12 powers of 2 are in the product.

DPatrick 2010-02-25 21:06:27
Thus, there are 1+2+3+...+12 = 6(13) = 78 powers of 2 in the product.

DPatrick 2010-02-25 21:06:40
(Too bad, if this had come out to 74, we'd be done. :( )

DPatrick 2010-02-25 21:06:47
Sadly, this doesn't rule out any answers.

DPatrick 2010-02-25 21:07:01
Let's try the other end. How many powers of 67 in the product?

rpond 2010-02-25 21:07:25
well, there are 79 multiples of 67

-$45! 2010-02-25 21:07:30
all multiples of 67 that don't have a larger prime

DPatrick 2010-02-25 21:07:35
Right. 79 * 67 < 5300 < 80 * 67, so there are 79 multiples of 67.

DPatrick 2010-02-25 21:07:42
We get a power of 67 for pow(n) whenever n is a multiple of 67 and has no larger prime factors.

-$45! 2010-02-25 21:07:51
so rule out 71, 73, and 79

spelljack825 2010-02-25 21:07:51
71, 73, 79 are primes

DPatrick 2010-02-25 21:08:06
Right: of the multiples of 67, we only have to rule out three: 71*67, 73*67, and 79*67.

DPatrick 2010-02-25 21:08:30
So that's 79 - 3 - 76 multiples of 67 that will contribute a 67 to the product of pow's...

karatemagic7 2010-02-25 21:08:36
67^2 adds an extra 67.

pirox 2010-02-25 21:08:36
67^2 is 2

stargroup 2010-02-25 21:08:36
67^2 has a power of 2, which we need to account for :D

moplam 2010-02-25 21:08:36
but we need to remember 67^2

DPatrick 2010-02-25 21:08:50
...and 67^2 will contribute an extra one, and that's the only extra.

DPatrick 2010-02-25 21:09:04
So that gives 76 + 1 = 77 powers of 67 in the product.

DPatrick 2010-02-25 21:09:12
Thus m <= 77. This rules out (E).

DPatrick 2010-02-25 21:09:34
Again, if you wanted to gamble, you could assume 3 and 5 have more powers, and go with answer (D).

DPatrick 2010-02-25 21:09:46
Let's continue checking though.

DPatrick 2010-02-25 21:09:53
How can we count powers of 3 in the product?

DPatrick 2010-02-25 21:10:04
Anything of the form 2^a * 3^b (with a >= 0 and b > 0) will give a power of 3.

DPatrick 2010-02-25 21:10:22
...so this is slightly more complicated.

DPatrick 2010-02-25 21:10:40
Let's start at the bottom. How many are there with a single power of 3?

karatemagic7 2010-02-25 21:11:04
10

ChickenSpeed 2010-02-25 21:11:04
12

DPatrick 2010-02-25 21:11:10
You've got it surrounded... :)

DPatrick 2010-02-25 21:11:18
(sorry, I couldn't resist)

DPatrick 2010-02-25 21:11:22
2^10 * 3 < 5300 < 2^11 * 3, so there are 11 with a single power of 3.

DPatrick 2010-02-25 21:11:30
(3, 6, 12, ..., up to 1024*3)

DPatrick 2010-02-25 21:11:58
Similarly 2^9 * 9 < 5300 < 2^10 * 9, so there are 10 with two powers of 3.

DPatrick 2010-02-25 21:12:03
2^7 * 27 < 5300 < 2^8 * 27, so there are 8 with three powers of 3.

DPatrick 2010-02-25 21:12:24
This'll take forever...can we speed this up at all? Maybe compute a lower bound instead of the exact number?

DPatrick 2010-02-25 21:13:35
There are lots of ways you could do it (including just brute-forcing it out), but this is what I did: every time we drop a power of 3, we lose at most 2 powers of 2. (This is because 4 > 3, so 2^(a-2) * 3^(b+1) < 2^a * 3^b.)

DPatrick 2010-02-25 21:14:06
So, starting with the 11 that had one power of 3 and dropping by 2 every time we increase a power of 3, we get that the powers of 3 in the product is AT LEAST 11(1) + 9(2) + 7(3) + 5(4) + 3(5) + 1(6) = 11 + 18 + 21 + 20 + 15 + 6 = 91.

-$45! 2010-02-25 21:14:19
But how do you know when you lose 1 and when you lose 2?

DPatrick 2010-02-25 21:14:27
We don't, exactly, but that's why I have "at least".

DPatrick 2010-02-25 21:14:39
91 is way more than 77, so no worries!

stargroup 2010-02-25 21:15:02
same for powers of 5: 2^a * 3^b * 5^c

DPatrick 2010-02-25 21:15:22
We can do essentially the same thing with powers of 5.

DPatrick 2010-02-25 21:15:35
We get a power of 5 whenever we have 2^a * 3^b * 5^c, where a,b >= 0 and c > 0.

DPatrick 2010-02-25 21:15:53
If we want a single power of 5, we must have 2^a * 3^b <= 5300/5 = 1060.

DPatrick 2010-02-25 21:16:18
Since 2^10 < 1060 < 2^11, and using the above logic (adding every power of 3 subtracts at most 2 powers of 2), that's AT LEAST 11 + 9 + 7 + 5 + 3 + 1 = 36.

DPatrick 2010-02-25 21:16:35
If we have 5^2 in there, we must have 2^a * 3^b <= 5300/25 = 424.

DPatrick 2010-02-25 21:16:41
We have 2^8 < 424 < 2^9, so that AT LEAST 2(9+7+5+3+1) = 2(25) = 50 more powers of 2.

-$45! 2010-02-25 21:16:46
These will be a lot more combinations than 77\

moplam 2010-02-25 21:16:46
It is just way more than 77

DPatrick 2010-02-25 21:16:50
That's already 36 + 50 = 86 > 77, so we can stop.

DPatrick 2010-02-25 21:16:59
Our conclusion is that 67 is the limiting prime factor: the given product of pow's has exactly 77 powers of 67, and strictly more powers of 2, 3, and 5.

RiteshR 2010-02-25 21:17:09
YES!! (D)

jxl28 2010-02-25 21:17:12
so our answer is D?

-$45! 2010-02-25 21:17:12
So D is the answer

DPatrick 2010-02-25 21:17:12
Thus the answer is (D) 77.

DPatrick 2010-02-25 21:17:28
In my opinion, this was a pretty time-consuming problem to be placed at #25.

DPatrick 2010-02-25 21:18:11
Let's again take a short 4-minute break. I'm all typed-out: my colleague Naoki Sato will step in and do some problems from 16-20 on both contests.

DPatrick 2010-02-25 21:18:23
Thanks...it's been fun! Stick around for Naoki at :22 past the hour.

nsato 2010-02-25 21:22:39
Hi everyone! I'm going to do the 16-20 problems that haven't been covered already.

nsato 2010-02-25 21:22:53
We'll start with AMC10, #16.

nsato 2010-02-25 21:23:01

nsato 2010-02-25 21:23:17
How do we start?

myyellowducky82 2010-02-25 21:23:47
Draw a diagram.

ProbaBillity 2010-02-25 21:23:48
draw it

Aeroalon 2010-02-25 21:23:48
Draw a picture?

sparkle123 2010-02-25 21:23:48
diagram

MathTwo 2010-02-25 21:23:48
diagram!

Infrared 2010-02-25 21:23:48
a picture is how to start

nsato 2010-02-25 21:23:53
Since this is a geometry problem, we start with an accurate diagram.

nsato 2010-02-25 21:24:00

nsato 2010-02-25 21:24:07
What should we add to the diagram?

sparkle123 2010-02-25 21:24:41
center

pirox 2010-02-25 21:24:41
lines from the center

sparkle123 2010-02-25 21:24:41
centre

v_Enhance 2010-02-25 21:24:43
Center of circle, radii.

Aeroalon 2010-02-25 21:24:45
Draw the radii to the points of intersection of the circle and the square

ernie 2010-02-25 21:24:49
the center, intersection points, and (soon) the lines that connect them

nsato 2010-02-25 21:24:53
Let's draw radii from the center of the circle to the points where the square intersects the circle. For good measure, we also draw a line from the center to the midpoint of a side.

nsato 2010-02-25 21:24:58

nsato 2010-02-25 21:25:07
The area inside the circle but outside the square consists of four circular segments, all congruent to the circular segment highlighted above.

nsato 2010-02-25 21:25:18
How can we find the area of this circular segment?

ProbaBillity 2010-02-25 21:26:05
find the area of the sector and then subtract the area of the triangle

mathforce1 2010-02-25 21:26:07
area of sector minus area of triangle

Infrared 2010-02-25 21:26:09
find the area of the sector and subtract the triangle

sj0201 2010-02-25 21:26:09
area of a sector minus area of the triangle

myyellowducky82 2010-02-25 21:26:11
find the area of the sector, then take away the area of the triangle

nsato 2010-02-25 21:26:16
The area of this circular segment is equal to the area of the circular sector OAB (which is the whole "pie wedge"), minus the area of triangle OAB.

nsato 2010-02-25 21:26:24
Let's see what we can do with the diagram. What is OA?

Aeroalon 2010-02-25 21:26:53
sqrt{3}/3

jxl28 2010-02-25 21:26:53
sqrt(3)/3

rpond 2010-02-25 21:26:53
sqrt(3)/3

letsruletheworldtogether 2010-02-25 21:26:53
sqrt(3)/3

MathTwo 2010-02-25 21:26:53
sqrt(3)/3

sj0201 2010-02-25 21:26:53

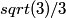
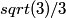
nsato 2010-02-25 21:26:58
OA is the radius of the circle, which is sqrt(3)/3.

nsato 2010-02-25 21:27:02
What is OM?

Aeroalon 2010-02-25 21:27:26
1/2: half the length of a side of the square

mathforce1 2010-02-25 21:27:26
1/2, half of square side length

-$45! 2010-02-25 21:27:34
1/2

jxl28 2010-02-25 21:27:34
1/2

sparkle123 2010-02-25 21:27:34
1/2

letsruletheworldtogether 2010-02-25 21:27:34
1/2

nsato 2010-02-25 21:27:37
OM is half the side length of the square, which is 1/2. Does this tell us anything interesting?

nsato 2010-02-25 21:27:45

Aeroalon 2010-02-25 21:28:32
Triangle OAM is a 30-60-90 right triangle

jxl28 2010-02-25 21:28:33
AOM is a 30-60-90 triangle

nsato 2010-02-25 21:28:39

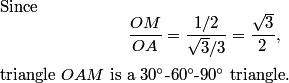
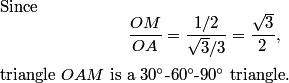
nsato 2010-02-25 21:28:50
So what is the area of triangle OAB, which is equilateral?

sparkle123 2010-02-25 21:29:31
sqrt3/12

jxl28 2010-02-25 21:29:32
sqrt(3)/12

pirox 2010-02-25 21:29:32
rt3/12

BarbieRocks 2010-02-25 21:29:32

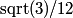
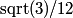
ernie 2010-02-25 21:29:32
sqrt(3)/12

Infrared 2010-02-25 21:29:32
(root3)/12

nsato 2010-02-25 21:29:35

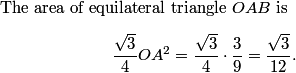
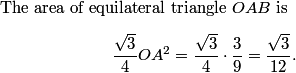
nsato 2010-02-25 21:29:39
What is the area of circular sector OAB?

jxl28 2010-02-25 21:30:23
pi/18

ernie 2010-02-25 21:30:23
pi/18

Aeroalon 2010-02-25 21:30:23
1/6 * pi/3 = pi/18

BarbieRocks 2010-02-25 21:30:23
1/6*1/3pi=pi/18

karatemagic7 2010-02-25 21:30:23
pi/18

nsato 2010-02-25 21:30:32

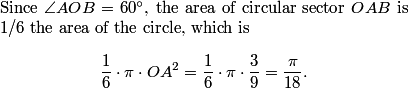
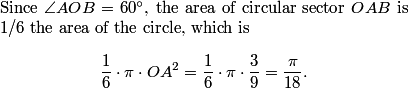
nsato 2010-02-25 21:30:40
So what is the area outside the square and inside the circle?

mathforce1 2010-02-25 21:31:11
sector minus triangle times four

pirox 2010-02-25 21:31:21
4(pi/18-rt3/12)

ernie 2010-02-25 21:31:22
$\frac{2\pi}{9} - \frac{\sqrt3}{3}$

BarbieRocks 2010-02-25 21:31:27
4(pi/18-sqrt(2)/12)=B

ProbaBillity 2010-02-25 21:31:32
so the answer is B.

ernie 2010-02-25 21:31:32
or B

letsruletheworldtogether 2010-02-25 21:31:32
so the answer is B

nsato 2010-02-25 21:31:37

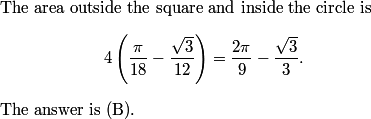
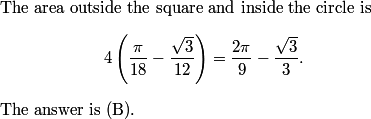
nsato 2010-02-25 21:31:52

nsato 2010-02-25 21:32:09
Since we seek the number of schools in the city, let n be this number.

nsato 2010-02-25 21:32:20
Then how many participants were there?

Just_Beginner 2010-02-25 21:32:50
there are 3n students and scoress

MathTwo 2010-02-25 21:32:50
3n participants

themehlman 2010-02-25 21:32:50
3n

Infrared 2010-02-25 21:32:50
3n

sreyesh 2010-02-25 21:32:50
3n

nsato 2010-02-25 21:32:56
Since each high school sent a team of 3 students, there were 3n participants.

nsato 2010-02-25 21:32:58
Can we say anything about 3n?

Aeroalon 2010-02-25 21:33:32
3n > 64

Just_Beginner 2010-02-25 21:33:32
it has to be greater than or equal to 64

MathTwo 2010-02-25 21:33:32
3n>64

BarbieRocks 2010-02-25 21:33:32
3n>64

nsato 2010-02-25 21:33:43
Since Carla placed 64th, 3n must be at least 64. What does this say about n?

pirox 2010-02-25 21:34:22
n>=22

ernie 2010-02-25 21:34:22
n >= 22 actually

nsato 2010-02-25 21:34:26
Since 3n >= 64 and n is a positive integer, n must be at least 22. (Actually, that's obvious from the choices.)

nsato 2010-02-25 21:34:34
Let's look at what we're given. We're given that Andrea had the median score, and that all participants had a different score. This means Andrea had the unique "middle" score, i.e. half the other students had a higher score, and half the other students had a lower score.

nsato 2010-02-25 21:34:52
What does this say about the number of participants?

pirox 2010-02-25 21:35:14
so 3n is odd

MathTwo 2010-02-25 21:35:15
it is odd

jxl28 2010-02-25 21:35:15
there is an odd number of them

Aeroalon 2010-02-25 21:35:15
It is an odd number.

sj0201 2010-02-25 21:35:16
it's odd

nsato 2010-02-25 21:35:21
The number of participants 3n must be an odd number.

ernie 2010-02-25 21:35:38
this implies that n is odd

Just_Beginner 2010-02-25 21:35:39
there must be an odd number of students

nsato 2010-02-25 21:35:49
But the number of participants is 3n, so n is odd number. So what can we say about n?

ernie 2010-02-25 21:36:26
n >= 23?

nsato 2010-02-25 21:36:31
We can say that n >= 23 (since n cannot be equal to 22).

Just_Beginner 2010-02-25 21:36:35
it can be 23, 25, 27, ...

nsato 2010-02-25 21:36:39
What piece of information haven't we used yet?

ernie 2010-02-25 21:37:09
beth was 37th

sj0201 2010-02-25 21:37:09
Beth is 37th

MathTwo 2010-02-25 21:37:09
Beth was 37th

nsato 2010-02-25 21:37:16
We haven't used the fact that Beth placed 37th. How can we use this fact?

PhireKaLk6781 2010-02-25 21:37:58
andrea must have scored 36th or better

themehlman 2010-02-25 21:37:58
andrea scored better than 37th

BarbieRocks 2010-02-25 21:37:58
Andrea's score was the highest, so she was better than 37th place

pirox 2010-02-25 21:38:01
andrea's highest on her team, at worst 36th

v_Enhance 2010-02-25 21:38:05
Andrea must place at least 36th,

nsato 2010-02-25 21:38:10
Andrea had the highest score on her team, so Andrea placed at least in 36th. But what is Andrea's place, in terms of n?

Infrared 2010-02-25 21:38:55
(3n+1)/2

JoeJack 2010-02-25 21:38:55
(3n+1)/2

BarbieRocks 2010-02-25 21:38:55
(3n+1)/2

nsato 2010-02-25 21:38:59
Since there were a total of 3n participants and Andrea had the median score, Andrea's place was (3n + 1)/2.

nsato 2010-02-25 21:39:05
Therefore, (3n + 1)/2 <= 36. What does this say about n?

sparkle123 2010-02-25 21:39:48
n<=23

pirox 2010-02-25 21:39:48
n<=23

nsato 2010-02-25 21:39:52
It says that 3n <= 71, so n <= 23.

-$45! 2010-02-25 21:40:17
So 23 is only possible answer

pirox 2010-02-25 21:40:17
so n=23 (b) :whistle:

dragoneye776 2010-02-25 21:40:17
and 23 is the only choice that fits

nsato 2010-02-25 21:40:21
But we have already determined that n >= 23, so n = 23. The answer is (B).

nsato 2010-02-25 21:40:36

nsato 2010-02-25 21:40:44
How do we start?

Just_Beginner 2010-02-25 21:41:02
draw a picuture

PhireKaLk6781 2010-02-25 21:41:02
draw a diagram

MathTwo 2010-02-25 21:41:02
draw the diagram

Aeroalon 2010-02-25 21:41:02
Draw a diagram

dragoneye776 2010-02-25 21:41:02
diagram!

nsato 2010-02-25 21:41:07
Since this is a geometry problem, we start with an accurate diagram.

nsato 2010-02-25 21:41:10

nsato 2010-02-25 21:41:15
http://s3.amazonaws.com/classroom.artofproblemsolving.com/Images/Transcripts/07bfaa1790ba39817560136a4f6fd9fe.png

nsato 2010-02-25 21:41:27
How do we know that point A is inside the circle?

PhireKaLk6781 2010-02-25 21:42:22
OA is less than radius

pirox 2010-02-25 21:42:22
oa is less than the radius

Just_Beginner 2010-02-25 21:42:22
OA is less than the radius's length

v_Enhance 2010-02-25 21:42:22
OA is less than the radius.

dragoneye776 2010-02-25 21:42:24
OA is less than the sqrt{156}

nsato 2010-02-25 21:42:31

nsato 2010-02-25 21:42:39
Let s be the side length of triangle ABC, since this is the quantity we seek. How can we find s?

Just_Beginner 2010-02-25 21:43:27
pythagorean theorem! draw oc and extend OA to BC as a height

v_Enhance 2010-02-25 21:43:27
Draw OB, the perpendicular from A to BC, and use the Pythagorean Theorem.

PhireKaLk6781 2010-02-25 21:43:27
first connect O to B and extend OA

dragoneye776 2010-02-25 21:43:27
Find the altitude of the triangle and make right triangles

JoeJack 2010-02-25 21:43:27
extend OA to touch BC to a point ill call P. then use pythagorean theorem on OPB

nsato 2010-02-25 21:43:30
One good way to find lengths is to construct right triangles. So let D be the midpoint of BC.

nsato 2010-02-25 21:43:33

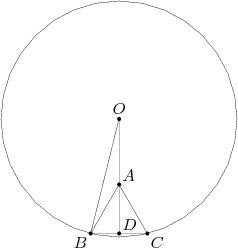
nsato 2010-02-25 21:43:41
This construction gives us several right triangles. For example, we know that BC is perpendicular to OD because BC is a chord of the circle.

nsato 2010-02-25 21:43:56

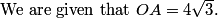
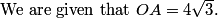
nsato 2010-02-25 21:44:00
What is AD in terms of s?

Just_Beginner 2010-02-25 21:44:34
BD=s/2, AD=s sqrt3/2

JoeJack 2010-02-25 21:44:34
sqrt3/2 * s

JoeJack 2010-02-25 21:44:34
s*sqrt3/2

yunhua98 2010-02-25 21:44:34
s*sqrt{3}/2

pirox 2010-02-25 21:44:36
rt3/2 s

nsato 2010-02-25 21:44:43

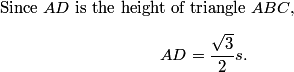
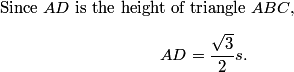
nsato 2010-02-25 21:44:53

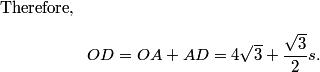
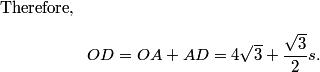
nsato 2010-02-25 21:45:01
But what is another expression for OD?

Just_Beginner 2010-02-25 21:46:06
OD=sqrt (OB^2-BD^2)

JoeJack 2010-02-25 21:46:11
sqrt(156-s^2/4)

pirox 2010-02-25 21:46:12
rt(156-s^2/4)

v_Enhance 2010-02-25 21:46:14
\sqrt{156-DB^2}

nsato 2010-02-25 21:46:19

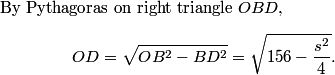
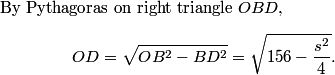
nsato 2010-02-25 21:46:24

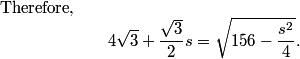
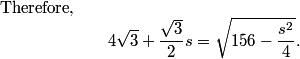
nsato 2010-02-25 21:46:37
How can we solve for s?

Just_Beginner 2010-02-25 21:47:05
square both sides

v_Enhance 2010-02-25 21:47:05
Square both sides and solve for s.

mathpi 2010-02-25 21:47:05
square it

dragoneye776 2010-02-25 21:47:05
square both sides

yunhua98 2010-02-25 21:47:05
square both sides????

nsato 2010-02-25 21:47:08
We can square both sides, to get rid of the square roots.

nsato 2010-02-25 21:47:12

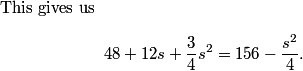
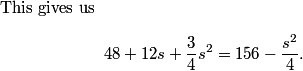
nsato 2010-02-25 21:47:21
This simplifies to the quadratic equation s^2 + 12s - 108 = 0.

nsato 2010-02-25 21:47:25
What are the solutions to this quadratic equation?

Just_Beginner 2010-02-25 21:48:11
6 and -18

sparkle123 2010-02-25 21:48:11
6 and -18

themehlman 2010-02-25 21:48:11
6, -18

mathpi 2010-02-25 21:48:11
-18,6

JoeJack 2010-02-25 21:48:11
6 and -18

v_Enhance 2010-02-25 21:48:12
(s-6)(s+18) = 0, so s=6 or s = -18.

Just_Beginner 2010-02-25 21:48:52
s can't be negative, so s=6

myyellowducky82 2010-02-25 21:48:52
Only the whole number solution works, so the answer is 6, or B.

-$45! 2010-02-25 21:48:52
But no negatives in geometry so it must be 6

dragoneye776 2010-02-25 21:48:54
s must be positive so its 6

Just_Beginner 2010-02-25 21:48:54
(B)

nsato 2010-02-25 21:48:56
This quadratic equation factors as (s - 6)(s + 18) = 0, so s = 6. The answer is (B).

nsato 2010-02-25 21:49:09

nsato 2010-02-25 21:49:18
How do we start?

nsato 2010-02-25 21:49:27
(You should know this by now.)

JoeJack 2010-02-25 21:49:42
draw a diagram

Just_Beginner 2010-02-25 21:49:43
draw a diagram again

letsruletheworldtogether 2010-02-25 21:49:43
draw diagram

BarbieRocks 2010-02-25 21:49:43
diagram\

MathTwo 2010-02-25 21:49:43
diagram

nsato 2010-02-25 21:49:46
Since this is a geometry problem, we start with an accurate diagram.

nsato 2010-02-25 21:49:54

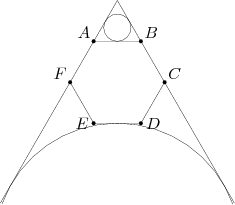
nsato 2010-02-25 21:50:00
Are there any additional points we should label?

letsruletheworldtogether 2010-02-25 21:50:46
where af and bc meet should be j

nsato 2010-02-25 21:50:47
We should label the intersection of AF and BC; let's call it G.

PhireKaLk6781 2010-02-25 21:50:59
points of tangency

MathTwo 2010-02-25 21:50:59
yeah the points of tangency

MathTwo 2010-02-25 21:50:59
label the points of tangency

JoeJack 2010-02-25 21:50:59
the points of tangency and the centers of the circles

JoeJack 2010-02-25 21:51:00
the centers of the 2 circles

nsato 2010-02-25 21:51:04
Let's also label the points of tangency of the circles with the sides. Let H be the midpoint of AB, let J be the midpoint of DE, and let L be the point where the second circle is tangent to BC. Finally, we let K be the center of the second circle.

nsato 2010-02-25 21:51:11

nsato 2010-02-25 21:51:16
What assumption can we make about the diagram that will make things easier?

MathTwo 2010-02-25 21:51:55
the sides of the hexagon have length one

nsato 2010-02-25 21:51:59
We are looking for the ratio of the area of the second circle to the area of the first circle. If we scale the diagram, then this ratio remains the same. Therefore, we can set any particular segment to be any length we want to, so let's assume that that side length of the hexagon is equal to 1.

nsato 2010-02-25 21:52:11
Then what is the radius of the first circle?

nsato 2010-02-25 21:52:17
(This is the small circle at the top.)

Just_Beginner 2010-02-25 21:53:24
it is sqrt3/6

letsruletheworldtogether 2010-02-25 21:53:24
1/6 sqrt3

sparkle123 2010-02-25 21:53:24
AGB is equilateral so sqrt3/6

BarbieRocks 2010-02-25 21:53:24
sqrt(3)/6

nsato 2010-02-25 21:53:29
There are several ways of calculating the radius of the first circle, which is the incircle of triangle ABG. For example, since triangle ABG is equilateral, the incenter coincides with the centroid.

nsato 2010-02-25 21:53:40

nsato 2010-02-25 21:53:53
Now we want to find the radius of the second circle. Let r be this radius.

nsato 2010-02-25 21:53:59
How can we find r? Which lengths in the diagram are equal to r?

nsato 2010-02-25 21:54:02

BarbieRocks 2010-02-25 21:54:36
KL, KJ

yunhua98 2010-02-25 21:54:36
JK and LK

-$45! 2010-02-25 21:54:36
JK and KL

Aeroalon 2010-02-25 21:54:36
Segments KL and KJ

Just_Beginner 2010-02-25 21:54:41
KL and KJ,

nsato 2010-02-25 21:54:43
We see that JK and KL are equal to r, so it may help to find GJ. What is GJ?

PhireKaLk6781 2010-02-25 21:55:36
nvrm 3sqrt3/2

BarbieRocks 2010-02-25 21:55:37
3aqrt(3)/2?

rpond 2010-02-25 21:55:37
3sqrt(3)/2

yunhua98 2010-02-25 21:55:37
3/2*root 3

-$45! 2010-02-25 21:55:37
3sqrt(3)/2

nsato 2010-02-25 21:55:43

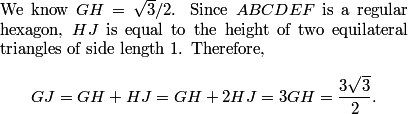
nsato 2010-02-25 21:55:58
How can we use these lengths?

nsato 2010-02-25 21:56:03

BarbieRocks 2010-02-25 21:56:16
GH+HJ=GH+2HJ?

nsato 2010-02-25 21:56:25
Sorry, that should say GH + HJ = GH + 2GH.

v_Enhance 2010-02-25 21:56:52
Note that since triangle GKL is 30-60-90, we can use ratios of that

nsato 2010-02-25 21:56:54
Exactly.

nsato 2010-02-25 21:56:57
We see that triangle GKL is a 30-60-90 triangle. (Since L is a tangent point, angle GLK is 90 degrees, and by symmetry, angle KGL is half of angle AGB.) What does this tell us?

MathTwo 2010-02-25 21:57:33
KL is half the length of the hypotenuse of the triangle

nsato 2010-02-25 21:58:06

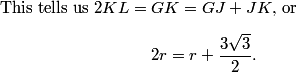
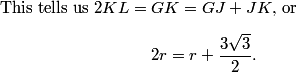
nsato 2010-02-25 21:58:36

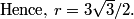
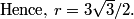
Just_Beginner 2010-02-25 21:58:38
r = 3sqrt3/2

nsato 2010-02-25 21:58:42
So what is the ratio of the areas of the circles?

letsruletheworldtogether 2010-02-25 21:59:19
81!!!

mathpi 2010-02-25 21:59:19
81

PhireKaLk6781 2010-02-25 21:59:19
81

-$45! 2010-02-25 21:59:19
81:1

-$45! 2010-02-25 21:59:19
D!

Just_Beginner 2010-02-25 21:59:19
3sart3/2 divided by sqrt 3/6, = 9, square to get 81

secondvegetable 2010-02-25 21:59:21
81

nsato 2010-02-25 21:59:25

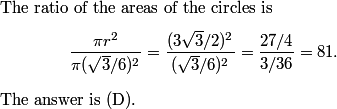
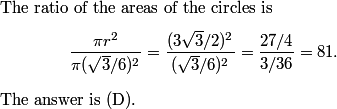
nsato 2010-02-25 21:59:46
Now I'll move onto the AMC 12 problems.

nsato 2010-02-25 21:59:58

nsato 2010-02-25 22:00:09
Where do we start?

MathTwo 2010-02-25 22:00:40
factor a out

BarbieRocks 2010-02-25 22:00:40
factor! a(bc+b+1)

nsato 2010-02-25 22:00:45
We start by factoring the expression: abc+ab+a = a(bc+b+1).

Just_Beginner 2010-02-25 22:01:08
if a is a mult 3, we have a mult. of 3 immediately

nsato 2010-02-25 22:01:10
If 'a' is divisible by 3, then the expression is divisible by 3. Fortunately, 2010 is divisible by 3, so 1/3 of the numbers in the set are divisible by 3, which means the probability that 'a' is divisible by 3 is 1/3. Therefore, the desired probability is 1/3 plus 2/3 times the probability bc+b+1 is divisible by 3.

nsato 2010-02-25 22:01:23
How do we find the probability that bc+b+1 is divisible by 3?

-$45! 2010-02-25 22:01:50
Put bc+b+1 in mod 3!

pirox 2010-02-25 22:01:50
put everything mod 3:

nsato 2010-02-25 22:02:03
We can tackle this with pretty straightforward casework based on b modulo 3. (By modulo 3, we mean the remainder when the number is divided by 3.)

nsato 2010-02-25 22:02:17
If b is divisible by 3, then bc+b+1 is 1 more than a multiple of 3, so bc+b+1 cannot be divisible by 3.

eat2thepieseye 2010-02-25 22:02:20
If b is divisible by 3, we lose.

nsato 2010-02-25 22:02:31
If b is 1 more than a multiple of 3, then bc+b+1 is divisible by 3 if and only if c+1+1 is divisible by 3, which is true if and only if c is also 1 more than a multiple of 3. What is the probability that this occurs?

v_Enhance 2010-02-25 22:02:41
If b = 1 mod 3, then only c=1 mod 3 works.

PhireKaLk6781 2010-02-25 22:03:06
1/9

pirox 2010-02-25 22:03:06
1/9

nsato 2010-02-25 22:03:07
The probability that b and c are both 1 more than a multiple of 3 is (1/3)(1/3) = 1/9.

v_Enhance 2010-02-25 22:03:15
If b=2 mod 3, only c=3 mod 3 works.

nsato 2010-02-25 22:03:17
Finally, if b is 2 more than a multiple of 3, then bc+b+1 is divisible by 3 if and only if 2c + 2 + 1 = 2c + 3 is. 2c+3 is divisible by 3 if and only if c is divisible by 3.

nsato 2010-02-25 22:03:25
What is the probability that this occurs?

-$45! 2010-02-25 22:03:43
Another 1/9!

v_Enhance 2010-02-25 22:03:43
Another 1/9.

mathpi 2010-02-25 22:03:43
1/9

rpond 2010-02-25 22:03:43
also 1/9

nsato 2010-02-25 22:03:46
The probability that b is 2 more than a multiple of 3 and c is a multiple of 3 is (1/3)(1/3) = 1/9.

nsato 2010-02-25 22:03:49
So, what is the final probability?

mathpi 2010-02-25 22:04:29
13/27

letsruletheworldtogether 2010-02-25 22:04:29
E

-$45! 2010-02-25 22:04:29
4/27 + 1/3 = 13/27! E is correct.

pirox 2010-02-25 22:04:29
1/3+2/3(2/9)=13/27 (E):whistle:

rpond 2010-02-25 22:04:29
2/9+1/3-2/9*1/3 = 13/27, E

Just_Beginner 2010-02-25 22:04:29
13/27

nsato 2010-02-25 22:04:32
The desired probability is P(a is a multiple of 3) + P(a is not a multiple of 3)*P(bc+b+1 is a multiple of 3) = 1/3 + (2/3)(1/9 + 1/9) = 13/27 This is choice (E).

nsato 2010-02-25 22:04:52

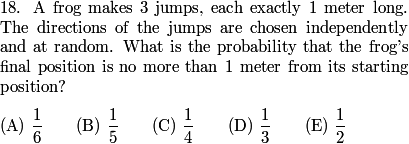
nsato 2010-02-25 22:05:24
How will we start?

v_Enhance 2010-02-25 22:05:55
Since this is invariant under rotation, start by fixing the first jump.

nsato 2010-02-25 22:05:59
We can simplify the problem a little bit by assuming the first jump is horizontal to the right. (Alternatively, we can place the problem on the coordinate plane with such that first jump is from (0,0) to (1,0).) We then want the probability the frog ends up back inside the unit circle centered at the starting point.

nsato 2010-02-25 22:06:13

nsato 2010-02-25 22:06:21
Then, the frog jumps again:

nsato 2010-02-25 22:06:23

nsato 2010-02-25 22:06:28
Now what must we evaluate?

pirox 2010-02-25 22:07:12
the probability

nsato 2010-02-25 22:07:16
We must evaluate the probability that the frog will end up back inside the circle on the next jump. Will this be the same no matter where B is?

letsruletheworldtogether 2010-02-25 22:07:38
no!

rpond 2010-02-25 22:07:38
no

pirox 2010-02-25 22:07:38
no

GoldenFrog1618 2010-02-25 22:07:39
no

nsato 2010-02-25 22:07:40
No, it won't, so we'll need a measure of how the frog took the second jump. Any suggestions?

MathTwo 2010-02-25 22:08:08
look at the angle

eat2thepieseye 2010-02-25 22:08:08
How about an angle?

MathTwo 2010-02-25 22:08:08
look at the angle the frog jumps

nsato 2010-02-25 22:08:12
We could use the angle that the frog uses relative to the horizontal (in kind of the same way we assign angles to points on the unit circle):

eat2thepieseye 2010-02-25 22:08:14
An angle with the horizontal will do.

nsato 2010-02-25 22:08:17

nsato 2010-02-25 22:08:23
We'll try to find the probability the frog ends up inside the circle on the next jump in terms of x. What should we think about first to help us find it?

nsato 2010-02-25 22:09:19
We can think about where the frog can possibly end up, which forms a circle centered at B with radius 1.

nsato 2010-02-25 22:09:23

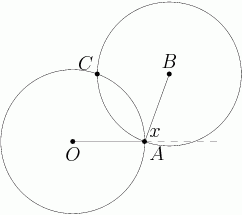
nsato 2010-02-25 22:09:28
Point C is the second point where the new circle hits the original one.

nsato 2010-02-25 22:09:33
So, the frog ends up back inside the original circle if it is on arc AC of this circle. Can we determine anything about this arc?

spelljack825 2010-02-25 22:10:21
equal to x

nsato 2010-02-25 22:10:26
Quadrilateral OABC is a rhombus! Therefore, <ABC = pi - <OAB = x. What does this tell us about the probability the frog ends up within 1 unit of O if its jump from A has angle x?

pirox 2010-02-25 22:11:30
x/2pi

nsato 2010-02-25 22:11:33
The third jump of the frog must be within an angle of x (arc AC of the second circle) out of a possible 2pi (the frog can jump in any direction from B), so the probability is x/2pi.

nsato 2010-02-25 22:11:53
But we should check this is always true.

nsato 2010-02-25 22:11:57
Our reasoning above may only hold if B is outside the original circle (we won't worry about B being below the horizontal line OA; that probability will obviously be the same as above OA). But we should check what happens if B is inside the original circle. Do we get the same result? That is, if we let x be the angle the second jump makes with the horizontal, does the frog have a range of x on its third jump to stay within the original circle?

nsato 2010-02-25 22:12:17
We start with a diagram:

nsato 2010-02-25 22:12:20

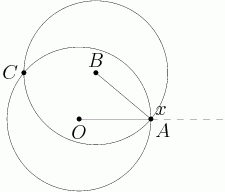
nsato 2010-02-25 22:12:26
Again, OABC is a rhombus, and again, we have <CBA = pi - <OAB = x. So, once again, the frog has an angle of x out of a possible 2pi in which it can jump and stay in the unit circle.

nsato 2010-02-25 22:12:59
We know that for any second jump of angle x, the frog has an angle of x out of 2pi in which it can jump to stay within the unit circle (where we limit x to be in the range 0 to pi, since the probability for when the frog jumps below the horizontal is the same as that above). So how do we compute the probability?

nsato 2010-02-25 22:13:42
We can't "count" the cases, since there are an infinite number of possible angles, so what technique can we use?

stargroup 2010-02-25 22:14:31
probability by geometry

nsato 2010-02-25 22:14:33
We use geometric probability. The second jump can be anything from 0 to pi. The third jump has a range of 2pi. For any second jump of angle x, the success region of the third jump covers a range of x. So, plotting the second jump on the horizontal and the third on the vertical, we get:

nsato 2010-02-25 22:14:39

nsato 2010-02-25 22:14:48
So what is the answer?

letsruletheworldtogether 2010-02-25 22:15:20
1/4!

MathTwo 2010-02-25 22:15:20
1/4

GoldenFrog1618 2010-02-25 22:15:20
1/4

MathTwo 2010-02-25 22:15:20
1/4 (c)

pirox 2010-02-25 22:15:20
so 1/4 (C) :bow:

stargroup 2010-02-25 22:15:20
1/4

monkeyman701 2010-02-25 22:15:22
C

nsato 2010-02-25 22:15:23
The successful region is 1/4 of the possible region, so the desired probability is 1/4. (Note that we only have x range from 0 to pi because we're only considering the possibility that the frog's second jump is above the horizontal -- the situation is the same below the horizontal, so the probability is 1/4 whether the frog jumps above or below the horizontal. Therefore, the overall probability is also 1/4.) The answer is (C).

nsato 2010-02-25 22:15:33
Here's the last problem of the night.

nsato 2010-02-25 22:15:38

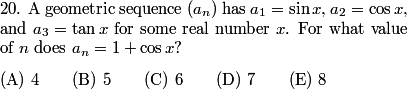
nsato 2010-02-25 22:16:10
Let's first get a feel for the problem by figuring out what the sequence looks like. What are the first few terms of the sequence?

nsato 2010-02-25 22:16:58
What is the common ratio?

rpond 2010-02-25 22:17:33
cos x / sin x = cot x

nsato 2010-02-25 22:17:35
From the first two terms, the common ratio must equal (cos x)/(sin x) = cot x.

nsato 2010-02-25 22:17:40
Then the sequence is: sin x, cos x, tan x, 1, cot x, cot^2 x, cot^3 x, cot^4 x, . . .

nsato 2010-02-25 22:17:45
We must determine which of these equals 1+cos x.

nsato 2010-02-25 22:17:49
What else do we know?

pirox 2010-02-25 22:18:37
cotx=tnax/cosx

rpond 2010-02-25 22:18:41
cos x * cot x = tan x

nsato 2010-02-25 22:18:44
We have an equation for x, since a_2/a_1 = a_3/a_2. This gives us (sin x)(tan x) = cos^2 x. We can rearrange this as sin^2 x = cos^3 x (when stuck on a trig problem, try looking at it in terms of sines and cosines!) What might we do with this?

rpond 2010-02-25 22:19:28
replace sin^2 x with 1-cos^2 x

kyuubi9 2010-02-25 22:19:28
sin^2x=1-cos^x

nsato 2010-02-25 22:19:30
Here, we'll write everything in terms of cosine both because it's easier to do so, and because the expression we want is in terms of cosine. Since sin^2 x + cos^2 x = 1, we have 1 - cos^2 x = cos^3 x.

nsato 2010-02-25 22:19:38
But we want 1 + cos x. Can we find a "1+cos x" in this equation?

v_Enhance 2010-02-25 22:20:36

nsato 2010-02-25 22:20:47

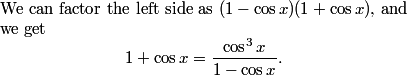
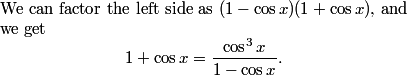
nsato 2010-02-25 22:20:51
That doesn't look too helpful. Any other suggestions?

rpond 2010-02-25 22:21:17
cos^3 x + cos^2 x = 1 -> cos^2 x(cos x + 1) = 1

zappy07 2010-02-25 22:21:18
1= cos^2x * (1+cosx)

stargroup 2010-02-25 22:21:18
divide equation by cos^2, so 1 + cos x = sec^2 x

nsato 2010-02-25 22:21:22

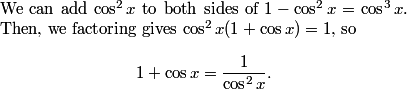
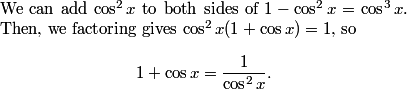
nsato 2010-02-25 22:21:28
That's at least a little promising.

nsato 2010-02-25 22:21:32
Let's look back at our geometric sequence: sin x, cos x, tan x, 1, cot x, cot^2 x, cot^3 x, cot^4 x, . . .

nsato 2010-02-25 22:21:39
We're looking for 1/(cos^2 x). I don't see one. Does anyone see where we might extract a 1/(cos^2x) (or even a 1/(cos x))?

stargroup 2010-02-25 22:22:20
a_4/a_2 = 1/cos x = r^2

rpond 2010-02-25 22:22:20
a4/a2 = 1/cos x = sec x (too bad i didn't see this when actually taking the test :/ )

nsato 2010-02-25 22:22:22
In going from the second term to the fourth, we go from cos x to 1. So, taking two steps in this geometric sequence is equivalent to multiplying twice by 1/(cos x).

nsato 2010-02-25 22:22:49
So what does 1/(cos^2 x) mean with respect to this geometric sequence?

rpond 2010-02-25 22:23:31
a4 = 1, a6 = sec x, a8 = sec^2 x

GoldenFrog1618 2010-02-25 22:23:36
a_2=cos x, a_4=1, a_6=1/cos x, a_8=1/cos^2 x

nsato 2010-02-25 22:23:37
We get 1/(cos^2 x) by multiplying 1 (the fourth term) by 1/(cos x) twice. So, we go 2 steps after the fourth term twice, and we get to the eighth term.

nsato 2010-02-25 22:24:03
The answer is (E).

nsato 2010-02-25 22:24:24
That's it for tonight's math jam. Thanks for coming out!

2010 AMC 10/12 B Math Jam

Facilitator: David Patrick