Math Jams

DPatrick 2010-04-02 19:01:33
Hello and welcome to the 2010 AIME II Math Jam!

DPatrick 2010-04-02 19:01:44
My name is Dave Patrick, and I'll be leading tonight's discussion.

DPatrick 2010-04-02 19:01:54
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.

DPatrick 2010-04-02 19:02:05
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.

DPatrick 2010-04-02 19:02:16
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read. Only write comments that are relevant to the discussion.

DPatrick 2010-04-02 19:02:37
There are a lot of students here, and I expect more will show up as we progress. As I said, only well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!

DPatrick 2010-04-02 19:02:54
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go.

DPatrick 2010-04-02 19:03:06
Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!

DPatrick 2010-04-02 19:03:27
We do have an assistant tonight who can help answer some of your questions--he is Miles Dillon Edwards (Boy Soprano II). Miles is an alumnus of Canada/USA Mathcamp, the Research Science Institute, the Hampshire College Summer Studies in Mathematics, and the Math Olympiad Program. He was a four-time USAMO qualifier. He also discovered a new proof of Heron's formula. He is currently studying math and cello performance at Indiana University.

DPatrick 2010-04-02 19:03:46
Miles can answer questions by whispering to you or by opening a window with you to chat 1-on-1.

DPatrick 2010-04-02 19:04:00
Please also remember that the purpose of this Math Jam is to work through the solutions to the AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics.

DPatrick 2010-04-02 19:04:17
So please, when a problem is posted, do not simply respond with the answer. That's not why we're here. We're going to work through the problems step-by-step, and people who post comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, are going to be ignored.

DPatrick 2010-04-02 19:04:34
I don't claim that the solutions that we'll present today are the "definitive" or "best" solutions to each problem. Many of the problems have more than one plausible approach. We don't have time to consider every possible approach to every problem.

DPatrick 2010-04-02 19:04:56
Also, these solutions are not necessarily the fastest or slickest, but these solutions are the ones that (to me) are the most logical, most elegant, or the ones that you'd be most likely to think of on your own.

DPatrick 2010-04-02 19:05:07
Let me also announce a few things up front.

DPatrick 2010-04-02 19:05:15
I will not speculate on the USAMO or USAJMO qualifying indexes.

DPatrick 2010-04-02 19:05:31
I will not speculate on whether the AIME I or AIME II will have statistically different score distributions (averages, etc.).

DPatrick 2010-04-02 19:05:55
In the event that the AIME II proves to be statistically more difficult or easier than the AIME I, there is precedent for the AMC to set different qualifying indexes for the two contests. (A lot of people ask this.)

DPatrick 2010-04-02 19:06:08
I do not know how soon you will get your scores. It has been suggested by the AMC office that it may be next week.

DPatrick 2010-04-02 19:06:17
I do not know when the USA(J)MO qualifiers will be announced. It also has been suggested by the AMC office that it may be next week.

DPatrick 2010-04-02 19:07:02
Our agenda tonight is to work through all 15 problems on the 2010 AIME II, in order.

DPatrick 2010-04-02 19:07:10
Let's get started!

DPatrick 2010-04-02 19:07:20

DPatrick 2010-04-02 19:07:36
As you can see, I'll always put the current problem at the top of the window.

DPatrick 2010-04-02 19:07:45
You can resize it by dragging the horizontal gray bar up or down.

letsruletheworldtogether 2010-04-02 19:08:11
remainder, not reminder

DPatrick 2010-04-02 19:08:21
oops, that's my first typo of the night. It won't be the last.

DPatrick 2010-04-02 19:08:28

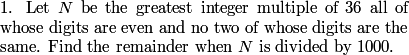
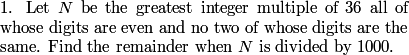
DPatrick 2010-04-02 19:08:32
(I won't change it up top.)

RunpengFAILS 2010-04-02 19:08:56
List the even digits: 0, 2, 4, 6, 8.

RiteshR 2010-04-02 19:08:57
First off, the digits of N must consist of 0,2,4,6,8

GoldenFrog1618 2010-04-02 19:08:57
the only possible digits are 0,2,4,6 and 8

vjnmath 2010-04-02 19:08:57
Only possible digits are 0,2,4,6,8

DPatrick 2010-04-02 19:09:04
We know that the digits must come from the set {0,2,4,6,8} and we can't use any twice.

MathTwo 2010-04-02 19:09:27
then the number must be divisible by 4 and 9

professordad 2010-04-02 19:09:27
and they have to add to a multiple of 9

sparkle123 2010-04-02 19:09:27
digits must add to 9 to be divisible by 9

letsruletheworldtogether 2010-04-02 19:09:27
36 is divisible by 9 and 4

DPatrick 2010-04-02 19:09:35
Right. Since N is a multiple of 9, the digits must sum to a multiple of 9.

RiteshR 2010-04-02 19:10:01
So we have to kick out a 2

NewAlbionAcademy 2010-04-02 19:10:01
8+6+4+0 is divisible by 9

superpi83 2010-04-02 19:10:01
so one digit can't be used. the 5 digits do not add to a multiple of 9.

vjnmath 2010-04-02 19:10:01
2 must be removed so the digit sum will be a multiple of 9

DPatrick 2010-04-02 19:10:27
Indeed, they sum to 20 now so we can't use them all. The only possibilities for the set of digits of N is {4,6,8} or {0,4,6,8}. (The only possible sum can be 18, since all the numbers are even.)

sparkle123 2010-04-02 19:10:40
8640 is the largest number

giratina150 2010-04-02 19:10:40
8640 is the biggest possible integer therefore

DPatrick 2010-04-02 19:10:50
We might as well check the largest possible N using these digits, which is 8640.

hellomynameis 2010-04-02 19:11:07
indeed 8640 works

nsun48 2010-04-02 19:11:07
which is divisible by 4!

DPatrick 2010-04-02 19:11:23
Yep, it works. (We already knew it was divisible by 9, and since the last two digits are 40 it's divisible by 4 too.)

DPatrick 2010-04-02 19:11:29
So N = 8640.

DPatrick 2010-04-02 19:11:36

DPatrick 2010-04-02 19:12:05

DPatrick 2010-04-02 19:12:35
(I'm going to move pretty quickly from problem to problem. The AIME I math jam took almost 3 hours, so we don't have a lot of time to waste!)

giratina150 2010-04-02 19:12:50
draw a diagram

letsruletheworldtogether 2010-04-02 19:12:50
draw a diagram!

ksun48 2010-04-02 19:12:50
draw a picture

number.sense 2010-04-02 19:12:50
draw the square

DPatrick 2010-04-02 19:12:54
A picture might be in order:

DPatrick 2010-04-02 19:12:58

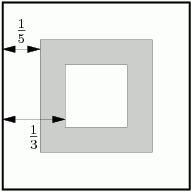
sparkle123 2010-04-02 19:13:34
draw two more concentric squares with side length 3/5 and 1/3

giratina150 2010-04-02 19:13:35
we need to find the shaded area

jdever 2010-04-02 19:13:35
The gray square has side length 3/5.

DPatrick 2010-04-02 19:13:41
P is more than 1/5 from the side of the square if it is inside the square whose sides are 1/5 from the sides of S.

DPatrick 2010-04-02 19:13:54
P is less than 1/3 from the side of the square if it is outside the square whose sides are 1/3 from the sides of S.

DPatrick 2010-04-02 19:14:05

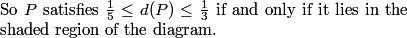
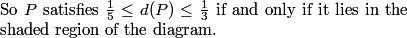
#H34N1 2010-04-02 19:14:24
find the area...(3/5)^2-(1/3)^2

letsruletheworldtogether 2010-04-02 19:14:24
find the area of the shaded region

DaNub123 2010-04-02 19:14:24
it would be (3/5^2-1/3^2)/1

scientistpatrick 2010-04-02 19:14:24
we need to find (3/5)^2 - (1/3)^2

RiteshR 2010-04-02 19:14:24

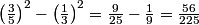
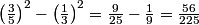
DPatrick 2010-04-02 19:14:32
Right: the probability we seek is the area of the shaded region (since the area of the entire square is 1).

DPatrick 2010-04-02 19:14:49
It is the area of a square of side length 1 - 2(1/5) = 3/5, minus the area of a square of side length 1 - 2(1/3) = 1/3.

DPatrick 2010-04-02 19:15:03

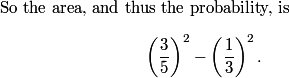
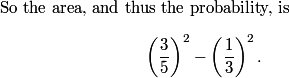
nsun48 2010-04-02 19:15:25
so 56+225=281

giratina150 2010-04-02 19:15:25
our answer is 56+225 = 281

hellomynameis 2010-04-02 19:15:25
56 + 225 = 281

superpi83 2010-04-02 19:15:25
since 56/225 is in lowest terms, the answer is 56+225=281

DPatrick 2010-04-02 19:15:31

DPatrick 2010-04-02 19:16:01
Let me quickly reiterate a couple of things for latecomers.

DPatrick 2010-04-02 19:16:12
There will be a transcript of the entire Math Jam on the website when we're finished.

DPatrick 2010-04-02 19:16:39
Also, due to the size of this Math Jam, we cannot respond to every comment or answer every question. But we'll do our best.

DPatrick 2010-04-02 19:16:45

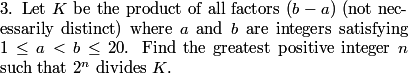
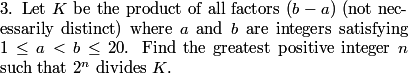
DPatrick 2010-04-02 19:16:59
What's a good strategy for this problem?

DaNub123 2010-04-02 19:17:37
find all possible b-a

letsruletheworldtogether 2010-04-02 19:17:37
list all possible b-a and how many times they appear

ksun48 2010-04-02 19:17:37
try it and find how many of each factor

DPatrick 2010-04-02 19:17:45
Yes -- we can count how many times each factor appears.

DPatrick 2010-04-02 19:18:02
For example, the factor 1 appears 19 times, since 1 <= a <= 19 gives b = a+1 satisfying b <= 20.

giratina150 2010-04-02 19:18:18
2 can happen 18

giratina150 2010-04-02 19:18:18
and so on

RiteshR 2010-04-02 19:18:18
20-n pairs (a,b) that differ by n

DPatrick 2010-04-02 19:18:24
Similarly, the factor 2 appears 18 times, since 1 <= a <= 18 gives b = a+2 satisfying b <= 20.

DPatrick 2010-04-02 19:18:33
3 appears 17 times, 4 appears 16 times, and so on, up to 19 appearing just once (a=1,b=20).

bridgemaster 2010-04-02 19:18:49
but we don't have to worry about 1, because it doesn't contain any two's

superpi83 2010-04-02 19:18:52
we only need to find factors of 2

DPatrick 2010-04-02 19:19:02
Since we want to count the powers of 2, we can ignore all the odd factors.

DPatrick 2010-04-02 19:19:12
Here's a little chart to keep things organized:

DPatrick 2010-04-02 19:19:18

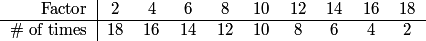
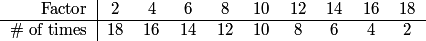
DPatrick 2010-04-02 19:19:33
How do we use this data?

giratina150 2010-04-02 19:20:08
now we need to count the number of times the factor 2 appears

superpi83 2010-04-02 19:20:08
make a new row called 'number of factors of 2 that number contains'

ksun48 2010-04-02 19:20:08
2 gives 1, 4 gives 2 6 gives 1 8 gives 3 10 gives 1 12 gives 2 14 gives 1 16 gives 4 18 gives 1 (factor of 2)

giratina150 2010-04-02 19:20:08
but for powers of 2 other than 2, you count them more

Chopstiks 2010-04-02 19:20:08
rewrite the factors by the exponent of 2 in its prime factorization

jdever 2010-04-02 19:20:08
Multiples of 2 each contribute 1 2, multiples of 4 contribute 2, etc.

DPatrick 2010-04-02 19:20:13
Some factors will contribute more than one power of 2. We can add this data to the chart:

DPatrick 2010-04-02 19:20:20

DPatrick 2010-04-02 19:20:35
(For example, each 8 contributes 2^3 to the product, and there are 12 factors of 8, so we get 12(3) = 36 total powers of 2)

number.sense 2010-04-02 19:20:43
add the elements of the bottome row

FuzzoMarx 2010-04-02 19:20:43
Then just sum the bottom row.

letsruletheworldtogether 2010-04-02 19:20:43
now addd

professordad 2010-04-02 19:20:43
just sum the last row.

DPatrick 2010-04-02 19:20:57
We just add the numbers in the bottom row of the table to get our answer of the total number of powers of 2 in the product.

DPatrick 2010-04-02 19:21:05

DPatrick 2010-04-02 19:21:30

DPatrick 2010-04-02 19:21:57
(I feel like they wrote this problem just for me, since I'm Dave and this happens to me a lot. Although I usually have to go further than 400 feet.)

superpi83 2010-04-02 19:22:27
casework?

hellomynameis 2010-04-02 19:22:27
Casework

centralbs 2010-04-02 19:22:27
Do we need to do casework?

DPatrick 2010-04-02 19:22:37
Sort of, but we can make it really simple.

DPatrick 2010-04-02 19:22:51
When I read this problem, my first thought was "this is almost exactly like the previous problem!".

DPatrick 2010-04-02 19:23:13
We just need to count how many pairs of gates are 4 or fewer units apart, and divide by the total number of pairs of gates.

DPatrick 2010-04-02 19:23:46
It's basically the same count we did in #3.

Bedro 2010-04-02 19:24:02
except now it's 12

DPatrick 2010-04-02 19:24:10
Right, so there are 11 pairs of gates that are 1 unit apart.

DPatrick 2010-04-02 19:24:16
There are 10 pairs of gates that are 2 units apart.

DPatrick 2010-04-02 19:24:25
And so on...

ksun48 2010-04-02 19:24:31
11+10+9+8=28

DPatrick 2010-04-02 19:24:46
I made the same mistake the first time too. :(

DPatrick 2010-04-02 19:24:50
It's 38.

DPatrick 2010-04-02 19:25:02
This is why you should always check your work.

DPatrick 2010-04-02 19:25:28
There are 38 pairs of gates that are 4 units apart or less.

DPatrick 2010-04-02 19:25:34
And how many total pairs?

Bedro 2010-04-02 19:25:47
over 12 C 2

superpi83 2010-04-02 19:25:47
total pairs=12C2=66

ProtestanT 2010-04-02 19:25:47
There are 66 pairs of gates in all

ksun48 2010-04-02 19:25:47
11*12/2=66

DPatrick 2010-04-02 19:26:02
Right, there are C(12,2) = 66 pairs of gates. (Or you could add 11+10+9+...+1.)

professordad 2010-04-02 19:26:28
so the probability is 38/66 = 19/33

DPatrick 2010-04-02 19:26:31

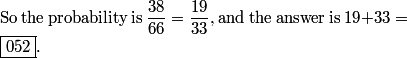
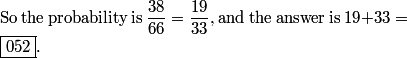
DPatrick 2010-04-02 19:27:00

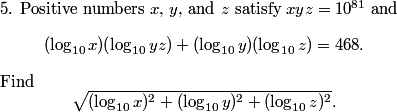
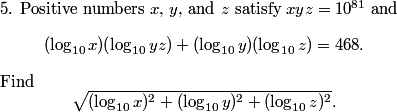
DPatrick 2010-04-02 19:27:21
What's going to make this problem a lot easier to work with?

anaverageaopser 2010-04-02 19:27:35
susbstitue log x = a, log y = b, log z = c?

ProtestanT 2010-04-02 19:27:35
Assign substitutions

sparkle123 2010-04-02 19:27:35
set logx=a

redsky 2010-04-02 19:27:35
let's substitute a = log x, b = log y, c = log z

RiteshR 2010-04-02 19:27:35
substitute for logs

DPatrick 2010-04-02 19:27:40
Those logs are ugly. Let's substitute to get rid of them.

DPatrick 2010-04-02 19:27:47

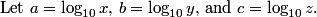
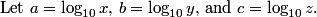
DPatrick 2010-04-02 19:28:02
Now we can rewrite the entire problem.

DPatrick 2010-04-02 19:28:23

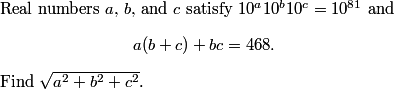
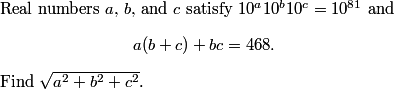
modularmarc101 2010-04-02 19:28:42
a+b+c = 81

sparkle123 2010-04-02 19:28:42
a+b+c=81

professordad 2010-04-02 19:28:42
wow a+b+c = 81

MathTwo 2010-04-02 19:28:42
then a+b+c=81

DPatrick 2010-04-02 19:28:49
The first equation is just a+b+c = 81.

Bedro 2010-04-02 19:29:02
ab + bc + ca = 468

letsruletheworldtogether 2010-04-02 19:29:08
ab+ac+bc=468

DPatrick 2010-04-02 19:29:09
The second equation is ab + ac + bc = 468.

DPatrick 2010-04-02 19:29:15
How can we get to a^2 + b^2 + c^2?

number.sense 2010-04-02 19:29:40
let's look at (a+b+c)^2

ritwik_anand 2010-04-02 19:29:40
we can square (a+b+c) as we have all other individual terms and solve for a^2 + b^2 +c^2

MathTwo 2010-04-02 19:29:40
square first equation and subtract twice the second from it

Bedro 2010-04-02 19:29:40
a^2 + b^2 + c^2 = (a+b+c)^2-2(ab+bc+ca)

pumpkinpi 2010-04-02 19:29:40
try squaring a+b+c

#H34N1 2010-04-02 19:29:40
(a+b+c)^2 expand the puppy

DPatrick 2010-04-02 19:29:51

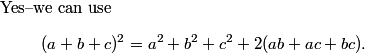
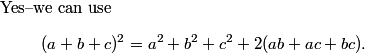
DPatrick 2010-04-02 19:30:13
Now we fill in what we know:

DPatrick 2010-04-02 19:30:23

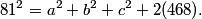
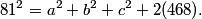
professordad 2010-04-02 19:30:32
81^2 - 2*468 and take the root of that

DPatrick 2010-04-02 19:30:38

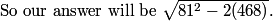
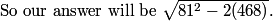
DPatrick 2010-04-02 19:30:53
A small tip: don't multiply out 81^2 unless you're sure you need to.

DPatrick 2010-04-02 19:31:02
I'd pull 9 out of each term first.

DPatrick 2010-04-02 19:31:21

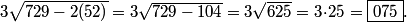
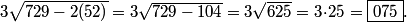
mathlead 2010-04-02 19:31:42
why do you write 075 and not just 75

DPatrick 2010-04-02 19:31:58
Only because the AMC writes them that way, since a 3-digit answer has to be filled in on the answer form.

DPatrick 2010-04-02 19:32:20

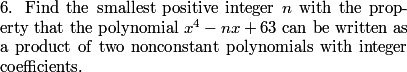
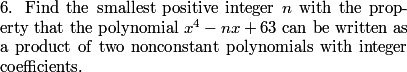
RiteshR 2010-04-02 19:32:47
For it to be factored, it must be a product of a linear and a cubic or 2 quadratics

cascadee 2010-04-02 19:32:47
try and factor the polynomial?

ksun48 2010-04-02 19:32:47
first try to factor that

DPatrick 2010-04-02 19:33:06
The possibilities for the factorization are either as a cubic times a linear, or as the product of two quadratics.

DPatrick 2010-04-02 19:33:20
We should examine each possibility.

anaverageaopser 2010-04-02 19:33:30
use undetermined coefficients

bananabunch 2010-04-02 19:33:30
Method of Undetermined Coefficients?

DPatrick 2010-04-02 19:33:45
Right, we'll write down a factorization with unknown coefficients, and see what we can fill in.

DPatrick 2010-04-02 19:33:55
Let's do the cubic * linear case first.

DPatrick 2010-04-02 19:34:02

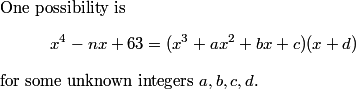
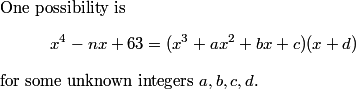
DPatrick 2010-04-02 19:34:23
What do we know about those coefficients?

theGoodGuy 2010-04-02 19:34:50
d*c=63

charzard96 2010-04-02 19:34:50
they're integers

pumpkinpi 2010-04-02 19:34:50
cd = 63

Chopstiks 2010-04-02 19:34:50
integers.

m4e9 2010-04-02 19:34:50
cd=63

bridgemaster 2010-04-02 19:34:50
cd = 63

DPatrick 2010-04-02 19:35:05
Certainly they're all integers (the problem tells us so), and cd = 63 since the constant terms have to match up.

DPatrick 2010-04-02 19:35:28
But some more fundamental data is present in this factorization.

centralbs 2010-04-02 19:35:38
-d is a root

DPatrick 2010-04-02 19:35:52
Right, we note that -d is a root, and d must divide 63.

DPatrick 2010-04-02 19:36:02
We can plug this back into the original quartic to solve for n in terms of d.

DPatrick 2010-04-02 19:36:10

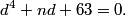
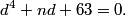
Bedro 2010-04-02 19:36:57
(d^4-63)/d

DPatrick 2010-04-02 19:37:01

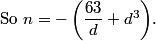
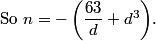
DPatrick 2010-04-02 19:37:20
What are the possible values of d that make n positive?

theGoodGuy 2010-04-02 19:37:48
-3

number.sense 2010-04-02 19:37:48
-1

DPatrick 2010-04-02 19:38:00
d must be a factor of 63 = 3*3*7.

professordad 2010-04-02 19:38:20
negative numbers

chhan92 2010-04-02 19:38:20
negative integer

anaverageaopser 2010-04-02 19:38:20
negative factors of 63

DPatrick 2010-04-02 19:38:30
n must be positive so we only need to check negative d.

DPatrick 2010-04-02 19:38:44
And remember that we are trying to minimize n.

DPatrick 2010-04-02 19:38:57
d=-1 gives n=64, d=-3 gives n=21+27=48, and any other d has -d^3 > 48.

modularmarc101 2010-04-02 19:39:08
-3 gives the smallest value : 48

DPatrick 2010-04-02 19:39:12
So the minimum from this case is 48.

bridgemaster 2010-04-02 19:39:30
however, we must also check the possibility that there are two quadratic factors, instead

DPatrick 2010-04-02 19:39:37
The other case is a product of quadratics:

DPatrick 2010-04-02 19:39:49

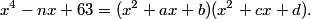
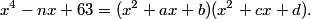
DPatrick 2010-04-02 19:40:08
How can we simplify this?

superpi83 2010-04-02 19:40:36
bd=63

anaverageaopser 2010-04-02 19:40:36
bd = 63 this time.

centralbs 2010-04-02 19:40:36
again bd=63

giratina150 2010-04-02 19:40:36
bd=63

sparkle123 2010-04-02 19:40:36
bd=63

GoldenFrog1618 2010-04-02 19:40:36
bd=63

ksun48 2010-04-02 19:40:36
bd=63

DPatrick 2010-04-02 19:40:44
Again we have bd = 63 by comparing constant terms.

GoldenFrog1618 2010-04-02 19:40:50
a=-c

ProtestanT 2010-04-02 19:40:50
a+c=0

modularmarc101 2010-04-02 19:40:50
a+c = 0

DPatrick 2010-04-02 19:41:06
By looking at the cubic terms, we must have a+c = 0. So let's set c = -a and rewrite it:

DPatrick 2010-04-02 19:41:14

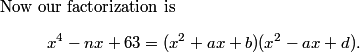
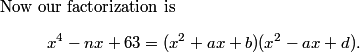
DPatrick 2010-04-02 19:41:39
What does the quadratic term tell us?

Bedro 2010-04-02 19:42:04
b+d-a^2=0

ksun48 2010-04-02 19:42:05
b+d=a^2

modularmarc101 2010-04-02 19:42:13
b + d = a^2

DPatrick 2010-04-02 19:42:14
Examining the quadratic term gives b + d - a^2 = 0, so a^2 = b+d.

DPatrick 2010-04-02 19:42:29
And from before, bd = 63.

DPatrick 2010-04-02 19:42:38
So we need a pair of factors of 63 whose sum is a perfect square.

RiteshR 2010-04-02 19:43:00
(1,63) and (7,9) are the only possibilites

dday25 2010-04-02 19:43:00
So (b,d) is either (1,63) or (7,9).

superpi83 2010-04-02 19:43:00
1+63 or 7+9

letsruletheworldtogether 2010-04-02 19:43:00
1,63 and 7,9

DPatrick 2010-04-02 19:43:11
The only possibilities (up to sign) are {1,63} and {7,9}.

DPatrick 2010-04-02 19:43:23
And what does n equal to?

ProtestanT 2010-04-02 19:44:05
n=a(b-d)

DPatrick 2010-04-02 19:44:15
Right, comparing the linear terms gives n = a(b-d).

DPatrick 2010-04-02 19:44:49
So we need to minimize a(b-d) positive, given that {b,d} is either {1,63} or {7,9}, and that a^2 = bd.

anaverageaopser 2010-04-02 19:45:05
n=4(9-7)=8

superpi83 2010-04-02 19:45:06
n=4(9-7)=8

DPatrick 2010-04-02 19:45:11
Right, we just check the two cases.

DPatrick 2010-04-02 19:45:37
{63,1} is going to give |a| = 8, so we get n = 8(63-1) = a big number (bigger than the 48 we found in the other case).

DPatrick 2010-04-02 19:45:49
{7,9} gives |a| = 4, so we get n = 4(9-7) = 8.

DPatrick 2010-04-02 19:45:55
That's the best!

DPatrick 2010-04-02 19:46:08

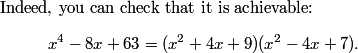
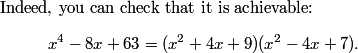
DPatrick 2010-04-02 19:46:21

DPatrick 2010-04-02 19:46:41

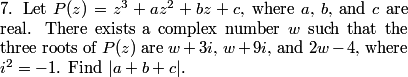
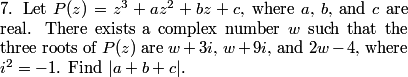
DPatrick 2010-04-02 19:46:53
What do we know about the roots of a cubic polynomial with real coefficients?

bridgemaster 2010-04-02 19:47:18
two of the roots must be conjugates of each other

RiteshR 2010-04-02 19:47:18
Two of the numbers must be conjugates, and the one number must be real

centralbs 2010-04-02 19:47:18
one has to be real

Bedro 2010-04-02 19:47:18
roots has to be conjucate pairs

sparkle123 2010-04-02 19:47:18
complex conjugates

Bedro 2010-04-02 19:47:18
imaginary roots has to come in conjugate pairs

redsky 2010-04-02 19:47:18
and one root must be real

DPatrick 2010-04-02 19:47:27
Right. Either all three are real (and that clearly can't happen in this problem)...

DPatrick 2010-04-02 19:47:32
...or one is real and the other two are complex conjugates (that is, of the form a+bi and a-bi).

DPatrick 2010-04-02 19:48:14
So what can we conclude about w?

centralbs 2010-04-02 19:48:36
it is either a - 3i or a - 9i

letsruletheworldtogether 2010-04-02 19:48:44
it is in the form -3i+b or -9i+b

DPatrick 2010-04-02 19:48:48
Since one of w+3i, w+9i, or 2w-4 must be real, the imaginary part of w must be -3i, -9i, or 0, to produce a real root.

DPatrick 2010-04-02 19:49:01
And it is clear that w cannot be real because w+3i and w+9i would not be a conjugate pair.

DPatrick 2010-04-02 19:49:22
We can quickly test the other two possibilities to see which produces a conjugate pair.

DPatrick 2010-04-02 19:49:37
If w = r - 3i for some real r, then the roots are: r, r+6i, and 2(r-3i)-4 = (2r-4)-6i. Hurray, a conjugate pair!

DPatrick 2010-04-02 19:50:00
If w = r - 9i for some real r, then the roots are: r-6i, r, and 2(r-9i)-4 = (2r-4)-18i. No good.

modularmarc101 2010-04-02 19:50:08
Vieta's formulas: since a is real, 4 - 4w - 12i is real so Im(w) = 3

DPatrick 2010-04-02 19:50:22
Indeed, you could also do this step using the fact that the sum of the three roots is real.

DPatrick 2010-04-02 19:50:38
Their sum is 4w + 12i - 4, so the imaginary part of 4w is -12i, and thus the imaginary part of w is -3i.

DPatrick 2010-04-02 19:50:56
So it must be w = r - 3i for some real r, and the roots are r, r+6i, and (2r-4)-6i.

number.sense 2010-04-02 19:51:18
2r-4 = r so r=4 b/c they are conjugates

bridgemaster 2010-04-02 19:51:18
r = 2r-4, so r = 4

Bedro 2010-04-02 19:51:18
r=2r-4

DPatrick 2010-04-02 19:51:27
For the latter two roots to be a conjugate pair, we must have the real parts equal...

DPatrick 2010-04-02 19:51:35
...so r = 2r-4, hence r = 4.

DPatrick 2010-04-02 19:51:46
Thus the roots are 4, 4+6i, and 4-6i.

RiteshR 2010-04-02 19:51:54
The answer is the polynomial with roots 4, 4+6i, 4-6i

DPatrick 2010-04-02 19:52:00

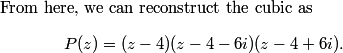
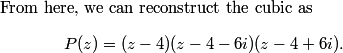
letsruletheworldtogether 2010-04-02 19:52:13
now use vietas to find the real part of w and a,b,c

ksun48 2010-04-02 19:52:13
so multiply it out

number.sense 2010-04-02 19:52:13
now we can either use vietta's formulas or just chug and plug and expand

DPatrick 2010-04-02 19:52:26
We could, or we could do something slightly nicer:

stickfigure 2010-04-02 19:52:29
plug in z = 1

DPatrick 2010-04-02 19:52:45
We use the fact that P(1) = 1 + a + b + c.

DPatrick 2010-04-02 19:52:57
So our answer is |P(1) - 1|.

DPatrick 2010-04-02 19:53:29
(It's useful to keep track of what we want as the final answer. We don't need to solve for a,b,c individually; it's slightly faster to just compute a+b+c.)

MathTwo 2010-04-02 19:53:43
now bash it out

giratina150 2010-04-02 19:53:43
the i' will cancel

DPatrick 2010-04-02 19:53:54

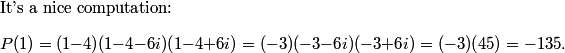
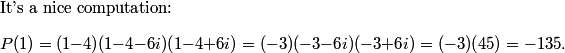
DPatrick 2010-04-02 19:54:22

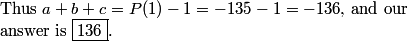
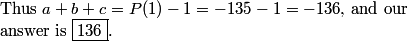
DPatrick 2010-04-02 19:54:51

DPatrick 2010-04-02 19:55:11
What do the first two conditions tell us?

#H34N1 2010-04-02 19:55:48
eacch number has to be assigned to either A or B

number.sense 2010-04-02 19:55:48
each element appears exactly once in A and B

modularmarc101 2010-04-02 19:55:48
THey partition a bigger set

FuzzoMarx 2010-04-02 19:55:48
We must have in our sets all the elements exactly once.

DPatrick 2010-04-02 19:55:52
Every element from {1,2,...,12} has to be in exactly one of A or B. (This is called a partition of the set {1,2,...,12}.)

DPatrick 2010-04-02 19:56:07
How do we construct a valid partition that satisfies the bottom two conditions?

pinkmuskrat 2010-04-02 19:56:33
try some cases of number of elements

stickfigure 2010-04-02 19:56:33
sorta caseworky: let there be x numbers in A and 12 - x numbers in B. then just count based on the number of ways to choose numbers for set A

MathTwo 2010-04-02 19:56:33
let A have n elements

ksun48 2010-04-02 19:56:33
first choose the number of elements

billy314 2010-04-02 19:56:33
Assign the number of elements in each set first

DPatrick 2010-04-02 19:56:45
Right, the sizes of the sets are important, so I like casework based on the sizes of the sets.

DPatrick 2010-04-02 19:56:59
Hopefully there will be a nice pattern to save us having to do thirteen different cases.

DPatrick 2010-04-02 19:57:09
First, we can decide the sizes of A and B. Call these a and b. (Note b = 12-a.)

number.sense 2010-04-02 19:57:18
note we can't have two elements w/ 6 in each

DPatrick 2010-04-02 19:57:37
Indeed, we cannot have a = b = 6, because then we can't place the 6 in either set.

giratina150 2010-04-02 19:57:51
each set can have 11 numbers maximum

letsruletheworldtogether 2010-04-02 19:57:51
nor can we have 12 in one set

DPatrick 2010-04-02 19:58:08
Right, we also cannot have a=0 or a=12, since then there's no place to put the 12.

dday25 2010-04-02 19:58:16
So a must be in B, and b must be in A.

DPatrick 2010-04-02 19:58:32
In all the remaining cases, the element "a" must go in B, and "b" must go in A.

DPatrick 2010-04-02 19:58:38
What about the remaining 10 elements?

centralbs 2010-04-02 19:58:52
Does not matter

superpi83 2010-04-02 19:58:52
can go anywhere...?

DPatrick 2010-04-02 19:59:09
They can go anywhere, but we know that a-1 of them have to go in A, and the remaining b-1 have to go in B.

RiteshR 2010-04-02 19:59:26
10Ca-1

ksun48 2010-04-02 19:59:26
so 10 choose a-1

dday25 2010-04-02 19:59:26
We "choose" a-1 of them to go in A, so we can do this in C(10,a-1) ways for each possible a.

DPatrick 2010-04-02 19:59:47

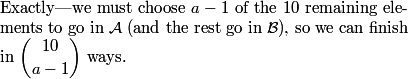
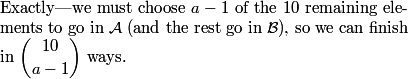
DPatrick 2010-04-02 20:00:06
And we've decided that any a in (1,2,3,4,5,7,8,9,10,11) will work.

DPatrick 2010-04-02 20:00:11
(a=0,6,12 won't work)

DPatrick 2010-04-02 20:00:18

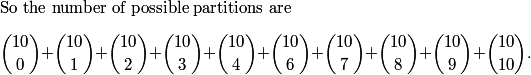
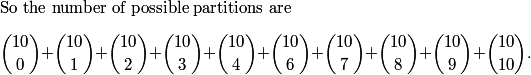
DPatrick 2010-04-02 20:00:31
What's this sum?

centralbs 2010-04-02 20:00:51
Looks like binomial expansion

pinkmuskrat 2010-04-02 20:00:51
if 10C5 was there, it would be 1024

bananabunch 2010-04-02 20:00:51
1024-C(10,5)

DPatrick 2010-04-02 20:01:01

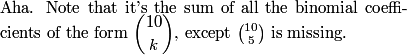
DPatrick 2010-04-02 20:01:18
If we had the missing C(10,5) term, then the sum would be 2^10 = 1024.

DPatrick 2010-04-02 20:01:36
(It's the sum of Row 10 of Pascal's Triangle.)

DPatrick 2010-04-02 20:01:44

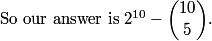
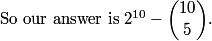
stickfigure 2010-04-02 20:01:55
subtracting that away, you get 772

anaverageaopser 2010-04-02 20:01:56
1024-252=772

DPatrick 2010-04-02 20:02:02

DPatrick 2010-04-02 20:02:13

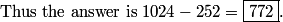
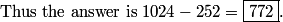
DPatrick 2010-04-02 20:02:37

number.sense 2010-04-02 20:02:56
Draw the pic!!

centralbs 2010-04-02 20:02:56
Picture!

stickfigure 2010-04-02 20:02:56
diagram :c

giratina150 2010-04-02 20:02:56
draw a diagram

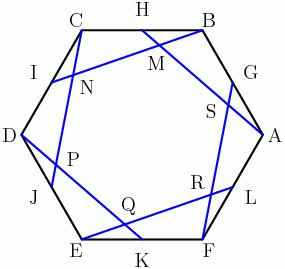
DPatrick 2010-04-02 20:03:05
You have to start by sketching a picture.

DPatrick 2010-04-02 20:03:10

DPatrick 2010-04-02 20:03:32
What might help simplify the computation in this problem?

Chopstiks 2010-04-02 20:03:43
Let the side length be 2

number.sense 2010-04-02 20:03:48
let BC = 2

DPatrick 2010-04-02 20:03:56
Yeah, I would set the side lengths of the big hexagon to be 2, so that AG = GB = BH = ... = LA = 1.

DPatrick 2010-04-02 20:04:17
Since we are only concerned about a ratio of areas, we can set the side length to be anything we want, and it won't change the ratio.

DPatrick 2010-04-02 20:04:44
Now, there are a few ways to do this problem. One option is to just throw the whole thing on the coordinate plane and bash away.

DPatrick 2010-04-02 20:04:54
It works, but it's potentially unpleasant.

DPatrick 2010-04-02 20:05:18
Instead, I suggest noticing something nice in the picture.

sparkle123 2010-04-02 20:05:40
similar triangles

number.sense 2010-04-02 20:05:40
similar triangles!!!

letsruletheworldtogether 2010-04-02 20:05:40
similar trianges DPJ and DCJ

MathTwo 2010-04-02 20:05:40
similar triangles

DPatrick 2010-04-02 20:05:53
There are six big triangles ABH, BCI, etc. They are all congruent.

DPatrick 2010-04-02 20:06:08
There are also six smaller triangles AGS, BHM, etc. They are all congruent too.

DPatrick 2010-04-02 20:06:12
And they are all similar!

DPatrick 2010-04-02 20:06:26
For example, angle GAS equals BAH, and angle AGS equals BHA, so ABH and ASG are similar.

DPatrick 2010-04-02 20:06:49
So we can try to chase the lengths to find the length of MS (a side of the smaller hexagon).

DPatrick 2010-04-02 20:06:58
Once we know MS, the ratio of the areas will be (MS/2)^2, the square of the ratio of the side lengths of the hexagons.

DPatrick 2010-04-02 20:07:17
Let's solve for the big triangle ABH. We know AB = 2 and BH = 1. What else do we know?

sparkle123 2010-04-02 20:07:39
angle b is 120

stickfigure 2010-04-02 20:07:39
ABH is 120 degrees

Bedro 2010-04-02 20:07:39
ABH = 120 degrees

DPatrick 2010-04-02 20:07:49
Right, angle ABH = 120 degrees.

pinkmuskrat 2010-04-02 20:07:59
by law of cosines, last side is sqrt{7}

ksun48 2010-04-02 20:07:59
ha = rt7 by law of cosines

RiteshR 2010-04-02 20:07:59
law of cosines?

anaverageaopser 2010-04-02 20:07:59
use law of cosines?

number.sense 2010-04-02 20:08:04
law of cosines bash, we have nice angles

DPatrick 2010-04-02 20:08:09
So we can use Law of Cosines to find AH:

DPatrick 2010-04-02 20:08:15

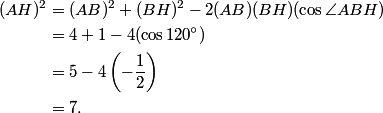
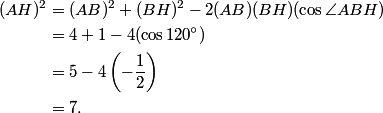
DPatrick 2010-04-02 20:08:27

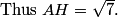
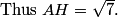
DPatrick 2010-04-02 20:08:40
But now all the little triangles are similar to 1-2-sqrt(7) triangles too!

DPatrick 2010-04-02 20:08:51
For example, what's HM?

number.sense 2010-04-02 20:09:31
1/sqrt(7)

letsruletheworldtogether 2010-04-02 20:09:31
1/sqrt7

Bedro 2010-04-02 20:09:31
1/rt7

quadraticfanatic 2010-04-02 20:09:31
(sqrt7)/7

DPatrick 2010-04-02 20:09:38
HM is the smaller leg of a 1-2-sqrt(7) similar triangle with long side 1.

DPatrick 2010-04-02 20:09:45
Thus HM is 1/sqrt(7).

DPatrick 2010-04-02 20:10:08
(I'd leave it as 1/sqrt(7) until it becomes clear we'd need it as sqrt(7)/7. 1/sqrt(7) is simpler.)

number.sense 2010-04-02 20:10:30
and AS=2/sqrt(7)

letsruletheworldtogether 2010-04-02 20:10:30
SA is 2/sqrt7

Bedro 2010-04-02 20:10:30
AS = 2/sqrt{7} the same way

ksun48 2010-04-02 20:10:30
we can also find as and ms

DPatrick 2010-04-02 20:10:38
In the same way, AS is the longer leg of a 1-2-sqrt(7) similar triangle with long side 1.

DPatrick 2010-04-02 20:10:47
Thus AS = 2/sqrt(7).

Bedro 2010-04-02 20:11:03
MS = AH - HM - AS

number.sense 2010-04-02 20:11:03
MS = AH-HM-AS = 4/sqrt(7)

DPatrick 2010-04-02 20:11:24

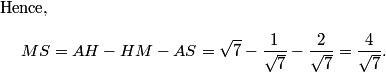
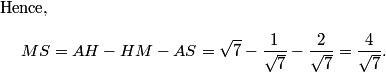
stickfigure 2010-04-02 20:11:46
divide that by 2, square it, and you get 4/7.... so it's 011

DPatrick 2010-04-02 20:11:50

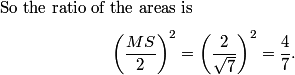
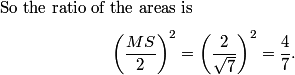
DPatrick 2010-04-02 20:11:59

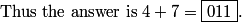
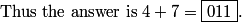
RiteshR 2010-04-02 20:12:05
i really like rcv's solution too

DPatrick 2010-04-02 20:12:30
Yes, there is a really nice solution posted by AoPS member rcv on our message board. It involves tiling the plane in a really creative way.

DPatrick 2010-04-02 20:12:53
We've finished all the single digit problems, so I'm going to take a 5-minute break to rest my typing fingers. :)

DPatrick 2010-04-02 20:13:01
We'll resume at about 8:18 ET / 5:18 PT.

DPatrick 2010-04-02 20:18:48
OK...I'm back and ready to tackle those double-digit problems.

DPatrick 2010-04-02 20:18:56

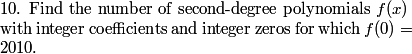
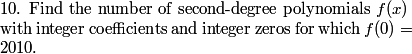
DPatrick 2010-04-02 20:19:26
What does such a polynomial look like?

modularmarc101 2010-04-02 20:19:41
constant term is 2010

Bedro 2010-04-02 20:19:41
f(x) = ax^2 + bx + 2010

ksun48 2010-04-02 20:19:41
constant term 2010

DaNub123 2010-04-02 20:19:45
ax^2+bx+2010

professordad 2010-04-02 20:19:45
ax^2 + bx + 2010

DPatrick 2010-04-02 20:20:09
That's true, but writing it in a form that also uses the fact that we have integer zeros would be especially helpful.

sparkle123 2010-04-02 20:20:16
f(x)=a(x-r1)(x-r2)

RiteshR 2010-04-02 20:20:16

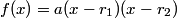
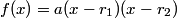
DPatrick 2010-04-02 20:20:30

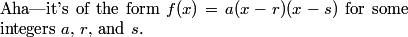
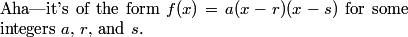
sparkle123 2010-04-02 20:20:55
ars=2010

number.sense 2010-04-02 20:20:56
ars=2010

giratina150 2010-04-02 20:20:56
(a)(r)s=2010

ksun48 2010-04-02 20:20:56
ars=2010

modularmarc101 2010-04-02 20:20:56
ars = 2010

DPatrick 2010-04-02 20:21:03
And comparing the two forms (or plugging in x=0) gives ars = 2010.

DPatrick 2010-04-02 20:21:14
So we need to count the numbers of ways that 2010 can be factored into three integer factors.

giratina150 2010-04-02 20:21:32
2010=2*3*5*67

FuzzoMarx 2010-04-02 20:21:32
We oughta factor 2010: 2*5*3*67

DPatrick 2010-04-02 20:21:38
Note that 2010 = 2 * 3 * 5 * 67.

DPatrick 2010-04-02 20:21:47
How do we get three factors a, r, s?

RiteshR 2010-04-02 20:22:09
3^4 ways

sparkle123 2010-04-02 20:22:10
3^4 since each of 2,3,5,67 can go 3 places

quadraticfanatic 2010-04-02 20:22:16
each prime factor can go in one of three categories

DPatrick 2010-04-02 20:22:20
Each prime can go into a, r, or s, so each prime has 3 choices for which factor to be in.

DPatrick 2010-04-02 20:22:37
That gives 3^4 = 81 possible ordered positive factorizations.

DPatrick 2010-04-02 20:22:48
What about the signs?

giratina150 2010-04-02 20:23:12
we need to account for negativs

centralbs 2010-04-02 20:23:12
we can have three positives, or 2 negatives and one positive

sparkle123 2010-04-02 20:23:26
81*4=324

DPatrick 2010-04-02 20:23:35
We can either have them all positive, or have 1 positive and 2 negative. That's 4 total possibilities.

DPatrick 2010-04-02 20:23:47
(since we have 3 choices for which one might be negative.)

DPatrick 2010-04-02 20:23:56
So that's a total of 4 * 81 = 324 ordered factorizations 2010 = a*r*s.

superpi83 2010-04-02 20:24:13
but there are repeats. for example 67(x-5)(x-6) and 67(x-6)(x-5) are the same

quadraticfanatic 2010-04-02 20:24:13
Now we need to remove any duplicates

sparkle123 2010-04-02 20:24:13
r and s are indistinguishable

DPatrick 2010-04-02 20:24:28
Right! If we swap r and s, we get the same polynomial.

DPatrick 2010-04-02 20:24:39
So should we just divide by 2, and get 324 / 2 = 162 polynomials?

panjia123 2010-04-02 20:24:59
Unless r=s?

FuzzoMarx 2010-04-02 20:25:06
That doesn't take into account when r and s are the same.

DPatrick 2010-04-02 20:25:11
We can't "swap" r and s if they are equal!

RiteshR 2010-04-02 20:25:19
(2010,1,1)

sparkle123 2010-04-02 20:25:22
aka when r=s=1 or -1

DPatrick 2010-04-02 20:25:27
There are two factorizations in which r and s are equal: 2010 * 1 * 1 and 2010 * (-1) * (-1).

DPatrick 2010-04-02 20:25:37
In each of the other 322 factorizations, we can swap r and s to get the same polynomial.

DPatrick 2010-04-02 20:25:53

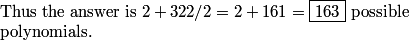
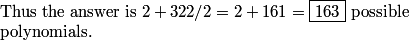
DPatrick 2010-04-02 20:26:14
It's this last step that made this problem relatively tricky.

DPatrick 2010-04-02 20:26:31
I'd be willing to bet that 162 is a very common wrong answer.

DPatrick 2010-04-02 20:26:44

DPatrick 2010-04-02 20:27:13
(As you probably figured out, this is really a game of tic-tac-toe in disguise. Hence the name T-grid.)

DPatrick 2010-04-02 20:27:35
So we are trying to count the number of full tic-tac-toe positions, with five 1's and four 0's (I actually used five X's and four O's in my notes), where there's not more than one winning line.

RiteshR 2010-04-02 20:28:09
With just the first condition, the answer would be 9C5 and many kids would be very happy. Unfortunately, there is a second condition.

quadraticfanatic 2010-04-02 20:28:09
There are 9!/5!4!= 126 ways to fulfill requirement (1)

panjia123 2010-04-02 20:28:15
Complementary counting?

DPatrick 2010-04-02 20:28:28
I agree--this is a great situation for complementary counting. It's seems hard (at least to me) to count positions when there are zero winning lines, but it seems easier to count positions with two or more winning lines and subtract from the total number of positions.

DPatrick 2010-04-02 20:28:59
As noted, to count the total possible positions (satisfying condition (1) only), we have to choose four spaces (out of nine) for the 0's.

DPatrick 2010-04-02 20:29:12

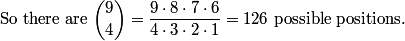
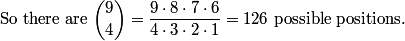
DPatrick 2010-04-02 20:29:28
Now we'll count positions with two or more winning lines, subtract from 126, and we'll have our answer.

DPatrick 2010-04-02 20:29:37
Can we have more than two winning lines?

DPatrick 2010-04-02 20:30:09
(To reiterate: a "winning line" is three 1's in a row or three 0's in a row, as described in condition (2).)

bananabunch 2010-04-02 20:30:28
No

centralbs 2010-04-02 20:30:28
No

quadraticfanatic 2010-04-02 20:30:28
No. It just doesn't work.

RiteshR 2010-04-02 20:30:31
no, but we can have exactly 2

DPatrick 2010-04-02 20:30:53
Right. We either have a line of 1's and a line of 0's, or we have two lines of 1's. (Think about why we can't have anything else.)

DPatrick 2010-04-02 20:31:02
So this naturally gives two cases.

DPatrick 2010-04-02 20:31:19
Case 1 is a line of 1's and a line of 0's. How do we construct it?

DPatrick 2010-04-02 20:31:44
("Construct" meaning: how do we count how many there are?)

billy314 2010-04-02 20:32:01
Lines cannot be diagonal

ksun48 2010-04-02 20:32:01
two the same direction

pumpkinpi 2010-04-02 20:32:01
obviously can't use long diagonals

sparkle123 2010-04-02 20:32:01
well they must be parallel

DPatrick 2010-04-02 20:32:22
Right. We can't use a diagonal line since then there's no room for the other number.

DPatrick 2010-04-02 20:32:36
This can only happen if the lines are parallel: both are horizontal or both are vertical. (A diagonal lines of either prevents the other number from making a line.)

DPatrick 2010-04-02 20:33:03
First, we have 2 choices for the direction (horizontal or vertical).

ksun48 2010-04-02 20:33:31
then 3*2 choices for the rest and 3 choices for the other 0

quadraticfanatic 2010-04-02 20:33:39
(2 directions, horizontal and vertical) x (6 ways to order 0's, 1's, and mixed) x (3 ways to order the 011 in the mixed row)= 36 possibilities

DPatrick 2010-04-02 20:33:41
Then, we have 3 choices for which line is the 1's, and 2 more choices after that for which line is the 0's.

DPatrick 2010-04-02 20:33:50
Finally, we have 3 ways to finish the grid: we must pick one of the 3 remaining empty squares to be 0.

DPatrick 2010-04-02 20:34:00
That's a total of 2*3*2*3 = 36 positions in this case.

DPatrick 2010-04-02 20:34:23
The other case, Case 2, is two rows of 1's.

DPatrick 2010-04-02 20:34:36
Since there are only five 1's total, the two lines must overlap.

DPatrick 2010-04-02 20:34:58
Here there are a few subcases: the lines of 1's could be (horizontal + vertical), or (horizontal + diagonal), or (vertical + diagonal), or (diagonal + diagonal).

DPatrick 2010-04-02 20:35:27
How about horiztonal + vertical? How many are there?

SnowEverywhere 2010-04-02 20:35:41
= 9

superpi83 2010-04-02 20:35:42
3*3=9 cases

RiteshR 2010-04-02 20:35:42
3*3=9

quadraticfanatic 2010-04-02 20:35:42
horizontal + vertical: 9 ways

DPatrick 2010-04-02 20:35:49
We must choose 1 of the 3 horizontal rows and 1 of the 3 vertical columns. That's 3*3 = 9 choices. The 0's will go in the remaining spaces, so there's no additional choice.

DPatrick 2010-04-02 20:36:02
How about horizontal + diagonal?

centralbs 2010-04-02 20:36:26
2 times 3

billy314 2010-04-02 20:36:26
2*3=6

RiteshR 2010-04-02 20:36:26
3*2=6, same for vertical+diagonal

Bedro 2010-04-02 20:36:26
3*2=6 choices

DPatrick 2010-04-02 20:36:42
We have 2 choices for which diagonal, and then 3 choices for the row. Again, no more choices after that (0's go in empty spaces), so 2*3 = 6 possibilities in this case.

DPatrick 2010-04-02 20:36:55
vertical + diagonal is the same, so that's 6 more in that case.

RiteshR 2010-04-02 20:37:13
and 1 for diagonal+diagonal

dajoe 2010-04-02 20:37:18
only 1

quadraticfanatic 2010-04-02 20:37:19
Only one.

superpi83 2010-04-02 20:37:19
diagonal+diagonal only 1 arrangement possible

DPatrick 2010-04-02 20:37:28
And for both diagonals, there's only 1 way.

quadraticfanatic 2010-04-02 20:37:34
h and v: 9 ways, h and d: 6 ways, v and d: 6 ways, d and d: 1 way. TOTAL : 22 WAYS

RiteshR 2010-04-02 20:37:39
that's 22 ways

DPatrick 2010-04-02 20:37:40
So 9 + 6 + 6 + 1 = 22 total in case 2.

DPatrick 2010-04-02 20:37:52
Adding cases 1 and 2, that's 36 + 22 = 58 total bad grids.

Bedro 2010-04-02 20:38:05
126-(36+22)=68

DPatrick 2010-04-02 20:38:13

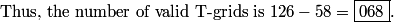
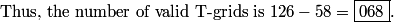
DPatrick 2010-04-02 20:38:47
I don't know of an easier way to do this problem that just listing all the cases as we did.

DPatrick 2010-04-02 20:38:59

DPatrick 2010-04-02 20:39:31
There are multiple ways that I know of to solve this problem.

SnowEverywhere 2010-04-02 20:39:38
Make equations and set variables

DPatrick 2010-04-02 20:39:53
They all end up doing this in one way or another.

DPatrick 2010-04-02 20:40:02
One method is to use the fact that, since the areas are the same, the heights must be in ratio 7:8. Then you can use the Pythagorean Theorem to get the lengths of the legs, and solve for the fact that the perimeters are equal.

DPatrick 2010-04-02 20:40:20
This method is straightforward, but slightly messy.

DPatrick 2010-04-02 20:40:32
Another method is to use the fact that since the areas and perimeters are equal, the radii of the incircles must be equal too. This leads to some elegant length-chasing. I'll leave it to you to fill in the details.

theax 2010-04-02 20:40:40
hmmm... let's try herons! algebra bash!

giratina150 2010-04-02 20:40:40
i used heron's formula

giratina150 2010-04-02 20:40:40
heron's formula

DPatrick 2010-04-02 20:40:45

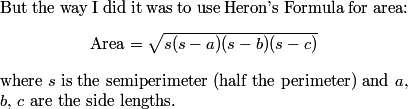
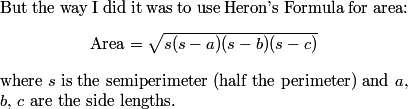
DPatrick 2010-04-02 20:41:11

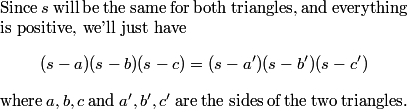
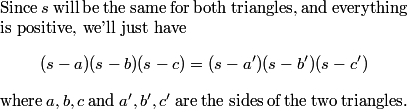
DPatrick 2010-04-02 20:41:29
Now we can set up our triangles.

giratina150 2010-04-02 20:41:49
we can draw diagrams and use the fact that the bases are in ratio 8:7

giratina150 2010-04-02 20:41:55
draw a diagram and label sides

RiteshR 2010-04-02 20:41:55
variables for lengths of triangles

DPatrick 2010-04-02 20:42:20
I'll omit drawing the diagrams, since we don't really use them for anything in particular, but we'll definitely introduce variables for the side lengths.

DPatrick 2010-04-02 20:42:47
Let's start with the bases, since that's the given data. What can we call them?

theax 2010-04-02 20:43:10
7x, 8x

jxl28 2010-04-02 20:43:10
7x and 8x?

GoldenFrog1618 2010-04-02 20:43:10
7x and 8x

pumpkinpi 2010-04-02 20:43:10
8b and 7b?

MathTwo 2010-04-02 20:43:10
8x and 7x

DPatrick 2010-04-02 20:43:18
You might write 8n and 7n for the bases, where n is some positive integer constant.

SnowEverywhere 2010-04-02 20:43:23
14a and 16a

RiteshR 2010-04-02 20:43:23
16a,14a

DPatrick 2010-04-02 20:43:34
But I wrote 16n and 14n instead.

DPatrick 2010-04-02 20:44:10
That's because if the legs of the first triangle (with base 16n) are a and a, then the legs of the second triangle (with base 14n) must be a+n and a+n in order to preserve the perimeter.

DPatrick 2010-04-02 20:44:25
If I had stuck with 8n and 7n, then I'd have to add n/2 to the other two sides, and it'd be a pain to keep track of the fact that n would have to be even. Starting with 16n and 14n avoids the need to do that.

DPatrick 2010-04-02 20:44:47
So to recap, one triangle has sides 16n, a, a, and the other has sides 14n, a+n, a+n. For both, the perimeter is 16n+2a and the semiperimeter is 8n + a.

DPatrick 2010-04-02 20:45:32
And now we plug these quantities into our Heron's equality for the areas, and really nice things happen.

DPatrick 2010-04-02 20:45:50

DPatrick 2010-04-02 20:46:08

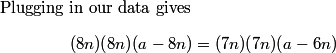
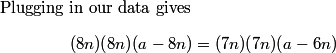
giratina150 2010-04-02 20:46:27
n^2 cancel

MathTwo 2010-04-02 20:46:27
yay stuff cancels

modularmarc101 2010-04-02 20:46:27
n^2 cancels out

DPatrick 2010-04-02 20:46:31
n^2 cancels, and what's left is 64a - 512n = 49a - 294n.

DPatrick 2010-04-02 20:46:49
So 15a = 218n.

DPatrick 2010-04-02 20:46:53
How does this help?

centralbs 2010-04-02 20:47:12
We can minimize the perimeter

Jongy 2010-04-02 20:47:12
Since both are integers, n=15 and a=218

ZHANGWENZHONGKK 2010-04-02 20:47:12
a=218,n=15

RiteshR 2010-04-02 20:47:17
the smallest possible perimeter iss when the side lengths are minimal

DPatrick 2010-04-02 20:47:23
The perimeter is 16n + 2a, and this is minimized when a and n are minimized.

DPatrick 2010-04-02 20:47:32
Since a and n must be positive integers, and 15 and 218 are relatively prime, the smallest solution is a = 218 and n =15.

ksun48 2010-04-02 20:47:49
16*15+2*218

DPatrick 2010-04-02 20:47:53

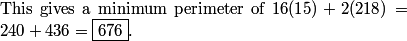
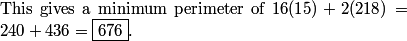
DPatrick 2010-04-02 20:48:23

DPatrick 2010-04-02 20:48:34
Wow. There's a lot of smoke and mirrors happening here.

DPatrick 2010-04-02 20:49:07
We need to cut through all the wordiness and get to the heart of the problem.

DPatrick 2010-04-02 20:49:30
For Alex and Dylan to be on the same team, what do Blair and Corey have to do?

mz94 2010-04-02 20:49:56
pick 2 cards either both greater than a+9 or less than a

ksun48 2010-04-02 20:49:57
get on the same side of alex and dylan, not different, or inbetween

DaNub123 2010-04-02 20:49:57
both higher or both lower

centralbs 2010-04-02 20:49:57
They have to either pick the highest cards or the lowest cards

SnowEverywhere 2010-04-02 20:49:57
both lower or both higher

DPatrick 2010-04-02 20:50:03
Right. They both have to be lower than a, or they both have to be higher than a+9.

DPatrick 2010-04-02 20:50:31
(oops, thanks to the several people who pointed out it's p(a) >= 1/2, not p(a) >= 12.)

DPatrick 2010-04-02 20:50:54
In other words, they both have to pick from {1,2,...,a-1} or they both have to pick from {a+10,a+11,...,52}.

DPatrick 2010-04-02 20:51:16
In how many ways can this happen?

mz94 2010-04-02 20:51:58
(a-1) nCr 2 + (43-a) nCr 2

RiteshR 2010-04-02 20:51:58
a-1 C 2 and 43-a C 2

MathTwo 2010-04-02 20:51:58
a-`1C2 and 43-aC2

DPatrick 2010-04-02 20:52:22
You could do it without regard to order using those numbers; I found it slightly cleaner to consider order so we don't have all the 1/2's.

DPatrick 2010-04-02 20:52:41
Blair and Corey pick from {1,2,...,a-1} in (a-1)(a-2) ways. (Blair has a-1 choices than Corey has a-2 choices.)

DPatrick 2010-04-02 20:52:54
Alternatively, they pick from {a+10,a+11,...,52} in (43-a)(42-a) ways. (Note that there are 43-a cards in this set.)

DPatrick 2010-04-02 20:53:05
These are disjoint possibilities (they can't both happen), so we just add to get the total number of ways they're on the same team.

DPatrick 2010-04-02 20:53:29
And since there are 50 cards remaining in the deck, there are 50 * 49 total ways for them to pick.

DPatrick 2010-04-02 20:53:36

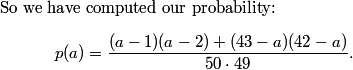
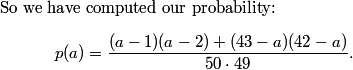
DPatrick 2010-04-02 20:53:55
We need this to be at least 1/2.

DPatrick 2010-04-02 20:54:01

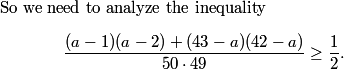
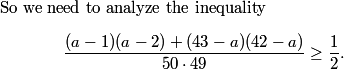
number.sense 2010-04-02 20:54:17
clear denominators

RiteshR 2010-04-02 20:54:17
simplify

DPatrick 2010-04-02 20:54:29

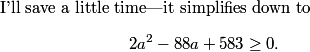
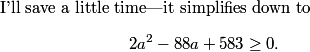
MathTwo 2010-04-02 20:54:50
complete the square or factor

DPatrick 2010-04-02 20:55:02
Since we don't need to explicitly solve it, we might find it easier to complete the square rather than use the quadratic formula.

DPatrick 2010-04-02 20:55:11

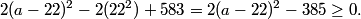
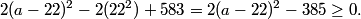
DPatrick 2010-04-02 20:55:24

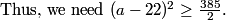
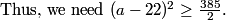
SnowEverywhere 2010-04-02 20:55:45
14

number.sense 2010-04-02 20:55:45
the rhs is about 190, so a-22=14 should suffice

DPatrick 2010-04-02 20:55:50
The right side is 192.5, which lies between 13^2 = 169 and 14^2 = 196.

DPatrick 2010-04-02 20:56:03

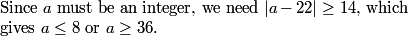
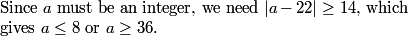
DPatrick 2010-04-02 20:56:18
By the symmetry of the problem, it doesn't matter whether we use a=8 or a=36. 8 seems simpler, but actually 36 gives the exact same calculation.

number.sense 2010-04-02 20:56:47
just plug it in now

DPatrick 2010-04-02 20:56:54

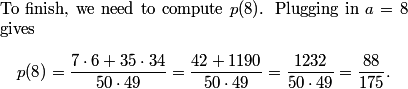
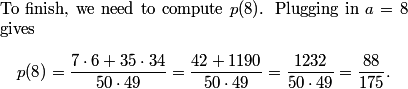
DPatrick 2010-04-02 20:57:05

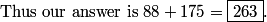
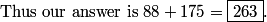
DPatrick 2010-04-02 20:57:50
This was the typical "looks really hard but it's not necessarily that hard" problem that often appears among 11-15 on the AIME.

DPatrick 2010-04-02 20:58:13
We'll finish with two nice geometry problems.

DPatrick 2010-04-02 20:58:20

DPatrick 2010-04-02 20:58:41
We can start by sketching a picture with all the provided information labeled. (Note: it may not be to scale.)

DPatrick 2010-04-02 20:58:45

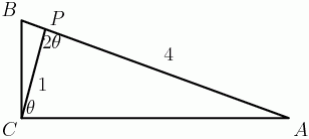
DPatrick 2010-04-02 20:59:09
The only other bit of relevant information that we should note in this diagram is that P is relatively close to B, much closer to B than to A. How do we know for sure?

RminusQ 2010-04-02 20:59:37
We're told that <A is <45 deg

SnowEverywhere 2010-04-02 20:59:37
THe inequality they gave us

DPatrick 2010-04-02 20:59:46
Right, why does that mean that P is closer to B than to A?

number.sense 2010-04-02 21:00:18
well 1<2, so it must be closer to the larger angle

DPatrick 2010-04-02 21:00:42
We know that the median from C to AB has length 2. Since the altitude from C to AB is closer to the short side, all cevians from C to AB with length less than 2 are closer to B than to A. (This is also a bit "obvious" from the picture.)

DPatrick 2010-04-02 21:01:02
So far so good; we've got a workable picture. Now what?

RminusQ 2010-04-02 21:01:29
Start with some liberal use of law of sines

stevenmeow 2010-04-02 21:01:29
Now we can use Law of sines to find the product AP*BP

DPatrick 2010-04-02 21:01:36
One valid solution method is chase angles (that is, write all the angles in the diagram in terms of theta), and then use Law of Sines and Law of Cosines all over the place to set up equations for the lengths.

DPatrick 2010-04-02 21:01:49
This works, and is not too bad, but is a bit inelegant.

DPatrick 2010-04-02 21:01:54
I have a nicer solution in mind.

SnowEverywhere 2010-04-02 21:02:10
Now consider the circumcircle of ABC?

DPatrick 2010-04-02 21:02:18
What might make us consider that option?

SnowEverywhere 2010-04-02 21:02:46
Right angle + double angles

letsruletheworldtogether 2010-04-02 21:02:47
AB is diameter

panjia123 2010-04-02 21:02:47
Right triangle?

ksun48 2010-04-02 21:02:47
ab is diameter

pumpkinpi 2010-04-02 21:02:47
AB is the diameter and we are given that length

number.sense 2010-04-02 21:02:47
AB is the diameter b/c its a right triangle

DPatrick 2010-04-02 21:03:11
Right triangles are nicely inscribed in their circumcircles: the hypotenuse AB will be the diameter, so the radius will be 2.

DPatrick 2010-04-02 21:03:48
But what really makes me eager to try the circumcircle is that we have angles of theta and 2theta, and those are naturally related in a circle as an inscribed angle and a central angle.

DPatrick 2010-04-02 21:03:56
So let's add the circumcircle of ABC and the corresponding central angle to the pic:

DPatrick 2010-04-02 21:04:02

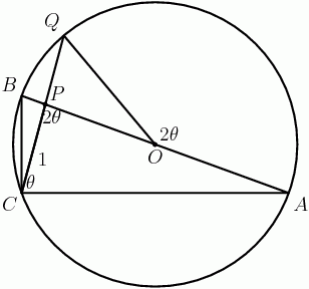
DPatrick 2010-04-02 21:04:59
I extended CP out to Q since it seems "obvious" we'd want to do that. Note QCA intercepts arc QA, so QOA is 2*theta.

DPatrick 2010-04-02 21:05:25
I've got two equal angles in this picture...surely that must be useful somewhere!

SnowEverywhere 2010-04-02 21:05:55
QPO is isosceles

stevenmeow 2010-04-02 21:05:55
QPO is isosceles with vertex Q

MathTwo 2010-04-02 21:05:55
QPO=180-2theta and QOP=180-2theta

billy314 2010-04-02 21:05:55
OPQ is isosceles

DPatrick 2010-04-02 21:06:09
Bingo. Angles QPO and QOP are each 180 - 2*theta, so triangle QPO is isosceles.

DPatrick 2010-04-02 21:06:15
Thus QP = QO.

MathTwo 2010-04-02 21:06:22
then QP=2

MathTwo 2010-04-02 21:06:24
that means QP=2

RminusQ 2010-04-02 21:06:24
But QO is a radius and thus 2

DPatrick 2010-04-02 21:06:33
Right, so now we have QP = 2.

RiteshR 2010-04-02 21:06:38
lol not to scale

mz94 2010-04-02 21:06:38
yay for not to scale diagrams

DPatrick 2010-04-02 21:06:48
Yeah, it's pretty hard to draw this to scale at the beginning.

DPatrick 2010-04-02 21:07:08
What do we do now?

MathTwo 2010-04-02 21:07:35
now use POP

RiteshR 2010-04-02 21:07:35
Power of a Point

modularmarc101 2010-04-02 21:07:35
POP on P?

DPatrick 2010-04-02 21:07:57
Right! We've got CP and QP, and we want to find info about AP and BP, so using Power of a Point at point P seems like a good idea.

DPatrick 2010-04-02 21:08:12
(CP)(PQ) = 1*2 = 2, so (BP)(AP) = 2 as well.

mz94 2010-04-02 21:08:30
x(4-x)=2?

Jongy 2010-04-02 21:08:30
BP(4-BP)=2*1

MathTwo 2010-04-02 21:08:30
but AP=4-BP

RunpengFAILS 2010-04-02 21:08:30
now we win because BP + AP =4....

DPatrick 2010-04-02 21:08:37
Right, on the other hand, AP + BP = 4.

DPatrick 2010-04-02 21:08:47
So it's just a little algebra to finish.

RminusQ 2010-04-02 21:08:56
xy = 2; x+y = 4 can be solved straightforwardly

DPatrick 2010-04-02 21:09:20
Indeed, just substitute one into the other however you see fit.

DPatrick 2010-04-02 21:09:50

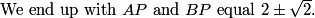
number.sense 2010-04-02 21:10:09
take the ratio

number.sense 2010-04-02 21:10:23
2+sqrt(2)/2-sqrt(2)

DPatrick 2010-04-02 21:10:31
We already decided that AP was larger than BP, so AP is the "+" root and BP is the "-" root.

DPatrick 2010-04-02 21:10:38

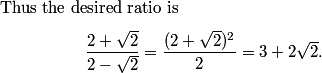
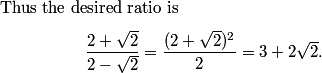
DPatrick 2010-04-02 21:10:48

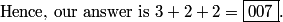
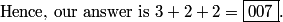
DPatrick 2010-04-02 21:11:14

DPatrick 2010-04-02 21:11:48
Yikes, there's a lot of data presented.

FuzzoMarx 2010-04-02 21:12:25
This picture was really hard to draw.

DPatrick 2010-04-02 21:12:48
It is. Let's just start to parse the data into a diagram. I also find this problem's picture to be a good advertisement for colored pencils.

DPatrick 2010-04-02 21:12:57
We start with M and N: they are just the midpoints of AC and AB. (I'll leave the lengths off for now.)

DPatrick 2010-04-02 21:13:01

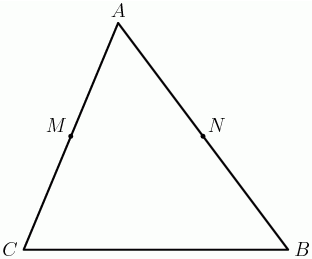
DPatrick 2010-04-02 21:13:13
D and E are the feet of the angle bisectors of ABC and ACB, respectively.

DPatrick 2010-04-02 21:13:25
Our first important question: which side of M does D lie on?

letsruletheworldtogether 2010-04-02 21:13:55
towards C

DPatrick 2010-04-02 21:13:58
How come?

letsruletheworldtogether 2010-04-02 21:14:31
because angle bisector theorem- AB>BC

Jongy 2010-04-02 21:14:31
Angle bisector theorem (AB>CB), so AD>CD

ksun48 2010-04-02 21:14:31
angle bisector theorem

DPatrick 2010-04-02 21:14:42
Right. We know AB = 15 and BC = 14. By the Angle Bisector Theorem, the foot of the bisector lies closer to the shorter side.

DPatrick 2010-04-02 21:14:50
So D lies closer to C than to A.

DPatrick 2010-04-02 21:15:03
In the same way, E lies closer to A than to B, since AC < BC.

DPatrick 2010-04-02 21:15:23
I'll add them to the picture. Note it will not be to scale. (If I drew it to scale, it'd be impossible to see the circles that are coming.)

DPatrick 2010-04-02 21:15:28

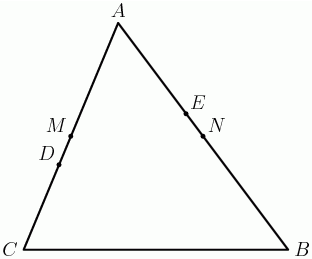
DPatrick 2010-04-02 21:15:45
Next, we draw the circumcircles. I'll draw the circumcircle of the median points in blue and the circumcircle of the bisector points in red. I'll also put in P and Q.

DPatrick 2010-04-02 21:15:51

DPatrick 2010-04-02 21:16:02
OK, there's the picture! :) Now the work begins.

DPatrick 2010-04-02 21:16:22
There's so much data it's hard to know where to start.

DPatrick 2010-04-02 21:16:47
You could bash it with coordinates, for sure. But the numbers are big and ugly.

DPatrick 2010-04-02 21:17:04
Let me try to present a logical, synthetic approach.

DPatrick 2010-04-02 21:17:17
Not knowing where to start, let's start at the end.

DPatrick 2010-04-02 21:17:24
We want to find BQ/CQ. Let's call this x so we can keep track of it.

DPatrick 2010-04-02 21:17:30
What else in the picture is equal to BQ/CQ?

sparkle123 2010-04-02 21:18:03
area abq/area acq

mz94 2010-04-02 21:18:03
area [ABQ]/area [ACQ]

DPatrick 2010-04-02 21:18:12
Since ABQ and ACQ are triangles with the same height, their areas are in the same ratio as the areas of the bases.

DPatrick 2010-04-02 21:18:32

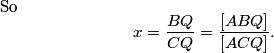
DPatrick 2010-04-02 21:18:49
That's our first step backwards.

DPatrick 2010-04-02 21:19:06
Our overall goal is to keep working backwards until we get something we can explicitly compute with our 13,14,15 data.

DPatrick 2010-04-02 21:19:15
What's the next step backwards? How do we get at those areas?

RunpengFAILS 2010-04-02 21:19:30
So bash the Sines of angles CAQ and QAB.

ksun48 2010-04-02 21:19:30
absinc/2

DPatrick 2010-04-02 21:19:39
We can get at those areas using the (1/2)ab(sin C) formula at point A.

DPatrick 2010-04-02 21:19:51

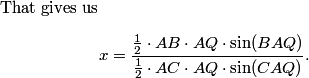
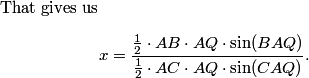
MathTwo 2010-04-02 21:20:26
yay we just have to find sinBAQ and sinCAQ now since we know everything else

DPatrick 2010-04-02 21:20:28
That's good! 1/2 AQ cancels, and we know AB and AC.

DPatrick 2010-04-02 21:20:37

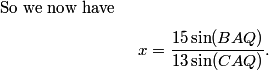
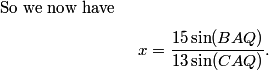
DPatrick 2010-04-02 21:20:51
How do we get at those sines?

FuzzoMarx 2010-04-02 21:21:08
Law of sines

DPatrick 2010-04-02 21:21:20
We need to turn that ratio of sines into a ratio of lengths. So we'll probably need to look to use Law of Sines at some point.

DPatrick 2010-04-02 21:21:45
One thing that will also probably help is that these angles appear in lots of places.

DPatrick 2010-04-02 21:22:02
For instance, angle BAQ is also angle NAP in the blue quadrilateral AMPN, and its also angle EAP in the red quadrilateral ADPE:

DPatrick 2010-04-02 21:22:06

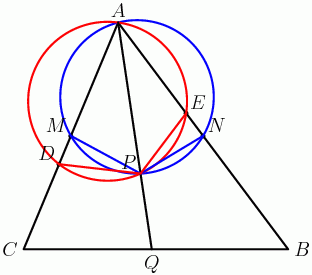
DPatrick 2010-04-02 21:22:31
(I'm trying to keep the important stuff up in the top window.)

DPatrick 2010-04-02 21:22:53
So what triangle(s) might we try Law of Sines on?

quadraticfanatic 2010-04-02 21:23:16
ADP, AEP

DPatrick 2010-04-02 21:23:43
That's a good choice: those are the two triangles that make up cyclic quadrilateral ADPE.

DPatrick 2010-04-02 21:23:49
(the red one in my pic)

sparkle123 2010-04-02 21:23:58
why not the blue ones?

number.sense 2010-04-02 21:24:00
ANP and APM

helloo 2010-04-02 21:24:00
ANP, AMP? since we know AM and AN

DPatrick 2010-04-02 21:24:19
The blue ones AMP and APN work equally well, and in fact I'll use them since that's the way I wrote it up in my notes. :)

DPatrick 2010-04-02 21:24:40
And we'll also want to use the fact that they have side AP in common.

DPatrick 2010-04-02 21:25:17
So we want to write the Law of Sines expressions for APM and APN that relate the side AP and the angles at the top that are part of our expression for x.

DPatrick 2010-04-02 21:25:30

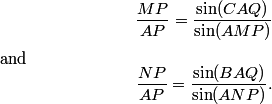
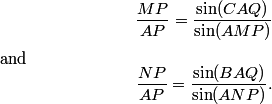
MathTwo 2010-04-02 21:26:10
but sinANP is equal to sinAMP

sparkle123 2010-04-02 21:26:10
sinAMP=sinANP supplementary

DPatrick 2010-04-02 21:26:24
Aha! Cyclic quadrilaterals again to the rescue!

DPatrick 2010-04-02 21:26:33
AMP and ANP are indeed supplementary, since they are opposite angles of the blue cyclic quadrilateral.

DPatrick 2010-04-02 21:26:40
So their sines are equal.

DPatrick 2010-04-02 21:26:47
Let me start doing some of the algebra involved:

DPatrick 2010-04-02 21:27:04

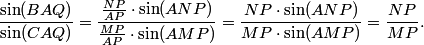
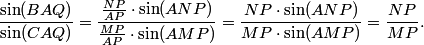
DPatrick 2010-04-02 21:27:26
The first step is just our two Law of Sines calculations from above, and then sin(ANP) = sin(AMP) as we mentioned.

DPatrick 2010-04-02 21:27:39

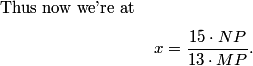
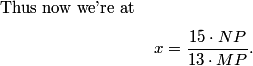
DPatrick 2010-04-02 21:28:00
So now all we need is the ratio NP/MP.

DPatrick 2010-04-02 21:28:24
A ratio of lengths.

DPatrick 2010-04-02 21:28:43
Let me put up the pic again with these segments drawn in:

DPatrick 2010-04-02 21:28:48

RiteshR 2010-04-02 21:29:04
Are triangles PMD and PME similar?

DPatrick 2010-04-02 21:29:13
I think you meant PNE, but that's an interesting question.

DPatrick 2010-04-02 21:29:19
That'd sure be handy if they were.

DPatrick 2010-04-02 21:29:21
Are they?

MathTwo 2010-04-02 21:29:53
yes they are!

RiteshR 2010-04-02 21:29:54
angle chase?

DPatrick 2010-04-02 21:30:09
We already noted that angles ANP and AMP are supplementary (opposite angles of the blue cyclic quadrilateral sum to 180).

DPatrick 2010-04-02 21:30:29
So angles ANP and PMD are equal!

DPatrick 2010-04-02 21:30:52
In the same way, using the red cyclic quadrilateral, angles ADP and AEP are supplementary, so angles ADP and PEN are equal.

DPatrick 2010-04-02 21:31:04
Therefore, triangles PMD and PNE are similar!

DPatrick 2010-04-02 21:31:11
How does that help?

RminusQ 2010-04-02 21:31:29
so that means we just need the ratio EN / MD

panjia123 2010-04-02 21:31:29
NP/MP=EN/MD

sparkle123 2010-04-02 21:31:29
NP/MP=EN/MD

DPatrick 2010-04-02 21:31:35

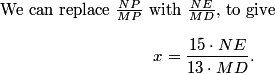
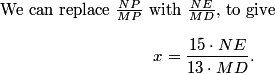
RiteshR 2010-04-02 21:31:57
use angle bisector theorem

sparkle123 2010-04-02 21:31:57
use angle bisector theorem to find AD and AE

RiteshR 2010-04-02 21:31:57
angle bisector theorem now

DPatrick 2010-04-02 21:32:11
Finally, something we can compute with the Angle Bisector Theorem! :)

DPatrick 2010-04-02 21:32:23
Let me put the basic pic back without the circles:

DPatrick 2010-04-02 21:32:31

DPatrick 2010-04-02 21:32:47
For instance, let NE = y. What equation can we write for y?

stevenmeow 2010-04-02 21:33:14
y=AN-AE

number.sense 2010-04-02 21:33:15
y=AN-AE

pumpkinpi 2010-04-02 21:33:15
AN - AE = y

DPatrick 2010-04-02 21:33:35
More importantly, AE = (15/2) - y and BE = (15/2) + y.

DPatrick 2010-04-02 21:33:50
But by the Angle Bisector Theorem, AE/BE = AC/BC = 13/14.

DPatrick 2010-04-02 21:33:59

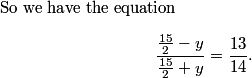
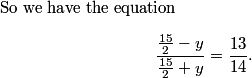
sparkle123 2010-04-02 21:34:16
its 5/18

DPatrick 2010-04-02 21:34:22

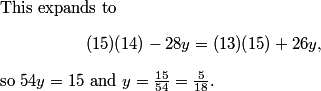
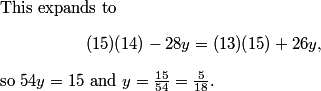
DPatrick 2010-04-02 21:34:49
We can do the same thing on the other side, by letting MD = z.

DPatrick 2010-04-02 21:35:09
We have AD = (13/2) + z and CD = (13/2) - z.

DPatrick 2010-04-02 21:35:19

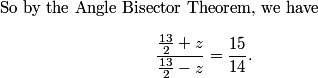
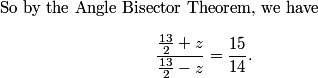
DPatrick 2010-04-02 21:35:41

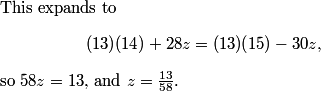
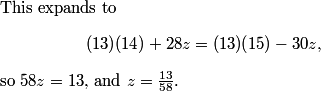
DPatrick 2010-04-02 21:35:52
Now we're at the finish line!

DPatrick 2010-04-02 21:36:08

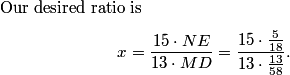
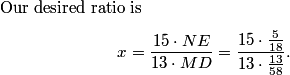
DPatrick 2010-04-02 21:36:31

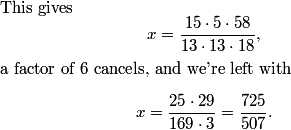
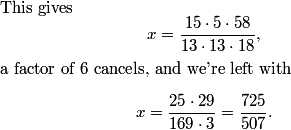
RiteshR 2010-04-02 21:36:53
don't add! m MINUS n!

DPatrick 2010-04-02 21:37:12
Fortunately, adding gives something larger than 1000, so we can't make that mistake.

DPatrick 2010-04-02 21:37:18

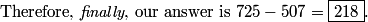
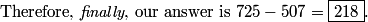
DPatrick 2010-04-02 21:37:49
What I hope you take away from this is how we started at the end and just proceeded, step by step, backwards, using the available data, until we got to something we could compute.

DPatrick 2010-04-02 21:38:26
That's it!

DPatrick 2010-04-02 21:38:35
Thanks for coming!

2010 AIME II Math Jam

Facilitator: David Patrick