Math Jams

DPatrick 2011-02-09 19:30:00
Welcome to the 2011 AMC 10A/12A Math Jam!

DPatrick 2011-02-09 19:30:10
I'm Dave Patrick, and I'll be leading our discussion tonight.

DPatrick 2011-02-09 19:30:23
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.

DPatrick 2011-02-09 19:30:36
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.

DPatrick 2011-02-09 19:30:52
This helps keep the session organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.

DPatrick 2011-02-09 19:31:15
There are a lot of students here! As I said, only well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. This Math Jam is much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!

DPatrick 2011-02-09 19:31:39
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the necessary material for every problem as we go.

DPatrick 2011-02-09 19:31:52
Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!

DPatrick 2011-02-09 19:32:24
Please: do not ask questions during the Math Jam about administrative aspects of the contests. We do not have time to answer them all.

DPatrick 2011-02-09 19:32:47
We do have an assistant tonight who can help answer some of the questions. He is Patrick Hulin (worthawholebean). Patrick started doing math competitions in elementary school and attended National MATHCOUNTS in 2006. In 2010, he received an honorable mention on the USA Math Olympiad. He currently studies math at MIT.

DPatrick 2011-02-09 19:33:02
He can answer questions by whispering to you or by opening a window with you to chat 1-on-1.

DPatrick 2011-02-09 19:33:28
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics.

DPatrick 2011-02-09 19:33:40
So please, when a question is posted, do not simply respond with the final answer. That's not why we're here.

DPatrick 2011-02-09 19:33:50
We're going to work through the problems step-by-step.

DPatrick 2011-02-09 19:34:04
The Math Jam will proceed as follows:

We will work the last 5 problems from the AMC 10A, then the last 5 problems from the AMC 12A. After that, time permitting, I will take requests for some other problems for discussion.

DPatrick 2011-02-09 19:34:24
We'll probably run for 1.5 to 2 hours.

DPatrick 2011-02-09 19:34:37
OK...let's get started with #21 from the AMC 10A:

DPatrick 2011-02-09 19:34:45

DPatrick 2011-02-09 19:34:56
Notice that I will always put the current problem at the top of the window. You can resize the area at the top by dragging the horizontal gray bar.

DPatrick 2011-02-09 19:35:11
How can it occur that the two weights are equal?

EricMathPath09 2011-02-09 19:35:48
There are only two possibilities- you select one couterfeit and one genuine coin both times, or you select two pairs of genuine coins.

Jerry1997 2011-02-09 19:35:48
1 genuine with 1 fake or two genuines on both sides

furrykid 2011-02-09 19:35:48
all real coins, or 1 real and 1 counterfeit in each pair.

DPatrick 2011-02-09 19:35:56
We could either have 4 genuine coins, or each pair could have 1 real and 1 fake coin.

DPatrick 2011-02-09 19:36:06
In how many ways can we pick two pairs of genuine coins?

BOGTRO 2011-02-09 19:36:38
8C2*6C2

christerson 2011-02-09 19:36:38
(8C2)(6C2)

tekgeek 2011-02-09 19:36:38
8C2*6C2

Maxima 2011-02-09 19:36:38
8C2 * 6C2.

DPatrick 2011-02-09 19:36:45
There are 8 genuine coins, so we can select C(8,2) = (8*7)/2 = 28 pairs for the first pair.

DPatrick 2011-02-09 19:36:56
Then, there are 6 genuine coins remaining, so we can select C(6,2) = (6*5)/2 = 15 pairs for the second pair.

DPatrick 2011-02-09 19:37:05
Thus, there are 28*15 ways to select two genuine pairs.

DPatrick 2011-02-09 19:37:16
How about the other possibility? How many ways to select two pairs, each of which is 1 real, 1 fake?

soulspeedy 2011-02-09 19:37:47
8*2*7

exmath89 2011-02-09 19:37:47
8*2*7*1

harukikara 2011-02-09 19:37:47
(2 x 8)(1 x 7)

Iggy Iguana 2011-02-09 19:37:47
8 for the first genuine, 2 for the first fake, 7 for the 2nd genuine, 1 for the 2nd fake.

DPatrick 2011-02-09 19:37:55
For the first pair, there are 8 real and 2 fake to select from, so there are 8*2 = 16 ways to select 1 real, 1 fake.

DPatrick 2011-02-09 19:38:05
For the second pair, there are 7 real and 1 fake remaining to select from, so there are 7*1 = 7 ways to select 1 real and 1 fake.

DPatrick 2011-02-09 19:38:16
So, there are 16*7 ways to select two pairs of 1 real, 1 fake.

DPatrick 2011-02-09 19:38:26
Thus, what is the probability that we want?

Spring 2011-02-09 19:38:55
(28*15)/(28*15+16*7)=15/19

rbhale12 2011-02-09 19:38:55
28*15/(28*15+16*7)

christerson 2011-02-09 19:38:55
the first case over the sum of both cases

Rocket95 2011-02-09 19:38:55
28*15/(28*15+16*7)

DPatrick 2011-02-09 19:39:01

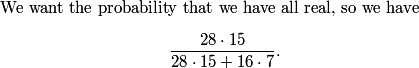
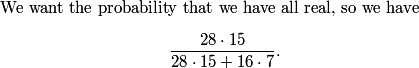
DPatrick 2011-02-09 19:39:13
Rather than expanding this out, what's the easiest way to simplify this?

ProbaBillity 2011-02-09 19:39:25
28 can be cancelled on top and bottom

exmath89 2011-02-09 19:39:25
cancel 28 out

DPatrick 2011-02-09 19:39:30
Divide numerator and denominator by 28.

DPatrick 2011-02-09 19:39:35

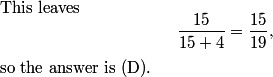
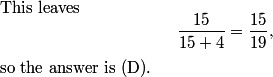
DPatrick 2011-02-09 19:40:05
To reiterate some points from the beginning:

DPatrick 2011-02-09 19:40:24
- yes, about 50 of you posted good comments each time, but I'm only going to post 3 or 4 each time. Please don't complain about this!

DPatrick 2011-02-09 19:40:35
- yes, there are other ways to do the problem. I don't have time to explain them all.

DPatrick 2011-02-09 19:40:50
OK, on to #22:

DPatrick 2011-02-09 19:41:01

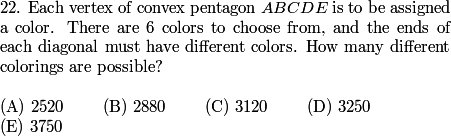
DPatrick 2011-02-09 19:41:31
This problem is also #16 on the AMC12A.

Lord.of.AMC 2011-02-09 19:41:37
casework

professordad 2011-02-09 19:41:37
casework on number of colors

megahertz 2011-02-09 19:41:37
casework!

calculatorwiz 2011-02-09 19:41:37
casework

DPatrick 2011-02-09 19:41:46
We can start with the easiest case. Clearly there are no problems if all the vertices are different colors.

DPatrick 2011-02-09 19:41:51
In how many ways can that happen?

chenboy3 2011-02-09 19:42:08
6*5*4*3*2=720 ways

RisingMathStar 2011-02-09 19:42:08
6*5*4*3*2

xxrxxhxx 2011-02-09 19:42:08
6*5*4*3*2=720

DPatrick 2011-02-09 19:42:18
6*5*4*3*2 = 720 ways. (6 choices for A, then 5 choices for B, and so on)

DPatrick 2011-02-09 19:42:30
For the other case(s): when are we allowed to reuse a color?

TruffleMaster 2011-02-09 19:42:49
when they are adjacent

bulutcocuk 2011-02-09 19:42:49
if they are next to each other

CRICKET229 2011-02-09 19:42:49
when they are adjacent

aopsmath1012 2011-02-09 19:42:49
if the vertices are adjacent

PowerOfPi 2011-02-09 19:42:49
The two vertices of the same color must be adjacent.

DPatrick 2011-02-09 19:42:55
Only when the vertices are next to each other.

DPatrick 2011-02-09 19:43:04
So for our next case, suppose we only decide to reuse 1 color. When can that happen?

DPatrick 2011-02-09 19:43:09
In how many ways?

chenboy3 2011-02-09 19:43:47
5*6*5*4*3=1800

peter6044 2011-02-09 19:43:48
5*6*5*4*3

theax 2011-02-09 19:43:48
there are five ways to pick the pair, so 5*6*5*4*3

DPatrick 2011-02-09 19:43:57
We pick a pair of vertices that are next to each other in 5 ways.
Then we pick a color for that pair in 6 ways.
Then we pick colors for the other three vertices in 5*4*3 ways.

DPatrick 2011-02-09 19:44:12
So the total number of ways to reuse 1 color is 5*6*5*4*3 = 1800.

DPatrick 2011-02-09 19:44:34
We can also reuse 2 colors. In how many ways can we do this?

GeorgiaTechMan 2011-02-09 19:45:06
5*6*5*4=600

remy1140 2011-02-09 19:45:06
5 (indistinguishable pair) * 6 * 5 * 4 = 600

JamesTianyQiaoMa 2011-02-09 19:45:06
5*6*5*4=600

simplyMathLete 2011-02-09 19:45:06
By having two pairs of sides with the same color on each vertex

DPatrick 2011-02-09 19:45:12
This involves choosing two pairs of adjacent vertices.

DPatrick 2011-02-09 19:45:36
This is most easily counted by choosing the fifth (non-matching) vertex, which we can do in 5 ways.
Then we color it in 6 ways.
Then we color the two pairs remaining in 5*4 ways.

DPatrick 2011-02-09 19:45:47
So the total number of ways to reuse two colors is 5*6*5*4 = 600.

DPatrick 2011-02-09 19:46:04
And clearly we can't reuse 3 or more colors -- we don't have enough vertices.

Relativity1618 2011-02-09 19:46:14
thats all the cases isnt it?

GeorgiaTechMan 2011-02-09 19:46:14
now add them up!

Lord.of.AMC 2011-02-09 19:46:22
600 + 1800 + 720 = 3120

PowerOfPi 2011-02-09 19:46:23
600+1800+720=3120

danielguo94 2011-02-09 19:46:23
720+1800+600=3120

DPatrick 2011-02-09 19:46:28
We add our cases, and get a total of 720+1800+600 = 3120 colorings. Answer (C).

DPatrick 2011-02-09 19:47:07
On to #23, which took me a long time to type up this morning:

DPatrick 2011-02-09 19:47:12

professordad 2011-02-09 19:47:40
shouldnt C be 365

ProbaBillity 2011-02-09 19:47:40
typo - answer choice C shold be 365

DPatrick 2011-02-09 19:47:51
oops. You're right. Answer (C) should be 365. (It's important too!)

DPatrick 2011-02-09 19:48:00
I'm not going to regenerate it because it will slow us down.

DPatrick 2011-02-09 19:48:21
Here's a little secret about the AMC and other similar contests: the longer a problem is, the easier it probably is.

DPatrick 2011-02-09 19:48:34
This problem is really wordy, but if you read it carefully, it's actually pretty easy. It's mostly just bookkeeping.

AlphaMath1 2011-02-09 19:48:53
Let's first look at the numbers Alice doesn't say, and try to spot a pattern or an expression for all of them

esque 2011-02-09 19:48:54
Count the first number of each sequence?

DPatrick 2011-02-09 19:49:16
We can just keep track of the first numbers and by how much they skip after each person.

omega1 2011-02-09 19:49:28
Alice doesn't say 2-5-8-11-14...

Ttocs45 2011-02-09 19:49:28
Count the first number and common difference of each sequence

DPatrick 2011-02-09 19:49:42
The numbers remaining after Alice are: 2,5,8,11,14,...

DPatrick 2011-02-09 19:49:51
This list starts at 2, and goes up by 3s.

DPatrick 2011-02-09 19:49:58
So after Barbara speaks, what numbers are remaining?

Caelestor 2011-02-09 19:50:19
5, 14, 23, ...

Rocket95 2011-02-09 19:50:19
5, 14, 23...

Iggy Iguana 2011-02-09 19:50:19
Remaining after Barbara is 5, 14, 23, ...

Ttocs45 2011-02-09 19:50:19
Starts at 5, common difference of 9

TruffleMaster 2011-02-09 19:50:19
5 going up by 9

DPatrick 2011-02-09 19:50:26
5,14,23,...
That is, they start at 5, and go up by 9s.

DPatrick 2011-02-09 19:50:48
After Candice? (Let's not list them anymore: we only need the starting number and by how much they go up by.)

Iggy Iguana 2011-02-09 19:51:04
Then 14 going up by 27

vcez 2011-02-09 19:51:04
14 going up by 27

Ttocs45 2011-02-09 19:51:04
Starts at 14, common difference of 27.

sup3rcrash3r 2011-02-09 19:51:04
14 and up by 27

xxrxxhxx 2011-02-09 19:51:04
14, up by 27

DPatrick 2011-02-09 19:51:10
The list starts at 5+9 = 14, and goes up by 9*3 = 27.

DPatrick 2011-02-09 19:51:18
After Debbie?

prezcoin 2011-02-09 19:51:32
41 and goes up by 81

agejiageji 2011-02-09 19:51:33
41 and up by 81

paperfury 2011-02-09 19:51:33
41 goung up by 81

superpi83 2011-02-09 19:51:33
41 going up by 81

JamesTianyQiaoMa 2011-02-09 19:51:33
41 going up by 81

DPatrick 2011-02-09 19:51:38
The list starts at 14+27 = 41, and goes up by 81s.

DPatrick 2011-02-09 19:51:43
After Eliza?

TruffleMaster 2011-02-09 19:51:55
122 going up by 243

christerson 2011-02-09 19:51:55
122 going up by 243

Jerry1997 2011-02-09 19:51:55
122 goes up by 243

pi31415926 2011-02-09 19:51:55
122 and up by 243

DPatrick 2011-02-09 19:52:00
The list starts at 41+81 = 122, and goes up by 243s.

DPatrick 2011-02-09 19:52:05
After Fatima?

lab 2011-02-09 19:52:17
365 going up by 729s and you're done.

fmasroor 2011-02-09 19:52:17
365 goin up by 729

henrypickle 2011-02-09 19:52:17
365 going up by 729s

DPatrick 2011-02-09 19:52:21
The list starts at 122+243 = 365, and goes up by 729s.

DPatrick 2011-02-09 19:52:27
So George says the only remaining number, 365. Answer (C).

DPatrick 2011-02-09 19:52:38
As a check, note that 365 + 729 > 1000, so indeed there is only one number left when it's George's turn.

DPatrick 2011-02-09 19:53:13
Let's continue on to #24:

DPatrick 2011-02-09 19:53:19

fmasroor 2011-02-09 19:53:35
can you put up a diagram?

flamingmath 2011-02-09 19:53:35
draw a diagram

DPatrick 2011-02-09 19:53:59
In order to make a diagram, what do we need to know about the vertices of the tetrahedra? How are they arranged?

gomath888 2011-02-09 19:54:28
no two adjacent

simplyMathLete 2011-02-09 19:54:28
No 2 of them adjacent

Shoelace Thm. 2011-02-09 19:54:28
Symetrically opposite

DPatrick 2011-02-09 19:54:35
They alternate vertices on the cube:

DPatrick 2011-02-09 19:54:41

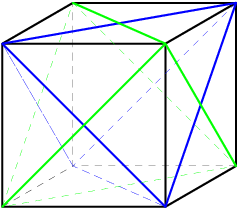
DPatrick 2011-02-09 19:54:52
One is blue, one is green.

DPatrick 2011-02-09 19:55:07
This picture is kind of noisy, though. Let's just look at the blue one.

DPatrick 2011-02-09 19:55:14

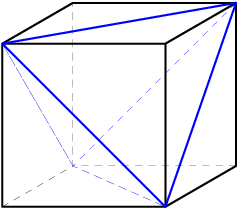
DPatrick 2011-02-09 19:55:25
What might be nice to know about this tetrahedron?

fmasroor 2011-02-09 19:55:40
so how much volume does that have

danielguo94 2011-02-09 19:55:40
its volume

the cliu 2011-02-09 19:55:40
its volume

DPatrick 2011-02-09 19:55:55
Right, that's probably helpful. How do we determine its volume?

Uday J Uppal 2011-02-09 19:56:35
you could do complimentary counting: find volume of total cube and then subtract certain places.

fmasroor 2011-02-09 19:56:35
subtracting the areas of the 'prisms' around it

DPatrick 2011-02-09 19:56:43
Right. It's the whole cube, minus 4 pieces.

DPatrick 2011-02-09 19:57:11
Each missing piece is a pyramid with height 1 and whose base is a isosceles right triangle with legs 1. (This is easiest to see in the pic by looking at the cube vertex on top in the front right.)

mathlead 2011-02-09 19:57:30
find the base's area and multiply by height/3

chenboy3 2011-02-09 19:57:30
base*height/3

2redpartyhats 2011-02-09 19:57:30
(1/3) base*height

DPatrick 2011-02-09 19:57:57
Right: each of these pyramidal pieces we have to cut away is a pyramid with height 1 and whose base is an isosceles right triangle with legs 1.

xxrxxhxx 2011-02-09 19:58:09
each piece has volume 1*1*1/2*1/3 = 1/6, subtract 4 of them to get 1/3 for the area of the tetrahedron

danielguo94 2011-02-09 19:58:11
The pieces have 1*1*1/2*1/3 = 1/6 volume each

DPatrick 2011-02-09 19:58:21
So each missing piece has volume (1/3)*(1/2)*1 = 1/6.

scgorantla 2011-02-09 19:58:37
and there are 4.

PowerOfPi 2011-02-09 19:58:41
1-4*1/6 = 1/3

DPatrick 2011-02-09 19:58:51
Thus, the volume of each tetrahedron is 1 - 4(1/6) = 1/3.

DPatrick 2011-02-09 19:59:07
Using this, how do we compute the volume of the overlap?

gaga654 2011-02-09 19:59:43
subtract the smaller tetrahedra not in the overlap

esque 2011-02-09 19:59:43
Subtract the smaller tetraherdons?

PowerOfPi 2011-02-09 19:59:43
subtract parts in blue tetrahedron but outside green tetrahedron

DPatrick 2011-02-09 19:59:51
Right: let me put up the combined picture again:

DPatrick 2011-02-09 19:59:57

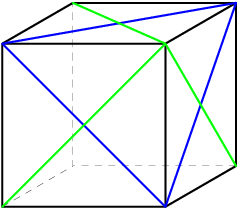
DPatrick 2011-02-09 20:00:05
(I took the hidden sides out to make it easier to see)

GeorgiaTechMan 2011-02-09 20:00:23
wouldn't there be four parts that are not in the green tetrahedron but in the blue tetrahedrons

DPatrick 2011-02-09 20:00:45
Right. Where do the blue and green tetrahedra intersect?

Spring 2011-02-09 20:01:05
At the midpoints of the sides

Uday J Uppal 2011-02-09 20:01:05
midpoint of the diagonals of the square faces

DPatrick 2011-02-09 20:01:08
Right.

DPatrick 2011-02-09 20:01:37
So there is a small tetrahedron, with sides exactly half the length, at each of the 4 vertices of the blue tetrahedron that is outside the green tetrahedron.

DPatrick 2011-02-09 20:01:50
(It can be hard to visualize this so think about it some more later if you don't see it right now.)

GeorgiaTechMan 2011-02-09 20:02:02
so the area of each small tetrahedron is 1/2^3=1/8 the area of each of the large tetrahedra

AlphaMath1 2011-02-09 20:02:03
ratio of volumes = (1/2)^3=1/8

Spring 2011-02-09 20:02:03
So the volume is 1/8 of the large tetrahedron

PowerOfPi 2011-02-09 20:02:03
thus, its volume is (1/2)^3 = 1/8 of the big one

DPatrick 2011-02-09 20:02:16
Right: each small tetrahedron has (1/2)^3 = 1/8 of the volume of the big one.

DPatrick 2011-02-09 20:02:22
So removing four of them leaves 4/8 = 1/2 of the volume of the whole.

AlphaMath1 2011-02-09 20:02:38
1/2*1/3=1/6

GausssWill 2011-02-09 20:02:39
So 1/6

DPatrick 2011-02-09 20:02:51
Since the whole blue tetrahedron has volume 1/3, the common region has volume 1/2 * 1/3 = 1/6. Answer (D).

DPatrick 2011-02-09 20:03:20
You could also do this problem directly by determining the region where they intersect and computing its volume directly, but I find this "cutting away pieces" solution more elegant.

DPatrick 2011-02-09 20:03:48
Next is #25 on the AMC 10A, which is also #22 on the AMC 12A:

DPatrick 2011-02-09 20:03:59

DPatrick 2011-02-09 20:04:38
How can we set this up?

GausssWill 2011-02-09 20:05:00
Draw a square

professordad 2011-02-09 20:05:00
diagram.

googol.plex 2011-02-09 20:05:00
draw a square

osmosis92 2011-02-09 20:05:00
first you need a square

DVA6102 2011-02-09 20:05:00
draw a square

DPatrick 2011-02-09 20:05:13
You could draw it if it helps you visualize, but I didn't do a drawing.

Iggy Iguana 2011-02-09 20:05:28
Let R be a unit square and let X be (a,b)

DPatrick 2011-02-09 20:05:47
I'll do this (almost). To help with the calculations, we can assume that R is the unit square with lower-left corner (0,0), and let X = (x,y) be the point.

DPatrick 2011-02-09 20:06:05
What do we know about the rays?

AlphaMath1 2011-02-09 20:06:29
they must meet the vertices

victorzhouaops 2011-02-09 20:06:30
4 of them must go to teh corners

briantix 2011-02-09 20:06:30
4 hit the corners

tan90 2011-02-09 20:06:30
Four of them must go through the verticies of the square

GeorgiaTechMan 2011-02-09 20:06:30
there must be 4 reaching the vertices or else we have quadrilaterals too

DPatrick 2011-02-09 20:06:41
Since each region must be a triangle, we must have rays to the four corners of the square. Otherwise the corner is part of a quadrilateral.

DPatrick 2011-02-09 20:06:57
So the triangles will all have their bases on one side of the square and have vertex X.

DPatrick 2011-02-09 20:07:20
What do we know about the points where the rays hit the sides of the square?

xixianxiang 2011-02-09 20:07:53
dividing sides into equal parts

Kestzh 2011-02-09 20:07:53
equal lengths

fmasroor 2011-02-09 20:07:53
they have to have the same base

happystuff123 2011-02-09 20:07:53
They interesect at equal intervals

CantonMathGuy 2011-02-09 20:07:53
they are equidistant

prezcoin 2011-02-09 20:07:53
evenly spaced for each side

JSGandora 2011-02-09 20:07:53
they must be evenly spaced on both sides.

DPatrick 2011-02-09 20:08:15
Right. Since to any side, all the triangles on that side will have the same height, and they must have the same area, they must all have the same base.

DPatrick 2011-02-09 20:08:23
So the rays must divide each side into pieces of equal size.

DPatrick 2011-02-09 20:08:41
Let's set up some more notation so we can more easily talk about what's going on. Suppose that the rays divide the four sides (bottom, right, top, and left) into a, b, c, and d pieces.

DPatrick 2011-02-09 20:08:53
What are the areas of the triangles?

connaissance 2011-02-09 20:09:08
1/n

prezcoin 2011-02-09 20:09:08
1/n

gaga654 2011-02-09 20:09:08
1/n

DPatrick 2011-02-09 20:09:17
Right. I didn't ask that question precisely enough.

DPatrick 2011-02-09 20:09:47
Let's look at the bottom first. If the point X = (x,y) and we divide the bottom into a pieces, what is the area of each triangle we get?

gh625 2011-02-09 20:10:23
y/2a

connaissance 2011-02-09 20:10:24
y/(2a)

ProbaBillity 2011-02-09 20:10:24
ay/2

limac 2011-02-09 20:10:24
the base is 1/a, and height is y, so y/2a.

DPatrick 2011-02-09 20:10:54
Right. The height is y and the bases are each 1/a, so the area is y/2a.

DPatrick 2011-02-09 20:11:20

DPatrick 2011-02-09 20:11:58
But the triangles on all four sides have to have the same areas.

DPatrick 2011-02-09 20:12:12

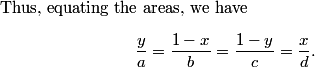
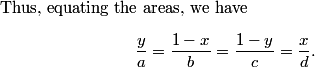
gaga654 2011-02-09 20:12:26
=1/n

DPatrick 2011-02-09 20:12:32
...and indeed they all equal 1/n.

DPatrick 2011-02-09 20:12:43
...actually I took the 1/2 out, so these all equal 2/n.

DPatrick 2011-02-09 20:12:51
How do we work with these equations?

simplyMathLete 2011-02-09 20:13:25
we could work with the a equation and the c one

DPatrick 2011-02-09 20:13:42
That's an idea: we can use the first and third to solve for y.

DPatrick 2011-02-09 20:13:51
Solving for y seems like a good idea since we want to count the possible (x,y).

simplyMathLete 2011-02-09 20:14:17
manipulating, y = a/(a + c)

AlphaMath1 2011-02-09 20:14:18
y/a=1-y/c cross multiplying gives cy=a-ay

DPatrick 2011-02-09 20:14:25

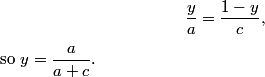
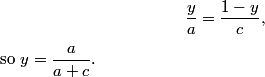
rubiks3.14 2011-02-09 20:14:39
now do it for x

chenboy3 2011-02-09 20:14:44
now solve for x

DPatrick 2011-02-09 20:14:50

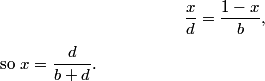
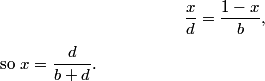
DPatrick 2011-02-09 20:15:37

DPatrick 2011-02-09 20:15:47
What else do we know?

Iggy Iguana 2011-02-09 20:16:04
doesn't a+c=b+d

DPatrick 2011-02-09 20:16:12
How do we know this?

csprunger95 2011-02-09 20:16:53
a little manipulation

mathcricket 2011-02-09 20:16:53
cross multiplication

AlphaMath1 2011-02-09 20:17:12
y/a=x/d ----> 1/a+c=1/b+d ----> a+c=b+d

DPatrick 2011-02-09 20:17:29

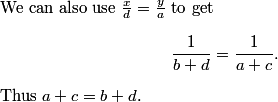
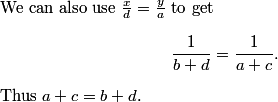
ilovepink 2011-02-09 20:17:39
doesn't a+c+b+d=n, because there are n triangles?

DPatrick 2011-02-09 20:17:46
Aha, we have that information too.

DPatrick 2011-02-09 20:17:55
Thus, since a+c = b+d, they are both equal to n/2.

gaga654 2011-02-09 20:18:13
so it's (2d/n,2a/n)

chenboy3 2011-02-09 20:18:17
so X is now (2d/n,2a/n)

DPatrick 2011-02-09 20:18:37

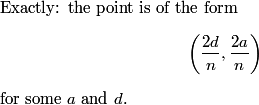
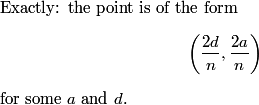
DPatrick 2011-02-09 20:18:48
What are the restrictions on a and d?

rubiks3.14 2011-02-09 20:19:20
have to be less than n/2

ilovepink 2011-02-09 20:19:20
a <n/2, d<n/2?

DPatrick 2011-02-09 20:19:33
We need at least 1 triangle on each side, so we must have a and d be strictly between 0 and n/2.

DPatrick 2011-02-09 20:19:44
Now what?

girishvar12 2011-02-09 20:20:12
plug in numbers?

bulutcocuk 2011-02-09 20:20:13
start counting!

vwu9 2011-02-09 20:20:21
plug in 60,100 for n?

DPatrick 2011-02-09 20:20:41

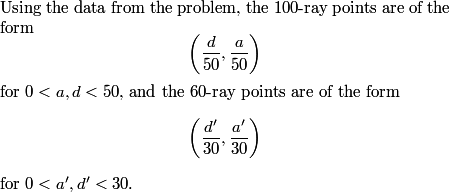
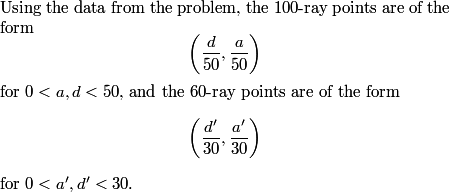
DPatrick 2011-02-09 20:21:05
First, how many of the 100-ray points are there?

Iggy Iguana 2011-02-09 20:21:25
49^2

gh625 2011-02-09 20:21:25
49^2

fractals 2011-02-09 20:21:25
49^2

danielguo94 2011-02-09 20:21:25
49^2

paperfury 2011-02-09 20:21:25
49*49

DPatrick 2011-02-09 20:21:36
a and d can each be between 1 and 49 (inclusive), so there are 49^2 of them.

DPatrick 2011-02-09 20:21:43
But when can a 100-ray point also be used as a 60-ray point?

TachyonPulse 2011-02-09 20:22:24
when d/50 = d'/30 and a/50 = a'/30

rubiks3.14 2011-02-09 20:22:25
when a or d/50 can be translated to something else /30

DPatrick 2011-02-09 20:22:33
Right: to do this, we need to be able to convert the denominator of 50 to a denominator of 30.

danielguo94 2011-02-09 20:22:37
when a and d are divisble by 5

DPatrick 2011-02-09 20:22:53
Right. This gives a' = (3/5)a and d' = (3/5)d. But we can only do this is a and d are multiples of 5.

gaga654 2011-02-09 20:23:10
there are 9^2 such points

Iggy Iguana 2011-02-09 20:23:10
there are 9*9=81 ways to not satisfy the problem.

VIPMaster 2011-02-09 20:23:10
there are 9 cases of this

DPatrick 2011-02-09 20:23:44
Indeed: there are 9 multiples of 5 between 0 and 50. When both a and d are both multiples of 5, those points have to be excluded from our earlier count. There are 9 multiples of 5, so there are 9^2 pairs.

Iggy Iguana 2011-02-09 20:23:56
49^2 - 9^2 = 58*40 = 2320.

briantix 2011-02-09 20:23:57
so 2401-81=2320?

DVA6102 2011-02-09 20:23:57
:.(49+9)(49-9)

fractals 2011-02-09 20:24:05
49^2 total and 9^2 that don't satisfy, so 49^2-9^2=(49-9)(49+9)=20*78=2320 (C)

DPatrick 2011-02-09 20:24:07

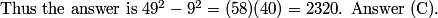
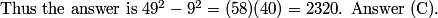
DPatrick 2011-02-09 20:24:41
To me this was clearly the hardest problem on the 10A. It required several steps to get from start to finish.

DPatrick 2011-02-09 20:25:30
I am going to take a 2-minute break to give my fingers a rest from typing, and then we'll come back with #21 on the AMC12.

DPatrick 2011-02-09 20:27:44
OK, I'm back and I've got my second wind now. :)

DPatrick 2011-02-09 20:27:56
We'll continue with #21 from the AMC 12:

DPatrick 2011-02-09 20:28:03

DPatrick 2011-02-09 20:28:27
First, be sure you understand the notation.

DPatrick 2011-02-09 20:28:33

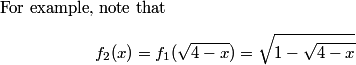
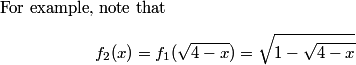
DPatrick 2011-02-09 20:28:56
How can we approach this problem?

lg5293 2011-02-09 20:29:17
find domain at each step

AlphaMath1 2011-02-09 20:29:17
Start with f_1 and work your way upwards?

moplam 2011-02-09 20:29:17
look at domain of f_1 then f_2, etc

BarbieRocks 2011-02-09 20:29:17
first few cases

DPatrick 2011-02-09 20:29:26
Let's just try to keep track of the domains and see where it gets us.

DPatrick 2011-02-09 20:29:33
What is the domain of f_1?

VIPMaster 2011-02-09 20:30:02
x<=1

Ttocs45 2011-02-09 20:30:02
x <= 1

connaissance 2011-02-09 20:30:02
x<=1

xxrxxhxx 2011-02-09 20:30:02
(-inf, 1]

DPatrick 2011-02-09 20:30:09

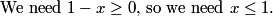
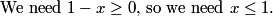
DPatrick 2011-02-09 20:30:31

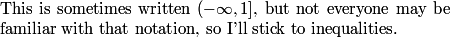
DPatrick 2011-02-09 20:30:41
What is the domain of f_2?

DPatrick 2011-02-09 20:31:20
How can we figure it out systematically?

gh625 2011-02-09 20:31:26
sqrt{4-x}<=1

DPatrick 2011-02-09 20:31:37

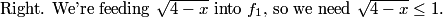
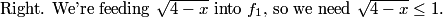
DPatrick 2011-02-09 20:32:03
What inequality does this give us for x?

EricMathPath09 2011-02-09 20:32:13
3<=x<=4

xxrxxhxx 2011-02-09 20:32:13
3<=x<=4

christerson 2011-02-09 20:32:13
3<= x <= 4

DPatrick 2011-02-09 20:32:28

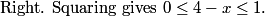
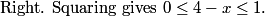
DPatrick 2011-02-09 20:32:36

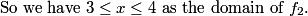
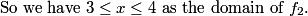
DPatrick 2011-02-09 20:32:42
Now what?

lg5293 2011-02-09 20:32:51
now go to f_3

BarbieRocks 2011-02-09 20:32:55
keep going?

theax 2011-02-09 20:32:55
same thing!

DPatrick 2011-02-09 20:32:59
What is the domain of f_3?

moplam 2011-02-09 20:33:17
3<=sqrt(9-x)<=4

iamnew 2011-02-09 20:33:18
feed sqrt(9-x) in that

lg5293 2011-02-09 20:33:18
3 <= sqrt{9-x} <= 4

gaga654 2011-02-09 20:33:18
3<=sqrt{9-x}<=4

DPatrick 2011-02-09 20:33:22

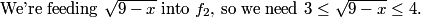
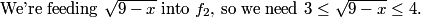
DPatrick 2011-02-09 20:33:40
What does that give for x?

moplam 2011-02-09 20:33:56
9<=9-x<=16 --> -7 <= x <=0

ilovepink 2011-02-09 20:33:56
-7<=x<=0

GeorgiaTechMan 2011-02-09 20:33:56
so -7 <=x<=0

fractals 2011-02-09 20:33:56
-7<=x<=0

DPatrick 2011-02-09 20:34:12

DPatrick 2011-02-09 20:34:18

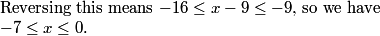
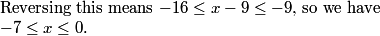
fmasroor 2011-02-09 20:34:26
isn't this eventually gonna end?

DPatrick 2011-02-09 20:34:29
I hope so!

centralbs 2011-02-09 20:34:34
and our next radical cannot be negative, so it must equal zero

DPatrick 2011-02-09 20:34:43
Aha...this seems important!

DPatrick 2011-02-09 20:34:57

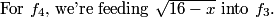
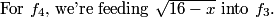
JamesTianyQiaoMa 2011-02-09 20:35:07
sqrt(16-x)=0

moplam 2011-02-09 20:35:07
well, for f_4, sqrt( 16 -x) = 0 is the only case

DPatrick 2011-02-09 20:35:25
But sqrt(16-x) is nonnegative by definition, and the only nonnegative number that f_3 can take is 0.

DPatrick 2011-02-09 20:35:35

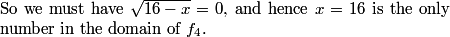
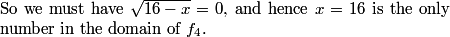
VIPMaster 2011-02-09 20:35:44
But be careful, this is not the last case

EricMathPath09 2011-02-09 20:35:47
We have not shown this to be the largest value of N, though./

DPatrick 2011-02-09 20:36:06
Indeed, there's a trap here. The problem asked for the LARGEST value of n with a single number in its domain, not the smallest.

DPatrick 2011-02-09 20:36:12
So we have to keep going!

DPatrick 2011-02-09 20:36:26

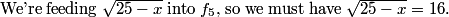
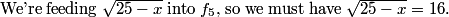
DPatrick 2011-02-09 20:36:36
oops...scratch that...

DPatrick 2011-02-09 20:36:45

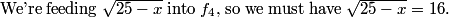
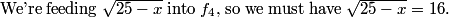
paperfury 2011-02-09 20:37:04
Thus, x=-231

Ttocs45 2011-02-09 20:37:04
x must be -231

simplyMathLete 2011-02-09 20:37:04
x = -231

JamesTianyQiaoMa 2011-02-09 20:37:04
x=-231

DPatrick 2011-02-09 20:37:10

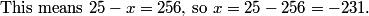
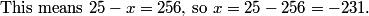
DPatrick 2011-02-09 20:37:17

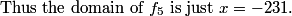
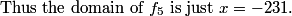
AlphaMath1 2011-02-09 20:37:29
next radical cannot equal -231

gaga654 2011-02-09 20:37:29
this is the last one that works

simplyMathLete 2011-02-09 20:37:29
and that's the last one! because x is negative

DPatrick 2011-02-09 20:37:44

DPatrick 2011-02-09 20:38:06
But that can't happen, since the left side of the above equation can't be negative.

paperfury 2011-02-09 20:38:13
So c=-231 and N=5

DPatrick 2011-02-09 20:38:19
Aha, we're done! We have N=5 and c = -231.

BarbieRocks 2011-02-09 20:38:29
5+(-231)=-226 (A)

xixianxiang 2011-02-09 20:38:29
hence -231+5 = -226

chenboy3 2011-02-09 20:38:29
therefore the sum is -231+5=-226

DPatrick 2011-02-09 20:38:34
Their sum is -226. Answer (A).

DPatrick 2011-02-09 20:38:59
We already did #22: it was the n-ray partition problem.

DPatrick 2011-02-09 20:39:03
So we'll press on to #23:

DPatrick 2011-02-09 20:39:10

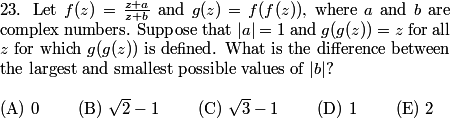
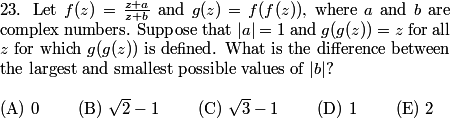
DPatrick 2011-02-09 20:39:32
How can we approach this?

Caelestor 2011-02-09 20:39:51
find an expression for g(z)

Cortana 2011-02-09 20:39:52
find g(z)

lg5293 2011-02-09 20:39:52
see what f(f(z)) is

DPatrick 2011-02-09 20:39:58
Maybe we should try to write down what these functions are.

DPatrick 2011-02-09 20:40:08
First, we can write down g(z) by plugging in f(z) for z in the definition of f(z):

DPatrick 2011-02-09 20:40:14

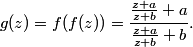
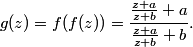
DPatrick 2011-02-09 20:40:29
(You guys shouldn't try to type in these expressions ... I'll do the icky algebra for you!)

fmasroor 2011-02-09 20:40:41
lets simplify that a little bit

DPatrick 2011-02-09 20:40:47
Multiplying numerator and denominator by z+b simplifies this:

DPatrick 2011-02-09 20:40:52

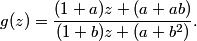
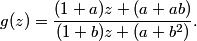
DPatrick 2011-02-09 20:41:12
We could try to write an expression for g(g(z)), but that seems messy.

DPatrick 2011-02-09 20:41:44
Rather than expand g(g(z)) all the way out, what else could we try?

theax 2011-02-09 20:41:54
g(z) is its own inverse function!

DPatrick 2011-02-09 20:42:01
How does that help?

PowerOfPi 2011-02-09 20:42:17
switch g(z) and z

DPatrick 2011-02-09 20:42:47
Aha! If we flip z and g(z) in the above expression, it will still be true! That's because g(z) is its own inverse.

DPatrick 2011-02-09 20:42:57

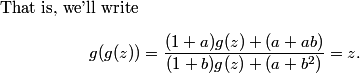
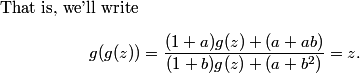
DPatrick 2011-02-09 20:43:17
What do we want to do with this?

BarbieRocks 2011-02-09 20:43:34
solve for g(z)

VIPMaster 2011-02-09 20:43:34
Now we can get g(z) in terms of z

centralbs 2011-02-09 20:43:34
Solve for g(z).... :(

GeorgiaTechMan 2011-02-09 20:43:34
could we find g(z) in terms of z using this?

gh625 2011-02-09 20:43:34
Solve for g(z) and set it equal to the original expression for g(z)

DPatrick 2011-02-09 20:43:40
Indeed: we can solve for g(z), and compare it to our earlier expression for g(z):

DPatrick 2011-02-09 20:43:51
Again, I'll do the messy algebra for you. :)

DPatrick 2011-02-09 20:43:57

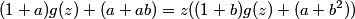
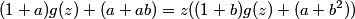
DPatrick 2011-02-09 20:44:08

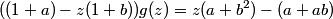
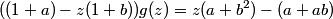
DPatrick 2011-02-09 20:44:17

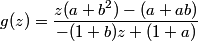
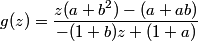
xixianxiang 2011-02-09 20:44:41
equate the two expressions

DPatrick 2011-02-09 20:44:43
And we can equate this to our earlier equation for g(z) (that I saved up at the top):

DPatrick 2011-02-09 20:44:48

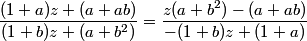
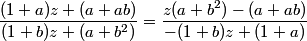
GeorgiaTechMan 2011-02-09 20:45:01
cross multiply

DPatrick 2011-02-09 20:45:06

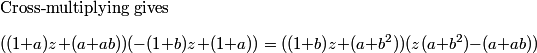
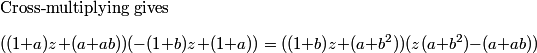
jeanlucwat 2011-02-09 20:45:11
this is getting messy...

DPatrick 2011-02-09 20:45:19
True, but the pretty part is coming up soon!

DPatrick 2011-02-09 20:45:39
I don't want to expand it all out necessarily...what do I want to do?

penguinshin 2011-02-09 20:46:00
equate the constants?

DPatrick 2011-02-09 20:46:20
Even more than that: I have a quadratic on both sides that are equal, so let's equal the z^2, z, and constant coefficents:

DPatrick 2011-02-09 20:46:26

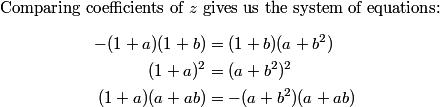
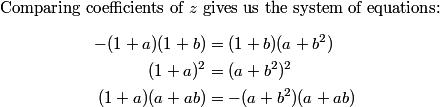
DPatrick 2011-02-09 20:46:37

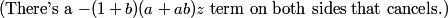
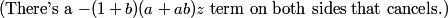
jeanlucwat 2011-02-09 20:46:59
divide by a+ab

Cortana 2011-02-09 20:46:59
(a+ab) cancel

DPatrick 2011-02-09 20:47:05
No can do. Why not?

gh625 2011-02-09 20:47:14
it could be 0

Caelestor 2011-02-09 20:47:14
might be 0

centralbs 2011-02-09 20:47:14
It could equal zero

andrewjjiang97 2011-02-09 20:47:14
Could be 0

DPatrick 2011-02-09 20:47:20
Right. And that's the whole point!

DPatrick 2011-02-09 20:47:32
If I clean up my system a little by factoring common factors, I get:

DPatrick 2011-02-09 20:47:41

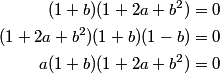
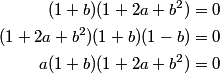
DPatrick 2011-02-09 20:48:02
What do we conclude from this system?

centralbs 2011-02-09 20:48:11
b=-1 works

calculus321 2011-02-09 20:48:12
b=-1

DPatrick 2011-02-09 20:48:22
b = -1 is certainly a solution.

DPatrick 2011-02-09 20:48:38
And if b is anything other than -1, what must we have?

simplyMathLete 2011-02-09 20:48:56
the other is 1 + 2a + b^2 = 0

fractals 2011-02-09 20:48:56
b^2+2a+1=0

gh625 2011-02-09 20:48:56
1+2a+b^2=0

xxrxxhxx 2011-02-09 20:48:56
1+2a+b^2 = 0

DPatrick 2011-02-09 20:49:12
Right, otherwise we must have 1 + 2a + b^2 = 0.

VIPMaster 2011-02-09 20:49:31
|a| = 1, that would be useful right about now!

DPatrick 2011-02-09 20:49:43
Indeed, given that |a| = 1, what do we know about |b|?

jeanlucwat 2011-02-09 20:50:01
-1-2a=b^2

DPatrick 2011-02-09 20:50:22

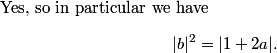
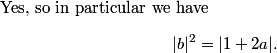
DPatrick 2011-02-09 20:50:39
What are the possible values of |1+2a| if we know |a| = 1?

jraz27 2011-02-09 20:51:12
3 or 1

andrewjjiang97 2011-02-09 20:51:12
3, 1

Iggy Iguana 2011-02-09 20:51:12
1 or 3

christerson 2011-02-09 20:51:12
3 or 1

bulutcocuk 2011-02-09 20:51:12
1 , 3

DPatrick 2011-02-09 20:51:33
Certainly a=1 gives |b|^2 = 3 and a=-1 gives |b| = 1.

DPatrick 2011-02-09 20:51:49
In the complex plane it can take any value in between too, but we only care about the largest and smallest.

DPatrick 2011-02-09 20:52:04

DPatrick 2011-02-09 20:52:31
We'll continue on to #24:

DPatrick 2011-02-09 20:52:37

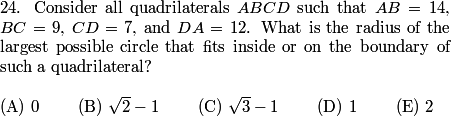
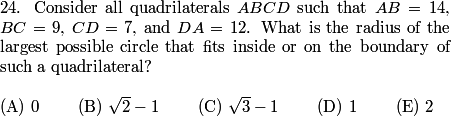
theone142857 2011-02-09 20:53:03
Answer choices

DPatrick 2011-02-09 20:53:14
Oops, these are the choices from the last problem! :(

DPatrick 2011-02-09 20:53:32
hang on a sec...

DPatrick 2011-02-09 20:54:03

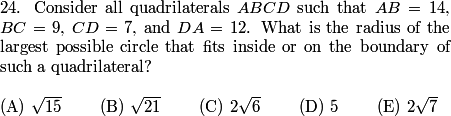
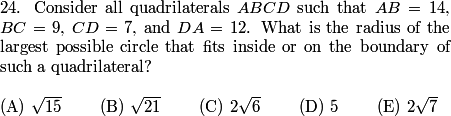
DPatrick 2011-02-09 20:54:10
Better? :)

DPatrick 2011-02-09 20:54:19
What can we say about the largest possible circle that fits inside quadrilateral ABCD?

BarbieRocks 2011-02-09 20:54:37
Opposite sides dd up to the same thing, so it MUST have an incircle.

gomath888 2011-02-09 20:54:37
inscribed

megahertz 2011-02-09 20:54:37
it is tangent to the sides

bulutcocuk 2011-02-09 20:54:37
it touches the boundaries

chenboy3 2011-02-09 20:54:37
it must border all sides of the quadrilateral

DPatrick 2011-02-09 20:54:41
The largest possible circle that fits inside quadrilateral ABCD is the circle that is tangent to all sides, also known as the incircle of quadrilateral ABCD.

DPatrick 2011-02-09 20:54:48

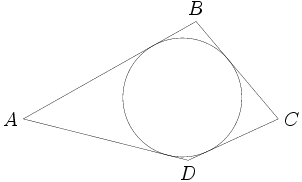
GeorgiaTechMan 2011-02-09 20:54:58
it is inscribed in quadrilateral ABCD since AB+CD=BC+AD

DPatrick 2011-02-09 20:55:09
Quadrilateral ABCD has an incircle if and only if AB + CD = BC + DA, which is the case here. This is a standard result in quadrilaterals. (It's also not hard to prove if you'd like to try it as an exercise, but I'll skip this now.)

DPatrick 2011-02-09 20:55:22
And if a quadrilateral has an incircle, then it is clearly the largest circle that fits inside the quadrilateral.

DPatrick 2011-02-09 20:55:33
What can we say about the radius of the incircle? How does it relate to the quadrilateral?

BarbieRocks 2011-02-09 20:55:54
Just like a triangle, A=rs

lg5293 2011-02-09 20:55:54
area = rs?

zero.destroyer 2011-02-09 20:55:54
rs=area

simplyMathLete 2011-02-09 20:55:54
rs = Area

DPatrick 2011-02-09 20:56:04
The radius of the incircle is given by r = K/s, where K is the area of the quadrilateral, and s is the semi-perimeter (half the perimeter) of the quadrilateral. This is the same formula as for the triangle, and it is derived the same way as well. (It's a fun exercise to try to do this yourself if you've never seen this before.)

DPatrick 2011-02-09 20:56:16
Since we are given the sides of the quadrilateral, we can compute the semi-perimeter s.

GeorgiaTechMan 2011-02-09 20:56:30
it is 21.

christopher.jedi 2011-02-09 20:56:30
21

DPatrick 2011-02-09 20:56:34
The semi-perimeter s is (14 + 9 + 7 + 12)/2 = 21.

DPatrick 2011-02-09 20:56:43
Hence, the radius we want is r = K/21. Thus, maximizing the radius is equivalent to maximizing the area.

DPatrick 2011-02-09 20:56:53
So how do we maximize the area?

BarbieRocks 2011-02-09 20:57:08
K is maximizied when its a cyclic quadrilateral.

Cortana 2011-02-09 20:57:08
ABCD is cyclic

AlphaMath1 2011-02-09 20:57:08
quadrilateral is cyclic?

Cortana 2011-02-09 20:57:08
Abcd is cyclic

bulutcocuk 2011-02-09 20:57:08
assume it's cyclic?

DPatrick 2011-02-09 20:57:46
Indeed, the area is maximized if the quadrilateral is cyclic (meaning we can circumscribe a circle around it containing all 4 vertices).

NuncChaos 2011-02-09 20:57:55
why necessarily cyclic?

antybash 2011-02-09 20:57:55
how do we prove it must be cyclic?

DPatrick 2011-02-09 20:58:09
Here's quickie argument since I don't have time for a full proof:

DPatrick 2011-02-09 20:58:17
Imagine it's cyclic to begin with:

DPatrick 2011-02-09 20:58:23

DPatrick 2011-02-09 20:58:32
The sides of the quadrilateral cut off four circular sectors in the circle.

DPatrick 2011-02-09 20:58:52
Now if I flex the quadrilateral and drag the sectors with it (but don't change them), I get something like this:

DPatrick 2011-02-09 20:59:01

DPatrick 2011-02-09 20:59:35
This has the same perimeter as my earlier circle, so it must have smaller area (since a circle is the maximum area for a given perimeter; this is often called the Isoperimetric Theorem).

DPatrick 2011-02-09 21:00:01
So the cyclic quadrilateral is the one with the largest area (given a fixed set of side lengths).

DPatrick 2011-02-09 21:00:18
So we'll want ABCD to be cyclic in order to maximize the area.

theone142857 2011-02-09 21:00:39
So A+C=180

simplyMathLete 2011-02-09 21:00:39
can we use Brahmagupta's formula?

bulutcocuk 2011-02-09 21:00:39
brahmagupta!

hrithikguy 2011-02-09 21:00:45
use brahmagupta

DPatrick 2011-02-09 21:00:56
There is a magic formula we could use now that blows the problem up.

DPatrick 2011-02-09 21:01:13
You can look this up on the forum.

DPatrick 2011-02-09 21:01:32
But let's assume you don't know the formula (like me).

DPatrick 2011-02-09 21:01:49
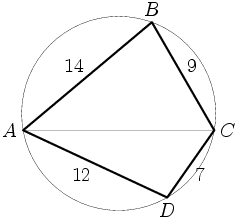
We can compute the area directly. Here's a picture:

DPatrick 2011-02-09 21:01:56

DPatrick 2011-02-09 21:02:22
I drew diagonal AC because I know how to work with triangles.

danielguo94 2011-02-09 21:02:47
law of cosines/sines

xixianxiang 2011-02-09 21:02:53
1/2 12*7sinD + 1/2 9*14 sinB

DPatrick 2011-02-09 21:02:56
Indeed.

DPatrick 2011-02-09 21:03:07

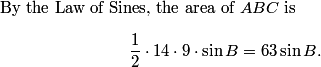
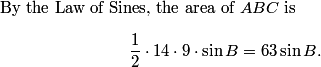
DPatrick 2011-02-09 21:03:15

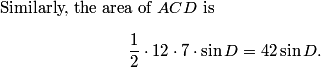
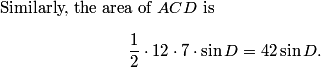
DPatrick 2011-02-09 21:03:25

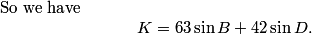
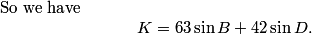
RisingMathStar 2011-02-09 21:03:35
angles B and D are supplementary

tan90 2011-02-09 21:03:36
sin B = sin D

exmath89 2011-02-09 21:03:36
<B+<D=180

TachyonPulse 2011-02-09 21:03:36
sin B = sin D because B + D = 180

DPatrick 2011-02-09 21:03:43
Aha: since our ABCD is cyclic, we do know sin B = sin D because the angles are supplementary.

DPatrick 2011-02-09 21:03:54
So K = 105 sin B.

DPatrick 2011-02-09 21:04:02
That's good, but we don't know sin B. What can we do?

JamesTianyQiaoMa 2011-02-09 21:04:14
law of cosines

silverchocolate 2011-02-09 21:04:14
law of cosineas

DPatrick 2011-02-09 21:04:22
We can compute AC two different ways by the Law of Cosines.

mathwiz314 2011-02-09 21:04:28
set the law of cos equal to each other

DPatrick 2011-02-09 21:04:33

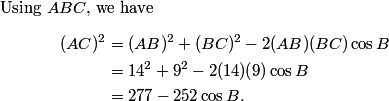
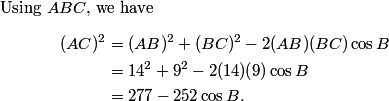
DPatrick 2011-02-09 21:04:47

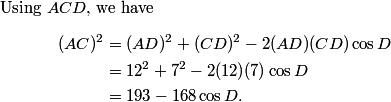
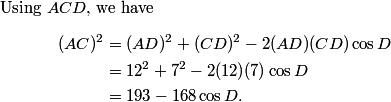
DPatrick 2011-02-09 21:05:03

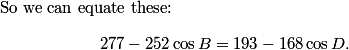
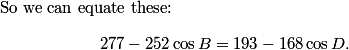
DVA6102 2011-02-09 21:05:17
B and D are supplementary

tan90 2011-02-09 21:05:17
cos B = -cos D

christerson 2011-02-09 21:05:17
cos B = -cos D

DPatrick 2011-02-09 21:05:24
But the quadrilateral is cyclic, so cos D = -cos B.

DPatrick 2011-02-09 21:05:38
Thus we have (after simplification) 21 = 105 cos B, hence cos B = 21/105 = 1/5.

DPatrick 2011-02-09 21:05:54
Now we just back everything out of our calculations.

DPatrick 2011-02-09 21:06:07

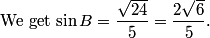
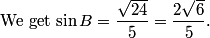
DPatrick 2011-02-09 21:06:18

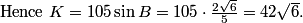
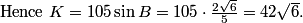
DPatrick 2011-02-09 21:06:28

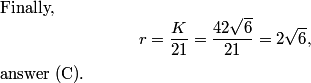
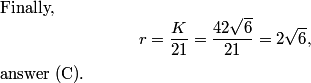
VIPMaster 2011-02-09 21:07:07
Would Brahmagupta's formula make this easier? i.e. Could you still use it and get the same answer?

DPatrick 2011-02-09 21:07:26
Yes, it does. But then you have to spend your time memorizing semi-obscure geometry formulas.

DPatrick 2011-02-09 21:07:43
Let's go on to #25:

DPatrick 2011-02-09 21:07:50

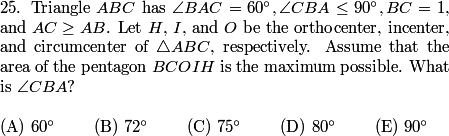
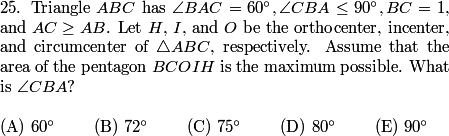
DPatrick 2011-02-09 21:08:08
(As a matter of taste, I'm not fond of both #24 and #25 being "maximize the area" problems, but on the other hand the methods are very different.)

Anamfija 2011-02-09 21:08:24
draw a picture

andrewjjiang97 2011-02-09 21:08:25
diagram

DPatrick 2011-02-09 21:08:32
Of course, we can start with a diagram. Unfortunately, it looks like this:

DPatrick 2011-02-09 21:08:38

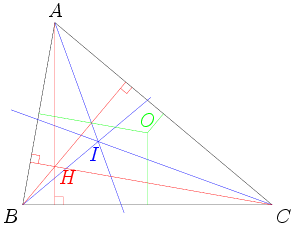
DPatrick 2011-02-09 21:08:45
I drew it with different colors to try to keep track of the different points, but it's still a bit of a mess.

DPatrick 2011-02-09 21:09:05
Not only is this a blizzard of lines and points, it we don't draw the diagram very precisely, we might end up being very unsure of the relative locations of H, I, and O. Moreover, there's so much going on in this diagram that it will be very hard to keep track of all the information we need to follow.

DPatrick 2011-02-09 21:09:19
Any ideas how to make it simpler?

centralbs 2011-02-09 21:09:29
Make 3 diagrams?

christopher.jedi 2011-02-09 21:09:38
one at a time

DPatrick 2011-02-09 21:09:47
We can break up the diagram and make one each for the circumcenter, incenter, and orthocenter, and learn what we can in each of those diagrams. Hopefully, we'll be able to combine that information in some useful way.

DPatrick 2011-02-09 21:10:14
Let's start with the circumcenter (for no particularly good reason):

DPatrick 2011-02-09 21:10:23

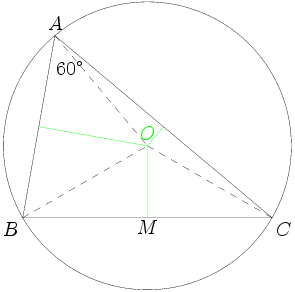
DPatrick 2011-02-09 21:10:35
What can we learn from this diagram?

Goutham 2011-02-09 21:10:54
BOC is isosceles

tan90 2011-02-09 21:11:02
The circumradius = sqrt3 / 3

DPatrick 2011-02-09 21:11:13
Since <BAC = 60, arc BC is 120 degrees, so <BOC = 120.

DPatrick 2011-02-09 21:11:28
Therefore, angles OBC and OCB are each 30 degrees.

thecmd999 2011-02-09 21:11:40
30 60 90?

DPatrick 2011-02-09 21:11:54
Right, BOM and COM are each 30-60-90, so we get some lengths too. (Recall BC = 1.)

GeorgiaTechMan 2011-02-09 21:12:03
so BO=OC=OA=1/sqrt3=sqrt3/3

DPatrick 2011-02-09 21:12:20
Since BC is 1, we have BM = 1/2, OM = 1/(2sqrt(3)), and the circumradius is 1/sqrt(3). Maybe that will be useful. I'll add this data to the pic:

DPatrick 2011-02-09 21:12:31

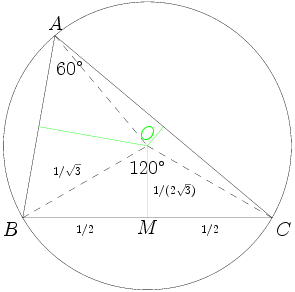
DPatrick 2011-02-09 21:12:53
Hmmm...we seem to have exhausted this picture.

DPatrick 2011-02-09 21:13:01
Let's move over to the incenter pic:

DPatrick 2011-02-09 21:13:08

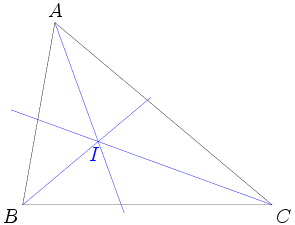
DPatrick 2011-02-09 21:13:36
Can we chase any angles or lengths?

mathtyro 2011-02-09 21:13:49
Yes, since we have angle bisectors.

mathnerd101 2011-02-09 21:13:49
the angles are bisected

Ttocs45 2011-02-09 21:14:08
angle BAI = angle CAI = 30

DPatrick 2011-02-09 21:14:48
Right, all of these blue lines are angle bisectors. So <BAI and <CAI are each 30.

DPatrick 2011-02-09 21:15:03
How about <BIC? Any info about it?

Cortana 2011-02-09 21:15:21
BIC= 120

capu 2011-02-09 21:15:22
120?

DPatrick 2011-02-09 21:15:24
How come?

Goutham 2011-02-09 21:15:47
90+A/2

Letti 2011-02-09 21:15:47
because 180-30-30=120

PowerOfPi 2011-02-09 21:15:47
use triangle BIC

william22 2011-02-09 21:15:47
because IBC+ICB=60..

DPatrick 2011-02-09 21:16:10
Right. <IBC is half of angle B, and <ICB is half of angle C.

DPatrick 2011-02-09 21:16:22
So their sum is half of <B + <C. But this sum is 120 (since A is 60).

DPatrick 2011-02-09 21:16:36
So <IBC + <ICB = (1/2)(120) = 60, and hence <BIC = 180-60 = 120.

DPatrick 2011-02-09 21:16:50
Hmmm.....

DPatrick 2011-02-09 21:17:17
Our first pic had a 120 degree angle too.

Iggy Iguana 2011-02-09 21:17:24
The first picture was 120 too

jraz27 2011-02-09 21:17:24
Is I=O?

DPatrick 2011-02-09 21:17:38
They're not necessary equal, but what do we know about B,I,O,C?

Goutham 2011-02-09 21:17:57
BIOC is cyclic

gomath888 2011-02-09 21:17:57
cyclic

capu 2011-02-09 21:17:57
cyclic

theax 2011-02-09 21:17:57
cyclic!!!!!!

DPatrick 2011-02-09 21:18:05
We previously saw <BOC =120, so <BOC = <BIC. This tells us that BIOC is a cyclic quadrilateral. That is, there is a circle that passes through B, I, O, and C.

DPatrick 2011-02-09 21:18:26
What should we wonder now?

xixianxiang 2011-02-09 21:18:29
does it pass through the final point too!?!?

DPatrick 2011-02-09 21:18:35
Does the circle go through H?

DPatrick 2011-02-09 21:18:44
Let's take a look at the orthocenter diagram.

DPatrick 2011-02-09 21:18:53

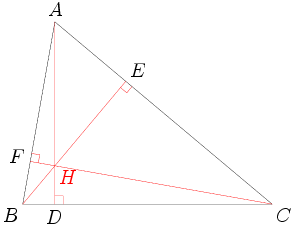
DPatrick 2011-02-09 21:19:06
We sure know where to look: what is <BHC?

VIPMaster 2011-02-09 21:19:38
120!!!

Cortana 2011-02-09 21:19:38
120

girishvar12 2011-02-09 21:19:38
120

Letti 2011-02-09 21:19:38
120

randomflyingtaco 2011-02-09 21:19:38
120? =_=

DPatrick 2011-02-09 21:19:44
I hope so...

xixianxiang 2011-02-09 21:19:53
*two angles above H are 120 because of right angles, thus two angles below H are too

DPatrick 2011-02-09 21:20:12
Indeed. AEHF is a quadrilateral with angle A 60 and two right angles. So FHE is 120.

DPatrick 2011-02-09 21:20:22
But BHC is vertical to FHE, so it's 120 too.

DPatrick 2011-02-09 21:20:35
Yep, H is on the circle that goes through B,I,O,C.

DPatrick 2011-02-09 21:20:43
So let's draw a new diagram with the circle drawn in too.

DPatrick 2011-02-09 21:20:50
In the interest of getting the diagram to stay on the page, we'll cut out the bottom half of the circle. We'll also connect the pentagon we care about with purple segments because we clearly need more color:

DPatrick 2011-02-09 21:21:00

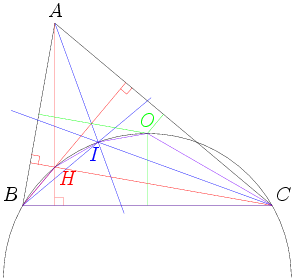
DPatrick 2011-02-09 21:21:08
Now what?

PowerOfPi 2011-02-09 21:21:27
maximize the area

mathtyro 2011-02-09 21:21:27
Maximize the area of the pentagon

DPatrick 2011-02-09 21:21:34
We want to find <ABC when the area of BHIOC is as great as possible. Do we know anything about the area of this pentagon yet?

DPatrick 2011-02-09 21:22:25
Do we know the area of any part of this pentagon? (Hint: I left one of the diagrams up top for a reason!)

firework 2011-02-09 21:22:52
BOC

GausssWill 2011-02-09 21:22:58
The BCO part of the pentagon can be caculated

Goutham 2011-02-09 21:22:58
We know BOC

DPatrick 2011-02-09 21:23:15
Right: we know all the lengths and angles in BOC, so its area is fixed regardless of where H and I end up.

DPatrick 2011-02-09 21:23:47
So, all we have to do is maximize the area of what's left over, which is the narrow cyclic quadrilateral BHIO:

DPatrick 2011-02-09 21:23:55

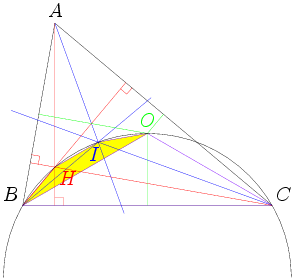
DPatrick 2011-02-09 21:24:17
BC is fixed; BC = 1. Point O is also fixed, so arc BO is fixed. So, our problem is to find the measure of angle B such that the resulting locations of H and I maximize the area of BHIO.

xixianxiang 2011-02-09 21:24:32
and to maximize remaining area, H, I should be spread out evenly

DPatrick 2011-02-09 21:24:35
How come?

DPatrick 2011-02-09 21:24:54
A reasonable guess is that the area is maximized when the arcs BH, HI, and IO are congruent. Is this true?

GeorgiaTechMan 2011-02-09 21:25:15
yes?

PowerOfPi 2011-02-09 21:25:15
yes

tan90 2011-02-09 21:25:15
yes

Cortana 2011-02-09 21:25:15
yes

osmosis92 2011-02-09 21:25:15
Yes

DPatrick 2011-02-09 21:25:18
How come?

DPatrick 2011-02-09 21:25:39
Let me make life a little easier by removing some of the noise from the picture:

DPatrick 2011-02-09 21:25:46

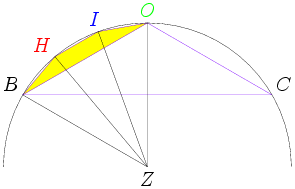
Shoelace Thm. 2011-02-09 21:26:04
The same stretching argument you used earlier

GausssWill 2011-02-09 21:26:04
Reasoning. If they are equal, the height of the quadrilaterial will be taller

DPatrick 2011-02-09 21:26:19
Essentially, yes, it's sort of the same argument as in the previous problem.

DPatrick 2011-02-09 21:26:54
If I move H closer to B, the triangle BHI gets smaller (since its height shrinks) and the rest stays the same.

DPatrick 2011-02-09 21:27:06
So I want H to be where the height of BHI is maximized, and that's in the center of arc BI.

DPatrick 2011-02-09 21:27:20
In the same way we want point I to be the midpoint of arc HO.

DPatrick 2011-02-09 21:27:29
So BH = HI = IO maximizes the yellow area.

DPatrick 2011-02-09 21:27:40
(This is a little hand-wavy but hopefully you get the idea.)

DPatrick 2011-02-09 21:27:48
Now, last step: back to the original diagram. Is it possible for H and I to divide arc BO in three equal pieces?

DPatrick 2011-02-09 21:27:58

VIPMaster 2011-02-09 21:28:19
yes it is

Cortana 2011-02-09 21:28:20
yes

1228panda 2011-02-09 21:28:20
yes

DPatrick 2011-02-09 21:28:32
How so, and what does <CBA end up as?

DPatrick 2011-02-09 21:29:38
Recall arc BO is 60 degrees of the circle (from the top picture), so BH and HI and IO will each span 20 degrees of the circle.

VIPMaster 2011-02-09 21:30:03
CBA becomes 80 because half of <B becomes 120/3 = 40

DPatrick 2011-02-09 21:30:28
Aha! CBI intercepts 80 degrees of arc of the circle (from I over to C).

DPatrick 2011-02-09 21:30:39
So <CBI = 80/2 = 40.

DPatrick 2011-02-09 21:30:47
But that's half of angle B, since BI is the bisector.

DPatrick 2011-02-09 21:30:53
So <B = 80, answer (D).

DPatrick 2011-02-09 21:31:07
This was pretty hard.

DPatrick 2011-02-09 21:31:36
We've been going for 2 hours, but I'm willing to do one more problem.

DPatrick 2011-02-09 21:31:52
Please vote for one of 16-20 on the 10A or 12A (and say which test).

DPatrick 2011-02-09 21:32:35
#20 on the 12A is the clear winner.

DPatrick 2011-02-09 21:32:46

DPatrick 2011-02-09 21:33:17
How can we use the fact that f(1) = 0?

lg5293 2011-02-09 21:33:28
plug in 1 to get a+b+c=0

xixianxiang 2011-02-09 21:33:28
a+b+c=0

AlphaMath1 2011-02-09 21:33:28
a+b+c=0

yankeesrule007 2011-02-09 21:33:28
c=-(a+b)

gh625 2011-02-09 21:33:28
a+b+c=0

rdj5933mile5 2011-02-09 21:33:28
a+b+c=0

DPatrick 2011-02-09 21:33:35
Right, plugging it in gives a+b+c = 0.

DPatrick 2011-02-09 21:33:38
So c = -(a+b)

DPatrick 2011-02-09 21:33:48
So the polynomial is f(x) = ax^2 + bx - (a+b).

DPatrick 2011-02-09 21:34:02
That factors pretty nicely!

DPatrick 2011-02-09 21:34:21
It factors as (x-1)(a(x+1) + b).

DPatrick 2011-02-09 21:34:36
In particular x-1 is a factor of f(x).

DPatrick 2011-02-09 21:34:56
So f(7) is a multiple of 6 and f(8) is a multiple of 7.

fractals 2011-02-09 21:35:01
so f(7)=54

girishvar12 2011-02-09 21:35:05
f(7)=54 because it has to be a multiple of 6

xxrxxhxx 2011-02-09 21:35:07
f(8) = 77

DPatrick 2011-02-09 21:35:17
Right, the only possibilities are f(7) = 54 and f(8) = 77.

DPatrick 2011-02-09 21:35:39
Plug those in to the equation of f(x) to solve for a and b. You should get a = 2 and b = -7.

DPatrick 2011-02-09 21:35:58
Thus f(x) = 2x^2 - 7x + 5, and f(100) = 20000 - 700 + 5.

DPatrick 2011-02-09 21:36:07
This is clearly between 15000 and 20000, so k=3 and the answer is (C).

DPatrick 2011-02-09 21:36:32
That was quick, so I'll do #20 on the 10A which was also in high demand and is also quick. :)

DPatrick 2011-02-09 21:36:42

DPatrick 2011-02-09 21:37:12
How much of the circle does a chord of length r cut off if the radius is also r?

Caelestor 2011-02-09 21:37:28
1/6

camath14 2011-02-09 21:37:28
1/6

fractals 2011-02-09 21:37:28
1/6

AlphaMath1 2011-02-09 21:37:28
1/6

Iggy Iguana 2011-02-09 21:37:28
1/6

$LaTeX$ 2011-02-09 21:37:28
1/6 of the circumference

esque 2011-02-09 21:37:28
1/6th, since the angle is 60 degrees

DPatrick 2011-02-09 21:37:36
Right: it cuts off 1/6 (or 60 degrees) of the circle.

girishvar12 2011-02-09 21:37:47
the first point can be anywhere on the circumfrence

PowerOfPi 2011-02-09 21:37:51
WLOG, let the first point be at the top

DPatrick 2011-02-09 21:38:00
Right: the first point can be anywhere on the circle.

DPatrick 2011-02-09 21:38:17
And we just concluded that the second point must be within 1/6th of the circle away from the first point.

xixianxiang 2011-02-09 21:38:26
then next point can be 1/6 to the right or to the left, which adds up to 1/3

DPatrick 2011-02-09 21:38:47
Right: so the second point must be on 1/3 of the circle, so the probability is 1/3. Answer (D).

DPatrick 2011-02-09 21:39:07
OK, that's 2 hours + 10 minutes, so I'm done for the night.

DPatrick 2011-02-09 21:39:20
Many people are posting their solutions on the AMC forum and/or the wiki on our website.

worthawholebean 2011-02-09 21:39:35
Thank you everyone for coming!

DPatrick 2011-02-09 21:39:44
You can also find the answers at amc.maa.org.

DPatrick 2011-02-09 21:39:56
Hope you did well on the contest and enjoyed the Math Jam.

DPatrick 2011-02-09 21:40:05
And good luck on the 10B/12B if you're taking it in two weeks!

DPatrick 2011-02-09 21:40:17
A transcript of this discussion will be available on the website shortly.

DPatrick 2011-02-09 21:40:23
Good night!

2011 AMC 10/12 A Discussion

Facilitator: Dave Patrick