2011 AMC 10/12 B Discussion
Go back to the Math Jam ArchiveA discussion of problems from the AMC 10/12 B, which is administered February 23. We will cover the last 5 problems on each test, as well as requested earlier problems on the tests.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Jeremy Copeland
copeland
2011-02-24 19:29:57
Welcome to the 2011 AMC 10B/12B Math Jam!
Welcome to the 2011 AMC 10B/12B Math Jam!
copeland
2011-02-24 19:30:07
I'm Jeremy Copeland, and I'll be leading our discussion tonight.
I'm Jeremy Copeland, and I'll be leading our discussion tonight.
willwang123
2011-02-24 19:30:10
Yay!
Yay!
mathcountsloser
2011-02-24 19:30:10
It's 6:30.
It's 6:30.
ctmusicgirl
2011-02-24 19:30:10
YAY :D
YAY :D
alex31415
2011-02-24 19:30:10
Start already!
Start already!
willwang123
2011-02-24 19:30:10
Hi!
Hi!
Joe10112
2011-02-24 19:30:10
Yay!
Yay!
minirafa
2011-02-24 19:30:10
hi
hi
chaos763
2011-02-24 19:30:10
Great!
Great!
gmarch89
2011-02-24 19:30:10
yay lol
yay lol
copeland
2011-02-24 19:30:19
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
copeland
2011-02-24 19:30:22
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
copeland
2011-02-24 19:30:30
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
copeland
2011-02-24 19:30:34
There are a lot of students here! As I said, only (a very small fraction of the) well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
There are a lot of students here! As I said, only (a very small fraction of the) well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
copeland
2011-02-24 19:30:41
Hmm.
Hmm.
copeland
2011-02-24 19:30:50
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
copeland
2011-02-24 19:30:53
We do have two assistants tonight who can help answer some of the questions.
We do have two assistants tonight who can help answer some of the questions.
copeland
2011-02-24 19:30:57
The first is Patrick Hulin (worthawholebean). Patrick started doing math competitions in elementary school and attended National MATHCOUNTS in 2006. In 2010, he received an honorable mention on the USA Math Olympiad. He currently studies math at MIT.
The first is Patrick Hulin (worthawholebean). Patrick started doing math competitions in elementary school and attended National MATHCOUNTS in 2006. In 2010, he received an honorable mention on the USA Math Olympiad. He currently studies math at MIT.
copeland
2011-02-24 19:31:11
We also have Vincent Le who is a sophomore at MIT. He has participated in MATHCOUNTS, ARML, USAMO, and also has been to Canada/USA Mathcamp and AwesomeMath. He's been at MIT for one more year than Patrick, and is thus one year more awesome.
We also have Vincent Le who is a sophomore at MIT. He has participated in MATHCOUNTS, ARML, USAMO, and also has been to Canada/USA Mathcamp and AwesomeMath. He's been at MIT for one more year than Patrick, and is thus one year more awesome.
copeland
2011-02-24 19:31:33
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1.
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1.
copeland
2011-02-24 19:31:42
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.
copeland
2011-02-24 19:31:46
Also notice that there will be several cases where we actually find the answer or almost the answer but instead wander off. The goal is always to find a proof that our answer is correct and not just find the answers. Of course on the AMC you should aim to do much less work than this.
Also notice that there will be several cases where we actually find the answer or almost the answer but instead wander off. The goal is always to find a proof that our answer is correct and not just find the answers. Of course on the AMC you should aim to do much less work than this.
copeland
2011-02-24 19:31:55
Oh.
Oh.
copeland
2011-02-24 19:31:59
Vincent = chessspro.
Vincent = chessspro.
copeland
2011-02-24 19:32:06
The Math Jam will proceed as follows:
The Math Jam will proceed as follows:
minirafa
2011-02-24 19:32:38
what about the other moderators?
what about the other moderators?
copeland
2011-02-24 19:32:40
They'll be grading each of your performances. tlcruickshank is especially concerned with your "style."
They'll be grading each of your performances. tlcruickshank is especially concerned with your "style."
copeland
2011-02-24 19:32:47
The Math Jam will proceed as follows:
The Math Jam will proceed as follows:
copeland
2011-02-24 19:32:50
We will work the last 5 problems from the AMC 10A, then the last 5 problems from the AMC 12A. After that, time permitting, I will take requests for some other problems for discussion.
We will work the last 5 problems from the AMC 10A, then the last 5 problems from the AMC 12A. After that, time permitting, I will take requests for some other problems for discussion.
Doink
2011-02-24 19:33:08
what is style?
what is style?
egbdf44
2011-02-24 19:33:08
What is "style"?
What is "style"?
copeland
2011-02-24 19:33:10
I don't think you're off to a good start. :)
I don't think you're off to a good start. :)
copeland
2011-02-24 19:33:20
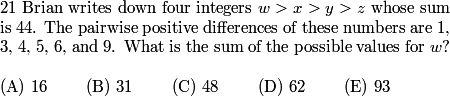
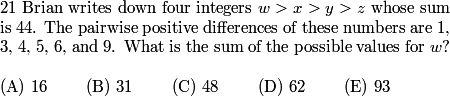
copeland
2011-02-24 19:33:34
Notice that I will always put the current problem at the top of the window. You can resize the area at the top by dragging the horizontal gray bar.
Notice that I will always put the current problem at the top of the window. You can resize the area at the top by dragging the horizontal gray bar.
copeland
2011-02-24 19:33:49
OK, which of the differences jump out at you?
OK, which of the differences jump out at you?
Tribefan
2011-02-24 19:34:28
9
9
Relativity1618
2011-02-24 19:34:28
9
9
jeff10
2011-02-24 19:34:28
The difference between w and z is 9.
The difference between w and z is 9.
AkshajKadaveru
2011-02-24 19:34:28
1
1
chaos763
2011-02-24 19:34:28
The 9.
The 9.
PowerOfPi
2011-02-24 19:34:28
w-z=9
w-z=9
RisingMathStar
2011-02-24 19:34:28
w - z = 9
w - z = 9
tekgeek
2011-02-24 19:34:28
w-z must equal 9
w-z must equal 9
.cpp
2011-02-24 19:34:28
The biggest difference, 9.
The biggest difference, 9.
jxihong
2011-02-24 19:34:28
1
1
davidx
2011-02-24 19:34:28
1
1
anonymous0
2011-02-24 19:34:29
diff. between w and z =9
diff. between w and z =9
curethekitten
2011-02-24 19:34:29
1
1
KKNC123
2011-02-24 19:34:29
1
1
copeland
2011-02-24 19:34:34
Since 1 is the smallest difference we know that two of the numbers must differ by 1.
Since 1 is the smallest difference we know that two of the numbers must differ by 1.
copeland
2011-02-24 19:34:37
Since 9 is the largest difference, we know that w-z=9.
Since 9 is the largest difference, we know that w-z=9.
copeland
2011-02-24 19:34:39
Now what?
Now what?
professordad
2011-02-24 19:35:48
casework on values
casework on values
AlphaMath1
2011-02-24 19:35:48
casework
casework
TruffleMaster
2011-02-24 19:35:48
the sum of the individual differences must equal 9
the sum of the individual differences must equal 9
jeff10
2011-02-24 19:35:48
The sum of the difference between w and x, x and y, and t and z is also 9.
The sum of the difference between w and x, x and y, and t and z is also 9.
NoWayHaze
2011-02-24 19:35:48
the sum of two of the differences is another
the sum of two of the differences is another
chaos763
2011-02-24 19:35:48
Some of the differences add up.
Some of the differences add up.
TrigMan
2011-02-24 19:35:48
You could start by guessing that x = w-1
You could start by guessing that x = w-1
capu
2011-02-24 19:35:48
1+3+5=9
1+3+5=9
dragonx
2011-02-24 19:35:48
We note that 3 differences must add up to 9 leaving us with two direct diffrrences being 3 and 5.
We note that 3 differences must add up to 9 leaving us with two direct diffrrences being 3 and 5.
gravel
2011-02-24 19:35:48
Casework?
Casework?
copeland
2011-02-24 19:35:52
Let's draw a number line.
Let's draw a number line.
copeland
2011-02-24 19:35:56


copeland
2011-02-24 19:35:58
Let's try to label the differences between the points on this line.
Let's try to label the differences between the points on this line.
copeland
2011-02-24 19:36:11
Anything can be 1 so far.
Anything can be 1 so far.
copeland
2011-02-24 19:36:15


copeland
2011-02-24 19:36:18


copeland
2011-02-24 19:36:20


copeland
2011-02-24 19:36:22
What else do we know?
What else do we know?
chaos763
2011-02-24 19:37:29
3 + 1 = 4.
3 + 1 = 4.
capu
2011-02-24 19:37:29
the differences in consecutive numbers are 1, 3, and 5
the differences in consecutive numbers are 1, 3, and 5
TruffleMaster
2011-02-24 19:37:29
no sum can equal 3 so one of the smaller differences is 3
no sum can equal 3 so one of the smaller differences is 3
Spring
2011-02-24 19:37:29
The first and third do not work because one of the differences would be 8.
The first and third do not work because one of the differences would be 8.
.cpp
2011-02-24 19:37:29
No difference of 8 exists, so cases 1 and 3 above are impossible.
No difference of 8 exists, so cases 1 and 3 above are impossible.
dragonx
2011-02-24 19:37:29
Other two add up to 8: 3 and 5.
Other two add up to 8: 3 and 5.
TrigMan
2011-02-24 19:37:29
The total is 9
The total is 9
Jasmine8925
2011-02-24 19:37:29
the other differences should add up to 8
the other differences should add up to 8
smallpeoples343
2011-02-24 19:37:29


willwang123
2011-02-24 19:37:29
w and z are 9 apart
w and z are 9 apart
greatwhiteshark98
2011-02-24 19:37:29
3 and 5 are the other differences?
3 and 5 are the other differences?
TruffleMaster
2011-02-24 19:37:29
so two of them must be 1 and 3 and the sum must be 9 so the third is 5
so two of them must be 1 and 3 and the sum must be 9 so the third is 5
AkshajKadaveru
2011-02-24 19:37:29
the other two add to 8
the other two add to 8
copeland
2011-02-24 19:37:36
Since 3 is the next smallest, there must be an edge of length 3.
Since 3 is the next smallest, there must be an edge of length 3.
copeland
2011-02-24 19:37:40
Since the total length is 9 we know that the other length must be 5.
Since the total length is 9 we know that the other length must be 5.
copeland
2011-02-24 19:37:44
Since 1+3 = 4 is the only way we can get 4, we must have the 3 next to the 1.
Since 1+3 = 4 is the only way we can get 4, we must have the 3 next to the 1.
copeland
2011-02-24 19:37:48
This gives us exactly four possibilities:
This gives us exactly four possibilities:
copeland
2011-02-24 19:37:51
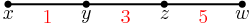
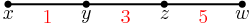
copeland
2011-02-24 19:37:53


copeland
2011-02-24 19:37:55


copeland
2011-02-24 19:37:58
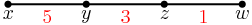
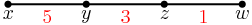
copeland
2011-02-24 19:38:01
Are these all the answers?
Are these all the answers?
jeff10
2011-02-24 19:38:39
NO only two are
NO only two are
theone142857
2011-02-24 19:38:39
5+3=8 bad
5+3=8 bad
sparkle123
2011-02-24 19:38:39
first and last not okay, must have diff of 6
first and last not okay, must have diff of 6
NoWayHaze
2011-02-24 19:38:39
no, some of them don't add up to other differences
no, some of them don't add up to other differences
professordad
2011-02-24 19:38:39
no because 8 is not a choice
no because 8 is not a choice
JSGandora
2011-02-24 19:38:39
no, we can't get 6 with the first or last onews
no, we can't get 6 with the first or last onews
Jasmine8925
2011-02-24 19:38:39
5 and 1 should be next to each other so we get 6 as a difference
5 and 1 should be next to each other so we get 6 as a difference
copeland
2011-02-24 19:38:43
Actually that's too many! We've narrowed it down to these possibilities, but two of these are bogus. Notice that the top and bottom options have lengths of 8. This is unacceptable.
Actually that's too many! We've narrowed it down to these possibilities, but two of these are bogus. Notice that the top and bottom options have lengths of 8. This is unacceptable.
copeland
2011-02-24 19:38:47
Fortunately the middle two have lengths 1, 3, 5, 4, 6, and 9, which is exactly what we wanted.
Fortunately the middle two have lengths 1, 3, 5, 4, 6, and 9, which is exactly what we wanted.
copeland
2011-02-24 19:38:49


copeland
2011-02-24 19:38:52


copeland
2011-02-24 19:38:55
How do we finish?
How do we finish?
jeff10
2011-02-24 19:39:36
Express everything in terms of z.
Express everything in terms of z.
hsm174
2011-02-24 19:39:36
find w
find w
Joe10112
2011-02-24 19:39:36
write equations!
write equations!
sindennisz
2011-02-24 19:39:36
find w
find w
RisingMathStar
2011-02-24 19:39:36
Their sum is 44
Their sum is 44
Iggy Iguana
2011-02-24 19:39:36
Now just plug them in to w+x+y+z=44
Now just plug them in to w+x+y+z=44
leinad47x
2011-02-24 19:39:36
add up possible values
add up possible values
andrewjjiang97
2011-02-24 19:39:36
find the values of w
find the values of w
Relativity1618
2011-02-24 19:39:36
w+x+y+z=44
w+x+y+z=44
AkshajKadaveru
2011-02-24 19:39:36
set variables
set variables
Jasmine8925
2011-02-24 19:39:36
we know the sum is 44, we should use that info now
we know the sum is 44, we should use that info now
theone142857
2011-02-24 19:39:36
sum=44
sum=44
smallpeoples343
2011-02-24 19:39:36
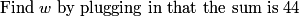
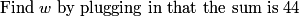
TruffleMaster
2011-02-24 19:39:36
x+x+3+x+3+1+x+3+1+5=44
x+x+3+x+3+1+x+3+1+5=44
copeland
2011-02-24 19:39:44


copeland
2011-02-24 19:39:48
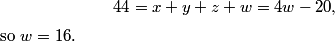
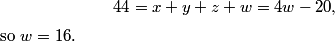
copeland
2011-02-24 19:39:58
What about the second case?
What about the second case?
ahaanomegas
2011-02-24 19:40:23
We can express our sets as {w, w - 5, w - 6, w - 9} or {w, w - 3, w - 4, w - 9}
We can express our sets as {w, w - 5, w - 6, w - 9} or {w, w - 3, w - 4, w - 9}
AlphaMath1
2011-02-24 19:40:23
w=15
w=15
theone142857
2011-02-24 19:40:23
15
15
Tribefan
2011-02-24 19:40:23
w=15
w=15
Iggy Iguana
2011-02-24 19:40:23
W=15
W=15
AstralMeson
2011-02-24 19:40:23
w = 15
w = 15
airplanes1
2011-02-24 19:40:23
w=15
w=15
luminate
2011-02-24 19:40:23
w = 15
w = 15
ahaanomegas
2011-02-24 19:40:23
In the second case, we have 4w - 16 = 44 --> w = 15
In the second case, we have 4w - 16 = 44 --> w = 15
alikimlynn
2011-02-24 19:40:23
w = 15
w = 15
TrigMan
2011-02-24 19:40:23
w=15, right?
w=15, right?
.cpp
2011-02-24 19:40:23
Do the same thing for w=15.
Do the same thing for w=15.
copeland
2011-02-24 19:40:27
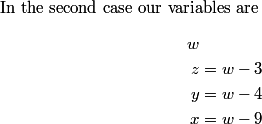
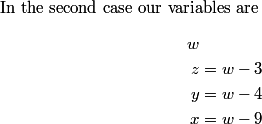
copeland
2011-02-24 19:40:30
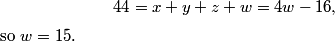
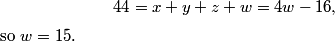
copeland
2011-02-24 19:40:33
And the solution?
And the solution?
anonymous0
2011-02-24 19:40:58
The answer is B
The answer is B
krmathcounts
2011-02-24 19:40:58
b
b
jeff10
2011-02-24 19:40:58
16+15=31
16+15=31
danielguo94
2011-02-24 19:40:58
B
B
davidx
2011-02-24 19:40:58
31
31
alikimlynn
2011-02-24 19:40:58
31
31
andrewjjiang97
2011-02-24 19:40:58
sum is 31, B
sum is 31, B
professordad
2011-02-24 19:40:58
16+15=31.
16+15=31.
calvinhobbesliker
2011-02-24 19:40:58
31
31
ooooo1
2011-02-24 19:40:58
b 31
b 31
luppleAOPS
2011-02-24 19:40:58
15+16=31
15+16=31
TrigMan
2011-02-24 19:40:58
B) 31 :)
B) 31 :)
Iggy Iguana
2011-02-24 19:40:58
16=15=31
16=15=31
j_f_c_w
2011-02-24 19:40:58
And the answer is 31=15+16
And the answer is 31=15+16
erica539
2011-02-24 19:40:58
31 the sum B
31 the sum B
christerson
2011-02-24 19:40:58
33
33
kangchangood
2011-02-24 19:40:58
(b)
(b)
aleCTY
2011-02-24 19:40:58
31
31
googol.plex
2011-02-24 19:40:58
16+15=31
16+15=31
LightningStreak
2011-02-24 19:40:58
31
31
alex31415
2011-02-24 19:40:58
so, 15+16=31 :)
so, 15+16=31 :)
NoWayHaze
2011-02-24 19:40:58
15+16=31
15+16=31
sayeramesh
2011-02-24 19:40:58
B => 31
B => 31
ooooo1
2011-02-24 19:40:58
B) 31
B) 31
TemurAmir
2011-02-24 19:40:58
The solution is 16+15=31 B
The solution is 16+15=31 B
theone142857
2011-02-24 19:40:58
31
31
kimmy12345
2011-02-24 19:40:58
15+16 = 31B
15+16 = 31B
LightningStreak
2011-02-24 19:40:58
B. 31
B. 31
TruffleMaster
2011-02-24 19:40:58
15+16=31
15+16=31
chengp
2011-02-24 19:40:58
31
31
infinity1
2011-02-24 19:40:58
15 + 16 = 31
15 + 16 = 31
chaos763
2011-02-24 19:40:58
31.
31.
RogLiu26
2011-02-24 19:40:58
B
B
Gosav3122
2011-02-24 19:40:58
31
31
.cpp
2011-02-24 19:40:58
16+15 = 31 => B.
16+15 = 31 => B.
ahaanomegas
2011-02-24 19:40:58
Sum of all possible values of w = 16 + 15 = 31 --> (B)
Sum of all possible values of w = 16 + 15 = 31 --> (B)
christerson
2011-02-24 19:40:58
31
31
spaceguy524
2011-02-24 19:40:58
B
B
mathcool2009
2011-02-24 19:40:58
16+15=31
16+15=31
supermathman
2011-02-24 19:40:58
16
16
mathletepower
2011-02-24 19:40:58
(b) 31
(b) 31
vwu9
2011-02-24 19:40:58
31
31
Tribefan
2011-02-24 19:40:58
(B) 31
(B) 31
copeland
2011-02-24 19:41:01
The solution is 16+15=31, answer (B).
The solution is 16+15=31, answer (B).
copeland
2011-02-24 19:41:26
MORE! That was fun.
MORE! That was fun.
copeland
2011-02-24 19:41:30
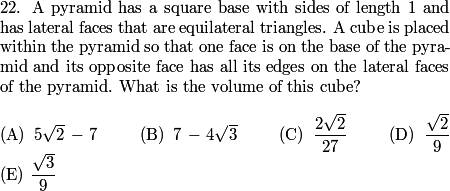
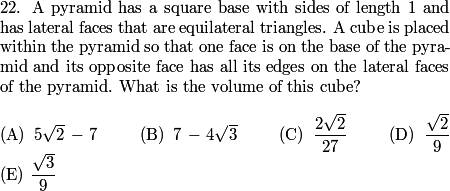
copeland
2011-02-24 19:41:41
First step?
First step?
AlphaMath1
2011-02-24 19:42:03
FIrst we need to try to visualize it
FIrst we need to try to visualize it
PowerOfPi
2011-02-24 19:42:03
diagram
diagram
Iggy Iguana
2011-02-24 19:42:03
draw a diagram
draw a diagram
minirafa
2011-02-24 19:42:03
draw a diagram?
draw a diagram?
luminate
2011-02-24 19:42:03
draw a picture
draw a picture
googol.plex
2011-02-24 19:42:03
draw it
draw it
AkshajKadaveru
2011-02-24 19:42:03
PICTURE TIME!
PICTURE TIME!
jxihong
2011-02-24 19:42:03
draw a picture
draw a picture
TemurAmir
2011-02-24 19:42:03
Draw a diagram?
Draw a diagram?
kimmy12345
2011-02-24 19:42:03
draw
draw
erica539
2011-02-24 19:42:03
diagram.
diagram.
sindennisz
2011-02-24 19:42:03
Draw a diagram.
Draw a diagram.
ilovepink
2011-02-24 19:42:03
picture!
picture!
copeland
2011-02-24 19:42:07
Draw a picture:
Draw a picture:
copeland
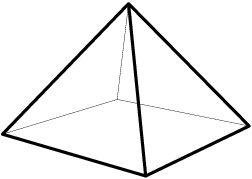
2011-02-24 19:42:11

copeland
2011-02-24 19:42:14
And we need our cube inside:
And we need our cube inside:
copeland
2011-02-24 19:42:17


mathcountsloser
2011-02-24 19:42:25
What if you are a fail drawer.
What if you are a fail drawer.
copeland
2011-02-24 19:42:27
Good thing I'm not.
Good thing I'm not.
copeland
2011-02-24 19:42:30
Awesome. Now what?
Awesome. Now what?
copeland
2011-02-24 19:43:14
Wow that's a lot of suggestions.
Wow that's a lot of suggestions.
copeland
2011-02-24 19:43:16
Coordinates.
Coordinates.
copeland
2011-02-24 19:43:17
Labels
Labels
copeland
2011-02-24 19:43:19
. . .
. . .
mhy123
2011-02-24 19:43:26
we must take a cross section
we must take a cross section
erica539
2011-02-24 19:43:26
do a cross-section
do a cross-section
.cpp
2011-02-24 19:43:26
Take an appropriate cross section.
Take an appropriate cross section.
aleCTY
2011-02-24 19:43:26
Right triangles
Right triangles
gmarch89
2011-02-24 19:43:26
calculate the volume of the pyramid?
calculate the volume of the pyramid?
LightningStreak
2011-02-24 19:43:26
draw an altitude?
draw an altitude?
luminate
2011-02-24 19:43:26
take a slice out of the pyramid and cube part
take a slice out of the pyramid and cube part
copeland
2011-02-24 19:43:35
OK.
OK.
copeland
2011-02-24 19:43:40
What cross-section?
What cross-section?
Jasmine8925
2011-02-24 19:44:46
through the middle of the pyramid and cube
through the middle of the pyramid and cube
krmathcounts
2011-02-24 19:44:46
Down the middle of the pyramid, so you can find the height
Down the middle of the pyramid, so you can find the height
dafjbomb
2011-02-24 19:44:46
from the top to the base so that the cube is cut into a perfect square cross section
from the top to the base so that the cube is cut into a perfect square cross section
ChipDale
2011-02-24 19:44:46
Through the middle
Through the middle
RisingMathStar
2011-02-24 19:44:46
center, laterally
center, laterally
TrigMan
2011-02-24 19:44:46
Right along the middle, so it hits the apex and the midpoints of two of the opposite base edges.
Right along the middle, so it hits the apex and the midpoints of two of the opposite base edges.
calvinhobbesliker
2011-02-24 19:44:46
The triangle whose altitude is the altidude of the pyramid
The triangle whose altitude is the altidude of the pyramid
mathcool2009
2011-02-24 19:44:46
I think he means cut the pyramid in half vertically
I think he means cut the pyramid in half vertically
copeland
2011-02-24 19:44:53
OK, I like this, but that's not enough info.
OK, I like this, but that's not enough info.
copeland
2011-02-24 19:44:58
There are lots of such slices.
There are lots of such slices.
copeland
2011-02-24 19:45:01
Which one do we want?
Which one do we want?
theone142857
2011-02-24 19:45:43
diagnal
diagnal
sparkle123
2011-02-24 19:45:43
along the diagonal of the base
along the diagonal of the base
gravel
2011-02-24 19:45:43
To the midpoint of the opposing base side
To the midpoint of the opposing base side
ChipDale
2011-02-24 19:45:43
Through the diagonal of the cube
Through the diagonal of the cube
briantix
2011-02-24 19:45:43
opposite corners of the base of the pyramid
opposite corners of the base of the pyramid
Candokevin
2011-02-24 19:45:43
slice it along the bottom diagnonal
slice it along the bottom diagnonal
copeland
2011-02-24 19:45:48
We want to try to find some 2D geometry somewhere that we can actually understand.
We want to try to find some 2D geometry somewhere that we can actually understand.
copeland
2011-02-24 19:45:52
If we look at one of the faces, that will give us some insight but it won't actually let us use the cube nicely.
If we look at one of the faces, that will give us some insight but it won't actually let us use the cube nicely.
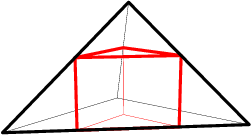
copeland
2011-02-24 19:45:54
Instead we ought to slice diagonally across the pyramid.
Instead we ought to slice diagonally across the pyramid.
copeland
2011-02-24 19:45:57

copeland
2011-02-24 19:46:01
OK, that's a little confusing so we'll push it into 2 dimensions:
OK, that's a little confusing so we'll push it into 2 dimensions:
copeland
2011-02-24 19:46:06


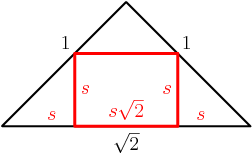
copeland
2011-02-24 19:46:08
What are the dimensions of this triangle?
What are the dimensions of this triangle?
theone142857
2011-02-24 19:46:38
1,1,xsqrt{2}
1,1,xsqrt{2}
AlphaMath1
2011-02-24 19:46:38
sqrt 2 1 1
sqrt 2 1 1
leinad47x
2011-02-24 19:46:38
1 by 1 by sqrt 2
1 by 1 by sqrt 2
luppleAOPS
2011-02-24 19:46:38
1,1, and sqrt2 for the base
1,1, and sqrt2 for the base
andrewjjiang97
2011-02-24 19:46:38
1, 1, sqrt{2}
1, 1, sqrt{2}
Iggy Iguana
2011-02-24 19:46:38
sqrt 2, 1, and 1
sqrt 2, 1, and 1
briantix
2011-02-24 19:46:38
1,1 sqrt2
1,1 sqrt2
willwang123
2011-02-24 19:46:38
1-1-sqrt2
1-1-sqrt2
PowerOfPi
2011-02-24 19:46:38
base is sqrt(2), legs are 1
base is sqrt(2), legs are 1
STan321
2011-02-24 19:46:38
1-1-rt2
1-1-rt2
copeland
2011-02-24 19:46:43
Since the pyramid has equilateral faces of length 1, the legs of this triangle are length 1. The base is the diagonal of a square (the base of the pyramid) with side length 1. Therefore the base has length sqrt(2).
Since the pyramid has equilateral faces of length 1, the legs of this triangle are length 1. The base is the diagonal of a square (the base of the pyramid) with side length 1. Therefore the base has length sqrt(2).
copeland
2011-02-24 19:46:47


copeland
2011-02-24 19:46:49
What kind of triangle is this?
What kind of triangle is this?
AkshajKadaveru
2011-02-24 19:47:12
Right
Right
dafjbomb
2011-02-24 19:47:12
right
right
sindennisz
2011-02-24 19:47:12
45-45-90
45-45-90
MrWhatWhen
2011-02-24 19:47:12
a right triangle
a right triangle
RisingMathStar
2011-02-24 19:47:12
isosceles right
isosceles right
briantix
2011-02-24 19:47:12
45-45-90
45-45-90
professordad
2011-02-24 19:47:12
its right triangle
its right triangle
usernamehi
2011-02-24 19:47:12
45, 45,90
45, 45,90
airplanes1
2011-02-24 19:47:12
right isoceles
right isoceles
Tribefan
2011-02-24 19:47:12
45,45,90
45,45,90
copeland
2011-02-24 19:47:16
It's an isosceles right triangle! We can use that later.
It's an isosceles right triangle! We can use that later.
copeland
2011-02-24 19:47:18
And the rectangle? (Of course the answer depends on the unknown side length, s, of the cube.)
And the rectangle? (Of course the answer depends on the unknown side length, s, of the cube.)
Spring
2011-02-24 19:48:05
s*sqrt2 by s
s*sqrt2 by s
aleCTY
2011-02-24 19:48:05
s, ssqrt2
s, ssqrt2
hsm174
2011-02-24 19:48:05
s,srt2
s,srt2
.cpp
2011-02-24 19:48:05
h sqrt(2) and h are the sides of the rectangle.
h sqrt(2) and h are the sides of the rectangle.
aunch
2011-02-24 19:48:05
has height s and width s*sqrt2
has height s and width s*sqrt2
erica539
2011-02-24 19:48:05
s by rt2s
s by rt2s
thedrummer
2011-02-24 19:48:05
s by srt2
s by srt2
sindennisz
2011-02-24 19:48:05
s by s*sqrt2
s by s*sqrt2
copeland
2011-02-24 19:48:07


copeland
2011-02-24 19:48:10
Now what do you see?
Now what do you see?
PowerOfPi
2011-02-24 19:48:41
top triangle is similar to the whole because of parallel lines
top triangle is similar to the whole because of parallel lines
NoWayHaze
2011-02-24 19:48:41
similar triangles!
similar triangles!
letrangere
2011-02-24 19:48:41
similar triangles
similar triangles
Iggy Iguana
2011-02-24 19:48:41
similar triangles
similar triangles
thedrummer
2011-02-24 19:48:41
similar triangles
similar triangles
az94566
2011-02-24 19:48:41
a shape
a shape
mthcz11
2011-02-24 19:48:41
similar triangles
similar triangles
luppleAOPS
2011-02-24 19:48:41
we see more similar triangles
we see more similar triangles
andrewjjiang97
2011-02-24 19:48:41
the two triangles on the bottom are 45-45-90
the two triangles on the bottom are 45-45-90
aleCTY
2011-02-24 19:48:41
similar triangles
similar triangles
copeland
2011-02-24 19:48:45
On the left and right we have two isosceles right triangles. We know this because the large triangle is isosceles (so, for example, the lines have slope 1 and -1).
On the left and right we have two isosceles right triangles. We know this because the large triangle is isosceles (so, for example, the lines have slope 1 and -1).
copeland
2011-02-24 19:48:49

copeland
2011-02-24 19:48:53
OK, now the easy part. How do we finish?
OK, now the easy part. How do we finish?
Moldytape
2011-02-24 19:49:39
2s + s rt2 = rt2
2s + s rt2 = rt2
Iggy Iguana
2011-02-24 19:49:39
WE know that 2s+ssqrt2 = sqrt2
WE know that 2s+ssqrt2 = sqrt2
hsm174
2011-02-24 19:49:39
2s+srt2=rt2
2s+srt2=rt2
Doink
2011-02-24 19:49:39
s(2+sqrt2)=sqrt2
s(2+sqrt2)=sqrt2
NoWayHaze
2011-02-24 19:49:39
2s+s*sqrt(2)=sqrt(2)
2s+s*sqrt(2)=sqrt(2)
sindennisz
2011-02-24 19:49:39
2s+s*sqrt2=sqrt2
2s+s*sqrt2=sqrt2
willwang123
2011-02-24 19:49:39
2s+s*sqrt2=sqrt2
2s+s*sqrt2=sqrt2
calvinhobbesliker
2011-02-24 19:49:39
sqrt2=2s+ssqrt2?
sqrt2=2s+ssqrt2?
awesomeusername
2011-02-24 19:49:39
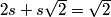
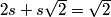
RisingMathStar
2011-02-24 19:49:39
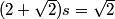
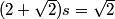
copeland
2011-02-24 19:49:44
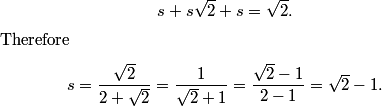
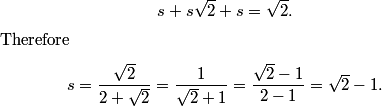
copeland
2011-02-24 19:49:48
And the volume is. . .
And the volume is. . .
professordad
2011-02-24 19:50:45
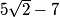
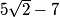
TruffleMaster
2011-02-24 19:50:45
5sqrt2-7
5sqrt2-7
briantix
2011-02-24 19:50:45
5sqrt2-7
5sqrt2-7
Iggy Iguana
2011-02-24 19:50:45
cube that to get 5sqrt2-7
cube that to get 5sqrt2-7
NoWayHaze
2011-02-24 19:50:45
5sqrt2-7
5sqrt2-7
erica539
2011-02-24 19:50:45
5rt2 - 7
5rt2 - 7
.cpp
2011-02-24 19:50:45
5sqrt(2) - 7 => A.
5sqrt(2) - 7 => A.
ahaanomegas
2011-02-24 19:50:45
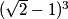
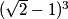
jxihong
2011-02-24 19:50:45
A 5 sq rt 2 -7
A 5 sq rt 2 -7
Relativity1618
2011-02-24 19:50:45
(sqrt2)-1 cubed
(sqrt2)-1 cubed
calvinhobbesliker
2011-02-24 19:50:45
Cube it to get 5sqrt2-7
Cube it to get 5sqrt2-7
theone142857
2011-02-24 19:50:45
cube it to get 5sqrt{2}-7
cube it to get 5sqrt{2}-7
kangchangood
2011-02-24 19:50:45
(a)..
(a)..
andrewjjiang97
2011-02-24 19:50:45
5sqrt{2}-7
5sqrt{2}-7
Spring
2011-02-24 19:50:45
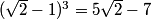
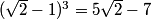
Relativity1618
2011-02-24 19:50:45
(5sqrt2)-7
(5sqrt2)-7
Doink
2011-02-24 19:50:45
5sqrt2-7 (A)
5sqrt2-7 (A)
MaggieKim
2011-02-24 19:50:45
5sqrt2-7
5sqrt2-7
sparkle123
2011-02-24 19:50:45
A 5sqrt2 -7
A 5sqrt2 -7
dragonx
2011-02-24 19:50:45
A) 5sqrt(2)-7
A) 5sqrt(2)-7
copeland
2011-02-24 19:50:47
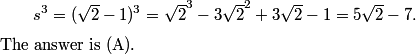
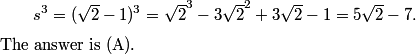
copeland
2011-02-24 19:50:57
I like that problem. It's fun to visualize.
I like that problem. It's fun to visualize.
mathcountsloser
2011-02-24 19:51:17
copeland
2011-02-24 19:51:19
(root(2)-1)^3 is prettier.
(root(2)-1)^3 is prettier.
copeland
2011-02-24 19:51:31
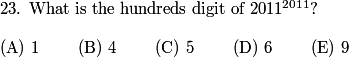
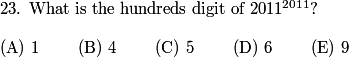
andrewjjiang97
2011-02-24 19:51:31
I think it's better when you look from one face, and use similar triangles
I think it's better when you look from one face, and use similar triangles
alikimlynn
2011-02-24 19:51:33
Since you only need the hundreds’ digit and you can’t use a calculator (wah), use 11 instead of 2011. You’ll find that there is a cycle of 1, 3, 6, 0, 5 for the hundreds digit. (Found by 11^1, 11^2, 11^3, 11^4, 11^5, respectively.) Then, 2011 – 1 = 2010. 2010/5 = 402 with no remainder. Therefore, 2011^2011 has a hundreds’ digit of 5, or (C).
Since you only need the hundreds’ digit and you can’t use a calculator (wah), use 11 instead of 2011. You’ll find that there is a cycle of 1, 3, 6, 0, 5 for the hundreds digit. (Found by 11^1, 11^2, 11^3, 11^4, 11^5, respectively.) Then, 2011 – 1 = 2010. 2010/5 = 402 with no remainder. Therefore, 2011^2011 has a hundreds’ digit of 5, or (C).
ahaanomegas
2011-02-24 19:51:36
Nothing is ugly in math if you know how to do it
Nothing is ugly in math if you know how to do it
copeland
2011-02-24 19:51:47
Dave did that.
Dave did that.
copeland
2011-02-24 19:51:53
Dave is passing things without permission.
Dave is passing things without permission.
copeland
2011-02-24 19:52:00
How do we feel about Dave?
How do we feel about Dave?
willwang123
2011-02-24 19:52:18
Gasp!!!
Gasp!!!
mathcountsloser
2011-02-24 19:52:18
Good job Dave.
Good job Dave.
davidx
2011-02-24 19:52:18
Dave is cool
Dave is cool
willwang123
2011-02-24 19:52:18
Boo!!!!
Boo!!!!
alikimlynn
2011-02-24 19:52:18
Badly?
Badly?
ChipDale
2011-02-24 19:52:18
Bad
Bad
sayeramesh
2011-02-24 19:52:18
bad
bad
DVA6102
2011-02-24 19:52:18
good
good
dragonx
2011-02-24 19:52:18
Banhammer TIME
Banhammer TIME
erica539
2011-02-24 19:52:18
shame on him!
shame on him!
Joe10112
2011-02-24 19:52:18
BAD DAVE!
BAD DAVE!
usernamehi
2011-02-24 19:52:18
MAD!!!!!
MAD!!!!!
smallpeoples343
2011-02-24 19:52:18
He's a bad person.
He's a bad person.
copeland
2011-02-24 19:52:21
Yes.
Yes.
copeland
2011-02-24 19:52:24
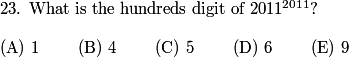
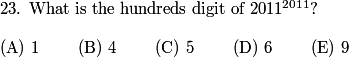
copeland
2011-02-24 19:52:35
What is it that we need to compute?
What is it that we need to compute?
AlphaMath1
2011-02-24 19:53:31
First reduce to mod 1000
First reduce to mod 1000
VIPMaster
2011-02-24 19:53:31
the first digit of 2011^2011 (mod 1000)
the first digit of 2011^2011 (mod 1000)
aleCTY
2011-02-24 19:53:31
2011^2011 mod 1000
2011^2011 mod 1000
mthcz11
2011-02-24 19:53:31
2011^2011 in mod 1000
2011^2011 in mod 1000
Iggy Iguana
2011-02-24 19:53:31
the thing mod 1000
the thing mod 1000
AlphaBetaTheta
2011-02-24 19:53:31
remainder in mod 1000, binomial theorem to the rescue
remainder in mod 1000, binomial theorem to the rescue
copeland
2011-02-24 19:53:34
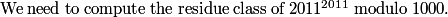
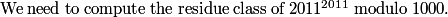
copeland
2011-02-24 19:53:46
Whenever you see one of these "hundreds" digits you know you should be reducing.
Whenever you see one of these "hundreds" digits you know you should be reducing.
copeland
2011-02-24 19:53:50
What's the first thing we notice?
What's the first thing we notice?
spaceguy524
2011-02-24 19:54:21
its the same as 11^(2011)
its the same as 11^(2011)
hi how are you doing toda
2011-02-24 19:54:21
get rid of 2000
get rid of 2000
luminate
2011-02-24 19:54:21
11^2011
11^2011
capu
2011-02-24 19:54:21
compute 11^2011
compute 11^2011
xxrxxhxx
2011-02-24 19:54:21
2011 == 11 mod 1000
2011 == 11 mod 1000
calculus321
2011-02-24 19:54:21
2011=2000+11
2011=2000+11
hi how are you doing toda
2011-02-24 19:54:21
2000 is unneccessary
2000 is unneccessary
briantix
2011-02-24 19:54:21
we can ignore the thoousands place
we can ignore the thoousands place
TruffleMaster
2011-02-24 19:54:21
2011 is 11 in mod 1000
2011 is 11 in mod 1000
mthcz11
2011-02-24 19:54:21
11^2011
11^2011
googol.plex
2011-02-24 19:54:21
2011^2011=11^2011
2011^2011=11^2011
AlphaBetaTheta
2011-02-24 19:54:21
2011^2011 = 11^2011 (mod 1000)
2011^2011 = 11^2011 (mod 1000)
copeland
2011-02-24 19:54:26
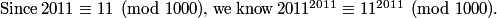
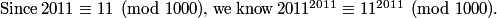
copeland
2011-02-24 19:54:30
Now how do we compute this?
Now how do we compute this?
AlphaBetaTheta
2011-02-24 19:55:14
binomial theorem
binomial theorem
AlphaMath1
2011-02-24 19:55:14
11=10+1 then BINOMIAL THEOREM!!!!!!
11=10+1 then BINOMIAL THEOREM!!!!!!
NoWayHaze
2011-02-24 19:55:14
binomial theorem
binomial theorem
Spring
2011-02-24 19:55:15
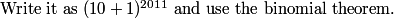
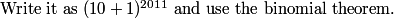
.cpp
2011-02-24 19:55:15
(10+1)^2011
(10+1)^2011
morpheus44
2011-02-24 19:55:15
binomial theorem?
binomial theorem?
Tribefan
2011-02-24 19:55:15
binomial theroem
binomial theroem
copeland
2011-02-24 19:55:18
We use the binomial theorem on 11 = 10 + 1.
We use the binomial theorem on 11 = 10 + 1.
copeland
2011-02-24 19:55:24
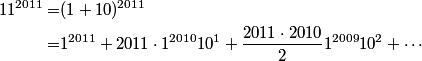
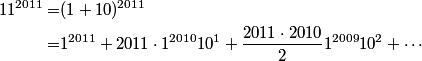
copeland
2011-02-24 19:55:26
Why did I stop there?
Why did I stop there?
VIPMaster
2011-02-24 19:55:59
because everything else cancels out mod 1000
because everything else cancels out mod 1000
calvinhobbesliker
2011-02-24 19:55:59
All else is 0 mod 1000
All else is 0 mod 1000
xxrxxhxx
2011-02-24 19:55:59
rest all have hundreds digit of 0 due to # of 10s as factors
rest all have hundreds digit of 0 due to # of 10s as factors
PowerOfPi
2011-02-24 19:55:59
everything after that is divisble by 10^3=1000
everything after that is divisble by 10^3=1000
AstralMeson
2011-02-24 19:55:59
that's the hundreds place
that's the hundreds place
aleCTY
2011-02-24 19:55:59
10^3 is 0 mod 1000
10^3 is 0 mod 1000
.cpp
2011-02-24 19:55:59
All the other terms are 0 mod 1000, so they are unnecessary.
All the other terms are 0 mod 1000, so they are unnecessary.
Spring
2011-02-24 19:55:59
Everything else is divisible by 1000 so they don't affect the hundreds digit.
Everything else is divisible by 1000 so they don't affect the hundreds digit.
Luminescence
2011-02-24 19:55:59
the others are 0mod1000
the others are 0mod1000
mathcountsloser
2011-02-24 19:55:59
10^3 = thousand, you only need the hundereds difit
10^3 = thousand, you only need the hundereds difit
copeland
2011-02-24 19:56:03
After that everything has a large power of 10. The next term, for example, is divisible by 10^3=1000, so is 0 mod 1000.
After that everything has a large power of 10. The next term, for example, is divisible by 10^3=1000, so is 0 mod 1000.
copeland
2011-02-24 19:56:05
Therefore removing all those ones gives
Therefore removing all those ones gives
copeland
2011-02-24 19:56:09
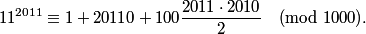
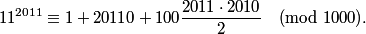
copeland
2011-02-24 19:56:10
What's the answer?
What's the answer?
quantammaths1234
2011-02-24 19:56:50
6.
6.
TruffleMaster
2011-02-24 19:56:50
6
6
vwu9
2011-02-24 19:56:50
6
6
willwang123
2011-02-24 19:56:50
6!
6!
soulspeedy
2011-02-24 19:56:50
6
6
NoWayHaze
2011-02-24 19:56:50
6
6
xxrxxhxx
2011-02-24 19:56:50
6 (D)
6 (D)
TemurAmir
2011-02-24 19:56:50
The answer is 6, D
The answer is 6, D
Luminescence
2011-02-24 19:56:50
6
6
DavidTong
2011-02-24 19:56:50
6 D
6 D
infinity1
2011-02-24 19:56:50
D 6
D 6
ahaanomegas
2011-02-24 19:56:50


Relativity1618
2011-02-24 19:56:50
6
6
CRICKET229
2011-02-24 19:56:50
6
6
knowmath
2011-02-24 19:56:50
d
d
j_f_c_w
2011-02-24 19:56:50
(d) 6
(d) 6
CRICKET229
2011-02-24 19:56:50
(D) 6
(D) 6
girishvar12
2011-02-24 19:56:50
D. 6
D. 6
Tribefan
2011-02-24 19:56:50
(D) 6
(D) 6
mthcz11
2011-02-24 19:56:50
D, 6
D, 6
AlphaBetaTheta
2011-02-24 19:56:50
6.
6.
capu
2011-02-24 19:56:50
D6
D6
LightningStreak
2011-02-24 19:56:50
d.6
d.6
spaceguy524
2011-02-24 19:56:50
D
D
jeff10
2011-02-24 19:56:50
the last three digits are 611, so the answer is 6.
the last three digits are 611, so the answer is 6.
Lalagato
2011-02-24 19:56:50
6
6
sincostanseccsccot
2011-02-24 19:56:50
6?
6?
agejiageji
2011-02-24 19:56:50
6
6
anonymous0
2011-02-24 19:56:50
D, 6
D, 6
copeland
2011-02-24 19:56:54
Since I'm lazy, I'll reduce before multiplying:
Since I'm lazy, I'll reduce before multiplying:
copeland
2011-02-24 19:56:57
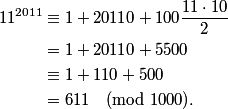
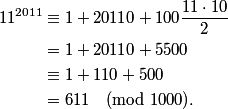
copeland
2011-02-24 19:57:03
The answer is (D) 6.
The answer is (D) 6.
aleCTY
2011-02-24 19:57:17
Couldn't we just use Euler's extension of FlT?
Couldn't we just use Euler's extension of FlT?
copeland
2011-02-24 19:57:25
Many people suggested Euler at the begnning.
Many people suggested Euler at the begnning.
copeland
2011-02-24 19:57:31
As an aside (and ignore this or come back to it if you don't understand), I assumed this problem was going to be much harder, so I started by computing:
As an aside (and ignore this or come back to it if you don't understand), I assumed this problem was going to be much harder, so I started by computing:
copeland
2011-02-24 19:57:36
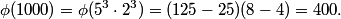
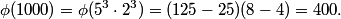
copeland
2011-02-24 19:57:38
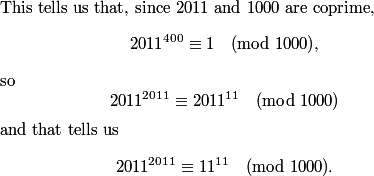
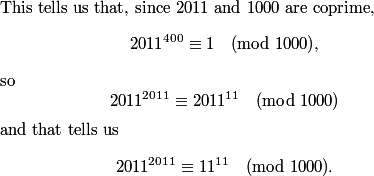
copeland
2011-02-24 19:57:48
This turns out to lead to fewer mistakes but in all I think it was the slower approach for this problem.
This turns out to lead to fewer mistakes but in all I think it was the slower approach for this problem.
ahaanomegas
2011-02-24 19:57:57
And what is Euler's Extension of FIT?
And what is Euler's Extension of FIT?
copeland
2011-02-24 19:58:04
It's a little "l." Get it?
It's a little "l." Get it?
mathletepower
2011-02-24 19:58:21
NO
NO
mthcz11
2011-02-24 19:58:21
no
no
willwang123
2011-02-24 19:58:21
No.
No.
usernamehi
2011-02-24 19:58:21
I dont get it.
I dont get it.
ChipDale
2011-02-24 19:58:21
No
No
davidx
2011-02-24 19:58:21
No
No
TemurAmir
2011-02-24 19:58:21
Nope
Nope
leinad47x
2011-02-24 19:58:21
no..
no..
MrWhatWhen
2011-02-24 19:58:21
What does phi mean in that
What does phi mean in that
Joe10112
2011-02-24 19:58:21
No. Please explain? XD
No. Please explain? XD
ctmusicgirl
2011-02-24 19:58:21
NO.
NO.
Relativity1618
2011-02-24 19:58:21
no
no
chaos763
2011-02-24 19:58:21
Not really.
Not really.
sparkle123
2011-02-24 19:58:21
no :(
no :(
copeland
2011-02-24 19:58:24
Hmm.
Hmm.
copeland
2011-02-24 19:58:40
Check out Fermat's little theorem and Euler's totient.
Check out Fermat's little theorem and Euler's totient.
copeland
2011-02-24 19:58:57
But for now we should move on. That wasn't actually necessary or even useful for this problem.
But for now we should move on. That wasn't actually necessary or even useful for this problem.
copeland
2011-02-24 19:59:04
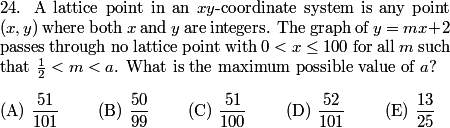
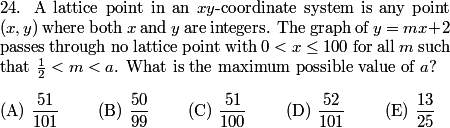
copeland
2011-02-24 19:59:13
Where should we start?
Where should we start?
lg5293
2011-02-24 19:59:44
graph?
graph?
erica539
2011-02-24 19:59:44
a diagram perhaps?
a diagram perhaps?
Iggy Iguana
2011-02-24 19:59:44
diagram?
diagram?
googol.plex
2011-02-24 19:59:44
graph it
graph it
supermathman
2011-02-24 19:59:44
draw it!!!!1
draw it!!!!1
ahaanomegas
2011-02-24 19:59:44
Draw an x-y plane?
Draw an x-y plane?
mthcz11
2011-02-24 19:59:44
draw a diagram
draw a diagram
mthcz11
2011-02-24 19:59:44
draw a graph
draw a graph
copeland
2011-02-24 19:59:53
You just like my drawins. I know you.
You just like my drawins. I know you.
copeland
2011-02-24 19:59:57
We could begin by subtracting 2 because it's irrelevant, but we won't bother. It turns out not to matter too much and only makes the computations a little easier.
We could begin by subtracting 2 because it's irrelevant, but we won't bother. It turns out not to matter too much and only makes the computations a little easier.
copeland
2011-02-24 20:00:00
Let's draw a graph:
Let's draw a graph:
copeland
2011-02-24 20:00:03
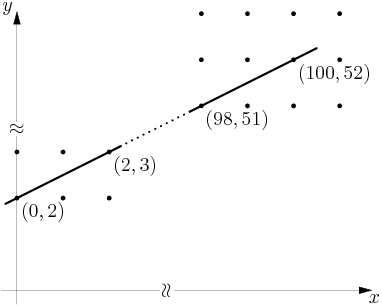

copeland
2011-02-24 20:00:09
What happens as we increase m?
What happens as we increase m?
Spring
2011-02-24 20:00:37
the slope increases
the slope increases
agejiageji
2011-02-24 20:00:37
slope increases
slope increases
ChipDale
2011-02-24 20:00:37
The line is steeper
The line is steeper
leinad47x
2011-02-24 20:00:37
slope goes up
slope goes up
Iggy Iguana
2011-02-24 20:00:37
the line gets steeper
the line gets steeper
luminate
2011-02-24 20:00:37
it becomes stteper
it becomes stteper
ahaanomegas
2011-02-24 20:00:37
The line becomes steeper
The line becomes steeper
mathcool2009
2011-02-24 20:00:37
the grafh becomes steeper
the grafh becomes steeper
professordad
2011-02-24 20:00:37
line gets steeper
line gets steeper
Doink
2011-02-24 20:00:37
it gets steeper
it gets steeper
pgmath
2011-02-24 20:00:37
The line becomes steeper.
The line becomes steeper.
copeland
2011-02-24 20:00:41
As we increase m the slope increases:
As we increase m the slope increases:
copeland
2011-02-24 20:00:43
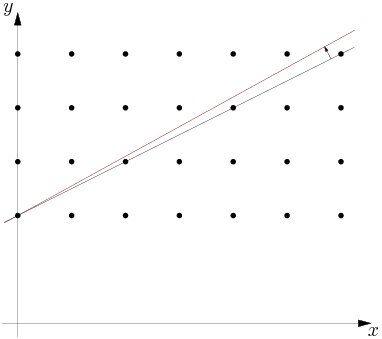

copeland
2011-02-24 20:00:47
lg5293
2011-02-24 20:01:41
the lowest lattice point we can hit
the lowest lattice point we can hit
Spring
2011-02-24 20:01:41
The maximum sloope the line can have and still not pass through any lattice points with x<100
The maximum sloope the line can have and still not pass through any lattice points with x<100
MrWhatWhen
2011-02-24 20:01:41
the maximum slope that won't pass through any lattice point
the maximum slope that won't pass through any lattice point
TrigMan
2011-02-24 20:01:41
The highest you can go without hitting more dots.
The highest you can go without hitting more dots.
Jasmine8925
2011-02-24 20:01:41
the next highest slope so that the line will go through a lattice point
the next highest slope so that the line will go through a lattice point
RisingMathStar
2011-02-24 20:01:41
The minimum slope at which the line touches the next lattice point
The minimum slope at which the line touches the next lattice point
.cpp
2011-02-24 20:01:41
The slope where y=mx+2 meets a lattice point first after m=1/2.
The slope where y=mx+2 meets a lattice point first after m=1/2.
xxrxxhxx
2011-02-24 20:01:41
when the line will be steep enough to hit a lattice point
when the line will be steep enough to hit a lattice point
AlphaMath1
2011-02-24 20:01:41
the next slope wheres there's an integral solution (x, y)
the next slope wheres there's an integral solution (x, y)
gh625
2011-02-24 20:01:41
The slope that goes through the next highest lattice point
The slope that goes through the next highest lattice point
JSGandora
2011-02-24 20:01:41
The slope at which the line first concides with another lattice point
The slope at which the line first concides with another lattice point
copeland
2011-02-24 20:01:43
The number a is the first slope larger than m=1/2 that hits another lattice point.
The number a is the first slope larger than m=1/2 that hits another lattice point.
copeland
2011-02-24 20:01:46
Where will this collision occur?
Where will this collision occur?
Spring
2011-02-24 20:02:39
(99,52)
(99,52)
AlphaMath1
2011-02-24 20:02:39
at x=99?
at x=99?
calvinhobbesliker
2011-02-24 20:02:39
99, 52
99, 52
RisingMathStar
2011-02-24 20:02:39
(99, 52)
(99, 52)
JSGandora
2011-02-24 20:02:39
At the upper right hand corner of the 100x52 rectangle
At the upper right hand corner of the 100x52 rectangle
copeland
2011-02-24 20:02:43
It'll occur somewhere at the end, so let me draw that for you:
It'll occur somewhere at the end, so let me draw that for you:
copeland
2011-02-24 20:02:45
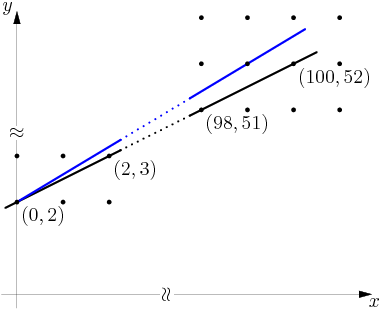

copeland
2011-02-24 20:02:48
For convenience we'll let L denote the line through (0,2) with slope 1/2.
For convenience we'll let L denote the line through (0,2) with slope 1/2.
copeland
2011-02-24 20:02:52
At this point we could compute the value of a right away, but it's only a tiny bit harder to get a nice, clean proof that our answer is correct, so instead we'll do everything the long way.
At this point we could compute the value of a right away, but it's only a tiny bit harder to get a nice, clean proof that our answer is correct, so instead we'll do everything the long way.
copeland
2011-02-24 20:02:58
For every integer x, there is a nearest lattice point above L with this x coordinate. What is this lattice point?
For every integer x, there is a nearest lattice point above L with this x coordinate. What is this lattice point?
copeland
2011-02-24 20:03:31
First of all, it depends on whether x is even or odd. If x is even then what is the lattice point?
First of all, it depends on whether x is even or odd. If x is even then what is the lattice point?
JSGandora
2011-02-24 20:04:18
(x,y+1)
(x,y+1)
Iggy Iguana
2011-02-24 20:04:18
(x,x+3)
(x,x+3)
.cpp
2011-02-24 20:04:18
1/2 x + 3.
1/2 x + 3.
Spring
2011-02-24 20:04:18
1/2x+3
1/2x+3
RisingMathStar
2011-02-24 20:04:18
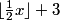
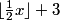
ahaanomegas
2011-02-24 20:04:18
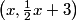
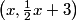
copeland
2011-02-24 20:04:28


copeland
2011-02-24 20:04:28
What about if x is odd?
What about if x is odd?
.cpp
2011-02-24 20:05:29
If x is odd, this is just (x,1/2x + 5/2).
If x is odd, this is just (x,1/2x + 5/2).
PowerOfPi
2011-02-24 20:05:29
(x, x/2+2.5)
(x, x/2+2.5)
Spring
2011-02-24 20:05:29
1/2x+2 rounded up to the nearest integer
1/2x+2 rounded up to the nearest integer
ahaanomegas
2011-02-24 20:05:29
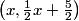
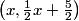
VIPMaster
2011-02-24 20:05:29
(x, x/2 + 2.5)
(x, x/2 + 2.5)
Iggy Iguana
2011-02-24 20:05:29
(x,x/2+2.5)
(x,x/2+2.5)
JSGandora
2011-02-24 20:05:29
(x,y+1/2)
(x,y+1/2)
copeland
2011-02-24 20:05:33
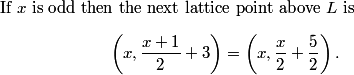
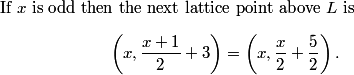
copeland
2011-02-24 20:05:38
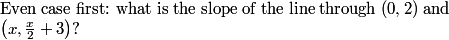
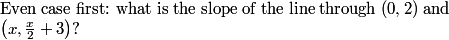
Spring
2011-02-24 20:06:26
(x/2+1)/x
(x/2+1)/x
ahaanomegas
2011-02-24 20:06:26
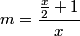
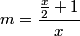
calvinhobbesliker
2011-02-24 20:06:26
0.5+1/x
0.5+1/x
Iggy Iguana
2011-02-24 20:06:26
(x/2+1)/x
(x/2+1)/x
luppleAOPS
2011-02-24 20:06:26
(x/2+1)/(x)
(x/2+1)/(x)
spaceguy524
2011-02-24 20:06:26
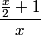
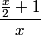
.cpp
2011-02-24 20:06:27
(x/2 + 1)/x
(x/2 + 1)/x
JSGandora
2011-02-24 20:06:27
(x/2+1)/x
(x/2+1)/x
TruffleMaster
2011-02-24 20:06:27
1/2+1/x
1/2+1/x
infinity1
2011-02-24 20:06:27
1/2 + 1/x
1/2 + 1/x
ChipDale
2011-02-24 20:06:27
1/2+1/x
1/2+1/x
sindennisz
2011-02-24 20:06:27
1/2+1/x
1/2+1/x
copeland
2011-02-24 20:06:29
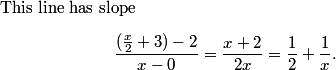
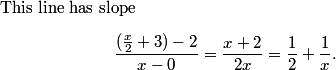
copeland
2011-02-24 20:06:31
Do we want to maximize or minimize that?
Do we want to maximize or minimize that?
ChipDale
2011-02-24 20:07:09
minimize
minimize
PowerOfPi
2011-02-24 20:07:09
minimize
minimize
erica539
2011-02-24 20:07:09
minimize
minimize
calvinhobbesliker
2011-02-24 20:07:09
Minimize
Minimize
Gosav3122
2011-02-24 20:07:09
min
min
mstoenescu
2011-02-24 20:07:09
minimize
minimize
Spring
2011-02-24 20:07:09
Minimize because we want the first collision with a lattice point
Minimize because we want the first collision with a lattice point
Gosav3122
2011-02-24 20:07:09
biggest slope, so minimize x
biggest slope, so minimize x
jeff10
2011-02-24 20:07:09
minimize
minimize
mathcool2009
2011-02-24 20:07:09
minimize
minimize
copeland
2011-02-24 20:07:11
We want the line to be under all of these points so we want the minimum. How small can that be for even x from 1 to 100?
We want the line to be under all of these points so we want the minimum. How small can that be for even x from 1 to 100?
willwang123
2011-02-24 20:07:50
51/100
51/100
PowerOfPi
2011-02-24 20:07:50
1/2+1/100=51/100
1/2+1/100=51/100
Iggy Iguana
2011-02-24 20:07:50
1/2 + 1/100 = 51/100
1/2 + 1/100 = 51/100
calvinhobbesliker
2011-02-24 20:07:50
1/2+1/100=51/100
1/2+1/100=51/100
Spring
2011-02-24 20:07:50
1/2+1/100=51/100
1/2+1/100=51/100
TrigMan
2011-02-24 20:07:50
51/100
51/100
RisingMathStar
2011-02-24 20:07:50
x should be 100
x should be 100
infinity1
2011-02-24 20:07:50
x = 100 ==> 0.51
x = 100 ==> 0.51
professordad
2011-02-24 20:07:50
1/2+1/100 or 51/100
1/2+1/100 or 51/100
copeland
2011-02-24 20:07:54
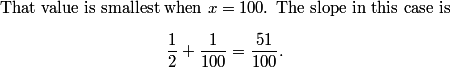
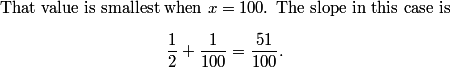
copeland
2011-02-24 20:07:55


Spring
2011-02-24 20:08:31
(x/2+1/2).x
(x/2+1/2).x
calvinhobbesliker
2011-02-24 20:08:31
1/2+1/2x
1/2+1/2x
Iggy Iguana
2011-02-24 20:08:31
(x/2+.5)/x
(x/2+.5)/x
VIPMaster
2011-02-24 20:08:31
1/2 + (1/2x)
1/2 + (1/2x)
spaceguy524
2011-02-24 20:08:31
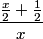
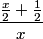
PowerOfPi
2011-02-24 20:08:31
1/2+1/(2x)
1/2+1/(2x)
.cpp
2011-02-24 20:08:31
1/2 + 1/(2x)
1/2 + 1/(2x)
MrWhatWhen
2011-02-24 20:08:31
(x/2-1/2)/x
(x/2-1/2)/x
ahaanomegas
2011-02-24 20:08:31
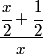
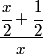
sindennisz
2011-02-24 20:08:31
1/2+1/2x
1/2+1/2x
copeland
2011-02-24 20:08:37
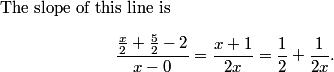
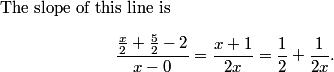
copeland
2011-02-24 20:08:39
What is the minimum over odd x between 1 and 100?
What is the minimum over odd x between 1 and 100?
LiBoy
2011-02-24 20:09:12
50/99
50/99
jeff10
2011-02-24 20:09:12
50/99
50/99
Iggy Iguana
2011-02-24 20:09:12
1/2 + 1/198 = 50/99
1/2 + 1/198 = 50/99
calvinhobbesliker
2011-02-24 20:09:12
1/2+1/198=100/198=50/99
1/2+1/198=100/198=50/99
ChipDale
2011-02-24 20:09:12
50/99
50/99
Spring
2011-02-24 20:09:12
1/2+1/(2*99)=50/99
1/2+1/(2*99)=50/99
Gosav3122
2011-02-24 20:09:12
99
99
PowerOfPi
2011-02-24 20:09:12
1/2+1/198=50/99
1/2+1/198=50/99
mstoenescu
2011-02-24 20:09:12
50/99
50/99
danielguo94
2011-02-24 20:09:12
50/99
50/99
AlphaMath1
2011-02-24 20:09:12
x=99 --->50/99
x=99 --->50/99
copeland
2011-02-24 20:09:16
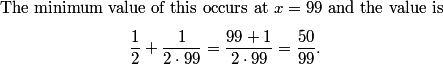
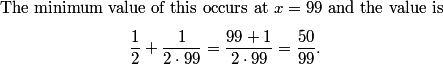
copeland
2011-02-24 20:09:19
And the answer?
And the answer?
LightningStreak
2011-02-24 20:10:08
B
B
AlphaMath1
2011-02-24 20:10:08
50/99
50/99
agejiageji
2011-02-24 20:10:08
50/99
50/99
PowerOfPi
2011-02-24 20:10:08
B
B
gh625
2011-02-24 20:10:08
B 50/99
B 50/99
professordad
2011-02-24 20:10:08
50/99 or B
50/99 or B
Jasmine8925
2011-02-24 20:10:08
50/99
50/99
minirafa
2011-02-24 20:10:08
b
b
supermathman
2011-02-24 20:10:08
50/99
50/99
Luminescence
2011-02-24 20:10:08
the smaller of the two, 50/99
the smaller of the two, 50/99
ahaanomegas
2011-02-24 20:10:08
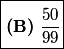
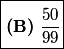
.cpp
2011-02-24 20:10:08
50/99 = (B).
50/99 = (B).
girishvar12
2011-02-24 20:10:08
B
B
willwang123
2011-02-24 20:10:08
B?
B?
ChipDale
2011-02-24 20:10:08
B
B
ctmusicgirl
2011-02-24 20:10:08
B
B
danielguo94
2011-02-24 20:10:08
B
B
TruffleMaster
2011-02-24 20:10:08
50/99
50/99
ooooo1
2011-02-24 20:10:08
50/99
50/99
mathletepower
2011-02-24 20:10:08
B for bee
B for bee
sayeramesh
2011-02-24 20:10:08
B
B
ctmusicgirl
2011-02-24 20:10:08
B
B
az94566
2011-02-24 20:10:08
50/99
50/99
ooooo1
2011-02-24 20:10:08
B) 50/99
B) 50/99
mathcounter7
2011-02-24 20:10:08
B
B
Spring
2011-02-24 20:10:08
50/99-5000/9900 and 51/100=5001/9900 so 50/99 is smaller
50/99-5000/9900 and 51/100=5001/9900 so 50/99 is smaller
LiBoy
2011-02-24 20:10:08
50/99!
50/99!
VIPMaster
2011-02-24 20:10:08
50/99
50/99
timelessmath
2011-02-24 20:10:08
50/99
50/99
knowmath
2011-02-24 20:10:08
b
b
mathletepower
2011-02-24 20:10:08
(B) 50/99
(B) 50/99
copeland
2011-02-24 20:10:12
Since 50/99 < 51/100, the answer must be 50/99, (B).
Since 50/99 < 51/100, the answer must be 50/99, (B).
copeland
2011-02-24 20:10:18
Alright!
Alright!
copeland
2011-02-24 20:10:33
Now it's time for the last problem on the 10.
Now it's time for the last problem on the 10.
copeland
2011-02-24 20:10:46


copeland
2011-02-24 20:10:55
OK, what first?
OK, what first?
Joe10112
2011-02-24 20:11:18
Draw a diagram for this one first!
Draw a diagram for this one first!
Iggy Iguana
2011-02-24 20:11:18
another diagram
another diagram
calvinhobbesliker
2011-02-24 20:11:18
Diagram
Diagram
mthcz11
2011-02-24 20:11:18
diagram
diagram
professordad
2011-02-24 20:11:18
draw the diagram :)
draw the diagram :)
chaos763
2011-02-24 20:11:18
Diagram?
Diagram?
ChipDale
2011-02-24 20:11:18
Draw a picture
Draw a picture
hoper190
2011-02-24 20:11:18
draw something
draw something
theone142857
2011-02-24 20:11:18
diagram
diagram
.cpp
2011-02-24 20:11:18
Diagram!
Diagram!
Luminescence
2011-02-24 20:11:18
draw a picture...?
draw a picture...?
az94566
2011-02-24 20:11:18
picture
picture
VIPMaster
2011-02-24 20:11:18
We love your diagrams!!
We love your diagrams!!
ahaanomegas
2011-02-24 20:11:18
Diagram
Diagram
copeland
2011-02-24 20:11:23
Well, drawing a picture has been useful for us so far. Let's draw another.
Well, drawing a picture has been useful for us so far. Let's draw another.
copeland
2011-02-24 20:11:27
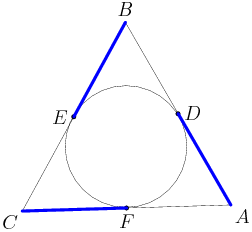

copeland
2011-02-24 20:11:31
At every step we start with a triangle, we draw the incircle and we look at the three edge lengths above. Let's start by giving them variables.
At every step we start with a triangle, we draw the incircle and we look at the three edge lengths above. Let's start by giving them variables.
copeland
2011-02-24 20:11:45
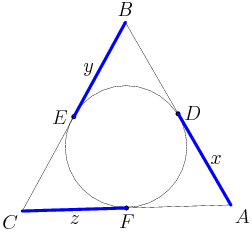

copeland
2011-02-24 20:11:52
Alright, what next? What else does geometry tell us?
Alright, what next? What else does geometry tell us?
AlphaMath1
2011-02-24 20:12:49
Congruent tangents
Congruent tangents
timelessmath
2011-02-24 20:12:49
tangent segments are congruent
tangent segments are congruent
Joe10112
2011-02-24 20:12:49
we note that z equals CE, and x equals FA, and y equals BD!
we note that z equals CE, and x equals FA, and y equals BD!
PowerOfPi
2011-02-24 20:12:49
CE=z, BD=y, AF=x because they are tangents from the same point
CE=z, BD=y, AF=x because they are tangents from the same point
Iggy Iguana
2011-02-24 20:12:49
AB - x = y, and same thiing for the other sides.
AB - x = y, and same thiing for the other sides.
professordad
2011-02-24 20:12:49
Two Tangent Theorem, so CE=CF, BE=BD, and AD=AF
Two Tangent Theorem, so CE=CF, BE=BD, and AD=AF
ChipDale
2011-02-24 20:12:49
equidistant from the sides
equidistant from the sides
copeland
2011-02-24 20:12:54
Since we're dealing with the incenter, we also know the other three edge lengths!
Since we're dealing with the incenter, we also know the other three edge lengths!
copeland
2011-02-24 20:12:57
Watch what happens if we draw the incenter and a couple of arcs:
Watch what happens if we draw the incenter and a couple of arcs:
copeland
2011-02-24 20:13:00
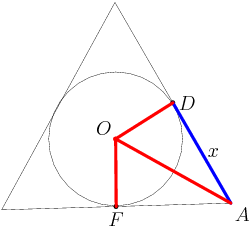

copeland
2011-02-24 20:13:04
Since the two triangles AOF and AOD are congruent (since these are right triangles with one equal edge and common hypotenuse) we know that AF = AD. (There's also a cute symmetry argument if you prefer, from flipping over OA.)
Since the two triangles AOF and AOD are congruent (since these are right triangles with one equal edge and common hypotenuse) we know that AF = AD. (There's also a cute symmetry argument if you prefer, from flipping over OA.)
copeland
2011-02-24 20:13:17
The picture fleshes out like this:
The picture fleshes out like this:
copeland
2011-02-24 20:13:19
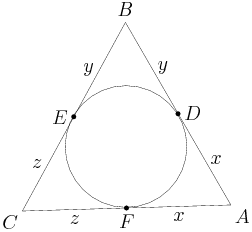

copeland
2011-02-24 20:13:24
OK, so back to the problem. Let's see how we include the initial conditions.
OK, so back to the problem. Let's see how we include the initial conditions.
copeland
2011-02-24 20:13:27
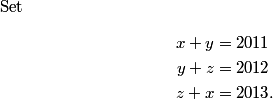
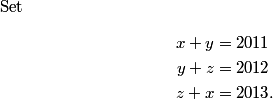
copeland
2011-02-24 20:13:29
Can we solve this system or is it under- or overdetermined?
Can we solve this system or is it under- or overdetermined?
DVA6102
2011-02-24 20:14:11
it is solvable
it is solvable
TruffleMaster
2011-02-24 20:14:11
you can solve it if you add them
you can solve it if you add them
Jasmine8925
2011-02-24 20:14:11
i think we can solve it
i think we can solve it
bbgun34
2011-02-24 20:14:11
you can solve it
you can solve it
timelessmath
2011-02-24 20:14:11
add all equations
add all equations
LightningStreak
2011-02-24 20:14:11
you can solve it
you can solve it
erica539
2011-02-24 20:14:11
we can solve
we can solve
AlphaMath1
2011-02-24 20:14:11
Add them up, divide by 2, then start subtracting each equation
Add them up, divide by 2, then start subtracting each equation
girishvar12
2011-02-24 20:14:11
solve
solve
PowerOfPi
2011-02-24 20:14:11
add 2 of them, subtract one, then divide by 2
add 2 of them, subtract one, then divide by 2
kangchangood
2011-02-24 20:14:11
we can. by sum/2 and subtraction
we can. by sum/2 and subtraction
TrigMan
2011-02-24 20:14:11
2x + 2y + 2z = 6036
2x + 2y + 2z = 6036
calvinhobbesliker
2011-02-24 20:14:11
We can solve it
We can solve it
TrigMan
2011-02-24 20:14:11
x + y + z = 3018
x + y + z = 3018
willwang123
2011-02-24 20:14:11
Add all the equations
Add all the equations
copeland
2011-02-24 20:14:16
We can solve it! First add the three equations:
We can solve it! First add the three equations:
copeland
2011-02-24 20:14:19
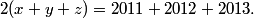
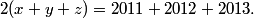
copeland
2011-02-24 20:14:22
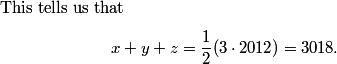
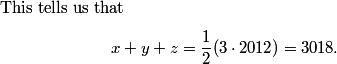
copeland
2011-02-24 20:14:24
What is x?
What is x?
jeff10
2011-02-24 20:14:55
x+y=2011, and x+y+z=3018
x+y=2011, and x+y+z=3018
.cpp
2011-02-24 20:14:55
1006.
1006.
airplanes1
2011-02-24 20:14:55
1006
1006
calvinhobbesliker
2011-02-24 20:14:55
1006
1006
ooooo1
2011-02-24 20:14:55
1006
1006
kangchangood
2011-02-24 20:14:55
1006
1006
Spring
2011-02-24 20:14:55
x=3018-(y+z)=3018-2012=1006
x=3018-(y+z)=3018-2012=1006
TruffleMaster
2011-02-24 20:14:55
1006
1006
PowerOfPi
2011-02-24 20:14:55
3018-2012=1006
3018-2012=1006
luppleAOPS
2011-02-24 20:14:55
3018-2012=1006
3018-2012=1006
copeland
2011-02-24 20:15:00
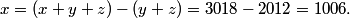
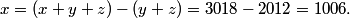
copeland
2011-02-24 20:15:00
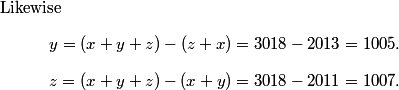
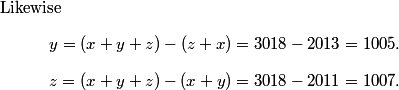
copeland
2011-02-24 20:15:05
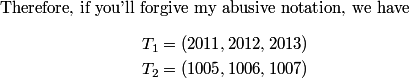
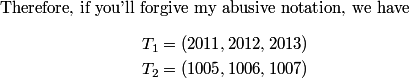
copeland
2011-02-24 20:15:18
Let's try one more iteration to see if we can't get an idea of what's going on.
Let's try one more iteration to see if we can't get an idea of what's going on.
copeland
2011-02-24 20:15:22
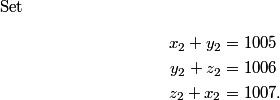
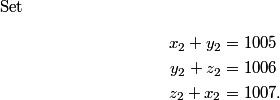
copeland
2011-02-24 20:15:29
(Notice that I'm using subscripts so I don't get confused. You don't have to care about them if you don't want. Also notice that x_2 is a partial edge of T_2 and a total edge of T_3. This is unfortunate but unavoidable.)
(Notice that I'm using subscripts so I don't get confused. You don't have to care about them if you don't want. Also notice that x_2 is a partial edge of T_2 and a total edge of T_3. This is unfortunate but unavoidable.)
copeland
2011-02-24 20:15:37
Now what?
Now what?
AlphaMath1
2011-02-24 20:16:15
Do the same thing
Do the same thing
professordad
2011-02-24 20:16:15
add and divide by 2
add and divide by 2
Iggy Iguana
2011-02-24 20:16:15
same thing
same thing
Relativity1618
2011-02-24 20:16:15
do the same thing
do the same thing
jxihong
2011-02-24 20:16:15
add the equations
add the equations
soulspeedy
2011-02-24 20:16:15
solve
solve
mthcz11
2011-02-24 20:16:15
add them all together again
add them all together again
kangchangood
2011-02-24 20:16:15
same thing again..
same thing again..
ooooo1
2011-02-24 20:16:15
add them and subtract again
add them and subtract again
mthcz11
2011-02-24 20:16:15
do the same as before
do the same as before
jeff10
2011-02-24 20:16:15
x(2)+y(2)+z(2)=1509
x(2)+y(2)+z(2)=1509
girishvar12
2011-02-24 20:16:15
add all three then solve like before
add all three then solve like before
Doink
2011-02-24 20:16:15
x+y+z=(1005+1006+1007)/2
x+y+z=(1005+1006+1007)/2
copeland
2011-02-24 20:16:17
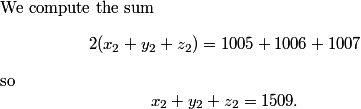
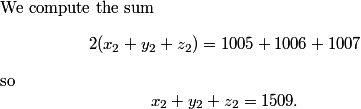
copeland
2011-02-24 20:16:20
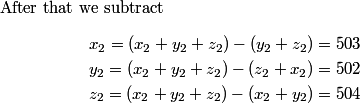
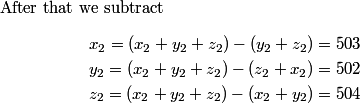
copeland
2011-02-24 20:16:26
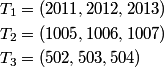
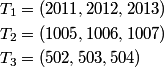
copeland
2011-02-24 20:16:33
I smell a pattern. What do you see?
I smell a pattern. What do you see?
PowerOfPi
2011-02-24 20:17:20
divide the middle by 2
divide the middle by 2
RisingMathStar
2011-02-24 20:17:20
consecutive numbers
consecutive numbers
TruffleMaster
2011-02-24 20:17:20
the middle term divides by 2
the middle term divides by 2
Iggy Iguana
2011-02-24 20:17:20
just divide middle term by 2 to get the next middle term.
just divide middle term by 2 to get the next middle term.
soulspeedy
2011-02-24 20:17:20
x,y,z increasing by 1
x,y,z increasing by 1
AlphaMath1
2011-02-24 20:17:20
Subtract y/2
Subtract y/2
BarbieRocks
2011-02-24 20:17:20
divide middle by 2, then plus 1 and minus 1
divide middle by 2, then plus 1 and minus 1
usernamehi
2011-02-24 20:17:20
increases by 1
increases by 1
briantix
2011-02-24 20:17:20
each triangle has half the perimeter of the one before it
each triangle has half the perimeter of the one before it
Spring
2011-02-24 20:17:20
The middle numbers are dividing by 2 each time
The middle numbers are dividing by 2 each time
qwerty323
2011-02-24 20:17:20
division by 2
division by 2
mathcool2009
2011-02-24 20:17:20
I notice that the middle term is halved each time
I notice that the middle term is halved each time
lg5293
2011-02-24 20:17:20
middle term divides by two, and right and left terms are less than one and greater than one respectively
middle term divides by two, and right and left terms are less than one and greater than one respectively
MrWhatWhen
2011-02-24 20:17:20
y is halved, x is 1 less than y, z is 1 more than y
y is halved, x is 1 less than y, z is 1 more than y
ilovepink
2011-02-24 20:17:20
middle term is halving
middle term is halving
kangchangood
2011-02-24 20:17:20
divide and the very right one down, middle one stays, and left one up
divide and the very right one down, middle one stays, and left one up
soulspeedy
2011-02-24 20:17:20
y,x,z increasing by 1
y,x,z increasing by 1
copeland
2011-02-24 20:17:24
It looks like the middle numbers are decreasing by half and the differences are always 1. Let's try to prove this.
It looks like the middle numbers are decreasing by half and the differences are always 1. Let's try to prove this.
copeland
2011-02-24 20:17:30
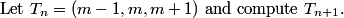
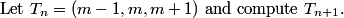
copeland
2011-02-24 20:17:38
Again we set things up:
Again we set things up:
copeland
2011-02-24 20:17:42
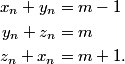
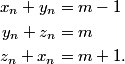
copeland
2011-02-24 20:17:50
What is the sum?
What is the sum?
AlphaMath1
2011-02-24 20:18:12
3m
3m
ooooo1
2011-02-24 20:18:12
3m
3m
morpheus44
2011-02-24 20:18:12
3m
3m
chimka
2011-02-24 20:18:12
3m
3m
briantix
2011-02-24 20:18:12
3m
3m
soulspeedy
2011-02-24 20:18:12
3m
3m
TrigMan
2011-02-24 20:18:12
3m
3m
qwerty323
2011-02-24 20:18:12
3m
3m
ChipDale
2011-02-24 20:18:12
3m
3m
mstoenescu
2011-02-24 20:18:12
3m
3m
BarbieRocks
2011-02-24 20:18:12
3m
3m
professordad
2011-02-24 20:18:12
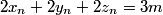
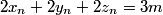
ChipDale
2011-02-24 20:18:12
3m
3m
copeland
2011-02-24 20:18:16
copeland
2011-02-24 20:18:25
And what does that make x, y, and z?
And what does that make x, y, and z?
PowerOfPi
2011-02-24 20:19:47
1/2m+1, 1/2m, 1/2m-1
1/2m+1, 1/2m, 1/2m-1
DVA6102
2011-02-24 20:19:47
1/2m-1,1/2m,1/2,+1
1/2m-1,1/2m,1/2,+1
briantix
2011-02-24 20:19:47
m/2-1,m/2,m/2+1
m/2-1,m/2,m/2+1
TrigMan
2011-02-24 20:19:47
m/2-1,m/2,m/2+1
m/2-1,m/2,m/2+1
math243
2011-02-24 20:19:47
consecutive
consecutive
NoWayHaze
2011-02-24 20:19:47
(m/2-1,m/2,m/2+1)
(m/2-1,m/2,m/2+1)
ChipDale
2011-02-24 20:19:47
m/2,m-1/2,m+1/2
m/2,m-1/2,m+1/2
agejiageji
2011-02-24 20:19:47
y = m/2, x = m/2-1, z = m/2 + 1
y = m/2, x = m/2-1, z = m/2 + 1
theone142857
2011-02-24 20:19:47
m/2,m/2-1,m/2+1
m/2,m/2-1,m/2+1
mathletepower
2011-02-24 20:19:47
m/2,m-2
m/2,m-2
BarbieRocks
2011-02-24 20:19:47
m/2-1, m/2, m/2+1
m/2-1, m/2, m/2+1
calvinhobbesliker
2011-02-24 20:19:47
m/2, m+2/2, m-2/2
m/2, m+2/2, m-2/2
mathcool2009
2011-02-24 20:19:47
x_n=m/2,y_n=m/2-1,z_n=m/2+1
x_n=m/2,y_n=m/2-1,z_n=m/2+1
professordad
2011-02-24 20:19:47
m/2-1,m/2,m/2+1
m/2-1,m/2,m/2+1
CRICKET229
2011-02-24 20:19:47
(m/2-1,m/2,m/2+1)
(m/2-1,m/2,m/2+1)
JSGandora
2011-02-24 20:19:47
x=m/2+1, y=m/2, z=m/2+1
x=m/2+1, y=m/2, z=m/2+1
girishvar12
2011-02-24 20:19:47
(m/2)-1=x y=m/2 z=(m/2)+1
(m/2)-1=x y=m/2 z=(m/2)+1
copeland
2011-02-24 20:19:49
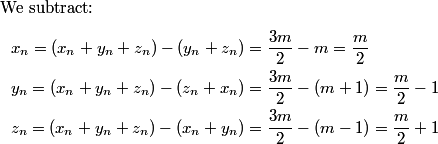
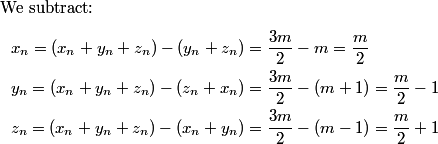
copeland
2011-02-24 20:19:53
(Notice that the order "changes," but that was also happening above.)
(Notice that the order "changes," but that was also happening above.)
copeland
2011-02-24 20:19:57
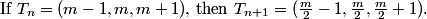
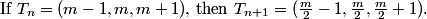
copeland
2011-02-24 20:20:01
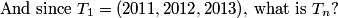
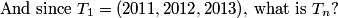
copeland
2011-02-24 20:20:09
Give me the middle term if you're feeling lazy.
Give me the middle term if you're feeling lazy.
LiBoy
2011-02-24 20:21:02
2012/2^N-1
2012/2^N-1
qwerty323
2011-02-24 20:21:06
2012/2^n-1
2012/2^n-1
BarbieRocks
2011-02-24 20:21:06
2012/2^(n-1)
2012/2^(n-1)
AlphaMath1
2011-02-24 20:21:06
2012/2^n-1
2012/2^n-1
ilovepink
2011-02-24 20:21:06
2012/2^(n-1)*
2012/2^(n-1)*
mathcool2009
2011-02-24 20:21:06
2012/2^(n-1) I think
2012/2^(n-1) I think
CRICKET229
2011-02-24 20:21:06
2012/2^n-1
2012/2^n-1
PowerOfPi
2011-02-24 20:21:06
2012/(2^(n-1))
2012/(2^(n-1))
willwang123
2011-02-24 20:21:06
2012/(2^(n-1))
2012/(2^(n-1))
copeland
2011-02-24 20:21:08
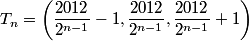
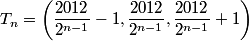
copeland
2011-02-24 20:21:12
Back to the problem. How do we know when we stop having a triangle?
Back to the problem. How do we know when we stop having a triangle?
Iggy Iguana
2011-02-24 20:22:04
We are trying to find the greatest value of T_n so that the triangle inequality still holds (x+y>z)
We are trying to find the greatest value of T_n so that the triangle inequality still holds (x+y>z)
andrewjjiang97
2011-02-24 20:22:04
triangle inequality
triangle inequality
erica539
2011-02-24 20:22:04
triangle inequality?
triangle inequality?
CRICKET229
2011-02-24 20:22:04
use triangle inequality
use triangle inequality
NoWayHaze
2011-02-24 20:22:04
triangle inequality
triangle inequality
willwang123
2011-02-24 20:22:04
sides do not satisfy triangle inequality
sides do not satisfy triangle inequality
sindennisz
2011-02-24 20:22:04
Triangle Inequality doesn't hold anymore.
Triangle Inequality doesn't hold anymore.
adhya
2011-02-24 20:22:04
when the trianlge inequality isnt satisfied
when the trianlge inequality isnt satisfied
LiBoy
2011-02-24 20:22:04
when sides do not conform to triangle inequality!
when sides do not conform to triangle inequality!
Spring
2011-02-24 20:22:04
When one of the sides is >= the sum of the other two
When one of the sides is >= the sum of the other two
ahaanomegas
2011-02-24 20:22:04
Triangle Inequality
Triangle Inequality
jxihong
2011-02-24 20:22:04
when two sides have a sum less than the third
when two sides have a sum less than the third
TemurAmir
2011-02-24 20:22:04
When the two smaller sides added together, is less than the largest
When the two smaller sides added together, is less than the largest
supermathman
2011-02-24 20:22:04
when a term < 0
when a term < 0
briantix
2011-02-24 20:22:04
when triangle inequalitie doesnt hold
when triangle inequalitie doesnt hold
professordad
2011-02-24 20:22:04
when it doesn't satisfy the triangle inequality
when it doesn't satisfy the triangle inequality
mathcool2009
2011-02-24 20:22:04
When the two shorter sides add up to not greater than the largest side.
When the two shorter sides add up to not greater than the largest side.
copeland
2011-02-24 20:22:06
We stop having a triangle when the triangle inequality fails (or when the smallest edge has negative length). The triangle inequality fails if the two smallest lengths add to less than the largest length.
We stop having a triangle when the triangle inequality fails (or when the smallest edge has negative length). The triangle inequality fails if the two smallest lengths add to less than the largest length.
copeland
2011-02-24 20:22:13
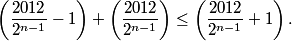
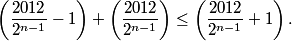
copeland
2011-02-24 20:22:16
Gross. Let me simplify that for you.
Gross. Let me simplify that for you.
copeland
2011-02-24 20:22:19
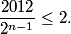
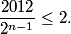
copeland
2011-02-24 20:22:27
or
or
copeland
2011-02-24 20:22:30
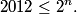
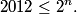
copeland
2011-02-24 20:22:45
What first power of 2 satisfies this first inequality with 2^{n-1}?
What first power of 2 satisfies this first inequality with 2^{n-1}?
calvinhobbesliker
2011-02-24 20:23:23
n>10
n>10
NoWayHaze
2011-02-24 20:23:23
11
11
professordad
2011-02-24 20:23:23
n=11
n=11
BarbieRocks
2011-02-24 20:23:23
n=11
n=11
erica539
2011-02-24 20:23:23
11
11
CRICKET229
2011-02-24 20:23:23
11
11
theone142857
2011-02-24 20:23:23
1024
1024
RisingMathStar
2011-02-24 20:23:23
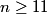
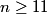
ChipDale
2011-02-24 20:23:23
11
11
math243
2011-02-24 20:23:23
11
11
copeland
2011-02-24 20:23:28
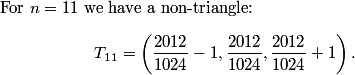
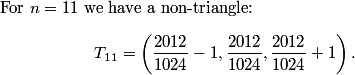
copeland
2011-02-24 20:23:31
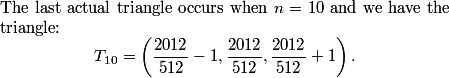
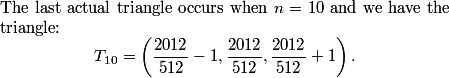
copeland
2011-02-24 20:23:35
So what's the answer to this problem?
So what's the answer to this problem?
mthcz11
2011-02-24 20:24:42
d
d
TemurAmir
2011-02-24 20:24:42
D, 1509/128
D, 1509/128
ksun48
2011-02-24 20:24:42
D
D
LiBoy
2011-02-24 20:24:42
2012/512=1509/128!
2012/512=1509/128!
gh625
2011-02-24 20:24:42
D 1509/128
D 1509/128
MrWhatWhen
2011-02-24 20:24:42
1509/128
1509/128
AlphaMath1
2011-02-24 20:24:42
(D) 1509/128
(D) 1509/128
theone142857
2011-02-24 20:24:42
1509/128
1509/128
knowmath
2011-02-24 20:24:42
d
d
Iggy Iguana
2011-02-24 20:24:42
3x2012/512 = D (1509/128)
3x2012/512 = D (1509/128)
mthcz11
2011-02-24 20:24:42
(D) 1509/128
(D) 1509/128
professordad
2011-02-24 20:24:42
so its D
so its D
Spring
2011-02-24 20:24:42
2012/512*3=1509/128, D
2012/512*3=1509/128, D
kangchangood
2011-02-24 20:24:42
(d)
(d)
infinity1
2011-02-24 20:24:42
D
D
az94566
2011-02-24 20:24:42
2
2
ahaanomegas
2011-02-24 20:24:42
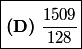
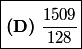
danielguo94
2011-02-24 20:24:42
D
D
Relativity1618
2011-02-24 20:24:42
1509/128
1509/128
ChipDale
2011-02-24 20:24:42
D
D
girishvar12
2011-02-24 20:24:42
1509/128 or D
1509/128 or D
mathletepower
2011-02-24 20:24:42
D
D
supermathman
2011-02-24 20:24:42
D
D
airplanes1
2011-02-24 20:24:42
1509/128
1509/128
willwang123
2011-02-24 20:24:42
D
D
airplanes1
2011-02-24 20:24:42
so D
so D
jeff10
2011-02-24 20:24:42
D
D
math_fun
2011-02-24 20:24:42
1509/128 or D
1509/128 or D
ooooo1
2011-02-24 20:24:42
D) 1509/128
D) 1509/128
PowerOfPi
2011-02-24 20:24:42
D
D
pgmath
2011-02-24 20:24:42
D) 1509/128
D) 1509/128
jxihong
2011-02-24 20:24:42
D
D
fortenforge
2011-02-24 20:24:42
D
D
copeland
2011-02-24 20:24:46
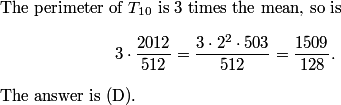
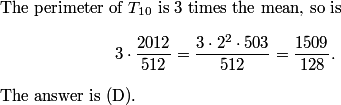
copeland
2011-02-24 20:24:52
(Notice that T_12, whatever that means, has a negative edge length. Therefore the negative edge length fear happens one term after the non-triangle case.)
(Notice that T_12, whatever that means, has a negative edge length. Therefore the negative edge length fear happens one term after the non-triangle case.)
copeland
2011-02-24 20:25:16
OK, crazy dance time. Three minute break then I want you back in your seats and exhausted.
OK, crazy dance time. Three minute break then I want you back in your seats and exhausted.
davidx
2011-02-24 20:28:17
*dances*
*dances*
DVA6102
2011-02-24 20:28:17
ahaanomegas
2011-02-24 20:28:17
Btw, I like that "crazy dance time".
Btw, I like that "crazy dance time".
1337Skills
2011-02-24 20:28:17
Time! Let's do this!
Time! Let's do this!
copeland
2011-02-24 20:28:22
Phew. Me too.
Phew. Me too.
copeland
2011-02-24 20:28:32
Time for the 12.
Time for the 12.
copeland
2011-02-24 20:28:40
We might call this "12 o-clock."
We might call this "12 o-clock."
copeland
2011-02-24 20:28:49
Or not. They can't all be winners.
Or not. They can't all be winners.
copeland
2011-02-24 20:29:02


copeland
2011-02-24 20:29:14
When you see the word "digits," what does that hint you should do?
When you see the word "digits," what does that hint you should do?
DVA6102
2011-02-24 20:29:51
expanded notation
expanded notation
profmusic
2011-02-24 20:29:51
Write it as 10a + b
Write it as 10a + b
danielguo94
2011-02-24 20:29:51
set variables as the digits
set variables as the digits
Gosav3122
2011-02-24 20:29:51
10a+b?
10a+b?
kangchangood
2011-02-24 20:29:51
set variables for each digit
set variables for each digit
bbgun34
2011-02-24 20:29:51
use 10a+b
use 10a+b
calvinhobbesliker
2011-02-24 20:29:51
10a+b
10a+b
lg5293
2011-02-24 20:29:51
separate into 10a + b
separate into 10a + b
TrigMan
2011-02-24 20:29:51
Write numbers as 10a + b
Write numbers as 10a + b
.cpp
2011-02-24 20:29:51
10A+B notation.
10A+B notation.
gh625
2011-02-24 20:29:51
let it equal 10a+b
let it equal 10a+b
soulspeedy
2011-02-24 20:29:51
write as 10a+b
write as 10a+b
RisingMathStar
2011-02-24 20:29:51
write it as 10a + b
write it as 10a + b
copeland
2011-02-24 20:29:58
clearly the tens digit is called a.
clearly the tens digit is called a.
copeland
2011-02-24 20:30:02
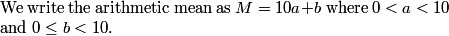
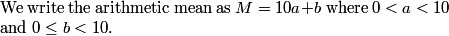
copeland
2011-02-24 20:30:07
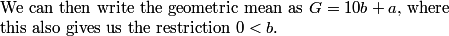
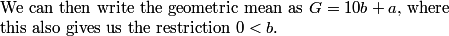
copeland
2011-02-24 20:30:14
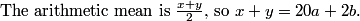
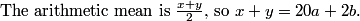
copeland
2011-02-24 20:30:16
How do we define the geometric mean?
How do we define the geometric mean?
morpheus44
2011-02-24 20:30:50
sqrtxy
sqrtxy
jeff10
2011-02-24 20:30:50
sqrt(xy)
sqrt(xy)
AlphaMath1
2011-02-24 20:30:50
square root of product
square root of product
lg5293
2011-02-24 20:30:50
sqrt{xy}
sqrt{xy}
DVA6102
2011-02-24 20:30:50
root(xy)
root(xy)
luppleAOPS
2011-02-24 20:30:50
sqrt(xy)
sqrt(xy)
erica539
2011-02-24 20:30:50
sqrt of xy
sqrt of xy
sindennisz
2011-02-24 20:30:50
sqrt(ab)
sqrt(ab)
adhya
2011-02-24 20:30:50
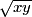
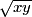
mstoenescu
2011-02-24 20:30:50
sqrt (xy)
sqrt (xy)
gqiao
2011-02-24 20:30:50
sqrt of x times y
sqrt of x times y
RisingMathStar
2011-02-24 20:30:50
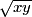
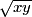
copeland
2011-02-24 20:30:55
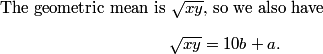
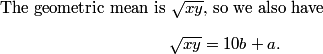
copeland
2011-02-24 20:30:58
What can we do to talk about |x-y|?
What can we do to talk about |x-y|?
calvinhobbesliker
2011-02-24 20:31:45
Square it?
Square it?
.cpp
2011-02-24 20:31:45
Find (x-y)^2.
Find (x-y)^2.
profmusic
2011-02-24 20:31:45
square both of those equations
square both of those equations
TrigMan
2011-02-24 20:31:45
Square the equation, to start.
Square the equation, to start.
soulspeedy
2011-02-24 20:31:45
square
square
bbgun34
2011-02-24 20:31:45
find (x-y)^2
find (x-y)^2
copeland
2011-02-24 20:31:51
If we square everything in sight we get good stuff.
If we square everything in sight we get good stuff.
copeland
2011-02-24 20:31:54
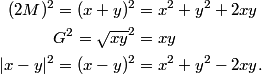
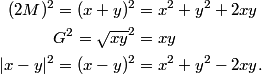
copeland
2011-02-24 20:32:00
So how do we get |x-y|^2?
So how do we get |x-y|^2?
VIPMaster
2011-02-24 20:32:53
(x+y)^2 - 4xy
(x+y)^2 - 4xy
erica539
2011-02-24 20:32:53
(2M)^2 -4G^2
(2M)^2 -4G^2
bbgun34
2011-02-24 20:32:53
(2M)^2-4G^2=|x-y|^2
(2M)^2-4G^2=|x-y|^2
.cpp
2011-02-24 20:32:53
(x+y)^2 - 4xy = (x-y)^2.
(x+y)^2 - 4xy = (x-y)^2.
PowerOfPi
2011-02-24 20:32:53
(x+y)^2-4xy
(x+y)^2-4xy
theone142857
2011-02-24 20:32:53
4M^2-4G^2
4M^2-4G^2
TrigMan
2011-02-24 20:32:53
(2M)^2 - 4(G)^2
(2M)^2 - 4(G)^2
profmusic
2011-02-24 20:32:53
subtract 4G^2, and we know a>b
subtract 4G^2, and we know a>b
luppleAOPS
2011-02-24 20:32:53
(2M)^2+4G^2
(2M)^2+4G^2
copeland
2011-02-24 20:32:57
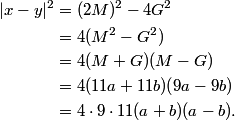
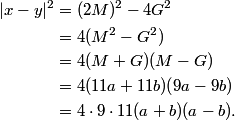
copeland
2011-02-24 20:33:15
That was a bunch of steps. I'll give you a moment.
That was a bunch of steps. I'll give you a moment.
copeland
2011-02-24 20:33:35
What do we know about this number?
What do we know about this number?
AlphaMath1
2011-02-24 20:34:18
It's a perfect square
It's a perfect square
PowerOfPi
2011-02-24 20:34:18
perfect square
perfect square
lg5293
2011-02-24 20:34:18
its a perfect square
its a perfect square
AlphaMath1
2011-02-24 20:34:18
(a+b)(a-b) must be divisible by 11
(a+b)(a-b) must be divisible by 11
bbgun34
2011-02-24 20:34:18
it is a square, so 11|(a+b)(a-b)
it is a square, so 11|(a+b)(a-b)
pi37
2011-02-24 20:34:18
it is a perfect square
it is a perfect square
professordad
2011-02-24 20:34:18
its a perfect square.
its a perfect square.
.cpp
2011-02-24 20:34:18
Therefore, (a+b)(a-b) must be a square times 11.
Therefore, (a+b)(a-b) must be a square times 11.
calvinhobbesliker
2011-02-24 20:34:18
It's a perfect square, so either a+b or a-bis 11
It's a perfect square, so either a+b or a-bis 11
kangchangood
2011-02-24 20:34:18
and one of them should be multiple of 11
and one of them should be multiple of 11
mstoenescu
2011-02-24 20:34:18
it is a square
it is a square
gqiao
2011-02-24 20:34:18
it's a perfect square?
it's a perfect square?
VIPMaster
2011-02-24 20:34:18
it's a perfect square!
it's a perfect square!
copeland
2011-02-24 20:34:26
We know it has to be a perfect square.
We know it has to be a perfect square.
copeland
2011-02-24 20:34:30
Since this is a perfect square and a and b are both less than 10, we know that 11 must divide a+b. In fact, since a and b are small we must have that a+b=11.
Since this is a perfect square and a and b are both less than 10, we know that 11 must divide a+b. In fact, since a and b are small we must have that a+b=11.
copeland
2011-02-24 20:34:42
What about a-b?
What about a-b?
dragoneye776
2011-02-24 20:35:29
a-b=1
a-b=1
willwang123
2011-02-24 20:35:29
1?
1?
bbgun34
2011-02-24 20:35:29
a-b=1
a-b=1
mstoenescu
2011-02-24 20:35:29
it is 1
it is 1
ahaanomegas
2011-02-24 20:35:29
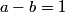
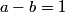
VIPMaster
2011-02-24 20:35:29
either 1, 4 or 9
either 1, 4 or 9
.cpp
2011-02-24 20:35:29
a-b=1.
a-b=1.
RisingMathStar
2011-02-24 20:35:29
either 1 or 9
either 1 or 9
libiamo
2011-02-24 20:35:29
1
1
kangchangood
2011-02-24 20:35:29
can be 1,4?
can be 1,4?
mstoenescu
2011-02-24 20:35:29
1 or 4 or 9
1 or 4 or 9
danielguo94
2011-02-24 20:35:29
a-b = 1 or 9
a-b = 1 or 9
TrigMan
2011-02-24 20:35:29
It equals 1
It equals 1
NoWayHaze
2011-02-24 20:35:29
=1
=1
kangchangood
2011-02-24 20:35:29
only 1,
only 1,
copeland
2011-02-24 20:35:38
That must be a perfect square? Which one?
That must be a perfect square? Which one?
copeland
2011-02-24 20:35:40
Since a and b are between 1 and 9, we know that a-b must be either 1 or 4. However, since a+b is odd we know a-b is also odd and a-b=1.
Since a and b are between 1 and 9, we know that a-b must be either 1 or 4. However, since a+b is odd we know a-b is also odd and a-b=1.
copeland
2011-02-24 20:35:46
So a and b are. . . .
So a and b are. . . .
ahaanomegas
2011-02-24 20:36:18
a = 6; b = 5
a = 6; b = 5
kthxbai
2011-02-24 20:36:18
6,5
6,5
mstoenescu
2011-02-24 20:36:18
6 and 5
6 and 5
airplanes1
2011-02-24 20:36:18
(a,b)=(6,5)
(a,b)=(6,5)
bbgun34
2011-02-24 20:36:18
a=6, b=5
a=6, b=5
danielguo94
2011-02-24 20:36:18
6 and 5
6 and 5
luppleAOPS
2011-02-24 20:36:18
a=6,b=5
a=6,b=5
PowerOfPi
2011-02-24 20:36:18
a=6, b=5
a=6, b=5
jeff10
2011-02-24 20:36:18
a=6, b=5
a=6, b=5
ooooo1
2011-02-24 20:36:18
6 and 5!!!???
6 and 5!!!???
copeland
2011-02-24 20:36:22
a=6 and b=5. The arithmetic mean is 65 and the geometric mean is 56. What is |x-y|?
a=6 and b=5. The arithmetic mean is 65 and the geometric mean is 56. What is |x-y|?
VIPMaster
2011-02-24 20:37:36
66
66
Jongy
2011-02-24 20:37:36
66
66
bbgun34
2011-02-24 20:37:36
66
66
AlphaMath1
2011-02-24 20:37:36
66!
66!
kangchangood
2011-02-24 20:37:36
66 (d)
66 (d)
.cpp
2011-02-24 20:37:36
66 => D.
66 => D.
willwin
2011-02-24 20:37:36
D
D
carmelninja
2011-02-24 20:37:36
66 --> D
66 --> D
professordad
2011-02-24 20:37:36
its 66.
its 66.
VIPMaster
2011-02-24 20:37:36
sqrt(4*9*11*11*1)
sqrt(4*9*11*11*1)
luppleAOPS
2011-02-24 20:37:36
sqrt(4*9*11*11*1)=66
sqrt(4*9*11*11*1)=66
ooooo1
2011-02-24 20:37:36
66
66
.cpp
2011-02-24 20:37:36
sqrt(4 x 9 x 11 x 11) = |x-y| =66 =>D.
sqrt(4 x 9 x 11 x 11) = |x-y| =66 =>D.
ksun48
2011-02-24 20:37:36
D66
D66
DavidTong
2011-02-24 20:37:36
66
66
knowmath
2011-02-24 20:37:36
d
d
copeland
2011-02-24 20:37:43
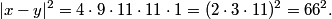
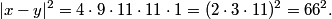
copeland
2011-02-24 20:37:44
Therefore |x-y|=66 and the answer is (D).
Therefore |x-y|=66 and the answer is (D).
copeland
2011-02-24 20:37:49
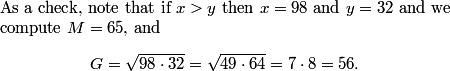
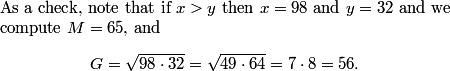
copeland
2011-02-24 20:38:11
Also notice that we were probably done a long time ago since we knew that |x-y|^2 was divisible by 2, 3, and 11.
Also notice that we were probably done a long time ago since we knew that |x-y|^2 was divisible by 2, 3, and 11.
copeland
2011-02-24 20:38:17
Not a lot of the choices have that property.
Not a lot of the choices have that property.
copeland
2011-02-24 20:38:22
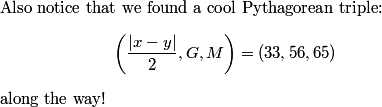
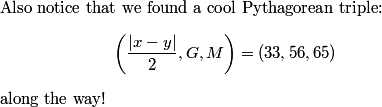
copeland
2011-02-24 20:38:34
From this formula:
From this formula:
copeland
2011-02-24 20:38:51
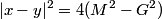
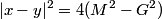
davidx
2011-02-24 20:38:58
That'll be helpful
That'll be helpful
copeland
2011-02-24 20:39:00
I bet.
I bet.
copeland
2011-02-24 20:39:21
I thought this was the trick when I first did this problem. That was a waste of 5 sure minutes.
I thought this was the trick when I first did this problem. That was a waste of 5 sure minutes.
copeland
2011-02-24 20:39:54
12B Problem 22 is the same as 10B Problem 25. It was fun, but let's skip it.
12B Problem 22 is the same as 10B Problem 25. It was fun, but let's skip it.
copeland
2011-02-24 20:40:00


copeland
2011-02-24 20:40:10
What first?
What first?
calvinhobbesliker
2011-02-24 20:40:41
Diagram
Diagram
danielguo94
2011-02-24 20:40:41
diagram
diagram
AlphaMath1
2011-02-24 20:40:41
Your awesome diagrams pl0x
Your awesome diagrams pl0x
jeff10
2011-02-24 20:40:41
Draw a diagram to visualize it.
Draw a diagram to visualize it.
willwin
2011-02-24 20:40:41
diagram
diagram
willwang123
2011-02-24 20:40:41
Draw!!!!!!!!!!!!!1
Draw!!!!!!!!!!!!!1
sindennisz
2011-02-24 20:40:41
Picture?
Picture?
mthcz11
2011-02-24 20:40:41
draw the graph :D
draw the graph :D
erica539
2011-02-24 20:40:41
draw a diagram once again?
draw a diagram once again?
copeland
2011-02-24 20:40:45
Let's draw another diagram. (I hope they gave you a lot of paper!)
Let's draw another diagram. (I hope they gave you a lot of paper!)
copeland
2011-02-24 20:40:48

copeland
2011-02-24 20:40:52
And a path looks something like this:
And a path looks something like this:
copeland
2011-02-24 20:40:59

copeland
2011-02-24 20:41:01
What are we trying to find here?
What are we trying to find here?
calvinhobbesliker
2011-02-24 20:42:02
All dots on all possible paths
All dots on all possible paths
gqiao
2011-02-24 20:42:02
number of lattice points total in the paths
number of lattice points total in the paths
mthcz11
2011-02-24 20:42:02
which points lie on the red path
which points lie on the red path
.cpp
2011-02-24 20:42:02
The number of lattice points the bug can reach.
The number of lattice points the bug can reach.
erica539
2011-02-24 20:42:02
lattice points that lie on these paths
lattice points that lie on these paths
ahaanomegas
2011-02-24 20:42:02
The number of paths which follow the rules given (one of which is what you drew)
The number of paths which follow the rules given (one of which is what you drew)
willwang123
2011-02-24 20:42:02
number of points within reach of a path.
number of points within reach of a path.
ChipDale
2011-02-24 20:42:02
number of paths
number of paths
carmelninja
2011-02-24 20:42:02
number of lattice points that could be included in such a path
number of lattice points that could be included in such a path
Gosav3122
2011-02-24 20:42:02
farthest point away from the two that can be covered
farthest point away from the two that can be covered
copeland
2011-02-24 20:42:04
We're trying to find all the points on all the paths of length at most 20 from (-3,2) to (3,-2). That path above has length 12.
We're trying to find all the points on all the paths of length at most 20 from (-3,2) to (3,-2). That path above has length 12.
copeland
2011-02-24 20:42:07
What points do we absolutely know we can reach?
What points do we absolutely know we can reach?
Jasmine8925
2011-02-24 20:43:05
anything within the rectangle that has those 2 points as corners
anything within the rectangle that has those 2 points as corners
ahaanomegas
2011-02-24 20:43:06
Those that are in the bounded rectangle
Those that are in the bounded rectangle
jeff10
2011-02-24 20:43:06
the points inside the rectangle, brcause the perimeter is 20 itself
the points inside the rectangle, brcause the perimeter is 20 itself
victorzhouaops
2011-02-24 20:43:06
the rectangle between the two points
the rectangle between the two points
erica539
2011-02-24 20:43:06
anything inside the rectangle.
anything inside the rectangle.
mathletepower
2011-02-24 20:43:06
ones that are between two paths
ones that are between two paths
.cpp
2011-02-24 20:43:06
All in rectangle with diagonal AB.
All in rectangle with diagonal AB.
professordad
2011-02-24 20:43:06
all points in the rectangle bounded by (-3,2),(3,2),(3,-2),(-3,-2)
all points in the rectangle bounded by (-3,2),(3,2),(3,-2),(-3,-2)
ooooo1
2011-02-24 20:43:06
the points in the rectangle: (x=-3, x=3, y=-2, y=2)
the points in the rectangle: (x=-3, x=3, y=-2, y=2)
willwang123
2011-02-24 20:43:06
Inside a rectangle w/ opposite corners A and B
Inside a rectangle w/ opposite corners A and B
jeff10
2011-02-24 20:43:06
with vertices (-2,3) amd (2, -3)
with vertices (-2,3) amd (2, -3)
VIPMaster
2011-02-24 20:43:06
all points around A and B
all points around A and B
copeland
2011-02-24 20:43:06
We can reach any point in the rectangle with our vertices as corners:
We can reach any point in the rectangle with our vertices as corners:
copeland
2011-02-24 20:43:11


copeland
2011-02-24 20:43:17
These points are all reachable by a path that only travels down and right, and such a path has length 10. Let's figure out where else we can go.
These points are all reachable by a path that only travels down and right, and such a path has length 10. Let's figure out where else we can go.
copeland
2011-02-24 20:43:21
How can we efficiently describe a path?
How can we efficiently describe a path?
kangchangood
2011-02-24 20:44:24
the.. letters?
the.. letters?
erica539
2011-02-24 20:44:24
steps up/down and steps left/right
steps up/down and steps left/right
kangchangood
2011-02-24 20:44:24
move = letters?
move = letters?
dragoneye776
2011-02-24 20:44:24
list of directions
list of directions
ChipDale
2011-02-24 20:44:24
A line where you have to go down or right except 10 instances
A line where you have to go down or right except 10 instances
adhya
2011-02-24 20:44:24
choose what directions the bug is going in
choose what directions the bug is going in
copeland
2011-02-24 20:44:29
We can write a path as a sequence of U (up), D (down), L (left), and R (right).
We can write a path as a sequence of U (up), D (down), L (left), and R (right).
copeland
2011-02-24 20:44:34
What do we know about each sequence?
What do we know about each sequence?
VIPMaster
2011-02-24 20:45:40
it must have at most 20 letters
it must have at most 20 letters
carmelninja
2011-02-24 20:45:40
at most 20 terms
at most 20 terms
luppleAOPS
2011-02-24 20:45:40
no more than twenty letters
no more than twenty letters
mathtyro
2011-02-24 20:45:40
Each sequence must containt at least 6R (in some order) and 4D(in some order)
Each sequence must containt at least 6R (in some order) and 4D(in some order)
dragoneye776
2011-02-24 20:45:40
20 terms, D - U = 4 and R - L = 6
20 terms, D - U = 4 and R - L = 6
tan90
2011-02-24 20:45:40
It must end with 4 more D's than U's and 6 more R's than L's
It must end with 4 more D's than U's and 6 more R's than L's
ooooo1
2011-02-24 20:45:40
D-U=4 and L-R=6
D-U=4 and L-R=6
BarbieRocks
2011-02-24 20:45:40
L-R=6, U-=4
L-R=6, U-=4
VIPMaster
2011-02-24 20:45:40
D = -U, L = -R
D = -U, L = -R
kangchangood
2011-02-24 20:45:40
(D-U) = 4 (R - L) = 6
(D-U) = 4 (R - L) = 6
professordad
2011-02-24 20:45:40
its 20 units long
its 20 units long
kangchangood
2011-02-24 20:45:40
and U + D + L + R <= 20
and U + D + L + R <= 20
RisingMathStar
2011-02-24 20:45:40
the maximum sum of the numbers of U and L is 5
the maximum sum of the numbers of U and L is 5
carmelninja
2011-02-24 20:45:40
there must be 6 more downs than ups, and 4 more rights than lefts
there must be 6 more downs than ups, and 4 more rights than lefts
erica539
2011-02-24 20:45:40
U+D+L+R is equal to or less than 20
U+D+L+R is equal to or less than 20
copeland
2011-02-24 20:45:42
Each sequence has at most 20 terms.
Each sequence has at most 20 terms.
copeland
2011-02-24 20:45:45
The number of times D appears is exactly 4 more than the number of times U appears.
The number of times D appears is exactly 4 more than the number of times U appears.
copeland
2011-02-24 20:45:48
The number of times R appears is exactly 6 more than the number of times L appears.
The number of times R appears is exactly 6 more than the number of times L appears.
copeland
2011-02-24 20:45:52
How far to the left of the rectangle can we go?
How far to the left of the rectangle can we go?
VIPMaster
2011-02-24 20:46:27
5 steps
5 steps
dragoneye776
2011-02-24 20:46:27
5
5
RisingMathStar
2011-02-24 20:46:27
5 units
5 units
bbgun34
2011-02-24 20:46:27
5
5
jeff10
2011-02-24 20:46:27
5 units
5 units
mathcool2009
2011-02-24 20:46:27
5 units
5 units
carmelninja
2011-02-24 20:46:27
5 units
5 units
willwang123
2011-02-24 20:46:27
5
5
calvinhobbesliker
2011-02-24 20:46:27
5
5
mathtyro
2011-02-24 20:46:27
5 (since we must use the 5 more to come back)
5 (since we must use the 5 more to come back)
copeland
2011-02-24 20:46:29
We can always go 5 units to the left of (-3,2) by the path LLLLLRRRRR*, where * goes from green to green.
We can always go 5 units to the left of (-3,2) by the path LLLLLRRRRR*, where * goes from green to green.
copeland
2011-02-24 20:46:33
We can go 5 units to the left of (-3,1) by a path DLLLLLRRRRR*.
We can go 5 units to the left of (-3,1) by a path DLLLLLRRRRR*.
copeland
2011-02-24 20:46:42
(reading left-to-right.)
(reading left-to-right.)
copeland
2011-02-24 20:46:50
etc.
etc.
copeland
2011-02-24 20:46:51
So we can get any point 5 units to the left of the rectangle.
So we can get any point 5 units to the left of the rectangle.
copeland
2011-02-24 20:46:55
What other points can we reach?
What other points can we reach?
dragoneye776
2011-02-24 20:47:44
5 units up and down and right
5 units up and down and right
ChipDale
2011-02-24 20:47:44
Down five more units
Down five more units
jeff10
2011-02-24 20:47:44
if you do not go left, you go 5 units up
if you do not go left, you go 5 units up
willwang123
2011-02-24 20:47:44
5 up
5 up
ChipDale
2011-02-24 20:47:44
Up five more units
Up five more units
RisingMathStar
2011-02-24 20:47:44
5 units from any edge of the rectangle
5 units from any edge of the rectangle
hsm174
2011-02-24 20:47:44
5 units right
5 units right
calvinhobbesliker
2011-02-24 20:47:44
5 above the rectangle
5 above the rectangle
carmelninja
2011-02-24 20:47:44
points 5 units below the above/below the rectangle
points 5 units below the above/below the rectangle
Jasmine8925
2011-02-24 20:47:44
5 units up
5 units up
.cpp
2011-02-24 20:47:44
5 units above rectangle, 5 units below rectangle, 5 units to the right of the rectangle.
5 units above rectangle, 5 units below rectangle, 5 units to the right of the rectangle.
gqiao
2011-02-24 20:47:44
any point 5 to the right
any point 5 to the right
copeland
2011-02-24 20:47:49
We can also reach 5 units above, 5 units right and 5 units below.
We can also reach 5 units above, 5 units right and 5 units below.
copeland
2011-02-24 20:47:52
(We're going to need a bigger picture!)
(We're going to need a bigger picture!)
copeland
2011-02-24 20:47:54

copeland
2011-02-24 20:47:57
Anywhere else?
Anywhere else?
jeff10
2011-02-24 20:48:53
If you took n units to the left, you take 5-n units up
If you took n units to the left, you take 5-n units up
VIPMaster
2011-02-24 20:48:53
anything with 4 Ls and 1 U, 3Ls and 2Us, ...
anything with 4 Ls and 1 U, 3Ls and 2Us, ...
RisingMathStar
2011-02-24 20:48:53
and any combination thereof
and any combination thereof
kangchangood
2011-02-24 20:48:53
make some stairs..
make some stairs..
theone142857
2011-02-24 20:48:53
or 2 and three or 1 and 4
or 2 and three or 1 and 4
dragoneye776
2011-02-24 20:48:53
in triangles of length and width 5, on each of the 4 corners
in triangles of length and width 5, on each of the 4 corners
theone142857
2011-02-24 20:48:53
in between
in between
professordad
2011-02-24 20:48:53
in the middle between the extensions, such as (5,5)
in the middle between the extensions, such as (5,5)
pikachoo
2011-02-24 20:48:53
units diagnal to the points?
units diagnal to the points?
carmelninja
2011-02-24 20:48:53
10 additional points in the corners
10 additional points in the corners
VIPMaster
2011-02-24 20:48:53
The lines between the vertices of the figure
The lines between the vertices of the figure
.cpp
2011-02-24 20:48:53
Four triangles to make an octagon.
Four triangles to make an octagon.
willwang123
2011-02-24 20:48:53
up and left
up and left
jeff10
2011-02-24 20:49:00
Yes, the points 5 unit steps away from the other green dot
Yes, the points 5 unit steps away from the other green dot
copeland
2011-02-24 20:49:03
We can also venture into the top left region by traveling a path like UULLLRRRDD* This gives us any point in the upper left triangle. We can similarly hit any point in any of the other three triangles.
We can also venture into the top left region by traveling a path like UULLLRRRDD* This gives us any point in the upper left triangle. We can similarly hit any point in any of the other three triangles.
copeland
2011-02-24 20:49:07

copeland
2011-02-24 20:49:10
Can we go any further than this?
Can we go any further than this?
copeland
2011-02-24 20:49:28
(This is the hard question so I'll give you a minute to write good arguments.)
(This is the hard question so I'll give you a minute to write good arguments.)
math243
2011-02-24 20:51:28
no, because when we go up or down, we need to come back
no, because when we go up or down, we need to come back
adhya
2011-02-24 20:51:28
no because we wont have enough moves left to come back
no because we wont have enough moves left to come back
jeff10
2011-02-24 20:51:28
No, because we will either go 6 or more units farther from our start, or 6 or more units past our finish point, which leads us to a perimeter more than 20.
No, because we will either go 6 or more units farther from our start, or 6 or more units past our finish point, which leads us to a perimeter more than 20.
calvinhobbesliker
2011-02-24 20:51:28
No, because all outside the region have x+y>5, so you can't get back.
No, because all outside the region have x+y>5, so you can't get back.
ChipDale
2011-02-24 20:51:28
No, if you go any further you can't get back to the other points
No, if you go any further you can't get back to the other points
dragoneye776
2011-02-24 20:51:28
we can only go a maximum of 5 lattice points from the center rectangle, and you have all possible points 5 lattice points away
we can only go a maximum of 5 lattice points from the center rectangle, and you have all possible points 5 lattice points away
agejiageji
2011-02-24 20:51:28
no, because you can only go 5 steps out of the rectangle defined by the green points
no, because you can only go 5 steps out of the rectangle defined by the green points
luppleAOPS
2011-02-24 20:51:28
no. any move either gets you one step closer to (-3,2), or one step further away. We need ten steps in total, and these are the only ways to do it.
no. any move either gets you one step closer to (-3,2), or one step further away. We need ten steps in total, and these are the only ways to do it.
carmelninja
2011-02-24 20:51:28
any path that goes from a green point to a boundary point to the other green point maxes out at 20 units, so if a path goes to a point not already included, it would be more than 20 units in length
any path that goes from a green point to a boundary point to the other green point maxes out at 20 units, so if a path goes to a point not already included, it would be more than 20 units in length
willwang123
2011-02-24 20:51:28
No, because we can only take 5 steps away from the starting point before we have to head towards the end. If we use more than 5 steps away (Up or left) we will not have enough steps to finish.
No, because we can only take 5 steps away from the starting point before we have to head towards the end. If we use more than 5 steps away (Up or left) we will not have enough steps to finish.
.cpp
2011-02-24 20:51:28
No, because otherwise we would stray more than 6 units from the rectangle; 6 more to get back + 10 extra moves for 7R and 3U gives more than 20 moves.
No, because otherwise we would stray more than 6 units from the rectangle; 6 more to get back + 10 extra moves for 7R and 3U gives more than 20 moves.
adhya
2011-02-24 20:51:28
no because at simplest it takes 10 moves to get from dot1 to dot 2, then we can move 5 more ahead and then come back with 5 but thats it because we can only have 20
no because at simplest it takes 10 moves to get from dot1 to dot 2, then we can move 5 more ahead and then come back with 5 but thats it because we can only have 20
gh625
2011-02-24 20:51:28
If you go more than five units up or to the left of A, then you would need more than 5 units to get back; combined wth the 10 needed to go from A to B, this would make more than 20 steps.
If you go more than five units up or to the left of A, then you would need more than 5 units to get back; combined wth the 10 needed to go from A to B, this would make more than 20 steps.
copeland
2011-02-24 20:51:33
No. The number of times we write U and L gives us a bound on how far away from the rectangle we can go. Therefore we can't possible go out of this octagon. (This isn't quite rigorous, but it encapsulates all of the aspects of a rigorous proof.)
No. The number of times we write U and L gives us a bound on how far away from the rectangle we can go. Therefore we can't possible go out of this octagon. (This isn't quite rigorous, but it encapsulates all of the aspects of a rigorous proof.)
copeland
2011-02-24 20:51:35
How many dots are there?
How many dots are there?
copeland
2011-02-24 20:51:38


wl2f
2011-02-24 20:53:20
195
195
lg5293
2011-02-24 20:53:20
195, use symmetry to make counting easier
195, use symmetry to make counting easier
dragoneye776
2011-02-24 20:53:20
195
195
professordad
2011-02-24 20:53:20
there are 195 dots.
there are 195 dots.
VIPMaster
2011-02-24 20:53:20
195
195
jeff10
2011-02-24 20:53:20
195, lost of counting
195, lost of counting
mathcool2009
2011-02-24 20:53:20
2(7+9+11+13+15)+5(17)
2(7+9+11+13+15)+5(17)
VIPMaster
2011-02-24 20:53:20
24*6 + 17*3 = 195
24*6 + 17*3 = 195
ahaanomegas
2011-02-24 20:53:20
195
195
ahaanomegas
2011-02-24 20:53:20
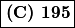
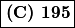
.cpp
2011-02-24 20:53:20
4x15 + 4x25 + 7x5 = 60+100+35 = 195 => C.
4x15 + 4x25 + 7x5 = 60+100+35 = 195 => C.
kangchangood
2011-02-24 20:53:20
195
195
danielguo94
2011-02-24 20:53:20
195
195
theone142857
2011-02-24 20:53:20
(C)195!!!:whistle:
(C)195!!!:whistle:
copeland
2011-02-24 20:53:24
We have 7+9+11+13+15+17+17+17+17+17+15+13+11+9+7 dots.
We have 7+9+11+13+15+17+17+17+17+17+15+13+11+9+7 dots.
copeland
2011-02-24 20:53:27
copeland
2011-02-24 20:53:40
This is where you hope that your arithmetic errors aren't actually possible answers.
This is where you hope that your arithmetic errors aren't actually possible answers.
copeland
2011-02-24 20:53:52
If you're curious, the concept of distance we're talking about here is the "taxicab metric." The taxicab metric is built by imagining a grid as Chicago or your favorite other metropolitan city and measuring how far a cab travels to get from one intersection to another.
If you're curious, the concept of distance we're talking about here is the "taxicab metric." The taxicab metric is built by imagining a grid as Chicago or your favorite other metropolitan city and measuring how far a cab travels to get from one intersection to another.
copeland
2011-02-24 20:54:03
The set of points satisfying d(P,X)+d(X,Q)<20 for fixed points P and Q (where d means distance) is just the interior of an ellipse. Therefore this question is asking us to compute the area of a taxicab ellipse.
The set of points satisfying d(P,X)+d(X,Q)<20 for fixed points P and Q (where d means distance) is just the interior of an ellipse. Therefore this question is asking us to compute the area of a taxicab ellipse.
copeland
2011-02-24 20:54:12
The cool thing we learned about a taxicab ellipse is that even though the major axis was not parallel to the x-axis, we still have a horizontal line of symmetry. That's pretty absurd and incredibly counter-intuitive.
The cool thing we learned about a taxicab ellipse is that even though the major axis was not parallel to the x-axis, we still have a horizontal line of symmetry. That's pretty absurd and incredibly counter-intuitive.
copeland
2011-02-24 20:54:25
Our argument in general shows that taxicab ellipses are nothing more than octagons. Later you should think about what shape a taxicab ellipse is when you start with foci whose x-coordinates are equal. Also think about what happens when the foci are the same point (a "taxicab circle").
Our argument in general shows that taxicab ellipses are nothing more than octagons. Later you should think about what shape a taxicab ellipse is when you start with foci whose x-coordinates are equal. Also think about what happens when the foci are the same point (a "taxicab circle").
copeland
2011-02-24 20:55:13
copeland
2011-02-24 20:55:25
Alright, octics are hard. Give me a hint here.
Alright, octics are hard. Give me a hint here.
jeff10
2011-02-24 20:55:36
What are octics?
What are octics?
ahaanomegas
2011-02-24 20:55:36
What are octics?
What are octics?
copeland
2011-02-24 20:55:40
octo = 8
octo = 8
copeland
2011-02-24 20:55:45
ics means, uh, polynomials.
ics means, uh, polynomials.
calvinhobbesliker
2011-02-24 20:56:11
Let x=z^4 and factor
Let x=z^4 and factor
adhya
2011-02-24 20:56:11
make x = z^4
make x = z^4
lg5293
2011-02-24 20:56:11
let u = z^4
let u = z^4
.cpp
2011-02-24 20:56:11
Let x=z^4, solve a quadratci
Let x=z^4, solve a quadratci
gqiao
2011-02-24 20:56:11
set z^4 as x?
set z^4 as x?
willwang123
2011-02-24 20:56:11
set x to z^4
set x to z^4
copeland
2011-02-24 20:56:16
This polynomial is quadratic in z^4. Let's write w=z^4.
This polynomial is quadratic in z^4. Let's write w=z^4.
copeland
2011-02-24 20:56:39
(I prefer x, too, but I've been told not to use x for complex coordinates, so we'll say w for now.)
(I prefer x, too, but I've been told not to use x for complex coordinates, so we'll say w for now.)
copeland
2011-02-24 20:56:45
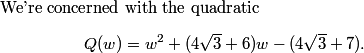
copeland
2011-02-24 20:56:53
Let's find the roots. Do you see them?
Let's find the roots. Do you see them?
airplanes1
2011-02-24 20:57:56
(z^4+4sqrt3+7)(z^4-1)
(z^4+4sqrt3+7)(z^4-1)
NoWayHaze
2011-02-24 20:57:56
(w-1)(w+(4sqrt3+7))
(w-1)(w+(4sqrt3+7))
professordad
2011-02-24 20:57:56
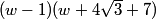
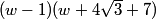
ilovepink
2011-02-24 20:57:56
(w+(4sqrt3+7))(w-1)
(w+(4sqrt3+7))(w-1)
professordad
2011-02-24 20:57:56
so w=1 or w=-4sqrt{3}-7
so w=1 or w=-4sqrt{3}-7
AlphaMath1
2011-02-24 20:57:56
Note that w=1 is a solution, so we already know that the fourth roots of unity are solutions to the octic.
Note that w=1 is a solution, so we already know that the fourth roots of unity are solutions to the octic.
wl2f
2011-02-24 20:57:56
z^4=1 and -4sqrt{3}-7
z^4=1 and -4sqrt{3}-7
hsm174
2011-02-24 20:57:56
uh 1 woruks
uh 1 woruks
airplanes1
2011-02-24 20:57:56
w=1, -(4sqrt3+7)
w=1, -(4sqrt3+7)
calvinhobbesliker
2011-02-24 20:57:56
Factor into (w-1)(w+4rad3+7) Roots are thus 4th roots of unity and 4th roots of -4sqrt3-7
Factor into (w-1)(w+4rad3+7) Roots are thus 4th roots of unity and 4th roots of -4sqrt3-7
.cpp
2011-02-24 20:57:56
w^2+(k)w-(k+1) = k+1 and -1 are roots.
w^2+(k)w-(k+1) = k+1 and -1 are roots.
bbgun34
2011-02-24 20:57:56
1 and -4rt3-7
1 and -4rt3-7
copeland
2011-02-24 20:57:59
There are two ways to proceed here.
There are two ways to proceed here.
copeland
2011-02-24 20:58:01
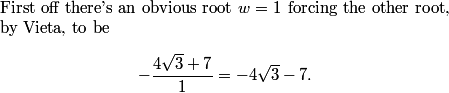
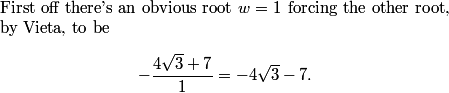
copeland
2011-02-24 20:58:10
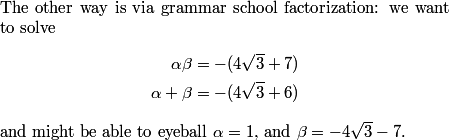
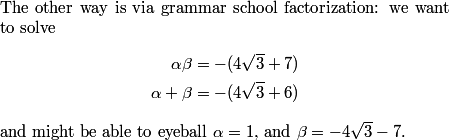
copeland
2011-02-24 20:58:36
Otherwise you might be skipping this one.
Otherwise you might be skipping this one.
copeland
2011-02-24 20:58:39
Therefore we can factor P a little bit.
Therefore we can factor P a little bit.
copeland
2011-02-24 20:58:44
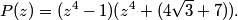
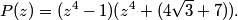
copeland
2011-02-24 20:58:46
I know 4 roots instantly. What are they?
I know 4 roots instantly. What are they?
airplanes1
2011-02-24 20:59:11
1, -1, i, -i
1, -1, i, -i
bbgun34
2011-02-24 20:59:11
4th roots of unity
4th roots of unity
willwang123
2011-02-24 20:59:11
1 -1 -i i
1 -1 -i i
kangchangood
2011-02-24 20:59:11
1 ,-1, i ,-i
1 ,-1, i ,-i
lg5293
2011-02-24 20:59:11
1, i, -i, -1
1, i, -i, -1
Jongy
2011-02-24 20:59:11
+-1 and +-i
+-1 and +-i
CRICKET229
2011-02-24 20:59:11
1, -1, i, -i
1, -1, i, -i
Aallisotsto
2011-02-24 20:59:11
1, -1, 1, -1
1, -1, 1, -1
RisingMathStar
2011-02-24 20:59:11
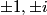
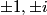
aleCTY
2011-02-24 20:59:11
1,-1,i,-i
1,-1,i,-i
.cpp
2011-02-24 20:59:11
z = i, -i, 1, or -1 work.
z = i, -i, 1, or -1 work.
bbgun34
2011-02-24 20:59:11
1,-1,i,-i
1,-1,i,-i
copeland
2011-02-24 20:59:14
The first quartic has roots 1, -1, i, and -i.
The first quartic has roots 1, -1, i, and -i.
copeland
2011-02-24 20:59:18
Now they want us to take a fourth root of -(4sqrt(3)+7). That's just mean.
Now they want us to take a fourth root of -(4sqrt(3)+7). That's just mean.
copeland
2011-02-24 20:59:25
First off, what's the argument (the angle it makes with the positive real axis) of -(4sqrt(3)+7)?
First off, what's the argument (the angle it makes with the positive real axis) of -(4sqrt(3)+7)?
calvinhobbesliker
2011-02-24 21:01:00
180 degrees
180 degrees
mstoenescu
2011-02-24 21:01:00
pi
pi
carmelninja
2011-02-24 21:01:00
pi, or 180 degrees
pi, or 180 degrees
Jasmine8925
2011-02-24 21:01:00
pi
pi
wl2f
2011-02-24 21:01:00
pi
pi
.cpp
2011-02-24 21:01:00
Or 180 degrees, if you consider it to be negative.
Or 180 degrees, if you consider it to be negative.
mstoenescu
2011-02-24 21:01:00
180°
180°
copeland
2011-02-24 21:01:06
This is a negative real number, so the argument is pi.
This is a negative real number, so the argument is pi.
copeland
2011-02-24 21:01:08
What are the arguments of the four fourth roots of this number?
What are the arguments of the four fourth roots of this number?
AlphaMath1
2011-02-24 21:02:06
180/4
180/4
gh625
2011-02-24 21:02:06
pi/4,3pi/4,5pi/4,7pi/4
pi/4,3pi/4,5pi/4,7pi/4
RisingMathStar
2011-02-24 21:02:06
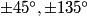
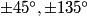
theone142857
2011-02-24 21:02:06
45,135,225,315
45,135,225,315
professordad
2011-02-24 21:02:06
45 degrees,135 degrees,225 degrees,315 degrees
45 degrees,135 degrees,225 degrees,315 degrees
nikeballa96
2011-02-24 21:02:06
by demoivre's theorem, they'll be 45 degrees
by demoivre's theorem, they'll be 45 degrees
copeland
2011-02-24 21:02:10
Taking the fourth roots divides the argument by 4. However there are four fourth roots and they differ by multiples of 2pi/4.
Taking the fourth roots divides the argument by 4. However there are four fourth roots and they differ by multiples of 2pi/4.
copeland
2011-02-24 21:02:13
Let's draw a picture. We know four of the roots. We also know the other four lie on the rays of slope 1 and -1.
Let's draw a picture. We know four of the roots. We also know the other four lie on the rays of slope 1 and -1.
copeland
2011-02-24 21:02:17
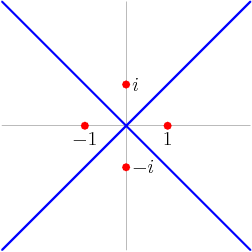

copeland
2011-02-24 21:02:22
The next thing we need to compute is the magnitude of the fourth root. Notice that we can forget the minus sign when we do this since we already know about the argument.
The next thing we need to compute is the magnitude of the fourth root. Notice that we can forget the minus sign when we do this since we already know about the argument.
copeland
2011-02-24 21:02:25
But fourth roots are hard. . . .
But fourth roots are hard. . . .
copeland
2011-02-24 21:02:28
Any ideas?
Any ideas?
profmusic
2011-02-24 21:03:09
square root of square root
square root of square root
carmelninja
2011-02-24 21:03:09
square root of square root
square root of square root
ilovepink
2011-02-24 21:03:09
square root twice
square root twice
jeff10
2011-02-24 21:03:09
sqrt(sqrtn)
sqrt(sqrtn)
mathman98
2011-02-24 21:03:09
take the square root, then take another square root?
take the square root, then take another square root?
jeff10
2011-02-24 21:03:09
sqrt(sqrt(n))
sqrt(sqrt(n))
professordad
2011-02-24 21:03:09
take the square root and then square root again?
take the square root and then square root again?
allicspteam
2011-02-24 21:03:09
make two sqrts
make two sqrts
copeland
2011-02-24 21:03:13
Let's try taking a square root first. That still a little daunting. What guess can we make about the square root that might make this a little simpler?
Let's try taking a square root first. That still a little daunting. What guess can we make about the square root that might make this a little simpler?
copeland
2011-02-24 21:03:41
We want the square root of 4sqrt(3)+7.
We want the square root of 4sqrt(3)+7.
Jasmine8925
2011-02-24 21:04:15
let the fourth root be a+bsqrt(c)
let the fourth root be a+bsqrt(c)
calvinhobbesliker
2011-02-24 21:04:15
a+bsqrtc?
a+bsqrtc?
Jasmine8925
2011-02-24 21:04:15
it'll have a sqrt(3) term
it'll have a sqrt(3) term
ilovepink
2011-02-24 21:04:15
(a+bsqrt3)
(a+bsqrt3)
profmusic
2011-02-24 21:04:15
it can be written as a + bsqrt(3)
it can be written as a + bsqrt(3)
professordad
2011-02-24 21:04:15
its going to be in the form a+bsqrt{3}
its going to be in the form a+bsqrt{3}
dragoneye776
2011-02-24 21:04:15
set it equal to a + bsqrt(c) and then square both sides
set it equal to a + bsqrt(c) and then square both sides
mathcool2009
2011-02-24 21:04:16
has form a(fourthrt(3))+b(sqrt(3))+c
has form a(fourthrt(3))+b(sqrt(3))+c
aleCTY
2011-02-24 21:04:16
(2+rt{3})^2
(2+rt{3})^2
AlphaMath1
2011-02-24 21:04:16
(sqrt{3}+2)^2
(sqrt{3}+2)^2
copeland
2011-02-24 21:04:18
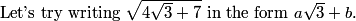
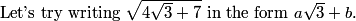
copeland
2011-02-24 21:04:20
This is a little bit naive. We don't have any reason to think that a and b here will be in any way nice.
This is a little bit naive. We don't have any reason to think that a and b here will be in any way nice.
copeland
2011-02-24 21:04:25
The only reason we have to even hope this will work is that we'd like to believe this problem is solvable and we're probably running short of other ideas.
The only reason we have to even hope this will work is that we'd like to believe this problem is solvable and we're probably running short of other ideas.
copeland
2011-02-24 21:04:39
What is the square of a*sqrt(3)+b?
What is the square of a*sqrt(3)+b?
gh625
2011-02-24 21:05:20
3a^2+b^2+2absqrt{3}
3a^2+b^2+2absqrt{3}
ilovepink
2011-02-24 21:05:20
3a^2 + b^2 + 2absqrt3
3a^2 + b^2 + 2absqrt3
nikeballa96
2011-02-24 21:05:20
3a^2+2absqrt3+b^2
3a^2+2absqrt3+b^2
CRICKET229
2011-02-24 21:05:20
3a^2+b^2+2absqrt3
3a^2+b^2+2absqrt3
professordad
2011-02-24 21:05:20
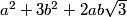
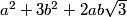
AlphaMath1
2011-02-24 21:05:20
3a^2+b^2+2ab*sqrt(3)
3a^2+b^2+2ab*sqrt(3)
Jasmine8925
2011-02-24 21:05:20
3a2+2absqrt(3)+b2
3a2+2absqrt(3)+b2
dragoneye776
2011-02-24 21:05:20
3a^2 + b^2 + 2absqrt(3)
3a^2 + b^2 + 2absqrt(3)
carmelninja
2011-02-24 21:05:20
(3a^2 + b^2) + (2ab)sqrt(3)
(3a^2 + b^2) + (2ab)sqrt(3)
copeland
2011-02-24 21:05:26
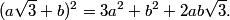
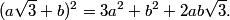
copeland
2011-02-24 21:05:27
Now IF a and b are rational then we should be able to solve this by equating the coefficients:
Now IF a and b are rational then we should be able to solve this by equating the coefficients:
copeland
2011-02-24 21:05:28
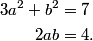
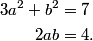
copeland
2011-02-24 21:05:31
Any ideas?
Any ideas?
mstoenescu
2011-02-24 21:06:04
2+sqrt3
2+sqrt3
carmelninja
2011-02-24 21:06:04
lucky guess!! --> 2+sqrt(3)
lucky guess!! --> 2+sqrt(3)
trigonometry456103
2011-02-24 21:06:04
2+sqrt3
2+sqrt3
theone142857
2011-02-24 21:06:04
sqrt{3}+2
sqrt{3}+2
wl2f
2011-02-24 21:06:04
2+sqrt3
2+sqrt3
kthxbai
2011-02-24 21:06:04
1,2
1,2
jeff10
2011-02-24 21:06:04
a=1, b=2
a=1, b=2
carmelninja
2011-02-24 21:06:04
a=1, b=2
a=1, b=2
.cpp
2011-02-24 21:06:04
a=1, b=2.
a=1, b=2.
professordad
2011-02-24 21:06:04
a=1,b=2
a=1,b=2
mstoenescu
2011-02-24 21:06:04
a=1 b=2
a=1 b=2
ChipDale
2011-02-24 21:06:04
a=1 b=2
a=1 b=2
copeland
2011-02-24 21:06:08
Neat! A solution: a = 1, b=2.
Neat! A solution: a = 1, b=2.
copeland
2011-02-24 21:06:11
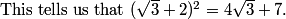
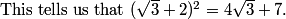
copeland
2011-02-24 21:06:13
What next?
What next?
ahaanomegas
2011-02-24 21:06:37
Oooooh, nice!
Oooooh, nice!
nikeballa96
2011-02-24 21:06:37
square root againnn
square root againnn
profmusic
2011-02-24 21:06:37
now we do it again...
now we do it again...
dragoneye776
2011-02-24 21:06:37
do it again
do it again
CRICKET229
2011-02-24 21:06:37
take square root of sqrt3+2
take square root of sqrt3+2
hsm174
2011-02-24 21:06:37
sqrt(sqrt3+2)
sqrt(sqrt3+2)
ChipDale
2011-02-24 21:06:37
Square root again
Square root again
gh625
2011-02-24 21:06:37
take the square root of 2+sqrt{3}
take the square root of 2+sqrt{3}
calvinhobbesliker
2011-02-24 21:06:37
Take the square root of 2+sqrt3 in a similar way
Take the square root of 2+sqrt3 in a similar way
Jasmine8925
2011-02-24 21:06:37
we need the square root of ;sqrt(3)+2
we need the square root of ;sqrt(3)+2
mathman98
2011-02-24 21:06:37
take the square root again'
take the square root again'
copeland
2011-02-24 21:06:39
That was so nice that we have to try it twice.
That was so nice that we have to try it twice.
copeland
2011-02-24 21:06:43
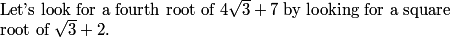
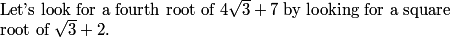
copeland
2011-02-24 21:06:45
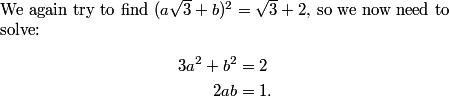
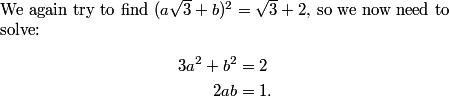
copeland
2011-02-24 21:06:49
Hmm. That's pretty disappointing.
Hmm. That's pretty disappointing.
copeland
2011-02-24 21:06:59
I don't see any nice solutions.
I don't see any nice solutions.
copeland
2011-02-24 21:07:02
Any ideas?
Any ideas?
copeland
2011-02-24 21:07:19
Does that look a little bit like a set of equations we COULD solve?
Does that look a little bit like a set of equations we COULD solve?
hsm174
2011-02-24 21:08:23
same thing?
same thing?
profmusic
2011-02-24 21:08:23
add a sqrt(2) term in place of b
add a sqrt(2) term in place of b
carmelninja
2011-02-24 21:08:23
instead, look for square root of 2(sqrt(3) + 2) = 4 + 2sqrt(3)
instead, look for square root of 2(sqrt(3) + 2) = 4 + 2sqrt(3)
theone142857
2011-02-24 21:08:23
multiply sqrt{2} to both
multiply sqrt{2} to both
professordad
2011-02-24 21:08:23
3a^2+b^2=4 and 2ab=2 is solvable
3a^2+b^2=4 and 2ab=2 is solvable
copeland
2011-02-24 21:08:30
I do see an equation that we can solve! Suppose we multiply the right sides only by 2, giving a new system of equations:
I do see an equation that we can solve! Suppose we multiply the right sides only by 2, giving a new system of equations:
copeland
2011-02-24 21:08:32
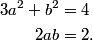
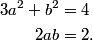
copeland
2011-02-24 21:08:36
What are the solutions to this?
What are the solutions to this?
calvinhobbesliker
2011-02-24 21:08:58
1 and 1
1 and 1
theone142857
2011-02-24 21:08:58
1,1
1,1
CRICKET229
2011-02-24 21:08:58
1,1
1,1
professordad
2011-02-24 21:08:58
a=b=1
a=b=1
.cpp
2011-02-24 21:08:58
a=1, b=1.
a=1, b=1.
willwang123
2011-02-24 21:08:58
a=b=1
a=b=1
christerson
2011-02-24 21:08:58
1,1
1,1
eb8368
2011-02-24 21:08:58
1,1
1,1
jeff10
2011-02-24 21:08:58
1 and 1
1 and 1
airplanes1
2011-02-24 21:08:58
a=b=1
a=b=1
carmelninja
2011-02-24 21:08:58
a=b=1
a=b=1
ooooo1
2011-02-24 21:08:58
1 and
1 and
evanteng1997
2011-02-24 21:08:58
b=1 a=1
b=1 a=1
danielguo94
2011-02-24 21:08:58
(1,1)
(1,1)
copeland
2011-02-24 21:09:02
a=b=1. Therefore we know that sqrt(3)+1 might be an interesting number. What is its square?
a=b=1. Therefore we know that sqrt(3)+1 might be an interesting number. What is its square?
BarbieRocks
2011-02-24 21:09:25
4+2sqrt(3)
4+2sqrt(3)
nikeballa96
2011-02-24 21:09:25
4 + 2sqrt3
4 + 2sqrt3
gqiao
2011-02-24 21:09:25
4+2root3
4+2root3
professordad
2011-02-24 21:09:25
4+2sqrt3
4+2sqrt3
calvinhobbesliker
2011-02-24 21:09:25
4+2sqrt3
4+2sqrt3
jeff10
2011-02-24 21:09:25
2sqrt3+4
2sqrt3+4
fries4guys
2011-02-24 21:09:25
4+2sqrt3
4+2sqrt3
LiBoy
2011-02-24 21:09:25
4+2sqrt3
4+2sqrt3
sindennisz
2011-02-24 21:09:25
4+2sqrt3
4+2sqrt3
mstoenescu
2011-02-24 21:09:25
4+2sqrt3
4+2sqrt3
ahaanomegas
2011-02-24 21:09:25
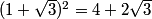
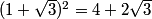
copeland
2011-02-24 21:09:34
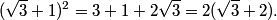
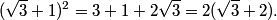
copeland
2011-02-24 21:09:34
So what is the fourth root of 4sqrt(3)+7?
So what is the fourth root of 4sqrt(3)+7?
theone142857
2011-02-24 21:10:33
doulble so divide sqrt 2
doulble so divide sqrt 2
AlphaMath1
2011-02-24 21:10:33
[sqrt(3)+1]/sqrt(2)
[sqrt(3)+1]/sqrt(2)
theone142857
2011-02-24 21:10:33
sqrt{6}/2+sqrt{2}/2
sqrt{6}/2+sqrt{2}/2
ilovepink
2011-02-24 21:10:33
sqrt(3/2) + (sqrt2)/2
sqrt(3/2) + (sqrt2)/2
mathcool2009
2011-02-24 21:10:33
(sqrt(3)+1)/sqrt(2)
(sqrt(3)+1)/sqrt(2)
gh625
2011-02-24 21:10:33
(1+sqrt{3})/sqrt{2}
(1+sqrt{3})/sqrt{2}
copeland
2011-02-24 21:10:38
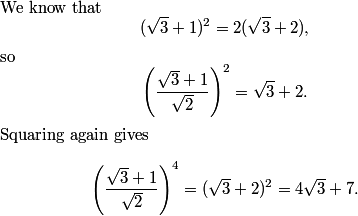
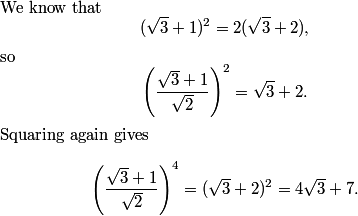
copeland
2011-02-24 21:10:45
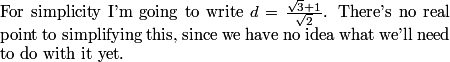
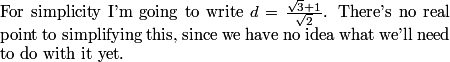
copeland
2011-02-24 21:10:52
I'll sticky those:
I'll sticky those:
copeland
2011-02-24 21:10:57
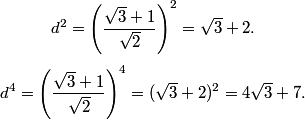
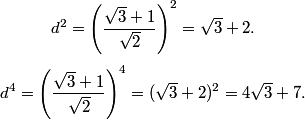
copeland
2011-02-24 21:11:05
And on the picture:
And on the picture:
copeland
2011-02-24 21:11:07
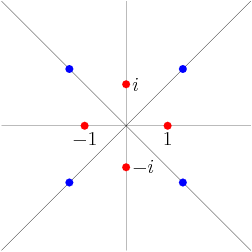

copeland
2011-02-24 21:11:10
What we've just discovered is that the blue dots are distance d from the origin.
What we've just discovered is that the blue dots are distance d from the origin.
copeland
2011-02-24 21:11:14
And the polygon we want?
And the polygon we want?
calvinhobbesliker
2011-02-24 21:11:54
Connect the dots wo intersection
Connect the dots wo intersection
professordad
2011-02-24 21:11:54
its an octagon (connect red with blue)
its an octagon (connect red with blue)
hsm174
2011-02-24 21:11:54
its a ninja star!!!
its a ninja star!!!
AlphaMath1
2011-02-24 21:11:54
A star
A star
ooooo1
2011-02-24 21:11:54
is the dots connected
is the dots connected
mathcool2009
2011-02-24 21:11:54
a concave star
a concave star
calvinhobbesliker
2011-02-24 21:11:54
4-sided star
4-sided star
.cpp
2011-02-24 21:11:54
The obvious, shuriken shaped one.
The obvious, shuriken shaped one.
copeland
2011-02-24 21:11:56
. . . . ninja star! Do you think it's a secret message?
. . . . ninja star! Do you think it's a secret message?
copeland
2011-02-24 21:11:59
We just connect the dots consecutively.
We just connect the dots consecutively.
copeland
2011-02-24 21:12:04
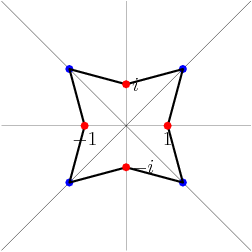

copeland
2011-02-24 21:12:06
Now how do we compute those distances?
Now how do we compute those distances?
professordad
2011-02-24 21:12:29
Distance Formula
Distance Formula
adhya
2011-02-24 21:12:29
distance formula?
distance formula?
calvinhobbesliker
2011-02-24 21:12:29
8 times distance between (0,1) and point d
8 times distance between (0,1) and point d
mathcool2009
2011-02-24 21:12:29
pythagoreabn theoroem
pythagoreabn theoroem
theone142857
2011-02-24 21:12:29
pythag
pythag
copeland
2011-02-24 21:12:32
yuck.
yuck.
RisingMathStar
2011-02-24 21:12:54
How do you prove that that has the smallest perimeter?
How do you prove that that has the smallest perimeter?
Jasmine8925
2011-02-24 21:12:54
why did the problem ask for the minimum perimeter? isn't there only one octagon?
why did the problem ask for the minimum perimeter? isn't there only one octagon?
copeland
2011-02-24 21:13:00
This is an interesting question.
This is an interesting question.
copeland
2011-02-24 21:13:15
However, once we do some computing we can actually show that these distances are even LOCALLY smallest
However, once we do some computing we can actually show that these distances are even LOCALLY smallest
copeland
2011-02-24 21:13:26
Therefore the blue neighbors are the closest points to the red dots.
Therefore the blue neighbors are the closest points to the red dots.
copeland
2011-02-24 21:13:33
And the red points are the closest neighbors to the blue dots.
And the red points are the closest neighbors to the blue dots.
copeland
2011-02-24 21:13:49
What's more awesome than the distance formula?
What's more awesome than the distance formula?
akscanb
2011-02-24 21:14:03
you
you
copeland
2011-02-24 21:14:06
and. . . .
and. . . .
tan90
2011-02-24 21:14:20
law of cosines
law of cosines
NoWayHaze
2011-02-24 21:14:20
law of cosines
law of cosines
carmelninja
2011-02-24 21:14:20
law of cosines
law of cosines
delta1
2011-02-24 21:14:20
law of cosines?
law of cosines?
RisingMathStar
2011-02-24 21:14:20
law of cosines
law of cosines
copeland
2011-02-24 21:14:25
Let's use the law of cosines
Let's use the law of cosines
copeland
2011-02-24 21:14:28
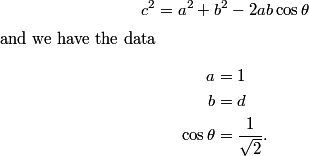
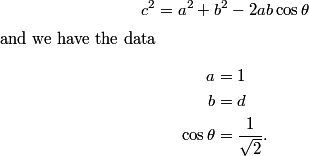
copeland
2011-02-24 21:14:41
I'll just compute for you.
I'll just compute for you.
copeland
2011-02-24 21:14:47
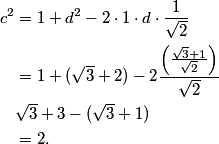
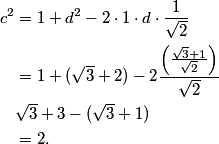
Jasmine8925
2011-02-24 21:15:11
can you give us another diagram with line segments labeled?
can you give us another diagram with line segments labeled?
copeland
2011-02-24 21:15:26
We're using the origin and two neighboring dots.
We're using the origin and two neighboring dots.
copeland
2011-02-24 21:15:43
For example, 1 and de^{2pi i/8}.
For example, 1 and de^{2pi i/8}.
copeland
2011-02-24 21:15:51
Oh. Well. That's pretty. What's the total perimeter?
Oh. Well. That's pretty. What's the total perimeter?
.cpp
2011-02-24 21:16:39
Wow! The answer is just B!
Wow! The answer is just B!
calvinhobbesliker
2011-02-24 21:16:39
8sqrt2 is the answer
8sqrt2 is the answer
nikeballa96
2011-02-24 21:16:39
multiply sqrt2 by 8 and our answer is (B) 8sqrt2
multiply sqrt2 by 8 and our answer is (B) 8sqrt2
professordad
2011-02-24 21:16:39
so the side is sqrt2 and the answer is 8sqrt2.
so the side is sqrt2 and the answer is 8sqrt2.
mstoenescu
2011-02-24 21:16:39
8sqrt2
8sqrt2
nikeballa96
2011-02-24 21:16:39
8sqrt2, or answer choice B
8sqrt2, or answer choice B
ilovepink
2011-02-24 21:16:39
B 8*sqrt2
B 8*sqrt2
AlphaMath1
2011-02-24 21:16:39
8sqrt{2}
8sqrt{2}
calculus321
2011-02-24 21:16:39
8sqrt2
8sqrt2
lg5293
2011-02-24 21:16:39
8sqrt{2}, B
8sqrt{2}, B
RisingMathStar
2011-02-24 21:16:39
8*sqrt{2}
8*sqrt{2}
.cpp
2011-02-24 21:16:39
8 sqrt 2 => B.
8 sqrt 2 => B.
professordad
2011-02-24 21:16:39
8sqrt2. or B.
8sqrt2. or B.
ChipDale
2011-02-24 21:16:39
B
B
NoWayHaze
2011-02-24 21:16:39
8sqrt2
8sqrt2
carmelninja
2011-02-24 21:16:39
8sqrt(2) --> (B)
8sqrt(2) --> (B)
eb8368
2011-02-24 21:16:39
(B) 8Root2
(B) 8Root2
copeland
2011-02-24 21:16:43
The lengths of the edges are all sqrt(2) by symmetry.
The lengths of the edges are all sqrt(2) by symmetry.
copeland
2011-02-24 21:16:48
Since there are 8 identical edges, the total perimeter must be 8sqrt(2), (B).
Since there are 8 identical edges, the total perimeter must be 8sqrt(2), (B).
copeland
2011-02-24 21:17:09
This problem was fun because none of the things we did should have worked.
This problem was fun because none of the things we did should have worked.
copeland
2011-02-24 21:17:20
You might have noticed cos(pi/12) in there somewhere. I have no idea how this forces the solution to be so clean, but if anybody sees the magic here you should definitely post it to the forums.
You might have noticed cos(pi/12) in there somewhere. I have no idea how this forces the solution to be so clean, but if anybody sees the magic here you should definitely post it to the forums.
willwang123
2011-02-24 21:17:37
didn't they do that on purpose?
didn't they do that on purpose?
copeland
2011-02-24 21:17:40
Of course.
Of course.
copeland
2011-02-24 21:17:53
That doesn't explain why those choices work, just what they achieve.
That doesn't explain why those choices work, just what they achieve.
copeland
2011-02-24 21:18:02
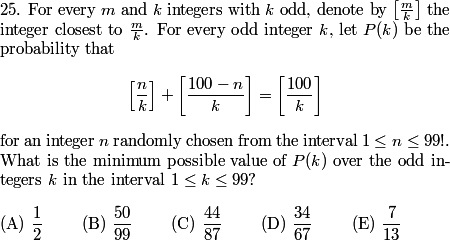
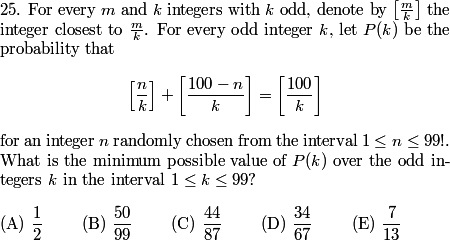
copeland
2011-02-24 21:18:15
Whew.
Whew.
copeland
2011-02-24 21:18:30
First thing's first. What is up with 99!? That number is what we in the business call "large."
First thing's first. What is up with 99!? That number is what we in the business call "large."
danielguo94
2011-02-24 21:19:02
what about 5000!?
what about 5000!?
copeland
2011-02-24 21:19:05
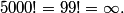
dragoneye776
2011-02-24 21:19:13
It's over 9000
It's over 9000
copeland
2011-02-24 21:19:16
Yes it is.
Yes it is.
copeland
2011-02-24 21:19:41
No ideas?
No ideas?
copeland
2011-02-24 21:19:57
What possible property does 99! have?
What possible property does 99! have?
narik
2011-02-24 21:20:23
something to do with divisible by the first 99 numbers
something to do with divisible by the first 99 numbers
Goldey
2011-02-24 21:20:23
its just a number divisible by every number 1-99. Since everything repeats every k and k can be any number 1-99
its just a number divisible by every number 1-99. Since everything repeats every k and k can be any number 1-99
calvinhobbesliker
2011-02-24 21:20:23
It's divisible by all possible k
It's divisible by all possible k
edrill4000
2011-02-24 21:20:23
divisible by numbers 1-99
divisible by numbers 1-99
airplanes1
2011-02-24 21:20:23
its divisible by every integer less than and equal to 99
its divisible by every integer less than and equal to 99
tan90
2011-02-24 21:20:23
It is divisible by all possible values of k
It is divisible by all possible values of k
Gosav3122
2011-02-24 21:20:23
divisible by all numbers 1-99?
divisible by all numbers 1-99?
copeland
2011-02-24 21:20:27
Super.
Super.
copeland
2011-02-24 21:20:53
There's another clue here, but I guess we might just leave it by the wayside until we find it later.
There's another clue here, but I guess we might just leave it by the wayside until we find it later.
copeland
2011-02-24 21:21:00
OK. There's no obvious way to start on this one. What should we do?
OK. There's no obvious way to start on this one. What should we do?
calvinhobbesliker
2011-02-24 21:21:41
Test a few k's?
Test a few k's?
Jasmine8925
2011-02-24 21:21:41
try some values of k and n
try some values of k and n
narik
2011-02-24 21:21:41
test the first few iterations out to see how it behaves
test the first few iterations out to see how it behaves
.cpp
2011-02-24 21:21:41
Try small examples of k.
Try small examples of k.
1nf1n1tyP1
2011-02-24 21:21:41
cry?
cry?
dragoneye776
2011-02-24 21:21:41
work with small numbers to find a pattern
work with small numbers to find a pattern
theone142857
2011-02-24 21:21:41
k=1,2,.........
k=1,2,.........
delta1
2011-02-24 21:21:41
experiment with small values?
experiment with small values?
ahaanomegas
2011-02-24 21:21:41
Try a few numbers and hope we see something interesting.
Try a few numbers and hope we see something interesting.
copeland
2011-02-24 21:21:43
Let's try some cases. Any idea which cases we should try?
Let's try some cases. Any idea which cases we should try?
akscanb
2011-02-24 21:22:13
1
1
ooooo1
2011-02-24 21:22:13
try 1 first
try 1 first
ahaanomegas
2011-02-24 21:22:13
k = 1, 2, ...
k = 1, 2, ...
wavelet
2011-02-24 21:22:13
5?
5?
willwang123
2011-02-24 21:22:13
Easy ones.
Easy ones.
adhya
2011-02-24 21:22:13
1,3
1,3
copeland
2011-02-24 21:22:15
We could try starting with k=1 or k=2. I have a better idea, though. What is it?
We could try starting with k=1 or k=2. I have a better idea, though. What is it?
copeland
2011-02-24 21:22:27
Well. . .not 2.
Well. . .not 2.
copeland
2011-02-24 21:22:30
since k is odd.
since k is odd.
BarbieRocks
2011-02-24 21:23:14
k=67
k=67
calvinhobbesliker
2011-02-24 21:23:14
The denoms of the answer choices?
The denoms of the answer choices?
copeland
2011-02-24 21:23:18
Looking at the answers we notice that the numbers 67 and 87 might be a good place to start.
Looking at the answers we notice that the numbers 67 and 87 might be a good place to start.
copeland
2011-02-24 21:23:25
Notice that these are even quite likely to be relevant numbers since 67/99 ~2/3 and 87/99~7/8.
Notice that these are even quite likely to be relevant numbers since 67/99 ~2/3 and 87/99~7/8.
copeland
2011-02-24 21:23:28
Let's try 67 first.
Let's try 67 first.
copeland
2011-02-24 21:23:31
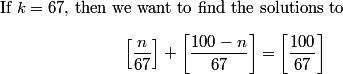
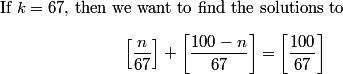
copeland
2011-02-24 21:23:38
(This is the point in the problem where I realized that right side is a constant.) What is the right side?
(This is the point in the problem where I realized that right side is a constant.) What is the right side?
calvinhobbesliker
2011-02-24 21:24:04
1
1
professordad
2011-02-24 21:24:04
its 1
its 1
jeff10
2011-02-24 21:24:04
the right side is 1.
the right side is 1.
ooooo1
2011-02-24 21:24:04
1?
1?
tan90
2011-02-24 21:24:04
1
1
RisingMathStar
2011-02-24 21:24:04
1
1
nikeballa96
2011-02-24 21:24:04
oh just kidding, it's 1
oh just kidding, it's 1
adhya
2011-02-24 21:24:06
1
1
snail2
2011-02-24 21:24:06
1 apparently
1 apparently
copeland
2011-02-24 21:24:10
The integer closest to 100/67 is 1. Therefore we have
The integer closest to 100/67 is 1. Therefore we have
copeland
2011-02-24 21:24:13
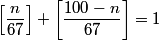
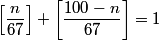
copeland
2011-02-24 21:24:16
What other simplification is there?
What other simplification is there?
copeland
2011-02-24 21:24:43
(Notice that this isn't an "equality." It's a logical doodad that's either true or false.)
(Notice that this isn't an "equality." It's a logical doodad that's either true or false.)
copeland
2011-02-24 21:25:14
Tell me specifically about [(100-n)/67].
Tell me specifically about [(100-n)/67].
copeland
2011-02-24 21:25:23
That looks pretty complicated.
That looks pretty complicated.
lg5293
2011-02-24 21:25:34
split it up?
split it up?
copeland
2011-02-24 21:25:43
yes, but NOT 100/67 - n/67.
yes, but NOT 100/67 - n/67.
MathAndKnowledge
2011-02-24 21:26:11
1 + (33 - n)/67
1 + (33 - n)/67
tan90
2011-02-24 21:26:11
you could split up the 67 and 33
you could split up the 67 and 33
Jasmine8925
2011-02-24 21:26:11
67/67+33/67-n/67?
67/67+33/67-n/67?
.cpp
2011-02-24 21:26:11
1+ 33/67 - n/67.
1+ 33/67 - n/67.
AlphaMath1
2011-02-24 21:26:11
1-(n-33)/67
1-(n-33)/67
nikeballa96
2011-02-24 21:26:11
1+(33-n/67)
1+(33-n/67)
copeland
2011-02-24 21:26:16
We notice [a+1]=[a]+1, so we can remove 67/67 from the middle term.
We notice [a+1]=[a]+1, so we can remove 67/67 from the middle term.
copeland
2011-02-24 21:26:18
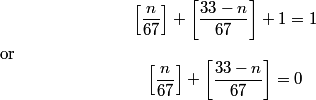
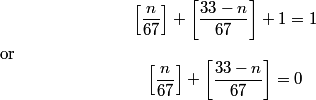
copeland
2011-02-24 21:26:27
When n ranges from 0 to 66, what happens to [n/67]?
When n ranges from 0 to 66, what happens to [n/67]?
.cpp
2011-02-24 21:27:28
It goes from 0 to 1.
It goes from 0 to 1.
delta1
2011-02-24 21:27:28
0 or 1
0 or 1
ChipDale
2011-02-24 21:27:28
It becomes 1
It becomes 1
calvinhobbesliker
2011-02-24 21:27:28
It is 0 until n is 34, after which it is 1
It is 0 until n is 34, after which it is 1
BarbieRocks
2011-02-24 21:27:28
=0 from n=1 to 33 and 1 from n=34 to 67
=0 from n=1 to 33 and 1 from n=34 to 67
Yongyi781
2011-02-24 21:27:28
It's 0 for n <= 33, and 1 for n >= 34
It's 0 for n <= 33, and 1 for n >= 34
RisingMathStar
2011-02-24 21:27:28
changes from 0 to 1 at n=34
changes from 0 to 1 at n=34
mathcool2009
2011-02-24 21:27:28
for n=0 to 33
for n=0 to 33
professordad
2011-02-24 21:27:28
it is first 0 and then becomes 1
it is first 0 and then becomes 1
mstoenescu
2011-02-24 21:27:28
goes from 0 to 1
goes from 0 to 1
copeland
2011-02-24 21:27:31
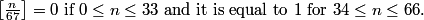
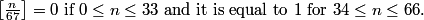
copeland
2011-02-24 21:27:37
What about [(33-n)/67] on this interval?
What about [(33-n)/67] on this interval?
agejiageji
2011-02-24 21:28:13
0
0
calvinhobbesliker
2011-02-24 21:28:13
It is always 0
It is always 0
ilovepink
2011-02-24 21:28:13
0.
0.
Goldey
2011-02-24 21:28:13
always 0.
always 0.
kad2361
2011-02-24 21:28:13
always 0
always 0
RisingMathStar
2011-02-24 21:28:13
always 0
always 0
jeff10
2011-02-24 21:28:13
it is always 0
it is always 0
ChipDale
2011-02-24 21:28:13
0
0
willwang123
2011-02-24 21:28:13
Always 0
Always 0
dragoneye776
2011-02-24 21:28:13
from 0 to 66, it is 0
from 0 to 66, it is 0
jeff10
2011-02-24 21:28:13
(33-0(/67=33/67 which is closer to 0
(33-0(/67=33/67 which is closer to 0
copeland
2011-02-24 21:28:18
Magically 33 is right in the middle of the interval, so 33-n ranges from 33 to -33. This ALWAYS gives zero. Therefore
Magically 33 is right in the middle of the interval, so 33-n ranges from 33 to -33. This ALWAYS gives zero. Therefore
copeland
2011-02-24 21:28:22
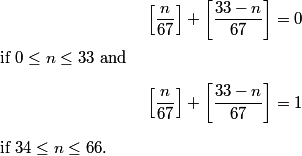
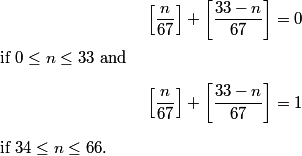
copeland
2011-02-24 21:28:29
What if n>=67? How can we deal with that?
What if n>=67? How can we deal with that?
kangchangood
2011-02-24 21:28:55
Well continuously I mistook it as floor function..
Well continuously I mistook it as floor function..
copeland
2011-02-24 21:28:57
Yes. Everyone has done this at least 3 times so far.
Yes. Everyone has done this at least 3 times so far.
RisingMathStar
2011-02-24 21:29:26
modulo 67
modulo 67
Yongyi781
2011-02-24 21:29:26
Subtract 67 from n
Subtract 67 from n
.cpp
2011-02-24 21:29:26
This can be tackled mod 67 like we did for the middle term.
This can be tackled mod 67 like we did for the middle term.
carmelninja
2011-02-24 21:29:26
n = 67x + y --> focus on y
n = 67x + y --> focus on y
kangchangood
2011-02-24 21:29:26
n = 67a + b
n = 67a + b
delta1
2011-02-24 21:29:26
split it up again
split it up again
copeland
2011-02-24 21:29:30
If n>=67 we can write n=67+m.
If n>=67 we can write n=67+m.
copeland
2011-02-24 21:29:34
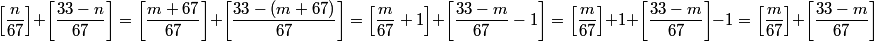
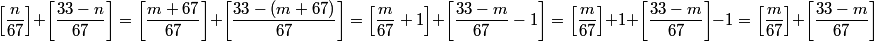
copeland
2011-02-24 21:29:45
Did that fall off the screen?
Did that fall off the screen?
copeland
2011-02-24 21:29:56
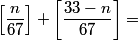
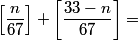
copeland
2011-02-24 21:30:05
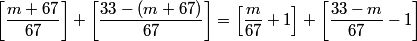
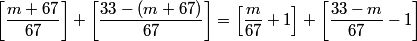
copeland
2011-02-24 21:30:09
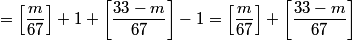
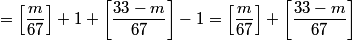
copeland
2011-02-24 21:30:17
And. . .
And. . .
lg5293
2011-02-24 21:31:01
back at the same place!
back at the same place!
kangchangood
2011-02-24 21:31:01
so that means it applies for every number..
so that means it applies for every number..
mstoenescu
2011-02-24 21:31:01
once again !
once again !
carmelninja
2011-02-24 21:31:01
its the exact same as before
its the exact same as before
dragoneye776
2011-02-24 21:31:01
Doesn't change, so just take mod 67
Doesn't change, so just take mod 67
mstoenescu
2011-02-24 21:31:01
the "same" !
the "same" !
ilovepink
2011-02-24 21:31:01
it repeats!
it repeats!
copeland
2011-02-24 21:31:29
So. . . .
So. . . .
copeland
2011-02-24 21:31:40
Let's go back to an old question.
Let's go back to an old question.
copeland
2011-02-24 21:31:47
Why do I care about 99!?
Why do I care about 99!?
maxw3ll
2011-02-24 21:32:24
everything comes in nice multiples
everything comes in nice multiples
dragoneye776
2011-02-24 21:32:24
its a factor of every value of k
its a factor of every value of k
snail2
2011-02-24 21:32:24
it is a multiple of everything from 1 to 99
it is a multiple of everything from 1 to 99
ilovepink
2011-02-24 21:32:24
it divides everything evenly and nothing is left over
it divides everything evenly and nothing is left over
adhya
2011-02-24 21:32:24
its the case for all numbers from 1-99
its the case for all numbers from 1-99
jeff10
2011-02-24 21:32:24
99! is divisible by all numbers from 1-99
99! is divisible by all numbers from 1-99
mathcool2009
2011-02-24 21:32:24
its 0(mod67)
its 0(mod67)
.cpp
2011-02-24 21:32:24
Because it has dividers for all the range of k.
Because it has dividers for all the range of k.
ahaanomegas
2011-02-24 21:32:24
Because our upper limit for k = 99
Because our upper limit for k = 99
carmelninja
2011-02-24 21:32:24
its divisible by 67
its divisible by 67
copeland
2011-02-24 21:32:32
It's divisible by 67 and. . ..
It's divisible by 67 and. . ..
RisingMathStar
2011-02-24 21:33:07
therefore each case is equally likely to happen
therefore each case is equally likely to happen
RisingMathStar
2011-02-24 21:33:07
making the probability 34/67
making the probability 34/67
copeland
2011-02-24 21:33:08
Every residue class is represented equally!
Every residue class is represented equally!
copeland
2011-02-24 21:33:15
Does that make sense?
Does that make sense?
copeland
2011-02-24 21:33:26
Therefore we really only care about the residue classes, by induction.
Therefore we really only care about the residue classes, by induction.
copeland
2011-02-24 21:33:30
This gives us P(67)=34/67.
This gives us P(67)=34/67.
copeland
2011-02-24 21:33:33
That's nice. We at least now know that D could be the answer and E cannot. However maybe 87 does the same thing, so we certainly couldn't rule out C (or either of the smaller ones).
That's nice. We at least now know that D could be the answer and E cannot. However maybe 87 does the same thing, so we certainly couldn't rule out C (or either of the smaller ones).
adhya
2011-02-24 21:33:49
no where diid the 34 come from
no where diid the 34 come from
copeland
2011-02-24 21:33:56
We wandered too far from that argument.
We wandered too far from that argument.
copeland
2011-02-24 21:33:59
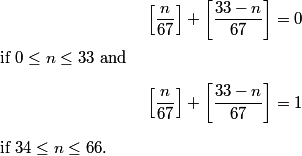
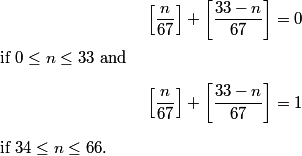
copeland
2011-02-24 21:34:06
We want to know the probability that this is not 0.
We want to know the probability that this is not 0.
copeland
2011-02-24 21:34:11
er, that this is zer.
er, that this is zer.
copeland
2011-02-24 21:34:19
That happens in 34 of the 67 cases.
That happens in 34 of the 67 cases.
copeland
2011-02-24 21:34:33
At this point I tried the same thing with 87 to see what happens. For the sake of everyone's sanity, though, I think we should go on to the general case.
At this point I tried the same thing with 87 to see what happens. For the sake of everyone's sanity, though, I think we should go on to the general case.
copeland
2011-02-24 21:34:43
zer = 0.
zer = 0.
copeland
2011-02-24 21:34:49
We fix k now, and consider the expression. What values of n concern us?
We fix k now, and consider the expression. What values of n concern us?
nikeballa96
2011-02-24 21:35:22
the values from 0 to k-1
the values from 0 to k-1
calvinhobbesliker
2011-02-24 21:35:22
n between 0 and k
n between 0 and k
Goldey
2011-02-24 21:35:22
0<=n<k
0<=n<k
copeland
2011-02-24 21:35:27
We only care about n such that 0<= n < k for the same inductive reason as above.
We only care about n such that 0<= n < k for the same inductive reason as above.
copeland
2011-02-24 21:35:36
(Oh, and there are 7 numbers from 0 to 6.)
(Oh, and there are 7 numbers from 0 to 6.)
copeland
2011-02-24 21:35:41
Furthermore we only care about the residue class of n as well.
Furthermore we only care about the residue class of n as well.
copeland
2011-02-24 21:35:44
We can write 100=qk+r for for some integers q and r. How should we choose q and r?
We can write 100=qk+r for for some integers q and r. How should we choose q and r?
nikeballa96
2011-02-24 21:36:57
maximize q and make sure r<k
maximize q and make sure r<k
carmelninja
2011-02-24 21:36:57
so r is minimized while still being positive
so r is minimized while still being positive
RisingMathStar
2011-02-24 21:36:57
q should be the floor of 100/k
q should be the floor of 100/k
Goldey
2011-02-24 21:36:57
0<=r<k
0<=r<k
copeland
2011-02-24 21:36:59
This is almost always the right choice.
This is almost always the right choice.
copeland
2011-02-24 21:37:01
However.
However.
copeland
2011-02-24 21:37:21
In this case there's a better option. Remember all that "Confused it with the floor," stuff from before?
In this case there's a better option. Remember all that "Confused it with the floor," stuff from before?
copeland
2011-02-24 21:37:38
We have a better option for the residue of 100.
We have a better option for the residue of 100.
Yongyi781
2011-02-24 21:38:22
-k/2 < r < k/2?
-k/2 < r < k/2?
RisingMathStar
2011-02-24 21:38:22
-k/2 < r < k/2
-k/2 < r < k/2
Goldey
2011-02-24 21:38:22
-k/2<r<k/2? or something like that
-k/2<r<k/2? or something like that
calvinhobbesliker
2011-02-24 21:38:22
Use the "closest integer" finction?
Use the "closest integer" finction?
copeland
2011-02-24 21:38:27
Excellent!
Excellent!
copeland
2011-02-24 21:38:27
We could force r to be between 0 an k, but I don't like that. Since we have [100/k] in our equation, let's instead let that be q. Therefore -k/2< r < k/2 is probably better.
We could force r to be between 0 an k, but I don't like that. Since we have [100/k] in our equation, let's instead let that be q. Therefore -k/2< r < k/2 is probably better.
copeland
2011-02-24 21:38:37
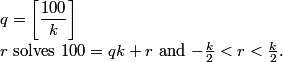
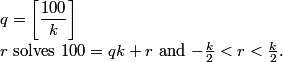
nikeballa96
2011-02-24 21:38:45
tricky tricky
tricky tricky
copeland
2011-02-24 21:39:01
Yeah. Actually we would have balled up our paper in about 3 minutes and done this anyway.
Yeah. Actually we would have balled up our paper in about 3 minutes and done this anyway.
copeland
2011-02-24 21:39:05
(And don't forget k is odd.)
(And don't forget k is odd.)
copeland
2011-02-24 21:39:08
It's now or never, I guess.
It's now or never, I guess.
copeland
2011-02-24 21:39:11
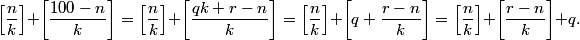
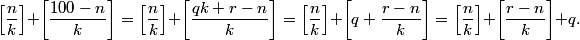
copeland
2011-02-24 21:39:29
Now how do we simplify that?
Now how do we simplify that?
ahaanomegas
2011-02-24 21:39:54
Can we?
Can we?
copeland
2011-02-24 21:40:01
We do want to compare this to something, right?
We do want to compare this to something, right?
copeland
2011-02-24 21:40:13
Maybe "simplify" is not the best term.
Maybe "simplify" is not the best term.
ahaanomegas
2011-02-24 21:40:27
What do we want to compare it with?
What do we want to compare it with?
copeland
2011-02-24 21:40:29
[100/k]
[100/k]
copeland
2011-02-24 21:40:33
Where do we see that?
Where do we see that?
.cpp
2011-02-24 21:40:46
For the original equation, we'll get [n/k] + [(r-n)/k] =0 again.
For the original equation, we'll get [n/k] + [(r-n)/k] =0 again.
calvinhobbesliker
2011-02-24 21:40:48
That's q
That's q
Gosav3122
2011-02-24 21:40:50
q
q
copeland
2011-02-24 21:40:54
We've assumed that q=[100/k], so
We've assumed that q=[100/k], so
copeland
2011-02-24 21:40:57
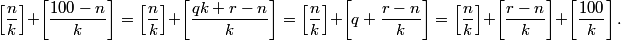
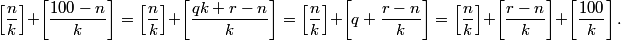
copeland
2011-02-24 21:41:07
(Deleting the middle stuff:)
(Deleting the middle stuff:)
copeland
2011-02-24 21:41:24
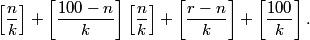
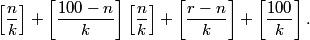
copeland
2011-02-24 21:41:30
Sorry. accidental smilie.
Sorry. accidental smilie.
copeland
2011-02-24 21:41:40
Gaar.
Gaar.
copeland
2011-02-24 21:41:51
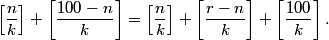
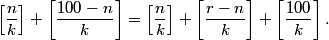
copeland
2011-02-24 21:42:17
Now what do we want?
Now what do we want?
jeff10
2011-02-24 21:42:48
we need q.
we need q.
copeland
2011-02-24 21:42:59
We need the right hand side to equal [100/k].
We need the right hand side to equal [100/k].
copeland
2011-02-24 21:43:03
So what's that tell us?
So what's that tell us?
ctmusicgirl
2011-02-24 21:43:41
isolate the term
isolate the term
narik
2011-02-24 21:43:41
that we need the probability that [n/k] + [r-n / k] = 0
that we need the probability that [n/k] + [r-n / k] = 0
mstoenescu
2011-02-24 21:43:41
that the other are zero !
that the other are zero !
calvinhobbesliker
2011-02-24 21:43:41
(n/k)+(r-n/k)=0
(n/k)+(r-n/k)=0
ooooo1
2011-02-24 21:43:41
the other two things on the right side equal to 0?
the other two things on the right side equal to 0?
copeland
2011-02-24 21:43:45
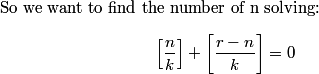
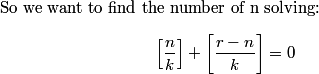
copeland
2011-02-24 21:43:49
We can simplify that further. How does the negative sign affect [x/k]?
We can simplify that further. How does the negative sign affect [x/k]?
ahaanomegas
2011-02-24 21:44:29
It opposes the direction or rounding
It opposes the direction or rounding
jeff10
2011-02-24 21:44:29
we will go the other direction
we will go the other direction
copeland
2011-02-24 21:44:31
Right, [-x/k]=-[x/k].
Right, [-x/k]=-[x/k].
copeland
2011-02-24 21:44:34
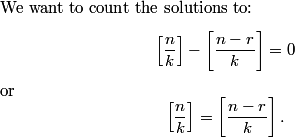
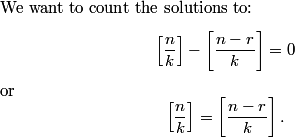
copeland
2011-02-24 21:44:39
OK, so we've algebrad ourselves out into the abyss. This equation is equivalent to the equation from the problem, except that we have introduced this new variable r.
OK, so we've algebrad ourselves out into the abyss. This equation is equivalent to the equation from the problem, except that we have introduced this new variable r.
copeland
2011-02-24 21:44:54
Thanks for enduring that. I promise it will pay off soon.
Thanks for enduring that. I promise it will pay off soon.
copeland
2011-02-24 21:44:55
Let's go back to the problem to see what this equation has to do with anything. First off, if r=0, what happens?
Let's go back to the problem to see what this equation has to do with anything. First off, if r=0, what happens?
calvinhobbesliker
2011-02-24 21:45:19
It's true for all n
It's true for all n
delta1
2011-02-24 21:45:19
always equal
always equal
RisingMathStar
2011-02-24 21:45:19
always true
always true
mathcool2009
2011-02-24 21:45:19
its always treu
its always treu
.cpp
2011-02-24 21:45:19
[n/k] = [n/k].
[n/k] = [n/k].
jeff10
2011-02-24 21:45:19
the two sides are equal by the reflexive property
the two sides are equal by the reflexive property
Gosav3122
2011-02-24 21:45:19
the statement is true
the statement is true
copeland
2011-02-24 21:45:21
The equation is always true if r=0. So what is P(k) when r=0?
The equation is always true if r=0. So what is P(k) when r=0?
Gosav3122
2011-02-24 21:45:42
1
1
mathcool2009
2011-02-24 21:45:42
1
1
mstoenescu
2011-02-24 21:45:42
1
1
narik
2011-02-24 21:45:42
1
1
ahaanomegas
2011-02-24 21:45:42
RisingMathStar
2011-02-24 21:45:42
1
1
jeff10
2011-02-24 21:45:46
1.
1.
copeland
2011-02-24 21:45:48
P=1. This isn't helpful since we want to minimize P.
P=1. This isn't helpful since we want to minimize P.
copeland
2011-02-24 21:45:52
To extend our little example further, when is r=0?
To extend our little example further, when is r=0?
RisingMathStar
2011-02-24 21:46:41
when k = 1, 5, or 25
when k = 1, 5, or 25
ilovepink
2011-02-24 21:46:41
when k divides 100
when k divides 100
.cpp
2011-02-24 21:46:41
k|100.
k|100.
jeff10
2011-02-24 21:46:41
k=1
k=1
tan90
2011-02-24 21:46:41
when k=1
when k=1
carmelninja
2011-02-24 21:46:41
k=1
k=1
copeland
2011-02-24 21:46:43
Since we defined r by 100 = qk+r, r is zero exactly when k divides 100. Therefore P(20)=1, P(50)=1, etc.
Since we defined r by 100 = qk+r, r is zero exactly when k divides 100. Therefore P(20)=1, P(50)=1, etc.
copeland
2011-02-24 21:46:50
OK, back to the task at hand. What values does [n/k] take?
OK, back to the task at hand. What values does [n/k] take?
copeland
2011-02-24 21:47:14
on 0<= n <k.
on 0<= n <k.
ahaanomegas
2011-02-24 21:47:38
0 and 1
0 and 1
calvinhobbesliker
2011-02-24 21:47:38
0 and 1
0 and 1
delta1
2011-02-24 21:47:38
0 or 1
0 or 1
.cpp
2011-02-24 21:47:38
0 or 1 only.
0 or 1 only.
mstoenescu
2011-02-24 21:47:38
0 and 1
0 and 1
copeland
2011-02-24 21:47:52
For 0 <= n < k/2 we have [n/k]=0.
For 0 <= n < k/2 we have [n/k]=0.
copeland
2011-02-24 21:47:55
For k/2 < n < k we have [n/k]=1.
For k/2 < n < k we have [n/k]=1.
copeland
2011-02-24 21:48:00
What are the values of [(n-r)/k]?
What are the values of [(n-r)/k]?
copeland
2011-02-24 21:48:14
on 0<=n < k
on 0<=n < k
tan90
2011-02-24 21:48:19
0 or 1
0 or 1
jeff10
2011-02-24 21:48:19
0 and 1
0 and 1
jeff10
2011-02-24 21:48:19
0 and 1
0 and 1
copeland
2011-02-24 21:48:24
When does it flip?
When does it flip?
Gosav3122
2011-02-24 21:49:21
n-r>k/2
n-r>k/2
copeland
2011-02-24 21:49:27
Since r is not that small, [(0-r)/k] must still be 0. The value continues to be zero until n-r>k/2 and then we get 1 from there on out.
Since r is not that small, [(0-r)/k] must still be 0. The value continues to be zero until n-r>k/2 and then we get 1 from there on out.
copeland
2011-02-24 21:49:38
When does equality fail then?
When does equality fail then?
copeland
2011-02-24 21:49:54
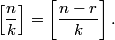
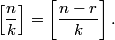
RisingMathStar
2011-02-24 21:50:56
between k/2 and k/2 +r
between k/2 and k/2 +r
Gosav3122
2011-02-24 21:50:56
when n<k/2 but n-r>k/2
when n<k/2 but n-r>k/2
Gosav3122
2011-02-24 21:50:56
and vice versa
and vice versa
copeland
2011-02-24 21:51:01
As n crosses k/2, the value of [n/k] flips from 0 to 1.
As n crosses k/2, the value of [n/k] flips from 0 to 1.
copeland
2011-02-24 21:51:04
As n crosses k/2 + r, the value of [(n-r)/k] flips from 0 to 1.
As n crosses k/2 + r, the value of [(n-r)/k] flips from 0 to 1.
copeland
2011-02-24 21:51:08
So the values are only different between k/2 and k/2 + r.
So the values are only different between k/2 and k/2 + r.
copeland
2011-02-24 21:51:11
Note that we don't know which is bigger, so we don't know which flip happens first. Or do we?
Note that we don't know which is bigger, so we don't know which flip happens first. Or do we?
copeland
2011-02-24 21:51:14
. . . .
. . . .
carmelninja
2011-02-24 21:52:16
r could be positive or negative
r could be positive or negative
copeland
2011-02-24 21:52:18
If r>0 then [n/k] flips first. If r<0 then [n-r/k] flips first.
If r>0 then [n/k] flips first. If r<0 then [n-r/k] flips first.
copeland
2011-02-24 21:52:23
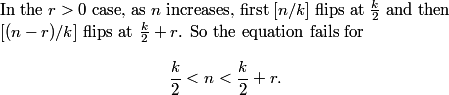
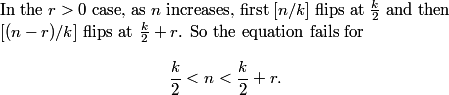
copeland
2011-02-24 21:52:33
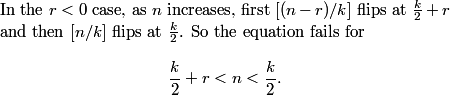
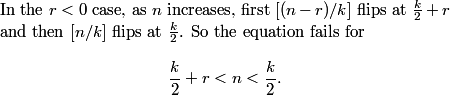
copeland
2011-02-24 21:52:43
What is P, as a function of r, in the first case?
What is P, as a function of r, in the first case?
RisingMathStar
2011-02-24 21:54:04
1 - r/k
1 - r/k
carmelninja
2011-02-24 21:54:04
r/k
r/k
copeland
2011-02-24 21:54:09
There are exactly r integers in this interval so P=1-r/k.
There are exactly r integers in this interval so P=1-r/k.
copeland
2011-02-24 21:54:12
Likewise, if r<0 then the interval contains exactly -r integers and P=1+r/k.
Likewise, if r<0 then the interval contains exactly -r integers and P=1+r/k.
copeland
2011-02-24 21:54:15
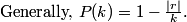
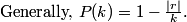
copeland
2011-02-24 21:54:18
We want to minimize P so we want to maximize |r|/k.
We want to minimize P so we want to maximize |r|/k.
copeland
2011-02-24 21:54:25
What is the naive bound on |r|?
What is the naive bound on |r|?
copeland
2011-02-24 21:54:39
(It's stickied.)
(It's stickied.)
.cpp
2011-02-24 21:54:59
k/2?
k/2?
carmelninja
2011-02-24 21:54:59
k/2
k/2
nikeballa96
2011-02-24 21:54:59
-k/2 to k/2
-k/2 to k/2
Gosav3122
2011-02-24 21:54:59
k/2
k/2
snail2
2011-02-24 21:54:59
-k/2<r<k/2
-k/2<r<k/2
calvinhobbesliker
2011-02-24 21:54:59
k/2
k/2
copeland
2011-02-24 21:55:03
Actually k is odd.
Actually k is odd.
copeland
2011-02-24 21:55:07
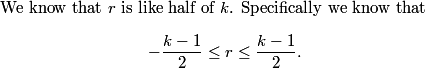
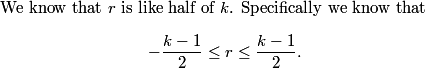
copeland
2011-02-24 21:55:14
Let's run with that. If 2r=k-1 then what does that say about the equation for 100?
Let's run with that. If 2r=k-1 then what does that say about the equation for 100?
copeland
2011-02-24 21:56:13
Recall 100 = qk+r
Recall 100 = qk+r
calvinhobbesliker
2011-02-24 21:56:57
100=(q+1/2)k-1/2
100=(q+1/2)k-1/2
LawrenceHan
2011-02-24 21:56:57
2qk+k-1
2qk+k-1
copeland
2011-02-24 21:57:01
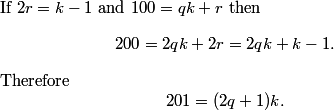
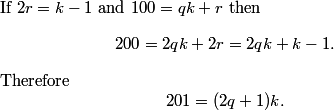
copeland
2011-02-24 21:57:07
And what do we know about 201?
And what do we know about 201?
RisingMathStar
2011-02-24 21:57:34
3 * 67
3 * 67
tan90
2011-02-24 21:57:34
3 * 67
3 * 67
.cpp
2011-02-24 21:57:34
Divisible by 67 and 3.
Divisible by 67 and 3.
ilovepink
2011-02-24 21:57:34
it's divisible by 3 and 67
it's divisible by 3 and 67
ChipDale
2011-02-24 21:57:34
It is 3*67
It is 3*67
calvinhobbesliker
2011-02-24 21:57:34
It's div by 67
It's div by 67
AlphaMath1
2011-02-24 21:57:34
it's divisible by 67
it's divisible by 67
willwang123
2011-02-24 21:57:34
3*67
3*67
copeland
2011-02-24 21:57:38
201=67*3. Therefore we care about k=3 and k=67. (I'm feeling pretty good about 67 right now. I was starting to worry that you were leading me astray!)
201=67*3. Therefore we care about k=3 and k=67. (I'm feeling pretty good about 67 right now. I was starting to worry that you were leading me astray!)
copeland
2011-02-24 21:57:44
If k=3 then 100=3*33+1, so r=1. What is P(3)?
If k=3 then 100=3*33+1, so r=1. What is P(3)?
RisingMathStar
2011-02-24 21:58:46
2/3
2/3
calvinhobbesliker
2011-02-24 21:58:46
2/3
2/3
ilovepink
2011-02-24 21:58:46
2/3
2/3
.cpp
2011-02-24 21:58:46
2/3.
2/3.
copeland
2011-02-24 21:58:55
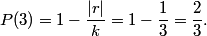
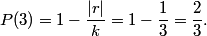
copeland
2011-02-24 21:58:57
If k=67 we know P(67)=34/67, which is much less.
If k=67 we know P(67)=34/67, which is much less.
copeland
2011-02-24 21:59:00
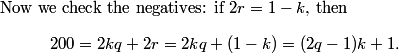
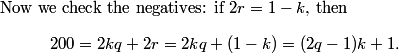
copeland
2011-02-24 21:59:09
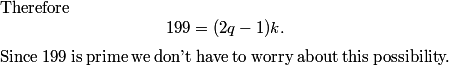
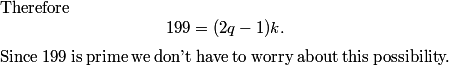
copeland
2011-02-24 21:59:23
Finally we need to knock out the non-edge cases. We assume that |r| is at most (k-3)/2. What does this make P?
Finally we need to knock out the non-edge cases. We assume that |r| is at most (k-3)/2. What does this make P?
ahaanomegas
2011-02-24 22:00:18
What are "non-edge cases"?
What are "non-edge cases"?
copeland
2011-02-24 22:00:19
I mean those r which aren't "maximal" in the sense that they bump into the k/2 bound.
I mean those r which aren't "maximal" in the sense that they bump into the k/2 bound.
calvinhobbesliker
2011-02-24 22:01:07
1/2-3/(2k)
1/2-3/(2k)
ilovepink
2011-02-24 22:01:07
(k+3)/2k*
(k+3)/2k*
copeland
2011-02-24 22:01:11
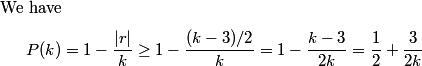
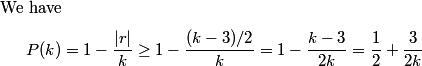
copeland
2011-02-24 22:01:38
Since k is at most 99, 1/k is at least 1/99. Therefore
Since k is at most 99, 1/k is at least 1/99. Therefore
copeland
2011-02-24 22:01:42
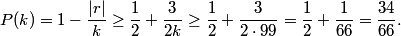
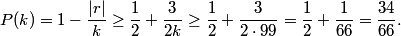
copeland
2011-02-24 22:01:44
Tell me about 34/66.
Tell me about 34/66.
RisingMathStar
2011-02-24 22:02:49
greater than 34/67
greater than 34/67
snail2
2011-02-24 22:02:49
it is bigger than 34/67
it is bigger than 34/67
airplanes1
2011-02-24 22:02:49
it's greater than 34/67
it's greater than 34/67
.cpp
2011-02-24 22:02:49
Greater than 34/67; also not an answer choice.
Greater than 34/67; also not an answer choice.
Yongyi781
2011-02-24 22:02:49
34/66 > 34/67
34/66 > 34/67
copeland
2011-02-24 22:02:54
This is MORE than 34/67, so we can't do any better than 34/67.
This is MORE than 34/67, so we can't do any better than 34/67.
copeland
2011-02-24 22:02:58
Therefore. . ..
Therefore. . ..
danielguo94
2011-02-24 22:03:42
THE ANSWER IS D
THE ANSWER IS D
nikeballa96
2011-02-24 22:03:42
so we should've given up waaay back then and guessed.
so we should've given up waaay back then and guessed.
hyunjoon123
2011-02-24 22:03:42
it's d
it's d
jeff10
2011-02-24 22:03:42
our answer is D
our answer is D
airplanes1
2011-02-24 22:03:42
D
D
.cpp
2011-02-24 22:03:42
Answer is D.
Answer is D.
snail2
2011-02-24 22:03:42
D!!!!!!!!!!!
D!!!!!!!!!!!
ChipDale
2011-02-24 22:03:42
The answer is 34/67 or D
The answer is 34/67 or D
calvinhobbesliker
2011-02-24 22:03:42
D is the answer
D is the answer
delta1
2011-02-24 22:03:42
D!!!
D!!!
copeland
2011-02-24 22:03:46
The answer, finally, is 34/67, (D).
The answer, finally, is 34/67, (D).
tan90
2011-02-24 22:03:54
Was there a quicker way to do this problem?
Was there a quicker way to do this problem?
RisingMathStar
2011-02-24 22:03:54
Moral of the story: don't attempt to solve #25
Moral of the story: don't attempt to solve #25
copeland
2011-02-24 22:04:17
Actually, I tried 87, realized that the computation that gives 44/87 is wrong and picked D.
Actually, I tried 87, realized that the computation that gives 44/87 is wrong and picked D.
willwang123
2011-02-24 22:04:24
that problem took almost an hour
that problem took almost an hour
hsm174
2011-02-24 22:04:24
Yes, that took around 15 mins
Yes, that took around 15 mins
jeff10
2011-02-24 22:04:24
unless you solve the rest really quiclky
unless you solve the rest really quiclky
copeland
2011-02-24 22:04:33
Yes. that problem took 15minute hours.
Yes. that problem took 15minute hours.
copeland
2011-02-24 22:04:53
Alright, that's it for tonight.
Alright, that's it for tonight.
copeland
2011-02-24 22:05:09
We've gone 2 hours and 36 minutes.
We've gone 2 hours and 36 minutes.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.









