Math Jams

DPatrick 2011-04-01 19:01:26
Welcome to the 2011 AIME II Math Jam!

DPatrick 2011-04-01 19:01:37
I'm Dave Patrick, and I'll be leading our discussion tonight.

DPatrick 2011-04-01 19:01:44
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.

DPatrick 2011-04-01 19:01:59
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.

DPatrick 2011-04-01 19:02:10
This helps keep the session organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.

DPatrick 2011-04-01 19:02:31
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go, or we'd be here all night.

DPatrick 2011-04-01 19:02:46
Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask.

DPatrick 2011-04-01 19:03:02
We usually get to every question in our classes, but we have a large number of students tonight. So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!

DPatrick 2011-04-01 19:03:32
We have a number of my AoPS colleagues here to help out tonight. They can answer questions by whispering to you or by opening a window with you to chat 1-on-1.

DPatrick 2011-04-01 19:03:55
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.

DPatrick 2011-04-01 19:04:38
I expect this to last between 2 and 3 hours. At a couple points during the Math Jam, I will get thirsty or hungry, or my fingers will get tired, and I'll take a 1-2 minute break.

DPatrick 2011-04-01 19:04:50
Other than that, the plan is to go through all 15 problems, in order.

DPatrick 2011-04-01 19:05:02
Before we get started, I have a question: for those of you who took the test, what was your favorite question on the test?

DPatrick 2011-04-01 19:05:45
Well, there doesn't seem to be much consensus on this, and we're going to do them all anyway. :)

DPatrick 2011-04-01 19:05:52
So, let's get started!

DPatrick 2011-04-01 19:05:57

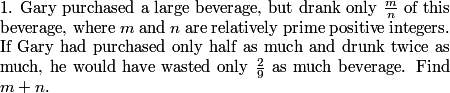
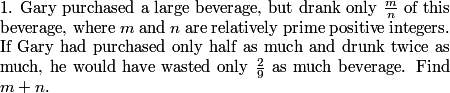
DPatrick 2011-04-01 19:06:24
(I'll always put the current question at the top of the chat window. You can resize the top area by dragging the horizontal gray bar near the top.)

policecap 2011-04-01 19:06:44
we can let the cup have size 1

mathswimmer 2011-04-01 19:06:44
Let m/n be x first

DPatrick 2011-04-01 19:06:55
There are a couple of simplifications that make solving the problem easier.

DPatrick 2011-04-01 19:07:02
We can assume that the (original) quantity of the beverage is 1.

DPatrick 2011-04-01 19:07:15

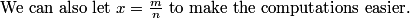
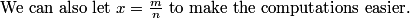
PiquantPeppers 2011-04-01 19:07:25
make an equation

supermathman 2011-04-01 19:07:26
set up an equation

DPatrick 2011-04-01 19:07:36
Now our goal is to set up an equation relating the two different wasted quantities.

DPatrick 2011-04-01 19:07:43
How much was wasted originally?

AlphaMath1 2011-04-01 19:08:11
1-x

DavidTong 2011-04-01 19:08:12
1-x

eb8368 2011-04-01 19:08:12
1-x

simplyMathLete 2011-04-01 19:08:12
he drank x, so 1-x

DPatrick 2011-04-01 19:08:18
He drank x, so 1-x was wasted.

DPatrick 2011-04-01 19:08:24
How much gets wasted in the hypothetical scenario?

tiger21 2011-04-01 19:08:46
1/2-2x

ksun48 2011-04-01 19:08:46
1/2-2x

superpi83 2011-04-01 19:08:46
1/2-2x

r31415 2011-04-01 19:08:46
1/2 -2x

DPatrick 2011-04-01 19:08:51
The total beverage is only 1/2, and he drinks 2x. So 1/2 - 2x gets wasted.

DPatrick 2011-04-01 19:09:01
What equation does this allow us to write?

tiger21 2011-04-01 19:09:41
1/2-2*x=2/9*(1-x)

.cpp 2011-04-01 19:09:41
2/9 (1-x) = 1/2 - 2x

AlphaMath1 2011-04-01 19:09:41
1/2-2x=2/9 (1-x)

DPatrick 2011-04-01 19:09:47

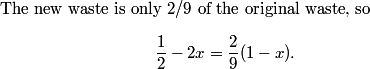
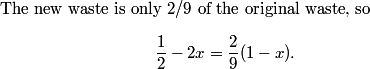
DPatrick 2011-04-01 19:10:06
(You have to read the problem carefully to be sure you have the right equation!)

mathlete5 2011-04-01 19:10:25
solve for x

policecap 2011-04-01 19:10:27
we get x=5/32

DPatrick 2011-04-01 19:10:35

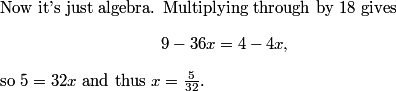
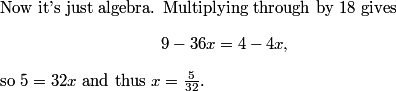
DPatrick 2011-04-01 19:10:46

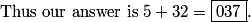
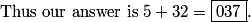
DPatrick 2011-04-01 19:11:15

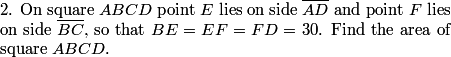
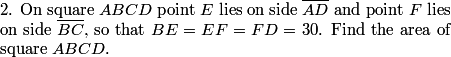
calculatorwiz 2011-04-01 19:11:28
diagram...

eb8368 2011-04-01 19:11:28
Draw a diagram

r31415 2011-04-01 19:11:28
picture!!!

.cpp 2011-04-01 19:11:28
Draw a diagram.

kubluck 2011-04-01 19:11:28
diagram!

DPatrick 2011-04-01 19:11:34
We probably want to sketch a diagram.

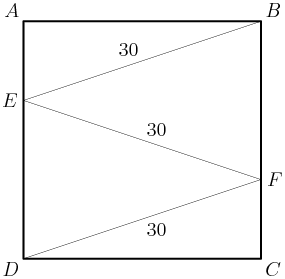
DPatrick 2011-04-01 19:11:38

DPatrick 2011-04-01 19:11:45
Now what?

GoldenFrog1618 2011-04-01 19:12:23
Draw perpendiculars from E and F

carmelninja 2011-04-01 19:12:28
draw lines parallel to AB that go through E and F

DPatrick 2011-04-01 19:12:35
If we draw lines from E and F parallel to AB and CD, we have 6 congruent triangles!

DPatrick 2011-04-01 19:12:41

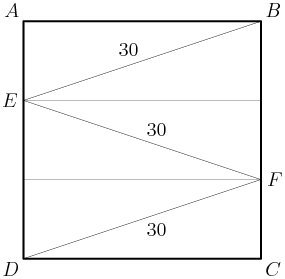
DPatrick 2011-04-01 19:13:05
Adding parallel lines to a diagram is one of the most useful geometric problem-solving techniques there is. (We'll see it again later tonight!)

BarbieRocks 2011-04-01 19:13:20
AE=x/3, AB=x

GoldenFrog1618 2011-04-01 19:13:20
CF=1/3 BC

billyg 2011-04-01 19:13:20
let AB=x and AE=x/3

DPatrick 2011-04-01 19:13:42
Right. We immediately see that AE = (1/3)AB since the three pieces of AD are all equal.

DPatrick 2011-04-01 19:13:53
So if we let AE = x, and AD = AB = 3x is the side of the square, then right triangle ABE has legs x and 3x and hypotenuse 30.

DPatrick 2011-04-01 19:14:09
(I prefer this to AB =x and AE = x/3, since no fractions!)

r31415 2011-04-01 19:14:20
x^2+3x^2=30^2

Duncanyang 2011-04-01 19:14:21
10x^2=900,

DPatrick 2011-04-01 19:14:29
Thus 10x^2 = 900, hence x^2 = 90.

policecap 2011-04-01 19:14:43
so (3x)^2=810

.cpp 2011-04-01 19:14:47
The area of the square is thus 9x^2, so the answer is 810.

DPatrick 2011-04-01 19:14:51
The area of the triangle is (3x)^2 = 9x^2 = 9(90) = 810.

DPatrick 2011-04-01 19:15:20
Onward...

DPatrick 2011-04-01 19:15:48
By the way, I should mention that all 15 problems are also discussed on our message board in our AMC forum, so if you have follow-up questions, that's probably a good place to go!

DPatrick 2011-04-01 19:15:53

GoldenFrog1618 2011-04-01 19:16:24
sum of angles is 18*160

eb8368 2011-04-01 19:16:25
Find the total degree measures of an 18-gon = (18-2)(180)

freddylukai 2011-04-01 19:16:25
first find the sum of all 18 angles

vlchen2 2011-04-01 19:16:25
Find the sum of the angle measures in an 18-sided polygon.

MrPibb 2011-04-01 19:16:25
Either find an arithmetic series of the interior angles or of the exterior angles. Start by finding the middle (9th and 10th) terms.

DPatrick 2011-04-01 19:16:40
You could certainly look at the (interior) angles, but whenever possible, I find it easier to work with exterior angles of a convex polygon, because they always sum to 360.

DPatrick 2011-04-01 19:17:28
And in particular, what is the average exterior angle?

jeff10 2011-04-01 19:17:52
20

ksun48 2011-04-01 19:17:52
20

math1000 2011-04-01 19:17:52
20

dlennon 2011-04-01 19:17:52
20 degrees

RisingMathStar 2011-04-01 19:17:52
360/18 = 20

vlchen2 2011-04-01 19:17:52
360/18=20

DPatrick 2011-04-01 19:17:57
The average exterior angle is 360/18 = 20. So the median of our sequence must be 20.

DPatrick 2011-04-01 19:18:17
But all the terms are integers, and they're all positive, so that doesn't leave very many possibilities...

eb8368 2011-04-01 19:18:45
so the 9th + 10th term / 2 = 20 and the 9th term + 10th term = 40

tiger21 2011-04-01 19:18:45
step 2 arithmetic sequence

DPatrick 2011-04-01 19:19:03
Right.

alex31415 2011-04-01 19:19:07
3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35,37

DPatrick 2011-04-01 19:19:19
Indeed. If the middle two terms are 19 and 21, then we get the sequence above.

DPatrick 2011-04-01 19:19:32
And if the middle two terms are spaced any farther apart, the first term ends up negative.

DPatrick 2011-04-01 19:19:42
So that sequence must be the sequence of exterior angles.

mathlete5 2011-04-01 19:20:06
so 180-37?

.cpp 2011-04-01 19:20:06
Thus the smallest interior angle is 180 - 37 = 143.

MrPibb 2011-04-01 19:20:06
Smallest interior angle = 180-37 = 143 degrees

RisingMathStar 2011-04-01 19:20:06
the smallest interior angle = 180 - 37 = 143

DPatrick 2011-04-01 19:20:18
Yes: the smallest (interior) angle is the angle that's supplementary to the largest exterior angle.

DPatrick 2011-04-01 19:20:24
This angle has measure 180 - 37 = 143.

DPatrick 2011-04-01 19:21:17
I always like working with exterior angles if possible for a problem like this. The numbers are smaller and they always sum to 360!

DPatrick 2011-04-01 19:21:33

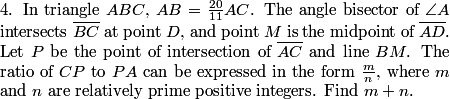
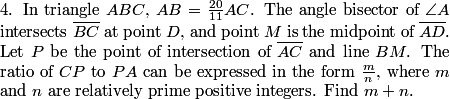
r31415 2011-04-01 19:21:48
picture!!!

asettipa 2011-04-01 19:21:48
Diagram!

DPatrick 2011-04-01 19:21:52
We can begin by sketching the figure.

DPatrick 2011-04-01 19:21:55

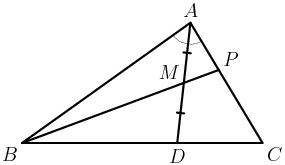
DPatrick 2011-04-01 19:22:04
I don't claim that this picture is in any way to scale, but it has all the key features marked.

DPatrick 2011-04-01 19:22:35
There are lots of ways to solve this problem. I'm going to present the most "low-tech" solution that I could find, that's still pretty straightforward.

r31415 2011-04-01 19:22:44
assign lengths for the sides

DPatrick 2011-04-01 19:22:53
I agree. Since we only care about ratios, we might as well set AB = 20 and AC = 11.

DPatrick 2011-04-01 19:23:03
Makes life a little simpler to be working with actual numbers.

DPatrick 2011-04-01 19:23:20
We care about AP and CP, so let's set AP = x so that CP = 11-x.

DPatrick 2011-04-01 19:23:40
How can we proceed from here?

Monkeyanator1 2011-04-01 19:23:49
Well, by angle bisector theoreom, AD/BD = AC/CD

math1000 2011-04-01 19:23:49
angle bisector theorem

AlphaMath1 2011-04-01 19:23:54
since AD is an angle bisector, BD/DC=20/11

DPatrick 2011-04-01 19:24:16
Right. The Angle Bisector Theorem tells us that the ratio BD/CD = 20/11.

DPatrick 2011-04-01 19:24:43
How does that help?

danielguo94 2011-04-01 19:24:58
ratios of areas

btilm305 2011-04-01 19:25:03
altitude of the triangle?

DPatrick 2011-04-01 19:25:29
That's one good way to proceed: you can next start "chasing areas" by noting that [ABD]/[ACD] = 20/11 as well.

DPatrick 2011-04-01 19:25:40
And you can continue finding other ratios of areas until you've solved the problem.

DPatrick 2011-04-01 19:26:06
In fact, that's how I first solved it, and it's not too hard, until my colleague nsato showed me an even simpler solution!

DPatrick 2011-04-01 19:26:22
Since we're want to find a ratio at the end of the problem, what else might be look for?

DPatrick 2011-04-01 19:26:25
...we look for?

nsun48 2011-04-01 19:26:49
similar triangles/parallel lines?

RisingMathStar 2011-04-01 19:26:51
similar triangles

DPatrick 2011-04-01 19:27:02
Right! But I don't see any parallel lines...

btilm305 2011-04-01 19:27:14
well make some

math1000 2011-04-01 19:27:14
draw them

smartalec17 2011-04-01 19:27:14
make some

tiger21 2011-04-01 19:27:14
Draw some!

DPatrick 2011-04-01 19:27:24
Sure, why not? What line should I draw?

DPatrick 2011-04-01 19:27:34

.cpp 2011-04-01 19:27:49
Parallel to BP from D.

DPatrick 2011-04-01 19:27:57
I like that idea.

DPatrick 2011-04-01 19:28:03

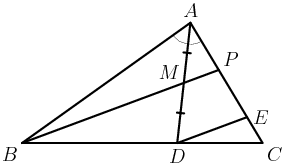
DPatrick 2011-04-01 19:28:16
Now I've got loads of similar triangles.

r31415 2011-04-01 19:28:25
Similar AMP and ADE!

GoldenFrog1618 2011-04-01 19:28:25
AP=PE

DPatrick 2011-04-01 19:28:43
Indeed. AMP and ADE are similar. So since AM = AD, we also get AP = AE.

DPatrick 2011-04-01 19:28:58
Remember we called AP = x (and CP = 11-x). So now PE = x too.

DPatrick 2011-04-01 19:29:02
...and CE = 11-2x.

.cpp 2011-04-01 19:29:18
CED ~ CPB!

mathswimmer 2011-04-01 19:29:18
CED ~ CPB

mathswimmer 2011-04-01 19:29:18
and we know CD/CB from angle bisector

DPatrick 2011-04-01 19:29:27
Aha, that's the other pair of similar triangles: CED and CPB>

.cpp 2011-04-01 19:29:36
CED~CPB with CD/CB = 11/31 = CE/CP.

DPatrick 2011-04-01 19:30:01
Right-o. CD/CB = 11/31 from the Angle Bisector Theorem observation from earlier, so CE/CP = 11/31 too.

aerrowfinn72 2011-04-01 19:30:13
(11-2x)/(11-x)=11/31

DPatrick 2011-04-01 19:30:15

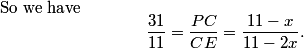
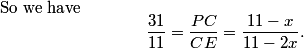
Duncanyang 2011-04-01 19:30:30
cross multiply and solve.

.cpp 2011-04-01 19:30:30
Solve for x.

DPatrick 2011-04-01 19:30:40
This gives 341 - 62x = 121 - 10x, hence 220 = 51x and x = 220/51.

DPatrick 2011-04-01 19:31:03
Finally, our desired ratio is CP/AP = (11-x)/x = (341/51)/(220/51) = 341/220.

.cpp 2011-04-01 19:31:30
Cancel a factor of 11.

DPatrick 2011-04-01 19:31:36
This simplifies to 31/20, so the answer is 31+20 = 051.

DPatrick 2011-04-01 19:31:48
(Don't forget you almost always have to simplify fractions to lowest terms on the AIME.)

AlphaMath1 2011-04-01 19:32:02
Mass points was a quick way to do this problem but it isn't as well known though

DPatrick 2011-04-01 19:32:21
Right: there are lots of ways to solve this problem, and a "high-tech" way is to use a technique called mass point geometry.

DPatrick 2011-04-01 19:32:41
I don't have time to cover that, but you can do a web search and/or ask on the forum about it.

DPatrick 2011-04-01 19:33:03
I like the solution we just did, though, because it doesn't use anything complicated!

DPatrick 2011-04-01 19:33:18

DPatrick 2011-04-01 19:33:47
How is the second sum related to the first sum?

professordad 2011-04-01 19:34:00
the sum of the next 2011 terms after the first 2011 terms is 180

DPatrick 2011-04-01 19:34:14
Yes -- we know that the second block of 2011 terms (that is, terms 2012 through 4022) sums to 180.

MrPibb 2011-04-01 19:34:25
Let common ratio = r

DPatrick 2011-04-01 19:34:41
Suppose r is the common ratio of the series. Given what we know about the sums, what do we know about r?

RisingMathStar 2011-04-01 19:35:08
r^2011 = 9/10

munygrubber 2011-04-01 19:35:08
r to the 2011 is 9/10

DPatrick 2011-04-01 19:35:31
Exactly. We know that each term in the second block is r^2011 times the corresponding term from the first block.

DPatrick 2011-04-01 19:35:40
So the sum of the second block is r^2011 times the sum of the first block.

DPatrick 2011-04-01 19:35:55
This tells us that r^2011 = (180/200) = 9/10.

RisingMathStar 2011-04-01 19:36:23
and the third block is r^2011 times the second block

simplyMathLete 2011-04-01 19:36:25
that is also the ratio between the third block and the second!

DPatrick 2011-04-01 19:36:41
Right. The sum of the third block is again (by the same reasoning) r^2011 times the sum of the second block.

professordad 2011-04-01 19:36:57
the third block sum is 9/10*180 or 162.

DPatrick 2011-04-01 19:37:11
So the sum of the third block is (9/10)*180 = 9*18 = 162.

.cpp 2011-04-01 19:37:30
380 + 162 = 542.

supermathman 2011-04-01 19:37:30
200+180+162=542

AbrahamKim 2011-04-01 19:37:30
542

simplyMathLete 2011-04-01 19:37:30
So the entire thing is 380 + 162 = 542

RisingMathStar 2011-04-01 19:37:30
therefore the desired sum is 380 + 162 = 542

DPatrick 2011-04-01 19:37:34
Thus our answer is the sum of all three blocks: 380 + 162 = 542.

AlphaMath1 2011-04-01 19:37:44
Wow this was a nice and celver way to do it rather than using the sum of geometric series formula

DPatrick 2011-04-01 19:38:23
Right. When the numbers in the problem are big (like 2011 and 4022 and 6033), that is often your clue that thinking about the problem a little can be a better way to go than trying to grind through a formula.

DPatrick 2011-04-01 19:38:47

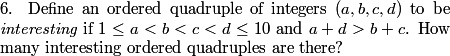
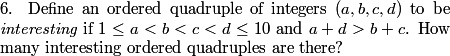
freddylukai 2011-04-01 19:39:16
casework?

tzhang1 2011-04-01 19:39:17
casework

AbrahamKim 2011-04-01 19:39:17
Bashing?

DPatrick 2011-04-01 19:39:23
We could certainly just brute-force count them all via casework, but let me show you a slightly more slick approach.

MrPibb 2011-04-01 19:39:35
Think in cases: Either a+d >,<, or = to b+c.

GoldenFrog1618 2011-04-01 19:39:35
(a,b,c,d) is interesting then (11-d,11-c,11-b,11-a) is not interesting

professordad 2011-04-01 19:39:35
a+d>b+c,a+d<b+c,or a+d=b+c,

DPatrick 2011-04-01 19:39:50
I agree, that's how I proceeded. Suppose we have an ordered quadruple with 1 <= a < b < c < d <= 10. There are three possibilities:

DPatrick 2011-04-01 19:39:56
(1) it's interesting, meaning a+d > b+c.
(2) it might have a+d < b+c. Let's call those uninteresting
(3) it might have a+d = b+c. Let's call those semi-interesting

AlphaMath1 2011-04-01 19:40:17
The probability that a+d>b+c is the same as the probability a+d<b+c

carmelninja 2011-04-01 19:40:17
the < and > cases are symmetric

professordad 2011-04-01 19:40:17
#uninteresting pairs = #interesting pairs

MrPibb 2011-04-01 19:40:17
The cases of > and < are equal because they are complements of each other.

DPatrick 2011-04-01 19:40:28
Yes. I claim that there are an equal number of interesting and uninteresting quadruples.

DPatrick 2011-04-01 19:40:56
GoldenFrog's comment above shows why. We have a correspondence (a,b,c,d) <---> (11-d,11-c,11-b,11-a).

DPatrick 2011-04-01 19:41:14
And we check that if a + d > b + c, then (11-d) + (11-a) = 22 - (a+d) < 22 - (b+c) = (11-b) + (11-c).

DPatrick 2011-04-01 19:41:40
This process is reversible, so this is a 1-1 matching of interesting and uninteresting quadruples.

Redeem 2011-04-01 19:41:49
so we simply need to count the semi interesting quadruples, subtract from total, and divide by two!!!

DPatrick 2011-04-01 19:42:05
Right. Our strategy is to count all the quadruples and subtract the semi-interesting ones. Then half of what remains are interesting (and the other half is uninteresting).

DPatrick 2011-04-01 19:42:21
How many total quadruples are there?

RisingMathStar 2011-04-01 19:42:44
There are (10 choose 4) total quadruples

MrPibb 2011-04-01 19:42:44
10 choose 4 = 210

simplyMathLete 2011-04-01 19:42:44
10 C 4, or 210 total

.cpp 2011-04-01 19:42:44
10 choose 4

munygrubber 2011-04-01 19:42:44
10 choose 4

Redeem 2011-04-01 19:42:44
10C4.... every way we pick 4 numbers corresponds to 1 way to arrange them in order

DPatrick 2011-04-01 19:42:48
Any choice of 4 numbers gives a unique ordered quadruple.

DPatrick 2011-04-01 19:42:55

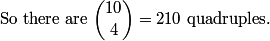
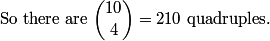
DPatrick 2011-04-01 19:43:02
How many of these are semi-interesting? That is, we want (a < b < c < d) with a+d = b+c.

DPatrick 2011-04-01 19:43:26
How can we count these?

simplyMathLete 2011-04-01 19:43:42
Casework is really easy here

Duncanyang 2011-04-01 19:43:42
JUST COUNT BY HAND!!!

mathswimmer 2011-04-01 19:43:42
go through different values of a+d?

DPatrick 2011-04-01 19:43:48
Now the brute force is not so bad. We have casework depending on what the sum a+d = b+c is.

DPatrick 2011-04-01 19:44:04
For instance, if a+d = b+c = 5 (the smallest possible), the only semi-interesting possibility is (1,2,3,4).

DPatrick 2011-04-01 19:44:15
Similarly, if the sum is 6, the only possibility is (1,2,4,5).

DPatrick 2011-04-01 19:44:28
How about 7?

RisingMathStar 2011-04-01 19:44:55
You choose 2 from the set of (1, 6), (2, 5), and (3, 4)

.cpp 2011-04-01 19:44:56
(1,2,5,6), (1,3,4,6), (2,3,4,5).

DPatrick 2011-04-01 19:45:04
For 7: there are three pairs (1,6),(2,5),(3,4) that sum to 7, and we must pick 2 of these pairs.

DPatrick 2011-04-01 19:45:23
So there are C(3,2) = 3 possibilities where the pairs sum to 7.

simplyMathLete 2011-04-01 19:45:47
the next is the same, because we can't use 4

DPatrick 2011-04-01 19:45:49
Same for a sum of 8: there are 3 pairs that sum to 8, so C(3,2) = 3 possibilities.

Redeem 2011-04-01 19:46:02
and therein lies the pattern!

simplyMathLete 2011-04-01 19:46:26
so the sums are 1, 1, 3, 3, 6, 6, or triangular numbers repeated

RisingMathStar 2011-04-01 19:46:27
9 and 10 have (4 choose 2) = 6, 11 has (5 choose 2) = 10, and so on

DPatrick 2011-04-01 19:46:31
Right: for sums of 9 or 10, there are 4 pairs summing to that number, so C(4,2) = 6 quadruples for each.

DPatrick 2011-04-01 19:46:42
The "middle" case is a sum of 11. There are 5 pairs, so C(5,2) = 10 semi-interesting quadruples whose pairs sum to 11.

DPatrick 2011-04-01 19:46:53
Then it goes back down...

DPatrick 2011-04-01 19:47:02
So the semi-interesting total is 2*1+2*3+2*6+10+2*6+2*3+2*1 = 4*(1+3+6) + 10 = 50.

DPatrick 2011-04-01 19:47:16
And to finish?

professordad 2011-04-01 19:47:35
210-50=160, half is 80.

RisingMathStar 2011-04-01 19:47:36
(210 - 50) / 2 = 80 is the answer

super_pi314 2011-04-01 19:47:36
so the total number of interesting quadruples is (210-50)/2=80

.cpp 2011-04-01 19:47:36
(210-50)/2 = 080.

DPatrick 2011-04-01 19:47:41
Out of 210 total quadruples, 50 are semi-interesting, so that leaves 160. Half of these are interesting, so the answer is 080.

Redeem 2011-04-01 19:48:01
is it required to put a leading 0?

DPatrick 2011-04-01 19:48:06
On the official AIME answer sheet, yes.

DPatrick 2011-04-01 19:48:17

DPatrick 2011-04-01 19:48:39
Let me first introduce some simple vocabulary to make this problem easier for us to talk about.

DPatrick 2011-04-01 19:48:55
Let's call two marbles next to each other of the same color a pair, and two marbles of opposite color next to each other a flip.

DPatrick 2011-04-01 19:49:05
The condition says that the number of pairs must equal the number of flips.

DPatrick 2011-04-01 19:49:14
So if there are n flips (and thus n pairs), how many total marbles are there?

CRICKET229 2011-04-01 19:49:56
2n+1

carmelninja 2011-04-01 19:49:56
2n+1 total

NoWayHaze 2011-04-01 19:49:59
2n+1

DPatrick 2011-04-01 19:50:28
Right, that gives 2n+1 total marbles. (Each marble starts either a pair or a flip, except the marble at the right end.)

DPatrick 2011-04-01 19:50:34
But what's the maximum number of pairs?

DPatrick 2011-04-01 19:50:58
...or, even easier, what's the maximum number of flips?

simplyMathLete 2011-04-01 19:51:33
each green marble contributes 2 flips maximum (1 on the left, one on the right)

carmelninja 2011-04-01 19:51:33
10 (two for each green marble)

simplyMathLete 2011-04-01 19:51:33
so, 2 flips per green * 5 greens = 10

munygrubber 2011-04-01 19:51:33
10, because there are only 5 green ones and one flip before and one after

DPatrick 2011-04-01 19:51:42
There are only 5 green marbles, and each one can be in at most two flips.

DPatrick 2011-04-01 19:52:04
So there can be at most 10 flips, and thus at most 21 marbles.

numberwiz 2011-04-01 19:52:15
So 21 marbles, 16 are red.

DPatrick 2011-04-01 19:52:21
Right. Can we arrange 16 reds and 5 green legally, and if so, in how many ways?

DPatrick 2011-04-01 19:52:52
Note each green must be in two pairs, so it must be surrounded by a red on each side.

nsun48 2011-04-01 19:53:18
stars and bars???

munygrubber 2011-04-01 19:53:18
as long as the greens are not next to each other or at the ends.... so just put in the 16 reds and insert the greens into the 15 slots availible

carmelninja 2011-04-01 19:53:18
choose 5 of the 15 slots between the 16 reds to put the greens in --> 15C5

DPatrick 2011-04-01 19:53:35
Exactly. This is a classic "stars and bars" or "balls and urn" or "objects and dividers" counting problem.

DPatrick 2011-04-01 19:53:39
Allow me to explain...

DPatrick 2011-04-01 19:53:46
Imagine the 16 reds lined up in a row:
RRRRRRRRRRRRRRRR

DPatrick 2011-04-01 19:53:57
We need to place the five greens in between the reds. One possibility is below:
RGRRGRRRRRGRRRGRRGRRR

DPatrick 2011-04-01 19:54:09
There are 15 "slots" between the reds, and we have to choose 5 of those slots to contain a green.

tiger21 2011-04-01 19:54:22
pick 5 from the 15 availeble spaces so 15C5=3003 -->003

DPatrick 2011-04-01 19:54:36

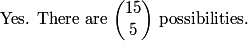
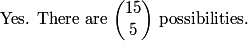
DPatrick 2011-04-01 19:54:56
C(15,5) = 3003, and we only want the last 3 digits, so our answer is 003.

DPatrick 2011-04-01 19:55:49

MrPibb 2011-04-01 19:56:18
Draw a unit circle on a polar coordinate grid! This helps to find the roots/zeros.

DPatrick 2011-04-01 19:56:30
I very much agree!

DPatrick 2011-04-01 19:56:35

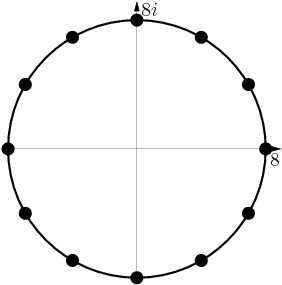
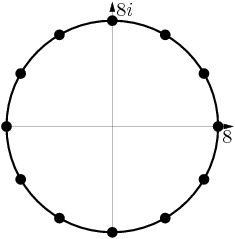
Duncanyang 2011-04-01 19:57:02
A dodecagon!!!!

AlphaMath1 2011-04-01 19:57:03
Un a unit circle with radius 8

MrPibb 2011-04-01 19:57:03
The numbers on a clock

simplyMathLete 2011-04-01 19:57:03
they form a dodecagon (12 sides)

numberwiz 2011-04-01 19:57:03
Evenly spaced 30 degrees, radius 8

ksun48 2011-04-01 19:57:03
roots of unity scaled up by 8

Maxima 2011-04-01 19:57:03
Each of the twelve roots of unity, just multiplied by 2^3 = 8.

DPatrick 2011-04-01 19:57:09
Yes. Clearly one solution is z = 2^3 = 8.

DPatrick 2011-04-01 19:57:19
The other are equally spaced around the circle centered at 0 with radius 8:

DPatrick 2011-04-01 19:57:23

DPatrick 2011-04-01 19:57:39
How do we maximize the sum?

supermathman 2011-04-01 19:58:11
You want everything to be as far right as possible:*-/

calculatorwiz 2011-04-01 19:58:25
have the most real parts

carmelninja 2011-04-01 19:58:25
create the most positive x-coordinates

DPatrick 2011-04-01 19:58:31
The real part of the sum is the same as the sum of the real parts, so we just need to maximize the real part of each w_j separately.

DPatrick 2011-04-01 19:58:48
Which has larger real part, z_j or iz_j?

Redeem 2011-04-01 19:59:01
it depends?

calculatorwiz 2011-04-01 19:59:01
depends on the z...

DPatrick 2011-04-01 19:59:06
It depends on which z we're looking at.

DPatrick 2011-04-01 19:59:14
What is the geometric meaning (in the complex plane) of multiplying by i?

freddylukai 2011-04-01 19:59:51
shift by 90 degress

.cpp 2011-04-01 19:59:51
Rotation ccw by 90 degrees.

simplyMathLete 2011-04-01 19:59:51
rotate by 90 degress

billyg 2011-04-01 19:59:51
rotating 90 degrees counterclockwise

DPatrick 2011-04-01 19:59:56
It rotates the point 90 degrees counterclockwise.

DPatrick 2011-04-01 20:00:08
So which roots have larger real parts if we leave them where they are, and which have larger real parts if we multiply them by i? (Remember the real part is the x-coordinate in the complex plane.)

DPatrick 2011-04-01 20:00:25
(It helps to talk about it if you think of the picture as a clock)

DPatrick 2011-04-01 20:00:39

billyg 2011-04-01 20:01:21
5-10

DPatrick 2011-04-01 20:02:03
Right. The points that are currently in the 5-10 o'clock positions will have larger real part if we rotate them 90 degrees counterclockwise.

DPatrick 2011-04-01 20:02:12
This is hard to see in text, so here's another picture:

DPatrick 2011-04-01 20:02:21

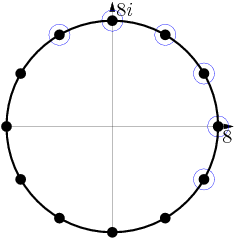
DPatrick 2011-04-01 20:02:38
The blue-circled roots have larger x-coordinate (larger real part) if we leave them along.

DPatrick 2011-04-01 20:02:40
...alone.

DPatrick 2011-04-01 20:02:57
The uncircled roots have larger x-coordinate if we rotate them each 3 positions counterclockwise.

DPatrick 2011-04-01 20:03:07
And the other (uncircled) roots will rotate to the red circled roots below:

DPatrick 2011-04-01 20:03:15

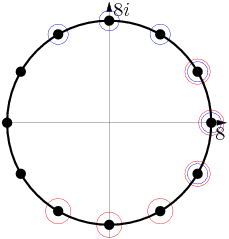
DPatrick 2011-04-01 20:03:33
Now we sum the real parts of all the circled roots (and if a root is circled twice, we count it twice).

GoldenFrog1618 2011-04-01 20:03:37
there is a bit of cancelling

DPatrick 2011-04-01 20:03:50
Yes, that makes it a bit simpler.

AlphaMath1 2011-04-01 20:03:58
top 3 and bottom 3 cancel

ktbroborg 2011-04-01 20:04:03
11 and 1 and 5 and 7

DPatrick 2011-04-01 20:04:13
First, the three roots with the blue circles only (at the top) will have real parts summing to 0.

DPatrick 2011-04-01 20:04:26
Same for the three roots with the red circles only.

DPatrick 2011-04-01 20:04:47
So we are left with twice the sum of the real parts of the three roots at the right (with the double-circles, at the 2-, 3- and 4-o'clock positions).

DPatrick 2011-04-01 20:05:06
Obviously the root on the real axis has real part 8.

DPatrick 2011-04-01 20:05:09
What about the other two?

Maxima 2011-04-01 20:05:29
both are 4sqrt3.

NoWayHaze 2011-04-01 20:05:30
cos pi/6

freddylukai 2011-04-01 20:05:30
cos 30 times 8

RisingMathStar 2011-04-01 20:05:30
8 * cos 30

DPatrick 2011-04-01 20:05:34

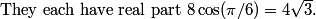
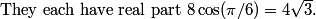
numberwiz 2011-04-01 20:06:09
16 + 16rt3

RisingMathStar 2011-04-01 20:06:09
2 * (8 + 2 * 4sqrt{3})

DPatrick 2011-04-01 20:06:12

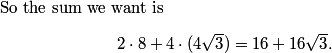
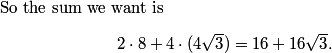
NoWayHaze 2011-04-01 20:06:34
we wan m +sqrt(n)

DPatrick 2011-04-01 20:06:42
This is not quite the format that's required.

RisingMathStar 2011-04-01 20:06:52

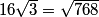
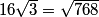
munygrubber 2011-04-01 20:06:53
move the 16 inside the radical

professordad 2011-04-01 20:06:53
16+sqrt(256*3)

.cpp 2011-04-01 20:06:55
Thus, the answer is 16 + 768 = 784.

Duncanyang 2011-04-01 20:06:56
16+768=784

DPatrick 2011-04-01 20:06:59

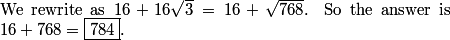
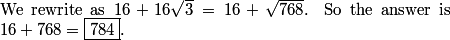
DPatrick 2011-04-01 20:07:22
We've finished page 1 of the contest!

DPatrick 2011-04-01 20:07:34
I've going to take a 2-minute "rest my fingers" break, and we'll resume at :10 past the hour.

DPatrick 2011-04-01 20:10:03
OK, we're back!

DPatrick 2011-04-01 20:10:09

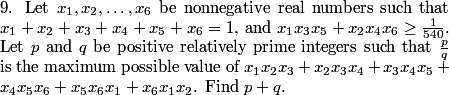
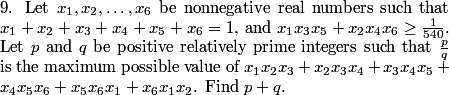
DPatrick 2011-04-01 20:10:44
Hmmm...we've got sums and products and inequalities and optimization (maximization). All these should suggest a tactic.

vliu 2011-04-01 20:10:58
am-gm

professordad 2011-04-01 20:10:58
AM-GM inequality?

mathepic 2011-04-01 20:10:58
AM-GM?

DPatrick 2011-04-01 20:11:05
AM-GM! That is, the arithmetic mean - geometric mean inequality, that says that the AM of a set of nonnegative numbers is always >= the GM of the same set, with equality if and only if all the numbers are equal.

DPatrick 2011-04-01 20:11:24
How can we use AM-GM in this problem?

mathswimmer 2011-04-01 20:12:30
note the symmetry of the sum we want to maximize so it goes nicely into the GM part

carmelninja 2011-04-01 20:12:38
treat each x_ix_jx_k as the geometric mean

DPatrick 2011-04-01 20:13:16
These are not bad ideas, and in fact I tried something similar the first time out, but in the interest of saving time I'll tell you that they don't really lead anywhere.

DPatrick 2011-04-01 20:13:44
We have two expressions that are sums of products of triples: the one that is given to be >= 1/540, and the one that we want to maximize. How do we work with them?

AlphaMath1 2011-04-01 20:14:34
We should start with the sum of the x_is that equal 1?

DPatrick 2011-04-01 20:14:49
In fact, that tells us that the AM of the x's is 1/6.

DPatrick 2011-04-01 20:15:50

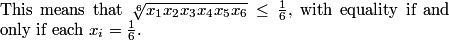
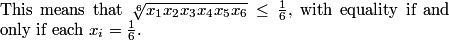
DPatrick 2011-04-01 20:18:10
It turns out that x_1 = x_2 = ... = x_6 = 1/6 is not the best value of the x's to maximum the sum we want.

simplyMathLete 2011-04-01 20:18:29
we could split up the product on the inside to (1,3,5), and (2, 4, 6)

centralbs 2011-04-01 20:18:30
Note that in our 8 products, x_1 never appears with x_4, x_2 never with x_5 and x_3 with x_6. This allows us to come up with a tricky factorization that involves all 6 products. (x_1 + x_4)(x_2 + x_5)(x_3 + x_6)

DPatrick 2011-04-01 20:19:12
Yes. All 8 terms that are products of three of the x's have something in common: they each have either x_1 or x_4, and either x_2 or x_5, and either x_3 or x_6.

DPatrick 2011-04-01 20:19:34
And they are all 8 possible terms with this property.

DPatrick 2011-04-01 20:19:43

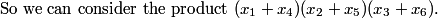
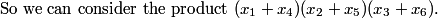
DPatrick 2011-04-01 20:20:13
This product expands to the sum in the given condition (call it r, so that r >= 1/540) and the expression we want (call it s, so that we want to maximize s).

DPatrick 2011-04-01 20:21:53
The AM of the three terms (x1+x4),(x2+x5),(x3+x6) is 1/3 (since they sum to 1). So the GM is at most 1/3, with equality if and only if they are all 1/3.

DPatrick 2011-04-01 20:25:11

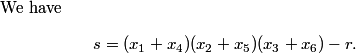
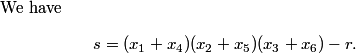
DPatrick 2011-04-01 20:25:26
We know r >= 1/540.

DPatrick 2011-04-01 20:25:46

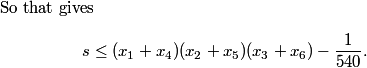
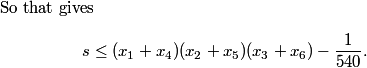
DPatrick 2011-04-01 20:26:13
Then AM-GM tells us the product is at most 1/27.

DPatrick 2011-04-01 20:26:34

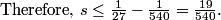
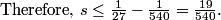
professordad 2011-04-01 20:27:16

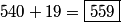
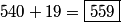
han2 2011-04-01 20:27:16
so the answer is 19 + 540 = 559?

freddylukai 2011-04-01 20:27:16
so we do have the right answer, 19+540=559

.cpp 2011-04-01 20:27:16
We should show that this is indeed achievable.

DPatrick 2011-04-01 20:27:39
Correct. This is a possible maximum, but it's not obvious that this maximum is achieveable.

DPatrick 2011-04-01 20:28:04
(On the actual contest, I might be tempted to guess that it is and move on.)

DPatrick 2011-04-01 20:28:28
But to check that we can achieve the maximum of 19/540, we have to have equality at all stages, meaning we must have x1x3x5 + x2x4x6 = 1/540, and we need equality in the AM-GM expression, so we must have x1+x4 = x2+x5 = x3+x6 = 1/3.

DPatrick 2011-04-01 20:28:35
Is this possible?

DPatrick 2011-04-01 20:28:54
We already know that setting them all equal to 1/6 doesn't work.

DPatrick 2011-04-01 20:29:03
Another easy thing to try is to make as any of them 0 as possible.

DPatrick 2011-04-01 20:29:09
...as many of them 0 as possible.

centralbs 2011-04-01 20:29:58
Yea, people on the forums got ;$ left(0,frac{1}{60}, 0,frac{1}{3},frac{19}{60},frac{1}{3}right) $

DPatrick 2011-04-01 20:30:07
This is probably the easiest way to achieve the equality.

DPatrick 2011-04-01 20:30:15
We could try to set x_1 = x_3 = 0. This means x_4 = x_6 = 1/3.

DPatrick 2011-04-01 20:30:24

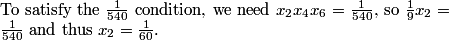
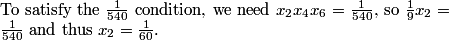
DPatrick 2011-04-01 20:32:42

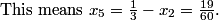
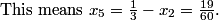
DPatrick 2011-04-01 20:32:42
Thus the maximum of 19/540 can be achieved, and our answer is 19+540 = 559.

han2 2011-04-01 20:32:42
so this means that the answer works

DPatrick 2011-04-01 20:33:05
(sorry, our classroom froze up for a sec there)

DPatrick 2011-04-01 20:33:16
Note that the "verification that the maximum can be achieved" is necessary for a proof, but on the AIME itself you might be tempted to "guess" that 19/540 is the answer without doing the verification. You might also be able to guess-and-check some values for the x's that work.

DPatrick 2011-04-01 20:33:30
That problem did not go as smoothly as I might have hoped. :(

DPatrick 2011-04-01 20:33:37
Let's hope this one is better...

DPatrick 2011-04-01 20:33:44

.cpp 2011-04-01 20:34:04
Diagram!

professordad 2011-04-01 20:34:05
draw a picture

tiger21 2011-04-01 20:34:05
draw a picture!

MrPibb 2011-04-01 20:34:05
Diagram

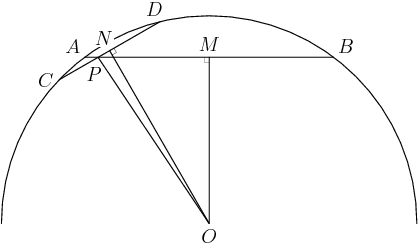
DPatrick 2011-04-01 20:34:08
Let's sketch a diagram. I'll label M and N to be the midpoints of the chords.

DPatrick 2011-04-01 20:34:12

DPatrick 2011-04-01 20:34:26
We're given MN = 12, AB = 30, CD = 14, and the radius is 25. We want (OP)^2.

DPatrick 2011-04-01 20:34:45
Any other lengths immediately pop out here?

RisingMathStar 2011-04-01 20:35:05
OM = 20, ON = 24

mhy123 2011-04-01 20:35:06
pythagorean theorem somehow

han2 2011-04-01 20:35:06
first of all OM is 20 from pythagoras

dragon96 2011-04-01 20:35:06
ON and OM (pythag)

kangchangood 2011-04-01 20:35:06
OM and ON

DPatrick 2011-04-01 20:35:13
MB = 15 and OB = 25, so MO = 20. (OMB is a 15-20-25 right triangle.)

DPatrick 2011-04-01 20:35:25
In the same way, ND = 7 and OD = 25, so ON = 24. (OND is 7-24-25.)

DPatrick 2011-04-01 20:35:49
So in particular we know all three sides of NMO. How does that help?

dragon96 2011-04-01 20:36:26
use Law of Cosines on OMN

.cpp 2011-04-01 20:36:27
Law of cosines.

RisingMathStar 2011-04-01 20:36:31
law of cosines

carmelninja 2011-04-01 20:36:32
can find angles

DPatrick 2011-04-01 20:37:02
We can use the Law of Cosines to find the angles in MNO, but before we decide to churn through that calculation, why will that help?

GoldenFrog1618 2011-04-01 20:37:40
MNPO is cyclic

DPatrick 2011-04-01 20:37:43
Aha!

DPatrick 2011-04-01 20:38:24
PNMO is cyclic! This is a very common type of cyclic quadrilateral to try to recognize, with the two right angles as in the diagram above. N and M both lie on the circle with diameter PO. (I won't draw it since it clutters the diagram.)

DPatrick 2011-04-01 20:39:17
Now we see a path to the answer. We use triangle NMO to find the trig data for angle NMO, and use that data at the supplementary angle NPO in right triangle NPO to find OP.

DPatrick 2011-04-01 20:39:52
So now I agree, using Law of Cosines to find angle NMO is the next step.

DPatrick 2011-04-01 20:40:15

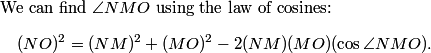
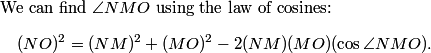
DPatrick 2011-04-01 20:40:40
We plug in our known NO = 24, NM = 12, and MO = 20:

DPatrick 2011-04-01 20:40:59

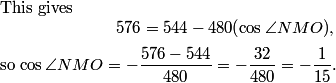
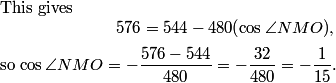
DPatrick 2011-04-01 20:41:14
What do we do with this information?

han2 2011-04-01 20:41:46
cos angle NPO is cos (180 - angle NMO) = -(cos angle NMO) = 1/15

dragon96 2011-04-01 20:41:46
find sine of <NPO

.cpp 2011-04-01 20:41:46
cos <NPO = 1/15.

RisingMathStar 2011-04-01 20:41:46
cos NPO = 1/15

DPatrick 2011-04-01 20:42:08
Right. Angles NMO and NPO are supplementary (they sum to 180 degrees), so cos NPO = - cos NMO = 1/15.

DPatrick 2011-04-01 20:42:26
And now we're just about done.

DPatrick 2011-04-01 20:42:44
We want OP, and we know sin(NPO) = NO/OP = 24/OP.

DPatrick 2011-04-01 20:42:59
(just using the right triangle PNO)

han2 2011-04-01 20:43:15
ah, so sin NPO = sqrt(224)/15?

professordad 2011-04-01 20:43:17
sin NPO= (sqrt224)/15

DPatrick 2011-04-01 20:43:27

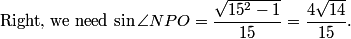
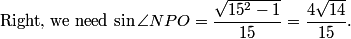
DPatrick 2011-04-01 20:44:05

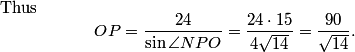
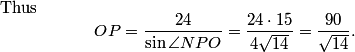
han2 2011-04-01 20:44:23
square it

kangchangood 2011-04-01 20:44:26
square it

DPatrick 2011-04-01 20:44:30
Squaring this gives (OP)^2 = 8100/14 = 4050/7, so the sum of numerator and denominator is 4057, and the reminder we want for our final answer is 057.

DPatrick 2011-04-01 20:45:23
As with most geometry problems, there are other ways you can solve it, and in particular there are other formulas involving cyclic quadrilaterals that you can use.

DPatrick 2011-04-01 20:45:42
But I think the key step is observing the cyclicness of PNMO.

DPatrick 2011-04-01 20:45:56
When you have lots of right angles, there are often cyclic quadrilaterals.

DPatrick 2011-04-01 20:46:12

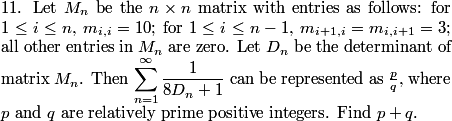
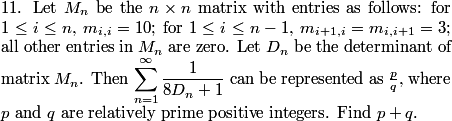
DPatrick 2011-04-01 20:46:28
There was a note explaining the determinant included with the problem (that I won't put up top):

DPatrick 2011-04-01 20:46:32

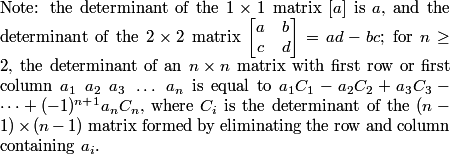
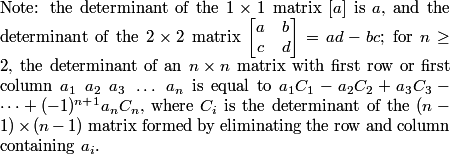
AlphaMath1 2011-04-01 20:47:02
We should list out the first few determinants

han2 2011-04-01 20:47:03
so... start with small matrices?

DPatrick 2011-04-01 20:47:12
Sure. Not knowing exactly what else to do, I just started computing a few for small values of n.

leinad47x 2011-04-01 20:47:21
|10|

DPatrick 2011-04-01 20:47:28

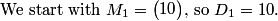
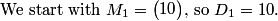
DPatrick 2011-04-01 20:47:49

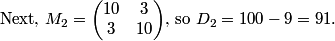
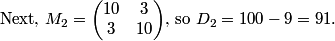
DPatrick 2011-04-01 20:48:03

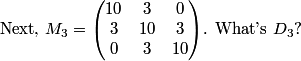
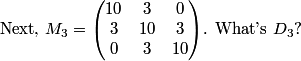
han2 2011-04-01 20:48:34
we have 10D2 - 3(30)

ksun48 2011-04-01 20:48:34
use the definition

DPatrick 2011-04-01 20:48:39

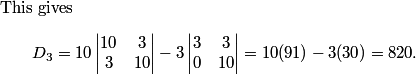
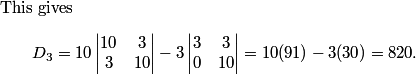
DPatrick 2011-04-01 20:48:59
The first three D's are 10, 91, 820. See any pattern?

DPatrick 2011-04-01 20:49:44
Some people I talked to (like rrusczyk) saw the patten right away. I didn't.

DPatrick 2011-04-01 20:50:14
Maybe the D's don't have a nice pattern....but it's not really what the problem asks for...

GoldenFrog1618 2011-04-01 20:50:40
plug into the sum!

DPatrick 2011-04-01 20:51:15
Right: we might want to compute the (8D_n + 1) denominators in the sum we want. Let's call those E_n.

DPatrick 2011-04-01 20:51:26

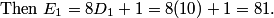
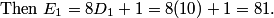
DPatrick 2011-04-01 20:51:38

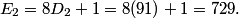
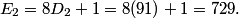
centralbs 2011-04-01 20:51:47
hmmmmmm

DPatrick 2011-04-01 20:51:50

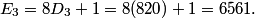
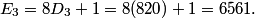
professordad 2011-04-01 20:51:54
wow, 1/81,1/729,1/9^4

dragon96 2011-04-01 20:51:55
powers of 9...

.cpp 2011-04-01 20:51:55
These are all powers of 9!

tiger21 2011-04-01 20:51:58
geometric sequence!

leinad47x 2011-04-01 20:51:59
powers of 9

DPatrick 2011-04-01 20:52:05
Even I could see the pattern now!

DPatrick 2011-04-01 20:52:11
Now the pattern is pretty clear. These are powers of 9, starting at 81.

centralbs 2011-04-01 20:52:19
a bunch of people guess at this point :)

DPatrick 2011-04-01 20:52:25
Yes...Assuming this pattern holds, what is the sum?

DPatrick 2011-04-01 20:52:41

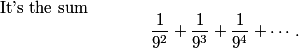
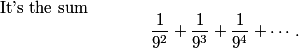
leinad47x 2011-04-01 20:52:52
Infinite geometric series with first term 1/81, ratio 1/9. a/(1-r)=1/81/(8/9)=1/72

.cpp 2011-04-01 20:52:52
1/81 * 9/8 = 1/72.

DPatrick 2011-04-01 20:53:18

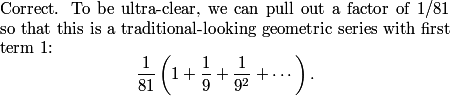
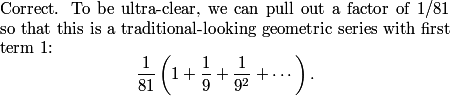
DPatrick 2011-04-01 20:53:31

DPatrick 2011-04-01 20:53:44

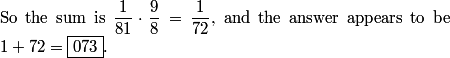
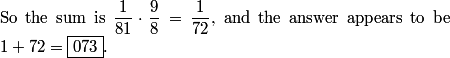
DPatrick 2011-04-01 20:53:56
In actual contest conditions, I might be tempted to go with this answer and move on.

freddylukai 2011-04-01 20:54:01
but we should show it does hold

nsun48 2011-04-01 20:54:01
do we need to prove it?

DPatrick 2011-04-01 20:54:13
We made a bold assumption about the D's. Can we prove it?

DPatrick 2011-04-01 20:54:24

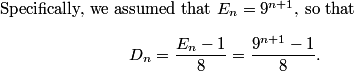
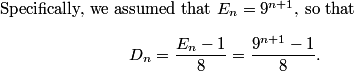
DPatrick 2011-04-01 20:54:26
How do we prove this?

professordad 2011-04-01 20:54:43
could we try induction?

carmelninja 2011-04-01 20:54:43
induction

dragon96 2011-04-01 20:54:43
induction?

.cpp 2011-04-01 20:54:43
Induction, maybe?

kangchangood 2011-04-01 20:54:43
Induction?

DPatrick 2011-04-01 20:55:16
We can try to prove this inductively, which requires expressing D_n in terms of smaller D's. Is there a recursion between the D_n's that we can exploit?

DPatrick 2011-04-01 20:55:40
(We already know it works for D_1, D_2, D_3, since we computed those, so any bases cases are already taken care of most likely.)

centralbs 2011-04-01 20:55:55
Expansion by minors, in the expansion you get previous D_n's

number.sense 2011-04-01 20:55:55
cofactors

DPatrick 2011-04-01 20:56:12
Right, we use the definition of derivative that they helpfully included in the contest.

han2 2011-04-01 20:56:31
... you meant determinant

Maxima 2011-04-01 20:56:31
^determinant

DPatrick 2011-04-01 20:56:49
Right, determinant! (I've been teaching calculus this year. We definitely don't want derivatives on the AIME.)

DPatrick 2011-04-01 20:57:04
The top row of D_n has a 10 and a 3, and the rest are 0s.

DPatrick 2011-04-01 20:57:16
(I should say the top row of the matrix M_n.)

DPatrick 2011-04-01 20:57:40
Let's go back to our n=3 example:

DPatrick 2011-04-01 20:57:49

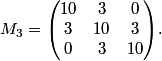
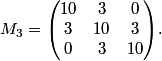
DPatrick 2011-04-01 20:57:58

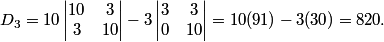
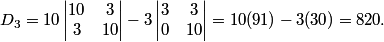
professordad 2011-04-01 20:58:20
hey, the first 2x2 matrix there is the previous matrix

simplyMathLete 2011-04-01 20:58:37
if we use the 10 minor, then we get the previous term. If we use the 3 minor, we get 9* the term before that

GoldenFrog1618 2011-04-01 20:58:40
10D_{n-1}-9D_{n-2}

DPatrick 2011-04-01 20:58:52

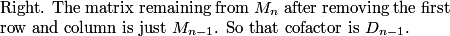
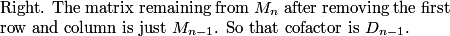
DPatrick 2011-04-01 20:59:26

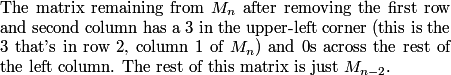
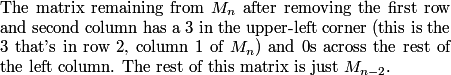
DPatrick 2011-04-01 20:59:46

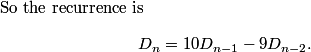
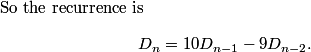
.cpp 2011-04-01 21:00:26
Simple induction to prove the recurrence from her.

DPatrick 2011-04-01 21:00:29
And to prove (by induction) that our formula for the D's works, we have to check it for D_1 and D_2 (which we already did), and then plug it into this recurrence to verify that it works.

DPatrick 2011-04-01 21:00:55
In fact, it does. I'll spare us the algebra in the interest of time, but if you plug in D_n = (9^(n+1) - 1)/8 into the above recurrence, it all works.

DPatrick 2011-04-01 21:01:46
Thus we had the correct formula: our bold assumption from earlier is correct, and the sum is 1/72, giving answer 073.

DPatrick 2011-04-01 21:02:04
OK, moving on..

DPatrick 2011-04-01 21:02:08

DPatrick 2011-04-01 21:02:33
First question: in how many ways can we seat the delegates?

Jarke 2011-04-01 21:02:59
8!

dragon96 2011-04-01 21:02:59
8! = 40320

Maxima 2011-04-01 21:02:59
8!, because we can rotate the table.

number.sense 2011-04-01 21:02:59
9!/9

leinad47x 2011-04-01 21:02:59
8!

.cpp 2011-04-01 21:02:59
8! ways, if they are each distinct.

DPatrick 2011-04-01 21:03:14
You might get a different answer, depending on what you consider a "seating".

DPatrick 2011-04-01 21:03:31
So we have to make a choice as to what a "seating" will be, and be consistent with that choice throughout.

DPatrick 2011-04-01 21:03:54
I found it easiest to have a seating be 9 distinct people into 9 seats, accounting for the rotational symmetry of the table.

DPatrick 2011-04-01 21:04:11
So there are 9! ways to arrange 9 people, but the round table is symmetric, so to account for rotating the table we must divide by 9 (since we can think of any of the 9 positions as being at the "top" of the table).

DPatrick 2011-04-01 21:04:22
Thus there are 9!/9 = 8! ways to seat the delegates. Note that 8! = 40320.

DPatrick 2011-04-01 21:04:42
How many of these seatings have every delegate next to at least one delegate from another country?

simplyMathLete 2011-04-01 21:05:21
complementary counting would be best

munygrubber 2011-04-01 21:05:21
everything that doesn't have three from the same country in a row

DPatrick 2011-04-01 21:05:34
I agree. What is asked for seems hard to count directly.

DPatrick 2011-04-01 21:05:53
But the complement is easier to count: the number of seatings that have some delegate next to no delegates from another country.

DPatrick 2011-04-01 21:06:21
In the "bad" seatings, somebody must have his/her countrymates on both sides. So all 3 people from one country must be seated together, and that seems (relatively) easier to get a handle on.

DPatrick 2011-04-01 21:06:38
Let's call the countries A, B, C for simplicity.

DPatrick 2011-04-01 21:06:42
How many seatings have all 3 people from A seated together?

professordad 2011-04-01 21:07:16
3! for people in A and 6! for people outside A, 3!*6!

gordgord 2011-04-01 21:07:16
3!x6!

number.sense 2011-04-01 21:07:16
3! * 6!

GoldenFrog1618 2011-04-01 21:07:16
6!3!

DPatrick 2011-04-01 21:07:22
Right.

DPatrick 2011-04-01 21:07:31
The way I like to think about this sort of counting is to glue the 3 people together into a "superperson".

DPatrick 2011-04-01 21:07:51
The 3 people from county A can be glued together in 3! ways.

DPatrick 2011-04-01 21:08:04
So now we think of having just 7 people to seat around the table: the superperson from A and the other 6 people from B and C.

DPatrick 2011-04-01 21:08:33
These people can be placed around the table in 7!/7 = 6! ways, accounting for rotation.

DPatrick 2011-04-01 21:08:56
So, all together, there are 3! * 6! ways to seat the people so that the three from A are together.

freddylukai 2011-04-01 21:09:19
same with B and C

han2 2011-04-01 21:09:19
this also applies for B and C

DPatrick 2011-04-01 21:09:38
Right. We have the same for the three from B all together and the three from C all together.

DPatrick 2011-04-01 21:09:46
This gives us a total count of 3*3!*6! ways to seat one country group all together.

simplyMathLete 2011-04-01 21:09:51
Now we need to use PIE, for the overcount

jeff10 2011-04-01 21:09:51
but don't we have to subtract the ways that two countries have that apply to them?

DPatrick 2011-04-01 21:10:04
Right. We've over-counted seatings in which the people from more than one country are all together. (For example, we've twice counted the arrangements when the 3 from A are together and the 3 from B are also together.)

DPatrick 2011-04-01 21:10:10
So we use the principle of inclusion-exclusion (or PIE) to correct for this. We must subtract off the seatings that we've overcounted.

DPatrick 2011-04-01 21:10:23
How many seatings have both the group from A and the group from B together?

.cpp 2011-04-01 21:11:11
3!*3!*4!

GoldenFrog1618 2011-04-01 21:11:11
3!*3!*4!

kangchangood 2011-04-01 21:11:11
no.. 3! 3! 5! /5

DPatrick 2011-04-01 21:11:15
Right.

DPatrick 2011-04-01 21:11:24
I use the same reasoning: we make an A-superperson in 3! ways. We make a B-superperson in 3! ways. We then have 5 "people" to seat (the two superpeople and the three people from C) in 5!/5 = 4! ways.

DPatrick 2011-04-01 21:11:32
So there are 3!*3!*4! such seatings.

kangchangood 2011-04-01 21:11:43
x 3

AlphaMath1 2011-04-01 21:11:48
multiply by 3 to account for all the parings

DPatrick 2011-04-01 21:11:54
Right, we have the same number of seatings in which each of the other two pairs of countries (A and C, and B and C) are all together.

DPatrick 2011-04-01 21:12:03
So that's 3*3!*3!*4! seatings we've overcounted in our initial count, that we now have to subtract off.

DPatrick 2011-04-01 21:12:10
Our total count of undesired seatings is now 3*3!*6! - 3*3!*3!*4!.

nsun48 2011-04-01 21:12:27
then add all three!

AlphaMath1 2011-04-01 21:12:28
However we must add the case where there is an A B C superperson

freddylukai 2011-04-01 21:12:28
but then add the case for A and B and C "superpeople"

DPatrick 2011-04-01 21:12:33
This is not yet accurate because we've undercounted the seatings in which all three countries' groups of people are together. These seatings were counted 3 times in the first step, but subtracted 3 times in the second step, so they're not in our count yet.

.cpp 2011-04-01 21:12:47
3!*3!*3!*2! ways to have all A, B, and C delegates together.

sparkle123 2011-04-01 21:12:48
3!3!3!2!

DPatrick 2011-04-01 21:12:53
We form a superperson for each country in 3! ways each, and then seat the 3 superpeople in 3!/3 = 2! ways around the table. So there are 3!*3!*3!*2! seatings.

DPatrick 2011-04-01 21:13:06

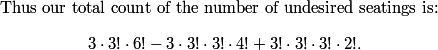
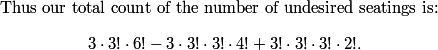
DPatrick 2011-04-01 21:13:25
This quantity is
3(6)(720) - 3(6)(6)(24) + (6)(6)(6)(2) = 12960 - 2592 + 432 = 10800.

number.sense 2011-04-01 21:13:39
over our original 8!

DPatrick 2011-04-01 21:13:41
So the probability of an undesired seating is 10800/40320 = 15/56.

DPatrick 2011-04-01 21:14:00
And we want to avoid a common mistake in complementary counting....forgetting that this is the complement of what we watn!

kangchangood 2011-04-01 21:14:12
1- undesired

carmelninja 2011-04-01 21:14:12
subtract from 1

number.sense 2011-04-01 21:14:12
subtract from 1, complementary counting! don't forget this is what we don't want

sparkle123 2011-04-01 21:14:12
41/56 is our answer

nsun48 2011-04-01 21:14:12
so desired is 41/56, 41+56=97!!!

freddylukai 2011-04-01 21:14:12
then the answer is 41/56

han2 2011-04-01 21:14:12
so we have 41 + 56 be the answer

jeff10 2011-04-01 21:14:12
41/56 is the desired

.cpp 2011-04-01 21:14:12
So we have m/n = 41/56, so m+n = 097.

DPatrick 2011-04-01 21:14:16
Thus the probability of a desired seating is 1 - 15/56 = 41/56, and the answer is 41+56 = 097.

DPatrick 2011-04-01 21:14:58
I think for many people this may have been the hardest problem on the contest.

DPatrick 2011-04-01 21:15:16

.cpp 2011-04-01 21:15:31
Diagram!

professordad 2011-04-01 21:15:31
draw a diagram

sindennisz 2011-04-01 21:15:31
picture

DPatrick 2011-04-01 21:15:40
We start off with a diagram. Of course, we start with P, the square, diagonal AC, and the circumcenters of ABP and CDP. Those circumcenters will be just floating out in space. What else should we include?

GoldenFrog1618 2011-04-01 21:16:04
the radii

han2 2011-04-01 21:16:12
O1P and PO2

jeff10 2011-04-01 21:16:12
radii

DPatrick 2011-04-01 21:16:28
Circumcenters mean circumcircles and circles mean radii. We can go ahead and include these, too. Colors help keep the pic organized!

DPatrick 2011-04-01 21:16:32

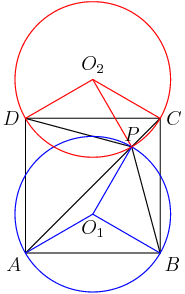
DPatrick 2011-04-01 21:16:51
Now what?

AlphaMath1 2011-04-01 21:17:32
P is equidistant from B and D

sparkle123 2011-04-01 21:17:32
by symmetry DP=PB

DPatrick 2011-04-01 21:17:43
Certainly PD = PB. That'll be useful.

GoldenFrog1618 2011-04-01 21:18:24
<O_2PD=45

ksun48 2011-04-01 21:18:24
DO2P is isoceles

DPatrick 2011-04-01 21:18:29
Aha...how come?

jeff10 2011-04-01 21:18:51
radii equals radii

.cpp 2011-04-01 21:18:52
Radii of circle are equal.

carmelninja 2011-04-01 21:18:52
two sides are radii

DPatrick 2011-04-01 21:19:04
Well, the isosceles part is pretty easy: DO_2 and PO_2 are each radii.

DPatrick 2011-04-01 21:19:14
Where did the 45 degree angle come from?

kangchangood 2011-04-01 21:19:55
DCP = 45

DPatrick 2011-04-01 21:20:15
Right.

.cpp 2011-04-01 21:20:22
Inscribe same arc of circle.

DPatrick 2011-04-01 21:20:47
Not quite...but close enough. Here's the pic again:

DPatrick 2011-04-01 21:20:51

DPatrick 2011-04-01 21:20:59
DCP is 45 degrees.

DPatrick 2011-04-01 21:21:21
Since it is an inscribed angle in the red circle and cuts off arc DP, we know that arc DP is 90 degrees.

DPatrick 2011-04-01 21:21:45

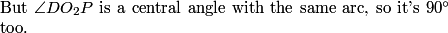
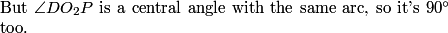
DPatrick 2011-04-01 21:22:02
So DO_2P is a 45-45-90 triangle.

jeff10 2011-04-01 21:22:06
isoceles right triangle found!

hurdler 2011-04-01 21:22:07
so its a 45-45 90 right triangle

DPatrick 2011-04-01 21:22:18
If there's a red one, there should be a blue one too by symmetry...

han2 2011-04-01 21:22:31
we could do the same with PO1B too...

hurdler 2011-04-01 21:22:31
PO_1B

sparkles257 2011-04-01 21:22:40
po1b

.cpp 2011-04-01 21:22:40
<PO_1B.

professordad 2011-04-01 21:22:40
BO1P

jeff10 2011-04-01 21:22:40
PO(1)B

DPatrick 2011-04-01 21:22:58
Right. PO1B is 45-45-90 too.

DPatrick 2011-04-01 21:23:01
How does that help?

supermathman 2011-04-01 21:23:31
dpb = 120;

professordad 2011-04-01 21:23:34
angle BPD is 120

DPatrick 2011-04-01 21:24:01

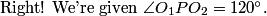
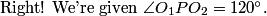
DPatrick 2011-04-01 21:24:24
If we remove the 45 degrees from DPO_2, and add the 45 degrees from BPO_1, we get angle DPB. So that's 120 degrees too!

DPatrick 2011-04-01 21:24:54
We're pretty much home free now. Drawing the other diagonal of the square helps us find AP quickly:

DPatrick 2011-04-01 21:24:58

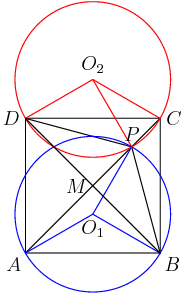
DPatrick 2011-04-01 21:25:16
We want AP.

DPatrick 2011-04-01 21:25:18
What's AM?

simplyMathLete 2011-04-01 21:25:41
6root2

ktbroborg 2011-04-01 21:25:41
6sqrt2

jeff10 2011-04-01 21:25:41
6sqrt2

.cpp 2011-04-01 21:25:41
6 sqrt(2).

kangchangood 2011-04-01 21:25:41
6 sqrt 2

DPatrick 2011-04-01 21:25:48
It's half the diagonal, so it's 6 * sqrt(2).

DPatrick 2011-04-01 21:25:50
What's MP?

hurdler 2011-04-01 21:26:15
MB/sqrt3

DPatrick 2011-04-01 21:26:39
Right: it's the shorter leg of a 30-60-90 triangle (PMB) with longer leg 3*sqrt(2).

DPatrick 2011-04-01 21:26:53
So not MB/sqrt(3) though, but 2*MB/sqrt(3).

hurdler 2011-04-01 21:27:05
=2sqrt6

.cpp 2011-04-01 21:27:05
2 sqrt6.

DPatrick 2011-04-01 21:27:10
Right.

DPatrick 2011-04-01 21:27:17

DPatrick 2011-04-01 21:27:25

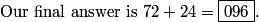
DPatrick 2011-04-01 21:28:09

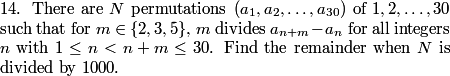
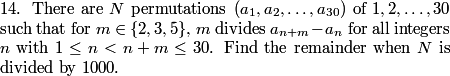
DPatrick 2011-04-01 21:28:41
This was one of those classic AIME problems where the notation makes the problem look hard, but if you can figure out what's going on, it's actually not that bad.

DPatrick 2011-04-01 21:28:48
What does that condition in the problem really mean?

number.sense 2011-04-01 21:29:20
2 divides differences of indeces sep by 2, same with 3 and 5

DPatrick 2011-04-01 21:29:32
Right, but can we write it using mods in an easy way?

.cpp 2011-04-01 21:30:07
a_(n+2) = a_n mod 2, similar for 3 and 5.

DPatrick 2011-04-01 21:30:17
Right. But it's even stronger than that.

number.sense 2011-04-01 21:30:31
all a_x such that x = i mod 2 are also congruent mod 2

DPatrick 2011-04-01 21:30:36

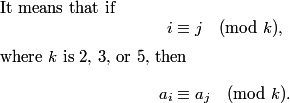
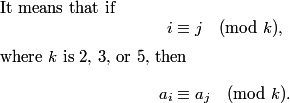
DPatrick 2011-04-01 21:31:08
So the mod of the index essentially determines the mod of the value, for each of the moduli 2, 3, and 5.

DPatrick 2011-04-01 21:31:53
For example, if we consider the condition k=2, what are the choices for the parities (the residues classes mod 2) of the a's?

number.sense 2011-04-01 21:32:31
all evens have even index and all odds have odd index/ all evens have odd index and all odds have even index

simplyMathLete 2011-04-01 21:32:31
even odd, alternating

.cpp 2011-04-01 21:32:43
a_odd = all even or all odd, vice versa for a_even.

jeff10 2011-04-01 21:32:43
parity alternation

DPatrick 2011-04-01 21:33:07
Right. We have the a_i with i odd can be odd or even, and the others are the opposite parity.

DPatrick 2011-04-01 21:33:56
That gives us 2 essential choices for the condition in mod 2.

DPatrick 2011-04-01 21:34:09
How about in mod 3? What's happening there?

policecap 2011-04-01 21:34:45
012012012012

GoldenFrog1618 2011-04-01 21:34:51
the mods we assign to a_1, a_2, a_3 fix all the others

number.sense 2011-04-01 21:34:56
every three, the residues repeat in pattern. the perm of the residues modulo 3 determines the scaffold for the rest of the seq

.cpp 2011-04-01 21:34:56
a_(1 mod 3) = mod3, a_(2mod 3) = mod 3, a_(0mod 3) = mod 3.

DPatrick 2011-04-01 21:35:00
All of a_1,a_4,...,a_28 are one choice of {0,1,2} mod 3
All of a_2,a_5,...,a_29 are another choice
All of a_3,a_6,...,a_30 are the remaining choice

DPatrick 2011-04-01 21:35:21
Right. There are 3! choices for how to assign the mods for k=3.

DPatrick 2011-04-01 21:35:38
And finally, what's happening mod 5?

number.sense 2011-04-01 21:35:53
and very similar for 5, perm of the 5 residues modulo 5 determines the pattern for the rest of the sequence

DPatrick 2011-04-01 21:36:10
By the same reasoning, there are 5! ways to assign the residues mod 5.

DPatrick 2011-04-01 21:36:29
Are these choices independent, and are they all possible?

DPatrick 2011-04-01 21:37:11
That is, if I pick a choice (out of 2!) of what the mod 2 residues should look like, a choice (out of 3!) of what the mod 3 residues should look like, and a choice (out of 5!) of what the mod 5 residues should look like, does it always work?

GoldenFrog1618 2011-04-01 21:37:22
each mod 2,3,5 combination makes a unique sequence by the Chinese remainder theorem

number.sense 2011-04-01 21:37:23
they are all possible since 30 is the lcm(2,3,5)

.cpp 2011-04-01 21:37:30
Well, 2*3*5 = 30, which might help here.

DPatrick 2011-04-01 21:37:41
Yes. Because 2, 3, and 5 are all relatively prime to each other, any two numbers between 1 and 30 will differ in at least one of the moduli 2, 3, and 5 (if they were equal mod 2 and mod 3 and mod 5, they'd be equal mod 2*3*5 = 30). And by the Chinese Remainder Theorem, given any choice of residue classes in mods 2, 3, and 5, there's exactly one number between 1 and 30 in all of the residue classes.

DPatrick 2011-04-01 21:38:08
So to get a valid sequence, we just have to pick how we want the residues arranges for each of mod 2, 3, and 5.

DPatrick 2011-04-01 21:38:27
So the number of permutations that we can have is 2 * 3! * 5! = 1440. The answer is 440.

DPatrick 2011-04-01 21:38:59

DPatrick 2011-04-01 21:39:17
I've italicized a portion of the problem statement because it turns out that the answer cannot satisfy that condition. More about that later.

DPatrick 2011-04-01 21:39:34

DPatrick 2011-04-01 21:39:53
What do we know about the equation in the problem?

nsun48 2011-04-01 21:40:13
floor of sqrt{P(x)} must be integer

Johan Gunardi 2011-04-01 21:40:21
LHS is integer

GoldenFrog1618 2011-04-01 21:40:23
sqrt(P([x])) must be an integer

DPatrick 2011-04-01 21:40:26
The left side is by definition an integer.

DPatrick 2011-04-01 21:40:31
So the right side must be an integer too.

number.sense 2011-04-01 21:40:48
so first we must det when exactly is the rhs an int

simplyMathLete 2011-04-01 21:40:49
which means P(floor(x)) is a square

DPatrick 2011-04-01 21:40:53

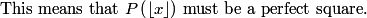
DPatrick 2011-04-01 21:41:02
What are the possibilities?

number.sense 2011-04-01 21:41:38
upper and lower bounds of the interval's value on the polynomial

DPatrick 2011-04-01 21:41:59
Right. We know that P(x) has Its minimum at x=3/2 (at the vertex of the graph of the parabola), so it is an increasing function between x=5 and x=15.

DPatrick 2011-04-01 21:42:15
We can compute P(5) = 1 and P(15) = 171.
So the possibilities for P([x]) being a perfect square lie between 1^2 = 1 and 13^2 = 169.

carmelninja 2011-04-01 21:42:31
find the integer values of x such that P(x) is a perfect square

DPatrick 2011-04-01 21:42:50
But [x] is an integer, of course.
So we need to find all the integers (between 5 and 15) that we can plug into P and get a perfect square.

number.sense 2011-04-01 21:42:53
plug in and solve

han2 2011-04-01 21:42:54
i used brute force

DPatrick 2011-04-01 21:42:57
Me too. :)

DPatrick 2011-04-01 21:43:01
There are only 11 integers to check, and it's pretty easy to run through the list.

DPatrick 2011-04-01 21:43:09

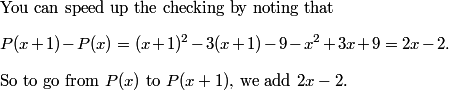
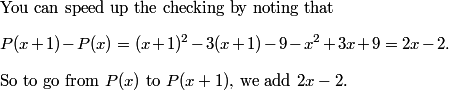
DPatrick 2011-04-01 21:43:20
P(5) = 25 - 15 - 9 = 1.  Yay this is 1^2.
P(6) = 1 + 8 = 9.  Yay this is 3^2.
P(7) = 9 + 10 = 19.  Nope.
P(8) = 19 + 12 = 31.  Nope.
P(9) = 31 + 14 = 45.  Nope.
P(10) = 45 + 16 = 61.  Nope.
P(11) = 61 + 18 = 79.  Nope.
P(12) = 79 + 20 = 99.  Nope.
P(13) = 99 + 22 = 121.  Yay this is 11^2.
P(14) = 121 + 24 = 145.  Nope.
P(15) = 145 + 26 = 171.  Nope.  (And as a check this matches the P(15) we got before.)

DPatrick 2011-04-01 21:43:42

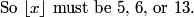
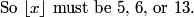
DPatrick 2011-04-01 21:43:51
Now what?

Johan Gunardi 2011-04-01 21:44:08
divide cases

number.sense 2011-04-01 21:44:13
test the intervals determined by this into the equation we wan

policecap 2011-04-01 21:44:17
we find what the corresponding vaues are

DPatrick 2011-04-01 21:44:32
Right. Now we check them separately to see what values of x work for each value of [x].

DPatrick 2011-04-01 21:44:42
Let's look at [x] = 5 first.

DPatrick 2011-04-01 21:44:50

GoldenFrog1618 2011-04-01 21:45:19
4>P(x)>=1

carmelninja 2011-04-01 21:45:19
find what value of x yields P(x) = 4

han2 2011-04-01 21:45:19
which makes P(x) between 1 and 4.

number.sense 2011-04-01 21:45:19
P(x) between 1 and 4

DPatrick 2011-04-01 21:45:24

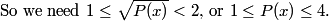
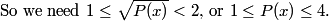
DPatrick 2011-04-01 21:45:41
(Actually, it's <4 at the end, but it doesn't matter)

DPatrick 2011-04-01 21:46:05

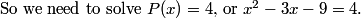
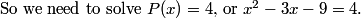
carmelninja 2011-04-01 21:46:23
quadratic formula

.cpp 2011-04-01 21:46:23
Use Quadratic theorem.

DPatrick 2011-04-01 21:46:25

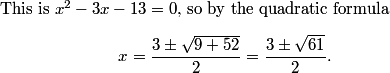
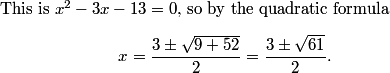
DPatrick 2011-04-01 21:46:35
Which root?

jeff10 2011-04-01 21:46:46
positive

number.sense 2011-04-01 21:46:46
the plus sign

AlphaMath1 2011-04-01 21:46:46
we dont care about the - because then x wouldn't be in the range

han2 2011-04-01 21:46:46
so positive one

DPatrick 2011-04-01 21:46:57
We need 5 <= x < 6, so it's got to be the positive one.

DPatrick 2011-04-01 21:47:05

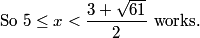
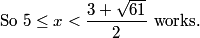
DPatrick 2011-04-01 21:47:27

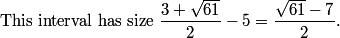
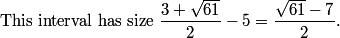
AlphaMath1 2011-04-01 21:47:40
We can do this similarly for 6 and 13

GoldenFrog1618 2011-04-01 21:47:41
do this again for 6 and 13

han2 2011-04-01 21:47:41
now for [6,7) case

DPatrick 2011-04-01 21:47:44
Next, let's go to [x] = 6.

DPatrick 2011-04-01 21:47:57
(Solving the problem is mostly careful bookkeeping from here on out...)

DPatrick 2011-04-01 21:48:09

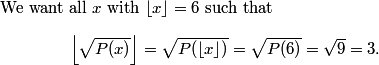
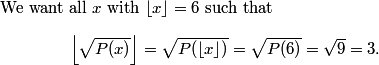
GoldenFrog1618 2011-04-01 21:48:28
16>P(x)>=9

policecap 2011-04-01 21:48:28
P(x)<16

DPatrick 2011-04-01 21:48:32

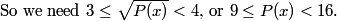
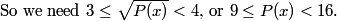
number.sense 2011-04-01 21:48:46
solve P(x) = 16

han2 2011-04-01 21:48:50
another quadratic formula plugging

DPatrick 2011-04-01 21:48:54

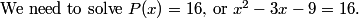
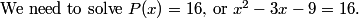
DPatrick 2011-04-01 21:49:01

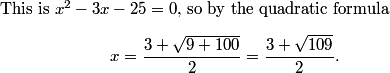
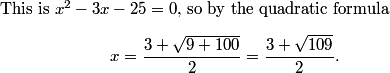
DPatrick 2011-04-01 21:49:16

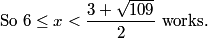
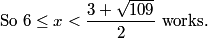
DPatrick 2011-04-01 21:49:29

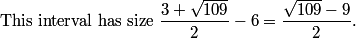
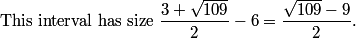
policecap 2011-04-01 21:49:37
one more case!

DPatrick 2011-04-01 21:49:41
Finally, let's go to [x] = 13.

DPatrick 2011-04-01 21:49:51

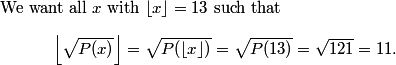
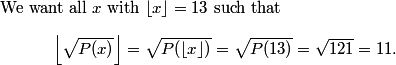
dlennon 2011-04-01 21:50:01
P(x)<144

DPatrick 2011-04-01 21:50:05

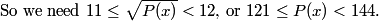
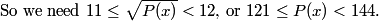
number.sense 2011-04-01 21:50:14
Solve P(x) = 144

.cpp 2011-04-01 21:50:15
For [13, 14), solve x^2 - 3x -153 =0.

DPatrick 2011-04-01 21:50:22

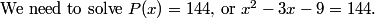
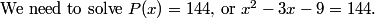
DPatrick 2011-04-01 21:50:30

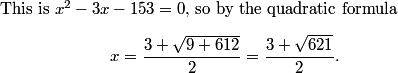
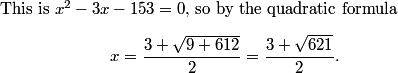
DPatrick 2011-04-01 21:50:46

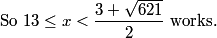
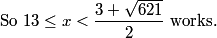
jeff10 2011-04-01 21:50:58
[(sqrt621)-23]/2

DPatrick 2011-04-01 21:50:59

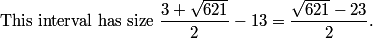
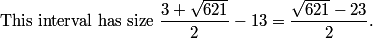
DPatrick 2011-04-01 21:51:22
So we've got the lengths of all the intervals for which it will work.

AlphaMath1 2011-04-01 21:51:30
Add all of them up and divide!

han2 2011-04-01 21:51:30
add them all and divide by 10

DPatrick 2011-04-01 21:51:42
We add up the lengths of the three intervals that we found to work, and divide by the total length of the "possible" x interval, which is 15-5 = 10.

DPatrick 2011-04-01 21:51:56

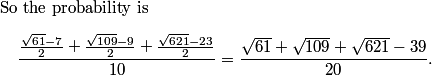
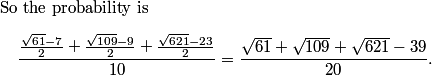
carmelninja 2011-04-01 21:52:17
850

DPatrick 2011-04-01 21:52:22
This matches the form of the answer that was asked for, so our answer is 61+109+621+39+20 = 850.

DPatrick 2011-04-01 21:52:37
Except...

GoldenFrog1618 2011-04-01 21:52:44
621= 9*69

.cpp 2011-04-01 21:52:44
621 has a factor of 9.

mathswimmer 2011-04-01 21:52:44
but 621 divides 9

DPatrick 2011-04-01 21:52:59
...621 does not satisfy the italicized condition above that it is not divisible by the square of a prime, since 9 divides 621.

DPatrick 2011-04-01 21:53:17
There is no way to make our answer fit the format that was asked for. So technically the problem asks for the impossible.

number.sense 2011-04-01 21:53:20
uh oh

nsun48 2011-04-01 21:53:22
typo..... AMC FAILED

DPatrick 2011-04-01 21:53:28
The AMC has published "850" as their official answer for #15, and yes, they are aware that the question has this error.

.cpp 2011-04-01 21:53:36
There was an errata, right?

DPatrick 2011-04-01 21:53:49
There was not. I have personally confirmed with the AMC that no errata was issued.

DPatrick 2011-04-01 21:54:05
I do not know what they are planning to do about it (if anything) with regard to the scoring.

jeff10 2011-04-01 21:55:37
are there going to be any math jams on USA(J)MO?

DPatrick 2011-04-01 21:56:11
No, we are not planning, in large part because they take too much time to prepare. But there will be a lively discussion on the forums, I'm sure!

binmu 2011-04-01 21:56:41
what do you need to get into the USA(J)MO?

DPatrick 2011-04-01 21:56:54
I do not know.

DPatrick 2011-04-01 21:57:06
The AMC is scheduled to announce the USA(J)MO qualifiers on April 8 (1 week from today).

2011 AIME II Math Jam

Facilitator: Dave Patrick