2013 AMC 10/12 A Discussion
Go back to the Math Jam ArchiveA discussion of problems from the AMC 10/12 A, which is administered February 6. We will cover the last 5 problems on each test, as well as requested earlier problems on the tests.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Dave Patrick
DPatrick
2013-02-06 19:30:12
Welcome to the 2013 AMC 10A/12A Math Jam!
Welcome to the 2013 AMC 10A/12A Math Jam!
DPatrick
2013-02-06 19:30:19
I'm Dave Patrick, and I'll be leading our discussion tonight.
I'm Dave Patrick, and I'll be leading our discussion tonight.
DPatrick
2013-02-06 19:30:27
Before we get started I would like to take a moment to explain our virtual classroom procedures to those who have not previously participated in a Math Jam or one of our online classes.
Before we get started I would like to take a moment to explain our virtual classroom procedures to those who have not previously participated in a Math Jam or one of our online classes.
DPatrick
2013-02-06 19:30:39
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
DPatrick
2013-02-06 19:30:52
This helps keep the session organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
This helps keep the session organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
DPatrick
2013-02-06 19:31:05
There are a lot of students here! As I said, only (a fraction of the) well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
There are a lot of students here! As I said, only (a fraction of the) well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
DPatrick
2013-02-06 19:31:17
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
DPatrick
2013-02-06 19:31:38
We do have two assistants tonight who can help answer some of your questions: baozhale and cppB.
We do have two assistants tonight who can help answer some of your questions: baozhale and cppB.
baozhale
2013-02-06 19:31:43
Hi!
Hi!
DPatrick
2013-02-06 19:31:49
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
DPatrick
2013-02-06 19:32:06
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.
DPatrick
2013-02-06 19:32:32
Also, there will be several cases where we actually find the answer or almost the answer but then wander off. The goal is always to find a proof that our answer is correct and not just find the answers. Of course on the AMC you should aim to do much less work than this.
Also, there will be several cases where we actually find the answer or almost the answer but then wander off. The goal is always to find a proof that our answer is correct and not just find the answers. Of course on the AMC you should aim to do much less work than this.
DPatrick
2013-02-06 19:32:54
We will work the last 5 problems from the AMC 10A, then the last 5 problems from the AMC 12A. (Three of the 10A problems, Problems 21-23, that we'll be working on also appeared as 17-19 on the 12A.) After that, time permitting, I may take requests for some other problems for discussion.
We will work the last 5 problems from the AMC 10A, then the last 5 problems from the AMC 12A. (Three of the 10A problems, Problems 21-23, that we'll be working on also appeared as 17-19 on the 12A.) After that, time permitting, I may take requests for some other problems for discussion.
DPatrick
2013-02-06 19:33:18
Let's kick things off with #21 from the 10A, which was also #17 on the 12A.
Let's kick things off with #21 from the 10A, which was also #17 on the 12A.
DPatrick
2013-02-06 19:33:22


DPatrick
2013-02-06 19:33:34
(The current problem under discussion will always be at the top of the screen.)
(The current problem under discussion will always be at the top of the screen.)
DPatrick
2013-02-06 19:33:46
Where can we begin?
Where can we begin?
Lord.of.AMC
2013-02-06 19:34:07
let the total number of coins be x
let the total number of coins be x
chuckmasters
2013-02-06 19:34:07
Work backwards
Work backwards
mathway
2013-02-06 19:34:07
assigning variables
assigning variables
math-rules
2013-02-06 19:34:07
Work backwards
Work backwards
DPatrick
2013-02-06 19:34:21
Sounds like a plan. Let's call the answer that we're looking for x.
Sounds like a plan. Let's call the answer that we're looking for x.
DPatrick
2013-02-06 19:34:31
Since x is what we want, it makes sense to start at x and work backwards.
Since x is what we want, it makes sense to start at x and work backwards.
DPatrick
2013-02-06 19:34:41
So there are x coins before the 12th pirate goes.
So there are x coins before the 12th pirate goes.
DPatrick
2013-02-06 19:34:47
How many coins before the 11th pirate takes his share?
How many coins before the 11th pirate takes his share?
willwin
2013-02-06 19:35:31
12x
12x
j2002
2013-02-06 19:35:31
12x
12x
mathwrath
2013-02-06 19:35:31
12x
12x
Funnymushman
2013-02-06 19:35:31
12x
12x
Tuxianeer
2013-02-06 19:35:31
12x
12x
mathwizard888
2013-02-06 19:35:31
12x
12x
DPatrick
2013-02-06 19:35:42
Right. He takes 11/12 of whatever was there.
Right. He takes 11/12 of whatever was there.
DPatrick
2013-02-06 19:35:50
So he leaves 1/12 of the stack for the last pirate...
So he leaves 1/12 of the stack for the last pirate...
DPatrick
2013-02-06 19:35:54
...but we also know that he leaves x for the last pirate.
...but we also know that he leaves x for the last pirate.
DPatrick
2013-02-06 19:36:02
So 1/12 of the stash before the 11th pirate chooses is x.
So 1/12 of the stash before the 11th pirate chooses is x.
DPatrick
2013-02-06 19:36:11
Therefore, the stash before the 11th pirate chooses is 12x.
Therefore, the stash before the 11th pirate chooses is 12x.
DPatrick
2013-02-06 19:36:19
No problem so far: if x is a positive integer, than so is 12x.
No problem so far: if x is a positive integer, than so is 12x.
DPatrick
2013-02-06 19:36:23
How many coins were there before the 10th pirate chose?
How many coins were there before the 10th pirate chose?
brian22
2013-02-06 19:36:50
72x for #10
72x for #10
kli2000
2013-02-06 19:36:50
The stash before the 10th pirate is 72x.
The stash before the 10th pirate is 72x.
flyrain
2013-02-06 19:36:50
72x?
72x?
foppotee
2013-02-06 19:36:50
72x
72x
DPatrick
2013-02-06 19:36:58
The 10th pirate takes 10/12 of the stack and leaves 2/12.
The 10th pirate takes 10/12 of the stack and leaves 2/12.
DPatrick
2013-02-06 19:37:02
So 2/12 of the stash is 12x.
So 2/12 of the stash is 12x.
DPatrick
2013-02-06 19:37:07
Thus the stash before the 10th pirate's turn is (12/2)*12x = 72x.
Thus the stash before the 10th pirate's turn is (12/2)*12x = 72x.
DPatrick
2013-02-06 19:37:14
Still good!
Still good!
DPatrick
2013-02-06 19:37:17
How does this generalize? That is, I don't want to do all 12 steps by hand.
How does this generalize? That is, I don't want to do all 12 steps by hand.
theone142857
2013-02-06 19:38:11
Multiply 12/k each time
Multiply 12/k each time
matticus42
2013-02-06 19:38:11
12/1*12/2*12/3*...*12/12
12/1*12/2*12/3*...*12/12
cerberus88
2013-02-06 19:38:11
each time, we multiply by (12/(12-k))
each time, we multiply by (12/(12-k))
StefRen
2013-02-06 19:38:16
x*(12/1)(12/2)(12/3)...etc
x*(12/1)(12/2)(12/3)...etc
DuoCapital
2013-02-06 19:38:16
x*(12/1)*(12/2)*(12/3)...
x*(12/1)*(12/2)*(12/3)...
DPatrick
2013-02-06 19:38:21
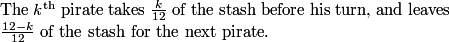
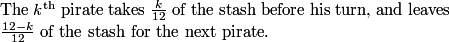
DPatrick
2013-02-06 19:38:36
Thus, to go backwards from after the kth pirate's turn to before his turn, we multiply by 12/(12-k).
Thus, to go backwards from after the kth pirate's turn to before his turn, we multiply by 12/(12-k).
DPatrick
2013-02-06 19:38:56
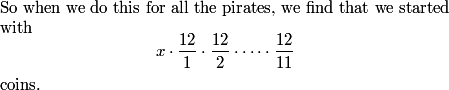
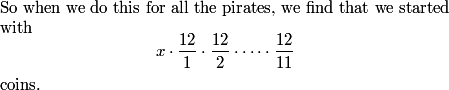
6stars
2013-02-06 19:39:16
The denominator is 11!
The denominator is 11!
DPatrick
2013-02-06 19:39:23
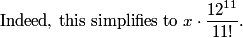
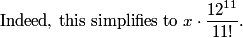
DPatrick
2013-02-06 19:39:39
How can this be ensured to be an integer at every step along the way?
How can this be ensured to be an integer at every step along the way?
thkim1011
2013-02-06 19:40:18
11, 7, 5 won't simplify.
11, 7, 5 won't simplify.
PertBanking
2013-02-06 19:40:18
So we just have to worry about the denominators that cant factor into 2^x * 3^x
So we just have to worry about the denominators that cant factor into 2^x * 3^x
sindennisz
2013-02-06 19:40:18
x needs to have a factor of 5,7,11.
x needs to have a factor of 5,7,11.
Samuel D
2013-02-06 19:40:18
X has to have 5^2, 7, 11
X has to have 5^2, 7, 11
DPatrick
2013-02-06 19:40:38
Right. Most of the 11! will cancel with all the 2's and 3's in 12^11.
Right. Most of the 11! will cancel with all the 2's and 3's in 12^11.
DPatrick
2013-02-06 19:40:56
But two 5's (one from 5 and one from 10), a 7, and an 11 won't cancel with the 12s, so these have to cancel with something in x.
But two 5's (one from 5 and one from 10), a 7, and an 11 won't cancel with the 12s, so these have to cancel with something in x.
ninjashiloh
2013-02-06 19:41:16
5^2*7*11=1925, so the answer is (D)
5^2*7*11=1925, so the answer is (D)
mathwrath
2013-02-06 19:41:16
x=1925
x=1925
jasontang
2013-02-06 19:41:16
5*5*7*11=1925
5*5*7*11=1925
dlennon
2013-02-06 19:41:16
x turns out to be 5^2*7*11=1925
x turns out to be 5^2*7*11=1925
DPatrick
2013-02-06 19:41:28
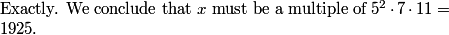
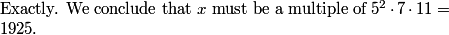
DPatrick
2013-02-06 19:41:31
And in fact x = 1925 works: for the first few steps we'll be multiplying by integers, and the factors of 1915 will allow us to cancel denominators when we multiply by 12/5, 12/7, 12/10, and 12/11. (There will be plenty of extra factors of 2's and 3's to cancel what's needed in 12/8 and 12/9 too.)
And in fact x = 1925 works: for the first few steps we'll be multiplying by integers, and the factors of 1915 will allow us to cancel denominators when we multiply by 12/5, 12/7, 12/10, and 12/11. (There will be plenty of extra factors of 2's and 3's to cancel what's needed in 12/8 and 12/9 too.)
DPatrick
2013-02-06 19:41:48
(oops: that should be 1925 above and not 1915)
(oops: that should be 1925 above and not 1915)
DPatrick
2013-02-06 19:41:59
So the answer is (D) 1925.
So the answer is (D) 1925.
DPatrick
2013-02-06 19:42:24
OK, let's move on to #22 on the 10A, which was also #18 on the 12A:
OK, let's move on to #22 on the 10A, which was also #18 on the 12A:
DPatrick
2013-02-06 19:42:30


DPatrick
2013-02-06 19:42:41
Yikes, 3-D!
Yikes, 3-D!
qwertyu
2013-02-06 19:42:56
Draw a cross-section
Draw a cross-section
Lord.of.AMC
2013-02-06 19:42:56
turn it into 2D
turn it into 2D
zhuangzhuang
2013-02-06 19:42:56
cross secrtions?
cross secrtions?
djmathman
2013-02-06 19:42:56
Cross-sections are nice.
Cross-sections are nice.
chuckmasters
2013-02-06 19:42:56
"Convert" it to 2-D
"Convert" it to 2-D
DPatrick
2013-02-06 19:43:00
The truth is, like many 3-D problems, it's really just a 2-D problem is disguise. Let's see.
The truth is, like many 3-D problems, it's really just a 2-D problem is disguise. Let's see.
DPatrick
2013-02-06 19:43:13
It probably makes sense to first figure out the radius of the big sphere. How do we do that?
It probably makes sense to first figure out the radius of the big sphere. How do we do that?
tluo5458
2013-02-06 19:43:40
shouldn't the spheres act like circles?
shouldn't the spheres act like circles?
Duncanyang
2013-02-06 19:43:40
circles centered at the vertices of a hexagon
circles centered at the vertices of a hexagon
minimario
2013-02-06 19:43:40
Draw a hexagon
Draw a hexagon
zhuj1198
2013-02-06 19:43:40
Draw the hexagon with circles on the vertices
Draw the hexagon with circles on the vertices
ic1999
2013-02-06 19:43:40
cross sections of 6 small spheres, draw the hexagon
cross sections of 6 small spheres, draw the hexagon
DPatrick
2013-02-06 19:43:43
We can take a cross-section that contains the hexagon.
We can take a cross-section that contains the hexagon.
DPatrick
2013-02-06 19:43:48
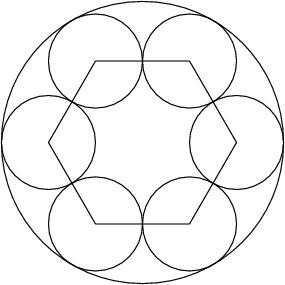

DPatrick
2013-02-06 19:43:58
The small circles are equatorial cross-sections of the small spheres, and each have radius 1. So what is the radius of the big sphere?
The small circles are equatorial cross-sections of the small spheres, and each have radius 1. So what is the radius of the big sphere?
anthonyjang
2013-02-06 19:44:25
the radius is 2+1
the radius is 2+1
mbt123
2013-02-06 19:44:25
radius of hexagon=2 + the radius of 1 sphere on a vertex=> radius of big sphere=3
radius of hexagon=2 + the radius of 1 sphere on a vertex=> radius of big sphere=3
Funnymushman
2013-02-06 19:44:25
3
3
bengals
2013-02-06 19:44:25
3
3
hawtsauze
2013-02-06 19:44:25
3
3
DPatrick
2013-02-06 19:44:29
The picture pretty much gives it to us for free: the big sphere has radius 3.
The picture pretty much gives it to us for free: the big sphere has radius 3.
DPatrick
2013-02-06 19:44:35
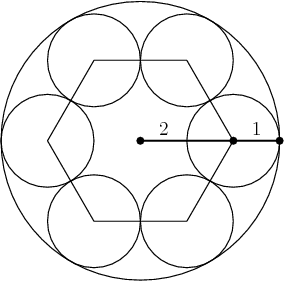

DPatrick
2013-02-06 19:44:46
Now what? How do we get a diagram with the eighth sphere in it?
Now what? How do we get a diagram with the eighth sphere in it?
calculatorwiz
2013-02-06 19:45:17
draw a vertical cross section
draw a vertical cross section
tan90
2013-02-06 19:45:17
vertical cross section
vertical cross section
sindennisz
2013-02-06 19:45:17
Take the cross-section perpendicular to it.
Take the cross-section perpendicular to it.
RedHydra
2013-02-06 19:45:17
take another cross section perpendicular to the current one
take another cross section perpendicular to the current one
jeff10
2013-02-06 19:45:17
how about a cross section from top to bottom instead of left to right?
how about a cross section from top to bottom instead of left to right?
supercomputer
2013-02-06 19:45:17
Take a vertical cross section (perpendicular to this)
Take a vertical cross section (perpendicular to this)
DPatrick
2013-02-06 19:45:22
We can take a vertical cross-section through the center of the hexagon and through two opposite small spheres:
We can take a vertical cross-section through the center of the hexagon and through two opposite small spheres:
DPatrick
2013-02-06 19:45:28


DPatrick
2013-02-06 19:45:47
The sphere we want has a cross-section centered at X in the above picture. Let's set r to be the radius that we're looking for: that is, the radius of the new sphere. What can we do with the above picture?
The sphere we want has a cross-section centered at X in the above picture. Let's set r to be the radius that we're looking for: that is, the radius of the new sphere. What can we do with the above picture?
jsk0301
2013-02-06 19:46:11
The centers make a triangle
The centers make a triangle
thkim1011
2013-02-06 19:46:11
Connect the centers
Connect the centers
SnapMaster
2013-02-06 19:46:11
I see a right triangle!
I see a right triangle!
kzhu98
2013-02-06 19:46:11
pythagorean theorem
pythagorean theorem
vinayak-kumar
2013-02-06 19:46:11
Draw a right triangle!
Draw a right triangle!
Chess4Everything
2013-02-06 19:46:11
We can connect the centers of the spheres.
We can connect the centers of the spheres.
DPatrick
2013-02-06 19:46:15
If we connect all the centers, we have a right triangle!
If we connect all the centers, we have a right triangle!
DPatrick
2013-02-06 19:46:20
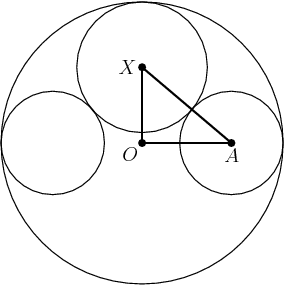

DPatrick
2013-02-06 19:46:34
What are the side lengths of this triangle? (Remember, r is the radius of the 8th sphere, centered at X.)
What are the side lengths of this triangle? (Remember, r is the radius of the 8th sphere, centered at X.)
ws5188
2013-02-06 19:47:10
OX=3-r, XA=r+1, OA=2
OX=3-r, XA=r+1, OA=2
SuperSnivy
2013-02-06 19:47:10
OX=3-r , OA=2 , AX=r+1
OX=3-r , OA=2 , AX=r+1
adelie
2013-02-06 19:47:10
OA is 2 as per the diagrams before, XO is 3-r by inspection
OA is 2 as per the diagrams before, XO is 3-r by inspection
PertBanking
2013-02-06 19:47:10
2, 1 + r, 3 - r
2, 1 + r, 3 - r
DPatrick
2013-02-06 19:47:17
OA is 2. (The radius of the big circle is 3 and the radius of the small circle is 1.)
OA is 2. (The radius of the big circle is 3 and the radius of the small circle is 1.)
DPatrick
2013-02-06 19:47:25
AX is 1+r (the sum of the radius of the circle at A and the radius of the circle at X).
AX is 1+r (the sum of the radius of the circle at A and the radius of the circle at X).
DPatrick
2013-02-06 19:47:32
OX is 3-r.
OX is 3-r.
DPatrick
2013-02-06 19:47:44
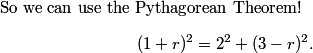
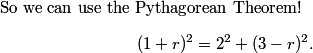
krmathcounts
2013-02-06 19:47:53
How do we know that the interior of circle X doesn't contain O?
How do we know that the interior of circle X doesn't contain O?
DPatrick
2013-02-06 19:48:09
That's a good observation...and in fact we're about to answer this.
That's a good observation...and in fact we're about to answer this.
mathwrath
2013-02-06 19:48:26
r=3/2
r=3/2
bharatputra
2013-02-06 19:48:26
r=3/2
r=3/2
mathwizard888
2013-02-06 19:48:26
r=3/2 (B)
r=3/2 (B)
Iwilllose
2013-02-06 19:48:30
r=3/2
r=3/2
DPatrick
2013-02-06 19:48:36
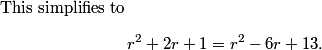
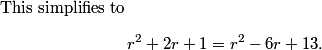
DPatrick
2013-02-06 19:48:46
This gives 8r = 12, so r = 3/2. Answer (B).
This gives 8r = 12, so r = 3/2. Answer (B).
mathwrath
2013-02-06 19:49:01
Circle X contains point O
Circle X contains point O
AdamGeller
2013-02-06 19:49:01
so O ends up being on circle X
so O ends up being on circle X
DPatrick
2013-02-06 19:49:07
Right: my picture was actually incorrect. We just determined that the diameter of the circle with center X is 3, so in fact that circle passes through O.
Right: my picture was actually incorrect. We just determined that the diameter of the circle with center X is 3, so in fact that circle passes through O.
math-rules
2013-02-06 19:49:17
How will we be able to draw such good drawings during the test?
How will we be able to draw such good drawings during the test?
DPatrick
2013-02-06 19:49:33
Bring a ruler, a compass, and a protractor. We'll see a problem later for which they're really valuable.
Bring a ruler, a compass, and a protractor. We'll see a problem later for which they're really valuable.
DPatrick
2013-02-06 19:49:47
Let's move on the 10A #23, which is also 12A #19:
Let's move on the 10A #23, which is also 12A #19:
DPatrick
2013-02-06 19:49:52
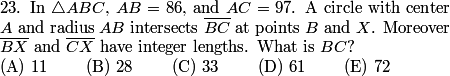
djmathman
2013-02-06 19:50:07
Draw a picture!
Draw a picture!
ic1999
2013-02-06 19:50:07
draw the diagram first
draw the diagram first
distortedwalrus
2013-02-06 19:50:07
diagram
diagram
cerberus88
2013-02-06 19:50:07
Diagram
Diagram
cr108x
2013-02-06 19:50:07
Draw Diagram
Draw Diagram
DPatrick
2013-02-06 19:50:11
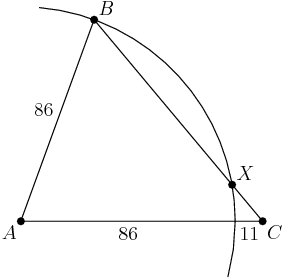
Let's sketch a picture of this.
Let's sketch a picture of this.
DPatrick
2013-02-06 19:50:16

DPatrick
2013-02-06 19:50:24
Note that I broke up AC into the 86 that's inside the circle, and the remaining 11 that's outside the circle.
Note that I broke up AC into the 86 that's inside the circle, and the remaining 11 that's outside the circle.
PranayMittal
2013-02-06 19:50:45
Power of the point!!!!
Power of the point!!!!
Doink
2013-02-06 19:50:45
Power of the point on C
Power of the point on C
qwertyu
2013-02-06 19:50:45
Power of a point
Power of a point
StefRen
2013-02-06 19:50:45
power of a point
power of a point
Smart Pi
2013-02-06 19:50:45
Power of a point!
Power of a point!
DPatrick
2013-02-06 19:50:50
Power of a point! We have lengths of lines that intersect a circle, so it's a good guess that power of a point will come in useful.
Power of a point! We have lengths of lines that intersect a circle, so it's a good guess that power of a point will come in useful.
DPatrick
2013-02-06 19:51:13
Point C looks like the best candidate. (Though there's no harm in trying other points too.)
Point C looks like the best candidate. (Though there's no harm in trying other points too.)
DPatrick
2013-02-06 19:51:17
What does using power of a point at point C tell us?
What does using power of a point at point C tell us?
djmathman
2013-02-06 19:51:55
CX * CB = 11* (11 + 86 + 86) = 11 * 183
CX * CB = 11* (11 + 86 + 86) = 11 * 183
ayqian22
2013-02-06 19:51:55
CX(CB)=11(183)
CX(CB)=11(183)
bengals
2013-02-06 19:51:55
BC*XC=11*183
BC*XC=11*183
DaChickenInc
2013-02-06 19:51:55
The power of point C is 11(11+2*86)=(XC)(BC)
The power of point C is 11(11+2*86)=(XC)(BC)
DPatrick
2013-02-06 19:52:12
Right. Power of a point says the product of the two distances from C to a circle, along any line, is constant.
Right. Power of a point says the product of the two distances from C to a circle, along any line, is constant.
DPatrick
2013-02-06 19:52:21
If we go along ray CB, we get (CX)(CB).
If we go along ray CB, we get (CX)(CB).
DPatrick
2013-02-06 19:52:29
If we go along ray CA, we get (11)(11+2*86).
If we go along ray CA, we get (11)(11+2*86).
DPatrick
2013-02-06 19:52:48
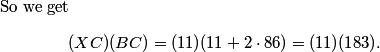
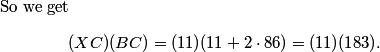
DPatrick
2013-02-06 19:52:57
But what else do we know?
But what else do we know?
Jzou
2013-02-06 19:53:29
we know that CX and CB are integers
we know that CX and CB are integers
Jzou
2013-02-06 19:53:29
XC and BC are integers
XC and BC are integers
adelie
2013-02-06 19:53:29
xc<bc
xc<bc
Iggy Iguana
2013-02-06 19:53:29
xc and bc are integers
xc and bc are integers
goldentail141
2013-02-06 19:53:29
XC and BX must be integers
XC and BX must be integers
ninjataco
2013-02-06 19:53:29
BX and CX are integers
BX and CX are integers
DPatrick
2013-02-06 19:53:31
We know that XC < BC are both positive integers.
We know that XC < BC are both positive integers.
DPatrick
2013-02-06 19:53:43
So just using this data, what are the possibilities for XC and BC?
So just using this data, what are the possibilities for XC and BC?
bobbyq
2013-02-06 19:54:12
33 and 61
33 and 61
SnapMaster
2013-02-06 19:54:12
33,61
33,61
guilt
2013-02-06 19:54:12
33, 61
33, 61
ninjashiloh
2013-02-06 19:54:12
33,61
33,61
infinity99
2013-02-06 19:54:12
So XC = 33, BC = 61
So XC = 33, BC = 61
DPatrick
2013-02-06 19:54:24
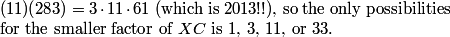
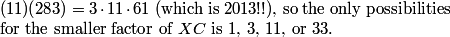
DPatrick
2013-02-06 19:54:43
(oops, that's (11)(183) = 2013.)
(oops, that's (11)(183) = 2013.)
DPatrick
2013-02-06 19:55:05
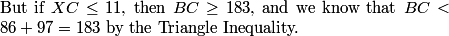
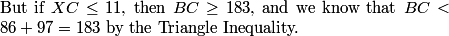
iguana123
2013-02-06 19:55:29
The answer is (D) 61
The answer is (D) 61
Smart Pi
2013-02-06 19:55:29
So BC = 61
So BC = 61
zhuj1198
2013-02-06 19:55:29
The answer is D
The answer is D
DPatrick
2013-02-06 19:55:31
Thus we must have XC = 33, leaving BC = 61. Answer (D).
Thus we must have XC = 33, leaving BC = 61. Answer (D).
tluo5458
2013-02-06 19:55:36
is the 2013 coincidental?
is the 2013 coincidental?
DPatrick
2013-02-06 19:55:47
I doubt it. They usually try to work in the current year in several problems.
They usually try to work in the current year in several problems.
I doubt it.
DPatrick
2013-02-06 19:56:05
OK, on to #24. (This one nor #25 was on the AMC 12A.)
OK, on to #24. (This one nor #25 was on the AMC 12A.)
DPatrick
2013-02-06 19:56:11


DPatrick
2013-02-06 19:56:32
The key to this problem -- indeed the key to many counting problems -- is staying organized.
The key to this problem -- indeed the key to many counting problems -- is staying organized.
DPatrick
2013-02-06 19:56:52
Let's start by naming one team A,B,C and the other team X,Y,Z.
Let's start by naming one team A,B,C and the other team X,Y,Z.
DPatrick
2013-02-06 19:57:08
What do we know?
What do we know?
kli2000
2013-02-06 19:57:34
6 rounds
6 rounds
apple.singer
2013-02-06 19:57:34
Person A plays XXYYZZ in some order
Person A plays XXYYZZ in some order
VietaFan
2013-02-06 19:57:34
A plays X, Y, and Z twice each
A plays X, Y, and Z twice each
tluo5458
2013-02-06 19:57:34
every person plays 6 games
every person plays 6 games
vinayak-kumar
2013-02-06 19:57:34
each player plays 2 games with each other
each player plays 2 games with each other
DPatrick
2013-02-06 19:57:39
In each round, each of {A,B,C} has to be paired with each of {X,Y,Z}.
In each round, each of {A,B,C} has to be paired with each of {X,Y,Z}.
DPatrick
2013-02-06 19:57:47
And each possible pairing (AX, AY, AZ, BX, BY, BZ, CX, CY, CZ) has to appear twice.
And each possible pairing (AX, AY, AZ, BX, BY, BZ, CX, CY, CZ) has to appear twice.
DPatrick
2013-02-06 19:58:04
How can we proceed?
How can we proceed?
Tuxianeer
2013-02-06 19:58:36
Consider the ways A's games can be scheduled, and then B's, and then you're done
Consider the ways A's games can be scheduled, and then B's, and then you're done
Nitzuga
2013-02-06 19:58:36
Start by placing the A's
Start by placing the A's
distortedwalrus
2013-02-06 19:58:36
look only at person A's games first
look only at person A's games first
pier17
2013-02-06 19:58:36
do A's matches first
do A's matches first
DPatrick
2013-02-06 19:58:41
I like to proceed via what I call "constructive counting": we imagine that we're the tournament organizer, and we're trying to construct a valid tournament. We keep track of our choices along the way.
I like to proceed via what I call "constructive counting": we imagine that we're the tournament organizer, and we're trying to construct a valid tournament. We keep track of our choices along the way.
DPatrick
2013-02-06 19:58:55
There are probably a lot of ways to do this for this problem. One way is to first focus on one particular player, let's say A.
There are probably a lot of ways to do this for this problem. One way is to first focus on one particular player, let's say A.
DPatrick
2013-02-06 19:59:03
In how many ways can we determine A's schedule?
In how many ways can we determine A's schedule?
apple.singer
2013-02-06 19:59:47
A has C(6,2)*C(4,2)*C(2,2) ways to have his/her matches
A has C(6,2)*C(4,2)*C(2,2) ways to have his/her matches
VietaFan
2013-02-06 19:59:47
$\frac{6!}{2^3}$, because there are 6 items with 3 doubled items. 90 ways
$\frac{6!}{2^3}$, because there are 6 items with 3 doubled items. 90 ways
jasontang
2013-02-06 19:59:47
6!/2*2*2
6!/2*2*2
math-rules
2013-02-06 19:59:47
6!/(2*2*2)=90
6!/(2*2*2)=90
jenniferwang
2013-02-06 19:59:47
There are 6!/2!2!2! ways.
There are 6!/2!2!2! ways.
mathwizard888
2013-02-06 19:59:47
6!/(2!2!2!)=90
6!/(2!2!2!)=90
centralbs
2013-02-06 19:59:47
6!/2!2!2!
6!/2!2!2!
DPatrick
2013-02-06 19:59:52
We need to arrange two AX's, two AY's, and two AZ's among the six rounds.
We need to arrange two AX's, two AY's, and two AZ's among the six rounds.
DPatrick
2013-02-06 20:00:00
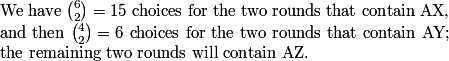
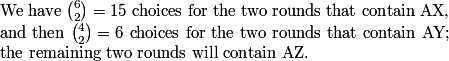
DPatrick
2013-02-06 20:00:07
So there are 15 * 6 = 90 ways to assign A's opponents in the six rounds.
So there are 15 * 6 = 90 ways to assign A's opponents in the six rounds.
DPatrick
2013-02-06 20:00:18
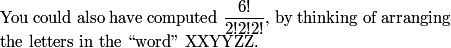
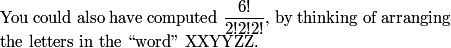
DPatrick
2013-02-06 20:00:25
Now what?
Now what?
Rocksolid
2013-02-06 20:01:02
We look at another player
We look at another player
fz0718
2013-02-06 20:01:02
continue the constuctive countoing!
continue the constuctive countoing!
Rocksolid
2013-02-06 20:01:02
We look at B or C
We look at B or C
pi_Plus_45x23
2013-02-06 20:01:02
do the same for b and c
do the same for b and c
googol.plex
2013-02-06 20:01:02
Assume he got XXYYZZ. This means B cannot have an X in first 2, no Y in second 2, and no Z in third 2
Assume he got XXYYZZ. This means B cannot have an X in first 2, no Y in second 2, and no Z in third 2
DPatrick
2013-02-06 20:01:06
To complete the construction, we have to determine how many ways there are to finish organizing the tournament: that is, in how many ways can the B's and C's be paired up.
To complete the construction, we have to determine how many ways there are to finish organizing the tournament: that is, in how many ways can the B's and C's be paired up.
DPatrick
2013-02-06 20:01:28
This count will be the same no matter how we arranged the A's, so for simplicity, let's suppose that A plays X in the first two rounds, then Y in the next two rounds, then Z in the last two rounds.
This count will be the same no matter how we arranged the A's, so for simplicity, let's suppose that A plays X in the first two rounds, then Y in the next two rounds, then Z in the last two rounds.
DPatrick
2013-02-06 20:01:40
So we have a diagram that looks something like this:
So we have a diagram that looks something like this:
DPatrick
2013-02-06 20:01:45


DPatrick
2013-02-06 20:01:51
How do we finish the pairing?
How do we finish the pairing?
3dot4teen
2013-02-06 20:02:31
Choose B's matches next
Choose B's matches next
bengals
2013-02-06 20:02:31
B pairs with Y,Z in first and second, C has no other choice
B pairs with Y,Z in first and second, C has no other choice
j2002
2013-02-06 20:02:31
Choose who B plays.
Choose who B plays.
jenniferwang
2013-02-06 20:02:41
But we need to keep in mind that one person cannot be paired up with two people at once.
But we need to keep in mind that one person cannot be paired up with two people at once.
DPatrick
2013-02-06 20:02:52
Let's just look at round 1 first. In the first round, it doesn't matter if we pair them BY,CZ or BZ,CY: the count of the remaining pairings will be the same either way.
Let's just look at round 1 first. In the first round, it doesn't matter if we pair them BY,CZ or BZ,CY: the count of the remaining pairings will be the same either way.
DPatrick
2013-02-06 20:03:04
So let's just assume that we have BY, CZ in the first round; we'll then double our count from here to get the total count.
So let's just assume that we have BY, CZ in the first round; we'll then double our count from here to get the total count.
DPatrick
2013-02-06 20:03:10

DPatrick
2013-02-06 20:03:22
What about round 2?
What about round 2?
Nitzuga
2013-02-06 20:03:41
There are still 2 ways!
There are still 2 ways!
sammyMaX
2013-02-06 20:03:41
BY CZ or BZ CY
BY CZ or BZ CY
Iwilllose
2013-02-06 20:03:41
We could have the same matches again.
We could have the same matches again.
supercomputer
2013-02-06 20:03:41
Same possiblities
Same possiblities
DPatrick
2013-02-06 20:03:47
It looks like we have two cases, depending on what we decide to do in round 2.
It looks like we have two cases, depending on what we decide to do in round 2.
DPatrick
2013-02-06 20:03:54
If we again pair BY, CZ in the second round, in how many ways can we finish?
If we again pair BY, CZ in the second round, in how many ways can we finish?
DPatrick
2013-02-06 20:03:59

bharatputra
2013-02-06 20:04:24
1.
1.
Lord.of.AMC
2013-02-06 20:04:24
1
1
krmathcounts
2013-02-06 20:04:24
ZZ,XX -- one way
ZZ,XX -- one way
ws5188
2013-02-06 20:04:24
1
1
footballfreak101
2013-02-06 20:04:24
1 way
1 way
DPatrick
2013-02-06 20:04:34
We're not allowed to have CZ in rounds 3 or 4, so those rounds have to be BZ and CX in both.
We're not allowed to have CZ in rounds 3 or 4, so those rounds have to be BZ and CX in both.
DPatrick
2013-02-06 20:04:39
That means we must have BX and CY in rounds 5 and 6.
That means we must have BX and CY in rounds 5 and 6.
DPatrick
2013-02-06 20:04:46
So in this case, there's only 1 way to finish.
So in this case, there's only 1 way to finish.
DPatrick
2013-02-06 20:04:58
And the other case: what if we switch and pair BZ, CY in the second round?
And the other case: what if we switch and pair BZ, CY in the second round?
DPatrick
2013-02-06 20:05:03

DPatrick
2013-02-06 20:05:06
Now in how many ways can we finish?
Now in how many ways can we finish?
Tuxianeer
2013-02-06 20:05:33
4
4
cherryclutch
2013-02-06 20:05:33
4
4
unknot
2013-02-06 20:05:33
4
4
zhuj1198
2013-02-06 20:05:33
4
4
vinayak-kumar
2013-02-06 20:05:33
4 ways
4 ways
mathwizard888
2013-02-06 20:05:33
2*2=4 ways (one Y and one Z)
2*2=4 ways (one Y and one Z)
DPatrick
2013-02-06 20:05:39
We need one more BY: that can be in either round 5 or round 6. So that's 2 choices.
We need one more BY: that can be in either round 5 or round 6. So that's 2 choices.
DPatrick
2013-02-06 20:05:47
And we need one more BZ: that can be in either round 3 or round 4. So that's also 2 choices.
And we need one more BZ: that can be in either round 3 or round 4. So that's also 2 choices.
DPatrick
2013-02-06 20:06:03
After that, the rest of the tournament is force.
After that, the rest of the tournament is force.
DPatrick
2013-02-06 20:06:05
...forced.
...forced.
DPatrick
2013-02-06 20:06:15
So there are 2*2 = 4 ways to finish in this case.
So there are 2*2 = 4 ways to finish in this case.
DPatrick
2013-02-06 20:06:24
How do we wrap all this up to get our final count?
How do we wrap all this up to get our final count?
fz0718
2013-02-06 20:06:45
4+1=5
4+1=5
countyguy
2013-02-06 20:06:45
90(2(1)+2(4))=E
90(2(1)+2(4))=E
Nitzuga
2013-02-06 20:06:45
So... $(4+1)2*90$?
So... $(4+1)2*90$?
googol.plex
2013-02-06 20:06:45
then you have to multiply by two because we assumed BY, CZ, so we have 5*2*90=900 E
then you have to multiply by two because we assumed BY, CZ, so we have 5*2*90=900 E
mathwizard888
2013-02-06 20:06:45
1+4=5, then 90*2*5=900 (E)
1+4=5, then 90*2*5=900 (E)
DPatrick
2013-02-06 20:06:58
Right, we just back up and carefully count our choices.
Right, we just back up and carefully count our choices.
DPatrick
2013-02-06 20:07:00
Once we paired BY and CZ in round 1, we had 1+4 = 5 ways to finish.
Once we paired BY and CZ in round 1, we had 1+4 = 5 ways to finish.
DPatrick
2013-02-06 20:07:22
But pairing BZ and CY in round 1 is identical and also gives 5 ways. So we have 10 ways to finish once we assign the A's.
But pairing BZ and CY in round 1 is identical and also gives 5 ways. So we have 10 ways to finish once we assign the A's.
DPatrick
2013-02-06 20:07:33
And recall that there were 90 ways to assign the A's, and once we did that there were 10 ways to finish.
And recall that there were 90 ways to assign the A's, and once we did that there were 10 ways to finish.
DPatrick
2013-02-06 20:07:39
So there are 90 * 10 = 900 possible tournaments. Answer (E).
So there are 90 * 10 = 900 possible tournaments. Answer (E).
nimblepanda
2013-02-06 20:07:56
is there an easier way to do it?
is there an easier way to do it?
DPatrick
2013-02-06 20:08:17
Possibly. I don't claim that my solutions are the easiest. But they're the most straightforward (to me, at least).
Possibly. I don't claim that my solutions are the easiest. But they're the most straightforward (to me, at least).
DPatrick
2013-02-06 20:08:25
And on to #25 on the 10A:
And on to #25 on the 10A:
DPatrick
2013-02-06 20:08:31


DPatrick
2013-02-06 20:08:43
This problem was quite guessable even if you didn't do all the work -- more about that as we go.
This problem was quite guessable even if you didn't do all the work -- more about that as we go.
brandbest1
2013-02-06 20:08:51
brute force drawing?
brute force drawing?
cerberus88
2013-02-06 20:08:51
Draw it and count
Draw it and count
ninjashiloh
2013-02-06 20:08:51
you could draw it if you had time
you could draw it if you had time
raptorw
2013-02-06 20:08:51
you can draw it
you can draw it
DPatrick
2013-02-06 20:09:03
You could try that. The answer choices would scare me off of that tactic, though.
You could try that. The answer choices would scare me off of that tactic, though.
forthegreatergood
2013-02-06 20:09:26
8C4 minus some stuff?
8C4 minus some stuff?
FlyingWombat
2013-02-06 20:09:26
It has to be less than 70
It has to be less than 70
zhuangzhuang
2013-02-06 20:09:26
you know <70...
you know <70...
kyuubinaruto
2013-02-06 20:09:26
can't you assume that the answer will be under 70
can't you assume that the answer will be under 70
DPatrick
2013-02-06 20:09:46
Indeed, if you know how to get "70" in this problem very quickly, it's easier to guess.
Indeed, if you know how to get "70" in this problem very quickly, it's easier to guess.
DPatrick
2013-02-06 20:10:04
But let's be a little more naive, and let's also try to prove our answer without guessing.
But let's be a little more naive, and let's also try to prove our answer without guessing.
DPatrick
2013-02-06 20:10:13
...and we'll see where the "70" comes from.
...and we'll see where the "70" comes from.
DPatrick
2013-02-06 20:10:28
My tactic is to first count all the pairs of diagonals that intersect, and then correct for when this overcounts intersection points.
My tactic is to first count all the pairs of diagonals that intersect, and then correct for when this overcounts intersection points.
DPatrick
2013-02-06 20:10:39
How do we count all the pairs of diagonals that intersect?
How do we count all the pairs of diagonals that intersect?
bluepin93
2013-02-06 20:11:01
considering the amount of intersections of one diagonal
considering the amount of intersections of one diagonal
3dot4teen
2013-02-06 20:11:01
By drawing just a little you can see how many times each line has an intersection point
By drawing just a little you can see how many times each line has an intersection point
DPatrick
2013-02-06 20:11:18
There's a slick way to count them, but let's do it the non-slick way first.
There's a slick way to count them, but let's do it the non-slick way first.
DPatrick
2013-02-06 20:11:33
The diagonals of an octagon come in three basic types.
The diagonals of an octagon come in three basic types.
DPatrick
2013-02-06 20:11:45
What I'll call "Type A: connects vertices that are 2 apart:
What I'll call "Type A: connects vertices that are 2 apart:
DPatrick
2013-02-06 20:11:50
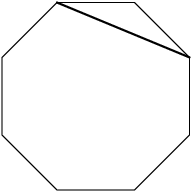

DPatrick
2013-02-06 20:11:56
How many of these are there?
How many of these are there?
calculatorwiz
2013-02-06 20:12:09
8
8
vincenthuang75025
2013-02-06 20:12:09
8
8
mathway
2013-02-06 20:12:09
8
8
bengals
2013-02-06 20:12:09
8
8
Seedleaf
2013-02-06 20:12:09
8
8
DuoCapital
2013-02-06 20:12:09
8
8
DPatrick
2013-02-06 20:12:23
There are 8 (one for each vertex that gets "cut off", like the upper-right vertex in the above pic).
There are 8 (one for each vertex that gets "cut off", like the upper-right vertex in the above pic).
DPatrick
2013-02-06 20:12:26
And how many other diagonals does each one of these intersect?
And how many other diagonals does each one of these intersect?
AopsKevin
2013-02-06 20:12:42
5
5
RotomPlasma
2013-02-06 20:12:42
5
5
kli2000
2013-02-06 20:12:42
5
5
ws5188
2013-02-06 20:12:42
5
5
Lalagato
2013-02-06 20:12:42
5
5
DPatrick
2013-02-06 20:12:46
They intersect any diagonal that runs from the "cut off" point to one of the other 5 points:
They intersect any diagonal that runs from the "cut off" point to one of the other 5 points:
DPatrick
2013-02-06 20:12:52
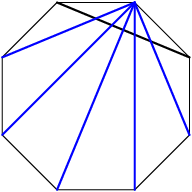

DPatrick
2013-02-06 20:13:03
So each of the 8 Type A diagonals intersects 5 other diagonals.
So each of the 8 Type A diagonals intersects 5 other diagonals.
DPatrick
2013-02-06 20:13:13
Next, "Type B" diagonals connect points that are 3 apart:
Next, "Type B" diagonals connect points that are 3 apart:
DPatrick
2013-02-06 20:13:18
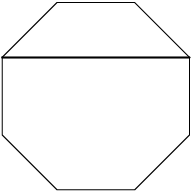

DPatrick
2013-02-06 20:13:20
How many of these are there?
How many of these are there?
mathwrath
2013-02-06 20:13:30
8
8
countyguy
2013-02-06 20:13:30
8 of them
8 of them
gundraja
2013-02-06 20:13:30
8
8
mathnerd101
2013-02-06 20:13:30
8
8
DaChickenInc
2013-02-06 20:13:30
8
8
DPatrick
2013-02-06 20:13:33
Again, there are 8 of them (one for each side of the octagon that gets "cut off").
Again, there are 8 of them (one for each side of the octagon that gets "cut off").
DPatrick
2013-02-06 20:13:40
And how many diagonals do each of these intersect?
And how many diagonals do each of these intersect?
coldsummer
2013-02-06 20:13:54
8
8
robinpark
2013-02-06 20:13:54
8
8
j610
2013-02-06 20:13:54
8
8
SuperSnivy
2013-02-06 20:13:54
8
8
hutyputy66
2013-02-06 20:13:54
8
8
Funnymushman
2013-02-06 20:13:54
8
8
DPatrick
2013-02-06 20:13:59
An intersecting diagonal must go from one of the 2 points on the "cut off" edge to one of the 4 point on the other side.
An intersecting diagonal must go from one of the 2 points on the "cut off" edge to one of the 4 point on the other side.
DPatrick
2013-02-06 20:14:05
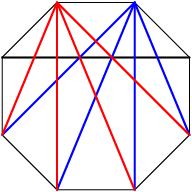

DPatrick
2013-02-06 20:14:10
So each type B diagonal intersects 8 other diagonals.
So each type B diagonal intersects 8 other diagonals.
DPatrick
2013-02-06 20:14:22
Don't worry, I'll make a chart of all our data once we've collected it.
Don't worry, I'll make a chart of all our data once we've collected it.
RotomPlasma
2013-02-06 20:14:30
But it's only 6 points!
But it's only 6 points!
DPatrick
2013-02-06 20:14:41
Indeed, we already see points where multiple diagonals intersect in the same point. Let's put that aside for now and worry about it later.
Indeed, we already see points where multiple diagonals intersect in the same point. Let's put that aside for now and worry about it later.
DPatrick
2013-02-06 20:14:49
Finally, type C diagonals connect opposite points:
Finally, type C diagonals connect opposite points:
DPatrick
2013-02-06 20:14:54
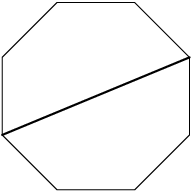

DPatrick
2013-02-06 20:14:57
How many of them are there?
How many of them are there?
unknot
2013-02-06 20:15:07
4
4
tuanyuan2008
2013-02-06 20:15:07
4
4
TigerSneak1
2013-02-06 20:15:07
4
4
oink
2013-02-06 20:15:07
4 of them
4 of them
minimario
2013-02-06 20:15:07
4
4
DPatrick
2013-02-06 20:15:12
Only 4: there's one for each pair of opposite points. (And notice 8+8+4 = 20, so in our three types we're accounted for all 20 diagonals.)
Only 4: there's one for each pair of opposite points. (And notice 8+8+4 = 20, so in our three types we're accounted for all 20 diagonals.)
DPatrick
2013-02-06 20:15:17
And how many other diagonals does each intersect?
And how many other diagonals does each intersect?
dragonkid
2013-02-06 20:15:30
9
9
RedHydra
2013-02-06 20:15:30
3*3 = 9
3*3 = 9
yangdongyan
2013-02-06 20:15:30
9
9
FlyingWombat
2013-02-06 20:15:30
9
9
fz0718
2013-02-06 20:15:30
9
9
ABCDE
2013-02-06 20:15:30
3*3=9
3*3=9
jeff10
2013-02-06 20:15:30
9
9
DPatrick
2013-02-06 20:15:35
An intersecting diagonal connects one of the 3 points on one side to one of the 3 points on the other side:
An intersecting diagonal connects one of the 3 points on one side to one of the 3 points on the other side:
DPatrick
2013-02-06 20:15:40
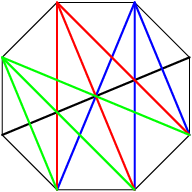

DPatrick
2013-02-06 20:15:45
So it intersects 3*3 = 9 other diagonals.
So it intersects 3*3 = 9 other diagonals.
DPatrick
2013-02-06 20:15:53
As promised, here's a summary of our data:
As promised, here's a summary of our data:
DPatrick
2013-02-06 20:16:43
Given this data, how many pairs of intersecting diagonals are there?
Given this data, how many pairs of intersecting diagonals are there?
DPatrick
2013-02-06 20:17:02
hang on...the table didn't post.
hang on...the table didn't post.
copeland
2013-02-06 20:17:18


Arghzoo
2013-02-06 20:18:19
40 + 64 + 36 = 140
40 + 64 + 36 = 140
RotomPlasma
2013-02-06 20:18:19
8*5+8*8+4*9=40+64+36=140
8*5+8*8+4*9=40+64+36=140
Nitzuga
2013-02-06 20:18:19
$8*8+8*5+4*9$? Maybe?
$8*8+8*5+4*9$? Maybe?
DPatrick
2013-02-06 20:18:25
The type As give us 8*5 = 40.
The type Bs give us 8*8 = 64.
The type Cs give us 4*9 = 36.
The type As give us 8*5 = 40.
The type Bs give us 8*8 = 64.
The type Cs give us 4*9 = 36.
DPatrick
2013-02-06 20:18:35
So we might think 40+64+36 = 140. But...
So we might think 40+64+36 = 140. But...
DuoCapital
2013-02-06 20:18:50
divide by 2
divide by 2
zhuangzhuang
2013-02-06 20:18:50
2 overcount
2 overcount
3dot4teen
2013-02-06 20:18:50
2 because they are pairs
2 because they are pairs
awesomeguy2
2013-02-06 20:18:50
divide by two
divide by two
IDMasterz
2013-02-06 20:18:50
overcounted divide by 2
overcounted divide by 2
DPatrick
2013-02-06 20:19:00
Right: 140 counts each pair twice: one time for when we consider each diagonal of the pair "first".
Right: 140 counts each pair twice: one time for when we consider each diagonal of the pair "first".
DPatrick
2013-02-06 20:19:05
So the number of intersecting pairs of diagonals is (40+64+36)/2 = 140/2 = 70.
So the number of intersecting pairs of diagonals is (40+64+36)/2 = 140/2 = 70.
DPatrick
2013-02-06 20:19:21
Now, a lot of you knew the slick way of finding the number of pairs of intersecting diagonals...
Now, a lot of you knew the slick way of finding the number of pairs of intersecting diagonals...
ravi1998
2013-02-06 20:19:39
or you could do 8 choose 4
or you could do 8 choose 4
djmathman
2013-02-06 20:19:39
For every four vertices of the octagon we choose, we can construct two chords whose endpoints are on each of the four vertices, creating a unique intersection point.
For every four vertices of the octagon we choose, we can construct two chords whose endpoints are on each of the four vertices, creating a unique intersection point.
supercomputer
2013-02-06 20:19:39
8C4
8C4
matholympiad25
2013-02-06 20:19:45
C(8,4). Every combination of 4 vertices makes an intersection point inside
C(8,4). Every combination of 4 vertices makes an intersection point inside
qwertyu
2013-02-06 20:19:45
8C4
8C4
teranz0
2013-02-06 20:19:45
Pick 4 points from 8, 8C4=70
Pick 4 points from 8, 8C4=70
DPatrick
2013-02-06 20:19:55
Right. We can get this number by computing C(8,4) = 70, since choosing any 4 vertices gives us a quadrilateral whose diagonals will intersect.
Right. We can get this number by computing C(8,4) = 70, since choosing any 4 vertices gives us a quadrilateral whose diagonals will intersect.
DPatrick
2013-02-06 20:20:27
You can think about this some more later.
You can think about this some more later.
DPatrick
2013-02-06 20:20:39
So is (C) 70 the answer?
So is (C) 70 the answer?
poweroftwo
2013-02-06 20:20:54
thats only pairs though
thats only pairs though
pranavsriram
2013-02-06 20:20:54
how about the ones where more then one diagonal intersected at the same point. Didn't we overcount those
how about the ones where more then one diagonal intersected at the same point. Didn't we overcount those
guilt
2013-02-06 20:20:54
no there were overlaps
no there were overlaps
Arghzoo
2013-02-06 20:20:54
nope there are concurrent pionts
nope there are concurrent pionts
rahulgupta1096
2013-02-06 20:20:54
no, we overcounted intersection points
no, we overcounted intersection points
DPatrick
2013-02-06 20:21:01
No. Many of these diagonals intersect at the same point. We don't want to count intersecting pairs of diagonals, we only want to count intersecting points.
No. Many of these diagonals intersect at the same point. We don't want to count intersecting pairs of diagonals, we only want to count intersecting points.
DPatrick
2013-02-06 20:21:07
For example, what about the center of the octagon?
For example, what about the center of the octagon?
DPatrick
2013-02-06 20:21:11
All four type C diagonals intersect in the center:
All four type C diagonals intersect in the center:
DPatrick
2013-02-06 20:21:15
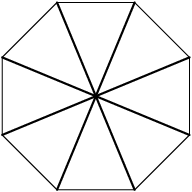

DPatrick
2013-02-06 20:21:21
How do we need to adjust our count of 70 to correct for the multiple diagonals intersecting in the center?
How do we need to adjust our count of 70 to correct for the multiple diagonals intersecting in the center?
unknot
2013-02-06 20:21:42
so subtract 4C2-1=5
so subtract 4C2-1=5
hamup1
2013-02-06 20:21:42
-5
-5
matholympiad25
2013-02-06 20:21:42
4 diagonals intersect in there. So it is counted 6 times. We need to subtract 5 from that count.
4 diagonals intersect in there. So it is counted 6 times. We need to subtract 5 from that count.
hamup1
2013-02-06 20:21:42
Subtract 5
Subtract 5
vinayak-kumar
2013-02-06 20:21:42
subtract 5?
subtract 5?
DPatrick
2013-02-06 20:21:51


DPatrick
2013-02-06 20:22:00
Therefore, we've counted this center point 6 times. But we only want to count it once.
Therefore, we've counted this center point 6 times. But we only want to count it once.
DPatrick
2013-02-06 20:22:07
So we have to subtract 5 from our previous count of 70, to correct for the fact that we've counted it 6 times and we only want to count it once.
So we have to subtract 5 from our previous count of 70, to correct for the fact that we've counted it 6 times and we only want to count it once.
DPatrick
2013-02-06 20:22:20
Now our count is 70 - 5 = 65.
Now our count is 70 - 5 = 65.
DPatrick
2013-02-06 20:22:24
Is (B) 65 the answer?
Is (B) 65 the answer?
mathwizard888
2013-02-06 20:22:41
brings it down to 65, but since there are more overcounts, it has to be 49 (A)
brings it down to 65, but since there are more overcounts, it has to be 49 (A)
sammyMaX
2013-02-06 20:22:41
And in our previous diagrams, we have encountered more overcount, so it is under 65 and therefore A
And in our previous diagrams, we have encountered more overcount, so it is under 65 and therefore A
coldsummer
2013-02-06 20:22:41
we know there are still more points to subtract so don't we know it's A right away?
we know there are still more points to subtract so don't we know it's A right away?
RedHydra
2013-02-06 20:22:41
No, there is still more overcounts
No, there is still more overcounts
Funnymushman
2013-02-06 20:22:41
no there's more
no there's more
fcc1234
2013-02-06 20:22:41
no there will be more overlaps
no there will be more overlaps
chessderek
2013-02-06 20:22:41
no, we still overcounted
no, we still overcounted
DPatrick
2013-02-06 20:22:45
No. There are other points at which more than 2 diagonals intersect. For example:
No. There are other points at which more than 2 diagonals intersect. For example:
DPatrick
2013-02-06 20:22:49
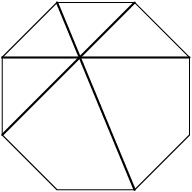

DPatrick
2013-02-06 20:23:14
(As you mentioned, at this point on the AMC contest, we now know the answer is less than 65, so we can go with (A) right away. But let's actually compute the answer.)
(As you mentioned, at this point on the AMC contest, we now know the answer is less than 65, so we can go with (A) right away. But let's actually compute the answer.)
mathnerd101
2013-02-06 20:23:28
there are 8 of those
there are 8 of those
cherryclutch
2013-02-06 20:23:33
subtract (8*2) = 16
subtract (8*2) = 16
DPatrick
2013-02-06 20:23:37
Right.
Right.
DPatrick
2013-02-06 20:23:44
There are 8 of these points. (The above picture can be rotated by any multiple of 45 degrees to get a new one.)
There are 8 of these points. (The above picture can be rotated by any multiple of 45 degrees to get a new one.)
DPatrick
2013-02-06 20:23:50
And each one is produced by 3 different pairs of diagonals. So each one is overcounted twice.
And each one is produced by 3 different pairs of diagonals. So each one is overcounted twice.
DPatrick
2013-02-06 20:23:59
Thus we must subtract another 2*8 = 16 from our count.
Thus we must subtract another 2*8 = 16 from our count.
ninjashiloh
2013-02-06 20:24:10
65-16=49 so the answer is (A)
65-16=49 so the answer is (A)
bluepie
2013-02-06 20:24:10
now the answer is A. 49
now the answer is A. 49
Iwilllose
2013-02-06 20:24:10
65-16-49, which is the answer....
65-16-49, which is the answer....
DPatrick
2013-02-06 20:24:15
That leaves us with 65 - 16 = 49 points.
Answer (A).
That leaves us with 65 - 16 = 49 points.
Answer (A).
DPatrick
2013-02-06 20:24:22
(It's the smallest answer choice, so we know there can't be any other intersection points that are overcounted.)
(It's the smallest answer choice, so we know there can't be any other intersection points that are overcounted.)
DuoCapital
2013-02-06 20:24:34
if this wasn't multiple choice, how would we know that there aren't any more?
if this wasn't multiple choice, how would we know that there aren't any more?
Showpar
2013-02-06 20:24:34
How do we know there aren't more intersection points?
How do we know there aren't more intersection points?
ninjataco
2013-02-06 20:24:34
How do we know that there aren't any other points that have multiple diagonals intersecting?
How do we know that there aren't any other points that have multiple diagonals intersecting?
DPatrick
2013-02-06 20:24:41
We'd just have to carefully look for them.
We'd just have to carefully look for them.
DPatrick
2013-02-06 20:25:03
You could look at our pictures of the individual types from earlier to get a better view.
You could look at our pictures of the individual types from earlier to get a better view.
gaberen
2013-02-06 20:25:09
Does it matter if the octagon isn't regular?
Does it matter if the octagon isn't regular?
DPatrick
2013-02-06 20:25:28
Indeed it would -- if the octagon were sufficiently irregular, it would be possible to get 70 distinct points.
Indeed it would -- if the octagon were sufficiently irregular, it would be possible to get 70 distinct points.
DPatrick
2013-02-06 20:25:52
As I said, this problem was pretty guessable. The "guessability" comes in because just looking at the center point is enough to tell you that the answer is going to be odd, and that eliminates all but (A) or (B).
As I said, this problem was pretty guessable. The "guessability" comes in because just looking at the center point is enough to tell you that the answer is going to be odd, and that eliminates all but (A) or (B).
DPatrick
2013-02-06 20:26:17
OK, I am going to take a 4 minute break to rest my hands, and we'll resume at 8:30 ET / 5:30 ET with problems 21-25 from the AMC 12A!
OK, I am going to take a 4 minute break to rest my hands, and we'll resume at 8:30 ET / 5:30 ET with problems 21-25 from the AMC 12A!
DPatrick
2013-02-06 20:29:51
I'm back!
I'm back!
DPatrick
2013-02-06 20:30:10
By the way, thanks to all you guys for your patience. This is by far the record number of AoPSers in the classroom at one time.
By the way, thanks to all you guys for your patience. This is by far the record number of AoPSers in the classroom at one time.
DPatrick
2013-02-06 20:30:33
I know we're not posting many of your replies, and I hope you understand it's because of the sheer number of them!
I know we're not posting many of your replies, and I hope you understand it's because of the sheer number of them!
DPatrick
2013-02-06 20:30:51
Anyway, on to the AMC 12A! We'll pick up with #21:
Anyway, on to the AMC 12A! We'll pick up with #21:
DPatrick
2013-02-06 20:30:55


ickathu
2013-02-06 20:31:20
is this natural log? Or what base?
is this natural log? Or what base?
DPatrick
2013-02-06 20:31:30
We should note that "log" means "log base 10". I feel that they should have made that explicit in the problem.
We should note that "log" means "log base 10". I feel that they should have made that explicit in the problem.
DPatrick
2013-02-06 20:31:52
And of course, there's no easy "rule" to compute something of the form log(a+b).
And of course, there's no easy "rule" to compute something of the form log(a+b).
DPatrick
2013-02-06 20:31:58
How can we start?
How can we start?
RelaxationUtopia
2013-02-06 20:32:19
is C typoed?
is C typoed?
catnpatx
2013-02-06 20:32:19
is answer c, 2109, a typo for 2019?
is answer c, 2109, a typo for 2019?
DPatrick
2013-02-06 20:32:23
oops, you're right.
oops, you're right.
DPatrick
2013-02-06 20:32:36


RexT95
2013-02-06 20:32:54
get rid of the log
get rid of the log
DuoCapital
2013-02-06 20:32:54
undo the first natural log in A and in the answers?
undo the first natural log in A and in the answers?
DPatrick
2013-02-06 20:33:10
Sure, one way to start is to get rid of at least the first log is to raise everything to the power of 10.
Sure, one way to start is to get rid of at least the first log is to raise everything to the power of 10.
DPatrick
2013-02-06 20:33:20
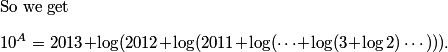
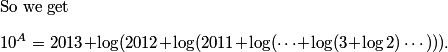
DPatrick
2013-02-06 20:33:38
oops, that's backwards, isn't it?
oops, that's backwards, isn't it?
DPatrick
2013-02-06 20:34:18
It's "10 to the power of everything", not "everything to the power of 10".
It's "10 to the power of everything", not "everything to the power of 10".
DPatrick
2013-02-06 20:34:32
What's nice about this is that we can rewrite the question a little more simply:
What's nice about this is that we can rewrite the question a little more simply:
DPatrick
2013-02-06 20:34:38
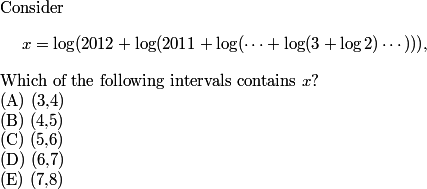
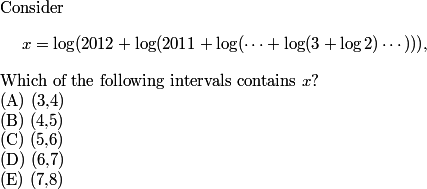
DPatrick
2013-02-06 20:34:57
Now what?
Now what?
Arghzoo
2013-02-06 20:35:24
3<log(2012....)<4
3<log(2012....)<4
jaymo
2013-02-06 20:35:28
log 2012+... won't be big enough to be more than 4
log 2012+... won't be big enough to be more than 4
DPatrick
2013-02-06 20:35:51
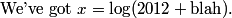
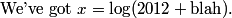
DPatrick
2013-02-06 20:36:03
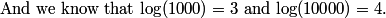
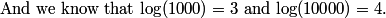
DPatrick
2013-02-06 20:36:08
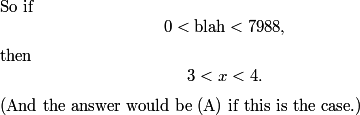
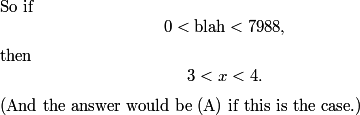
DPatrick
2013-02-06 20:36:22
Is "blah" really that small?
Is "blah" really that small?
brian22
2013-02-06 20:36:46
it's pretty tiny
it's pretty tiny
mathrocks11
2013-02-06 20:36:46
blah can't be greater than 7988 b/c blah = log(2011 + log(2010
blah can't be greater than 7988 b/c blah = log(2011 + log(2010
tluo5458
2013-02-06 20:36:46
it is 3<blah<4
it is 3<blah<4
DPatrick
2013-02-06 20:37:02
Seems very very likely that "blah" is small. Remember that "blah" is itself a log.
Seems very very likely that "blah" is small. Remember that "blah" is itself a log.
DPatrick
2013-02-06 20:37:13
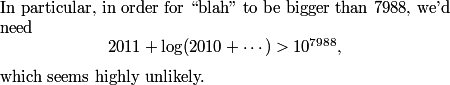
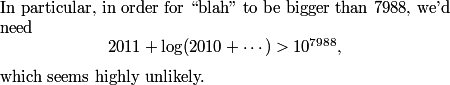
mathrocks11
2013-02-06 20:37:36
blah is less than A, so it must be less than 4
blah is less than A, so it must be less than 4
brian22
2013-02-06 20:37:36
on the test, we put A and move on!
on the test, we put A and move on!
DPatrick
2013-02-06 20:38:06
Indeed, we can easily see that blah is less than A, so it must be less than 8 (based on the answer choices), so the answer must be (A) and we can move on!
Indeed, we can easily see that blah is less than A, so it must be less than 8 (based on the answer choices), so the answer must be (A) and we can move on!
DPatrick
2013-02-06 20:38:15
In fact, it's pretty easy to prove by induction that all the logs in the expression for x are between 0 and 4.
In fact, it's pretty easy to prove by induction that all the logs in the expression for x are between 0 and 4.
DPatrick
2013-02-06 20:38:28


DPatrick
2013-02-06 20:38:33
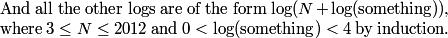
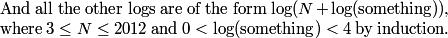
DPatrick
2013-02-06 20:38:48
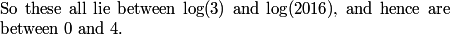
DPatrick
2013-02-06 20:39:06
Thus, indeed, x is less than 4. (And it's clearly greater than 3, since it's at least log(2012) which is a little more than 3.)
Thus, indeed, x is less than 4. (And it's clearly greater than 3, since it's at least log(2012) which is a little more than 3.)
DPatrick
2013-02-06 20:39:12
Thus the answer is (A).
Thus the answer is (A).
DPatrick
2013-02-06 20:39:38
This question was basically a test of whether you understood what a "log" meant or not.
This question was basically a test of whether you understood what a "log" meant or not.
DPatrick
2013-02-06 20:39:43
Let's move on to #22:
Let's move on to #22:
DPatrick
2013-02-06 20:39:47
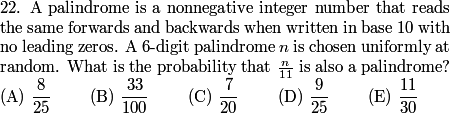
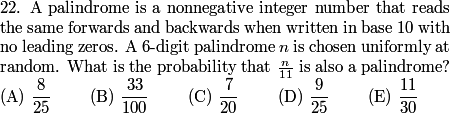
DPatrick
2013-02-06 20:40:04
What does a 6-digit palindrome look like?
What does a 6-digit palindrome look like?
matholympiad25
2013-02-06 20:40:15
write as abccba
write as abccba
DuoCapital
2013-02-06 20:40:15
abccba
abccba
guilt
2013-02-06 20:40:15
abccba
abccba
RotomPlasma
2013-02-06 20:40:15
abccba
abccba
matticus42
2013-02-06 20:40:15
abccba
abccba
RelaxationUtopia
2013-02-06 20:40:15
abccba
abccba
alex31415
2013-02-06 20:40:15
abccba
abccba
DPatrick
2013-02-06 20:40:20
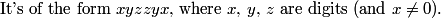
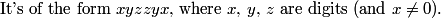
DPatrick
2013-02-06 20:40:24
So how many of them are there?
So how many of them are there?
adelie
2013-02-06 20:40:43
900
900
Jpl2000
2013-02-06 20:40:43
900
900
gundraja
2013-02-06 20:40:43
900
900
monkey8
2013-02-06 20:40:43
9*10*10
9*10*10
Arghzoo
2013-02-06 20:40:43
9*10*10 = 900
9*10*10 = 900
DPatrick
2013-02-06 20:40:48
There are 9 choices for x and 10 each for y and z, so there are 9*10*10 = 900 of them.
There are 9 choices for x and 10 each for y and z, so there are 9*10*10 = 900 of them.
DPatrick
2013-02-06 20:40:56
How many are divisible by 11?
How many are divisible by 11?
ninjataco
2013-02-06 20:41:13
all of them
all of them
mathnerd101
2013-02-06 20:41:13
all of them
all of them
calculatorwiz
2013-02-06 20:41:13
all of them
all of them
qfoam
2013-02-06 20:41:13
all of them
all of them
Double_Double
2013-02-06 20:41:13
all of them
all of them
DPatrick
2013-02-06 20:41:18
All of them! The divisibility test for 11 is to take the alternating sum of the digits. But that gives us x-y+z-z+y-x = 0.
All of them! The divisibility test for 11 is to take the alternating sum of the digits. But that gives us x-y+z-z+y-x = 0.
DPatrick
2013-02-06 20:41:43
So we want to investigate n/11 where n is one of our 6-digit palindromes. What do we get when we divide xyzzyx by 11?
So we want to investigate n/11 where n is one of our 6-digit palindromes. What do we get when we divide xyzzyx by 11?
DPatrick
2013-02-06 20:42:04
Maybe that's a bad question to ask...what's another way we can approach this?
Maybe that's a bad question to ask...what's another way we can approach this?
adelie
2013-02-06 20:42:31
go backwards
go backwards
centralbs
2013-02-06 20:42:31
consider the result after division: a palindrome in the form abcba
consider the result after division: a palindrome in the form abcba
ChenthuranA
2013-02-06 20:42:31
abcba
abcba
djmathman
2013-02-06 20:42:36
Consider the palindrome that results, and find all of them such that 11 times it is also a palindrome
Consider the palindrome that results, and find all of them such that 11 times it is also a palindrome
DPatrick
2013-02-06 20:42:47
Right, we can come at this from the other direction: we can start with a palindrome, multiply it by 11, and see if we get a 6-digit palindrome.
Right, we can come at this from the other direction: we can start with a palindrome, multiply it by 11, and see if we get a 6-digit palindrome.
DPatrick
2013-02-06 20:42:53
Can we do this by starting with a 4-digit palindrome?
Can we do this by starting with a 4-digit palindrome?
bobthesmartypants
2013-02-06 20:43:17
no
no
ic1999
2013-02-06 20:43:17
9aa9
9aa9
DPatrick
2013-02-06 20:43:43
Well.. it might be big enough: 11*(a four digit number starting with 9) can have 6 digits.
Well.. it might be big enough: 11*(a four digit number starting with 9) can have 6 digits.
DPatrick
2013-02-06 20:44:00
(11*9999 = 109989 for example, but that's not a palindrome)
(11*9999 = 109989 for example, but that's not a palindrome)
qwertyu
2013-02-06 20:44:17
But the unit digit is always 9
But the unit digit is always 9
brian22
2013-02-06 20:44:17
but the result would end in 9
but the result would end in 9
Porteradams
2013-02-06 20:44:17
but wont be a palindrome
but wont be a palindrome
mcdonalds106_7
2013-02-06 20:44:25
no; it will start with 1 and end with 9
no; it will start with 1 and end with 9
DPatrick
2013-02-06 20:44:40
Right. Regardless of what the digit b is, 11(9bb9) ends in 9 but begins with a 1.
Right. Regardless of what the digit b is, 11(9bb9) ends in 9 but begins with a 1.
DPatrick
2013-02-06 20:44:47
So it can never be a palindrome.
So it can never be a palindrome.
DPatrick
2013-02-06 20:45:00
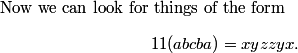
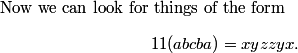
DPatrick
2013-02-06 20:45:18
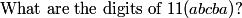
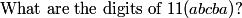
VietaFan
2013-02-06 20:45:47
a_(a+b)_(c+b)_(c+b)_(a+b)_a
a_(a+b)_(c+b)_(c+b)_(a+b)_a
jaymo
2013-02-06 20:45:47
a, a+b, b+c, etc
a, a+b, b+c, etc
VietaFan
2013-02-06 20:45:47
It's a palindrome!
It's a palindrome!
ChenthuranA
2013-02-06 20:45:47
a,a+b, b+c,c+b,b+a,a
a,a+b, b+c,c+b,b+a,a
pl210741
2013-02-06 20:45:47
abcba0+abcba
abcba0+abcba
DPatrick
2013-02-06 20:45:52
Well...maybe.
Well...maybe.
centralbs
2013-02-06 20:45:57
a, a+b, b+c, c+b , b+a , a before carrying
a, a+b, b+c, c+b , b+a , a before carrying
rahulgupta1096
2013-02-06 20:46:00
a(a+b)(b+c)(c+b)(b+a)(a) with carrying where necessary
a(a+b)(b+c)(c+b)(b+a)(a) with carrying where necessary
DPatrick
2013-02-06 20:46:14
Let's pretend we're back in 3rd grade. We just write out the multiplication, the long way:
Let's pretend we're back in 3rd grade. We just write out the multiplication, the long way:
DPatrick
2013-02-06 20:46:18


DPatrick
2013-02-06 20:46:36
The digits look like a, a+b, b+c, c+b, b+a, and a. That's a palindrome!
The digits look like a, a+b, b+c, c+b, b+a, and a. That's a palindrome!
DPatrick
2013-02-06 20:46:45
...but only if there's no carrying when we add.
...but only if there's no carrying when we add.
DPatrick
2013-02-06 20:47:16
Is it possible that it might still sum to give a 6-digit palindrome, even if there was carrying?
Is it possible that it might still sum to give a 6-digit palindrome, even if there was carrying?
gengkev
2013-02-06 20:47:55
no; a + b < 10 because the a must be the same, so b + c < 10 to not interfere
no; a + b < 10 because the a must be the same, so b + c < 10 to not interfere
Doink
2013-02-06 20:47:55
no, because then the first digit would be a+1 and the last would be a
no, because then the first digit would be a+1 and the last would be a
AdamGeller
2013-02-06 20:47:55
no. we can't have a first digit of a from carrying
no. we can't have a first digit of a from carrying
teranz0
2013-02-06 20:47:55
not if a+b>9, because then the first and last digit would be different
not if a+b>9, because then the first and last digit would be different
DPatrick
2013-02-06 20:48:20
Well, let's be careful and make sure. (Again, you might not do this on the actual contest, where there's more time-pressure.)
Well, let's be careful and make sure. (Again, you might not do this on the actual contest, where there's more time-pressure.)
DPatrick
2013-02-06 20:48:26
The last digit is a, so the first digit has to be a as well.
The last digit is a, so the first digit has to be a as well.
DPatrick
2013-02-06 20:48:39
This means that the addition in the ten-thousands column (the second column from the left) cannot carry a "1" over to the hundred-thousands column.
This means that the addition in the ten-thousands column (the second column from the left) cannot carry a "1" over to the hundred-thousands column.
DPatrick
2013-02-06 20:48:52
But also the ten-thousands column has to match the tens column, which is a+b, and this can't carry either.
But also the ten-thousands column has to match the tens column, which is a+b, and this can't carry either.
DPatrick
2013-02-06 20:49:05
So the addition of b+c in the thousands column can't carry either. So this has to match the b+c in the hundreds column, and it can't carry either.
So the addition of b+c in the thousands column can't carry either. So this has to match the b+c in the hundreds column, and it can't carry either.
sonaal
2013-02-06 20:49:19
so no carrying
so no carrying
catnpatx
2013-02-06 20:49:26
therefore there cannot be any carrying
therefore there cannot be any carrying
DPatrick
2013-02-06 20:49:29
The summary is: this is a palindrome if and only if the addition has no carrying.
The summary is: this is a palindrome if and only if the addition has no carrying.
mathrocks11
2013-02-06 20:49:50
so both a+b and b+c are less than 10
so both a+b and b+c are less than 10
math-rules
2013-02-06 20:49:50
a+b<10 and b+c<10
a+b<10 and b+c<10
jkoj25
2013-02-06 20:49:57
so a+b<10 and c+b<10
so a+b<10 and c+b<10
Oboeplayer311
2013-02-06 20:50:04
so a+b < 10 and c+b < 10
so a+b < 10 and c+b < 10
ninjataco
2013-02-06 20:50:04
so a + b < 10 and b+c <10
so a + b < 10 and b+c <10
DPatrick
2013-02-06 20:50:14


DPatrick
2013-02-06 20:50:27
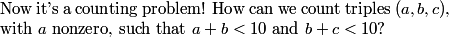
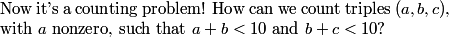
zhuangzhuang
2013-02-06 20:50:54
casework on b
casework on b
calculatorwiz
2013-02-06 20:50:54
casework on b?
casework on b?
bobthesmartypants
2013-02-06 20:51:01
first pick a b and count a and c accordingly
first pick a b and count a and c accordingly
ic1999
2013-02-06 20:51:01
casework with b
casework with b
DPatrick
2013-02-06 20:51:03
Usually we count based on the most severe restriction. Here b is the most restrictive since it appears in both conditions.
Usually we count based on the most severe restriction. Here b is the most restrictive since it appears in both conditions.
DPatrick
2013-02-06 20:51:09
So let's use casework on the value of b.
So let's use casework on the value of b.
DPatrick
2013-02-06 20:51:17
How many (a,b,c) with b=0?
How many (a,b,c) with b=0?
jsani0102
2013-02-06 20:51:42
90
90
sammyMaX
2013-02-06 20:51:42
90
90
djmathman
2013-02-06 20:51:42
9*10=90
9*10=90
ickathu
2013-02-06 20:51:42
9*1*10
9*1*10
DaChickenInc
2013-02-06 20:51:42
90
90
DPatrick
2013-02-06 20:51:47
We have 9 choices for a (any digit except 0) and 10 choices for c (any digit), so 9*10 = 90 such triples.
We have 9 choices for a (any digit except 0) and 10 choices for c (any digit), so 9*10 = 90 such triples.
DPatrick
2013-02-06 20:51:51
How many with b=1?
How many with b=1?
DuoCapital
2013-02-06 20:52:09
8*9=72
8*9=72
cherryclutch
2013-02-06 20:52:09
72
72
distortedwalrus
2013-02-06 20:52:09
72
72
Arghzoo
2013-02-06 20:52:09
8 and 9 = 72
8 and 9 = 72
MathBrain2000
2013-02-06 20:52:09
72=9*8
72=9*8
DPatrick
2013-02-06 20:52:13
We now have 8 choices for a (any digit 1-8) and 9 choices for c (any digit 1-9), so 8*9 = 72 such triples.
We now have 8 choices for a (any digit 1-8) and 9 choices for c (any digit 1-9), so 8*9 = 72 such triples.
DPatrick
2013-02-06 20:52:23
You can see the pattern: there will be 7*8 triples with b=2, 6*7 triples with b=3, and so on up to 1*2 triples with b=8.
You can see the pattern: there will be 7*8 triples with b=2, 6*7 triples with b=3, and so on up to 1*2 triples with b=8.
DPatrick
2013-02-06 20:52:28
So how many triples altogether?
So how many triples altogether?
mathnerd101
2013-02-06 20:52:50
any digit 0-8 you mean?
any digit 0-8 you mean?
DPatrick
2013-02-06 20:53:05
Oops, right, c is any digit 0-8 in the "b=1" case.
Oops, right, c is any digit 0-8 in the "b=1" case.
brian22
2013-02-06 20:53:12
90+72+56+42+30+20+12+6+2=330
90+72+56+42+30+20+12+6+2=330
Arghzoo
2013-02-06 20:53:12
2 + 6 + 12 + 20 + 30 + 42 + 56 + 72 + 90 =
2 + 6 + 12 + 20 + 30 + 42 + 56 + 72 + 90 =
viker
2013-02-06 20:53:23
330 triples
330 triples
tluo5458
2013-02-06 20:53:23
2+6+12+20+30+42+56+72+90=330
2+6+12+20+30+42+56+72+90=330
DPatrick
2013-02-06 20:53:28
We get 90 + 72 + 56 + 42 + 30 + 20 + 12 + 6 + 2 = 330 triples.
We get 90 + 72 + 56 + 42 + 30 + 20 + 12 + 6 + 2 = 330 triples.
DPatrick
2013-02-06 20:53:53
Each triple gives abcba that when multiplied by 11, corresponds to a unique 6-digit palindrome satisfying the problem condition.
Each triple gives abcba that when multiplied by 11, corresponds to a unique 6-digit palindrome satisfying the problem condition.
gundraja
2013-02-06 20:54:02
330/900 gives 11/30 E)
330/900 gives 11/30 E)
matholympiad25
2013-02-06 20:54:02
330/900 = 11/30 E
330/900 = 11/30 E
bzhou5
2013-02-06 20:54:02
330/990=11/30 E
330/990=11/30 E
DPatrick
2013-02-06 20:54:24
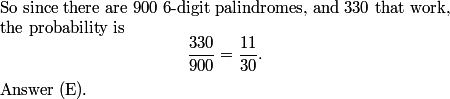
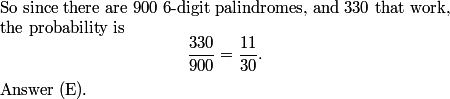
DPatrick
2013-02-06 20:54:39
OK, on to #23!
OK, on to #23!
DPatrick
2013-02-06 20:54:44
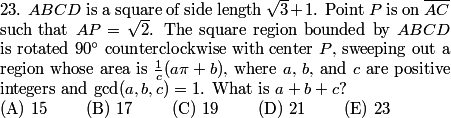
Iwilllose
2013-02-06 20:55:01
Draw a diagram?
Draw a diagram?
tuanyuan2008
2013-02-06 20:55:01
draw a diagram
draw a diagram
Iggy Iguana
2013-02-06 20:55:01
draw a diagram
draw a diagram
DPatrick
2013-02-06 20:55:08
We should start by drawing a picture:
We should start by drawing a picture:
DPatrick
2013-02-06 20:55:12
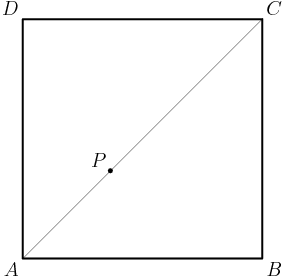

djmathman
2013-02-06 20:55:22
Is this the problem where you said that a compass and protractor were helpful?
Is this the problem where you said that a compass and protractor were helpful?
DPatrick
2013-02-06 20:55:42
Absolutely. Put your compass point on P and draw. Here's the picture after the rotation.
Absolutely. Put your compass point on P and draw. Here's the picture after the rotation.
DPatrick
2013-02-06 20:55:46


DPatrick
2013-02-06 20:56:00
Now I used fancy drawing software. You probably just made a hand-sketch (but if you brought a ruler and compass and protractor, your sketch likely was pretty good too). It looks like A' and D' lie on AB, and B' and C' lie on CD. How do we know this for sure?
Now I used fancy drawing software. You probably just made a hand-sketch (but if you brought a ruler and compass and protractor, your sketch likely was pretty good too). It looks like A' and D' lie on AB, and B' and C' lie on CD. How do we know this for sure?
panjia123
2013-02-06 20:56:44
P lies on the diagonal so APA' is 45-45-90
P lies on the diagonal so APA' is 45-45-90
DPatrick
2013-02-06 20:56:55
Right: we know that APA' is an isosceles right triangle (since it's a 90-degree rotation), so angle A'AP must be 45 degrees. That forces A' to be on AB. The same argument forces C' to be on CD.
Right: we know that APA' is an isosceles right triangle (since it's a 90-degree rotation), so angle A'AP must be 45 degrees. That forces A' to be on AB. The same argument forces C' to be on CD.
DPatrick
2013-02-06 20:57:24
And what about B' and D'?
And what about B' and D'?
DPatrick
2013-02-06 20:58:05
The same argument won't work because angle PBC is not 45 degrees.
The same argument won't work because angle PBC is not 45 degrees.
panjia123
2013-02-06 20:58:22
it still has to be a square region
it still has to be a square region
JFC
2013-02-06 20:58:30
But B'D'A' is!
But B'D'A' is!
DPatrick
2013-02-06 20:58:48
Right! The square rotates rigidly -- that is, we know A'B'C'D' is still a square, rotated 90 degrees.
Right! The square rotates rigidly -- that is, we know A'B'C'D' is still a square, rotated 90 degrees.
DPatrick
2013-02-06 20:58:55
So A'B' must be parallel to BC and the same length, putting B' on CD. The same argument places D' on AB.
So A'B' must be parallel to BC and the same length, putting B' on CD. The same argument places D' on AB.
DPatrick
2013-02-06 20:59:18
Moral of the story: you might not have noticed/guessed that A' was on AB without an accurate diagram! So bring accurate-diagram-drawing tools with you.
Moral of the story: you might not have noticed/guessed that A' was on AB without an accurate diagram! So bring accurate-diagram-drawing tools with you.
DPatrick
2013-02-06 20:59:37
The area we want is the entire region inside this diagram: anything that is inside either square (ABCD or A'B'C'D') or any of the arcs is part of the region.
The area we want is the entire region inside this diagram: anything that is inside either square (ABCD or A'B'C'D') or any of the arcs is part of the region.
DPatrick
2013-02-06 20:59:44
How do we compute this area?
How do we compute this area?
mathrocks11
2013-02-06 21:00:07
split it into sectors and triangles?
split it into sectors and triangles?
Rocksolid
2013-02-06 21:00:10
Take it piece by piece
Take it piece by piece
heliootrope
2013-02-06 21:00:10
divide it into a rectangle and four sectors
divide it into a rectangle and four sectors
prezcoin
2013-02-06 21:00:13
divide the diagram into sectors and triangles centered at P
divide the diagram into sectors and triangles centered at P
DPatrick
2013-02-06 21:00:17
This region is ugly-looking, but it's made up of nice-looking pieces.
This region is ugly-looking, but it's made up of nice-looking pieces.
DPatrick
2013-02-06 21:00:29
We have some choices about how to break up this region, but here's one idea:
We have some choices about how to break up this region, but here's one idea:
DPatrick
2013-02-06 21:00:33

DPatrick
2013-02-06 21:01:05
(Compare the two pics that I've posted to the top, to be sure they're the same!)
(Compare the two pics that I've posted to the top, to be sure they're the same!)
DPatrick
2013-02-06 21:01:10
So we have four sectors (pieces of circles) and 4 little triangles.
So we have four sectors (pieces of circles) and 4 little triangles.
DPatrick
2013-02-06 21:01:18
Now we angle-chase and length-chase and crunch numbers.
Now we angle-chase and length-chase and crunch numbers.
DPatrick
2013-02-06 21:01:22
Let's do the sectors first. What's the area of the bottom sector?
Let's do the sectors first. What's the area of the bottom sector?
tiger11
2013-02-06 21:01:52
pi/2
pi/2
cherryclutch
2013-02-06 21:01:52
pi r^2 /4
pi r^2 /4
bobthesmartypants
2013-02-06 21:01:52
1/2 pi
1/2 pi
memphis_tiger
2013-02-06 21:01:52
pi/2
pi/2
Duncanyang
2013-02-06 21:01:52
pi/2
pi/2
qfoam
2013-02-06 21:01:52
pi/2
pi/2
DPatrick
2013-02-06 21:01:57
It's a 90-degree sector of a circle of radius sqrt(2).
It's a 90-degree sector of a circle of radius sqrt(2).
DPatrick
2013-02-06 21:02:08


DPatrick
2013-02-06 21:02:18
How about the top sector?
How about the top sector?
ChenthuranA
2013-02-06 21:02:54
3pi/2
3pi/2
ic1999
2013-02-06 21:02:54
3pi/2
3pi/2
zhuangzhuang
2013-02-06 21:02:54
3pi/2
3pi/2
guilt
2013-02-06 21:02:54
3pi/2
3pi/2
DPatrick
2013-02-06 21:02:59
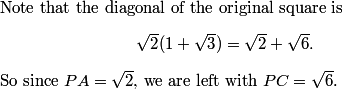
DPatrick
2013-02-06 21:03:19


DPatrick
2013-02-06 21:03:40
How about the two side sectors?
How about the two side sectors?
DPatrick
2013-02-06 21:03:50
What is length PB?
What is length PB?
Calebhe1290
2013-02-06 21:04:19
2
2
centralbs
2013-02-06 21:04:19
2
2
alexlin9008
2013-02-06 21:04:19
2
2
chessderek
2013-02-06 21:04:19
2
2
gengkev
2013-02-06 21:04:19
2
2
DPatrick
2013-02-06 21:04:34
It might help to drop an altitude from P down to AB. Here it is in the original square:
It might help to drop an altitude from P down to AB. Here it is in the original square:
DPatrick
2013-02-06 21:04:38
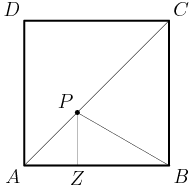

mathrocks11
2013-02-06 21:04:54
PZ is 1
PZ is 1
MrMerchant
2013-02-06 21:04:54
30-60-90 triangle
30-60-90 triangle
DPatrick
2013-02-06 21:04:59
DPatrick
2013-02-06 21:05:11


DPatrick
2013-02-06 21:05:21
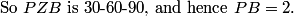
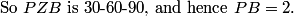
DPatrick
2013-02-06 21:05:56
So sector BPX is part of a circle of radius 2. What's the angle BPX?
So sector BPX is part of a circle of radius 2. What's the angle BPX?
mydogcanpur
2013-02-06 21:06:27
60
60
minimario
2013-02-06 21:06:27
60
60
ClassClown
2013-02-06 21:06:27
60
60
tuanyuan2008
2013-02-06 21:06:27
60
60
ickathu
2013-02-06 21:06:27
60 degrees
60 degrees
DPatrick
2013-02-06 21:06:49
Again, it might help to drop an altitude from P down to BC in our original square:
Again, it might help to drop an altitude from P down to BC in our original square:
DPatrick
2013-02-06 21:06:53
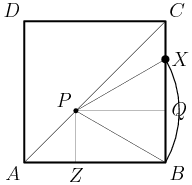

DPatrick
2013-02-06 21:07:13


bzhou5
2013-02-06 21:07:35
the area is 2pi/3
the area is 2pi/3
bzhou5
2013-02-06 21:07:35
the area of the right sector is 2pi/3
the area of the right sector is 2pi/3
Rocksolid
2013-02-06 21:07:35
2pi/3 is the area of the sector
2pi/3 is the area of the sector
DPatrick
2013-02-06 21:07:43
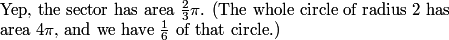
Iwilllose
2013-02-06 21:07:54
so the combined area is 4pi/3
so the combined area is 4pi/3
bobthesmartypants
2013-02-06 21:07:57
2/3 pi for one sector, 2/3 pi for other sector, plus 1/2 pi and 3/2 pi gives 10/3 pi for all the sectors
2/3 pi for one sector, 2/3 pi for other sector, plus 1/2 pi and 3/2 pi gives 10/3 pi for all the sectors
DPatrick
2013-02-06 21:08:17
Right: the left sector (YPD' in the funky picture up top) is symmetric to the right sector. So it also has area (2/3)pi.
Right: the left sector (YPD' in the funky picture up top) is symmetric to the right sector. So it also has area (2/3)pi.
DPatrick
2013-02-06 21:08:32


ickathu
2013-02-06 21:08:46
what about the triangles PYC', PXC, PA'B, and PD'A?
what about the triangles PYC', PXC, PA'B, and PD'A?
DPatrick
2013-02-06 21:08:56
Yes: now on to the four little triangles.
Yes: now on to the four little triangles.
DPatrick
2013-02-06 21:09:02
The two on the bottom are identical, as are the two on the top. Let's look at the bottom first.
The two on the bottom are identical, as are the two on the top. Let's look at the bottom first.
DPatrick
2013-02-06 21:09:17
What is the area of PA'B?
What is the area of PA'B?
empoleon
2013-02-06 21:09:32
all have height of 1
all have height of 1
DPatrick
2013-02-06 21:09:42
Indeed, the height is PZ = 1.
Indeed, the height is PZ = 1.
DPatrick
2013-02-06 21:09:48
What is A'B?
What is A'B?
kli2000
2013-02-06 21:10:14
sqrt3-1
sqrt3-1
guilt
2013-02-06 21:10:14
sqrt3 -1
sqrt3 -1
Calebhe1290
2013-02-06 21:10:14
rt3-1
rt3-1
gundraja
2013-02-06 21:10:14
SQRT(3) - 1
SQRT(3) - 1
mathrocks11
2013-02-06 21:10:14
we found ZA' is 1 so A'B is sqrt(3)-1
we found ZA' is 1 so A'B is sqrt(3)-1
DPatrick
2013-02-06 21:10:21
The length is AB - 2(AZ) = (1 + sqrt(3)) - 2 = sqrt(3) - 1.
The length is AB - 2(AZ) = (1 + sqrt(3)) - 2 = sqrt(3) - 1.
chessderek
2013-02-06 21:10:33
so area of PA'B is (sqrt3-1)/2
so area of PA'B is (sqrt3-1)/2
DPatrick
2013-02-06 21:10:36


DPatrick
2013-02-06 21:10:48
Now what about the top triangles? What is the area of PXC?
Now what about the top triangles? What is the area of PXC?
DPatrick
2013-02-06 21:10:55
This guy might help:
This guy might help:
DPatrick
2013-02-06 21:11:00


DuoCapital
2013-02-06 21:11:24
height = sqrt(3)
height = sqrt(3)
DPatrick
2013-02-06 21:11:39
Right: earlier we found the height is PQ = ZB = sqrt(3).
Right: earlier we found the height is PQ = ZB = sqrt(3).
ic1999
2013-02-06 21:11:52
XC=sqrt3-1
XC=sqrt3-1
VietaFan
2013-02-06 21:11:52
base = sqrt 3 - 1
base = sqrt 3 - 1
empoleon
2013-02-06 21:11:52
base = sqrt(3)-1
base = sqrt(3)-1
DPatrick
2013-02-06 21:12:02
And the base is CX = CB - BX = (1 + sqrt(3)) - 2 = sqrt(3) - 1.
And the base is CX = CB - BX = (1 + sqrt(3)) - 2 = sqrt(3) - 1.
DPatrick
2013-02-06 21:12:25
cherryclutch
2013-02-06 21:12:50
now add em up!
now add em up!
Iwilllose
2013-02-06 21:12:50
so then the total for the two top is 3-sqrt3, and the entire total is 2?
so then the total for the two top is 3-sqrt3, and the entire total is 2?
guilt
2013-02-06 21:12:50
3-sqrt3 +sqrt3 -1 =2
3-sqrt3 +sqrt3 -1 =2
DPatrick
2013-02-06 21:12:58
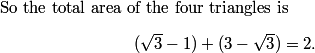
DPatrick
2013-02-06 21:13:21


bobthesmartypants
2013-02-06 21:13:48
and we can represent total area as 1/3(10 pi + 6)
and we can represent total area as 1/3(10 pi + 6)
VietaFan
2013-02-06 21:13:48
or $\frac{1}{3}(10 \pi + 6)$
or $\frac{1}{3}(10 \pi + 6)$
tluo5458
2013-02-06 21:13:48
but it has to 1/c time (a\pi+b)
but it has to 1/c time (a\pi+b)
jaymo
2013-02-06 21:14:01
c=3, a=10, b=6
c=3, a=10, b=6
ClassClown
2013-02-06 21:14:01
the answer is (C) 19
the answer is (C) 19
DPatrick
2013-02-06 21:14:04
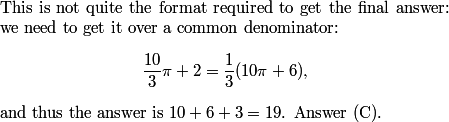
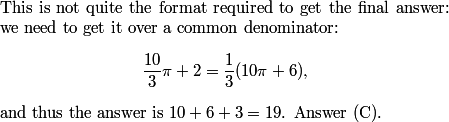
DPatrick
2013-02-06 21:14:42
I would say that this problem was certainly complicated, but --- provided you drew an accurate picture to start with! --- was not super-hard.
I would say that this problem was certainly complicated, but --- provided you drew an accurate picture to start with! --- was not super-hard.
DPatrick
2013-02-06 21:15:00
On to #24:
On to #24:
DPatrick
2013-02-06 21:15:05


DPatrick
2013-02-06 21:15:55
Let's count for our denominator first. (I usually like to start counting problems that way -- we might see something that'll help with the presumably harder numerator count.)
Let's count for our denominator first. (I usually like to start counting problems that way -- we might see something that'll help with the presumably harder numerator count.)
DPatrick
2013-02-06 21:15:59
How many segments are there?
How many segments are there?
Arghzoo
2013-02-06 21:16:20
so we have 12C2 distinct segments
so we have 12C2 distinct segments
Arghzoo
2013-02-06 21:16:20
12C2=66
12C2=66
colinhy
2013-02-06 21:16:20
12c2 = 66
12c2 = 66
mathemagician1729
2013-02-06 21:16:20
12C2 = 66
12C2 = 66
ickathu
2013-02-06 21:16:20
C(12,2) = 66
C(12,2) = 66
DPatrick
2013-02-06 21:16:26
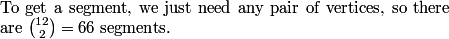
DPatrick
2013-02-06 21:16:30
So how many sets of 3 segments?
So how many sets of 3 segments?
giratina150
2013-02-06 21:16:49
66C3
66C3
alligator112
2013-02-06 21:16:49
66C3
66C3
gqiao
2013-02-06 21:16:49
66C3=11x65x64
66C3=11x65x64
awesomemathlete
2013-02-06 21:16:49
66 choose 3
66 choose 3
Seedleaf
2013-02-06 21:16:49
66C3
66C3
gundraja
2013-02-06 21:16:49
66C3
66C3
DPatrick
2013-02-06 21:16:54
DPatrick
2013-02-06 21:17:12
Now what?
Now what?
sammy1615
2013-02-06 21:17:26
find the ones that make a triangle
find the ones that make a triangle
VietaFan
2013-02-06 21:17:38
Count the degenerates and subtract.
Count the degenerates and subtract.
DPatrick
2013-02-06 21:17:58
We'll need some way to organize our work.
We'll need some way to organize our work.
DPatrick
2013-02-06 21:18:04
Let's give a segment a "size" based on how many vertices away its endpoints are (counting the shorter distance around the outside of the 12-gon). So an edge of the 12-gon has size 1, a segment connecting vertices two apart has size 2, and so on.
Let's give a segment a "size" based on how many vertices away its endpoints are (counting the shorter distance around the outside of the 12-gon). So an edge of the 12-gon has size 1, a segment connecting vertices two apart has size 2, and so on.
DPatrick
2013-02-06 21:18:30
One approach is to compute all the lengths of all the different sizes, and then start applying the triangle inequality.
One approach is to compute all the lengths of all the different sizes, and then start applying the triangle inequality.
DPatrick
2013-02-06 21:18:48
The downside is that some of the lengths are a little messy (involving sin(15) and such).
The downside is that some of the lengths are a little messy (involving sin(15) and such).
DPatrick
2013-02-06 21:19:03
We actually don't need to compute the lengths -- we can reason geometrically just by drawing the right pictures.
We actually don't need to compute the lengths -- we can reason geometrically just by drawing the right pictures.
DPatrick
2013-02-06 21:19:13
First of all, though, how many segments are there of each size?
First of all, though, how many segments are there of each size?
yangwy
2013-02-06 21:19:43
12 of each except largest, which has 6
12 of each except largest, which has 6
Jpl2000
2013-02-06 21:19:43
6 of the longest, 12 of the rest
6 of the longest, 12 of the rest
jaymo
2013-02-06 21:19:43
12, 12, 12, 12, 12, 6
12, 12, 12, 12, 12, 6
guilt
2013-02-06 21:19:43
12 for each except six for size 6
12 for each except six for size 6
DPatrick
2013-02-06 21:19:48
There are 12 segments of each of sizes 1-5 (each one can be rotated 30 degrees to get a new one), and 6 segments of size 6 (there are the 6 long diagonals of the 12-gon that pass through the center). Note that 5*12 + 6 = 66, so all segments are accounted for.
There are 12 segments of each of sizes 1-5 (each one can be rotated 30 degrees to get a new one), and 6 segments of size 6 (there are the 6 long diagonals of the 12-gon that pass through the center). Note that 5*12 + 6 = 66, so all segments are accounted for.
DPatrick
2013-02-06 21:20:05
Now for the ugly part: which sets of sizes produce a triangle with positive area?
Or maybe a better question is: which sets don't?
Now for the ugly part: which sets of sizes produce a triangle with positive area?
Or maybe a better question is: which sets don't?
DPatrick
2013-02-06 21:20:14
Which question seems better to try to count?
Which question seems better to try to count?
vinayak-kumar
2013-02-06 21:20:34
the latter
the latter
matticus42
2013-02-06 21:20:34
2nd
2nd
minimario
2013-02-06 21:20:34
The 2nd one
The 2nd one
crastybow
2013-02-06 21:20:34
Which sets don't?
Which sets don't?
Oboeplayer311
2013-02-06 21:20:34
which don't
which don't
ic1999
2013-02-06 21:20:34
which ones don't
which ones don't
DPatrick
2013-02-06 21:20:51
Probably the second question, judging by the answer choices: the answers choices are all a lot closer to 1 than to 0, so counting sets of three segments that fail to produce a nontrivial triangle will be a smaller count.
Probably the second question, judging by the answer choices: the answers choices are all a lot closer to 1 than to 0, so counting sets of three segments that fail to produce a nontrivial triangle will be a smaller count.
DPatrick
2013-02-06 21:21:01
Are there any "obvious" claims?
Are there any "obvious" claims?
DPatrick
2013-02-06 21:21:50
What combinations of sizes do we not have to bother looking at if we're trying to find segments that fail to make a nontrivial triangle?
What combinations of sizes do we not have to bother looking at if we're trying to find segments that fail to make a nontrivial triangle?
DPatrick
2013-02-06 21:22:02
(There are a lot of negatives in that sentences...)
(There are a lot of negatives in that sentences...)
Iwilllose
2013-02-06 21:22:22
3 consecutvie sides?
3 consecutvie sides?
guilt
2013-02-06 21:22:22
equilateral triangles....
equilateral triangles....
yangwy
2013-02-06 21:22:22
ones that are part of the 12-gon already
ones that are part of the 12-gon already
ic1999
2013-02-06 21:22:22
3 of the same length
3 of the same length
theGoodGuy
2013-02-06 21:22:22
large sizes
large sizes
DuoCapital
2013-02-06 21:22:22
all sides equal
all sides equal
mathemagician1729
2013-02-06 21:22:22
equilateral
equilateral
DPatrick
2013-02-06 21:22:37
Yes, there are some good ideas here.
Yes, there are some good ideas here.
DPatrick
2013-02-06 21:22:59
My first claim is that if all the segments are size 3 or bigger, we're OK. How come?
My first claim is that if all the segments are size 3 or bigger, we're OK. How come?
DPatrick
2013-02-06 21:23:17
Clearly we have a size 3-3-6 triangle (indeed it's a right triangle):
Clearly we have a size 3-3-6 triangle (indeed it's a right triangle):
DPatrick
2013-02-06 21:23:21
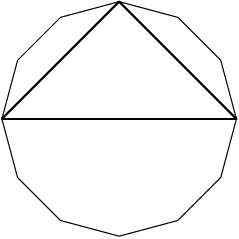

DPatrick
2013-02-06 21:23:32
So 3-3-n works for any 3 <= n <= 6.
So 3-3-n works for any 3 <= n <= 6.
DPatrick
2013-02-06 21:23:41
And increasing either 3 makes the triangle closer to equilateral, rather than closer to degenerate. (For instance, 3-4-6 is acute.)
And increasing either 3 makes the triangle closer to equilateral, rather than closer to degenerate. (For instance, 3-4-6 is acute.)
DPatrick
2013-02-06 21:23:56
Can we fail to have a triangle if all the sides are size 2 or larger?
Can we fail to have a triangle if all the sides are size 2 or larger?
VietaFan
2013-02-06 21:24:21
yes; 2, 2, 6
yes; 2, 2, 6
teranz0
2013-02-06 21:24:21
Yes, 2 size 2s add up to a size 6
Yes, 2 size 2s add up to a size 6
ksun48
2013-02-06 21:24:21
2-2-6 is degenerate
2-2-6 is degenerate
j2002
2013-02-06 21:24:24
2,2,6
2,2,6
DPatrick
2013-02-06 21:24:32
The worst case scenario is 2-2-6: the middle side is as short as possible and the longest side is as long as possible.
The worst case scenario is 2-2-6: the middle side is as short as possible and the longest side is as long as possible.
DPatrick
2013-02-06 21:24:52
But a 2-2-6 "triangle" is actually a line. The size 2 segments are exactly half the size 6 segments, because the triangle in the picture below is 30-60-90:
But a 2-2-6 "triangle" is actually a line. The size 2 segments are exactly half the size 6 segments, because the triangle in the picture below is 30-60-90:
DPatrick
2013-02-06 21:24:57
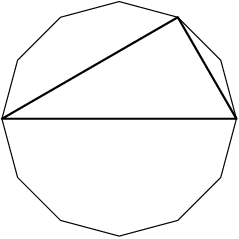

DPatrick
2013-02-06 21:25:12
But if 2-2-6 is a line, what can we conclude about 2-a-b, where a<=b and (a>2 or b<6)?
But if 2-2-6 is a line, what can we conclude about 2-a-b, where a<=b and (a>2 or b<6)?
matholympiad25
2013-02-06 21:25:45
it will always be a triangle
it will always be a triangle
tluo5458
2013-02-06 21:25:45
it is a triangle
it is a triangle
brian22
2013-02-06 21:25:45
we're fine
we're fine
bobthesmartypants
2013-02-06 21:25:45
so anything 2 or above except 2-2-6 is good
so anything 2 or above except 2-2-6 is good
mydogcanpur
2013-02-06 21:25:45
It's a triangle
It's a triangle
djmathman
2013-02-06 21:25:45
It's a triangle!
It's a triangle!
DPatrick
2013-02-06 21:25:53
These all work. Starting with a degenerate triangle (that is, a line) and making the middle side longer and/or the longest side shorter will always allow us to make a non-degenerate triangle.
These all work. Starting with a degenerate triangle (that is, a line) and making the middle side longer and/or the longest side shorter will always allow us to make a non-degenerate triangle.
DPatrick
2013-02-06 21:26:11
So the only triple that fails where all the sides are size 2 or larger is (2,2,6).
So the only triple that fails where all the sides are size 2 or larger is (2,2,6).
DPatrick
2013-02-06 21:26:29
(I'll put that datum up top for safe-keeping.)
(I'll put that datum up top for safe-keeping.)
DPatrick
2013-02-06 21:26:39
This leaves triples with at least one side of size 1. We need to determine which of these succeed and which of these fail.
This leaves triples with at least one side of size 1. We need to determine which of these succeed and which of these fail.
DPatrick
2013-02-06 21:26:53
Again, one way is to use trig to compute all the lengths and then analyze them algebraically. That works but is perhaps inelegant.
Again, one way is to use trig to compute all the lengths and then analyze them algebraically. That works but is perhaps inelegant.
DPatrick
2013-02-06 21:27:09
Let's instead try to use the geometry of the 12-gon to analyze which triples work and which fail when size 1 is the shortest side.
Let's instead try to use the geometry of the 12-gon to analyze which triples work and which fail when size 1 is the shortest side.
DPatrick
2013-02-06 21:27:16
Clearly 1-1-1 and 1-1-2 work (the first is equilateral and the second is formed by three consecutive vertices).
Clearly 1-1-1 and 1-1-2 work (the first is equilateral and the second is formed by three consecutive vertices).
DPatrick
2013-02-06 21:27:22
How about 1-1-3?
How about 1-1-3?
minimario
2013-02-06 21:27:56
No
No
Ani10
2013-02-06 21:27:56
no
no
Porteradams
2013-02-06 21:27:56
nope
nope
matticus42
2013-02-06 21:27:56
nope
nope
Seedleaf
2013-02-06 21:27:56
no
no
bzhou5
2013-02-06 21:28:08
no the side of length 3 is greater than 1+1
no the side of length 3 is greater than 1+1
DPatrick
2013-02-06 21:28:16
We can look at the following trapezoid:
We can look at the following trapezoid:
DPatrick
2013-02-06 21:28:19
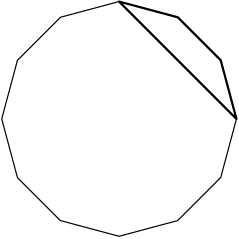

DPatrick
2013-02-06 21:28:36
If the side length of the 12-gon is s, what is the length of the size 3 segment (in terms of s)?
If the side length of the 12-gon is s, what is the length of the size 3 segment (in terms of s)?
DPatrick
2013-02-06 21:28:44
(Note that we don't need its exact length -- we just need to determine if it is at least 2s or not.)
(Note that we don't need its exact length -- we just need to determine if it is at least 2s or not.)
sonaal
2013-02-06 21:29:01
is more than 2s
is more than 2s
ahaanomegas
2013-02-06 21:29:06
It is more than 2s.
It is more than 2s.
DPatrick
2013-02-06 21:29:09
How do we know?
How do we know?
guilt
2013-02-06 21:29:17
(sqrt3 +1 )s
(sqrt3 +1 )s
DPatrick
2013-02-06 21:29:27
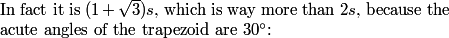
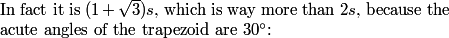
DPatrick
2013-02-06 21:29:32

DPatrick
2013-02-06 21:30:05
So the lengths of a size 1-1-3 "triangle" would have to be s, s, and (1+sqrt(3))s. That fails the triangle inequality since 1 + sqrt(3) is a lot bigger than 2.
So the lengths of a size 1-1-3 "triangle" would have to be s, s, and (1+sqrt(3))s. That fails the triangle inequality since 1 + sqrt(3) is a lot bigger than 2.
countyguy
2013-02-06 21:30:18
1-1-3, 1-1-4, 1-1-5, 1-1-6 don't work
1-1-3, 1-1-4, 1-1-5, 1-1-6 don't work
matholympiad25
2013-02-06 21:30:18
so 1-1-3, 1-1-4, 1-1-5, and 1-1-6 don't work
so 1-1-3, 1-1-4, 1-1-5, and 1-1-6 don't work
DPatrick
2013-02-06 21:30:35
So 1-1-3 fails. Hence, so does 1-1-4, 1-1-5, and 1-1-6, because trying to make the longest side even longer just makes things worse.
So 1-1-3 fails. Hence, so does 1-1-4, 1-1-5, and 1-1-6, because trying to make the longest side even longer just makes things worse.
DPatrick
2013-02-06 21:30:49
Continuing, we easily see that 1-2-2 and 1-2-3 succeed. How about 1-2-4?
Continuing, we easily see that 1-2-2 and 1-2-3 succeed. How about 1-2-4?
Iwilllose
2013-02-06 21:31:07
No, because 1+2<4
No, because 1+2<4
Oboeplayer311
2013-02-06 21:31:07
nope 1+2 < 4
nope 1+2 < 4
DPatrick
2013-02-06 21:31:27
How do we know that (size 1) + (size 2) < (size 4)? (Remember, 1, 2, and 4 are just labels; they're not the actual side lengths.)
How do we know that (size 1) + (size 2) < (size 4)? (Remember, 1, 2, and 4 are just labels; they're not the actual side lengths.)
jiujianxian
2013-02-06 21:32:05
calculate then length?
calculate then length?
DPatrick
2013-02-06 21:32:19
We could do that, but I can again draw a picture of a trapezoid:
We could do that, but I can again draw a picture of a trapezoid:
DPatrick
2013-02-06 21:32:24

DPatrick
2013-02-06 21:32:45
I just let t be the length of the size 2 side -- I don't need to bother computing it!
I just let t be the length of the size 2 side -- I don't need to bother computing it!
ic1999
2013-02-06 21:32:52
it doesn't work because 1<sqrt2
it doesn't work because 1<sqrt2
bobthesmartypants
2013-02-06 21:32:52
and sqrt{2}s>s
and sqrt{2}s>s
DPatrick
2013-02-06 21:33:15
Right! We see that the size 4 side is t + sqrt(2)*s, and that's bigger than (size 1) + (size 2) = s + t.
Right! We see that the size 4 side is t + sqrt(2)*s, and that's bigger than (size 1) + (size 2) = s + t.
DPatrick
2013-02-06 21:33:25
So 1-2-4 fails as a triangle.
So 1-2-4 fails as a triangle.
guilt
2013-02-06 21:33:38
so 1-2-5, 1-2-6 also dont work
so 1-2-5, 1-2-6 also dont work
sonaal
2013-02-06 21:33:38
anything bigger also fails
anything bigger also fails
bobthesmartypants
2013-02-06 21:33:41
and that means so do 1-2-5- and 1-2-6
and that means so do 1-2-5- and 1-2-6
VietaFan
2013-02-06 21:33:41
so dose 1-2-5 and 1-2-6
so dose 1-2-5 and 1-2-6
DPatrick
2013-02-06 21:33:58
Right. 1-2-4 fails and making the long side bigger makes it words. Thus so does 1-2-5 and 1-2-6.
Right. 1-2-4 fails and making the long side bigger makes it words. Thus so does 1-2-5 and 1-2-6.
DPatrick
2013-02-06 21:34:11
On we go...
1-3-3 and 1-3-4 trivially succeed. How about 1-3-5?
On we go...
1-3-3 and 1-3-4 trivially succeed. How about 1-3-5?
tluo5458
2013-02-06 21:34:29
1-3-5 and 1-3-6 also fail (for nxt part)
1-3-5 and 1-3-6 also fail (for nxt part)
tluo5458
2013-02-06 21:34:29
1-3-5 doesn't work nor does 1-3-6
1-3-5 doesn't work nor does 1-3-6
DPatrick
2013-02-06 21:34:35
Again, let's try for a relevant trapezoid.
Again, let's try for a relevant trapezoid.
DPatrick
2013-02-06 21:34:38

DPatrick
2013-02-06 21:34:53
Note the side of size 5 is on the bottom. The two little triangles on the ends are 30-60-90.
Note the side of size 5 is on the bottom. The two little triangles on the ends are 30-60-90.
stickman1668
2013-02-06 21:35:00
it is equal, not larger
it is equal, not larger
ic1999
2013-02-06 21:35:00
1-3-5 is a line
1-3-5 is a line
ksun48
2013-02-06 21:35:00
oh... it's equal...
oh... it's equal...
kx1001678
2013-02-06 21:35:05
135 makes a line so that fails
135 makes a line so that fails
DPatrick
2013-02-06 21:35:08
So in fact (size 5) = (size 1) + (size 3), and 1-3-5 is a degenerate triangle (a line).
So in fact (size 5) = (size 1) + (size 3), and 1-3-5 is a degenerate triangle (a line).
DPatrick
2013-02-06 21:35:16
Thus 1-3-5 fails, and so does 1-3-6.
Thus 1-3-5 fails, and so does 1-3-6.
DPatrick
2013-02-06 21:35:29
Keep on truckin'...
1-4-4, 1-4-5, 1-5-5, 1-5-6, and 1-6-6 all trivially succeed. The only one missing from this list is 1-4-6. Does it fail or succeed?
Keep on truckin'...
1-4-4, 1-4-5, 1-5-5, 1-5-6, and 1-6-6 all trivially succeed. The only one missing from this list is 1-4-6. Does it fail or succeed?
gundraja
2013-02-06 21:35:54
succeeds.
succeeds.
googol.plex
2013-02-06 21:35:54
seems to work actually
seems to work actually
ksun48
2013-02-06 21:35:54
draw the trapezoids, but it succeeds
draw the trapezoids, but it succeeds
DPatrick
2013-02-06 21:35:59
It succeeds! Again we draw a trapezoid:
It succeeds! Again we draw a trapezoid:
DPatrick
2013-02-06 21:36:03

DPatrick
2013-02-06 21:36:12
Now the two small triangles on the ends are 15-75-90. So the side adjacent to each of the size 1 segments is smaller than s/2, so their sum is smaller than s, and thus:
(size 6) < (size 1) + (size 4).
Thus 1-4-6 succeeds as a triangle.
Now the two small triangles on the ends are 15-75-90. So the side adjacent to each of the size 1 segments is smaller than s/2, so their sum is smaller than s, and thus:
(size 6) < (size 1) + (size 4).
Thus 1-4-6 succeeds as a triangle.
DPatrick
2013-02-06 21:36:30
Whew!
Whew!
DPatrick
2013-02-06 21:36:37
To summarize, here is the list of all the size triples that fail:
1-1-3, 1-1-4, 1-1-5, 1-1-6, 1-2-4, 1-2-5, 1-2-6, 1-3-5, 1-3-6, 2-2-6
To summarize, here is the list of all the size triples that fail:
1-1-3, 1-1-4, 1-1-5, 1-1-6, 1-2-4, 1-2-5, 1-2-6, 1-3-5, 1-3-6, 2-2-6
DPatrick
2013-02-06 21:36:50
Now we can count. How many of each type of triple are there?
Now we can count. How many of each type of triple are there?
Calebhe1290
2013-02-06 21:37:21
depends on whether or not 6 is included
depends on whether or not 6 is included
ksun48
2013-02-06 21:37:21
well, there are 12 of each segment except 6 has 6 segments only
well, there are 12 of each segment except 6 has 6 segments only
DPatrick
2013-02-06 21:37:46
Right, what's annoying is that some have repeated sizes, and some have that annoying size 6 which has fewer possibilities.
Right, what's annoying is that some have repeated sizes, and some have that annoying size 6 which has fewer possibilities.
DPatrick
2013-02-06 21:38:22
The three triples 1-1-{3,4,5} each have C(12,2) = 66 ways to choose the two size 1 segments and then 12 ways to choose the larger segment. So there are 66*12 of each of these three.
The three triples 1-1-{3,4,5} each have C(12,2) = 66 ways to choose the two size 1 segments and then 12 ways to choose the larger segment. So there are 66*12 of each of these three.
DPatrick
2013-02-06 21:38:44
The 1-1-6 triple is the same, but there are only 6 ways to choose the segment of size 6, so there are 66*6 such triples.
The 1-1-6 triple is the same, but there are only 6 ways to choose the segment of size 6, so there are 66*6 such triples.
Jpl2000
2013-02-06 21:38:48
so we have 12 C 2 * (12 + 12 + 12 + 6)
so we have 12 C 2 * (12 + 12 + 12 + 6)
DPatrick
2013-02-06 21:38:54
Right: that takes care of all the 1-1-n.
Right: that takes care of all the 1-1-n.
DPatrick
2013-02-06 21:39:17
How many of each of 1-2-4, 1-2-5, and 1-3-5?
How many of each of 1-2-4, 1-2-5, and 1-3-5?
blub212212
2013-02-06 21:39:29
12^3
12^3
jiujianxian
2013-02-06 21:39:29
12^3
12^3
JohnPeanuts
2013-02-06 21:39:32
12^3
12^3
DPatrick
2013-02-06 21:39:42
The 1-2-4, 1-2-5, and 1-3-5 triples each have 12*12*12 ways to choose the segments. (12 choices for a segment of each size.)
The 1-2-4, 1-2-5, and 1-3-5 triples each have 12*12*12 ways to choose the segments. (12 choices for a segment of each size.)
DPatrick
2013-02-06 21:39:55
Similarly, the 1-2-6 and 1-3-6 triples each have 12*12*6 ways to choose the segments.
Similarly, the 1-2-6 and 1-3-6 triples each have 12*12*6 ways to choose the segments.
DPatrick
2013-02-06 21:40:13
Lastly, the 2-2-6 triple has 66*6 ways to choose the segments.
Lastly, the 2-2-6 triple has 66*6 ways to choose the segments.
DPatrick
2013-02-06 21:40:38
I recommend not multiplying these out -- a lot of factors will probably cancel.
I recommend not multiplying these out -- a lot of factors will probably cancel.
bobthesmartypants
2013-02-06 21:40:43
add em up!
add em up!
DPatrick
2013-02-06 21:40:53
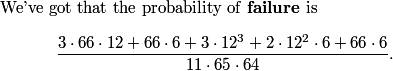
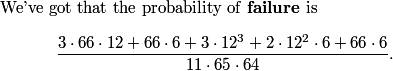
DPatrick
2013-02-06 21:41:07
(The 11*65*64 in the denominator is our count from way back at the beginning.)
(The 11*65*64 in the denominator is our count from way back at the beginning.)
DPatrick
2013-02-06 21:41:16
Now to simplify this -- without a calcuator!
Now to simplify this -- without a calcuator!
DPatrick
2013-02-06 21:41:40
I'd try to combine terms first.
I'd try to combine terms first.
bzhou5
2013-02-06 21:41:51
take out a 66 in the 3 terms and 12s in the others
take out a 66 in the 3 terms and 12s in the others
DPatrick
2013-02-06 21:41:55
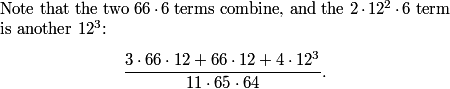
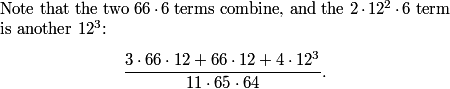
DPatrick
2013-02-06 21:42:09
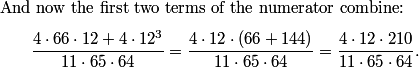
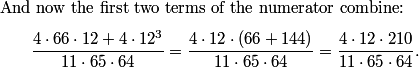
DPatrick
2013-02-06 21:42:23
(I'm going to run through this quickly because it's kinda boring and we still have #25 to go!)
(I'm going to run through this quickly because it's kinda boring and we still have #25 to go!)
kx1001678
2013-02-06 21:42:33
we can cancel out some 2s
we can cancel out some 2s
matholympiad25
2013-02-06 21:42:33
cancel 2 out from the numerator's terms
cancel 2 out from the numerator's terms
DPatrick
2013-02-06 21:42:38
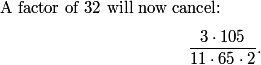
sonaal
2013-02-06 21:42:51
cancel 5
cancel 5
jaymo
2013-02-06 21:42:51
cancel 5's
cancel 5's
bookie331
2013-02-06 21:42:51
cancel out the 5
cancel out the 5
DPatrick
2013-02-06 21:42:53
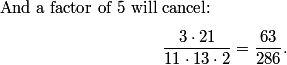
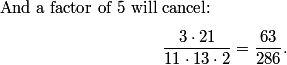
DPatrick
2013-02-06 21:43:02
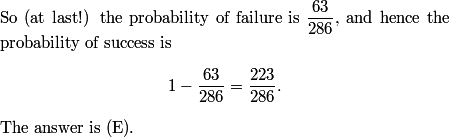
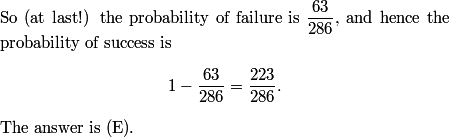
math-rules
2013-02-06 21:43:15
This problem would take at least 15 min. on the real amc, right?
This problem would take at least 15 min. on the real amc, right?
DPatrick
2013-02-06 21:43:43
This was our least-favorite of the hard problems here at the AoPS office. It's way way way long and somewhat unpleasant.
This was our least-favorite of the hard problems here at the AoPS office. It's way way way long and somewhat unpleasant.
DPatrick
2013-02-06 21:44:21
Believe it or not, I think this was probably the most elegant way. You could bash out the actual segments lengths and do it that way, but I don't think it's any faster.
Believe it or not, I think this was probably the most elegant way. You could bash out the actual segments lengths and do it that way, but I don't think it's any faster.
DPatrick
2013-02-06 21:44:37
Anyway, let's leave this one behind and go on to #25, which was probably my favorite.
Anyway, let's leave this one behind and go on to #25, which was probably my favorite.
DPatrick
2013-02-06 21:44:42
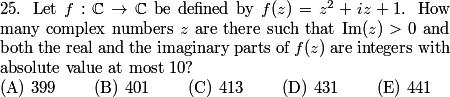
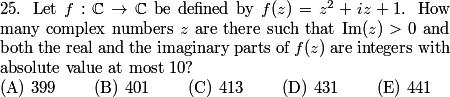
DPatrick
2013-02-06 21:44:57
You may need to read it over a couple of times to see what they're asking.
You may need to read it over a couple of times to see what they're asking.
viker
2013-02-06 21:45:07
Im means the imaginary art of a+bi right
Im means the imaginary art of a+bi right
DPatrick
2013-02-06 21:45:27
Right, Im(z) is the imaginary part of z. So if z = a+bi where a and b are real, then Im(z) = b.
Right, Im(z) is the imaginary part of z. So if z = a+bi where a and b are real, then Im(z) = b.
DPatrick
2013-02-06 21:45:39
There are a lot of ideas you could try here.
There are a lot of ideas you could try here.
DPatrick
2013-02-06 21:45:54
Suppose c is one of our "target" points: that is, c is a complex number whose real and imaginary parts are integers between -10 and 10 (inclusive).
Suppose c is one of our "target" points: that is, c is a complex number whose real and imaginary parts are integers between -10 and 10 (inclusive).
DPatrick
2013-02-06 21:46:05
Forgetting about the Im(z) > 0 restriction right now... how many complex numbers z are there with f(z) = c?
Forgetting about the Im(z) > 0 restriction right now... how many complex numbers z are there with f(z) = c?
brian22
2013-02-06 21:46:22
2
2
Tuxianeer
2013-02-06 21:46:22
2
2
alex31415
2013-02-06 21:46:22
2
2
distortedwalrus
2013-02-06 21:46:22
2
2
JohnPeanuts
2013-02-06 21:46:22
at most 2
at most 2
DPatrick
2013-02-06 21:46:37
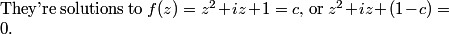
DPatrick
2013-02-06 21:47:05
Since we have all of the complex numbers to work with, this quadratic has 2 solutions for every c....right?
Since we have all of the complex numbers to work with, this quadratic has 2 solutions for every c....right?
Tuxianeer
2013-02-06 21:47:26
it could have 1
it could have 1
Iwilllose
2013-02-06 21:47:26
unless it is perfect square?
unless it is perfect square?
mprashker
2013-02-06 21:47:26
double roots
double roots
Seedleaf
2013-02-06 21:47:34
unless when you set it equal to c, the discriminant is 0
unless when you set it equal to c, the discriminant is 0
DPatrick
2013-02-06 21:47:38
Right. If z^2 + iz + (1-c) has discriminant 0, then there's only one z. When does that happen?
Right. If z^2 + iz + (1-c) has discriminant 0, then there's only one z. When does that happen?
ssilwa
2013-02-06 21:48:14
-1-4(1-c)= 0
-1-4(1-c)= 0
ssilwa
2013-02-06 21:48:14
c= 5/4
c= 5/4
bobthesmartypants
2013-02-06 21:48:14
-1-4+4c=0
-1-4+4c=0
Tuxianeer
2013-02-06 21:48:14
c=5/4
c=5/4
brian22
2013-02-06 21:48:14
4c-5=0, c=5/4
4c-5=0, c=5/4
DPatrick
2013-02-06 21:48:24
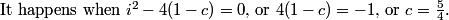
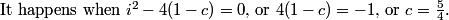
DPatrick
2013-02-06 21:48:55
But that's not one of our target points (because it doesn't have an integer real part), so we don't have to worry about that exception. Thus we conclude that every one of our target points has two z's that map to it via f.
But that's not one of our target points (because it doesn't have an integer real part), so we don't have to worry about that exception. Thus we conclude that every one of our target points has two z's that map to it via f.
DPatrick
2013-02-06 21:49:27
DPatrick
2013-02-06 21:49:39
What else do we know about the two z's that map to any target point?
What else do we know about the two z's that map to any target point?
DPatrick
2013-02-06 21:49:48
Could they both have Im(z) > 0?
Could they both have Im(z) > 0?
DPatrick
2013-02-06 21:50:24
Many of you are saying that z1 and z2 must be conjugates. That is not the case! The quadratic we started with doesn't have real coefficients.
Many of you are saying that z1 and z2 must be conjugates. That is not the case! The quadratic we started with doesn't have real coefficients.
JohnPeanuts
2013-02-06 21:50:32
No, since z_1+z_2 = -i
No, since z_1+z_2 = -i
DPatrick
2013-02-06 21:50:40
Aha...Vieta's Formulas still apply though!
Aha...Vieta's Formulas still apply though!
DPatrick
2013-02-06 21:51:17
We know that z1 + z2 = -i by Vieta's Formulas. (More generally, the sum of the roots of x^2 + bx + c is -b for any quadratic.)
We know that z1 + z2 = -i by Vieta's Formulas. (More generally, the sum of the roots of x^2 + bx + c is -b for any quadratic.)
ahaanomegas
2013-02-06 21:51:27
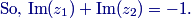
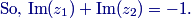
DPatrick
2013-02-06 21:51:41
Right, the imaginary parts of z1 and z2 thus must add to -1. So they can't both be positive.
Right, the imaginary parts of z1 and z2 thus must add to -1. So they can't both be positive.
awesomemathlete
2013-02-06 21:51:50
so only one at most could be positive
so only one at most could be positive
DPatrick
2013-02-06 21:52:17
Right. So we've learned something important: each target point c has at most one z such that f(z) = c with Im(z) > 0.
Right. So we've learned something important: each target point c has at most one z such that f(z) = c with Im(z) > 0.
DPatrick
2013-02-06 21:52:35
Another way to say this is that the function f is 1-1 on the set of complex numbers with Im(z) > 0: they all get mapped to different points.
Another way to say this is that the function f is 1-1 on the set of complex numbers with Im(z) > 0: they all get mapped to different points.
blub212212
2013-02-06 21:52:44
so we only need to know the number of C's now
so we only need to know the number of C's now
DPatrick
2013-02-06 21:52:57
Well, let's stop and count them. How many "target" points are there?
Well, let's stop and count them. How many "target" points are there?
jiujianxian
2013-02-06 21:53:28
21^2=441
21^2=441
matholympiad25
2013-02-06 21:53:28
21*21=441
21*21=441
Jpl2000
2013-02-06 21:53:28
21^2
21^2
dinoboy
2013-02-06 21:53:28
21*21 = 441
21*21 = 441
DPatrick
2013-02-06 21:53:49
Right: the real part is any integer from -10 to 10 (inclusive), so that's 21 choices for the real part, and same for the imaginary part.
Right: the real part is any integer from -10 to 10 (inclusive), so that's 21 choices for the real part, and same for the imaginary part.
DPatrick
2013-02-06 21:53:55
So there are 21*21 = 441 target points.
So there are 21*21 = 441 target points.
DPatrick
2013-02-06 21:54:14
And each target point c has at most one z with Im(z) > 0 so that f(z) = c, by our earlier discussion.
And each target point c has at most one z with Im(z) > 0 so that f(z) = c, by our earlier discussion.
DPatrick
2013-02-06 21:54:20
So is the answer necessarily (E) 441?
So is the answer necessarily (E) 441?
bobsanders
2013-02-06 21:54:44
no
no
blub212212
2013-02-06 21:54:44
no, because some C's may have no solution
no, because some C's may have no solution
brian22
2013-02-06 21:54:44
so 441 is a MAXIMUM
so 441 is a MAXIMUM
pr0likethis
2013-02-06 21:54:44
no, 441 is just an upper bound
no, 441 is just an upper bound
memphis_tiger
2013-02-06 21:54:44
couldnt some C's have 0 z's with positive Imaginary parts
couldnt some C's have 0 z's with positive Imaginary parts
DPatrick
2013-02-06 21:55:05
Certainly. For some of the target points, both z's that map to that point might have Im(z) <= 0, so that point might not have any z's.
Certainly. For some of the target points, both z's that map to that point might have Im(z) <= 0, so that point might not have any z's.
DPatrick
2013-02-06 21:55:13
So how do we proceed from here?
So how do we proceed from here?
DPatrick
2013-02-06 21:55:37
Inequalities (like Im(z) > 0) are often unpleasant to deal with.
Inequalities (like Im(z) > 0) are often unpleasant to deal with.
DPatrick
2013-02-06 21:55:55
Replacing them with equalities often clears things up a bit.
Replacing them with equalities often clears things up a bit.
djmathman
2013-02-06 21:56:07
Maybe deal with equality then?
Maybe deal with equality then?
sonaal
2013-02-06 21:56:07
make it an equality?
make it an equality?
distortedwalrus
2013-02-06 21:56:11
IM=0!
IM=0!
DPatrick
2013-02-06 21:56:16
Can we find where the points with Im(z) = 0 map to? That is, where does the real line map to?
Can we find where the points with Im(z) = 0 map to? That is, where does the real line map to?
Acstar
2013-02-06 21:56:33
x axis
x axis
DPatrick
2013-02-06 21:56:59
Right: we're taking the points z on the "real" (or "x") axis of the complex plane, and we want to know where f(z) is.
Right: we're taking the points z on the "real" (or "x") axis of the complex plane, and we want to know where f(z) is.
sonaal
2013-02-06 21:57:13
graph it?
graph it?
DPatrick
2013-02-06 21:57:16
How do we do that?
How do we do that?
DPatrick
2013-02-06 21:57:44
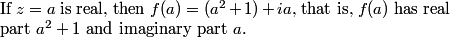
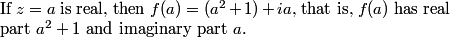
DPatrick
2013-02-06 21:58:14
So the point (a,0) on the real axis of the complex plane gets mapped to the point (a^2+1,a) on the complex plane.
So the point (a,0) on the real axis of the complex plane gets mapped to the point (a^2+1,a) on the complex plane.
DPatrick
2013-02-06 21:58:19
What do all these points look like?
What do all these points look like?
Jpl2000
2013-02-06 21:58:30
so just a parabola
so just a parabola
mydogcanpur
2013-02-06 21:58:30
Parabola?
Parabola?
DPatrick
2013-02-06 21:58:34
It's a parabola!
It's a parabola!
DPatrick
2013-02-06 21:58:42
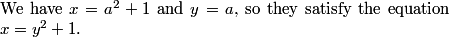
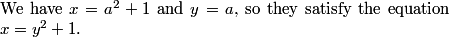
Calebhe1290
2013-02-06 21:58:50
horizontal parabola
horizontal parabola
ahaanomegas
2013-02-06 21:58:50
A horizontal parabola?
A horizontal parabola?
DPatrick
2013-02-06 21:59:06
Indeed, it's a "horizontal" parabola opening to the right, with vertex at (1,0).
Indeed, it's a "horizontal" parabola opening to the right, with vertex at (1,0).
DPatrick
2013-02-06 21:59:08
Here's a picture:
Here's a picture:
DPatrick
2013-02-06 21:59:14
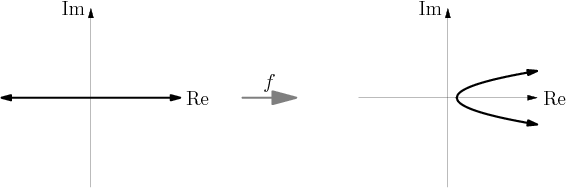

DPatrick
2013-02-06 21:59:57
So now we know where the points with Im(z) = 0 go when we apply the function f.
So now we know where the points with Im(z) = 0 go when we apply the function f.
DPatrick
2013-02-06 22:00:27
And we decided that the points with Im(z) > 0 get mapped 1-1 when we apply f (that is, two of them can't go to the same point).
And we decided that the points with Im(z) > 0 get mapped 1-1 when we apply f (that is, two of them can't go to the same point).
DPatrick
2013-02-06 22:00:36
So where do they go? Inside the parabola or outside?
So where do they go? Inside the parabola or outside?
Jpl2000
2013-02-06 22:01:09
test a point
test a point
DPatrick
2013-02-06 22:01:24
Based on your comments, you're voting about 3-to-1 for inside. But let's test a point to be sure.
Based on your comments, you're voting about 3-to-1 for inside. But let's test a point to be sure.
DPatrick
2013-02-06 22:01:34
What's an easy point to test that has Im > 0?
What's an easy point to test that has Im > 0?
memphis_tiger
2013-02-06 22:01:47
i
i
ic1999
2013-02-06 22:01:47
i
i
Tuxianeer
2013-02-06 22:01:47
i
i
DPatrick
2013-02-06 22:01:55
Sure, let's test with z=i. What is f(i)?
Sure, let's test with z=i. What is f(i)?
pr0likethis
2013-02-06 22:02:12
f(i)=-1
f(i)=-1
blub212212
2013-02-06 22:02:12
-1
-1
jiujianxian
2013-02-06 22:02:12
-1
-1
mssmath
2013-02-06 22:02:12
-1
-1
ssilwa
2013-02-06 22:02:12
-1
-1
DPatrick
2013-02-06 22:02:18
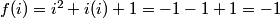
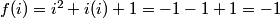
mydogcanpur
2013-02-06 22:02:32
So outside?
So outside?
DPatrick
2013-02-06 22:02:44
Yes, that's outside the parabola!
Yes, that's outside the parabola!
DPatrick
2013-02-06 22:02:54
So the region with Im(z) > 0 maps to the region outside the parabola.
So the region with Im(z) > 0 maps to the region outside the parabola.
DPatrick
2013-02-06 22:02:58
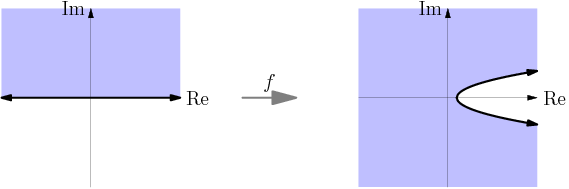

DPatrick
2013-02-06 22:03:21
So we can conclude: the points outside the parabola are exactly the points that succeed, and the points on or inside the parabola are exactly the points that fail.
So we can conclude: the points outside the parabola are exactly the points that succeed, and the points on or inside the parabola are exactly the points that fail.
DPatrick
2013-02-06 22:03:45
So to get our answer, we need to count the target points that are outside the parabola.
So to get our answer, we need to count the target points that are outside the parabola.
DPatrick
2013-02-06 22:03:54

VietaFan
2013-02-06 22:04:10
Count inside and subtract; that's easier.
Count inside and subtract; that's easier.
blub212212
2013-02-06 22:04:10
wouldn't it be easier to do 441-points inside the parabola
wouldn't it be easier to do 441-points inside the parabola
Seedleaf
2013-02-06 22:04:15
or just count the number of points inside and subtract
or just count the number of points inside and subtract
kli2000
2013-02-06 22:04:15
complementary is better
complementary is better
DPatrick
2013-02-06 22:04:30
Right: it's going to be way easier to count the point inside (or on) the parabola.
Right: it's going to be way easier to count the point inside (or on) the parabola.
DPatrick
2013-02-06 22:04:40
(Don't forget that the ones on the parabola fail too.)
(Don't forget that the ones on the parabola fail too.)
countyguy
2013-02-06 22:05:01
42 fail, so 441-42=399 A
42 fail, so 441-42=399 A
ksun48
2013-02-06 22:05:01
42
42
memphis_tiger
2013-02-06 22:05:01
total is 42
total is 42
pr0likethis
2013-02-06 22:05:01
10+9+9+6+6+1+1=42
10+9+9+6+6+1+1=42
DPatrick
2013-02-06 22:05:20
Right. You don't need to draw a fancy picture with all the dots like I did, you can just make a chart.
Right. You don't need to draw a fancy picture with all the dots like I did, you can just make a chart.
DPatrick
2013-02-06 22:05:25
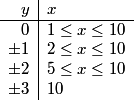
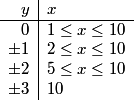
DPatrick
2013-02-06 22:05:37
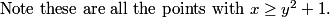
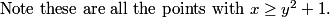
ahaanomegas
2013-02-06 22:05:44
Test the parabola inequality, basically.
Test the parabola inequality, basically.
DPatrick
2013-02-06 22:05:49
So there are 10 + 2(9) + 2(6) + 2(1) = 42 target points that fail.
So there are 10 + 2(9) + 2(6) + 2(1) = 42 target points that fail.
DPatrick
2013-02-06 22:05:56
Hence, the answer is 441 - 42 = 399. Answer (A).
Hence, the answer is 441 - 42 = 399. Answer (A).
DPatrick
2013-02-06 22:06:37
Richard Rusczyk is planning to make videos for all the problems we did tonight -- he is really looking forward to this one because there's lots of cool math that comes up in this problem, much of which we glossed over.
Richard Rusczyk is planning to make videos for all the problems we did tonight -- he is really looking forward to this one because there's lots of cool math that comes up in this problem, much of which we glossed over.
DPatrick
2013-02-06 22:06:53
His AMC 10 videos should be up on the website sometime tomorrow, with the AMC 12 videos following in a few days.
His AMC 10 videos should be up on the website sometime tomorrow, with the AMC 12 videos following in a few days.
DPatrick
2013-02-06 22:07:41
Well, we've already been going for over 2.5 hours, so I think I'll stop so that I (and you all) can eat dinner (if you live in the west like me) or go to bed (if you live in the east).
Well, we've already been going for over 2.5 hours, so I think I'll stop so that I (and you all) can eat dinner (if you live in the west like me) or go to bed (if you live in the east).
DPatrick
2013-02-06 22:07:56
There are discussions of virtually all of the problems in the AMC forum on the AoPS website.
There are discussions of virtually all of the problems in the AMC forum on the AoPS website.
DPatrick
2013-02-06 22:08:04
Please join us again on Thursday, February 21, when we will discuss the AMC 10B/12B contests.
Please join us again on Thursday, February 21, when we will discuss the AMC 10B/12B contests.
DPatrick
2013-02-06 22:08:09
Have a great night!
Have a great night!
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.









