Math Jams

copeland 2013-02-21 18:58:16
The Math Jam will start at 7:30 PM Eastern / 4:30 PM Pacific.

copeland 2013-02-21 18:58:21
The classroom is moderated, meaning that you can type into the classroom, but these comments will not go directly into the room.

copeland 2013-02-21 18:58:36
Please do not ask about administrative aspects of the contests, and please do not ask me to speculate about the results.

ic1999 2013-02-21 19:24:45
Are we starting with the AMC 10?

copeland 2013-02-21 19:24:55
We'll start at AMC10B, Problem 21.

1ph0ne 2013-02-21 19:25:35
Will we only to probs 21+?

copeland 2013-02-21 19:25:36
Probably, unless we have a lot of time at the end, but I'm pretty slow and that usually doesn't happen.

Super 2013-02-21 19:25:58
Can we request problems afterward

copeland 2013-02-21 19:25:59
If there's time.

NextEinstein 2013-02-21 19:27:01
These were some very nice problems

copeland 2013-02-21 19:27:04
I liked a lot of them.

wcao9311 2013-02-21 19:27:30
when are the questions posted/

copeland 2013-02-21 19:27:31
You can find all the problems as well as discussions of them on our message boards:

copeland 2013-02-21 19:27:35
http://www.artofproblemsolving.com/Forum/viewforum.php?f=133

FrozenFury 2013-02-21 19:28:47
Will there be a transcript afterwards?

copeland 2013-02-21 19:29:02
Yes. You can find the transcript here later:
http://www.artofproblemsolving.com/School/mathjams.php

copeland 2013-02-21 19:29:31
Oh, and I'm not going to speculate on the cutoff.

copeland 2013-02-21 19:29:40
Because I have no idea.

mathmaster2012 2013-02-21 19:29:51
Last math jam was very long. Good luck today.

copeland 2013-02-21 19:29:53
Thanks.

copeland 2013-02-21 19:30:22
Dave's faster than I am, but I got 9 problems instead of 10.

Archimedes10 2013-02-21 19:30:35
YAAY! IT'S MATH TIME!!!!!!!!

copeland 2013-02-21 19:30:40
Welcome to the 2013 AMC 10B/12B Math Jam!

copeland 2013-02-21 19:30:44
I'm Jeremy Copeland, and I'll be leading our discussion tonight.

copeland 2013-02-21 19:30:49
Before we get started I would like to take a moment to explain our virtual classroom procedures to those who have not previously participated in a Math Jam or one of our online classes.

copeland 2013-02-21 19:30:55
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.

copeland 2013-02-21 19:31:02
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.

copeland 2013-02-21 19:31:11
There are a lot of students here! As I said, only (a fraction of the) well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!

copeland 2013-02-21 19:32:04
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!

copeland 2013-02-21 19:32:21
Our main assistant tonight is Rachel Kulikoff.

copeland 2013-02-21 19:32:23

Rachel Kulikoff is currently a second-year student at the University
of Chicago. She has a wide variety of interests, including
science/math, policy, and education, and has yet to find a major (or
potential career) that combines these interests. Rachel was a
late-comer to mathematical contests, but she did place in the top 40
at the University of Georgia high school math tournament and had the
privilege of competing in the Math Prize for Girls Competition in
2010. Rachel was on the executive board of The Triple Helix, an
interdisciplinary undergraduate research magazine, on house council
(sort of like a Prefect in Harry Potter), and hopes to join the club
water polo team this year. In her dwindled free time, Rachel loves to
swim, think, experiment, and hike.

AdmireEuler 2013-02-21 19:32:27
hey guys!

Andrew 2013-02-21 19:32:48
Hello!

planetpeter91 2013-02-21 19:32:48
hello

jeremylu 2013-02-21 19:32:48
hi Rachel Kulikoff.

distortedwalrus 2013-02-21 19:32:48
hello

french01math 2013-02-21 19:32:48
hello

flyrain 2013-02-21 19:32:48
hi

smart99 2013-02-21 19:32:48
hi

NathanV 2013-02-21 19:32:48
Hi!

copeland 2013-02-21 19:33:05
Rachel can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, she may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.

copeland 2013-02-21 19:33:08
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.

copeland 2013-02-21 19:33:21
We will work the last 5 problems from the AMC 10B, then the last 5 problems from the AMC 12B. Two of these problems are the same, 10A Problem 25 and 12A Problem 23. We'll only solve that problem once.

copeland 2013-02-21 19:33:31
Oh, and there's a half a bajillion folks here tonight. It hurts me to say it, but we're probably going to miss some of the things that some of you say. (Especially during the geometry problems - sheesh.) Please forgive me in advance. That doesn't happen in our classes.

copeland 2013-02-21 19:33:43
Ready to get started?

medianpi 2013-02-21 19:33:56
yes

Lord.of.AMC 2013-02-21 19:33:56
YES

coldsummer 2013-02-21 19:33:56
yes

fcc1234 2013-02-21 19:33:56
yeah!!!

JigglykongisFUM16 2013-02-21 19:33:56
Sure

abhishek26 2013-02-21 19:33:56
sure

OISHIKA_DAS 2013-02-21 19:33:56
Yes

kdokmeci 2013-02-21 19:33:56
Yes!

lakshmi_leo 2013-02-21 19:33:56
yup

iRezizt 2013-02-21 19:33:56
yes!

djmathman 2013-02-21 19:33:56
Let's go!

wcao9311 2013-02-21 19:33:56
Yes!!

AbsoluteFriend 2013-02-21 19:33:56
yess!!

swe1 2013-02-21 19:33:56
Yes

Archimedes10 2013-02-21 19:33:56
YES!!!!!!!!!!!!

sparkles257 2013-02-21 19:33:56
yes

distortedwalrus 2013-02-21 19:33:56
yes.

vinayak-kumar 2013-02-21 19:33:56
YEA

alquila 2013-02-21 19:33:56
YES!!!

a1pha 2013-02-21 19:33:56
Yes

Andrew 2013-02-21 19:33:56
Yes!

DavidLiu729 2013-02-21 19:33:56
yes

JFC 2013-02-21 19:33:56
Yeah!

theone142857 2013-02-21 19:33:56
yes

gaberen 2013-02-21 19:33:56
LETS GOOOOO

bobthesmartypants 2013-02-21 19:33:56
yes!

VietaFan 2013-02-21 19:33:56
yes, I am

henrikjb 2013-02-21 19:33:56
yes sir

smart99 2013-02-21 19:33:56
yes

mathman500 2013-02-21 19:33:56
Yes!

ProblemSolver1026 2013-02-21 19:33:56
yup

dardarmath 2013-02-21 19:33:56
YES!

planetpeter91 2013-02-21 19:33:56
yup

copeland 2013-02-21 19:34:05

copeland 2013-02-21 19:34:13
Not a bad problem to kick things off. How should we start?

NextEinstein 2013-02-21 19:35:01
Have one sequence start a, b and the other start c, d

RotomPlasma 2013-02-21 19:35:01
Express the seventh term in terms of the first term (a) and second term (b)

Hydroxide 2013-02-21 19:35:01
let the sequences start with a, b and x, y

PERFECTION 2013-02-21 19:35:01
Start by assigning variables to the first and second terms

distortedwalrus 2013-02-21 19:35:01
call the first two terms of each sequence a, b and c, d

theone142857 2013-02-21 19:35:01
Set up variables

j2002 2013-02-21 19:35:01
a, b, a +b...

i8sumpi 2013-02-21 19:35:01
Second sequence first two terms: y1 y2

centralbs 2013-02-21 19:35:01
Let the first two terms of one sequence be a and b and find an expression for the 7th term

copeland 2013-02-21 19:35:03
Since the recurrence depends on the previous two terms, every number is determined once you're given the first two numbers. I want to know how the seventh number is related to the first two numbers.

copeland 2013-02-21 19:35:08
If the sequence starts
\[a,b,\ldots,\]
what is the seventh term?

guilt 2013-02-21 19:35:39
5a+8b

Voytek 2013-02-21 19:35:39
5a+8b

jiujianxian 2013-02-21 19:35:39
5a+8b

gengkev 2013-02-21 19:35:39
5a+8b

mathwizard888 2013-02-21 19:35:39
5a+8b

RunpengFAILS 2013-02-21 19:35:39
5a+8b

thecmd999 2013-02-21 19:35:39
5a+8b

Sesquipedalian 2013-02-21 19:35:39
5a+8b

dantx5 2013-02-21 19:35:39
5a+8b

copeland 2013-02-21 19:35:42
The sequence continues
\[a,b,a+b,a+2b,2a+3b,3a+5b,5a+8b,\ldots\]and the seventh term is $5a+8b$. (Notice that the coefficients are Fibonacci numbers!)

copeland 2013-02-21 19:35:46
Now we have two sequences
\[a,b,a+b,a+2b,2a+3b,3a+5b,5a+8b,\ldots,\]and
\[x,y,x+y,x+2y,2x+3y,3x+5y,5x+8y,\ldots\]and we also assume that \[5a+8b=5x+8y.\]

copeland 2013-02-21 19:36:02
What can we do with such an equation?

centralbs 2013-02-21 19:36:31
Group the multiples of 5 on one side and the multiples of 8 on the other

Hydroxide 2013-02-21 19:36:31
Rearrange to get 5(a-x)=8(y-b)

lazorpenguin27143 2013-02-21 19:36:31
move terms and factor

Seedleaf 2013-02-21 19:36:31
5(a-x) = 8(y-b)

Aequilipse 2013-02-21 19:36:31
move the numbers with 5 coeffs to one side and 8 coeffs to the other side

mbt123 2013-02-21 19:36:31
factor on both sides, 5(a-x)=8(y-b)

bookie331 2013-02-21 19:36:31
subtract 5x and 8b

copeland 2013-02-21 19:36:34
Let's isolate the multiples of 5 and the multiples 8 to get \[5(a-x)=8(y-b).\]

copeland 2013-02-21 19:36:37
How's that useful?

19oshawott98 2013-02-21 19:37:13
a-x is mult of 8

googol.plex 2013-02-21 19:37:13
a-x is multiple of 8, y-b is multiple of 5

19oshawott98 2013-02-21 19:37:13
y-b is mult of 5

joshxiong 2013-02-21 19:37:13
We know that a-x is a multiple of 8 and y-b is a multiple of 5.

copeland 2013-02-21 19:37:18
Since those are integers, both sides are multiple of 40. Specifically we can write \[5(x-a)=8(b-y)=40k,\] telling us that
\begin{align*}
x&=a+8k\\
y&=b-5k
\end{align*}

copeland 2013-02-21 19:37:25
To get from one such sequence to another, we increase (or decrease) the first term by a multiple of 8 and decrease (or increase) the second term by the corresponding multiple of 5.

copeland 2013-02-21 19:37:32
If we start with a pair $(a,b)$ where $a\leq b$, then eventually this stepping will give us a first term that is larger than the second term.

copeland 2013-02-21 19:37:35
What are we looking for in this problem?

matholympiad25 2013-02-21 19:37:54
Smallest possible value of N

mapletree14 2013-02-21 19:37:54
the smallest N

VietaFan 2013-02-21 19:37:54
The smallest possible N

klpt 2013-02-21 19:37:54
Smallest possible value of N?

thecmd999 2013-02-21 19:37:54
we're trying to minimize N

copeland 2013-02-21 19:37:57
such that. . . .

Voytek 2013-02-21 19:38:31
there are two ways to represent it using multiples of 5 and 8

bobthesmartypants 2013-02-21 19:38:31
a not equal to x

mbt123 2013-02-21 19:38:31
there are two integer solutions to the above equation

math-rules 2013-02-21 19:38:31
a is not x and increasing

rafa2be 2013-02-21 19:38:31
It's the same seventh number but different sequence

copeland 2013-02-21 19:38:33
We are looking for a pair for which we can make this step at least once. That is, we want a pair $(a,b)$ where $a\leq b$ and also where \[a+8\leq b-5,\]meaning that \[b\geq a+13.\]

copeland 2013-02-21 19:38:43
What pair should we try first, and what $N$ do we get?

jeremylu 2013-02-21 19:39:30
0, and 13

number.sense 2013-02-21 19:39:30
zero and 13

Lord.of.AMC 2013-02-21 19:39:30
b = 13, a = 0, N=104

swe1 2013-02-21 19:39:30
(0,13)

numbertheory 2013-02-21 19:39:30
n=104

anthonyjang 2013-02-21 19:39:30
(0,13) to 104

numbertheory 2013-02-21 19:39:30
a=8 b=8, n=104

sarvottam 2013-02-21 19:39:30
(0,13)

Imsacred 2013-02-21 19:39:30
a=0, b=13, N=104

linpaws 2013-02-21 19:39:30
(0,13)

thecmd999 2013-02-21 19:39:30
(a,b)=(0, 13) ==> N=104

mprashker 2013-02-21 19:39:30
b = 13, a = 0, N = 104

copeland 2013-02-21 19:39:34
If $(a,b)=(0,13)$, then $N=5a+8b=104.$ Furthermore, we can get from here to the pair \[(x,y)=(8,8)\] and again $N=5x+8y=104.$

copeland 2013-02-21 19:39:36
Can we get any smaller answer?

distortedwalrus 2013-02-21 19:40:03
no, because we can't use anything less than 0

number.sense 2013-02-21 19:40:03
no, then a would be negative which results in a decreasing sequence

Lord.of.AMC 2013-02-21 19:40:03
no, a is non-negative

lakshmi_leo 2013-02-21 19:40:03
it is nonnegative numbers

bobthesmartypants 2013-02-21 19:40:03
no because a has to be non-negative

mathman98 2013-02-21 19:40:03
no we can't because a has to be nonnegative

copeland 2013-02-21 19:40:07
No. In order to satisfy $b\geq a+13,$ we need to have $a\geq0$ and $b\geq13$, and increasing either will increase the seventh term.

copeland 2013-02-21 19:40:10
So what's the answer?

Ty330 2013-02-21 19:40:24

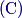
kdokmeci 2013-02-21 19:40:24
104

NathanV 2013-02-21 19:40:24
C 104

sn1per 2013-02-21 19:40:24
C

ninjataco 2013-02-21 19:40:24
C 104

planetpeter91 2013-02-21 19:40:24
C, 104

mydogcanpur 2013-02-21 19:40:24
C

sparkles257 2013-02-21 19:40:24
104!

dardarmath 2013-02-21 19:40:24
C. 104

copeland 2013-02-21 19:40:27
The answer is (C), 104.

copeland 2013-02-21 19:40:33
OK, great.

copeland 2013-02-21 19:40:38
Time for more!

copeland 2013-02-21 19:40:42

copeland 2013-02-21 19:40:55

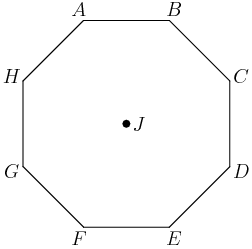
copeland 2013-02-21 19:40:57
What are we trying to find?

sn1per 2013-02-21 19:41:40
its like a magic square sort of

planetpeter91 2013-02-21 19:41:40
how many ways we can assign numbers 1-9 to points.

1ph0ne 2013-02-21 19:41:40
Combinations of number arrangements on octagon.

Jerry1997 2013-02-21 19:41:40
counting number of ways to make all diagonals through the center equal sum

billgates42 2013-02-21 19:41:40
In how many ways the sums of the numbers are equal

PERFECTION 2013-02-21 19:41:40
The ways we can complete this "number puzzle"

fcc1234 2013-02-21 19:41:40
how many ways you can enter number 1-9 so that AJE is equal to BJF and CJG and DJH

jeremylu 2013-02-21 19:41:40
how many ways the vertices, plus J, can be associated with 1 - 9

copeland 2013-02-21 19:41:44
You might have notice a lack of geometry in this geometry problem. Instead we are just trying to solve a set of equations,\[
a+j+e
=
b+j+f
=
c+j+g
=
d+j+h.\]Where these are the values associated to the obvious vertices.

copeland 2013-02-21 19:41:54
Those can probably be simplified. . .

viperstrike 2013-02-21 19:42:16
subtract j

swe1 2013-02-21 19:42:16
cancel j

sammyMaX 2013-02-21 19:42:16
remove the j

Jerry1997 2013-02-21 19:42:16
j's cancel

NextEinstein 2013-02-21 19:42:16
Subtract j

djmathman 2013-02-21 19:42:16
subtract j from both sides

dantx5 2013-02-21 19:42:16
get rid of the j's

ProblemSolver1026 2013-02-21 19:42:16
a+e=b+f=c+g=d+h

copeland 2013-02-21 19:42:20
\[a+e=b+f=c+g=d+h,\] and let's call that value $S.$

copeland 2013-02-21 19:42:23
OK, the picture's now irrelevant.

copeland 2013-02-21 19:42:26
Can we write down any other equations?

swe1 2013-02-21 19:43:03
4S+j=45?

matholympiad25 2013-02-21 19:43:03
4S+j=45

centralbs 2013-02-21 19:43:03
4S+j = 45

jeremylu 2013-02-21 19:43:03
No...

Hydroxide 2013-02-21 19:43:03
a+b+c+d+e+f+g+h=45

kli2000 2013-02-21 19:43:03
4S + center_number = 45

mathman500 2013-02-21 19:43:03
a+b+c+d+e+f+g+h=45-j

copeland 2013-02-21 19:43:09
Since all the numbers are distinct, we know\[a+b+c+d+e+f+g+h+j=45.\]

copeland 2013-02-21 19:43:13
We can substitute our value for $S$ in there to get \[4S+j=45.\]

copeland 2013-02-21 19:43:16
What's that tell us about $j?$

Lord.of.AMC 2013-02-21 19:43:42
j = 1, 5, or 9

matholympiad25 2013-02-21 19:43:42
j is 1 mod 4

Hydroxide 2013-02-21 19:43:42
1 mod 4

djmathman 2013-02-21 19:43:42
45-j must be divisible by 4!

theone142857 2013-02-21 19:43:42
j must be 1 mod 4

dantx5 2013-02-21 19:43:42
j=1,5,9

henrikjb 2013-02-21 19:43:42
j = 1,5,9

mathmaster2012 2013-02-21 19:43:42
j is 1 mod 4

Royalreter1 2013-02-21 19:43:42
it must be 1,5 or 9

trophies 2013-02-21 19:43:42
j is either 1,5, or 9. Now we can make cases on j...

copeland 2013-02-21 19:43:47
Now we know that $45-j$ has to be a multiple of 4. Therefore $j$ is either 1, 5, or 9.

copeland 2013-02-21 19:43:56
If $j=9,$ is it possible to pair the other 8 digits up?

matholympiad25 2013-02-21 19:44:35
1-8, 2-7, 3-6, 4-5. Yes

djmathman 2013-02-21 19:44:35
Mhm. {1,8},{2,7},{3,6},{4,5}

Lord.of.AMC 2013-02-21 19:44:35
(1,8) (2,7) (3,6) (4,5)

dantx5 2013-02-21 19:44:35
1-8,2-7,3-6,4-5

Sesquipedalian 2013-02-21 19:44:35
Yes: (1,8),(2,7),etc

numbertheory 2013-02-21 19:44:35
yes 1+8, 2+7, 3+6, 4+5

swe1 2013-02-21 19:44:35
(1,8) (2,7) (3,6) (4,5)

bobthesmartypants 2013-02-21 19:44:35
yes: 1, 8; 2, 7; 3, 6; 4, 5

burch_c 2013-02-21 19:44:35
1+8,2+7,3+6,4+5

copeland 2013-02-21 19:45:01
If $j=9,$ then $S=(45-9)/4=9$, and we get $S=1+8=2+7=3+6=4+5.$

copeland 2013-02-21 19:45:09
The pairs are unique.

copeland 2013-02-21 19:45:12
How many ways can we label the 8 outer vertices with these pairs?

Lord.of.AMC 2013-02-21 19:45:42
4! * 2^4 = 384

Hydroxide 2013-02-21 19:45:42
8*6*4*2

i8sumpi 2013-02-21 19:45:42
8*6*4*2

VietaFan 2013-02-21 19:45:42
24*2^4 ways

thecmd999 2013-02-21 19:45:42
4!*2^4

RelaxationUtopia 2013-02-21 19:45:42
8x6x4x2

RelaxationUtopia 2013-02-21 19:45:42
=384

shimfamily2012 2013-02-21 19:45:42
8*6*4*2

hjia1 2013-02-21 19:45:42
8*6*4*2

ws5188 2013-02-21 19:45:42
4!*2^4=384

mathwizard888 2013-02-21 19:45:42
4!*2^4=384

copeland 2013-02-21 19:45:48
There are 8 choices for $a$ and that fixes $e$. Then there are 6 more choices for $b$ and that fixes $f$. Then there are 4 choices left for $c$, fixing $g$. Finally there are 2 choices left for $d$ and $h.$

copeland 2013-02-21 19:45:53
There are a total of $8\cdot6\cdot4\cdot2=384$ labellings with $j=9$. Here is one of them:

copeland 2013-02-21 19:45:57

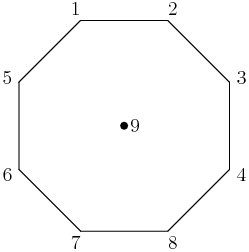
copeland 2013-02-21 19:46:00
Alternatively, there are $4!$ ways to assign each pair, and then $2^4$ ways to order the pairs.

copeland 2013-02-21 19:46:07
How many labellings are there with $j=1?$

alquila 2013-02-21 19:46:26
384

EpicMath31415 2013-02-21 19:46:26
Same?

bestwillcui1 2013-02-21 19:46:26
384 as well

AlcumusGuy 2013-02-21 19:46:26
same thing: 384

NathanV 2013-02-21 19:46:26
same number, 384

googol.plex 2013-02-21 19:46:26
same, 384

crastybow 2013-02-21 19:46:26
Same. 384

kdokmeci 2013-02-21 19:46:26
The same number.

lakshmi_leo 2013-02-21 19:46:26
same number 384

nuggetfan 2013-02-21 19:46:26
the same - 384

copeland 2013-02-21 19:46:31
If $j=1$ then $S=(45-1)/4=11.$ We could go through a similar argument from before to show that there are 384 of them, but there are a couple of simpler ways to see that. How?

i8sumpi 2013-02-21 19:47:22
symmetry tells the same

thecmd999 2013-02-21 19:47:22
just reflect over 5

centralbs 2013-02-21 19:47:22
the sums are symmetric about 5.5

theone142857 2013-02-21 19:47:22
Send i to 9-i. It's a bijection

AlcumusGuy 2013-02-21 19:47:22
1 and 9 are symmetric about 5

alwinwillwin 2013-02-21 19:47:22
it's the complement

j2002 2013-02-21 19:47:22
j-8, everything else +1.

copeland 2013-02-21 19:47:26
We can just add one to each of the 8 outer values in a $j=9$ configuration to get a $j=1$ configuration.

copeland 2013-02-21 19:47:31

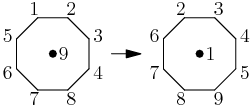
copeland 2013-02-21 19:47:32
Or we could subtract every value from 10:

copeland 2013-02-21 19:48:07

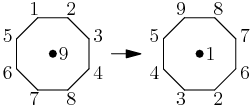
copeland 2013-02-21 19:48:49
How many labellings are there with $j=5?$

ninjataco 2013-02-21 19:49:11
same 384

JFC 2013-02-21 19:49:11
Again, 384

jeremylu 2013-02-21 19:49:11
384

chenmichael9 2013-02-21 19:49:11
384

anthonyjang 2013-02-21 19:49:11
384. same thing

sparkles257 2013-02-21 19:49:11
384

mathfuns 2013-02-21 19:49:11
384

Archimedes10 2013-02-21 19:49:11
384 again!

Ty330 2013-02-21 19:49:11
384 the same

vinayak-kumar 2013-02-21 19:49:11
384

copeland 2013-02-21 19:49:19
If we add 1 to all the bigger values in a $j=9$ solution we get a $j=5$ solution.

copeland 2013-02-21 19:49:25

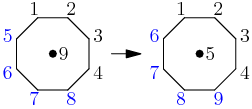
copeland 2013-02-21 19:49:27
There are also 384 of these.

copeland 2013-02-21 19:49:31
How many total labellings are there?

regularperson 2013-02-21 19:49:56
1152

kli2000 2013-02-21 19:49:56
1152

Iwilllose 2013-02-21 19:49:56
Adding these up, we get 1152, answerr C

viker 2013-02-21 19:49:56
1152

54math 2013-02-21 19:49:56
384*3

mydogcanpur 2013-02-21 19:49:56
1152 (C)

austintatious 2013-02-21 19:49:56
384 X 3

swimmerstar 2013-02-21 19:49:56
c 1152

ProblemSolver1026 2013-02-21 19:49:56
C, 1152

HiddenMathlete 2013-02-21 19:49:56
3*384

Voytek 2013-02-21 19:49:56
384*3=1152 or answer C

copeland 2013-02-21 19:49:59
The answer is $384+384+384=1152,$ (C).

copeland 2013-02-21 19:50:20
I seem to have a poor missing picture up there for some of you.

copeland 2013-02-21 19:50:23
It should be like this:

copeland 2013-02-21 19:50:31

copeland 2013-02-21 19:51:03

copeland 2013-02-21 19:51:11
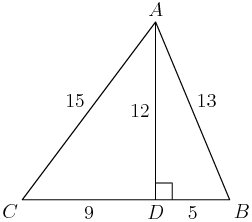
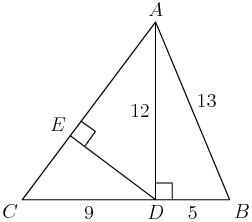
Let's stop at the first sentence, "In triangle $ABC$, $AB=13$, $BC=14$, and $CA=15.$" This triangle should be in your bag of tricks.

copeland 2013-02-21 19:51:17
What is the length of the altitude to $\overline{BC}?$

swe1 2013-02-21 19:51:48
altitude is 12

Lord.of.AMC 2013-02-21 19:51:48
12

guilt 2013-02-21 19:51:48
12

RelaxationUtopia 2013-02-21 19:51:48
12

henrikjb 2013-02-21 19:51:48
altituda of 12

matholympiad25 2013-02-21 19:51:48
12

blueberrysc7 2013-02-21 19:51:48
12

USAMOREAPER 2013-02-21 19:51:48
12

matticus42 2013-02-21 19:51:48
12

mbt123 2013-02-21 19:51:48
12

19oshawott98 2013-02-21 19:51:48
12

linpaws 2013-02-21 19:51:48
12

mapletree14 2013-02-21 19:51:48
12

copeland 2013-02-21 19:51:53

copeland 2013-02-21 19:51:55
The other altitudes are also almost as nice.

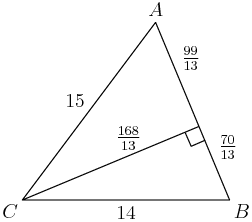
copeland 2013-02-21 19:51:59

copeland 2013-02-21 19:52:03

copeland 2013-02-21 19:52:08
You can get these last two by chasing similar triangles from the first triangle or by applying the Pythagorean Theorem.

vinayak-kumar 2013-02-21 19:52:20
Wow, thats really nice

copeland 2013-02-21 19:52:23
Yeah.

copeland 2013-02-21 19:52:35
You'll see this triangle pop up every few years on some contest or another.

copeland 2013-02-21 19:52:39
When I solved this problem, I used a lot of these facts, and made a great big mess. It worked, but it's not something I'd be comfortable doing again with all of you watching.

copeland 2013-02-21 19:52:47
Instead we'll be a little smarter.

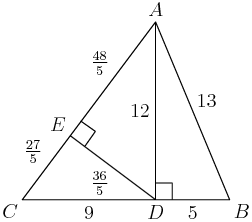
copeland 2013-02-21 19:52:53
Our point $D$ is good, though:

copeland 2013-02-21 19:52:56

copeland 2013-02-21 19:53:03
Next we drop a perpendicular from $D$ to $AC$.

copeland 2013-02-21 19:53:08

copeland 2013-02-21 19:53:16
Can we say anything about lengths in this diagram?

kdokmeci 2013-02-21 19:54:15
Simlar triangles?

wcao9311 2013-02-21 19:54:15
similar

nalaxone44 2013-02-21 19:54:15
DE=36/5

PERFECTION 2013-02-21 19:54:15
DE=36/5

coldsummer 2013-02-21 19:54:15
DE=36/5

dantx5 2013-02-21 19:54:15
ED = 36/5

VietaFan 2013-02-21 19:54:15
3-4-5 and 5-12-13 right triangles

theone142857 2013-02-21 19:54:15
We can find DE, AE, CE by using similar triangles

googol.plex 2013-02-21 19:54:15
yes, we have similar triangles so CE=27/5, DE=36/5, AE=48/5

centralbs 2013-02-21 19:54:15
ED is 36/5 by similar triangles

copeland 2013-02-21 19:54:19
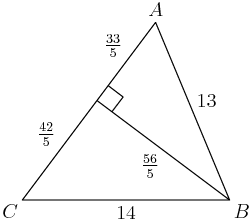
$\triangle CED$ is similar to $\triangle CDA$, which is 3-4-5. Therefore \[CE=\frac35\cdot9=\frac{27}5.\] That makes \[EA=CA-CE=15-\frac{27}5=\frac {48}5.\]

copeland 2013-02-21 19:54:24

copeland 2013-02-21 19:54:28
Now $F$ is somewhere on $\overline{DE}$ such that $\angle AFB$ is a right angle. What is the locus of all the points that give right angles?

nuggetfan 2013-02-21 19:55:09
circle

ic1999 2013-02-21 19:55:09
circle

Piya31415 2013-02-21 19:55:09
circle with diameter ab

bobthesmartypants 2013-02-21 19:55:09
a circle!

theone142857 2013-02-21 19:55:09
circle with diameter AB

flyrain 2013-02-21 19:55:09
a circle

mathwizard888 2013-02-21 19:55:09
circle with diameter AB

Lord.of.AMC 2013-02-21 19:55:09
the ones on the semicircle with diameter AB

joshxiong 2013-02-21 19:55:09
The circle with diameter AB.

copeland 2013-02-21 19:55:11
In order for $\angle AFB$ to be a right angle, $F$ must be on the circle with diameter $\overline{AB}$, and all of these points do produce a right angle.

copeland 2013-02-21 19:55:24
(And a "locus" is just a fancy word for set, if you are a geometer.)

copeland 2013-02-21 19:55:30
Know anything else about this circle?

mcdonalds106_7 2013-02-21 19:55:56
circle with AB on diameter, this happens to contain D as well

alwinwillwin 2013-02-21 19:55:56
it's a cyclic quadrilateral!

mcdonalds106_7 2013-02-21 19:55:56
D is on it

theone142857 2013-02-21 19:55:56
It's the circumcircle of ABD

coldsummer 2013-02-21 19:55:56
intersects D

number.sense 2013-02-21 19:55:56
cicumcircle of ABD

Aplus95 2013-02-21 19:55:56
Passes through D

mbt123 2013-02-21 19:55:56
amust go throguh point D

copeland 2013-02-21 19:56:00
$D$ is also on this circle. Here it is:

copeland 2013-02-21 19:56:04

copeland 2013-02-21 19:56:06
OK, that's a lot of stuff. How can we get an expression with $EF$ in it?

nuggetfan 2013-02-21 19:56:41
power of a point?

number.sense 2013-02-21 19:56:41
Power of a point should be good

AkshajK 2013-02-21 19:56:41
Powerpoint

anthonyjang 2013-02-21 19:56:41
power of a point

pi37 2013-02-21 19:56:41
POP

TigerSneak1 2013-02-21 19:56:41
power of a point

Smokkala 2013-02-21 19:56:41
power of a point

kli2000 2013-02-21 19:56:41
power of a point!

copeland 2013-02-21 19:56:57
Yeah. If you got this far on the test and haven't used Power of a Point, now must be the time.

copeland 2013-02-21 19:57:01
We can use power of a point on the line through $E$ and $D$. However we need another line through $E$ to compare to. The obvious choice is the line through $E$ and $A$. Let's name that other intersection $X$.

copeland 2013-02-21 19:57:06

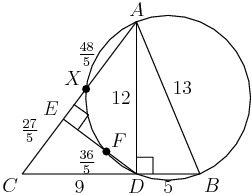
copeland 2013-02-21 19:57:11
What does Power of a Point say for $E$?

matholympiad25 2013-02-21 19:57:58
EF*ED=EX*EA

swe1 2013-02-21 19:57:58
EF*ED=EX*EA

Doooooooooot 2013-02-21 19:57:58
EX*EA = EF*ED

Hydroxide 2013-02-21 19:57:58
EF*ED=EX*EA

Colomnt 2013-02-21 19:57:58
EF * ED = EX * EA

RelaxationUtopia 2013-02-21 19:57:58
EF X ED = EX x EA

planetpeter91 2013-02-21 19:57:58
EX*EA=EF*ED

crastybow 2013-02-21 19:57:58
EF*ED = EX*EA

bookworm83197 2013-02-21 19:57:58
EF*ED=EX*EA

i8sumpi 2013-02-21 19:57:58
EX*(48/5)=EF*(36/5)

copeland 2013-02-21 19:58:02
We get \[EX\cdot EA=EF\cdot ED,\]so\[EX\cdot\frac{48}5=EF\cdot\frac{36}5.\] We can simplify that to

copeland 2013-02-21 19:58:07
\[4EX=3EF.\]

copeland 2013-02-21 19:58:10
(Another 3:4:5 triangle, for what it's worth - that's how Power of a Point works.)

copeland 2013-02-21 19:58:22
Now what can we use to get $EX?$

Lord.of.AMC 2013-02-21 19:59:15
POP C

viker 2013-02-21 19:59:15
Power of a point?

vinayak-kumar 2013-02-21 19:59:15
similar triangles

regularperson 2013-02-21 19:59:15
Similar Triangles

mydogcanpur 2013-02-21 19:59:15
Connect XF and use similar triangles

flyrain 2013-02-21 19:59:15
Power of a point on C?

ic1999 2013-02-21 19:59:15
power of a point again

copeland 2013-02-21 19:59:33
(Those are, philosophically, the same answer since they'll give the same proportion.)

copeland 2013-02-21 19:59:35
We can also apply Power of a Point to $C$, giving\[CD\cdot CB=CX\cdot CA.\]

copeland 2013-02-21 19:59:39
Substituting what we know gives\[9\cdot14=CX\cdot15.\]

copeland 2013-02-21 19:59:44
Therefore $CX=\frac{42}5$, so

copeland 2013-02-21 20:00:03
\[EX=CX-CE=\frac{42}5-\frac{27}5=3.\]

googol.plex 2013-02-21 20:01:07
EX must be 3

guilt 2013-02-21 20:01:07
ex = 3 ef =4

ws5188 2013-02-21 20:01:07
EX=3

zhuangzhuang 2013-02-21 20:01:07
ex=3, so ef=4

swe1 2013-02-21 20:01:07
So EF=4

kdokmeci 2013-02-21 20:01:07
EF=4, then

googol.plex 2013-02-21 20:01:07
so EF is 4 and DF is 16/5

number.sense 2013-02-21 20:01:07
We could drop a perpendicular from B (we know the altitude), and then use that to get AX by pythagorean theorem on BXA - then EA - AX = EX --> our answer (16/5) --> 21

Lord.of.AMC 2013-02-21 20:01:07
EX = 3 and thus EF = 4 and thus FD = 16/5 and 16+5 = 21

nalaxone44 2013-02-21 20:01:07
EF=4, so DF=36/5-4=16/5

mathmaster2012 2013-02-21 20:01:07
EF=4

AkshajK 2013-02-21 20:01:07

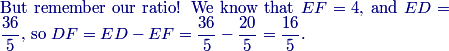
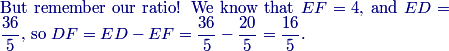
PERFECTION 2013-02-21 20:01:07
so therefore EF=4

sarvottam 2013-02-21 20:01:07
EF=4

anthonyjang 2013-02-21 20:01:07
EF=4, 36/5 - 4=16/5, sum is 21

Aplus95 2013-02-21 20:01:07
EF = 4, DF = DE-EF = 36/5 - 4 = 16/5

i8sumpi 2013-02-21 20:01:07
Therefore EF=16/5. 16+5=21 B.

guilt 2013-02-21 20:01:07
and ef =4. thus df = 36/5 - 4 = 16/5 16+5 =21 B

ninjataco 2013-02-21 20:01:08
and DF is 36/5 - 4 = 16/5?

copeland 2013-02-21 20:01:11
Since $EX=3,$ we get $EF=4$. This makes
\[DF=ED-EF=\frac{36}5-4=\frac{16}5.\]

copeland 2013-02-21 20:01:14
Therefore the answer is $16+5=21,$ (B).

copeland 2013-02-21 20:01:24
There were a lot of ways to solve this problem.

copeland 2013-02-21 20:01:45
I see many of you mentioning some other ways to approach our steps or other ways to get some of these values.

copeland 2013-02-21 20:01:59
I agree. This problem really lends itself to some cool exploration.

vinayak-kumar 2013-02-21 20:02:11
is there a slick one?

rpant1 2013-02-21 20:02:11
was this the quickest?

copeland 2013-02-21 20:02:17
It's an interesting question.

copeland 2013-02-21 20:02:45
I think that POP has many cousins, and those all give different approaches that are spiritually the same.

copeland 2013-02-21 20:02:58
You can use that cyclic quadrilateral to the same ends, for example.

djmathman 2013-02-21 20:03:08
I think the solution involving cyclic quadrilaterals is quickest, but then again that's probably because that's the way I solved it.

copeland 2013-02-21 20:03:17
Alright, next problem.

copeland 2013-02-21 20:03:21

copeland 2013-02-21 20:03:27
What kinds of numbers have exactly 4 positive divisors?

RelaxationUtopia 2013-02-21 20:03:56
P^3 or P1P2

googol.plex 2013-02-21 20:03:56
prime*different prime

crastybow 2013-02-21 20:03:56
Cubes of primes, or product of two primes

kli2000 2013-02-21 20:03:56
cubes, and prime * prime

AlcumusGuy 2013-02-21 20:03:56
numbers in the form p_1*p_2 and p_1^3

Colomnt 2013-02-21 20:03:56
p_1*p_2 or p^3

thecmd999 2013-02-21 20:03:56
p^3 or pq for primes p, q

centralbs 2013-02-21 20:03:56
p^3 or pq where p and q are primes

copeland 2013-02-21 20:04:00
A number with 4 positive divisors is either $p^3$ for some prime $p$ or is $pq$ with $p$ and $q$ prime.

copeland 2013-02-21 20:04:04
I bet there are some of each. Let's explore the $m=p^3$ type first. If $m=p^3$ then what is $n?$

theone142857 2013-02-21 20:04:29
1+p+p^2+p^3

Hydroxide 2013-02-21 20:04:29
1+p+p^2+p^3

RotomPlasma 2013-02-21 20:04:29
1+p+p^2+p^3

mathwizard888 2013-02-21 20:04:29
p^3+p^2+p+1

crastybow 2013-02-21 20:04:29
p^3+p^2+p+1

bobthesmartypants 2013-02-21 20:04:29
$p^3+p^2+p+1$

copeland 2013-02-21 20:04:33
$n=1+p+p^2+p^3$.

copeland 2013-02-21 20:04:38
For what $p$ is that in the neighborhood of 2000? (This is the painful part of the problem.)

matholympiad25 2013-02-21 20:05:18
12, 13ish

IMGUNNA 2013-02-21 20:05:18
12

mydogcanpur 2013-02-21 20:05:18
12

viperstrike 2013-02-21 20:05:18
p=13?

rafa2be 2013-02-21 20:05:18
13

copeland 2013-02-21 20:05:22
If $p=10$ then \[1+p+p^2+p^3=1111\]is too small.

copeland 2013-02-21 20:05:26
If $p=11$ then \[1+p+p^2+p^3=\frac{11^4-1}{11-1}=1464.\]

copeland 2013-02-21 20:05:32
Getting closer. . .

copeland 2013-02-21 20:05:35
If $p=12$ then \[1+p+p^2+p^3=(1+12)(1+144)=1885\]

copeland 2013-02-21 20:05:38
OK, one more.

copeland 2013-02-21 20:05:46
If $p=13$ then \[1+p+p^2+p^3=(1+13)(1+169)=2380.\]

Lord.of.AMC 2013-02-21 20:06:06
nope!

Archimedes10 2013-02-21 20:06:06
NOOOOOOO!!!!

centralbs 2013-02-21 20:06:06
so none from that case

viker 2013-02-21 20:06:06
That is too big

j2002 2013-02-21 20:06:06
None of that type.

NextEinstein 2013-02-21 20:06:06
so none for that case.

copeland 2013-02-21 20:06:08
Huh. Crazy. They didn't pick a range with any of these type. Crazy. . .

apple.singer 2013-02-21 20:06:11
(When solving this, I totally didn't realize that m could be p^3. Thankfully it didn't matter

)

copeland 2013-02-21 20:06:14
I know, right?

copeland 2013-02-21 20:06:23
Let's look at the $m=pq$. What is $n$ in this case?

AkshajK 2013-02-21 20:06:29
Saem

regularperson 2013-02-21 20:06:29
Same

VietaFan 2013-02-21 20:06:29
me too

mathdoggy 2013-02-21 20:06:29
Me too!

mathmaster2012 2013-02-21 20:06:29
Same here!

copeland 2013-02-21 20:06:30

swe1 2013-02-21 20:06:51
(p+1)(q+1)

planetpeter91 2013-02-21 20:06:51
(p+1)(q+1)

ben7 2013-02-21 20:06:51
1+p+q+pq

Wickedestjr 2013-02-21 20:06:51
(p + 1)(q + 1)

bestwillcui1 2013-02-21 20:06:51
1+p+q+pq

number.sense 2013-02-21 20:06:51
(p+1)(q+1)

nuggetfan 2013-02-21 20:06:51
1+p+q+pq

EpicMath31415 2013-02-21 20:06:51
1+p+q+pq

OCed 2013-02-21 20:06:51
(p+1)(q+1)

distortedwalrus 2013-02-21 20:06:51
(p+1)(q+1)

sparkles257 2013-02-21 20:06:51
(1 + p)(1+q)

nalaxone44 2013-02-21 20:06:51
1+p+pq+q

copeland 2013-02-21 20:06:52
The sum of the divisors of $pq$ is \[1+p+q+pq=(p+1)(q+1).\]

copeland 2013-02-21 20:06:56
Alright, so let's check 2010. How does that factor?

copeland 2013-02-21 20:07:10
(Was anybody working on math contests 3 years ago?

)

djmathman 2013-02-21 20:07:32
2*3*5*67

Piya31415 2013-02-21 20:07:32
2,3,67,5

kdokmeci 2013-02-21 20:07:32
67*2*3*5

mathdoggy 2013-02-21 20:07:32
2 * 67 * 5 * 3

Imsacred 2013-02-21 20:07:32
2*3*5*67

VietaFan 2013-02-21 20:07:32
2010 = 5*3*2*67

googol.plex 2013-02-21 20:07:32
2*3*5*67

flyrain 2013-02-21 20:07:32
2*5*3*67

kdokmeci 2013-02-21 20:07:32
67*2*3*5

blippy1998 2013-02-21 20:07:32
2*3*5*67

guilt 2013-02-21 20:07:32
2*3*5*67

ic1999 2013-02-21 20:07:32
2*3*5*67

copeland 2013-02-21 20:07:36
\[2010=2\cdot3\cdot5\cdot67.\]

copeland 2013-02-21 20:07:41
Is that of the form $(p+1)(q+1)?$

RelaxationUtopia 2013-02-21 20:08:26
Notice that the product is divisible by 4, unless one of the primes is 2. Therefore any even number must be divisible by 4.

AlcumusGuy 2013-02-21 20:08:26
No; we need at least 2 factors of 2

RelaxationUtopia 2013-02-21 20:08:26
nope - must have factor of 2 in each product

theone142857 2013-02-21 20:08:26
No, because one is even and one is odd.

regularperson 2013-02-21 20:08:26
No, because p and q cannot both be odd

copeland 2013-02-21 20:08:27
If $p$ and $q$ are both odd, then $(p+1)(q+1)$ is a multiple of 4, but 2010 is not a multiple of 4. The only possibility is that \[2010=(2+1)(q+1).\]

copeland 2013-02-21 20:08:32
Is the solution, $q,$ to this equation prime?

wmcho1007 2013-02-21 20:08:56
cant be, since if p is 2, then q must be 669 which is not prime

matholympiad25 2013-02-21 20:08:56
q=669, not prime

wmcho1007 2013-02-21 20:08:56
in which case, q=669 which is not prime

theone142857 2013-02-21 20:08:56
no 669, is not prime

googol.plex 2013-02-21 20:08:56
669 is 3*223

AlcumusGuy 2013-02-21 20:08:56
q = 669, which is divisible by 3

regularperson 2013-02-21 20:08:56
It is 669, which is divisible by

copeland 2013-02-21 20:08:59
We write \[2010=(2+1)(669+1).\]

copeland 2013-02-21 20:09:02
But 669 is not prime since it is a multipile of 3.

copeland 2013-02-21 20:09:05
One down. . .

copeland 2013-02-21 20:09:12
Let's explore the parity of $p$ and $q$ a little more.

copeland 2013-02-21 20:09:16
If $p=2$ then $(p+1)(q+1)=3(q+1)$ is a multiple of 6.

copeland 2013-02-21 20:09:19
If $p$ and $q$ are both odd, then $(p+1)(q+1)$ is a multiple of 4.

copeland 2013-02-21 20:09:25
\[\begin{array}{c|c|c}
N~&~\text{div by 4}~&~\text{div by 6}~\\
\hline
2010&\text{No}&{\color{red}{\text{Yes}}}\\
2011&\text{No}&\text{No}\\
2012&{\color{red}{\text{Yes}}}&\text{No}\\
2013&\text{No}&\text{No}\\
2014&\text{No}&\text{No}\\
2015&\text{No}&\text{No}\\
2016&{\color{red}{\text{Yes}}}&{\color{red}{\text{Yes}}}\\
2017&\text{No}&\text{No}\\
2018&\text{No}&\text{No}\\
2019&\text{No}&\text{No}
\end{array}\]

copeland 2013-02-21 20:09:32
We know that 2010 fails.

copeland 2013-02-21 20:09:35
What about 2012?

AlcumusGuy 2013-02-21 20:10:37
2^2 * 503, but it won't work

VietaFan 2013-02-21 20:10:37
2012 = 503*4 fails

bobthesmartypants 2013-02-21 20:10:37
2012=2*2*503

zhuangzhuang 2013-02-21 20:10:37
2^2*503, fails

Lord.of.AMC 2013-02-21 20:10:37
no, 2012 = 2*503 but 503 is prime already

mikhailgromov 2013-02-21 20:10:37
2012/4=503

RelaxationUtopia 2013-02-21 20:10:37
It fails too - try with two fours and get 503 as prime and it doesn't work

ws5188 2013-02-21 20:10:37
2*2*503

dardarmath 2013-02-21 20:10:37
2012= 4*503

willwin 2013-02-21 20:10:37
2^2*503

copeland 2013-02-21 20:10:41
When we factor 2012, we get $2012=2^2\cdot503,$ and 503 is prime. This one fails, too.

copeland 2013-02-21 20:10:56
So what's the answer to this problem?

theone142857 2013-02-21 20:11:29
Looking at the answer choices we see that it must be 1

mydogcanpur 2013-02-21 20:11:29
2016 is the only one left (A)

mathfuns 2013-02-21 20:11:29
1

Hydroxide 2013-02-21 20:11:29
1

Lord.of.AMC 2013-02-21 20:11:29
ans is 1

guilt 2013-02-21 20:11:29
since there is no answer choice 0 it must be a 1

PERFECTION 2013-02-21 20:11:29
so only one that is nice is 2016, so 1, A

willwang123 2013-02-21 20:11:29
(A)=1

AlcumusGuy 2013-02-21 20:11:29
2016 must work, so 1

VietaFan 2013-02-21 20:11:29
Since 1 is the lowest it is 1

AnishS 2013-02-21 20:11:29
1 the only number is 2016

wmcho1007 2013-02-21 20:11:29
only 2016 is possible choice, so A

copeland 2013-02-21 20:11:33
Since 2016 is the only possible success, and we know the smallest available answer is 1, 2016 must be a success. The answer must be (A).

copeland 2013-02-21 20:11:38
That's pretty unsatisfying, using the answer choices to show existence. Do you see an actual factorization?

Lord.of.AMC 2013-02-21 20:12:27
2016 works, (1+41)(1+47)

RelaxationUtopia 2013-02-21 20:12:27
The number m is 1509, because 1509+503+3+1 = 2016

VietaFan 2013-02-21 20:12:27
Testing 2016, we get 2016 = 2*1008 = 8*252. 7 and 251 are both prime.

mathwizard888 2013-02-21 20:12:27
BTW, 2016=(41+1)(47+1)

PERFECTION 2013-02-21 20:12:27
(41,47) and (3,503) works

djmathman 2013-02-21 20:12:27
2016=(3+1)(503+1)

AlcumusGuy 2013-02-21 20:12:27
2^5 * 3^2 * 7 = 41(47)

copeland 2013-02-21 20:12:33
Since we already factored $2012=4\cdot503,$ and $2016$ is 4 greater, we find \[2016=(3+1)(503+1)\]with 503 prime.

copeland 2013-02-21 20:12:42
We also get lots of other valid factorizations,\[2016=(7+1)(251+1)=(11+1)(167+1)=(23+1)(83+1)=(41+1)(47+1).\]

Imsacred 2013-02-21 20:13:00
maybe in the year 2380ish AMC will recycle this problem so p^3 becomes relevant

copeland 2013-02-21 20:13:12
"Memmed it. That was on the AMC 3 centuries ago. . ."

copeland 2013-02-21 20:13:23
Alright. This problem. . .

copeland 2013-02-21 20:13:26

copeland 2013-02-21 20:13:37
Ever notice how the confused characters in math problems are all number theorists? It's never, "Bernardo draws a circle on the blackboard and later Leroy thinks it's a pentagon. . ."

copeland 2013-02-21 20:13:48
In this type of number theory problem, where we take an integer as input ($N$ here) and get something as output (the last two digits of whatever LeRoy created), I like to start by figuring out the period of operation. What's the period here? (When does the output start repeating?)

matholympiad25 2013-02-21 20:14:51
Every 900

googol.plex 2013-02-21 20:14:51
well we have obvious repeats every 900...

willwang123 2013-02-21 20:14:51
no wait 25*36=900

joshxiong 2013-02-21 20:14:51
25*36=900

Piya31415 2013-02-21 20:14:51
900?

googol.plex 2013-02-21 20:14:51
25*36 is 900, and when you do that the tens and units stay the same

theone142857 2013-02-21 20:14:51
5^2*6^2=900

copeland 2013-02-21 20:14:53
Since the last two digits base 5 representation repeat every 25 terms and the last 2 digits of the base 6 representation repeat every 36 terms, the whole sequence repeats every $25\cdot36=900$ terms.

copeland 2013-02-21 20:14:57
The period is thus (a factor of) 900.

copeland 2013-02-21 20:15:00
Is that interesting?

apple.singer 2013-02-21 20:15:26
There are 900 3-digit numbers

Relativity1618 2013-02-21 20:15:26
same number of values for N

willwang123 2013-02-21 20:15:26
yes because 100-999 is 900 numbers.

j2002 2013-02-21 20:15:26
yes all three digit numbers are different mod 900

Seedleaf 2013-02-21 20:15:26
theres only 900 three digit integers

copeland 2013-02-21 20:15:30
Well, there are exactly 900 three-digit integers, so the set of outputs (counting repeats) from $N=100-999$ is the same as the set of outputs from $1-900$ or $0-899.$

RelaxationUtopia 2013-02-21 20:15:37
Why are there so many problems involving Bernardo?

kdokmeci 2013-02-21 20:15:37
By the way, there were Bernardo and LeRoy on a previuos test, too.

copeland 2013-02-21 20:15:54
These are the chairs of the AMC 10 and AMC 12.

copeland 2013-02-21 20:16:10
I'm sure when they actually write numbers on a chalkboard, they make a note of the base.

Sesquipedalian 2013-02-21 20:16:22
Why do math people name the things they sit on?

copeland 2013-02-21 20:16:32
OK, back to the problem. . .

copeland 2013-02-21 20:16:35
I'm overwhelmed. What should you do when you're overwhelmed with a problem like this?

Lord.of.AMC 2013-02-21 20:17:11
make it easier

theone142857 2013-02-21 20:17:11
Small values

mathmaster2012 2013-02-21 20:17:11
Experiment!

jasonmathcounts 2013-02-21 20:17:11
try out some numbers

AlcumusGuy 2013-02-21 20:17:11
do a simpler problem

Wickedestjr 2013-02-21 20:17:11
Test a few example numbers

richard4912 2013-02-21 20:17:11
smaller cases

54math 2013-02-21 20:17:11
try a simplier version

copeland 2013-02-21 20:17:14
Two important strategies come to mind here: reduce to a simpler problem and try some examples.

copeland 2013-02-21 20:17:18
What's the simpler problem?

Jerry1997 2013-02-21 20:17:44
1 digit

RelaxationUtopia 2013-02-21 20:17:44
Just base 5 or base 6 unit digit

googol.plex 2013-02-21 20:17:44
only last digits?

willwang123 2013-02-21 20:17:44
a 1-digit positive integer

mikhailgromov 2013-02-21 20:17:44
Last digit

mathman98 2013-02-21 20:17:44
One digit integers

colinhy 2013-02-21 20:17:44
only the last digit is the same as that of 2N?

copeland 2013-02-21 20:17:49
Let's just look at the units digits. What's the period when we look at only the units digit?

AkshajK 2013-02-21 20:18:11
30

nuggetfan 2013-02-21 20:18:11
30

Hydroxide 2013-02-21 20:18:11
30

AnishS 2013-02-21 20:18:11
30

sparkles257 2013-02-21 20:18:11
30

VietaFan 2013-02-21 20:18:11
30

regularperson 2013-02-21 20:18:11
30

swe1 2013-02-21 20:18:11
30

vinayak-kumar 2013-02-21 20:18:11
5*6=30

copeland 2013-02-21 20:18:13
The period is $5\cdot6=30.$

copeland 2013-02-21 20:18:16
I can write a table for the first few, only keeping track of the units digit:

copeland 2013-02-21 20:18:18
\[\begin{array}{c|c|c|c}
N~&~\text{base 5}~&~\text{base 6}~&~~~S~~~\\
\hline
0&0&0&0\\
1&1&1&2\\
2&2&2&4\\
3&3&3&6\\
4&4&4&8
\end{array}\]

copeland 2013-02-21 20:18:27
Huh. The first 5 all have units digit equal to $2N.$ I'm starting to think the answer might be 900. . . .

copeland 2013-02-21 20:18:31
\[\begin{array}{c|c|c|c}
~~~N~~~&~\text{base 5}~&~\text{base 6}~&~~~S~~~\\
\hline
{\color{red}{0}}&0&0&0\\
{\color{red}{1}}&1&1&2\\
{\color{red}{2}}&2&2&4\\
{\color{red}{3}}&3&3&6\\
{\color{red}{4}}&4&4&8\\
5&0&5&5\\
6&1&0&1\\
7&2&1&3\\
8&3&2&5\\
9&4&3&7\\
10&0&4&4
\end{array}\]

copeland 2013-02-21 20:18:35
OK, the next few are not so hot.

copeland 2013-02-21 20:18:48
I don't have any bright ideas. However, I do have a lot of paper, and this is going pretty fast.

copeland 2013-02-21 20:18:54
What other $N$ from 0-29 work?

Seedleaf 2013-02-21 20:19:47
just 0,1,2,3,4

regularperson 2013-02-21 20:19:47
None

theone142857 2013-02-21 20:19:47
none

alphaReally 2013-02-21 20:19:47
none

anonymous0 2013-02-21 20:19:47
none?

OCed 2013-02-21 20:19:47
None.

billgates42 2013-02-21 20:19:47
None

burch_c 2013-02-21 20:19:47
none

copeland 2013-02-21 20:19:51
None of them do!

copeland 2013-02-21 20:19:54
\[\begin{array}{c|c|c|c}
~~~N~~~&~\text{base 5}~&~\text{base 6}~&~~~S~~~\\
\hline
{\color{red}{0}}&0&0&{\color{red}{0}}\\
{\color{red}{1}}&1&1&{\color{red}{2}}\\
{\color{red}{2}}&2&2&{\color{red}{4}}\\
{\color{red}{3}}&3&3&{\color{red}{6}}\\
{\color{red}{4}}&4&4&{\color{red}{8}}\\
5&0&5&5\\
6&1&0&1\\
7&2&1&3\\
8&3&2&5\\
9&4&3&7\\
10&0&4&4\\
11&1&5&6\\
12&2&0&2\\
13&3&1&4\\
14&4&2&6\\
15&0&3&3\\
16&1&4&5\\
17&2&5&7\\
18&3&0&3\\
19&4&1&5\\
20&0&2&2\\
21&1&3&4\\
22&2&4&6\\
23&3&5&8\\
24&4&0&4\\
25&0&1&1\\
26&1&2&3\\
27&2&3&6\\
28&3&4&7\\
29&4&5&9
\end{array}\]

copeland 2013-02-21 20:20:07
Alright, what did we just show? Does our 1-digit experiment tell us anything about the 2-digit case?

RelaxationUtopia 2013-02-21 20:21:10
OH so the only ones we have to consider for the second condition are those congruent to the first 5 mod 30!!

matholympiad25 2013-02-21 20:21:10
We can simplify our work even more by just considering the unit digit equalling 0 case

apple.singer 2013-02-21 20:21:10
Well all the numbers in the 2-digit case must be 0-4 mod 30

Jerry1997 2013-02-21 20:21:10
only 0,1,2,3,4 mod (30) can work at all for 2 digits?

ic1999 2013-02-21 20:21:10
we only need to try first 5 of every 30

copeland 2013-02-21 20:21:11
We know that the units digit in the 2-digit case is just the 1-digit case again. We also know that the units digits repeat every 30 and that we need $N$ to be 0,1,2,3,4, or 5 modulo 30 in order to work. Therefore we know $N=30M+0,$ $30M+1,$ $30M+2,$ $30M+3,$ or $30M+4.$

copeland 2013-02-21 20:21:19
And how does the choice 0, 1, 2, 3, or 4 affect the tens digit?

Voytek 2013-02-21 20:22:17
It doesn't.

mydogcanpur 2013-02-21 20:22:17
It doesn't

billgates42 2013-02-21 20:22:17
It doesnt affect it

numbertheory 2013-02-21 20:22:17
it doesn't

apple.singer 2013-02-21 20:22:17
not at all?

Ty330 2013-02-21 20:22:17
None whatsoever

copeland 2013-02-21 20:22:21
It doesn't. There is no carrying since the largest value we get is 4+4<10.

copeland 2013-02-21 20:22:28
So for each $M$, either all 5 work or none of them work.

copeland 2013-02-21 20:22:31
So now is it time to think of something clever to do?

regularperson 2013-02-21 20:23:13
No, keep on going

anwang16 2013-02-21 20:23:13
try each one? not very clever

mathmaster2012 2013-02-21 20:23:13
Test 1 for each case.

Jerry1997 2013-02-21 20:23:13
look at 0,30,60,90 and find a pattern

RelaxationUtopia 2013-02-21 20:23:13
Notice that there are 30 repeats so consider one of the unit digits as case and try that for different ten's digits

mathman98 2013-02-21 20:23:13
Treat tens digit like one's digit

copeland 2013-02-21 20:23:16
No. Let's just make another chart and be done with it.

copeland 2013-02-21 20:23:21
Cleverness is for suckers.

copeland 2013-02-21 20:23:26
\[\begin{array}{c|c|c|c}
~~~30M+0~~~&~\text{base 5}~&~\text{base 6}~&~~~S~~~\\
\hline
0&00&00&00\\
30&10&50&60\\
60&20&40&60\\
90&30&30&60\\
120&40&20&60\\
150&00&10&10\\
180&10&00&10\\
210&20&50&70\\
240&30&40&70\\
270&40&30&70\\
300&00&20&20\\
330&10&10&20\\
360&20&00&20\\
390&30&50&80\\
420&40&40&80\\
450&00&30&30\\
480&10&20&30\\
510&20&10&30\\
540&30&00&30\\
570&40&50&90\\
600&00&40&40\\
630&10&30&40\\
660&20&20&40\\
690&30&10&40\\
720&40&00&40\\
750&00&50&50\\
780&10&40&50\\
810&20&30&50\\
840&30&20&50\\
870&40&10&50
\end{array}\]

copeland 2013-02-21 20:23:29
Which ones of those are good?

1ph0ne 2013-02-21 20:24:42
0

C00LDUDE 2013-02-21 20:24:42
30

Jerry1997 2013-02-21 20:24:42
0 and 30

copeland 2013-02-21 20:24:44
OK, those work.

copeland 2013-02-21 20:24:48
See any others?

mcdonalds106_7 2013-02-21 20:25:27
360,390,720

bookie331 2013-02-21 20:25:27
720

alquila 2013-02-21 20:25:27
360,390,720,

Cobra2010 2013-02-21 20:25:27
720

googol.plex 2013-02-21 20:25:27
just 360 390 and 720

DaChickenInc 2013-02-21 20:25:27
720

AlcumusGuy 2013-02-21 20:25:27
and 720

mathmaster2012 2013-02-21 20:25:27
390,720

bookie331 2013-02-21 20:25:27
390 and 720

nuggetfan 2013-02-21 20:25:27
360, 390, 720

danielguo94 2013-02-21 20:25:27
360

distortedwalrus 2013-02-21 20:25:27
720

copeland 2013-02-21 20:25:41
Here are the winners, 0, 30, 360, 390, and 720.

copeland 2013-02-21 20:25:45
\[\begin{array}{c|c|c|c}
~~~30M+0~~~&~\text{base 5}~&~\text{base 6}~&~~~S~~~\\
\hline
{\color{red}{0}}&00&00&{\color{red}{00}}\\
{\color{red}{30}}&10&50&{\color{red}{60}}\\
60&20&40&60\\
90&30&30&60\\
120&40&20&60\\
150&00&10&10\\
180&10&00&10\\
210&20&50&70\\
240&30&40&70\\
270&40&30&70\\
300&00&20&20\\
330&10&10&20\\
{\color{red}{360}}&20&00&{\color{red}{20}}\\
{\color{red}{390}}&30&50&{\color{red}{80}}\\
420&40&40&80\\
450&00&30&30\\
480&10&20&30\\
510&20&10&30\\
540&30&00&30\\
570&40&50&90\\
600&00&40&40\\
630&10&30&40\\
660&20&20&40\\
690&30&10&40\\
{\color{red}{720}}&40&00&{\color{red}{40}}\\
750&00&50&50\\
780&10&40&50\\
810&20&30&50\\
840&30&20&50\\
870&40&10&50
\end{array}\]

copeland 2013-02-21 20:25:53
So what's the answer?

anthonyjang 2013-02-21 20:26:42
E, 25?

vinayak-kumar 2013-02-21 20:26:42
5*5=(E) 25

regularperson 2013-02-21 20:26:42
WE HAVE 5 WINNERS! 5 CHOICES FOR EACH, OUR ANSWER IS 25!

Ty330 2013-02-21 20:26:42
5*5 = 25

savefiles 2013-02-21 20:26:42
E!

Lord.of.AMC 2013-02-21 20:26:42
5*5 = 25

VietaFan 2013-02-21 20:26:42
25, 5 last digits for each

amoghgaitonde 2013-02-21 20:26:42
25 (E)

zhuangzhuang 2013-02-21 20:26:42
25

Mrdavid445 2013-02-21 20:26:42
25

Lord.of.AMC 2013-02-21 20:26:42
5 for the units, 5 for tens, 5*5 = 25.

JFC 2013-02-21 20:26:42
5*5=(E) 25

ws5188 2013-02-21 20:26:42
25

copeland 2013-02-21 20:27:21
There are 5 successful tens digits, and each gets 5 successful ones digits, so the answer is $5\cdot5=25,$ (E).

copeland 2013-02-21 20:28:35
A couple of people are unhappy that we included, say, 33. Why is that cool?

copeland 2013-02-21 20:28:41
Why is it cool to include 33?

copeland 2013-02-21 20:28:45
What are we really saying when we count 33?

apple.singer 2013-02-21 20:29:11
because 933 works just as well

mcdonalds106_7 2013-02-21 20:29:11
add 900 to it

nuggetfan 2013-02-21 20:29:11
33 (mod 900)

Imsacred 2013-02-21 20:29:11
that 933 works

copeland 2013-02-21 20:29:21
33 is just the residue class mod 900. We're really counting 933 when we say 33 up there.

copeland 2013-02-21 20:29:29
Incidentally, you might have noticed that in the 1-digit case, there was exactly one solution for each of the five possible ones digits of $2N$. You might have conjectured that the same holds for the tens digit. This conjecture does hold and gives a nice quick way to guess that the answer is 25.

copeland 2013-02-21 20:29:42
(There are more sophisticated ways to solve this problem, but they're not any easier, definitely not any faster, not really that enlightening, and more prone to error.)

copeland 2013-02-21 20:30:00
Oh, look! We just finished the AMC10. Congrats everyone.

copeland 2013-02-21 20:30:24
Let's take a small break.

copeland 2013-02-21 20:30:47
Everyone give me your favorite one-line proof for Problem 12B, #16.

copeland 2013-02-21 20:30:50

Voytek 2013-02-21 20:33:49
Since 2013=61*3*11 it must have a 61! on top and since 59 is the biggest prime under 61 it must have a 59! on bottom so 61-59=2 (B)

crastybow 2013-02-21 20:33:49
2013 = 3*11*61, b_1 must be the largest prime under 61, so 61-59=2 (B)

wcao9311 2013-02-21 20:33:49
2013=61x11x 3, smallest prime under 61 is 59, and 61-59 is 2, we have 59 because you must cancel it out frm r

flyrain 2013-02-21 20:33:49
We have 2013=3*11*61. Thus, a_1 has to be 61. We can have 3 included in the 60, and since 59 is prime, we have a_1=61 and b_1=59. Thus, We have 61-59=B) 2

RotomPlasma 2013-02-21 20:33:49
2013=61*11*3, so the top will have 61! as the first term, and the bottom needs to eliminate 60! but 60 can be expressed in smaller factorials so the first term of the denominator will actually be the largest prime smaller than 60 which is 59, so 61-59=2 (B)

ajb 2013-02-21 20:33:49
There must be a 61 in the numerator, but the 59 must cancel out, and 60 is clearly possible to cancel without using 60!, so 61-59=2

teranz0 2013-02-21 20:33:49
61 is the largest prime factor of 2013. 60 has 12 in it, which does not divide 12, so we need to cancel it wit the 60 in 61! by putting 60! on the bottom. 61-60=1

googol.plex 2013-02-21 20:33:49
We have to have 61 in the numerator, and 59 in the denominator so lets use 61! and 59!. We also need an 11 and a 3 so we have 11! and 3! in numerator and 10! and 2! in denominator. We need another 60 in the denominator, so we put a 5! in the denominator and a 2! in the numerator. Thus 61 is a_1 and 59 is b_1 so we have B 2

RelaxationUtopia 2013-02-21 20:33:49
Or "Oh factorials take up every composite numbers, only ones that matter are the prime ones, namely the largest one. Top must be 61 and bottom can be as low as 59, so 2". I wish I got this on the actual test instead of looking at it and saying 61 and 60 so 1.

copeland 2013-02-21 20:33:51
When we factor, we get $2013=3\cdot11\cdot61$. We know that we HAVE to have at least $61!$ in the numerator and we have to have at least a $51!$ in the denominator. We can build such a representation with those values, so the answer must be $a_1+b_1=61+59=120.$ These have a diference of 2.

copeland 2013-02-21 20:34:22
Who's ready for the 12 now?

AkshajK 2013-02-21 20:35:15
me

lostinhyperspace 2013-02-21 20:35:15
me!

theone142857 2013-02-21 20:35:15
me

clear 2013-02-21 20:35:15
lets go!

Archimedes10 2013-02-21 20:35:15
I am.

mathman500 2013-02-21 20:35:15
I am!

mathgenius64 2013-02-21 20:35:15
me

gab9810 2013-02-21 20:35:15
2013=7*61*359! not 51!

mathdoggy 2013-02-21 20:35:15
everyone

IceBeam 2013-02-21 20:35:15
I"m Ready!

copeland 2013-02-21 20:35:20

copeland 2013-02-21 20:35:23
Uh-oh! Vocabulary question. What's a directrix?

thecmd999 2013-02-21 20:36:23
parabolas are equidistant from a fixed point (focus) and a line (directrix)

1ph0ne 2013-02-21 20:36:23
Opposite from the focus, same distance with the focus fro the vertex.

kdokmeci 2013-02-21 20:36:23
Its the line where theparabola is the same distance from the focus. Uh, so much vocab

sammyMaX 2013-02-21 20:36:23
A line. The distance between the directrix and focus is constant

mrwoodpusher 2013-02-21 20:36:23
Parabolas are defined by a line, the directrix, and a point, the focus, and the distance from each point on the parabola to the point and the line are equal.

bookworm83197 2013-02-21 20:36:23
the line which is the same distance away from the point as the focus? :-/

trophies 2013-02-21 20:36:23
Any point on a parabola is equidistant from the focus and the directrix...

distortedwalrus 2013-02-21 20:36:23
the line such that the distance between any point on the parabola and the focus of the parabola equals the distance to that line

copeland 2013-02-21 20:36:29

copeland 2013-02-21 20:36:31
Given a point and a line not containing that point, we can construct the locus of all points that are equidistant from the point and line. The line used in this construction is called the directrix of the parabola.

copeland 2013-02-21 20:36:40
Let's think about when parabolas that share a focus intersect. If we have a parabola with directrix $L$ and focus $F$ and a parabola with directrix $K$ and focus $F$, and we also have a point $X$ on the parabolas associated to each, what can we say about $X?$

copeland 2013-02-21 20:37:07

OCed 2013-02-21 20:38:02
It's equidistant from both lines

Imsacred 2013-02-21 20:38:02
X is equidistant to K and L

swe1 2013-02-21 20:38:02
X is on the angle bisector of directrixes?

linpaws 2013-02-21 20:38:02
X is equidistant from L and K.

kdokmeci 2013-02-21 20:38:02
Equidistant from each directesx?

mrwoodpusher 2013-02-21 20:38:02
it is equidistant from both lines

copeland 2013-02-21 20:38:06
The distance from $X$ to $F$ is the same as the distance from $X$ to $L$ and from $X$ to $K$.

copeland 2013-02-21 20:38:09
Therefore the circle with center $F$ and radius $XF$ passes through $F$. It also has to be tangent to each directrix at the point nearest to $X$.

copeland 2013-02-21 20:38:19

copeland 2013-02-21 20:38:27
How many times do parabolas with non-parallel directrices intersect?

RelaxationUtopia 2013-02-21 20:39:04
TWO

Voytek 2013-02-21 20:39:04
2

Jerry1997 2013-02-21 20:39:04
2

VietaFan 2013-02-21 20:39:04
2

djmathman 2013-02-21 20:39:04
twice

roilior 2013-02-21 20:39:04
2 times

RexT95 2013-02-21 20:39:04
2

ninjataco 2013-02-21 20:39:04
twice?

mathwizard888 2013-02-21 20:39:04
2

mprashker 2013-02-21 20:39:04
twice

mssmath 2013-02-21 20:39:04
two

joshxiong 2013-02-21 20:39:04
Twice

copeland 2013-02-21 20:39:08
Two. Given any two lines and any point not on those lines, there are two circles tangent to both lines that contain the point.

copeland 2013-02-21 20:39:11

copeland 2013-02-21 20:39:15

copeland 2013-02-21 20:39:23
There's a nice way to see that.

copeland 2013-02-21 20:39:38
The "smaller arc" of the circle, as we move the center away from the intersection, sweeps out the entire region.

copeland 2013-02-21 20:39:44
The "larger arc" does so as well.

copeland 2013-02-21 20:40:12
There's one time, as we are increasing the radius, that the smaller arc hits the point in its sweeping.

copeland 2013-02-21 20:40:17
The same holds for the larger arc.

copeland 2013-02-21 20:40:42
What about when the lines are parallel?

ic1999 2013-02-21 20:41:31
none or twice

program4 2013-02-21 20:41:31
the parabolae either intersect twice or never

colinhy 2013-02-21 20:41:31
Sometimes it will intersect twice but other times it won't intersect

kli2000 2013-02-21 20:41:31
sometimes 2, sometimes 0

copeland 2013-02-21 20:41:35
Ah! There are cases.

copeland 2013-02-21 20:41:43
When do they intersect?

RexT95 2013-02-21 20:42:22
when one is upside down

number.sense 2013-02-21 20:42:22
when they are oriented in opposite directions

flyrain 2013-02-21 20:42:22
the point is betwwen the directrixes

nuggetfan 2013-02-21 20:42:22
when one is on one side and one is on the other

mcdonalds106_7 2013-02-21 20:42:22
2 iff directrix is on same side of focus

copeland 2013-02-21 20:42:38
If two lines are parallel and we are given a point between them, there are exactly two circles that contain that point.

copeland 2013-02-21 20:42:43

copeland 2013-02-21 20:42:47

copeland 2013-02-21 20:42:53
However, no circles that are tangent to both lines contain any points outside, so if $F$ is not between the directrices, the two parabolas cannot intersect.

copeland 2013-02-21 20:43:06

copeland 2013-02-21 20:43:11
What parabolas intersect the parabola with directrix $y=2x+3?$

copeland 2013-02-21 20:44:44
What about when the slope is -2?

nuggetfan 2013-02-21 20:45:38
yes, all

kli2000 2013-02-21 20:45:38
yes

ninjataco 2013-02-21 20:45:38
yes, they will intersect.

roilior 2013-02-21 20:45:38
you forgot to post their answers

VietaFan 2013-02-21 20:45:38
2 hits

copeland 2013-02-21 20:45:54
Yes, those all intersect because they point a different direction.

copeland 2013-02-21 20:45:56
Every directrix with slope $-2,$ $-1,$ or $1$ gives a parabola that intersects twice. There are $6\cdot4=24$ such parabolas giving $48$ intersections.

copeland 2013-02-21 20:46:07
What about when $a=2?$

copeland 2013-02-21 20:46:24
What values of $b$ give us an intersection with the parabola defined by $y=2x+3?$

sammyMaX 2013-02-21 20:46:36
you forgot to list a=0

copeland 2013-02-21 20:46:43
Right, thank you.

copeland 2013-02-21 20:46:49
We'll correct the count at the end.

VietaFan 2013-02-21 20:47:16
All parabolas with directrix slope != 2 and y = 2x+k where k <= -3

piguy314 2013-02-21 20:47:16
All except when b is 1 or 2?

number.sense 2013-02-21 20:47:16
-1, -2, and -3 are the y intercepts of directrices of those parabolas

program4 2013-02-21 20:47:16
those with b negative

kli2000 2013-02-21 20:47:16
-1, -2, -3

piguy314 2013-02-21 20:47:16
-1,-2,-3

ParallelProcess 2013-02-21 20:47:16
it has to be on the other side of the focus, so b<0

program4 2013-02-21 20:47:16
b=-3, -2, -1

copeland 2013-02-21 20:47:19
If the slope of the directrix is 2, then we get either 2 or 0 intersections. We get 2 intersections from those directrices on the opposite side of $F=(0,0)$. We can determine this by the $y$-intercepts.

copeland 2013-02-21 20:47:25
The directrices $2x-3,$ $2x-2,$ and $2x-1$ each give two more intersections and the directrices $2x+1$ and $2x+2$ do not give parabolas that intersect the given parabola at all.

copeland 2013-02-21 20:47:59
This parabola has $48+6=54$ intersections.

copeland 2013-02-21 20:48:05
Generally, when do two parabolas fail to intersect?

Voytek 2013-02-21 20:48:41
When their directrices are parallel and they are facing the same side

ic1999 2013-02-21 20:48:41
when they have parallel directrices and they are facing the same direction

program4 2013-02-21 20:48:41
same a, same sign of b

kli2000 2013-02-21 20:48:41
when slopes are the same, and (0, 0) is not inbeween the lines

VietaFan 2013-02-21 20:48:41
When there are parallel directrixes on the same side of the origin.

mcdonalds106_7 2013-02-21 20:48:41
iff directrices have same slope and are on same side of focus

copeland 2013-02-21 20:48:45
A pair of parabolas will only fail to intersect when their directrices have the same slope and the $y$-intercepts have the same sign.

copeland 2013-02-21 20:48:48
So how many total intersections are there?

FrozenFury 2013-02-21 20:50:28
810

number.sense 2013-02-21 20:50:28
60 overcounts

mcdonalds106_7 2013-02-21 20:50:28

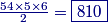
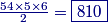
ksun48 2013-02-21 20:50:28
I mean 870 - 60 = 810

kli2000 2013-02-21 20:50:28
(has to be a multiple of 54)

VietaFan 2013-02-21 20:50:28
54*30/2 or 810 (C)

roilior 2013-02-21 20:50:28
810

program4 2013-02-21 20:50:28
810

copeland 2013-02-21 20:50:31
There are \[\frac{30\cdot27}2\]intersecting pairs and each pair intersects twice, so the total number of intersections is $30\cdot27=810.$ (C)

copeland 2013-02-21 20:50:34
Alternatively, you could just draw all 30 parabolas and count:

copeland 2013-02-21 20:50:39

matholympiad25 2013-02-21 20:51:04
WHOA how could we count that...

copeland 2013-02-21 20:51:05
Come on. There are only 810 intersections there. . . .

copeland 2013-02-21 20:51:13
I get the feeling that this was pretty hard for a 21.

copeland 2013-02-21 20:51:44
Next problem. Back to the world of algebra.

copeland 2013-02-21 20:51:48

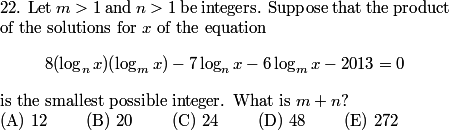
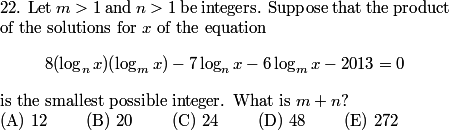
copeland 2013-02-21 20:51:56
(I bet it's probably not 272. . . .)

copeland 2013-02-21 20:52:04
And ew. Logs.

copeland 2013-02-21 20:52:09
And logs with different bases, which are hard to work with.

copeland 2013-02-21 20:52:12
What could make them easier to work with?

sparkles257 2013-02-21 20:52:38
base change?

Voytek 2013-02-21 20:52:38
Use change of base

mrwoodpusher 2013-02-21 20:52:38
change of base

esque 2013-02-21 20:52:38
change of base formula

Jayjayliu 2013-02-21 20:52:38
make them the smae base

hamup1 2013-02-21 20:52:38
Change bases! Or exponents

djmathman 2013-02-21 20:52:38
Change of base!

mapletree14 2013-02-21 20:52:38
change of base

mssmath 2013-02-21 20:52:38
Log rules/ change of base

copeland 2013-02-21 20:52:42
Logs are usually easier to work with if they have the same base.

copeland 2013-02-21 20:52:47
So let's convert everything to the same base.

copeland 2013-02-21 20:52:55
Let's leave the base undecided for now. We'll just write "log" for our new log with the yet-to-be decided base. (You can use base 10 if you feel happier that way.)

copeland 2013-02-21 20:53:03
What is $log_n x$ as a log in our new base?

ic1999 2013-02-21 20:53:24
logx/logn

Voytek 2013-02-21 20:53:24
logx/logn

UrInvalid 2013-02-21 20:53:24
log x/ logn

nuggetfan 2013-02-21 20:53:24
logx/logn

RexT95 2013-02-21 20:53:24
log x / log n

RelaxationUtopia 2013-02-21 20:53:24
logx/logn

toodles9 2013-02-21 20:53:24
logx/logn

piguy314 2013-02-21 20:53:24
log(x)/log(n)

theone142857 2013-02-21 20:53:24
log x/log n

kdokmeci 2013-02-21 20:53:24
logx/logn

copeland 2013-02-21 20:53:28
$$log_n x = \frac{\log x}{\log n}.$$

copeland 2013-02-21 20:53:31
Similarly,
$$
log_m x = \frac{\log x}{\log m}.
$$

copeland 2013-02-21 20:53:34
Now our equation is:
$$
8\left(\frac{\log x}{\log n}\right)\left(\frac{\log x}{\log m}\right) - 7\left(\frac{\log x}{\log n}\right) - 6\left(\frac{\log x}{\log m}\right) - 2013 = 0.
$$

copeland 2013-02-21 20:53:37
Why is this nicer?

thecmd999 2013-02-21 20:54:46
it's a quadratic in log x!

matholympiad25 2013-02-21 20:54:46
Quadratic in log x

mathman500 2013-02-21 20:54:46
Quadratic in logx

UrInvalid 2013-02-21 20:54:46
looks like quadratic equation

axwscedv 2013-02-21 20:54:46
quadratic

copeland 2013-02-21 20:54:49
Because it's a quadratic in log x!

copeland 2013-02-21 20:54:53
In fact, let's set $y = \log x$ to make it look nicer.

copeland 2013-02-21 20:54:56
We can also set $a = \log m$ and $b = \log n$ to make it look even nicer still!

copeland 2013-02-21 20:54:59
Now our equation is just
$$
\frac{8}{ab}y^2 - \left(\frac{6}{a} + \frac{7}{b}\right)y - 2013 = 0.
$$

copeland 2013-02-21 20:55:05
What are we trying to do?

centralbs 2013-02-21 20:55:43
we want product of x's

nuggetfan 2013-02-21 20:55:43
find smallest product

RelaxationUtopia 2013-02-21 20:55:43
minimize prodct of solutions

swe1 2013-02-21 20:55:43
find m and n so that products of solutions is smallest?

copeland 2013-02-21 20:55:49
We want the product of the x's in the original equation to be as small a positive integer as possible. What does that mean for the y's?

mcdonalds106_7 2013-02-21 20:56:24
smallest sum for y's

OCed 2013-02-21 20:56:24
We need the sum of the y's

ic1999 2013-02-21 20:56:24
smallest sum

delta1 2013-02-21 20:56:24
make the sum smallest

number.sense 2013-02-21 20:56:24
minimize product of solutions --> mnimize sum of roots of this quadratic

ParallelProcess 2013-02-21 20:56:24
sum of ys should be smallest

suparnoghoshal100 2013-02-21 20:56:24
summation of the ys

copeland 2013-02-21 20:56:33
Remember, $y = \log x$. So if $x_1$ and $x_2$ are the roots of the original equation, and $y_1 = \log x_1$ and $y_2 = \log x_2.$

copeland 2013-02-21 20:56:37
We see that $\log x_1x_2 = \log x_1 + \log x_2 = y_1 + y_2$.

copeland 2013-02-21 20:56:41
So, to examine the product of the x's, we examine the sum of the y's.

copeland 2013-02-21 20:56:43
But what is the sum of the y's?

ic1999 2013-02-21 20:57:29
vieta's formulas: (6/1 + 7/b)/(8/ab)

evanyao10 2013-02-21 20:57:29
6/a + 7/b all over 8/ab

program4 2013-02-21 20:57:29
$\frac{\frac6a+\frac7b}{\frac8{ab}}$

Imsacred 2013-02-21 20:57:29
(6/a+7/b)/(8/ab)

DaChickenInc 2013-02-21 20:57:29

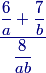
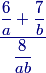
mathwizard888 2013-02-21 20:57:29
(6/a+7/b)/(8/(ab))

distortedwalrus 2013-02-21 20:57:29
(6/a+7/b)/(8/ab)

copeland 2013-02-21 20:57:33
The sum of the roots of our quadratic is
$$
\frac{\frac{6}{a} + \frac{7}{b}}{\frac{8}{ab}}.
$$

copeland 2013-02-21 20:57:37
This can be simplified by multiplying numerator and denominator by $ab$:
$$
\frac{6b + 7a}{8} = \frac78a + \frac34b.
$$

copeland 2013-02-21 20:57:41
And recall that this equals $\log x_1x_2$, where $x_1$ and $x_2$ are the root of the original equation.

copeland 2013-02-21 20:57:51
So what?

copeland 2013-02-21 20:58:40
I don't know much about $a$ and $b$. . . .

copeland 2013-02-21 20:58:51
Let's remember what $a$ and $b$ are! They're the logs of $m$ and $n.$

copeland 2013-02-21 20:59:21
This gives us
$$
\log x_1x_2 = \frac78 \log m + \frac34 \log n.
$$

copeland 2013-02-21 20:59:30
Now what?

number.sense 2013-02-21 20:59:52
raise 10 to the power of this

Voytek 2013-02-21 20:59:52
Combine using log rules

centralbs 2013-02-21 20:59:52
use rule of logs to write the constant as exponents

ic1999 2013-02-21 20:59:52
log(m^(7/8)n^(3/4))

nuggetfan 2013-02-21 20:59:52
power rule?

delta1 2013-02-21 20:59:52
unlog

copeland 2013-02-21 20:59:54
This gives us
$$
\log x_1x_2 = \frac78 \log m + \frac34 \log n.
$$

copeland 2013-02-21 20:59:57
But we can simplify that right side!

copeland 2013-02-21 21:00:01
We get
$$
\log x_1x_2 = \log\left( m^{7/8}n^{3/4} \right).
$$

copeland 2013-02-21 21:00:07
That tells us that $x_1x_2 = m^{7/8}n^{3/4}$.

copeland 2013-02-21 21:00:15
Great. $m$ and $n$ are the integers that we control in the problem. We want to minimize $x_1x_2$, assuming that it, also, is an integer.

copeland 2013-02-21 21:00:20
How do we make this as small a positive integer as possible?

copeland 2013-02-21 21:01:15
We can write it as
$$
x_1x_2 = \sqrt[8]{m^7n^6},
$$
does that help?

centralbs 2013-02-21 21:01:34
try powers of 2

mcdonalds106_7 2013-02-21 21:01:34
m and n are powers of 2

ksun48 2013-02-21 21:01:34
m and n being powers of $2$

copeland 2013-02-21 21:01:43
We need $m^7n^6$ to be as small an 8th power as possible.

copeland 2013-02-21 21:01:46
But also remember that $m$ and $n$ themselves are positive integers greater than 1.

copeland 2013-02-21 21:01:51
We should make $m$ and $n$ both powers of 2. (Throwing in any extra prime factors will just make it larger.) We want to make $m^7n^6 = 2^{8z}$ for some positive $z$.

copeland 2013-02-21 21:01:55
If $m = 2^p$ and $n = 2^q$, what is this equivalent to?

swe1 2013-02-21 21:02:40
7p+6q=8z

evanyao10 2013-02-21 21:02:40
7p + 6q = 8z

nuggetfan 2013-02-21 21:02:40
7p + 6q = 8z

matholympiad25 2013-02-21 21:02:40
7p+6q=8z

flyrain 2013-02-21 21:02:40
6p+6q=8z

kdokmeci 2013-02-21 21:02:40
7p+6q=8z

copeland 2013-02-21 21:02:44
We have to solve $7p + 6q = 8z$ for the smallest possible $z$.

copeland 2013-02-21 21:02:46
What the smallest solution?

program4 2013-02-21 21:03:27
z=4 (p=2, q=3)

bharatputra 2013-02-21 21:03:27
(p, q) (2, 3)

colinhy 2013-02-21 21:03:27
p = 2 q = 3

ParallelProcess 2013-02-21 21:03:27
m = 2^2 and n =2^3?

mathmaster2012 2013-02-21 21:03:27
p=2,q=3,z=4

colinhy 2013-02-21 21:03:27
p = 2 q = 3 z = 4

copeland 2013-02-21 21:03:30
It's $7(2) + 6(3) = 32$. (You can easily check that we can solve for $z < 4$.)

copeland 2013-02-21 21:03:32
And what's the answer to our problem?

sammyMaX 2013-02-21 21:04:11
$\boxed{12}$

bookie331 2013-02-21 21:04:11
2^2 + 2^3 = 12

ksun48 2013-02-21 21:04:11
$4+8 = \fbox{12}$

distortedwalrus 2013-02-21 21:04:11
(A) 12

planetpeter91 2013-02-21 21:04:11
A,12

mathwizard888 2013-02-21 21:04:11
8+4=12 (A)

mydogcanpur 2013-02-21 21:04:11
12 (A)

piguy314 2013-02-21 21:04:11
4+8=12 (A)

VietaFan 2013-02-21 21:04:11
2^3+2^2 = 12(A)

flyrain 2013-02-21 21:04:11
12 A hey...

copeland 2013-02-21 21:04:15
We find $m = 2^2 = 4$ and $n = 2^3 = 8$ produces a product of $x$'s of 32, and that's the smallest possible.

copeland 2013-02-21 21:04:18
The answer is $4+8 = 12$. Answer (A).

copeland 2013-02-21 21:04:24
Good job.

copeland 2013-02-21 21:04:40
Problem 23 on the 10B was the same as that digits problem (Problem 25) from the 12B, so we've handled that one already.

copeland 2013-02-21 21:04:51
7 down, 2 to go!

copeland 2013-02-21 21:04:54

copeland 2013-02-21 21:05:01
Let's start by sketching a picture. I've labeled the known lengths and known angles given by the data in the problem.

copeland 2013-02-21 21:05:06

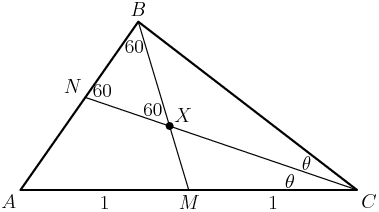
copeland 2013-02-21 21:05:13
As you can tell, BNX is perfectly equilateral.

copeland 2013-02-21 21:05:25
What game do we play with this one?

flyrain 2013-02-21 21:05:59
angle chasing

distortedwalrus 2013-02-21 21:05:59
angle chasing

VietaFan 2013-02-21 21:05:59
Angle chasing

mydogcanpur 2013-02-21 21:05:59
Angle chasing

misgiven 2013-02-21 21:05:59
angle chase?

copeland 2013-02-21 21:06:05
That's actually a great idea here.

copeland 2013-02-21 21:06:18
We have a lot of 60s, so it might turn out fine.

copeland 2013-02-21 21:06:22
I'll save you the trouble:

copeland 2013-02-21 21:06:27

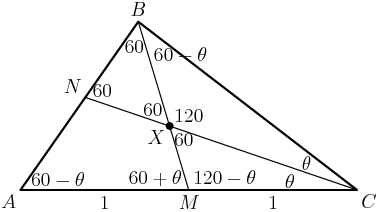
copeland 2013-02-21 21:06:29
Notice anything?

mrwoodpusher 2013-02-21 21:07:38
similar triangles?

ssilwa 2013-02-21 21:07:38
similar triangles!

copeland 2013-02-21 21:07:40
Where?

giratina150 2013-02-21 21:08:05
BCM~ACB

colinhy 2013-02-21 21:08:05
CBM = CAB

sammyMaX 2013-02-21 21:08:05
ABC is similar to BCM

UrInvalid 2013-02-21 21:08:05
ABC and BMC

copeland 2013-02-21 21:08:08
ABC and BMC are similar!

copeland 2013-02-21 21:08:14

copeland 2013-02-21 21:08:20
So?

ssilwa 2013-02-21 21:08:41
we can set up ratios

kdokmeci 2013-02-21 21:08:41
Find proportions

kli2000 2013-02-21 21:08:41
ratios of side lengths

copeland 2013-02-21 21:08:53
Let $x$ be the side length $BC$.

copeland 2013-02-21 21:08:57
What is $x?$

kli2000 2013-02-21 21:09:30
x = $\sqrt{2}$

ic1999 2013-02-21 21:09:30
sqrt2

nuggetfan 2013-02-21 21:09:30
1/x = x/2

colinhy 2013-02-21 21:09:30
sqrt2

nuggetfan 2013-02-21 21:09:30
x = sqrt(2)

sieb11 2013-02-21 21:09:30
sqrt(2)

copeland 2013-02-21 21:09:34
Then we have $\dfrac{AC}{BC} = \dfrac{BC}{MC}$, so $\dfrac{2}{x} = \dfrac{x}{1}$, so $x = \sqrt2$.

copeland 2013-02-21 21:09:40

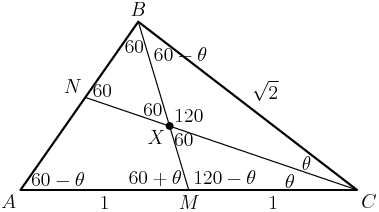
copeland 2013-02-21 21:09:45
Any other similar triangles?

DaChickenInc 2013-02-21 21:10:16

kdokmeci 2013-02-21 21:10:16
BNC~MXC

DaChickenInc 2013-02-21 21:10:16

RexT95 2013-02-21 21:10:16
bxc and xmc

piguy314 2013-02-21 21:10:16
BNC and MXC

OCed 2013-02-21 21:10:16
XMC, BNC

Cradin 2013-02-21 21:10:16
XMC and BNC

henrikjb 2013-02-21 21:10:16
BNC ~ MXC

guilt 2013-02-21 21:10:16
bxc and anc

piguy314 2013-02-21 21:10:16
BNC and MXC

Voytek 2013-02-21 21:10:16
BNC and XMC

copeland 2013-02-21 21:10:19
BNC and MXC are similar!

copeland 2013-02-21 21:10:26

copeland 2013-02-21 21:10:28
And we know $\dfrac{BC}{MC} = \sqrt2$, so
$$
\frac{BN}{MX} = \frac{NC}{XC} = \sqrt2
$$
as well. Which ratio looks more useful?

VietaFan 2013-02-21 21:11:48
Nc/XC

ksun48 2013-02-21 21:11:48
I guess NC/XC

UrInvalid 2013-02-21 21:11:48
NC/XC

flyrain 2013-02-21 21:11:48
NC/XC

misgiven 2013-02-21 21:11:48
NC/XC

thedealer1994 2013-02-21 21:11:48
NC/XC = $\sqrt2$

copeland 2013-02-21 21:11:51
MX doesn't look all that useful. But NC/XC looks useful, because $NC = XC + NX$, and $NX$ is what we want.

copeland 2013-02-21 21:11:55
In fact, let's set $t = BN = BX = NX$. What equation do we have for $t$?

bharatputra 2013-02-21 21:13:20
XCsqrt2=XC+t

VietaFan 2013-02-21 21:13:20
XC+t=sqrt{2}XC; t=sqrt(2)-1XC

nuggetfan 2013-02-21 21:13:20
t+XC/XC = sqrt(2)

VietaFan 2013-02-21 21:13:20
$t = \sqrt{2}-1 (XC)$

thedealer1994 2013-02-21 21:13:20
t/XC=$\sqrt2 - 1$

kli2000 2013-02-21 21:13:20
t/MX = (t+XC)/XC = sqrt2

copeland 2013-02-21 21:13:23

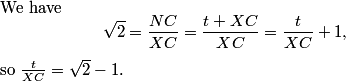
copeland 2013-02-21 21:13:27
But that means
$$
XC = \frac{t}{\sqrt2 - 1} = \frac{t(\sqrt2 + 1)}{(\sqrt2 - 1)(\sqrt2 + 1)} = t(\sqrt2 + 1).
$$

copeland 2013-02-21 21:13:38
Here are our lengths:

copeland 2013-02-21 21:13:40

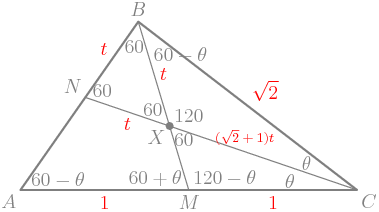
copeland 2013-02-21 21:13:43
Now what?

ksun48 2013-02-21 21:14:24
I guess the only think we can do is LOC then

mprashker 2013-02-21 21:14:24
law of cosines?

thedealer1994 2013-02-21 21:14:24
Law of cosines!

giratina150 2013-02-21 21:14:24
law of cosines

Cradin 2013-02-21 21:14:24
law of cosines

distortedwalrus 2013-02-21 21:14:24
use the law of cosines

Voytek 2013-02-21 21:14:24
Law of cosines

copeland 2013-02-21 21:14:29
On what?

mydogcanpur 2013-02-21 21:15:08
on triangle BXC

theone142857 2013-02-21 21:15:08
BXC

kdokmeci 2013-02-21 21:15:08
BXC

OCed 2013-02-21 21:15:08
BXC

VietaFan 2013-02-21 21:15:08
on BXC

bookie331 2013-02-21 21:15:08
bxc?

fireonice18 2013-02-21 21:15:08
on triangle bxc to find BN

copeland 2013-02-21 21:15:14
We can use the Law of Cosines on BXC.

copeland 2013-02-21 21:15:17
$$
(BC)^2 = (BX)^2 + (XC)^2 - 2(BX)(XC)\cos\angle BXC.
$$

copeland 2013-02-21 21:15:22
This gives
$$
2 = t^2 + \left((\sqrt2 + 1)t\right)^2 - 2t(\sqrt2 + 1)t\cos(120).
$$

copeland 2013-02-21 21:15:26
But $\cos(120) = -\frac12$, so this is
$$
2 = t^2\left(1 + (\sqrt2 + 1)^2 + (\sqrt2 + 1)\right).
$$

copeland 2013-02-21 21:15:38
I'm not going to torture you by asking you to solve that.

copeland 2013-02-21 21:15:41
This simplifies to
$$
2 = t^2(1 + (3 + 2\sqrt2) + (1 + \sqrt2)) = t^2(5 + 3\sqrt2).
$$

copeland 2013-02-21 21:15:49
Hence,
\begin{align*}
t^2 &= \frac{2}{5 + 3\sqrt2} \\
&= \frac{2(5-3\sqrt2)}{(5+3\sqrt2)(5-3\sqrt2)} \\
&= \frac{10 - 6\sqrt2}{25 - 18} \\
&= \frac{10 - 6\sqrt2}{7}, \\
\end{align*}
answer (A).

kdokmeci 2013-02-21 21:16:05
Whew!

copeland 2013-02-21 21:16:07
Whew.

sparkles257 2013-02-21 21:16:17
whoa...

Archimedes10 2013-02-21 21:16:17
What. Just. Happened.

copeland 2013-02-21 21:16:24
Aritmhmetic.

copeland 2013-02-21 21:16:40
Angle chase -> Law of Cosines -> radical manipulating -> Profit.

Voytek 2013-02-21 21:16:59
You mean arithmetic?

copeland 2013-02-21 21:17:08
One man's arithmetic is another man's radical manipulation.

copeland 2013-02-21 21:17:39
I feel like such a subversive when I radically manipulate.

copeland 2013-02-21 21:17:51
OK, one more problem.

Archimedes10 2013-02-21 21:18:07
You mean, one man's Aritmhmetic is another man's radical manipulation.

copeland 2013-02-21 21:18:11
Yes. Gesundheit.

matholympiad25 2013-02-21 21:19:00
What does gesundheit mean?

minimario 2013-02-21 21:19:00
Gesundheit?

sparkles257 2013-02-21 21:19:00
whats a gesundheit?

copeland 2013-02-21 21:19:02
It's German for "Don't sneeze on me."

copeland 2013-02-21 21:19:05

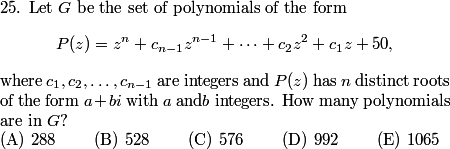
copeland 2013-02-21 21:19:14
OK, great!

copeland 2013-02-21 21:19:16
Polynomials.

copeland 2013-02-21 21:19:21
I like polynomials.

copeland 2013-02-21 21:19:22
What do we know about the roots?

kdokmeci 2013-02-21 21:19:53
Conjugates!

mapletree14 2013-02-21 21:19:53
they occur in conjugate pairs

giratina150 2013-02-21 21:19:53
complex conjugate?

kdokmeci 2013-02-21 21:19:53
They are complex and conjugates!

ic1999 2013-02-21 21:19:53
conjugates of each other

noobynoob 2013-02-21 21:19:53
conjugates

copeland 2013-02-21 21:19:55
Always?

program4 2013-02-21 21:20:31
the complex roots are in conjugates

ksun48 2013-02-21 21:20:31
unless real

ic1999 2013-02-21 21:20:31
unless b is 0

centralbs 2013-02-21 21:20:31
as long as b is not 0

nuggetfan 2013-02-21 21:20:31
unless b = 0

theone142857 2013-02-21 21:20:31
unless b=0

copeland 2013-02-21 21:20:41
Right. Don't forget the possibility of real roots.

copeland 2013-02-21 21:20:44
The real roots are all integers.

copeland 2013-02-21 21:20:47
The non-real roots come in conjugate pairs, $a\pm bi$.

copeland 2013-02-21 21:20:51
Therefore we can factor $P$ as a product of linear pieces, $(z+r)$, and a product of pairs of non-real linear terms,\[(z-(a-bi))(z-(a+bi)).\]

copeland 2013-02-21 21:20:56
What do we get when we expand such a quadratic?

program4 2013-02-21 21:21:50
$z^2-2az+(a^2+b^2)$

alphaReally 2013-02-21 21:21:50
z^2-2za+a^2+b^2

Archimedes10 2013-02-21 21:21:50
This is a difference of two squares factored

mapletree14 2013-02-21 21:21:50

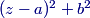
mssmath 2013-02-21 21:21:50
z^2-2z-a^2+b^2

matholympiad25 2013-02-21 21:21:50
z^2-2a+(a^2+b^2)

thedealer1994 2013-02-21 21:21:50
$(z-a)^2+b^2$

VietaFan 2013-02-21 21:21:50
$z^2-2az+a^2+b^2$

copeland 2013-02-21 21:21:54
\[(z-(a-bi))(z-(a+bi))=z^2-2az+(a^2+b^2).\]

copeland 2013-02-21 21:22:03
Now we can factor $P$ as a product of pieces of the form $z+r$ with $r$ an integer and pieces of the form
\[z^2-2az+(a^2+b^2),\]
where $a$ and $b$ are integers.

copeland 2013-02-21 21:22:11
When we factor $P$ into linear terms and quadratic terms with nonreal roots (we'll call such factors "irreducibles"), that determines a factorization of 50.

copeland 2013-02-21 21:22:26
Make sure you understand that statement. One example is the factorization\[(z-5)(z-2)(z^2+1)(z^2+z+5),\] with 2 irreducible linear factors and 2 irreducible quadratic factors.

copeland 2013-02-21 21:22:33
How should we organize our solution?

Doink 2013-02-21 21:23:37
they are all distinct and all multiply to either 50 or -50

ic1999 2013-02-21 21:23:37
use vieta's and factor 50

kdokmeci 2013-02-21 21:23:37
Cases of factors of 50

Voytek 2013-02-21 21:23:37
By the different factors of 50

nuggetfan 2013-02-21 21:23:37
factorize 50?

1ph0ne 2013-02-21 21:23:37
Casework?

copeland 2013-02-21 21:23:43
We can solve this problem via casework on all possible factorizations of 50. All we have to do is count the ways to multiply all such polynomials together to get a constant term of $+50.$

copeland 2013-02-21 21:23:54
Let's look at all irreducibles with particular constant terms. The list of factors of 50 is \[-50,-25,-10,-5,-2,-1,1,2,5,10,25,50.\]

copeland 2013-02-21 21:24:01
What are all irreducible polynomials with constant term $-50?$

theone142857 2013-02-21 21:24:50
(x-50)

nuggetfan 2013-02-21 21:24:50
x-50

ic1999 2013-02-21 21:24:50
x-50 and that's it

copeland 2013-02-21 21:24:54
Since $z^2-2az+(a^2+b^2)$ has a nonnegative constant term, the only possible polynomial is the linear one, $x-50$.

copeland 2013-02-21 21:24:57
What about irreducibles with constant term $-25?$

kz190 2013-02-21 21:25:16
x-25

program4 2013-02-21 21:25:16
just x-25

Doink 2013-02-21 21:25:16
x-25

mathwizard888 2013-02-21 21:25:16
x-25

ABCDE 2013-02-21 21:25:16
x-25

mydogcanpur 2013-02-21 21:25:16
x-25

lucylai 2013-02-21 21:25:16
x-25

Cradin 2013-02-21 21:25:16
x-25

copeland 2013-02-21 21:25:20
Again there are no quadratics, just the linear polynomial $z-25$.

copeland 2013-02-21 21:25:25
In fact, we get one possible linear polynomial for each factor.

copeland 2013-02-21 21:25:30
\[\begin{array}{c|c}
\text{constant}~&~\text{polynomial}\\
\hline
-50&z-50\\
-25&z-25\\
-10&z-10\\
-5&z-5\\
-2&z-2\\
-1&z-1\\
1&z+1\\
2&z+2\\
5&z+5\\
10&z+10\\
25&z+25\\
50&z+50
\end{array}\]

copeland 2013-02-21 21:25:38
Now let's find the quadratics.

copeland 2013-02-21 21:25:42
For $a^2+b^2=1$, what are all irreducibles \[z^2-2az+(a^2+b^2)?\]

kdokmeci 2013-02-21 21:26:39
z^2+1

chenboy3 2013-02-21 21:26:39
z^2 + 1

theone142857 2013-02-21 21:26:39
z^2_+1

ABCDE 2013-02-21 21:26:39
just x^2+1

program4 2013-02-21 21:26:39
z^2+1

copeland 2013-02-21 21:26:41
If $a=1$ or $a=-1$ then $b=0$ and the roots are $1\pm0i$, which are real. That gives \[z^2\pm 2z+1=(z\pm1)^2.\] This is not irreducible. The only irreducible quadratic has $a=0$ and is\[z^2+1.\]

copeland 2013-02-21 21:27:00
Does that make sense?

copeland 2013-02-21 21:27:11
We throw $z^2+2z+1$ away because it factors.

copeland 2013-02-21 21:27:15
\[\begin{array}{c|c}
\text{constant}~&~\text{polynomials}\\
\hline
-50&z-50\\
-25&z-25\\
-10&z-10\\
-5&z-5\\
-2&z-2\\
-1&z-1\\
1&z+1,~z^2+1\\
2&z+2,~\ldots\\
5&z+5,~\ldots\\
10&z+10,~\ldots\\
25&z+25,~\ldots\\
50&z+50,~\ldots
\end{array}\]

copeland 2013-02-21 21:28:11
What are all possible values of $a$ when $a=2$ and $z^2-2az+(a^2+b^2)$ is irreducible?

copeland 2013-02-21 21:28:57
What can we choose for $a$ if $a^2+b^2=2?$

sammyMaX 2013-02-21 21:29:23
$a=\pm1$

Cradin 2013-02-21 21:29:23
a = 1

nuggetfan 2013-02-21 21:29:23
a = +- 1

mikhailgromov 2013-02-21 21:29:23
1

Voytek 2013-02-21 21:29:23
1

mathwizard888 2013-02-21 21:29:23
1, -1

distortedwalrus 2013-02-21 21:29:23
a=b=1

sparkles257 2013-02-21 21:29:23
1 or -1?

program4 2013-02-21 21:29:23
a=-1, 1

copeland 2013-02-21 21:29:29
The only way to write 2 as a sum of squares is $2=1+1$. Therefore $a=\pm1$.

copeland 2013-02-21 21:29:34
\[\begin{array}{c|c}
\text{constant}~&~\text{polynomials}\\
\hline
-50&z-50\\
-25&z-25\\
-10&z-10\\
-5&z-5\\
-2&z-2\\
-1&z-1\\
1&(z+1),~(z^2+1)\\
2&(z+2),~(z^2\pm2z+2)\\
5&z+5,~\ldots\\
10&z+10,~\ldots\\
25&z+25,~\ldots\\
50&z+50,~\ldots
\end{array}\]

copeland 2013-02-21 21:29:38
OK, I'm starting to see where this is going. What are the possible values for $a$ when $a^2+b^2=5?$

bharatputra 2013-02-21 21:30:20
-2,-1,1,2

nuggetfan 2013-02-21 21:30:20
+-2, +-1

program4 2013-02-21 21:30:20
a=1, 2, -1, -2

Cradin 2013-02-21 21:30:20
a = +-2, +-1

linpaws 2013-02-21 21:30:20
-2,-1,1,2

VietaFan 2013-02-21 21:30:20
a = 1 or 2 or -1 or -2

flyrain 2013-02-21 21:30:20
5=1+4

Imsacred 2013-02-21 21:30:20
+-1, +-2

copeland 2013-02-21 21:30:23
We can write $5=1+4$ or $5=4+1$. Therefore $a=\pm1$ or $a=\pm2.$

copeland 2013-02-21 21:30:27
\[\begin{array}{c|c}
\text{constant}~&~\text{polynomials}\\
\hline
-50&z-50\\
-25&z-25\\
-10&z-10\\
-5&z-5\\
-2&z-2\\
-1&z-1\\
1&(z+1),~(z^2+1)\\
2&(z+2),~(z^2\pm2z+2)\\
5&~z+5,~(z^2\pm2z+5),~(z^2\pm4z+5)\\
10&z+10,~\ldots\\
25&z+25,~\ldots\\
50&z+50,~\ldots
\end{array}\]

copeland 2013-02-21 21:30:31
What are the possible values for $a$ when $a^2+b^2=10?$

Cradin 2013-02-21 21:30:59
a = +/-3, +/- 1

Imsacred 2013-02-21 21:30:59
+-1, +-3

ic1999 2013-02-21 21:30:59
+-1, +-3

kli2000 2013-02-21 21:30:59
+- 1, +-3

mapletree14 2013-02-21 21:30:59
+-3, +-1

distortedwalrus 2013-02-21 21:30:59
+-1, +-2, +-3

aux770 2013-02-21 21:30:59
+-1，+-3

pi_Plus_45x23 2013-02-21 21:30:59
+-1,+-3

1ph0ne 2013-02-21 21:30:59
+- 3, +- 1

bookie331 2013-02-21 21:30:59
+-1, +-3

guilt 2013-02-21 21:31:05
a = +-1, +- 3

copeland 2013-02-21 21:31:07
We can write $10=1+9=9+1$, so $a=\pm1$ or $a=\pm3.$

copeland 2013-02-21 21:31:11
\[\begin{array}{c|c}
\text{constant}~&~\text{polynomials}\\
\hline
-50&z-50\\
-25&z-25\\
-10&z-10\\
-5&z-5\\
-2&z-2\\
-1&z-1\\
1&(z+1),~(z^2+1)\\
2&(z+2),~(z^2\pm2z+2)\\
5&~z+5,~(z^2\pm2z+5),~(z^2\pm4z+5)\\
10&~z+10,~(z^2\pm2z+10),~(z^2\pm6z+10)\\
25&z+25,~\ldots\\
50&z+50,~\ldots
\end{array}\]

copeland 2013-02-21 21:31:15
What are the possible values for $a$ when $a^2+b^2=25?$

copeland 2013-02-21 21:31:58
There seems to be contention here.

copeland 2013-02-21 21:32:12
Specifically, we can't decide whether to inclued -5, 0, or 5.

copeland 2013-02-21 21:32:20
What are the possible values of $a?$

mathwizard888 2013-02-21 21:33:16
-4, -3, 0, 3, 4

program4 2013-02-21 21:33:16
3, 4, -3, -4, 0 (not 5 and -5 since those are not irreducible)

program4 2013-02-21 21:33:16
3, 4, -3, -4, 0

sammyMaX 2013-02-21 21:33:16
we need some imaginary part, so a cannot equal 5 or -5

Imsacred 2013-02-21 21:33:16
rather, we include 0, but not +-5 because we already counted both of them

kdokmeci 2013-02-21 21:33:16
a doesnt have to be nonzero

copeland 2013-02-21 21:33:20
We can write $25=9+16=16+9,$ so $a=\pm3$ or $a=\pm4.$ Notice also that 25 is a square, so we could have $a=0$ as well.

copeland 2013-02-21 21:33:29
\[\begin{array}{c|c}
\text{constant}~&~\text{polynomials}\\
\hline
-50&z-50\\
-25&z-25\\
-10&z-10\\
-5&z-5\\
-2&z-2\\
-1&z-1\\
1&(z+1),~(z^2+1)\\
2&(z+2),~(z^2\pm2z+2)\\
5&~z+5,~(z^2\pm2z+5),~(z^2\pm4z+5)\\
10&~z+10,~(z^2\pm2z+10),~(z^2\pm6z+10)\\
25&~z+25,~(z^2+25),~(z^2\pm6z+25),~(z^2\pm8z+25)\\
50&z+50,~\ldots
\end{array}\]

copeland 2013-02-21 21:33:44
And finally, what about 50?

Imsacred 2013-02-21 21:34:38
+-1, +-7, +-5

kdokmeci 2013-02-21 21:34:38
a=+-7,+-5,+-1

mathwizard888 2013-02-21 21:34:38
-7, -5, -1, 1, 5, 7

mydogcanpur 2013-02-21 21:34:38
a= +-1, +-5, +-7

matholympiad25 2013-02-21 21:34:38
+-1, +-7, +-5

darrench12 2013-02-21 21:34:38
+-5,+-7,+-1

program4 2013-02-21 21:34:38
1, 7, -1, -7, 5, -5

sparkles257 2013-02-21 21:34:38
+-1, +-7, +- 5

copeland 2013-02-21 21:34:43
Since $50=1+49=49+1$ we could have $a=\pm1$ or $a=\pm7.$ We can also write $5=25+25$, so we get $a=\pm5$ as well.

copeland 2013-02-21 21:34:47
\[\begin{array}{c|c}
\text{constant}~&~\text{polynomials}\\
\hline
-50&z-50\\
-25&z-25\\
-10&z-10\\
-5&z-5\\
-2&z-2\\
-1&z-1\\
1&(z+1),~(z^2+1)\\
2&(z+2),~(z^2\pm2z+2)\\
5&~z+5,~(z^2\pm2z+5),~(z^2\pm4z+5)\\
10&~z+10,~(z^2\pm2z+10),~(z^2\pm6z+10)\\
25&~z+25,~(z^2+25),~(z^2\pm6z+25),~(z^2\pm8z+25)\\
50&~z+50,~(z^2\pm2z+50),~(z^2\pm5z+50),~(z^2\pm14z+50)
\end{array}\]

copeland 2013-02-21 21:34:51
\[\begin{array}{c|c|c}
\text{constant}~&~\text{polynomials}~&~\text{number}\\
\hline
-50&z-50&1\\
-25&z-25&1\\
-10&z-10&1\\
-5&z-5&1\\
-2&z-2&1\\
-1&z-1&1\\
1&(z+1),~(z^2+1)&2\\
2&(z+2),~(z^2\pm2z+2)&3\\
5&~z+5,~(z^2\pm2z+5),~(z^2\pm4z+5)&5\\
10&~z+10,~(z^2\pm2z+10),~(z^2\pm6z+10)&5\\
25&~z+25,~(z^2+25),~(z^2\pm6z+25),~(z^2\pm8z+25)&6\\
50&~z+50,~(z^2\pm2z+50),~(z^2\pm5z+50),~(z^2\pm14z+50)~&7
\end{array}\]

copeland 2013-02-21 21:35:01
That's all the polynomials. Now we just need to count all the ways to multiply things in the middle column such that the product of the constant terms is 50.

copeland 2013-02-21 21:35:11
I have a serious phobia of signs and casework, and it looks like we've got a lot of those to take care of up there. Is there a way we can streamline our casework to avoid dealing with signs in our factorization? Tell me something that will make those worries go away.

copeland 2013-02-21 21:36:48
Is there any way to flip the sign of the constant term?

Imsacred 2013-02-21 21:38:17
we can choose whether or not to have a root of +1 so we dont have to worry about the resulting sign of the rest

mydogcanpur 2013-02-21 21:38:17
Multiply by -1?

mikhailgromov 2013-02-21 21:38:17
Multiply by ;$-1$

sammyMaX 2013-02-21 21:38:17
Use the (z-1) to flip signs

copeland 2013-02-21 21:38:22
We have the linear polynomial $z-1$. If we find all polynomials with constant term $\pm50$ while ignoring this polynomial, then we can multiply by $z-1$ in the end to fix all those polynomials that have constant term $-50.$

copeland 2013-02-21 21:38:32
While we're cleaning things up, what other constant should we discuss and why?

kdokmeci 2013-02-21 21:39:47
1?

sammyMaX 2013-02-21 21:39:47
(z+1). It doesn't contribute anything, so each polynomial we can either add it or not add it

centralbs 2013-02-21 21:39:47
z+1

VietaFan 2013-02-21 21:39:47
The 1. It can go over and over and not change the product.

sammyMaX 2013-02-21 21:39:47
same with $(z^2+1)$

kdokmeci 2013-02-21 21:39:52

copeland 2013-02-21 21:39:53
We can multiply a polynomial by $z+1$ or $z^2+1$ and not change the constant term. Therefore we can ignore these two possible factors, too, and then multiply by $2^2=4$ at the end based on whether these two appear or not.

copeland 2013-02-21 21:40:00
Now we've dramatically simplified our table:

copeland 2013-02-21 21:40:03
\[\begin{array}{c|c|c}
\text{constant}~&~\text{polynomials}~&~\text{number}\\
\hline
\pm2&(z-2),~(z+2),~(z^2\pm2z+2)&4\\
\pm5&(z-5),~z+5,~(z^2\pm2z+5),~(z^2\pm4z+5)&6\\
\pm10&(z-10),~(z+10),~(z^2\pm2z+10),~(z^2\pm6z+10)&6\\
\pm25&(z-25),~(z+25),~(z^2+25),~(z^2\pm6z+25),~(z^2\pm8z+25)&7\\
\pm50&~~(z-50),~(z+50),~(z^2\pm2z+50),~(z^2\pm5z+50),~(z^2\pm14z+50)~&8
\end{array}\]

copeland 2013-02-21 21:40:06
Now we count! What are all the factorizations of 50 (with positive factors)?

copeland 2013-02-21 21:41:33
Factorizations!

copeland 2013-02-21 21:41:47
We want to write 50 as a product of some number of numbers, each of which is greater than 1.

Imsacred 2013-02-21 21:42:30
2*5*5, 10*5, 2*25, 50

lucylai 2013-02-21 21:42:30
50, 2*25, 5*10, 2*5*5

linpaws 2013-02-21 21:42:30
2x5x5,2x25,5x10

kdokmeci 2013-02-21 21:42:30

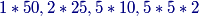
Imsacred 2013-02-21 21:42:30
2*5*5, 2*25, 10*5, 50

kli2000 2013-02-21 21:42:30
2*5*5, 5*10, 2*25, 50

UrInvalid 2013-02-21 21:42:30
50,2*25,5*10,2*5*5

copeland 2013-02-21 21:42:33
$50=50=2\cdot25=5\cdot10=2\cdot5\cdot5.$

copeland 2013-02-21 21:42:38
How many polynomials correspond to the trivial factorization of $\pm50$?

UrInvalid 2013-02-21 21:43:20
8

Imsacred 2013-02-21 21:43:20
8

Iggy Iguana 2013-02-21 21:43:20
8

sammyMaX 2013-02-21 21:43:20
8

lucylai 2013-02-21 21:43:20
8

joshxiong 2013-02-21 21:43:20
8

UrInvalid 2013-02-21 21:43:20
8 polynomials

copeland 2013-02-21 21:43:21
There are 8 polynomials. (Later we will get a total of 32 when we include $(z+1)$ and $(z^2+1).$

copeland 2013-02-21 21:43:25
\[\begin{array}{c|c|c|c|c}
\text{factorization}~~&~~50~~&~~2\cdot25~~&~~5\cdot10~~&~~2\cdot5\cdot5\\
\hline
\text{count}&8&&&
\end{array}\]

copeland 2013-02-21 21:43:28
How many polynomials correspond to the factorization $50=2\cdot25?$

OCed 2013-02-21 21:43:51
28

UrInvalid 2013-02-21 21:43:51
28

mssmath 2013-02-21 21:43:51
28

bharatputra 2013-02-21 21:43:51
28

Iggy Iguana 2013-02-21 21:43:51
28

pi_Plus_45x23 2013-02-21 21:43:51
28

mathwizard888 2013-02-21 21:43:51
28

copeland 2013-02-21 21:43:55
We pick one factor of constant 2 and one factor of constant 25, giving $4\cdot7=28$ polynomials.

copeland 2013-02-21 21:43:58
\[\begin{array}{c|c|c|c|c}
\text{factorization}~~&~~50~~&~~2\cdot25~~&~~5\cdot10~~&~~2\cdot5\cdot5\\
\hline
\text{count}&8&4\cdot7&&
\end{array}\]

copeland 2013-02-21 21:44:01
What about $5\cdot10?$

mathwizard888 2013-02-21 21:44:32
36

bharatputra 2013-02-21 21:44:32
36

Imsacred 2013-02-21 21:44:32
36

UrInvalid 2013-02-21 21:44:32
6*6=36

VietaFan 2013-02-21 21:44:32
36

mssmath 2013-02-21 21:44:32
36

dsrndm 2013-02-21 21:44:32
36

numbertheorist17 2013-02-21 21:44:32
36

copeland 2013-02-21 21:44:36
\[\begin{array}{c|c|c|c|c}
\text{factorization}~~&~~50~~&~~2\cdot25~~&~~5\cdot10~~&~~2\cdot5\cdot5\\
\hline
\text{count}&8&4\cdot7&6\cdot6&
\end{array}\]

copeland 2013-02-21 21:44:39
And finally, $2\cdot5\cdot5?$

mathwizard888 2013-02-21 21:45:19
4*6C2=60

Iggy Iguana 2013-02-21 21:45:19
60

OCed 2013-02-21 21:45:19
15*4=60

numbertheorist17 2013-02-21 21:45:19
60

sammyMaX 2013-02-21 21:45:19
60

copeland 2013-02-21 21:45:43
Here we have to pick one of the 4 polynomials in the 2-row and two from the 5-row giving $4\binom62=4\cdot15.$

copeland 2013-02-21 21:45:55
\[\begin{array}{c|c|c|c|c}
\text{factorization}~~&~~50~~&~~2\cdot25~~&~~5\cdot10~~&~~2\cdot5\cdot5\\
\hline
\text{count}&8&4\cdot7&6\cdot6&4\cdot15
\end{array}\]

copeland 2013-02-21 21:45:58
So what's the answer?

numbertheorist17 2013-02-21 21:47:11
total: 4(8+28+36+60)=4(132)=528 B

Voytek 2013-02-21 21:47:11
B) 528

mssmath 2013-02-21 21:47:11
(B)

bharatputra 2013-02-21 21:47:11
132*4=528 (b)

sparkles257 2013-02-21 21:47:11
B

kdokmeci 2013-02-21 21:47:11
A 288

Iggy Iguana 2013-02-21 21:47:11
528

danzhi 2013-02-21 21:47:11
528

kz190 2013-02-21 21:47:11
i got b

lucylai 2013-02-21 21:47:11
528

Imsacred 2013-02-21 21:47:11
4(8+28+36+60)=528 B

theone142857 2013-02-21 21:47:11
528

pi_Plus_45x23 2013-02-21 21:47:11
B. 528

mathwizard888 2013-02-21 21:47:11
528 (B)

mydogcanpur 2013-02-21 21:47:11
528 (B)

Math99 2013-02-21 21:47:11
c.

copeland 2013-02-21 21:47:16
Here we have counted $8+4\cdot7+6\cdot6+4\cdot15=132$ total polynomials. Then we multiply by 2 to account for the presence or absence of $z+1,$ and multiply by 2 again to handle $z^2+1.$

copeland 2013-02-21 21:47:23
The final count is $4\cdot132=528.$ The answer is (B).

copeland 2013-02-21 21:47:50
Good work. This problem was cool, except I got the wrong answer about 5 times before finally getting my arithmetic right.

copeland 2013-02-21 21:48:13
I spent 10 minutes tracking down my error in $8+4\cdot7+6\cdot6+4\cdot15=102$

VietaFan 2013-02-21 21:48:34
Thanks for doing this class; it was interesting.

copeland 2013-02-21 21:48:37
Thank you guys.

copeland 2013-02-21 21:48:42
Oh, there was a good question above:

sammyMaX 2013-02-21 21:48:46
what if they didn't specify it had $n$ roots? would it make the problem more complicated?

copeland 2013-02-21 21:48:55
What happens when you allow repeated roots here?

Iggy Iguana 2013-02-21 21:49:26
you can use a lot of 1's

program4 2013-02-21 21:49:26
the answer would be infinity

OCed 2013-02-21 21:49:26
You can have an infinite amount of polynomials.

matholympiad25 2013-02-21 21:49:26
Then you can get infinitely many (z+1)^k in the factors

bharatputra 2013-02-21 21:49:26
answer would be infinity

program4 2013-02-21 21:49:26
because x+1 can be used as many times as you want

sammyMaX 2013-02-21 21:49:26
You could keep adding the 1's and -1

colinhy 2013-02-21 21:49:26
You could have infinitely mant (x+1)s

Imsacred 2013-02-21 21:49:26
you could have infinite roots of -1 or 1

copeland 2013-02-21 21:49:37
Right. That's the only point of forcing the roots to be distinct.

copeland 2013-02-21 21:50:21
Alright, I'm starting to wane here, and we're done with the last 5 of each test.

copeland 2013-02-21 21:50:29
So. . .

copeland 2013-02-21 21:50:30
That's all for tonight's Math Jam!

mprashker 2013-02-21 21:50:32
Thank you very much. Will Richard Rusczyk make the videos again? those are very helpful.

copeland 2013-02-21 21:50:43
Yes. He plans to think about starting them next week.

copeland 2013-02-21 21:51:09
Please join us again on Saturday, March 16, when we will discuss the AIME I contest.

1ph0ne 2013-02-21 21:51:24
Where can we find the transcript for this math jam?

copeland 2013-02-21 21:51:33
You can find the Math Jam transcript here:

copeland 2013-02-21 21:51:39
http://www.artofproblemsolving.com/School/mathjams.php

copeland 2013-02-21 21:51:41
once I post it.

kli2000 2013-02-21 21:52:24
what are the AIME math jams like?

copeland 2013-02-21 21:52:29
Like this, with AIME problems.

copeland 2013-02-21 21:52:38
We'll do all 15 and it will take a little over 3 hours.

Royalreter1 2013-02-21 21:52:42
Will the transcript be everything from the beginning?

copeland 2013-02-21 21:52:43
Yes.

kdokmeci 2013-02-21 21:53:42
There weren't any circle problems in the final five (involving pi and stuff)

hamup1 2013-02-21 21:53:42
So we can attend the AIME math jams even if we don't get into the AIME contest right?

copeland 2013-02-21 21:53:46
Absolutely.

trophies 2013-02-21 21:54:16
wait what day is the AIME on

copeland 2013-02-21 21:54:22
March 14 and April 3.

copeland 2013-02-21 21:54:31
http://amc.maa.org/calendar.shtml

ic1999 2013-02-21 21:55:04
pi day!!!!!

crastybow 2013-02-21 21:55:04
March 14 is Pi Day! And it happens to be my birthday XD

djmathman 2013-02-21 21:56:27
And MIT Admissions Day!

mapletree14 2013-02-21 21:56:27
and when MIT RD results come out. . .

SteinsChaos 2013-02-21 21:56:27
and it happens to be MIT results day

copeland 2013-02-21 21:56:28
Funny thing for many of you to have on your minds. . . .

copeland 2013-02-21 21:57:29
Alright, I'm going home. Everyone have a good night!

2013 AMC 10/12 B Discussion

Facilitator: Jeremy Copeland