rrusczyk (19:31:38)
Tonight we have Dan Zaharopol from USAMTS sponsor Canada/USA Mathcamp. He is going to lead an intriguing discussion about how mathematicians think about the sizes of infinite sets.

rrusczyk (19:31:46)
Canada/USA Mathcamp is providing $200 scholarships to the top 30 female and top 30 male scorers in the USAMTS. (These students must pass the Mathcamp admission quiz to qualify.) Mathcamp is a very popular summer program for outstanding math students. Many top USAMTS students are alumni of Mathcamp. More information about Mathcamp can be found at www.mathcamp.org. Dan will be back on March 20 to speak about Mathcamp in more detail. Tonight he's going to talk about math. (But if you have Mathcamp questions at the end of class, you might be able to talk him into responding! Please don't ask him questions during class, though.)

rrusczyk (19:32:00)
Dan Zaharopol graduated from MIT in 2004 and is now in the PhD program at the University of Illinois, studying algebraic topology. He teaches advanced mathematics each summer at Canada/USA Mathcamp, as well as with various programs at MIT; he also occasionally teaches calculus (which he says is much more boring!) at the U of I.

rrusczyk (19:32:13)
And now I'll turn the classroom over to Dan!

DanZ (19:32:34)
I'd like to clarify that "Please don't ask him questions during class, though" refers entirely to Mathcamp questions. Math questions you are welcome to ask.

DanZ (19:32:40)
And Mathcamp questions are indeed welcome after class.

DanZ (19:32:42)
So, hello everyone!

DanZ (19:32:51)
This class is an experiment. It's unlike other AoPS classes, which focus on solving problems we understand, and it's certainly unlike anything I've ever done before. We're going to discover whole new areas of math that will give us new questions and problems to solve. I think it's really interesting, and I hope that you will, too!

DanZ (19:33:15)
Also, my font is going to be weird because I'll be using a lot of LaTeX! :)

DanZ (19:33:31)


DanZ (19:33:41)


DanZ (19:33:49)


DanZ (19:33:58)


DanZ (19:34:06)


DanZ (19:34:36)
(It's possible you've already seen an introduction to such things, in which case today will probably be review, but you're welcome to enjoy the experience nonetheless. If you haven't, though, great!)

DanZ (19:34:54)
(Also, I do plan on talking about ordinal and cardinal numbers sometime, but not tonight.)

DanZ (19:35:02)


DanZ (19:35:15)


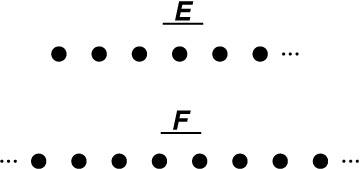
DanZ (19:35:25)
By the way, every image in this Math Jam is also online, in higher resolution. You can see this one at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/EFlarge.jpg

DanZ (19:35:46)
(You may need to disable your popup blocker to see that image, or hold CTRL while clicking it.)

DanZ (19:35:58)


DanZ (19:36:42)
A sampling of replies shows some disagreement:

Jayson Lynch (19:36:10)
Same

b-flat (19:36:13)
E looks smaller than F

ruth-bruce-ted@sbcglobal. (19:36:21)
different i meant

davidyko (19:36:51)
I think they're the same...

ragnarok23 (19:36:53)
different

DanZ (19:37:10)
...and so on...

henry.zheng (19:37:12)
different. e is almost certainly smaller than f

DanZ (19:38:02)
Okay.

DanZ (19:38:12)
So, some of you look at these and go, well, "E fits inside F, so F must be bigger."

DanZ (19:38:35)
Others of you pointed out that we might be able to rearrange the points of F to get E back, and if we can rearrange one into the other, then they ought to be the same.

DanZ (19:38:43)


DanZ (19:38:55)


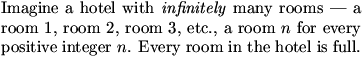
DanZ (19:39:03)


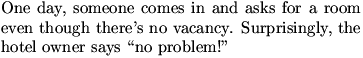
DanZ (19:39:15)


DanZ (19:39:25)


DanZ (19:39:32)
Here's the same thing in pictures: we start at

DanZ (19:39:44)


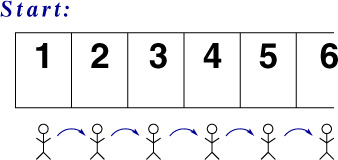
DanZ (19:39:51)
and then, after the move, we're at

DanZ (19:39:59)


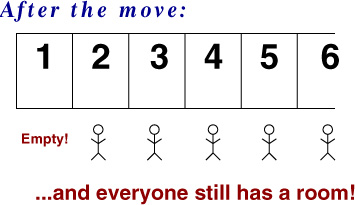
DanZ (19:40:08)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/hotel-plus-onelarge.jpg

elephantmaster (19:39:33)
How can every room be full if there are an infinite number of rooms

DanZ (19:40:28)
That's a good question. The answer is that I'm cheating, I'm not talking about a real hotel.

DanZ (19:40:43)
But because we can think about infinite sets in mathematics (like, "all numbers"), I want to play with a model.

DanZ (19:40:50)
A hotel is an easy way to understand what we'll be doing.

ragnarok23 (19:40:44)
but if all the rooms are full, how will the last person move to another

DanZ (19:41:17)
The answer is that there's always a next room, because there are infinitely many.

DanZ (19:41:22)
So there's no "last" person!

DanZ (19:41:31)
Just like the numbers go on and on, the rooms of this imaginary hotel go on and on.

plucesiar (19:41:47)
So are you saying in that sense, F can be similarly be fit into E just by a smarter way of pairing?

DanZ (19:42:13)
Quite possibly, and "pairing" is a great word for it.

DanZ (19:42:20)
Let's consider another sample problem.

bagladyrockstar_2 (19:41:54)
Is the owner of the hotel aware of this? He shouldn't but up a "no vacancy" sign

DanZ (19:42:30)
(And yes, that was his mistake!)

DanZ (19:42:37)
(But all the rooms [i]were[/i] full!)

DanZ (19:42:45)
The next day, the hotel owner is working at the desk when suddenly he hears some fire engines. Turns out that the hotel next door --- which is just like his! --- has burned down. All the people got out alive, but now they all need space. So infinitely many people come to his hotel and ask for rooms all at once --- and he's already booked up! Does he have a way to make space for them?

davidyko (19:42:43)
More money for the owner of the hotel...

DanZ (19:43:13)
(Yeah, but he's practically infinitely rich already...)

bubka (19:43:15)
in a similar way!

Jayson Lynch (19:43:16)
yes, use the same type of process.

Krazul (19:43:12)
He can tell everyone to move to the room with double their current room number...

b-flat (19:43:17)
yes - double the room number of all current occupants & then add in the rest to the now empty rooms

variable (19:43:28)
Each person doubles his/her room number.

Jayson Lynch (19:43:30)
Move everyone into their room number x2

DanZ (19:43:46)
Okay! Lots of people got this.

DanZ (19:44:00)
Right! Now the hotel owner gets on the loudspeaker and announces, "Attention! Attention! If you are occupying a room, please move to the room whose number i twice your own room." Everyone gets up and goes twice as far into the hotel --- precisely filling all the even rooms, but leaving the odd rooms free! Now he just sorts all the arrivals from the other hotel into the odd rooms.

DanZ (19:44:09)
We start at:

DanZ (19:44:17)


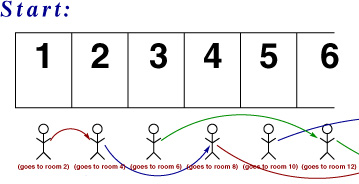
DanZ (19:44:24)
and end up with:

DanZ (19:44:31)


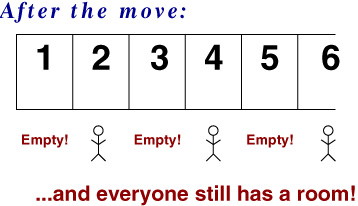
DanZ (19:44:35)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/hotel-times-twolarge.jpg

DanZ (19:44:57)
Now, you wouldn't want to be in room one million, because then you'd have to walk a million room spaces...

DanZ (19:45:06)
But this is all imaginary, so it's ok! :)

meenamathgirl (19:44:58)
so the sets from before are equal!

DanZ (19:45:30)
Very good! I'll show you an explicit way to do that in just a minute. But this works to show that they're equal.

henry.zheng (19:45:15)
infinitely fast elevators...

hestia (19:45:22)
couldn't the people just move an inifinite number of rooms?

DanZ (19:45:52)
Hestia: the only problem with that is you need to tell everyone where to go.

DanZ (19:46:08)
Each person needs a room to go to; if you tell the person in room 100 to move infinitely many rooms forward, he's not actually getting to any new room!

DanZ (19:46:29)
But the way we've done it, everyone really does have somewhere to go, so it's OK.

DanZ (19:46:52)
It's a good question.

DanZ (19:46:54)
It seems like somehow we can take infinity and fit *more* into the *same size* infinity! It seems like even two infinities is the same as one infinity! Understanding this --- and what kinds of infinities might actually be larger --- is going to be the point of this math jam.

DanZ (19:47:01)


DanZ (19:47:20)
Feel free to send your answer, but I'm not going to send it on just yet. This one's tougher!

ragnarok23 (19:47:07)
could you tell them to go to the room number 3 times their number?

DanZ (19:47:45)
Yes, and that lets you fit *two* hotels in. But infinitely many more hotels at once?

plucesiar (19:47:47)
I have a feeling you're gonna be talking about power sets or something of the sort

DanZ (19:48:10)
Yes, I will.

DanZ (19:48:35)
If you don't know what power sets are, don't worry about it.

DanZ (19:49:00)
By the way, if anyone is having a tough time viewing what I post, let me know. Using all this LaTeX might make it take a while to download on slower connections.

DanZ (19:49:05)


DanZ (19:49:23)


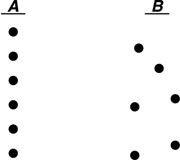
DanZ (19:49:28)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/ABlarge.jpg

DanZ (19:49:37)
Do these two sets have the same number of dots?

meenamathgirl (19:49:45)
yes

DanZ (19:49:58)
Right, so there was a lot more consensus on that one.

DanZ (19:50:09)
How did you tell?

not_trig (19:50:14)
you count?

davidyko (19:50:15)
I counted.

ruth-bruce-ted@sbcglobal. (19:50:18)
i counted them

bagladyrockstar_2 (19:50:23)
I counted one side and then the other

DanZ (19:50:47)


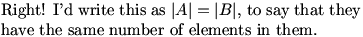
DanZ (19:51:00)


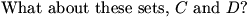
DanZ (19:51:06)


DanZ (19:51:11)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/CDlarge.jpg

ragnarok23 (19:51:13)
no

nicholaskramer (19:51:15)
no

plucesiar (19:51:16)
no

DanZ (19:51:28)
Okay, no disputes here either.

DanZ (19:51:33)
Again, you can count them.

DanZ (19:51:37)
So, here's a strange question. What if you didn't know how to count? Could you compare the sizes of the sets in that case?

Hamster1800 (19:51:49)
sure, cross out one from each until one's empty

EgUaLuEsRs07_2 (19:51:52)
pair them up, there will be one left over

davidyko (19:51:52)
You line them up one-on-one

perfectnumber628 (19:52:01)
pair up the dots

plucesiar (19:52:03)
see if one belongs in the other?

DanZ (19:52:24)
Okay, lots of good ideas..

DanZ (19:52:35)
One good way to do it is to "pair them up."

DanZ (19:52:46)
I want to find a method that will generalize.

DanZ (19:52:50)
We can't count to infinity (yet).

DanZ (19:52:59)
But maybe we can still compare sizes by doing the same thing we do for finite sets!

DanZ (19:53:21)
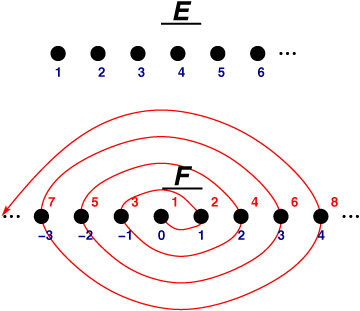
Now, we already saw E and F:

DanZ (19:53:25)


DanZ (19:53:43)
Let's think about what it means to say that they're the same, or different sizes.

DanZ (19:54:02)
Now, if you think about it as pairing them up: can you do it?

DanZ (19:54:09)
Can you pair up E with F?

hestia (19:54:10)
so could you call e=n and then f=2n?

DanZ (19:54:35)
(Since I haven't defined bijection, keep away from using that word.)

henry.zheng (19:54:23)
well, according to the pair up logic, then they would be the same...infinite

plucesiar (19:54:27)
Yes, you can send each one of E to F and you can send one of F to E (trickier), so they pair up and thus are the same size

DanZ (19:55:03)
Does pairing them up mean that all infinite sets are the same size?

DanZ (19:55:14)
We need to come up with a reliable way that sends each dot of one to a dot of the other, with no overlaps.

Austin Texas (19:54:59)
You could put the next member of E on the front of F and the next after that on the back of F and alternate to pair them u

Krazul (19:55:04)
yes... you match the first one with one in the middle of F... then for the next ones you can switch between pairing with the right side and the left side.

DanZ (19:55:38)
Very good!

DanZ (19:55:40)
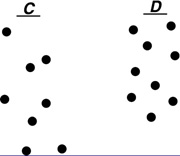
Okay, let's see this first in pictures.

DanZ (19:55:44)
So we can get a good idea of what's going on.

DanZ (19:55:53)


DanZ (19:56:01)


DanZ (19:56:07)
So it looks like this:

DanZ (19:56:12)
//s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/EF-morph2.jpg

DanZ (19:56:16)


DanZ (19:56:23)


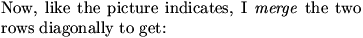
DanZ (19:56:31)


DanZ (19:56:39)
But that's just E!

DanZ (19:56:46)


DanZ (19:56:52)
You can see the whole process at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/EF-morphlarge.jpg

henry.zheng (19:56:54)
so then they are equal?!

DanZ (19:57:19)
Yes! Well, you can pair them up. And if you accept that pairing up two sets means that they're the same size, then E and F are the same size.

scunliffe (19:56:50)
pretty

DanZ (19:57:32)
This stuff will be gorgeous.

nicholaskramer (19:57:26)
so 2?=??

DanZ (19:57:46)
Well, we're going to need better notation to understand that question.

DanZ (19:58:01)
When you put in an infinity sign, you're assuming all of them are the same! Maybe there's something bigger we haven't seen yet.

DanZ (19:58:11)
Speaking of:

DanZ (19:58:16)


DanZ (19:58:22)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/EGlarge.jpg

DanZ (19:58:28)
What do you think about these guys?

plucesiar (19:57:56)
So basically it kind of depends on how you define them as "equal"?

DanZ (19:58:44)
It does, but this is the definition most mathematicians use, because it makes sense.

DanZ (19:58:49)
And it works for the finite case too.

Hamster1800 (19:58:27)
This is the infinity of infinite hotels!

DanZ (19:58:55)
Yes!

meenamathgirl (19:58:49)
are those the same size too by taking diagonals and merging them?

Krazul (19:58:52)
G seems to be bigger... collapsing it into E is hard.

Jayson Lynch (19:58:58)
but as afore stated much harder to show

not_trig (19:59:05)
line them up diagonally in this case, top left to bottom right

davidyko (19:59:08)
Wait...no...

davidyko (19:59:12)
Never mind, you can't pair them up.

Hamster1800 (19:59:15)
If we sort G by diagonals w/ slopes of -1, then going from left-to-right on those diagonals, we can sort them and make a pairing like that...I think

DanZ (19:59:55)
Lots of interesting ideas, some "yes," some "no."

DanZ (20:00:11)
It turns out that the answer is yes.

DanZ (20:00:13)
Let's rearrange.

DanZ (20:00:34)


DanZ (20:00:38)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/EG-rearrange-with-arrowslarge.jpg

DanZ (20:00:51)
You see the diagonals that people mentioned.

DanZ (20:00:57)
Every dot in G has somewhere to go in E!

Jayson Lynch (20:01:00)
once again, very nice illustrations...

DanZ (20:01:16)
(Thank you. These took a long time! :))

plucesiar (20:00:51)
oh thats clever

davidyko (20:00:52)
Hmm!

meenamathgirl (20:01:12)
So they are the same size!

DanZ (20:01:31)
Yeah, I love this stuff. Does everyone see it?

DanZ (20:01:59)
Excellent.

DanZ (20:02:14)
Okay! Now, let's just quickly rewrite stuff.

DanZ (20:02:20)
So that we can make this all a bit cleaner.

DanZ (20:02:29)
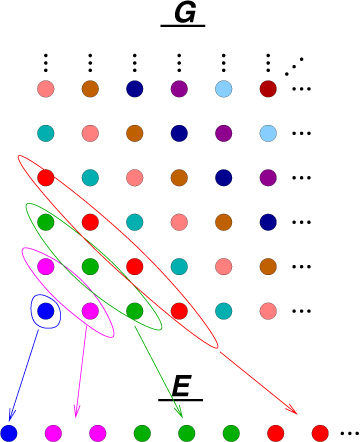
First, pairing up E and F.

DanZ (20:02:43)
The "rearrangement" that I showed you before leads to this pairing:

DanZ (20:02:59)


DanZ (20:03:01)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/EF-pairing-plainlarge.jpg

DanZ (20:03:13)
The red numbers show where the dots of E went.

DanZ (20:03:17)
Notice how they go back and forth along F.

DanZ (20:03:28)


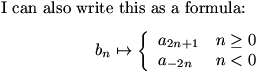
DanZ (20:03:34)


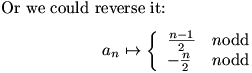
DanZ (20:03:40)
It's a pairing, so it goes both ways.

DanZ (20:03:56)
Yes, that second one should be n even!

DanZ (20:03:59)
Sorry about that.

DanZ (20:04:13)
And there should be a space after the [i]n[/i].

DanZ (20:04:29)
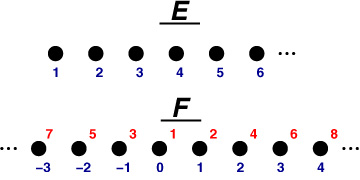
Another way to see it:

DanZ (20:04:39)


DanZ (20:04:48)
We take E, which is a line, and "spiral it around" F.

DanZ (20:04:52)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/EF-pairing-arrowslarge.jpg

DanZ (20:05:02)
Someone before talked about finding a center point --- well, pick any point, and make it the center; then spiral around it.

DanZ (20:05:09)
There are [b]lots[/b] of different pairings!

not_trig (20:04:50)
wow

nicholaskramer (20:04:54)
cool!!

DanZ (20:05:27)
Now, let's show how E pairs with G:

DanZ (20:05:39)


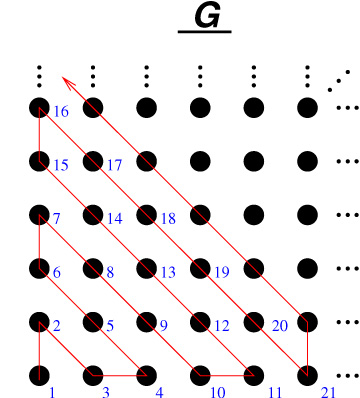
DanZ (20:05:43)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/EG-pairinglarge.jpg

davidyko (20:05:26)
That's sweet.

hestia (20:05:28)
are you saying inifity is a spiral?

DanZ (20:06:04)
I'm saying that we can match one size of infinity with another by spiralling it around.

DanZ (20:06:14)
So it turns out they were the same after all.

DanZ (20:06:29)
The only thing I'm willing to say about infinity is this: there should never be an "end," whatever that means.

DanZ (20:06:39)
If something is infinite, you should never be able to pair it up with a finite set.

meenamathgirl (20:06:31)
So by transitivity the size of F is equal to the size of G, right?

DanZ (20:06:50)
Yes, very good.

DanZ (20:06:54)
= works like we want it to.

DanZ (20:07:06)


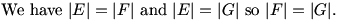
DanZ (20:07:20)
In other words, reverse the pairing from E to F, then pair E to G, and that gets you a pairing F to G.

plucesiar (20:06:16)
so as long as we find a way to pair two sets in a systematic order then we can say somethin about the sizes of them?

DanZ (20:07:32)
Exactly.

not_trig (20:07:09)
countably infinite

DanZ (20:07:53)
The word for a set that is the same size as E is [b]countable[/b].

DanZ (20:07:57)
So all these sets are "countable."

davidyko (20:07:23)
So these aren't absolute value signs.

DanZ (20:08:17)
No; just like absolute value is like the "size" of a number, this is the "size" of a set.

DanZ (20:08:25)
Okay, great.

DanZ (20:08:38)


henry.zheng (20:08:27)
and our hotel owner is no more overworked and no richer before and after the tornado?

DanZ (20:08:52)
Yeah, well, that's the problem with running an infinite hotel!

DanZ (20:09:00)
Once you're full, you're as rich as you're ever going to get!

DanZ (20:09:47)
By the way, you may hear people using the word [b]cardinality[/b] --- it's another way of saying size.

DanZ (20:09:51)


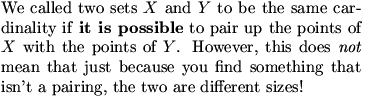
DanZ (20:10:16)
So now, suppose we want to find something bigger than E.

DanZ (20:10:28)
This is hard, if it's possible at all, because we'd need to prove that no pairing exists at all!

plucesiar (20:10:50)
can you give an example of just because you find something that isn't a pairing means that they're different sizes?

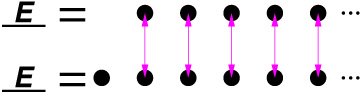
DanZ (20:11:17)
Well, just because you find something that isn't a pairing, they might still [b]be[/b] the same size!

DanZ (20:11:21)
For example:

DanZ (20:11:27)


DanZ (20:11:31)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/E-paired-Elarge.jpg

DanZ (20:11:43)
So we need to prove that no one, no matter how smart they are, can possibly pair up some set with E.

DanZ (20:11:55)
Everyone ok so far?

DanZ (20:12:25)
Ok. A lot of people have mentioned "power sets" or "irrational numbers."

DanZ (20:12:27)
You are all correct.

DanZ (20:12:38)
But I'm going to start off doing this in a different way, which turns out to actually be the same way. :)

DanZ (20:12:54)


DanZ (20:13:00)


DanZ (20:13:12)
We're going to have to be very clever about sneaking "more" infinity into it.

DanZ (20:13:17)


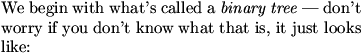
DanZ (20:13:22)


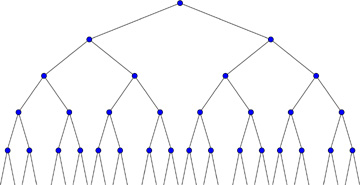
DanZ (20:13:28)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/binarytreelarge.jpg

DanZ (20:13:42)


DanZ (20:13:50)
This one is infinitely long: no matter how go, you never reach the bottom.

DanZ (20:13:56)


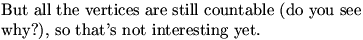
DanZ (20:14:02)
Here are a couple of paths:

DanZ (20:14:38)


DanZ (20:14:40)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/treewithpathslarge.jpg

DanZ (20:14:42)


DanZ (20:15:03)
Hold on, my TeX died on me...

DanZ (20:15:12)


DanZ (20:15:15)
There we go.

DanZ (20:15:25)
You see why we can't draw it.

DanZ (20:15:35)
For the experts, this is correct:

variable (20:15:12)
Oh - the number of paths is equal to the number of real numbers between 0 and 1 when written in binary.

DanZ (20:15:59)
Okay, so we're going to think about a set where every point is an infinite path.

DanZ (20:16:03)
And this will turn out to be bigger.

DanZ (20:16:11)


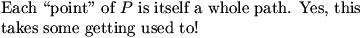
DanZ (20:16:15)


DanZ (20:16:23)


DanZ (20:16:39)


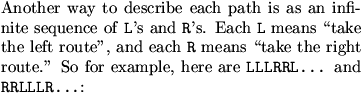
DanZ (20:16:46)


DanZ (20:16:52)
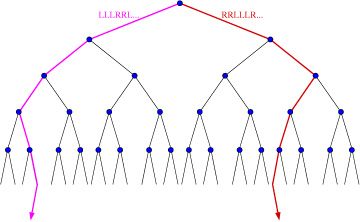
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/secondtreewithpathslarge.jpg

DanZ (20:17:10)
Everyone see that so far? I just posted a bunch.

EgUaLuEsRs07_2 (20:17:53)
so if you call the "Ls" 0s and the "Rs" 1s, u get every possible real numebr between 0 and 1, in binary?

DanZ (20:18:11)
Yes.

DanZ (20:18:17)
Okay!

DanZ (20:18:21)
So:

DanZ (20:18:22)
Remember the original paths I gave you from before?

DanZ (20:18:49)


DanZ (20:18:51)
What do these correspond to?

DanZ (20:18:55)
i.e. what are the first letters of each of the two paths?

DanZ (20:19:15)
Give me the first six.

not_trig (20:19:05)
RL, LR

Hamster1800 (20:19:11)
LRRLRR... and RLRLRL...

DanZ (20:19:27)
There we go.

nicholaskramer (20:19:27)
LRRLR

DanZ (20:19:56)
By the way,

DanZ (20:19:58)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/secondtreewithpathslarge.jpg

DanZ (20:20:09)


DanZ (20:20:22)
Remember, just finding a pairing that doesn't work isn't enough.

DanZ (20:20:35)
You need to start with some way to match them up and prove that it's not actually a pairing!

123s (20:20:39)
proof by contradiction

meenamathgirl (20:20:43)
Can we prove it by contradiction?

DanZ (20:20:53)
Yes!

DanZ (20:20:55)
Precisely.

Goistein (20:20:53)
Is |P|=2^|E|?

DanZ (20:21:12)
Yes, but I haven't explained what that means yet!

EgUaLuEsRs07_2 (20:20:53)
o is this the diagonal proof?

DanZ (20:21:23)
That's a good hint, perhaps...

exponent (20:21:15)
you can pair E with the set of paths , but then each path has an infinite number of points

DanZ (20:21:44)
Okay, but you need to think of why that's a problem.

bubka (20:21:56)
yes we first assume a pairing exists and then say that we choose a path that is different from the ith path at the ith point

DanZ (20:22:12)
Good.

Jayson Lynch (20:22:07)
Let us pair up 1 with LLL..., 2 with LRLl..., 3 with LLRl..., 4 with LLlR... and so on

DanZ (20:22:28)
Right, we need to start with a pairing, and then prove that it [i]misses[/i] something.

DanZ (20:22:32)
So let me start us off with a sample pairing.

DanZ (20:22:43)
And explain it from the beginning.

DanZ (20:22:45)


DanZ (20:22:55)


DanZ (20:23:01)


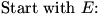
DanZ (20:23:06)


DanZ (20:23:13)
The first point might go like:

DanZ (20:23:19)


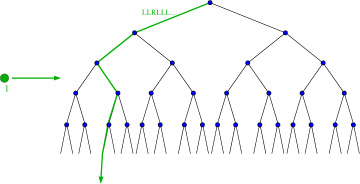
DanZ (20:23:24)
The second point like:

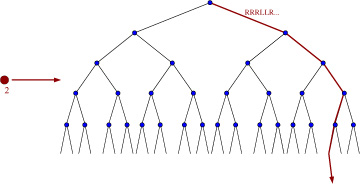
DanZ (20:23:32)


DanZ (20:23:36)
The third point like:

DanZ (20:23:43)


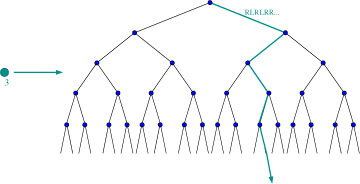
DanZ (20:23:47)
And so on.

DanZ (20:23:51)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/EP-pairinglarge.jpg

DanZ (20:23:53)


DanZ (20:24:12)


DanZ (20:24:43)
(Imagine, of course, that the matching goes on for all the points of E...)

henry.zheng (20:25:18)
well, if u are to match one series of LRLR... then there will be at least one other (RLRL...) that will be missing

DanZ (20:25:51)
The problem here is that maybe point eight goes to LRLR... and point 56 goes to RLRL...

meenamathgirl (20:25:26)
Follow a particular numbered path completely and then branch off one at the "end"? But wait, there is no end...

DanZ (20:26:08)
You're right. So think about building a whole new path.

DanZ (20:26:20)
Let me ask you this. What's an easy way to make a path that's different from where the first point of E goes to?

whitesoxfan (20:26:12)
paths where the Ls and Rs dont repeat

whitesoxfan (20:26:17)
irrational paths

DanZ (20:26:56)
This isn't necessarily good enough: maybe I'm crazy and I make the first point go to the path that corresponds to the digits of pi.

henry.zheng (20:26:50)
go the other direction

DanZ (20:27:03)
Yes!

Goistein (20:27:07)
Change the "last" direction?

DanZ (20:27:20)
Actually, change the first.

DanZ (20:27:35)
Suppose that we make a new path, which goes R first instead of L.

DanZ (20:27:47)
Just to remind you, we have:

DanZ (20:27:50)


DanZ (20:28:02)
So point 1 goes to a path that starts of L. Let's start a new path going R.

DanZ (20:28:11)
But now it might be the same as the second point... how do we fix that?

not_trig (20:27:36)
and then the second, and then the third... ?

DanZ (20:28:29)
What do you mean? What should our new path do as its second move?

b-flat (20:28:24)
second point L

DanZ (20:28:32)
Yes!

DanZ (20:28:55)
So we're building a new path, and it starts off going RL. Which means that it's already guaranteed to be different from where the first two points are paired up with.

bubka (20:28:51)
thirs point L

DanZ (20:29:18)
Right: because the third thing the third path does is go R, and we need to do the opposite.

henry.zheng (20:29:09)
so the final conclusion is that for every path, there always exists at least one point from which a point can deviate. Hence, we can never pair up the points.

davidyko (20:29:17)
And then go L, then R

DanZ (20:29:41)
Now we're getting there. We're going to build just one path that's different from every path E was matched to!

Jayson Lynch (20:29:29)
Repeat ad infinum...

Hamster1800 (20:29:41)
and we continue this for a long time until we get one different from all of paths corresponding to the countable infinity of points in E

DanZ (20:29:53)
Exactly.

DanZ (20:30:00)
We end up with:

DanZ (20:30:08)


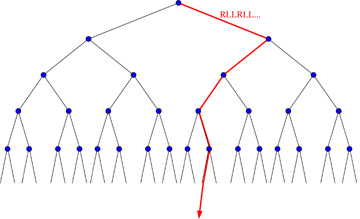
DanZ (20:30:12)
Image at: //s3.amazonaws.com/classroom.artofproblemsolving.com/Community/MJImages/DanZ/newpathlarge.jpg

DanZ (20:30:18)
It's always doing the opposite.

DanZ (20:30:33)
Since we know where everything in E was going, and it wasn't going to this, there's a path that it missed!

DanZ (20:30:42)
There are actually lots more that the matching missed, but we only needed to find one.

DanZ (20:30:50)
Since now we know that the "pairing" was a fake!

DanZ (20:31:25)


DanZ (20:31:34)


DanZ (20:31:41)


DanZ (20:31:55)


meenamathgirl (20:30:58)
So what cardinality is this?

DanZ (20:32:13)
This is called the cardinality of the "continuum," i.e. the real numbers.

DanZ (20:32:23)
It's also written

DanZ (20:32:29)


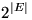
DanZ (20:32:46)
Which means that it's the same as the [i]power set[/i] of E.

bubka (20:31:11)
in fact the matching missed almost all the paths!

DanZ (20:32:55)
Yes, you're right!

DanZ (20:33:01)
You can build lots more paths it missed if you want.

davidyko (20:31:36)
So there[i]are[/i] bigger different sizes of infinities.

davidyko (20:32:24)
So we had countable, now we have continuum?

DanZ (20:33:10)
Yup.

bubka (20:32:22)
aleph one

DanZ (20:33:20)
That, however, is dangerous to say!

DanZ (20:33:33)
It's actually impossible to prove that this is aleph one.

meenamathgirl (20:33:35)
Can you talk about how much bigger the cardinality of the continuum is than the countable sets?

DanZ (20:33:50)
It depends what you mean by "how much."

DanZ (20:34:01)
It turns out that, unless you add an extra axiom, you can't prove if there's any other size of infinity between them!

DanZ (20:34:20)
However, there are a *lot* more points in the continuum than in countable sets. You get a better idea of this the more you work with it.

DanZ (20:34:27)
This is a crazy big infinity, and there are much larger!

not_trig (20:34:13)
what is aleph one vs. aleph null?

meenamathgirl (20:34:15)
Isn't that called the continuum hypothesis?

b-flat (20:34:19)
what is "aleph one?"

bubka (20:34:28)
what is the definition of aleph one?

DanZ (20:34:53)
Aleph one is the biggest infinity after |E|.

DanZ (20:34:59)
Err, smallest.

DanZ (20:35:04)
Sorry. Aleph one is the smallest infinity after |E|.

DanZ (20:35:17)
But you can't prove which one that is unless you add an extra axiom.

whitesoxfan (20:33:25)
what about 3^|E|? and 1.5^E?

DanZ (20:35:38)
Well, 1.5^E is weird.

DanZ (20:35:39)
But:

exponent (20:34:09)
would this have the same cardinality as a tree where each point splits into 3 more paths?

DanZ (20:35:52)
3^|E| has the same size as a tree where you split into three paths.

DanZ (20:36:07)
I'm going to leave you with the question of if those are the same; you can think about it your own, and I'd be happy to answer it later.

DanZ (20:36:16)
Okay, I want to wrap up the discussion for a minute.

DanZ (20:36:50)
This proof is very deep, and for that reason it's a good place to stop and let you think about it. I do want to say a few other things before we close for the night, including the possibility of continuing this.

DanZ (20:36:54)


DanZ (20:36:57)


DanZ (20:37:16)


DanZ (20:37:25)


DanZ (20:37:50)
(It's counterintuitive because there are infinitely many rationals "between" any two integers, and yet you can still pair them up!)

DanZ (20:37:52)


DanZ (20:38:15)
So, guys, did you enjoy the Math Jam?

Goistein (20:38:11)
So next is complex numbers?

DanZ (20:38:32)
That's a good thing to think about!

meenamathgirl (20:38:24)
Yes!

b-flat (20:38:26)
yeah

davidyko (20:38:31)
Yeah, definitely, it was great.

exponent (20:38:34)
yeah, thanks

Hamster1800 (20:38:35)
If I say no, will you stop it from going to the classroom?

plucesiar (20:38:35)
yes this was pretty sweet

henry.zheng (20:38:52)
wow. amazing. so there are as many numbers as there are even numbers. i had a feeling that was true, but now it's proven.

DanZ (20:39:08)
Thank you! A few more things:

DanZ (20:39:25)


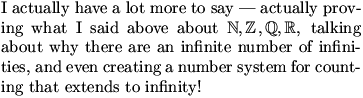
DanZ (20:39:36)
I don't want to keep going now --- we're all tired, and that was a lot of math --- but Richard gave me permission to hold two other Math Jams, at this time next week, and then this time the week after --- so that's March 7 and March 14, also at 7:30pm ET. I guess I don't know if you guys would be interested in seeing more of this stuff. So if we were to meet next week, do you think you'd come? (Please reply so I can get an idea!)

DanZ (20:40:20)
Okay, that was so many "yes" replies I'm not going to even post them. That's really awesome!

bubka (20:40:17)
the time is a bit tough: it is seven in the morning here now

DanZ (20:40:38)
Except that might be difficult to deal with!

DanZ (20:40:41)
I'm sorry, but thank you for coming!

daermon (20:40:37)
is it okay if i missed a bunch of this?

DanZ (20:40:58)
There will be a log posted.

DanZ (20:41:03)
A few more notes:

DanZ (20:41:10)
You can also feel free to invite others; they can look over the transcript of this math jam, or if they feel up to a huge challenge, they could just jump in --- I'm going to briefly review what we did here today.

DanZ (20:41:26)
Now, for those of you who are looking for a new kind of challenge in math --- or if you want to sharpen your skills at solving problems in theoretical math --- I've put up some interesting problems that relate to this material. It's worth looking at these! They'll help you understand and extend everything that's happened here, and they'll improve your problem solving a bit, too. If you want to take a look, you can find them on my webpage:

DanZ (20:41:32)
http://www.math.uiuc.edu/~dzaharo2/teaching/mathjam/

DanZ (20:41:46)
These problems are really interesting; you'll see things that are even weirder, and you'll also get your first look at an even bigger infinity.

DanZ (20:41:53)
You don't need to look at them to understand next time.

DanZ (20:41:55)
But they're cool!

DanZ (20:42:02)
And they're fun, and some of them are pretty hard, too!

plucesiar (20:41:25)
Do you have any recommendations for further reading?

DanZ (20:42:24)
Yes, but let me think about that so I can find the best book to recommend.

DanZ (20:42:36)
I'll suggest something next time. Keith Devlin's The Joy of Sets is definitely a good bet, however.

DanZ (20:42:58)
Okay, that's all for today. I'm going to hang around and keep talking for as long as you guys have questions, but I'll leave stuff for next time, too.

Question-and-answer session starts here.

DanZ (20:43:15)
Also, as Richard says, I teach at Mathcamp each summer, and if you have questions about that, feel free to ask them once the infinity questions die down.

Goistein (20:42:45)
What's aleph 3?

DanZ (20:43:46)
"Aleph n" is the nth largest infinity (yes, you can order them). You write these like:

DanZ (20:44:10)
(Waiting for my LaTeX to render...)

DanZ (20:45:16)


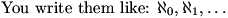
DanZ (20:45:21)
Ah, there we go.

DanZ (20:45:28)
Now, it turns out there are bigger ones yet!

DanZ (20:45:30)
For example,

DanZ (20:45:53)


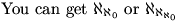
DanZ (20:45:58)
You can even go down for an infinite chain!

DanZ (20:46:09)
So there's a lot of stuff in there.

variable (20:43:23)
Is |E| the smallest infinity, please? If 2^|E| is a larger infinity than |E|, does this mean that log_2 (|E|) is a lesser infinity than |E|?

DanZ (20:46:40)
Yes, |E| is the smallest. Because if you have infinitely many elements, there must always be a "next" one --- so start at one, then find a "next" one, then the "next" one after that, and so on, and you get E inside your set.

DanZ (20:46:47)
So any infinite set is at least as large as E.

DanZ (20:46:54)
Logs are not really well-defined for infinity, I'm afraid!

mechtech (20:43:35)
Does .99999999999999999... = 1

DanZ (20:47:15)
Yes: .999... = 0.333... + 0.333... + 0.333... = 1/3 + 1/3 + 1/3 = 1.

DanZ (20:47:23)
There's a formal definition of the real numbers and this comes out of that.

E^(pi*i)=-1 (20:43:41)
Just wondering: is it possible that there is no such thing as the "smallest infinity after |E|" because infinities are like the real numbers: infinitely dense?

DanZ (20:47:35)
It depends on your assumptions, but in general, there's always a next one.

EgUaLuEsRs07_2 (20:43:50)
this is a little off topic, but do u think i could ask a few questions about what MIT is like?

DanZ (20:47:50)
I'd be happy to answer questions about that a bit later, but I'd like to let the others finish first.

daermon (20:45:35)
dan, isn't aleph 3 the number of subsets of reals?

DanZ (20:48:06)
That depends on the continuum hypthesis.

DanZ (20:48:22)
If you assume the continuum hypothesis, then (I believe) aleph 2 is the number of subsets of the reals.

DanZ (20:48:27)
But I might be wrong on that, I'd have to look it up.

bubka (20:46:23)
how do you know the set of infinities is ordered?

DanZ (20:48:55)
If you assume the axiom of choice (which just about everyone does), that implies something called the "well ordering principle," which tells you that you have an order on them!

DanZ (20:48:58)
(In fact, it's a very special order.)

daermon (20:46:59)
is there any commonsense way to describe the alephs that go down in an infinite chain?

DanZ (20:49:26)
If you've seen power sets --- and if not, you will next time --- then you can get a lot of them. But there's such a large infinity of alephs that you couldn't possibly describe them all.

DanZ (20:49:39)
In particular, there are more alephs than there are sentences you can write in the English language --- *lots* more.

variable (20:48:33)
What is the cardinality of the number of infinities, please?

DanZ (20:50:05)
The number of infinities is actually *bigger* than any infinity. Now you're getting into deep set theory!

DanZ (20:50:22)
The problem is that you can't have the set of all sets, and if you allow a set of all infinities, you get the same contradiction.

bubka (20:50:25)
then how can you enumerate them?

DanZ (20:51:05)
(Responding to there being more alephs than there are sentences in the English language.)

DanZ (20:51:10)
The answer is that there's no way to write down every oen.

DanZ (20:51:32)
But you can say "assume that this aleph is 'large enough'" and then work with it. You don't know which one it is [i]exactly[/i], but you can still prove stuff about how it behaves.

DanZ (20:51:35)
This stuff is really crazy. :)

Hamster1800 (20:51:29)
If you don't assume the axiom of choice, is it possible that they aren't ordered?

DanZ (20:52:09)
Again, I believe so, but I don't know for sure. Unfortunately, you're stretching my knowledge, since I'm not a logician.

DanZ (20:52:27)
(Logicians deal with this; I deal with topology, which is more the shape of a space, but I know some logic on the side which lets me teach this.)

Goistein (20:51:46)
Is 2^(Aleph n)=Aleph (n+1) true?

DanZ (20:52:37)
Depends on the continuum hypothesis!

EgUaLuEsRs07_2 (20:51:48)
if the alephs can be indexed with the natural numbers, doesnt that mean there are countable many of them, since there are contably many natural numbers?

DanZ (20:53:00)


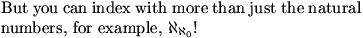
bubka (20:52:29)
then aleph knot, aleph one, aleph two, ... is only a small subset of them?

DanZ (20:53:16)
*Very* small subset.

daermon (20:51:58)
what is the axiom of choice? i might've missed this earlier...

DanZ (20:53:34)
The axiom of choice is a pretty technical statement, actually.

DanZ (20:53:44)
So, a while ago a lot of people came up with axioms for set theory.

DanZ (20:53:51)
Look on Wikipedia for the Zermelo-Frankel set theory axioms, for example.

DanZ (20:54:05)
They realized afterwards that there are some questions that these axioms don't answer!

DanZ (20:54:21)
One of them is if there's any infinite set between |E| and |P| --- that's called the continuum hypothesis.

DanZ (20:54:45)
Another is called the axiom of choice, and in some sense it's really simple. It asks if there is always a function that can take on element out of an infinite collection of sets.

DanZ (20:54:57)
It's a weird question to ask, but it has profound consequences.

DanZ (20:55:15)
One of which is if you can find a "well ordering" on every set. (That's called the well ordering principle.)

DanZ (20:55:23)
Which would allow you to find a nice ordering on sizes of infinity!

bubka (20:55:12)
but hang on the set : aleph knot, aleph one, aleph two, ..., aleph aleph knot, leph aleph one, aleph aleph two, ... aleph aleph aleph knot, ... is still countable?!

DanZ (20:55:52)
No --- even aleph one isn't countable.

DanZ (20:55:58)
But that *list* of infinities is countable.

DanZ (20:56:10)
You haven't even begun to touch just how many infinities they are. They keep going way beyond that list!

DanZ (20:56:58)
For example, I can do aleph sub an *infinite descending chain of alephs*, and then much higher.

daermon (20:56:54)
so my counting doesn't work?

DanZ (20:57:17)
I'm afraid so. :)

EgUaLuEsRs07_2 (20:56:47)
wait, didnt u just say that list of infinities is not countable?

DanZ (20:57:27)
Yes --- there are lots more beyond that list.

DanZ (20:57:47)
(Hrm. So that last bit of discussion was surprisingly technical. To those that aren't following, don't panic!)

Hamster1800 (20:57:36)
is it possible to have a chain of aleph one alephs?

DanZ (20:57:54)
Yes.

DanZ (20:58:04)
And now we're starting to get somewhere.

bubka (20:57:58)
ok its like the paradox: a well ordered set isn't necessarily countable, because the list of minima obtained by removing the minimum each time is nowhere near exhaustive!

DanZ (20:58:15)
Yes!

DanZ (20:58:22)
That's a fantastic observation.

DanZ (20:58:37)
Back in high school, I was convinced I'd proved that the real numbers were countable assuming the axiom of choice. :)

daermon (20:58:55)
tsk tsk

DanZ (20:59:23)
Yeah, I got a teacher at Mathcamp (back when I was a student) to correct me then.

sangsang (20:59:08)
Would aleph aleph aleph aleph...etc. exist?

DanZ (20:59:34)
Yes.

DanZ (20:59:46)
So, here's a formal way of saying it.

DanZ (21:00:02)
You can take the [i]union[/i] of any collection of sets.

DanZ (21:00:44)


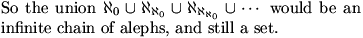
DanZ (21:00:49)
A new one, that's bigger.

Goistein (21:00:40)
tan(90) is which infinity?

DanZ (21:01:30)
That's actually a different kind of thing. This infinity system is *different* from what you get with functions, which doesn't really have any system beyond just "infinity."

daermon (21:01:02)
it would be nice if somebody proved that undecidability thing wrong so we could have the continuim hypothesis lol

DanZ (21:01:47)
Well, we can just assume it.

daermon (21:01:57)
thats like some religion of math :P

DanZ (21:02:33)
Heh, you'd be surprised. Mathematicians get pretty passionate about what they think "must" be true.

DanZ (21:03:13)
It turns out that if you assume the axiom of choice, you can prove something called the "Banach Tarski paradox." It says that if you take a sphere, and cut it up into a bunch of pieces, then reassemble them in just the right way, you get two spheres of the same size as the original!

DanZ (21:03:27)
Now, the cuts you have to make are totally insane (they're called "unmeasurable"), so you could never do this in real life.

DanZ (21:03:39)
Banach and Tarski didn't like the axiom of choice, so they proved this to convince mathematicians not to use it.

DanZ (21:03:53)
Instead, when they published it, everyone went "that's so cool!" and wanted to assume the axiom of choice!

daermon (21:04:04)
ooh burn

Jayson Lynch (21:04:11)
Think of 'proving' and assuming the continum hypothesis like you would look at Euclid's fifth axom. There are different types of geomety. No one is correct.

DanZ (21:04:35)
Yes, that's a very good point. However, the axiom of choice is so incredibly useful that lots of people want to use it.

EgUaLuEsRs07_2 (21:04:22)
well its only counterintuitive to us because we think of trying to do that with a physical sphere, which isnt infinitely divisible, whereas a mathematical sphere is

bubka (21:04:31)
we can have two branches of maths: one assuming it and one not assuming it

DanZ (21:05:09)
And in some sense we do --- but most people work in one particular branch, or what they do doesn't depend on which branch they're in (it's true in both).

bubka (21:05:43)
like proving |E| = |F|

DanZ (21:06:03)
Exactly --- you can do that in either.

alienfreakk (21:05:57)
what is infinity times infinity

DanZ (21:06:33)
It actually depends on what kind of number system you're using (ordinals or cardinals), and the answer is not always what you hope it will be.

DanZ (21:06:43)
You'll actually see a kind of example of that on those problems I mentioned.

daermon (21:07:00)
isn't this college stuff? it doesn't seem too hard, just confusing

DanZ (21:07:11)
So, it depends.

DanZ (21:07:19)
You'd be surprised how much math you'd do as a math major that never uses calculus, for example.

DanZ (21:07:37)
And you wouldn't see this in college unless you were a math major or took some extra math courses for fun.

DanZ (21:07:47)
Engineers, for example, only take calculus and linear algebra.

DanZ (21:07:52)
Which wouldn't cover this.

DanZ (21:07:59)
But you can find those fun courses in there and get some really neat stuff.

bubka (21:07:40)
graph theory

DanZ (21:08:18)
That's another example of math that just doesn't need calculus, at least for most of it.

daermon (21:07:55)
i learned some of this at CTY

DanZ (21:08:38)
There are lots of places to see it. I think I first saw some of it there, too.

DanZ (21:08:46)
But this is only the tip of the iceberg.

DanZ (21:09:21)
There's so much interesting mathematics out there --- group theory, which is a generalization of algebra, and topology, which studies the shape of things and bending them, and so much else --- that it's just impossible to learn it all. You can just navigate through the ocean and learn what looks interesting!

daermon (21:09:02)
ok now i cant wait to be in high school so i can go to mathcamp... i guess mathpath will have to do

DanZ (21:09:42)
Tangentially, Mathcamp is open to middle school students who do well on the qualifying quiz.

DanZ (21:09:54)
So you're welcome to apply, but it's much more difficult to get in when you're in middle school.

Goistein (21:09:17)
90% we don't understand.

DanZ (21:10:23)
For me, it sure feels like that sometimes! :)

bookaholic (21:10:20)
I went to Mathcamp the summer after eighth grade--so definitely try to apply

bubka (21:10:52)
topology and graph theory rock! i think rigorous proofs involving Riemann integrals and epsilons and deltas are on their way out

DanZ (21:11:16)
You still need those rigorous proofs, and they can be neat too. But I'd agree with you on the math I prefer!

Goistein (21:10:56)
What math do you take?

DanZ (21:12:11)


DanZ (21:12:28)
It's a lot more complicated than that, but I'd have to do a lot of teaching to explain it all!

whitesoxfan (21:11:39)
infinity was just the tip of the iceburg, the real numbers was just the tip of the iceburg, all this is just the tip of the iceburg---what's the whole thing?

DanZ (21:12:36)
Crazy.

daermon (21:12:11)
aren't you a teacher?

DanZ (21:12:56)
I teach at Mathcamp and at other places, but I'm a graduate student at UIUC. That means I teach some classes here, but I'm still studying for my PhD.

bubka (21:12:29)
rigorous proofs are frightfully neat, but as for reproducing them at the exams, it's pretty boring and horrible

DanZ (21:13:20)
I agree. However, thinking about new problems and coming up with proofs [i]is[/i] interesting!

DanZ (21:13:58)


E^(pi*i)=-1 (21:13:50)
Who was it that said "When more than 0% of a field of mathematics is understood, it has become boring"?

DanZ (21:14:07)
Heh.

DanZ (21:14:21)
I think that ought to do it for tonight.

DanZ (21:14:22)
I still have to eat dinner!

DanZ (21:14:33)
However, I'll arrange for the next Math Jam and I think you'll all get e-mail about it.

DanZ (21:14:53)
Feel free to look over those problems and send me messages if you have questions; they'll be interesting!

E^(pi*i)=-1 (21:14:49)
Hey Dan are you planning a TCS MAth Jam? :-)

DanZ (21:15:06)
Shush, you. :)

DanZ (21:15:21)
I am going to be teaching at cSplash in New York City, where I'll do a bit of TCS. So you can Google that if you're in the area.

bubka (21:14:54)
can we PM we?

DanZ (21:15:34)
You're welcome to send me messages.

daermon (21:15:13)
whats TCS?

DanZ (21:15:57)
It's a course I taught at Mathcamp last summer --- "Theoretical Computer Science." There's even a little bit of it in the problems for this class!

DanZ (21:16:06)
It's a field of mathematics that studies the limits of what computers can do.

daermon (21:16:09)
oh like turning stuff?

DanZ (21:16:40)
"Turing," actually.

daermon (21:16:36)
turing?

DanZ (21:16:45)
Ah, yes.

DanZ (21:17:02)
Alan Turing, a mathematician who came up with a mathematical model of a computer, called a Turing machine.

EgUaLuEsRs07_2 (21:15:54)
im a senior, and i applied for MIT for class of '11, and i was wondering if maybe i could ask you a few questions, or maybe it would be better to do that next time...

DanZ (21:17:15)
Do you mind sending me a PM? That might be the best way to communicate about it.

EgUaLuEsRs07_2 (21:17:29)
what is a PM?

DanZ (21:17:41)
Private Message: it's something AoPS lets you send.

DanZ (21:17:57)
When you go to the forums, for example, there'll be a button at the top for "private message."

daermon (21:17:53)
look on the toolbar on top of the screen

bubka (21:18:36)
P vs NP is also great, eh?

DanZ (21:19:01)
It's an interesting problem indeed!

daermon (21:18:42)
okay maybe i should do my homework now :(

daermon (21:18:53)
[img id=em-1]

DanZ (21:19:08)
All right guys --- thanks! This was a lot of fun. Next week, things will get even more crazy!

DanZ (21:19:20)
So hopefully I'll see you then; I think you'll see that it's really interesting.

DanZ (21:19:29)
Until then, good night, or good morning, depending on where you are!

DanZ (21:19:52)
(Ok, I got one more math question I'll quickly attend to:)

Goistein (21:19:34)
Is 8/0 just plain infinity as well as tan(90)?

DanZ (21:20:05)
Dividing by 0 is undefined for a good reason.

DanZ (21:20:13)
You want to be able to multiply back by that thing and get where you started.

DanZ (21:20:22)
But if you multiply anything by 0, you'll never get 8!

DanZ (21:20:31)
If you make it infinity, then you lose a property of division that you really want.

DanZ (21:20:35)
So it's not even infinity, it's just undefined!

DanZ (21:20:51)
Good night, all!