Math Jams

DPatrick 2013-02-06 19:30:12
Welcome to the 2013 AMC 10A/12A Math Jam!

DPatrick 2013-02-06 19:30:19
I'm Dave Patrick, and I'll be leading our discussion tonight.

DPatrick 2013-02-06 19:30:27
Before we get started I would like to take a moment to explain our virtual classroom procedures to those who have not previously participated in a Math Jam or one of our online classes.

DPatrick 2013-02-06 19:30:39
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.

DPatrick 2013-02-06 19:30:52
This helps keep the session organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.

DPatrick 2013-02-06 19:31:05
There are a lot of students here! As I said, only (a fraction of the) well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!

DPatrick 2013-02-06 19:31:17
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!

DPatrick 2013-02-06 19:31:38
We do have two assistants tonight who can help answer some of your questions: baozhale and cppB.

baozhale 2013-02-06 19:31:43
Hi!

DPatrick 2013-02-06 19:31:49
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.

DPatrick 2013-02-06 19:32:06
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.

DPatrick 2013-02-06 19:32:32
Also, there will be several cases where we actually find the answer or almost the answer but then wander off. The goal is always to find a proof that our answer is correct and not just find the answers. Of course on the AMC you should aim to do much less work than this.

DPatrick 2013-02-06 19:32:54
We will work the last 5 problems from the AMC 10A, then the last 5 problems from the AMC 12A. (Three of the 10A problems, Problems 21-23, that we'll be working on also appeared as 17-19 on the 12A.) After that, time permitting, I may take requests for some other problems for discussion.

DPatrick 2013-02-06 19:33:18
Let's kick things off with #21 from the 10A, which was also #17 on the 12A.

DPatrick 2013-02-06 19:33:22

DPatrick 2013-02-06 19:33:34
(The current problem under discussion will always be at the top of the screen.)

DPatrick 2013-02-06 19:33:46
Where can we begin?

Lord.of.AMC 2013-02-06 19:34:07
let the total number of coins be x

chuckmasters 2013-02-06 19:34:07
Work backwards

mathway 2013-02-06 19:34:07
assigning variables

math-rules 2013-02-06 19:34:07
Work backwards

DPatrick 2013-02-06 19:34:21
Sounds like a plan. Let's call the answer that we're looking for x.

DPatrick 2013-02-06 19:34:31
Since x is what we want, it makes sense to start at x and work backwards.

DPatrick 2013-02-06 19:34:41
So there are x coins before the 12th pirate goes.

DPatrick 2013-02-06 19:34:47
How many coins before the 11th pirate takes his share?

willwin 2013-02-06 19:35:31
12x

j2002 2013-02-06 19:35:31
12x

mathwrath 2013-02-06 19:35:31
12x

Funnymushman 2013-02-06 19:35:31
12x

Tuxianeer 2013-02-06 19:35:31
12x

mathwizard888 2013-02-06 19:35:31
12x

DPatrick 2013-02-06 19:35:42
Right. He takes 11/12 of whatever was there.

DPatrick 2013-02-06 19:35:50
So he leaves 1/12 of the stack for the last pirate...

DPatrick 2013-02-06 19:35:54
...but we also know that he leaves x for the last pirate.

DPatrick 2013-02-06 19:36:02
So 1/12 of the stash before the 11th pirate chooses is x.

DPatrick 2013-02-06 19:36:11
Therefore, the stash before the 11th pirate chooses is 12x.

DPatrick 2013-02-06 19:36:19
No problem so far: if x is a positive integer, than so is 12x.

DPatrick 2013-02-06 19:36:23
How many coins were there before the 10th pirate chose?

brian22 2013-02-06 19:36:50
72x for #10

kli2000 2013-02-06 19:36:50
The stash before the 10th pirate is 72x.

flyrain 2013-02-06 19:36:50
72x?

foppotee 2013-02-06 19:36:50
72x

DPatrick 2013-02-06 19:36:58
The 10th pirate takes 10/12 of the stack and leaves 2/12.

DPatrick 2013-02-06 19:37:02
So 2/12 of the stash is 12x.

DPatrick 2013-02-06 19:37:07
Thus the stash before the 10th pirate's turn is (12/2)*12x = 72x.

DPatrick 2013-02-06 19:37:14
Still good!

DPatrick 2013-02-06 19:37:17
How does this generalize? That is, I don't want to do all 12 steps by hand.

theone142857 2013-02-06 19:38:11
Multiply 12/k each time

matticus42 2013-02-06 19:38:11
12/1*12/2*12/3*...*12/12

cerberus88 2013-02-06 19:38:11
each time, we multiply by (12/(12-k))

StefRen 2013-02-06 19:38:16
x*(12/1)(12/2)(12/3)...etc

DuoCapital 2013-02-06 19:38:16
x*(12/1)*(12/2)*(12/3)...

DPatrick 2013-02-06 19:38:21

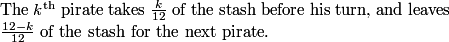
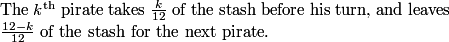
DPatrick 2013-02-06 19:38:36
Thus, to go backwards from after the kth pirate's turn to before his turn, we multiply by 12/(12-k).

DPatrick 2013-02-06 19:38:56

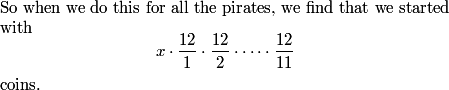
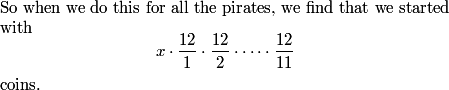
6stars 2013-02-06 19:39:16
The denominator is 11!

DPatrick 2013-02-06 19:39:23

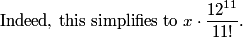
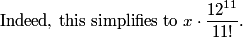
DPatrick 2013-02-06 19:39:39
How can this be ensured to be an integer at every step along the way?

thkim1011 2013-02-06 19:40:18
11, 7, 5 won't simplify.

PertBanking 2013-02-06 19:40:18
So we just have to worry about the denominators that cant factor into 2^x * 3^x

sindennisz 2013-02-06 19:40:18
x needs to have a factor of 5,7,11.

Samuel D 2013-02-06 19:40:18
X has to have 5^2, 7, 11

DPatrick 2013-02-06 19:40:38
Right. Most of the 11! will cancel with all the 2's and 3's in 12^11.

DPatrick 2013-02-06 19:40:56
But two 5's (one from 5 and one from 10), a 7, and an 11 won't cancel with the 12s, so these have to cancel with something in x.

ninjashiloh 2013-02-06 19:41:16
5^2*7*11=1925, so the answer is (D)

mathwrath 2013-02-06 19:41:16
x=1925

jasontang 2013-02-06 19:41:16
5*5*7*11=1925

dlennon 2013-02-06 19:41:16
x turns out to be 5^2*7*11=1925

DPatrick 2013-02-06 19:41:28

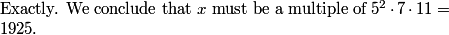
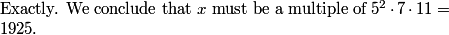
DPatrick 2013-02-06 19:41:31
And in fact x = 1925 works: for the first few steps we'll be multiplying by integers, and the factors of 1915 will allow us to cancel denominators when we multiply by 12/5, 12/7, 12/10, and 12/11. (There will be plenty of extra factors of 2's and 3's to cancel what's needed in 12/8 and 12/9 too.)

DPatrick 2013-02-06 19:41:48
(oops: that should be 1925 above and not 1915)

DPatrick 2013-02-06 19:41:59
So the answer is (D) 1925.

DPatrick 2013-02-06 19:42:24
OK, let's move on to #22 on the 10A, which was also #18 on the 12A:

DPatrick 2013-02-06 19:42:30

DPatrick 2013-02-06 19:42:41
Yikes, 3-D!

qwertyu 2013-02-06 19:42:56
Draw a cross-section

Lord.of.AMC 2013-02-06 19:42:56
turn it into 2D

zhuangzhuang 2013-02-06 19:42:56
cross secrtions?

djmathman 2013-02-06 19:42:56
Cross-sections are nice.

chuckmasters 2013-02-06 19:42:56
"Convert" it to 2-D

DPatrick 2013-02-06 19:43:00
The truth is, like many 3-D problems, it's really just a 2-D problem is disguise. Let's see.

DPatrick 2013-02-06 19:43:13
It probably makes sense to first figure out the radius of the big sphere. How do we do that?

tluo5458 2013-02-06 19:43:40
shouldn't the spheres act like circles?

Duncanyang 2013-02-06 19:43:40
circles centered at the vertices of a hexagon

minimario 2013-02-06 19:43:40
Draw a hexagon

zhuj1198 2013-02-06 19:43:40
Draw the hexagon with circles on the vertices

ic1999 2013-02-06 19:43:40
cross sections of 6 small spheres, draw the hexagon

DPatrick 2013-02-06 19:43:43
We can take a cross-section that contains the hexagon.

DPatrick 2013-02-06 19:43:48

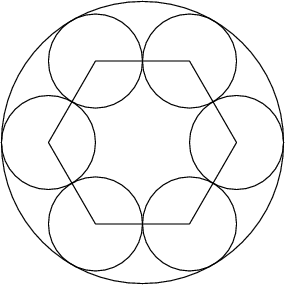
DPatrick 2013-02-06 19:43:58
The small circles are equatorial cross-sections of the small spheres, and each have radius 1. So what is the radius of the big sphere?

anthonyjang 2013-02-06 19:44:25
the radius is 2+1

mbt123 2013-02-06 19:44:25
radius of hexagon=2 + the radius of 1 sphere on a vertex=> radius of big sphere=3

Funnymushman 2013-02-06 19:44:25
3

bengals 2013-02-06 19:44:25
3

hawtsauze 2013-02-06 19:44:25
3

DPatrick 2013-02-06 19:44:29
The picture pretty much gives it to us for free: the big sphere has radius 3.

DPatrick 2013-02-06 19:44:35

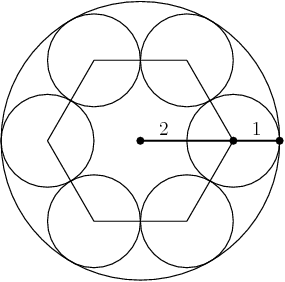
DPatrick 2013-02-06 19:44:46
Now what? How do we get a diagram with the eighth sphere in it?

calculatorwiz 2013-02-06 19:45:17
draw a vertical cross section

tan90 2013-02-06 19:45:17
vertical cross section

sindennisz 2013-02-06 19:45:17
Take the cross-section perpendicular to it.

RedHydra 2013-02-06 19:45:17
take another cross section perpendicular to the current one

jeff10 2013-02-06 19:45:17
how about a cross section from top to bottom instead of left to right?

supercomputer 2013-02-06 19:45:17
Take a vertical cross section (perpendicular to this)

DPatrick 2013-02-06 19:45:22
We can take a vertical cross-section through the center of the hexagon and through two opposite small spheres:

DPatrick 2013-02-06 19:45:28

DPatrick 2013-02-06 19:45:47
The sphere we want has a cross-section centered at X in the above picture. Let's set r to be the radius that we're looking for: that is, the radius of the new sphere. What can we do with the above picture?

jsk0301 2013-02-06 19:46:11
The centers make a triangle

thkim1011 2013-02-06 19:46:11
Connect the centers

SnapMaster 2013-02-06 19:46:11
I see a right triangle!

kzhu98 2013-02-06 19:46:11
pythagorean theorem

vinayak-kumar 2013-02-06 19:46:11
Draw a right triangle!

Chess4Everything 2013-02-06 19:46:11
We can connect the centers of the spheres.

DPatrick 2013-02-06 19:46:15
If we connect all the centers, we have a right triangle!

DPatrick 2013-02-06 19:46:20

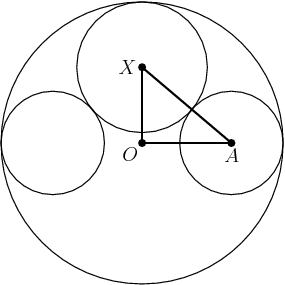
DPatrick 2013-02-06 19:46:34
What are the side lengths of this triangle? (Remember, r is the radius of the 8th sphere, centered at X.)

ws5188 2013-02-06 19:47:10
OX=3-r, XA=r+1, OA=2

SuperSnivy 2013-02-06 19:47:10
OX=3-r , OA=2 , AX=r+1

adelie 2013-02-06 19:47:10
OA is 2 as per the diagrams before, XO is 3-r by inspection

PertBanking 2013-02-06 19:47:10
2, 1 + r, 3 - r

DPatrick 2013-02-06 19:47:17
OA is 2. (The radius of the big circle is 3 and the radius of the small circle is 1.)

DPatrick 2013-02-06 19:47:25
AX is 1+r (the sum of the radius of the circle at A and the radius of the circle at X).

DPatrick 2013-02-06 19:47:32
OX is 3-r.

DPatrick 2013-02-06 19:47:44

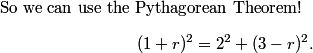
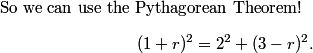
krmathcounts 2013-02-06 19:47:53
How do we know that the interior of circle X doesn't contain O?

DPatrick 2013-02-06 19:48:09
That's a good observation...and in fact we're about to answer this.

mathwrath 2013-02-06 19:48:26
r=3/2

bharatputra 2013-02-06 19:48:26
r=3/2

mathwizard888 2013-02-06 19:48:26
r=3/2 (B)

Iwilllose 2013-02-06 19:48:30
r=3/2

DPatrick 2013-02-06 19:48:36

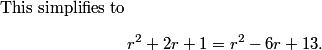
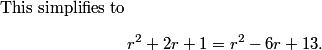
DPatrick 2013-02-06 19:48:46
This gives 8r = 12, so r = 3/2. Answer (B).

mathwrath 2013-02-06 19:49:01
Circle X contains point O

AdamGeller 2013-02-06 19:49:01
so O ends up being on circle X

DPatrick 2013-02-06 19:49:07
Right: my picture was actually incorrect. We just determined that the diameter of the circle with center X is 3, so in fact that circle passes through O.

math-rules 2013-02-06 19:49:17
How will we be able to draw such good drawings during the test?

DPatrick 2013-02-06 19:49:33
Bring a ruler, a compass, and a protractor. We'll see a problem later for which they're really valuable.

DPatrick 2013-02-06 19:49:47
Let's move on the 10A #23, which is also 12A #19:

DPatrick 2013-02-06 19:49:52

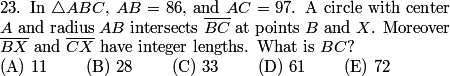
djmathman 2013-02-06 19:50:07
Draw a picture!

ic1999 2013-02-06 19:50:07
draw the diagram first

distortedwalrus 2013-02-06 19:50:07
diagram

cerberus88 2013-02-06 19:50:07
Diagram

cr108x 2013-02-06 19:50:07
Draw Diagram

DPatrick 2013-02-06 19:50:11
Let's sketch a picture of this.

DPatrick 2013-02-06 19:50:16

DPatrick 2013-02-06 19:50:24
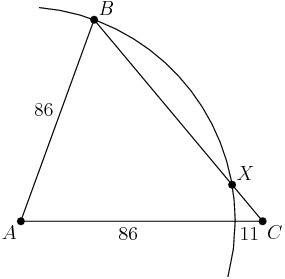
Note that I broke up AC into the 86 that's inside the circle, and the remaining 11 that's outside the circle.

PranayMittal 2013-02-06 19:50:45
Power of the point!!!!

Doink 2013-02-06 19:50:45
Power of the point on C

qwertyu 2013-02-06 19:50:45
Power of a point

StefRen 2013-02-06 19:50:45
power of a point

Smart Pi 2013-02-06 19:50:45
Power of a point!

DPatrick 2013-02-06 19:50:50
Power of a point! We have lengths of lines that intersect a circle, so it's a good guess that power of a point will come in useful.

DPatrick 2013-02-06 19:51:13
Point C looks like the best candidate. (Though there's no harm in trying other points too.)

DPatrick 2013-02-06 19:51:17
What does using power of a point at point C tell us?

djmathman 2013-02-06 19:51:55
CX * CB = 11* (11 + 86 + 86) = 11 * 183

ayqian22 2013-02-06 19:51:55
CX(CB)=11(183)

bengals 2013-02-06 19:51:55
BC*XC=11*183

DaChickenInc 2013-02-06 19:51:55
The power of point C is 11(11+2*86)=(XC)(BC)

DPatrick 2013-02-06 19:52:12
Right. Power of a point says the product of the two distances from C to a circle, along any line, is constant.

DPatrick 2013-02-06 19:52:21
If we go along ray CB, we get (CX)(CB).

DPatrick 2013-02-06 19:52:29
If we go along ray CA, we get (11)(11+2*86).

DPatrick 2013-02-06 19:52:48

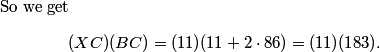
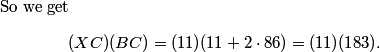
DPatrick 2013-02-06 19:52:57
But what else do we know?

Jzou 2013-02-06 19:53:29
we know that CX and CB are integers

Jzou 2013-02-06 19:53:29
XC and BC are integers

adelie 2013-02-06 19:53:29
xc<bc

Iggy Iguana 2013-02-06 19:53:29
xc and bc are integers

goldentail141 2013-02-06 19:53:29
XC and BX must be integers

ninjataco 2013-02-06 19:53:29
BX and CX are integers

DPatrick 2013-02-06 19:53:31
We know that XC < BC are both positive integers.

DPatrick 2013-02-06 19:53:43
So just using this data, what are the possibilities for XC and BC?

bobbyq 2013-02-06 19:54:12
33 and 61

SnapMaster 2013-02-06 19:54:12
33,61

guilt 2013-02-06 19:54:12
33, 61

ninjashiloh 2013-02-06 19:54:12
33,61

infinity99 2013-02-06 19:54:12
So XC = 33, BC = 61

DPatrick 2013-02-06 19:54:24

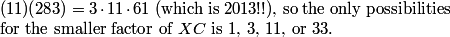
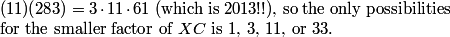
DPatrick 2013-02-06 19:54:43
(oops, that's (11)(183) = 2013.)

DPatrick 2013-02-06 19:55:05

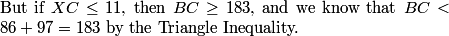
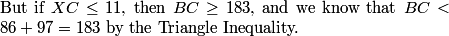
iguana123 2013-02-06 19:55:29
The answer is (D) 61

Smart Pi 2013-02-06 19:55:29
So BC = 61

zhuj1198 2013-02-06 19:55:29
The answer is D

DPatrick 2013-02-06 19:55:31
Thus we must have XC = 33, leaving BC = 61. Answer (D).

tluo5458 2013-02-06 19:55:36
is the 2013 coincidental?

DPatrick 2013-02-06 19:55:47
I doubt it.

They usually try to work in the current year in several problems.

DPatrick 2013-02-06 19:56:05
OK, on to #24. (This one nor #25 was on the AMC 12A.)

DPatrick 2013-02-06 19:56:11

DPatrick 2013-02-06 19:56:32
The key to this problem -- indeed the key to many counting problems -- is staying organized.

DPatrick 2013-02-06 19:56:52
Let's start by naming one team A,B,C and the other team X,Y,Z.

DPatrick 2013-02-06 19:57:08
What do we know?

kli2000 2013-02-06 19:57:34
6 rounds

apple.singer 2013-02-06 19:57:34
Person A plays XXYYZZ in some order

VietaFan 2013-02-06 19:57:34
A plays X, Y, and Z twice each

tluo5458 2013-02-06 19:57:34
every person plays 6 games

vinayak-kumar 2013-02-06 19:57:34
each player plays 2 games with each other

DPatrick 2013-02-06 19:57:39
In each round, each of {A,B,C} has to be paired with each of {X,Y,Z}.

DPatrick 2013-02-06 19:57:47
And each possible pairing (AX, AY, AZ, BX, BY, BZ, CX, CY, CZ) has to appear twice.

DPatrick 2013-02-06 19:58:04
How can we proceed?

Tuxianeer 2013-02-06 19:58:36
Consider the ways A's games can be scheduled, and then B's, and then you're done

Nitzuga 2013-02-06 19:58:36
Start by placing the A's

distortedwalrus 2013-02-06 19:58:36
look only at person A's games first

pier17 2013-02-06 19:58:36
do A's matches first

DPatrick 2013-02-06 19:58:41
I like to proceed via what I call "constructive counting": we imagine that we're the tournament organizer, and we're trying to construct a valid tournament. We keep track of our choices along the way.

DPatrick 2013-02-06 19:58:55
There are probably a lot of ways to do this for this problem. One way is to first focus on one particular player, let's say A.

DPatrick 2013-02-06 19:59:03
In how many ways can we determine A's schedule?

apple.singer 2013-02-06 19:59:47
A has C(6,2)*C(4,2)*C(2,2) ways to have his/her matches

VietaFan 2013-02-06 19:59:47
$\frac{6!}{2^3}$, because there are 6 items with 3 doubled items. 90 ways

jasontang 2013-02-06 19:59:47
6!/2*2*2

math-rules 2013-02-06 19:59:47
6!/(2*2*2)=90

jenniferwang 2013-02-06 19:59:47
There are 6!/2!2!2! ways.

mathwizard888 2013-02-06 19:59:47
6!/(2!2!2!)=90

centralbs 2013-02-06 19:59:47
6!/2!2!2!

DPatrick 2013-02-06 19:59:52
We need to arrange two AX's, two AY's, and two AZ's among the six rounds.

DPatrick 2013-02-06 20:00:00

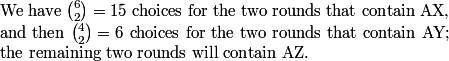
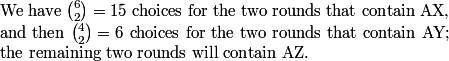
DPatrick 2013-02-06 20:00:07
So there are 15 * 6 = 90 ways to assign A's opponents in the six rounds.

DPatrick 2013-02-06 20:00:18

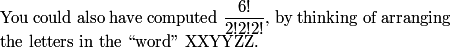
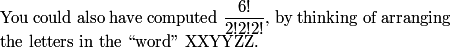
DPatrick 2013-02-06 20:00:25
Now what?

Rocksolid 2013-02-06 20:01:02
We look at another player

fz0718 2013-02-06 20:01:02
continue the constuctive countoing!

Rocksolid 2013-02-06 20:01:02
We look at B or C

pi_Plus_45x23 2013-02-06 20:01:02
do the same for b and c

googol.plex 2013-02-06 20:01:02
Assume he got XXYYZZ. This means B cannot have an X in first 2, no Y in second 2, and no Z in third 2

DPatrick 2013-02-06 20:01:06
To complete the construction, we have to determine how many ways there are to finish organizing the tournament: that is, in how many ways can the B's and C's be paired up.

DPatrick 2013-02-06 20:01:28
This count will be the same no matter how we arranged the A's, so for simplicity, let's suppose that A plays X in the first two rounds, then Y in the next two rounds, then Z in the last two rounds.

DPatrick 2013-02-06 20:01:40
So we have a diagram that looks something like this:

DPatrick 2013-02-06 20:01:45

DPatrick 2013-02-06 20:01:51
How do we finish the pairing?

3dot4teen 2013-02-06 20:02:31
Choose B's matches next

bengals 2013-02-06 20:02:31
B pairs with Y,Z in first and second, C has no other choice

j2002 2013-02-06 20:02:31
Choose who B plays.

jenniferwang 2013-02-06 20:02:41
But we need to keep in mind that one person cannot be paired up with two people at once.

DPatrick 2013-02-06 20:02:52
Let's just look at round 1 first. In the first round, it doesn't matter if we pair them BY,CZ or BZ,CY: the count of the remaining pairings will be the same either way.

DPatrick 2013-02-06 20:03:04
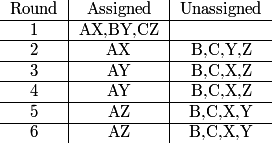
So let's just assume that we have BY, CZ in the first round; we'll then double our count from here to get the total count.

DPatrick 2013-02-06 20:03:10

DPatrick 2013-02-06 20:03:22
What about round 2?

Nitzuga 2013-02-06 20:03:41
There are still 2 ways!

sammyMaX 2013-02-06 20:03:41
BY CZ or BZ CY

Iwilllose 2013-02-06 20:03:41
We could have the same matches again.

supercomputer 2013-02-06 20:03:41
Same possiblities

DPatrick 2013-02-06 20:03:47
It looks like we have two cases, depending on what we decide to do in round 2.

DPatrick 2013-02-06 20:03:54
If we again pair BY, CZ in the second round, in how many ways can we finish?

DPatrick 2013-02-06 20:03:59

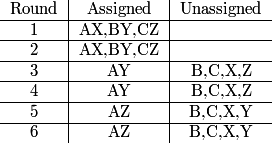
bharatputra 2013-02-06 20:04:24
1.

Lord.of.AMC 2013-02-06 20:04:24
1

krmathcounts 2013-02-06 20:04:24
ZZ,XX -- one way

ws5188 2013-02-06 20:04:24
1

footballfreak101 2013-02-06 20:04:24
1 way

DPatrick 2013-02-06 20:04:34
We're not allowed to have CZ in rounds 3 or 4, so those rounds have to be BZ and CX in both.

DPatrick 2013-02-06 20:04:39
That means we must have BX and CY in rounds 5 and 6.

DPatrick 2013-02-06 20:04:46
So in this case, there's only 1 way to finish.

DPatrick 2013-02-06 20:04:58
And the other case: what if we switch and pair BZ, CY in the second round?

DPatrick 2013-02-06 20:05:03

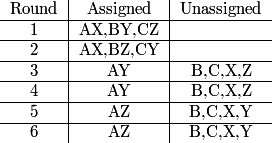
DPatrick 2013-02-06 20:05:06
Now in how many ways can we finish?

Tuxianeer 2013-02-06 20:05:33
4

cherryclutch 2013-02-06 20:05:33
4

unknot 2013-02-06 20:05:33
4

zhuj1198 2013-02-06 20:05:33
4

vinayak-kumar 2013-02-06 20:05:33
4 ways

mathwizard888 2013-02-06 20:05:33
2*2=4 ways (one Y and one Z)

DPatrick 2013-02-06 20:05:39
We need one more BY: that can be in either round 5 or round 6. So that's 2 choices.

DPatrick 2013-02-06 20:05:47
And we need one more BZ: that can be in either round 3 or round 4. So that's also 2 choices.

DPatrick 2013-02-06 20:06:03
After that, the rest of the tournament is force.

DPatrick 2013-02-06 20:06:05
...forced.

DPatrick 2013-02-06 20:06:15
So there are 2*2 = 4 ways to finish in this case.

DPatrick 2013-02-06 20:06:24
How do we wrap all this up to get our final count?

fz0718 2013-02-06 20:06:45
4+1=5

countyguy 2013-02-06 20:06:45
90(2(1)+2(4))=E

Nitzuga 2013-02-06 20:06:45
So... $(4+1)2*90$?

googol.plex 2013-02-06 20:06:45
then you have to multiply by two because we assumed BY, CZ, so we have 5*2*90=900 E

mathwizard888 2013-02-06 20:06:45
1+4=5, then 90*2*5=900 (E)

DPatrick 2013-02-06 20:06:58
Right, we just back up and carefully count our choices.

DPatrick 2013-02-06 20:07:00
Once we paired BY and CZ in round 1, we had 1+4 = 5 ways to finish.

DPatrick 2013-02-06 20:07:22
But pairing BZ and CY in round 1 is identical and also gives 5 ways. So we have 10 ways to finish once we assign the A's.

DPatrick 2013-02-06 20:07:33
And recall that there were 90 ways to assign the A's, and once we did that there were 10 ways to finish.

DPatrick 2013-02-06 20:07:39
So there are 90 * 10 = 900 possible tournaments. Answer (E).

nimblepanda 2013-02-06 20:07:56
is there an easier way to do it?

DPatrick 2013-02-06 20:08:17
Possibly. I don't claim that my solutions are the easiest. But they're the most straightforward (to me, at least).

DPatrick 2013-02-06 20:08:25
And on to #25 on the 10A:

DPatrick 2013-02-06 20:08:31

DPatrick 2013-02-06 20:08:43
This problem was quite guessable even if you didn't do all the work -- more about that as we go.

brandbest1 2013-02-06 20:08:51
brute force drawing?

cerberus88 2013-02-06 20:08:51
Draw it and count

ninjashiloh 2013-02-06 20:08:51
you could draw it if you had time

raptorw 2013-02-06 20:08:51
you can draw it

DPatrick 2013-02-06 20:09:03
You could try that. The answer choices would scare me off of that tactic, though.

forthegreatergood 2013-02-06 20:09:26
8C4 minus some stuff?

FlyingWombat 2013-02-06 20:09:26
It has to be less than 70

zhuangzhuang 2013-02-06 20:09:26
you know <70...

kyuubinaruto 2013-02-06 20:09:26
can't you assume that the answer will be under 70

DPatrick 2013-02-06 20:09:46
Indeed, if you know how to get "70" in this problem very quickly, it's easier to guess.

DPatrick 2013-02-06 20:10:04
But let's be a little more naive, and let's also try to prove our answer without guessing.

DPatrick 2013-02-06 20:10:13
...and we'll see where the "70" comes from.

DPatrick 2013-02-06 20:10:28
My tactic is to first count all the pairs of diagonals that intersect, and then correct for when this overcounts intersection points.

DPatrick 2013-02-06 20:10:39
How do we count all the pairs of diagonals that intersect?

bluepin93 2013-02-06 20:11:01
considering the amount of intersections of one diagonal

3dot4teen 2013-02-06 20:11:01
By drawing just a little you can see how many times each line has an intersection point

DPatrick 2013-02-06 20:11:18
There's a slick way to count them, but let's do it the non-slick way first.

DPatrick 2013-02-06 20:11:33
The diagonals of an octagon come in three basic types.

DPatrick 2013-02-06 20:11:45
What I'll call "Type A: connects vertices that are 2 apart:

DPatrick 2013-02-06 20:11:50

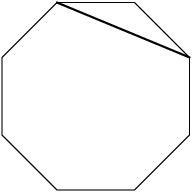
DPatrick 2013-02-06 20:11:56
How many of these are there?

calculatorwiz 2013-02-06 20:12:09
8

vincenthuang75025 2013-02-06 20:12:09
8

mathway 2013-02-06 20:12:09
8

bengals 2013-02-06 20:12:09
8

Seedleaf 2013-02-06 20:12:09
8

DuoCapital 2013-02-06 20:12:09
8

DPatrick 2013-02-06 20:12:23
There are 8 (one for each vertex that gets "cut off", like the upper-right vertex in the above pic).

DPatrick 2013-02-06 20:12:26
And how many other diagonals does each one of these intersect?

AopsKevin 2013-02-06 20:12:42
5

RotomPlasma 2013-02-06 20:12:42
5

kli2000 2013-02-06 20:12:42
5

ws5188 2013-02-06 20:12:42
5

Lalagato 2013-02-06 20:12:42
5

DPatrick 2013-02-06 20:12:46
They intersect any diagonal that runs from the "cut off" point to one of the other 5 points:

DPatrick 2013-02-06 20:12:52

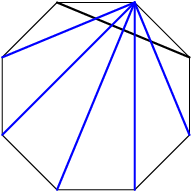
DPatrick 2013-02-06 20:13:03
So each of the 8 Type A diagonals intersects 5 other diagonals.

DPatrick 2013-02-06 20:13:13
Next, "Type B" diagonals connect points that are 3 apart:

DPatrick 2013-02-06 20:13:18

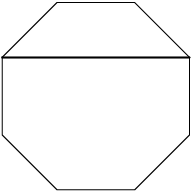
DPatrick 2013-02-06 20:13:20
How many of these are there?

mathwrath 2013-02-06 20:13:30
8

countyguy 2013-02-06 20:13:30
8 of them

gundraja 2013-02-06 20:13:30
8

mathnerd101 2013-02-06 20:13:30
8

DaChickenInc 2013-02-06 20:13:30
8

DPatrick 2013-02-06 20:13:33
Again, there are 8 of them (one for each side of the octagon that gets "cut off").

DPatrick 2013-02-06 20:13:40
And how many diagonals do each of these intersect?

coldsummer 2013-02-06 20:13:54
8

robinpark 2013-02-06 20:13:54
8

j610 2013-02-06 20:13:54
8

SuperSnivy 2013-02-06 20:13:54
8

hutyputy66 2013-02-06 20:13:54
8

Funnymushman 2013-02-06 20:13:54
8

DPatrick 2013-02-06 20:13:59
An intersecting diagonal must go from one of the 2 points on the "cut off" edge to one of the 4 point on the other side.

DPatrick 2013-02-06 20:14:05

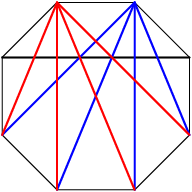
DPatrick 2013-02-06 20:14:10
So each type B diagonal intersects 8 other diagonals.

DPatrick 2013-02-06 20:14:22
Don't worry, I'll make a chart of all our data once we've collected it.

RotomPlasma 2013-02-06 20:14:30
But it's only 6 points!

DPatrick 2013-02-06 20:14:41
Indeed, we already see points where multiple diagonals intersect in the same point. Let's put that aside for now and worry about it later.

DPatrick 2013-02-06 20:14:49
Finally, type C diagonals connect opposite points:

DPatrick 2013-02-06 20:14:54

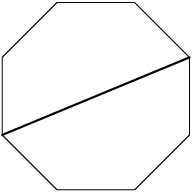
DPatrick 2013-02-06 20:14:57
How many of them are there?

unknot 2013-02-06 20:15:07
4

tuanyuan2008 2013-02-06 20:15:07
4

TigerSneak1 2013-02-06 20:15:07
4

oink 2013-02-06 20:15:07
4 of them

minimario 2013-02-06 20:15:07
4

DPatrick 2013-02-06 20:15:12
Only 4: there's one for each pair of opposite points. (And notice 8+8+4 = 20, so in our three types we're accounted for all 20 diagonals.)

DPatrick 2013-02-06 20:15:17
And how many other diagonals does each intersect?

dragonkid 2013-02-06 20:15:30
9

RedHydra 2013-02-06 20:15:30
3*3 = 9

yangdongyan 2013-02-06 20:15:30
9

FlyingWombat 2013-02-06 20:15:30
9

fz0718 2013-02-06 20:15:30
9

ABCDE 2013-02-06 20:15:30
3*3=9

jeff10 2013-02-06 20:15:30
9

DPatrick 2013-02-06 20:15:35
An intersecting diagonal connects one of the 3 points on one side to one of the 3 points on the other side:

DPatrick 2013-02-06 20:15:40

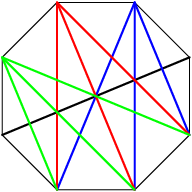
DPatrick 2013-02-06 20:15:45
So it intersects 3*3 = 9 other diagonals.

DPatrick 2013-02-06 20:15:53
As promised, here's a summary of our data:

DPatrick 2013-02-06 20:16:43
Given this data, how many pairs of intersecting diagonals are there?

DPatrick 2013-02-06 20:17:02
hang on...the table didn't post.

copeland 2013-02-06 20:17:18

Arghzoo 2013-02-06 20:18:19
40 + 64 + 36 = 140

RotomPlasma 2013-02-06 20:18:19
8*5+8*8+4*9=40+64+36=140

Nitzuga 2013-02-06 20:18:19
$8*8+8*5+4*9$? Maybe?

DPatrick 2013-02-06 20:18:25
The type As give us 8*5 = 40.
The type Bs give us 8*8 = 64.
The type Cs give us 4*9 = 36.

DPatrick 2013-02-06 20:18:35
So we might think 40+64+36 = 140. But...

DuoCapital 2013-02-06 20:18:50
divide by 2

zhuangzhuang 2013-02-06 20:18:50
2 overcount

3dot4teen 2013-02-06 20:18:50
2 because they are pairs

awesomeguy2 2013-02-06 20:18:50
divide by two

IDMasterz 2013-02-06 20:18:50
overcounted divide by 2

DPatrick 2013-02-06 20:19:00
Right: 140 counts each pair twice: one time for when we consider each diagonal of the pair "first".

DPatrick 2013-02-06 20:19:05
So the number of intersecting pairs of diagonals is (40+64+36)/2 = 140/2 = 70.

DPatrick 2013-02-06 20:19:21
Now, a lot of you knew the slick way of finding the number of pairs of intersecting diagonals...

ravi1998 2013-02-06 20:19:39
or you could do 8 choose 4

djmathman 2013-02-06 20:19:39
For every four vertices of the octagon we choose, we can construct two chords whose endpoints are on each of the four vertices, creating a unique intersection point.

supercomputer 2013-02-06 20:19:39
8C4

matholympiad25 2013-02-06 20:19:45
C(8,4). Every combination of 4 vertices makes an intersection point inside

qwertyu 2013-02-06 20:19:45
8C4

teranz0 2013-02-06 20:19:45
Pick 4 points from 8, 8C4=70

DPatrick 2013-02-06 20:19:55
Right. We can get this number by computing C(8,4) = 70, since choosing any 4 vertices gives us a quadrilateral whose diagonals will intersect.

DPatrick 2013-02-06 20:20:27
You can think about this some more later.

DPatrick 2013-02-06 20:20:39
So is (C) 70 the answer?

poweroftwo 2013-02-06 20:20:54
thats only pairs though

pranavsriram 2013-02-06 20:20:54
how about the ones where more then one diagonal intersected at the same point. Didn't we overcount those

guilt 2013-02-06 20:20:54
no there were overlaps

Arghzoo 2013-02-06 20:20:54
nope there are concurrent pionts

rahulgupta1096 2013-02-06 20:20:54
no, we overcounted intersection points

DPatrick 2013-02-06 20:21:01
No. Many of these diagonals intersect at the same point. We don't want to count intersecting pairs of diagonals, we only want to count intersecting points.

DPatrick 2013-02-06 20:21:07
For example, what about the center of the octagon?

DPatrick 2013-02-06 20:21:11
All four type C diagonals intersect in the center:

DPatrick 2013-02-06 20:21:15

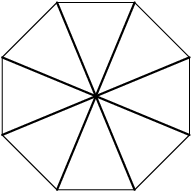
DPatrick 2013-02-06 20:21:21
How do we need to adjust our count of 70 to correct for the multiple diagonals intersecting in the center?

unknot 2013-02-06 20:21:42
so subtract 4C2-1=5

hamup1 2013-02-06 20:21:42
-5

matholympiad25 2013-02-06 20:21:42
4 diagonals intersect in there. So it is counted 6 times. We need to subtract 5 from that count.

hamup1 2013-02-06 20:21:42
Subtract 5

vinayak-kumar 2013-02-06 20:21:42
subtract 5?

DPatrick 2013-02-06 20:21:51

DPatrick 2013-02-06 20:22:00
Therefore, we've counted this center point 6 times. But we only want to count it once.

DPatrick 2013-02-06 20:22:07
So we have to subtract 5 from our previous count of 70, to correct for the fact that we've counted it 6 times and we only want to count it once.

DPatrick 2013-02-06 20:22:20
Now our count is 70 - 5 = 65.

DPatrick 2013-02-06 20:22:24
Is (B) 65 the answer?

mathwizard888 2013-02-06 20:22:41
brings it down to 65, but since there are more overcounts, it has to be 49 (A)

sammyMaX 2013-02-06 20:22:41
And in our previous diagrams, we have encountered more overcount, so it is under 65 and therefore A

coldsummer 2013-02-06 20:22:41
we know there are still more points to subtract so don't we know it's A right away?

RedHydra 2013-02-06 20:22:41
No, there is still more overcounts

Funnymushman 2013-02-06 20:22:41
no there's more

fcc1234 2013-02-06 20:22:41
no there will be more overlaps

chessderek 2013-02-06 20:22:41
no, we still overcounted

DPatrick 2013-02-06 20:22:45
No. There are other points at which more than 2 diagonals intersect. For example:

DPatrick 2013-02-06 20:22:49

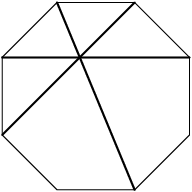
DPatrick 2013-02-06 20:23:14
(As you mentioned, at this point on the AMC contest, we now know the answer is less than 65, so we can go with (A) right away. But let's actually compute the answer.)

mathnerd101 2013-02-06 20:23:28
there are 8 of those

cherryclutch 2013-02-06 20:23:33
subtract (8*2) = 16

DPatrick 2013-02-06 20:23:37
Right.

DPatrick 2013-02-06 20:23:44
There are 8 of these points. (The above picture can be rotated by any multiple of 45 degrees to get a new one.)

DPatrick 2013-02-06 20:23:50
And each one is produced by 3 different pairs of diagonals. So each one is overcounted twice.

DPatrick 2013-02-06 20:23:59
Thus we must subtract another 2*8 = 16 from our count.

ninjashiloh 2013-02-06 20:24:10
65-16=49 so the answer is (A)

bluepie 2013-02-06 20:24:10
now the answer is A. 49

Iwilllose 2013-02-06 20:24:10
65-16-49, which is the answer....

DPatrick 2013-02-06 20:24:15
That leaves us with 65 - 16 = 49 points.
Answer (A).

DPatrick 2013-02-06 20:24:22
(It's the smallest answer choice, so we know there can't be any other intersection points that are overcounted.)

DuoCapital 2013-02-06 20:24:34
if this wasn't multiple choice, how would we know that there aren't any more?

Showpar 2013-02-06 20:24:34
How do we know there aren't more intersection points?

ninjataco 2013-02-06 20:24:34
How do we know that there aren't any other points that have multiple diagonals intersecting?

DPatrick 2013-02-06 20:24:41
We'd just have to carefully look for them.

DPatrick 2013-02-06 20:25:03
You could look at our pictures of the individual types from earlier to get a better view.

gaberen 2013-02-06 20:25:09
Does it matter if the octagon isn't regular?

DPatrick 2013-02-06 20:25:28
Indeed it would -- if the octagon were sufficiently irregular, it would be possible to get 70 distinct points.

DPatrick 2013-02-06 20:25:52
As I said, this problem was pretty guessable. The "guessability" comes in because just looking at the center point is enough to tell you that the answer is going to be odd, and that eliminates all but (A) or (B).

DPatrick 2013-02-06 20:26:17
OK, I am going to take a 4 minute break to rest my hands, and we'll resume at 8:30 ET / 5:30 ET with problems 21-25 from the AMC 12A!

DPatrick 2013-02-06 20:29:51
I'm back!

DPatrick 2013-02-06 20:30:10
By the way, thanks to all you guys for your patience. This is by far the record number of AoPSers in the classroom at one time.

DPatrick 2013-02-06 20:30:33
I know we're not posting many of your replies, and I hope you understand it's because of the sheer number of them!

DPatrick 2013-02-06 20:30:51
Anyway, on to the AMC 12A! We'll pick up with #21:

DPatrick 2013-02-06 20:30:55

ickathu 2013-02-06 20:31:20
is this natural log? Or what base?

DPatrick 2013-02-06 20:31:30
We should note that "log" means "log base 10". I feel that they should have made that explicit in the problem.

DPatrick 2013-02-06 20:31:52
And of course, there's no easy "rule" to compute something of the form log(a+b).

DPatrick 2013-02-06 20:31:58
How can we start?

RelaxationUtopia 2013-02-06 20:32:19
is C typoed?

catnpatx 2013-02-06 20:32:19
is answer c, 2109, a typo for 2019?

DPatrick 2013-02-06 20:32:23
oops, you're right.

DPatrick 2013-02-06 20:32:36

RexT95 2013-02-06 20:32:54
get rid of the log

DuoCapital 2013-02-06 20:32:54
undo the first natural log in A and in the answers?

DPatrick 2013-02-06 20:33:10
Sure, one way to start is to get rid of at least the first log is to raise everything to the power of 10.

DPatrick 2013-02-06 20:33:20

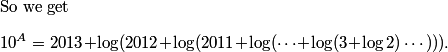
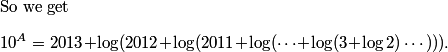
DPatrick 2013-02-06 20:33:38
oops, that's backwards, isn't it?

DPatrick 2013-02-06 20:34:18
It's "10 to the power of everything", not "everything to the power of 10".

DPatrick 2013-02-06 20:34:32
What's nice about this is that we can rewrite the question a little more simply:

DPatrick 2013-02-06 20:34:38

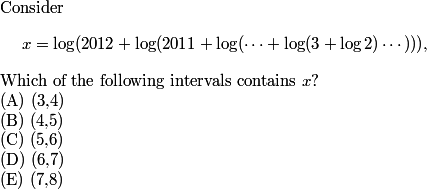
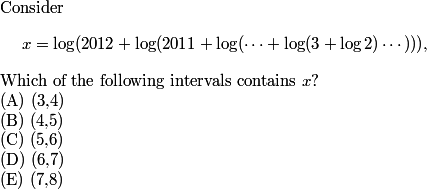
DPatrick 2013-02-06 20:34:57
Now what?

Arghzoo 2013-02-06 20:35:24
3<log(2012....)<4

jaymo 2013-02-06 20:35:28
log 2012+... won't be big enough to be more than 4

DPatrick 2013-02-06 20:35:51

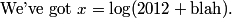
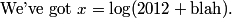
DPatrick 2013-02-06 20:36:03

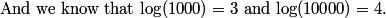
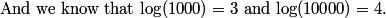
DPatrick 2013-02-06 20:36:08

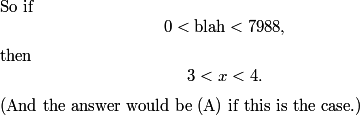
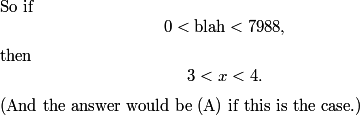
DPatrick 2013-02-06 20:36:22
Is "blah" really that small?

brian22 2013-02-06 20:36:46
it's pretty tiny

mathrocks11 2013-02-06 20:36:46
blah can't be greater than 7988 b/c blah = log(2011 + log(2010

tluo5458 2013-02-06 20:36:46
it is 3<blah<4

DPatrick 2013-02-06 20:37:02
Seems very very likely that "blah" is small. Remember that "blah" is itself a log.

DPatrick 2013-02-06 20:37:13

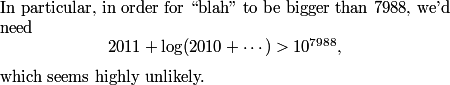
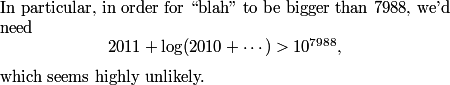
mathrocks11 2013-02-06 20:37:36
blah is less than A, so it must be less than 4

brian22 2013-02-06 20:37:36
on the test, we put A and move on!

DPatrick 2013-02-06 20:38:06
Indeed, we can easily see that blah is less than A, so it must be less than 8 (based on the answer choices), so the answer must be (A) and we can move on!

DPatrick 2013-02-06 20:38:15
In fact, it's pretty easy to prove by induction that all the logs in the expression for x are between 0 and 4.

DPatrick 2013-02-06 20:38:28

DPatrick 2013-02-06 20:38:33

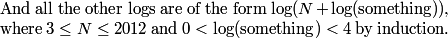
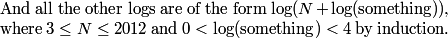
DPatrick 2013-02-06 20:38:48

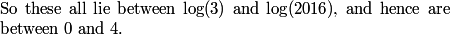
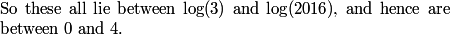
DPatrick 2013-02-06 20:39:06
Thus, indeed, x is less than 4. (And it's clearly greater than 3, since it's at least log(2012) which is a little more than 3.)

DPatrick 2013-02-06 20:39:12
Thus the answer is (A).

DPatrick 2013-02-06 20:39:38
This question was basically a test of whether you understood what a "log" meant or not.

DPatrick 2013-02-06 20:39:43
Let's move on to #22:

DPatrick 2013-02-06 20:39:47

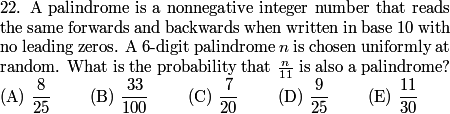
DPatrick 2013-02-06 20:40:04
What does a 6-digit palindrome look like?

matholympiad25 2013-02-06 20:40:15
write as abccba

DuoCapital 2013-02-06 20:40:15
abccba

guilt 2013-02-06 20:40:15
abccba

RotomPlasma 2013-02-06 20:40:15
abccba

matticus42 2013-02-06 20:40:15
abccba

RelaxationUtopia 2013-02-06 20:40:15
abccba

alex31415 2013-02-06 20:40:15
abccba

DPatrick 2013-02-06 20:40:20

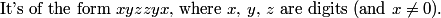
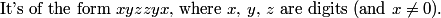
DPatrick 2013-02-06 20:40:24
So how many of them are there?

adelie 2013-02-06 20:40:43
900

Jpl2000 2013-02-06 20:40:43
900

gundraja 2013-02-06 20:40:43
900

monkey8 2013-02-06 20:40:43
9*10*10

Arghzoo 2013-02-06 20:40:43
9*10*10 = 900

DPatrick 2013-02-06 20:40:48
There are 9 choices for x and 10 each for y and z, so there are 9*10*10 = 900 of them.

DPatrick 2013-02-06 20:40:56
How many are divisible by 11?

ninjataco 2013-02-06 20:41:13
all of them

mathnerd101 2013-02-06 20:41:13
all of them

calculatorwiz 2013-02-06 20:41:13
all of them

qfoam 2013-02-06 20:41:13
all of them

Double_Double 2013-02-06 20:41:13
all of them

DPatrick 2013-02-06 20:41:18
All of them! The divisibility test for 11 is to take the alternating sum of the digits. But that gives us x-y+z-z+y-x = 0.

DPatrick 2013-02-06 20:41:43
So we want to investigate n/11 where n is one of our 6-digit palindromes. What do we get when we divide xyzzyx by 11?

DPatrick 2013-02-06 20:42:04
Maybe that's a bad question to ask...what's another way we can approach this?

adelie 2013-02-06 20:42:31
go backwards

centralbs 2013-02-06 20:42:31
consider the result after division: a palindrome in the form abcba

ChenthuranA 2013-02-06 20:42:31
abcba

djmathman 2013-02-06 20:42:36
Consider the palindrome that results, and find all of them such that 11 times it is also a palindrome

DPatrick 2013-02-06 20:42:47
Right, we can come at this from the other direction: we can start with a palindrome, multiply it by 11, and see if we get a 6-digit palindrome.

DPatrick 2013-02-06 20:42:53
Can we do this by starting with a 4-digit palindrome?

bobthesmartypants 2013-02-06 20:43:17
no

ic1999 2013-02-06 20:43:17
9aa9

DPatrick 2013-02-06 20:43:43
Well.. it might be big enough: 11*(a four digit number starting with 9) can have 6 digits.

DPatrick 2013-02-06 20:44:00
(11*9999 = 109989 for example, but that's not a palindrome)

qwertyu 2013-02-06 20:44:17
But the unit digit is always 9

brian22 2013-02-06 20:44:17
but the result would end in 9

Porteradams 2013-02-06 20:44:17
but wont be a palindrome

mcdonalds106_7 2013-02-06 20:44:25
no; it will start with 1 and end with 9

DPatrick 2013-02-06 20:44:40
Right. Regardless of what the digit b is, 11(9bb9) ends in 9 but begins with a 1.

DPatrick 2013-02-06 20:44:47
So it can never be a palindrome.

DPatrick 2013-02-06 20:45:00

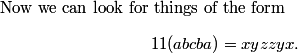
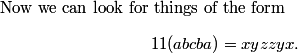
DPatrick 2013-02-06 20:45:18

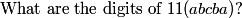
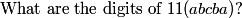
VietaFan 2013-02-06 20:45:47
a_(a+b)_(c+b)_(c+b)_(a+b)_a

jaymo 2013-02-06 20:45:47
a, a+b, b+c, etc

VietaFan 2013-02-06 20:45:47
It's a palindrome!

ChenthuranA 2013-02-06 20:45:47
a,a+b, b+c,c+b,b+a,a

pl210741 2013-02-06 20:45:47
abcba0+abcba

DPatrick 2013-02-06 20:45:52
Well...maybe.

centralbs 2013-02-06 20:45:57
a, a+b, b+c, c+b , b+a , a before carrying

rahulgupta1096 2013-02-06 20:46:00
a(a+b)(b+c)(c+b)(b+a)(a) with carrying where necessary

DPatrick 2013-02-06 20:46:14
Let's pretend we're back in 3rd grade. We just write out the multiplication, the long way:

DPatrick 2013-02-06 20:46:18

DPatrick 2013-02-06 20:46:36
The digits look like a, a+b, b+c, c+b, b+a, and a. That's a palindrome!

DPatrick 2013-02-06 20:46:45
...but only if there's no carrying when we add.

DPatrick 2013-02-06 20:47:16
Is it possible that it might still sum to give a 6-digit palindrome, even if there was carrying?

gengkev 2013-02-06 20:47:55
no; a + b < 10 because the a must be the same, so b + c < 10 to not interfere

Doink 2013-02-06 20:47:55
no, because then the first digit would be a+1 and the last would be a

AdamGeller 2013-02-06 20:47:55
no. we can't have a first digit of a from carrying

teranz0 2013-02-06 20:47:55
not if a+b>9, because then the first and last digit would be different

DPatrick 2013-02-06 20:48:20
Well, let's be careful and make sure. (Again, you might not do this on the actual contest, where there's more time-pressure.)

DPatrick 2013-02-06 20:48:26
The last digit is a, so the first digit has to be a as well.

DPatrick 2013-02-06 20:48:39
This means that the addition in the ten-thousands column (the second column from the left) cannot carry a "1" over to the hundred-thousands column.

DPatrick 2013-02-06 20:48:52
But also the ten-thousands column has to match the tens column, which is a+b, and this can't carry either.

DPatrick 2013-02-06 20:49:05
So the addition of b+c in the thousands column can't carry either. So this has to match the b+c in the hundreds column, and it can't carry either.

sonaal 2013-02-06 20:49:19
so no carrying

catnpatx 2013-02-06 20:49:26
therefore there cannot be any carrying

DPatrick 2013-02-06 20:49:29
The summary is: this is a palindrome if and only if the addition has no carrying.

mathrocks11 2013-02-06 20:49:50
so both a+b and b+c are less than 10

math-rules 2013-02-06 20:49:50
a+b<10 and b+c<10

jkoj25 2013-02-06 20:49:57
so a+b<10 and c+b<10

Oboeplayer311 2013-02-06 20:50:04
so a+b < 10 and c+b < 10

ninjataco 2013-02-06 20:50:04
so a + b < 10 and b+c <10

DPatrick 2013-02-06 20:50:14

DPatrick 2013-02-06 20:50:27

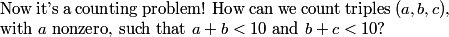
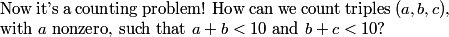
zhuangzhuang 2013-02-06 20:50:54
casework on b

calculatorwiz 2013-02-06 20:50:54
casework on b?

bobthesmartypants 2013-02-06 20:51:01
first pick a b and count a and c accordingly

ic1999 2013-02-06 20:51:01
casework with b

DPatrick 2013-02-06 20:51:03
Usually we count based on the most severe restriction. Here b is the most restrictive since it appears in both conditions.

DPatrick 2013-02-06 20:51:09
So let's use casework on the value of b.

DPatrick 2013-02-06 20:51:17
How many (a,b,c) with b=0?

jsani0102 2013-02-06 20:51:42
90

sammyMaX 2013-02-06 20:51:42
90

djmathman 2013-02-06 20:51:42
9*10=90

ickathu 2013-02-06 20:51:42
9*1*10

DaChickenInc 2013-02-06 20:51:42
90

DPatrick 2013-02-06 20:51:47
We have 9 choices for a (any digit except 0) and 10 choices for c (any digit), so 9*10 = 90 such triples.

DPatrick 2013-02-06 20:51:51
How many with b=1?

DuoCapital 2013-02-06 20:52:09
8*9=72

cherryclutch 2013-02-06 20:52:09
72

distortedwalrus 2013-02-06 20:52:09
72

Arghzoo 2013-02-06 20:52:09
8 and 9 = 72

MathBrain2000 2013-02-06 20:52:09
72=9*8

DPatrick 2013-02-06 20:52:13
We now have 8 choices for a (any digit 1-8) and 9 choices for c (any digit 1-9), so 8*9 = 72 such triples.

DPatrick 2013-02-06 20:52:23
You can see the pattern: there will be 7*8 triples with b=2, 6*7 triples with b=3, and so on up to 1*2 triples with b=8.

DPatrick 2013-02-06 20:52:28
So how many triples altogether?

mathnerd101 2013-02-06 20:52:50
any digit 0-8 you mean?

DPatrick 2013-02-06 20:53:05
Oops, right, c is any digit 0-8 in the "b=1" case.

brian22 2013-02-06 20:53:12
90+72+56+42+30+20+12+6+2=330

Arghzoo 2013-02-06 20:53:12
2 + 6 + 12 + 20 + 30 + 42 + 56 + 72 + 90 =

viker 2013-02-06 20:53:23
330 triples

tluo5458 2013-02-06 20:53:23
2+6+12+20+30+42+56+72+90=330

DPatrick 2013-02-06 20:53:28
We get 90 + 72 + 56 + 42 + 30 + 20 + 12 + 6 + 2 = 330 triples.

DPatrick 2013-02-06 20:53:53
Each triple gives abcba that when multiplied by 11, corresponds to a unique 6-digit palindrome satisfying the problem condition.

gundraja 2013-02-06 20:54:02
330/900 gives 11/30 E)

matholympiad25 2013-02-06 20:54:02
330/900 = 11/30 E

bzhou5 2013-02-06 20:54:02
330/990=11/30 E

DPatrick 2013-02-06 20:54:24

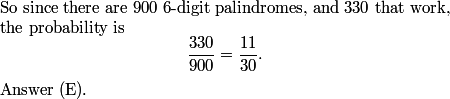
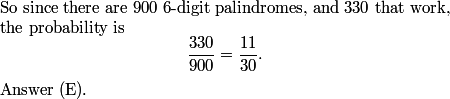
DPatrick 2013-02-06 20:54:39
OK, on to #23!

DPatrick 2013-02-06 20:54:44

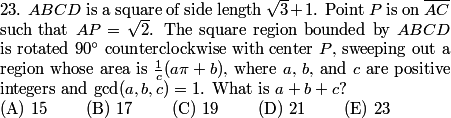
Iwilllose 2013-02-06 20:55:01
Draw a diagram?

tuanyuan2008 2013-02-06 20:55:01
draw a diagram

Iggy Iguana 2013-02-06 20:55:01
draw a diagram

DPatrick 2013-02-06 20:55:08
We should start by drawing a picture:

DPatrick 2013-02-06 20:55:12

djmathman 2013-02-06 20:55:22
Is this the problem where you said that a compass and protractor were helpful?

DPatrick 2013-02-06 20:55:42
Absolutely. Put your compass point on P and draw. Here's the picture after the rotation.

DPatrick 2013-02-06 20:55:46

DPatrick 2013-02-06 20:56:00
Now I used fancy drawing software. You probably just made a hand-sketch (but if you brought a ruler and compass and protractor, your sketch likely was pretty good too). It looks like A' and D' lie on AB, and B' and C' lie on CD. How do we know this for sure?

panjia123 2013-02-06 20:56:44
P lies on the diagonal so APA' is 45-45-90

DPatrick 2013-02-06 20:56:55
Right: we know that APA' is an isosceles right triangle (since it's a 90-degree rotation), so angle A'AP must be 45 degrees. That forces A' to be on AB. The same argument forces C' to be on CD.

DPatrick 2013-02-06 20:57:24
And what about B' and D'?

DPatrick 2013-02-06 20:58:05
The same argument won't work because angle PBC is not 45 degrees.

panjia123 2013-02-06 20:58:22
it still has to be a square region

JFC 2013-02-06 20:58:30
But B'D'A' is!

DPatrick 2013-02-06 20:58:48
Right! The square rotates rigidly -- that is, we know A'B'C'D' is still a square, rotated 90 degrees.

DPatrick 2013-02-06 20:58:55
So A'B' must be parallel to BC and the same length, putting B' on CD. The same argument places D' on AB.

DPatrick 2013-02-06 20:59:18
Moral of the story: you might not have noticed/guessed that A' was on AB without an accurate diagram! So bring accurate-diagram-drawing tools with you.

DPatrick 2013-02-06 20:59:37
The area we want is the entire region inside this diagram: anything that is inside either square (ABCD or A'B'C'D') or any of the arcs is part of the region.

DPatrick 2013-02-06 20:59:44
How do we compute this area?

mathrocks11 2013-02-06 21:00:07
split it into sectors and triangles?

Rocksolid 2013-02-06 21:00:10
Take it piece by piece

heliootrope 2013-02-06 21:00:10
divide it into a rectangle and four sectors

prezcoin 2013-02-06 21:00:13
divide the diagram into sectors and triangles centered at P

DPatrick 2013-02-06 21:00:17
This region is ugly-looking, but it's made up of nice-looking pieces.

DPatrick 2013-02-06 21:00:29
We have some choices about how to break up this region, but here's one idea:

DPatrick 2013-02-06 21:00:33

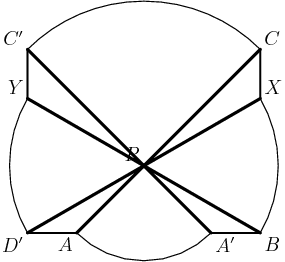
DPatrick 2013-02-06 21:01:05
(Compare the two pics that I've posted to the top, to be sure they're the same!)

DPatrick 2013-02-06 21:01:10
So we have four sectors (pieces of circles) and 4 little triangles.

DPatrick 2013-02-06 21:01:18
Now we angle-chase and length-chase and crunch numbers.

DPatrick 2013-02-06 21:01:22
Let's do the sectors first. What's the area of the bottom sector?

tiger11 2013-02-06 21:01:52
pi/2

cherryclutch 2013-02-06 21:01:52
pi r^2 /4

bobthesmartypants 2013-02-06 21:01:52
1/2 pi

memphis_tiger 2013-02-06 21:01:52
pi/2

Duncanyang 2013-02-06 21:01:52
pi/2

qfoam 2013-02-06 21:01:52
pi/2

DPatrick 2013-02-06 21:01:57
It's a 90-degree sector of a circle of radius sqrt(2).

DPatrick 2013-02-06 21:02:08

DPatrick 2013-02-06 21:02:18
How about the top sector?

ChenthuranA 2013-02-06 21:02:54
3pi/2

ic1999 2013-02-06 21:02:54
3pi/2

zhuangzhuang 2013-02-06 21:02:54
3pi/2

guilt 2013-02-06 21:02:54
3pi/2

DPatrick 2013-02-06 21:02:59

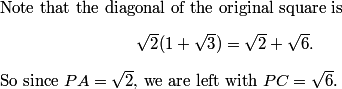
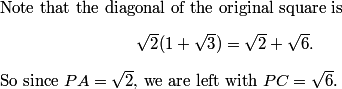
DPatrick 2013-02-06 21:03:19

DPatrick 2013-02-06 21:03:40
How about the two side sectors?

DPatrick 2013-02-06 21:03:50
What is length PB?

Calebhe1290 2013-02-06 21:04:19
2

centralbs 2013-02-06 21:04:19
2

alexlin9008 2013-02-06 21:04:19
2

chessderek 2013-02-06 21:04:19
2

gengkev 2013-02-06 21:04:19
2

DPatrick 2013-02-06 21:04:34
It might help to drop an altitude from P down to AB. Here it is in the original square:

DPatrick 2013-02-06 21:04:38

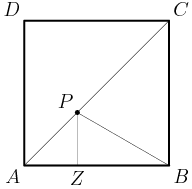
mathrocks11 2013-02-06 21:04:54
PZ is 1

MrMerchant 2013-02-06 21:04:54
30-60-90 triangle

DPatrick 2013-02-06 21:04:59

DPatrick 2013-02-06 21:05:11

DPatrick 2013-02-06 21:05:21

DPatrick 2013-02-06 21:05:56
So sector BPX is part of a circle of radius 2. What's the angle BPX?

mydogcanpur 2013-02-06 21:06:27
60

minimario 2013-02-06 21:06:27
60

ClassClown 2013-02-06 21:06:27
60

tuanyuan2008 2013-02-06 21:06:27
60

ickathu 2013-02-06 21:06:27
60 degrees

DPatrick 2013-02-06 21:06:49
Again, it might help to drop an altitude from P down to BC in our original square:

DPatrick 2013-02-06 21:06:53

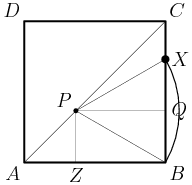
DPatrick 2013-02-06 21:07:13

bzhou5 2013-02-06 21:07:35
the area is 2pi/3

bzhou5 2013-02-06 21:07:35
the area of the right sector is 2pi/3

Rocksolid 2013-02-06 21:07:35
2pi/3 is the area of the sector

DPatrick 2013-02-06 21:07:43

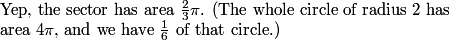
Iwilllose 2013-02-06 21:07:54
so the combined area is 4pi/3

bobthesmartypants 2013-02-06 21:07:57
2/3 pi for one sector, 2/3 pi for other sector, plus 1/2 pi and 3/2 pi gives 10/3 pi for all the sectors

DPatrick 2013-02-06 21:08:17
Right: the left sector (YPD' in the funky picture up top) is symmetric to the right sector. So it also has area (2/3)pi.

DPatrick 2013-02-06 21:08:32

ickathu 2013-02-06 21:08:46
what about the triangles PYC', PXC, PA'B, and PD'A?

DPatrick 2013-02-06 21:08:56
Yes: now on to the four little triangles.

DPatrick 2013-02-06 21:09:02
The two on the bottom are identical, as are the two on the top. Let's look at the bottom first.

DPatrick 2013-02-06 21:09:17
What is the area of PA'B?

empoleon 2013-02-06 21:09:32
all have height of 1

DPatrick 2013-02-06 21:09:42
Indeed, the height is PZ = 1.

DPatrick 2013-02-06 21:09:48
What is A'B?

kli2000 2013-02-06 21:10:14
sqrt3-1

guilt 2013-02-06 21:10:14
sqrt3 -1

Calebhe1290 2013-02-06 21:10:14
rt3-1

gundraja 2013-02-06 21:10:14
SQRT(3) - 1

mathrocks11 2013-02-06 21:10:14
we found ZA' is 1 so A'B is sqrt(3)-1

DPatrick 2013-02-06 21:10:21
The length is AB - 2(AZ) = (1 + sqrt(3)) - 2 = sqrt(3) - 1.

chessderek 2013-02-06 21:10:33
so area of PA'B is (sqrt3-1)/2

DPatrick 2013-02-06 21:10:36

DPatrick 2013-02-06 21:10:48
Now what about the top triangles? What is the area of PXC?

DPatrick 2013-02-06 21:10:55
This guy might help:

DPatrick 2013-02-06 21:11:00

DuoCapital 2013-02-06 21:11:24
height = sqrt(3)

DPatrick 2013-02-06 21:11:39
Right: earlier we found the height is PQ = ZB = sqrt(3).

ic1999 2013-02-06 21:11:52
XC=sqrt3-1

VietaFan 2013-02-06 21:11:52
base = sqrt 3 - 1

empoleon 2013-02-06 21:11:52
base = sqrt(3)-1

DPatrick 2013-02-06 21:12:02
And the base is CX = CB - BX = (1 + sqrt(3)) - 2 = sqrt(3) - 1.

DPatrick 2013-02-06 21:12:25

cherryclutch 2013-02-06 21:12:50
now add em up!

Iwilllose 2013-02-06 21:12:50
so then the total for the two top is 3-sqrt3, and the entire total is 2?

guilt 2013-02-06 21:12:50
3-sqrt3 +sqrt3 -1 =2

DPatrick 2013-02-06 21:12:58

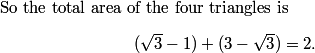
DPatrick 2013-02-06 21:13:21

bobthesmartypants 2013-02-06 21:13:48
and we can represent total area as 1/3(10 pi + 6)

VietaFan 2013-02-06 21:13:48
or $\frac{1}{3}(10 \pi + 6)$

tluo5458 2013-02-06 21:13:48
but it has to 1/c time (a\pi+b)

jaymo 2013-02-06 21:14:01
c=3, a=10, b=6

ClassClown 2013-02-06 21:14:01
the answer is (C) 19

DPatrick 2013-02-06 21:14:04

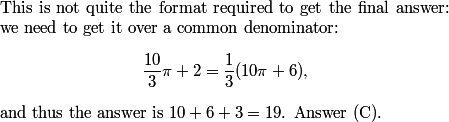
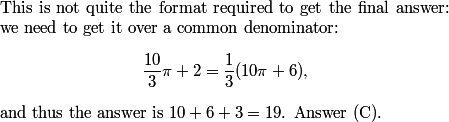
DPatrick 2013-02-06 21:14:42
I would say that this problem was certainly complicated, but --- provided you drew an accurate picture to start with! --- was not super-hard.

DPatrick 2013-02-06 21:15:00
On to #24:

DPatrick 2013-02-06 21:15:05

DPatrick 2013-02-06 21:15:55
Let's count for our denominator first. (I usually like to start counting problems that way -- we might see something that'll help with the presumably harder numerator count.)

DPatrick 2013-02-06 21:15:59
How many segments are there?

Arghzoo 2013-02-06 21:16:20
so we have 12C2 distinct segments

Arghzoo 2013-02-06 21:16:20
12C2=66

colinhy 2013-02-06 21:16:20
12c2 = 66

mathemagician1729 2013-02-06 21:16:20
12C2 = 66

ickathu 2013-02-06 21:16:20
C(12,2) = 66

DPatrick 2013-02-06 21:16:26

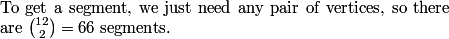
DPatrick 2013-02-06 21:16:30
So how many sets of 3 segments?

giratina150 2013-02-06 21:16:49
66C3

alligator112 2013-02-06 21:16:49
66C3

gqiao 2013-02-06 21:16:49
66C3=11x65x64

awesomemathlete 2013-02-06 21:16:49
66 choose 3

Seedleaf 2013-02-06 21:16:49
66C3

gundraja 2013-02-06 21:16:49
66C3

DPatrick 2013-02-06 21:16:54

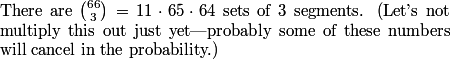
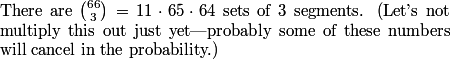
DPatrick 2013-02-06 21:17:12
Now what?

sammy1615 2013-02-06 21:17:26
find the ones that make a triangle

VietaFan 2013-02-06 21:17:38
Count the degenerates and subtract.

DPatrick 2013-02-06 21:17:58
We'll need some way to organize our work.

DPatrick 2013-02-06 21:18:04
Let's give a segment a "size" based on how many vertices away its endpoints are (counting the shorter distance around the outside of the 12-gon). So an edge of the 12-gon has size 1, a segment connecting vertices two apart has size 2, and so on.

DPatrick 2013-02-06 21:18:30
One approach is to compute all the lengths of all the different sizes, and then start applying the triangle inequality.

DPatrick 2013-02-06 21:18:48
The downside is that some of the lengths are a little messy (involving sin(15) and such).

DPatrick 2013-02-06 21:19:03
We actually don't need to compute the lengths -- we can reason geometrically just by drawing the right pictures.

DPatrick 2013-02-06 21:19:13
First of all, though, how many segments are there of each size?

yangwy 2013-02-06 21:19:43
12 of each except largest, which has 6

Jpl2000 2013-02-06 21:19:43
6 of the longest, 12 of the rest

jaymo 2013-02-06 21:19:43
12, 12, 12, 12, 12, 6

guilt 2013-02-06 21:19:43
12 for each except six for size 6

DPatrick 2013-02-06 21:19:48
There are 12 segments of each of sizes 1-5 (each one can be rotated 30 degrees to get a new one), and 6 segments of size 6 (there are the 6 long diagonals of the 12-gon that pass through the center). Note that 5*12 + 6 = 66, so all segments are accounted for.

DPatrick 2013-02-06 21:20:05
Now for the ugly part: which sets of sizes produce a triangle with positive area?
Or maybe a better question is: which sets don't?

DPatrick 2013-02-06 21:20:14
Which question seems better to try to count?

vinayak-kumar 2013-02-06 21:20:34
the latter

matticus42 2013-02-06 21:20:34
2nd

minimario 2013-02-06 21:20:34
The 2nd one

crastybow 2013-02-06 21:20:34
Which sets don't?

Oboeplayer311 2013-02-06 21:20:34
which don't

ic1999 2013-02-06 21:20:34
which ones don't

DPatrick 2013-02-06 21:20:51
Probably the second question, judging by the answer choices: the answers choices are all a lot closer to 1 than to 0, so counting sets of three segments that fail to produce a nontrivial triangle will be a smaller count.

DPatrick 2013-02-06 21:21:01
Are there any "obvious" claims?

DPatrick 2013-02-06 21:21:50
What combinations of sizes do we not have to bother looking at if we're trying to find segments that fail to make a nontrivial triangle?

DPatrick 2013-02-06 21:22:02
(There are a lot of negatives in that sentences...)

Iwilllose 2013-02-06 21:22:22
3 consecutvie sides?

guilt 2013-02-06 21:22:22
equilateral triangles....

yangwy 2013-02-06 21:22:22
ones that are part of the 12-gon already

ic1999 2013-02-06 21:22:22
3 of the same length

theGoodGuy 2013-02-06 21:22:22
large sizes

DuoCapital 2013-02-06 21:22:22
all sides equal

mathemagician1729 2013-02-06 21:22:22
equilateral

DPatrick 2013-02-06 21:22:37
Yes, there are some good ideas here.

DPatrick 2013-02-06 21:22:59
My first claim is that if all the segments are size 3 or bigger, we're OK. How come?

DPatrick 2013-02-06 21:23:17
Clearly we have a size 3-3-6 triangle (indeed it's a right triangle):

DPatrick 2013-02-06 21:23:21

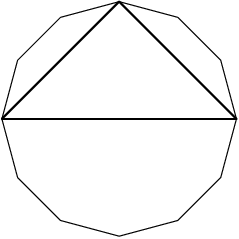
DPatrick 2013-02-06 21:23:32
So 3-3-n works for any 3 <= n <= 6.

DPatrick 2013-02-06 21:23:41
And increasing either 3 makes the triangle closer to equilateral, rather than closer to degenerate. (For instance, 3-4-6 is acute.)

DPatrick 2013-02-06 21:23:56
Can we fail to have a triangle if all the sides are size 2 or larger?

VietaFan 2013-02-06 21:24:21
yes; 2, 2, 6

teranz0 2013-02-06 21:24:21
Yes, 2 size 2s add up to a size 6

ksun48 2013-02-06 21:24:21
2-2-6 is degenerate

j2002 2013-02-06 21:24:24
2,2,6

DPatrick 2013-02-06 21:24:32
The worst case scenario is 2-2-6: the middle side is as short as possible and the longest side is as long as possible.

DPatrick 2013-02-06 21:24:52
But a 2-2-6 "triangle" is actually a line. The size 2 segments are exactly half the size 6 segments, because the triangle in the picture below is 30-60-90:

DPatrick 2013-02-06 21:24:57

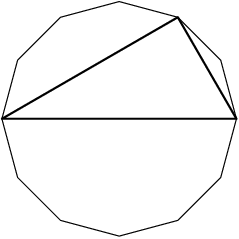
DPatrick 2013-02-06 21:25:12
But if 2-2-6 is a line, what can we conclude about 2-a-b, where a<=b and (a>2 or b<6)?

matholympiad25 2013-02-06 21:25:45
it will always be a triangle

tluo5458 2013-02-06 21:25:45
it is a triangle

brian22 2013-02-06 21:25:45
we're fine

bobthesmartypants 2013-02-06 21:25:45
so anything 2 or above except 2-2-6 is good

mydogcanpur 2013-02-06 21:25:45
It's a triangle

djmathman 2013-02-06 21:25:45
It's a triangle!

DPatrick 2013-02-06 21:25:53
These all work. Starting with a degenerate triangle (that is, a line) and making the middle side longer and/or the longest side shorter will always allow us to make a non-degenerate triangle.

DPatrick 2013-02-06 21:26:11
So the only triple that fails where all the sides are size 2 or larger is (2,2,6).

DPatrick 2013-02-06 21:26:29
(I'll put that datum up top for safe-keeping.)

DPatrick 2013-02-06 21:26:39
This leaves triples with at least one side of size 1. We need to determine which of these succeed and which of these fail.

DPatrick 2013-02-06 21:26:53
Again, one way is to use trig to compute all the lengths and then analyze them algebraically. That works but is perhaps inelegant.

DPatrick 2013-02-06 21:27:09
Let's instead try to use the geometry of the 12-gon to analyze which triples work and which fail when size 1 is the shortest side.

DPatrick 2013-02-06 21:27:16
Clearly 1-1-1 and 1-1-2 work (the first is equilateral and the second is formed by three consecutive vertices).

DPatrick 2013-02-06 21:27:22
How about 1-1-3?

minimario 2013-02-06 21:27:56
No

Ani10 2013-02-06 21:27:56
no

Porteradams 2013-02-06 21:27:56
nope

matticus42 2013-02-06 21:27:56
nope

Seedleaf 2013-02-06 21:27:56
no

bzhou5 2013-02-06 21:28:08
no the side of length 3 is greater than 1+1

DPatrick 2013-02-06 21:28:16
We can look at the following trapezoid:

DPatrick 2013-02-06 21:28:19

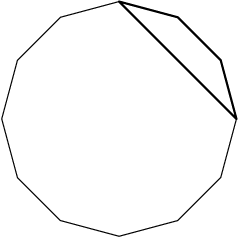
DPatrick 2013-02-06 21:28:36
If the side length of the 12-gon is s, what is the length of the size 3 segment (in terms of s)?

DPatrick 2013-02-06 21:28:44
(Note that we don't need its exact length -- we just need to determine if it is at least 2s or not.)

sonaal 2013-02-06 21:29:01
is more than 2s

ahaanomegas 2013-02-06 21:29:06
It is more than 2s.

DPatrick 2013-02-06 21:29:09
How do we know?

guilt 2013-02-06 21:29:17
(sqrt3 +1 )s

DPatrick 2013-02-06 21:29:27

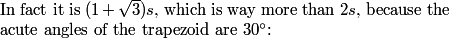
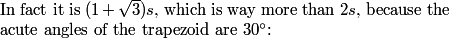
DPatrick 2013-02-06 21:29:32

DPatrick 2013-02-06 21:30:05
So the lengths of a size 1-1-3 "triangle" would have to be s, s, and (1+sqrt(3))s. That fails the triangle inequality since 1 + sqrt(3) is a lot bigger than 2.

countyguy 2013-02-06 21:30:18
1-1-3, 1-1-4, 1-1-5, 1-1-6 don't work

matholympiad25 2013-02-06 21:30:18
so 1-1-3, 1-1-4, 1-1-5, and 1-1-6 don't work

DPatrick 2013-02-06 21:30:35
So 1-1-3 fails. Hence, so does 1-1-4, 1-1-5, and 1-1-6, because trying to make the longest side even longer just makes things worse.

DPatrick 2013-02-06 21:30:49
Continuing, we easily see that 1-2-2 and 1-2-3 succeed. How about 1-2-4?

Iwilllose 2013-02-06 21:31:07
No, because 1+2<4

Oboeplayer311 2013-02-06 21:31:07
nope 1+2 < 4

DPatrick 2013-02-06 21:31:27
How do we know that (size 1) + (size 2) < (size 4)? (Remember, 1, 2, and 4 are just labels; they're not the actual side lengths.)

jiujianxian 2013-02-06 21:32:05
calculate then length?

DPatrick 2013-02-06 21:32:19
We could do that, but I can again draw a picture of a trapezoid:

DPatrick 2013-02-06 21:32:24

DPatrick 2013-02-06 21:32:45
I just let t be the length of the size 2 side -- I don't need to bother computing it!

ic1999 2013-02-06 21:32:52
it doesn't work because 1<sqrt2

bobthesmartypants 2013-02-06 21:32:52
and sqrt{2}s>s

DPatrick 2013-02-06 21:33:15
Right! We see that the size 4 side is t + sqrt(2)*s, and that's bigger than (size 1) + (size 2) = s + t.

DPatrick 2013-02-06 21:33:25
So 1-2-4 fails as a triangle.

guilt 2013-02-06 21:33:38
so 1-2-5, 1-2-6 also dont work

sonaal 2013-02-06 21:33:38
anything bigger also fails

bobthesmartypants 2013-02-06 21:33:41
and that means so do 1-2-5- and 1-2-6

VietaFan 2013-02-06 21:33:41
so dose 1-2-5 and 1-2-6

DPatrick 2013-02-06 21:33:58
Right. 1-2-4 fails and making the long side bigger makes it words. Thus so does 1-2-5 and 1-2-6.

DPatrick 2013-02-06 21:34:11
On we go...
1-3-3 and 1-3-4 trivially succeed. How about 1-3-5?

tluo5458 2013-02-06 21:34:29
1-3-5 and 1-3-6 also fail (for nxt part)

tluo5458 2013-02-06 21:34:29
1-3-5 doesn't work nor does 1-3-6

DPatrick 2013-02-06 21:34:35
Again, let's try for a relevant trapezoid.

DPatrick 2013-02-06 21:34:38

DPatrick 2013-02-06 21:34:53
Note the side of size 5 is on the bottom. The two little triangles on the ends are 30-60-90.

stickman1668 2013-02-06 21:35:00
it is equal, not larger

ic1999 2013-02-06 21:35:00
1-3-5 is a line

ksun48 2013-02-06 21:35:00
oh... it's equal...

kx1001678 2013-02-06 21:35:05
135 makes a line so that fails

DPatrick 2013-02-06 21:35:08
So in fact (size 5) = (size 1) + (size 3), and 1-3-5 is a degenerate triangle (a line).

DPatrick 2013-02-06 21:35:16
Thus 1-3-5 fails, and so does 1-3-6.

DPatrick 2013-02-06 21:35:29
Keep on truckin'...
1-4-4, 1-4-5, 1-5-5, 1-5-6, and 1-6-6 all trivially succeed. The only one missing from this list is 1-4-6. Does it fail or succeed?

gundraja 2013-02-06 21:35:54
succeeds.

googol.plex 2013-02-06 21:35:54
seems to work actually

ksun48 2013-02-06 21:35:54
draw the trapezoids, but it succeeds

DPatrick 2013-02-06 21:35:59
It succeeds! Again we draw a trapezoid:

DPatrick 2013-02-06 21:36:03

DPatrick 2013-02-06 21:36:12
Now the two small triangles on the ends are 15-75-90. So the side adjacent to each of the size 1 segments is smaller than s/2, so their sum is smaller than s, and thus:
(size 6) < (size 1) + (size 4).
Thus 1-4-6 succeeds as a triangle.

DPatrick 2013-02-06 21:36:30
Whew!

DPatrick 2013-02-06 21:36:37
To summarize, here is the list of all the size triples that fail:
1-1-3, 1-1-4, 1-1-5, 1-1-6, 1-2-4, 1-2-5, 1-2-6, 1-3-5, 1-3-6, 2-2-6

DPatrick 2013-02-06 21:36:50
Now we can count. How many of each type of triple are there?

Calebhe1290 2013-02-06 21:37:21
depends on whether or not 6 is included

ksun48 2013-02-06 21:37:21
well, there are 12 of each segment except 6 has 6 segments only

DPatrick 2013-02-06 21:37:46
Right, what's annoying is that some have repeated sizes, and some have that annoying size 6 which has fewer possibilities.

DPatrick 2013-02-06 21:38:22
The three triples 1-1-{3,4,5} each have C(12,2) = 66 ways to choose the two size 1 segments and then 12 ways to choose the larger segment. So there are 66*12 of each of these three.

DPatrick 2013-02-06 21:38:44
The 1-1-6 triple is the same, but there are only 6 ways to choose the segment of size 6, so there are 66*6 such triples.

Jpl2000 2013-02-06 21:38:48
so we have 12 C 2 * (12 + 12 + 12 + 6)

DPatrick 2013-02-06 21:38:54
Right: that takes care of all the 1-1-n.

DPatrick 2013-02-06 21:39:17
How many of each of 1-2-4, 1-2-5, and 1-3-5?

blub212212 2013-02-06 21:39:29
12^3

jiujianxian 2013-02-06 21:39:29
12^3

JohnPeanuts 2013-02-06 21:39:32
12^3

DPatrick 2013-02-06 21:39:42
The 1-2-4, 1-2-5, and 1-3-5 triples each have 12*12*12 ways to choose the segments. (12 choices for a segment of each size.)

DPatrick 2013-02-06 21:39:55
Similarly, the 1-2-6 and 1-3-6 triples each have 12*12*6 ways to choose the segments.

DPatrick 2013-02-06 21:40:13
Lastly, the 2-2-6 triple has 66*6 ways to choose the segments.

DPatrick 2013-02-06 21:40:38
I recommend not multiplying these out -- a lot of factors will probably cancel.

bobthesmartypants 2013-02-06 21:40:43
add em up!

DPatrick 2013-02-06 21:40:53

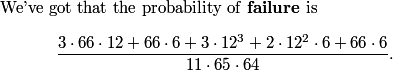
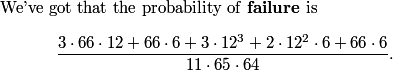
DPatrick 2013-02-06 21:41:07
(The 11*65*64 in the denominator is our count from way back at the beginning.)

DPatrick 2013-02-06 21:41:16
Now to simplify this -- without a calcuator!

DPatrick 2013-02-06 21:41:40
I'd try to combine terms first.

bzhou5 2013-02-06 21:41:51
take out a 66 in the 3 terms and 12s in the others

DPatrick 2013-02-06 21:41:55

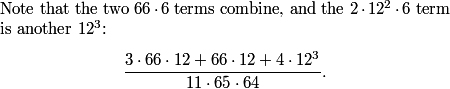
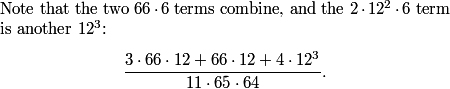
DPatrick 2013-02-06 21:42:09

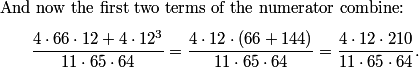
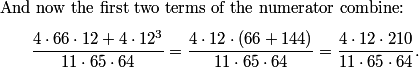
DPatrick 2013-02-06 21:42:23
(I'm going to run through this quickly because it's kinda boring and we still have #25 to go!)

kx1001678 2013-02-06 21:42:33
we can cancel out some 2s

matholympiad25 2013-02-06 21:42:33
cancel 2 out from the numerator's terms

DPatrick 2013-02-06 21:42:38

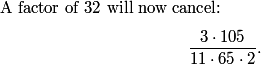
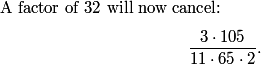
sonaal 2013-02-06 21:42:51
cancel 5

jaymo 2013-02-06 21:42:51
cancel 5's

bookie331 2013-02-06 21:42:51
cancel out the 5

DPatrick 2013-02-06 21:42:53

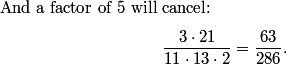
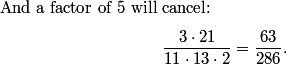
DPatrick 2013-02-06 21:43:02

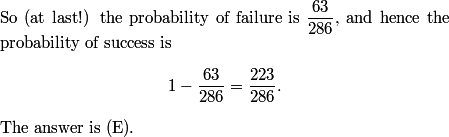
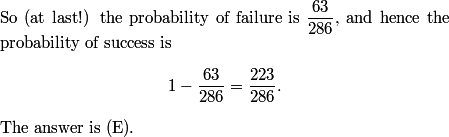
math-rules 2013-02-06 21:43:15
This problem would take at least 15 min. on the real amc, right?

DPatrick 2013-02-06 21:43:43
This was our least-favorite of the hard problems here at the AoPS office. It's way way way long and somewhat unpleasant.

DPatrick 2013-02-06 21:44:21
Believe it or not, I think this was probably the most elegant way. You could bash out the actual segments lengths and do it that way, but I don't think it's any faster.

DPatrick 2013-02-06 21:44:37
Anyway, let's leave this one behind and go on to #25, which was probably my favorite.

DPatrick 2013-02-06 21:44:42

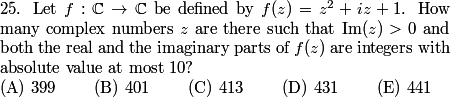
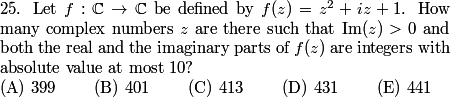
DPatrick 2013-02-06 21:44:57
You may need to read it over a couple of times to see what they're asking.

viker 2013-02-06 21:45:07
Im means the imaginary art of a+bi right

DPatrick 2013-02-06 21:45:27
Right, Im(z) is the imaginary part of z. So if z = a+bi where a and b are real, then Im(z) = b.

DPatrick 2013-02-06 21:45:39
There are a lot of ideas you could try here.

DPatrick 2013-02-06 21:45:54
Suppose c is one of our "target" points: that is, c is a complex number whose real and imaginary parts are integers between -10 and 10 (inclusive).

DPatrick 2013-02-06 21:46:05
Forgetting about the Im(z) > 0 restriction right now... how many complex numbers z are there with f(z) = c?

brian22 2013-02-06 21:46:22
2

Tuxianeer 2013-02-06 21:46:22
2

alex31415 2013-02-06 21:46:22
2

distortedwalrus 2013-02-06 21:46:22
2

JohnPeanuts 2013-02-06 21:46:22
at most 2

DPatrick 2013-02-06 21:46:37

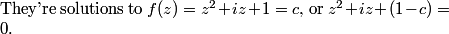
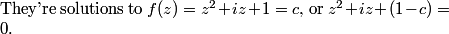
DPatrick 2013-02-06 21:47:05
Since we have all of the complex numbers to work with, this quadratic has 2 solutions for every c....right?

Tuxianeer 2013-02-06 21:47:26
it could have 1

Iwilllose 2013-02-06 21:47:26
unless it is perfect square?

mprashker 2013-02-06 21:47:26
double roots

Seedleaf 2013-02-06 21:47:34
unless when you set it equal to c, the discriminant is 0

DPatrick 2013-02-06 21:47:38
Right. If z^2 + iz + (1-c) has discriminant 0, then there's only one z. When does that happen?

ssilwa 2013-02-06 21:48:14
-1-4(1-c)= 0

ssilwa 2013-02-06 21:48:14
c= 5/4

bobthesmartypants 2013-02-06 21:48:14
-1-4+4c=0

Tuxianeer 2013-02-06 21:48:14
c=5/4

brian22 2013-02-06 21:48:14
4c-5=0, c=5/4

DPatrick 2013-02-06 21:48:24

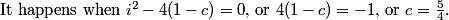
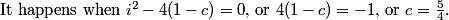
DPatrick 2013-02-06 21:48:55
But that's not one of our target points (because it doesn't have an integer real part), so we don't have to worry about that exception. Thus we conclude that every one of our target points has two z's that map to it via f.

DPatrick 2013-02-06 21:49:27

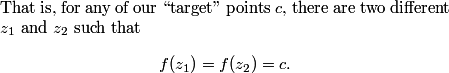
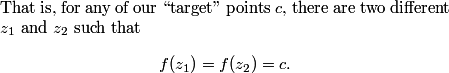
DPatrick 2013-02-06 21:49:39
What else do we know about the two z's that map to any target point?

DPatrick 2013-02-06 21:49:48
Could they both have Im(z) > 0?

DPatrick 2013-02-06 21:50:24
Many of you are saying that z1 and z2 must be conjugates. That is not the case! The quadratic we started with doesn't have real coefficients.

JohnPeanuts 2013-02-06 21:50:32
No, since z_1+z_2 = -i

DPatrick 2013-02-06 21:50:40
Aha...Vieta's Formulas still apply though!

DPatrick 2013-02-06 21:51:17
We know that z1 + z2 = -i by Vieta's Formulas. (More generally, the sum of the roots of x^2 + bx + c is -b for any quadratic.)

ahaanomegas 2013-02-06 21:51:27

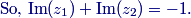
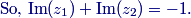
DPatrick 2013-02-06 21:51:41
Right, the imaginary parts of z1 and z2 thus must add to -1. So they can't both be positive.

awesomemathlete 2013-02-06 21:51:50
so only one at most could be positive

DPatrick 2013-02-06 21:52:17
Right. So we've learned something important: each target point c has at most one z such that f(z) = c with Im(z) > 0.

DPatrick 2013-02-06 21:52:35
Another way to say this is that the function f is 1-1 on the set of complex numbers with Im(z) > 0: they all get mapped to different points.

blub212212 2013-02-06 21:52:44
so we only need to know the number of C's now

DPatrick 2013-02-06 21:52:57
Well, let's stop and count them. How many "target" points are there?

jiujianxian 2013-02-06 21:53:28
21^2=441

matholympiad25 2013-02-06 21:53:28
21*21=441

Jpl2000 2013-02-06 21:53:28
21^2

dinoboy 2013-02-06 21:53:28
21*21 = 441

DPatrick 2013-02-06 21:53:49
Right: the real part is any integer from -10 to 10 (inclusive), so that's 21 choices for the real part, and same for the imaginary part.

DPatrick 2013-02-06 21:53:55
So there are 21*21 = 441 target points.

DPatrick 2013-02-06 21:54:14
And each target point c has at most one z with Im(z) > 0 so that f(z) = c, by our earlier discussion.

DPatrick 2013-02-06 21:54:20
So is the answer necessarily (E) 441?

bobsanders 2013-02-06 21:54:44
no

blub212212 2013-02-06 21:54:44
no, because some C's may have no solution

brian22 2013-02-06 21:54:44
so 441 is a MAXIMUM

pr0likethis 2013-02-06 21:54:44
no, 441 is just an upper bound

memphis_tiger 2013-02-06 21:54:44
couldnt some C's have 0 z's with positive Imaginary parts

DPatrick 2013-02-06 21:55:05
Certainly. For some of the target points, both z's that map to that point might have Im(z) <= 0, so that point might not have any z's.

DPatrick 2013-02-06 21:55:13
So how do we proceed from here?

DPatrick 2013-02-06 21:55:37
Inequalities (like Im(z) > 0) are often unpleasant to deal with.

DPatrick 2013-02-06 21:55:55
Replacing them with equalities often clears things up a bit.

djmathman 2013-02-06 21:56:07
Maybe deal with equality then?

sonaal 2013-02-06 21:56:07
make it an equality?

distortedwalrus 2013-02-06 21:56:11
IM=0!

DPatrick 2013-02-06 21:56:16
Can we find where the points with Im(z) = 0 map to? That is, where does the real line map to?

Acstar 2013-02-06 21:56:33
x axis

DPatrick 2013-02-06 21:56:59
Right: we're taking the points z on the "real" (or "x") axis of the complex plane, and we want to know where f(z) is.

sonaal 2013-02-06 21:57:13
graph it?

DPatrick 2013-02-06 21:57:16
How do we do that?

DPatrick 2013-02-06 21:57:44

DPatrick 2013-02-06 21:58:14
So the point (a,0) on the real axis of the complex plane gets mapped to the point (a^2+1,a) on the complex plane.

DPatrick 2013-02-06 21:58:19
What do all these points look like?

Jpl2000 2013-02-06 21:58:30
so just a parabola

mydogcanpur 2013-02-06 21:58:30
Parabola?

DPatrick 2013-02-06 21:58:34
It's a parabola!

DPatrick 2013-02-06 21:58:42

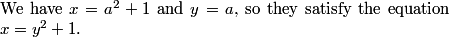
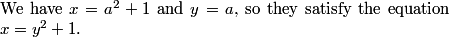
Calebhe1290 2013-02-06 21:58:50
horizontal parabola

ahaanomegas 2013-02-06 21:58:50
A horizontal parabola?

DPatrick 2013-02-06 21:59:06
Indeed, it's a "horizontal" parabola opening to the right, with vertex at (1,0).

DPatrick 2013-02-06 21:59:08
Here's a picture:

DPatrick 2013-02-06 21:59:14

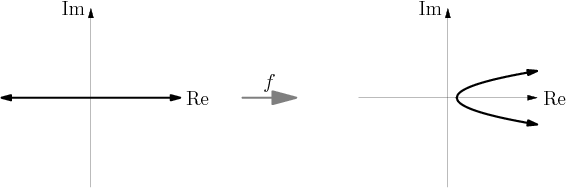
DPatrick 2013-02-06 21:59:57
So now we know where the points with Im(z) = 0 go when we apply the function f.

DPatrick 2013-02-06 22:00:27
And we decided that the points with Im(z) > 0 get mapped 1-1 when we apply f (that is, two of them can't go to the same point).

DPatrick 2013-02-06 22:00:36
So where do they go? Inside the parabola or outside?

Jpl2000 2013-02-06 22:01:09
test a point

DPatrick 2013-02-06 22:01:24
Based on your comments, you're voting about 3-to-1 for inside. But let's test a point to be sure.

DPatrick 2013-02-06 22:01:34
What's an easy point to test that has Im > 0?

memphis_tiger 2013-02-06 22:01:47
i

ic1999 2013-02-06 22:01:47
i

Tuxianeer 2013-02-06 22:01:47
i

DPatrick 2013-02-06 22:01:55
Sure, let's test with z=i. What is f(i)?

pr0likethis 2013-02-06 22:02:12
f(i)=-1

blub212212 2013-02-06 22:02:12
-1

jiujianxian 2013-02-06 22:02:12
-1

mssmath 2013-02-06 22:02:12
-1

ssilwa 2013-02-06 22:02:12
-1

DPatrick 2013-02-06 22:02:18

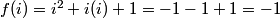
mydogcanpur 2013-02-06 22:02:32
So outside?

DPatrick 2013-02-06 22:02:44
Yes, that's outside the parabola!

DPatrick 2013-02-06 22:02:54
So the region with Im(z) > 0 maps to the region outside the parabola.

DPatrick 2013-02-06 22:02:58

DPatrick 2013-02-06 22:03:21
So we can conclude: the points outside the parabola are exactly the points that succeed, and the points on or inside the parabola are exactly the points that fail.

DPatrick 2013-02-06 22:03:45
So to get our answer, we need to count the target points that are outside the parabola.

DPatrick 2013-02-06 22:03:54

VietaFan 2013-02-06 22:04:10
Count inside and subtract; that's easier.

blub212212 2013-02-06 22:04:10
wouldn't it be easier to do 441-points inside the parabola

Seedleaf 2013-02-06 22:04:15
or just count the number of points inside and subtract

kli2000 2013-02-06 22:04:15
complementary is better

DPatrick 2013-02-06 22:04:30
Right: it's going to be way easier to count the point inside (or on) the parabola.

DPatrick 2013-02-06 22:04:40
(Don't forget that the ones on the parabola fail too.)

countyguy 2013-02-06 22:05:01
42 fail, so 441-42=399 A

ksun48 2013-02-06 22:05:01
42

memphis_tiger 2013-02-06 22:05:01
total is 42

pr0likethis 2013-02-06 22:05:01
10+9+9+6+6+1+1=42

DPatrick 2013-02-06 22:05:20
Right. You don't need to draw a fancy picture with all the dots like I did, you can just make a chart.

DPatrick 2013-02-06 22:05:25

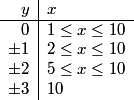
DPatrick 2013-02-06 22:05:37

ahaanomegas 2013-02-06 22:05:44
Test the parabola inequality, basically.

DPatrick 2013-02-06 22:05:49
So there are 10 + 2(9) + 2(6) + 2(1) = 42 target points that fail.

DPatrick 2013-02-06 22:05:56
Hence, the answer is 441 - 42 = 399. Answer (A).

DPatrick 2013-02-06 22:06:37
Richard Rusczyk is planning to make videos for all the problems we did tonight -- he is really looking forward to this one because there's lots of cool math that comes up in this problem, much of which we glossed over.

DPatrick 2013-02-06 22:06:53
His AMC 10 videos should be up on the website sometime tomorrow, with the AMC 12 videos following in a few days.

DPatrick 2013-02-06 22:07:41
Well, we've already been going for over 2.5 hours, so I think I'll stop so that I (and you all) can eat dinner (if you live in the west like me) or go to bed (if you live in the east).

DPatrick 2013-02-06 22:07:56
There are discussions of virtually all of the problems in the AMC forum on the AoPS website.

DPatrick 2013-02-06 22:08:04
Please join us again on Thursday, February 21, when we will discuss the AMC 10B/12B contests.

DPatrick 2013-02-06 22:08:09
Have a great night!

2013 AMC 10/12 A Discussion

Facilitator: Dave Patrick