2013 AIME I Math Jam
Go back to the Math Jam ArchiveAoPS instructors discuss all 15 problems of the 2013 AIME I.
Copyright © 2024 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Dave Patrick
DPatrick
2013-03-16 18:57:32
Before we get started (in about 2 minutes), I have a question: for those of you who took the test, what was your favorite question on the test.
Before we get started (in about 2 minutes), I have a question: for those of you who took the test, what was your favorite question on the test.
DPatrick
2013-03-16 18:57:35
?
?
DPatrick
2013-03-16 18:59:12
#11 seems to be winning the vote. I liked it too. We'll get to it...
#11 seems to be winning the vote. I liked it too. We'll get to it...
anthonyjang
2013-03-16 19:00:02
When are the official answers coming out?
When are the official answers coming out?
DPatrick
2013-03-16 19:00:11
I believe on Monday. But you'll see all 15 answers tonight.
I believe on Monday. But you'll see all 15 answers tonight.
DPatrick
2013-03-16 19:00:18
Let's get started!
Let's get started!
DPatrick
2013-03-16 19:00:23
Welcome to the 2013 AIME I Math Jam!
Welcome to the 2013 AIME I Math Jam!
DPatrick
2013-03-16 19:00:30
I'm Dave Patrick, and I'll be leading our discussion tonight.
I'm Dave Patrick, and I'll be leading our discussion tonight.
DPatrick
2013-03-16 19:00:38
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
DPatrick
2013-03-16 19:00:48
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
DPatrick
2013-03-16 19:01:03
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
DPatrick
2013-03-16 19:01:27
There are a lot of students here, much more than our regular online classes! As I said, only a relatively small fraction of the well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. This Math Jam is much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
There are a lot of students here, much more than our regular online classes! As I said, only a relatively small fraction of the well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. This Math Jam is much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
DPatrick
2013-03-16 19:01:43
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the necessary material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We always to try do so in our regular online classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the necessary material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We always to try do so in our regular online classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
DPatrick
2013-03-16 19:01:55
We do have two teaching assistants with us tonight to help answer your questions: Luis Ares (Duelist) and Lizard (Elizabeth) Reiland (Entropy).
We do have two teaching assistants with us tonight to help answer your questions: Luis Ares (Duelist) and Lizard (Elizabeth) Reiland (Entropy).
DPatrick
2013-03-16 19:02:02
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
DPatrick
2013-03-16 19:02:31
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. Also on occasion we may stop to prove things that you wouldn't necessary need to prove while doing the contest.
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. Also on occasion we may stop to prove things that you wouldn't necessary need to prove while doing the contest.
DPatrick
2013-03-16 19:02:48
So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be acknowledged.
So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be acknowledged.
DPatrick
2013-03-16 19:03:07
Let's get started! We're going to work through all 15 problems, in order.
Let's get started! We're going to work through all 15 problems, in order.
DPatrick
2013-03-16 19:03:14
DPatrick
2013-03-16 19:03:19
(You'll notice that the current problem will always be posted to the top of the window. You can resize the top part of the window by dragging on the horizontal bar separating it from the main part of the window.)
(You'll notice that the current problem will always be posted to the top of the window. You can resize the top part of the window by dragging on the horizontal bar separating it from the main part of the window.)
kiwiluver75
2013-03-16 19:03:51
d=rt
d=rt
cxiong
2013-03-16 19:03:51
Use a system of equations, D = RT
Use a system of equations, D = RT
btilm305
2013-03-16 19:03:51
Distance = rate * time
Distance = rate * time
DPatrick
2013-03-16 19:04:03
Of course, you know that distance = rate * time. We'll obviously want to use that!
Of course, you know that distance = rate * time. We'll obviously want to use that!
teranz0
2013-03-16 19:04:19
Express the rate at which he swims as x, runs as 5x, and bikes as 10x
Express the rate at which he swims as x, runs as 5x, and bikes as 10x
pieslinger
2013-03-16 19:04:19
set a variable for swiming speed
set a variable for swiming speed
kdokmeci
2013-03-16 19:04:19
We make our variables
We make our variables
akalykid012
2013-03-16 19:04:19
Let x equal speed when swimming
Let x equal speed when swimming
ClassicCalculator
2013-03-16 19:04:19
Express the swimming rate (d/t) as "x".
Express the swimming rate (d/t) as "x".
DPatrick
2013-03-16 19:04:36
I like setting the problem up in terms of the swimming rate, because the other two rates are then multiples of it.
I like setting the problem up in terms of the swimming rate, because the other two rates are then multiples of it.
DPatrick
2013-03-16 19:04:42
So let's set $r$ to be the rate (in miles per hour) that Tom swims.
So let's set $r$ to be the rate (in miles per hour) that Tom swims.
DPatrick
2013-03-16 19:04:56
He runs 5 times faster than he swims, so he runs at a rate of $5r$.
He runs 5 times faster than he swims, so he runs at a rate of $5r$.
DPatrick
2013-03-16 19:05:02
And he bikes twice as fast as he runs, so he bikes at a rate of $10r$.
And he bikes twice as fast as he runs, so he bikes at a rate of $10r$.
DPatrick
2013-03-16 19:05:09
So how long does Tom take to complete the triathlon?
So how long does Tom take to complete the triathlon?
billgates42
2013-03-16 19:05:30
4 adn 1/4 hr
4 adn 1/4 hr
Wickedestjr
2013-03-16 19:05:30
4 and a quarter hours
4 and a quarter hours
bugegg3
2013-03-16 19:05:30
4.25 hours
4.25 hours
phoenix827
2013-03-16 19:05:30
17/4 hr
17/4 hr
jeff10
2013-03-16 19:05:30
17/4 hours: I think writing this as an improper fraction helps later on
17/4 hours: I think writing this as an improper fraction helps later on
DPatrick
2013-03-16 19:05:45
Right, on the one hand the problem tells us: 4.25 or 17/4 hours.
Right, on the one hand the problem tells us: 4.25 or 17/4 hours.
DPatrick
2013-03-16 19:05:57
But on the other hand, we can compute his time in terms of r.
But on the other hand, we can compute his time in terms of r.
akalykid012
2013-03-16 19:06:31
1/2r + 8/5r + 30/10r hours
1/2r + 8/5r + 30/10r hours
Annabeth
2013-03-16 19:06:31
0.5/r+30/10r+8/5r
0.5/r+30/10r+8/5r
btilm305
2013-03-16 19:06:31
1/2r, 3/r, and 8/5r respectively
1/2r, 3/r, and 8/5r respectively
joshxiong
2013-03-16 19:06:31
1/2r+8/5r+30/10r
1/2r+8/5r+30/10r
ucantbeatmario
2013-03-16 19:06:31
t=.5/r+8/5r+30/10r
t=.5/r+8/5r+30/10r
DPatrick
2013-03-16 19:06:36
The swimming takes $\frac{0.5}{r}$ hours.
The swimming takes $\frac{0.5}{r}$ hours.
DPatrick
2013-03-16 19:06:45
The cycling takes $\frac{30}{10r} = \frac{3}{r}$ hours.
The cycling takes $\frac{30}{10r} = \frac{3}{r}$ hours.
DPatrick
2013-03-16 19:06:51
The running takes $\frac{8}{5r} = \frac{1.6}{r}$ hours.
The running takes $\frac{8}{5r} = \frac{1.6}{r}$ hours.
DPatrick
2013-03-16 19:06:59
So the whole thing takes $\frac{0.5}{r} + \frac{3}{r} + \frac{1.6}{r} = \frac{5.1}{r}$ hours.
So the whole thing takes $\frac{0.5}{r} + \frac{3}{r} + \frac{1.6}{r} = \frac{5.1}{r}$ hours.
DPatrick
2013-03-16 19:07:17
(All of those used "time = distance / rate".)
(All of those used "time = distance / rate".)
kdokmeci
2013-03-16 19:07:30
5.1/r=17/4
5.1/r=17/4
ninjataco
2013-03-16 19:07:30
then 5.1/r = 17/4
then 5.1/r = 17/4
DPatrick
2013-03-16 19:07:46
Exactly: the two times are equal, so $\frac{5.1}{r} = \frac{17}{4}$.
Exactly: the two times are equal, so $\frac{5.1}{r} = \frac{17}{4}$.
mg13
2013-03-16 19:08:26
r=1.2 miles per hours
r=1.2 miles per hours
poponono
2013-03-16 19:08:26
r=1.2
r=1.2
csmath
2013-03-16 19:08:26
r=1.2
r=1.2
amoghgaitonde
2013-03-16 19:08:26
r = 1.2
r = 1.2
25120012jsy21
2013-03-16 19:08:26
r=1.2
r=1.2
willabc
2013-03-16 19:08:26
r=1.2
r=1.2
DPatrick
2013-03-16 19:08:40
Right: we solve this to get $r = \frac65$ (or $r=1.2$) (miles per hour).
Right: we solve this to get $r = \frac65$ (or $r=1.2$) (miles per hour).
DPatrick
2013-03-16 19:08:51
And what's the finish?
And what's the finish?
mathwizard888
2013-03-16 19:09:20
Tom spends 3/1.2 hrs=150 minutes biking
Tom spends 3/1.2 hrs=150 minutes biking
csmath
2013-03-16 19:09:20
Cycling takes 2.5 hours which is 150 minutes
Cycling takes 2.5 hours which is 150 minutes
sahilp
2013-03-16 19:09:20
3/1.2=2.5 hr= 150 mins
3/1.2=2.5 hr= 150 mins
avi1234
2013-03-16 19:09:20
30/1.2*60
30/1.2*60
sunny2000
2013-03-16 19:09:20
We plug this into the other equation
We plug this into the other equation
ProbaBillity
2013-03-16 19:09:20
The answer is 3/r = 2.5 hours, or 150 minutes.
The answer is 3/r = 2.5 hours, or 150 minutes.
DPatrick
2013-03-16 19:09:28
Right. The bicycling time is $\frac{3}{r} = \frac{3}{\frac65} = \frac52$ hours, which is $\boxed{150}$ minutes.
Right. The bicycling time is $\frac{3}{r} = \frac{3}{\frac65} = \frac52$ hours, which is $\boxed{150}$ minutes.
DPatrick
2013-03-16 19:09:54
DPatrick
2013-03-16 19:10:05
What do we know about $n$?
What do we know about $n$?
thkim1011
2013-03-16 19:10:22
Since 0 can't be the first digit, we must have 5 as the first and last digits.
Since 0 can't be the first digit, we must have 5 as the first and last digits.
minimario
2013-03-16 19:10:22
The first and last digits must be 5
The first and last digits must be 5
swe1
2013-03-16 19:10:22
First and last digits have to be 5
First and last digits have to be 5
54math
2013-03-16 19:10:22
first and last digits of n have to be 5
first and last digits of n have to be 5
sparkles257
2013-03-16 19:10:22
has to begin and end with 5
has to begin and end with 5
lcamhie142857
2013-03-16 19:10:22
first and last digits are 5
first and last digits are 5
anthonyjang
2013-03-16 19:10:22
5_ _ _ 5 is the form
5_ _ _ 5 is the form
mathcool2009
2013-03-16 19:10:22
n = 5_ _ _5
n = 5_ _ _5
DPatrick
2013-03-16 19:10:27
Condition (a) says that $n$ ends in 0 or 5.
Condition (a) says that $n$ ends in 0 or 5.
DPatrick
2013-03-16 19:10:33
But condition (b) says that $n$ begins with the same digit that it ends with, and a number can't begin with 0.
But condition (b) says that $n$ begins with the same digit that it ends with, and a number can't begin with 0.
DPatrick
2013-03-16 19:10:43
So $n$ starts and ends with 5.
So $n$ starts and ends with 5.
DPatrick
2013-03-16 19:10:54
Or in other words, $n = 5xyz5$ for digits $x$, $y$, and $z$.
Or in other words, $n = 5xyz5$ for digits $x$, $y$, and $z$.
DPatrick
2013-03-16 19:10:59
How do we count these that satisfy condition (c)?
How do we count these that satisfy condition (c)?
cxiong
2013-03-16 19:11:26
abcde, b+c+d=5,10,15,20,25
abcde, b+c+d=5,10,15,20,25
ProbaBillity
2013-03-16 19:11:26
bobthesmartypants
2013-03-16 19:11:26
casework
casework
simon1221
2013-03-16 19:11:26
x+y+z is divisible by 5
x+y+z is divisible by 5
andrewlin
2013-03-16 19:11:26
x+y+z=5,10,15,20 or 25 because 27 is the largest sum
x+y+z=5,10,15,20 or 25 because 27 is the largest sum
wjli
2013-03-16 19:11:26
the sum of xyz must be a multiple of 5
the sum of xyz must be a multiple of 5
az_phx_brandon_jiang
2013-03-16 19:11:26
x+y+z=5, 10, 15, 20, 25
x+y+z=5, 10, 15, 20, 25
DPatrick
2013-03-16 19:11:32
We could do cases: $x+y+z=0$, $x+y+z=5$, $x+y+z=10$, and so on, but is there a more clever way?
We could do cases: $x+y+z=0$, $x+y+z=5$, $x+y+z=10$, and so on, but is there a more clever way?
lucylai
2013-03-16 19:12:02
x and y can be anything, and z just has to be congruent to -x-y (mod 5)
x and y can be anything, and z just has to be congruent to -x-y (mod 5)
lcamhie142857
2013-03-16 19:12:02
Use mod 5 on the 4th digit
Use mod 5 on the 4th digit
ucantbeatmario
2013-03-16 19:12:02
yes. Fore very choice of x and y, there two choices for z
yes. Fore very choice of x and y, there two choices for z
ABCDE
2013-03-16 19:12:02
2 possibilities for z for every pair of x and y
2 possibilities for z for every pair of x and y
anwang16
2013-03-16 19:12:02
its 1/5 of the total ways to have x,y,z
its 1/5 of the total ways to have x,y,z
billgates42
2013-03-16 19:12:02
there are 2 possible values of c for every a and b
there are 2 possible values of c for every a and b
footballer
2013-03-16 19:12:02
for each pair of digits, there is 2 possible third digits for the sum to be a multiple of 5
for each pair of digits, there is 2 possible third digits for the sum to be a multiple of 5
DPatrick
2013-03-16 19:12:07
Right!
Right!
DPatrick
2013-03-16 19:12:21
Given any choices for $x$ and $y$, how many $z$'s are there?
Given any choices for $x$ and $y$, how many $z$'s are there?
apple.singer
2013-03-16 19:12:33
2
2
kiwiluver75
2013-03-16 19:12:33
2
2
akalykid012
2013-03-16 19:12:33
2
2
bugegg3
2013-03-16 19:12:33
2
2
noobynoob
2013-03-16 19:12:33
$2$
$2$
Wickedestjr
2013-03-16 19:12:33
TWO!
TWO!
DPatrick
2013-03-16 19:12:48
Indeed, there are exactly 2.
Indeed, there are exactly 2.
DPatrick
2013-03-16 19:12:55
For example, if $x+y=2$, then we need $z$ to be 3 or 8.
For example, if $x+y=2$, then we need $z$ to be 3 or 8.
DPatrick
2013-03-16 19:13:13
No matter what x and y are, there will be two z's that make x+y+z a multiple of 5.
No matter what x and y are, there will be two z's that make x+y+z a multiple of 5.
DPatrick
2013-03-16 19:13:30
(In the language of modular arithmetic, we need $z \equiv -(x+y) \pmod{5}$, and there are always two digits that satisfy this.)
(In the language of modular arithmetic, we need $z \equiv -(x+y) \pmod{5}$, and there are always two digits that satisfy this.)
number.sense
2013-03-16 19:13:57
so we have 10*10*2 = 200 choices
so we have 10*10*2 = 200 choices
andrewlin
2013-03-16 19:13:57
so there are 10 choices for x, 10 for y and 2 for z. 10*10*2=200
so there are 10 choices for x, 10 for y and 2 for z. 10*10*2=200
billgates42
2013-03-16 19:13:57
There are 10*10 pairs for a and b because a can be 0.
There are 10*10 pairs for a and b because a can be 0.
csmath
2013-03-16 19:13:57
There are 10 ways to pick each of x and y so 100 total *2=200 (final answer)
There are 10 ways to pick each of x and y so 100 total *2=200 (final answer)
DPatrick
2013-03-16 19:14:12
Right: for every pair of digits $(x,y)$, there are two such $z$.
Right: for every pair of digits $(x,y)$, there are two such $z$.
DPatrick
2013-03-16 19:14:24
And since there are $10 \cdot 10 = 100$ pairs $(x,y)$, there are $2 \cdot 100 = \boxed{200}$ numbers satisfying all the conditions.
And since there are $10 \cdot 10 = 100$ pairs $(x,y)$, there are $2 \cdot 100 = \boxed{200}$ numbers satisfying all the conditions.
DPatrick
2013-03-16 19:15:01
Of course, counting all the x+y+z = 0, x+y+z = 5, and so on by brute-force works too.
Of course, counting all the x+y+z = 0, x+y+z = 5, and so on by brute-force works too.
mathnerd101
2013-03-16 19:15:12
2 down 13 more to go
2 down 13 more to go
DPatrick
2013-03-16 19:15:16
ninjataco
2013-03-16 19:15:34
draw a picture!
draw a picture!
katelynnsmith
2013-03-16 19:15:34
draw a diagram first
draw a diagram first
DPatrick
2013-03-16 19:15:38
Sure, let's sketch a quick picture:
Sure, let's sketch a quick picture:
DPatrick
2013-03-16 19:15:47
DPatrick
2013-03-16 19:16:07
(You might have had F closer to B than to C -- it doesn't matter)
(You might have had F closer to B than to C -- it doesn't matter)
ninjataco
2013-03-16 19:16:27
set AE equal to "x"
set AE equal to "x"
jeff10
2013-03-16 19:16:27
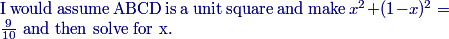
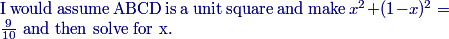
mg13
2013-03-16 19:16:27
label sides and assign variables
label sides and assign variables
mathman500
2013-03-16 19:16:27
WLOG let AB=1
WLOG let AB=1
DPatrick
2013-03-16 19:16:44
That's how I did it too. You could also use two variables but I like setting things to equal 1 if I can.
That's how I did it too. You could also use two variables but I like setting things to equal 1 if I can.
DPatrick
2013-03-16 19:16:54
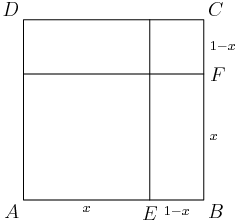
So let's set $AB = 1$ and $AE = x$.
So let's set $AB = 1$ and $AE = x$.
DPatrick
2013-03-16 19:17:05
This gives $EB = 1-x$, $BF = x$, and $FC = 1-x$.
This gives $EB = 1-x$, $BF = x$, and $FC = 1-x$.
DPatrick
2013-03-16 19:17:18
n1000
2013-03-16 19:17:52
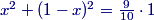
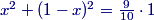
cxiong
2013-03-16 19:17:52
x² + (1-x)² = 9/10
x² + (1-x)² = 9/10
TMTOLBTWNTOF
2013-03-16 19:17:52
x^2 + 1-x ^2 = 9/10
x^2 + 1-x ^2 = 9/10
Mrdavid445
2013-03-16 19:17:52
(1-x)^2+x^2=(9/10)
(1-x)^2+x^2=(9/10)
DPatrick
2013-03-16 19:18:23
Right, the sum of the areas of the two smaller squares is $x^2 + (1-x)^2$.
Right, the sum of the areas of the two smaller squares is $x^2 + (1-x)^2$.
DPatrick
2013-03-16 19:18:27
And we know this equals 9/10.
And we know this equals 9/10.
DPatrick
2013-03-16 19:18:36
So we have
$$
2x^2 - 2x + 1 = \frac{9}{10}.
$$
So we have
$$
2x^2 - 2x + 1 = \frac{9}{10}.
$$
DPatrick
2013-03-16 19:18:54
Let's not solve for $x$ just yet, because that's not what we're asked for. What are we asked for?
Let's not solve for $x$ just yet, because that's not what we're asked for. What are we asked for?
cxiong
2013-03-16 19:19:17
find x/1-x + 1-x/x
find x/1-x + 1-x/x
lucylai
2013-03-16 19:19:17
(1-x)/x+x/(1-x)
(1-x)/x+x/(1-x)
avi1234
2013-03-16 19:19:17
x/(1-x)+(1-x)/x?
x/(1-x)+(1-x)/x?
mathcool2009
2013-03-16 19:19:17
x/1-x + 1-x/x
x/1-x + 1-x/x
JRY
2013-03-16 19:19:17
x/(1-x)+(1-x)/x
x/(1-x)+(1-x)/x
VietaFan
2013-03-16 19:19:17
x/(1-x)+(1-x)/x
x/(1-x)+(1-x)/x
DPatrick
2013-03-16 19:19:28
Yes: we want $\dfrac{AE}{EB} + \dfrac{EB}{AE} = \dfrac{x}{1-x} + \dfrac{1-x}{x}$.
Yes: we want $\dfrac{AE}{EB} + \dfrac{EB}{AE} = \dfrac{x}{1-x} + \dfrac{1-x}{x}$.
DPatrick
2013-03-16 19:19:40
This simplifies to
$$
\frac{x^2 + (1-x)^2}{x(1-x)} = \frac{2x^2 - 2x + 1}{x - x^2}.
$$
This simplifies to
$$
\frac{x^2 + (1-x)^2}{x(1-x)} = \frac{2x^2 - 2x + 1}{x - x^2}.
$$
DPatrick
2013-03-16 19:19:48
Aha, I recognize the numerator!
Aha, I recognize the numerator!
kdokmeci
2013-03-16 19:20:16
9/10
9/10
promathist99
2013-03-16 19:20:16
It's the same!
It's the same!
SuperSnivy
2013-03-16 19:20:16
9/10 for numerator
9/10 for numerator
csmath
2013-03-16 19:20:16
That = 9/10
That = 9/10
billgates42
2013-03-16 19:20:16
9/10
9/10
DPatrick
2013-03-16 19:20:22
The numerator is just $\frac{9}{10}$.
The numerator is just $\frac{9}{10}$.
DPatrick
2013-03-16 19:20:27
What about the denominator?
What about the denominator?
akalykid012
2013-03-16 19:20:57
denominator = 1/20
denominator = 1/20
mapletree14
2013-03-16 19:20:57
And subtract one and divide by 2 to get the denominator.
And subtract one and divide by 2 to get the denominator.
nikoma
2013-03-16 19:20:57
Isolate 2x^2 - 2x
Isolate 2x^2 - 2x
ucantbeatmario
2013-03-16 19:20:57
x-x^2=(1-9/10)/2=1/20
x-x^2=(1-9/10)/2=1/20
DPatrick
2013-03-16 19:21:04
Rearranging our area equation a little bit gives us
$$
2x^2 - 2x = -\frac{1}{10},
$$
so $x - x^2 = \frac{1}{20}$.
Rearranging our area equation a little bit gives us
$$
2x^2 - 2x = -\frac{1}{10},
$$
so $x - x^2 = \frac{1}{20}$.
lcamhie142857
2013-03-16 19:21:35
dividing gives 18
dividing gives 18
mathwizard888
2013-03-16 19:21:35
(9/10)/(1/20)=018 answer
(9/10)/(1/20)=018 answer
Nitzuga
2013-03-16 19:21:35
So our answer is $018$
So our answer is $018$
DPatrick
2013-03-16 19:21:40
Therefore, the quantity we want is
$$
\frac{\frac{9}{10}}{\frac{1}{20}} = \frac{180}{10} = \boxed{018}.
$$
Therefore, the quantity we want is
$$
\frac{\frac{9}{10}}{\frac{1}{20}} = \frac{180}{10} = \boxed{018}.
$$
DPatrick
2013-03-16 19:22:32
You can also get a perhaps more elegant solution by using two variables: letting AE = x and EB = y. It requires you to be slightly more clever. You can post it on the forum if you like.
You can also get a perhaps more elegant solution by using two variables: letting AE = x and EB = y. It requires you to be slightly more clever. You can post it on the forum if you like.
DPatrick
2013-03-16 19:22:49
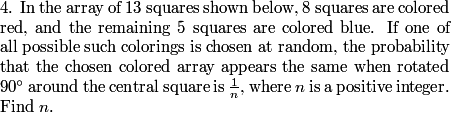
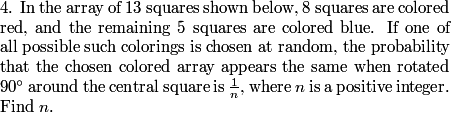
DPatrick
2013-03-16 19:22:58
DPatrick
2013-03-16 19:23:09
What exactly does the rotation condition mean?
What exactly does the rotation condition mean?
steve123456
2013-03-16 19:23:40
all the corresponding positions have to be the same color
all the corresponding positions have to be the same color
TMTOLBTWNTOF
2013-03-16 19:23:40
All the L's on the outside need the same arrangement
All the L's on the outside need the same arrangement
andrewlin
2013-03-16 19:23:40
it means that all of the L's have the same colouring
it means that all of the L's have the same colouring
pedronr
2013-03-16 19:23:40
Each of the sets of three has to have the same pattern.
Each of the sets of three has to have the same pattern.
mathman98
2013-03-16 19:23:40
It's the same on all four "sides"
It's the same on all four "sides"
n1000
2013-03-16 19:23:40
that the four little Ls have the same coloring
that the four little Ls have the same coloring
DPatrick
2013-03-16 19:23:47
Right. In other words, all of the lettered squares in the picture below must be the same color (that is, all the X's must be the same, all the Y's must be the same, and all the Z's must be the same):
Right. In other words, all of the lettered squares in the picture below must be the same color (that is, all the X's must be the same, all the Y's must be the same, and all the Z's must be the same):
DPatrick
2013-03-16 19:23:52
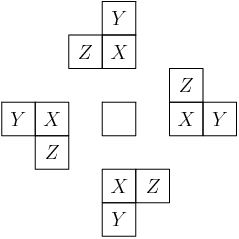
DPatrick
2013-03-16 19:24:05
And how is that possible with the given colors (8 red and 5 blue)?
And how is that possible with the given colors (8 red and 5 blue)?
swe1
2013-03-16 19:24:25
Middle has to be blue
Middle has to be blue
mathnerd101
2013-03-16 19:24:25
blue has to be in the middle
blue has to be in the middle
timoteomo3
2013-03-16 19:24:25
center must be blue
center must be blue
thkim1011
2013-03-16 19:24:25
Middle must be blue
Middle must be blue
mathman27
2013-03-16 19:24:25
middle is blue
middle is blue
bugegg3
2013-03-16 19:24:25
the center must be blue
the center must be blue
ClassicCalculator
2013-03-16 19:24:42
The center square must be blue, and each surrounding group must have 2 reds and 1 blue.
The center square must be blue, and each surrounding group must have 2 reds and 1 blue.
sahilp
2013-03-16 19:24:42
x y or z is blue
x y or z is blue
countingkg
2013-03-16 19:24:42
so either X = blue, Y = blue, or Z=blue
so either X = blue, Y = blue, or Z=blue
hi how are you doing toda
2013-03-16 19:24:42
so each coloring of L can only be 2 red and 1 blue
so each coloring of L can only be 2 red and 1 blue
DPatrick
2013-03-16 19:24:51
Right. We need to pick one of X, Y, or Z to be 4 of the five blues (along with the center square). The other two letters will all be red.
Right. We need to pick one of X, Y, or Z to be 4 of the five blues (along with the center square). The other two letters will all be red.
DPatrick
2013-03-16 19:25:10
So how many colorings work?
So how many colorings work?
ninjataco
2013-03-16 19:25:25
3 ways to do this
3 ways to do this
distortedwalrus
2013-03-16 19:25:25
3
3
btilm305
2013-03-16 19:25:25
3
3
Math_Kirby
2013-03-16 19:25:25
3
3
sparkles257
2013-03-16 19:25:25
3
3
anwang16
2013-03-16 19:25:25
3
3
number.sense
2013-03-16 19:25:25
3 total
3 total
Wickedestjr
2013-03-16 19:25:25
Three
Three
anthonyjang
2013-03-16 19:25:25
3
3
lucylai
2013-03-16 19:25:25
3
3
willabc
2013-03-16 19:25:25
3
3
DPatrick
2013-03-16 19:25:42
Right: just 3. Either X+center blue, or Y+center blue, or Z+center blue.
Right: just 3. Either X+center blue, or Y+center blue, or Z+center blue.
kouhong
2013-03-16 19:25:49
now we find how many possibilites there are total
now we find how many possibilites there are total
DPatrick
2013-03-16 19:25:58
Right...and how many ways to color the 13 squares overall?
Right...and how many ways to color the 13 squares overall?
ABCDE
2013-03-16 19:26:18
13 choose 5 total ways
13 choose 5 total ways
mg13
2013-03-16 19:26:18
13C5
13C5
SuperSnivy
2013-03-16 19:26:18
54math
2013-03-16 19:26:18
13C5
13C5
VietaFan
2013-03-16 19:26:18
$\binom{13}{5}$
$\binom{13}{5}$
ryanyoo
2013-03-16 19:26:18
13c5
13c5
koel17
2013-03-16 19:26:18
13 choose 8
13 choose 8
noobynoob
2013-03-16 19:26:18
$\frac{13!}{8!5!}$
$\frac{13!}{8!5!}$
moana314
2013-03-16 19:26:18
13 choose 5
13 choose 5
DPatrick
2013-03-16 19:26:22
There are 13 squares, and we must pick any 5 of them to be blue.
There are 13 squares, and we must pick any 5 of them to be blue.
DPatrick
2013-03-16 19:26:37
So there are
$$
\binom{13}{5} = \frac{13 \cdot 12 \cdot 11 \cdot 10 \cdot 9}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 13 \cdot 11 \cdot 9 = 1287
$$
total colorings.
So there are
$$
\binom{13}{5} = \frac{13 \cdot 12 \cdot 11 \cdot 10 \cdot 9}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 13 \cdot 11 \cdot 9 = 1287
$$
total colorings.
DPatrick
2013-03-16 19:26:55
(I wrote it out because that's what you had to do on the contest too -- no calcuators!)
(I wrote it out because that's what you had to do on the contest too -- no calcuators!)
DPatrick
2013-03-16 19:27:01
...or calcuLators even!
...or calcuLators even!
ucantbeatmario
2013-03-16 19:27:21
and 3/1287=1/429, so n=429
and 3/1287=1/429, so n=429
gaberen
2013-03-16 19:27:21
3/1287 = 1/429 so n = 429
3/1287 = 1/429 so n = 429
SurrealisticStranger
2013-03-16 19:27:21
Divide by 3, we get 429
Divide by 3, we get 429
kdokmeci
2013-03-16 19:27:21
Our probability is 3/1287=1/429 so the answer is 429
Our probability is 3/1287=1/429 so the answer is 429
Annabeth
2013-03-16 19:27:21
3/1287=1/429, so n=429
3/1287=1/429, so n=429
DPatrick
2013-03-16 19:27:26
Hence, the probability of a successful coloring is $\frac{3}{1287} = \frac{1}{429}$, and the answer is $\boxed{429}$.
Hence, the probability of a successful coloring is $\frac{3}{1287} = \frac{1}{429}$, and the answer is $\boxed{429}$.
DPatrick
2013-03-16 19:27:51
DPatrick
2013-03-16 19:28:15
Since there's no easy formula for the roots of a cubic, what should we do?
Since there's no easy formula for the roots of a cubic, what should we do?
cxiong
2013-03-16 19:28:46
(x + 1)³ = x³ + 3x² + 3x + 1
(x + 1)³ = x³ + 3x² + 3x + 1
Wickedestjr
2013-03-16 19:28:46
Notice the last three terms of the equation
Notice the last three terms of the equation
mathman500
2013-03-16 19:28:46
The polynomial almost looks like -(x+1)^3
The polynomial almost looks like -(x+1)^3
timoteomo3
2013-03-16 19:28:46
-3x^2-3x-1 looks just like (x+1)^3
-3x^2-3x-1 looks just like (x+1)^3
DPatrick
2013-03-16 19:29:08
Aha, most of the coefficients look nice. In particular the 3,3,1 in the final three terms are suggestive of a perfect cube.
Aha, most of the coefficients look nice. In particular the 3,3,1 in the final three terms are suggestive of a perfect cube.
DPatrick
2013-03-16 19:29:17
But the 8 up front is annoying.
But the 8 up front is annoying.
mathman98
2013-03-16 19:29:49
Write 8x^3 as 9x^3-x^3
Write 8x^3 as 9x^3-x^3
az_phx_brandon_jiang
2013-03-16 19:29:49
9x^3-x^3
9x^3-x^3
photondragon314
2013-03-16 19:29:49
rewrite as: 9x^3 - x^3 - 3x^2 - 3x - 1 = 0
rewrite as: 9x^3 - x^3 - 3x^2 - 3x - 1 = 0
DPatrick
2013-03-16 19:30:08
Let's force the perfect cube in there!
Let's force the perfect cube in there!
DPatrick
2013-03-16 19:30:15
Let's write it as
$$
9x^3 {\color{red}{- x^3 - 3x^2 - 3x - 1}} = 0.
$$
What good did that do?
Let's write it as
$$
9x^3 {\color{red}{- x^3 - 3x^2 - 3x - 1}} = 0.
$$
What good did that do?
Hydroxide
2013-03-16 19:30:36
it's -(x+1)^3
it's -(x+1)^3
sparkles257
2013-03-16 19:30:36
-(x+1)^3
-(x+1)^3
pedronr
2013-03-16 19:30:36
So 9x^3-(x+1)^3=0.
So 9x^3-(x+1)^3=0.
Aplus95
2013-03-16 19:30:36
9x^3 = (x+1)^3
9x^3 = (x+1)^3
mathwizard888
2013-03-16 19:30:36
9x^3=(x+1)^3
9x^3=(x+1)^3
DPatrick
2013-03-16 19:30:41
Now it's really nice:
$$
9x^3 = x^3 + 3x^2 + 3x + 1 = (x+1)^3.
$$
Now it's really nice:
$$
9x^3 = x^3 + 3x^2 + 3x + 1 = (x+1)^3.
$$
mathnerd101
2013-03-16 19:31:06
cube root both sides
cube root both sides
billgates42
2013-03-16 19:31:06
cubed root time!
cubed root time!
mjoshi
2013-03-16 19:31:06
take the cube root
take the cube root
n1000
2013-03-16 19:31:06
take the cube root of both sides
take the cube root of both sides
DPatrick
2013-03-16 19:31:19
So taking the cube root of both sides, we get $\sqrt[3]{9}\cdot x = x+1$.
So taking the cube root of both sides, we get $\sqrt[3]{9}\cdot x = x+1$.
Wickedestjr
2013-03-16 19:31:51
Solve for x!
Solve for x!
trophies
2013-03-16 19:31:51
now solve for x!
now solve for x!
mssmath
2013-03-16 19:31:51
x=1/(9^(1/3)-1)
x=1/(9^(1/3)-1)
ninjataco
2013-03-16 19:31:51
subtract x from each side and factor it out
subtract x from each side and factor it out
number.sense
2013-03-16 19:31:51
solve for x: 1/(cbrt9-1)
solve for x: 1/(cbrt9-1)
DPatrick
2013-03-16 19:32:00
Solving for $x$ gives $x = \dfrac{1}{\sqrt[3]{9} - 1}$.
Solving for $x$ gives $x = \dfrac{1}{\sqrt[3]{9} - 1}$.
DPatrick
2013-03-16 19:32:08
So far, so good, but it's not in the form that the answer requires. What do we do?
So far, so good, but it's not in the form that the answer requires. What do we do?
anwang16
2013-03-16 19:32:42
use difference of cubes backwards
use difference of cubes backwards
sindennisz
2013-03-16 19:32:42
Complete the cube on the bottom using difference of cubes.
Complete the cube on the bottom using difference of cubes.
tiger21
2013-03-16 19:32:42
multiply to get a difference of cubes in the denominator
multiply to get a difference of cubes in the denominator
DPatrick
2013-03-16 19:32:53
Maybe if we let $y = \sqrt[3]{9}$ it's easier to see: $x = \dfrac{1}{y-1}$. We need something with just $y^3$ and 1 in the denominator.
Maybe if we let $y = \sqrt[3]{9}$ it's easier to see: $x = \dfrac{1}{y-1}$. We need something with just $y^3$ and 1 in the denominator.
DPatrick
2013-03-16 19:33:11
Since we know $y^3,$ we should multiply numerator and denominator by $y^2 + y + 1$, noting that
$$
(y-1)(y^2+y+1) = y^3 - 1.
$$
Since we know $y^3,$ we should multiply numerator and denominator by $y^2 + y + 1$, noting that
$$
(y-1)(y^2+y+1) = y^3 - 1.
$$
DPatrick
2013-03-16 19:33:21
(That's a special case of the difference-of-cubes factorization.)
(That's a special case of the difference-of-cubes factorization.)
Math_Kirby
2013-03-16 19:33:45
multiply top and bottom with (sqrt[3](81)+sqrt[3]{9}+1)
multiply top and bottom with (sqrt[3](81)+sqrt[3]{9}+1)
awesomeusername
2013-03-16 19:34:00
multiply numerator and denominator by y^2 + y + 1
multiply numerator and denominator by y^2 + y + 1
mathawesomeness777
2013-03-16 19:34:00
multiply by y^2 + y + 1
multiply by y^2 + y + 1
DPatrick
2013-03-16 19:34:05
So now we have
$$
x = \frac{y^2 + y + 1}{y^3 - 1} = \frac{\sqrt[3]{81} + \sqrt[3]{9} + 1}{8}.
$$
So now we have
$$
x = \frac{y^2 + y + 1}{y^3 - 1} = \frac{\sqrt[3]{81} + \sqrt[3]{9} + 1}{8}.
$$
zhuangzhuang
2013-03-16 19:34:29
81+9+8=98=ans
81+9+8=98=ans
ucantbeatmario
2013-03-16 19:34:29
so answer =81+9+8=98
so answer =81+9+8=98
amoghgaitonde
2013-03-16 19:34:29
a = 81, b = 9, c = 8 so a + b + c = 98
a = 81, b = 9, c = 8 so a + b + c = 98
Annabeth
2013-03-16 19:34:29
81+9+8=98
81+9+8=98
coldsummer
2013-03-16 19:34:29
so the answer is 81 + 9 + 8 = 098
so the answer is 81 + 9 + 8 = 098
chiku
2013-03-16 19:34:29
81+9+8=98
81+9+8=98
DPatrick
2013-03-16 19:34:36
This is the form we need, and the answer is $81 + 9 + 8 = \boxed{098}$.
This is the form we need, and the answer is $81 + 9 + 8 = \boxed{098}$.
DPatrick
2013-03-16 19:35:00
DPatrick
2013-03-16 19:35:29
There are many many ways to solve this problem -- the main hitch is to keep track of your assumptions carefully.
There are many many ways to solve this problem -- the main hitch is to keep track of your assumptions carefully.
TMTOLBTWNTOF
2013-03-16 19:35:48
does order within the box matter?
does order within the box matter?
DPatrick
2013-03-16 19:35:56
That's one assumption we have to decide upon.
That's one assumption we have to decide upon.
DPatrick
2013-03-16 19:36:08
I found it easier to count if we assume that it DOES matter.
I found it easier to count if we assume that it DOES matter.
DPatrick
2013-03-16 19:36:16
(You can do it the other way too.)
(You can do it the other way too.)
timoteomo3
2013-03-16 19:36:26
indistinguishable math textbooks! much more convenient
indistinguishable math textbooks! much more convenient
DPatrick
2013-03-16 19:36:52
Yes, I also found it easiest to assume the books themselves are indistinguishable.
Yes, I also found it easiest to assume the books themselves are indistinguishable.
DPatrick
2013-03-16 19:37:08
Let's think about it as arranging the 12 books in order -- 3 M's (for math) and 9 O's (for other) -- from which the first 3 books will go in the first box, and then the next 4 books will go in the second box, and the last 5 books into the third box.
Let's think about it as arranging the 12 books in order -- 3 M's (for math) and 9 O's (for other) -- from which the first 3 books will go in the first box, and then the next 4 books will go in the second box, and the last 5 books into the third box.
DPatrick
2013-03-16 19:37:41
First, how many ways to arrange the books in any order?
First, how many ways to arrange the books in any order?
gaberen
2013-03-16 19:38:09
12!/9!3!
12!/9!3!
54math
2013-03-16 19:38:09
12C3
12C3
QuantumandMath
2013-03-16 19:38:09
(12 3)
(12 3)
Annabeth
2013-03-16 19:38:09
12!/9!*3!
12!/9!*3!
cerberus88
2013-03-16 19:38:09
12!/3!9!
12!/3!9!
bugegg3
2013-03-16 19:38:09
12 choose 3
12 choose 3
Flamewire
2013-03-16 19:38:09
12!/9!3! since they're indistinguishable
12!/9!3! since they're indistinguishable
billgates42
2013-03-16 19:38:09
There are 12 choose 3
There are 12 choose 3
TheUnChosenOne
2013-03-16 19:38:09
12C3
12C3
DPatrick
2013-03-16 19:38:22
Right. I'm just thinking of arranging 3 M's and 9 O's into a 12-letter "word".
Right. I'm just thinking of arranging 3 M's and 9 O's into a 12-letter "word".
DPatrick
2013-03-16 19:38:32
We only need to choose the 3 slots (among the 12) for the math books.
We only need to choose the 3 slots (among the 12) for the math books.
DPatrick
2013-03-16 19:38:43
So there are $\dbinom{12}{3} = \dfrac{12 \cdot 11 \cdot 10}{6} = 220$ arrangements.
So there are $\dbinom{12}{3} = \dfrac{12 \cdot 11 \cdot 10}{6} = 220$ arrangements.
DPatrick
2013-03-16 19:39:03
And now we count "successes": where the M's all end up in the same box.
And now we count "successes": where the M's all end up in the same box.
QuantumandMath
2013-03-16 19:39:23
ror left box, 1 way for math
ror left box, 1 way for math
kdokmeci
2013-03-16 19:39:23
Casework into wwhich box
Casework into wwhich box
d95776
2013-03-16 19:39:23
Count the number of cases.
Count the number of cases.
mathnerd101
2013-03-16 19:39:23
the first box with 3 only has one way
the first box with 3 only has one way
DPatrick
2013-03-16 19:39:30
Right, there are 3 cases, depending on which box they end up in.
Right, there are 3 cases, depending on which box they end up in.
DPatrick
2013-03-16 19:39:44
The first case of the first box has just 1 way: MMMOOOOOOOOO (where O is an "other" non-math book).
The first case of the first box has just 1 way: MMMOOOOOOOOO (where O is an "other" non-math book).
DPatrick
2013-03-16 19:39:55
How about the second box?
How about the second box?
jeff10
2013-03-16 19:40:14
the number of ways to put the 3 math books into the "4 box" is 4
the number of ways to put the 3 math books into the "4 box" is 4
cxiong
2013-03-16 19:40:14
second has 4
second has 4
mikhailgromov
2013-03-16 19:40:14
second 4 ways
second 4 ways
csmath
2013-03-16 19:40:14
There are 4 ways for the second box.
There are 4 ways for the second box.
JRY
2013-03-16 19:40:14
4C3=4
4C3=4
DVA6102
2013-03-16 19:40:14
4 C 3 = 4
4 C 3 = 4
cjquines0
2013-03-16 19:40:14
4C3
4C3
VietaFan
2013-03-16 19:40:14
4 choose 3 or 4 ways
4 choose 3 or 4 ways
DPatrick
2013-03-16 19:40:20
We must have OOOXXXXOOOOO where XXXX is the middle box. 3 of the X's have to be M's.
We must have OOOXXXXOOOOO where XXXX is the middle box. 3 of the X's have to be M's.
DPatrick
2013-03-16 19:40:30
So there are $\binom43 = 4$ ways (choose 3 of the 4 X's to be M's, or alternatively just choose one of them to be an O).
So there are $\binom43 = 4$ ways (choose 3 of the 4 X's to be M's, or alternatively just choose one of them to be an O).
DPatrick
2013-03-16 19:40:48
How about the case for the last box?
How about the case for the last box?
tiger21
2013-03-16 19:41:10
5C3 or 10 ways
5C3 or 10 ways
phoenix827
2013-03-16 19:41:10
5C3
5C3
SuperSnivy
2013-03-16 19:41:10
10 ways for last box
10 ways for last box
sahilp
2013-03-16 19:41:10
5C3=10
5C3=10
flyrain
2013-03-16 19:41:10
5C3=10
5C3=10
davidkim2106
2013-03-16 19:41:10
5C3
5C3
ninjataco
2013-03-16 19:41:10
5C3=10 ways
5C3=10 ways
AlcumusGuy
2013-03-16 19:41:10
5C3 = 10 ways
5C3 = 10 ways
DPatrick
2013-03-16 19:41:22
Now we must have OOOOOOOXXXXX where XXXXX is the last box. 3 of the X's have to be M's.
Now we must have OOOOOOOXXXXX where XXXXX is the last box. 3 of the X's have to be M's.
DPatrick
2013-03-16 19:41:27
So there are $\binom53 = 10$ ways (choose 3 of the 5 X's to be M's).
So there are $\binom53 = 10$ ways (choose 3 of the 5 X's to be M's).
Annabeth
2013-03-16 19:41:49
In all, 15 ways
In all, 15 ways
kdokmeci
2013-03-16 19:41:49
The total number of ways is 1+4+10=15 ways.
The total number of ways is 1+4+10=15 ways.
pedronr
2013-03-16 19:41:53
So (1+4+10)/220 is the answer
So (1+4+10)/220 is the answer
mathwizard888
2013-03-16 19:41:58
probability is 15/220=3/44, so 047 answer
probability is 15/220=3/44, so 047 answer
DPatrick
2013-03-16 19:42:02
All together, there are $1+4+10 = 15$ successful orderings of the books.
All together, there are $1+4+10 = 15$ successful orderings of the books.
promathist99
2013-03-16 19:42:52
Answer: 047
Answer: 047
distortedwalrus
2013-03-16 19:42:52
15/220 = 3/44 --> 47
15/220 = 3/44 --> 47
n1000
2013-03-16 19:42:52
Sun7777
2013-03-16 19:42:52
47
47
kouhong
2013-03-16 19:42:52
so3+44=47 (answer)
so3+44=47 (answer)
DPatrick
2013-03-16 19:43:00
Thus the probability is $\frac{15}{220} = \frac{3}{44}$ in lowest terms, so the answer is $3+44 = \boxed{047}$.
Thus the probability is $\frac{15}{220} = \frac{3}{44}$ in lowest terms, so the answer is $3+44 = \boxed{047}$.
DPatrick
2013-03-16 19:43:52
Mattchu386
2013-03-16 19:44:07
Diagram!
Diagram!
mathman500
2013-03-16 19:44:07
Draw a diagram
Draw a diagram
andrewlin
2013-03-16 19:44:07
should we attempt a diagram?
should we attempt a diagram?
billgates42
2013-03-16 19:44:07
Draw a picture!!!
Draw a picture!!!
DPatrick
2013-03-16 19:44:14
I would certainly attempt to sketch a picture.
I would certainly attempt to sketch a picture.
DPatrick
2013-03-16 19:44:26
Fortunately, I have a whizzy drawing program. With my whizzy drawing program, I can make this:
Fortunately, I have a whizzy drawing program. With my whizzy drawing program, I can make this:
DPatrick
2013-03-16 19:44:31
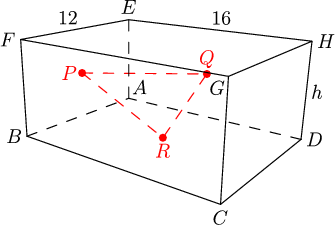
btilm305
2013-03-16 19:44:37
height = h
height = h
DPatrick
2013-03-16 19:44:57
Indeed, I've called the height h (what they called m/n in the problem).
Indeed, I've called the height h (what they called m/n in the problem).
DPatrick
2013-03-16 19:45:12
OK. That's not very illuminating. Point A is the corner where the three faces mentioned in the problem meet, and the dashed red triangle is the triangle with area 30. But that red triangle is still just plain hard to think about.
OK. That's not very illuminating. Point A is the corner where the three faces mentioned in the problem meet, and the dashed red triangle is the triangle with area 30. But that red triangle is still just plain hard to think about.
DPatrick
2013-03-16 19:45:18
Any ideas?
Any ideas?
Knightone
2013-03-16 19:45:53
dilate the midpoints to the corners and use area(FCH)=120
dilate the midpoints to the corners and use area(FCH)=120
DPatrick
2013-03-16 19:46:25
I like this idea. If we blow up the triangle to FHC, we get a triangle whose side lengths are two as big, so whose area is 2^2 = 4 times as big:
I like this idea. If we blow up the triangle to FHC, we get a triangle whose side lengths are two as big, so whose area is 2^2 = 4 times as big:
DPatrick
2013-03-16 19:46:31
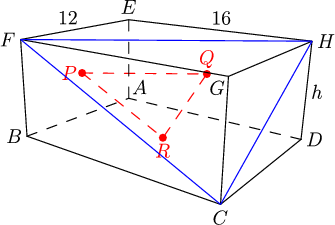
DPatrick
2013-03-16 19:46:56
I find that triangle CFH is way easier to think about than PQR, because we already have a mess of right triangles. (Note that we could have reached an essentially equivalent position by considering the box with A, P, R, and Q as vertices. But blowing things up is more fun.)
I find that triangle CFH is way easier to think about than PQR, because we already have a mess of right triangles. (Note that we could have reached an essentially equivalent position by considering the box with A, P, R, and Q as vertices. But blowing things up is more fun.)
DPatrick
2013-03-16 19:47:14
So now the area of the blue triangle is 4*30 = 120, and we still want to find h.
So now the area of the blue triangle is 4*30 = 120, and we still want to find h.
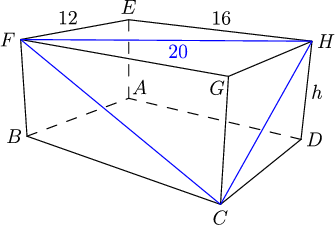
Wickedestjr
2013-03-16 19:47:31
Then note that FH = 20, thus the altitude to FH = 12.
Then note that FH = 20, thus the altitude to FH = 12.
csmath
2013-03-16 19:47:31
FH=20
FH=20
Polynomial
2013-03-16 19:47:31
FH is 20
FH is 20
bugegg3
2013-03-16 19:47:31
12^2+16^2=20^2
12^2+16^2=20^2
Wickedestjr
2013-03-16 19:47:31
The altitude from C to FH must be equal to 12.
The altitude from C to FH must be equal to 12.
DPatrick
2013-03-16 19:47:35
Aha!
Aha!
DPatrick
2013-03-16 19:47:43
We know that FE = 12 and EH = 16.
We know that FE = 12 and EH = 16.
DPatrick
2013-03-16 19:48:07
So FEH is a 12-16-20 right triangle! And FH = 20. (You could use the Pythagorean Theorem too if you didn't see it right away.)
So FEH is a 12-16-20 right triangle! And FH = 20. (You could use the Pythagorean Theorem too if you didn't see it right away.)
DPatrick
2013-03-16 19:48:13
We don't need PQR anymore, so I'll wipe that out to make our diagram cleaner:
We don't need PQR anymore, so I'll wipe that out to make our diagram cleaner:
DPatrick
2013-03-16 19:48:22
Polynomial
2013-03-16 19:48:57
And the altitude from C to FH is 12. Use variables and solve for h
And the altitude from C to FH is 12. Use variables and solve for h
kdokmeci
2013-03-16 19:49:00
Connect C to FH
Connect C to FH
billgates42
2013-03-16 19:49:00
FIND THE ALTITUDE from C
FIND THE ALTITUDE from C
DPatrick
2013-03-16 19:49:27
Right, as mentioned a bit earlier, the area of the blue triangle is 120, and if we think of FH as the base, with length 20, then the height from C to FH must be 12:
Right, as mentioned a bit earlier, the area of the blue triangle is 120, and if we think of FH as the base, with length 20, then the height from C to FH must be 12:
DPatrick
2013-03-16 19:49:36
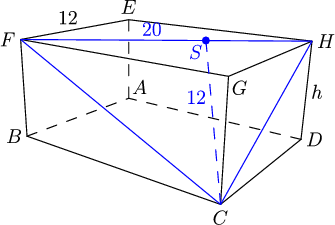
DPatrick
2013-03-16 19:49:45
All right, how are we going to get h?
All right, how are we going to get h?
QuantumandMath
2013-03-16 19:50:11
CGS
CGS
forthegreatergood
2013-03-16 19:50:11
make a triangle
make a triangle
cxiong
2013-03-16 19:50:11
pythagorean theorem from SG, SC, GC
pythagorean theorem from SG, SC, GC
DPatrick
2013-03-16 19:50:22
We go back to that classic strategy of "build right triangles and hope good things happen". We draw GS to make right triangle CGS. Once we find GS, we're home free.
We go back to that classic strategy of "build right triangles and hope good things happen". We draw GS to make right triangle CGS. Once we find GS, we're home free.
DPatrick
2013-03-16 19:50:27
akalykid012
2013-03-16 19:51:06
GS * 20 = 12 * 16
GS * 20 = 12 * 16
chiku
2013-03-16 19:51:19
SG=9.6
SG=9.6
tiger21
2013-03-16 19:51:19
GS=12*16/20
GS=12*16/20
DPatrick
2013-03-16 19:51:28
Aha! Look at the area of the top face EFGH.
Aha! Look at the area of the top face EFGH.
DPatrick
2013-03-16 19:51:57
On the one hand, it's 12*16. (Sorry, EH = 16 got lost from the diagram somewhere.)
On the one hand, it's 12*16. (Sorry, EH = 16 got lost from the diagram somewhere.)
DPatrick
2013-03-16 19:52:31
On the other hand, FH is a diagonal and GS is an altitude to FH, so the area of 2 * (1/2 * FH * SG) = 20 * SG.
On the other hand, FH is a diagonal and GS is an altitude to FH, so the area of 2 * (1/2 * FH * SG) = 20 * SG.
DPatrick
2013-03-16 19:52:58
So we have $12 \cdot 16 = 20 \cdot SG$, which makes $SG = \frac{48}{5}$.
So we have $12 \cdot 16 = 20 \cdot SG$, which makes $SG = \frac{48}{5}$.
DPatrick
2013-03-16 19:53:10
And to finish?
And to finish?
cerberus88
2013-03-16 19:53:34
We get that h=36/5, so the answer is 041
We get that h=36/5, so the answer is 041
akalykid012
2013-03-16 19:53:34
h= 36/5
h= 36/5
ssilwa
2013-03-16 19:53:34
now use pythagorean theorem to find GC or h
now use pythagorean theorem to find GC or h
mathwizard888
2013-03-16 19:53:34
CG=36/5, so 041 answer
CG=36/5, so 041 answer
cerberus88
2013-03-16 19:53:34
h^2=12^2-9.6^2=7.2^2, so h=36/5->041
h^2=12^2-9.6^2=7.2^2, so h=36/5->041
anwang16
2013-03-16 19:53:34
so h=36/5
so h=36/5
cxiong
2013-03-16 19:53:34
(48/5)² + h² = 12²
(48/5)² + h² = 12²
SuperSnivy
2013-03-16 19:53:34
h=36/5, so ans is 041
h=36/5, so ans is 041
cjquines0
2013-03-16 19:53:34
sqrt(12^2 - (48/5)^2) = h
sqrt(12^2 - (48/5)^2) = h
DPatrick
2013-03-16 19:54:17
Right. We know CS = 12 and GS = 48/5 and CGS is a right triangle, so we can use the Pythagorean Theorem again to find CG = h, or again notice that CGS is similar to a 3-4-5 triangle with sides (36/5)-(48/5)-(60/5).
Right. We know CS = 12 and GS = 48/5 and CGS is a right triangle, so we can use the Pythagorean Theorem again to find CG = h, or again notice that CGS is similar to a 3-4-5 triangle with sides (36/5)-(48/5)-(60/5).
DPatrick
2013-03-16 19:54:37
In any event, h = 36/5, so our answer is $36 + 5 = \boxed{041}$.
In any event, h = 36/5, so our answer is $36 + 5 = \boxed{041}$.
DPatrick
2013-03-16 19:55:01
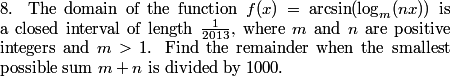
mathawesomeness777
2013-03-16 19:55:20
nasty expression
nasty expression
DPatrick
2013-03-16 19:55:37
Often the nastiest-looking AIME questions are really not that hard once you get past the notation.
Often the nastiest-looking AIME questions are really not that hard once you get past the notation.
DPatrick
2013-03-16 19:55:42
What are the conditions for this function to be defined?
What are the conditions for this function to be defined?
lcamhie142857
2013-03-16 19:55:56
domain of arcsin is [-1,1]
domain of arcsin is [-1,1]
AlcumusGuy
2013-03-16 19:55:56
start with the big picture or arcsin, whose domain is [-1, 1]
start with the big picture or arcsin, whose domain is [-1, 1]
Aplus95
2013-03-16 19:55:56
domain of arcsin is [-1,1]
domain of arcsin is [-1,1]
lucylai
2013-03-16 19:55:56
the domain of arcsin(x) is [-1, 1]
the domain of arcsin(x) is [-1, 1]
Wickedestjr
2013-03-16 19:55:56
-1 </= arcsin </= 1
-1 </= arcsin </= 1
steve123456
2013-03-16 19:55:56
log(m)nx must be between -1 and 1
log(m)nx must be between -1 and 1
VietaFan
2013-03-16 19:55:56
arcsin's domain is [-1, 1]
arcsin's domain is [-1, 1]
billgates42
2013-03-16 19:55:56
The domain of arcsin=[-1,1]
The domain of arcsin=[-1,1]
mathman500
2013-03-16 19:55:56
Domain of arcsin(x) is [-1,1]
Domain of arcsin(x) is [-1,1]
DPatrick
2013-03-16 19:56:22
Right. Since sines are always between -1 and 1, the arcsin function must take an input between -1 and 1 (since sine's output is between -1 and 1).
Right. Since sines are always between -1 and 1, the arcsin function must take an input between -1 and 1 (since sine's output is between -1 and 1).
DPatrick
2013-03-16 19:56:29
So we must have $-1 \le \log_m(nx) \le 1$.
So we must have $-1 \le \log_m(nx) \le 1$.
DPatrick
2013-03-16 19:56:36
What does that mean?
What does that mean?
distortedwalrus
2013-03-16 19:57:08
raise everything to the mth power
raise everything to the mth power
Hydroxide
2013-03-16 19:57:08
1/m <= nx <= m
1/m <= nx <= m
swe1
2013-03-16 19:57:08
Raise both sides with base m
Raise both sides with base m
QuantumandMath
2013-03-16 19:57:08
1/m<=nx<=m
1/m<=nx<=m
JRY
2013-03-16 19:57:08
1/m <= nx <=m
1/m <= nx <=m
bromine
2013-03-16 19:57:08
1/m <= nx <= m
1/m <= nx <= m
DPatrick
2013-03-16 19:57:24
Right, we get rid of the log by raising m to all the terms in our inequality.
Right, we get rid of the log by raising m to all the terms in our inequality.
DPatrick
2013-03-16 19:57:30
This means that $\frac{1}{m} \le nx \le m$.
This means that $\frac{1}{m} \le nx \le m$.
lucylai
2013-03-16 19:57:47
divide everything by n
divide everything by n
billgates42
2013-03-16 19:57:47
ISOLATE X!!!!!!
ISOLATE X!!!!!!
QuantumandMath
2013-03-16 19:57:47
1/nm<=x<=m/n
1/nm<=x<=m/n
DPatrick
2013-03-16 19:58:04
This gives us $\frac{1}{mn} \le x \le \frac{m}{n}$.
This gives us $\frac{1}{mn} \le x \le \frac{m}{n}$.
DPatrick
2013-03-16 19:58:12
So what is the length of the interval?
So what is the length of the interval?
DVA6102
2013-03-16 19:58:34
1/2013
1/2013
promathist99
2013-03-16 19:58:34
1/2013
1/2013
pedronr
2013-03-16 19:58:34
1/2013
1/2013
bugegg3
2013-03-16 19:58:34
1/2013
1/2013
sparkles257
2013-03-16 19:58:34
1/2013
1/2013
d95776
2013-03-16 19:58:34
1/2013
1/2013
mathematician153
2013-03-16 19:58:34
m/n-1/mn
m/n-1/mn
VietaFan
2013-03-16 19:58:34
That means that m/n-1/mn = 1/2013
That means that m/n-1/mn = 1/2013
joshxiong
2013-03-16 19:58:34
m/n-1/mn
m/n-1/mn
DPatrick
2013-03-16 19:58:39
We must have $\frac{1}{mn} \le x \le \frac{m}{n}$, so the interval has length
$$
\frac{m}{n} - \frac{1}{mn} = \frac{1}{2013}.
$$
We must have $\frac{1}{mn} \le x \le \frac{m}{n}$, so the interval has length
$$
\frac{m}{n} - \frac{1}{mn} = \frac{1}{2013}.
$$
DPatrick
2013-03-16 19:58:51
Now what?
Now what?
AlcumusGuy
2013-03-16 19:59:19
Clear the denominators and solve for n
Clear the denominators and solve for n
kdokmeci
2013-03-16 19:59:19
Solve for n or m
Solve for n or m
DPatrick
2013-03-16 19:59:30
Well, we want to examine m+n, and that's hard to do at present.
Well, we want to examine m+n, and that's hard to do at present.
DPatrick
2013-03-16 19:59:40
It'll probably help to solve for one of m or n in terms of the other.
It'll probably help to solve for one of m or n in terms of the other.
DPatrick
2013-03-16 19:59:53
And n looks easier to solve for because it only appears in denominators.
And n looks easier to solve for because it only appears in denominators.
DPatrick
2013-03-16 20:00:10
Let's isolate the two variables by multiplying by $n$ and simplifying the left side:
$$
\frac{m^2-1}{m} = \frac{n}{2013}.
$$
Let's isolate the two variables by multiplying by $n$ and simplifying the left side:
$$
\frac{m^2-1}{m} = \frac{n}{2013}.
$$
DPatrick
2013-03-16 20:00:33
And now we can solve for $n$ in terms of $m$:
$$
n = \frac{2013(m^2-1)}{m}.
$$
And now we can solve for $n$ in terms of $m$:
$$
n = \frac{2013(m^2-1)}{m}.
$$
DPatrick
2013-03-16 20:00:40
What does this tell us?
What does this tell us?
ssilwa
2013-03-16 20:01:01
so m|2013
so m|2013
Knightone
2013-03-16 20:01:01
m divides 2013
m divides 2013
ABCDE
2013-03-16 20:01:01
m is a factor of 2013
m is a factor of 2013
number.sense
2013-03-16 20:01:01
m divides 2013
m divides 2013
calculatorwiz
2013-03-16 20:01:01
as m increases so does n
as m increases so does n
cerberus88
2013-03-16 20:01:01
m divides 2013
m divides 2013
tiger21
2013-03-16 20:01:01
m is a factor of 2013
m is a factor of 2013
mathwizard888
2013-03-16 20:01:01
m is a factor of 2013
m is a factor of 2013
DPatrick
2013-03-16 20:01:11
Right -- it tells us two important things.
Right -- it tells us two important things.
DPatrick
2013-03-16 20:01:31
Remember that $m$ and $n$ must be positive integers, and $m>1$. So $m$ must be a factor of 2013 other than 1.
Remember that $m$ and $n$ must be positive integers, and $m>1$. So $m$ must be a factor of 2013 other than 1.
DPatrick
2013-03-16 20:01:49
Of course, you've all memorized that $2013 = 3 \cdot 11 \cdot 61$ (or you can easily work it out again).
Of course, you've all memorized that $2013 = 3 \cdot 11 \cdot 61$ (or you can easily work it out again).
DPatrick
2013-03-16 20:02:15
But also, as calculatorwiz pointed out, as m increases, so does n.
But also, as calculatorwiz pointed out, as m increases, so does n.
DPatrick
2013-03-16 20:02:35
So making m as small as possible will also make n as small as possible.
So making m as small as possible will also make n as small as possible.
steve123456
2013-03-16 20:02:51
so to minimize m+n, m=3
so to minimize m+n, m=3
tc1729
2013-03-16 20:02:51
so minimizing m minimizes n, so take m=3
so minimizing m minimizes n, so take m=3
n1000
2013-03-16 20:02:51
so we want the smallest value of m, namely three
so we want the smallest value of m, namely three
cxiong
2013-03-16 20:02:51
m = 3
m = 3
csmath
2013-03-16 20:02:51
m=3?
m=3?
DPatrick
2013-03-16 20:03:04
...and the smallest m we can take that's >1 and a factor of 2013 is m=3/
...and the smallest m we can take that's >1 and a factor of 2013 is m=3/
sahilp
2013-03-16 20:03:16
so m=3 and n=671*8
so m=3 and n=671*8
DPatrick
2013-03-16 20:03:23
Indeed, for $m=3$ we get
$$
n = \frac{2013(3^2-1)}{3} = 671 \cdot 8 = 5368.
$$
Indeed, for $m=3$ we get
$$
n = \frac{2013(3^2-1)}{3} = 671 \cdot 8 = 5368.
$$
SuperSnivy
2013-03-16 20:03:48
m = 3, so n = 5368 ==> ans 371
m = 3, so n = 5368 ==> ans 371
number.sense
2013-03-16 20:03:48
m+n = 5371, so our answer is 371
m+n = 5371, so our answer is 371
AlcumusGuy
2013-03-16 20:03:48
so m + n = 5371, so answer is 371
so m + n = 5371, so answer is 371
lucylai
2013-03-16 20:03:48
371
371
davidkim2106
2013-03-16 20:03:48
5368+3=5371
5368+3=5371
SuperSnivy
2013-03-16 20:03:48
3+368 = 371
3+368 = 371
billgates42
2013-03-16 20:03:48
368+3=371!!!
368+3=371!!!
DPatrick
2013-03-16 20:03:54
So $m+n = 5371$, and the answer is $\boxed{371}$.
So $m+n = 5371$, and the answer is $\boxed{371}$.
DPatrick
2013-03-16 20:04:22
Let's do one more (#9), and then I'm going to take a little break before going on to the double-digit problems.
Let's do one more (#9), and then I'm going to take a little break before going on to the double-digit problems.
DPatrick
2013-03-16 20:04:29
DPatrick
2013-03-16 20:04:44
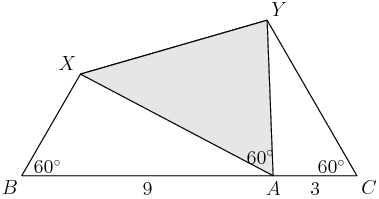
Here's the picture they gave:
Here's the picture they gave:
DPatrick
2013-03-16 20:04:49
DPatrick
2013-03-16 20:04:57
Let's blow up that second picture a bit, and label the points, angles, and lengths that we know:
Let's blow up that second picture a bit, and label the points, angles, and lengths that we know:
DPatrick
2013-03-16 20:05:02
DPatrick
2013-03-16 20:05:12
Anything else that we know that we can label?
Anything else that we know that we can label?
teranz0
2013-03-16 20:05:37
Call XB 12 -x, XA : x
Call XB 12 -x, XA : x
ssilwa
2013-03-16 20:05:37
let BX = x and XA = 12-x same for YC and AY
let BX = x and XA = 12-x same for YC and AY
clear
2013-03-16 20:05:37
label Bx as x, and AX as 12-x, and same for CY and AY
label Bx as x, and AX as 12-x, and same for CY and AY
VietaFan
2013-03-16 20:05:37
AB+BX = 12
AB+BX = 12
DPatrick
2013-03-16 20:06:01
Right: we know that the folded sides AB = 12 and AC = 12 before the folding, so we know AX + XB = 12 and AY + YC = 12 after the folding.
Right: we know that the folded sides AB = 12 and AC = 12 before the folding, so we know AX + XB = 12 and AY + YC = 12 after the folding.
DPatrick
2013-03-16 20:06:07
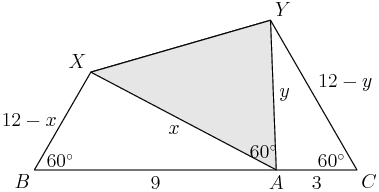
So let's call $AX = x$ and $AY = y$, and label the other lengths accordingly:
So let's call $AX = x$ and $AY = y$, and label the other lengths accordingly:
DPatrick
2013-03-16 20:06:12
DPatrick
2013-03-16 20:06:23
And let's keep in mind what we're trying to find: we want the length $XY$.
And let's keep in mind what we're trying to find: we want the length $XY$.
DPatrick
2013-03-16 20:06:27
I think we've collected the data -- how do we proceed?
I think we've collected the data -- how do we proceed?
noobynoob
2013-03-16 20:06:42
LoC
LoC
d95776
2013-03-16 20:06:42
Use the law of cosines
Use the law of cosines
mathcool2009
2013-03-16 20:06:42
LAW OF COSINES
LAW OF COSINES
joshxiong
2013-03-16 20:06:42
We can use the Law of Cosines
We can use the Law of Cosines
mprashker
2013-03-16 20:06:42
law of cosines!!!
law of cosines!!!
trumpetjean
2013-03-16 20:06:42
law of cosines
law of cosines
noobynoob
2013-03-16 20:06:42
LoC
LoC
thkim1011
2013-03-16 20:06:42
laws of cosine?
laws of cosine?
cire_il
2013-03-16 20:06:42
LOC to find x and y
LOC to find x and y
sunny2000
2013-03-16 20:06:42
laws of cosine!
laws of cosine!
DPatrick
2013-03-16 20:07:01
I can't think of a more elegant way to proceed than to just bash with the Law of Cosines.
I can't think of a more elegant way to proceed than to just bash with the Law of Cosines.
DPatrick
2013-03-16 20:07:36
We have two triangles ($ABX$ and $ACY$) in which we have all three sides and a 60-degree angle. That means we can use the Law of Cosines in each triangle to solve for $x$ and $y$. (60-degree angles are especially nice with Law of Cosines, of course, since $\cos(60^\circ) = \frac12$.)
We have two triangles ($ABX$ and $ACY$) in which we have all three sides and a 60-degree angle. That means we can use the Law of Cosines in each triangle to solve for $x$ and $y$. (60-degree angles are especially nice with Law of Cosines, of course, since $\cos(60^\circ) = \frac12$.)
DPatrick
2013-03-16 20:07:51
What does triangle $ABX$ give us?
What does triangle $ABX$ give us?
steve123456
2013-03-16 20:08:46
x=39/5
x=39/5
kdokmeci
2013-03-16 20:08:46
x=39/5
x=39/5
msinghal
2013-03-16 20:08:46
x=39/5
x=39/5
ws5188
2013-03-16 20:08:46
x^2=81+(12-x)^2-9(12-x)
x^2=81+(12-x)^2-9(12-x)
DPatrick
2013-03-16 20:08:56
Plugging in the data gives us
$$
x^2 = 9^2 + (12-x)^2 - 2(9)(12-x)(\cos 60^\circ).
$$
Plugging in the data gives us
$$
x^2 = 9^2 + (12-x)^2 - 2(9)(12-x)(\cos 60^\circ).
$$
DPatrick
2013-03-16 20:09:10
Conveniently, $\cos 60^\circ = \frac12$, so this is just
$$
x^2 = 81 + 144 - 24x + x^2 - 108 + 9x.
$$
Conveniently, $\cos 60^\circ = \frac12$, so this is just
$$
x^2 = 81 + 144 - 24x + x^2 - 108 + 9x.
$$
DPatrick
2013-03-16 20:09:29
The $x^2$'s cancel, and we have $0 = 117 - 15x$, which solves to give $x = \frac{39}{5}$.
The $x^2$'s cancel, and we have $0 = 117 - 15x$, which solves to give $x = \frac{39}{5}$.
DPatrick
2013-03-16 20:09:48
(I'm not belaboring the routine algebra -- you all can manage that I'm sure!)
(I'm not belaboring the routine algebra -- you all can manage that I'm sure!)
brandbest1
2013-03-16 20:10:00
same thing for y
same thing for y
cxiong
2013-03-16 20:10:00
Find y, use cosine law again
Find y, use cosine law again
DPatrick
2013-03-16 20:10:13
In triangle $ACY$, the Law of Cosines gives us
$$
y^2 = 3^2 + (12-y)^2 - 2(3)(12-y)(\cos 60^\circ).
$$
In triangle $ACY$, the Law of Cosines gives us
$$
y^2 = 3^2 + (12-y)^2 - 2(3)(12-y)(\cos 60^\circ).
$$
lcamhie142857
2013-03-16 20:10:22
y=39/7
y=39/7
lucylai
2013-03-16 20:10:22
y=39/7
y=39/7
distortedwalrus
2013-03-16 20:10:22
similarly we can get y=39/7 using the other triangle
similarly we can get y=39/7 using the other triangle
DPatrick
2013-03-16 20:10:26
This simplifies to $0 = 117 - 21y$, so $y = \frac{39}{7}$.
This simplifies to $0 = 117 - 21y$, so $y = \frac{39}{7}$.
DPatrick
2013-03-16 20:10:34
And how do we finish?
And how do we finish?
davidkim2106
2013-03-16 20:10:48
law of cosines again
law of cosines again
ryanyoo
2013-03-16 20:10:48
one more time
one more time
onta
2013-03-16 20:10:48
Law of Cosines AGAIN!
Law of Cosines AGAIN!
pedronr
2013-03-16 20:10:48
Use LOC again for side XY.
Use LOC again for side XY.
Wickedestjr
2013-03-16 20:10:48
Law of cosines again!
Law of cosines again!
DPatrick
2013-03-16 20:10:51
We again use Law of Cosines, on triangle $XAY$:
$$
(XY)^2 = x^2 + y^2 - 2xy(\cos60^\circ) = x^2 + y^2 - xy.
$$
We again use Law of Cosines, on triangle $XAY$:
$$
(XY)^2 = x^2 + y^2 - 2xy(\cos60^\circ) = x^2 + y^2 - xy.
$$
DPatrick
2013-03-16 20:11:04
This gives
$$
(XY)^2 = \left(\frac{39}{5}\right)^2 + \left(\frac{39}{7}\right)^2 - \left(\frac{39}{5}\right)\left(\frac{39}{7}\right).
$$
This gives
$$
(XY)^2 = \left(\frac{39}{5}\right)^2 + \left(\frac{39}{7}\right)^2 - \left(\frac{39}{5}\right)\left(\frac{39}{7}\right).
$$
DPatrick
2013-03-16 20:11:19
How do we simplify this most efficiently?
How do we simplify this most efficiently?
pickten
2013-03-16 20:11:35
factor out 39^2
factor out 39^2
calculatorwiz
2013-03-16 20:11:35
factor out 39^2
factor out 39^2
scgorantla
2013-03-16 20:11:35
factor out 39^2
factor out 39^2
ws5188
2013-03-16 20:11:35
factor out 39^2
factor out 39^2
kdokmeci
2013-03-16 20:11:35
Remove the 39's
Remove the 39's
DPatrick
2013-03-16 20:11:39
We can pull out the $39^2$ term:
$$
(XY)^2 = (39)^2 \left(\frac{1}{5^2} + \frac{1}{7^2} - \frac{1}{5 \cdot 7}\right).
$$
We can pull out the $39^2$ term:
$$
(XY)^2 = (39)^2 \left(\frac{1}{5^2} + \frac{1}{7^2} - \frac{1}{5 \cdot 7}\right).
$$
number.sense
2013-03-16 20:11:48
factor out the 39^2 and common denominator of 25*49
factor out the 39^2 and common denominator of 25*49
DPatrick
2013-03-16 20:12:02
We see that the common denominator of the expression in the parentheses is $5^2 \cdot 7^2$, so we have:
$$
(XY)^2 = (39)^2 \left(\frac{7^2 + 5^2 - 5 \cdot 7}{5^2 \cdot 7^2}\right) = (39)^2 \left(\frac{39}{5^2 \cdot 7^2}\right).
$$
We see that the common denominator of the expression in the parentheses is $5^2 \cdot 7^2$, so we have:
$$
(XY)^2 = (39)^2 \left(\frac{7^2 + 5^2 - 5 \cdot 7}{5^2 \cdot 7^2}\right) = (39)^2 \left(\frac{39}{5^2 \cdot 7^2}\right).
$$
cerberus88
2013-03-16 20:12:15
so XY=39sqrt(39)/35
so XY=39sqrt(39)/35
DPatrick
2013-03-16 20:12:23
Taking the square root gives us
$$
XY = \frac{39\sqrt{39}}{35},
$$
which is in the required format, so the answer is $39 + 39 + 35 = \boxed{113}$.
Taking the square root gives us
$$
XY = \frac{39\sqrt{39}}{35},
$$
which is in the required format, so the answer is $39 + 39 + 35 = \boxed{113}$.
DPatrick
2013-03-16 20:12:50
I'm going to take a quick 2-minute break to stretch my legs...we'll resume at :15 past!
I'm going to take a quick 2-minute break to stretch my legs...we'll resume at :15 past!
DPatrick
2013-03-16 20:15:06
A couple of quick reminders before we continue...
A couple of quick reminders before we continue...
DPatrick
2013-03-16 20:15:46
First, if you're new to AoPS, please note that this Math Jam is not like our usual online classes! Our regular classes have many fewer students and we're able to answer all your questions during regular classtime.
First, if you're new to AoPS, please note that this Math Jam is not like our usual online classes! Our regular classes have many fewer students and we're able to answer all your questions during regular classtime.
DPatrick
2013-03-16 20:16:24
Second, there will be a complete transcript of this Math Jam posted on the website once we're finished, so if you came late or just want to go back and review, you'll be able to see everything we did.
Second, there will be a complete transcript of this Math Jam posted on the website once we're finished, so if you came late or just want to go back and review, you'll be able to see everything we did.
DPatrick
2013-03-16 20:16:38
And now, on to the double-digit problems!
And now, on to the double-digit problems!
DPatrick
2013-03-16 20:16:43
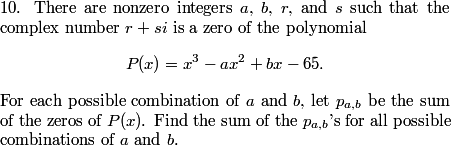
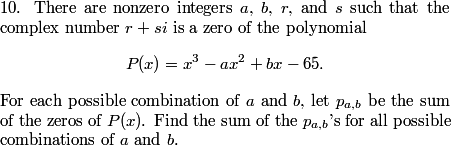
DPatrick
2013-03-16 20:17:12
What do we know about $P(x)$?
What do we know about $P(x)$?
onta
2013-03-16 20:17:27
vieta?
vieta?
billgates42
2013-03-16 20:17:27
Use VIETA!!!
Use VIETA!!!
QuantumandMath
2013-03-16 20:17:27
a is sum of zero's
a is sum of zero's
TMTOLBTWNTOF
2013-03-16 20:17:32
r - si is therefore also a root
r - si is therefore also a root
tc1729
2013-03-16 20:17:32
r-si is also a root of P(x)
r-si is also a root of P(x)
kdokmeci
2013-03-16 20:17:32
If r+si is a root, so is r-si
If r+si is a root, so is r-si
ssilwa
2013-03-16 20:17:32
it also has root r-si
it also has root r-si
calculatorwiz
2013-03-16 20:17:32
it has roots r+si and r-si
it has roots r+si and r-si
distortedwalrus
2013-03-16 20:17:38
it has three roots
it has three roots
anthonyjang
2013-03-16 20:17:38
it has 2 imaginary roots and one real root
it has 2 imaginary roots and one real root
lazorpenguin27143
2013-03-16 20:17:38
r-si is also a zero since the coefficients are rational
r-si is also a zero since the coefficients are rational
Flamewire
2013-03-16 20:17:38
Two of its zeros are r+si and r-si
Two of its zeros are r+si and r-si
pickten
2013-03-16 20:17:38
p_A,B = a
p_A,B = a
AlcumusGuy
2013-03-16 20:17:41
sum of roots = a and product = 65
sum of roots = a and product = 65
DVA6102
2013-03-16 20:17:41
65 is product of zeroes
65 is product of zeroes
DPatrick
2013-03-16 20:17:51
Right, all good observations! Let me organize them,
Right, all good observations! Let me organize them,
DPatrick
2013-03-16 20:18:00
The sum of its roots is $a$.
The sum of its roots is $a$.
DPatrick
2013-03-16 20:18:04
The product of its roots is 65.
The product of its roots is 65.
DPatrick
2013-03-16 20:18:15
(These are both consequences of Vieta's Formulas for polynomials.)
(These are both consequences of Vieta's Formulas for polynomials.)
DPatrick
2013-03-16 20:18:41
We also know that if $r+si$ is a root, then so is $r-si$, and the third root is real.
We also know that if $r+si$ is a root, then so is $r-si$, and the third root is real.
DPatrick
2013-03-16 20:18:57
So what does this tell us about $r$ and $s$?
So what does this tell us about $r$ and $s$?
cerberus88
2013-03-16 20:19:28
we know that r^2+s^2 divides 65
we know that r^2+s^2 divides 65
OCed
2013-03-16 20:19:28
r^2+s^2|65
r^2+s^2|65
calculatorwiz
2013-03-16 20:19:28
r^2 + s^2 is the product of those too roots
r^2 + s^2 is the product of those too roots
DVA6102
2013-03-16 20:19:28
(r^2+s^2)k=65, where k is the third real root
(r^2+s^2)k=65, where k is the third real root
lucylai
2013-03-16 20:19:28
the third root is 65/(r^2+s^2)
the third root is 65/(r^2+s^2)
DPatrick
2013-03-16 20:19:51
Aha!
Aha!
DPatrick
2013-03-16 20:19:58
Let's call the third (real) root $t$.
Let's call the third (real) root $t$.
DPatrick
2013-03-16 20:20:08
Then we have $(r+si)(r-si)t = (r^2+s^2)t = 65$.
Then we have $(r+si)(r-si)t = (r^2+s^2)t = 65$.
DPatrick
2013-03-16 20:20:20
So $r^2+s^2$ is a factor of 65.
So $r^2+s^2$ is a factor of 65.
DPatrick
2013-03-16 20:20:29
What are the possibilites?
What are the possibilites?
minimario
2013-03-16 20:20:34
what is t isn't an integer?
what is t isn't an integer?
DPatrick
2013-03-16 20:21:07
That's a good question. But we certainly know that t is rational, so one way we can tell is by the Rational Root Theorem that it must be an integer (because the coefficient of x^3 is 1).
That's a good question. But we certainly know that t is rational, so one way we can tell is by the Rational Root Theorem that it must be an integer (because the coefficient of x^3 is 1).
DPatrick
2013-03-16 20:21:15
We can also tell by looking at the sum of the roots.
We can also tell by looking at the sum of the roots.
DPatrick
2013-03-16 20:21:37
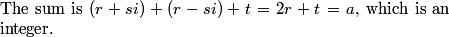
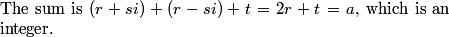
DPatrick
2013-03-16 20:22:02
In fact, let's file that fact up top for future use...
In fact, let's file that fact up top for future use...
DPatrick
2013-03-16 20:22:25
But back to the product...what are the possibilities for $r$ and $s$ given that $r^2 + s^2$ is a factor of 65?
But back to the product...what are the possibilities for $r$ and $s$ given that $r^2 + s^2$ is a factor of 65?
number.sense
2013-03-16 20:22:45
r^2+s^2 = 5, 13, 65 (cannot be 1 because r,s >0)
r^2+s^2 = 5, 13, 65 (cannot be 1 because r,s >0)
kdokmeci
2013-03-16 20:22:45
1,5,13,65
1,5,13,65
davidkim2106
2013-03-16 20:22:45
13,5 1,65
13,5 1,65
DPatrick
2013-03-16 20:23:03
Right: the only positive integer factors of 65 are 1, 5, 13, and 65. And we can't have $r^2 + s^2 = 1$ because they both have to be nonzero.
Right: the only positive integer factors of 65 are 1, 5, 13, and 65. And we can't have $r^2 + s^2 = 1$ because they both have to be nonzero.
DPatrick
2013-03-16 20:23:18
So we only need to look for nonzero perfect squares that sum to 5, 13, or 65.
So we only need to look for nonzero perfect squares that sum to 5, 13, or 65.
DPatrick
2013-03-16 20:23:25
And there aren't very many...
And there aren't very many...
Flamewire
2013-03-16 20:23:47
5 = 1^2 + 2^2
5 = 1^2 + 2^2
JRY
2013-03-16 20:23:47
5:1+4, 13:4+9
5:1+4, 13:4+9
ssilwa
2013-03-16 20:23:47
5 = 1+4
5 = 1+4
Flamewire
2013-03-16 20:23:47
13 = 2^2 + 3^2
13 = 2^2 + 3^2
QuantumandMath
2013-03-16 20:23:47
5=1^2+2^2
5=1^2+2^2
mathcool2009
2013-03-16 20:24:05
r,s = 8,1 7,4 1,2 2,3
r,s = 8,1 7,4 1,2 2,3
JRY
2013-03-16 20:24:05
65:64+1
65:64+1
Flamewire
2013-03-16 20:24:05
65 = 7^2 + 4^2
65 = 7^2 + 4^2
billgates42
2013-03-16 20:24:05
DONT FORGET that r can be negative!!!
DONT FORGET that r can be negative!!!
Knightone
2013-03-16 20:24:05
(r,s)=plus/minus (1,8),(8,1) (2,3),(3,2), (1,2),(2,1) (4,7),(7,4)
(r,s)=plus/minus (1,8),(8,1) (2,3),(3,2), (1,2),(2,1) (4,7),(7,4)
DPatrick
2013-03-16 20:24:13
Indeed, the only possibilities are:
\begin{align*}
1^2 + 2^2 &= 5, \\
2^2 + 3^2 &= 13, \\
1^2 + 8^2 &= 65, \\
4^2 + 7^2 &= 65.
\end{align*}
Indeed, the only possibilities are:
\begin{align*}
1^2 + 2^2 &= 5, \\
2^2 + 3^2 &= 13, \\
1^2 + 8^2 &= 65, \\
4^2 + 7^2 &= 65.
\end{align*}
DPatrick
2013-03-16 20:24:24
Of course, as you mention, r and/or s can be negative too!
Of course, as you mention, r and/or s can be negative too!
DPatrick
2013-03-16 20:24:53
Perhaps its better to think in terms of the polynomials rather than choices for r and s. How many different cubic polynomials does each of these give us?
Perhaps its better to think in terms of the polynomials rather than choices for r and s. How many different cubic polynomials does each of these give us?
d95776
2013-03-16 20:25:19
4
4
sjag
2013-03-16 20:25:19
4
4
davidkim2106
2013-03-16 20:25:19
4?
4?
jasonmathcounts
2013-03-16 20:25:19
4
4
DPatrick
2013-03-16 20:25:32
Right. Each solution above gives 4 cubics, for the four different choices of r. (So there are 16 cubics total.)
Right. Each solution above gives 4 cubics, for the four different choices of r. (So there are 16 cubics total.)
DPatrick
2013-03-16 20:25:46
For example, the equation $1^2 + 2^2 = 5$ gives a different cubic for $r = 1$, $r=-1$, $r=2$, and $r=-2$.
For example, the equation $1^2 + 2^2 = 5$ gives a different cubic for $r = 1$, $r=-1$, $r=2$, and $r=-2$.
DPatrick
2013-03-16 20:26:11
Or to expand on this a bit further, each of the four triples below are a possible set of roots of the polynomial:
\begin{align*}
(+1+2i,~~ +1-2i,~~& 13), \\
(-1+2i,~~ -1-2i,~~& 13), \\
(+2+1i,~~ +2-1i,~~& 13), \\
(-2+1i,~~ -2-1i,~~& 13).
\end{align*}
Or to expand on this a bit further, each of the four triples below are a possible set of roots of the polynomial:
\begin{align*}
(+1+2i,~~ +1-2i,~~& 13), \\
(-1+2i,~~ -1-2i,~~& 13), \\
(+2+1i,~~ +2-1i,~~& 13), \\
(-2+1i,~~ -2-1i,~~& 13).
\end{align*}
DPatrick
2013-03-16 20:26:27
What do we get when we sum all these roots?
What do we get when we sum all these roots?
DPatrick
2013-03-16 20:26:38
(Just for the four cubics above that I've listed.)
(Just for the four cubics above that I've listed.)
calculatorwiz
2013-03-16 20:26:56
52
52
sahilp
2013-03-16 20:26:56
52
52
AlcumusGuy
2013-03-16 20:26:56
imaginary parts simplify to 0!
imaginary parts simplify to 0!
cerberus88
2013-03-16 20:26:56
52
52
lucylai
2013-03-16 20:26:56
52
52
csmath
2013-03-16 20:26:56
13*4=52
13*4=52
tiger21
2013-03-16 20:26:56
52
52
VietaFan
2013-03-16 20:26:56
52 = 13*4
52 = 13*4
mikhailgromov
2013-03-16 20:26:56
52
52
sunny2000
2013-03-16 20:26:56
52
52
jaymo
2013-03-16 20:26:56
52
52
flyrain
2013-03-16 20:26:56
52
52
DPatrick
2013-03-16 20:27:14
Right! Notice that not only do all the imaginary parts cancel out, but all the real parts of the complex roots cancel out too!
Right! Notice that not only do all the imaginary parts cancel out, but all the real parts of the complex roots cancel out too!
DPatrick
2013-03-16 20:27:26
Except for the 13's, everything cancels. $1+2i$ can be paired with $-1-2i$, $-1+2i$ can be paired with $1-2i$, etc. So we're just left with $4 \cdot 13 = 52$.
Except for the 13's, everything cancels. $1+2i$ can be paired with $-1-2i$, $-1+2i$ can be paired with $1-2i$, etc. So we're just left with $4 \cdot 13 = 52$.
DPatrick
2013-03-16 20:27:59
So the four cubics coming from $1^2 + 2^2 = 5$ give roots that sum to $4 \cdot 13 = 52$.
So the four cubics coming from $1^2 + 2^2 = 5$ give roots that sum to $4 \cdot 13 = 52$.
DPatrick
2013-03-16 20:28:12
How about the four cubics coming from $2^2 + 3^2 = 13$? What do their roots sum to?
How about the four cubics coming from $2^2 + 3^2 = 13$? What do their roots sum to?
distortedwalrus
2013-03-16 20:28:32
20
20
number.sense
2013-03-16 20:28:32
20
20
joshxiong
2013-03-16 20:28:32
4*5=20
4*5=20
mathwizard888
2013-03-16 20:28:32
4*5=20
4*5=20
Sanqiang3
2013-03-16 20:28:32
20?
20?
Superwiz
2013-03-16 20:28:32
20
20
DPatrick
2013-03-16 20:29:02
Right! Each of those four cubics will have two complex roots and a real root of 5 (so that 13*5 = 65 gives the correct product). But when we sum them, all the complex roots will cancel out, and we'll just have 4*5 = 20.
Right! Each of those four cubics will have two complex roots and a real root of 5 (so that 13*5 = 65 gives the correct product). But when we sum them, all the complex roots will cancel out, and we'll just have 4*5 = 20.
DPatrick
2013-03-16 20:29:20
And how about the third and fourth equations above?
And how about the third and fourth equations above?
SuperSnivy
2013-03-16 20:29:35
4 each
4 each
empoleon
2013-03-16 20:29:35
4 and 4 each
4 and 4 each
akalykid012
2013-03-16 20:29:35
4, 4
4, 4
mathcool2009
2013-03-16 20:29:35
4 and 4
4 and 4
kdokmeci
2013-03-16 20:29:35
2*(4*1)=8
2*(4*1)=8
anthonyjang
2013-03-16 20:29:35
8, total
8, total
DPatrick
2013-03-16 20:30:01
Right: each has four cubics with two complex roots and a real root of 1. The complex roots cancel when we sum them, so we're left with 4*1 = 4 for each set of four cubics.
Right: each has four cubics with two complex roots and a real root of 1. The complex roots cancel when we sum them, so we're left with 4*1 = 4 for each set of four cubics.
cerberus88
2013-03-16 20:30:15
the answer is 080
the answer is 080
number.sense
2013-03-16 20:30:15
so our answer is 52 + 20 + 8 = 80
so our answer is 52 + 20 + 8 = 80
distortedwalrus
2013-03-16 20:30:15
for a total of 80 = 52+20+4+4
for a total of 80 = 52+20+4+4
VietaFan
2013-03-16 20:30:15
The sum is 20+52+8 = 080.
The sum is 20+52+8 = 080.
DPatrick
2013-03-16 20:30:25
Adding them all up, we see that all the roots over all the cubics sum to $52 + 20 + 4 + 4 = \boxed{080}$.
Adding them all up, we see that all the roots over all the cubics sum to $52 + 20 + 4 + 4 = \boxed{080}$.
DPatrick
2013-03-16 20:30:48
DPatrick
2013-03-16 20:31:06
First let's look at (a). What does that tell us?
First let's look at (a). What does that tell us?
mathworld1
2013-03-16 20:31:35
N divisible by 14,15,16
N divisible by 14,15,16
andrewlin
2013-03-16 20:31:35
N is div by 16,15 and 14
N is div by 16,15 and 14
wjq8g6
2013-03-16 20:31:35
N = 0 mod 16, 15 and 14
N = 0 mod 16, 15 and 14
gengkev
2013-03-16 20:31:35
N is a multiple of lcm(16,15,14)
N is a multiple of lcm(16,15,14)
pedronr
2013-03-16 20:31:35
N is a multiple of LCM(14,15,16)
N is a multiple of LCM(14,15,16)
ksun48
2013-03-16 20:31:35
14|N, 15|N, 16|N
14|N, 15|N, 16|N
TheUnChosenOne
2013-03-16 20:31:35
multiple of 16 15 and 14
multiple of 16 15 and 14
ABCDE
2013-03-16 20:31:35
N is a multiple of 2^4*3*5*7
N is a multiple of 2^4*3*5*7
Hydroxide
2013-03-16 20:31:35
lcm(14, 15, 16) | N
lcm(14, 15, 16) | N
DPatrick
2013-03-16 20:31:41
Right, $N$ must be a multiple of the least common multiple of 16, 15, and 14.
Right, $N$ must be a multiple of the least common multiple of 16, 15, and 14.
DPatrick
2013-03-16 20:31:47
So $N = 2^4 \cdot 3 \cdot 5 \cdot 7 \cdot k$ for some positive integer $k$.
So $N = 2^4 \cdot 3 \cdot 5 \cdot 7 \cdot k$ for some positive integer $k$.
DPatrick
2013-03-16 20:32:11
(Let's leave the primes as-is instead of multiplying them out right now -- we may not have to.)
(Let's leave the primes as-is instead of multiplying them out right now -- we may not have to.)
DPatrick
2013-03-16 20:32:17
Now on to part (b).
Now on to part (b).
DPatrick
2013-03-16 20:32:21
What numbers less than 14 are not already divisors of $N$?
What numbers less than 14 are not already divisors of $N$?
cire_il
2013-03-16 20:32:48
9 11 13
9 11 13
mathematician153
2013-03-16 20:32:48
9,11,13
9,11,13
billgates42
2013-03-16 20:32:48
13 11 9
13 11 9
willabc
2013-03-16 20:32:48
9,11,13
9,11,13
Flamewire
2013-03-16 20:32:48
9, 11, 13
9, 11, 13
Knightone
2013-03-16 20:32:48
9,11,13
9,11,13
sparkles257
2013-03-16 20:32:48
9 and 11 and 13
9 and 11 and 13
lastenemytobeconquered
2013-03-16 20:32:48
9 11 and 13
9 11 and 13
lcamhie142857
2013-03-16 20:32:48
9, 11, 13
9, 11, 13
ws5188
2013-03-16 20:32:48
9, 11, 13
9, 11, 13
DPatrick
2013-03-16 20:33:04
1,2,3,4,5,6,7,8,10,12 are already divisors of $2^4 \cdot 3 \cdot 5 \cdot 7$, so the blocks will get distributed evenly to those numbers of students.
1,2,3,4,5,6,7,8,10,12 are already divisors of $2^4 \cdot 3 \cdot 5 \cdot 7$, so the blocks will get distributed evenly to those numbers of students.
DPatrick
2013-03-16 20:33:12
This just leaves 9,11,13. So we must have $x=9$, $y=11$, and $z=13$.
This just leaves 9,11,13. So we must have $x=9$, $y=11$, and $z=13$.
DPatrick
2013-03-16 20:33:27
In particular, we now know that $N$ is 3 more than a multiple of 9, and 3 more than a multiple of 11, and 3 more than a multiple of 13.
In particular, we now know that $N$ is 3 more than a multiple of 9, and 3 more than a multiple of 11, and 3 more than a multiple of 13.
mathworld1
2013-03-16 20:33:43
So N leaves a remainder of 3 when divided by 9,11,13
So N leaves a remainder of 3 when divided by 9,11,13
fmasroor
2013-03-16 20:33:43
and thus 3+(9*11*13)k
and thus 3+(9*11*13)k
DPatrick
2013-03-16 20:33:52
Right...but I've already used "k".
Right...but I've already used "k".
DPatrick
2013-03-16 20:34:03
We can write this as $N = 9 \cdot 11 \cdot 13 \cdot m + 3$, for some positive integer $m$.
We can write this as $N = 9 \cdot 11 \cdot 13 \cdot m + 3$, for some positive integer $m$.
DPatrick
2013-03-16 20:34:13
So now we have two equations for $N$:
\begin{align*}
N &= 2^4 \cdot 3 \cdot 5 \cdot 7 \cdot k, \\
N &= 9 \cdot 11 \cdot 13 \cdot m + 3,
\end{align*}
where $m$ and $k$ are some positive integers.
So now we have two equations for $N$:
\begin{align*}
N &= 2^4 \cdot 3 \cdot 5 \cdot 7 \cdot k, \\
N &= 9 \cdot 11 \cdot 13 \cdot m + 3,
\end{align*}
where $m$ and $k$ are some positive integers.
DPatrick
2013-03-16 20:34:23
How do we find the minimal such $N$?
How do we find the minimal such $N$?
billgates42
2013-03-16 20:34:41
factor out a 3!!!
factor out a 3!!!
andrewlin
2013-03-16 20:34:41
well we can divide by 3 on both sides
well we can divide by 3 on both sides
DPatrick
2013-03-16 20:34:47
Getting rid of the factor of 3 might help: let $N' = N/3$. (Both equations are multiples of 3.)
Getting rid of the factor of 3 might help: let $N' = N/3$. (Both equations are multiples of 3.)
DPatrick
2013-03-16 20:34:54
Now we have
$$
N' = 2^4 \cdot 5 \cdot 7 \cdot k = 3 \cdot 11 \cdot 13 \cdot m + 1.
$$
Now we have
$$
N' = 2^4 \cdot 5 \cdot 7 \cdot k = 3 \cdot 11 \cdot 13 \cdot m + 1.
$$
mprashker
2013-03-16 20:35:08
euclidean algorithm
euclidean algorithm
noobynoob
2013-03-16 20:35:08
Euclidean algorithm?
Euclidean algorithm?
DPatrick
2013-03-16 20:35:40
One very good idea at this point is to use the Euclidean Algorithm to solve this equation. You can use this algorithm to solve ax + by = 1 where a and b are relatively prime.
One very good idea at this point is to use the Euclidean Algorithm to solve this equation. You can use this algorithm to solve ax + by = 1 where a and b are relatively prime.
DPatrick
2013-03-16 20:35:49
In fact that's how I solved the problem the first time.
In fact that's how I solved the problem the first time.
DPatrick
2013-03-16 20:36:14
But I think I'll solve it using modular arithmetic right now, because it's a little less messy.
But I think I'll solve it using modular arithmetic right now, because it's a little less messy.
DPatrick
2013-03-16 20:36:40
We're trying to solve for k, so we can look at mod 3, mod 11, and mod 13 separately.
We're trying to solve for k, so we can look at mod 3, mod 11, and mod 13 separately.
DPatrick
2013-03-16 20:36:55
What do we get if we look at our equation mod 3?
What do we get if we look at our equation mod 3?
ssilwa
2013-03-16 20:37:32
k == 2 mod 3
k == 2 mod 3
SuperSnivy
2013-03-16 20:37:32
2k = 1 mod 3
2k = 1 mod 3
number.sense
2013-03-16 20:37:32
we get that the lhs = 1 mod 3
we get that the lhs = 1 mod 3
mathwizard888
2013-03-16 20:37:32
2^4*5*7*k==1 (mod 3)
2^4*5*7*k==1 (mod 3)
kdokmeci
2013-03-16 20:37:32
2k=1mod3
2k=1mod3
nikoma
2013-03-16 20:37:32
2^4*5*7*k = 1 (mod 3)
2^4*5*7*k = 1 (mod 3)
cerberus88
2013-03-16 20:37:32
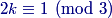
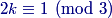
DPatrick
2013-03-16 20:37:39
We get
$$
2^4 \cdot 5 \cdot 7 \cdot k \equiv 1 \cdot 2 \cdot 1 \cdot k \equiv 2k \equiv 1 \pmod{3}.
$$
So $k \equiv 2 \pmod{3}$.
We get
$$
2^4 \cdot 5 \cdot 7 \cdot k \equiv 1 \cdot 2 \cdot 1 \cdot k \equiv 2k \equiv 1 \pmod{3}.
$$
So $k \equiv 2 \pmod{3}$.
DPatrick
2013-03-16 20:38:03
How about mod 11?
How about mod 11?
cerberus88
2013-03-16 20:38:36
SuperSnivy
2013-03-16 20:38:36
10k = 1 mod 11
10k = 1 mod 11
kdokmeci
2013-03-16 20:38:36
10k=1mod11, or -1k=1mod11
10k=1mod11, or -1k=1mod11
n1000
2013-03-16 20:38:36
10k=1(mod11)
10k=1(mod11)
DPatrick
2013-03-16 20:38:43
We get
$$
5 \cdot 5 \cdot 7 \cdot k \equiv 3 \cdot 7 \cdot k \equiv 10k \equiv 1 \pmod{11},
$$
We get
$$
5 \cdot 5 \cdot 7 \cdot k \equiv 3 \cdot 7 \cdot k \equiv 10k \equiv 1 \pmod{11},
$$
DPatrick
2013-03-16 20:39:16
And 10k is the same as -k mod 11, so we have that k = -1 mod 11.
And 10k is the same as -k mod 11, so we have that k = -1 mod 11.
DPatrick
2013-03-16 20:39:22
Before we go on to mod 13, what do you notice about the mod 3 and mod 11 results?
Before we go on to mod 13, what do you notice about the mod 3 and mod 11 results?
mathwizard888
2013-03-16 20:39:48
both -1
both -1
fmasroor
2013-03-16 20:39:48
both =-1 mod M
both =-1 mod M
mathworld1
2013-03-16 20:39:48
k = -1 of both mods
k = -1 of both mods
anwang16
2013-03-16 20:39:48
both -1
both -1
mathworld1
2013-03-16 20:39:48
so k = -1 mod 33
so k = -1 mod 33
DPatrick
2013-03-16 20:39:52
We note that $k \equiv -1 \pmod{3}$ and $k \equiv -1 \pmod{11}$, so $k \equiv -1 \pmod{33}$. That is, $k$ is one less than a multiple of 33.
We note that $k \equiv -1 \pmod{3}$ and $k \equiv -1 \pmod{11}$, so $k \equiv -1 \pmod{33}$. That is, $k$ is one less than a multiple of 33.
DPatrick
2013-03-16 20:40:22
How about mod 13?
How about mod 13?
goran
2013-03-16 20:40:40
k=1 mod 13
k=1 mod 13
Annabeth
2013-03-16 20:40:40
k=1 (mod 13)
k=1 (mod 13)
cerberus88
2013-03-16 20:40:40
cire_il
2013-03-16 20:40:40
k=1 mod 13
k=1 mod 13
flyrain
2013-03-16 20:40:40
k=1 mod 13
k=1 mod 13
DPatrick
2013-03-16 20:40:45
We get
$$
3 \cdot 5 \cdot 7 \cdot k \equiv 2 \cdot 7 \cdot k \equiv k \equiv 1 \pmod{13}.
$$
So $k \equiv 1 \pmod{13}$.
We get
$$
3 \cdot 5 \cdot 7 \cdot k \equiv 2 \cdot 7 \cdot k \equiv k \equiv 1 \pmod{13}.
$$
So $k \equiv 1 \pmod{13}$.
DPatrick
2013-03-16 20:40:56
So we've concluded that k is 1 more than a multiple of 13 but 1 less than a multiple of 33.
So we've concluded that k is 1 more than a multiple of 13 but 1 less than a multiple of 33.
DPatrick
2013-03-16 20:41:03
You could guess-and-check from here, but what's a systematic way to solve it?
You could guess-and-check from here, but what's a systematic way to solve it?
anthonyjang
2013-03-16 20:41:27
CRT?
CRT?
mathworld1
2013-03-16 20:41:27
chinese remainder thm!
chinese remainder thm!
nikoma
2013-03-16 20:41:27
Chinese remainder theorem
Chinese remainder theorem
mprashker
2013-03-16 20:41:27
chinese remainder theorem
chinese remainder theorem
Hydroxide
2013-03-16 20:41:27
CRT
CRT
pickten
2013-03-16 20:41:27
CRT
CRT
DPatrick
2013-03-16 20:41:31
What does that mean?
What does that mean?
DPatrick
2013-03-16 20:41:55
The Chinese Remainder Theorem says that there is a solution, but how do we find it?
The Chinese Remainder Theorem says that there is a solution, but how do we find it?
nsun48
2013-03-16 20:42:17
substitute 1+13a in for k, and use another one of the equations
substitute 1+13a in for k, and use another one of the equations
DPatrick
2013-03-16 20:42:36
That's a good idea. I like working with the bigger number though (but it doesn't matter much).
That's a good idea. I like working with the bigger number though (but it doesn't matter much).
DPatrick
2013-03-16 20:42:46
In other words, we can let $k = 33c - 1$ for some positive integer $c$. Then we have
$$
33c - 1 \equiv 1 \pmod{13},
$$
which reduces to $7c \equiv 2 \pmod{13}$.
In other words, we can let $k = 33c - 1$ for some positive integer $c$. Then we have
$$
33c - 1 \equiv 1 \pmod{13},
$$
which reduces to $7c \equiv 2 \pmod{13}$.
Hydroxide
2013-03-16 20:43:20
so c=4 (mod 13)
so c=4 (mod 13)
anwang16
2013-03-16 20:43:20
c==4
c==4
ws5188
2013-03-16 20:43:20
c==4(mod 13)
c==4(mod 13)
DPatrick
2013-03-16 20:43:24
Now multiplying by 2 gives $14c \equiv c \equiv 4 \pmod{13}$.
Now multiplying by 2 gives $14c \equiv c \equiv 4 \pmod{13}$.
DPatrick
2013-03-16 20:43:38
Now we just unravel everything we've done...
Now we just unravel everything we've done...
DPatrick
2013-03-16 20:43:48
We have $c = 4$ and $k = 4(33)-1 = 131$ is the smallest positive solution.
We have $c = 4$ and $k = 4(33)-1 = 131$ is the smallest positive solution.
kdokmeci
2013-03-16 20:44:06
131 is prime
131 is prime
DPatrick
2013-03-16 20:44:12
And indeed 131 is prime.
And indeed 131 is prime.
DPatrick
2013-03-16 20:44:16
Thus $N = 2^4 \cdot 3 \cdot 5 \cdot 7 \cdot 131$.
Thus $N = 2^4 \cdot 3 \cdot 5 \cdot 7 \cdot 131$.
lucylai
2013-03-16 20:44:39
2+3+5+7+131=148, so 148 is the answer
2+3+5+7+131=148, so 148 is the answer
mathwizard888
2013-03-16 20:44:39
c=4 gives k=131, and 131 is prime, so 2+3+5+7+131=148 answer
c=4 gives k=131, and 131 is prime, so 2+3+5+7+131=148 answer
kdokmeci
2013-03-16 20:44:39
2+3+5+7+131=148
2+3+5+7+131=148
cerberus88
2013-03-16 20:44:39
2+3+5+7+131=148'
2+3+5+7+131=148'
viker
2013-03-16 20:44:39
$ 2+3+5+7+131 =\boxed{148} $
$ 2+3+5+7+131 =\boxed{148} $
akalykid012
2013-03-16 20:44:39
2+3+5+7+131= 148
2+3+5+7+131= 148
wjq8g6
2013-03-16 20:44:39
131 + 2 + 3 + 5 + 7 = 148
131 + 2 + 3 + 5 + 7 = 148
DPatrick
2013-03-16 20:44:50
And the sum of the distinct primes of $N$ is $2+3+5+7+131 = \boxed{148}$.
And the sum of the distinct primes of $N$ is $2+3+5+7+131 = \boxed{148}$.
jasonmathcounts
2013-03-16 20:45:16
I thought this problem was kind of unfair because part B in the question doesn't specifically rule out x=1 . If there was one student present then the blocks could technically be distributed equally (the one student gets total number - 3 blocks). If you do that you'll get 17 (like me and a lot of other people did).
I thought this problem was kind of unfair because part B in the question doesn't specifically rule out x=1 . If there was one student present then the blocks could technically be distributed equally (the one student gets total number - 3 blocks). If you do that you'll get 17 (like me and a lot of other people did).
DPatrick
2013-03-16 20:45:27
I do not agree with this interpretation, but if you feel strongly about it, you should write to the AMC.
I do not agree with this interpretation, but if you feel strongly about it, you should write to the AMC.
DPatrick
2013-03-16 20:45:42
DPatrick
2013-03-16 20:46:02
Before I try to draw the picture, which is the point on side RP: is it E or F?
Before I try to draw the picture, which is the point on side RP: is it E or F?
SuperSnivy
2013-03-16 20:46:28
F
F
AayushGupta
2013-03-16 20:46:28
F
F
distortedwalrus
2013-03-16 20:46:28
F
F
sindennisz
2013-03-16 20:46:28
F
F
jeff10
2013-03-16 20:46:28
F
F
DPatrick
2013-03-16 20:46:32
Well, to be honest, I couldn't tell until I drew both pictures and looked at the angles. If you try to put E on side RP, you get too much angle at point E (you can draw it and see for yourself). It is point F that is on RP.
Well, to be honest, I couldn't tell until I drew both pictures and looked at the angles. If you try to put E on side RP, you get too much angle at point E (you can draw it and see for yourself). It is point F that is on RP.
DPatrick
2013-03-16 20:46:53
So the picture looks something like this:
So the picture looks something like this:
DPatrick
2013-03-16 20:46:58
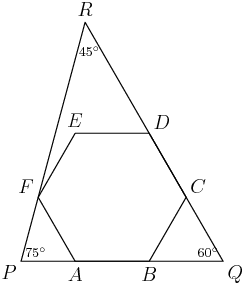
DPatrick
2013-03-16 20:47:08
All the side lengths of the hexagon are 1. Any other lengths we know?
All the side lengths of the hexagon are 1. Any other lengths we know?
lucylai
2013-03-16 20:47:32
CB=CQ=BQ=1
CB=CQ=BQ=1
superpi83
2013-03-16 20:47:32
CBQ is equilateral with side length 1
CBQ is equilateral with side length 1
billgates42
2013-03-16 20:47:32
BQ=1
BQ=1
cerberus88
2013-03-16 20:47:32
CQ and BQ are also 1
CQ and BQ are also 1
Hydroxide
2013-03-16 20:47:32
BQ=CQ=1
BQ=CQ=1
AceOfDiamonds
2013-03-16 20:47:32
BQ, CQ
BQ, CQ
Polynomial
2013-03-16 20:47:32
BQ and CQ
BQ and CQ
OCed
2013-03-16 20:47:32
BC=CQ=QB=1
BC=CQ=QB=1
DPatrick
2013-03-16 20:47:37
CBQ is equilateral, so $CQ = BQ = 1$ too.
CBQ is equilateral, so $CQ = BQ = 1$ too.
DPatrick
2013-03-16 20:48:24
Any other length in this picture that we can quickly figure out?
Any other length in this picture that we can quickly figure out?
DPatrick
2013-03-16 20:48:54
We can do a lot with the Law of Sines, but there's a simpler (in my opinion) non-trig solution.
We can do a lot with the Law of Sines, but there's a simpler (in my opinion) non-trig solution.
davidkim2106
2013-03-16 20:49:03
RD=RQ-2
RD=RQ-2
QuantumandMath
2013-03-16 20:49:08
rd?
rd?
DPatrick
2013-03-16 20:49:23
We actually also know $RD$ too! We just need to draw in $DF:$
We actually also know $RD$ too! We just need to draw in $DF:$
DPatrick
2013-03-16 20:49:30
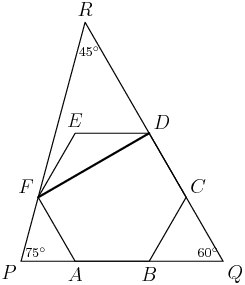
Flamewire
2013-03-16 20:49:51
Then we get a 45-45-90 triangle
Then we get a 45-45-90 triangle
Piya31415
2013-03-16 20:49:51
45 45 90 triangle!
45 45 90 triangle!
mathworld1
2013-03-16 20:49:51
45-45-90
45-45-90
DPatrick
2013-03-16 20:50:02
Right! DEF is 120-30-30. So angle RDF is 60+30 = 90 degrees, a right angle!
Right! DEF is 120-30-30. So angle RDF is 60+30 = 90 degrees, a right angle!
cerberus88
2013-03-16 20:50:18
so RD=FD=sqrt(3)
so RD=FD=sqrt(3)
DPatrick
2013-03-16 20:50:24
So RDF is an isosceles right triangle, and hence $RD = DF = \sqrt3$.
So RDF is an isosceles right triangle, and hence $RD = DF = \sqrt3$.
DPatrick
2013-03-16 20:50:36
We're actually almost done: how do we finish?
We're actually almost done: how do we finish?
kdokmeci
2013-03-16 20:50:52
Make ALTITUDE to RQ
Make ALTITUDE to RQ
DPatrick
2013-03-16 20:51:14
Yes! We want the area, and side $RQ = 2 + \sqrt3$, so if we can compute the length of the altitude from $P$ to $RQ$, we'll be done.
Yes! We want the area, and side $RQ = 2 + \sqrt3$, so if we can compute the length of the altitude from $P$ to $RQ$, we'll be done.
noobynoob
2013-03-16 20:51:26
30-60-90 and 45-45-90
30-60-90 and 45-45-90
mdlu
2013-03-16 20:51:26
altitude forms a 30-60-90 and a 45-45-90
altitude forms a 30-60-90 and a 45-45-90
DPatrick
2013-03-16 20:51:36
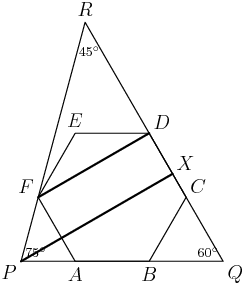
DPatrick
2013-03-16 20:51:50
Oh, now we're in great shape! PXR is 45-45-90 and PXQ is 30-60-90!
Oh, now we're in great shape! PXR is 45-45-90 and PXQ is 30-60-90!
DPatrick
2013-03-16 20:52:16
Let's call $PX = h$. What do we know about $RX$ and $XQ$?
Let's call $PX = h$. What do we know about $RX$ and $XQ$?
csmath
2013-03-16 20:52:39
They sum to 2 +sqrt 3
They sum to 2 +sqrt 3
cjquines0
2013-03-16 20:52:39
RX + XQ = 2 + sqrt(3)
RX + XQ = 2 + sqrt(3)
VietaFan
2013-03-16 20:52:39
RX+XQ = 2+sqrt3
RX+XQ = 2+sqrt3
mondi
2013-03-16 20:52:42
RX=h
RX=h
anthonyjang
2013-03-16 20:52:46
RX=h, XQ=h/\sqrt{3}
RX=h, XQ=h/\sqrt{3}
DPatrick
2013-03-16 20:52:53
Right, and that's all the data we need!
Right, and that's all the data we need!
DPatrick
2013-03-16 20:52:58
$PXR$ is an isosceles right triangle angle, so $RX = PX = h$.
$PXR$ is an isosceles right triangle angle, so $RX = PX = h$.
DPatrick
2013-03-16 20:53:17
...(I meant to say "right triangle *again*" above)...
...(I meant to say "right triangle *again*" above)...
DPatrick
2013-03-16 20:53:27
And...$PXQ$ is 30-60-90! So $XQ = \frac{h}{\sqrt3}$.
And...$PXQ$ is 30-60-90! So $XQ = \frac{h}{\sqrt3}$.
DPatrick
2013-03-16 20:53:37
Thus, since $RX + XQ = RQ$, we have
$$
h + \frac{h}{\sqrt3} = 2 + \sqrt3.
$$
Thus, since $RX + XQ = RQ$, we have
$$
h + \frac{h}{\sqrt3} = 2 + \sqrt3.
$$
VietaFan
2013-03-16 20:53:43
just algebra now
just algebra now
Flamewire
2013-03-16 20:53:52
h
h
viker
2013-03-16 20:53:52
solve for h
solve for h
DPatrick
2013-03-16 20:54:00
Indeed, this solves to gives us
$$
h = \frac{2+\sqrt3}{1+\frac{1}{\sqrt3}}.
$$
Indeed, this solves to gives us
$$
h = \frac{2+\sqrt3}{1+\frac{1}{\sqrt3}}.
$$
DPatrick
2013-03-16 20:54:14
We can multiply numerator and denominator by $\sqrt3$ to get the slightly nicer
$$
h = \frac{3 + 2\sqrt3}{1 + \sqrt3}.
$$
We can multiply numerator and denominator by $\sqrt3$ to get the slightly nicer
$$
h = \frac{3 + 2\sqrt3}{1 + \sqrt3}.
$$
VietaFan
2013-03-16 20:54:35
rationalize denominator
rationalize denominator
Flamewire
2013-03-16 20:54:35
multiply top and bottom by 1 - sqrt3
multiply top and bottom by 1 - sqrt3
n1000
2013-03-16 20:54:35
multiply top and bottom by 1-sqrt(3)
multiply top and bottom by 1-sqrt(3)
DPatrick
2013-03-16 20:54:55
We could do that now, but let's write the expression for the area of the triangle first. (Doesn't really matter.)
We could do that now, but let's write the expression for the area of the triangle first. (Doesn't really matter.)
DPatrick
2013-03-16 20:55:05
Our desired area is
$$
\frac12h(RQ) = \frac{(3+2\sqrt3)(2+\sqrt3)}{2(1+\sqrt3)}.
$$
Our desired area is
$$
\frac12h(RQ) = \frac{(3+2\sqrt3)(2+\sqrt3)}{2(1+\sqrt3)}.
$$
DPatrick
2013-03-16 20:55:27
I'll brush through the algebra: this cleans up a bit to
$$
\frac{12 + 7\sqrt3}{2 + 2\sqrt3},
$$
and we can rationalize the denominator by multiplying by $2\sqrt3 - 2$:
$$
\frac{(12+7\sqrt3)(2\sqrt3-2)}{12-4} = \frac{18 + 10\sqrt3}{8} = \frac{9 + 5\sqrt3}{4}.
$$
I'll brush through the algebra: this cleans up a bit to
$$
\frac{12 + 7\sqrt3}{2 + 2\sqrt3},
$$
and we can rationalize the denominator by multiplying by $2\sqrt3 - 2$:
$$
\frac{(12+7\sqrt3)(2\sqrt3-2)}{12-4} = \frac{18 + 10\sqrt3}{8} = \frac{9 + 5\sqrt3}{4}.
$$
cerberus88
2013-03-16 20:55:55
so the answer is 021
so the answer is 021
mathworld1
2013-03-16 20:55:55
a+b+c+d=021
a+b+c+d=021
kdokmeci
2013-03-16 20:55:55
Now our answer is 9+5+3+4=21
Now our answer is 9+5+3+4=21
flyrain
2013-03-16 20:55:55
021
021
mssmath
2013-03-16 20:55:55
or 021
or 021
DPatrick
2013-03-16 20:56:00
This is in the proper format, so the answer is $9+5+3+4 = \boxed{021}$.
This is in the proper format, so the answer is $9+5+3+4 = \boxed{021}$.
DPatrick
2013-03-16 20:56:27
DPatrick
2013-03-16 20:56:40
Yikes. So many subscripts.
Yikes. So many subscripts.
DPatrick
2013-03-16 20:56:51
Let's try to draw a picture. Note that the angle at B is obtuse. I'll also use colors to label the angles that are equal (via the similar triangles):
Let's try to draw a picture. Note that the angle at B is obtuse. I'll also use colors to label the angles that are equal (via the similar triangles):
DPatrick
2013-03-16 20:57:01
DPatrick
2013-03-16 20:57:20
I shaded $B_0C_1B_1$, because that's what we want to try to keep track of the area of.
I shaded $B_0C_1B_1$, because that's what we want to try to keep track of the area of.
DPatrick
2013-03-16 20:57:31
There are of course many many more triangles, but let's start with this picture.
There are of course many many more triangles, but let's start with this picture.
DPatrick
2013-03-16 20:57:48
What length can we try to compute?
What length can we try to compute?
thecmd999
2013-03-16 20:58:23
C_0C_1
C_0C_1
mdlu
2013-03-16 20:58:23
c1-b0 or c1-c0
c1-b0 or c1-c0
DPatrick
2013-03-16 20:59:17
$C_0C_1$ is common to the two similar triangles $B_0C_1C_0$ and $AB_0C_0$, so let's set $x = C_0C_1$ and try to compute it.
$C_0C_1$ is common to the two similar triangles $B_0C_1C_0$ and $AB_0C_0$, so let's set $x = C_0C_1$ and try to compute it.
DPatrick
2013-03-16 20:59:23
mathwizard888
2013-03-16 20:59:47
x/17=17/25
x/17=17/25
superpi83
2013-03-16 20:59:47
17/25=x/17 --> x=289/25
17/25=x/17 --> x=289/25
DPatrick
2013-03-16 20:59:56
We get that the ratio of the sides opposite red angles equals the ratio of sides opposite blue angles, or
$$
\frac{x}{17} = \frac{17}{25}.
$$
We get that the ratio of the sides opposite red angles equals the ratio of sides opposite blue angles, or
$$
\frac{x}{17} = \frac{17}{25}.
$$
DPatrick
2013-03-16 21:00:17
So $x = \frac{289}{25}$.
So $x = \frac{289}{25}$.
DPatrick
2013-03-16 21:00:30
Well, that's a bit of data, but how does it help?
Well, that's a bit of data, but how does it help?
goran
2013-03-16 21:00:45
We can find AC_{1}
We can find AC_{1}
mondi
2013-03-16 21:00:45
so now we know AC1
so now we know AC1
cerberus88
2013-03-16 21:00:59
then we can find AC_1 and then use similar triangles to find B_1C_1
then we can find AC_1 and then use similar triangles to find B_1C_1
viker
2013-03-16 21:01:08
we can find $ AC_! $
we can find $ AC_! $
jigglypuff
2013-03-16 21:01:08
find a c1
find a c1
DPatrick
2013-03-16 21:01:29
These are probably all good ideas, but before we get bogged in too many computations, what's the general strategy here?
These are probably all good ideas, but before we get bogged in too many computations, what's the general strategy here?
DPatrick
2013-03-16 21:01:42
Maybe we should draw some more shaded triangles to get an idea of the big picture:
Maybe we should draw some more shaded triangles to get an idea of the big picture:
DPatrick
2013-03-16 21:01:49
DPatrick
2013-03-16 21:01:55
Notice anything helpful?
Notice anything helpful?
flyrain
2013-03-16 21:02:27
all the shadeds are similar
all the shadeds are similar
Math99
2013-03-16 21:02:27
similar triangles
similar triangles
Math_Kirby
2013-03-16 21:02:27
infinite geometric series and sim. triangles
infinite geometric series and sim. triangles
VietaFan
2013-03-16 21:02:27
infinite geometric series of triangles
infinite geometric series of triangles
fz0718
2013-03-16 21:02:27
they're summing to a geometric series
they're summing to a geometric series
calculatorwiz
2013-03-16 21:02:27
they're all similar to each other
they're all similar to each other
lucylai
2013-03-16 21:02:27
the areas form geometric sequence
the areas form geometric sequence
DPatrick
2013-03-16 21:02:50
There's a lot of similarity, and it suggested that the areas of the shaded triangles will be a geometric series.
There's a lot of similarity, and it suggested that the areas of the shaded triangles will be a geometric series.
DPatrick
2013-03-16 21:03:00
But there's another clever idea that I like...
But there's another clever idea that I like...
superpi83
2013-03-16 21:03:09
The fraction of grey in AB1C1 is, by similarity, the same as the fraction of grey in AB0C0, and therefore also equal to the fraction of grey in B0B1C1C0. So, we can find the total grey area by finding the fraction of grey in B0B1C1C0 and multiplying by the area of triangle AB0C0.
The fraction of grey in AB1C1 is, by similarity, the same as the fraction of grey in AB0C0, and therefore also equal to the fraction of grey in B0B1C1C0. So, we can find the total grey area by finding the fraction of grey in B0B1C1C0 and multiplying by the area of triangle AB0C0.
DPatrick
2013-03-16 21:03:40
That's a great idea (and I should also credit by AoPS colleague Palmer Mebane for suggesting this idea to me too).
That's a great idea (and I should also credit by AoPS colleague Palmer Mebane for suggesting this idea to me too).
DPatrick
2013-03-16 21:03:51
Let me try to explain what this means in the picture.
Let me try to explain what this means in the picture.
DPatrick
2013-03-16 21:04:10
Let's break up the picture into quadrilaterals:
Let's break up the picture into quadrilaterals:
DPatrick
2013-03-16 21:04:15
DPatrick
2013-03-16 21:04:42
Notice that the ratio of (shaded area) : (total area) within each quadrilateral is the same, by the similarity.
Notice that the ratio of (shaded area) : (total area) within each quadrilateral is the same, by the similarity.
DPatrick
2013-03-16 21:05:16
So if we can compute that ratio just for the first quadrilateral, that's all we need! We then just take that ratio times the total are of $AB_0C_0$ to get our answer.
So if we can compute that ratio just for the first quadrilateral, that's all we need! We then just take that ratio times the total are of $AB_0C_0$ to get our answer.
DPatrick
2013-03-16 21:05:43
So we don't need to bother with a geometric series: we just do it once for the first quadrilateral.
So we don't need to bother with a geometric series: we just do it once for the first quadrilateral.
DPatrick
2013-03-16 21:05:55
In other words, we want the ratio of shaded area to the total area in the brown-bordered quadrilateral below:
In other words, we want the ratio of shaded area to the total area in the brown-bordered quadrilateral below:
DPatrick
2013-03-16 21:05:59
DPatrick
2013-03-16 21:06:11
Multiplying this ratio by the total area of $AB_0C_0$ will give us the total shaded area of all the little triangles, and hence our answer.
Multiplying this ratio by the total area of $AB_0C_0$ will give us the total shaded area of all the little triangles, and hence our answer.
DPatrick
2013-03-16 21:06:36
(This might get a little clearer as we go. Or you may need to come back and think about it more later.)
(This might get a little clearer as we go. Or you may need to come back and think about it more later.)
DPatrick
2013-03-16 21:06:43
So how do we compute this ratio?
So how do we compute this ratio?
billgates42
2013-03-16 21:07:03
Ratio of C1B1 to 17
Ratio of C1B1 to 17
QuantumandMath
2013-03-16 21:07:03
find C1B1
find C1B1
pickten
2013-03-16 21:07:10
fractions of the entire area?
fractions of the entire area?
DPatrick
2013-03-16 21:07:21
I like this last idea. Note that our original triangle has three pieces:
I like this last idea. Note that our original triangle has three pieces:
DPatrick
2013-03-16 21:07:26
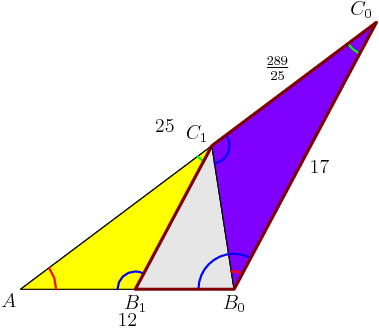
DPatrick
2013-03-16 21:07:56
We want the ratio of (gray) / (gray + purple). Rather than compute the actual areas, we can find out the fraction that each piece makes up of the whole.
We want the ratio of (gray) / (gray + purple). Rather than compute the actual areas, we can find out the fraction that each piece makes up of the whole.
DPatrick
2013-03-16 21:08:04
What fraction of the total triangle's area is the purple piece?
What fraction of the total triangle's area is the purple piece?
cire_il
2013-03-16 21:08:35
289/625
289/625
mathcool2009
2013-03-16 21:08:35
289/625
289/625
cerberus88
2013-03-16 21:08:35
289/25
289/25
wjq8g6
2013-03-16 21:08:35
17/25 ^2
17/25 ^2
dandedude
2013-03-16 21:08:35
289/625?
289/625?
superpi83
2013-03-16 21:08:35
(17/25)^2
(17/25)^2
distortedwalrus
2013-03-16 21:08:35
289/625
289/625
DPatrick
2013-03-16 21:09:01
This is not so bad, because the purple triangle is similar to the entire large triangle. The ratio of similarity is $\frac{B_0C_0}{AC_0} = \frac{17}{25}$, so it is $\left(\frac{17}{25}\right)^2$ of the total triangle's area.
This is not so bad, because the purple triangle is similar to the entire large triangle. The ratio of similarity is $\frac{B_0C_0}{AC_0} = \frac{17}{25}$, so it is $\left(\frac{17}{25}\right)^2$ of the total triangle's area.
DPatrick
2013-03-16 21:09:23
The gray one is hard to get at directly, but the yellow one is also similar to the whole.
The gray one is hard to get at directly, but the yellow one is also similar to the whole.
DPatrick
2013-03-16 21:09:27
What fraction of the total triangle's area is the yellow piece?
What fraction of the total triangle's area is the yellow piece?
wjq8g6
2013-03-16 21:09:57
(25 - 289/25)/ 25 squared
(25 - 289/25)/ 25 squared
DPatrick
2013-03-16 21:10:06
Unfortunately, yeah.
Unfortunately, yeah.
DPatrick
2013-03-16 21:10:11
The ratio of similarity is a little more complicated. It's:
$$
\frac{AC_1}{AC_0} = \frac{25-\frac{289}{25}}{25} = \frac{625 - 289}{625} = \frac{336}{625}.
$$
So it is $\left(\frac{336}{625}\right)^2$ of the total area.
The ratio of similarity is a little more complicated. It's:
$$
\frac{AC_1}{AC_0} = \frac{25-\frac{289}{25}}{25} = \frac{625 - 289}{625} = \frac{336}{625}.
$$
So it is $\left(\frac{336}{625}\right)^2$ of the total area.
dandedude
2013-03-16 21:10:24
ouch
ouch
fmasroor
2013-03-16 21:10:24
eww
eww
DPatrick
2013-03-16 21:10:28
This is getting complicated. What can we do to make it simpler?
This is getting complicated. What can we do to make it simpler?
lcamhie142857
2013-03-16 21:10:47
don't calculate anything out until the end
don't calculate anything out until the end
DPatrick
2013-03-16 21:11:04
And what's a really good way to avoid the temptation of calculating anything?
And what's a really good way to avoid the temptation of calculating anything?
jameswangisb
2013-03-16 21:11:09
give it a varible?
give it a varible?
zqjx
2013-03-16 21:11:16
use variables
use variables
gengkev
2013-03-16 21:11:16
assign vars!
assign vars!
AayushGupta
2013-03-16 21:11:16
variables!
variables!
DPatrick
2013-03-16 21:11:19
The quantity 17/25 comes up a lot so let's give it a name. Let's call it r.
The quantity 17/25 comes up a lot so let's give it a name. Let's call it r.
DPatrick
2013-03-16 21:11:33
So now the purple piece is $r^2$ of the total area, and the yellow piece is what in terms of $r$?
So now the purple piece is $r^2$ of the total area, and the yellow piece is what in terms of $r$?
VietaFan
2013-03-16 21:12:10
$\frac{25-17r}{25}$
$\frac{25-17r}{25}$
DPatrick
2013-03-16 21:12:26
That's the ratio of the lengths, so we'll have to square that to get the fraction of the area.
That's the ratio of the lengths, so we'll have to square that to get the fraction of the area.
superpi83
2013-03-16 21:12:37
(1-r^2)^2
(1-r^2)^2
DPatrick
2013-03-16 21:12:57
Indeed, let's write it out:
$$
\frac{AC_1}{AC_0} = \frac{25 - 17r}{25} = 1 - \frac{17}{25}r = 1-r^2,
$$
so the yellow piece's area is $(1-r^2)^2$ of the total area.
Indeed, let's write it out:
$$
\frac{AC_1}{AC_0} = \frac{25 - 17r}{25} = 1 - \frac{17}{25}r = 1-r^2,
$$
so the yellow piece's area is $(1-r^2)^2$ of the total area.
DPatrick
2013-03-16 21:13:17
And thus the gray area is what's left, which is $1 - r^2 - (1-r^2)^2$.
And thus the gray area is what's left, which is $1 - r^2 - (1-r^2)^2$.
DPatrick
2013-03-16 21:13:39
So the ratio that we wanted is:
$$
\frac{\text{gray}}{\text{gray} + \text{purple}} = \frac{1-r^2-(1-r^2)^2}{1-(1-r^2)^2}.
$$
So the ratio that we wanted is:
$$
\frac{\text{gray}}{\text{gray} + \text{purple}} = \frac{1-r^2-(1-r^2)^2}{1-(1-r^2)^2}.
$$
DPatrick
2013-03-16 21:14:13
So we just compute this ratio, and multiply it by the area of the original triangle, and we've got our total area that we want!
So we just compute this ratio, and multiply it by the area of the original triangle, and we've got our total area that we want!
DPatrick
2013-03-16 21:14:33
By the way, what is the area of the original triangle?
By the way, what is the area of the original triangle?
DVA6102
2013-03-16 21:15:06
By Heron, the area of the original is 90.
By Heron, the area of the original is 90.
davidkim2106
2013-03-16 21:15:06
herons
herons
mondi
2013-03-16 21:15:06
herons formula
herons formula
cerberus88
2013-03-16 21:15:06
90
90
lucylai
2013-03-16 21:15:06
90 by Heron's formula
90 by Heron's formula
bestwillcui1
2013-03-16 21:15:06
use herons
use herons
DPatrick
2013-03-16 21:15:11
One option is to use Heron's Formula, noting that the semiperimeter is (12+17+25)/2 = 27:
$$
[AB_0C_0] = \sqrt{27(27-12)(27-17)(27-25)}.
$$
One option is to use Heron's Formula, noting that the semiperimeter is (12+17+25)/2 = 27:
$$
[AB_0C_0] = \sqrt{27(27-12)(27-17)(27-25)}.
$$
DPatrick
2013-03-16 21:15:20
This simplifies to
$$
\sqrt{27 \cdot 15 \cdot 10 \cdot 2} = \sqrt{2^2 \cdot 3^4 \cdot 5^2} = 2 \cdot 9 \cdot 5 = 90.
$$
This simplifies to
$$
\sqrt{27 \cdot 15 \cdot 10 \cdot 2} = \sqrt{2^2 \cdot 3^4 \cdot 5^2} = 2 \cdot 9 \cdot 5 = 90.
$$
DPatrick
2013-03-16 21:15:41
Or, you might notice that the triangle sits as the difference of two nice right triangles:
Or, you might notice that the triangle sits as the difference of two nice right triangles:
ryanyoo
2013-03-16 21:15:46
or you could think of it as a 15-20-25 triangle minus a 8-15-17 one
or you could think of it as a 15-20-25 triangle minus a 8-15-17 one
mdlu
2013-03-16 21:15:46
we can see that fitting in an 8-15-17 on the right hand side works
we can see that fitting in an 8-15-17 on the right hand side works
DPatrick
2013-03-16 21:15:51
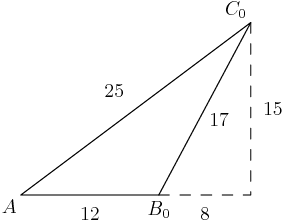
DPatrick
2013-03-16 21:16:12
So $AB_0C_0$ is the difference between a 15-20-15 right triangle and a 8-15-17 right triangle, and its area is thus the difference of areas: 150 - 60 = 90.
So $AB_0C_0$ is the difference between a 15-20-15 right triangle and a 8-15-17 right triangle, and its area is thus the difference of areas: 150 - 60 = 90.
davidkim2106
2013-03-16 21:16:29
multiply the ratio with 90
multiply the ratio with 90
DPatrick
2013-03-16 21:16:47
Thus the area of all the shaded triangles is $$
\frac{90(1-r^2-(1-r^2)^2)}{1-(1-r^2)^2},
$$
where $r = \frac{17}{25}$.
Thus the area of all the shaded triangles is $$
\frac{90(1-r^2-(1-r^2)^2)}{1-(1-r^2)^2},
$$
where $r = \frac{17}{25}$.
pedronr
2013-03-16 21:16:58
then do all of the calculation
then do all of the calculation
jigglypuff
2013-03-16 21:17:09
simplify
simplify
DPatrick
2013-03-16 21:17:21
It simplifies quite a bit:
$$
\frac{90(1-r^2-(1-2r^2+r^4))}{1-(1-2r^2+r^4)} = \frac{90(r^2-r^4)}{2r^2-r^4} = \frac{90(1-r^2)}{2-r^2}.
$$
It simplifies quite a bit:
$$
\frac{90(1-r^2-(1-2r^2+r^4))}{1-(1-2r^2+r^4)} = \frac{90(r^2-r^4)}{2r^2-r^4} = \frac{90(1-r^2)}{2-r^2}.
$$
DPatrick
2013-03-16 21:17:36
(Using r instead of 17/25 was a very good idea!)
(Using r instead of 17/25 was a very good idea!)
DPatrick
2013-03-16 21:17:49
But now we don't have much choice but to plug r back in.
But now we don't have much choice but to plug r back in.
DPatrick
2013-03-16 21:17:59
We plug $r = \frac{17}{25}$ in, and multiply numerator and denominator by $25^2$ to clear fractions:
$$
\frac{90(25^2 - 17^2)}{2 \cdot 25^2 - 17^2}.
$$
We plug $r = \frac{17}{25}$ in, and multiply numerator and denominator by $25^2$ to clear fractions:
$$
\frac{90(25^2 - 17^2)}{2 \cdot 25^2 - 17^2}.
$$
DPatrick
2013-03-16 21:18:13
This is $\dfrac{90 \cdot 336}{961}$.
This is $\dfrac{90 \cdot 336}{961}$.
viker
2013-03-16 21:18:40
superpi83
2013-03-16 21:18:40
therefore 961
therefore 961
kdokmeci
2013-03-16 21:18:40
Answer;961
Answer;961
mathmaster2012
2013-03-16 21:18:40
so 961
so 961
fmasroor
2013-03-16 21:18:40
961
961
kdokmeci
2013-03-16 21:18:40
961
961
DPatrick
2013-03-16 21:18:45
Since 961 doesn't have any factors in common with the numerator, and we only want the denominator as our final answer, we're done. The final answer is $\boxed{961}$.
Since 961 doesn't have any factors in common with the numerator, and we only want the denominator as our final answer, we're done. The final answer is $\boxed{961}$.
distortedwalrus
2013-03-16 21:19:12
so it's 31^2...coincidence that it's a perfect square?
so it's 31^2...coincidence that it's a perfect square?
DPatrick
2013-03-16 21:19:19
I think so, but I'm not sure...
I think so, but I'm not sure...
DPatrick
2013-03-16 21:19:37
I thought #13 was the hardest and the least elegant problem on the contest. #14 and #15 are much prettier!
I thought #13 was the hardest and the least elegant problem on the contest. #14 and #15 are much prettier!
DPatrick
2013-03-16 21:19:46
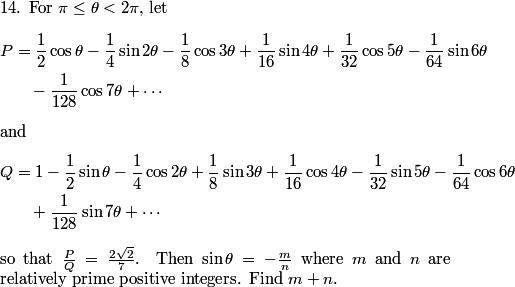
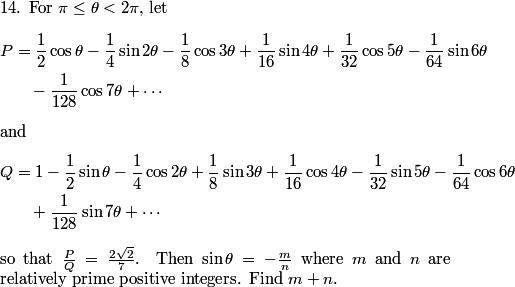
Sun7777
2013-03-16 21:20:05
that looks complex
that looks complex
DPatrick
2013-03-16 21:20:10
...in more than one way.
...in more than one way.
DPatrick
2013-03-16 21:20:21
There are a lot of clues here for what to try...
There are a lot of clues here for what to try...
DPatrick
2013-03-16 21:20:25
...trig functions...
...trig functions...
DPatrick
2013-03-16 21:20:35
...alternating signs...in particular in cycles of 4...
...alternating signs...in particular in cycles of 4...
DPatrick
2013-03-16 21:20:40
...powers...
...powers...
mathmaster2012
2013-03-16 21:21:06
thecmd999
2013-03-16 21:21:06
complex number BASH
complex number BASH
kdokmeci
2013-03-16 21:21:06
complex numbers!
complex numbers!
lucylai
2013-03-16 21:21:06
complex numbers
complex numbers
vlchen888
2013-03-16 21:21:06
i
i
lcamhie142857
2013-03-16 21:21:06
Demoivre's?
Demoivre's?
lucylai
2013-03-16 21:21:06
complex numbers with demoivre's
complex numbers with demoivre's
danielguo94
2013-03-16 21:21:06
de moivre's
de moivre's
DPatrick
2013-03-16 21:21:16
Right. We want to convert the trig functions to something that works nicely with powers.
Right. We want to convert the trig functions to something that works nicely with powers.
DPatrick
2013-03-16 21:21:31
This (plus the other clues) strongly suggest trying to use complex exponentials (or deMoivre's Theorem if you prefer) in some way.
This (plus the other clues) strongly suggest trying to use complex exponentials (or deMoivre's Theorem if you prefer) in some way.
DPatrick
2013-03-16 21:21:49
In particular, we might want to try looking at some combination of $P \pm iQ$ or $Q \pm iP$ and seeing which one works.
In particular, we might want to try looking at some combination of $P \pm iQ$ or $Q \pm iP$ and seeing which one works.
DPatrick
2013-03-16 21:22:11
You have to experiment a little bit to see exactly what combination works.
You have to experiment a little bit to see exactly what combination works.
QuantumandMath
2013-03-16 21:22:22
Q+I*p
Q+I*p
DPatrick
2013-03-16 21:22:31
A little experimentation will lead you to look at $Q + iP$:
A little experimentation will lead you to look at $Q + iP$:
DPatrick
2013-03-16 21:22:38
\begin{align*}
Q + iP &= 1 \\
&+ \frac12(-\sin\theta + i\cos\theta) \\
&+ \frac14(-\cos 2\theta - i\sin 2\theta) \\
&+ \frac18(\sin 3\theta -i\cos 3\theta) \\
&+ \frac{1}{16}(\cos 4\theta + i\sin 4\theta) \\
&+ \frac{1}{32}(-\sin 5\theta + i\cos 5\theta) \\
&+ \cdots.
\end{align*}
\begin{align*}
Q + iP &= 1 \\
&+ \frac12(-\sin\theta + i\cos\theta) \\
&+ \frac14(-\cos 2\theta - i\sin 2\theta) \\
&+ \frac18(\sin 3\theta -i\cos 3\theta) \\
&+ \frac{1}{16}(\cos 4\theta + i\sin 4\theta) \\
&+ \frac{1}{32}(-\sin 5\theta + i\cos 5\theta) \\
&+ \cdots.
\end{align*}
DPatrick
2013-03-16 21:22:46
Notice the nice pattern?
Notice the nice pattern?
QuantumandMath
2013-03-16 21:23:18
geometric powers
geometric powers
viker
2013-03-16 21:23:18
kdokmeci
2013-03-16 21:23:18
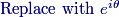
Math99
2013-03-16 21:23:21
geometric serieis?
geometric serieis?
DPatrick
2013-03-16 21:23:29
Conveniently, all of the terms are of the form
$$
\frac{1}{2^k} i^k (\cos k\theta + i\sin k\theta)
$$
where $k$ is a nonnegative integer.
Conveniently, all of the terms are of the form
$$
\frac{1}{2^k} i^k (\cos k\theta + i\sin k\theta)
$$
where $k$ is a nonnegative integer.
DPatrick
2013-03-16 21:23:53
Look at the coefficients of the cosine term: 1, i, -1, -i, 1, i, ...
Look at the coefficients of the cosine term: 1, i, -1, -i, 1, i, ...
DPatrick
2013-03-16 21:23:59
They're the powers of i.
They're the powers of i.
DPatrick
2013-03-16 21:24:12
And the sine coefficients: -1, -i, 1, i, -1, ...
And the sine coefficients: -1, -i, 1, i, -1, ...
DPatrick
2013-03-16 21:24:28
Also the powers of i, just shifted ahead by an extra multiple of i.
Also the powers of i, just shifted ahead by an extra multiple of i.
DPatrick
2013-03-16 21:24:41
So that's pretty cool!
So that's pretty cool!
DPatrick
2013-03-16 21:24:56
And we also know that $\cos k\theta + i\sin k\theta = e^{ik\theta} = (e^{i\theta})^k$.
And we also know that $\cos k\theta + i\sin k\theta = e^{ik\theta} = (e^{i\theta})^k$.
DPatrick
2013-03-16 21:26:41
Or in the language of deMoivre's Theorem,
$$
\cos k\theta + i \sin k\theta = \left(\cos\theta + i\sin\theta\right)^k.
$$
Or in the language of deMoivre's Theorem,
$$
\cos k\theta + i \sin k\theta = \left(\cos\theta + i\sin\theta\right)^k.
$$
DPatrick
2013-03-16 21:27:03
(that was exciting!)
(that was exciting!)
superpi83
2013-03-16 21:27:17
geometric series with first term 1 and common ratio e^(itheta)*i/2
geometric series with first term 1 and common ratio e^(itheta)*i/2
DPatrick
2013-03-16 21:27:36
Right! Our sum $Q+iP$ is now an infinite geometric series!
Right! Our sum $Q+iP$ is now an infinite geometric series!
DPatrick
2013-03-16 21:27:41
$$
Q + iP = \sum_{k=0}^\infty \left(\frac{ie^{i\theta}}{2}\right)^k.
$$
$$
Q + iP = \sum_{k=0}^\infty \left(\frac{ie^{i\theta}}{2}\right)^k.
$$
DPatrick
2013-03-16 21:27:57
What is its sum?
What is its sum?
QuantumandMath
2013-03-16 21:28:16
1/(1-x)
1/(1-x)
Flamewire
2013-03-16 21:28:37
1/(1-ie^itheta/2)
1/(1-ie^itheta/2)
cerberus88
2013-03-16 21:28:37
superpi83
2013-03-16 21:28:37
1/(1-(ie^(itheta))/2)
1/(1-(ie^(itheta))/2)
pickten
2013-03-16 21:28:37
1/(1-ie^{itheta}/2)
1/(1-ie^{itheta}/2)
DPatrick
2013-03-16 21:28:47
Right. The sum $1 + r + r^2 + r^3 + \cdots = \frac{1}{1-r}$, provided $|r| < 1$. But $\left|\frac{ie^{i\theta}}{2}\right| = \frac12$, so we're safe.
Right. The sum $1 + r + r^2 + r^3 + \cdots = \frac{1}{1-r}$, provided $|r| < 1$. But $\left|\frac{ie^{i\theta}}{2}\right| = \frac12$, so we're safe.
DPatrick
2013-03-16 21:28:55
Thus we have
$$
Q + iP = \frac{1}{1-\frac{ie^{i\theta}}{2}} = \frac{2}{2-ie^{i\theta}}.
$$
Thus we have
$$
Q + iP = \frac{1}{1-\frac{ie^{i\theta}}{2}} = \frac{2}{2-ie^{i\theta}}.
$$
DPatrick
2013-03-16 21:29:04
Now what?
Now what?
AceOfDiamonds
2013-03-16 21:29:27
find P/Q
find P/Q
DVA6102
2013-03-16 21:29:27
We haven't used P/Q=2root2/7 yet.
We haven't used P/Q=2root2/7 yet.
DPatrick
2013-03-16 21:29:50
Correct, we still have that data to use. What does $\frac{P}{Q} = \frac{2\sqrt2}{7}$ mean in terms of the complex number $Q + iP$?
Correct, we still have that data to use. What does $\frac{P}{Q} = \frac{2\sqrt2}{7}$ mean in terms of the complex number $Q + iP$?
mapletree14
2013-03-16 21:30:17
argument?
argument?
thecmd999
2013-03-16 21:30:17
it's the tangent of the angle formed by the complex number with the real axis in the complex plane
it's the tangent of the angle formed by the complex number with the real axis in the complex plane
centralbs
2013-03-16 21:30:17
the tangent of the angle is 2sqrt2/7
the tangent of the angle is 2sqrt2/7
mathmaster2012
2013-03-16 21:30:17
argument is arctan(2sqrt2/7)
argument is arctan(2sqrt2/7)
DPatrick
2013-03-16 21:30:25
Not exactly, but you all have the right idea...
Not exactly, but you all have the right idea...
DPatrick
2013-03-16 21:30:56
Well, let's see..
Well, let's see..
DPatrick
2013-03-16 21:31:10
It means that $7P = 2\sqrt2Q$. In other words, 7 times the imaginary part of $Q+iP$ equals $2\sqrt2$ times the real part of $Q+iP$.
It means that $7P = 2\sqrt2Q$. In other words, 7 times the imaginary part of $Q+iP$ equals $2\sqrt2$ times the real part of $Q+iP$.
DPatrick
2013-03-16 21:31:32
And this means that $Q + iP$ is a real multiple of $7 + i2\sqrt2$. (The key is that it's a real multiple.)
And this means that $Q + iP$ is a real multiple of $7 + i2\sqrt2$. (The key is that it's a real multiple.)
DPatrick
2013-03-16 21:32:01
The "imaginary"/"real" ratio is the constant $2\sqrt2 / 7$.
The "imaginary"/"real" ratio is the constant $2\sqrt2 / 7$.
DPatrick
2013-03-16 21:32:31
In other words, now we know that
$$
Q + iP = \frac{2}{2 - ie^{i\theta}} = c(7 + i2\sqrt2)
$$
for some real constant $c$.
In other words, now we know that
$$
Q + iP = \frac{2}{2 - ie^{i\theta}} = c(7 + i2\sqrt2)
$$
for some real constant $c$.
DPatrick
2013-03-16 21:32:51
How does this help?
How does this help?
zqjx
2013-03-16 21:33:30
we can separate the real and imaginary parts?
we can separate the real and imaginary parts?
pickten
2013-03-16 21:33:30
expand using cis?
expand using cis?
DPatrick
2013-03-16 21:33:37
It's annoying to have the polar form on the left side but the rectangular form on the right side, so let's go back to cosine and sine:
It's annoying to have the polar form on the left side but the rectangular form on the right side, so let's go back to cosine and sine:
DPatrick
2013-03-16 21:33:44
$$
Q + iP = \frac{2}{(2 + \sin\theta) - i\cos\theta)} = c(7 + i2\sqrt2)
$$
for some real constant $c$.
$$
Q + iP = \frac{2}{(2 + \sin\theta) - i\cos\theta)} = c(7 + i2\sqrt2)
$$
for some real constant $c$.
nsun48
2013-03-16 21:34:01
cross multiply
cross multiply
nsun48
2013-03-16 21:34:11
and both sides should be real
and both sides should be real
DPatrick
2013-03-16 21:34:20
Right. This means that the imaginary part of
$$
\left((2 + \sin\theta) - i\cos\theta\right)\left(7 + i2\sqrt2\right)
$$
must be 0, because this product must be real (it must equal 2/c).
Right. This means that the imaginary part of
$$
\left((2 + \sin\theta) - i\cos\theta\right)\left(7 + i2\sqrt2\right)
$$
must be 0, because this product must be real (it must equal 2/c).
DPatrick
2013-03-16 21:34:34
But what is that imaginary part?
But what is that imaginary part?
QuantumandMath
2013-03-16 21:35:01
-7cos+2sqrt2(2+sin)
-7cos+2sqrt2(2+sin)
DPatrick
2013-03-16 21:35:10
Multiply it out: it's $2\sqrt2(2 + \sin\theta) - 7\cos\theta$.
Multiply it out: it's $2\sqrt2(2 + \sin\theta) - 7\cos\theta$.
DPatrick
2013-03-16 21:35:23
Since this must be 0, we now have the equation
$$
4\sqrt2 + 2\sqrt2\sin\theta = 7\cos\theta.
$$
Since this must be 0, we now have the equation
$$
4\sqrt2 + 2\sqrt2\sin\theta = 7\cos\theta.
$$
DPatrick
2013-03-16 21:35:33
Now what?
Now what?
lucylai
2013-03-16 21:35:49
square both sides
square both sides
thecmd999
2013-03-16 21:35:49
square and solve for sine with the pythagorean identity
square and solve for sine with the pythagorean identity
DPatrick
2013-03-16 21:35:54
I'd square both sides: both to get rid of the square roots, and to hopefully be able to apply $\sin^2\theta + \cos^2\theta = 1$.
I'd square both sides: both to get rid of the square roots, and to hopefully be able to apply $\sin^2\theta + \cos^2\theta = 1$.
DPatrick
2013-03-16 21:36:02
We get:
$$
32 + 32\sin\theta + 8\sin^2\theta = 49\cos^2\theta.
$$
We get:
$$
32 + 32\sin\theta + 8\sin^2\theta = 49\cos^2\theta.
$$
gengkev
2013-03-16 21:36:15
cos^2=1-sin^2?
cos^2=1-sin^2?
DPatrick
2013-03-16 21:36:22
Aha, now that's
$$
32 + 32\sin\theta + 8\sin^2\theta = 49 - 49\sin^2\theta.
$$
Aha, now that's
$$
32 + 32\sin\theta + 8\sin^2\theta = 49 - 49\sin^2\theta.
$$
DVA6102
2013-03-16 21:36:35
solve for sin(theta)
solve for sin(theta)
cerberus88
2013-03-16 21:36:35
quadratic so solve fro sin(theta)
quadratic so solve fro sin(theta)
AayushGupta
2013-03-16 21:36:38
assign sin a variable and solve
assign sin a variable and solve
DPatrick
2013-03-16 21:36:44
Since $\sin\theta$ is what we want to solve for, let's call it $x$, and what we have is just a quadratic in $x$:
$$
32 + 32x + 8x^2 = 49 - 49x^2.
$$
Since $\sin\theta$ is what we want to solve for, let's call it $x$, and what we have is just a quadratic in $x$:
$$
32 + 32x + 8x^2 = 49 - 49x^2.
$$
DPatrick
2013-03-16 21:36:58
This simplifies to $57x^2 + 32x - 17 = 0$.
This simplifies to $57x^2 + 32x - 17 = 0$.
DVA6102
2013-03-16 21:37:12
factor!
factor!
SkinnySanta
2013-03-16 21:37:12
rational root theorem
rational root theorem
DPatrick
2013-03-16 21:37:16
Since we're told it has rational roots, it's probably not too difficult to factor.
Since we're told it has rational roots, it's probably not too difficult to factor.
DPatrick
2013-03-16 21:37:29
And since 17 is prime, there aren't too many possibilities.
And since 17 is prime, there aren't too many possibilities.
mathmaster2012
2013-03-16 21:37:40
(19x+17)(3x-1)=0
(19x+17)(3x-1)=0
DPatrick
2013-03-16 21:37:42
Indeed, we get $(19x + 17)(3x - 1) = 0$.
Indeed, we get $(19x + 17)(3x - 1) = 0$.
cire_il
2013-03-16 21:37:49
-17/19 happens to work
-17/19 happens to work
DPatrick
2013-03-16 21:37:56
To finish, note that we want the negative root, so we have $x = -\frac{17}{19}$. Our final answer is $17 + 19 = \boxed{036}$.
To finish, note that we want the negative root, so we have $x = -\frac{17}{19}$. Our final answer is $17 + 19 = \boxed{036}$.
DPatrick
2013-03-16 21:38:22
The finish line is in sight!
The finish line is in sight!
DPatrick
2013-03-16 21:38:27
DPatrick
2013-03-16 21:38:47
We normally try to write arithmetic sequences in terms of their common differences; how can we do that here?
We normally try to write arithmetic sequences in terms of their common differences; how can we do that here?
DPatrick
2013-03-16 21:39:23
This is where a clever choice can simplify things later quite a bit.
This is where a clever choice can simplify things later quite a bit.
lucylai
2013-03-16 21:39:31
let x and y be common differences for (A, B, C) and (b, a, c), respectively
let x and y be common differences for (A, B, C) and (b, a, c), respectively
DPatrick
2013-03-16 21:39:44
That's a good idea, but to keep better track, I'm going to call them D and d.
That's a good idea, but to keep better track, I'm going to call them D and d.
SuperSnivy
2013-03-16 21:40:15
(B-D , B , B+D) and (b-d , b , b+d)
(B-D , B , B+D) and (b-d , b , b+d)
DPatrick
2013-03-16 21:40:32
That's what I normally like to do, and indeed on my first attempt I did it that way. It was needlessly messy.
That's what I normally like to do, and indeed on my first attempt I did it that way. It was needlessly messy.
DPatrick
2013-03-16 21:40:44
Then my AoPS colleague Jeremy Copeland gave be a better idea.
Then my AoPS colleague Jeremy Copeland gave be a better idea.
DPatrick
2013-03-16 21:41:05
Notice that in part (d) of the problem statement, the $C$'s line up ($C$ with $c$), whereas the $A$'s and $B$'s are mismatched ($b$ is in $A$'s position and $a$ is in $B$'s position).
Notice that in part (d) of the problem statement, the $C$'s line up ($C$ with $c$), whereas the $A$'s and $B$'s are mismatched ($b$ is in $A$'s position and $a$ is in $B$'s position).
DPatrick
2013-03-16 21:41:22
So this suggests making the third term the "base" term, and writing the other two terms using that base.
So this suggests making the third term the "base" term, and writing the other two terms using that base.
DPatrick
2013-03-16 21:41:35
In other words, we'll write
$$
(A,B,C) = (C-2D,C-D,C)
$$
where $D>0$ is the common difference, and
$$
(b,a,c) = (c-2d,c-d,c)
$$
where $d>0$ is the common difference.
In other words, we'll write
$$
(A,B,C) = (C-2D,C-D,C)
$$
where $D>0$ is the common difference, and
$$
(b,a,c) = (c-2d,c-d,c)
$$
where $d>0$ is the common difference.
DPatrick
2013-03-16 21:42:03
Now what does condition (c) say?
Now what does condition (c) say?
distortedwalrus
2013-03-16 21:42:27
A == a (mod p) and similarly for the others
A == a (mod p) and similarly for the others
kdokmeci
2013-03-16 21:42:36
A-a, B-b, C-c have a factor of p
A-a, B-b, C-c have a factor of p
DPatrick
2013-03-16 21:42:47
Right. But let's write them all out in terms of C,c,D,d.
Right. But let's write them all out in terms of C,c,D,d.
DPatrick
2013-03-16 21:42:58
It says that
\begin{align*}
A-a &= (C-2D) - (c-d) = (C-c) - (2D-d), \\
B-b &= (C-D) - (c-2d) = (C-c) - (D-2d), \\
C-c
\end{align*}
are all multiples of $p$.
It says that
\begin{align*}
A-a &= (C-2D) - (c-d) = (C-c) - (2D-d), \\
B-b &= (C-D) - (c-2d) = (C-c) - (D-2d), \\
C-c
\end{align*}
are all multiples of $p$.
superpi83
2013-03-16 21:43:18
so 2D-d and D-2d are both multiples of p
so 2D-d and D-2d are both multiples of p
mathworld1
2013-03-16 21:43:24
So p divides 2D-d and D-2d!
So p divides 2D-d and D-2d!
kdokmeci
2013-03-16 21:43:26
2D-d, D-2d are multiples of p
2D-d, D-2d are multiples of p
DPatrick
2013-03-16 21:43:42
Aha! It tells us that $2D-d$ and $D-2d$ are also multiples of $p$. (These could possibly be negative or 0, depending on what $D$ and $d$ are.)
Aha! It tells us that $2D-d$ and $D-2d$ are also multiples of $p$. (These could possibly be negative or 0, depending on what $D$ and $d$ are.)
mathmaster2012
2013-03-16 21:43:58
3d is a multiple of p
3d is a multiple of p
superpi83
2013-03-16 21:43:58
This means p divides 3d
This means p divides 3d
DPatrick
2013-03-16 21:44:14
Right! We also then get $p\mid (2D-d)-2(D-2d)=3d.$
Right! We also then get $p\mid (2D-d)-2(D-2d)=3d.$
DPatrick
2013-03-16 21:44:29
So $3d$ is a multiple of $p$. What does that mean?
So $3d$ is a multiple of $p$. What does that mean?
countingkg
2013-03-16 21:45:12
because d < p, p = 3
because d < p, p = 3
DPatrick
2013-03-16 21:45:25
Right!
Right!
DPatrick
2013-03-16 21:45:32
We know that $p$ is prime, and $0 < d < p$, and $3d$ is a multiple of $p$.
We know that $p$ is prime, and $0 < d < p$, and $3d$ is a multiple of $p$.
DPatrick
2013-03-16 21:46:10
The only possibility is that $p = 3$.
The only possibility is that $p = 3$.
mathwizard888
2013-03-16 21:46:27
(b,a,c)=(0,1,2)
(b,a,c)=(0,1,2)
DPatrick
2013-03-16 21:46:47
Right: we have to have $d=1$, and the little sequence $(b,a,c) = (0,1,2)$ is the only one that works.
Right: we have to have $d=1$, and the little sequence $(b,a,c) = (0,1,2)$ is the only one that works.
DPatrick
2013-03-16 21:47:08
So now let's go back and use this data in the problem statement...
So now let's go back and use this data in the problem statement...
DPatrick
2013-03-16 21:47:22
We have an arithmetic sequence $(A,B,C)$ with $0 \le A < B < C \le 99$, such that $A-1$, $B$, and $C-2$ are all multiples of 3.
We have an arithmetic sequence $(A,B,C)$ with $0 \le A < B < C \le 99$, such that $A-1$, $B$, and $C-2$ are all multiples of 3.
fmasroor
2013-03-16 21:47:50
write in terms of B, R
write in terms of B, R
DPatrick
2013-03-16 21:48:09
I agree: now $B$ is the nice term (it's just a multiple of 3), so I'd write the sequence in terms of $B$.
I agree: now $B$ is the nice term (it's just a multiple of 3), so I'd write the sequence in terms of $B$.
DPatrick
2013-03-16 21:48:15
That is, we want to count the ordered pairs $(B,X)$ of positive integers such that:
(i) $0 \le B-X < B < B+X \le 99$, and
(ii) $B$ is a multiple of 3, and
(iii) $X \equiv 1 \pmod 3$
That is, we want to count the ordered pairs $(B,X)$ of positive integers such that:
(i) $0 \le B-X < B < B+X \le 99$, and
(ii) $B$ is a multiple of 3, and
(iii) $X \equiv 1 \pmod 3$
DPatrick
2013-03-16 21:48:38
(I'm calling the common difference $X$ now, for no good reason -- I probably should have just stuck with $D$.)
(I'm calling the common difference $X$ now, for no good reason -- I probably should have just stuck with $D$.)
DPatrick
2013-03-16 21:48:56
How do we count these?
How do we count these?
VietaFan
2013-03-16 21:49:21
Count the B first.
Count the B first.
mathworld1
2013-03-16 21:49:28
For each B, find the number of possible X
For each B, find the number of possible X
DPatrick
2013-03-16 21:49:32
The choices for B are easy: 3, 6, 9, 12, ..., 96=3*32. There are 32 of them.
The choices for B are easy: 3, 6, 9, 12, ..., 96=3*32. There are 32 of them.
DPatrick
2013-03-16 21:49:42
How many X's for each B?
How many X's for each B?
pedronr
2013-03-16 21:49:54
The number of possible values of X per every B is like a pyramid centering at closest to 50
The number of possible values of X per every B is like a pyramid centering at closest to 50
DPatrick
2013-03-16 21:50:04
Right. Note that if $B < 50$, then the $0 \le B-X$ is going to be the limiting condition on $X$; but if $B > 50$, then the $B+X \le 99$ is the limiting condition on $X$, and indeed the two cases are symmetric.
Right. Note that if $B < 50$, then the $0 \le B-X$ is going to be the limiting condition on $X$; but if $B > 50$, then the $B+X \le 99$ is the limiting condition on $X$, and indeed the two cases are symmetric.
superpi83
2013-03-16 21:50:11
3 has 1, 6 has 2, 9 has 3...
3 has 1, 6 has 2, 9 has 3...
DPatrick
2013-03-16 21:50:32
Exactly. If $B = 3k$ (where $1 \le k \le 16$), then $X$ can be $1, 4, 7, \ldots$, up to $3k-2$. So there are $k$ choices for $X$.
Exactly. If $B = 3k$ (where $1 \le k \le 16$), then $X$ can be $1, 4, 7, \ldots$, up to $3k-2$. So there are $k$ choices for $X$.
DPatrick
2013-03-16 21:50:48
Hence, there are $1+2+3+\cdots+16 = \frac{16 \cdot 17}{2} = 136$ pairs $(B,X)$ with $B < 50$.
Hence, there are $1+2+3+\cdots+16 = \frac{16 \cdot 17}{2} = 136$ pairs $(B,X)$ with $B < 50$.
mathworld1
2013-03-16 21:51:06
Symmetric for B>50
Symmetric for B>50
DPatrick
2013-03-16 21:51:22
Right. If $B = 99 - 3k$ (where $1 \le k \le 16$), then again $X$ can be $1, 4, 7, \ldots$, again up to $3k-2$. So again there are $k$ choices for $X$.
Right. If $B = 99 - 3k$ (where $1 \le k \le 16$), then again $X$ can be $1, 4, 7, \ldots$, again up to $3k-2$. So again there are $k$ choices for $X$.
DPatrick
2013-03-16 21:51:29
So that gives another 136 pairs $(B,X)$ with $B>50$.
So that gives another 136 pairs $(B,X)$ with $B>50$.
countingkg
2013-03-16 21:51:35
272!!!!!!!!!!!!!!!
272!!!!!!!!!!!!!!!
cerberus88
2013-03-16 21:51:35
so the answer is 272
so the answer is 272
kdokmeci
2013-03-16 21:51:35
272 total
272 total
DPatrick
2013-03-16 21:51:38
Hence our answer is $2(136) = \boxed{272}$.
Hence our answer is $2(136) = \boxed{272}$.
DPatrick
2013-03-16 21:52:00
And that's it for the AIME I! We just got in under 3 hours. Thanks for hanging out with my on a Saturday night.
And that's it for the AIME I! We just got in under 3 hours. Thanks for hanging out with my on a Saturday night.
DPatrick
2013-03-16 21:52:04
*me*!
*me*!
DPatrick
2013-03-16 21:52:09
And please join us again for the AIME II Math Jam on Friday, April 5, when we'll do all this again for the AIME II.
And please join us again for the AIME II Math Jam on Friday, April 5, when we'll do all this again for the AIME II.
anwang16
2013-03-16 21:52:26
wait are we allowed to take both tests
wait are we allowed to take both tests
DPatrick
2013-03-16 21:52:37
No, you're not. But we're certainly allowed to discuss them both!
No, you're not. But we're certainly allowed to discuss them both!
zero.destroyer
2013-03-16 21:52:59
what would you predict the usamo cutoff is?
what would you predict the usamo cutoff is?
DPatrick
2013-03-16 21:53:03
I wouldn't. I never do.
I wouldn't. I never do.
distortedwalrus
2013-03-16 21:53:19
is there a reason why we can take both AMCs but not both AIMEs?
is there a reason why we can take both AMCs but not both AIMEs?
DPatrick
2013-03-16 21:53:26
I have no idea. You'd have to ask the AMC that.
I have no idea. You'd have to ask the AMC that.
apple.singer
2013-03-16 21:53:36
What was your favorite problem?
What was your favorite problem?
DPatrick
2013-03-16 21:53:49
I liked #11 and #14.
I liked #11 and #14.
DPatrick
2013-03-16 21:53:55
#10 was kind of nice too.
#10 was kind of nice too.
DPatrick
2013-03-16 21:54:01
I hated #13, to be honest.
I hated #13, to be honest.
Klu2014
2013-03-16 21:54:37
Is this a new rule? That you can only take one AIME?
Is this a new rule? That you can only take one AIME?
DPatrick
2013-03-16 21:54:40
That's always been the rule.
That's always been the rule.
tRIG
2013-03-16 21:56:01
would you say this years Aime was easier than previous years?
would you say this years Aime was easier than previous years?
Wickedestjr
2013-03-16 21:56:01
It seemed like this was a particularly easy AIME in comparison to previous years.
It seemed like this was a particularly easy AIME in comparison to previous years.
mapletree14
2013-03-16 21:56:01
Was this an easy AIME?
Was this an easy AIME?
DPatrick
2013-03-16 21:56:35
It's hard for me to say. There didn't seem to be a "killer" question in my opinion.
It's hard for me to say. There didn't seem to be a "killer" question in my opinion.
DPatrick
2013-03-16 21:57:10
The geometry seemed a bit easier than usual (to me anyway), except perhaps for #13.
The geometry seemed a bit easier than usual (to me anyway), except perhaps for #13.
DPatrick
2013-03-16 21:57:21
...which was more messy than really hard.
...which was more messy than really hard.
forthegreatergood
2013-03-16 21:57:33
when will transcripts be up
when will transcripts be up
DPatrick
2013-03-16 21:57:45
About 5 minutes or so after I close the classroom.
About 5 minutes or so after I close the classroom.
minimario
2013-03-16 21:57:50
Will Richard be making videos?
Will Richard be making videos?
DPatrick
2013-03-16 21:57:53
I'm not sure.
I'm not sure.
csmath
2013-03-16 21:58:31
When does the classroom close?
When does the classroom close?
DPatrick
2013-03-16 21:58:43
When I decide to close it, which is going to be in just a few minutes.
When I decide to close it, which is going to be in just a few minutes.
mapletree14
2013-03-16 21:58:48
What did you score on the AIME?
What did you score on the AIME?
DPatrick
2013-03-16 21:59:10
I honestly do not remember. (And perhaps that's a commentary on how important your AIME scores is in the long term.) Not a 15.
I honestly do not remember. (And perhaps that's a commentary on how important your AIME scores is in the long term.) Not a 15.
scgorantla
2013-03-16 21:59:28
Are AIME 1 and 2 on the same difficulty, or how is the difficulty of each exam defined?
Are AIME 1 and 2 on the same difficulty, or how is the difficulty of each exam defined?
DPatrick
2013-03-16 21:59:34
Two contests are written, and then they flip a coin,
Two contests are written, and then they flip a coin,
DPatrick
2013-03-16 21:59:36
Really.
Really.
mathmaster2012
2013-03-16 21:59:56
How do you know they flip a coin?
How do you know they flip a coin?
DPatrick
2013-03-16 22:00:03
Because I've been told so by the Director of the AMC>
Because I've been told so by the Director of the AMC>
DPatrick
2013-03-16 22:01:15
OK, I'm going to start the process for closing the classroom and doing the transcript, in part because I'm hungry for dinner (it's 7 PM here), so very shortly you'll all be ejected from the room.
OK, I'm going to start the process for closing the classroom and doing the transcript, in part because I'm hungry for dinner (it's 7 PM here), so very shortly you'll all be ejected from the room.
DPatrick
2013-03-16 22:01:25
Good night and enjoy St. Patrick's Day tomorrow!
Good night and enjoy St. Patrick's Day tomorrow!
DPatrick
2013-03-16 22:02:44
Bye!
Bye!
Copyright © 2024 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
