2013 AIME II Math Jam
Go back to the Math Jam ArchiveAoPS instructors discuss all 15 problems of the 2013 AIME II.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Dave Patrick
DPatrick
2013-04-05 19:00:10
Welcome to the 2013 AIME II Math Jam!
Welcome to the 2013 AIME II Math Jam!
DPatrick
2013-04-05 19:00:15
I'm Dave Patrick, and I'll be leading our discussion tonight.
I'm Dave Patrick, and I'll be leading our discussion tonight.
DPatrick
2013-04-05 19:00:21
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
DPatrick
2013-04-05 19:00:28
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
DPatrick
2013-04-05 19:00:38
This helps keep the session organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
This helps keep the session organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
DPatrick
2013-04-05 19:01:00
There are a lot of students here already, and there will likely be more people arriving as we go. As I said, only a relatively small fraction of the well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
There are a lot of students here already, and there will likely be more people arriving as we go. As I said, only a relatively small fraction of the well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
DPatrick
2013-04-05 19:01:18
Also, we won't be going through all the math quite as thoroughly as we do in our classes -- I can't teach all the necessary material for every problem as we go.
Also, we won't be going through all the math quite as thoroughly as we do in our classes -- I can't teach all the necessary material for every problem as we go.
DPatrick
2013-04-05 19:01:28
Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We always to try do so in our regular online classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all.
Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We always to try do so in our regular online classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all.
DPatrick
2013-04-05 19:01:38
We do have two teaching assistants with us tonight to help answer your questions: Catherine Sheard (greekpanda) and Elena Sizikova (Anna Smith).
We do have two teaching assistants with us tonight to help answer your questions: Catherine Sheard (greekpanda) and Elena Sizikova (Anna Smith).
DPatrick
2013-04-05 19:01:53
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
DPatrick
2013-04-05 19:02:10
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. Also on occasion we may stop to prove things that you wouldn't necessary need to prove while doing the contest.
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. Also on occasion we may stop to prove things that you wouldn't necessary need to prove while doing the contest.
DPatrick
2013-04-05 19:02:30
So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem most likely won't be acknowledged.
So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem most likely won't be acknowledged.
DPatrick
2013-04-05 19:02:44
Let's get started! We're going to work through all 15 problems, in order.
Let's get started! We're going to work through all 15 problems, in order.
DPatrick
2013-04-05 19:02:55


DPatrick
2013-04-05 19:03:06
Notice that the current problem under discussion will always be placed at the top of the window. You can resize that top region by dragging the horizontal bar separating the top pane from the main pane.
Notice that the current problem under discussion will always be placed at the top of the window. You can resize that top region by dragging the horizontal bar separating the top pane from the main pane.
mathmaster2012
2013-04-05 19:03:47
Fractional parts of the day
Fractional parts of the day
sunny2000
2013-04-05 19:03:47
make proportions and use the information that they give you already! (metric, etc)
make proportions and use the information that they give you already! (metric, etc)
DPatrick
2013-04-05 19:03:59
Right, that's a productive way to think about it.
Right, that's a productive way to think about it.
DPatrick
2013-04-05 19:04:11
In terms of a fraction of a day, what does the time A:BC mean?
In terms of a fraction of a day, what does the time A:BC mean?
sibirica
2013-04-05 19:04:41
(100*A+10*B+10*C)/1000ths of a day
(100*A+10*B+10*C)/1000ths of a day
genesis2
2013-04-05 19:04:41
ABC/1000
ABC/1000
sarvottam
2013-04-05 19:04:41
ABC/1000?
ABC/1000?
Tommy2000
2013-04-05 19:04:46
100A+10B+c/1000
100A+10B+c/1000
DPatrick
2013-04-05 19:04:50
Yes: ABC1000 is the fraction of the day that has gone by. (Here, we're thinking of ABC as a 3-digit number, which conveniently happens to be what we want our final answer to be.)
Yes: ABC1000 is the fraction of the day that has gone by. (Here, we're thinking of ABC as a 3-digit number, which conveniently happens to be what we want our final answer to be.)
DPatrick
2013-04-05 19:05:10
So the question becomes: at 6:36 AM, what fraction of the day has passed?
So the question becomes: at 6:36 AM, what fraction of the day has passed?
mathmaster2012
2013-04-05 19:05:42
11/40
11/40
bobthesmartypants
2013-04-05 19:05:42
(6*60+36)/1440
(6*60+36)/1440
countyguy
2013-04-05 19:05:42
11/40
11/40
JWK750
2013-04-05 19:05:42
11/40
11/40
stellalau
2013-04-05 19:05:42
ABC/1000 = (60*6 + 36) / (1440)
ABC/1000 = (60*6 + 36) / (1440)
kdokmeci
2013-04-05 19:05:42
1/4+(3/5)/24=11/40
1/4+(3/5)/24=11/40
DPatrick
2013-04-05 19:05:46
Right.
Right.
DPatrick
2013-04-05 19:05:51
The 6 hours have consumed 624=14 of the day.
The 6 hours have consumed 624=14 of the day.
DPatrick
2013-04-05 19:06:01
The 36 minutes have consumed 3660=35 of the next hour...
The 36 minutes have consumed 3660=35 of the next hour...
DPatrick
2013-04-05 19:06:05
...but that hour itself is 124 of the day.
...but that hour itself is 124 of the day.
DPatrick
2013-04-05 19:06:14
So the 36 minutes consume another 35⋅124=140 of the day.
So the 36 minutes consume another 35⋅124=140 of the day.
DPatrick
2013-04-05 19:06:30
Thus, at 6:36 AM, 14+140=1140 of the day is gone.
Thus, at 6:36 AM, 14+140=1140 of the day is gone.
DPatrick
2013-04-05 19:06:46
But we need this as thousandths of the day in order to find the metric time.
But we need this as thousandths of the day in order to find the metric time.
mathmaster2012
2013-04-05 19:07:01
1000*(11/40)=275
1000*(11/40)=275
lazorpenguin27143
2013-04-05 19:07:01
multiply by 1000 to get answer
multiply by 1000 to get answer
kdokmeci
2013-04-05 19:07:01
11/40=0.275, so answer is 275
11/40=0.275, so answer is 275
sunny2000
2013-04-05 19:07:01
proportions!
proportions!
ZZmath9
2013-04-05 19:07:01
2751000
2751000
countyguy
2013-04-05 19:07:01
11/40=275/1000
11/40=275/1000
DPatrick
2013-04-05 19:07:11
Yep: 1140=11⋅2540⋅25=2751000,
so 2751000 of the day is gone at 6:36 AM.
Yep: 1140=11⋅2540⋅25=2751000,
so 2751000 of the day is gone at 6:36 AM.
DPatrick
2013-04-05 19:07:20
So we set the alarm for 2:75 metric time. Answer 275.
So we set the alarm for 2:75 metric time. Answer 275.
DPatrick
2013-04-05 19:07:34
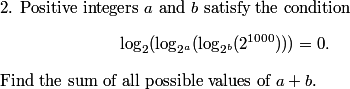
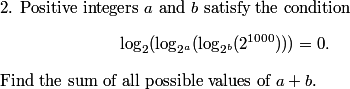
sunny2000
2013-04-05 19:08:10
first simplify by getting the logs out
first simplify by getting the logs out
genesis2
2013-04-05 19:08:10
Try to turn these into exponents.
Try to turn these into exponents.
AayushGupta
2013-04-05 19:08:10
remove the log 2
remove the log 2
DPatrick
2013-04-05 19:08:23
Right, we want to get rid of the logs and write this in a way that we can better understand.
Right, we want to get rid of the logs and write this in a way that we can better understand.
DPatrick
2013-04-05 19:08:42
Let's work from the outside in.
Let's work from the outside in.
distortedwalrus
2013-04-05 19:08:49
this means that the part inside the argument of the first log expression must be equal to 1.
this means that the part inside the argument of the first log expression must be equal to 1.
bobthesmartypants
2013-04-05 19:08:49
If log2x=0, then x must equal 1
If log2x=0, then x must equal 1
DPatrick
2013-04-05 19:09:09
Good start. If log2(x)=0, then x=1, since 20=1.
Good start. If log2(x)=0, then x=1, since 20=1.
DPatrick
2013-04-05 19:09:26
So now we have
log2a(log2b(21000))=1.
So now we have
log2a(log2b(21000))=1.
DPatrick
2013-04-05 19:09:57
Now what?
Now what?
DPatrick
2013-04-05 19:10:07
Next: if log2a(y)=1, then what's y?
Next: if log2a(y)=1, then what's y?
countyguy
2013-04-05 19:10:21
2^a
2^a
sunny2000
2013-04-05 19:10:21
2^a
2^a
lazorpenguin27143
2013-04-05 19:10:21
2^a
2^a
Superwiz
2013-04-05 19:10:21
2^a
2^a
tc1729
2013-04-05 19:10:21
2^a
2^a
DPatrick
2013-04-05 19:10:30
Yes: y=2a, since (2a)1=2a.
Yes: y=2a, since (2a)1=2a.
DPatrick
2013-04-05 19:10:37
So now we have
log2b(21000)=2a.
So now we have
log2b(21000)=2a.
DPatrick
2013-04-05 19:10:55
But what is the log that remains?
But what is the log that remains?
kdokmeci
2013-04-05 19:11:15
Simplify log: It equals 1000/b
Simplify log: It equals 1000/b
wpk
2013-04-05 19:11:15
2^1000 = (2^b)^(1000/b)
2^1000 = (2^b)^(1000/b)
matholympiad25
2013-04-05 19:11:15
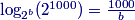
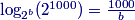
turkeybob777
2013-04-05 19:11:15
1000/b
1000/b
ZZmath9
2013-04-05 19:11:15
1000b
1000b
mathwrath
2013-04-05 19:11:15
1000/b
1000/b
DPatrick
2013-04-05 19:11:23


sibirica
2013-04-05 19:11:35
simplify as 1000/b=2^a
simplify as 1000/b=2^a
DPatrick
2013-04-05 19:11:46
Thus our equation is simply 1000b=2a.
Thus our equation is simply 1000b=2a.
DPatrick
2013-04-05 19:11:55
What now?
What now?
MathPerson060375
2013-04-05 19:12:03
So 1000 = b*2^a
So 1000 = b*2^a
AlcumusGuy
2013-04-05 19:12:03
multiply both sides by b
multiply both sides by b
DPatrick
2013-04-05 19:12:08
We need to solve 1000=2a⋅b where a and b are positive integers.
We need to solve 1000=2a⋅b where a and b are positive integers.
bobthesmartypants
2013-04-05 19:12:29
now we factor 1000=2^3 x 5^3
now we factor 1000=2^3 x 5^3
wpk
2013-04-05 19:12:29
1000 = 2^3 * 5^3
1000 = 2^3 * 5^3
TheStrangeCharm
2013-04-05 19:12:29
1000 = 2^3*5^3
1000 = 2^3*5^3
DPatrick
2013-04-05 19:12:39
Aha, perhaps writing it as 23⋅53=2a⋅b will help.
Aha, perhaps writing it as 23⋅53=2a⋅b will help.
vyzw
2013-04-05 19:13:00
a = 1,2,3
a = 1,2,3
AlcumusGuy
2013-04-05 19:13:00
so a = 1, 2, or 3
so a = 1, 2, or 3
DPatrick
2013-04-05 19:13:23
Right. We see that a must be 1, 2, or 3. (Note that a must be positive, so a≠0.)
Right. We see that a must be 1, 2, or 3. (Note that a must be positive, so a≠0.)
Tommy2000
2013-04-05 19:13:47
a=1,2,3 and b= 500, 250,125 respectively
a=1,2,3 and b= 500, 250,125 respectively
mathmaster2012
2013-04-05 19:13:47
(1,500), (2,250), and (3,125) are our solution sets
(1,500), (2,250), and (3,125) are our solution sets
DPatrick
2013-04-05 19:13:55
Right: this gives the solutions
(a,b)={(1,500),(2,250),(3,125)}.
Right: this gives the solutions
(a,b)={(1,500),(2,250),(3,125)}.
ZZmath9
2013-04-05 19:14:12
1+500+2+250+3+125=881 is the answer
1+500+2+250+3+125=881 is the answer
matholympiad25
2013-04-05 19:14:12
1+2+3+500+250+125=881
1+2+3+500+250+125=881
ninjataco
2013-04-05 19:14:12
so we have 881
so we have 881
genesis2
2013-04-05 19:14:12


DPatrick
2013-04-05 19:14:16
The sum of all of these is
1+500+2+250+3+125=881.
The sum of all of these is
1+500+2+250+3+125=881.
DPatrick
2013-04-05 19:14:48
By the way, I should mention that there will be a full transcript of this entire session posted on the web page once we're done.
By the way, I should mention that there will be a full transcript of this entire session posted on the web page once we're done.
DPatrick
2013-04-05 19:15:01
So you don't have to take notes, and you'll be able to go back and review anything you might have missed.
So you don't have to take notes, and you'll be able to go back and review anything you might have missed.
DPatrick
2013-04-05 19:15:09


kdokmeci
2013-04-05 19:15:32
Find T
Find T
mathwrath
2013-04-05 19:15:32
Find the time it takes to burn down!
Find the time it takes to burn down!
DPatrick
2013-04-05 19:15:39
Seems like a good place to start. What is T?
Seems like a good place to start. What is T?
ninjataco
2013-04-05 19:16:00
T = 10(1+2+3+...+118+119)
T = 10(1+2+3+...+118+119)
JWK750
2013-04-05 19:16:00
T=10(1+2..+119)
T=10(1+2..+119)
piguy314
2013-04-05 19:16:00
(10+20+30+...+1190)
(10+20+30+...+1190)
DPatrick
2013-04-05 19:16:06
We know that
T=10+20+30+⋯+1190=10(1+2+3+⋯+119).
We know that
T=10+20+30+⋯+1190=10(1+2+3+⋯+119).
DPatrick
2013-04-05 19:16:13
What is that sum?
What is that sum?
ninjataco
2013-04-05 19:16:32
T=10* (119*120)/2
T=10* (119*120)/2
sibirica
2013-04-05 19:16:32
119*120*10/2
119*120*10/2
fmasroor
2013-04-05 19:16:32
5(119)(120)
5(119)(120)
MathPerson060375
2013-04-05 19:16:32
Which is (119*120/2)*10
Which is (119*120/2)*10
viva
2013-04-05 19:16:32
119*120*5
119*120*5
Ronnicus
2013-04-05 19:16:32
10*(119*120/2)
10*(119*120/2)
countyguy
2013-04-05 19:16:40
triangular numbers
triangular numbers
DPatrick
2013-04-05 19:16:46
It's T=10⋅(119)(120)2=5(119)(120).
It's T=10⋅(119)(120)2=5(119)(120).
DPatrick
2013-04-05 19:17:12
(Let's not multiply it out -- it doesn't look like it'll help us at the moment.)
(Let's not multiply it out -- it doesn't look like it'll help us at the moment.)
sunny2000
2013-04-05 19:17:17
divide that time by half
divide that time by half
DPatrick
2013-04-05 19:17:24
So T/2=5(119)(60), and we need to find out how much has burned (and hence how much is left) after this many seconds.
So T/2=5(119)(60), and we need to find out how much has burned (and hence how much is left) after this many seconds.
DPatrick
2013-04-05 19:17:32
What now?
What now?
kdokmeci
2013-04-05 19:17:48
T/2 is also a triangular number.
T/2 is also a triangular number.
ninjataco
2013-04-05 19:17:48
another triangular number because it is 10(1+2+...+x)
another triangular number because it is 10(1+2+...+x)
DPatrick
2013-04-05 19:18:17
Right. If x is an integer, then it takes 10(1+2+⋯+x)=5x(x+1) seconds to burn x centimeters.
Right. If x is an integer, then it takes 10(1+2+⋯+x)=5x(x+1) seconds to burn x centimeters.
DPatrick
2013-04-05 19:18:43
(If x is not an integer we might have a problem. But let's assume it is for the moment and hope we get lucky.)
(If x is not an integer we might have a problem. But let's assume it is for the moment and hope we get lucky.)
DPatrick
2013-04-05 19:18:55
So if we get lucky, we might be able to solve
5x(x+1)=5(119)(60).
So if we get lucky, we might be able to solve
5x(x+1)=5(119)(60).
ninjataco
2013-04-05 19:19:09
x(x+1) = 119 * 60
x(x+1) = 119 * 60
sunny2000
2013-04-05 19:19:09
divide by 5 on both sides
divide by 5 on both sides
DPatrick
2013-04-05 19:19:13
This is x(x+1)=119(60).
This is x(x+1)=119(60).
DPatrick
2013-04-05 19:19:21
How do we solve this (without a calculator)?
How do we solve this (without a calculator)?
matholympiad25
2013-04-05 19:19:41
estimate the square root
estimate the square root
piguy314
2013-04-05 19:19:51
119=17*7, then use 17 for some trial and error to get 84*85
119=17*7, then use 17 for some trial and error to get 84*85
fmasroor
2013-04-05 19:19:51
factor 119 as 7*17, maybe something comes up
factor 119 as 7*17, maybe something comes up
DPatrick
2013-04-05 19:19:56
That's basically what I did.
That's basically what I did.
DPatrick
2013-04-05 19:20:13
The left side is almost a perfect square...so we can guess what perfect square is the right side close to.
The left side is almost a perfect square...so we can guess what perfect square is the right side close to.
DPatrick
2013-04-05 19:20:46
119(60)=7140 (you don't even need to compute it exactly, just estimate that it's about 120(60)=7200, and that's between 802=6400 and 902=8100. Probably close to halfway.
119(60)=7140 (you don't even need to compute it exactly, just estimate that it's about 120(60)=7200, and that's between 802=6400 and 902=8100. Probably close to halfway.
DPatrick
2013-04-05 19:21:20
And we'll need a factor of 5, so x=84 and x=85 are the only reasonable things to try.
And we'll need a factor of 5, so x=84 and x=85 are the only reasonable things to try.
ZZmath9
2013-04-05 19:21:29
The last digit is 0, so it's either 84×85 or 85×86. Checking, we find it's 84×85
The last digit is 0, so it's either 84×85 or 85×86. Checking, we find it's 84×85
kdokmeci
2013-04-05 19:21:29
84*85
84*85
matholympiad25
2013-04-05 19:21:29
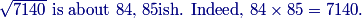
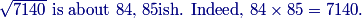
DPatrick
2013-04-05 19:21:38
And indeed, x=84 works, since 84⋅85=7140.
And indeed, x=84 works, since 84⋅85=7140.
DPatrick
2013-04-05 19:21:44
We got lucky. After exactly 84 centimeters have burned, we've used up T2 seconds.
We got lucky. After exactly 84 centimeters have burned, we've used up T2 seconds.
epicpwn314
2013-04-05 19:21:58
yeah so x=84 and 119-84=35 so the answer is 350
yeah so x=84 and 119-84=35 so the answer is 350
mathwrath
2013-04-05 19:21:58
119-84=35
119-84=35
wpk
2013-04-05 19:22:01
leaving 35
leaving 35
DPatrick
2013-04-05 19:22:07
Be careful at the end! The final answer is 10 times how much is left. There are 119−84=35 centimeters remaining, so the final answer is 350.
Be careful at the end! The final answer is 10 times how much is left. There are 119−84=35 centimeters remaining, so the final answer is 350.
DPatrick
2013-04-05 19:22:37
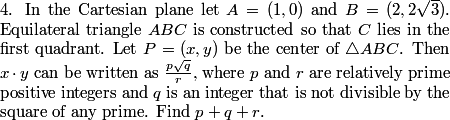
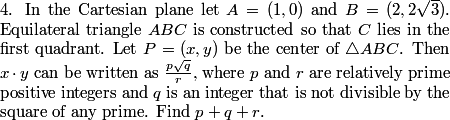
DPatrick
2013-04-05 19:22:55
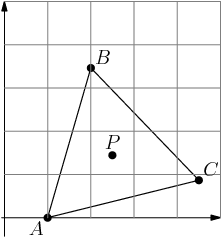
If you brought graph paper and a ruler and protractor to the contest (which I hope you did!), you can draw a pretty accurate picture:
If you brought graph paper and a ruler and protractor to the contest (which I hope you did!), you can draw a pretty accurate picture:
DPatrick
2013-04-05 19:23:02

DPatrick
2013-04-05 19:23:13
(There's already a quick sanity check for our answer for P: it looks like it's close to (52,32).)
(There's already a quick sanity check for our answer for P: it looks like it's close to (52,32).)
DPatrick
2013-04-05 19:23:20
What will make this problem a little easier to solve?
What will make this problem a little easier to solve?
stellalau
2013-04-05 19:23:57
Easy to shift A to the origin to work with it. So A' = (0,0), B' = (1,2root3)
Easy to shift A to the origin to work with it. So A' = (0,0), B' = (1,2root3)
TheStrangeCharm
2013-04-05 19:23:57
shifting the triangle over 1 so A is the origin
shifting the triangle over 1 so A is the origin
DPatrick
2013-04-05 19:24:07
I like the idea of moving everything in the diagram 1 unit to the left, so that A becomes the origin. But if we do this: DO NOT FORGET TO MOVE IT BACK BEFORE COMPUTING THE FINAL ANSWER!!
I like the idea of moving everything in the diagram 1 unit to the left, so that A becomes the origin. But if we do this: DO NOT FORGET TO MOVE IT BACK BEFORE COMPUTING THE FINAL ANSWER!!
DPatrick
2013-04-05 19:24:16
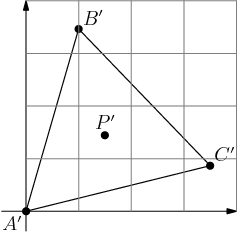

DPatrick
2013-04-05 19:24:26
I've given them new names. A′=(0,0) and B′=(1,2√3) now.
I've given them new names. A′=(0,0) and B′=(1,2√3) now.
DPatrick
2013-04-05 19:24:37
How do we find C′?
How do we find C′?
tc1729
2013-04-05 19:25:14
toss onto the complex plane
toss onto the complex plane
matholympiad25
2013-04-05 19:25:14
Complex numbers!
Complex numbers!
TheStrangeCharm
2013-04-05 19:25:14
complex number!
complex number!
sunny2000
2013-04-05 19:25:14
rotation of 60 degrees=polar coordinates
rotation of 60 degrees=polar coordinates
tc1729
2013-04-05 19:25:14
C' is a -60 degree rotation of B', which is easy to deal with on the complex plane
C' is a -60 degree rotation of B', which is easy to deal with on the complex plane
DPatrick
2013-04-05 19:25:24
There are many ways to proceed (in fact the AMC published 3 different "official" solutions for this problem). For example, you could compute the midpoint of A′B′ (call it M′), and then compute the line through M perpendicular to A′B′, and then go down this line the correct distance (specifically, √3(A′B′)) to find C′.
There are many ways to proceed (in fact the AMC published 3 different "official" solutions for this problem). For example, you could compute the midpoint of A′B′ (call it M′), and then compute the line through M perpendicular to A′B′, and then go down this line the correct distance (specifically, √3(A′B′)) to find C′.
DPatrick
2013-04-05 19:25:42
But I like the method of thinking of these as points in the complex plane. (Or in terms of polar coordinates, which is essentially the same thing.)
But I like the method of thinking of these as points in the complex plane. (Or in terms of polar coordinates, which is essentially the same thing.)
DPatrick
2013-04-05 19:25:56
What point is B′ if we think of it as a complex number?
What point is B′ if we think of it as a complex number?
bobthesmartypants
2013-04-05 19:26:20
1+2isqrt3
1+2isqrt3
ZZmath9
2013-04-05 19:26:20
1+2i√3
1+2i√3
matholympiad25
2013-04-05 19:26:20
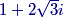
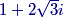
kdokmeci
2013-04-05 19:26:20
1+2i root 3
1+2i root 3
DPatrick
2013-04-05 19:26:24
We have B′=1+2√3i. (The x-coordinate becomes the real part, and the y-coordinate becomes the imaginary part.)
We have B′=1+2√3i. (The x-coordinate becomes the real part, and the y-coordinate becomes the imaginary part.)
DPatrick
2013-04-05 19:26:39
And what do we do to B' to get C'?
And what do we do to B' to get C'?
matholympiad25
2013-04-05 19:27:04
Multiply by cos(−60∘)+isin(−60∘)
Multiply by cos(−60∘)+isin(−60∘)
fmasroor
2013-04-05 19:27:04
rotate by -60 degrees
rotate by -60 degrees
twin77
2013-04-05 19:27:04
rotate -60 degrees
rotate -60 degrees
TheStrangeCharm
2013-04-05 19:27:04
multiply by cis(-pi/3)
multiply by cis(-pi/3)
DPatrick
2013-04-05 19:27:18
We rotate B′ by 60 degrees clockwise. (Which is easy to do now that A' is the origin!)
We rotate B′ by 60 degrees clockwise. (Which is easy to do now that A' is the origin!)
DPatrick
2013-04-05 19:27:41
That's the same as multiplying B′ by the complex number e−π3i. (Or \cis(−60∘) if you prefer.)
That's the same as multiplying B′ by the complex number e−π3i. (Or \cis(−60∘) if you prefer.)
DPatrick
2013-04-05 19:28:07
Either way, e−π3i=cos(−π3)+isin(−π3).
Either way, e−π3i=cos(−π3)+isin(−π3).
DPatrick
2013-04-05 19:28:26
What is this complex number?
What is this complex number?
twin77
2013-04-05 19:29:03
1/2 - sqrt3/2 i
1/2 - sqrt3/2 i
vyzw
2013-04-05 19:29:06
1/2-isqrt3/2
1/2-isqrt3/2
theGoodGuy
2013-04-05 19:29:13
1/2 - isqrt3/2
1/2 - isqrt3/2
matholympiad25
2013-04-05 19:29:13
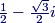
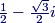
DPatrick
2013-04-05 19:29:33
This is 12−√32i. (The real part is cos(−60∘), and the imaginary part is sin(−60∘).)
This is 12−√32i. (The real part is cos(−60∘), and the imaginary part is sin(−60∘).)
DPatrick
2013-04-05 19:29:45
So we multiply B′ by this to get:
C′=(1+2√3i)(12−√32i).
So we multiply B′ by this to get:
C′=(1+2√3i)(12−√32i).
DPatrick
2013-04-05 19:29:51
What does this simplify to?
What does this simplify to?
theGoodGuy
2013-04-05 19:30:37
7/2+isqrt3/2
7/2+isqrt3/2
MathPerson060375
2013-04-05 19:30:43
7/2 + (sqrt(3)/2)i
7/2 + (sqrt(3)/2)i
DPatrick
2013-04-05 19:31:17
Multiplying it out gives C′=12−√32i+2√32i−2√3√32i2.
Multiplying it out gives C′=12−√32i+2√32i−2√3√32i2.
DPatrick
2013-04-05 19:31:30
This simplifies to C′=72+√32i.
This simplifies to C′=72+√32i.
DPatrick
2013-04-05 19:31:44
(Note that the last term in the expansion is +3.)
(Note that the last term in the expansion is +3.)
DPatrick
2013-04-05 19:32:11
Also this is a good point to check that this C′ is consistent with our original picture, which it is!
Also this is a good point to check that this C′ is consistent with our original picture, which it is!
kdokmeci
2013-04-05 19:32:22
C'=(7/2, root 3 /2)
C'=(7/2, root 3 /2)
DPatrick
2013-04-05 19:32:30
Right. Which is about where it looks to be.
Right. Which is about where it looks to be.
DPatrick
2013-04-05 19:32:35
Now, what is P′?
Now, what is P′?
matholympiad25
2013-04-05 19:32:54


vyzw
2013-04-05 19:32:54
average the 3 points
average the 3 points
TheStrangeCharm
2013-04-05 19:32:54
centroid or just average of all the corrdinates
centroid or just average of all the corrdinates
DPatrick
2013-04-05 19:33:00
Right. It's the average of A′, B′, and C′.
Right. It's the average of A′, B′, and C′.
DPatrick
2013-04-05 19:33:20
That is,
P′=(13(0+1+72),13(0+2√3+√32)).
That is,
P′=(13(0+1+72),13(0+2√3+√32)).
DPatrick
2013-04-05 19:33:46
This simplifies to P′=(32,5√36).
This simplifies to P′=(32,5√36).
vyzw
2013-04-05 19:33:57
(3/2,5sqrt3/6) but then shift it back
(3/2,5sqrt3/6) but then shift it back
twin77
2013-04-05 19:34:06
shift it 1 to the right
shift it 1 to the right
MathPerson060375
2013-04-05 19:34:06
And move back to P (not prime)
And move back to P (not prime)
DPatrick
2013-04-05 19:34:07
BUT DON'T FORGET TO SHIFT IT BACK!
BUT DON'T FORGET TO SHIFT IT BACK!
DPatrick
2013-04-05 19:34:12
So we have P=(52,5√36).
So we have P=(52,5√36).
DPatrick
2013-04-05 19:34:23
(And looking at our sanity check from the picture, we indeed see that this is close to (52,32).)
(And looking at our sanity check from the picture, we indeed see that this is close to (52,32).)
DPatrick
2013-04-05 19:34:41
(From the original picture, I mean!)
(From the original picture, I mean!)
ninjataco
2013-04-05 19:34:51
then we have 25root3/12, and then the answer is 040
then we have 25root3/12, and then the answer is 040
ZZmath9
2013-04-05 19:34:51
Product: 25√312, answer: 25+3+12=40
Product: 25√312, answer: 25+3+12=40
kdokmeci
2013-04-05 19:34:51
x*y=25root3 /12; 25+3+12=040
x*y=25root3 /12; 25+3+12=040
DPatrick
2013-04-05 19:34:58
And to finish: the product of the coordinates of P is 25√312, so our final answer is 25+3+12=040.
And to finish: the product of the coordinates of P is 25√312, so our final answer is 25+3+12=040.
DPatrick
2013-04-05 19:35:23
On to another back-to-back problem involving an equilateral triangle...
On to another back-to-back problem involving an equilateral triangle...
DPatrick
2013-04-05 19:35:28
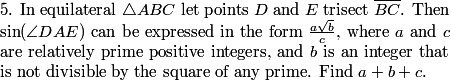
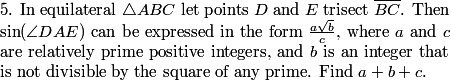
DPatrick
2013-04-05 19:35:40
Let's draw a picture.
Let's draw a picture.
DPatrick
2013-04-05 19:35:49
But there's a clever tactic we can use...
But there's a clever tactic we can use...
mathwrath
2013-04-05 19:35:56
I plugged in values.
I plugged in values.
DPatrick
2013-04-05 19:36:05
Right. Since we have flexibility with the lengths, let's pick some convenient ones. I made the trisected lengths 2 and the big triangle's side length 6, so as to avoid fractions:
Right. Since we have flexibility with the lengths, let's pick some convenient ones. I made the trisected lengths 2 and the big triangle's side length 6, so as to avoid fractions:
DPatrick
2013-04-05 19:36:12
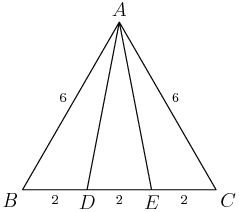

DPatrick
2013-04-05 19:36:27
How can we get data for sin(DAE)?
How can we get data for sin(DAE)?
epicpwn314
2013-04-05 19:36:46
draw the altitude
draw the altitude
sunny2000
2013-04-05 19:36:46
draw altitude
draw altitude
Lemon123
2013-04-05 19:36:46
Draw Altitude/Median
Draw Altitude/Median
tenniskidperson3
2013-04-05 19:36:46
Area
Area
ssilwa
2013-04-05 19:36:46
Use area
Use area
Tommy2000
2013-04-05 19:36:46
make a right triangle?
make a right triangle?
bobthesmartypants
2013-04-05 19:36:46
First draw height from A to BC
First draw height from A to BC
DPatrick
2013-04-05 19:37:05
First let's think about the area. What do we know about this picture?
First let's think about the area. What do we know about this picture?
kdokmeci
2013-04-05 19:37:28
Area is trisected
Area is trisected
ZZmath9
2013-04-05 19:37:28
All three triangles have same area
All three triangles have same area
sparkles257
2013-04-05 19:37:28
three triangles have equal areas
three triangles have equal areas
DPatrick
2013-04-05 19:37:33
Right. Each small triangle is one-third the area of the big triangle.
Right. Each small triangle is one-third the area of the big triangle.
DPatrick
2013-04-05 19:37:51
What's the area of the big triangle (using the lengths I've chosen)?
What's the area of the big triangle (using the lengths I've chosen)?
countyguy
2013-04-05 19:38:12
9sqrt3
9sqrt3
theGoodGuy
2013-04-05 19:38:12
9sqrt3
9sqrt3
AayushGupta
2013-04-05 19:38:12
9sqrt3 is the area of the big one
9sqrt3 is the area of the big one
fmasroor
2013-04-05 19:38:12
9sqrt3
9sqrt3
az_phx_brandon_jiang
2013-04-05 19:38:12
9sqrt3
9sqrt3
NumberGiant
2013-04-05 19:38:12
9sqrt3
9sqrt3
DPatrick
2013-04-05 19:38:16
[ABC]=62⋅√34=9√3.
[ABC]=62⋅√34=9√3.
DPatrick
2013-04-05 19:38:24
So each small triangle has area 3√3.
So each small triangle has area 3√3.
DPatrick
2013-04-05 19:38:37
How does that help?
How does that help?
vyzw
2013-04-05 19:38:53
so the height is 3sqrt3.
so the height is 3sqrt3.
bobthesmartypants
2013-04-05 19:38:53
so the height is 3sqrt3/2*2=3sqrt3
so the height is 3sqrt3/2*2=3sqrt3
yrushi
2013-04-05 19:38:53
so altitude is 3√3
so altitude is 3√3
ZZmath9
2013-04-05 19:38:53
We now can find the height
We now can find the height
DPatrick
2013-04-05 19:39:15
Indeed, the height of any of them is 3√3.
Indeed, the height of any of them is 3√3.
DPatrick
2013-04-05 19:39:18
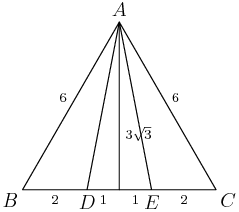

kdokmeci
2013-04-05 19:39:49
So we can find AD
So we can find AD
Lemon123
2013-04-05 19:39:49
pythogras Theorem for AE or AD
pythogras Theorem for AE or AD
noobynoob
2013-04-05 19:39:49
Area = $(AD)(DE)\sin DAE
Area = $(AD)(DE)\sin DAE
DPatrick
2013-04-05 19:39:55
Aha, all the pieces are falling into place!
Aha, all the pieces are falling into place!
yrushi
2013-04-05 19:40:14
find AD=2√7
find AD=2√7
vyzw
2013-04-05 19:40:14
AD=2sqrt7
AD=2sqrt7
DPatrick
2013-04-05 19:40:16
We have
(AD)2=12+(3√3)2=28,
so AD=√28=2√7.
We have
(AD)2=12+(3√3)2=28,
so AD=√28=2√7.
DPatrick
2013-04-05 19:40:43
But now the thing we want -- sin(DAE) -- is part of the area formula for the middle triangle.
But now the thing we want -- sin(DAE) -- is part of the area formula for the middle triangle.
matholympiad25
2013-04-05 19:40:54
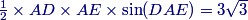
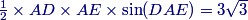
az_phx_brandon_jiang
2013-04-05 19:40:54
[ADE]=3sqrt3=1/2 sin(DAE)*AD*DE
[ADE]=3sqrt3=1/2 sin(DAE)*AD*DE
mxie
2013-04-05 19:41:02
now use the area formula, Area = AD * AD * sin DAE * 1/2
now use the area formula, Area = AD * AD * sin DAE * 1/2
DPatrick
2013-04-05 19:41:11
We use the area formula for triangle ADE:
3√3=[ADE]=12(AD)2sin(DAE).
We use the area formula for triangle ADE:
3√3=[ADE]=12(AD)2sin(DAE).
ninjataco
2013-04-05 19:41:22
and we can substitute in the values we know
and we can substitute in the values we know
DPatrick
2013-04-05 19:41:31
We know (AD)2=28, so
3√3=14sin(DAE),
hence sin(DAE)=3√314.
We know (AD)2=28, so
3√3=14sin(DAE),
hence sin(DAE)=3√314.
ninjataco
2013-04-05 19:41:43
and the answer is 020
and the answer is 020
matholympiad25
2013-04-05 19:41:49
3+3+14=020
3+3+14=020
twin77
2013-04-05 19:41:49
the answer is 020
the answer is 020
mathmaster2012
2013-04-05 19:41:49
3+3+14=20, which is our answer!
3+3+14=20, which is our answer!
DPatrick
2013-04-05 19:41:53
Our final answer is 3+3+14=020.
Our final answer is 3+3+14=020.
sunny2000
2013-04-05 19:41:56
wait, couldn't you just have drawn altitude, use pythagorean, and use double angle sine formula?
wait, couldn't you just have drawn altitude, use pythagorean, and use double angle sine formula?
DPatrick
2013-04-05 19:42:02
Certainly!
Certainly!
DPatrick
2013-04-05 19:42:19
But I trust myself to remember the area formula more than the double-angle formula.
But I trust myself to remember the area formula more than the double-angle formula.
DPatrick
2013-04-05 19:42:38
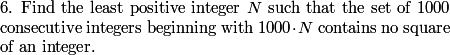
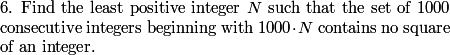
DPatrick
2013-04-05 19:42:57
Just to agree on some terminology, let's call a "block" a set of 1000 consecutive digits beginning with 1000N for some N. These are all the numbers that share the same digits except for the final three.
Just to agree on some terminology, let's call a "block" a set of 1000 consecutive digits beginning with 1000N for some N. These are all the numbers that share the same digits except for the final three.
DPatrick
2013-04-05 19:43:05
How high do we have to go before the perfect squares get at least 1000 apart?
How high do we have to go before the perfect squares get at least 1000 apart?
mathwrath
2013-04-05 19:43:21
500^2 and 501^2 are the first two more than 1000 apart.
500^2 and 501^2 are the first two more than 1000 apart.
yrushi
2013-04-05 19:43:21
we have (n+1)2−n2=2n+1
we have (n+1)2−n2=2n+1
ssilwa
2013-04-05 19:43:21
500
500
davidkim2106
2013-04-05 19:43:21
500?
500?
epicpwn314
2013-04-05 19:43:21
500
500
JWK750
2013-04-05 19:43:21
N=500
N=500
genesis2
2013-04-05 19:43:21
250000
250000
DPatrick
2013-04-05 19:43:33
Right. Notice that (k+1)2−k2=2k+1.
Right. Notice that (k+1)2−k2=2k+1.
DPatrick
2013-04-05 19:43:40
So we need k≥500 for k2 and (k+1)2 to be at least 1000 apart.
So we need k≥500 for k2 and (k+1)2 to be at least 1000 apart.
DPatrick
2013-04-05 19:43:52
So 500 is the smallest we need to even consider looking at.
So 500 is the smallest we need to even consider looking at.
DPatrick
2013-04-05 19:43:58
Does k=500 work? That is, does the block after k2 avoid perfect squares?
Does k=500 work? That is, does the block after k2 avoid perfect squares?
kdokmeci
2013-04-05 19:44:20
500^2=250000, 501^2=2510001
500^2=250000, 501^2=2510001
math-rules
2013-04-05 19:44:20
no
no
AayushGupta
2013-04-05 19:44:20
no because it includes 500^2
no because it includes 500^2
mathmaster2012
2013-04-05 19:44:26
No, 501^2=500^2+1001 so no avoidance
No, 501^2=500^2+1001 so no avoidance
DPatrick
2013-04-05 19:44:36
Right. 5002=250000 doesn't work.
Right. 5002=250000 doesn't work.
DPatrick
2013-04-05 19:44:56
And 5012=251001, so we don't avoid a perfect square in the 251xxx block.
And 5012=251001, so we don't avoid a perfect square in the 251xxx block.
mathwrath
2013-04-05 19:45:12
(500+x)^2=500^2+2*500*x+x^2=500^2+100x+x^2
(500+x)^2=500^2+2*500*x+x^2=500^2+100x+x^2
bobthesmartypants
2013-04-05 19:45:12
can we represent k as x+500, such that x≥0
can we represent k as x+500, such that x≥0
twin77
2013-04-05 19:45:12
use (500+n)^2 to test
use (500+n)^2 to test
DPatrick
2013-04-05 19:45:24
Good idea. (500+a)2=250000+1000a+a2, so choosing k=500+a will give us a perfect square in the block beginning with 1000⋅(250+a):
Good idea. (500+a)2=250000+1000a+a2, so choosing k=500+a will give us a perfect square in the block beginning with 1000⋅(250+a):
DPatrick
2013-04-05 19:45:29
5012=251001,5022=252004,5032=253009,5042=254016,etc.
5012=251001,5022=252004,5032=253009,5042=254016,etc.
swimmerstar
2013-04-05 19:45:45
wait the last 3 digits are perfect squares
wait the last 3 digits are perfect squares
ZZmath9
2013-04-05 19:45:45
There's a pattern
There's a pattern
DPatrick
2013-04-05 19:45:50
Aha.
Aha.
DPatrick
2013-04-05 19:46:10
The last three digits of (500+a)2 are just a2.
The last three digits of (500+a)2 are just a2.
DPatrick
2013-04-05 19:46:25
So if a2≥1000, then we might be able to skip a block.
So if a2≥1000, then we might be able to skip a block.
Tommy2000
2013-04-05 19:46:46
it will stop when it gets to 961 or 31^2
it will stop when it gets to 961 or 31^2
Superwiz
2013-04-05 19:46:46
a^2>1000[
a^2>1000[
mathworld1
2013-04-05 19:46:46
we need a >= 32
we need a >= 32
vyzw
2013-04-05 19:46:46
so then since 31^2<1000 we check 32
so then since 31^2<1000 we check 32
stellalau
2013-04-05 19:46:46
so then we choose a were a^2 > 1000, smallest of this would be 32^2
so then we choose a were a^2 > 1000, smallest of this would be 32^2
DPatrick
2013-04-05 19:46:54
Notice that 312=961 and 322=1024.
Notice that 312=961 and 322=1024.
DPatrick
2013-04-05 19:47:01
5312=(500+31)2=250000+31000+961=281961
5312=(500+31)2=250000+31000+961=281961
DPatrick
2013-04-05 19:47:06
5322=(500+32)2=250000+32000+1024=283024
5322=(500+32)2=250000+32000+1024=283024
DPatrick
2013-04-05 19:47:16
We win!
We win!
mathwrath
2013-04-05 19:47:38
282000 has none.
282000 has none.
ninjataco
2013-04-05 19:47:38
it skipped 282000
it skipped 282000
bobthesmartypants
2013-04-05 19:47:38
It skips 282000, so 282 is the answer
It skips 282000, so 282 is the answer
NumberGiant
2013-04-05 19:47:38


DPatrick
2013-04-05 19:47:46
The 282xxx block doesn't have any perfect squares!
The 282xxx block doesn't have any perfect squares!
DPatrick
2013-04-05 19:47:52
So our answer is 282.
So our answer is 282.
DPatrick
2013-04-05 19:48:14


ninjataco
2013-04-05 19:48:39
assign variables for the original number of clerks and the number that are reassigned
assign variables for the original number of clerks and the number that are reassigned
matholympiad25
2013-04-05 19:48:39
Let original number of clerks = c, number removed every hour = r.
Let original number of clerks = c, number removed every hour = r.
DPatrick
2013-04-05 19:48:46
Good idea. Suppose we start with c clerks, and reassign r of them every hour.
Good idea. Suppose we start with c clerks, and reassign r of them every hour.
DPatrick
2013-04-05 19:48:59
How many files get sorted in the first hour?
How many files get sorted in the first hour?
MathPerson060375
2013-04-05 19:49:14
30c
30c
19bobhu
2013-04-05 19:49:14
30c
30c
az_phx_brandon_jiang
2013-04-05 19:49:14
30c
30c
countyguy
2013-04-05 19:49:14
30c
30c
dan2012
2013-04-05 19:49:14
30c
30c
DPatrick
2013-04-05 19:49:18
In the first hour, they sort 30c files.
In the first hour, they sort 30c files.
DPatrick
2013-04-05 19:49:23
How about the second hour?
How about the second hour?
number.sense
2013-04-05 19:49:34
30c-30r
30c-30r
JWK750
2013-04-05 19:49:34
30(c-r)
30(c-r)
wpk
2013-04-05 19:49:34
30(c-r)
30(c-r)
yrushi
2013-04-05 19:49:34
30(c-r)
30(c-r)
mxie
2013-04-05 19:49:34
30(c-r)
30(c-r)
fmasroor
2013-04-05 19:49:34
30(c-r)
30(c-r)
DPatrick
2013-04-05 19:49:38
In the second hour, there are only c−r clerks remaining, so they sort another 30(c−r) files.
In the second hour, there are only c−r clerks remaining, so they sort another 30(c−r) files.
DPatrick
2013-04-05 19:49:43
How about the third hour?
How about the third hour?
sparkles257
2013-04-05 19:50:00
30(c-2r)
30(c-2r)
genesis2
2013-04-05 19:50:00
30(c-2r)
30(c-2r)
ssilwa
2013-04-05 19:50:00
30c-60r
30c-60r
davidkim2106
2013-04-05 19:50:00
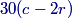
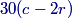
distortedwalrus
2013-04-05 19:50:00
30(c-2r)
30(c-2r)
atmath2011
2013-04-05 19:50:00
30(c-2r)
30(c-2r)
DPatrick
2013-04-05 19:50:04
In the third hour, there are only c−2r clerks remaining, so they sort another 30(c−2r) files.
In the third hour, there are only c−2r clerks remaining, so they sort another 30(c−2r) files.
DPatrick
2013-04-05 19:50:11
And how about the final 10 minutes?
And how about the final 10 minutes?
AayushGupta
2013-04-05 19:50:30
5(c-3r)
5(c-3r)
matholympiad25
2013-04-05 19:50:30
10/60*30(c-3r)=5(c-3r)
10/60*30(c-3r)=5(c-3r)
kdokmeci
2013-04-05 19:50:30
5(c-3r)
5(c-3r)
mathmaster2012
2013-04-05 19:50:30
5(c-3r)
5(c-3r)
math-rules
2013-04-05 19:50:30
5(c-3r)
5(c-3r)
ilikepie333
2013-04-05 19:50:30
(30(c-3r))/6
(30(c-3r))/6
DPatrick
2013-04-05 19:50:35
In the final 10 minutes (which is 16 of an hour), there are only c−3r clerks remaining, so they sort the final 5(c−3r) files.
In the final 10 minutes (which is 16 of an hour), there are only c−3r clerks remaining, so they sort the final 5(c−3r) files.
fmasroor
2013-04-05 19:50:44
add them up, we should get 1775
add them up, we should get 1775
DPatrick
2013-04-05 19:50:50
Hence, the total number of files sorted is
30c+30(c−r)+30(c−2r)+5(c−3r)=1775.'
Hence, the total number of files sorted is
30c+30(c−r)+30(c−2r)+5(c−3r)=1775.'
DPatrick
2013-04-05 19:51:02
This simplifies to 95c−105r=1775.
This simplifies to 95c−105r=1775.
mathmaster2012
2013-04-05 19:51:11
Divide by 5
Divide by 5
twin77
2013-04-05 19:51:11
divide by 5
divide by 5
mathworld1
2013-04-05 19:51:11
19c-21r = 355
19c-21r = 355
DPatrick
2013-04-05 19:51:14
We can divide by 5 to get 19c−21r=355.
We can divide by 5 to get 19c−21r=355.
DPatrick
2013-04-05 19:51:20
How do we solve this?
How do we solve this?
matholympiad25
2013-04-05 19:51:33
c-3r>0, since there were still some clerks in the last 10 minutes
c-3r>0, since there were still some clerks in the last 10 minutes
DPatrick
2013-04-05 19:51:47
That's an important condition to note. We must have c and r positive integers, and c-3r > 0.
That's an important condition to note. We must have c and r positive integers, and c-3r > 0.
yrushi
2013-04-05 19:52:20
just add 21 to 355 until we get a multiple of 19
just add 21 to 355 until we get a multiple of 19
ninjataco
2013-04-05 19:52:20
c= (21r+355)/19, create a table?
c= (21r+355)/19, create a table?
DPatrick
2013-04-05 19:52:29
You could certainly guess-and-check to find the answer from here.
You could certainly guess-and-check to find the answer from here.
number.sense
2013-04-05 19:52:41
consider modulo 19
consider modulo 19
ssilwa
2013-04-05 19:52:41
take mod 19
take mod 19
bobthesmartypants
2013-04-05 19:52:41
use modular arithmetic
use modular arithmetic
DPatrick
2013-04-05 19:52:52
A more systematic way to solve is to look at the equation either mod 19 or mod 21.
A more systematic way to solve is to look at the equation either mod 19 or mod 21.
DPatrick
2013-04-05 19:53:20
Funnily enough, you all suggested mod 19. I actually used mod 21 at the time. But let's do mod 19 since you all suggested it.
Funnily enough, you all suggested mod 19. I actually used mod 21 at the time. But let's do mod 19 since you all suggested it.
DPatrick
2013-04-05 19:54:42
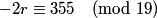
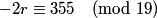
DPatrick
2013-04-05 19:54:51
And what is 355 mod 19?
And what is 355 mod 19?
stellalau
2013-04-05 19:55:12
13
13
Tommy2000
2013-04-05 19:55:12
13
13
mathwrath
2013-04-05 19:55:12
also -6
also -6
hjia1
2013-04-05 19:55:12
13
13
Debdut
2013-04-05 19:55:12
13
13
Superwiz
2013-04-05 19:55:12
-6 (mod 19)
-6 (mod 19)
MathPerson060375
2013-04-05 19:55:12
Is 13 mod 19
Is 13 mod 19
DPatrick
2013-04-05 19:56:03
You could divide it out to compute that 355 = 13 (mod 19).
You could divide it out to compute that 355 = 13 (mod 19).
DPatrick
2013-04-05 19:56:44
But 13 is the same as -6 (mod 19), so our equation is just −2r≡−6(mod19).
But 13 is the same as -6 (mod 19), so our equation is just −2r≡−6(mod19).
math-rules
2013-04-05 19:56:58
r=3
r=3
vyzw
2013-04-05 19:56:58
r=3 is possible from -6
r=3 is possible from -6
dilei
2013-04-05 19:56:58
r=3
r=3
19bobhu
2013-04-05 19:56:58
r=3
r=3
DPatrick
2013-04-05 19:57:11
This gives r=3 as the smallest possible solution. Does it work?
This gives r=3 as the smallest possible solution. Does it work?
countyguy
2013-04-05 19:57:29
plug r=3 into the original equation
plug r=3 into the original equation
ninjataco
2013-04-05 19:57:29
yes and then c = 22
yes and then c = 22
wpk
2013-04-05 19:57:29
c = 22
c = 22
DPatrick
2013-04-05 19:57:35
It does!
It does!
DPatrick
2013-04-05 19:58:01


DPatrick
2013-04-05 19:58:15
So we get a solution with 22 clerks, with 3 being removed every hour.
So we get a solution with 22 clerks, with 3 being removed every hour.
noobynoob
2013-04-05 19:58:26
what if r were bigger?
what if r were bigger?
DPatrick
2013-04-05 19:58:38
That's a good question to ask. You can observe that this is the only solution, since to get any other potential solution we'd have to increase the number of clerks by 21 and the number removed by 19. But 43 clerks, removing 22 per hour, would leave a negative number of clerks after 2 hours! And if we went up to 64 clerks, they'd finish all the sorting in the first hour!
That's a good question to ask. You can observe that this is the only solution, since to get any other potential solution we'd have to increase the number of clerks by 21 and the number removed by 19. But 43 clerks, removing 22 per hour, would leave a negative number of clerks after 2 hours! And if we went up to 64 clerks, they'd finish all the sorting in the first hour!
DPatrick
2013-04-05 19:59:04
So (c,r) = (22,3) is in fact the only solution that works.
So (c,r) = (22,3) is in fact the only solution that works.
DPatrick
2013-04-05 19:59:11
So we have 22 clerks in the first hour, with 3 being removed every hour. What's the final answer?
So we have 22 clerks in the first hour, with 3 being removed every hour. What's the final answer?
yrushi
2013-04-05 19:59:20
now we need 30c+15(c−r)
now we need 30c+15(c−r)
twin77
2013-04-05 19:59:36
so the answer is 30(22) + 15(19) = 945
so the answer is 30(22) + 15(19) = 945
bobthesmartypants
2013-04-05 19:59:36
now to find the 1.5 hour we do 30(22)+15(19)
now to find the 1.5 hour we do 30(22)+15(19)
dan2012
2013-04-05 19:59:40
the answer is 945 then
the answer is 945 then
DPatrick
2013-04-05 19:59:43
In 1.5 hours, they sort 30c+15(c−r)=45c−15r=15(3c−r) files. Hence our answer is
15(3(22)−3)=15(63)=945.
In 1.5 hours, they sort 30c+15(c−r)=45c−15r=15(3c−r) files. Hence our answer is
15(3(22)−3)=15(63)=945.
DPatrick
2013-04-05 20:00:06


DPatrick
2013-04-05 20:00:17
Let's sketch a picture:
Let's sketch a picture:
DPatrick
2013-04-05 20:00:22

DPatrick
2013-04-05 20:00:26
Let's also call the unknown radius r.
Let's also call the unknown radius r.
DPatrick
2013-04-05 20:00:28
Now what?
Now what?
ssilwa
2013-04-05 20:01:11
draw some lines
draw some lines
MSTang
2013-04-05 20:01:11
draw radii to the vertices
draw radii to the vertices
kdokmeci
2013-04-05 20:01:11
Draw radii
Draw radii
AayushGupta
2013-04-05 20:01:11
connect the center to each of the vertices
connect the center to each of the vertices
DPatrick
2013-04-05 20:01:33
There are a lot of complicated things you could do, or one really simple thing you could do.
There are a lot of complicated things you could do, or one really simple thing you could do.
DPatrick
2013-04-05 20:01:56
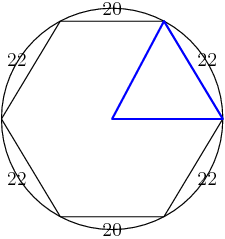
In fact, we only need to draw two radii:
In fact, we only need to draw two radii:
DPatrick
2013-04-05 20:02:02

DPatrick
2013-04-05 20:02:11
What do we know about this triangle?
What do we know about this triangle?
matholympiad25
2013-04-05 20:02:28
it is isosceles
it is isosceles
sparkles257
2013-04-05 20:02:28
isosclees
isosclees
sunny2000
2013-04-05 20:02:28
it's isoceles
it's isoceles
vyzw
2013-04-05 20:02:28
isosceles
isosceles
fmasroor
2013-04-05 20:02:28
isosceles
isosceles
stellalau
2013-04-05 20:02:28
isosceles
isosceles
DPatrick
2013-04-05 20:02:48
Sure: both blue radii have length r. But surely we know a little more than that...
Sure: both blue radii have length r. But surely we know a little more than that...
genesis2
2013-04-05 20:03:04
the triangle seems to cry out to draw an altitude
the triangle seems to cry out to draw an altitude
DPatrick
2013-04-05 20:03:22

DPatrick
2013-04-05 20:03:39
So what?
So what?
Apollo13
2013-04-05 20:04:11
use pythagarean theroem
use pythagarean theroem
Apollo13
2013-04-05 20:04:11
use Pythagorean theorem
use Pythagorean theorem
zhuangzhuang
2013-04-05 20:04:11
Pythagorean theo
Pythagorean theo
Tommy2000
2013-04-05 20:04:11
call the height h and solve for it using the pythagorean theorm
call the height h and solve for it using the pythagorean theorm
MathPerson060375
2013-04-05 20:04:11
pythag!
pythag!
math-rules
2013-04-05 20:04:11
pythag for the altitude on both right triangles and equate
pythag for the altitude on both right triangles and equate
ico_the_psycho
2013-04-05 20:04:11
Equate the two expressions for the altitude, obtained by Pythagoras' Thm?
Equate the two expressions for the altitude, obtained by Pythagoras' Thm?
DPatrick
2013-04-05 20:04:23
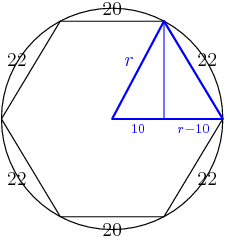
If we call the height h, then by the Pythagorean Theorem (twice):
h2=r2−102=222−(r−10)2.
If we call the height h, then by the Pythagorean Theorem (twice):
h2=r2−102=222−(r−10)2.
ilikepie333
2013-04-05 20:04:49
simplify for r
simplify for r
DPatrick
2013-04-05 20:04:54
This gives
r2−100=484−r2+20r−100,
or 2r2−20r−484=0.
This gives
r2−100=484−r2+20r−100,
or 2r2−20r−484=0.
HYP135peppers
2013-04-05 20:05:12
divide by 2
divide by 2
bobthesmartypants
2013-04-05 20:05:12
divide by 2
divide by 2
DPatrick
2013-04-05 20:05:16
Dividing by 2 gives r2−10r−242=0.
Dividing by 2 gives r2−10r−242=0.
DPatrick
2013-04-05 20:05:53
(Note: several people are asking where the 10 and r-10 came from. The "10" is half of the "20" from the top side.)
(Note: several people are asking where the 10 and r-10 came from. The "10" is half of the "20" from the top side.)
mathwrath
2013-04-05 20:06:05
quadratic formula
quadratic formula
19bobhu
2013-04-05 20:06:05
Quadratic
Quadratic
DPatrick
2013-04-05 20:06:10
Now the quadratic formula gives
r=10±√100+4(242)2=5±√25+242=5±√267.
Now the quadratic formula gives
r=10±√100+4(242)2=5±√25+242=5±√267.
tapir1729
2013-04-05 20:06:22


MSTang
2013-04-05 20:06:22
disregard negative solution
disregard negative solution
DPatrick
2013-04-05 20:06:27
We clearly want the positive value of r, so r=5+√267, and our final answer is 5+267=272.
We clearly want the positive value of r, so r=5+√267, and our final answer is 5+267=272.
DPatrick
2013-04-05 20:07:00


DPatrick
2013-04-05 20:07:15
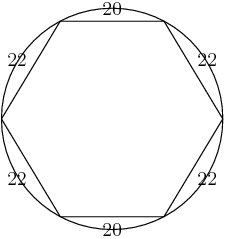
I found that a little picture helped me visualize the problem. Here's the sample that they gave:
I found that a little picture helped me visualize the problem. Here's the sample that they gave:
DPatrick
2013-04-05 20:07:20


DPatrick
2013-04-05 20:07:24
And here's the blank board:
And here's the blank board:
DPatrick
2013-04-05 20:07:29


DPatrick
2013-04-05 20:07:36
How do we count the tilings?
How do we count the tilings?
DPatrick
2013-04-05 20:07:56
Let's suppose we tried to build one of these tilings. How could we do so?
Let's suppose we tried to build one of these tilings. How could we do so?
HYP135peppers
2013-04-05 20:08:30
fill in with different colors and size
fill in with different colors and size
AayushGupta
2013-04-05 20:08:36
assign a first color, then a second, and so on, adding tile breaks as well
assign a first color, then a second, and so on, adding tile breaks as well
DPatrick
2013-04-05 20:08:57
Let's just move left-to-right along the board.
Let's just move left-to-right along the board.
DPatrick
2013-04-05 20:09:06
How many choices for the first square?
How many choices for the first square?
yrushi
2013-04-05 20:09:21
3
3
dan2012
2013-04-05 20:09:21
3
3
kdokmeci
2013-04-05 20:09:21
3
3
ssilwa
2013-04-05 20:09:21
3
3
stellalau
2013-04-05 20:09:21
3
3
19JasonH
2013-04-05 20:09:21
3
3
DPatrick
2013-04-05 20:09:28
We need to pick a color for the first square. That's 3 choices.
We need to pick a color for the first square. That's 3 choices.
DPatrick
2013-04-05 20:09:37
Then, for the next square, what are the choices?
Then, for the next square, what are the choices?
MathPerson060375
2013-04-05 20:09:57
4 choices
4 choices
zhuangzhuang
2013-04-05 20:09:57
same or new tile
same or new tile
AayushGupta
2013-04-05 20:09:57
4
4
MSTang
2013-04-05 20:10:04
extend tile from first square, or build another separate tile in 3 ways
extend tile from first square, or build another separate tile in 3 ways
DPatrick
2013-04-05 20:10:16
Right: We could continue the previous tile, or we could start a new tile in any of the 3 colors. So there are 4 choices for the next square.
Right: We could continue the previous tile, or we could start a new tile in any of the 3 colors. So there are 4 choices for the next square.
DPatrick
2013-04-05 20:10:46
The same is true for every subsequent square: we could continue the previous tile, or we could start a new tile in any of the 3 colors. So there are 4 choices for each subsequent square.
The same is true for every subsequent square: we could continue the previous tile, or we could start a new tile in any of the 3 colors. So there are 4 choices for each subsequent square.
DPatrick
2013-04-05 20:10:58
For example, the sample tiling above is from the choices:
red, green, continue, green, blue, continue, green
For example, the sample tiling above is from the choices:
red, green, continue, green, blue, continue, green
AayushGupta
2013-04-05 20:11:13
so 3 x 4^6
so 3 x 4^6
viva
2013-04-05 20:11:13
3*(4^6)
3*(4^6)
19bobhu
2013-04-05 20:11:13
so it's 3*4^6
so it's 3*4^6
dan2012
2013-04-05 20:11:13
3x4^6
3x4^6
DPatrick
2013-04-05 20:11:40
Right, there are 3 choices for the first square, then 4 choices for each of the 6 subsequent square, so that's 3⋅46=3⋅4096=12288 tilings total.
Right, there are 3 choices for the first square, then 4 choices for each of the 6 subsequent square, so that's 3⋅46=3⋅4096=12288 tilings total.
number.sense
2013-04-05 20:11:50
have to correct for not using all 3 colors
have to correct for not using all 3 colors
TheStrangeCharm
2013-04-05 20:11:50
but we need to use each color exactly once?
but we need to use each color exactly once?
math-rules
2013-04-05 20:11:50
but you need to make sure all colors are used
but you need to make sure all colors are used
sume
2013-04-05 20:11:50
now count tilings that dont have three colors
now count tilings that dont have three colors
DPatrick
2013-04-05 20:12:16
Indeed, it's not quite so simple. We've counted some tilings that don't use all three colors, as required.
Indeed, it's not quite so simple. We've counted some tilings that don't use all three colors, as required.
DPatrick
2013-04-05 20:12:37
We need to ensure that we use each color at least once.
We need to ensure that we use each color at least once.
DPatrick
2013-04-05 20:12:54
So we must subtract off the colorings that don't use some color.
So we must subtract off the colorings that don't use some color.
DPatrick
2013-04-05 20:12:58
How many tilings don't use red?
How many tilings don't use red?
kdokmeci
2013-04-05 20:13:24
2x3^6
2x3^6
atmath2011
2013-04-05 20:13:24
2*3^6
2*3^6
shreyash
2013-04-05 20:13:24
2*3^6
2*3^6
Tommy2000
2013-04-05 20:13:24
2*3^6
2*3^6
twin77
2013-04-05 20:13:24
2*3^6
2*3^6
DPatrick
2013-04-05 20:13:36
Right, we can use the same logic: now we have 2 choices (blue or green) for the first square, and 3 choices (continue, blue, or green) for each of the 6 subsequent squares.
Right, we can use the same logic: now we have 2 choices (blue or green) for the first square, and 3 choices (continue, blue, or green) for each of the 6 subsequent squares.
DPatrick
2013-04-05 20:13:44
So there are 2⋅36=2⋅729=1458 tilings that don't use red.
So there are 2⋅36=2⋅729=1458 tilings that don't use red.
Tommy2000
2013-04-05 20:13:50
same for blue and green
same for blue and green
matholympiad25
2013-04-05 20:13:53
similar for blue, green
similar for blue, green
JoshH
2013-04-05 20:13:53
Same with other two colors
Same with other two colors
DPatrick
2013-04-05 20:13:57
Similarly, there are 1458 that don't use blue, and 1458 that don't use green.
Similarly, there are 1458 that don't use blue, and 1458 that don't use green.
ilikepie333
2013-04-05 20:14:04
4374 tilings that are not good
4374 tilings that are not good
DPatrick
2013-04-05 20:14:08
So our tiling count is now 12288−3(1458)=12288−4374=7914.
So our tiling count is now 12288−3(1458)=12288−4374=7914.
DPatrick
2013-04-05 20:14:14
Are we done?
Are we done?
matholympiad25
2013-04-05 20:14:40
now we count back those that have only one color.
now we count back those that have only one color.
twin77
2013-04-05 20:14:40
but we need to add the ones with only 1 color
but we need to add the ones with only 1 color
bobthesmartypants
2013-04-05 20:14:40
no, undercounted
no, undercounted
DPatrick
2013-04-05 20:14:49
We're not done! We've doubly-subtracted the tilings that only use one color.
We're not done! We've doubly-subtracted the tilings that only use one color.
DPatrick
2013-04-05 20:14:53
(For example, a tiling that's all blue will have been subtracted twice, once in the "no red" group and once in the "no green" group.)
(For example, a tiling that's all blue will have been subtracted twice, once in the "no red" group and once in the "no green" group.)
DPatrick
2013-04-05 20:15:05
So we need to add the one-color tilings back in.
So we need to add the one-color tilings back in.
DPatrick
2013-04-05 20:15:11
How many are there?
How many are there?
MathPerson060375
2013-04-05 20:15:38
So add in 3*2^6
So add in 3*2^6
MSTang
2013-04-05 20:15:38
There are 3*2^6 of them
There are 3*2^6 of them
HYP135peppers
2013-04-05 20:15:38
2^6 for each color
2^6 for each color
willabc
2013-04-05 20:15:38
3*2^6
3*2^6
countyguy
2013-04-05 20:15:38
3*2^6=192
3*2^6=192
coldsummer
2013-04-05 20:15:38
for red its 2^6, multiply by 3 to get 192 not counted cases
for red its 2^6, multiply by 3 to get 192 not counted cases
DPatrick
2013-04-05 20:15:48
Right. There are 3 choices for which color to use, and then 26=64 choices for whether to start a new tile or not at each subsequent square.
Right. There are 3 choices for which color to use, and then 26=64 choices for whether to start a new tile or not at each subsequent square.
DPatrick
2013-04-05 20:15:57
So there are 3⋅64=192 one-color tilings.
So there are 3⋅64=192 one-color tilings.
DPatrick
2013-04-05 20:16:03
We add these back in to get 7914+192=8106 legal tilings.
We add these back in to get 7914+192=8106 legal tilings.
DPatrick
2013-04-05 20:16:08
Are we done?
Are we done?
sume
2013-04-05 20:16:26
yes
yes
mathwrath
2013-04-05 20:16:26
Yes
Yes
TheStrangeCharm
2013-04-05 20:16:26
yes
yes
MathPerson060375
2013-04-05 20:16:26
I hope
I hope
biddyxm
2013-04-05 20:16:26
Yes
Yes
ilikepie333
2013-04-05 20:16:26
106=final answer
106=final answer
Tommy2000
2013-04-05 20:16:26
8106mod 100= 106
8106mod 100= 106
twin77
2013-04-05 20:16:26
yes, so the answer is 106
yes, so the answer is 106
DPatrick
2013-04-05 20:16:38
Now we're done! There are 8106 tilings, so mod 1000 our answer is 106.
Now we're done! There are 8106 tilings, so mod 1000 our answer is 106.
DPatrick
2013-04-05 20:17:13
We've finish all the single-digit problems (1-9). I'm going to take a quick break to rest my typing hands, and we'll resume at :22 past the hours to look at problems 10-15.
We've finish all the single-digit problems (1-9). I'm going to take a quick break to rest my typing hands, and we'll resume at :22 past the hours to look at problems 10-15.
DPatrick
2013-04-05 20:21:39
:30 second warning
:30 second warning
DPatrick
2013-04-05 20:22:16


DPatrick
2013-04-05 20:22:36
Obviously we want a picture!
Obviously we want a picture!
DPatrick
2013-04-05 20:22:41


DPatrick
2013-04-05 20:22:44
We want to maximize the area of the red triangle.
We want to maximize the area of the red triangle.
DPatrick
2013-04-05 20:22:51
Any ideas?
Any ideas?
DPatrick
2013-04-05 20:23:58
To me, the given lengths suggest to try to set up areas of triangles with bases OB or AB or AO. We want to be able to isolate [BKL] but let's see what we can find out.
To me, the given lengths suggest to try to set up areas of triangles with bases OB or AB or AO. We want to be able to isolate [BKL] but let's see what we can find out.
math-rules
2013-04-05 20:24:05
[BKL]=[ABL]-[ABK]
[BKL]=[ABL]-[ABK]
DPatrick
2013-04-05 20:24:31
Indeed, so let's look at ABL and ABK. And let's get O in there too. So let me add OK and OL to the picture.
Indeed, so let's look at ABL and ABK. And let's get O in there too. So let me add OK and OL to the picture.
DPatrick
2013-04-05 20:24:37


DPatrick
2013-04-05 20:25:10
DPatrick
2013-04-05 20:25:29
What triangle(s) can we relate [ABK] to easily?
What triangle(s) can we relate [ABK] to easily?
DPatrick
2013-04-05 20:25:42
(By the way, for those who don't know, [ABK] is a shorthand for the area of ABK.)
(By the way, for those who don't know, [ABK] is a shorthand for the area of ABK.)
MSTang
2013-04-05 20:26:07
OBK?
OBK?
ilikepie333
2013-04-05 20:26:07
OBK?
OBK?
sparkles257
2013-04-05 20:26:07
ako
ako
matholympiad25
2013-04-05 20:26:07
AKO
AKO
HYP135peppers
2013-04-05 20:26:07
[OBK]
[OBK]
atmath2011
2013-04-05 20:26:07
obk
obk
DPatrick
2013-04-05 20:26:34
Either OBK or OAK share the same height from K down to the line A--B--O, and we also know how the lengths of the bases relate.
Either OBK or OAK share the same height from K down to the line A--B--O, and we also know how the lengths of the bases relate.
DPatrick
2013-04-05 20:27:00
It turns out that using OAK will be better in the end (though admittedly it's not so easy maybe to see that now).
It turns out that using OAK will be better in the end (though admittedly it's not so easy maybe to see that now).
DPatrick
2013-04-05 20:27:09
What's the ratio [KAB]/[KAO]?
What's the ratio [KAB]/[KAO]?
ninjataco
2013-04-05 20:27:20
their areas are in the same proportion as their bases
their areas are in the same proportion as their bases
They
2013-04-05 20:27:33
4/(4+rt13)
4/(4+rt13)
kdokmeci
2013-04-05 20:27:33
4/(4+root 13)
4/(4+root 13)
mathwrath
2013-04-05 20:27:33
4/(4+sqrt13)
4/(4+sqrt13)
ssilwa
2013-04-05 20:27:33
4/(4+sqrt13)
4/(4+sqrt13)
MSTang
2013-04-05 20:27:33
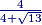
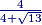
DPatrick
2013-04-05 20:27:51
KAB and KAO have the same height from K, so the ratio of their areas is the ratio of their bases:
[KAB][KAO]=44+√13.
KAB and KAO have the same height from K, so the ratio of their areas is the ratio of their bases:
[KAB][KAO]=44+√13.
DPatrick
2013-04-05 20:28:15
So far, so good.
So far, so good.
DPatrick
2013-04-05 20:28:57
We earlier observed that [BKL] is the difference between [KAB] and [LAB], so maybe we should try to do the same thing with [LAB]?
We earlier observed that [BKL] is the difference between [KAB] and [LAB], so maybe we should try to do the same thing with [LAB]?
matholympiad25
2013-04-05 20:29:20
yes, indeed, the areas are in same ratio
yes, indeed, the areas are in same ratio
bobthesmartypants
2013-04-05 20:29:23
[LAB] with [LOB]
[LAB] with [LOB]
DPatrick
2013-04-05 20:29:37
Right, we can do the same thing with point L:
[LAB][LAO]=44+√13.
Right, we can do the same thing with point L:
[LAB][LAO]=44+√13.
DPatrick
2013-04-05 20:30:03
And keep in mind that what's nice is that the red triangle is the difference between LAB and KAB, the two numerators of our ratios of areas.
And keep in mind that what's nice is that the red triangle is the difference between LAB and KAB, the two numerators of our ratios of areas.
DPatrick
2013-04-05 20:30:13
So we have two ratios that are the same. What does that mean?
So we have two ratios that are the same. What does that mean?
DPatrick
2013-04-05 20:30:34
...and we want [LAB] - [KAB]....
...and we want [LAB] - [KAB]....
bobthesmartypants
2013-04-05 20:30:47
subtract them
subtract them
kdokmeci
2013-04-05 20:30:53
subtract ratios?
subtract ratios?
DPatrick
2013-04-05 20:31:02
Right! If two ratios are the same, we're allowed to subtract them!
Right! If two ratios are the same, we're allowed to subtract them!
DPatrick
2013-04-05 20:31:08
That is, if ab=cd=k, then a−cb−d=k too. (This is worth learning, and proving, if you haven't seen it before!)
That is, if ab=cd=k, then a−cb−d=k too. (This is worth learning, and proving, if you haven't seen it before!)
DPatrick
2013-04-05 20:31:25
So let's use that with our area ratios!
So let's use that with our area ratios!
DPatrick
2013-04-05 20:31:32
[LAB]−[KAB][LAO]−[KAO]=[LKB][LKO]=44+√13.
[LAB]−[KAB][LAO]−[KAO]=[LKB][LKO]=44+√13.
DPatrick
2013-04-05 20:31:45
What have we accomplished by doing this?
What have we accomplished by doing this?
zhuangzhuang
2013-04-05 20:32:03
maximise area of LKO
maximise area of LKO
number.sense
2013-04-05 20:32:03
so you want to maximize LKO's area.... which is much easier to think about
so you want to maximize LKO's area.... which is much easier to think about
DPatrick
2013-04-05 20:32:28
Exactly. Our goal is to maximize [LKB]. But now we can maximize [LKO] instead and use it to compute [LKB].
Exactly. Our goal is to maximize [LKB]. But now we can maximize [LKO] instead and use it to compute [LKB].
DPatrick
2013-04-05 20:32:41
How do we maximize the area of LKO?
How do we maximize the area of LKO?
mathwrath
2013-04-05 20:33:12
best with 90 degree arc KL
best with 90 degree arc KL
noobynoob
2013-04-05 20:33:12
measure of ∠LOK=90
measure of ∠LOK=90
They
2013-04-05 20:33:12
Remember it's isosceles
Remember it's isosceles
matholympiad25
2013-04-05 20:33:12
LKO area is easy to maximize, it is just 1/2*OK*OL*sin LKO, so max sin LKO is just 1, so it is just 13/2
LKO area is easy to maximize, it is just 1/2*OK*OL*sin LKO, so max sin LKO is just 1, so it is just 13/2
bobthesmartypants
2013-04-05 20:33:12
LKO is maximized in area when LOK=90 degrees
LKO is maximized in area when LOK=90 degrees
zhuangzhuang
2013-04-05 20:33:12
make it right
make it right
shreyash
2013-04-05 20:33:19
OK and OL are perpendicular
OK and OL are perpendicular
DPatrick
2013-04-05 20:33:28
Exactly. LKO is isosceles with sides LO=KO=√13.
Exactly. LKO is isosceles with sides LO=KO=√13.
DPatrick
2013-04-05 20:33:44
So its area is maximized when ∠LOK is a right angle. Is that in fact possible to do in our construction?
So its area is maximized when ∠LOK is a right angle. Is that in fact possible to do in our construction?
ws0414
2013-04-05 20:34:08
yes?
yes?
ssilwa
2013-04-05 20:34:08
yes
yes
sunny2000
2013-04-05 20:34:08
yes
yes
MSTang
2013-04-05 20:34:08
yes
yes
They
2013-04-05 20:34:08
Why not?
Why not?
ico_the_psycho
2013-04-05 20:34:26
Yes, because there is enough wiggle room for the angle to vary from 0 to 180 degrees.
Yes, because there is enough wiggle room for the angle to vary from 0 to 180 degrees.
DPatrick
2013-04-05 20:34:28
Sure -- we just draw the ray from A to cut off a 90-degree arc of the circle.
Sure -- we just draw the ray from A to cut off a 90-degree arc of the circle.
DPatrick
2013-04-05 20:34:51
(The picture I drew looks a little too big an arc is cut off, but I was close!)
(The picture I drew looks a little too big an arc is cut off, but I was close!)
ninjataco
2013-04-05 20:35:02
then the area is 13/2
then the area is 13/2
fmasroor
2013-04-05 20:35:02
[LOK]=13/2
[LOK]=13/2
Tommy2000
2013-04-05 20:35:02
lko's area is 13\2
lko's area is 13\2
kdokmeci
2013-04-05 20:35:02
Maximum area of LOK is 13/2
Maximum area of LOK is 13/2
DPatrick
2013-04-05 20:35:16
So we get a maximum area of [LKO]=12(√13)2=132.
So we get a maximum area of [LKO]=12(√13)2=132.
ninjataco
2013-04-05 20:35:24
so, knowing that [LKO] is 13/2, we can substitute and solve for [LKB]
so, knowing that [LKO] is 13/2, we can substitute and solve for [LKB]
ssilwa
2013-04-05 20:35:24
now just cross multiply ansd solve for LKB
now just cross multiply ansd solve for LKB
DPatrick
2013-04-05 20:35:37
Right, we go back to our ratio to get:
[LKB]=(44+√13)[LKO]=264+√13.
Right, we go back to our ratio to get:
[LKB]=(44+√13)[LKO]=264+√13.
DPatrick
2013-04-05 20:35:52
Almost there, one small step to finish...
Almost there, one small step to finish...
Debdut
2013-04-05 20:36:07
Rationalize
Rationalize
countyguy
2013-04-05 20:36:07
conjugates to rationalize
conjugates to rationalize
distortedwalrus
2013-04-05 20:36:07
woohoo rationalize!
woohoo rationalize!
Hamliet
2013-04-05 20:36:07
CONJUGATE
CONJUGATE
muhaboug
2013-04-05 20:36:07
no sqrts in the denoms
no sqrts in the denoms
AayushGupta
2013-04-05 20:36:07
rationalize the denominator
rationalize the denominator
DPatrick
2013-04-05 20:36:16
We've still got to rationalize the denominator:
[LKB]=264+√13⋅4−√134−√13=104−26√133.
We've still got to rationalize the denominator:
[LKB]=264+√13⋅4−√134−√13=104−26√133.
kdokmeci
2013-04-05 20:36:30
104+26+13+3=146
104+26+13+3=146
DPatrick
2013-04-05 20:36:33
Now it's in the correct format, so our answer is 104+26+13+3=146.
Now it's in the correct format, so our answer is 104+26+13+3=146.
DPatrick
2013-04-05 20:36:55
This may have been my favorite problem, and I rarely say that about geometry problems!
This may have been my favorite problem, and I rarely say that about geometry problems!
DPatrick
2013-04-05 20:37:09
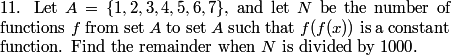
DPatrick
2013-04-05 20:37:26
As with the tiling problem, let's think about how we would construct such a function.
As with the tiling problem, let's think about how we would construct such a function.
DPatrick
2013-04-05 20:37:36
What do we have to decide?
What do we have to decide?
ico_the_psycho
2013-04-05 20:38:01
What the constant is going to be.
What the constant is going to be.
MSTang
2013-04-05 20:38:01
which constant f(f(x)) should be
which constant f(f(x)) should be
DPatrick
2013-04-05 20:38:06
We first need to pick the constant. Let's call it c, so that f(f(x))=c for all x∈A.
We first need to pick the constant. Let's call it c, so that f(f(x))=c for all x∈A.
DPatrick
2013-04-05 20:38:14
There are obviously 7 choices for c.
There are obviously 7 choices for c.
DPatrick
2013-04-05 20:38:28
Now what?
Now what?
matholympiad25
2013-04-05 20:39:00
now we pick the numbers n such that f(n)=c
now we pick the numbers n such that f(n)=c
ico_the_psycho
2013-04-05 20:39:00
Now we decide which subset of A collapses to c under the action of f.
Now we decide which subset of A collapses to c under the action of f.
DPatrick
2013-04-05 20:39:41
Right. Next we think about the rest of the numbers in A. They either map to c directly in one step (that is, f(x)=c), or in two steps (so that f(x)≠c but f(f(x))=c).
Right. Next we think about the rest of the numbers in A. They either map to c directly in one step (that is, f(x)=c), or in two steps (so that f(x)≠c but f(f(x))=c).
matholympiad25
2013-04-05 20:39:47
c needs to map to c
c needs to map to c
DPatrick
2013-04-05 20:39:55
This may seem obvious, but how do we know that?
This may seem obvious, but how do we know that?
DPatrick
2013-04-05 20:40:03
That is, how do we know that f(c)=c?
That is, how do we know that f(c)=c?
DPatrick
2013-04-05 20:40:40
Why can't we have f(c)=d for some d≠c and then f(d)=c?
Why can't we have f(c)=d for some d≠c and then f(d)=c?
q12
2013-04-05 20:41:13
then f(f(d))=d
then f(f(d))=d
They
2013-04-05 20:41:13
Then f(d) will be c and the second round will make it d.
Then f(d) will be c and the second round will make it d.
DPatrick
2013-04-05 20:42:12
Right, if d≠c, then we get f(f(d))=f(c)=d, which isn't allowed.
Right, if d≠c, then we get f(f(d))=f(c)=d, which isn't allowed.
DPatrick
2013-04-05 20:42:28
So we must have f(c)=c.
So we must have f(c)=c.
DPatrick
2013-04-05 20:42:52
But for each of the other 6 elements, they might map to c in one step or two steps.
But for each of the other 6 elements, they might map to c in one step or two steps.
matholympiad25
2013-04-05 20:43:00
now we pick the other ones that map to c
now we pick the other ones that map to c
DPatrick
2013-04-05 20:43:23
Right. And we have to keep in mind that the ones that don't map directly to c then have to map to one of the elements that does map to c.
Right. And we have to keep in mind that the ones that don't map directly to c then have to map to one of the elements that does map to c.
DPatrick
2013-04-05 20:43:38
This is getting a little confusing in words, so I decided to make a little chart to keep track of everything.
This is getting a little confusing in words, so I decided to make a little chart to keep track of everything.
DPatrick
2013-04-05 20:43:43
# of add'l elements# of choices for# of choices formapping to celements mapping to cother elementstotal123456
# of add'l elements# of choices for# of choices formapping to celements mapping to cother elementstotal123456
MSTang
2013-04-05 20:43:59
at least one must map to c
at least one must map to c
mathwrath
2013-04-05 20:43:59
At least one maps directly to c.
At least one maps directly to c.
DPatrick
2013-04-05 20:44:20
Indeed, we can't have all other 6 elements not map to c in one step, because they'd never map to c in two steps either.
Indeed, we can't have all other 6 elements not map to c in one step, because they'd never map to c in two steps either.
DPatrick
2013-04-05 20:44:29
So I don't have a "0" row in my left column.
So I don't have a "0" row in my left column.
DPatrick
2013-04-05 20:44:45
For each row, in how many ways can we choose the elements that map to c?
For each row, in how many ways can we choose the elements that map to c?
DPatrick
2013-04-05 20:45:01
If we need k elements, how many ways are there to pick them?
If we need k elements, how many ways are there to pick them?
DPatrick
2013-04-05 20:45:15
(Note that "add'l" is an abbreviation for "additional" in the chart.)
(Note that "add'l" is an abbreviation for "additional" in the chart.)
math-rules
2013-04-05 20:45:26
6ck, where k is the number in the left column
6ck, where k is the number in the left column
zhuangzhuang
2013-04-05 20:45:26
if the number in the row is x, then we can do 6CX
if the number in the row is x, then we can do 6CX
distortedwalrus
2013-04-05 20:45:26
6Ck
6Ck
TheStrangeCharm
2013-04-05 20:45:26
6 choose k
6 choose k
zhuangzhuang
2013-04-05 20:45:26
6Ck
6Ck
PlatinumFalcon
2013-04-05 20:45:26
6Ck
6Ck
DPatrick
2013-04-05 20:45:42
If we need k elements from the other 6 elements to map to c (besides c itself), then there are (6k) choices.
If we need k elements from the other 6 elements to map to c (besides c itself), then there are (6k) choices.
DPatrick
2013-04-05 20:45:47
So let's fill in the second column of the table:
So let's fill in the second column of the table:
DPatrick
2013-04-05 20:45:53
# of add'l elements# of choices for# of choices formapping to celements mapping to cother elementstotal162153204155661
# of add'l elements# of choices for# of choices formapping to celements mapping to cother elementstotal162153204155661
DPatrick
2013-04-05 20:46:07
How about the third column?
How about the third column?
DPatrick
2013-04-05 20:46:15
Each of the other items must map to one of the other elements mapping to c.
Each of the other items must map to one of the other elements mapping to c.
ico_the_psycho
2013-04-05 20:46:38
Then the remaining 6−k elements must map to these k elements. This can be done in k6−k ways.
Then the remaining 6−k elements must map to these k elements. This can be done in k6−k ways.
DPatrick
2013-04-05 20:46:47
Right. Let's see how this works.
Right. Let's see how this works.
DPatrick
2013-04-05 20:46:58
The first row has 5 other elements, but they each only have 1 choice: they must map to the element (other than c) that maps to c. So that's 15 choices.
The first row has 5 other elements, but they each only have 1 choice: they must map to the element (other than c) that maps to c. So that's 15 choices.
DPatrick
2013-04-05 20:47:24
The second row has 4 other elements, and each has 2 choices of where to map to: one of the 2 elements (other than c) that maps to c. So that's 24 choices.
The second row has 4 other elements, and each has 2 choices of where to map to: one of the 2 elements (other than c) that maps to c. So that's 24 choices.
DPatrick
2013-04-05 20:47:33
And so on.
And so on.
DPatrick
2013-04-05 20:47:37
We continue like this and fill in the third column:
We continue like this and fill in the third column:
DPatrick
2013-04-05 20:47:41
# of add'l elements# of choices for# of choices formapping to celements mapping to cother elementstotal161521524320334154256516160
# of add'l elements# of choices for# of choices formapping to celements mapping to cother elementstotal161521524320334154256516160
DPatrick
2013-04-05 20:48:03
What's the fourth column? What is the total possibilities for each row?
What's the fourth column? What is the total possibilities for each row?
Tommy2000
2013-04-05 20:48:15
multipy
multipy
number.sense
2013-04-05 20:48:15
multiple pairwise the second and third columns to get the total column
multiple pairwise the second and third columns to get the total column
sparkles257
2013-04-05 20:48:15
multiply them
multiply them
Tommy2000
2013-04-05 20:48:19
multiply column2 *column 3
multiply column2 *column 3
DPatrick
2013-04-05 20:48:58
Right. To construct a legal function we must make the choices indicated in both the second *and* third columns, so we multiply to get the total choices for that row:
Right. To construct a legal function we must make the choices indicated in both the second *and* third columns, so we multiply to get the total choices for that row:
DPatrick
2013-04-05 20:49:03
# of add'l elements# of choices for# of choices formapping to celements mapping to cother elementstotal16156⋅1=62152415⋅16=2403203320⋅27=5404154215⋅16=24056516⋅5=3061601⋅1=1
# of add'l elements# of choices for# of choices formapping to celements mapping to cother elementstotal16156⋅1=62152415⋅16=2403203320⋅27=5404154215⋅16=24056516⋅5=3061601⋅1=1
MSTang
2013-04-05 20:49:22
add totals
add totals
distortedwalrus
2013-04-05 20:49:22
add em up
add em up
DPatrick
2013-04-05 20:49:26
So that gives a total of
6+240+540+240+30+1=1057
ways to finish constructing the function, once we've chosen c.
So that gives a total of
6+240+540+240+30+1=1057
ways to finish constructing the function, once we've chosen c.
zhuangzhuang
2013-04-05 20:49:40
*7.
*7.
mathwrath
2013-04-05 20:49:40
7 possibilities for c...
7 possibilities for c...
DPatrick
2013-04-05 20:49:53
And there were 7 choices for c at the beginning. Thus, there are 7⋅1057=7399 such functions.
And there were 7 choices for c at the beginning. Thus, there are 7⋅1057=7399 such functions.
DPatrick
2013-04-05 20:50:00
Our answer is 399.
Our answer is 399.
DPatrick
2013-04-05 20:50:29
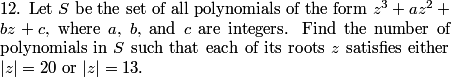
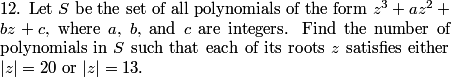
DPatrick
2013-04-05 20:50:45
Broadly speaking, what do we know about the roots of a cubic?
Broadly speaking, what do we know about the roots of a cubic?
countyguy
2013-04-05 20:51:12
three of them
three of them
kdokmeci
2013-04-05 20:51:12
Either all real, or 2 complex one real
Either all real, or 2 complex one real
TheStrangeCharm
2013-04-05 20:51:12
either all 3 are real, or one is real and the others are complex conjugates
either all 3 are real, or one is real and the others are complex conjugates
zhuangzhuang
2013-04-05 20:51:12
they have at least one real root
they have at least one real root
fmasroor
2013-04-05 20:51:12
all real or 2 imaginaries 1 real
all real or 2 imaginaries 1 real
matholympiad25
2013-04-05 20:51:12
complex conjugates if the coefficients are real
complex conjugates if the coefficients are real
DPatrick
2013-04-05 20:51:26
Right. I suppose I should have asked "a cubic with real coefficients" to be more clear, sorry.
Right. I suppose I should have asked "a cubic with real coefficients" to be more clear, sorry.
DPatrick
2013-04-05 20:51:30
We either have 3 real roots, or 1 real root and a conjugate pair of complex roots.
We either have 3 real roots, or 1 real root and a conjugate pair of complex roots.
kdokmeci
2013-04-05 20:51:37
Casework?
Casework?
DPatrick
2013-04-05 20:51:44
Yeah: we'll count cubics in each case, and add them.
Yeah: we'll count cubics in each case, and add them.
DPatrick
2013-04-05 20:52:03
(Note that since the cubics in S are monic, they are uniquely determined by their roots.)
(Note that since the cubics in S are monic, they are uniquely determined by their roots.)
DPatrick
2013-04-05 20:52:08
How many possibilities are there for three real roots?
How many possibilities are there for three real roots?
DPatrick
2013-04-05 20:52:19
Note that the roots have to be in the set {−20,−13,13,20}, and we can take any three elements of this set (with repetition) and get a different cubic.
Note that the roots have to be in the set {−20,−13,13,20}, and we can take any three elements of this set (with repetition) and get a different cubic.
DPatrick
2013-04-05 20:52:33
How many are there?
How many are there?
DPatrick
2013-04-05 20:52:54
I mean, how many sets of 3 roots from the set (with possible repetition)?
I mean, how many sets of 3 roots from the set (with possible repetition)?
giftedbee
2013-04-05 20:53:18
20
20
googol.plex
2013-04-05 20:53:18
we have 20, 4 from n^3, 12 from n^2*m, and 4 from taking 3 different ones
we have 20, 4 from n^3, 12 from n^2*m, and 4 from taking 3 different ones
countyguy
2013-04-05 20:53:18
20
20
DPatrick
2013-04-05 20:53:45
Right. You could do something semi-complicated (like a "stars and bars" or "balls and urns" argument) to count them, but I found it easy to just think about the cases.
Right. You could do something semi-complicated (like a "stars and bars" or "balls and urns" argument) to count them, but I found it easy to just think about the cases.
DPatrick
2013-04-05 20:53:57
There are (43)=4 with three distinct roots.
There are (43)=4 with three distinct roots.
DPatrick
2013-04-05 20:54:09
There are 4*3=12 with a double root (4 choices) and a third different root (3 choices).
There are 4*3=12 with a double root (4 choices) and a third different root (3 choices).
DPatrick
2013-04-05 20:54:15
And there are 4 with a triple root.
And there are 4 with a triple root.
DPatrick
2013-04-05 20:54:19
So there are 4+12+4 = 20 with three real roots.
So there are 4+12+4 = 20 with three real roots.
DPatrick
2013-04-05 20:54:39
Now on to the other case: a complex (non-real) conjugate pair and a real root.
Now on to the other case: a complex (non-real) conjugate pair and a real root.
DPatrick
2013-04-05 20:54:57
There are obviously 4 choices for the real root.
There are obviously 4 choices for the real root.
DPatrick
2013-04-05 20:55:02
How about the conjugate pair?
How about the conjugate pair?
DPatrick
2013-04-05 20:55:12
What do we know about it?
What do we know about it?
MSTang
2013-04-05 20:55:26
have the same magnitude
have the same magnitude
countyguy
2013-04-05 20:55:26
absolute value of 20 or 13
absolute value of 20 or 13
kdokmeci
2013-04-05 20:55:29
Their magnitude is 20 or 13
Their magnitude is 20 or 13
DPatrick
2013-04-05 20:55:34
Right. If our conjugate pair is p±qi, then we must have p2+q2=132 or p2+q2=202.
Right. If our conjugate pair is p±qi, then we must have p2+q2=132 or p2+q2=202.
DPatrick
2013-04-05 20:55:46
What are the conditions on p and/or q?
What are the conditions on p and/or q?
DPatrick
2013-04-05 20:56:22
A lot of you are saying they have to be integers...why?
A lot of you are saying they have to be integers...why?
DPatrick
2013-04-05 20:56:47
In fact there's no reason either of them has to be an integer.
In fact there's no reason either of them has to be an integer.
zhuangzhuang
2013-04-05 20:57:07
2p is an integer(by vieta) and q is not 0
2p is an integer(by vieta) and q is not 0
Sayan
2013-04-05 20:57:17
2p is an integer
2p is an integer
DPatrick
2013-04-05 20:57:41
We do know that the sum of the three roots is an integer: it's −a from the original cubic, by Vieta's Formulas.
We do know that the sum of the three roots is an integer: it's −a from the original cubic, by Vieta's Formulas.
DPatrick
2013-04-05 20:58:07
But if p±qi and r are our roots (where r is some real number), what is their sum?
But if p±qi and r are our roots (where r is some real number), what is their sum?
mathmaster2012
2013-04-05 20:58:28
2p+r!
2p+r!
matholympiad25
2013-04-05 20:58:28
2p+r
2p+r
ssilwa
2013-04-05 20:58:28
2p+r
2p+r
shreyash
2013-04-05 20:58:28
2p + r
2p + r
JWK750
2013-04-05 20:58:28
2p+r
2p+r
DPatrick
2013-04-05 20:58:44
Their sum is (p+qi)+(p−qi)+r=2p+r.
Their sum is (p+qi)+(p−qi)+r=2p+r.
DPatrick
2013-04-05 20:59:04
We already know r is an integer, so 2p must be an integer too. (We sometimes say that p is a half-integer.)
We already know r is an integer, so 2p must be an integer too. (We sometimes say that p is a half-integer.)
DPatrick
2013-04-05 20:59:34
There actually is no condition at all on q, except that it's non-zero (so that the roots are non-real).
There actually is no condition at all on q, except that it's non-zero (so that the roots are non-real).
DPatrick
2013-04-05 20:59:54
So if p2+q2=132, how many choices are there for the complex roots?
So if p2+q2=132, how many choices are there for the complex roots?
MSTang
2013-04-05 21:00:34
from -12.5 to 12.5 on p, so 51
from -12.5 to 12.5 on p, so 51
aux770
2013-04-05 21:00:34
51
51
DPatrick
2013-04-05 21:00:54
We must have |p|<13. (We can't have |p|=13 because that would make q=0.)
We must have |p|<13. (We can't have |p|=13 because that would make q=0.)
DPatrick
2013-04-05 21:01:00
So p must be in the set
{−252,−242,…,0,…,242,252}.
So p must be in the set
{−252,−242,…,0,…,242,252}.
DPatrick
2013-04-05 21:01:14
So there are 51 choices for p, and once we choose p, the imaginary part q is uniquely determined by p2+q2=132.
So there are 51 choices for p, and once we choose p, the imaginary part q is uniquely determined by p2+q2=132.
DPatrick
2013-04-05 21:01:25
How about if p2+q2=202? How many choices?
How about if p2+q2=202? How many choices?
mathwrath
2013-04-05 21:01:43
79
79
mathwrath
2013-04-05 21:01:43
79
79
tapir1729
2013-04-05 21:01:43
79
79
Tommy2000
2013-04-05 21:01:43
79
79
AayushGupta
2013-04-05 21:01:43
79
79
DPatrick
2013-04-05 21:01:47
Now p must be in the set
{−392,−382,…,0,…,382,392}.
Now p must be in the set
{−392,−382,…,0,…,382,392}.
DPatrick
2013-04-05 21:01:57
So there are 79 choices for p, and once we choose p, the imaginary part q is uniquely determined.
So there are 79 choices for p, and once we choose p, the imaginary part q is uniquely determined.
DPatrick
2013-04-05 21:02:22
Hence combined there are 51+79=130 possible non-real conjugate pairs.
Hence combined there are 51+79=130 possible non-real conjugate pairs.
DPatrick
2013-04-05 21:02:32
So how many cubics with non-real roots?
So how many cubics with non-real roots?
kdokmeci
2013-04-05 21:02:54
130x4=520
130x4=520
piguy314
2013-04-05 21:02:54
4*130 = 520
4*130 = 520
DPatrick
2013-04-05 21:03:04
Right, don't forget each of these has 4 choices for the third (real) root!
Right, don't forget each of these has 4 choices for the third (real) root!
DPatrick
2013-04-05 21:03:28
So there are 4⋅130=520 cubics in the case of "1 real, 2 non-real conjugate roots".
So there are 4⋅130=520 cubics in the case of "1 real, 2 non-real conjugate roots".
zhuangzhuang
2013-04-05 21:03:40
520+20--=540 as our answer
520+20--=540 as our answer
mathmaster2012
2013-04-05 21:03:40
520+20=540, which is our answer!
520+20=540, which is our answer!
shreyash
2013-04-05 21:03:40
520 + 20 = 540
520 + 20 = 540
googol.plex
2013-04-05 21:03:40
so adding the cases we have 540
so adding the cases we have 540
DPatrick
2013-04-05 21:03:47
And to finish: adding the 20 cubics with real roots, we get an answer of 520+20=540.
And to finish: adding the 20 cubics with real roots, we get an answer of 520+20=540.
DPatrick
2013-04-05 21:04:12
I actually liked that problem a lot too. #10 and #12 were my co-favorites.
I actually liked that problem a lot too. #10 and #12 were my co-favorites.
MSTang
2013-04-05 21:04:29
which was your least favorite?
which was your least favorite?
DPatrick
2013-04-05 21:04:36
#15. And we'll soon see why.
#15. And we'll soon see why.
DPatrick
2013-04-05 21:04:43


DPatrick
2013-04-05 21:04:58
Here's a picture. I've used x and y for unknown lengths, incorporating the given data.
Here's a picture. I've used x and y for unknown lengths, incorporating the given data.
DPatrick
2013-04-05 21:05:03
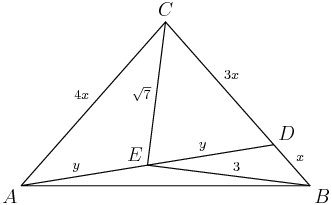

DPatrick
2013-04-05 21:05:33
There are some really clever ways to solve this by extending lots of lines, or by using some high-powered machinery, but I just did a lot of Law of Cosines bashing.
There are some really clever ways to solve this by extending lots of lines, or by using some high-powered machinery, but I just did a lot of Law of Cosines bashing.
DPatrick
2013-04-05 21:05:51
I've got lots of lengths and lots of triangles that share either common angles or supplementary angles.
I've got lots of lengths and lots of triangles that share either common angles or supplementary angles.
matholympiad25
2013-04-05 21:06:15
Stewart's Theorem on ACD and CEB
Stewart's Theorem on ACD and CEB
DPatrick
2013-04-05 21:06:38
That's essentially what I did, except without actually using Stewart's Theorem, for the very good reason that I can never remember it.
That's essentially what I did, except without actually using Stewart's Theorem, for the very good reason that I can never remember it.
DPatrick
2013-04-05 21:06:49
And you don't actually need it if you know the Law of Cosines.
And you don't actually need it if you know the Law of Cosines.
RelaxationUtopia
2013-04-05 21:06:53
Law of Cos on supplementary angles is essentially Stewart's Theorem in disguise xD
Law of Cos on supplementary angles is essentially Stewart's Theorem in disguise xD
kdokmeci
2013-04-05 21:06:58
cos x =-cos (180-x)
cos x =-cos (180-x)
DPatrick
2013-04-05 21:07:02
Indeed it is.
Indeed it is.
DPatrick
2013-04-05 21:07:08
One place to start is the supplementary angles at E: AEC and DEC. Note that cos(AEC)=−cos(DEC).
One place to start is the supplementary angles at E: AEC and DEC. Note that cos(AEC)=−cos(DEC).
DPatrick
2013-04-05 21:07:20
So we can set up two Law of Cosines expressions, using triangles AEC and DEC and the common cosine.
So we can set up two Law of Cosines expressions, using triangles AEC and DEC and the common cosine.
DPatrick
2013-04-05 21:07:25
(4x)2=y2+7−2y√7cos(AEC)(3x)2=y2+7−2y√7cos(DEC)
(4x)2=y2+7−2y√7cos(AEC)(3x)2=y2+7−2y√7cos(DEC)
DPatrick
2013-04-05 21:07:59
We substitute our observation about the supplementary angles:
We substitute our observation about the supplementary angles:
DPatrick
2013-04-05 21:08:03
(4x)2=y2+7+2y√7cos(DEC)(3x)2=y2+7−2y√7cos(DEC)
(4x)2=y2+7+2y√7cos(DEC)(3x)2=y2+7−2y√7cos(DEC)
DPatrick
2013-04-05 21:08:18
And it should be "obvious" what to do next...
And it should be "obvious" what to do next...
fmasroor
2013-04-05 21:08:35
add?
add?
googol.plex
2013-04-05 21:08:35
if we add the equations they go away
if we add the equations they go away
AayushGupta
2013-04-05 21:08:35
add both
add both
Sayan
2013-04-05 21:08:35
add them
add them
genesis2
2013-04-05 21:08:35
addd them together
addd them together
DPatrick
2013-04-05 21:08:54
If we add the equations, all the icky parts go away!
If we add the equations, all the icky parts go away!
DPatrick
2013-04-05 21:08:59
25x2=2y2+14
25x2=2y2+14
Tommy2000
2013-04-05 21:09:11
solve for x^2 in terms of y^2
solve for x^2 in terms of y^2
DPatrick
2013-04-05 21:09:19
Or, to match my notes, solve for y^2 in terms of x^2.
Or, to match my notes, solve for y^2 in terms of x^2.
DPatrick
2013-04-05 21:09:35
It doesn't really matter but my notes for the rest of the problem will be hopeless otherwise.
It doesn't really matter but my notes for the rest of the problem will be hopeless otherwise.
DPatrick
2013-04-05 21:09:45
We get y2=252x2−7.
We get y2=252x2−7.
DPatrick
2013-04-05 21:10:00
Now what?
Now what?
kdokmeci
2013-04-05 21:10:13
Law of cosine on new triangle
Law of cosine on new triangle
ssilwa
2013-04-05 21:10:17
again on CEB
again on CEB
DPatrick
2013-04-05 21:10:41
I'd like to find triangles with a common angle, to use the same sort of trick. Since I don't know AB (yet?) I can't use the other two supplementary angles at E.
I'd like to find triangles with a common angle, to use the same sort of trick. Since I don't know AB (yet?) I can't use the other two supplementary angles at E.
AayushGupta
2013-04-05 21:10:49
do the law of cosines on DEB and DEC, and add again
do the law of cosines on DEB and DEC, and add again
DPatrick
2013-04-05 21:11:18
That's an idea too. And there are lots of ways that work. But (again, to match my notes) I chose ECD and ECB.
That's an idea too. And there are lots of ways that work. But (again, to match my notes) I chose ECD and ECB.
DPatrick
2013-04-05 21:11:26
Let's use the Law of Cosines on the two triangles ECD and ECB with the common angle at C.
Let's use the Law of Cosines on the two triangles ECD and ECB with the common angle at C.
DPatrick
2013-04-05 21:11:42
y2=7+(3x)2−6x√7cos(ECD)32=7+(4x)2−8x√7cos(ECB)
y2=7+(3x)2−6x√7cos(ECD)32=7+(4x)2−8x√7cos(ECB)
herro66
2013-04-05 21:12:06
make the cos parts equal
make the cos parts equal
DPatrick
2013-04-05 21:12:10
Now we'll use our info about y2 from above, and also the fact the ECD and ECB are the same angle.
Now we'll use our info about y2 from above, and also the fact the ECD and ECB are the same angle.
DPatrick
2013-04-05 21:12:14
252x2−7=7+9x2−6x√7cos(ECD)9=7+16x2−8x√7cos(ECD)
252x2−7=7+9x2−6x√7cos(ECD)9=7+16x2−8x√7cos(ECD)
19bobhu
2013-04-05 21:12:30
add?
add?
kdokmeci
2013-04-05 21:12:30
add as planned
add as planned
hatchguy
2013-04-05 21:12:30
multiply first by 4, second by two 3
multiply first by 4, second by two 3
kdokmeci
2013-04-05 21:12:34
Multiply top by 4, bottom by 3
Multiply top by 4, bottom by 3
DPatrick
2013-04-05 21:12:47
It's not quite as straightforward as before, but we multiply the first by 4, the second by -3, and then add:
50x2−28=28+36x2−24x√7cos(ECD)−27=−21−48x2+24x2√7cos(ECD)50x2−55=7−12x2
It's not quite as straightforward as before, but we multiply the first by 4, the second by -3, and then add:
50x2−28=28+36x2−24x√7cos(ECD)−27=−21−48x2+24x2√7cos(ECD)50x2−55=7−12x2
DPatrick
2013-04-05 21:13:07
Again, the icky goes away.
Again, the icky goes away.
zhuangzhuang
2013-04-05 21:13:21
so x=1!
so x=1!
mathwrath
2013-04-05 21:13:21
x=1
x=1
kdokmeci
2013-04-05 21:13:21
x=1! 1! NOT SOME CRAZY VALUE!
x=1! 1! NOT SOME CRAZY VALUE!
AayushGupta
2013-04-05 21:13:21
x^2 = 1
x^2 = 1
MSTang
2013-04-05 21:13:21
x=1
x=1
DPatrick
2013-04-05 21:13:26
Well, whad'ya know?
Well, whad'ya know?
DPatrick
2013-04-05 21:13:30
62x2=62, so x=1.
62x2=62, so x=1.
matholympiad25
2013-04-05 21:13:40
x=1, y=sqrt(11/2)
x=1, y=sqrt(11/2)
DPatrick
2013-04-05 21:13:44
This makes y2=252−7=112, so y=√112.
This makes y2=252−7=112, so y=√112.
DPatrick
2013-04-05 21:13:51
Let's update the picture with the now-known lengths:
Let's update the picture with the now-known lengths:
DPatrick
2013-04-05 21:13:58


DPatrick
2013-04-05 21:14:30
Now we can continue to do ugly things from here to finish, or if we're sufficiently observant we might notice something interesting.
Now we can continue to do ugly things from here to finish, or if we're sufficiently observant we might notice something interesting.
zhuangzhuang
2013-04-05 21:14:53
so the triangle CEB is right!
so the triangle CEB is right!
az_phx_brandon_jiang
2013-04-05 21:14:53
So CEB is right?
So CEB is right?
matholympiad25
2013-04-05 21:14:53
CEB is right!!!!!!!!!!!!!!!!!!1
CEB is right!!!!!!!!!!!!!!!!!!1
hatchguy
2013-04-05 21:14:53
CEB has a right angle, by pythagoras
CEB has a right angle, by pythagoras
mathwrath
2013-04-05 21:14:53
BEC=90 degrees
BEC=90 degrees
DPatrick
2013-04-05 21:15:07
CEB is a 3-√7-4 right triangle!
CEB is a 3-√7-4 right triangle!
DPatrick
2013-04-05 21:15:32
So how do we finish from here, now that we've noticed this really really useful fact?
So how do we finish from here, now that we've noticed this really really useful fact?
mathwrath
2013-04-05 21:15:50
CEB=half of ACB
CEB=half of ACB
DPatrick
2013-04-05 21:16:19
Exactly. Note that CED and CEA have the same area (same bases AE = ED, and same altitude from C to AED).
Exactly. Note that CED and CEA have the same area (same bases AE = ED, and same altitude from C to AED).
DPatrick
2013-04-05 21:16:28
Also BED and BEA have the same area for the same reason.
Also BED and BEA have the same area for the same reason.
DPatrick
2013-04-05 21:16:42
So CEB is exactly half the entire triangle.
So CEB is exactly half the entire triangle.
DPatrick
2013-04-05 21:17:00
And since CEB is a right triangle, its area is pretty easy to compute.
And since CEB is a right triangle, its area is pretty easy to compute.
mxie
2013-04-05 21:17:11
so [ACB] = 2 * (1/2) * sqrt7 * 3
so [ACB] = 2 * (1/2) * sqrt7 * 3
cheese1000
2013-04-05 21:17:11
So 3sqrt7 is the answer?
So 3sqrt7 is the answer?
googol.plex
2013-04-05 21:17:11
so the answer is 3sqrt 7
so the answer is 3sqrt 7
DPatrick
2013-04-05 21:17:21
Hence our area of ABC is
[ABC]=2[CEB]=2(12⋅3⋅√7)=3√7.
Hence our area of ABC is
[ABC]=2[CEB]=2(12⋅3⋅√7)=3√7.
DPatrick
2013-04-05 21:17:30
The final answer is 3+7=010.
The final answer is 3+7=010.
noobynoob
2013-04-05 21:17:55
easily guessable
easily guessable
ssilwa
2013-04-05 21:17:55
its funny how we had teh 3 and the sqrt7 all along
its funny how we had teh 3 and the sqrt7 all along
DPatrick
2013-04-05 21:18:15
Unfortunately, yes. I would have preferred something more interesting to happen along the way.
Unfortunately, yes. I would have preferred something more interesting to happen along the way.
DPatrick
2013-04-05 21:18:23
DPatrick
2013-04-05 21:18:43
Alright, I read it and I don't get it. Anybody have any good ideas?
Alright, I read it and I don't get it. Anybody have any good ideas?
matholympiad25
2013-04-05 21:19:04
try out a few n starting from 20
try out a few n starting from 20
kdokmeci
2013-04-05 21:19:04
Pattern?
Pattern?
twin77
2013-04-05 21:19:04
try some numbers
try some numbers
trophies
2013-04-05 21:19:08
try a few cases.
try a few cases.
DPatrick
2013-04-05 21:19:30
I don't have any clever ideas, so let's just pick a few small n's and compute the f(n,k)'s and see if we learn anything.
I don't have any clever ideas, so let's just pick a few small n's and compute the f(n,k)'s and see if we learn anything.
DPatrick
2013-04-05 21:19:43
I'm going to save us some time...I did a bunch of these ahead of time:
I'm going to save us some time...I did a bunch of these ahead of time:
DPatrick
2013-04-05 21:19:47
n→k↓ 20 21 22 23 24 25 26 271000000002010101013201201204012301235012340126234501237601234568456701239234567801001234567110123451201231301
n→k↓ 20 21 22 23 24 25 26 271000000002010101013201201204012301235012340126234501237601234568456701239234567801001234567110123451201231301
DPatrick
2013-04-05 21:20:06
Notice that the rows just cycle through the residues mod k, and each new row starts with a 0 (because k divides n=2k evenly).
Notice that the rows just cycle through the residues mod k, and each new row starts with a 0 (because k divides n=2k evenly).
DPatrick
2013-04-05 21:20:35
So the rows are easy to understand, but F(n) is (by definition) the largest value in n's column.
So the rows are easy to understand, but F(n) is (by definition) the largest value in n's column.
matholympiad25
2013-04-05 21:20:51
wow it happens when k=7,8,8,8,9,9,9,10,10,10,...
wow it happens when k=7,8,8,8,9,9,9,10,10,10,...
DPatrick
2013-04-05 21:20:58
Yeah, let's mark them in the table:
Yeah, let's mark them in the table:
DPatrick
2013-04-05 21:21:02
n→k↓ 20 21 22 23 24 25 26 271000000002010101013201201204012301235012340126234501237601234568456701239234567801001234567110123451201231301
n→k↓ 20 21 22 23 24 25 26 271000000002010101013201201204012301235012340126234501237601234568456701239234567801001234567110123451201231301
DPatrick
2013-04-05 21:21:19
It looks kinda like a staircase with slope -1/3. If we're not confident yet, we can collect a little more data:
It looks kinda like a staircase with slope -1/3. If we're not confident yet, we can collect a little more data:
DPatrick
2013-04-05 21:21:29
n→k↓ 20 21 22 23 24 25 26 27 28 29 30100000000000201010101010320120120120401230123012501234012340623450123450760123456012845670123456923456780123100123456789011012345678120123456130123414012150
n→k↓ 20 21 22 23 24 25 26 27 28 29 30100000000000201010101010320120120120401230123012501234012340623450123450760123456012845670123456923456780123100123456789011012345678120123456130123414012150
DPatrick
2013-04-05 21:21:39
OK, I'm convinced.
OK, I'm convinced.
DPatrick
2013-04-05 21:22:18
On the actual contest, if you were confident that the pattern continues, you could assume such and proceed.
On the actual contest, if you were confident that the pattern continues, you could assume such and proceed.
DPatrick
2013-04-05 21:22:35
But let's at least try to quickly convince ourselves why this pattern holds.
But let's at least try to quickly convince ourselves why this pattern holds.
DPatrick
2013-04-05 21:22:54
What do you notice as you read up each column from the bottom?
What do you notice as you read up each column from the bottom?
thehanbro
2013-04-05 21:23:26
+2
+2
ssilwa
2013-04-05 21:23:26
0246 or 1357
0246 or 1357
jmvc003
2013-04-05 21:23:26
it's increasing by 2
it's increasing by 2
19JasonH
2013-04-05 21:23:26
0 or 1
0 or 1
DPatrick
2013-04-05 21:23:50
Right. Every column starts at the bottom with either 0 or 1 (if n is even or odd, respectively), then the numbers increase by 2 for a while.
Right. Every column starts at the bottom with either 0 or 1 (if n is even or odd, respectively), then the numbers increase by 2 for a while.
DPatrick
2013-04-05 21:24:27
It's hopefully pretty clear why we get the 0's and 1's at the bottom: we know that n/(n/2) is an integer if n is even, so it has remainder 0.
It's hopefully pretty clear why we get the 0's and 1's at the bottom: we know that n/(n/2) is an integer if n is even, so it has remainder 0.
DPatrick
2013-04-05 21:24:46
If n is odd, then n=2(n−12)+1, so the remainder is 1.
If n is odd, then n=2(n−12)+1, so the remainder is 1.
DPatrick
2013-04-05 21:25:05
Why does it go up by 2 every time as we climb from the bottom towards the maximum?
Why does it go up by 2 every time as we climb from the bottom towards the maximum?
DPatrick
2013-04-05 21:26:14
For example, 27/12 has a remainder of 3. Why does this mean that 27/11 has a remainder of 5, and why does this generalize?
For example, 27/12 has a remainder of 3. Why does this mean that 27/11 has a remainder of 5, and why does this generalize?
DPatrick
2013-04-05 21:27:26
At times in number theory, it pays to appeal to algebra. Suppose n=2k+r for some "large" k close to ⌊n2⌋ (that is, some k close to the bottom of a column).
At times in number theory, it pays to appeal to algebra. Suppose n=2k+r for some "large" k close to ⌊n2⌋ (that is, some k close to the bottom of a column).
DPatrick
2013-04-05 21:27:42
What equation do we write when we try to divide n by k−1?
What equation do we write when we try to divide n by k−1?
giftedbee
2013-04-05 21:28:09
2(k-1)+r+2
2(k-1)+r+2
kdokmeci
2013-04-05 21:28:26
n=2(k-1)+r+2
n=2(k-1)+r+2
DPatrick
2013-04-05 21:28:33
We get n=2(k−1)+(r+2), assuming that k is still "large enough".
We get n=2(k−1)+(r+2), assuming that k is still "large enough".
DPatrick
2013-04-05 21:28:49
So by decreasing the divisor from k to k−1, we've increased the remainder from r to r+2.
So by decreasing the divisor from k to k−1, we've increased the remainder from r to r+2.
DPatrick
2013-04-05 21:29:04
So that's why the remainders in the columns are increasing by 2's near the bottom.
So that's why the remainders in the columns are increasing by 2's near the bottom.
DPatrick
2013-04-05 21:29:11
But at some point this fails...when?
But at some point this fails...when?
centralbs
2013-04-05 21:29:22
below n/3
below n/3
AayushGupta
2013-04-05 21:29:22
when it goes over
when it goes over
DPatrick
2013-04-05 21:29:34
Right, this only works as long as the quotient part of n/k is 2.
Right, this only works as long as the quotient part of n/k is 2.
DPatrick
2013-04-05 21:29:47
When the quotient increases to 3, then the remainder drops back to 0, 1, or 2 again.
When the quotient increases to 3, then the remainder drops back to 0, 1, or 2 again.
kdokmeci
2013-04-05 21:29:53
And thats why slope is -1/3!
And thats why slope is -1/3!
DPatrick
2013-04-05 21:29:55
Indeed.
Indeed.
DPatrick
2013-04-05 21:30:10
Here's the chart again, with the "groups of threes" highlighted a little more:
Here's the chart again, with the "groups of threes" highlighted a little more:
DPatrick
2013-04-05 21:30:13
n→k↓ 20 21 22 23 24 25 26 27 28 29 30 31100000000000020101010101013201201201201401230123012350123401234016234501234501760123456012384567012345679234567801234100123456789011101234567891201234567130123451401231501
n→k↓ 20 21 22 23 24 25 26 27 28 29 30 31100000000000020101010101013201201201201401230123012350123401234016234501234501760123456012384567012345679234567801234100123456789011101234567891201234567130123451401231501
DPatrick
2013-04-05 21:30:47
Notice that the maximum value for n's column always is as ⌊n3⌋+1, right before the quotient of n/k jumps from 2 to 3.
Notice that the maximum value for n's column always is as ⌊n3⌋+1, right before the quotient of n/k jumps from 2 to 3.
DPatrick
2013-04-05 21:31:06
("as" should have been "at" in the previous sentence!)
("as" should have been "at" in the previous sentence!)
DPatrick
2013-04-05 21:31:49
OK, so I'm more convinced now! Again, using test-taking strategy, your better option during the contest probably is to assume the pattern and try to answer the problem.
OK, so I'm more convinced now! Again, using test-taking strategy, your better option during the contest probably is to assume the pattern and try to answer the problem.
DPatrick
2013-04-05 21:31:56
Now that we've established the pattern, how do we compute the sum of the boxed numbers over 20≤n≤100?
Now that we've established the pattern, how do we compute the sum of the boxed numbers over 20≤n≤100?
kdokmeci
2013-04-05 21:32:26
6+5+6+(7+6+7)+8+7+8+(9+8+9(+...
6+5+6+(7+6+7)+8+7+8+(9+8+9(+...
DPatrick
2013-04-05 21:33:04
Right, I've grouped the columns into groups of three, with each group centered at some multiple of 3. (For example, the first group is centered at n=21=3⋅7.)
Right, I've grouped the columns into groups of three, with each group centered at some multiple of 3. (For example, the first group is centered at n=21=3⋅7.)
DPatrick
2013-04-05 21:33:18
For the group centered at n=3m, what is the sum of the numbers?
For the group centered at n=3m, what is the sum of the numbers?
Sayan
2013-04-05 21:33:53
3m-4
3m-4
twin77
2013-04-05 21:33:53
3m - 4
3m - 4
DPatrick
2013-04-05 21:34:05
Right: their sum is
F(3m−1)+F(3m)+F(3m+1)=(m−1)+(m−2)+(m−1)=3m−4.
Right: their sum is
F(3m−1)+F(3m)+F(3m+1)=(m−1)+(m−2)+(m−1)=3m−4.
DPatrick
2013-04-05 21:34:15
So each group sums to 3m−4.
So each group sums to 3m−4.
DPatrick
2013-04-05 21:34:20
(As a quick check: when m=7 we get 3(7)−4=17, which is 6+5+6; when m=8 we get 3(8)−4=20, which is 7+6+7, and so on.)
(As a quick check: when m=7 we get 3(7)−4=17, which is 6+5+6; when m=8 we get 3(8)−4=20, which is 7+6+7, and so on.)
DPatrick
2013-04-05 21:34:29
So the triples sum to
17+20+23+⋯
Where does it stop?
So the triples sum to
17+20+23+⋯
Where does it stop?
twin77
2013-04-05 21:35:08
when it is centered at n=99
when it is centered at n=99
matholympiad25
2013-04-05 21:35:08
stops at 3(33)-4=95
stops at 3(33)-4=95
DPatrick
2013-04-05 21:35:27
Right. The last triple is centered at n=99.
Right. The last triple is centered at n=99.
DPatrick
2013-04-05 21:35:33
This last triple is for m=33, where we get
F(98)+F(99)+F(100)=3(33)−4=95.
This last triple is for m=33, where we get
F(98)+F(99)+F(100)=3(33)−4=95.
DPatrick
2013-04-05 21:35:42
So our answer is just the arithmetic series
17+20+23+⋯+95.
So our answer is just the arithmetic series
17+20+23+⋯+95.
DPatrick
2013-04-05 21:35:49
What is this sum?
What is this sum?
kdokmeci
2013-04-05 21:36:18
1512
1512
zhuangzhuang
2013-04-05 21:36:18
56*27=1512, ans=512
56*27=1512, ans=512
matholympiad25
2013-04-05 21:36:18
1512, so answer is 512
1512, so answer is 512
ZZmath9
2013-04-05 21:36:18
1512
1512
distortedwalrus
2013-04-05 21:36:18
56*# of terms...
56*# of terms...
DPatrick
2013-04-05 21:36:23
We run from m=7 to m=33, so there are 33−7+1=27 terms.
We run from m=7 to m=33, so there are 33−7+1=27 terms.
DPatrick
2013-04-05 21:36:27
And the average term is 17+952=56.
And the average term is 17+952=56.
DPatrick
2013-04-05 21:36:34
So our sum is (27)(56)=1512. Our final answer is 512.
So our sum is (27)(56)=1512. Our final answer is 512.
DPatrick
2013-04-05 21:36:53
And finally...
And finally...
DPatrick
2013-04-05 21:36:58
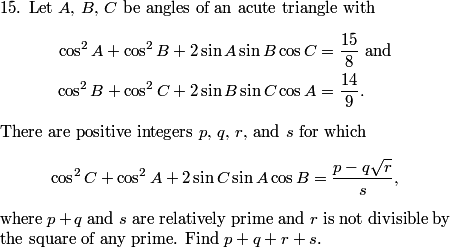
AayushGupta
2013-04-05 21:37:15
the problem of doom!
the problem of doom!
MSTang
2013-04-05 21:37:17
I now see why you didn't like this problem.
I now see why you didn't like this problem.
DPatrick
2013-04-05 21:37:39
Well, I could have liked this problem, but we'll see as we go why I ultimately didn't like it.
Well, I could have liked this problem, but we'll see as we go why I ultimately didn't like it.
DPatrick
2013-04-05 21:37:56
First of all, let's assign variables to the right sides of the equations, so I don't have to keep writing them out:
First of all, let's assign variables to the right sides of the equations, so I don't have to keep writing them out:
DPatrick
2013-04-05 21:38:02
cos2A+cos2B+2sinAsinBcosC=x,cos2B+cos2C+2sinBsinCcosA=y,cos2C+cos2A+2sinCsinAcosB=z.
cos2A+cos2B+2sinAsinBcosC=x,cos2B+cos2C+2sinBsinCcosA=y,cos2C+cos2A+2sinCsinAcosB=z.
DPatrick
2013-04-05 21:38:13
We're given x and y, and we want to find z.
We're given x and y, and we want to find z.
kdokmeci
2013-04-05 21:38:19
Symmetry!
Symmetry!
DPatrick
2013-04-05 21:38:26
There is a lot of symmetry here.
There is a lot of symmetry here.
trophies
2013-04-05 21:38:38
the first thought that comes into my head right now (I didnt take the AIME II) is subtracting the equations
the first thought that comes into my head right now (I didnt take the AIME II) is subtracting the equations
DPatrick
2013-04-05 21:39:05
That's often a very good idea with a symmetric-looking system of equations: either add or subtract them together and see if something nicer comes out.
That's often a very good idea with a symmetric-looking system of equations: either add or subtract them together and see if something nicer comes out.
borntobeweild
2013-04-05 21:39:15
maybe add equations and use triangle identities
maybe add equations and use triangle identities
DPatrick
2013-04-05 21:39:22
Let's add the first two and see what happens.
Let's add the first two and see what happens.
DPatrick
2013-04-05 21:39:31
cos2A+2cos2B+cos2C+2sinB(sinAcosC+sinCcosA)=x+y
cos2A+2cos2B+cos2C+2sinB(sinAcosC+sinCcosA)=x+y
DPatrick
2013-04-05 21:39:45
What's the term in the parentheses?
What's the term in the parentheses?
kdokmeci
2013-04-05 21:39:59
Sin addtion formula!
Sin addtion formula!
kdokmeci
2013-04-05 21:39:59
sin(A+C)
sin(A+C)
RelaxationUtopia
2013-04-05 21:39:59
sin (A+C)
sin (A+C)
Debdut
2013-04-05 21:39:59
sin(A+c)
sin(A+c)
number.sense
2013-04-05 21:39:59
sin (A+C)
sin (A+C)
teethpaste
2013-04-05 21:39:59
the stuff in parentheses is sin(A+C)!
the stuff in parentheses is sin(A+C)!
DPatrick
2013-04-05 21:40:08
It's sin(A+C)! That's good, but what's even better?
It's sin(A+C)! That's good, but what's even better?
Sayan
2013-04-05 21:40:24
sin(A+C)=sinB
sin(A+C)=sinB
matholympiad25
2013-04-05 21:40:24
sin A cos C + sin C cos A = sin(A+C)=sin (180-B)=sin B
sin A cos C + sin C cos A = sin(A+C)=sin (180-B)=sin B
zhuangzhuang
2013-04-05 21:40:24
its also sin B!
its also sin B!
AayushGupta
2013-04-05 21:40:24
sin A+C = sin 180-B
sin A+C = sin 180-B
teethpaste
2013-04-05 21:40:24
A+C=180-B!
A+C=180-B!
DPatrick
2013-04-05 21:40:32
That's even better: it's sinB! Note that
sinB=sin(180∘−B)=sin(A+C).
That's even better: it's sinB! Note that
sinB=sin(180∘−B)=sin(A+C).
DPatrick
2013-04-05 21:40:44
So now our equation is
cos2A+2cos2B+cos2C+2sinB(sinB)=x+y
So now our equation is
cos2A+2cos2B+cos2C+2sinB(sinB)=x+y
DPatrick
2013-04-05 21:40:57
And it keeps getting better and better!
And it keeps getting better and better!
AayushGupta
2013-04-05 21:41:12
sin^2 B + cos^2 B = 1
sin^2 B + cos^2 B = 1
Tuxianeer
2013-04-05 21:41:12
sin^2+cos^2=1
sin^2+cos^2=1
zhuangzhuang
2013-04-05 21:41:12
get rid of sin^2 +cos^2 b
get rid of sin^2 +cos^2 b
kdokmeci
2013-04-05 21:41:12
sin^2+cos^2=1
sin^2+cos^2=1
cheese1000
2013-04-05 21:41:12
cos^2+sin^2 equals 1
cos^2+sin^2 equals 1
DPatrick
2013-04-05 21:41:16
Well, that's convenient! 2cos2B+2sin2B is just 2.
Well, that's convenient! 2cos2B+2sin2B is just 2.
DPatrick
2013-04-05 21:41:22
So our equation is just
cos2A+cos2C+2=x+y.
So our equation is just
cos2A+cos2C+2=x+y.
DPatrick
2013-04-05 21:41:38
That is way way way better than anything we started with.
That is way way way better than anything we started with.
number.sense
2013-04-05 21:41:45
no reason these two equations were special
no reason these two equations were special
centralbs
2013-04-05 21:41:49
we can get 3 equations like this by symmetry
we can get 3 equations like this by symmetry
DPatrick
2013-04-05 21:42:00
Right, we can do the same thing by adding the other two pairs of equations.
Right, we can do the same thing by adding the other two pairs of equations.
DPatrick
2013-04-05 21:42:09
We get a new system of 3 equations:
cos2A+cos2C+2=x+y,cos2A+cos2B+2=y+z,cos2B+cos2C+2=x+z.
We get a new system of 3 equations:
cos2A+cos2C+2=x+y,cos2A+cos2B+2=y+z,cos2B+cos2C+2=x+z.
DPatrick
2013-04-05 21:42:38
Life seems good so far. Now what?
Life seems good so far. Now what?
kdokmeci
2013-04-05 21:42:53
Add them up again?
Add them up again?
19bobhu
2013-04-05 21:42:53
subtract, or add
subtract, or add
borntobeweild
2013-04-05 21:42:53
We can add them all and subtract each one
We can add them all and subtract each one
Sayan
2013-04-05 21:42:53
subtract first 2 and add it with the third
subtract first 2 and add it with the third
number.sense
2013-04-05 21:42:53
what if we added them all up?
what if we added them all up?
DPatrick
2013-04-05 21:43:05
Now there are lots of ways to isolate the individual cosine terms.
Now there are lots of ways to isolate the individual cosine terms.
DPatrick
2013-04-05 21:43:12
For example, add the first two and subtract the third.
For example, add the first two and subtract the third.
DPatrick
2013-04-05 21:43:34
The B and C parts cancel, and we're left with
2cos2A+2=(x+y)+(y+z)−(x+z)=2y.
The B and C parts cancel, and we're left with
2cos2A+2=(x+y)+(y+z)−(x+z)=2y.
kdokmeci
2013-04-05 21:44:05
cos^2 A+1=y
cos^2 A+1=y
mathwrath
2013-04-05 21:44:05
cos^2A+1=y
cos^2A+1=y
fprosk
2013-04-05 21:44:05
cos^2A=y-1
cos^2A=y-1
DPatrick
2013-04-05 21:44:06
Sweet! So cos2A+1=y, and hence cos2A=y−1.
Sweet! So cos2A+1=y, and hence cos2A=y−1.
DPatrick
2013-04-05 21:44:13
Similarly cos2B=z−1 and cos2C=x−1.
Similarly cos2B=z−1 and cos2C=x−1.
DPatrick
2013-04-05 21:44:41
Remember, we know x = 15/8 and y = 14/9, and we want to find z.
Remember, we know x = 15/8 and y = 14/9, and we want to find z.
kdokmeci
2013-04-05 21:44:48
Plug in x, y
Plug in x, y
DPatrick
2013-04-05 21:44:54
So we know that cos2A=59 and cos2C=78, and we want to find z=cos2B+1.
So we know that cos2A=59 and cos2C=78, and we want to find z=cos2B+1.
AayushGupta
2013-04-05 21:45:07
B = 180-C-A, so we can solve
B = 180-C-A, so we can solve
DPatrick
2013-04-05 21:45:16
Right, recall that cosB=cos(180∘−(A+C))=−cos(A+C).
Right, recall that cosB=cos(180∘−(A+C))=−cos(A+C).
DPatrick
2013-04-05 21:45:34
So we can use the cosine angle-sum formula:
cosB=−(cosAcosC−sinAsinC)
So we can use the cosine angle-sum formula:
cosB=−(cosAcosC−sinAsinC)
sparkles257
2013-04-05 21:45:54
substitute in values of cosA and c
substitute in values of cosA and c
DPatrick
2013-04-05 21:46:07
We plug in numbers, using the fact that sin2A=1−cos2A=49 and sin2C=1−cos2C=18.
We plug in numbers, using the fact that sin2A=1−cos2A=49 and sin2C=1−cos2C=18.
DPatrick
2013-04-05 21:46:40
So the sines and cosines are the square roots of all these numbers, and recall that we were given that the angles are acute, so we use the positive square root for the cosine terms.
So the sines and cosines are the square roots of all these numbers, and recall that we were given that the angles are acute, so we use the positive square root for the cosine terms.
DPatrick
2013-04-05 21:46:55
This gives us
cosB=−(√59⋅√78−√49⋅√18)
This gives us
cosB=−(√59⋅√78−√49⋅√18)
DPatrick
2013-04-05 21:47:36
A little algebra that I triple-checked (believe me) shows that this simplifies to cosB=2−√35√72.
A little algebra that I triple-checked (believe me) shows that this simplifies to cosB=2−√35√72.
matholympiad25
2013-04-05 21:47:51
WHAT!? THE COSINE IS NEGATIVE!!!!!!!!!!!!!????????????
WHAT!? THE COSINE IS NEGATIVE!!!!!!!!!!!!!????????????
henrikjb
2013-04-05 21:47:51
How can that be negative?
How can that be negative?
wfu
2013-04-05 21:47:51
But why is cos B negative...
But why is cos B negative...
DPatrick
2013-04-05 21:48:00
Uh-oh. Now we see the flaw.
Uh-oh. Now we see the flaw.
DPatrick
2013-04-05 21:48:13
This cosine is negative. That means that angle B is obtuse, contrary to what the problem statement says.
This cosine is negative. That means that angle B is obtuse, contrary to what the problem statement says.
trophies
2013-04-05 21:48:27
What did we do wrong?
What did we do wrong?
DPatrick
2013-04-05 21:48:40
We didn't do anything wrong. There's no way to get around this. The problem statement is incorrect -- there is no solution with A, B, C all acute. This also brings into question our assumption a moment ago to use the positive square roots for cosA and cosC, but I'll address that at the end.
We didn't do anything wrong. There's no way to get around this. The problem statement is incorrect -- there is no solution with A, B, C all acute. This also brings into question our assumption a moment ago to use the positive square roots for cosA and cosC, but I'll address that at the end.
Sayan
2013-04-05 21:49:04
So that's why it was your least favourite!
So that's why it was your least favourite!
DPatrick
2013-04-05 21:49:20
Yes, I prefer my AIME problems to have solutions. This one doesn't as written.
Yes, I prefer my AIME problems to have solutions. This one doesn't as written.
DPatrick
2013-04-05 21:49:27
For now, let's ignore (or pretend we didn't notice) that B is obtuse, and finish the problem.
For now, let's ignore (or pretend we didn't notice) that B is obtuse, and finish the problem.
distortedwalrus
2013-04-05 21:49:58
now just square this and add 1 and you're done.
now just square this and add 1 and you're done.
DPatrick
2013-04-05 21:50:08
Right: to finish, we compute z=cos2B+1:
z=(2−√35√72)2+1.
Right: to finish, we compute z=cos2B+1:
z=(2−√35√72)2+1.
DPatrick
2013-04-05 21:50:25
This simplifies to
z=4−4√35+35+7272=111−4√3572.
This simplifies to
z=4−4√35+35+7272=111−4√3572.
DPatrick
2013-04-05 21:50:37
This is in the correct format, so our final "answer" is 111+4+35+72=222.
This is in the correct format, so our final "answer" is 111+4+35+72=222.
19bobhu
2013-04-05 21:51:01
is that actually the answer in the answer sheet
is that actually the answer in the answer sheet
DPatrick
2013-04-05 21:51:04
It is.
It is.
DPatrick
2013-04-05 21:51:09
Unfortunately, as I mentioned, there is no solution with A,B,C all acute, contrary to the problem statement.
Unfortunately, as I mentioned, there is no solution with A,B,C all acute, contrary to the problem statement.
DPatrick
2013-04-05 21:51:21
Equally unfortunately, there are actually two solutions to the system of equations.
Equally unfortunately, there are actually two solutions to the system of equations.
DPatrick
2013-04-05 21:51:33
As you may recall, we assumed that A and C were acute when we did our cos(A+C) calculation. If you instead assume that A is obtuse, you get a different triangle and a different answer for z, though not one that can be put in the required format. (It doesn't work with C obtuse.)
As you may recall, we assumed that A and C were acute when we did our cos(A+C) calculation. If you instead assume that A is obtuse, you get a different triangle and a different answer for z, though not one that can be put in the required format. (It doesn't work with C obtuse.)
MSTang
2013-04-05 21:51:46
could they have removed the word acute and fixed the problem?
could they have removed the word acute and fixed the problem?
DPatrick
2013-04-05 21:52:10
Well...there still would have been two solutions. They could have worded it to force one or the other I suppose.
Well...there still would have been two solutions. They could have worded it to force one or the other I suppose.
number.sense
2013-04-05 21:52:26
what's the amc doing with this problem?
what's the amc doing with this problem?
19oshawott98
2013-04-05 21:52:26
what are they going to do about the problem for AIME test-takers?
what are they going to do about the problem for AIME test-takers?
DPatrick
2013-04-05 21:52:37
I can report that the AMC is aware of the error in this problem, because many people (including myself) have told them. I do not know what (if anything) they intend to do.
I can report that the AMC is aware of the error in this problem, because many people (including myself) have told them. I do not know what (if anything) they intend to do.
DPatrick
2013-04-05 21:53:11
Anyway...that's it for the AIME II!
Anyway...that's it for the AIME II!
DPatrick
2013-04-05 21:53:15
Good luck on the USA(J)MO if you qualify for it!
Good luck on the USA(J)MO if you qualify for it!
Superwiz
2013-04-05 21:53:59
What do you think the cutoff score for USA(J)MO will be?
What do you think the cutoff score for USA(J)MO will be?
DPatrick
2013-04-05 21:54:10
No idea, and I prefer not to speculate.
No idea, and I prefer not to speculate.
henrikjb
2013-04-05 21:54:29
When do we find out the cutoff?
When do we find out the cutoff?
DPatrick
2013-04-05 21:54:41
Probably next week. Maybe the week after, I'm not sure.
Probably next week. Maybe the week after, I'm not sure.
DPatrick
2013-04-05 21:55:08
They tend to score the AIME II fairly quickly, because the USA(J)MO is only 4 weeks away.
They tend to score the AIME II fairly quickly, because the USA(J)MO is only 4 weeks away.
atmath2011
2013-04-05 21:55:36
anybody feel the probs on the AIME II (even though i didn't take it) were easier than the AIME I?
anybody feel the probs on the AIME II (even though i didn't take it) were easier than the AIME I?
number.sense
2013-04-05 21:55:36
What do you think the difficulty of AIME 2 was relative to 1
What do you think the difficulty of AIME 2 was relative to 1
Knightone
2013-04-05 21:55:36
Which AIME did you find harder?
Which AIME did you find harder?
DPatrick
2013-04-05 21:55:54
I thought they were about the same.
I thought they were about the same.
DPatrick
2013-04-05 21:56:20
The AIME I had an unusually-difficult early problem (#5 if I remember, with a cubic polynomial) that the AIME II didn't really have.
The AIME I had an unusually-difficult early problem (#5 if I remember, with a cubic polynomial) that the AIME II didn't really have.
centralbs
2013-04-05 21:56:38
Which problem did you find the most difficult?
Which problem did you find the most difficult?
DPatrick
2013-04-05 21:56:47
Besides the one that was actually impossible?
Besides the one that was actually impossible?
DPatrick
2013-04-05 21:57:06
#13 was ugly to do correctly, but as we mentioned perhaps easy to cut corners and/or guess.
#13 was ugly to do correctly, but as we mentioned perhaps easy to cut corners and/or guess.
DPatrick
2013-04-05 21:57:30
#11 was hard because it was a little technical with the language.
#11 was hard because it was a little technical with the language.
DPatrick
2013-04-05 21:57:51
But I've seen so many counting problems in my lifetime that I can do them almost in my sleep.
But I've seen so many counting problems in my lifetime that I can do them almost in my sleep.
DPatrick
2013-04-05 21:57:53

DPatrick
2013-04-05 21:58:47
#10 is still probably my favorite. It had a nice elegant solution.
#10 is still probably my favorite. It had a nice elegant solution.
DPatrick
2013-04-05 21:59:21
OK, I'm going to close up the classroom now so that I can generate and post the transcript of the session.
OK, I'm going to close up the classroom now so that I can generate and post the transcript of the session.
DPatrick
2013-04-05 21:59:32
Have a nice weekend!
Have a nice weekend!
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.









