2014 AMC 10/12 A Discussion
Go back to the Math Jam ArchiveA discussion of problems from the AMC 10/12 A, which is administered February 4. We will cover the last 5 problems on each test, as well as requested earlier problems on the tests.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Jeremy Copeland
copeland
2014-02-05 18:47:31
The Math Jam will start at 7:00 PM Eastern / 4:00 PM Pacific.
The Math Jam will start at 7:00 PM Eastern / 4:00 PM Pacific.
copeland
2014-02-05 18:47:35
The classroom is moderated, meaning that you can type into the classroom, but these comments will not go directly into the room.
The classroom is moderated, meaning that you can type into the classroom, but these comments will not go directly into the room.
copeland
2014-02-05 18:53:39
Please do not ask about administrative aspects of the contests, and please do not ask me to speculate about the results.
Please do not ask about administrative aspects of the contests, and please do not ask me to speculate about the results.
ws0414
2014-02-05 18:54:00
how about passing scores?
how about passing scores?
copeland
2014-02-05 18:54:00
Please do not ask about administrative aspects of the contests, and please do not ask me to speculate about the results.
Please do not ask about administrative aspects of the contests, and please do not ask me to speculate about the results.
arpanliku
2014-02-05 18:54:38
Hello, Mr. Copeland.
Hello, Mr. Copeland.
copeland
2014-02-05 18:54:40
Hi there!
Hi there!
copeland
2014-02-05 18:56:37
Welcome to the 2014 AMC 10A/12A Math Jam!
Welcome to the 2014 AMC 10A/12A Math Jam!
copeland
2014-02-05 18:56:43
We will be starting a minute or 2 after 7pm ET.
We will be starting a minute or 2 after 7pm ET.
copeland
2014-02-05 18:57:03
I will explain the structure of the Math Jam shortly.
I will explain the structure of the Math Jam shortly.
kajay88
2014-02-05 18:57:36
so we cannot ask you about the cutoff score?
so we cannot ask you about the cutoff score?
copeland
2014-02-05 18:57:39
You can, but it won't help you. I won't answer.
You can, but it won't help you. I won't answer.
jigglypuff
2014-02-05 18:58:25
do you know what the cutoff score is?
do you know what the cutoff score is?
copeland
2014-02-05 18:58:26
Please do not ask about administrative aspects of the contests, and please do not ask me to speculate about the results.
Please do not ask about administrative aspects of the contests, and please do not ask me to speculate about the results.
AkshajK
2014-02-05 18:58:36
what is your stance on rainbows?
what is your stance on rainbows?
copeland
2014-02-05 18:58:36
Rainbows rule.
Rainbows rule.
VinTheSad
2014-02-05 18:59:05
peanut butter?
peanut butter?
copeland
2014-02-05 18:59:14
Yep. Peanut butter and rainbows are definitely my thing.
Yep. Peanut butter and rainbows are definitely my thing.
copeland
2014-02-05 18:59:16
How'd you know?
How'd you know?
mathman121
2014-02-05 19:00:09
What's your favorite topic in math? (algebra, geometry, number theory, etc.)
What's your favorite topic in math? (algebra, geometry, number theory, etc.)
adno
2014-02-05 19:00:09
i hate peanut butter
i hate peanut butter
copeland
2014-02-05 19:00:11
Lots of very good, cheap calories. How could you hate it?
Lots of very good, cheap calories. How could you hate it?
pi37
2014-02-05 19:01:02
Geometry has lots of good cheap calories
Geometry has lots of good cheap calories
copeland
2014-02-05 19:01:05
That's right.
That's right.
bpnyc
2014-02-05 19:01:49
are we starting now?
are we starting now?
Art123
2014-02-05 19:01:49
are we starting?
are we starting?
copeland
2014-02-05 19:01:51
Don't mind if I do!
Don't mind if I do!
copeland
2014-02-05 19:01:56
Welcome to the 2014 AMC 10A/12A Math Jam!
Welcome to the 2014 AMC 10A/12A Math Jam!
copeland
2014-02-05 19:01:56
I'm Jeremy Copeland, and I'll be leading our discussion tonight.
I'm Jeremy Copeland, and I'll be leading our discussion tonight.
copeland
2014-02-05 19:01:59
I'm the school director here at AoPS. That means when something goes wrong, I either get yelled at or have to yell at someone else. Before AoPS, I was an instructor at MIT, and before that I got my Ph.D. from the University of Chicago. Before that I was an undergrad at Reed College and going back even further, I can't really remember. I used to have hobbies, but I'm a parent now, so those days are all over.
I'm the school director here at AoPS. That means when something goes wrong, I either get yelled at or have to yell at someone else. Before AoPS, I was an instructor at MIT, and before that I got my Ph.D. from the University of Chicago. Before that I was an undergrad at Reed College and going back even further, I can't really remember. I used to have hobbies, but I'm a parent now, so those days are all over.
copeland
2014-02-05 19:02:09
Before we get started I would like to take a moment to explain our virtual classroom procedures to those who have not previously participated in a Math Jam or one of our online classes.
Before we get started I would like to take a moment to explain our virtual classroom procedures to those who have not previously participated in a Math Jam or one of our online classes.
copeland
2014-02-05 19:02:17
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
copeland
2014-02-05 19:02:22
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
copeland
2014-02-05 19:02:36
There are a lot of students here! As I said, only (a fraction of the) well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
There are a lot of students here! As I said, only (a fraction of the) well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
copeland
2014-02-05 19:02:40
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
AlanMTuring
2014-02-05 19:02:59
How can you type that fast
How can you type that fast
copeland
2014-02-05 19:03:00
I have 2 keyboards.
I have 2 keyboards.
copeland
2014-02-05 19:03:09
We have 2 scheduled assistants tonight: Jessica Hyde (i, imaginary) and Benjamin Engwall bluecarneal.
We have 2 scheduled assistants tonight: Jessica Hyde (i, imaginary) and Benjamin Engwall bluecarneal.
copeland
2014-02-05 19:03:10
Jessica started her career in math education in middle school, helping her classmates with their homework. From there she moved on to tutoring with the Math Honors Society in high school and taking courses at the University of Connecticut. In 2014 she will enroll at the Massachusetts Institute of Technology as a physics major, although she adores physics and mathematics equally and wants it to be known that she does not play favorites between the two. In her spare time she attempts to knit and (fruitlessly) to teach her cat and two rats to obey her authority.
Jessica started her career in math education in middle school, helping her classmates with their homework. From there she moved on to tutoring with the Math Honors Society in high school and taking courses at the University of Connecticut. In 2014 she will enroll at the Massachusetts Institute of Technology as a physics major, although she adores physics and mathematics equally and wants it to be known that she does not play favorites between the two. In her spare time she attempts to knit and (fruitlessly) to teach her cat and two rats to obey her authority.
copeland
2014-02-05 19:03:11
Benjamin is a Junior in college who enjoys studying both mathematics and computer science. He has been an active member of the AoPS community for over 5 years, and has enjoyed the opportunities he has had as Moderator, Grader, and TA. In his spare time, he enjoys swimming, golfing, and creating nifty Python programs.
Benjamin is a Junior in college who enjoys studying both mathematics and computer science. He has been an active member of the AoPS community for over 5 years, and has enjoyed the opportunities he has had as Moderator, Grader, and TA. In his spare time, he enjoys swimming, golfing, and creating nifty Python programs.
bluecarneal
2014-02-05 19:03:39
Hi!
Hi!
copeland
2014-02-05 19:03:43
We also have a guest assistant who happened to drop in: Alyssa Zisk (baozhale). Say hi to her, too!
We also have a guest assistant who happened to drop in: Alyssa Zisk (baozhale). Say hi to her, too!
i, imaginary
2014-02-05 19:03:44
Hello!
Hello!
baozhale
2014-02-05 19:03:55
Hi
Hi
simon1221
2014-02-05 19:04:13
hi
hi
aburules
2014-02-05 19:04:13
I am form
I am form
adno
2014-02-05 19:04:13
hi
hi
simranK
2014-02-05 19:04:13
hello!
hello!
1915933
2014-02-05 19:04:13
Hello!
Hello!
sunny2000
2014-02-05 19:04:13
hi
hi
ZZmath9
2014-02-05 19:04:13
Hi!
Hi!
AlanMTuring
2014-02-05 19:04:13
Hi!
Hi!
APSFUNJJJ
2014-02-05 19:04:13
hi
hi
mualphatheta
2014-02-05 19:04:13
Hi!
Hi!
1023ong
2014-02-05 19:04:13
nice to meet you all
nice to meet you all
LukeCell
2014-02-05 19:04:13
Hello
Hello
MrMerchant
2014-02-05 19:04:13
Hi!
Hi!
NikhilP
2014-02-05 19:04:13
Hi
Hi
15Pandabears
2014-02-05 19:04:13
hi!
hi!
pranavkrishna
2014-02-05 19:04:13
Hello
Hello
jigglypuff
2014-02-05 19:04:13
hi
hi
PiesAreSquared
2014-02-05 19:04:13
Hi!
Hi!
AbsoluteFriend
2014-02-05 19:04:13
Hi!
Hi!
IsabeltheCat
2014-02-05 19:04:13
Hellow!
Hellow!
ninjataco
2014-02-05 19:04:13
Hello!
Hello!
ljiang528
2014-02-05 19:04:13
hi
hi
DaChickenInc
2014-02-05 19:04:13
Hello
Hello
Ericaops
2014-02-05 19:04:13
Hello
Hello
tigergirl
2014-02-05 19:04:13
Hello
Hello
lucylai
2014-02-05 19:04:13
hi
hi
poweroftwo
2014-02-05 19:04:13
Hello!
Hello!
nahor123
2014-02-05 19:04:13
Hi
Hi
itsqueencaro
2014-02-05 19:04:13
hi benjamin and jessica!
hi benjamin and jessica!
kbird
2014-02-05 19:04:13
Hi!
Hi!
mathnerd101
2014-02-05 19:04:13
Hello!
Hello!
copeland
2014-02-05 19:04:20
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the incredibly large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the incredibly large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
copeland
2014-02-05 19:04:25
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.
copeland
2014-02-05 19:04:35
We will work the last 5 problems from the AMC 10A, then the last 5 problems from the AMC 12A. Two of these problems are the same, 10A Problem 25 and 12A Problem 22. We'll only solve that problem once.
We will work the last 5 problems from the AMC 10A, then the last 5 problems from the AMC 12A. Two of these problems are the same, 10A Problem 25 and 12A Problem 22. We'll only solve that problem once.
copeland
2014-02-05 19:04:48
We usually promise to chat about other problems on the test, but honestly, I tend to meander and most of us will be exhausted by the end of these 9 problems.
We usually promise to chat about other problems on the test, but honestly, I tend to meander and most of us will be exhausted by the end of these 9 problems.
copeland
2014-02-05 19:05:00
Oh, and there's a metric ton of people here tonight (375 and rising). I really don't like saying it, but we're probably going to miss some of the things that some of you say. (Especially during the geometry problems - sheesh.) Please forgive me in advance. That doesn't happen in our classes.
Oh, and there's a metric ton of people here tonight (375 and rising). I really don't like saying it, but we're probably going to miss some of the things that some of you say. (Especially during the geometry problems - sheesh.) Please forgive me in advance. That doesn't happen in our classes.
distortedwalrus
2014-02-05 19:05:20
I'm already exhausted
I'm already exhausted
copeland
2014-02-05 19:05:21
You should see it from my side. . .
You should see it from my side. . .
copeland
2014-02-05 19:05:30
Let's get started, huh?
Let's get started, huh?
2kev111
2014-02-05 19:05:50
ok
ok
Anno
2014-02-05 19:05:50
Okay
Okay
Turtle
2014-02-05 19:05:50
sure.
sure.
rmflute
2014-02-05 19:05:50
yes
yes
ferrastacie
2014-02-05 19:05:50
yes!
yes!
mualphatheta
2014-02-05 19:05:50
Yay!
Yay!
6stars
2014-02-05 19:05:50
Aye
Aye
kj2002
2014-02-05 19:05:50
Yeah
Yeah
dli00105
2014-02-05 19:05:50
yes!!
yes!!
mathman121
2014-02-05 19:05:50
YEAH!
YEAH!
Pythonprogrammer
2014-02-05 19:05:50
yes!
yes!
2kev111
2014-02-05 19:05:50
i cant wait to begin!
i cant wait to begin!
copeland
2014-02-05 19:05:56
21. Positive integers a and b are such that the graphs of y=ax+5 and y=3x+b intersect the x-axis at the same point. What is the sum of all possible x-coordinates of these points of intersection?
peekaboo!
(A) −20(B) −18(C) −15(D) −12(E) −8
21. Positive integers a and b are such that the graphs of y=ax+5 and y=3x+b intersect the x-axis at the same point. What is the sum of all possible x-coordinates of these points of intersection?
peekaboo!
(A) −20(B) −18(C) −15(D) −12(E) −8
copeland
2014-02-05 19:06:03
What does it mean for y=ax+5 and y=3x+b to have the same x-intercept?
What does it mean for y=ax+5 and y=3x+b to have the same x-intercept?
njaladan
2014-02-05 19:07:18
They both have the same x-value when y=0.
They both have the same x-value when y=0.
jungyeon
2014-02-05 19:07:18
they intersect at one point with y=0
they intersect at one point with y=0
mathwizard888
2014-02-05 19:07:18
when y is 0, the x-coordinates are equal
when y is 0, the x-coordinates are equal
copeland
2014-02-05 19:07:28
That's good. Can we make that into equations?
That's good. Can we make that into equations?
SuperSnivy
2014-02-05 19:07:57
ax+5=3x+b=0
ax+5=3x+b=0
chenmichael9
2014-02-05 19:07:57
ax+5=3x+b
ax+5=3x+b
mathwizard888
2014-02-05 19:07:57
ax+5=0 and 3x+b=0 have the same solution
ax+5=0 and 3x+b=0 have the same solution
Jessicatian
2014-02-05 19:07:57
ax+5=3x+b=0
ax+5=3x+b=0
alex31415
2014-02-05 19:07:57
ax+5=0 and 3x+b=0 for positive integers a,b
ax+5=0 and 3x+b=0 for positive integers a,b
copeland
2014-02-05 19:08:00
Right.
Right.
copeland
2014-02-05 19:08:01
This means that there's a specific x such that for our a and b,
0=ax+50=3x+b.
This means that there's a specific x such that for our a and b,
0=ax+50=3x+b.
copeland
2014-02-05 19:08:03
What should we do now?
What should we do now?
MathematicsOfPi
2014-02-05 19:08:54
Solve for x in both equations
Solve for x in both equations
thkim1011
2014-02-05 19:08:54
solve for x and let them equal
solve for x and let them equal
coldsummer
2014-02-05 19:08:54
solve for a and b
solve for a and b
Smokkala
2014-02-05 19:08:54
solve for a and b
solve for a and b
0_o
2014-02-05 19:08:54
add/subtract equations from each other
add/subtract equations from each other
mathmaster2012
2014-02-05 19:08:54
solve for a in terms of b
solve for a in terms of b
copeland
2014-02-05 19:09:03
That's good, let's try solving these equations.
That's good, let's try solving these equations.
copeland
2014-02-05 19:09:21
We have 2 equations in 3 unknowns, so we should probably try to eliminate something. What variable don't we want?
We have 2 equations in 3 unknowns, so we should probably try to eliminate something. What variable don't we want?
ScottBusche
2014-02-05 19:09:37
x
x
ChenthuranA
2014-02-05 19:09:37
x
x
surajsreddy
2014-02-05 19:09:37
x
x
sharonmath
2014-02-05 19:09:37
x
x
Sesquipedalian
2014-02-05 19:09:37
x
x
jdew192837
2014-02-05 19:09:37
x
x
BobCat128
2014-02-05 19:09:37
x
x
copeland
2014-02-05 19:09:42
Let's eliminate x from the equations. That will give us something Diophantine (meaning an integer equation) in terms of a and b.
Let's eliminate x from the equations. That will give us something Diophantine (meaning an integer equation) in terms of a and b.
copeland
2014-02-05 19:09:44
There are lots of ways to do this, and probably several of you want to substitute, but if we use elimination we won't have any nasty denominators. What should we multiply the equations by?
There are lots of ways to do this, and probably several of you want to substitute, but if we use elimination we won't have any nasty denominators. What should we multiply the equations by?
ninjataco
2014-02-05 19:10:17
the first one by 3, second one by a
the first one by 3, second one by a
swe1
2014-02-05 19:10:17
top one by 3 and bottom by a
top one by 3 and bottom by a
mjoshi
2014-02-05 19:10:17
3, and a
3, and a
Tuxianeer
2014-02-05 19:10:17
3 and a respectively
3 and a respectively
simpleasthat
2014-02-05 19:10:17
3 and -a
3 and -a
flyrain
2014-02-05 19:10:17
3 and a
3 and a
mjoshi
2014-02-05 19:10:17
the first one by 3, the second one by a?
the first one by 3, the second one by a?
copeland
2014-02-05 19:10:20
If we multiply the first equation by 3 and the second equation by a then we can subtract to eliminate x.
If we multiply the first equation by 3 and the second equation by a then we can subtract to eliminate x.
copeland
2014-02-05 19:10:25
0=3ax+150=3ax+ab0=15−ab.
0=3ax+150=3ax+ab0=15−ab.
copeland
2014-02-05 19:10:28
Therefore ab=15.
Therefore ab=15.
copeland
2014-02-05 19:10:30
What are the possible values of a?
What are the possible values of a?
willwang123
2014-02-05 19:10:50
1 3 5 15
1 3 5 15
eyux
2014-02-05 19:10:50
1, 3, 5, 15
1, 3, 5, 15
etothei
2014-02-05 19:10:50
1,3,5,15
1,3,5,15
fz0718
2014-02-05 19:10:50
1,3,5,15
1,3,5,15
VinTheSad
2014-02-05 19:10:50
a can equal, 1, 3, 5, or 15
a can equal, 1, 3, 5, or 15
fadebekun
2014-02-05 19:10:50
All factors of 15 which are 1,3,5,15
All factors of 15 which are 1,3,5,15
blueferret
2014-02-05 19:10:50
1,3,5,15
1,3,5,15
ajoy
2014-02-05 19:10:50
1,3,5,15
1,3,5,15
golden_ratio
2014-02-05 19:10:50
1,3,15
1,3,15
Emmettshell
2014-02-05 19:10:50
1,3,5,15
1,3,5,15
pranavkrishna
2014-02-05 19:10:50
1,3,5,15
1,3,5,15
copeland
2014-02-05 19:10:54
We can have a=1, 3, 5, or 15.
We can have a=1, 3, 5, or 15.
copeland
2014-02-05 19:10:57
But now we need x. When we solve the first equation for x we get x=−5a.
But now we need x. When we solve the first equation for x we get x=−5a.
copeland
2014-02-05 19:10:58
What is the sum of all possible values of x?
What is the sum of all possible values of x?
jeremylu
2014-02-05 19:11:20
-8
-8
Vishnu09
2014-02-05 19:11:20
-8
-8
UrInvalid
2014-02-05 19:11:20
-8
-8
ws5188
2014-02-05 19:11:20
-8
-8
tangaroo
2014-02-05 19:11:20
-8
-8
jigglypuff
2014-02-05 19:11:20
-8
-8
maxplanck
2014-02-05 19:11:20
-8
-8
Offendo
2014-02-05 19:11:20
-8
-8
1915933
2014-02-05 19:11:20
(E)-8
(E)-8
copeland
2014-02-05 19:11:24
We add−51+−53+−55+−515=−5−53−1−13=−8.
We add−51+−53+−55+−515=−5−53−1−13=−8.
copeland
2014-02-05 19:11:25
The answer is (E).
The answer is (E).
copeland
2014-02-05 19:11:33
Good. I hope everyone's warmed up.
Good. I hope everyone's warmed up.
mualphatheta
2014-02-05 19:11:45
yay! one down
one down
yay!
copeland
2014-02-05 19:12:02
Yep. We're working through the AMC10 right now in order from 21 through 25.
Yep. We're working through the AMC10 right now in order from 21 through 25.
copeland
2014-02-05 19:12:04
22. In rectangle ABCD, AB=20 and BC=10. Let E be a point on ¯CD such that ∠CBE=15∘. What is AE?
peekaboo!
(A) 20√33(B) 10√3(C) 18(D) 11√3(E) 20
22. In rectangle ABCD, AB=20 and BC=10. Let E be a point on ¯CD such that ∠CBE=15∘. What is AE?
peekaboo!
(A) 20√33(B) 10√3(C) 18(D) 11√3(E) 20
copeland
2014-02-05 19:12:17
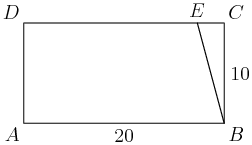

copeland
2014-02-05 19:12:19
Anybody have any ideas here?
Anybody have any ideas here?
trumpeter
2014-02-05 19:12:58
trig?
trig?
Tuxianeer
2014-02-05 19:12:58
trig
trig
2kev111
2014-02-05 19:12:58
use trigonometry?
use trigonometry?
Eunectus
2014-02-05 19:12:58
trig
trig
simon1221
2014-02-05 19:12:58
trig?
trig?
jillu1947
2014-02-05 19:12:58
i used trig
i used trig
simranK
2014-02-05 19:12:58
trigonometry...?
trigonometry...?
Mathdolphin
2014-02-05 19:12:58
Trig bash
Trig bash
copeland
2014-02-05 19:13:00
Trig bash works, but it's a little slower than the "intended" solution.
Trig bash works, but it's a little slower than the "intended" solution.
jeremylu
2014-02-05 19:13:35
15-75-90 triangle
15-75-90 triangle
copeland
2014-02-05 19:13:38
I see it!
I see it!
copeland
2014-02-05 19:13:41
What can we do wit hthat guy?
What can we do wit hthat guy?
connor0728
2014-02-05 19:14:41
split it up
split it up
guilt
2014-02-05 19:14:41
split 75 into 15 and 60
split 75 into 15 and 60
lightning23
2014-02-05 19:14:41
Split the 15-75-90 into a 30-60 -90 and an isosceles
Split the 15-75-90 into a 30-60 -90 and an isosceles
NikhilP
2014-02-05 19:14:41
75=15+60
75=15+60
copeland
2014-02-05 19:14:47
The easiest solution I have for this problem relies on a trick you might want to know.
The easiest solution I have for this problem relies on a trick you might want to know.
copeland
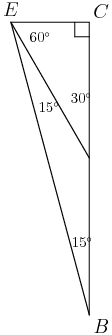
2014-02-05 19:14:48
The trick is: if you ever see a 15-75-90 triangle, draw a new segment that makes a 30-60-90 triangle inside:
The trick is: if you ever see a 15-75-90 triangle, draw a new segment that makes a 30-60-90 triangle inside:
copeland
2014-02-05 19:14:51

copeland
2014-02-05 19:14:57
This is really nice because we have on 30-60-90 triangle and we also have an isosceles triangle. This is just one of those tricks you either know or you don't. It's kind of an unfortunate twist to the problem.
This is really nice because we have on 30-60-90 triangle and we also have an isosceles triangle. This is just one of those tricks you either know or you don't. It's kind of an unfortunate twist to the problem.
copeland
2014-02-05 19:15:01
Write this in your Big Book of Tricks. It doesn't come up that often, but if a problem has a 15-75-90 triangle, you probably should consider starting here.
Write this in your Big Book of Tricks. It doesn't come up that often, but if a problem has a 15-75-90 triangle, you probably should consider starting here.
copeland
2014-02-05 19:15:05
There actually is a more general idea here. If you're give weird angles, start looking for isosceles triangles. That gives you an opportunity to transport side lengths around and it sometimes allows you to double your angles. You can also solve this problem by creating a nice 75-75-30 isosceles triangle somewhere as well, but that solution is a little too mysterious for me.
There actually is a more general idea here. If you're give weird angles, start looking for isosceles triangles. That gives you an opportunity to transport side lengths around and it sometimes allows you to double your angles. You can also solve this problem by creating a nice 75-75-30 isosceles triangle somewhere as well, but that solution is a little too mysterious for me.
copeland
2014-02-05 19:15:10
There actually is a more general idea here. If you're given weird angles, start looking for isosceles triangles. That gives you an opportunity to transport side lengths around and it sometimes allows you to double your angles.
There actually is a more general idea here. If you're given weird angles, start looking for isosceles triangles. That gives you an opportunity to transport side lengths around and it sometimes allows you to double your angles.
copeland
2014-02-05 19:15:27
Incidentally, we can get another nice triangle that we can use the Angle Bisector Theorem on by placing a new point on DC and forcing BC to be an angle bisector in a 30-60-90 triangle.
Incidentally, we can get another nice triangle that we can use the Angle Bisector Theorem on by placing a new point on DC and forcing BC to be an angle bisector in a 30-60-90 triangle.
copeland
2014-02-05 19:15:30
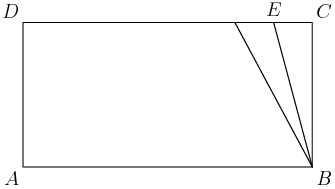

copeland
2014-02-05 19:15:40
Some of you also suggested this. It leads to a fine solution as well.
Some of you also suggested this. It leads to a fine solution as well.
copeland
2014-02-05 19:15:53
Back to this triangle:
Back to this triangle:
copeland
2014-02-05 19:15:55


copeland
2014-02-05 19:16:00
Now what?
Now what?
jdew192837
2014-02-05 19:16:44
Use the ratios 1 2 square root of 3
Use the ratios 1 2 square root of 3
coldsummer
2014-02-05 19:16:44
let CE = x
let CE = x
guor
2014-02-05 19:16:44
Get side lengths.
Get side lengths.
blueferret
2014-02-05 19:16:44
call EC x
call EC x
somepersonoverhere
2014-02-05 19:16:44
calculate EC
calculate EC
UrInvalid
2014-02-05 19:16:44
set ec as x, use special triangle formulae
set ec as x, use special triangle formulae
ChenthuranA
2014-02-05 19:16:44
write everything in terms of EC
write everything in terms of EC
copeland
2014-02-05 19:16:50
Let's introduce a variable. I'm going to let x=EC.
Let's introduce a variable. I'm going to let x=EC.
copeland
2014-02-05 19:16:54


copeland
2014-02-05 19:17:00
What other distances do we get?
What other distances do we get?
Richardq
2014-02-05 19:17:43
EF=2x
EF=2x
CountDown
2014-02-05 19:17:43
EF = 2x
EF = 2x
Emmettshell
2014-02-05 19:17:43
EF=2x
EF=2x
CountDown
2014-02-05 19:17:43
CF = x * \sqrt{3}
CF = x * \sqrt{3}
Vishnu09
2014-02-05 19:17:43
EF: 2X
EF: 2X
alex31415
2014-02-05 19:17:43
CF=sqrt3*x, EF=2x, FB=2x
CF=sqrt3*x, EF=2x, FB=2x
jenmath666
2014-02-05 19:17:43
CF=x sqrt3
CF=x sqrt3
Turtle
2014-02-05 19:17:43
CF xsqrt3. EF = 2x
CF xsqrt3. EF = 2x
dli00105
2014-02-05 19:17:43
CF=xsqrt(3)
CF=xsqrt(3)
pedronr
2014-02-05 19:17:43
CF is x√3
CF is x√3
copeland
2014-02-05 19:17:45
CF=x√3.
CF=x√3.
copeland
2014-02-05 19:17:45
EF=FB=2x.
EF=FB=2x.
copeland
2014-02-05 19:17:49


copeland
2014-02-05 19:17:56
Now what?
Now what?
NumberNinja
2014-02-05 19:18:32
CB=10
CB=10
carjacker
2014-02-05 19:18:32
x*sqrt(3)+2x=10
x*sqrt(3)+2x=10
swe1
2014-02-05 19:18:32
solve for 2x+xsqrt3=10
solve for 2x+xsqrt3=10
DigitalKing257
2014-02-05 19:18:32
CB=10=2x+x√3
CB=10=2x+x√3
mjoshi
2014-02-05 19:18:32
x(2+\sqrt{3}) = 10
x(2+\sqrt{3}) = 10
njaladan
2014-02-05 19:18:32
2x + sqrt(3)*x = 10
2x + sqrt(3)*x = 10
droid347
2014-02-05 19:18:32
2x+xsqrt(3)=10
2x+xsqrt(3)=10
copeland
2014-02-05 19:18:36
Oh, now we can solve for x with BC. We have10=BC=BF+FC=2x+x√3. Therefore x=102+√3.
Oh, now we can solve for x with BC. We have10=BC=BF+FC=2x+x√3. Therefore x=102+√3.
copeland
2014-02-05 19:18:38
What do we get when we rationalize the denominator?
What do we get when we rationalize the denominator?
ZZmath9
2014-02-05 19:19:03
20-10sqrt3
20-10sqrt3
jigglypuff
2014-02-05 19:19:03
20-10sqrt3
20-10sqrt3
mathwizard888
2014-02-05 19:19:03
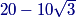
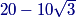
zoroark12345
2014-02-05 19:19:03
20-10/sqrt{3}
20-10/sqrt{3}
simranK
2014-02-05 19:19:03
20-10sqrt{3}
20-10sqrt{3}
scgorantla
2014-02-05 19:19:03
20-10sqrt3
20-10sqrt3
suli
2014-02-05 19:19:03
20 - 10sqrt(3)
20 - 10sqrt(3)
mualphatheta
2014-02-05 19:19:03
20-10sqrt(3)
20-10sqrt(3)
trumpeter
2014-02-05 19:19:03
20-10sqrt(3)
20-10sqrt(3)
ninjataco
2014-02-05 19:19:03
20−10√3
20−10√3
jeremylu
2014-02-05 19:19:03
20−10√3
20−10√3
copeland
2014-02-05 19:19:06
x=102+√3⋅2−√32−√3=10(2−√3)4−3=20−10√3.
x=102+√3⋅2−√32−√3=10(2−√3)4−3=20−10√3.
copeland
2014-02-05 19:19:09
Now what should we find?
Now what should we find?
mathmaster2012
2014-02-05 19:19:48
DE and pythgagorean
DE and pythgagorean
chying1
2014-02-05 19:19:48
DE
DE
zoroark12345
2014-02-05 19:19:48
DE for pythagorean theorem
DE for pythagorean theorem
mathmaster2012
2014-02-05 19:19:48
DE and pythagorean
DE and pythagorean
DrMath
2014-02-05 19:19:48
DE and pythagoras for AE
DE and pythagoras for AE
want2learn
2014-02-05 19:19:48
ED
ED
buzzyun
2014-02-05 19:19:48
DE = 20 -x
DE = 20 -x
copeland
2014-02-05 19:19:55
Since we have AD=10, all we need is DE and the Pythagorean Theorem to get AE. What is DE?
Since we have AD=10, all we need is DE and the Pythagorean Theorem to get AE. What is DE?
Mathlete25
2014-02-05 19:20:19
DE=10\sqrt{3}
DE=10\sqrt{3}
jiyer99
2014-02-05 19:20:19
10sqrt3
10sqrt3
JixuanW
2014-02-05 19:20:19
DE = 10rt(3)
DE = 10rt(3)
15Pandabears
2014-02-05 19:20:19
10sqrt3
10sqrt3
surajsreddy
2014-02-05 19:20:19
10sqrt(3)
10sqrt(3)
AndrewK
2014-02-05 19:20:19
10 root 3
10 root 3
ZekromReshiram
2014-02-05 19:20:19
10sqrt3
10sqrt3
ajc01
2014-02-05 19:20:19
10sqrt3
10sqrt3
mathwizard888
2014-02-05 19:20:19
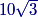
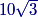
copeland
2014-02-05 19:20:22
This is nice, DE=DC−EC=20−(20−10√3)=10√3.
This is nice, DE=DC−EC=20−(20−10√3)=10√3.
copeland
2014-02-05 19:20:23
Here's our diagram:
Here's our diagram:
copeland
2014-02-05 19:21:08
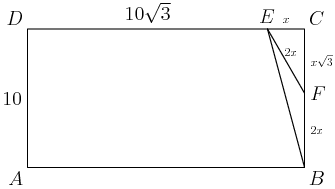

pedronr
2014-02-05 19:21:50
ADE is a 30-60-90 triangle
ADE is a 30-60-90 triangle
25120012jsy21
2014-02-05 19:21:50
And now we use the pythagorean theorem to get (E), 20?
And now we use the pythagorean theorem to get (E), 20?
kajay88
2014-02-05 19:21:50
AE now=20
AE now=20
fadebekun
2014-02-05 19:21:50
So we have AE=√(10√3)2+100=√400=20
So we have AE=√(10√3)2+100=√400=20
MathematicsOfPi
2014-02-05 19:21:50
so △ADE is also 30-60-90 and we can use the ratios or Pythagorean Theorem to find AE
so △ADE is also 30-60-90 and we can use the ratios or Pythagorean Theorem to find AE
blueferret
2014-02-05 19:21:50
AE=20
AE=20
IsabeltheCat
2014-02-05 19:21:50
AE=20 by 30-60-90
AE=20 by 30-60-90
WolfOfAtlantis
2014-02-05 19:21:50
30 60 90
30 60 90
pl210741
2014-02-05 19:21:50
30-60-90 triangle
30-60-90 triangle
Eunectus
2014-02-05 19:21:50
hey is that a 30-60-90
hey is that a 30-60-90
zacchro
2014-02-05 19:21:50
AE=;20
AE=;20
sunny2000
2014-02-05 19:21:50
30, 60, 90 triangle
30, 60, 90 triangle
yuunderstand168
2014-02-05 19:21:50
and that's a 30-60-90 triangle (DAE)
and that's a 30-60-90 triangle (DAE)
Tuxianeer
2014-02-05 19:21:50
(E) 20
(E) 20
copeland
2014-02-05 19:21:55
Look! It's a 30-60-90 triangle. We don't even need the Pythagorean Theorem. The hypotenuse is 2⋅10=20. The answer is (E).
Look! It's a 30-60-90 triangle. We don't even need the Pythagorean Theorem. The hypotenuse is 2⋅10=20. The answer is (E).
copeland
2014-02-05 19:21:58
Incidentally, if you drew a very big, very clear diagram here, you might be able to see either that △ADE is 30-60-90 or that △AEB is isosceles. Either one gives you a good opportunity to guess the answer if you don't see the trick.
Incidentally, if you drew a very big, very clear diagram here, you might be able to see either that △ADE is 30-60-90 or that △AEB is isosceles. Either one gives you a good opportunity to guess the answer if you don't see the trick.
copeland
2014-02-05 19:22:12
Phew. 2 down.
Phew. 2 down.
laegolas
2014-02-05 19:22:25
I didn't know any of the theorems. I used a ruler and got the answer correct!
I didn't know any of the theorems. I used a ruler and got the answer correct!
fz0718
2014-02-05 19:22:25
If you drew a clear diagram, you could've just used a ruler and got it...
If you drew a clear diagram, you could've just used a ruler and got it...
Smokkala
2014-02-05 19:22:25
Somebody used their ruler and found the scale and got 20
Somebody used their ruler and found the scale and got 20
copeland
2014-02-05 19:22:29
Absolutely.
Absolutely.
mualphatheta
2014-02-05 19:22:45
Finger measurements = Reliable.
Finger measurements = Reliable.
copeland
2014-02-05 19:22:46
Depends on your fingers.
Depends on your fingers.
copeland
2014-02-05 19:22:48
23. A rectangular piece of paper whose length is √3 times the width has area A. The paper is divided into three equal sections along the opposite lengths, and then a dotted line is drawn from the first divider to the second divider on the opposite side as shown. The paper is then folded flat along this dotted line to create a new shape with area B. What is the ratio B:A?
peekaboo!
(A) 1:2(B) 3:5(C) 2:3(D) 3:4(E) 4:5
23. A rectangular piece of paper whose length is √3 times the width has area A. The paper is divided into three equal sections along the opposite lengths, and then a dotted line is drawn from the first divider to the second divider on the opposite side as shown. The paper is then folded flat along this dotted line to create a new shape with area B. What is the ratio B:A?
peekaboo!
(A) 1:2(B) 3:5(C) 2:3(D) 3:4(E) 4:5
copeland
2014-02-05 19:23:00
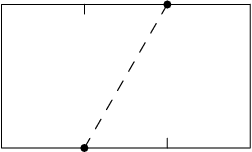

copeland
2014-02-05 19:23:03
Just so we're in the same place on this one, we are going to fold the bottom right corner up and to the left.
Just so we're in the same place on this one, we are going to fold the bottom right corner up and to the left.
copeland
2014-02-05 19:23:24
It probably helps to have some actual scale here. What should we pick for the length of the short edge?
It probably helps to have some actual scale here. What should we pick for the length of the short edge?
va2010
2014-02-05 19:23:54
\sqrt{3}
\sqrt{3}
ScottBusche
2014-02-05 19:23:54
sqrt3?
sqrt3?
LightningX48
2014-02-05 19:23:54
sqrt(3)
sqrt(3)
DaChickenInc
2014-02-05 19:23:54
√3
√3
guilt
2014-02-05 19:23:54
sqrt3
sqrt3
abishek99
2014-02-05 19:23:54
sqrt3
sqrt3
GeorgCantor
2014-02-05 19:23:54
root 3?
root 3?
copeland
2014-02-05 19:23:57
Since the long edge is trisected, we should make that 3 and the short edge will be √3.
Since the long edge is trisected, we should make that 3 and the short edge will be √3.
copeland
2014-02-05 19:24:02
It doesn't matter, but I like this choice.
It doesn't matter, but I like this choice.
copeland
2014-02-05 19:24:08
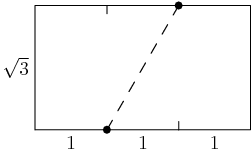

copeland
2014-02-05 19:24:13
Now what do you notice?
Now what do you notice?
UrInvalid
2014-02-05 19:24:37
30-60-90
30-60-90
hexagram
2014-02-05 19:24:37
30-60-90!
30-60-90!
2kev111
2014-02-05 19:24:37
it is a 30 60 90 triangle
it is a 30 60 90 triangle
swe1
2014-02-05 19:24:37
30-60-90 triangle
30-60-90 triangle
Nitzuga
2014-02-05 19:24:37
30-60-90
30-60-90
LMA
2014-02-05 19:24:37
30-60-90 triangle!
30-60-90 triangle!
ChenthuranA
2014-02-05 19:24:37
30-60-90
30-60-90
Eudokia
2014-02-05 19:24:37
30-60-90
30-60-90
MasterChief1096
2014-02-05 19:24:37
30-60-90 ratios
30-60-90 ratios
Vishnu09
2014-02-05 19:24:37
30-60-90 triangles
30-60-90 triangles
copeland
2014-02-05 19:24:40
Every interesting angle in this diagram is in the 30-60-90 triangle family.
Every interesting angle in this diagram is in the 30-60-90 triangle family.
copeland
2014-02-05 19:24:45
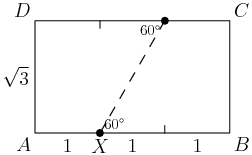

copeland
2014-02-05 19:24:47
We need to figure out where the bottom right corner lands when we fold it. What is the angle it makes with the horizontal axis after the fold?
We need to figure out where the bottom right corner lands when we fold it. What is the angle it makes with the horizontal axis after the fold?
harvey2014
2014-02-05 19:25:37
60
60
pickten
2014-02-05 19:25:37
60
60
ninjataco
2014-02-05 19:25:37
60
60
dli00105
2014-02-05 19:25:37
60
60
Anthrax
2014-02-05 19:25:37
60
60
ingridzhang97
2014-02-05 19:25:37
60
60
SuperSnivy
2014-02-05 19:25:37
60
60
rjw98
2014-02-05 19:25:37
120
120
6stars
2014-02-05 19:25:37
60 degrees?
60 degrees?
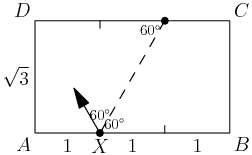
copeland
2014-02-05 19:25:39
The point lands along a ray from X that is 120∘ counter-clockwise from B. This is 60 degrees from horizontal to the left.
The point lands along a ray from X that is 120∘ counter-clockwise from B. This is 60 degrees from horizontal to the left.
copeland
2014-02-05 19:25:51

copeland
2014-02-05 19:25:58
Since XB=2, it lies 2 units along this ray. What do you notice?
Since XB=2, it lies 2 units along this ray. What do you notice?
mymathboy
2014-02-05 19:26:48
B to D
B to D
checkmate1021
2014-02-05 19:26:48
B => D
B => D
xianmingli
2014-02-05 19:26:48
lies on D
lies on D
pinetree1
2014-02-05 19:26:48
It is at D
It is at D
etothei
2014-02-05 19:26:48
B IS ON D
B IS ON D
hliu70
2014-02-05 19:26:48
B lands on D
B lands on D
DrMath
2014-02-05 19:26:48
it lands on D
it lands on D
2kev111
2014-02-05 19:26:48
b will touch d
b will touch d
copeland
2014-02-05 19:26:53
Since ∠AXD=60∘, AX=1, and XB=2 we get that B lands on D after the fold. Wow is that going to be convenient!
Since ∠AXD=60∘, AX=1, and XB=2 we get that B lands on D after the fold. Wow is that going to be convenient!
copeland
2014-02-05 19:26:56


copeland
2014-02-05 19:27:08
Now we just need to compute. What fraction of the rectangle overlaps?
Now we just need to compute. What fraction of the rectangle overlaps?
teachm
2014-02-05 19:27:35
1/3
1/3
flyingsledge
2014-02-05 19:27:35
1/3
1/3
Mathdolphin
2014-02-05 19:27:35
1/3
1/3
15Pandabears
2014-02-05 19:27:35
1/3
1/3
rmflute
2014-02-05 19:27:35
1/3
1/3
flyrain
2014-02-05 19:27:35
1/3
1/3
treemath
2014-02-05 19:27:35
1/3
1/3
vincenthuang75025
2014-02-05 19:27:35
1/3
1/3
njaladan
2014-02-05 19:27:35
1/3
1/3
Kevinyang2000
2014-02-05 19:27:35
1/3
1/3
mxgo
2014-02-05 19:27:35
1/3
1/3
copeland
2014-02-05 19:27:42
The new figure looks something like this with a few suggestive congruent triangles drawn in.
The new figure looks something like this with a few suggestive congruent triangles drawn in.
copeland
2014-02-05 19:27:44
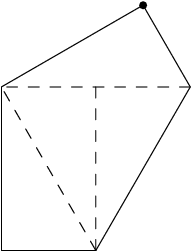

copeland
2014-02-05 19:27:46
We can dissect the rectangle into 6 congruent triangles. Two pairs of the triangles will overlap when we fold giving us just four triangles.
We can dissect the rectangle into 6 congruent triangles. Two pairs of the triangles will overlap when we fold giving us just four triangles.
copeland
2014-02-05 19:27:52
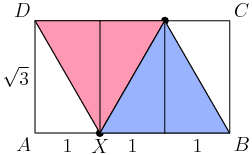

copeland
2014-02-05 19:28:09
That means 2/6 of the triangles overlap (a larger equilateral triangle).
That means 2/6 of the triangles overlap (a larger equilateral triangle).
copeland
2014-02-05 19:28:12
What is the answer?
What is the answer?
pedronr
2014-02-05 19:28:37
so the answer is 2/3
so the answer is 2/3
joshualee2000
2014-02-05 19:28:37
so the answer is C 2:3
so the answer is C 2:3
kajay88
2014-02-05 19:28:37
2/3
2/3
LightningX48
2014-02-05 19:28:37
so its 2/3 or (C)
so its 2/3 or (C)
brandonbigbrother
2014-02-05 19:28:37
2:3
2:3
El_Ectric
2014-02-05 19:28:37
2/3
2/3
want2learn
2014-02-05 19:28:37
2:3
2:3
kangrui
2014-02-05 19:28:37
2:3, C
2:3, C
jfu
2014-02-05 19:28:37
C
C
copeland
2014-02-05 19:28:49
The ratio of the new figure's area to the old figure's area is 46=23. The answer is (C).
The ratio of the new figure's area to the old figure's area is 46=23. The answer is (C).
blueberry7
2014-02-05 19:29:24
number 24...
number 24...
arpanliku
2014-02-05 19:29:24
Three down! This is fun!
Three down! This is fun!
Basking
2014-02-05 19:29:27
3 down!!
3 down!!
copeland
2014-02-05 19:29:31
24. A sequence of natural numbers is constructed by listing the first 4, then skipping one, listing the next 5, skipping 2, listing 6, skipping 3, and, on the nth iteration, listing n+3 and skipping n. The sequence begins 1,2,3,4,6,7,8,9,10,13. What is the 500,000th number in the sequence?
peekaboo!
(A) 996,506(B) 996,507(C) 996,508(D) 996,509(E) 996,510
24. A sequence of natural numbers is constructed by listing the first 4, then skipping one, listing the next 5, skipping 2, listing 6, skipping 3, and, on the nth iteration, listing n+3 and skipping n. The sequence begins 1,2,3,4,6,7,8,9,10,13. What is the 500,000th number in the sequence?
peekaboo!
(A) 996,506(B) 996,507(C) 996,508(D) 996,509(E) 996,510
copeland
2014-02-05 19:29:36
Oh, goodie. The bookkeeping problem. Let's have at it, then.
Oh, goodie. The bookkeeping problem. Let's have at it, then.
copeland
2014-02-05 19:29:43
What should be the first step in any problem like this?
What should be the first step in any problem like this?
Tuxianeer
2014-02-05 19:30:12
small cases
small cases
fcc1234
2014-02-05 19:30:12
Smaller cases?
Smaller cases?
mjoshi
2014-02-05 19:30:12
patterns?
patterns?
simon1221
2014-02-05 19:30:12
find a pattern
find a pattern
ninjackbrosky
2014-02-05 19:30:12
grouping
grouping
blueferret
2014-02-05 19:30:12
try to find a pattern
try to find a pattern
suli
2014-02-05 19:30:12
Find patterns
Find patterns
kbird
2014-02-05 19:30:12
pattern-finding
pattern-finding
aburules
2014-02-05 19:30:12
find a pattern
find a pattern
sarvottam
2014-02-05 19:30:12
write the first few terms
write the first few terms
lightning23
2014-02-05 19:30:12
Find a pattern
Find a pattern
BobCat128
2014-02-05 19:30:12
look for a pattern
look for a pattern
copeland
2014-02-05 19:30:23
On basically any bookkeeping problem, I promise you that starting off with a nice clear example will help you. It cleans up all the possible off-by-one errors you might have and gives you some nice test cases for all the general things you'll need to say.
On basically any bookkeeping problem, I promise you that starting off with a nice clear example will help you. It cleans up all the possible off-by-one errors you might have and gives you some nice test cases for all the general things you'll need to say.
copeland
2014-02-05 19:30:24
Here is the first four blocks of our sequence. This is probably more than you would need. The sequence is in black and the skipped numbers are in red.
Here is the first four blocks of our sequence. This is probably more than you would need. The sequence is in black and the skipped numbers are in red.
copeland
2014-02-05 19:30:26
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,…
1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,…
copeland
2014-02-05 19:30:33
This example will help us to find a pattern.
This example will help us to find a pattern.
copeland
2014-02-05 19:30:35
We want the 500,000th black term in this list. What should we count?
We want the 500,000th black term in this list. What should we count?
gaussian
2014-02-05 19:31:17
terms in each row
terms in each row
Tuxianeer
2014-02-05 19:31:17
number of numbers skipped
number of numbers skipped
willwang123
2014-02-05 19:31:17
how many terms there are in all
how many terms there are in all
Eudokia
2014-02-05 19:31:17
the reds
the reds
ingridzhang97
2014-02-05 19:31:17
the black terms
the black terms
TheCrafter
2014-02-05 19:31:17
Number of terms skipped
Number of terms skipped
mathwizard888
2014-02-05 19:31:17
black and total
black and total
angel27
2014-02-05 19:31:17
The number of black numbers in each row
The number of black numbers in each row
DrMath
2014-02-05 19:31:17
which iteration it is in
which iteration it is in
gengkev
2014-02-05 19:31:17
black terms and red terms
black terms and red terms
mathmaster2012
2014-02-05 19:31:17
4,10,18,28, etc.
4,10,18,28, etc.
copeland
2014-02-05 19:31:23
Let's count the number of black terms in the first n blocks and the total number of terms in the first n blocks. How many black terms are there in the first n blocks?
Let's count the number of black terms in the first n blocks and the total number of terms in the first n blocks. How many black terms are there in the first n blocks?
Nahmid
2014-02-05 19:33:01
n(n+7)/2
n(n+7)/2
UrInvalid
2014-02-05 19:33:01
n(n+7)/2
n(n+7)/2
alex31415
2014-02-05 19:33:01
4+5+6+...+(n+3)
4+5+6+...+(n+3)
dli00105
2014-02-05 19:33:01
4+5+6+...+n+3
4+5+6+...+n+3
linhhuynh
2014-02-05 19:33:01
n(n+7)/2
n(n+7)/2
copeland
2014-02-05 19:33:04
The first n blocks have 4+5+6+⋯+(n+3)terms. That is n(n+7)2 total black terms in the first n rows.
The first n blocks have 4+5+6+⋯+(n+3)terms. That is n(n+7)2 total black terms in the first n rows.
copeland
2014-02-05 19:33:11
Now let's find the last (red) number in the nth block. Before that, how many total numbers are on the nth row?
Now let's find the last (red) number in the nth block. Before that, how many total numbers are on the nth row?
jigglypuff
2014-02-05 19:34:10
2n+3
2n+3
wpk
2014-02-05 19:34:10
2n+3
2n+3
JFC
2014-02-05 19:34:10
3+2n
3+2n
MaYang
2014-02-05 19:34:10
2n+3
2n+3
Turtwig123
2014-02-05 19:34:10
2n+3
2n+3
harvey2014
2014-02-05 19:34:10
2n+3
2n+3
copeland
2014-02-05 19:34:13
The first row has 5 terms. The second has 7, the third has 9. The nth row has 2n+3 total terms.
The first row has 5 terms. The second has 7, the third has 9. The nth row has 2n+3 total terms.
copeland
2014-02-05 19:34:15
Now what is the last number in row n?
Now what is the last number in row n?
UrInvalid
2014-02-05 19:35:12
n(n+4)
n(n+4)
mathwizard888
2014-02-05 19:35:12
n(n+4)
n(n+4)
mathwizard888
2014-02-05 19:35:12
n(n+4)
n(n+4)
Michael_Huang23
2014-02-05 19:35:12
(n)(n+4)
(n)(n+4)
Nahmid
2014-02-05 19:35:12
n(n+4)
n(n+4)
brainiac1
2014-02-05 19:35:12
n^2+4n
n^2+4n
copeland
2014-02-05 19:35:15
Since the list starts at 1, the last number in row n is equal to the total number of terms in the first n rows. That is 5+7+9+⋯+(2n+3)=n(2n+8)2=n(n+4).
Since the list starts at 1, the last number in row n is equal to the total number of terms in the first n rows. That is 5+7+9+⋯+(2n+3)=n(2n+8)2=n(n+4).
copeland
2014-02-05 19:35:22
A lot of people are asking where these formulas are coming from.
A lot of people are asking where these formulas are coming from.
copeland
2014-02-05 19:35:44
If you have an arithmetic progression that starts with a and ends with b, what is the average value?
If you have an arithmetic progression that starts with a and ends with b, what is the average value?
AndrewK
2014-02-05 19:36:14
a+b/2
a+b/2
NumberNinja
2014-02-05 19:36:14
(a+b)/2
(a+b)/2
richard4912
2014-02-05 19:36:14
(a+b)/2
(a+b)/2
Darn
2014-02-05 19:36:14
(A+B)/2
(A+B)/2
Mathdolphin
2014-02-05 19:36:14
(a+b)/2
(a+b)/2
MathematicsOfPi
2014-02-05 19:36:14
a+b2
a+b2
1023ong
2014-02-05 19:36:14
(a+b)/2
(a+b)/2
SHARKYBOY
2014-02-05 19:36:14
(a+b)/2
(a+b)/2
Anthrax
2014-02-05 19:36:14
(a+b)/2
(a+b)/2
eddy55
2014-02-05 19:36:14
(a+b)/2
(a+b)/2
willwin4sure
2014-02-05 19:36:14
(a+b)/2
(a+b)/2
copeland
2014-02-05 19:36:19
The average value will be a+b2.
The average value will be a+b2.
copeland
2014-02-05 19:36:30
All you need to do to find the sum is multiply this average by the total number of terms.
All you need to do to find the sum is multiply this average by the total number of terms.
copeland
2014-02-05 19:36:55
If we start at 5 and end at 2n+3, the average is 2n+82 and the number of terms is n.
If we start at 5 and end at 2n+3, the average is 2n+82 and the number of terms is n.
copeland
2014-02-05 19:37:08
This is where we get n(2n+8)2.
This is where we get n(2n+8)2.
copeland
2014-02-05 19:37:18
The last omitted (red) number in row n is n(n+4).
The last omitted (red) number in row n is n(n+4).
copeland
2014-02-05 19:37:33
Now we're looking for the 500,000th number in our sequence, which is the 500,000th black number listed. How do we find out what row that term is in?
Now we're looking for the 500,000th number in our sequence, which is the 500,000th black number listed. How do we find out what row that term is in?
Nitzuga
2014-02-05 19:38:32
Solve n(n+7)/2=500000
Solve n(n+7)/2=500000
UrInvalid
2014-02-05 19:38:32
n(n+7)=1000000, ceil(n)
n(n+7)=1000000, ceil(n)
ingridzhang97
2014-02-05 19:38:32
first set n(n+7)/2 equal to 500,000 to find n
first set n(n+7)/2 equal to 500,000 to find n
blueferret
2014-02-05 19:38:32
n(n+7)/2>500000
n(n+7)/2>500000
AaaDuhLoo
2014-02-05 19:38:32
n(n+7)/2 = 500,000
n(n+7)/2 = 500,000
checkmate1021
2014-02-05 19:38:32
n(n+7)/2 = 500000
n(n+7)/2 = 500000
JFC
2014-02-05 19:38:32
Find what value of n, when in n(n+7)/2, exceeds 500000
Find what value of n, when in n(n+7)/2, exceeds 500000
ingridzhang97
2014-02-05 19:38:32
first set n(n+7)/2 equal to 500,000 to find the iteration/row
first set n(n+7)/2 equal to 500,000 to find the iteration/row
copeland
2014-02-05 19:38:37
We want to find the n such that n(n+7)2<500,000≤(n+1)(n+8)2.
We want to find the n such that n(n+7)2<500,000≤(n+1)(n+8)2.
copeland
2014-02-05 19:38:39
Let's look at n(n+7)≈1,000,000. What is an obvious place to start?
Let's look at n(n+7)≈1,000,000. What is an obvious place to start?
Emmettshell
2014-02-05 19:38:59
1000
1000
zoroark12345
2014-02-05 19:38:59
1000
1000
joshualee2000
2014-02-05 19:38:59
1000
1000
ninjackbrosky
2014-02-05 19:38:59
1000
1000
DrMath
2014-02-05 19:38:59
1000
1000
geo31415926
2014-02-05 19:38:59
1000
1000
DuoCapital
2014-02-05 19:38:59
1000
1000
gengkev
2014-02-05 19:38:59
1000!
1000!
15Pandabears
2014-02-05 19:38:59
1000
1000
LightningX48
2014-02-05 19:38:59
1000
1000
dli00105
2014-02-05 19:38:59
n=1000
n=1000
dlin
2014-02-05 19:38:59
1000
1000
matthewzou
2014-02-05 19:38:59
1000
1000
copeland
2014-02-05 19:39:02
If we let n=1000 we get n(n+7)=1000⋅1007=1,007,000 which is about 7000 too much.
If we let n=1000 we get n(n+7)=1000⋅1007=1,007,000 which is about 7000 too much.
copeland
2014-02-05 19:39:08
You could decrease n a few times and find the right row, but here's a quick trick that might shave some seconds off your time:
You could decrease n a few times and find the right row, but here's a quick trick that might shave some seconds off your time:
copeland
2014-02-05 19:39:10
If n≈1000 and we decrease n by 1, about how much do we decrease n(n+7)?
If n≈1000 and we decrease n by 1, about how much do we decrease n(n+7)?
Michael_Huang23
2014-02-05 19:39:52
2000
2000
JFC
2014-02-05 19:39:52
2000
2000
dli00105
2014-02-05 19:39:52
2000
2000
Darn
2014-02-05 19:39:52
2000>
2000>
NathanV
2014-02-05 19:39:52
2000
2000
willwin4sure
2014-02-05 19:39:52
2000
2000
checkmate1021
2014-02-05 19:39:52
2000?
2000?
alex31415
2014-02-05 19:39:52
2000
2000
billgates42
2014-02-05 19:39:52
2000
2000
copeland
2014-02-05 19:39:54
The Binomial Theorem tells us that if (a−1)(b−1)=ab−a−b+1. So if a and b are close to 1000, decreasing both by 1 decreases the product by about a+b≈2000. Every time we decrease n by 1 we decrease the product by approximately 2000.
The Binomial Theorem tells us that if (a−1)(b−1)=ab−a−b+1. So if a and b are close to 1000, decreasing both by 1 decreases the product by about a+b≈2000. Every time we decrease n by 1 we decrease the product by approximately 2000.
copeland
2014-02-05 19:40:03
Therefore, what n should we start with?
Therefore, what n should we start with?
poweroftwo
2014-02-05 19:40:28
996
996
pedronr
2014-02-05 19:40:28
996
996
ssk9208
2014-02-05 19:40:28
996
996
Turtwig123
2014-02-05 19:40:28
996
996
DaChickenInc
2014-02-05 19:40:28
996
996
CornSaltButter
2014-02-05 19:40:28
996
996
scgorantla
2014-02-05 19:40:28
996
996
joshualee2000
2014-02-05 19:40:28
996
996
BobCat128
2014-02-05 19:40:28
996
996
copeland
2014-02-05 19:40:32
We know n=1000 is about 7000 too big so replacing n by n−4 should decrease the product by about 4⋅2000=8000. That is the row before the 5000,000th term.
We know n=1000 is about 7000 too big so replacing n by n−4 should decrease the product by about 4⋅2000=8000. That is the row before the 5000,000th term.
copeland
2014-02-05 19:40:34
How many terms are in the first 996 rows?
How many terms are in the first 996 rows?
guilt
2014-02-05 19:41:33
996000
996000
UrInvalid
2014-02-05 19:41:33
996000
996000
LightningX48
2014-02-05 19:41:33
996000
996000
Richardq
2014-02-05 19:41:33
996000
996000
mathwizard888
2014-02-05 19:41:33
996000
996000
mxgo
2014-02-05 19:41:33
996000
996000
Nitzuga
2014-02-05 19:41:33
996,000
996,000
hametm
2014-02-05 19:41:33
n(n+4), which is 996(1000)=996000
n(n+4), which is 996(1000)=996000
copeland
2014-02-05 19:41:35
The first 996 rows have 996⋅(996+7)2=12(1000−4)(1000+3)=12(1,000,000−4000+3000−12)=500,000−506terms.
The first 996 rows have 996⋅(996+7)2=12(1000−4)(1000+3)=12(1,000,000−4000+3000−12)=500,000−506terms.
copeland
2014-02-05 19:41:39
What does that tell us?
What does that tell us?
IsabeltheCat
2014-02-05 19:42:25
997th row
997th row
pedronr
2014-02-05 19:42:25
the 500000th term is in the 997th row
the 500000th term is in the 997th row
ferrastacie
2014-02-05 19:42:25
its the 997 row
its the 997 row
anwang16
2014-02-05 19:42:25
its in the 997th row
its in the 997th row
copeland
2014-02-05 19:42:32
Yep. Where is it in that row?
Yep. Where is it in that row?
mathstar10
2014-02-05 19:43:02
506 of the 997 row
506 of the 997 row
billgates42
2014-02-05 19:43:02
506 more in the next row
506 more in the next row
Eudokia
2014-02-05 19:43:02
506th term
506th term
jigglypuff
2014-02-05 19:43:02
506th number
506th number
trumpeter
2014-02-05 19:43:02
the 507th term
the 507th term
mathstar10
2014-02-05 19:43:02
506
506
mjoshi
2014-02-05 19:43:02
506th
506th
vincenthuang75025
2014-02-05 19:43:02
506th
506th
rmflute
2014-02-05 19:43:02
506th place
506th place
angel27
2014-02-05 19:43:02
506th
506th
VinTheSad
2014-02-05 19:43:02
506th place
506th place
NikhilP
2014-02-05 19:43:02
506th term
506th term
golden_ratio
2014-02-05 19:43:02
506
506
copeland
2014-02-05 19:43:05
This tells us that we want the 506th term in the 997th row.
This tells us that we want the 506th term in the 997th row.
copeland
2014-02-05 19:43:06
To finish, we need to know the last (red) number in the 996th row. What is it?
To finish, we need to know the last (red) number in the 996th row. What is it?
mathwizard888
2014-02-05 19:43:43
996000
996000
bookie331
2014-02-05 19:43:43
996000
996000
Darn
2014-02-05 19:43:43
996000?
996000?
mymathboy
2014-02-05 19:43:43
996,000
996,000
copeland
2014-02-05 19:43:51
Right. We already computed this.
Right. We already computed this.
copeland
2014-02-05 19:43:52
The last red number in row 996 is 996(996+4)=996,000.
The last red number in row 996 is 996(996+4)=996,000.
copeland
2014-02-05 19:43:57
And what's the final answer?
And what's the final answer?
simon1221
2014-02-05 19:44:23
996506
996506
SuperSnivy
2014-02-05 19:44:23
996506
996506
kbird
2014-02-05 19:44:23
A is the answer!
A is the answer!
Tuxianeer
2014-02-05 19:44:23
(A)996,506
(A)996,506
buzzyun
2014-02-05 19:44:23
A
A
jkyman
2014-02-05 19:44:23
A
A
kajay88
2014-02-05 19:44:23
a
a
LogPolarBear
2014-02-05 19:44:23
996506, or A
996506, or A
flamesofpi
2014-02-05 19:44:23
A
A
MathematicsOfPi
2014-02-05 19:44:23
996,506
996,506
njaladan
2014-02-05 19:44:23
996506
996506
ZekromReshiram
2014-02-05 19:44:23
996506
996506
lightning23
2014-02-05 19:44:23
996506
996506
ZZmath9
2014-02-05 19:44:23
996506
996506
ChenthuranA
2014-02-05 19:44:23
996506
996506
copeland
2014-02-05 19:44:26
The answer is 996,000+506=996,506. (A)
The answer is 996,000+506=996,506. (A)
copeland
2014-02-05 19:44:43
Alright, good work.
Alright, good work.
copeland
2014-02-05 19:44:49
We're moving right along it seems.
We're moving right along it seems.
copeland
2014-02-05 19:44:59
The next problem is the only overlap between the tests:
The next problem is the only overlap between the tests:
copeland
2014-02-05 19:45:15
25. The number 5867 is between 22013 and 22014. How many pairs of integers (m,n) are there such that 1≤m≤2012 and
5n<2m<2m+2<5n+1?
(A) 278(B) 279(C) 280(D) 281(E) 282
25. The number 5867 is between 22013 and 22014. How many pairs of integers (m,n) are there such that 1≤m≤2012 and
5n<2m<2m+2<5n+1?
(A) 278(B) 279(C) 280(D) 281(E) 282
copeland
2014-02-05 19:45:25
This was also Problem 22 on the AMC12.
This was also Problem 22 on the AMC12.
copeland
2014-02-05 19:45:45
Here's a neat problem. It's not quite clear what the purpose of the first sentence is yet, so let's focus on the second. In words, what are we trying to find?
Here's a neat problem. It's not quite clear what the purpose of the first sentence is yet, so let's focus on the second. In words, what are we trying to find?
DrMath
2014-02-05 19:46:41
three powers of 2 in between consecutive powers of 5
three powers of 2 in between consecutive powers of 5
jweisblat14
2014-02-05 19:46:41
how many times, when we order all the powers of 2 and 5, we get a 5 2 2 2 5 pattern
how many times, when we order all the powers of 2 and 5, we get a 5 2 2 2 5 pattern
Nahmid
2014-02-05 19:46:41
trying to find 3 powers of 2 in between 2 powers of 5
trying to find 3 powers of 2 in between 2 powers of 5
jigglypuff
2014-02-05 19:46:41
3 powers of 2 are between 2 powers of 5
3 powers of 2 are between 2 powers of 5
alex31415
2014-02-05 19:46:41
The number of triplets on consecutive powers of 2 that are between the same two powers of 5
The number of triplets on consecutive powers of 2 that are between the same two powers of 5
wpk
2014-02-05 19:46:41
3 powers of two between consecutive powers of 5
3 powers of two between consecutive powers of 5
copeland
2014-02-05 19:46:42
We are trying to find the pairs of consecutive powers of 5 that have at least 3 different powers of 2 in between them.
We are trying to find the pairs of consecutive powers of 5 that have at least 3 different powers of 2 in between them.
copeland
2014-02-05 19:46:50
Now the target is clear, but I'm not really sure where to start. What should we do?
Now the target is clear, but I'm not really sure where to start. What should we do?
pl210741
2014-02-05 19:47:34
check small cases?
check small cases?
alex31415
2014-02-05 19:47:34
Try small cases
Try small cases
pedronr
2014-02-05 19:47:34
find small examples
find small examples
dli00105
2014-02-05 19:47:34
smaller values
smaller values
willwin4sure
2014-02-05 19:47:34
try some small numbers?
try some small numbers?
joshualee2000
2014-02-05 19:47:34
find the first number then find a pattern?
find the first number then find a pattern?
anwang16
2014-02-05 19:47:34
Try small cases.
Try small cases.
suli
2014-02-05 19:47:34
List some examples
List some examples
AndrewK
2014-02-05 19:47:34
Find an example case
Find an example case
mjoshi
2014-02-05 19:47:34
test out some values?
test out some values?
JFC
2014-02-05 19:47:34
Find the first solution?
Find the first solution?
want2learn
2014-02-05 19:47:34
the smallest number m this works for
the smallest number m this works for
copeland
2014-02-05 19:47:39
Let's look at the first few. The powers of 5 start 1,5,25,125,625,3125,….The powers of 2 start2,4,8,16,32,64,128,256,512,1024,….(We've omitted 1 from our 2's list because of the m≥1 condition.)
Let's look at the first few. The powers of 5 start 1,5,25,125,625,3125,….The powers of 2 start2,4,8,16,32,64,128,256,512,1024,….(We've omitted 1 from our 2's list because of the m≥1 condition.)
copeland
2014-02-05 19:47:53
That's a little confusing. When I was solving, I found it much easier to put those all in the same list. This is where having two colors of ink really helps.
That's a little confusing. When I was solving, I found it much easier to put those all in the same list. This is where having two colors of ink really helps.
copeland
2014-02-05 19:47:56
1,2,4,5,8,16,25,32,64,125,128,256,512,625,1024,2048,3125,….
1,2,4,5,8,16,25,32,64,125,128,256,512,625,1024,2048,3125,….
copeland
2014-02-05 19:48:04
What do we notice from our list?
What do we notice from our list?
ABCDE
2014-02-05 19:48:51
so 2 or 3 powers of 2 between each power of 5
so 2 or 3 powers of 2 between each power of 5
jweisblat14
2014-02-05 19:48:51
2,2,2,3,2,...
2,2,2,3,2,...
MasterChief1096
2014-02-05 19:48:51
there are 2 or 3 powers of 2 between every two powers of 5
there are 2 or 3 powers of 2 between every two powers of 5
fz0718
2014-02-05 19:48:51
2,2,2,3,2
2,2,2,3,2
Sesquipedalian
2014-02-05 19:48:51
2,2,3,2,2,3,2,2,3,2,2,3
2,2,3,2,2,3,2,2,3,2,2,3
hexagram
2014-02-05 19:48:51
only gaps of 2 and 3
only gaps of 2 and 3
blueferret
2014-02-05 19:48:51
theres always 2 powers of 2, but only occasionally 3
theres always 2 powers of 2, but only occasionally 3
chying1
2014-02-05 19:48:51
there is a power of 5 between every 2 or 3 powers of 2
there is a power of 5 between every 2 or 3 powers of 2
copeland
2014-02-05 19:48:55
For all the powers of 5 (in red) in our list, there's always two powers of 2 between them, except for 125 and 625 that have three power of 2 between them.
For all the powers of 5 (in red) in our list, there's always two powers of 2 between them, except for 125 and 625 that have three power of 2 between them.
copeland
2014-02-05 19:48:57
So we might conjecture that there's always either two or three powers of 2 between every consecutive pairs of powers of 5.
So we might conjecture that there's always either two or three powers of 2 between every consecutive pairs of powers of 5.
copeland
2014-02-05 19:49:02
Can we prove this?
Can we prove this?
VinVinB
2014-02-05 19:49:19
Yes.
Yes.
hexagram
2014-02-05 19:49:19
yes
yes
Tuxianeer
2014-02-05 19:49:19
yes
yes
suli
2014-02-05 19:49:19
Yes
Yes
jigglypuff
2014-02-05 19:49:19
yes
yes
mathwizard888
2014-02-05 19:49:19
yes
yes
hshiems
2014-02-05 19:49:19
Yes.
Yes.
goldentail141
2014-02-05 19:49:19
yes!
yes!
Richardq
2014-02-05 19:49:19
yes
yes
copeland
2014-02-05 19:49:23
I love the confidence!
I love the confidence!
copeland
2014-02-05 19:49:35
Let's just look between two consecutive powers of 5. Suppose the smallest power of 2 in between them is 2a and the largest is 2b:
5n<2a<2b<5n+1
Let's just look between two consecutive powers of 5. Suppose the smallest power of 2 in between them is 2a and the largest is 2b:
5n<2a<2b<5n+1
copeland
2014-02-05 19:49:38
What are we interested in?
What are we interested in?
UrInvalid
2014-02-05 19:50:23
b-a
b-a
poweroftwo
2014-02-05 19:50:23
b-a
b-a
DrMath
2014-02-05 19:50:23
a-b=1 or 2
a-b=1 or 2
mymathboy
2014-02-05 19:50:23
b-a
b-a
guilt
2014-02-05 19:50:23
b-a
b-a
DaChickenInc
2014-02-05 19:50:23
possible values of b-a
possible values of b-a
jigglypuff
2014-02-05 19:50:23
b-a
b-a
pl210741
2014-02-05 19:50:23
b-a
b-a
copeland
2014-02-05 19:50:28
We're interested in how many powers of 2 there can be, so we're interested in b−a.
We're interested in how many powers of 2 there can be, so we're interested in b−a.
copeland
2014-02-05 19:50:30
How can we get at b−a algebraically?
How can we get at b−a algebraically?
buzzyun
2014-02-05 19:51:35
dividing
dividing
pattycakechichi
2014-02-05 19:51:35
logs
logs
Pythonprogrammer
2014-02-05 19:51:35
divide
divide
simon1221
2014-02-05 19:51:35
log base 2
log base 2
trumpeter
2014-02-05 19:51:35
logarithms
logarithms
Nitzuga
2014-02-05 19:51:35
logarithms?
logarithms?
hwl0304
2014-02-05 19:51:35
logs?
logs?
Eudokia
2014-02-05 19:51:35
dividing
dividing
MathPro1000
2014-02-05 19:51:35
Divide
Divide
copeland
2014-02-05 19:51:38
This is a mixed bag here. We'll talk about logarithms in a bit, but since we're solving this in the context of the AMC10, let's skip the idea for a moment.
This is a mixed bag here. We'll talk about logarithms in a bit, but since we're solving this in the context of the AMC10, let's skip the idea for a moment.
copeland
2014-02-05 19:51:43
Well, we know that 2b−a=2b2a.
Well, we know that 2b−a=2b2a.
copeland
2014-02-05 19:51:46
And how can we relate that fraction to powers of 5?
And how can we relate that fraction to powers of 5?
copeland
2014-02-05 19:52:43
Let's try to bound this above. I know something about 2b, right?
Let's try to bound this above. I know something about 2b, right?
ninjataco
2014-02-05 19:53:23
less than 5n+1
less than 5n+1
suli
2014-02-05 19:53:23
2^b < 5^(n+1)
2^b < 5^(n+1)
distortedwalrus
2014-02-05 19:53:23
it's less than 5^{n+1}
it's less than 5^{n+1}
VinTheSad
2014-02-05 19:53:23
yeah, 2^b<5^n+1
yeah, 2^b<5^n+1
checkmate1021
2014-02-05 19:53:23
2b<5(n−1)
2b<5(n−1)
ferrastacie
2014-02-05 19:53:23
2^b < 5^(n+1)
2^b < 5^(n+1)
pedronr
2014-02-05 19:53:23
2^b<5^(n+1)
2^b<5^(n+1)
copeland
2014-02-05 19:53:29
Right. We know that 2b<5n+1, so replacing the numerator with the larger 5n+1 makes the fraction larger.
Right. We know that 2b<5n+1, so replacing the numerator with the larger 5n+1 makes the fraction larger.
copeland
2014-02-05 19:53:38
And I know something about 2a, right?
And I know something about 2a, right?
joshualee2000
2014-02-05 19:54:07
bigger than 5^n
bigger than 5^n
lee42
2014-02-05 19:54:07
greater than 5^n
greater than 5^n
fcc1234
2014-02-05 19:54:07
2a>5^n
2a>5^n
golden_ratio
2014-02-05 19:54:07
greater than 5^n
greater than 5^n
ingridzhang97
2014-02-05 19:54:07
it's larger 5^n
it's larger 5^n
dli00105
2014-02-05 19:54:07
2^a>5^n
2^a>5^n
flamefoxx99
2014-02-05 19:54:07
It's larger than 5^n
It's larger than 5^n
angel27
2014-02-05 19:54:07
It's bigger than 5^n
It's bigger than 5^n
AndrewK
2014-02-05 19:54:07
Its greater thatn 5n
Its greater thatn 5n
MaYang
2014-02-05 19:54:07
5^n < 2^a
5^n < 2^a
ChenthuranA
2014-02-05 19:54:07
5^n<2^a
5^n<2^a
copeland
2014-02-05 19:54:10
We also know that 5n<2a, so replacing the denominator with the smaller 5n also make the fraction larger.
We also know that 5n<2a, so replacing the denominator with the smaller 5n also make the fraction larger.
copeland
2014-02-05 19:54:13
Therefore, 2b−a=2b2a<5n+15n=5.
Therefore, 2b−a=2b2a<5n+15n=5.
copeland
2014-02-05 19:54:13
What have we concluded?
What have we concluded?
ninjataco
2014-02-05 19:55:48
b−a≤2
b−a≤2
DrMath
2014-02-05 19:55:48
2^b-a is at most 5 so b-a<=2
2^b-a is at most 5 so b-a<=2
chying1
2014-02-05 19:55:48
b-a<3
b-a<3
ZekromReshiram
2014-02-05 19:55:48
which means the interval can only be 0, 1, or 2
which means the interval can only be 0, 1, or 2
DaChickenInc
2014-02-05 19:55:48
b−a≤2
b−a≤2
Kevinyang2000
2014-02-05 19:55:48
b-a<=2
b-a<=2
IceFireGold1
2014-02-05 19:55:48
2>=b-a
2>=b-a
AopsKevin
2014-02-05 19:55:48
b-a<log2(5)
b-a<log2(5)
copeland
2014-02-05 19:55:52
2b−a<5, so b−a≤2.
2b−a<5, so b−a≤2.
copeland
2014-02-05 19:55:55
So there can only be at most 3 different powers of 2 between any two consecutive powers of 5.
So there can only be at most 3 different powers of 2 between any two consecutive powers of 5.
copeland
2014-02-05 19:56:04
Notice that we haven't ruled out b=a yet.
Notice that we haven't ruled out b=a yet.
copeland
2014-02-05 19:56:07
How about the other side of the argument? We had conjectured that there always had to be exactly two or three powers of 2, and we've just proved that there can't be more than three -- how do we show that there can't be fewer than two?
How about the other side of the argument? We had conjectured that there always had to be exactly two or three powers of 2, and we've just proved that there can't be more than three -- how do we show that there can't be fewer than two?
1915933
2014-02-05 19:56:33
Show that b-a>0.
Show that b-a>0.
flamefoxx99
2014-02-05 19:56:33
We show that a-b \ge 1
We show that a-b \ge 1
copeland
2014-02-05 19:56:39
Sounds like a noble goal.
Sounds like a noble goal.
copeland
2014-02-05 19:56:51
How do we get an inequality that is reversed?
How do we get an inequality that is reversed?
copeland
2014-02-05 19:57:13
Specifically, we want something in terms of b to be bigger than someting with a 5.
Specifically, we want something in terms of b to be bigger than someting with a 5.
jweisblat14
2014-02-05 19:58:28
2^(b+1)>5
2^(b+1)>5
jweisblat14
2014-02-05 19:58:28
and 2^(a-1)<5^n
and 2^(a-1)<5^n
zoroark12345
2014-02-05 19:58:28
take the largest b and then take 2^(b+1)
take the largest b and then take 2^(b+1)
pedronr
2014-02-05 19:58:28
2^(b+1)>5^(n+1)
2^(b+1)>5^(n+1)
copeland
2014-02-05 19:58:38
Good. Nice.
Good. Nice.
copeland
2014-02-05 19:58:42
Let's look and the next powers of two immediately before and after those in the middle: that is, we'll extend our inequality a little bit.
2a−1<5n<2a<2b<5n+1<2b+1
Let's look and the next powers of two immediately before and after those in the middle: that is, we'll extend our inequality a little bit.
2a−1<5n<2a<2b<5n+1<2b+1
copeland
2014-02-05 19:58:52
Now what? Are we in business?
Now what? Are we in business?
copeland
2014-02-05 19:59:05
What should we divide now?
What should we divide now?
UrInvalid
2014-02-05 19:59:52
the outer terms
the outer terms
ingridzhang97
2014-02-05 19:59:52
2^(b+1) and 2^(a-1)
2^(b+1) and 2^(a-1)
pedronr
2014-02-05 19:59:52
2^(b+1)/2(a-1)>5
2^(b+1)/2(a-1)>5
blueferret
2014-02-05 19:59:52
2^(b+1)/2^(a-1)
2^(b+1)/2^(a-1)
jiecut
2014-02-05 19:59:52
2^b+1/2^a-1
2^b+1/2^a-1
hametm
2014-02-05 19:59:52
2^(b+1) and 2^(a-1)
2^(b+1) and 2^(a-1)
VinTheSad
2014-02-05 19:59:52
2^b+1 and 2^a-1
2^b+1 and 2^a-1
jweisblat14
2014-02-05 19:59:57
divide the powers of 5, and divide the outer powers of 2
divide the powers of 5, and divide the outer powers of 2
tfmtoto
2014-02-05 20:00:00
2^(b+1)/2^(a-1)
2^(b+1)/2^(a-1)
copeland
2014-02-05 20:00:02
We can look at the ratio of the new powers of 2, just like we did before.
We can look at the ratio of the new powers of 2, just like we did before.
copeland
2014-02-05 20:00:03
We start with 2b−a+2=2b+12a−1.
We start with 2b−a+2=2b+12a−1.
copeland
2014-02-05 20:00:06
Now what?
Now what?
lee42
2014-02-05 20:00:54
compare with powers of 5
compare with powers of 5
pedronr
2014-02-05 20:00:54
greater than 5^(n+1)/5^n
greater than 5^(n+1)/5^n
hametm
2014-02-05 20:00:54
Bound it from above like before
Bound it from above like before
ingridzhang97
2014-02-05 20:00:54
and that is greater than 5^(n+1)/5^n=5
and that is greater than 5^(n+1)/5^n=5
dli00105
2014-02-05 20:00:54
round top down and bottom up
round top down and bottom up
angel27
2014-02-05 20:00:54
2^b+1/2^a-1 > 5^n+1/5^n
2^b+1/2^a-1 > 5^n+1/5^n
bigc08
2014-02-05 20:00:54
that is greater than 5^n+1/5^n
that is greater than 5^n+1/5^n
copeland
2014-02-05 20:00:57
If we replace the numerator with 5n+1, we make the fraction smaller (since the numerator becomes smaller).
If we replace the numerator with 5n+1, we make the fraction smaller (since the numerator becomes smaller).
copeland
2014-02-05 20:01:00
And if we replace the denominator with 5n, we also make the fraction smaller (since the denominator becomes larger).
And if we replace the denominator with 5n, we also make the fraction smaller (since the denominator becomes larger).
copeland
2014-02-05 20:01:04
Therefore,
2b−a+2=2b+12a−1>5n+15n=5.
Therefore,
2b−a+2=2b+12a−1>5n+15n=5.
copeland
2014-02-05 20:01:07
What have we concluded?
What have we concluded?
DrMath
2014-02-05 20:01:52
b-a>0
b-a>0
Tuxianeer
2014-02-05 20:01:52
b-a>0
b-a>0
ChenthuranA
2014-02-05 20:01:52
b-a+2>2
b-a+2>2
joshualee2000
2014-02-05 20:01:52
b-a+2>2
b-a+2>2
MaYang
2014-02-05 20:01:52
b-a+2>=2
b-a+2>=2
mathbeida
2014-02-05 20:01:52
b-a+2 > 2
b-a+2 > 2
goldentail141
2014-02-05 20:01:52
a cannot be equal to b
a cannot be equal to b
hamup1
2014-02-05 20:01:52
b-a+2>2, or b-a>0
b-a+2>2, or b-a>0
djmathman
2014-02-05 20:01:52
That b−a+2≥3⟹b−a≥1
That b−a+2≥3⟹b−a≥1
copeland
2014-02-05 20:01:59
and also. . .
and also. . .
MATHCOUNTSmath
2014-02-05 20:02:03
that math is awesome
that math is awesome
copeland
2014-02-05 20:02:05
2b−a+2>5, so b−a+2≥3, and thus b−a≥1.
2b−a+2>5, so b−a+2≥3, and thus b−a≥1.
copeland
2014-02-05 20:02:18
We've shown that if 2a and 2b are the smallest and largest powers of 2 between any two consecutive powers of 5, then 1≤b−a≤2.
We've shown that if 2a and 2b are the smallest and largest powers of 2 between any two consecutive powers of 5, then 1≤b−a≤2.
copeland
2014-02-05 20:02:27
What does that mean?
What does that mean?
ferrastacie
2014-02-05 20:03:13
b-a = 1 or 2
b-a = 1 or 2
JFC
2014-02-05 20:03:13
There are always 2 or 3 powers of 2 between powers of 5
There are always 2 or 3 powers of 2 between powers of 5
simon1221
2014-02-05 20:03:13
there are 2 or 3 powers of 2
there are 2 or 3 powers of 2
hamup1
2014-02-05 20:03:13
There is either 2 or 3 powers of two in between two consecutive powers of 5
There is either 2 or 3 powers of two in between two consecutive powers of 5
VinTheSad
2014-02-05 20:03:13
there must be either 2 or 3 powers of 2 between each power of 5
there must be either 2 or 3 powers of 2 between each power of 5
pedronr
2014-02-05 20:03:13
there are either 2 or 3 consecutive powers of 2 between each two powers of 5
there are either 2 or 3 consecutive powers of 2 between each two powers of 5
LMA
2014-02-05 20:03:13
there can only be 2 or 3 integer powers of 2 between any 2 consecutive powers of 5
there can only be 2 or 3 integer powers of 2 between any 2 consecutive powers of 5
AlcumusGuy
2014-02-05 20:03:13
we've proven the conjecture that there must be either 2 or 3 powers of 2 between two consecutive powers of 5
we've proven the conjecture that there must be either 2 or 3 powers of 2 between two consecutive powers of 5
UltimateChampion1235
2014-02-05 20:03:13
there can be 2-3 powers of 2 between cons. powers of 5
there can be 2-3 powers of 2 between cons. powers of 5
wpk
2014-02-05 20:03:13
2 or 3 powers of 2 between consecutive powers of 5
2 or 3 powers of 2 between consecutive powers of 5
mxgo
2014-02-05 20:03:13
there can only be 2-3 powers of 2
there can only be 2-3 powers of 2
checkmate1021
2014-02-05 20:03:13
we can only have 2 or 3 powers of 2 petween two consecutive powers of five
we can only have 2 or 3 powers of 2 petween two consecutive powers of five
1915933
2014-02-05 20:03:13
Only two or three consecutive powers of 2 can be between two consecutive powers of 5.
Only two or three consecutive powers of 2 can be between two consecutive powers of 5.
abishek99
2014-02-05 20:03:13
there are 2 or 3 powers of 2 between each pair of consecutive powers of 5
there are 2 or 3 powers of 2 between each pair of consecutive powers of 5
firemike
2014-02-05 20:03:13
there can only two or three terms between the two powers of 5
there can only two or three terms between the two powers of 5
copeland
2014-02-05 20:03:27
Putting these two results together tell us that every consecutive pair of powers of 5 has exactly two or three powers of 2 between them. We've proved our conjecture.
Putting these two results together tell us that every consecutive pair of powers of 5 has exactly two or three powers of 2 between them. We've proved our conjecture.
copeland
2014-02-05 20:03:30
Great! How do we use this information to solve the problem?
Great! How do we use this information to solve the problem?
copeland
2014-02-05 20:04:32
A lot of you are suggesting that we find a pattern now.
A lot of you are suggesting that we find a pattern now.
copeland
2014-02-05 20:04:42
You can actually PROVE that there is no pattern.
You can actually PROVE that there is no pattern.
coldsummer
2014-02-05 20:04:57
we want the number of cases in which there are three powers of two in between two consecutive powers of 5
we want the number of cases in which there are three powers of two in between two consecutive powers of 5
fadebekun
2014-02-05 20:04:57
We want the number of intervals with 3 powers of 2.
We want the number of intervals with 3 powers of 2.
copeland
2014-02-05 20:05:01
All we want is this.
All we want is this.
copeland
2014-02-05 20:05:06
Remember the barnyard problem?
Remember the barnyard problem?
copeland
2014-02-05 20:05:44
If I have a farm and there are 100 animals and they have 150 feet, how many animals are sheep and how many are cows?
If I have a farm and there are 100 animals and they have 150 feet, how many animals are sheep and how many are cows?
zacchro
2014-02-05 20:05:54
I can guess--x cows with 4 legs and y chickens with 2?
I can guess--x cows with 4 legs and y chickens with 2?
copeland
2014-02-05 20:06:12
So now we have a happy analogy.
So now we have a happy analogy.
copeland
2014-02-05 20:06:19
Oh, wait.
Oh, wait.
copeland
2014-02-05 20:06:22
That doesn't work.
That doesn't work.
willwin
2014-02-05 20:06:31
sheep and cows both have 4 legs though
sheep and cows both have 4 legs though
copeland
2014-02-05 20:06:36
Sheep and cows happen to have the same number of legs.
Sheep and cows happen to have the same number of legs.
copeland
2014-02-05 20:06:55
Let's try something else. How about alpacas and flamingos?
Let's try something else. How about alpacas and flamingos?
copeland
2014-02-05 20:07:06
What are our flamingos in this example?
What are our flamingos in this example?
angel27
2014-02-05 20:07:36
The 2s
The 2s
tekgeek
2014-02-05 20:07:36
the number of powers of 2
the number of powers of 2
want2learn
2014-02-05 20:07:36
an interval with 2
an interval with 2
anonymous0
2014-02-05 20:07:36
2 powers of 2
2 powers of 2
Offendo
2014-02-05 20:07:36
2 powers
2 powers
Lord.of.AMC
2014-02-05 20:07:36
the cases in which there are 2 powers of 2 in between
the cases in which there are 2 powers of 2 in between
copeland
2014-02-05 20:07:43
Yes, and the alpacas are the cases of 3.
Yes, and the alpacas are the cases of 3.
copeland
2014-02-05 20:07:57
We just need to count the consecutive powers of 5 that have three powers of 2 between them. (Each such pair will contribute exactly one ordered pair (m,n) to our final count.)
We just need to count the consecutive powers of 5 that have three powers of 2 between them. (Each such pair will contribute exactly one ordered pair (m,n) to our final count.)
copeland
2014-02-05 20:08:05
Hmmm...what data haven't we used yet?
Hmmm...what data haven't we used yet?
blueferret
2014-02-05 20:09:01
the first sentence
the first sentence
suli
2014-02-05 20:09:01
First sentence
First sentence
AaaDuhLoo
2014-02-05 20:09:01
The first sentence!
The first sentence!
lee42
2014-02-05 20:09:01
the first sentence
the first sentence
DVA6102
2014-02-05 20:09:01
the first sentence
the first sentence
UrInvalid
2014-02-05 20:09:01
the first sentence
the first sentence
Nitzuga
2014-02-05 20:09:01
The first sentence!
The first sentence!
jkyman
2014-02-05 20:09:01
the first sentence
the first sentence
copeland
2014-02-05 20:09:08
We haven't used 22013<5867<22014 yet. How does that figure in?
We haven't used 22013<5867<22014 yet. How does that figure in?
goodbear
2014-02-05 20:09:50
5^867 is between 2^2013 and 2^2014
5^867 is between 2^2013 and 2^2014
bigc08
2014-02-05 20:09:50
only 866 intervals
only 866 intervals
ingridzhang97
2014-02-05 20:09:50
the highest power of 5 that we can consider is 867, and there are a total of 2013 powers of 2
the highest power of 5 that we can consider is 867, and there are a total of 2013 powers of 2
Richardq
2014-02-05 20:09:50
it shows that n cannot be 867
it shows that n cannot be 867
jweisblat14
2014-02-05 20:09:50
there are 2013 legs and 867 animals - how many have 3 feet?
there are 2013 legs and 867 animals - how many have 3 feet?
zoroark12345
2014-02-05 20:09:50
tells us that there are 2013 powers of 2 under 5^867
tells us that there are 2013 powers of 2 under 5^867
copeland
2014-02-05 20:09:53
It tells us that 5867 is the largest power of 5 that we need to look at (since m≤2012).
It tells us that 5867 is the largest power of 5 that we need to look at (since m≤2012).
copeland
2014-02-05 20:09:55
So we're looking at the powers of 2 that lie in:
50<⋯<51<⋯<52<⋯<⋯⋯<⋯<5866<⋯<5867
So we're looking at the powers of 2 that lie in:
50<⋯<51<⋯<52<⋯<⋯⋯<⋯<5866<⋯<5867
copeland
2014-02-05 20:09:59
That gives us 867 possible pairs of consecutive powers of 5.
That gives us 867 possible pairs of consecutive powers of 5.
copeland
2014-02-05 20:10:03
Let's finish our sequence. Now we know that it ends
Let's finish our sequence. Now we know that it ends
copeland
2014-02-05 20:10:04
…,22012,22013,5867,22014
…,22012,22013,5867,22014
copeland
2014-02-05 20:10:16
And how many powers of 2 do we care about?
And how many powers of 2 do we care about?
fadebekun
2014-02-05 20:10:51
2013 powers
2013 powers
ChenthuranA
2014-02-05 20:10:51
2013
2013
Darn
2014-02-05 20:10:51
2013
2013
alex31415
2014-02-05 20:10:51
2013
2013
Showpar
2014-02-05 20:10:51
2013
2013
Eudokia
2014-02-05 20:10:51
2013
2013
pedronr
2014-02-05 20:10:51
2013 powers
2013 powers
coldsummer
2014-02-05 20:10:51
2013
2013
Emmettshell
2014-02-05 20:10:51
2013
2013
hametm
2014-02-05 20:10:51
2013
2013
brainiac1
2014-02-05 20:10:51
2013
2013
mathsd
2014-02-05 20:10:51
2013
2013
copeland
2014-02-05 20:10:55
We start at 21 and end at 22013, so there are 2013 of them.
We start at 21 and end at 22013, so there are 2013 of them.
copeland
2014-02-05 20:11:08
That's where having the example protects us from off-by-one errors.
That's where having the example protects us from off-by-one errors.
copeland
2014-02-05 20:11:11
And we know that there are either two of three of them in each of the 867 gaps between powers of 5.
And we know that there are either two of three of them in each of the 867 gaps between powers of 5.
copeland
2014-02-05 20:11:28
If we go ahead and allot 2 legs to each animal,, how many legs are left over?
If we go ahead and allot 2 legs to each animal,, how many legs are left over?
Tuxianeer
2014-02-05 20:12:12
279
279
joshualee2000
2014-02-05 20:12:12
279
279
Ericaops
2014-02-05 20:12:12
279
279
jigglypuff
2014-02-05 20:12:12
279 (B)
279 (B)
coldsummer
2014-02-05 20:12:12
279
279
UrInvalid
2014-02-05 20:12:12
279
279
DrMath
2014-02-05 20:12:12
279
279
dli00105
2014-02-05 20:12:12
279
279
flamesofpi
2014-02-05 20:12:12
279
279
kgator
2014-02-05 20:12:12
279
279
ninjataco
2014-02-05 20:12:12
279
279
copeland
2014-02-05 20:12:15
There are 2013−2(867)=2013−1734=279 remaining. That's how many of the gaps that must have a third power of 2 in order to fit all 2013 of them in there.
There are 2013−2(867)=2013−1734=279 remaining. That's how many of the gaps that must have a third power of 2 in order to fit all 2013 of them in there.
GeorgCantor
2014-02-05 20:12:23
2*the number of alpacas
2*the number of alpacas
ksun48
2014-02-05 20:12:23
er wait 2 legs to each
er wait 2 legs to each
copeland
2014-02-05 20:12:39
Yeah, well, no. For the purposes of this exercise, we've modified our alpacas.
Yeah, well, no. For the purposes of this exercise, we've modified our alpacas.
lightning23
2014-02-05 20:13:02
279
279
1915933
2014-02-05 20:13:02
279
279
mathwizard888
2014-02-05 20:13:02
279
279
smith_ch
2014-02-05 20:13:02
279
279
dli00105
2014-02-05 20:13:02
(B)279
(B)279
copeland
2014-02-05 20:13:05
So there are 279 consecutive powers of 5 with exactly three powers of 2 between them. Our answer is 279, answer (B).
So there are 279 consecutive powers of 5 with exactly three powers of 2 between them. Our answer is 279, answer (B).
mathnerd101
2014-02-05 20:13:43
Why didn't you use bicycles and tricycles?
Why didn't you use bicycles and tricycles?
copeland
2014-02-05 20:13:45
They are not useful if you want to shear them for sweater yarn.
They are not useful if you want to shear them for sweater yarn.
LMA
2014-02-05 20:14:09
so, are flamingos useful for sweaters???
so, are flamingos useful for sweaters???
copeland
2014-02-05 20:14:12
You should see my flamingo sweaters. They're fabulous.
You should see my flamingo sweaters. They're fabulous.
baozhale
2014-02-05 20:14:33
Very feathery
Very feathery
copeland
2014-02-05 20:14:34
This problem was also on the AMC12, and if you solved it there, you might have used a little more machinery.
This problem was also on the AMC12, and if you solved it there, you might have used a little more machinery.
copeland
2014-02-05 20:14:37
If you're anything like me (and most people aren't), then you instead took the log of everything immediately after seeing the problem. In this point of view, we want to put the powers of two sequence log2,2log2,3log2,…,2014log2 in between the terms of the sequence log5,2log5,3log5,…,867log5.
If you're anything like me (and most people aren't), then you instead took the log of everything immediately after seeing the problem. In this point of view, we want to put the powers of two sequence log2,2log2,3log2,…,2014log2 in between the terms of the sequence log5,2log5,3log5,…,867log5.
copeland
2014-02-05 20:14:52
What's cool about those sequences?
What's cool about those sequences?
pl210741
2014-02-05 20:15:22
arithmetic?
arithmetic?
suli
2014-02-05 20:15:22
Arithmetic
Arithmetic
MATHCOUNTSmath
2014-02-05 20:15:22
arithmetic
arithmetic
pattycakechichi
2014-02-05 20:15:22
arithmetic
arithmetic
Dragon6point1
2014-02-05 20:15:22
arithmetic?
arithmetic?
joshualee2000
2014-02-05 20:15:22
arithmetic
arithmetic
bengals
2014-02-05 20:15:22
arithmetic
arithmetic
simranK
2014-02-05 20:15:22
arithmetic!
arithmetic!
MATHCOUNTSmath
2014-02-05 20:15:22
They are arithmetic series
They are arithmetic series
AkshajK
2014-02-05 20:15:22
they are arithmetic sequences
they are arithmetic sequences
WildTurtle
2014-02-05 20:15:22
Arithmetic sequence
Arithmetic sequence
copeland
2014-02-05 20:15:24
These are arithmetic sequences! The 2-sequence is much closer together than the 5-sequence. Anybody see a nice rational approximation to log5log2?
These are arithmetic sequences! The 2-sequence is much closer together than the 5-sequence. Anybody see a nice rational approximation to log5log2?
Tuxianeer
2014-02-05 20:16:19
2013/867
2013/867
lucylai
2014-02-05 20:16:19
use the first sentence
use the first sentence
pi37
2014-02-05 20:16:19
2013.5/867
2013.5/867
pattycakechichi
2014-02-05 20:16:19
2014/867?
2014/867?
copeland
2014-02-05 20:16:23
We know for sure that the sequence end around the same place so 865log5≈2014log2 and in particular, the ratio of the common differences is log5log2≈2014865 which is a little bit more than 2.
We know for sure that the sequence end around the same place so 865log5≈2014log2 and in particular, the ratio of the common differences is log5log2≈2014865 which is a little bit more than 2.
copeland
2014-02-05 20:16:29
Now it's quite useful to know that if you have two infinite arithmetic progressions with common ratio between n and n+1 then (whenever there are no terms in common) the shorter-period progression appears either n or n+1 times in every gap of the longer period one. In our case, we see that we always get 2 or 3 terms in each gap.
Now it's quite useful to know that if you have two infinite arithmetic progressions with common ratio between n and n+1 then (whenever there are no terms in common) the shorter-period progression appears either n or n+1 times in every gap of the longer period one. In our case, we see that we always get 2 or 3 terms in each gap.
copeland
2014-02-05 20:16:40
Incidentally, things are even cleaner if we take the logarithm base to be 5. Then we're fitting the sequence log52,2log52,3log52,…,2014log52 in between the terms of the sequence 1,2,3…,867.
Incidentally, things are even cleaner if we take the logarithm base to be 5. Then we're fitting the sequence log52,2log52,3log52,…,2014log52 in between the terms of the sequence 1,2,3…,867.
copeland
2014-02-05 20:16:53
This is another place you might have seen this type of problem. If we let α=log52=log2log5 then we're now asking what the sequence ⌊αn⌋ looks like, since that's the left endpoint of the interval.
This is another place you might have seen this type of problem. If we let α=log52=log2log5 then we're now asking what the sequence ⌊αn⌋ looks like, since that's the left endpoint of the interval.
copeland
2014-02-05 20:17:00
The general result here is that since 1α is between 2 and 3, each integer appears either 2 or 3 times in the sequence. I strongly encourage you to try some examples later because these techniques are really powerful.
The general result here is that since 1α is between 2 and 3, each integer appears either 2 or 3 times in the sequence. I strongly encourage you to try some examples later because these techniques are really powerful.
copeland
2014-02-05 20:18:10
Alright, everyone take 2 minutes to stretch and we'll start back in on the AMC12.
Alright, everyone take 2 minutes to stretch and we'll start back in on the AMC12.
LMA
2014-02-05 20:20:21
will there be a transcript available for this?
will there be a transcript available for this?
copeland
2014-02-05 20:20:23
Yes. After class I will try to convince the transcripter to work. It should be up tonight.
Yes. After class I will try to convince the transcripter to work. It should be up tonight.
DrMath
2014-02-05 20:20:47
the transcripter?
the transcripter?
copeland
2014-02-05 20:20:52
It transcripts the transcripts.
It transcripts the transcripts.
copeland
2014-02-05 20:20:57
Seems like a natural name to me.
Seems like a natural name to me.
Bomist0
2014-02-05 20:21:51
should we start now?
should we start now?
copeland
2014-02-05 20:21:53
Yes we should.
Yes we should.
copeland
2014-02-05 20:21:57
21. For every real number x, let ⌊x⌋ denote the greatest integer not exceeding x, and let f(x)=⌊x⌋(2014x−⌊x⌋−1). The set of all numbers x such that 1≤x<2014 and f(x)≤1 is a union of disjoint intervals. What is the sum of the lengths of those intervals?
peekaboo!
(A) 1(B) log2015log2014(C) log2014log2013(D) 20142013(E) 201412014
21. For every real number x, let ⌊x⌋ denote the greatest integer not exceeding x, and let f(x)=⌊x⌋(2014x−⌊x⌋−1). The set of all numbers x such that 1≤x<2014 and f(x)≤1 is a union of disjoint intervals. What is the sum of the lengths of those intervals?
peekaboo!
(A) 1(B) log2015log2014(C) log2014log2013(D) 20142013(E) 201412014
copeland
2014-02-05 20:22:06
Our function is f(x)=⌊x⌋(2014x−⌊x⌋−1). Is there a way we can simplify this?
Our function is f(x)=⌊x⌋(2014x−⌊x⌋−1). Is there a way we can simplify this?
ninjataco
2014-02-05 20:22:57
x−⌊x⌋={x}
x−⌊x⌋={x}
lucylai
2014-02-05 20:22:57
let x=[x]+r
let x=[x]+r
brian22
2014-02-05 20:22:57
[x]=x-floor(x)
[x]=x-floor(x)
Tuxianeer
2014-02-05 20:22:57
x-floor(x)={x}
x-floor(x)={x}
AkshajK
2014-02-05 20:22:57
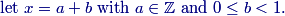
copeland
2014-02-05 20:23:06
The quantity x−⌊x⌋ is the "fractional part" of x, which we usually write as {x}. Now we want to talk about when ⌊x⌋(2014{x}−1)≤1.
The quantity x−⌊x⌋ is the "fractional part" of x, which we usually write as {x}. Now we want to talk about when ⌊x⌋(2014{x}−1)≤1.
copeland
2014-02-05 20:23:23
What does the function ⌊x⌋ look like?
What does the function ⌊x⌋ look like?
dasobson
2014-02-05 20:24:00
lots of steps
lots of steps
dli00105
2014-02-05 20:24:00
a staircase
a staircase
Tuxianeer
2014-02-05 20:24:00
discrete steps
discrete steps
swe1
2014-02-05 20:24:00
Staircase
Staircase
dieButteristalle
2014-02-05 20:24:00
a staircase
a staircase
alex31415
2014-02-05 20:24:00
Steps
Steps
CornSaltButter
2014-02-05 20:24:00
A staircase
A staircase
DrMath
2014-02-05 20:24:00
it is a bunch of line segments
it is a bunch of line segments
AaaDuhLoo
2014-02-05 20:24:00
Step function.
Step function.
simon1221
2014-02-05 20:24:00
a set of stairs (graphicly)
a set of stairs (graphicly)
checkmate1021
2014-02-05 20:24:00
a staircase without the thing on the side
a staircase without the thing on the side
AaaDuhLoo
2014-02-05 20:24:00
Staircase.
Staircase.
copeland
2014-02-05 20:24:05
(risers)
(risers)
copeland
2014-02-05 20:24:23
The things on stairs that keep your change from going away and keep you from getting vertigo are called risers.
The things on stairs that keep your change from going away and keep you from getting vertigo are called risers.
copeland
2014-02-05 20:24:29
It's a "step function":
It's a "step function":
copeland
2014-02-05 20:24:32


copeland
2014-02-05 20:24:35
What does the function (2014{x}−1) look like?
What does the function (2014{x}−1) look like?
dasobson
2014-02-05 20:25:25
repeats over and over
repeats over and over
brian22
2014-02-05 20:25:25
periodic
periodic
Tuxianeer
2014-02-05 20:25:25
repeated unit of a curve
repeated unit of a curve
lucylai
2014-02-05 20:25:25
it goes from 0 to 2013
it goes from 0 to 2013
alex31415
2014-02-05 20:25:25
Many exponential curves
Many exponential curves
DrMath
2014-02-05 20:25:25
exponential segments not exceeding 2013
exponential segments not exceeding 2013
anwang16
2014-02-05 20:25:25
diagonal repeats
diagonal repeats
blueferret
2014-02-05 20:25:25
repeated curves
repeated curves
fz0718
2014-02-05 20:25:25
a bunch of curves starting at the x axis
a bunch of curves starting at the x axis
vincenthuang75025
2014-02-05 20:25:25
A weird curve thingy that keeps repeating
A weird curve thingy that keeps repeating
awesomemathlete
2014-02-05 20:25:25
the same exponential function repeated every integer
the same exponential function repeated every integer
copeland
2014-02-05 20:25:27
The fractional part is periodic with period 1, so this function is periodic with period 1. In any period, it increases like a very sharp exponential, except it's shifted down by 1. When x is an integer, the value is 0 and it approaches 2013 (a very big number) as x increases to the next integer.
The fractional part is periodic with period 1, so this function is periodic with period 1. In any period, it increases like a very sharp exponential, except it's shifted down by 1. When x is an integer, the value is 0 and it approaches 2013 (a very big number) as x increases to the next integer.
copeland
2014-02-05 20:25:31


copeland
2014-02-05 20:25:44
The product of the two functions will look like a bunch of copies of the exponential function scaled by different values.
The product of the two functions will look like a bunch of copies of the exponential function scaled by different values.
copeland
2014-02-05 20:25:48
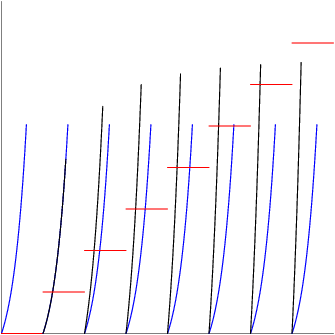

copeland
2014-02-05 20:26:20
Note: the curves start at 0 since 20140−1=1−1=0.
Note: the curves start at 0 since 20140−1=1−1=0.
copeland
2014-02-05 20:26:25
In function problems, it's often nice to have a picture of what's happening in mind. In this particular problem, the picture helps nail down what the intervals are. What are they?
In function problems, it's often nice to have a picture of what's happening in mind. In this particular problem, the picture helps nail down what the intervals are. What are they?
copeland
2014-02-05 20:27:25
The intervals are the places where f is less than 1.
The intervals are the places where f is less than 1.
copeland
2014-02-05 20:27:33
Can you tell me a place where f is definitely less than 1?
Can you tell me a place where f is definitely less than 1?
Tuxianeer
2014-02-05 20:27:59
integers
integers
lucylai
2014-02-05 20:27:59
integers
integers
swe1
2014-02-05 20:27:59
At the integers
At the integers
jweisblat14
2014-02-05 20:27:59
when x is an integer
when x is an integer
coldsummer
2014-02-05 20:27:59
at integers
at integers
pedronr
2014-02-05 20:27:59
any integer
any integer
copeland
2014-02-05 20:28:08
f is zero at all the integers, then f increases.
f is zero at all the integers, then f increases.
copeland
2014-02-05 20:28:20
Therefore, what does our set of intervals look like?
Therefore, what does our set of intervals look like?
swe1
2014-02-05 20:29:08
Intervals starting at the integers and get shorter
Intervals starting at the integers and get shorter
jweisblat14
2014-02-05 20:29:08
a little bit after each integer
a little bit after each integer
blueferret
2014-02-05 20:29:08
they start from integers
they start from integers
Tuxianeer
2014-02-05 20:29:08
very small intervals starting at each integer
very small intervals starting at each integer
hametm
2014-02-05 20:29:08
From an integer to the point where the curve intersects y=1
From an integer to the point where the curve intersects y=1
ingridzhang97
2014-02-05 20:29:08
(0, something), (1, something) , (2, something), etc
(0, something), (1, something) , (2, something), etc
checkmate1021
2014-02-05 20:29:08
a bunch of line segments starting at each integer that get smaller and smaller (exponentially?)
a bunch of line segments starting at each integer that get smaller and smaller (exponentially?)
Dragon6point1
2014-02-05 20:29:08
A set of 2013 or so intervals starting at each integers and ending before the next.
A set of 2013 or so intervals starting at each integers and ending before the next.
jweisblat14
2014-02-05 20:29:08
a bunch of really short intervals, one startng at each integer and getting shorter and shorter
a bunch of really short intervals, one startng at each integer and getting shorter and shorter
jiecut
2014-02-05 20:29:08
the intervals decrease
the intervals decrease
copeland
2014-02-05 20:29:17
For every integer 1 through 2013, there is one interval with left endpoint equal to that integer. The right endpoint occurs when the function f hits the value 1.
For every integer 1 through 2013, there is one interval with left endpoint equal to that integer. The right endpoint occurs when the function f hits the value 1.
copeland
2014-02-05 20:29:20
So we have 2013 intervals. The intervals are [1,??] and [2,??] and [3,??] and [4,??], etc. Now our goal is to figure out what the lengths of all these intervals are and add those up.
So we have 2013 intervals. The intervals are [1,??] and [2,??] and [3,??] and [4,??], etc. Now our goal is to figure out what the lengths of all these intervals are and add those up.
copeland
2014-02-05 20:29:30
Let's use casework on the left endpoints and then sum.
Let's use casework on the left endpoints and then sum.
copeland
2014-02-05 20:29:32
The first left endpoint is 1. How wide is this interval?
The first left endpoint is 1. How wide is this interval?
alex31415
2014-02-05 20:30:22
log_2014(2)
log_2014(2)
lucylai
2014-02-05 20:30:22
log_2014(2)
log_2014(2)
joshxiong
2014-02-05 20:30:22
log20142
log20142
mathwizard888
2014-02-05 20:30:22


brian22
2014-02-05 20:30:22
log_2014(2)
log_2014(2)
Verjok
2014-02-05 20:30:22
log base 2014 of 2
log base 2014 of 2
ingridzhang97
2014-02-05 20:30:22
until 2014^{x}=2
until 2014^{x}=2
copeland
2014-02-05 20:30:30
The right endpoint of the interval occurs when f(x)=1. Therefore we want to solve ⌊x⌋(2014{x}−1)=1 when ⌊x⌋=1. That means we want to find the fractional part that solves 2014{x}−1=1.
The right endpoint of the interval occurs when f(x)=1. Therefore we want to solve ⌊x⌋(2014{x}−1)=1 when ⌊x⌋=1. That means we want to find the fractional part that solves 2014{x}−1=1.
copeland
2014-02-05 20:31:22
When we take the log of this equation we get {x}log2014=log2.
When we take the log of this equation we get {x}log2014=log2.
copeland
2014-02-05 20:31:28
The solution to this equation is {x}=log2log2014.
The solution to this equation is {x}=log2log2014.
copeland
2014-02-05 20:31:35
Now I reflexively don't worry about the base of logs. It looks like a lot of you chose to take your logs with base 2014.
Now I reflexively don't worry about the base of logs. It looks like a lot of you chose to take your logs with base 2014.
copeland
2014-02-05 20:32:11
That is also a fine approach, but only if you have the foresight to know that any logs we take in this problem are base 2014.
That is also a fine approach, but only if you have the foresight to know that any logs we take in this problem are base 2014.
copeland
2014-02-05 20:32:29
I'm going to stick with the more general log for the moment, just to avoid getting in trouble.
I'm going to stick with the more general log for the moment, just to avoid getting in trouble.
copeland
2014-02-05 20:32:36
The first interval ends when ⌊x⌋=1 and {x}=log2log2014. The interval is [1,1+log2log2014] and the length is just log2log2014.
The first interval ends when ⌊x⌋=1 and {x}=log2log2014. The interval is [1,1+log2log2014] and the length is just log2log2014.
copeland
2014-02-05 20:33:05
Let's make a chart that keeps track of the lengths of the intervals:
⌊x⌋length1log2log2014
Let's make a chart that keeps track of the lengths of the intervals:
⌊x⌋length1log2log2014
copeland
2014-02-05 20:33:08
The second left endpoint is 2. How wide is this interval?
The second left endpoint is 2. How wide is this interval?
jweisblat14
2014-02-05 20:33:46
the next one is log(3/2)/log(2014)
the next one is log(3/2)/log(2014)
blueferret
2014-02-05 20:33:46
log2014(3/2)
log2014(3/2)
lucylai
2014-02-05 20:33:46
log(3/2)/log(2014)
log(3/2)/log(2014)
alex31415
2014-02-05 20:33:46
log(3/2)/log(2014)
log(3/2)/log(2014)
Fibonacci97
2014-02-05 20:33:46
log(3/2)/log(2014)
log(3/2)/log(2014)
DrMath
2014-02-05 20:33:46
log (3/2)/log(2014)
log (3/2)/log(2014)
swe1
2014-02-05 20:33:46
log_2014(3/2)
log_2014(3/2)
hametm
2014-02-05 20:33:46
log(3/2)/log 2014
log(3/2)/log 2014
copeland
2014-02-05 20:33:49
The right endpoint is where f(x)=1 when ⌊x⌋=2.
The right endpoint is where f(x)=1 when ⌊x⌋=2.
copeland
2014-02-05 20:33:52
So we want to solve 2(2014{x}−1)=1. That means we want to find the fractional part that solves 2014{x}−1=12.
So we want to solve 2(2014{x}−1)=1. That means we want to find the fractional part that solves 2014{x}−1=12.
copeland
2014-02-05 20:33:59
So 2014{x}=32, which means that {x}log2014=log32.
So 2014{x}=32, which means that {x}log2014=log32.
copeland
2014-02-05 20:34:10
The solution to this equation is {x}=log32log2014.
The solution to this equation is {x}=log32log2014.
copeland
2014-02-05 20:34:16
Can we make that prettier?
Can we make that prettier?
Pythonprogrammer
2014-02-05 20:34:48
log 3 - log2/ log 2014
log 3 - log2/ log 2014
mishai
2014-02-05 20:34:48
(log 3-log 2)/log 2014
(log 3-log 2)/log 2014
lucylai
2014-02-05 20:34:48
(log(3)-log(2))/log(2014)
(log(3)-log(2))/log(2014)
checkmate1021
2014-02-05 20:34:48
log(3) - log(2)
log(3) - log(2)
AaaDuhLoo
2014-02-05 20:34:48
(log3-log2)/(log2014) ?
(log3-log2)/(log2014) ?
mathbeida
2014-02-05 20:34:48
log3 - log 2
log3 - log 2
dasobson
2014-02-05 20:34:48
log 3 - log 2 over log 2014?
log 3 - log 2 over log 2014?
Fibonacci97
2014-02-05 20:34:48
log(3)-log(2)
log(3)-log(2)
copeland
2014-02-05 20:35:04
The solution to this equation simplifies as {x}=log32log2014=log3−log2log2014.
The solution to this equation simplifies as {x}=log32log2014=log3−log2log2014.
copeland
2014-02-05 20:35:08
The interval is [2,2+log3−log2log2014] and its length is log3−log2log2014
The interval is [2,2+log3−log2log2014] and its length is log3−log2log2014
copeland
2014-02-05 20:35:11
Let's add this to the chart:⌊x⌋length1log2log20142log3−log2log2014
Let's add this to the chart:⌊x⌋length1log2log20142log3−log2log2014
copeland
2014-02-05 20:35:14
The third left endpoint is 3. How wide is this interval?
The third left endpoint is 3. How wide is this interval?
Dragon6point1
2014-02-05 20:35:43
(log4 - log3)/log2014
(log4 - log3)/log2014
anwang16
2014-02-05 20:35:43
(log4-log3)/log2014
(log4-log3)/log2014
joshualee2000
2014-02-05 20:35:43
log 4-log 3/log2014
log 4-log 3/log2014
tekgeek
2014-02-05 20:35:43
(log4-log3)/log2014
(log4-log3)/log2014
LightningX48
2014-02-05 20:35:43
(log4 - log3)/log(2014)
(log4 - log3)/log(2014)
CornSaltButter
2014-02-05 20:35:43
log4−log3log2014
log4−log3log2014
1915933
2014-02-05 20:35:48
(log 4 - log 3)/log 2014
(log 4 - log 3)/log 2014
bigc08
2014-02-05 20:35:48
log 4-log 3/log 2014
log 4-log 3/log 2014
simon1221
2014-02-05 20:35:48
log4 - log3 / log201
log4 - log3 / log201
copeland
2014-02-05 20:35:53
We need f(x)=1 when ⌊x⌋=3.
We need f(x)=1 when ⌊x⌋=3.
copeland
2014-02-05 20:35:55
Now we want to solve 3(2014{x}−1)=1. That means we want to find the fractional part that solves 2014{x}−1=13.
Now we want to solve 3(2014{x}−1)=1. That means we want to find the fractional part that solves 2014{x}−1=13.
copeland
2014-02-05 20:36:01
So 2014{x}=43, and hence {x}log2014=log43=log4−log3.
So 2014{x}=43, and hence {x}log2014=log43=log4−log3.
copeland
2014-02-05 20:36:07
The solution to this equation is {x}=log43log2014=log4−log3log2014.
The solution to this equation is {x}=log43log2014=log4−log3log2014.
copeland
2014-02-05 20:36:10
⌊x⌋length1log2log20142log3−log2log20143log4−log3log2014
⌊x⌋length1log2log20142log3−log2log20143log4−log3log2014
copeland
2014-02-05 20:36:12
I bet you see the pattern now. What is the last term?
I bet you see the pattern now. What is the last term?
tekgeek
2014-02-05 20:37:14
+....+(log2014-log2013)/log2014
+....+(log2014-log2013)/log2014
jweisblat14
2014-02-05 20:37:14
log 2014 - log 2013 / log 2014
log 2014 - log 2013 / log 2014
Dragon6point1
2014-02-05 20:37:14
(log2014 - log2013)/log2014
(log2014 - log2013)/log2014
DrMath
2014-02-05 20:37:14
(log 2014-log 2013)/log 2014
(log 2014-log 2013)/log 2014
ingridzhang97
2014-02-05 20:37:14
(log2014-log2013)/log2014
(log2014-log2013)/log2014
mathnerd101
2014-02-05 20:37:14
(log2014-log2013)/log2014
(log2014-log2013)/log2014
LMA
2014-02-05 20:37:14
(log 2014-log2013)/log2014
(log 2014-log2013)/log2014
DaChickenInc
2014-02-05 20:37:14
log2014−log2013log2014
log2014−log2013log2014
Tuxianeer
2014-02-05 20:37:14
(log(2014)-log(2013))/log(2014)
(log(2014)-log(2013))/log(2014)
ferrastacie
2014-02-05 20:37:14
(log 2014 - log 2013)/ log 2014
(log 2014 - log 2013)/ log 2014
ZekromReshiram
2014-02-05 20:37:14
(log2015-log2014)/log2014
(log2015-log2014)/log2014
copeland
2014-02-05 20:37:20
The final left endpoint is 2013.
The final left endpoint is 2013.
copeland
2014-02-05 20:37:21
We need f(x)=1 when ⌊x⌋=2013.
We need f(x)=1 when ⌊x⌋=2013.
copeland
2014-02-05 20:37:24
Now we want to solve 2013(2014{x}−1)=1. That means we want to find the fractional part that solves 2014{x}−1=12013.
Now we want to solve 2013(2014{x}−1)=1. That means we want to find the fractional part that solves 2014{x}−1=12013.
copeland
2014-02-05 20:37:29
This gives 2014{x}=20142013, so {x}log2014=log20142013=log2014−log2013.
This gives 2014{x}=20142013, so {x}log2014=log20142013=log2014−log2013.
copeland
2014-02-05 20:37:37
The solution to this equation is {x}=log20142013log2014=log2014−log2013log2014.
The solution to this equation is {x}=log20142013log2014=log2014−log2013log2014.
copeland
2014-02-05 20:37:40
⌊x⌋length1log2log20142log3−log2log20143log4−log3log2014⋮ ⋮2013log2014−log2013log2014
⌊x⌋length1log2log20142log3−log2log20143log4−log3log2014⋮ ⋮2013log2014−log2013log2014
copeland
2014-02-05 20:37:48
What do we get when we add these?
What do we get when we add these?
want2learn
2014-02-05 20:38:27
1
1
ws0414
2014-02-05 20:38:27
A
A
hi how are you doing toda
2014-02-05 20:38:27
1
1
matholympiad25
2014-02-05 20:38:27
1 A
1 A
coldsummer
2014-02-05 20:38:27
1
1
ssk9208
2014-02-05 20:38:27
Cancel and cancel
Cancel and cancel
mathtastic
2014-02-05 20:38:27
log2014/log2014=1
log2014/log2014=1
junat3
2014-02-05 20:38:27
A) 1
A) 1
mathwizard888
2014-02-05 20:38:27
adding them gives log 2014/log 2014=1 (A)
adding them gives log 2014/log 2014=1 (A)
doodlemaster7
2014-02-05 20:38:27
log 2014/2014
log 2014/2014
raylgheeheehee
2014-02-05 20:38:27
1
1
jiecut
2014-02-05 20:38:27
1
1
brainiac1
2014-02-05 20:38:27
1
1
Jayjayliu
2014-02-05 20:38:27
1
1
quackman
2014-02-05 20:38:27
1
1
IsabeltheCat
2014-02-05 20:38:27
1
1
tfmtoto
2014-02-05 20:38:27
1
1
jiecut
2014-02-05 20:38:27
log2014/log2014 = 1
log2014/log2014 = 1
flamefoxx99
2014-02-05 20:38:27
log2014/log2014
log2014/log2014
born_in_1999
2014-02-05 20:38:27
log2014/log2014
log2014/log2014
copeland
2014-02-05 20:38:32
When we add these the sum telescopes. The log2 in row 1 cancels the log2 in row 2. The log3 in row 2 cancels the log3 in row 3. The only thing left is the final termlog2014log2014=1.The answer is (A).
When we add these the sum telescopes. The log2 in row 1 cancels the log2 in row 2. The log3 in row 2 cancels the log3 in row 3. The only thing left is the final termlog2014log2014=1.The answer is (A).
copeland
2014-02-05 20:39:05
Incidentally, the first term ought to be log2−log1log2014.
Incidentally, the first term ought to be log2−log1log2014.
copeland
2014-02-05 20:39:32
Problem 12-22 was the same as 10-25.
Problem 12-22 was the same as 10-25.
copeland
2014-02-05 20:39:35
Nailed it.
Nailed it.
simon1221
2014-02-05 20:39:53
3 left
3 left
copeland
2014-02-05 20:40:02
For anybody not keeping score.
For anybody not keeping score.
copeland
2014-02-05 20:40:03
Let's keep going.
Let's keep going.
copeland
2014-02-05 20:40:05
23. The fraction 1992=0.¯bn−1bn−2…b2b1b0, where n is the length of the period of the repeating decimal expansion. What is the sum b0+b1+⋯+bn−1?
peekaboo!
(A) 874(B) 883(C) 887(D) 891(E) 892
23. The fraction 1992=0.¯bn−1bn−2…b2b1b0, where n is the length of the period of the repeating decimal expansion. What is the sum b0+b1+⋯+bn−1?
peekaboo!
(A) 874(B) 883(C) 887(D) 891(E) 892
copeland
2014-02-05 20:40:16
I love repeating decimal problems. I find them soothing.
I love repeating decimal problems. I find them soothing.
copeland
2014-02-05 20:40:30
Know any well-known repeating decimals that we could possibly use here (assuming you don't already know the expansion of 1/992)?
Know any well-known repeating decimals that we could possibly use here (assuming you don't already know the expansion of 1/992)?
mathmaster2012
2014-02-05 20:41:01
1/99=0.010101010101
1/99=0.010101010101
mssmath
2014-02-05 20:41:01
1/99
1/99
tapir1729
2014-02-05 20:41:01
1/99
1/99
distortedwalrus
2014-02-05 20:41:01
1/99 = .01010101...
1/99 = .01010101...
mishai
2014-02-05 20:41:01
1/99 by itself
1/99 by itself
blueferret
2014-02-05 20:41:01
1/99=0.010101...
1/99=0.010101...
hametm
2014-02-05 20:41:01
1/99=.0101010101....
1/99=.0101010101....
Dragon6point1
2014-02-05 20:41:01
199=0.01010101...
199=0.01010101...
maxplanck
2014-02-05 20:41:01
1/99
1/99
minimario
2014-02-05 20:41:01


vinayak-kumar
2014-02-05 20:41:01
1/99=.010101010101010101010101...
1/99=.010101010101010101010101...
copeland
2014-02-05 20:41:04
You should definitely know that 199=.0101010101⋯.
You should definitely know that 199=.0101010101⋯.
copeland
2014-02-05 20:41:06
As a quick reminder because it's useful, we write 1=.99999999…. Now we are looking at a list of 99s:1=.99⏟99⏟99⏟99⏟….
As a quick reminder because it's useful, we write 1=.99999999…. Now we are looking at a list of 99s:1=.99⏟99⏟99⏟99⏟….
copeland
2014-02-05 20:41:15
Once we see this, we can just divide each of these 99s by 99 to get 1:199=.01⏟01⏟01⏟01⏟….
Once we see this, we can just divide each of these 99s by 99 to get 1:199=.01⏟01⏟01⏟01⏟….
copeland
2014-02-05 20:41:19
Now for the fun part. How do we get 1992?
Now for the fun part. How do we get 1992?
copeland
2014-02-05 20:41:33
There are (at least) four nice ways to get at this. What do you see?
There are (at least) four nice ways to get at this. What do you see?
zoroark12345
2014-02-05 20:42:03
divide 99 again
divide 99 again
DrMath
2014-02-05 20:42:03
divide by 99 again
divide by 99 again
bengals
2014-02-05 20:42:03
divide again
divide again
copeland
2014-02-05 20:42:13
There are multiple ways to divide, actually.
There are multiple ways to divide, actually.
copeland
2014-02-05 20:42:15
We could use long division. This is a really nice approach and is often the best thing to turn to in a repeating decimals problem if you aren't struck with any other bit of inspiriation.
We could use long division. This is a really nice approach and is often the best thing to turn to in a repeating decimals problem if you aren't struck with any other bit of inspiriation.
copeland
2014-02-05 20:42:25
We could also break the sum into a geometric series of powers of 10−2 as
199=+.010000000000…+.000100000000…+.000001000000…+.000000010000…+.000000000100… ⋮
Then we could use our expression for 199 to divide each of the terms by 99 and add.
We could also break the sum into a geometric series of powers of 10−2 as
199=+.010000000000…+.000100000000…+.000001000000…+.000000010000…+.000000000100… ⋮
Then we could use our expression for 199 to divide each of the terms by 99 and add.
copeland
2014-02-05 20:42:31
What else could we do?
What else could we do?
DVA6102
2014-02-05 20:43:04
well 1/9801 = something/999....9999
well 1/9801 = something/999....9999
bigc08
2014-02-05 20:43:04
divide each period in 0.0101010101 by 99
divide each period in 0.0101010101 by 99
bigc08
2014-02-05 20:43:04
separate the decimal into periods
separate the decimal into periods
copeland
2014-02-05 20:43:10
We could figure out the period and write 199=010101…010101999999…999999and then just divide the numerator by 99. That definitely isn't a bad solution.
We could figure out the period and write 199=010101…010101999999…999999and then just divide the numerator by 99. That definitely isn't a bad solution.
blueberry7
2014-02-05 20:43:47
square it!
square it!
blueferret
2014-02-05 20:43:47
square our number
square our number
swe1
2014-02-05 20:43:47
Squaring! Yaaayyy!
Squaring! Yaaayyy!
Tuxianeer
2014-02-05 20:43:47
square it
square it
doodlemaster7
2014-02-05 20:43:47
square it!
square it!
yangwy
2014-02-05 20:43:47
1/99*1/99
1/99*1/99
awesomemathlete
2014-02-05 20:43:47
Square that decimal.
Square that decimal.
CornSaltButter
2014-02-05 20:43:47
square 1/99?
square 1/99?
sirknightingfail
2014-02-05 20:43:47


copeland
2014-02-05 20:43:51
We could also just take the expression for 199 and square it.
We could also just take the expression for 199 and square it.
copeland
2014-02-05 20:43:56
Since the squaring solution is the most exotic-looking one here, I think we'll learn most from going with that one.
Since the squaring solution is the most exotic-looking one here, I think we'll learn most from going with that one.
copeland
2014-02-05 20:44:00
1992=(.0101010101010…)2.
1992=(.0101010101010…)2.
copeland
2014-02-05 20:44:14
How does the square of this number start?
How does the square of this number start?
joshualee2000
2014-02-05 20:45:16
1/9801=0.00010203040506070809..........
1/9801=0.00010203040506070809..........
jweisblat14
2014-02-05 20:45:16
.00010101010101...+.0000010101010101...+.000000010101010101...
.00010101010101...+.0000010101010101...+.000000010101010101...
dli00105
2014-02-05 20:45:16
0.00010203...
0.00010203...
DigitalKing257
2014-02-05 20:45:16
0.0001020...
0.0001020...
joshualee2000
2014-02-05 20:45:16
0.0001020304050607...
0.0001020304050607...
alex31415
2014-02-05 20:45:16
.00010203...
.00010203...
blueferret
2014-02-05 20:45:16
0.01020304...
0.01020304...
sirknightingfail
2014-02-05 20:45:16


MrMerchant
2014-02-05 20:45:16
it turns out to be 0.001020304050607......
it turns out to be 0.001020304050607......
extremeaxe6
2014-02-05 20:45:16
0.00010203040506070809...
0.00010203040506070809...
Pythonprogrammer
2014-02-05 20:45:16
000102030405...
000102030405...
jweisblat14
2014-02-05 20:45:16
.0001020304...
.0001020304...
swe1
2014-02-05 20:45:16
0.000102030405?
0.000102030405?
copeland
2014-02-05 20:45:19
Long multiplication makes this easier.
Long multiplication makes this easier.
copeland
2014-02-05 20:45:21
×.01010101010101…×.01010101010101…×.00010101010101010…+.00000101010101010…+.00000001010101010…+.00000000010101010…abcdefg⋮+.0001020304050607…
×.01010101010101…×.01010101010101…×.00010101010101010…+.00000101010101010…+.00000001010101010…+.00000000010101010…abcdefg⋮+.0001020304050607…
copeland
2014-02-05 20:45:26
(Fun fact: this is actually the same sum you'd get if you divided the terms of the geometric series by 99 like in our other proposed solution.)
(Fun fact: this is actually the same sum you'd get if you divided the terms of the geometric series by 99 like in our other proposed solution.)
copeland
2014-02-05 20:45:31
That's intriguing, but I'm not sure what happens when we start carrying or how it ends or when it starts to repeat, so we need to think about those things.
That's intriguing, but I'm not sure what happens when we start carrying or how it ends or when it starts to repeat, so we need to think about those things.
copeland
2014-02-05 20:45:35
If we think of these as two-digit blocks, when does it start to carry from block to block?
If we think of these as two-digit blocks, when does it start to carry from block to block?
jweisblat14
2014-02-05 20:46:26
99 to 100
99 to 100
lucylai
2014-02-05 20:46:26
at 9899...
at 9899...
superpi83
2014-02-05 20:46:26
at the 100th summand
at the 100th summand
brian22
2014-02-05 20:46:26
after ...9899
after ...9899
copeland
2014-02-05 20:46:28
We actually make it all the way up to 98 before anything weird happens.
We actually make it all the way up to 98 before anything weird happens.
copeland
2014-02-05 20:46:31
.000102030405…969798?????
.000102030405…969798?????
copeland
2014-02-05 20:46:37
Now the next block is 99 then 100 then 101, but that's definitely going to make a mess of things. Is there any way to fix this?
Now the next block is 99 then 100 then 101, but that's definitely going to make a mess of things. Is there any way to fix this?
copeland
2014-02-05 20:46:59
Here's a hint: you almost always need to use 1=.99999… somewhere in arguments like this.
Here's a hint: you almost always need to use 1=.99999… somewhere in arguments like this.
swe1
2014-02-05 20:47:43
Subtract 0.999999999?
Subtract 0.999999999?
copeland
2014-02-05 20:47:46
Well that's too big.
Well that's too big.
copeland
2014-02-05 20:47:55
But is there a nice way to get a stream of nines out of this?
But is there a nice way to get a stream of nines out of this?
DrMath
2014-02-05 20:48:36
0.000......000999999.....
0.000......000999999.....
brainiac1
2014-02-05 20:48:36
subtract 0.00000.........9999999999
subtract 0.00000.........9999999999
hametm
2014-02-05 20:48:36
Subtract .999999....*10^-9899
Subtract .999999....*10^-9899
zoroark12345
2014-02-05 20:48:36
starting 99 subtract a bunch of 9's
starting 99 subtract a bunch of 9's
Tuxianeer
2014-02-05 20:48:36
-0.000000000000(to lie with the 9899)999999999
-0.000000000000(to lie with the 9899)999999999
copeland
2014-02-05 20:48:43
Let's pull out a 99 from all of the remaining terms. Then 99=99+0 and 100=99+01 and 101=99+02, etc. Now if we pull all the 99s out into a different series, we find something neat:
Let's pull out a 99 from all of the remaining terms. Then 99=99+0 and 100=99+01 and 101=99+02, etc. Now if we pull all the 99s out into a different series, we find something neat:
copeland
2014-02-05 20:48:44
+.000102030405…96979800010203…+.000000000000…00000099999999…
+.000102030405…96979800010203…+.000000000000…00000099999999…
copeland
2014-02-05 20:48:51
Now that is the same as
.000102030405…96979800010203…+.000000000000…00000100000000… .000102030405…96979900010203…
and at this point, we could reasonably be convinced that we've found where the expansion starts to repeat.
Now that is the same as
.000102030405…96979800010203…+.000000000000…00000100000000… .000102030405…96979900010203…
and at this point, we could reasonably be convinced that we've found where the expansion starts to repeat.
copeland
2014-02-05 20:49:01
Let's prove that. We could figure out the period and divide things out, but now that we have a target, let's just see what happens when we multiply x=.¯000102…969799 by 99.
Let's prove that. We could figure out the period and divide things out, but now that we have a target, let's just see what happens when we multiply x=.¯000102…969799 by 99.
copeland
2014-02-05 20:49:09
Ugh. Multiplying by 99 is hard. What is easy?
Ugh. Multiplying by 99 is hard. What is easy?
ksun48
2014-02-05 20:49:33
*100 - 1
*100 - 1
fcc1234
2014-02-05 20:49:33
Multiplying by 100-1
Multiplying by 100-1
mathtastic
2014-02-05 20:49:33
multiplying by 100 then subtracting
multiplying by 100 then subtracting
CornSaltButter
2014-02-05 20:49:33
multiplying by 100, subtracting 1
multiplying by 100, subtracting 1
tekgeek
2014-02-05 20:49:33
multiplying by 100-1
multiplying by 100-1
simon1221
2014-02-05 20:49:33
times 100, minus 1
times 100, minus 1
mathtastic
2014-02-05 20:49:33
99x=100x-x
99x=100x-x
treemath
2014-02-05 20:49:33
multiplying by (100-1)
multiplying by (100-1)
bookie331
2014-02-05 20:49:35
multiplying by 100 and subtract 1
multiplying by 100 and subtract 1
copeland
2014-02-05 20:49:38
We could multiply x by 100 and subtract x because 99x=100x−x.
We could multiply x by 100 and subtract x because 99x=100x−x.
copeland
2014-02-05 20:49:41
−100x=.¯01020304…96979900−100x=.¯00010203…95969799.¯01010101…01010101
At the end we get the really tricky 9900−9799=0101.
−100x=.¯01020304…96979900−100x=.¯00010203…95969799.¯01010101…01010101
At the end we get the really tricky 9900−9799=0101.
copeland
2014-02-05 20:49:53
That is our expansion for 199, so we're right!
That is our expansion for 199, so we're right!
copeland
2014-02-05 20:49:56
Now we need the sum of the digits of .00010203…969799. How can we get at this sum?
Now we need the sum of the digits of .00010203…969799. How can we get at this sum?
copeland
2014-02-05 20:50:18
WWGD?
WWGD?
doodlemaster7
2014-02-05 20:50:52
99*100/2 gauss
99*100/2 gauss
LMA
2014-02-05 20:50:52
does that stand for what would gauss do?
does that stand for what would gauss do?
copeland
2014-02-05 20:50:57
Gauss, folks!
Gauss, folks!
copeland
2014-02-05 20:51:05
How can we make the sum of these things easier?
How can we make the sum of these things easier?
bacca2002
2014-02-05 20:51:29
failed copeland
failed copeland
copeland
2014-02-05 20:51:33
Yeah, they can't all be winners.
Yeah, they can't all be winners.
checkmate1021
2014-02-05 20:52:02
sum in pairs
sum in pairs
alex31415
2014-02-05 20:52:02
find the average
find the average
acegikmoqsuwy2000
2014-02-05 20:52:02
grouping them together?
grouping them together?
extremeaxe6
2014-02-05 20:52:02
take 0+99, 1+98 etc and each summand adds to 99 or a digit sum of 18
take 0+99, 1+98 etc and each summand adds to 99 or a digit sum of 18
copeland
2014-02-05 20:52:05
We're missing 98, but otherwise we have everything from 00 to 99.
We're missing 98, but otherwise we have everything from 00 to 99.
copeland
2014-02-05 20:52:07
Let's pair the 2-digit numbers from 00 to 99 up and then subtract the contribution of 98.
Let's pair the 2-digit numbers from 00 to 99 up and then subtract the contribution of 98.
copeland
2014-02-05 20:52:08
What do 00 and 99 contribute collectively to the sum?
What do 00 and 99 contribute collectively to the sum?
mishai
2014-02-05 20:52:54
18
18
DrMath
2014-02-05 20:52:54
18
18
Pythonprogrammer
2014-02-05 20:52:54
18
18
jweisblat14
2014-02-05 20:52:54
18
18
dli00105
2014-02-05 20:52:54
18
18
distortedwalrus
2014-02-05 20:52:54
18
18
Dragon6point1
2014-02-05 20:52:54
18
18
lucylai
2014-02-05 20:52:54
18
18
ingridzhang97
2014-02-05 20:52:54
18
18
mssmath
2014-02-05 20:52:54
18
18
dli00105
2014-02-05 20:52:54
18
18
blueferret
2014-02-05 20:52:54
18
18
mathwizard888
2014-02-05 20:52:54
18
18
copeland
2014-02-05 20:52:57
00 and 99 contribute 0+0+9+9=18.
00 and 99 contribute 0+0+9+9=18.
copeland
2014-02-05 20:52:58
What do 47 and 52 contribute?
What do 47 and 52 contribute?
hametm
2014-02-05 20:53:17
18
18
ninjashiloh
2014-02-05 20:53:17
18
18
joshualee2000
2014-02-05 20:53:17
18
18
flamesofpi
2014-02-05 20:53:17
18
18
mathsd
2014-02-05 20:53:17
18
18
Chronix
2014-02-05 20:53:17
18
18
Weegee13
2014-02-05 20:53:17
18
18
hi how are you doing toda
2014-02-05 20:53:17
18
18
copeland
2014-02-05 20:53:20
47 and 52 contribute 4+7+5+2=18 to the sum as well.
47 and 52 contribute 4+7+5+2=18 to the sum as well.
copeland
2014-02-05 20:53:21
What's the average sum of digits for a 2-digit number?
What's the average sum of digits for a 2-digit number?
bigc08
2014-02-05 20:53:45
9
9
mxgo
2014-02-05 20:53:45
9
9
bacca2002
2014-02-05 20:53:45
9.
9.
Dragon6point1
2014-02-05 20:53:45
9
9
jweisblat14
2014-02-05 20:53:45
9
9
treemath
2014-02-05 20:53:45
9
9
bengals
2014-02-05 20:53:45
9
9
math0127
2014-02-05 20:53:45
9
9
CyclicRain
2014-02-05 20:53:45
9
9
copeland
2014-02-05 20:53:47
The average sum of the digits of a 2-digit number is 9. How many total 2-digit numbers are there?
The average sum of the digits of a 2-digit number is 9. How many total 2-digit numbers are there?
joshualee2000
2014-02-05 20:54:20
100
100
speck
2014-02-05 20:54:20
100
100
hametm
2014-02-05 20:54:20
100
100
WalkerTesla
2014-02-05 20:54:20
100
100
jiecut
2014-02-05 20:54:20
100
100
Tuxianeer
2014-02-05 20:54:20
100
100
copeland
2014-02-05 20:54:23
There are 100 total 2-digit numbers, so the sum of all the digits is 900.
There are 100 total 2-digit numbers, so the sum of all the digits is 900.
copeland
2014-02-05 20:54:24
And the final answer?
And the final answer?
jweisblat14
2014-02-05 20:55:00
883
883
lucylai
2014-02-05 20:55:00
883
883
CornSaltButter
2014-02-05 20:55:00
900-17=883
900-17=883
bacca2002
2014-02-05 20:55:00
since you have to subtract 9 and 8
since you have to subtract 9 and 8
pattycakechichi
2014-02-05 20:55:00
883 --> B
883 --> B
jweisblat14
2014-02-05 20:55:00
remove a 9+8-17 and get 883
remove a 9+8-17 and get 883
howie2000
2014-02-05 20:55:00
18⋅50=900, then 900−17=883
18⋅50=900, then 900−17=883
WalkerTesla
2014-02-05 20:55:00
900-17 = 883
900-17 = 883
bacca2002
2014-02-05 20:55:00
so the final answer is (B) 883
so the final answer is (B) 883
guilt
2014-02-05 20:55:00
subtrat 17
subtrat 17
abishek99
2014-02-05 20:55:00
900-17=883 B
900-17=883 B
howie2000
2014-02-05 20:55:00
883
883
harvey2014
2014-02-05 20:55:00
900-17=883
900-17=883
copeland
2014-02-05 20:55:02
We need to subtract the 9+8 that we lose by skipping 98. That leaves 900−17=883 as the sum. The answer is (B).
We need to subtract the 9+8 that we lose by skipping 98. That leaves 900−17=883 as the sum. The answer is (B).
copeland
2014-02-05 20:55:52
(Incidentally, when I solved this one, I decided the average was something and I decided that the number of them was a multiple of 10, so the units digit had to be the same as the units digit of -9-8. There's only one answer here that ends in 3.)
(Incidentally, when I solved this one, I decided the average was something and I decided that the number of them was a multiple of 10, so the units digit had to be the same as the units digit of -9-8. There's only one answer here that ends in 3.)
pi37
2014-02-05 20:56:44
I did exactly that, except I subtracted 98 and chose the only answer that ended in 2
I did exactly that, except I subtracted 98 and chose the only answer that ended in 2
copeland
2014-02-05 20:56:51
So, there's a downside too.
So, there's a downside too.
copeland
2014-02-05 20:57:00
24. Let f0(x)=x+|x−100|−|x+100|, and for n≥1, let fn(x)=|fn−1(x)|−1. For how many values of x is f100(x)=0?
peekaboo!
(A) 299(B) 300(C) 301(D) 302(E) 303
24. Let f0(x)=x+|x−100|−|x+100|, and for n≥1, let fn(x)=|fn−1(x)|−1. For how many values of x is f100(x)=0?
peekaboo!
(A) 299(B) 300(C) 301(D) 302(E) 303
copeland
2014-02-05 20:57:08
What are some ways we can start in on this problem?
What are some ways we can start in on this problem?
6stars
2014-02-05 20:58:05
We could graph?
We could graph?
mathtastic
2014-02-05 20:58:05
graphing it and trying values to get a feel for the function
graphing it and trying values to get a feel for the function
ksun48
2014-02-05 20:58:05
and just try to solve for possible values of f_0(x)
and just try to solve for possible values of f_0(x)
DVA6102
2014-02-05 20:58:05
compute f_n for small n
compute f_n for small n
joshualee2000
2014-02-05 20:58:05
find f1(x) ?
find f1(x) ?
zoroark12345
2014-02-05 20:58:05
draw a graph
draw a graph
joshxiong
2014-02-05 20:58:05
Graph f0(x)
Graph f0(x)
flyrain
2014-02-05 20:58:05
work with the recursive function
work with the recursive function
copeland
2014-02-05 20:58:10
There are generally two approaches to this problem - graphical and algebraic. I think we'll learn more from the graphical approach so that's the one I'm going to take.
There are generally two approaches to this problem - graphical and algebraic. I think we'll learn more from the graphical approach so that's the one I'm going to take.
copeland
2014-02-05 20:58:12
First let's graph the three components of f0. The first part is just x which is easy to graph.
First let's graph the three components of f0. The first part is just x which is easy to graph.
copeland
2014-02-05 20:58:16


copeland
2014-02-05 20:58:47
(To be honest, we'll graph for a while and probably switch to something more algebraic.)
(To be honest, we'll graph for a while and probably switch to something more algebraic.)
copeland
2014-02-05 20:58:48
What does the graph of y=|x−100| look like?
What does the graph of y=|x−100| look like?
blueferret
2014-02-05 20:59:03
a v shape
a v shape
Pythonprogrammer
2014-02-05 20:59:03
like a V!
like a V!
dli00105
2014-02-05 20:59:03
aV s
aV s
copeland
2014-02-05 20:59:06
Where?
Where?
checkmate1021
2014-02-05 20:59:24
v centered at 100
v centered at 100
blueferret
2014-02-05 20:59:24
the bottom is at x=100
the bottom is at x=100
fmasroor
2014-02-05 20:59:24
shifted -> 100
shifted -> 100
checkmate1021
2014-02-05 20:59:24
centered at 100
centered at 100
lee42
2014-02-05 20:59:24
A V shifted right by 100
A V shifted right by 100
LMA
2014-02-05 20:59:24
shifted right 100
shifted right 100
mishai
2014-02-05 20:59:24
100 to the right of the origin
100 to the right of the origin
stonewater
2014-02-05 20:59:24
right 100
right 100
copeland
2014-02-05 20:59:26
It is an absolute value with slope ±1 and vertex at 100.
It is an absolute value with slope ±1 and vertex at 100.
copeland
2014-02-05 20:59:37
What about y=−|x+100|?
What about y=−|x+100|?
copeland
2014-02-05 20:59:38
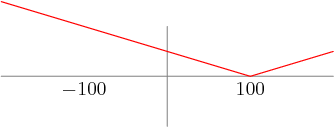

trumpeter
2014-02-05 21:00:25
upside down v 100 left of the origin
upside down v 100 left of the origin
DrMath
2014-02-05 21:00:25
similar, a minus V with vertex -100
similar, a minus V with vertex -100
az_phx_brandon_jiang
2014-02-05 21:00:25
upside down V at -100
upside down V at -100
bigc08
2014-02-05 21:00:25
flipped and vertex at -100,0
flipped and vertex at -100,0
swe1
2014-02-05 21:00:25
Its the same except at -100 and flipped upside down
Its the same except at -100 and flipped upside down
mathmaster2012
2014-02-05 21:00:25
same thing except base is on -100 and it is upside down
same thing except base is on -100 and it is upside down
hamzacooly
2014-02-05 21:00:25
and upside down V centered at -100
and upside down V centered at -100
mathbeida
2014-02-05 21:00:25
upside down v centered at -100
upside down v centered at -100
copeland
2014-02-05 21:00:28
This one is below the axis and has its vertex, a maximum, at -100.
This one is below the axis and has its vertex, a maximum, at -100.
copeland
2014-02-05 21:00:30

copeland
2014-02-05 21:00:39
Here are all three.
Here are all three.
copeland
2014-02-05 21:00:42

copeland
2014-02-05 21:00:49
When we add these, we get a continuous, piecewise linear function. It has kinks at x=±100. What are the values of f0 at ±100?
When we add these, we get a continuous, piecewise linear function. It has kinks at x=±100. What are the values of f0 at ±100?
brian22
2014-02-05 21:01:43
-+100
-+100
joshualee2000
2014-02-05 21:01:43
+/-100
+/-100
DrMath
2014-02-05 21:01:43
-100, 100
-100, 100
acegikmoqsuwy2000
2014-02-05 21:01:43
-100, and 100
-100, and 100
blueferret
2014-02-05 21:01:43
-100 and +100
-100 and +100
bigc08
2014-02-05 21:01:43
at 100 it is -100 and at -100 it is 100
at 100 it is -100 and at -100 it is 100
WalkerTesla
2014-02-05 21:01:43
-100 and 100 for x = 100 and -100
-100 and 100 for x = 100 and -100
speck
2014-02-05 21:01:43
-100 and 100
-100 and 100
speck
2014-02-05 21:01:43
reverse the signs
reverse the signs
ingridzhang97
2014-02-05 21:01:43
-100 and 100
-100 and 100
copeland
2014-02-05 21:01:46
The values are
f0(−100)=−100+200−0=+100f0(100)=100+0−200=−100.
The values are
f0(−100)=−100+200−0=+100f0(100)=100+0−200=−100.
copeland
2014-02-05 21:01:52
Here is the graph.
Here is the graph.
copeland
2014-02-05 21:01:57
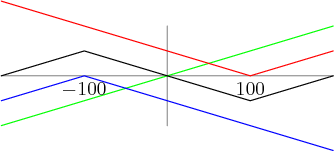

copeland
2014-02-05 21:01:59
Notice how there's always one slope that's different from the other two. That means the slope is always either +1 or −1.
Notice how there's always one slope that's different from the other two. That means the slope is always either +1 or −1.
copeland
2014-02-05 21:02:08
The graph rises from −∞ to (−100,100) then falls to (100,−100) then rises again to +∞.
The graph rises from −∞ to (−100,100) then falls to (100,−100) then rises again to +∞.
copeland
2014-02-05 21:02:14


copeland
2014-02-05 21:02:25
We will solve the problem with a little algebra from here, but let's take a few moments to graph a few more of these. My original solution was entirely via graphs, but the algebraic ideas generalize a little better.
We will solve the problem with a little algebra from here, but let's take a few moments to graph a few more of these. My original solution was entirely via graphs, but the algebraic ideas generalize a little better.
copeland
2014-02-05 21:02:35
Generalize to other problems, that is.
Generalize to other problems, that is.
copeland
2014-02-05 21:02:37
Now how do we get f1?
Now how do we get f1?
ws0414
2014-02-05 21:03:17
absolute, shift down one
absolute, shift down one
dli00105
2014-02-05 21:03:17
absolute value minus 1
absolute value minus 1
bacca2002
2014-02-05 21:03:17
take the absolute value and subtract 1
take the absolute value and subtract 1
swe1
2014-02-05 21:03:17
Flip the part that is negative and shift down by one
Flip the part that is negative and shift down by one
pi37
2014-02-05 21:03:17
flip some stuff over and move it down
flip some stuff over and move it down
shandongboy
2014-02-05 21:03:17
turn all negatives into positive, shift down one unit
turn all negatives into positive, shift down one unit
copeland
2014-02-05 21:03:20
We take the negative part of the graph and flip it. Then we move everything down 1.
We take the negative part of the graph and flip it. Then we move everything down 1.
copeland
2014-02-05 21:03:26

copeland
2014-02-05 21:03:31
For f2 we do the same thing. We flip those little peaks and we subtract 1.
For f2 we do the same thing. We flip those little peaks and we subtract 1.
copeland
2014-02-05 21:03:33

copeland
2014-02-05 21:03:48
All of the values are shrinking to the x-axis and then the oscillate back and forth between -1 and 0.
All of the values are shrinking to the x-axis and then the oscillate back and forth between -1 and 0.
copeland
2014-02-05 21:03:50
Alright, let's break from this and work purely algebraically.
Alright, let's break from this and work purely algebraically.
copeland
2014-02-05 21:03:53
What should we do to determine if f100(x)=0?
What should we do to determine if f100(x)=0?
DrMath
2014-02-05 21:04:43
look at f99?
look at f99?
Dragon6point1
2014-02-05 21:04:43
Find when f99=1
Find when f99=1
blueferret
2014-02-05 21:04:43
f99(x)=1 or -1
f99(x)=1 or -1
1915933
2014-02-05 21:04:43
Determine if f_99=1 or -1.
Determine if f_99=1 or -1.
DVA6102
2014-02-05 21:04:43
sorry f_99(x) = +-1
sorry f_99(x) = +-1
ws0414
2014-02-05 21:04:43
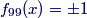
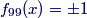
copeland
2014-02-05 21:04:48
If f100(x)=0 then f99(x) must have been −1 or +1.
If f100(x)=0 then f99(x) must have been −1 or +1.
copeland
2014-02-05 21:04:51
Now what?
Now what?
dli00105
2014-02-05 21:05:18
f98(x)
f98(x)
jweisblat14
2014-02-05 21:05:18
f98
f98
copeland
2014-02-05 21:05:22
Good. What about it?
Good. What about it?
zacchro
2014-02-05 21:05:51
f98 is -2,0,2
f98 is -2,0,2
Tuxianeer
2014-02-05 21:05:51
f_98=0,2,-2
f_98=0,2,-2
joshxiong
2014-02-05 21:05:51
f_98(x) = 0, -2, 2
f_98(x) = 0, -2, 2
mathwizard888
2014-02-05 21:05:51
f98(x) is 0, -2, or 2
f98(x) is 0, -2, or 2
Tuxianeer
2014-02-05 21:05:51
f_98=0,2,-2 if f_100=0
f_98=0,2,-2 if f_100=0
awesomemathlete
2014-02-05 21:05:51
-2,0,2
-2,0,2
LMA
2014-02-05 21:05:51
it must have been 0, 2, or -2?
it must have been 0, 2, or -2?
joshualee2000
2014-02-05 21:05:51
then $f_(98)=0 or +/- 2
then $f_(98)=0 or +/- 2
hametm
2014-02-05 21:05:51
It must have been 2, -2, or 0
It must have been 2, -2, or 0
copeland
2014-02-05 21:05:53
If f99(x)∈{−1,+1} then |f98(x)|−1=−1or|f98(x)|−1=+1.
If f99(x)∈{−1,+1} then |f98(x)|−1=−1or|f98(x)|−1=+1.
copeland
2014-02-05 21:06:01
In the first case, f98(x)=0. In the second case f98(x)=±2. Therefore we must have f98(x)∈{−2,0,2}.
In the first case, f98(x)=0. In the second case f98(x)=±2. Therefore we must have f98(x)∈{−2,0,2}.
copeland
2014-02-05 21:06:08
What does that tell us about f97(x)?
What does that tell us about f97(x)?
ksun48
2014-02-05 21:06:50
3,1,-1,or negative thr3e
3,1,-1,or negative thr3e
willwin4sure
2014-02-05 21:06:50
-3, -1, 1, 3
-3, -1, 1, 3
mathtastic
2014-02-05 21:06:50
-3 -1 1 3
-3 -1 1 3
ws0414
2014-02-05 21:06:50
then -2, -1, 0, 1, 2
then -2, -1, 0, 1, 2
DaChickenInc
2014-02-05 21:06:50
-3,-1,1,3
-3,-1,1,3
CornSaltButter
2014-02-05 21:06:50
{1,-1,3,-3}
{1,-1,3,-3}
copeland
2014-02-05 21:06:53
We know that |f98(x)| is one more than an element of {−2,0,2} so has to be 1 or 3. That means f98(x)∈{−3,−1,1,3}.
We know that |f98(x)| is one more than an element of {−2,0,2} so has to be 1 or 3. That means f98(x)∈{−3,−1,1,3}.
copeland
2014-02-05 21:06:55
The pattern is clear from here. |f97(x)| has to be one more than an element of {−3,−1,1,3} so must be in {0,2,4}. That means f97(x)∈{−4,−2,0,2,4}.
The pattern is clear from here. |f97(x)| has to be one more than an element of {−3,−1,1,3} so must be in {0,2,4}. That means f97(x)∈{−4,−2,0,2,4}.
copeland
2014-02-05 21:06:57
And what set contains f0(x)?
And what set contains f0(x)?
colinhy
2014-02-05 21:07:48
following the pattern gives us f0∈−100,−98,…,100
following the pattern gives us f0∈−100,−98,…,100
blueferret
2014-02-05 21:07:48
-100, -98, -96, ... +100
-100, -98, -96, ... +100
viva
2014-02-05 21:07:48
100, 98, ... 0, -98, ... -100
100, 98, ... 0, -98, ... -100
joshualee2000
2014-02-05 21:07:48
{-100,-98....98,100}
{-100,-98....98,100}
copeland
2014-02-05 21:07:54
We note that the index added to the largest element is constant, 100+0=99+1=98+2=97+3, etc. Therefore
f100(x)=0⇒f99(x)∈{−1,1}⇒f98(x)∈{−2,0,2}⇒f97(x)∈{−3,−1,1,3}⋮⇒f0(x)∈{−100,−98,−96,…,96,98,100}
We note that the index added to the largest element is constant, 100+0=99+1=98+2=97+3, etc. Therefore
f100(x)=0⇒f99(x)∈{−1,1}⇒f98(x)∈{−2,0,2}⇒f97(x)∈{−3,−1,1,3}⋮⇒f0(x)∈{−100,−98,−96,…,96,98,100}
copeland
2014-02-05 21:08:07
Here's our graph again:
Here's our graph again:
copeland
2014-02-05 21:08:12


copeland
2014-02-05 21:08:17
How many times is f0(x)=−100?
How many times is f0(x)=−100?
joshualee2000
2014-02-05 21:08:42
2
2
Dragon6point1
2014-02-05 21:08:42
Twice.
Twice.
blueferret
2014-02-05 21:08:42
2
2
WalkerTesla
2014-02-05 21:08:42
2
2
sirknightingfail
2014-02-05 21:08:42
2
2
simon1221
2014-02-05 21:08:42
2
2
zohee
2014-02-05 21:08:42
twice?
twice?
jkyman
2014-02-05 21:08:42
2
2
acegikmoqsuwy2000
2014-02-05 21:08:42
2
2
speck
2014-02-05 21:08:42
2
2
distortedwalrus
2014-02-05 21:08:45
2
2
roitishk
2014-02-05 21:08:45
2
2
copeland
2014-02-05 21:08:48
We noted that that is the minimum on the right. We hit the value 100 twice.
We noted that that is the minimum on the right. We hit the value 100 twice.
copeland
2014-02-05 21:08:49
How many times is f0(x)=−98?
How many times is f0(x)=−98?
stonewater
2014-02-05 21:09:27
3
3
az_phx_brandon_jiang
2014-02-05 21:09:27
3
3
treemath
2014-02-05 21:09:27
3
3
checkmate1021
2014-02-05 21:09:27
3
3
speck
2014-02-05 21:09:27
3
3
guilt
2014-02-05 21:09:27
3
3
ingridzhang97
2014-02-05 21:09:27
3
3
Jayjayliu
2014-02-05 21:09:27
3
3
mikep
2014-02-05 21:09:27
3
3
lee42
2014-02-05 21:09:27
thrice?
thrice?
copeland
2014-02-05 21:09:30
We're between the peak and the trough so we hit this value three times. What else?
We're between the peak and the trough so we hit this value three times. What else?
ksun48
2014-02-05 21:10:15
here are the possible values 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2
here are the possible values 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2
blueferret
2014-02-05 21:10:15
all of them hit 3 times except -100 and 100
all of them hit 3 times except -100 and 100
Tuxianeer
2014-02-05 21:10:15
3 for everything -98 to 98
3 for everything -98 to 98
Dragon6point1
2014-02-05 21:10:15
We hit all other values except 100 three times.
We hit all other values except 100 three times.
speck
2014-02-05 21:10:15
100 and -100 are 2, the rest are 3
100 and -100 are 2, the rest are 3
mathtastic
2014-02-05 21:10:15
you wtill hit everything else 3 times as well, but 100 you will only hit twice
you wtill hit everything else 3 times as well, but 100 you will only hit twice
swe1
2014-02-05 21:10:15
Every number from -98 to 98 intersects three times
Every number from -98 to 98 intersects three times
stonewater
2014-02-05 21:10:15
it's always 3 until +100, which is 2
it's always 3 until +100, which is 2
zohee
2014-02-05 21:10:15
It'll be three for everything except for the two extreme values
It'll be three for everything except for the two extreme values
copeland
2014-02-05 21:10:18
We hit all the values three times except f0(x)=−100 twice and f0(x)=100 twice.
We hit all the values three times except f0(x)=−100 twice and f0(x)=100 twice.
copeland
2014-02-05 21:10:19
How many total solutions are there?
How many total solutions are there?
bacca2002
2014-02-05 21:10:51
so the answer is just 3*99+4
so the answer is just 3*99+4
bacca2002
2014-02-05 21:10:51
301
301
bacca2002
2014-02-05 21:10:51
99*3+4
99*3+4
bacca2002
2014-02-05 21:10:51
answer is C.
answer is C.
WalkerTesla
2014-02-05 21:10:51
99*3+4 = 301
99*3+4 = 301
1915933
2014-02-05 21:10:51
(c) 301
(c) 301
dantheman567
2014-02-05 21:10:51
301
301
blueferret
2014-02-05 21:10:51
3*99+2*2
3*99+2*2
speck
2014-02-05 21:10:51
2*2+3*99=301
2*2+3*99=301
sirknightingfail
2014-02-05 21:10:51
3*99+2*2=301
3*99+2*2=301
DrMath
2014-02-05 21:10:51
303-2=301C
303-2=301C
Pythonprogrammer
2014-02-05 21:10:51
(C) 301
(C) 301
copeland
2014-02-05 21:10:53
We have 101 total numbers on the list. We hit all of them three times except the first and last. Therefore the total is 99⋅3+2⋅2=301. The answer is (C).
We have 101 total numbers on the list. We hit all of them three times except the first and last. Therefore the total is 99⋅3+2⋅2=301. The answer is (C).
copeland
2014-02-05 21:10:59
Hm.
Hm.
copeland
2014-02-05 21:11:04
Does anybody know what time it is?
Does anybody know what time it is?
CornSaltButter
2014-02-05 21:11:25
The big one!!!!
The big one!!!!
brainiac1
2014-02-05 21:11:25
YAY One laft
YAY One laft
zohee
2014-02-05 21:11:25
Final problem time?
Final problem time?
DVA6102
2014-02-05 21:11:25
time for number 25
time for number 25
CornSaltButter
2014-02-05 21:11:25
adventure time
adventure time
copeland
2014-02-05 21:11:42
Yes. We're at 12-25. Let's have at it.
Yes. We're at 12-25. Let's have at it.
copeland
2014-02-05 21:11:43
25. The parabola P has focus (0,0) and goes through the points (4,3) and (−4,−3). For how many points (x,y)∈P with integer coordinates is it true that |4x+3y|≤1000?
peekaboo!
(A) 38(B) 40(C) 42(D) 44(E) 46
25. The parabola P has focus (0,0) and goes through the points (4,3) and (−4,−3). For how many points (x,y)∈P with integer coordinates is it true that |4x+3y|≤1000?
peekaboo!
(A) 38(B) 40(C) 42(D) 44(E) 46
copeland
2014-02-05 21:12:18
Alright, we're given the focus (0,0) and two points (4,3) and (−4,−3). Usually how many points do you need to describe a conic section?
Alright, we're given the focus (0,0) and two points (4,3) and (−4,−3). Usually how many points do you need to describe a conic section?
swe1
2014-02-05 21:12:50
5
5
DrMath
2014-02-05 21:12:50
5
5
brandbest1
2014-02-05 21:12:50
5
5
distortedwalrus
2014-02-05 21:12:50
5
5
quackman
2014-02-05 21:12:50
5
5
dantheman567
2014-02-05 21:12:50
FIVE!!!
FIVE!!!
copeland
2014-02-05 21:12:53
Usually you need 5 points to define a conic section. Well, at least when the points are on the conic.
Usually you need 5 points to define a conic section. Well, at least when the points are on the conic.
copeland
2014-02-05 21:12:55
That's what jumped out at me at first when I saw this problem. Something weird is definitely going on here. Let's just say we have no idea how many parabolas fit this description.
That's what jumped out at me at first when I saw this problem. Something weird is definitely going on here. Let's just say we have no idea how many parabolas fit this description.
copeland
2014-02-05 21:13:00
Incidentally, there are two things that we missed in our "three points" analysis. First is that we know it's a parabola: any 4 well-chosen points define exactly 2 parabolas.
Incidentally, there are two things that we missed in our "three points" analysis. First is that we know it's a parabola: any 4 well-chosen points define exactly 2 parabolas.
copeland
2014-02-05 21:13:11
Second, we're not just given random points - we're given a focus. It turns out that foci are just magicially twice as good as other points for defining a conic.
Second, we're not just given random points - we're given a focus. It turns out that foci are just magicially twice as good as other points for defining a conic.
copeland
2014-02-05 21:13:19
Now, none of what we just said is going to help us too much on this problem, but if you have all these ideas on-hand you can look at this problem and say to yourself, "Self, there are two parabolas here. That's not too scary and might come in handy. At least we need to hope that both parabolas give the same answer."
Now, none of what we just said is going to help us too much on this problem, but if you have all these ideas on-hand you can look at this problem and say to yourself, "Self, there are two parabolas here. That's not too scary and might come in handy. At least we need to hope that both parabolas give the same answer."
copeland
2014-02-05 21:13:34
Incidentally, I assume you don't know any of that stuff - it's a shame that nobody really teaches conics. It's really beautiful mathematics.
Incidentally, I assume you don't know any of that stuff - it's a shame that nobody really teaches conics. It's really beautiful mathematics.
copeland
2014-02-05 21:13:39
Let's get started.
Let's get started.
copeland
2014-02-05 21:13:49
What is the focus of a parabola? What is the pertinent definition for a parabola?
What is the focus of a parabola? What is the pertinent definition for a parabola?
blueferret
2014-02-05 21:14:51
identical distance between focus and a line, the directrix
identical distance between focus and a line, the directrix
dasobson
2014-02-05 21:14:51
equidistant from focus and directrix
equidistant from focus and directrix
LMA
2014-02-05 21:14:51
the set of points equidistant from the focus and the directrix
the set of points equidistant from the focus and the directrix
ws0414
2014-02-05 21:14:51
set of points equidistant from a point and a line
set of points equidistant from a point and a line
djmathman
2014-02-05 21:14:51
A parabola is the locus of points that are equidistant from the focus and a line called the directrix
A parabola is the locus of points that are equidistant from the focus and a line called the directrix
joshxiong
2014-02-05 21:14:51
A parabola is the set of points that are equidistant to a point (focus) and a line (directrix)
A parabola is the set of points that are equidistant to a point (focus) and a line (directrix)
alex31415
2014-02-05 21:14:51
Distance from any point to the focus is the same as distance to directrix
Distance from any point to the focus is the same as distance to directrix
richard4912
2014-02-05 21:14:51
Distance from any point on the parabola is equidistant from the focus and the directrix
Distance from any point on the parabola is equidistant from the focus and the directrix
math_posse
2014-02-05 21:14:51
Distance from focus and directrix is equal
Distance from focus and directrix is equal
hexagram
2014-02-05 21:14:51
same distance from directrix to focus
same distance from directrix to focus
copeland
2014-02-05 21:14:54
Given a point (the focus) and a line (the directrix) we can define a parabola as the locus of all points equidistant from the focus and the directrix.
Given a point (the focus) and a line (the directrix) we can define a parabola as the locus of all points equidistant from the focus and the directrix.
copeland
2014-02-05 21:15:06
I'm impressed.
I'm impressed.
copeland
2014-02-05 21:15:08
What do you notice about our three points?
What do you notice about our three points?
MSTang
2014-02-05 21:15:49
symmetric about origin
symmetric about origin
guilt
2014-02-05 21:15:49
collinear
collinear
dli00105
2014-02-05 21:15:49
collinear
collinear
mathwizard888
2014-02-05 21:15:49
collinear
collinear
DaChickenInc
2014-02-05 21:15:49
collinear
collinear
checkmate1021
2014-02-05 21:15:49
colinear
colinear
mathnerd101
2014-02-05 21:15:49
the 2 points are 5 units away from the focus
the 2 points are 5 units away from the focus
swe1
2014-02-05 21:15:49
They are symmetrical around the origin
They are symmetrical around the origin
checkmate1021
2014-02-05 21:15:49
collinear
collinear
willwin4sure
2014-02-05 21:15:49
all on the same line
all on the same line
hametm
2014-02-05 21:15:49
Origen and two points that have rotational symmetry
Origen and two points that have rotational symmetry
mssmath
2014-02-05 21:15:49
the midpoint is the origin
the midpoint is the origin
acegikmoqsuwy2000
2014-02-05 21:15:49
they are reflected about the origin?
they are reflected about the origin?
copeland
2014-02-05 21:15:52
These three points are collinear. I bet that's going to make things easier.
These three points are collinear. I bet that's going to make things easier.
copeland
2014-02-05 21:15:54
The focus is also the midpoint between the other two.
The focus is also the midpoint between the other two.
copeland
2014-02-05 21:15:56
What does that make the segment connecting A=(4,3) to B=(−4,−3)?
What does that make the segment connecting A=(4,3) to B=(−4,−3)?
ws0414
2014-02-05 21:16:19
the something...
the something...
copeland
2014-02-05 21:16:20
Exactly!
Exactly!
swe1
2014-02-05 21:16:33
latus rectum
latus rectum
joshxiong
2014-02-05 21:16:33
latus rectum
latus rectum
djmathman
2014-02-05 21:16:33
the latus rectum of the parabola
the latus rectum of the parabola
ingridzhang97
2014-02-05 21:16:33
the latus something
the latus something
storm7
2014-02-05 21:16:33
latus rectum
latus rectum
copeland
2014-02-05 21:16:37
That's the latus rectum of the parabola. A chord in a conic that is bisected by the focus is called a latus rectum. In a circle, diameters are latus recti. In a hyperbola or ellipse, there are two of these - one for each focus.
That's the latus rectum of the parabola. A chord in a conic that is bisected by the focus is called a latus rectum. In a circle, diameters are latus recti. In a hyperbola or ellipse, there are two of these - one for each focus.
copeland
2014-02-05 21:16:46
What do you know about the latus rectum that will probably be useful?
What do you know about the latus rectum that will probably be useful?
Tuxianeer
2014-02-05 21:17:25
parallel to the directrix
parallel to the directrix
ingridzhang97
2014-02-05 21:17:25
parallel to the directrix
parallel to the directrix
djmathman
2014-02-05 21:17:25
it's parallel to the directrix
it's parallel to the directrix
shandongboy
2014-02-05 21:17:25
parallel to directrix?
parallel to directrix?
DaChickenInc
2014-02-05 21:17:25
parallel to directrix?
parallel to directrix?
mathwizard888
2014-02-05 21:17:25
parallel to the directrix
parallel to the directrix
dantheman567
2014-02-05 21:17:25
parallel to the conic section directrix
parallel to the conic section directrix
1915933
2014-02-05 21:17:25
The latus rectum is always parallel to the directix.
The latus rectum is always parallel to the directix.
copeland
2014-02-05 21:17:28
The latus rectum is parallel to the directrix. Therefore we know the slope of the directrix. The latus rectum is also perpendicular to the axis of symmetry. Now we're on our way to being able to draw a really nice picture.
The latus rectum is parallel to the directrix. Therefore we know the slope of the directrix. The latus rectum is also perpendicular to the axis of symmetry. Now we're on our way to being able to draw a really nice picture.
copeland
2014-02-05 21:17:44
What else?
What else?
bradleyramunas
2014-02-05 21:18:15
1/4p
1/4p
dasobson
2014-02-05 21:18:15
equal to |4a|
equal to |4a|
DrMath
2014-02-05 21:18:15
its length is 4a or something like that
its length is 4a or something like that
trumpeter
2014-02-05 21:18:15
four times distance from focus to vertex
four times distance from focus to vertex
ws0414
2014-02-05 21:18:15
four times distance from focus to center of parabola
four times distance from focus to center of parabola
mikep
2014-02-05 21:18:15
its length is 4p
its length is 4p
joshualee2000
2014-02-05 21:18:15
4a?
4a?
copeland
2014-02-05 21:18:28
That's good. We will draw a picture to get that in a second.
That's good. We will draw a picture to get that in a second.
copeland
2014-02-05 21:18:34
What about the axis of symmetry?
What about the axis of symmetry?
Modest_Ked
2014-02-05 21:19:25
perpendicular
perpendicular
dasobson
2014-02-05 21:19:25
perpendicular and goes through the origin
perpendicular and goes through the origin
bacca2002
2014-02-05 21:19:25
it's perpendicular to the directrizx
it's perpendicular to the directrizx
CornSaltButter
2014-02-05 21:19:25
it's perpendicular to the axis of symmetry
it's perpendicular to the axis of symmetry
LMA
2014-02-05 21:19:25
it's perpindicular to the directrix/latus rectum
it's perpindicular to the directrix/latus rectum
ingridzhang97
2014-02-05 21:19:25
perpendicular to the latus rectum
perpendicular to the latus rectum
yvetal27
2014-02-05 21:19:25
the axis is perpendicular to the directx
the axis is perpendicular to the directx
jweisblat14
2014-02-05 21:19:25
perpendicular to the latus rectum, through the focus
perpendicular to the latus rectum, through the focus
copeland
2014-02-05 21:19:27
The axis of symmetry ought to be perpendicular to our segment.
The axis of symmetry ought to be perpendicular to our segment.
copeland
2014-02-05 21:19:37


copeland
2014-02-05 21:19:40
Here's our latus rectum.
Here's our latus rectum.
copeland
2014-02-05 21:19:43
How far is A=(4,3) from the directrix?
How far is A=(4,3) from the directrix?
mathtastic
2014-02-05 21:20:04
5
5
DaChickenInc
2014-02-05 21:20:04
5
5
DrMath
2014-02-05 21:20:04
5
5
bacca2002
2014-02-05 21:20:04
5.
5.
ksun48
2014-02-05 21:20:04
5
5
Allan Z
2014-02-05 21:20:04
5
5
viva
2014-02-05 21:20:04
5
5
copeland
2014-02-05 21:20:07
The point A is 5 units from the focus (0,0) so it is 5 units from the directrix.
The point A is 5 units from the focus (0,0) so it is 5 units from the directrix.
copeland
2014-02-05 21:20:13
How far is the focus from the directrix?
How far is the focus from the directrix?
dantheman567
2014-02-05 21:20:41
also 5?
also 5?
mathtastic
2014-02-05 21:20:41
again 5
again 5
awesomemathlete
2014-02-05 21:20:41
5
5
blueferret
2014-02-05 21:20:41
5
5
legozelda
2014-02-05 21:20:41
5
5
DVA6102
2014-02-05 21:20:41
5
5
copeland
2014-02-05 21:20:46
Since the directrix is parallel to the latus rectum and the line of symmetry of the diagram is perpendicular to the latus rectum, when we drop the altitudes from A and B to the directrix, we get a rectangle.
Since the directrix is parallel to the latus rectum and the line of symmetry of the diagram is perpendicular to the latus rectum, when we drop the altitudes from A and B to the directrix, we get a rectangle.
copeland
2014-02-05 21:20:55

copeland
2014-02-05 21:20:58
This is a 5×10 rectangle. The distance from the focus to the directrix is the height of this rectangle, 5. Now we can draw our parabola:
This is a 5×10 rectangle. The distance from the focus to the directrix is the height of this rectangle, 5. Now we can draw our parabola:
copeland
2014-02-05 21:21:05

copeland
2014-02-05 21:21:16
Notice that here is where we see our two parabolas. The directrix could be located either direction from the latus rectum.
Notice that here is where we see our two parabolas. The directrix could be located either direction from the latus rectum.
copeland
2014-02-05 21:21:21

copeland
2014-02-05 21:21:24
Let's just hope that the answer is independent of this choice.
Let's just hope that the answer is independent of this choice.
copeland
2014-02-05 21:21:26
First off, what is bad about this parabola?
First off, what is bad about this parabola?
blueferret
2014-02-05 21:22:13
its slanted
its slanted
dantheman567
2014-02-05 21:22:13
its slanted
its slanted
TheUnChosenOne
2014-02-05 21:22:13
tilted
tilted
Dragon6point1
2014-02-05 21:22:13
It's tilted.
It's tilted.
checkmate1021
2014-02-05 21:22:13
it is tilted
it is tilted
ScottBusche
2014-02-05 21:22:13
It's slanted.
It's slanted.
hametm
2014-02-05 21:22:13
It's axis of symmetry isn't parallel to an axis
It's axis of symmetry isn't parallel to an axis
flyrain
2014-02-05 21:22:13
it's not vertical or horizontal it is not a function
it's not vertical or horizontal it is not a function
copeland
2014-02-05 21:22:19
It's all wonky. It would be way better if it weren't. How can we fix it?
It's all wonky. It would be way better if it weren't. How can we fix it?
acegikmoqsuwy2000
2014-02-05 21:22:54
rotate it
rotate it
joshualee2000
2014-02-05 21:22:54
turn it
turn it
flyrain
2014-02-05 21:22:54
rotate the axis
rotate the axis
Pythonprogrammer
2014-02-05 21:22:54
rotation
rotation
blueferret
2014-02-05 21:22:54
tilt the axes?
tilt the axes?
quackman
2014-02-05 21:22:54
rotation
rotation
hametm
2014-02-05 21:22:54
Tilt the axis?
Tilt the axis?
distortedwalrus
2014-02-05 21:22:54
introduce a new coordinate system
introduce a new coordinate system
dli00105
2014-02-05 21:22:54
rotate it
rotate it
sirknightingfail
2014-02-05 21:22:54
rotate your axis
rotate your axis
copeland
2014-02-05 21:23:08
We could rotate the parabola or rotate the axes.
We could rotate the parabola or rotate the axes.
copeland
2014-02-05 21:23:34
It's morally the same. Since we actually care about x and y, let's introduce new coordinates and leave the parabola alone.
It's morally the same. Since we actually care about x and y, let's introduce new coordinates and leave the parabola alone.
copeland
2014-02-05 21:23:46
Let the u-axis go through A and B and let the v-axis be perpendicular to that through the focus.
Let the u-axis go through A and B and let the v-axis be perpendicular to that through the focus.
copeland
2014-02-05 21:23:51

copeland
2014-02-05 21:24:15
I want to come clean with you here. I'm morally obligated to pretend that this problem can be solved in a reasonable amount of time without using any linear algebra. I'll stick to that narrative, but I don't really believe it's possible. Anyway, let's keep going.
I want to come clean with you here. I'm morally obligated to pretend that this problem can be solved in a reasonable amount of time without using any linear algebra. I'll stick to that narrative, but I don't really believe it's possible. Anyway, let's keep going.
copeland
2014-02-05 21:24:29
What is the equation for the u-axis?
What is the equation for the u-axis?
joshxiong
2014-02-05 21:25:15
y = 3/4 x
y = 3/4 x
CornSaltButter
2014-02-05 21:25:15
y= 3x/4
y= 3x/4
blueferret
2014-02-05 21:25:15
y=3/4x
y=3/4x
simon1221
2014-02-05 21:25:15
y=-3/4x
y=-3/4x
distortedwalrus
2014-02-05 21:25:15
y=3/4x
y=3/4x
stonewater
2014-02-05 21:25:15
y=3/4x
y=3/4x
mathwizard888
2014-02-05 21:25:15
4y=3x
4y=3x
math_posse
2014-02-05 21:25:15
y=3/4x
y=3/4x
copeland
2014-02-05 21:25:18
The u-axis has slope of 34 and goes through the origin so its equation is y=34x. That looks better in standard form as 3x−4y=0.
The u-axis has slope of 34 and goes through the origin so its equation is y=34x. That looks better in standard form as 3x−4y=0.
copeland
2014-02-05 21:25:23
What is the equation for the v-axis?
What is the equation for the v-axis?
storm7
2014-02-05 21:25:58
y=-4/3x
y=-4/3x
dasobson
2014-02-05 21:25:58
y=-4x/3
y=-4x/3
Modest_Ked
2014-02-05 21:25:58
y=-4/3x
y=-4/3x
hametm
2014-02-05 21:25:58
4x+3y=0
4x+3y=0
blueferret
2014-02-05 21:25:58
3y+4x=0
3y+4x=0
az_phx_brandon_jiang
2014-02-05 21:25:58
4x+3y=0
4x+3y=0
joshualee2000
2014-02-05 21:25:58
4x+3y=0
4x+3y=0
stonewater
2014-02-05 21:25:58
4x+3y=0
4x+3y=0
storm7
2014-02-05 21:25:58
4x+3y=0
4x+3y=0
LMA
2014-02-05 21:25:58
y=-4/3x
y=-4/3x
bradleyramunas
2014-02-05 21:25:58
y=-4/3x
y=-4/3x
copeland
2014-02-05 21:26:00
The v-axis is perpendicular to the u-axis. It has slope −43 and goes through the origin. Its equation is 4x+3y=0.
The v-axis is perpendicular to the u-axis. It has slope −43 and goes through the origin. Its equation is 4x+3y=0.
copeland
2014-02-05 21:26:10
Incidentally, why is standard form useful in a problem like this?
Incidentally, why is standard form useful in a problem like this?
ingridzhang97
2014-02-05 21:27:08
to find distance between point and line and such
to find distance between point and line and such
qwertyu
2014-02-05 21:27:08
Can easily find distance
Can easily find distance
joshxiong
2014-02-05 21:27:08
distance formula for a point and a line
distance formula for a point and a line
copeland
2014-02-05 21:27:11
The distance formula from a point to a line needs the standard form.
The distance formula from a point to a line needs the standard form.
copeland
2014-02-05 21:27:13
Now the u-coordinate is the signed distance from the v-axis. What is the (u,v) coordinate for a point with coordinate (x,y) in our original frame?
Now the u-coordinate is the signed distance from the v-axis. What is the (u,v) coordinate for a point with coordinate (x,y) in our original frame?
copeland
2014-02-05 21:28:16
We need the distance from a point to a line. (Hopefully you remember the formula for the distance from a point to a line!)
We need the distance from a point to a line. (Hopefully you remember the formula for the distance from a point to a line!)
copeland
2014-02-05 21:28:39
What is the distance from (x,y) to the line 4x+3y=0?
What is the distance from (x,y) to the line 4x+3y=0?
mathbeida
2014-02-05 21:29:22
|4x+3y|/5
|4x+3y|/5
blueferret
2014-02-05 21:29:22
(4x+3y)/5
(4x+3y)/5
DrMath
2014-02-05 21:29:22
|4x+3y|/5
|4x+3y|/5
zhuangzhuang
2014-02-05 21:29:22
|4x+3y|/5
|4x+3y|/5
mikep
2014-02-05 21:29:22
abs(4x+3y)/5
abs(4x+3y)/5
ingridzhang97
2014-02-05 21:29:22
|4x+3y|/sqrt(4^2+3^2)
|4x+3y|/sqrt(4^2+3^2)
1915933
2014-02-05 21:29:22
(4x+3y)/5
(4x+3y)/5
mishai
2014-02-05 21:29:22
|4x+3y|/5
|4x+3y|/5
copeland
2014-02-05 21:29:26
The distance from (x,y) to 4x+3y=0 is |4x+3y|√32+42.Since we want a signed distance, we drop the absolute values and just get u=4x+3y5. This is positive in the first (x,y)-quadrant.
The distance from (x,y) to 4x+3y=0 is |4x+3y|√32+42.Since we want a signed distance, we drop the absolute values and just get u=4x+3y5. This is positive in the first (x,y)-quadrant.
copeland
2014-02-05 21:29:34
Likewise, the v-coordinate is the distance from (x,y) to the u-axis, −3x+4y5.I picked the sign here that is positive in the second (x,y)-quadrant.
Likewise, the v-coordinate is the distance from (x,y) to the u-axis, −3x+4y5.I picked the sign here that is positive in the second (x,y)-quadrant.
copeland
2014-02-05 21:29:44
u=4x+3y5,v=−3x+4y5.
u=4x+3y5,v=−3x+4y5.
copeland
2014-02-05 21:29:53
Look back at the problem. What tells us we're on the right track?
Look back at the problem. What tells us we're on the right track?
DVA6102
2014-02-05 21:30:42
the equation is |4x+3y|<=1000
the equation is |4x+3y|<=1000
zhuangzhuang
2014-02-05 21:30:42
the desired involves |4x+3y|
the desired involves |4x+3y|
ws0414
2014-02-05 21:30:42
the 4x+3y
the 4x+3y
infiniteturtle
2014-02-05 21:30:42
the 4x+3y part
the 4x+3y part
jweisblat14
2014-02-05 21:30:42
4x + 3y
4x + 3y
acegikmoqsuwy2000
2014-02-05 21:30:42
we have the |4x+3y| part
we have the |4x+3y| part
mathnerd101
2014-02-05 21:30:42
Theres a 4x+3y in the question?
Theres a 4x+3y in the question?
dli00105
2014-02-05 21:30:42
5|u|<=1000
5|u|<=1000
copeland
2014-02-05 21:30:44
One of our constraints is |4x+3y|≤1000. That is a multiple of u. We can divide by 5 and rewrite the constraint as
One of our constraints is |4x+3y|≤1000. That is a multiple of u. We can divide by 5 and rewrite the constraint as
copeland
2014-02-05 21:30:45
|u|≤200.
|u|≤200.
copeland
2014-02-05 21:31:08
We just want the lattice points between these two lines, u=−200 and u=200.
We just want the lattice points between these two lines, u=−200 and u=200.
copeland
2014-02-05 21:31:12
Alright, good. Now let's get an equation for the parabola in our u,v-coordinates. We have the distance definition for the parabola. What is the distance from the (u,v) to the focus?
Alright, good. Now let's get an equation for the parabola in our u,v-coordinates. We have the distance definition for the parabola. What is the distance from the (u,v) to the focus?
mishai
2014-02-05 21:32:02
sqrt(u^2+v^2)
sqrt(u^2+v^2)
brainiac1
2014-02-05 21:32:02
sqrt(u^2+v^2)
sqrt(u^2+v^2)
joshualee2000
2014-02-05 21:32:02
√(u2+v2)
√(u2+v2)
AkshajK
2014-02-05 21:32:02


copeland
2014-02-05 21:32:07
The distance is just √u2+v2. (Cool computation: check later that √u2+v2=√x2+y2. It's neat and helps to clarify the coordinates some.)
The distance is just √u2+v2. (Cool computation: check later that √u2+v2=√x2+y2. It's neat and helps to clarify the coordinates some.)
copeland
2014-02-05 21:32:12
Now we need the directrix. What do we know about it?
Now we need the directrix. What do we know about it?
copeland
2014-02-05 21:32:26
Specifically we need its equation.
Specifically we need its equation.
zhuangzhuang
2014-02-05 21:33:01
parallel to axis
parallel to axis
ingridzhang97
2014-02-05 21:33:01
parallel to the u-axis
parallel to the u-axis
LMA
2014-02-05 21:33:01
it's parallel to u
it's parallel to u
1915933
2014-02-05 21:33:01
It is parallel to the u-axis.
It is parallel to the u-axis.
ingridzhang97
2014-02-05 21:33:01
5 units below the u axis
5 units below the u axis
LMA
2014-02-05 21:33:01
v=-5
v=-5
hametm
2014-02-05 21:33:01
v=-5
v=-5
joshualee2000
2014-02-05 21:33:01
its equation is v=-5
its equation is v=-5
brainiac1
2014-02-05 21:33:01
it's 5 below the latus rectum
it's 5 below the latus rectum
DaChickenInc
2014-02-05 21:33:01
v=−5
v=−5
storm7
2014-02-05 21:33:01
v=-5
v=-5
copeland
2014-02-05 21:33:04
We know it's parallel to the u-axis, so its equation is v=something. We also know it is a distance of 5 from the focus, so it must be v=5 or v=−5. Let's pick v=−5 since that's the one we drew above.
We know it's parallel to the u-axis, so its equation is v=something. We also know it is a distance of 5 from the focus, so it must be v=5 or v=−5. Let's pick v=−5 since that's the one we drew above.
copeland
2014-02-05 21:33:05
What is the distance from (u,v) to the directrix?
What is the distance from (u,v) to the directrix?
blueferret
2014-02-05 21:34:42
v+5
v+5
mathwizard888
2014-02-05 21:34:42
|v+5|
|v+5|
DaChickenInc
2014-02-05 21:34:42
|v+5|
|v+5|
jweisblat14
2014-02-05 21:34:42
v+5
v+5
joshualee2000
2014-02-05 21:34:48
v+5
v+5
copeland
2014-02-05 21:34:50
The distance to the directrix is just |v+5|.
The distance to the directrix is just |v+5|.
copeland
2014-02-05 21:34:53
Therefore the equation for the parabola is √u2+v2=|v+5|.
Therefore the equation for the parabola is √u2+v2=|v+5|.
copeland
2014-02-05 21:34:56
That's ugly. . .
That's ugly. . .
DrMath
2014-02-05 21:35:14
square
square
awesomemath123
2014-02-05 21:35:14
square it
square it
dli00105
2014-02-05 21:35:14
square it
square it
WalkerTesla
2014-02-05 21:35:14
Square both sides
Square both sides
1915933
2014-02-05 21:35:14
Square both sides!
Square both sides!
prime235
2014-02-05 21:35:14
square both sides
square both sides
copeland
2014-02-05 21:35:18
If we square it we get u2+v2=(v+5)2.
If we square it we get u2+v2=(v+5)2.
copeland
2014-02-05 21:35:18
What happens when we simplify this?
What happens when we simplify this?
zhuangzhuang
2014-02-05 21:35:59
u^2=10v+25
u^2=10v+25
Tuxianeer
2014-02-05 21:35:59
u^2=10v+25
u^2=10v+25
mathtastic
2014-02-05 21:35:59
v^2 cancel
v^2 cancel
dasobson
2014-02-05 21:35:59
u^2-10v-25=0
u^2-10v-25=0
mathtastic
2014-02-05 21:35:59
u^2=10v+25
u^2=10v+25
nowunkie
2014-02-05 21:35:59
u^2+v^2=v^2+10v+25
u^2+v^2=v^2+10v+25
maxplanck
2014-02-05 21:35:59
u^2 = 10v + 25
u^2 = 10v + 25
prime235
2014-02-05 21:35:59
v^2 disappears!
v^2 disappears!
CornSaltButter
2014-02-05 21:35:59
u2−10v−25=0
u2−10v−25=0
nowunkie
2014-02-05 21:35:59
u^2=10v+25
u^2=10v+25
AkshajK
2014-02-05 21:35:59
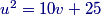
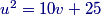
mikeli380
2014-02-05 21:35:59
$u^2=10v+25
$u^2=10v+25
checkmate1021
2014-02-05 21:35:59
u2−10v−25=0
u2−10v−25=0
copeland
2014-02-05 21:36:03
First we get u2+v2=v2+10v+25and then the v2 terms cancel giving us the parabola
First we get u2+v2=v2+10v+25and then the v2 terms cancel giving us the parabola
copeland
2014-02-05 21:36:04
u2=10v+25.
u2=10v+25.
copeland
2014-02-05 21:36:11
Gosh, that's pretty. That means we have the right coordinate system.
Gosh, that's pretty. That means we have the right coordinate system.
copeland
2014-02-05 21:36:14
Usually a parabola would have the squares of both coordinates. It's only when you pick the axis of symmetry as one of your coordinates that one of the squares drops away.
Usually a parabola would have the squares of both coordinates. It's only when you pick the axis of symmetry as one of your coordinates that one of the squares drops away.
copeland
2014-02-05 21:36:39
"to be parallel to one of the coordinate axes," I should have said.
"to be parallel to one of the coordinate axes," I should have said.
copeland
2014-02-05 21:36:41
Now it is time to go looking for our integer solutions. Remember, though, that u and v don't have to be integers. Just x and y. What should we do?
Now it is time to go looking for our integer solutions. Remember, though, that u and v don't have to be integers. Just x and y. What should we do?
blueferret
2014-02-05 21:37:27
substitute them back in
substitute them back in
dasobson
2014-02-05 21:37:27
write in terms of x and y maybe?
write in terms of x and y maybe?
mssmath
2014-02-05 21:37:27
convert back
convert back
ws0414
2014-02-05 21:37:27
convert back
convert back
hametm
2014-02-05 21:37:27
Plug in x and y
Plug in x and y
mishai
2014-02-05 21:37:27
u=(4x+3y)/5
u=(4x+3y)/5
checkmate1021
2014-02-05 21:37:27
use what we found for u and v in terms of x and y
use what we found for u and v in terms of x and y
copeland
2014-02-05 21:37:30
Let's rewrite the equation in terms of x and y. That gives(4x+3y5)2=10(−3x+4y5)+25.
Let's rewrite the equation in terms of x and y. That gives(4x+3y5)2=10(−3x+4y5)+25.
copeland
2014-02-05 21:37:34
What do you notice?
What do you notice?
copeland
2014-02-05 21:38:19
Specifically, we have some diophantine thing here.
Specifically, we have some diophantine thing here.
copeland
2014-02-05 21:38:34
We're looking for our integer solutions so we need to put our number theory hats on.
We're looking for our integer solutions so we need to put our number theory hats on.
distortedwalrus
2014-02-05 21:38:53
I don't own one of those.
I don't own one of those.
copeland
2014-02-05 21:38:56
Borrow one?
Borrow one?
copeland
2014-02-05 21:39:22
We want to talk about the integer solutions in x and y now. Say something that is like, "something something integer something."
We want to talk about the integer solutions in x and y now. Say something that is like, "something something integer something."
DVA6102
2014-02-05 21:40:27
because 5|10, RHS must be an integer, so LHS must be an integer as well
because 5|10, RHS must be an integer, so LHS must be an integer as well
copeland
2014-02-05 21:40:46
OK, what?
OK, what?
copeland
2014-02-05 21:41:03
What happens when we start plugging integers in for x and y?
What happens when we start plugging integers in for x and y?
blueferret
2014-02-05 21:41:30
both sides are integers!
both sides are integers!
Allan Z
2014-02-05 21:41:30
5|(4x+3y)
5|(4x+3y)
ilikepie333
2014-02-05 21:41:30
4x+3y is divisible by 5
4x+3y is divisible by 5
mishai
2014-02-05 21:41:30
4x+3y must be divisible by 5
4x+3y must be divisible by 5
ingridzhang97
2014-02-05 21:41:30
4x+3y must be divisible by 5
4x+3y must be divisible by 5
copeland
2014-02-05 21:41:46
v is not an integer. It has a 5 in the denominator.
v is not an integer. It has a 5 in the denominator.
copeland
2014-02-05 21:41:54
However, 10v is an integer. The right side of the equation is always an integer so the left side must be. That forces u to be an integer and specifically we know that 4x+3y≡0(mod5).
However, 10v is an integer. The right side of the equation is always an integer so the left side must be. That forces u to be an integer and specifically we know that 4x+3y≡0(mod5).
copeland
2014-02-05 21:42:21
There's a chance that says something about v also. Can we learn anything about −3x+4y now?
There's a chance that says something about v also. Can we learn anything about −3x+4y now?
bob12345678
2014-02-05 21:42:59
its also 0 in mod 5
its also 0 in mod 5
dli00105
2014-02-05 21:42:59
-3x+4y=0(mod5)
-3x+4y=0(mod5)
mathtastic
2014-02-05 21:42:59
yes it must also be congruent to 0 mod 5!!!
yes it must also be congruent to 0 mod 5!!!
tim9099xxzz
2014-02-05 21:42:59
Also divisble by 5
Also divisble by 5
copeland
2014-02-05 21:43:02
Why?
Why?
AkshajK
2014-02-05 21:43:29
multiply by 3 and take mod 5
multiply by 3 and take mod 5
nowunkie
2014-02-05 21:43:29
4y-3x has to be divisible by 5
4y-3x has to be divisible by 5
CornSaltButter
2014-02-05 21:43:29
2(-3x+4y), so 5 | 4y-3x
2(-3x+4y), so 5 | 4y-3x
copeland
2014-02-05 21:43:36
If we multiply 4x+3y≡0(mod5) by 3 we get 12x+9y≡0(mod5). That is equivalent to −3x+4y≡0(mod5).
If we multiply 4x+3y≡0(mod5) by 3 we get 12x+9y≡0(mod5). That is equivalent to −3x+4y≡0(mod5).
copeland
2014-02-05 21:43:55
There are other ways to get the same result. Like:
There are other ways to get the same result. Like:
DaChickenInc
2014-02-05 21:43:57
x≡3y(mod5)
x≡3y(mod5)
copeland
2014-02-05 21:44:04
And then grind through.
And then grind through.
copeland
2014-02-05 21:44:13
Specifically, though, we just learned that v is also an integer. Awesome.
Specifically, though, we just learned that v is also an integer. Awesome.
copeland
2014-02-05 21:44:20
Let's go back to the parabola,u2=10v+25. Now we know u and v are integers. However we notice that the right side is now divisible by 5. That makes the left side divisible by 5 and u is a multiple of 5.
Let's go back to the parabola,u2=10v+25. Now we know u and v are integers. However we notice that the right side is now divisible by 5. That makes the left side divisible by 5 and u is a multiple of 5.
copeland
2014-02-05 21:44:31
This forces u to be on the list −200,−195,−190,…,190,195,200. There are still 81 numbers in the list and that's not one of the possible answer choices so we need to keep going.
This forces u to be on the list −200,−195,−190,…,190,195,200. There are still 81 numbers in the list and that's not one of the possible answer choices so we need to keep going.
copeland
2014-02-05 21:44:37
What have we missed?
What have we missed?
copeland
2014-02-05 21:45:41
Here's a hint; the answers are all around 40. . . .
Here's a hint; the answers are all around 40. . . .
mathwizard888
2014-02-05 21:46:07
multiples of 10 don't work
multiples of 10 don't work
zhuangzhuang
2014-02-05 21:46:07
parity of v
parity of v
ABCDE
2014-02-05 21:46:07
odd multiple of 5
odd multiple of 5
pi37
2014-02-05 21:46:07
u is odd
u is odd
yangwy
2014-02-05 21:46:07
u must be odd
u must be odd
copeland
2014-02-05 21:46:34
Notice that 81 is about twice all of the possible answer choices. This implies that we may have missed a parity constraint. Indeed, the right side of the equation is always odd, so u has to be odd as well.
Notice that 81 is about twice all of the possible answer choices. This implies that we may have missed a parity constraint. Indeed, the right side of the equation is always odd, so u has to be odd as well.
copeland
2014-02-05 21:46:43
How many values of u does that leave?
How many values of u does that leave?
nowunkie
2014-02-05 21:47:20
40!
40!
MSTang
2014-02-05 21:47:20
40
40
LMA
2014-02-05 21:47:20
40
40
dli00105
2014-02-05 21:47:20
40
40
CornSaltButter
2014-02-05 21:47:20
40 values
40 values
mathwizard888
2014-02-05 21:47:20
40 (B)
40 (B)
Modest_Ked
2014-02-05 21:47:20
40
40
brainiac1
2014-02-05 21:47:20
40 values
40 values
bobthesmartypants
2014-02-05 21:47:20
40
40
CornSaltButter
2014-02-05 21:47:20
B!
B!
blueferret
2014-02-05 21:47:20
40
40
AkshajK
2014-02-05 21:47:20
40
40
dli00105
2014-02-05 21:47:20
(B)40
(B)40
WalkerTesla
2014-02-05 21:47:20
40
40
mathtastic
2014-02-05 21:47:20
40!!
40!!
ingridzhang97
2014-02-05 21:47:20
40
40
joshualee2000
2014-02-05 21:47:20
40
40
yangwy
2014-02-05 21:47:20
40
40
simon1221
2014-02-05 21:47:20
40
40
Acstar00
2014-02-05 21:47:20
40
40
distortedwalrus
2014-02-05 21:47:20
40
40
tfmtoto
2014-02-05 21:47:20
40
40
copeland
2014-02-05 21:47:22
That leaves −195,−185,−175,…,175,185,195. There are 40 numbers on this list. The answer must be (B).
That leaves −195,−185,−175,…,175,185,195. There are 40 numbers on this list. The answer must be (B).
copeland
2014-02-05 21:47:26
As upastanding, conscientious mathematicians, we really should check that we can get all of these. Notice for sure that u=±5 gives solutions since these are our points A and B.
As upastanding, conscientious mathematicians, we really should check that we can get all of these. Notice for sure that u=±5 gives solutions since these are our points A and B.
copeland
2014-02-05 21:47:34
As rushed and sleepy mathematicians, we probably ought to assume that we are right. Here's a nice compelling picture anyway:
As rushed and sleepy mathematicians, we probably ought to assume that we are right. Here's a nice compelling picture anyway:
copeland
2014-02-05 21:47:38

copeland
2014-02-05 21:47:49
Notice that we hit the lattice points A and B and these correspond to u=±5. We miss the u=0 point because the vertex has half-integer v=−25. Now the rest of the claim is that the solution set to some Diophantine equation corresponds to some arithmetic progression with these two points as consecutive terms. That feels very reasonable and natural to me.
Notice that we hit the lattice points A and B and these correspond to u=±5. We miss the u=0 point because the vertex has half-integer v=−25. Now the rest of the claim is that the solution set to some Diophantine equation corresponds to some arithmetic progression with these two points as consecutive terms. That feels very reasonable and natural to me.
copeland
2014-02-05 21:48:02
In the interest of time, I will leave it to you to figure out what x and y are in terms of u and v (the answer is pretty neat) and then prove that u=10n+5 forces x and y to be integers.
In the interest of time, I will leave it to you to figure out what x and y are in terms of u and v (the answer is pretty neat) and then prove that u=10n+5 forces x and y to be integers.
Tuxianeer
2014-02-05 21:48:39
upastanding
upastanding
copeland
2014-02-05 21:48:42
Indeed. We have upas on our farm as well.
Indeed. We have upas on our farm as well.
copeland
2014-02-05 21:48:52
They help with any legs problems that have sixes in them.
They help with any legs problems that have sixes in them.
copeland
2014-02-05 21:49:19
Alright, speaking of sleepy. Is anybody else exhausted?
Alright, speaking of sleepy. Is anybody else exhausted?
nowunkie
2014-02-05 21:49:52
yes
yes
Modest_Ked
2014-02-05 21:49:52
yes I have school tom
yes I have school tom
dli00105
2014-02-05 21:49:52
me!!
me!!
1915933
2014-02-05 21:49:52
Yes!
Yes!
bob12345678
2014-02-05 21:49:52
me i should be doing my science fair
me i should be doing my science fair
mishai
2014-02-05 21:49:52
I should be doing my homework right now.
I should be doing my homework right now.
david_sun
2014-02-05 21:49:52
no, math makes me energized
no, math makes me energized
copeland
2014-02-05 21:50:17
Well I'm getting tired and it's coming up on 7, so I think we should call it for the night.
Well I'm getting tired and it's coming up on 7, so I think we should call it for the night.
copeland
2014-02-05 21:50:23
Any questions before we go?
Any questions before we go?
copeland
2014-02-05 21:50:44
There WILL be a transcript for the Math Jam on the Math Jams transcripts page.
There WILL be a transcript for the Math Jam on the Math Jams transcripts page.
copeland
2014-02-05 21:51:09
I'll try to put that up in the next few minutes.
I'll try to put that up in the next few minutes.
Modest_Ked
2014-02-05 21:51:14
How do you type so fast?
How do you type so fast?
copeland
2014-02-05 21:51:18
I have two keyboards.
I have two keyboards.
simon1221
2014-02-05 21:51:40
and 4 arms
and 4 arms
copeland
2014-02-05 21:51:42
There are phenomenal discussions about the rest of the problems in our forum:
There are phenomenal discussions about the rest of the problems in our forum:
copeland
2014-02-05 21:51:56
That answers a large number of the questions that many of you have.
That answers a large number of the questions that many of you have.
DaChickenInc
2014-02-05 21:52:05
Should I look in the last 5 problems of every test to get bookkeeping problems?
Should I look in the last 5 problems of every test to get bookkeeping problems?
copeland
2014-02-05 21:52:20
You will seen lots of bookkeeping problems on the AMC.
You will seen lots of bookkeeping problems on the AMC.
copeland
2014-02-05 21:52:39
Practicing these is very useful and you can find them every year.
Practicing these is very useful and you can find them every year.
copeland
2014-02-05 21:52:51
The main trick is to write a lot of examples. Small cases. Etc.
The main trick is to write a lot of examples. Small cases. Etc.
copeland
2014-02-05 21:53:08
Be sure to test where things start and where they end so you don't get off-by-one errors.
Be sure to test where things start and where they end so you don't get off-by-one errors.
fz0718
2014-02-05 21:53:27
Should we make a real, tangible book of tricks?
Should we make a real, tangible book of tricks?
copeland
2014-02-05 21:53:29
Couldn't hurt.
Couldn't hurt.
mathtastic
2014-02-05 21:54:36
is mr rusczyk gonna make videos for the last few problems?
is mr rusczyk gonna make videos for the last few problems?
copeland
2014-02-05 21:54:38
Yes!
Yes!
copeland
2014-02-05 21:54:46
You can find videos for all of the problems we covered today on our videos page:
http://www.artofproblemsolving.com/Videos/index.php?type=amc
Richard chose some different tactics in his videos than we used today, so it might be worth checking them out.
You can find videos for all of the problems we covered today on our videos page:
http://www.artofproblemsolving.com/Videos/index.php?type=amc
Richard chose some different tactics in his videos than we used today, so it might be worth checking them out.
ws0414
2014-02-05 21:55:02
why called bookkeeping?
why called bookkeeping?
copeland
2014-02-05 21:55:07
Because it's fun to type.
Because it's fun to type.
copeland
2014-02-05 21:55:20
You know that bookkeeping is one of 3 words in the English language with 3 double letters?
You know that bookkeeping is one of 3 words in the English language with 3 double letters?
DrMath
2014-02-05 21:56:02
i clicked AMC 10B but nothing came up
i clicked AMC 10B but nothing came up
copeland
2014-02-05 21:56:11
You just jumped to that list on the page.
You just jumped to that list on the page.
copeland
2014-02-05 21:58:05
Alright, it looks like it's time to wind this down. thanks to everyone for coming to tonight's Math Jam.
Alright, it looks like it's time to wind this down. thanks to everyone for coming to tonight's Math Jam.
copeland
2014-02-05 21:58:16
I'm going to close the room here in a few moments.
I'm going to close the room here in a few moments.
copeland
2014-02-05 21:59:03
Please join us again on Thursday, February 20, when we will discuss the AMC 10B/12B contests and on again in March when we will be discussing the AIME I and II contests.
Please join us again on Thursday, February 20, when we will discuss the AMC 10B/12B contests and on again in March when we will be discussing the AIME I and II contests.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.









