2014 AMC 10/12 B Discussion
Go back to the Math Jam ArchiveA discussion of problems from the AMC 10/12 B, which is administered February 19. We will cover the last 5 problems on each test, as well as requested earlier problems on the tests.
Copyright © 2024 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Dave Patrick
DPatrick
2014-02-20 18:59:37
Welcome to the 2014 AMC 10B/12B Math Jam!
Welcome to the 2014 AMC 10B/12B Math Jam!
DPatrick
2014-02-20 18:59:47
I'm Dave Patrick, and I'll be leading our discussion tonight.
I'm Dave Patrick, and I'll be leading our discussion tonight.
DPatrick
2014-02-20 19:00:00
Before we get started I would like to take a moment to quickly explain our virtual classroom procedures to those who have not previously participated in a Math Jam or one of our online classes.
Before we get started I would like to take a moment to quickly explain our virtual classroom procedures to those who have not previously participated in a Math Jam or one of our online classes.
DPatrick
2014-02-20 19:00:08
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
DPatrick
2014-02-20 19:00:21
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
DPatrick
2014-02-20 19:00:39
There are a lot of students here! As I said, only (a fraction of the) well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
There are a lot of students here! As I said, only (a fraction of the) well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
DPatrick
2014-02-20 19:01:01
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
Also, we won't be going through the math quite as thoroughly as we do in our classes -- I can't teach all the prerequisite material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We usually do in our classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
DPatrick
2014-02-20 19:01:30
We have at least one teaching assistant here tonight to help out: Alyssa (aka baozhale).
We have at least one teaching assistant here tonight to help out: Alyssa (aka baozhale).
DPatrick
2014-02-20 19:01:46
I think a second TA is on her way, she may be running a little late.
I think a second TA is on her way, she may be running a little late.
copeland
2014-02-20 19:02:00
Alyssa is in her third years at URI. She is in the International Engineering Program for Mechanical Engineering and Chinese, which means that she learns how to be a mechanical engineer in Chinese as well as in English. She is also studying mathematics, and began in the masters program for that this fall. Alyssa wants to do research and teach, though she has not yet decided between mathematics and nanotechnology. Right now, she is helping teach math while doing nanotechnology research, which seems a reasonable compromise. In case anyone was wondering about the username, it's the pinyin (English spelling) of the Chinese word ``exploded\" (爆�,�了.)
Alyssa is in her third years at URI. She is in the International Engineering Program for Mechanical Engineering and Chinese, which means that she learns how to be a mechanical engineer in Chinese as well as in English. She is also studying mathematics, and began in the masters program for that this fall. Alyssa wants to do research and teach, though she has not yet decided between mathematics and nanotechnology. Right now, she is helping teach math while doing nanotechnology research, which seems a reasonable compromise. In case anyone was wondering about the username, it's the pinyin (English spelling) of the Chinese word ``exploded\" (爆�,�了.)
DPatrick
2014-02-20 19:02:14
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the incredibly large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the incredibly large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
DPatrick
2014-02-20 19:02:33
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.
Please also remember that the purpose of this Math Jam is to work through the solutions to AMC problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be posted.
thejet
2014-02-20 19:02:48
Hi baozhale (sorry don't really know who you are :/)
Hi baozhale (sorry don't really know who you are :/)
sojourner1
2014-02-20 19:02:48
你好爆炸了!
你好爆炸了!
DPatrick
2014-02-20 19:03:07
We will work the last 5 problems from the AMC 10B, then the last 5 problems from the AMC 12B. Two of these problems are the same, 10B Problem 25 and 12B Problem 22. We'll only solve that problem once.
We will work the last 5 problems from the AMC 10B, then the last 5 problems from the AMC 12B. Two of these problems are the same, 10B Problem 25 and 12B Problem 22. We'll only solve that problem once.
DPatrick
2014-02-20 19:03:31
Then we'll see how long we've been here -- we might do another problem or two if we're not all too tired.
Then we'll see how long we've been here -- we might do another problem or two if we're not all too tired.
DPatrick
2014-02-20 19:03:47
Let's get started with 10B Problem 21:
Let's get started with 10B Problem 21:
DPatrick
2014-02-20 19:03:55
21. Trapezoid $ABCD$ has parallel sides $\overline{AB}$ of length 33 and $\overline{CD}$ of length 21. The other two sides are of lengths 10 and 14. The angles at $A$ and $B$ are acute. What is the length of the shorter diagonal of $ABCD?$
$\phantom{10B:21}$
$\text{(A) } 10\sqrt6 \quad \text{(B) } 25 \quad \text{(C) } 8\sqrt{10} \quad \text{(D) } 18\sqrt2 \quad \text{(E) } 26$
21. Trapezoid $ABCD$ has parallel sides $\overline{AB}$ of length 33 and $\overline{CD}$ of length 21. The other two sides are of lengths 10 and 14. The angles at $A$ and $B$ are acute. What is the length of the shorter diagonal of $ABCD?$
$\phantom{10B:21}$
$\text{(A) } 10\sqrt6 \quad \text{(B) } 25 \quad \text{(C) } 8\sqrt{10} \quad \text{(D) } 18\sqrt2 \quad \text{(E) } 26$
DPatrick
2014-02-20 19:04:20
(You'll notice the current problem will always be posted to the top. You can resize that top region by dragging the horizontal bar that separates it from the main discussion window.)
(You'll notice the current problem will always be posted to the top. You can resize that top region by dragging the horizontal bar that separates it from the main discussion window.)
gkhsieh
2014-02-20 19:04:44
draw a picture
draw a picture
liuh008
2014-02-20 19:04:44
Draw a diagram;
Draw a diagram;
DrMath
2014-02-20 19:04:44
Diagram always!
Diagram always!
dli00105
2014-02-20 19:04:44
draw a picture!!
draw a picture!!
Wiggle Wam
2014-02-20 19:04:44
First draw a picture!!!
First draw a picture!!!
DPatrick
2014-02-20 19:04:52
Of course, we should draw a diagram:
Of course, we should draw a diagram:
DPatrick
2014-02-20 19:04:57
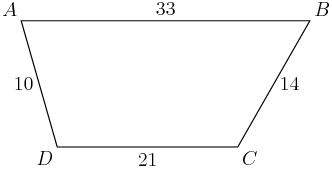
DPatrick
2014-02-20 19:05:03
Anything you think we should add to this diagram?
Anything you think we should add to this diagram?
mathbeida
2014-02-20 19:05:21
then drop two perpendicular line from C and D
then drop two perpendicular line from C and D
DivideBy0
2014-02-20 19:05:21
altitudes!
altitudes!
alex766
2014-02-20 19:05:21
heights from D and C?
heights from D and C?
math0127
2014-02-20 19:05:21
the heights from points c and d
the heights from points c and d
xXpapayaXx
2014-02-20 19:05:21
Draw altitudes
Draw altitudes
brandbest1
2014-02-20 19:05:21
Draw the heights of the trapezoid.
Draw the heights of the trapezoid.
Bomist0
2014-02-20 19:05:21
extra perpendicular lines from C and D to AB
extra perpendicular lines from C and D to AB
DPatrick
2014-02-20 19:05:27
Yes, the altitudes from $C$ and $D$ to $\overline{AB}$. I'll also label some unknown edges:
Yes, the altitudes from $C$ and $D$ to $\overline{AB}$. I'll also label some unknown edges:
DPatrick
2014-02-20 19:05:32
DPatrick
2014-02-20 19:05:46
Great -- what equations can we now write?
Great -- what equations can we now write?
tanuagg13
2014-02-20 19:06:03
pythagorean theorem to find a and b
pythagorean theorem to find a and b
SockFoot
2014-02-20 19:06:03
pythagorean theorem stuff
pythagorean theorem stuff
codyj
2014-02-20 19:06:03
pythagorean theorem
pythagorean theorem
DPatrick
2014-02-20 19:06:12
Yes, we have two equations given by the Pythagorean Theorem on the little triangles.
Yes, we have two equations given by the Pythagorean Theorem on the little triangles.
joshualee2000
2014-02-20 19:06:33
$a^2 + h^2 = 100$
$a^2 + h^2 = 100$
steve123456
2014-02-20 19:06:33
a^2+h^2=100 and b^2+h^2=196
a^2+h^2=100 and b^2+h^2=196
WOLFHEART
2014-02-20 19:06:33
a^2 + h^2 = 10^2
a^2 + h^2 = 10^2
joshualee2000
2014-02-20 19:06:33
$b^2 + h^2 = 196$
$b^2 + h^2 = 196$
ChenthuranA
2014-02-20 19:06:33
b^2+h^2=196
b^2+h^2=196
sparkles257
2014-02-20 19:06:33
b^2 + h^2 = 196
b^2 + h^2 = 196
DPatrick
2014-02-20 19:06:41
\begin{align*}
a^2 + h^2 &= 10^2, \\
b^2 + h^2 &= 14^2.
\end{align*}
\begin{align*}
a^2 + h^2 &= 10^2, \\
b^2 + h^2 &= 14^2.
\end{align*}
DivideBy0
2014-02-20 19:06:55
we know a+b=33-21=12
we know a+b=33-21=12
CreativeNinja
2014-02-20 19:06:55
a+b=12
a+b=12
2kev111
2014-02-20 19:06:55
a plus b equals 12
a plus b equals 12
oink
2014-02-20 19:06:55
a+b=12
a+b=12
ingridzhang97
2014-02-20 19:06:55
a+b=12
a+b=12
hotstuffFTW
2014-02-20 19:06:55
A + B = 12
A + B = 12
DPatrick
2014-02-20 19:07:00
We also have $a+b = 33-21 = 12$ from the length $AB$.
We also have $a+b = 33-21 = 12$ from the length $AB$.
DPatrick
2014-02-20 19:07:09
How do we use these equations?
How do we use these equations?
fprosk
2014-02-20 19:07:32
subtract the second equation from the first
subtract the second equation from the first
mathtastic
2014-02-20 19:07:32
subtract first from second and factor as (b-a)(b+a)
subtract first from second and factor as (b-a)(b+a)
mathawesomeness777
2014-02-20 19:07:32
Subtract the two top equations?
Subtract the two top equations?
harvey2014
2014-02-20 19:07:32
b^2-a^2
b^2-a^2
syrup827
2014-02-20 19:07:32
subtract out h^2
subtract out h^2
DPatrick
2014-02-20 19:07:53
There are lots of ways to proceed. I like equating the two expressions for $h^2$ from the two Pythagorean equations.
There are lots of ways to proceed. I like equating the two expressions for $h^2$ from the two Pythagorean equations.
DPatrick
2014-02-20 19:08:05
(Which is really the same thing as subtracting them to cancel the $h^2$ term.)
(Which is really the same thing as subtracting them to cancel the $h^2$ term.)
DPatrick
2014-02-20 19:08:17
Equating $h^2$ in our Pythagorean expressions gives us $100 - a^2 = 196 - b^2.$ So we have $b^2 - a^2 = 96.$
Equating $h^2$ in our Pythagorean expressions gives us $100 - a^2 = 196 - b^2.$ So we have $b^2 - a^2 = 96.$
DaChickenInc
2014-02-20 19:08:37
b-a=8
b-a=8
yajaniaj
2014-02-20 19:08:37
$12(b-a)=96$
$12(b-a)=96$
brandbest1
2014-02-20 19:08:37
difference of two squares
difference of two squares
Bomist0
2014-02-20 19:08:37
difference of squares
difference of squares
IsabeltheCat
2014-02-20 19:08:37
b-a=8
b-a=8
Eudokia
2014-02-20 19:08:37
divide by b+a
divide by b+a
aaa16797
2014-02-20 19:08:37
you can write it in (b-a)(b+a)
you can write it in (b-a)(b+a)
DPatrick
2014-02-20 19:08:47
Aha! Dividing this by $a+b = 12$ gives us $b-a = 96/12 = 8.$
Aha! Dividing this by $a+b = 12$ gives us $b-a = 96/12 = 8.$
ahaanomegas
2014-02-20 19:09:14
Therefore, a = 2, b = 10.
Therefore, a = 2, b = 10.
rraj411
2014-02-20 19:09:14
2 eqn 2 variable
2 eqn 2 variable
dli00105
2014-02-20 19:09:14
a=2 and b=10
a=2 and b=10
abishek99
2014-02-20 19:09:14
a=2, b=10
a=2, b=10
WalkerTesla
2014-02-20 19:09:14
b= 10, a=2
b= 10, a=2
sojourner1
2014-02-20 19:09:14
2b is 20, b=10, a = 2
2b is 20, b=10, a = 2
DPatrick
2014-02-20 19:09:23
Right, now we have the simple system $a+b = 12$ and $b-a = 8$, which solves to give $b = 10$ and $a= 2.$
Right, now we have the simple system $a+b = 12$ and $b-a = 8$, which solves to give $b = 10$ and $a= 2.$
DPatrick
2014-02-20 19:09:33
And so what is $h$?
And so what is $h$?
mathmaster2012
2014-02-20 19:09:49
ws5188
2014-02-20 19:09:49
4sqrt6
4sqrt6
ahaanomegas
2014-02-20 19:09:49
sqrt(96)
sqrt(96)
mathmaster2012
2014-02-20 19:09:49
LightningX48
2014-02-20 19:09:49
4sqrt6
4sqrt6
acegikmoqsuwy2000
2014-02-20 19:09:49
sqrt96?
sqrt96?
DPatrick
2014-02-20 19:09:53
We have $h^2 = 100-a^2 = 100-4 = 96,$ so $h = \sqrt{96}.$
We have $h^2 = 100-a^2 = 100-4 = 96,$ so $h = \sqrt{96}.$
DPatrick
2014-02-20 19:10:11
Here's the updated picture with the lengths filled in:
Here's the updated picture with the lengths filled in:
DPatrick
2014-02-20 19:10:21
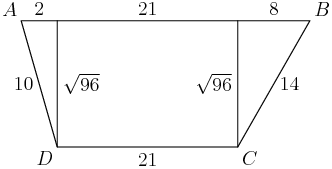
DPatrick
2014-02-20 19:10:28
Great -- how do we finish from here?
Great -- how do we finish from here?
iguana123
2014-02-20 19:10:52
AC is the shorter diagonal
AC is the shorter diagonal
flyrain
2014-02-20 19:10:52
draw the shorter diagonal
draw the shorter diagonal
joshxiong
2014-02-20 19:10:52
Clearly AC is shorter
Clearly AC is shorter
guilt
2014-02-20 19:10:52
find AC using pythagorean theorem
find AC using pythagorean theorem
johnguolex
2014-02-20 19:10:52
draw AC and use pythag to figure out the length
draw AC and use pythag to figure out the length
masalvada12
2014-02-20 19:10:52
draw in diagonals
draw in diagonals
blueferret
2014-02-20 19:10:52
pythagorean theorem with 23 and sqrt(96)
pythagorean theorem with 23 and sqrt(96)
DPatrick
2014-02-20 19:11:01
Right. We want the length $AC,$ which we can get from the right triangle below:
Right. We want the length $AC,$ which we can get from the right triangle below:
DPatrick
2014-02-20 19:11:05
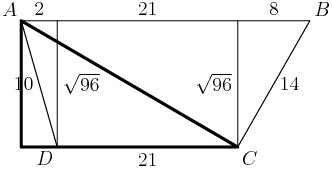
DPatrick
2014-02-20 19:11:17
This triangle has height $h=\sqrt{96}$ and length $21+a = 21+2 = 23.$
This triangle has height $h=\sqrt{96}$ and length $21+a = 21+2 = 23.$
wehac
2014-02-20 19:11:33
23^2+96=625. So the answer is B) 25
23^2+96=625. So the answer is B) 25
summitwei
2014-02-20 19:11:33
AC=25
AC=25
hesa57
2014-02-20 19:11:33
96+23^2=x^2
96+23^2=x^2
ajoy
2014-02-20 19:11:33
23^2 + 96 = 625. so the square root of that is 25!
23^2 + 96 = 625. so the square root of that is 25!
blueberry7
2014-02-20 19:11:33
so AC=25
so AC=25
DPatrick
2014-02-20 19:11:47
Its hypotenuse is \[\sqrt{(\sqrt{96})^2 + 23^2} = \sqrt{96 + 529} = \sqrt{625}.\]
Its hypotenuse is \[\sqrt{(\sqrt{96})^2 + 23^2} = \sqrt{96 + 529} = \sqrt{625}.\]
DPatrick
2014-02-20 19:11:51
This is 25, so the answer is (B).
This is 25, so the answer is (B).
ingridzhang97
2014-02-20 19:11:54
wasn't b=10? not 8
wasn't b=10? not 8
DPatrick
2014-02-20 19:12:12
Oops, you're right. That "8" should be a "10" in the last two pictures.
Oops, you're right. That "8" should be a "10" in the last two pictures.
DPatrick
2014-02-20 19:12:19
Fortunately we didn't use it!
Fortunately we didn't use it!
DPatrick
2014-02-20 19:12:34
On to 10B Problem #22:
On to 10B Problem #22:
DPatrick
2014-02-20 19:12:38
22. Eight semicircles line the inside of a square with side length 2 as shown. What is the radius of the circle tangent to all of these semicircles?
$\phantom{10B:22}$
$\text{(A) } \dfrac{1+\sqrt2}4 \quad \text{(B) } \dfrac{\sqrt5-1}2 \quad \text{(C) } \dfrac{\sqrt3+1}4 \quad \text{(D) } \dfrac{2\sqrt3}5 \quad \text{(E) } \dfrac{\sqrt5}3$
22. Eight semicircles line the inside of a square with side length 2 as shown. What is the radius of the circle tangent to all of these semicircles?
$\phantom{10B:22}$
$\text{(A) } \dfrac{1+\sqrt2}4 \quad \text{(B) } \dfrac{\sqrt5-1}2 \quad \text{(C) } \dfrac{\sqrt3+1}4 \quad \text{(D) } \dfrac{2\sqrt3}5 \quad \text{(E) } \dfrac{\sqrt5}3$
DPatrick
2014-02-20 19:12:43
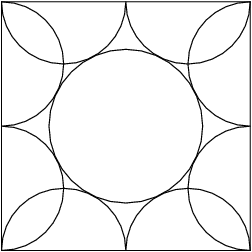
DPatrick
2014-02-20 19:12:59
What segment is begging to be added to the picture?
What segment is begging to be added to the picture?
nsd
2014-02-20 19:13:35
draw from center of semicircle to center of circle.
draw from center of semicircle to center of circle.
Darn
2014-02-20 19:13:35
Connect the center of the circle to the edge of the square
Connect the center of the circle to the edge of the square
CreativeNinja
2014-02-20 19:13:35
a line going through the point of tangency
a line going through the point of tangency
sparkles257
2014-02-20 19:13:35
the segment from center to midpt of side
the segment from center to midpt of side
starwars123
2014-02-20 19:13:35
the segment from the center to the edge of the square
the segment from the center to the edge of the square
fprosk
2014-02-20 19:13:35
center of circle to edge of quare
center of circle to edge of quare
briantix
2014-02-20 19:13:35
the centers of the circles
the centers of the circles
mathbeida
2014-02-20 19:13:35
connect the center of the circle to a semicirle center
connect the center of the circle to a semicirle center
DPatrick
2014-02-20 19:13:51
Right, arguably there are two segments begging to be added.
Right, arguably there are two segments begging to be added.
DPatrick
2014-02-20 19:13:57
Whenever we have tangent circles, it's almost always helpful to draw the segment that connects the centers of the circles, which also passes through the point of tangency. So let's draw it:
Whenever we have tangent circles, it's almost always helpful to draw the segment that connects the centers of the circles, which also passes through the point of tangency. So let's draw it:
DPatrick
2014-02-20 19:14:03
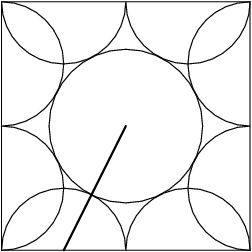
DPatrick
2014-02-20 19:14:25
And, there's a right triangle if we draw the segment from the center of the big circle straight down to the bottom base. I'll also label the edges that we know:
And, there's a right triangle if we draw the segment from the center of the big circle straight down to the bottom base. I'll also label the edges that we know:
DPatrick
2014-02-20 19:14:32
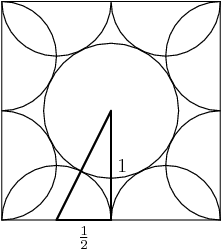
DPatrick
2014-02-20 19:14:45
And now what do we have?
And now what do we have?
DaChickenInc
2014-02-20 19:15:00
right triangle w/ side lengths 1/2, 1, 1/2+r=$\sqrt{5}/2$
right triangle w/ side lengths 1/2, 1, 1/2+r=$\sqrt{5}/2$
DrMath
2014-02-20 19:15:00
so hypotenuse is 1/2 root 5
so hypotenuse is 1/2 root 5
Darn
2014-02-20 19:15:00
Hypotenuse is sqrt5/2
Hypotenuse is sqrt5/2
joshualee2000
2014-02-20 19:15:00
so the hypotenuse is $\sqrt{5}/2$
so the hypotenuse is $\sqrt{5}/2$
DPatrick
2014-02-20 19:15:27
On the one hand, by the Pythagorean Theorem, the hypotenuse of that right triangle is $\sqrt{1^2 + \left(\frac12\right)^2} = \sqrt{\frac54} = \frac{\sqrt5}{2}.$
On the one hand, by the Pythagorean Theorem, the hypotenuse of that right triangle is $\sqrt{1^2 + \left(\frac12\right)^2} = \sqrt{\frac54} = \frac{\sqrt5}{2}.$
DPatrick
2014-02-20 19:15:43
(You might recognize a 1-2-$\sqrt5$ right triangle, and this one is half that size.)
(You might recognize a 1-2-$\sqrt5$ right triangle, and this one is half that size.)
johnguolex
2014-02-20 19:16:04
a right triangle!
a right triangle!
MATHCOUNTSmath
2014-02-20 19:16:04
and subtract 1/2
and subtract 1/2
pkbehl
2014-02-20 19:16:04
the radius of the semicircle is 1/2 so we subtract
the radius of the semicircle is 1/2 so we subtract
alex766
2014-02-20 19:16:04
then you have to subtract 1/2 for the radius of the smaller circle
then you have to subtract 1/2 for the radius of the smaller circle
DPatrick
2014-02-20 19:16:19
Right, on the other hand, it's $\frac12 + r$, where $r$ is the radius of the big circle.
Right, on the other hand, it's $\frac12 + r$, where $r$ is the radius of the big circle.
hexagram
2014-02-20 19:16:32
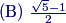
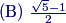
mathmaster2012
2014-02-20 19:16:32
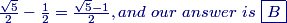
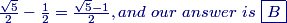
19CindyW
2014-02-20 19:16:34
so the radius of the circle is sqrt(5)-1/2
so the radius of the circle is sqrt(5)-1/2
cnnwy1282
2014-02-20 19:16:38
Subtracting the radius of the semicircle, we get (sqrt5-1)/2
Subtracting the radius of the semicircle, we get (sqrt5-1)/2
DPatrick
2014-02-20 19:16:46
Yep: $r = \frac{\sqrt5}{2}-\frac12 = \frac{\sqrt5-1}{2},$ answer (B).
Yep: $r = \frac{\sqrt5}{2}-\frac12 = \frac{\sqrt5-1}{2},$ answer (B).
DPatrick
2014-02-20 19:17:18
That problem was probably the easiest of all the problems we'll do tonight.
That problem was probably the easiest of all the problems we'll do tonight.
DPatrick
2014-02-20 19:17:32
On to 10B #23, which is also 12B #19:
On to 10B #23, which is also 12B #19:
DPatrick
2014-02-20 19:17:38
23. A sphere is inscribed in a truncated right circular cone as shown. The volume of the truncated cone is twice that of the sphere. What is the ratio of the radius of the bottom base of the truncated cone to the radius of the top base of the truncated cone?
$\phantom{10B:23}$
$\text{(A) } \dfrac32 \quad \text{(B) } \dfrac{1+\sqrt5}2 \quad \text{(C) } \sqrt3 \quad \text{(D) } 2 \quad \text{(E) } \dfrac{3+\sqrt5}2$
23. A sphere is inscribed in a truncated right circular cone as shown. The volume of the truncated cone is twice that of the sphere. What is the ratio of the radius of the bottom base of the truncated cone to the radius of the top base of the truncated cone?
$\phantom{10B:23}$
$\text{(A) } \dfrac32 \quad \text{(B) } \dfrac{1+\sqrt5}2 \quad \text{(C) } \sqrt3 \quad \text{(D) } 2 \quad \text{(E) } \dfrac{3+\sqrt5}2$
DPatrick
2014-02-20 19:17:46
DPatrick
2014-02-20 19:17:58
(copeland did the diagram!)
(copeland did the diagram!)
dli00105
2014-02-20 19:18:34
cross section
cross section
Nahmid
2014-02-20 19:18:34
take a 2-d cross section!
take a 2-d cross section!
DPatrick
2014-02-20 19:18:41
Indeed, like many 3D geometry problems, it's really a 2D problem in disguise.
Indeed, like many 3D geometry problems, it's really a 2D problem in disguise.
DPatrick
2014-02-20 19:18:46
We can look at a cross-section of the object sliced down the middle:
We can look at a cross-section of the object sliced down the middle:
DPatrick
2014-02-20 19:18:53
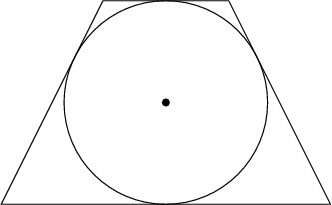
DPatrick
2014-02-20 19:19:04
We might find it helpful to assign variables to the lengths. How can we do that?
We might find it helpful to assign variables to the lengths. How can we do that?
brandbest1
2014-02-20 19:19:39
let the top radius be 1, then let the radius be r
let the top radius be 1, then let the radius be r
mapletree14
2014-02-20 19:19:39
Let the top have length 1, we can assume this WLOG.
Let the top have length 1, we can assume this WLOG.
Nahmid
2014-02-20 19:19:39
let the radius of the top be 1, the bottom be R
let the radius of the top be 1, the bottom be R
WalkerTesla
2014-02-20 19:19:39
We can let the top radius be 1 and solve for the bottom radius
We can let the top radius be 1 and solve for the bottom radius
DPatrick
2014-02-20 19:19:47
I like this idea. Since we the data that we care about (the ratio of the volumes that we're given, and the ratio of the radii that we want), we have a little flexibility in assign variables to lengths -- we can pick one length to be 1 if we want, for convenience.
I like this idea. Since we the data that we care about (the ratio of the volumes that we're given, and the ratio of the radii that we want), we have a little flexibility in assign variables to lengths -- we can pick one length to be 1 if we want, for convenience.
DPatrick
2014-02-20 19:20:00
And since the answer we want is (radius of bottom face)/(radius of top face), it seems likely that things may turn out nice if we make the radius of the top face equal to 1, so that our answer is just the radius of the bottom face.
And since the answer we want is (radius of bottom face)/(radius of top face), it seems likely that things may turn out nice if we make the radius of the top face equal to 1, so that our answer is just the radius of the bottom face.
DPatrick
2014-02-20 19:20:17
So let's let the radius of the top face be 1 and the radius of the bottom face be $r$. (Again, note that our final answer will be just $r.$) Let's also call the radius of the sphere $s.$
So let's let the radius of the top face be 1 and the radius of the bottom face be $r$. (Again, note that our final answer will be just $r.$) Let's also call the radius of the sphere $s.$
DPatrick
2014-02-20 19:20:23
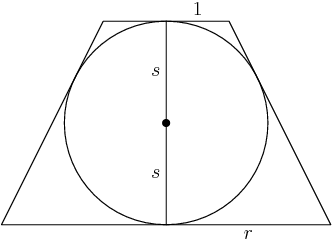
DPatrick
2014-02-20 19:20:35
Can we relate $r$ and $s$?
Can we relate $r$ and $s$?
acegikmoqsuwy2000
2014-02-20 19:20:59
pythegorean theorem
pythegorean theorem
joshxiong
2014-02-20 19:20:59
Use the pythagorean theorem
Use the pythagorean theorem
Arcmage101
2014-02-20 19:20:59
pythagorean theorem
pythagorean theorem
hwl0304
2014-02-20 19:20:59
pythagorean theorem??
pythagorean theorem??
fireonice18
2014-02-20 19:20:59
pythagorean theorem
pythagorean theorem
DPatrick
2014-02-20 19:21:07
How? I don't see a right triangle anywhere...
How? I don't see a right triangle anywhere...
SockFoot
2014-02-20 19:21:30
make on
make on
SirNinja
2014-02-20 19:21:30
draw one
draw one
guilt
2014-02-20 19:21:30
draw the altitude
draw the altitude
NikhilP
2014-02-20 19:21:30
draw one
draw one
awesomethree
2014-02-20 19:21:30
draw it
draw it
brandbest1
2014-02-20 19:21:30
drop an altitude from the top vertex
drop an altitude from the top vertex
medianpi
2014-02-20 19:21:30
make one
make one
abishek99
2014-02-20 19:21:30
drop an altitiude
drop an altitiude
DPatrick
2014-02-20 19:21:43
Sure, if we need a right triangle, there's no law that says we can't just go ahead and make one!
Sure, if we need a right triangle, there's no law that says we can't just go ahead and make one!
DPatrick
2014-02-20 19:21:47
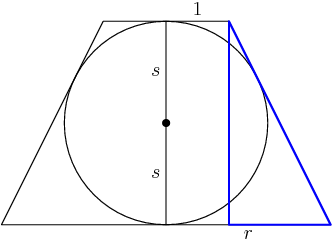
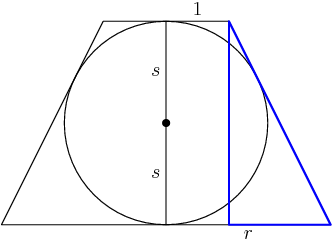
DPatrick
2014-02-20 19:22:07
It has legs $2s$ and $r-1$. But don't we also know its hypotenuse?
It has legs $2s$ and $r-1$. But don't we also know its hypotenuse?
blueferret
2014-02-20 19:22:32
1+r
1+r
sophiazhi
2014-02-20 19:22:32
1+r
1+r
DaChickenInc
2014-02-20 19:22:32
1+r by equal tangents
1+r by equal tangents
urmilla
2014-02-20 19:22:32
r+1
r+1
fdas
2014-02-20 19:22:32
r+1
r+1
blueferret
2014-02-20 19:22:32
the hypotenuse is 1+r
the hypotenuse is 1+r
Nahmid
2014-02-20 19:22:37
the tangents to a circle are equivalent, so the hyp is r+1
the tangents to a circle are equivalent, so the hyp is r+1
brandbest1
2014-02-20 19:22:37
by the two tangent theorem, the two segments of the hyp have length r and 1, so it's length is r+1
by the two tangent theorem, the two segments of the hyp have length r and 1, so it's length is r+1
DPatrick
2014-02-20 19:22:51
Right! It's clearer if we add the point of tangency from the circle to the hypotenuse...
Right! It's clearer if we add the point of tangency from the circle to the hypotenuse...
DPatrick
2014-02-20 19:22:56
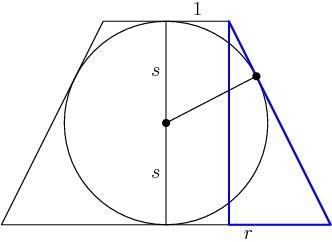
DPatrick
2014-02-20 19:23:06
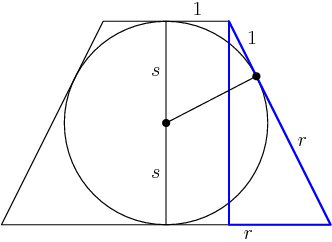
The distances from a point outside a circle to its two corresponding points of tangency are equal:
The distances from a point outside a circle to its two corresponding points of tangency are equal:
DPatrick
2014-02-20 19:23:14
DPatrick
2014-02-20 19:23:21
So the blue triangle has hypotenuse $r+1$.
So the blue triangle has hypotenuse $r+1$.
SirNinja
2014-02-20 19:23:37
(2s)^2+(r-1)^2=(r+1)^2
(2s)^2+(r-1)^2=(r+1)^2
hjl00
2014-02-20 19:23:37
pythagrean theorem
pythagrean theorem
DPatrick
2014-02-20 19:23:42
Therefore by the Pythagorean Theorem we have \[(2s)^2 + (r-1)^2 = (r+1)^2.\]
Therefore by the Pythagorean Theorem we have \[(2s)^2 + (r-1)^2 = (r+1)^2.\]
Eudokia
2014-02-20 19:24:10
s^2=r
s^2=r
parley999
2014-02-20 19:24:10
s^2=r
s^2=r
joshualee2000
2014-02-20 19:24:10
so s^2 = r
so s^2 = r
dli00105
2014-02-20 19:24:10
which simplifies to s^2=r
which simplifies to s^2=r
LightningX48
2014-02-20 19:24:10
s^2 = r
s^2 = r
DPatrick
2014-02-20 19:24:17
Right: expanding this out gives \[4s^2 + r^2 - 2r + 1 = r^2 + 2r + 1,\]
so $4s^2 = 4r,$ hence $r = s^2.$
Right: expanding this out gives \[4s^2 + r^2 - 2r + 1 = r^2 + 2r + 1,\]
so $4s^2 = 4r,$ hence $r = s^2.$
DPatrick
2014-02-20 19:24:35
OK, let's file $r=s^2$ away for now.
OK, let's file $r=s^2$ away for now.
rraj411
2014-02-20 19:24:42
volume relation now
volume relation now
DPatrick
2014-02-20 19:24:52
Right. We know that the volume of the sphere is $\frac43\pi s^3.$
Right. We know that the volume of the sphere is $\frac43\pi s^3.$
DPatrick
2014-02-20 19:25:00
Therefore the volume of the frustum (the truncated cone) is twice that, or $\frac83\pi s^3.$
Therefore the volume of the frustum (the truncated cone) is twice that, or $\frac83\pi s^3.$
DPatrick
2014-02-20 19:25:05
How do we compute the volume of the frustum in terms of its bases and its height?
How do we compute the volume of the frustum in terms of its bases and its height?
ingridzhang97
2014-02-20 19:25:38
extend the two sides of the "trapezoid" to meet at a point
extend the two sides of the "trapezoid" to meet at a point
Nahmid
2014-02-20 19:25:38
a bigger cone minus a smaller one
a bigger cone minus a smaller one
blueferret
2014-02-20 19:25:38
big cone minus little cone?
big cone minus little cone?
alex31415
2014-02-20 19:25:38
add a "top" and subtract
add a "top" and subtract
DrMath
2014-02-20 19:25:38
volume of total-chopped off pary
volume of total-chopped off pary
tanishq1
2014-02-20 19:25:38
draw the missing pyramid on top
draw the missing pyramid on top
AlcumusGuy
2014-02-20 19:25:38
volume of large cone minus volume of chopped off cone
volume of large cone minus volume of chopped off cone
DPatrick
2014-02-20 19:25:45
Many solutions I've seen, at this point, magically use the "formula" for volume of a right circular frustum. I suspect that most of you, like me, don't know this formula. Fortunately, it's not that hard to determine the volume of a frustum.
Many solutions I've seen, at this point, magically use the "formula" for volume of a right circular frustum. I suspect that most of you, like me, don't know this formula. Fortunately, it's not that hard to determine the volume of a frustum.
DPatrick
2014-02-20 19:25:55
We can "untruncate" it and draw the original cone:
We can "untruncate" it and draw the original cone:
DPatrick
2014-02-20 19:26:00
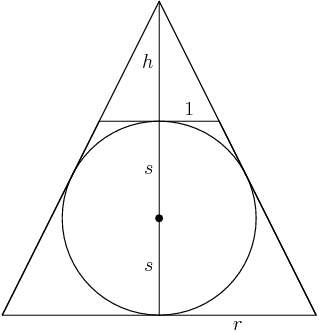
DPatrick
2014-02-20 19:26:14
I've labeled the additional height as $h$ -- how can we compute $h$ in terms of $r$ and/or $s$?
I've labeled the additional height as $h$ -- how can we compute $h$ in terms of $r$ and/or $s$?
mathbeida
2014-02-20 19:26:31
h/(h+2s) = 1/r
h/(h+2s) = 1/r
VD8M9
2014-02-20 19:26:31
similar triangles
similar triangles
MathStudent2002
2014-02-20 19:26:31
similar triangles!
similar triangles!
pl210741
2014-02-20 19:26:31
Similar triangles
Similar triangles
geogirl08
2014-02-20 19:26:31
similarity
similarity
nuggetfan
2014-02-20 19:26:31
similar triangles!!!
similar triangles!!!
iguana123
2014-02-20 19:26:31
similar triangles!
similar triangles!
DPatrick
2014-02-20 19:26:38
Yes! By similar triangles, we know that \[\frac{h}{1} = \frac{h+2s}{r}.\]
Yes! By similar triangles, we know that \[\frac{h}{1} = \frac{h+2s}{r}.\]
DaChickenInc
2014-02-20 19:26:50
by similarity, $h=\frac{2s}{r-1}$
by similarity, $h=\frac{2s}{r-1}$
DPatrick
2014-02-20 19:27:00
Indeed, this simplifies to $rh = h+2s$, and hence $h = \dfrac{2s}{r-1}.$
Indeed, this simplifies to $rh = h+2s$, and hence $h = \dfrac{2s}{r-1}.$
DPatrick
2014-02-20 19:27:16
So the volume of the frustum is the volume of the entire cone minus the volume of the little cone on top.
So the volume of the frustum is the volume of the entire cone minus the volume of the little cone on top.
DPatrick
2014-02-20 19:27:25
This is \[\frac13\pi r^2(2s+h) - \frac13\pi 1^2(h).\]
This is \[\frac13\pi r^2(2s+h) - \frac13\pi 1^2(h).\]
tennis1729
2014-02-20 19:27:58
which is equal to 8/3 s^3 pi
which is equal to 8/3 s^3 pi
DrMath
2014-02-20 19:28:10
DPatrick
2014-02-20 19:28:21
Right, let's simplify a little first before making that equality though. (It doesn't matter much what order you finish up in.)
Right, let's simplify a little first before making that equality though. (It doesn't matter much what order you finish up in.)
DrMath
2014-02-20 19:28:29
*s^3,my bad
*s^3,my bad
DPatrick
2014-02-20 19:28:39
The frustum volume simplifies to \[\frac13\pi\left(r^2(2s+h)-h\right).\]
The frustum volume simplifies to \[\frac13\pi\left(r^2(2s+h)-h\right).\]
DPatrick
2014-02-20 19:28:54
And as we just mentioned, we need this to equal $\frac83\pi s^3$, so we have \[r^2(2s+h)-h = 8s^3.\]
And as we just mentioned, we need this to equal $\frac83\pi s^3$, so we have \[r^2(2s+h)-h = 8s^3.\]
DPatrick
2014-02-20 19:29:15
And this simplifies to $2r^2s + (r^2-1)h = 8s^3.$ How do we get rid of the $h$ from this?
And this simplifies to $2r^2s + (r^2-1)h = 8s^3.$ How do we get rid of the $h$ from this?
SockFoot
2014-02-20 19:29:39
plug in h
plug in h
tanishq1
2014-02-20 19:29:39
plug in 2s/(r-1)
plug in 2s/(r-1)
crastybow
2014-02-20 19:29:39
plug in what we got before
plug in what we got before
DrMath
2014-02-20 19:29:39
h=2s/(r-1)
h=2s/(r-1)
wehac
2014-02-20 19:29:39
h=2s/(r-1)
h=2s/(r-1)
DPatrick
2014-02-20 19:29:52
Right, we had $h = \dfrac{2s}{r-1}.$
Right, we had $h = \dfrac{2s}{r-1}.$
DPatrick
2014-02-20 19:30:18
So $(r^2-1)h = \frac{2s(r^2-1)}{r-1}$...
So $(r^2-1)h = \frac{2s(r^2-1)}{r-1}$...
ingridzhang97
2014-02-20 19:30:26
and that r-1 cancels out with r^2-1=(r-1)(r+1)
and that r-1 cancels out with r^2-1=(r-1)(r+1)
dli00105
2014-02-20 19:30:26
it cancels nicely
it cancels nicely
DPatrick
2014-02-20 19:30:33
...indeed, it's just $2s(r+1)$.
...indeed, it's just $2s(r+1)$.
DPatrick
2014-02-20 19:30:43
So our equation becomes \[2r^2s + (r+1)2s = 8s^3.\]
So our equation becomes \[2r^2s + (r+1)2s = 8s^3.\]
ingridzhang97
2014-02-20 19:31:00
and we can also cancel out an s
and we can also cancel out an s
blueferret
2014-02-20 19:31:00
reduce the 2s
reduce the 2s
Tommy2000
2014-02-20 19:31:00
divide by s
divide by s
dli00105
2014-02-20 19:31:00
divide by 2
divide by 2
mikhailgromov
2014-02-20 19:31:00
Divide by s
Divide by s
leejp1998
2014-02-20 19:31:00
cancle s
cancle s
DPatrick
2014-02-20 19:31:26
Let's divide by $2s$ and we're down to $r^2 + r + 1 = 4s^2.$
Let's divide by $2s$ and we're down to $r^2 + r + 1 = 4s^2.$
Royalreter1
2014-02-20 19:31:47
substitte r=s^2 in
substitte r=s^2 in
geogirl08
2014-02-20 19:31:47
LightningX48
2014-02-20 19:31:47
r = s^2!
r = s^2!
guilt
2014-02-20 19:31:47
s^2 = r
s^2 = r
MathStudent2002
2014-02-20 19:31:47
And we have r=s^2 so the right side is 4r!
And we have r=s^2 so the right side is 4r!
joshualee2000
2014-02-20 19:31:47
4s^2= 4r
4s^2= 4r
DPatrick
2014-02-20 19:31:57
Aha, we had filed away $r = s^2$.
Aha, we had filed away $r = s^2$.
DPatrick
2014-02-20 19:32:07
So we just have $r^2 + r + 1 = 4r$, or $r^2 - 3r + 1 = 0.$
So we just have $r^2 + r + 1 = 4r$, or $r^2 - 3r + 1 = 0.$
crastybow
2014-02-20 19:32:25
so use quadratic formula to find r to finish it off
so use quadratic formula to find r to finish it off
brandbest1
2014-02-20 19:32:25
solve it for our answer
solve it for our answer
Mathgeek727
2014-02-20 19:32:25
quadritic equation?
quadritic equation?
guilt
2014-02-20 19:32:25
r^2 - 3r +1 = 0 -> r = (3+sqrt5)/2 or E
r^2 - 3r +1 = 0 -> r = (3+sqrt5)/2 or E
urmilla
2014-02-20 19:32:25
(E) (3+ sqrt 5) /2 by quadratic formula
(E) (3+ sqrt 5) /2 by quadratic formula
DPatrick
2014-02-20 19:32:33
Yep. Solving gives \[r = \frac{3 \pm \sqrt5}{2}.\]
Yep. Solving gives \[r = \frac{3 \pm \sqrt5}{2}.\]
DPatrick
2014-02-20 19:32:40
Only the "+" is an answer choice (and only the "+" is greater than 1, which we need).
Only the "+" is an answer choice (and only the "+" is greater than 1, which we need).
DPatrick
2014-02-20 19:32:49
So $r = \dfrac{3 + \sqrt5}{2}$ is the answer. Answer (E).
So $r = \dfrac{3 + \sqrt5}{2}$ is the answer. Answer (E).
DPatrick
2014-02-20 19:33:27
This was the hardest problem of the 21-25 group on the 10B, in my opinion.
This was the hardest problem of the 21-25 group on the 10B, in my opinion.
DPatrick
2014-02-20 19:33:44
Let's move on to 10B #24, which was also 12B #18:
Let's move on to 10B #24, which was also 12B #18:
DPatrick
2014-02-20 19:33:49
24. The numbers 1, 2, 3, 4, 5 are to be arranged in a circle. An arrangement is bad if it is not true that for every $n$ from 1 to 15 one can find a subset of the numbers that appear consecutively on the circle that sum to $n.$ Arrangements that differ only by a rotation or a reflection are considered the same. How many different bad arrangements are there?
$\phantom{10B:24}$
$\text{(A) } 1 \quad \text{(B) } 2 \quad \text{(C) } 3 \quad \text{(D) } 4 \quad \text{(E) } 5$
24. The numbers 1, 2, 3, 4, 5 are to be arranged in a circle. An arrangement is bad if it is not true that for every $n$ from 1 to 15 one can find a subset of the numbers that appear consecutively on the circle that sum to $n.$ Arrangements that differ only by a rotation or a reflection are considered the same. How many different bad arrangements are there?
$\phantom{10B:24}$
$\text{(A) } 1 \quad \text{(B) } 2 \quad \text{(C) } 3 \quad \text{(D) } 4 \quad \text{(E) } 5$
DPatrick
2014-02-20 19:34:07
Yikes. We need to untangle the words.
Yikes. We need to untangle the words.
DPatrick
2014-02-20 19:34:13
Is there a simpler way to describe a bad arrangement?
Is there a simpler way to describe a bad arrangement?
brandbest1
2014-02-20 19:34:44
if there's a value of n such that you can't find consecutive numbers that sum to n
if there's a value of n such that you can't find consecutive numbers that sum to n
checkmate1021
2014-02-20 19:34:48
There exists an n from 1 to 15 that cannot be expressed as a sum of consecutive numbers on the circle
There exists an n from 1 to 15 that cannot be expressed as a sum of consecutive numbers on the circle
Tommy2000
2014-02-20 19:34:56
the sum of any group of numbers doesnt equal n for some number from 1-15
the sum of any group of numbers doesnt equal n for some number from 1-15
Quadratic64
2014-02-20 19:34:56
an arrangement where one cannot find consecutive numbers that sum to n
an arrangement where one cannot find consecutive numbers that sum to n
DPatrick
2014-02-20 19:35:03
A bad arrangement is an arrangement for which there's some number (between 1 and 15) that cannot be found in our circle as a sum of consecutive elements.
A bad arrangement is an arrangement for which there's some number (between 1 and 15) that cannot be found in our circle as a sum of consecutive elements.
DPatrick
2014-02-20 19:35:45
For some reason (maybe it's just me) I find this reformulation easier that what's stated in the problem. "if it is not true that.." is harder to parse.
For some reason (maybe it's just me) I find this reformulation easier that what's stated in the problem. "if it is not true that.." is harder to parse.
DPatrick
2014-02-20 19:36:19
So we need to count arrangements where some sum from 1 to 15 can't be found.
So we need to count arrangements where some sum from 1 to 15 can't be found.
DPatrick
2014-02-20 19:36:22
How can we simplify the search?
How can we simplify the search?
DiscipulusBonus
2014-02-20 19:36:43
1-5 and 10-15 are automatic (for 10-14, only one number is missing), so we only need to check if an arrangement can sum to 6,7,8, and 9.
1-5 and 10-15 are automatic (for 10-14, only one number is missing), so we only need to check if an arrangement can sum to 6,7,8, and 9.
WalkerTesla
2014-02-20 19:36:43
We can always get 1,2,3,4,5,10,11,12,13,14, and 15. Therefore we only need to worry about 6,7,8, and 9
We can always get 1,2,3,4,5,10,11,12,13,14, and 15. Therefore we only need to worry about 6,7,8, and 9
mathcool2009
2014-02-20 19:36:43
n = 1,2,3,4,5,10,11,12,13,14,15 always can be found as a sum
n = 1,2,3,4,5,10,11,12,13,14,15 always can be found as a sum
Joe10112
2014-02-20 19:36:43
1-5 can all be found, 10-15 can all be found
1-5 can all be found, 10-15 can all be found
Eudokia
2014-02-20 19:36:43
We don't have to look at 1-5 and 10-15
We don't have to look at 1-5 and 10-15
abishek99
2014-02-20 19:36:43
1-5 and 10-15 have to be sums
1-5 and 10-15 have to be sums
DPatrick
2014-02-20 19:36:51
We can always find the sums 1 through 5 -- just take a single number.
We can always find the sums 1 through 5 -- just take a single number.
DPatrick
2014-02-20 19:36:58
We can also always find the sums 10 through 15 -- just omit a single number, or take all five numbers to get 15.
We can also always find the sums 10 through 15 -- just omit a single number, or take all five numbers to get 15.
DPatrick
2014-02-20 19:37:06
So the only way that an arrangement can be bad is if one of 6, 7, 8, or 9 is not a sum.
So the only way that an arrangement can be bad is if one of 6, 7, 8, or 9 is not a sum.
mssmath
2014-02-20 19:37:28
6 and 7 imply 8 and 9 so we need only check 6 and 7
6 and 7 imply 8 and 9 so we need only check 6 and 7
DivideBy0
2014-02-20 19:37:28
Once we have found a set summing to 6, we can choose everything else and obtain a set summing to 9, and similarly for 7 and 8. Thus, we only need to check each case for weather or not we can obtain 6 or 7.
Once we have found a set summing to 6, we can choose everything else and obtain a set summing to 9, and similarly for 7 and 8. Thus, we only need to check each case for weather or not we can obtain 6 or 7.
Rogman
2014-02-20 19:37:28
but no 6 implies no 9 and no 7 implies no 8
but no 6 implies no 9 and no 7 implies no 8
joshxiong
2014-02-20 19:37:28
also if 6 can be achieved, 9 can
also if 6 can be achieved, 9 can
mathmaster2012
2014-02-20 19:37:28
If we can find 6, we can find 15-6=9. If we can find 7, we can find 15-7=8.
If we can find 6, we can find 15-6=9. If we can find 7, we can find 15-7=8.
DPatrick
2014-02-20 19:37:38
Right, there's a further simplification! 6 is a sum if and only if 9 is a sum: if some consecutive elements sum to 6, then the remaining elements sum to 9, and vice versa.
Right, there's a further simplification! 6 is a sum if and only if 9 is a sum: if some consecutive elements sum to 6, then the remaining elements sum to 9, and vice versa.
DPatrick
2014-02-20 19:37:43
In the same way, 7 is a sum if and only if 8 is a sum.
In the same way, 7 is a sum if and only if 8 is a sum.
DPatrick
2014-02-20 19:37:48
So an arrangement is bad if and only if either 6 or 7 is not realizable as a sum.
So an arrangement is bad if and only if either 6 or 7 is not realizable as a sum.
DPatrick
2014-02-20 19:37:56
At this point we can probably just try to construct them.
At this point we can probably just try to construct them.
DPatrick
2014-02-20 19:38:02
How do we construct a bad arrangement that doesn't contain a sum of 6?
How do we construct a bad arrangement that doesn't contain a sum of 6?
DPatrick
2014-02-20 19:38:33
Here's a blank arrangement to start:
Here's a blank arrangement to start:
DPatrick
2014-02-20 19:38:37
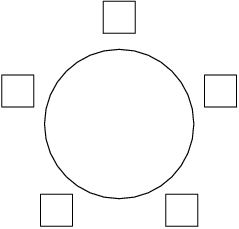
Tuxianeer
2014-02-20 19:38:57
5 and 1 are not adjacent, same with 2 and 4
5 and 1 are not adjacent, same with 2 and 4
lucylai
2014-02-20 19:38:57
1 and 5 have to be across from each other
1 and 5 have to be across from each other
mentalgenius
2014-02-20 19:38:57
just put 5 somewhere to account for rotations
just put 5 somewhere to account for rotations
DPatrick
2014-02-20 19:39:22
Sure, let's just put the 5 in the top position -- it doesn't matter where we put it, and fixing it to the top will account for the rotations:
Sure, let's just put the 5 in the top position -- it doesn't matter where we put it, and fixing it to the top will account for the rotations:
DPatrick
2014-02-20 19:39:27
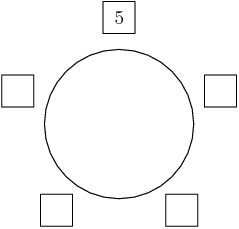
DPatrick
2014-02-20 19:39:46
And we need the 1 not to be next to the 5. Since reflections don't matter, there's only 1 place (up to reflection) to put the 1:
And we need the 1 not to be next to the 5. Since reflections don't matter, there's only 1 place (up to reflection) to put the 1:
DPatrick
2014-02-20 19:39:52
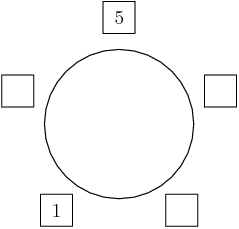
johnguolex
2014-02-20 19:39:59
also 4/5 can't be adjacent
also 4/5 can't be adjacent
jon167
2014-02-20 19:40:12
4 goes near 1
4 goes near 1
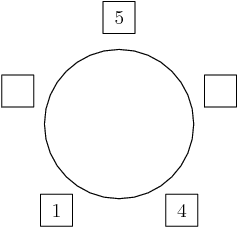
DPatrick
2014-02-20 19:40:22
Right: if we don't have a sum of 6, then we also don't have a sum of 9.
Right: if we don't have a sum of 6, then we also don't have a sum of 9.
DPatrick
2014-02-20 19:40:31
So the 4 has to go in the blank next to the 1, away from the 5:
So the 4 has to go in the blank next to the 1, away from the 5:
DPatrick
2014-02-20 19:40:43
blueberry7
2014-02-20 19:40:58
2 cannot be next to the 4 either
2 cannot be next to the 4 either
joshualee2000
2014-02-20 19:40:58
since 2 has to be away from 4, it goes on the left
since 2 has to be away from 4, it goes on the left
alex31415
2014-02-20 19:40:58
The 2 is between the 5 and the 1.
The 2 is between the 5 and the 1.
willabc
2014-02-20 19:40:58
2 can't be next to 4
2 can't be next to 4
VD8M9
2014-02-20 19:40:58
2 between 5/1??
2 between 5/1??
19bobhu
2014-02-20 19:40:58
2 has to go between 1 and 5
2 has to go between 1 and 5
DPatrick
2014-02-20 19:41:16
At this point, we're done: the 2 can't be next to the 4, so it has to go on the left, and the 3 goes in the remaining spot on the right:
At this point, we're done: the 2 can't be next to the 4, so it has to go on the left, and the 3 goes in the remaining spot on the right:
DPatrick
2014-02-20 19:41:21
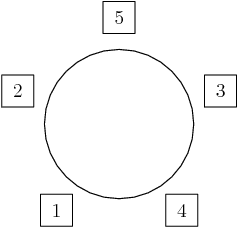
DPatrick
2014-02-20 19:41:40
This is the only bad arrangement that doesn't have a sum of 6 or 9.
This is the only bad arrangement that doesn't have a sum of 6 or 9.
guilt
2014-02-20 19:41:53
now check the case of 7
now check the case of 7
19bobhu
2014-02-20 19:41:53
And now we have to make the ones that can't make 7
And now we have to make the ones that can't make 7
acegikmoqsuwy2000
2014-02-20 19:41:53
now we try doing it for 7
now we try doing it for 7
ssk9208
2014-02-20 19:41:53
now 7
now 7
Royalreter1
2014-02-20 19:41:53
Now we look for 7/8
Now we look for 7/8
DPatrick
2014-02-20 19:42:06
Right: now we have to do the same exercise for bad arrangement(s) that don't have a sum of 7 or 8.
Right: now we have to do the same exercise for bad arrangement(s) that don't have a sum of 7 or 8.
DPatrick
2014-02-20 19:42:15
It's pretty much the same...
It's pretty much the same...
geogirl08
2014-02-20 19:42:27
5 is not adjacent to 2, nor is 3 adjacent to 5 for no 7
5 is not adjacent to 2, nor is 3 adjacent to 5 for no 7
alex31415
2014-02-20 19:42:27
Place 5 at the top, and 2 at the bottom.
Place 5 at the top, and 2 at the bottom.
mathbeida
2014-02-20 19:42:33
start with 5 again, 2 can not be adjacent
start with 5 again, 2 can not be adjacent
blueberry7
2014-02-20 19:42:33
the 5 cannot be next to the 2... or the 3
the 5 cannot be next to the 2... or the 3
DPatrick
2014-02-20 19:42:39
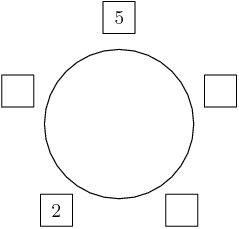
Again, we start with the 5 on top, and the 2 in the lower-left (since it can't be next to the 5):
Again, we start with the 5 on top, and the 2 in the lower-left (since it can't be next to the 5):
DPatrick
2014-02-20 19:42:46
awesomethree
2014-02-20 19:43:02
and 3 in the lower right
and 3 in the lower right
starwars123
2014-02-20 19:43:02
3 in the lower right
3 in the lower right
guilt
2014-02-20 19:43:02
also 3 can't be next to 5
also 3 can't be next to 5
DPatrick
2014-02-20 19:43:17
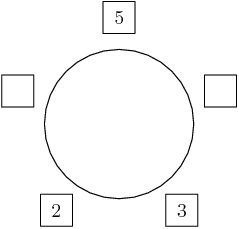
Right, if we don't have a sum of 7, we also don't have a sum of 8, and that forces the 3 not to be next to the 5:
Right, if we don't have a sum of 7, we also don't have a sum of 8, and that forces the 3 not to be next to the 5:
DPatrick
2014-02-20 19:43:28
elsw
2014-02-20 19:43:42
4 can't be next to 3
4 can't be next to 3
Eudokia
2014-02-20 19:43:42
4 can't be next to 3
4 can't be next to 3
wehac
2014-02-20 19:43:42
4 is in between 2 and 5
4 is in between 2 and 5
Tommy2000
2014-02-20 19:43:42
4 can't be next to 3, so 4 is between 2 and 5
4 can't be next to 3, so 4 is between 2 and 5
hotstuffFTW
2014-02-20 19:43:42
4 between 5,2 and 1 between 3,5
4 between 5,2 and 1 between 3,5
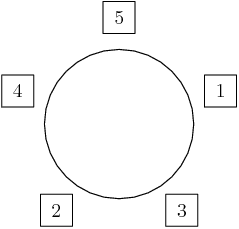
DPatrick
2014-02-20 19:43:59
And now we're forced again: the 4 has to go on the left (it can't be next to the 3), and the 1 is what remains:
And now we're forced again: the 4 has to go on the left (it can't be next to the 3), and the 1 is what remains:
DPatrick
2014-02-20 19:44:03
DPatrick
2014-02-20 19:44:12
And thus this is the only bad arrangement (up to reflections and rotations) that doesn't have a sum of 7.
And thus this is the only bad arrangement (up to reflections and rotations) that doesn't have a sum of 7.
abishek99
2014-02-20 19:44:25
only 2 arrangements B
only 2 arrangements B
pinkrock
2014-02-20 19:44:25
so the answer in B
so the answer in B
Bomist0
2014-02-20 19:44:25
2=>(B)
2=>(B)
ericding
2014-02-20 19:44:25
so the answer is B
so the answer is B
masalvada12
2014-02-20 19:44:25
therefore answer is 2
therefore answer is 2
DPatrick
2014-02-20 19:44:33
Correct: there are only 2 bad arrangements (one with no 6s or 9s, and one with no 7s or 8s). The answer is (B).
Correct: there are only 2 bad arrangements (one with no 6s or 9s, and one with no 7s or 8s). The answer is (B).
DPatrick
2014-02-20 19:44:59
OK, on to 10B #25 which is also 12B #22:
OK, on to 10B #25 which is also 12B #22:
DPatrick
2014-02-20 19:45:04
25. In a small pond there are eleven lily pads in a row labeled 0 through 10. A frog is sitting on pad 1. When the frog is on pad $N,$ $0<N<10,$ it will jump to pad $N-1$ with probability $\dfrac N{10}$ and to pad $N+1$ with probability $1-\dfrac N{10}.$ Each jump is independent of the previous jumps. If the frog reaches pad 0 it will be eaten by a patiently waiting snake. If the frog reaches pad 10 it will exit the pond, never to return. What is the probability that the frog will escape being eaten by the snake?
$\phantom{10B:25,12B:22}$
$\text{(A) } \dfrac{32}{79} \quad \text{(B) } \dfrac{161}{384} \quad \text{(C) } \dfrac{63}{146} \quad \text{(D) } \dfrac7{16} \quad \text{(E) } \dfrac12$
25. In a small pond there are eleven lily pads in a row labeled 0 through 10. A frog is sitting on pad 1. When the frog is on pad $N,$ $0<N<10,$ it will jump to pad $N-1$ with probability $\dfrac N{10}$ and to pad $N+1$ with probability $1-\dfrac N{10}.$ Each jump is independent of the previous jumps. If the frog reaches pad 0 it will be eaten by a patiently waiting snake. If the frog reaches pad 10 it will exit the pond, never to return. What is the probability that the frog will escape being eaten by the snake?
$\phantom{10B:25,12B:22}$
$\text{(A) } \dfrac{32}{79} \quad \text{(B) } \dfrac{161}{384} \quad \text{(C) } \dfrac{63}{146} \quad \text{(D) } \dfrac7{16} \quad \text{(E) } \dfrac12$
DPatrick
2014-02-20 19:45:18
Yikes again. Many many words.
Yikes again. Many many words.
DPatrick
2014-02-20 19:45:44
Let's set $p_i$ to be the probability that the frog lives starting from lily pad $i$. So we're trying to find $p_1.$
Let's set $p_i$ to be the probability that the frog lives starting from lily pad $i$. So we're trying to find $p_1.$
checkmate1021
2014-02-20 19:45:53
state diagram?
state diagram?
Rogman
2014-02-20 19:45:53
stages?
stages?
dli00105
2014-02-20 19:45:53
state diagram
state diagram
DPatrick
2014-02-20 19:46:26
You could draw a diagram (often called a "state diagram") for this problem if you wanted, but I'm not sure this problem is complicated enough to need one.
You could draw a diagram (often called a "state diagram") for this problem if you wanted, but I'm not sure this problem is complicated enough to need one.
DPatrick
2014-02-20 19:46:43
The diagram would basically just be the lily pads, with arrows showing the probabilities of jumping between them.
The diagram would basically just be the lily pads, with arrows showing the probabilities of jumping between them.
DPatrick
2014-02-20 19:46:53
Do we know any of the $p$'s right away?
Do we know any of the $p$'s right away?
joshxiong
2014-02-20 19:47:16
p_0 = 0, p_10 = 1
p_0 = 0, p_10 = 1
Bomist0
2014-02-20 19:47:16
0 and 10
0 and 10
checkmate1021
2014-02-20 19:47:16
p0 is 0
p0 is 0
bli1999
2014-02-20 19:47:16
p0 is 0.
p0 is 0.
mathwizard888
2014-02-20 19:47:16
p_0=0, p_10=1
p_0=0, p_10=1
Tuxianeer
2014-02-20 19:47:16
$p_0=0$ $p_{10}=1$
$p_0=0$ $p_{10}=1$
DPatrick
2014-02-20 19:47:20
$p_0 = 0$ -- the frog has become snake food.
$p_0 = 0$ -- the frog has become snake food.
DPatrick
2014-02-20 19:47:28
$p_{10} = 1$ -- freedom!
$p_{10} = 1$ -- freedom!
DPatrick
2014-02-20 19:47:53
(Many of you have also noticed another key fact. I'm going to play dumb for a moment, but we'll get to your observation soon!)
(Many of you have also noticed another key fact. I'm going to play dumb for a moment, but we'll get to your observation soon!)
DPatrick
2014-02-20 19:48:01
How are the other $p$'s related?
How are the other $p$'s related?
XxAndreixX
2014-02-20 19:48:43
p(n) = (1-n/10)p(n+1) + (n/10)p(n-1)
p(n) = (1-n/10)p(n+1) + (n/10)p(n-1)
Arcmage101
2014-02-20 19:48:43
1-i/10 and i/10
1-i/10 and i/10
DPatrick
2014-02-20 19:48:54
Right, we've got the data about the jumping that's given in the problem.
Right, we've got the data about the jumping that's given in the problem.
DPatrick
2014-02-20 19:49:00
The frog moves from pad $i$ to pad $i+1$ with probability $1-\frac{i}{10}$ and to pad $i-1$ with probability $\frac{i}{10}.$
The frog moves from pad $i$ to pad $i+1$ with probability $1-\frac{i}{10}$ and to pad $i-1$ with probability $\frac{i}{10}.$
DPatrick
2014-02-20 19:49:26
If the frog moves to pad $i+1$, his new probability of freedom is $p_{i+1}$.
If the frog moves to pad $i+1$, his new probability of freedom is $p_{i+1}$.
DPatrick
2014-02-20 19:49:36
If the frog moves to pad $i-1$, his new probability of freedom is $p_{i-1}$.
If the frog moves to pad $i-1$, his new probability of freedom is $p_{i-1}$.
DPatrick
2014-02-20 19:49:47
Therefore, \[ p_i = \left(1 - \frac{i}{10}\right)p_{i+1} + \frac{i}{10}p_{i-1}.\]
Therefore, \[ p_i = \left(1 - \frac{i}{10}\right)p_{i+1} + \frac{i}{10}p_{i-1}.\]
ingridzhang97
2014-02-20 19:50:01
so we can write some equations
so we can write some equations
DPatrick
2014-02-20 19:50:19
Indeed we can, but first, let's multiply this through by 10 to get rid of the fractions.
Indeed we can, but first, let's multiply this through by 10 to get rid of the fractions.
DPatrick
2014-02-20 19:50:26
\[ 10p_i = (10-i)p_{i+1} + ip_{i-1}.\]
\[ 10p_i = (10-i)p_{i+1} + ip_{i-1}.\]
DPatrick
2014-02-20 19:50:38
So now we have a system of 10 equations in 10 variables (using $p_0=0$ and $p_{10}=1$):
\begin{align*}
10p_1 &= 9p_2, \\
10p_2 &= 8p_3 + 2p_1, \\
10p_3 &= 7p_4 + 3p_2, \\
10p_4 &= 6p_5 + 4p_3, \\
10p_5 &= 5p_6 + 5p_4, \\
10p_6 &= 4p_7 + 6p_5, \\
10p_7 &= 3p_8 + 7p_6, \\
10p_8 &= 2p_9 + 8p_7, \\
10p_9 &= 1 + 9p_8.
\end{align*}
So now we have a system of 10 equations in 10 variables (using $p_0=0$ and $p_{10}=1$):
\begin{align*}
10p_1 &= 9p_2, \\
10p_2 &= 8p_3 + 2p_1, \\
10p_3 &= 7p_4 + 3p_2, \\
10p_4 &= 6p_5 + 4p_3, \\
10p_5 &= 5p_6 + 5p_4, \\
10p_6 &= 4p_7 + 6p_5, \\
10p_7 &= 3p_8 + 7p_6, \\
10p_8 &= 2p_9 + 8p_7, \\
10p_9 &= 1 + 9p_8.
\end{align*}
matholympiad25
2014-02-20 19:50:58
yikes
yikes
DPatrick
2014-02-20 19:51:10
Actually, I lied...it's "only" 9 equations in 9 variables.
Actually, I lied...it's "only" 9 equations in 9 variables.
DPatrick
2014-02-20 19:51:25
But that'll still take forever to solve. We could, mind you...
But that'll still take forever to solve. We could, mind you...
DPatrick
2014-02-20 19:51:40
...but there's an important observation that we can make to simplify things immensely.
...but there's an important observation that we can make to simplify things immensely.
mentalgenius
2014-02-20 19:52:01
in the middle, 1/2 chance to go either way
in the middle, 1/2 chance to go either way
joshualee2000
2014-02-20 19:52:01
$p_5 = \frac{1}{2}$
$p_5 = \frac{1}{2}$
pi37
2014-02-20 19:52:01
p_5=1/2
p_5=1/2
ABCDE
2014-02-20 19:52:01
p_5=1/2
p_5=1/2
Nahmid
2014-02-20 19:52:01
p5 = 1/2
p5 = 1/2
joshualee2000
2014-02-20 19:52:01
but $p_5 = \frac{1}{2}$
but $p_5 = \frac{1}{2}$
mentalgenius
2014-02-20 19:52:01
p5 = 1/2
p5 = 1/2
mathtastic
2014-02-20 19:52:09
ohhh p5=1/2 using logic!!!!!!!! (i think)
ohhh p5=1/2 using logic!!!!!!!! (i think)
DrMath
2014-02-20 19:52:13
Remember $p_5=\frac{1}{2}$!
Remember $p_5=\frac{1}{2}$!
DPatrick
2014-02-20 19:52:38
Right! Everything in this problem is symmetric with respect to the middle lily pad. So if the frog is in the middle, it's 50-50 that he'll live or get eaten. So $p_5 = \frac12.$
Right! Everything in this problem is symmetric with respect to the middle lily pad. So if the frog is in the middle, it's 50-50 that he'll live or get eaten. So $p_5 = \frac12.$
DPatrick
2014-02-20 19:52:49
That's very useful, because it reduces our 9-equation system to a 4-equation system:
\begin{align*}
10p_1 &= 9p_2, \\
10p_2 &= 8p_3 + 2p_1, \\
10p_3 &= 7p_4 + 3p_2, \\
10p_4 &= 3 + 4p_3.
\end{align*}
That's very useful, because it reduces our 9-equation system to a 4-equation system:
\begin{align*}
10p_1 &= 9p_2, \\
10p_2 &= 8p_3 + 2p_1, \\
10p_3 &= 7p_4 + 3p_2, \\
10p_4 &= 3 + 4p_3.
\end{align*}
SockFoot
2014-02-20 19:53:07
solving time
solving time
Royalreter1
2014-02-20 19:53:07
Now we can solve!
Now we can solve!
TheMaskedMagician
2014-02-20 19:53:07
Now this is something we can manage.
Now this is something we can manage.
DPatrick
2014-02-20 19:53:16
At this point I don't think there's anything clever to do except to slog through and solve this for $p_1.$
At this point I don't think there's anything clever to do except to slog through and solve this for $p_1.$
DPatrick
2014-02-20 19:53:33
We want to end with $p_1$, so we'll work from the bottom up. Let's eliminate $p_4$ first.
We want to end with $p_1$, so we'll work from the bottom up. Let's eliminate $p_4$ first.
DPatrick
2014-02-20 19:54:04
I'm basically going to zip through this because it's rather boring. But notice how I make choices as I go to make the simplification as painless as possible.
I'm basically going to zip through this because it's rather boring. But notice how I make choices as I go to make the simplification as painless as possible.
Tommy2000
2014-02-20 19:54:11
multiply equation 3 by 10 and equation 4 by 7
multiply equation 3 by 10 and equation 4 by 7
DPatrick
2014-02-20 19:54:21
Good idea: multiplying the third equation by 10 and the fourth equation by 7 gives:
\begin{align*}
100p_3 &= 70p_4 + 30p_2, \\
70p_4 &= 21 + 28p_3.
\end{align*}
Good idea: multiplying the third equation by 10 and the fourth equation by 7 gives:
\begin{align*}
100p_3 &= 70p_4 + 30p_2, \\
70p_4 &= 21 + 28p_3.
\end{align*}
DPatrick
2014-02-20 19:54:33
Then substitution gives $100p_3 = 21 + 28p_3 + 30p_2,$ or $72p_3 = 21 + 30p_2.$
Then substitution gives $100p_3 = 21 + 28p_3 + 30p_2,$ or $72p_3 = 21 + 30p_2.$
DPatrick
2014-02-20 19:54:44
Now our system is:
\begin{align*}
10p_1 &= 9p_2, \\
10p_2 &= 8p_3 + 2p_1, \\
72p_3 &= 21 + 30p_2.
\end{align*}
Now our system is:
\begin{align*}
10p_1 &= 9p_2, \\
10p_2 &= 8p_3 + 2p_1, \\
72p_3 &= 21 + 30p_2.
\end{align*}
DivideBy0
2014-02-20 19:54:59
mult eq 2 by 9
mult eq 2 by 9
sojourner1
2014-02-20 19:54:59
multiply through by 9
multiply through by 9
DPatrick
2014-02-20 19:55:05
Multiplying the second equation by 9 gives $90p_2 = 72p_3 + 18p_1.$
Multiplying the second equation by 9 gives $90p_2 = 72p_3 + 18p_1.$
DPatrick
2014-02-20 19:55:15
Now we can substitute the third equation into the second to get $90p_2 = 21 + 30p_2 + 18p_1,$ or $60p_2 = 21 + 18p_1.$
Now we can substitute the third equation into the second to get $90p_2 = 21 + 30p_2 + 18p_1,$ or $60p_2 = 21 + 18p_1.$
DPatrick
2014-02-20 19:55:26
Now our system is just 2 equations:
\begin{align*}
10p_1 &= 9p_2, \\
60p_2 &= 21 + 18p_1.
\end{align*}
Now our system is just 2 equations:
\begin{align*}
10p_1 &= 9p_2, \\
60p_2 &= 21 + 18p_1.
\end{align*}
LightningX48
2014-02-20 19:55:43
multiply first equation by 20, second by 3
multiply first equation by 20, second by 3
blueberry7
2014-02-20 19:55:47
multiply the first by 20, the second by 3
multiply the first by 20, the second by 3
bestwillcui1
2014-02-20 19:55:47
multiply first equation by 20, second equation by 3
multiply first equation by 20, second equation by 3
DPatrick
2014-02-20 19:55:51
Multiply the first by 20 and the second by 3 to get:
\begin{align*}
200p_1 &= 180p_2, \\
180p_2 &= 63 + 54p_1.
\end{align*}
Multiply the first by 20 and the second by 3 to get:
\begin{align*}
200p_1 &= 180p_2, \\
180p_2 &= 63 + 54p_1.
\end{align*}
DPatrick
2014-02-20 19:56:00
So $200p_1 = 63 + 54p_1,$ and hence $p_1 = \dfrac{63}{146}.$ Answer (C).
So $200p_1 = 63 + 54p_1,$ and hence $p_1 = \dfrac{63}{146}.$ Answer (C).
DPatrick
2014-02-20 19:56:52
While this was an OK problem, it was somewhat less-than-elegant for a #25 in my opinion.
While this was an OK problem, it was somewhat less-than-elegant for a #25 in my opinion.
VD8M9
2014-02-20 19:56:58
is this the simplest possible way?
is this the simplest possible way?
wehac
2014-02-20 19:56:58
Is there a quicker way to do this?
Is there a quicker way to do this?
DPatrick
2014-02-20 19:57:15
We talked about this around the office this morning, and we didn't really see a better way.
We talked about this around the office this morning, and we didn't really see a better way.
DPatrick
2014-02-20 19:57:37
I'm going to take a 3-minute rest break...we'll resume at 8:01 Eastern.
I'm going to take a 3-minute rest break...we'll resume at 8:01 Eastern.
DPatrick
2014-02-20 20:01:07
OK, we're back! On to the AMC 12B!
OK, we're back! On to the AMC 12B!
DPatrick
2014-02-20 20:01:13
21. In the figure, $ABCD$ is a square of side length 1. The rectangles $JKHG$ and $EBCF$ are congruent. What is $BE?$
$\phantom{12B:21}$
$\text{(A) } \dfrac12(\sqrt6-2) \quad \text{(B) } \dfrac14 \quad \text{(C) } 2-\sqrt3 \quad \text{(D) } \dfrac{\sqrt3}6 \quad \text{(E) } 1-\dfrac{\sqrt2}2$
21. In the figure, $ABCD$ is a square of side length 1. The rectangles $JKHG$ and $EBCF$ are congruent. What is $BE?$
$\phantom{12B:21}$
$\text{(A) } \dfrac12(\sqrt6-2) \quad \text{(B) } \dfrac14 \quad \text{(C) } 2-\sqrt3 \quad \text{(D) } \dfrac{\sqrt3}6 \quad \text{(E) } 1-\dfrac{\sqrt2}2$
DPatrick
2014-02-20 20:01:20
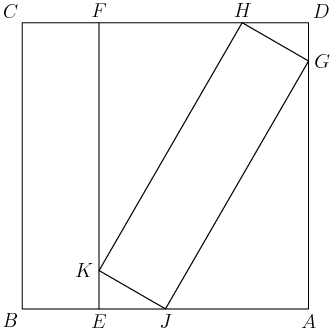
DPatrick
2014-02-20 20:01:39
Let's set $x = BE$ to be what we want. Notice that $GH = JK = x$ too.
Let's set $x = BE$ to be what we want. Notice that $GH = JK = x$ too.
DPatrick
2014-02-20 20:01:46
What do you notice in this picture?
What do you notice in this picture?
guilt
2014-02-20 20:01:57
similar triangles!
similar triangles!
XxAndreixX
2014-02-20 20:01:57
Similar triangles
Similar triangles
HYP135peppers
2014-02-20 20:01:57
similar triangles!
similar triangles!
Tommy2000
2014-02-20 20:01:57
similar triangle
similar triangle
Tuxianeer
2014-02-20 20:01:57
similar triangles
similar triangles
sahilp
2014-02-20 20:01:57
similar triangles
similar triangles
brandongeren
2014-02-20 20:01:57
similar triangles
similar triangles
DPatrick
2014-02-20 20:02:05
Ding ding ding! We've got similar triangles!
Ding ding ding! We've got similar triangles!
DPatrick
2014-02-20 20:02:22
Specifically, $AGJ \sim DHG.$ (And a couple of others too, but I'll use those two.) I'll color the corresponding sides in the diagram:
Specifically, $AGJ \sim DHG.$ (And a couple of others too, but I'll use those two.) I'll color the corresponding sides in the diagram:
DPatrick
2014-02-20 20:02:28
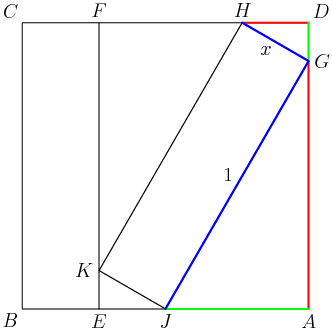
DPatrick
2014-02-20 20:02:39
And since $GJ = 1$ and $GH = x$, we know that the constant of proportionality from $AGJ$ to $DGH$ is $x$ -- that is, every length in $DGH$ is $x$ times the corresponding length from $AGJ$.
And since $GJ = 1$ and $GH = x$, we know that the constant of proportionality from $AGJ$ to $DGH$ is $x$ -- that is, every length in $DGH$ is $x$ times the corresponding length from $AGJ$.
DPatrick
2014-02-20 20:02:59
What can we do now?
What can we do now?
guilt
2014-02-20 20:03:28
set up ratios
set up ratios
va2010
2014-02-20 20:03:28
AG+GD=1
AG+GD=1
Sesquipedalian
2014-02-20 20:03:28
DG+GA=1
DG+GA=1
tanishq1
2014-02-20 20:03:28
pythag theorem if you set a couple more variables
pythag theorem if you set a couple more variables
Larklight
2014-02-20 20:03:28
pythagorean theorem
pythagorean theorem
XxAndreixX
2014-02-20 20:03:28
Set AJ = a, AG = b and write equations
Set AJ = a, AG = b and write equations
DPatrick
2014-02-20 20:03:45
Yeah, let's label some more lengths so that we can write some equations using some of these facts.
Yeah, let's label some more lengths so that we can write some equations using some of these facts.
DPatrick
2014-02-20 20:03:52
I set $AG = y$ and $AJ = z$. Then we know that $DH = xy$ and $DG = xz$.
I set $AG = y$ and $AJ = z$. Then we know that $DH = xy$ and $DG = xz$.
DPatrick
2014-02-20 20:03:57
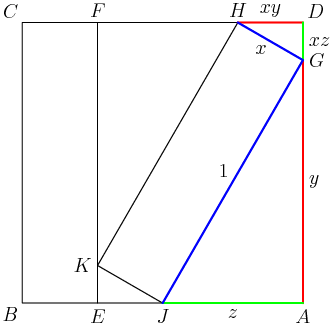
DPatrick
2014-02-20 20:04:28
A couple of you mentioned that $AD = 1$, so we have the equation $y + xz = 1.$
A couple of you mentioned that $AD = 1$, so we have the equation $y + xz = 1.$
DPatrick
2014-02-20 20:04:41
What about the other side of the square? What equation do we get from that?
What about the other side of the square? What equation do we get from that?
SockFoot
2014-02-20 20:05:20
z+xy+x=y+xz=1
z+xy+x=y+xz=1
joshualee2000
2014-02-20 20:05:20
xz+y=1, z+xy+x =1
xz+y=1, z+xy+x =1
Larklight
2014-02-20 20:05:20
z+x+xy =1
z+x+xy =1
Tinyyy
2014-02-20 20:05:20
xy+z+x=1
xy+z+x=1
ingridzhang97
2014-02-20 20:05:20
AB=1 so x+xy+z=1
AB=1 so x+xy+z=1
sparkles257
2014-02-20 20:05:20
xy + z = 1- BE
xy + z = 1- BE
DPatrick
2014-02-20 20:05:44
Right: on the bottom, $BE = x$ and $EJ = xy$ (same as $DH$) and $AJ = z$, so adding these gives $x + xy + z = 1.$
Right: on the bottom, $BE = x$ and $EJ = xy$ (same as $DH$) and $AJ = z$, so adding these gives $x + xy + z = 1.$
DPatrick
2014-02-20 20:06:18
Therefore we have the equations
\begin{align*}
xy + x + z &= 1, \\
xz + y &= 1,
\end{align*}from the two sides of the big square.
Therefore we have the equations
\begin{align*}
xy + x + z &= 1, \\
xz + y &= 1,
\end{align*}from the two sides of the big square.
DPatrick
2014-02-20 20:06:30
Now what?
Now what?
distortedwalrus
2014-02-20 20:06:45
y^2 + z^2 = 1
y^2 + z^2 = 1
XxAndreixX
2014-02-20 20:06:45
y^2 + z^2 = 1
y^2 + z^2 = 1
PertBanking
2014-02-20 20:06:45
Pythagorean Theorem!
Pythagorean Theorem!
dli00105
2014-02-20 20:06:45
y^2+z^2=1
y^2+z^2=1
DPatrick
2014-02-20 20:06:57
Right! We also have $y^2 + z^2 = 1$ from triangle $AGJ$.
Right! We also have $y^2 + z^2 = 1$ from triangle $AGJ$.
DPatrick
2014-02-20 20:07:23
So we've got 3 equations in 3 variables, and even though they're not linear, we can probably solve them.
So we've got 3 equations in 3 variables, and even though they're not linear, we can probably solve them.
Nahmid
2014-02-20 20:07:38
solve for x in the second equation and plug in
solve for x in the second equation and plug in
blueberry7
2014-02-20 20:07:38
solve for x
solve for x
DPatrick
2014-02-20 20:08:03
There are lots of ways to finish from here -- one way is to substitute $x = \dfrac{1-y}{z}$ from the second equation into the first, to get
\[ \frac{y(1-y)}{z} + \frac{1-y}{z} + z = 1. \]
There are lots of ways to finish from here -- one way is to substitute $x = \dfrac{1-y}{z}$ from the second equation into the first, to get
\[ \frac{y(1-y)}{z} + \frac{1-y}{z} + z = 1. \]
DPatrick
2014-02-20 20:08:26
It's just algebra from here, so again I'll kind of zip through it. Multiply through by $z$ to get \[y(1-y) = z - (1-y) - z^2,\] which simplifies to $0 = z - 1 - z^2 + y^2$ (the $y$ terms cancel).
It's just algebra from here, so again I'll kind of zip through it. Multiply through by $z$ to get \[y(1-y) = z - (1-y) - z^2,\] which simplifies to $0 = z - 1 - z^2 + y^2$ (the $y$ terms cancel).
joshualee2000
2014-02-20 20:08:59
1=z^2+y^2
1=z^2+y^2
DrMath
2014-02-20 20:08:59
z^2+y^2=1
z^2+y^2=1
DPatrick
2014-02-20 20:09:21
Right, we can replace $y^2$ with $1-z^2$ in the above equation, to get something just in terms of $z$.
Right, we can replace $y^2$ with $1-z^2$ in the above equation, to get something just in terms of $z$.
DPatrick
2014-02-20 20:09:28
We substitute to get $0 = z - 1 - z^2 + (1-z^2),$ or $0 = z - 2z^2.$
We substitute to get $0 = z - 1 - z^2 + (1-z^2),$ or $0 = z - 2z^2.$
matholympiad25
2014-02-20 20:09:44
z = 1/2
z = 1/2
wehac
2014-02-20 20:09:44
z=1/2
z=1/2
SockFoot
2014-02-20 20:09:44
z=1/2
z=1/2
DrMath
2014-02-20 20:09:44
z=1/2
z=1/2
DPatrick
2014-02-20 20:09:49
Thus (since $z$ is clearly not zero!) we have $z = \frac12$.
Thus (since $z$ is clearly not zero!) we have $z = \frac12$.
DPatrick
2014-02-20 20:10:14
Now we just unravel the equations to find $x$ (our answer).
Now we just unravel the equations to find $x$ (our answer).
mathawesomeness777
2014-02-20 20:10:20
y=sqrt(3)/2
y=sqrt(3)/2
LightningX48
2014-02-20 20:10:20
y = sqrt3 / 2
y = sqrt3 / 2
crastybow
2014-02-20 20:10:27
JAG is 30-60-90
JAG is 30-60-90
DPatrick
2014-02-20 20:10:31
We then have $y^2 = 1-z^2 = \frac34,$ so $y = \frac{\sqrt3}{2}.$ (In fact, notice that all the right triangles in the picture turn out to be 30-60-90.)
We then have $y^2 = 1-z^2 = \frac34,$ so $y = \frac{\sqrt3}{2}.$ (In fact, notice that all the right triangles in the picture turn out to be 30-60-90.)
joshualee2000
2014-02-20 20:10:55
x= 1-y/z
x= 1-y/z
DPatrick
2014-02-20 20:10:57
And to finish, we want \[x = \frac{1-y}{z} = \frac{1-\frac{\sqrt3}{2}}{\frac12} = 2-\sqrt3.\] Answer (C).
And to finish, we want \[x = \frac{1-y}{z} = \frac{1-\frac{\sqrt3}{2}}{\frac12} = 2-\sqrt3.\] Answer (C).
DrMath
2014-02-20 20:11:14
is there a reason to see that at first without digging thru algebra?
is there a reason to see that at first without digging thru algebra?
DPatrick
2014-02-20 20:11:24
The 30-60-90 triangles? Not that I can obviously see.
The 30-60-90 triangles? Not that I can obviously see.
DPatrick
2014-02-20 20:11:51
There are certainly other ways to solve this problem -- one of the AMC's published solutions used trigonometry.
There are certainly other ways to solve this problem -- one of the AMC's published solutions used trigonometry.
DPatrick
2014-02-20 20:12:11
Anyway, we already did #22 (it was 10B #25), so on to #23:
Anyway, we already did #22 (it was 10B #25), so on to #23:
DPatrick
2014-02-20 20:12:16
23. The number 2017 is prime. Let $\displaystyle S=\sum_{k=0}^{62}\binom{2014}k.$ What is the remainder when $S$ is divided by 2017?
$\phantom{12B:23}$
$\text{(A) } 32 \quad \text{(B) } 684 \quad \text{(C) } 1024 \quad \text{(D) } 1576 \quad \text{(E) } 2016$
23. The number 2017 is prime. Let $\displaystyle S=\sum_{k=0}^{62}\binom{2014}k.$ What is the remainder when $S$ is divided by 2017?
$\phantom{12B:23}$
$\text{(A) } 32 \quad \text{(B) } 684 \quad \text{(C) } 1024 \quad \text{(D) } 1576 \quad \text{(E) } 2016$
DPatrick
2014-02-20 20:12:36
Weird.
Weird.
DPatrick
2014-02-20 20:12:55
What's a better way to write $\dbinom{2014}{k}$ mod 2017?
What's a better way to write $\dbinom{2014}{k}$ mod 2017?
DPatrick
2014-02-20 20:13:28
It might help to write out the binomial coefficient: \[\dbinom{2014}{k} = \frac{(2014)(2013)\cdots(2014-k+1)}{k!}.\]
It might help to write out the binomial coefficient: \[\dbinom{2014}{k} = \frac{(2014)(2013)\cdots(2014-k+1)}{k!}.\]
crastybow
2014-02-20 20:13:51
-3 * -4 * -5 * ...
-3 * -4 * -5 * ...
Allan Z
2014-02-20 20:13:51
expand, write 2014=-3 mod 2017, 2013=-4 mod 2017 etc
expand, write 2014=-3 mod 2017, 2013=-4 mod 2017 etc
ingridzhang97
2014-02-20 20:13:51
2014=-3 mod 2017
2014=-3 mod 2017
DPatrick
2014-02-20 20:14:00
Right: $2014 \equiv -3 \pmod{2017}.$
Right: $2014 \equiv -3 \pmod{2017}.$
DPatrick
2014-02-20 20:14:12
So mod 2017 this is \[ \frac{(-3)(-4)\cdots(-3-k+1)}{k!}.\]
So mod 2017 this is \[ \frac{(-3)(-4)\cdots(-3-k+1)}{k!}.\]
DPatrick
2014-02-20 20:14:29
By the way -- and this is important! -- this is the step where we use the fact that 2017 is prime.
By the way -- and this is important! -- this is the step where we use the fact that 2017 is prime.
DPatrick
2014-02-20 20:14:43
You can't replace numbers in the numerator of a fraction modulo some residue if the denominator isn't relatively prime to the residue. For example, 6/2 is 3, and 6 = -4 mod 10, but -4/2 is -2, which is not the same as 3 mod 10. It failed because 2 isn't relatively prime to 10, so we're not allowed to "divide by 2" mod 10. If the modulus is prime, however, we can divide by anything we want (provided it's not a multiple of the prime, of course.)
You can't replace numbers in the numerator of a fraction modulo some residue if the denominator isn't relatively prime to the residue. For example, 6/2 is 3, and 6 = -4 mod 10, but -4/2 is -2, which is not the same as 3 mod 10. It failed because 2 isn't relatively prime to 10, so we're not allowed to "divide by 2" mod 10. If the modulus is prime, however, we can divide by anything we want (provided it's not a multiple of the prime, of course.)
Allan Z
2014-02-20 20:14:56
the fact that 2017 is prime makes multiplicative inverse exist
the fact that 2017 is prime makes multiplicative inverse exist
starwars123
2014-02-20 20:14:58
it has no factors other than 1 and 2017
it has no factors other than 1 and 2017
DPatrick
2014-02-20 20:15:04
Indeed, that's the technical fact that we're using.
Indeed, that's the technical fact that we're using.
DPatrick
2014-02-20 20:15:19
(If this doesn't mean anything to you, it might when you take a more advanced number theory course.)
(If this doesn't mean anything to you, it might when you take a more advanced number theory course.)
DPatrick
2014-02-20 20:15:45
Anyway, so we've got that \[ \binom{2014}{k} \equiv \frac{(-3)(-4)\cdots(-3-k+1)}{k!} \pmod{2017}.\]
Anyway, so we've got that \[ \binom{2014}{k} \equiv \frac{(-3)(-4)\cdots(-3-k+1)}{k!} \pmod{2017}.\]
DPatrick
2014-02-20 20:15:50
What do we do with this?
What do we do with this?
TheStrangeCharm
2014-02-20 20:16:08
factor out the negatives and then cancel with the $k!$
factor out the negatives and then cancel with the $k!$
Allan Z
2014-02-20 20:16:08
a lot of terms cancel!
a lot of terms cancel!
lucylai
2014-02-20 20:16:08
cancel
cancel
DPatrick
2014-02-20 20:16:20
Indeed, if we pull the minus signs out, this is \[ (-1)^k\frac{(3)(4)\cdots(k+2)}{k!}.\]
Indeed, if we pull the minus signs out, this is \[ (-1)^k\frac{(3)(4)\cdots(k+2)}{k!}.\]
DPatrick
2014-02-20 20:16:48
And then a lot of stuff cancels...
And then a lot of stuff cancels...
DPatrick
2014-02-20 20:17:05
This is just $$(-1)^k\frac{(k+1)(k+2)}{2}.$$
This is just $$(-1)^k\frac{(k+1)(k+2)}{2}.$$
joshxiong
2014-02-20 20:17:21
This becomes $\binom{k+2}{2}$
This becomes $\binom{k+2}{2}$
DPatrick
2014-02-20 20:17:45
Aha, so our sum is just \[ S \equiv \sum_{k=0}^{62} (-1)^k\binom{k+2}{2} \pmod{2017}.\]
Aha, so our sum is just \[ S \equiv \sum_{k=0}^{62} (-1)^k\binom{k+2}{2} \pmod{2017}.\]
DPatrick
2014-02-20 20:18:00
That is, writing it without the $\Sigma$, our sum (mod 2017) is \[ \binom22 - \binom32 + \binom42 - \binom52 + \cdots - \binom{63}{2} + \binom{64}{2}.\]
That is, writing it without the $\Sigma$, our sum (mod 2017) is \[ \binom22 - \binom32 + \binom42 - \binom52 + \cdots - \binom{63}{2} + \binom{64}{2}.\]
DPatrick
2014-02-20 20:18:15
Does this sum telescope or collapse in a nice way?
Does this sum telescope or collapse in a nice way?
DPatrick
2014-02-20 20:18:36
It may help to think of $\dbinom{n}{2}$ in another way...
It may help to think of $\dbinom{n}{2}$ in another way...
awesome2478
2014-02-20 20:18:51
triangular numbers?
triangular numbers?
DrMath
2014-02-20 20:18:51
1+2+3+...+(n-2)+(n-1)
1+2+3+...+(n-2)+(n-1)
DPatrick
2014-02-20 20:18:59
Right! $\dbinom{n}{2}$ is the sum of the first $n-1$ positive integers: $\dfrac{n(n-1)}{2}.$
Right! $\dbinom{n}{2}$ is the sum of the first $n-1$ positive integers: $\dfrac{n(n-1)}{2}.$
DPatrick
2014-02-20 20:19:16
So, for instance, what is $\binom42 - \binom32?$
So, for instance, what is $\binom42 - \binom32?$
sparkles257
2014-02-20 20:19:33
3
3
XxAndreixX
2014-02-20 20:19:33
3
3
guilt
2014-02-20 20:19:33
3
3
wehac
2014-02-20 20:19:33
3
3
ahaanomegas
2014-02-20 20:19:33
bestwillcui1
2014-02-20 20:19:33
3
3
mathwizard888
2014-02-20 20:19:33
3
3
TheMaskedMagician
2014-02-20 20:19:33
$3$
$3$
DPatrick
2014-02-20 20:19:37
It's just 3: $\binom42 - \binom32 = (1+2+3)-(1+2) = 3.$
It's just 3: $\binom42 - \binom32 = (1+2+3)-(1+2) = 3.$
DPatrick
2014-02-20 20:19:50
In the same way $\binom62 - \binom52 = (1+2+3+4+5)-(1+2+3+4) = 5$, and $\binom82 - \binom72 = 7$, and so on.
In the same way $\binom62 - \binom52 = (1+2+3+4+5)-(1+2+3+4) = 5$, and $\binom82 - \binom72 = 7$, and so on.
sahilp
2014-02-20 20:20:06
1+3+5+7.....+61+63
1+3+5+7.....+61+63
ingridzhang97
2014-02-20 20:20:11
that sum becomes the sum of the first 32 odds
that sum becomes the sum of the first 32 odds
DPatrick
2014-02-20 20:20:37
Right. When we pair up the terms like this (don't forget the $\binom22$ term at the front), our sum becomes: \[1+3+5+\cdots+63.\]
Right. When we pair up the terms like this (don't forget the $\binom22$ term at the front), our sum becomes: \[1+3+5+\cdots+63.\]
mjlove
2014-02-20 20:20:48
32^2
32^2
Jayjayliu
2014-02-20 20:20:48
32^2
32^2
DaChickenInc
2014-02-20 20:20:48
32^2=1024
32^2=1024
ssk9208
2014-02-20 20:20:48
which is $32^2 = 1024$
which is $32^2 = 1024$
blueferret
2014-02-20 20:20:48
32^2
32^2
dli00105
2014-02-20 20:20:48
sum=32^2=1024
sum=32^2=1024
1023megabytes
2014-02-20 20:20:48
32^2 = 1024 (C)
32^2 = 1024 (C)
mathawesomeness777
2014-02-20 20:20:48
= 32^2
= 32^2
DPatrick
2014-02-20 20:20:53
That is, it's just the sum of the first 32 positive odd integers.
That is, it's just the sum of the first 32 positive odd integers.
DPatrick
2014-02-20 20:21:01
And you should all know that this sum is just $32^2$, or $1024.$ Answer (C).
And you should all know that this sum is just $32^2$, or $1024.$ Answer (C).
DPatrick
2014-02-20 20:21:05
(If you don't know this, try to prove it on your own.)
(If you don't know this, try to prove it on your own.)
DPatrick
2014-02-20 20:21:39
I liked this problem, but the bit about 2017 having to be prime made it a bit technical.
I liked this problem, but the bit about 2017 having to be prime made it a bit technical.
DPatrick
2014-02-20 20:21:49
Anyway, on to #24:
Anyway, on to #24:
DPatrick
2014-02-20 20:21:53
24. Let $ABCDE$ be a pentagon inscribed in a circle such that $AB=CD=3,$ $BC=DE=10,$ and $AE=14.$ The sum of the lengths of all diagonals of $ABCDE$ is equal to $\dfrac mn,$ where $m$ and $n$ are relatively prime positive integers. What is $m+n?$
$\phantom{12B:24}$
$\text{(A) } 129 \quad \text{(B) } 247 \quad \text{(C) } 353 \quad \text{(D) } 391 \quad \text{(E) } 421$
24. Let $ABCDE$ be a pentagon inscribed in a circle such that $AB=CD=3,$ $BC=DE=10,$ and $AE=14.$ The sum of the lengths of all diagonals of $ABCDE$ is equal to $\dfrac mn,$ where $m$ and $n$ are relatively prime positive integers. What is $m+n?$
$\phantom{12B:24}$
$\text{(A) } 129 \quad \text{(B) } 247 \quad \text{(C) } 353 \quad \text{(D) } 391 \quad \text{(E) } 421$
xXpapayaXx
2014-02-20 20:22:12
draw a picture
draw a picture
ompatel99
2014-02-20 20:22:12
picture!
picture!
SheilaMajumdar
2014-02-20 20:22:12
image please
image please
dli00105
2014-02-20 20:22:12
draw a picture!!
draw a picture!!
DPatrick
2014-02-20 20:22:16
Here's a picture:
Here's a picture:
DPatrick
2014-02-20 20:22:22
DPatrick
2014-02-20 20:22:34
What do we notice about the diagonals?
What do we notice about the diagonals?
joshxiong
2014-02-20 20:23:06
AC=BD=CE
AC=BD=CE
Rogman
2014-02-20 20:23:06
some are congruent
some are congruent
mssmath
2014-02-20 20:23:06
AC=CE
AC=CE
1023megabytes
2014-02-20 20:23:06
DB=EC
DB=EC
blueferret
2014-02-20 20:23:06
some of them have equal lengths
some of them have equal lengths
distortedwalrus
2014-02-20 20:23:06
a lot of them are equal in length
a lot of them are equal in length
DPatrick
2014-02-20 20:23:15
Three of them -- $\overline{AC},\,\overline{BD},\,\overline{CE}$ -- are the same length, since they all cut out the same length arc (specifically, an arc cut out by a segment of length 3 followed by a segment of length 10 in either order).
Three of them -- $\overline{AC},\,\overline{BD},\,\overline{CE}$ -- are the same length, since they all cut out the same length arc (specifically, an arc cut out by a segment of length 3 followed by a segment of length 10 in either order).
DPatrick
2014-02-20 20:23:30
So that we have a better picture of what's going on, I'll draw those in red below; the other two diagonals I'll draw in green ($\overline{AD}$) and blue ($\overline{BE}$):
So that we have a better picture of what's going on, I'll draw those in red below; the other two diagonals I'll draw in green ($\overline{AD}$) and blue ($\overline{BE}$):
DPatrick
2014-02-20 20:23:36
Arcmage101
2014-02-20 20:23:59
Do you have any techniques for quickly drawing approximate figures and/or diagrams?
Do you have any techniques for quickly drawing approximate figures and/or diagrams?
mathtastic
2014-02-20 20:23:59
wow those are colorful
wow those are colorful
mathtastic
2014-02-20 20:23:59
are we allowed to use colors on the test?
are we allowed to use colors on the test?
DPatrick
2014-02-20 20:24:13
That's my suggestion: use colors. Bring lots of colors writing implements.
That's my suggestion: use colors. Bring lots of colors writing implements.
DPatrick
2014-02-20 20:24:28
Let's call the red length $r$, the green length $g$, and the blue length $b$. So we're trying to find $3r + g + b.$
Let's call the red length $r$, the green length $g$, and the blue length $b$. So we're trying to find $3r + g + b.$
DPatrick
2014-02-20 20:24:42
(That's another reason to use colors -- easier to remember which variable is which!)
(That's another reason to use colors -- easier to remember which variable is which!)
DPatrick
2014-02-20 20:24:55
OK. What do we do now?
OK. What do we do now?
joshxiong
2014-02-20 20:25:15
we can use Ptolemy's Theorem
we can use Ptolemy's Theorem
va2010
2014-02-20 20:25:15
Use ptolemy?
Use ptolemy?
Larklight
2014-02-20 20:25:15
ptolmey's theorem?
ptolmey's theorem?
guilt
2014-02-20 20:25:15
use ptolemy's theorem
use ptolemy's theorem
Allan Z
2014-02-20 20:25:15
Notice cyclic quadrilaterals : ptolemy's theorem to get systems of 3 equations
Notice cyclic quadrilaterals : ptolemy's theorem to get systems of 3 equations
distortedwalrus
2014-02-20 20:25:15
ptolemy's theorem
ptolemy's theorem
DPatrick
2014-02-20 20:25:26
From here, there are two major paths to the solution, depending on whether you know (or want to use) Ptolemy's Theorem or not. I'll show you the Ptolemy's Theorem solution, but then I'll also show you a solution where you don't need Ptolemy's Theorem at all.
From here, there are two major paths to the solution, depending on whether you know (or want to use) Ptolemy's Theorem or not. I'll show you the Ptolemy's Theorem solution, but then I'll also show you a solution where you don't need Ptolemy's Theorem at all.
DPatrick
2014-02-20 20:25:37
Ptolemy's Theorem states that in a cyclic quadrilateral, the sum of the product of the lengths of the opposite sides equals the product of the diagonals.
Ptolemy's Theorem states that in a cyclic quadrilateral, the sum of the product of the lengths of the opposite sides equals the product of the diagonals.
DPatrick
2014-02-20 20:26:03
And a "cyclic quadrilateral" is one whose four vertices all lie on the same circle.
And a "cyclic quadrilateral" is one whose four vertices all lie on the same circle.
DPatrick
2014-02-20 20:26:13
For example, using cyclic quadrilateral $BCDE$, we have \[(BC)(DE) + (BE)(CD) = (BD)(CE).\] Plugging in the numbers and the variables that we have, this is $100 + 3b = r^2.$
For example, using cyclic quadrilateral $BCDE$, we have \[(BC)(DE) + (BE)(CD) = (BD)(CE).\] Plugging in the numbers and the variables that we have, this is $100 + 3b = r^2.$
DPatrick
2014-02-20 20:26:18
Tommy2000
2014-02-20 20:26:42
MORE equations
MORE equations
DPatrick
2014-02-20 20:26:49
Yeah, we have 5 cyclic quadrilateral in our picture, so we have 5 equations that result from Ptolemy's Theorem. I'll list them below, and I'll label them by the point on the pentagon that's omitted (so, for example, equation ($A$) comes from quadrilateral $BCDE$, omitting $A$):
\begin{align*}
3b + 100 &= r^2 \qquad (A) \\
10r + 42 &= rg \qquad (B) \\
14r + 30 &= bg \qquad (C) \\
3r + 140 &= rb \qquad (D) \\
10g + 9 &= r^2 \qquad (E)
\end{align*}
Yeah, we have 5 cyclic quadrilateral in our picture, so we have 5 equations that result from Ptolemy's Theorem. I'll list them below, and I'll label them by the point on the pentagon that's omitted (so, for example, equation ($A$) comes from quadrilateral $BCDE$, omitting $A$):
\begin{align*}
3b + 100 &= r^2 \qquad (A) \\
10r + 42 &= rg \qquad (B) \\
14r + 30 &= bg \qquad (C) \\
3r + 140 &= rb \qquad (D) \\
10g + 9 &= r^2 \qquad (E)
\end{align*}
DPatrick
2014-02-20 20:27:07
This seems like a lot of data. How can we use these equations?
This seems like a lot of data. How can we use these equations?
DPatrick
2014-02-20 20:28:19
There are probably lots of ways to solve this system. Nobody suggested what I happened to do, but I'm sure what you might have done is just as good.
There are probably lots of ways to solve this system. Nobody suggested what I happened to do, but I'm sure what you might have done is just as good.
DPatrick
2014-02-20 20:28:37
I thought that (B) and (D) were easy ways to solve for $g$ and $b$ in terms of $r$.
I thought that (B) and (D) were easy ways to solve for $g$ and $b$ in terms of $r$.
DPatrick
2014-02-20 20:28:51
Specifically, (B) and (D) let us solve for $g$ and $b$ in terms of $r$:
\begin{align*}
g &= 10 + \frac{42}{r}, \\
b &= 3 + \frac{140}{r}.
\end{align*}
Specifically, (B) and (D) let us solve for $g$ and $b$ in terms of $r$:
\begin{align*}
g &= 10 + \frac{42}{r}, \\
b &= 3 + \frac{140}{r}.
\end{align*}
DPatrick
2014-02-20 20:29:32
(I think you could have used (A) and (E) in this first step as well -- a lot of you suggested that. But I don't have that one written up in my notes!)
(I think you could have used (A) and (E) in this first step as well -- a lot of you suggested that. But I don't have that one written up in my notes!)
blueberry7
2014-02-20 20:29:39
then we can plug into equations A and E
then we can plug into equations A and E
joshxiong
2014-02-20 20:29:39
now we can plug these into (A) and (E)
now we can plug these into (A) and (E)
DPatrick
2014-02-20 20:29:53
Right, in fact, we really only need one of them.
Right, in fact, we really only need one of them.
DPatrick
2014-02-20 20:30:01
One way to continue is to plug the expression for $b$ into equation (A) and get an equation for $r$:
\[ 3\left(3 + \frac{140}{r}\right) + 100 = r^2.\]
One way to continue is to plug the expression for $b$ into equation (A) and get an equation for $r$:
\[ 3\left(3 + \frac{140}{r}\right) + 100 = r^2.\]
Tommy2000
2014-02-20 20:30:17
solve for r
solve for r
oink
2014-02-20 20:30:17
then solve for r
then solve for r
Rogman
2014-02-20 20:30:17
but we'll get a cubic!
but we'll get a cubic!
DPatrick
2014-02-20 20:30:25
True: we can multiply through by $r$ to get $9r + 420 + 100r = r^3,$ or $r^3 - 109r - 420 = 0.$
True: we can multiply through by $r$ to get $9r + 420 + 100r = r^3,$ or $r^3 - 109r - 420 = 0.$
mathlearning920
2014-02-20 20:30:39
It might be easier if you plugged the expression into E
It might be easier if you plugged the expression into E
DPatrick
2014-02-20 20:30:46
I bet we get the same cubic.
I bet we get the same cubic.
crastybow
2014-02-20 20:31:01
try RRT
try RRT
guilt
2014-02-20 20:31:01
rrt!
rrt!
va2010
2014-02-20 20:31:01
Use Rational root theorem
Use Rational root theorem
alex31415
2014-02-20 20:31:01
Rational Roots Theorem?
Rational Roots Theorem?
DPatrick
2014-02-20 20:31:22
It is tricky to solve cubics in general, but we have some clues.
It is tricky to solve cubics in general, but we have some clues.
DPatrick
2014-02-20 20:31:29
Because the problem strongly implies that $r$ is rational, we look for rational roots, which have to be factors of 420. Also because there's no quadratic term, the roots have to sum to 0.
Because the problem strongly implies that $r$ is rational, we look for rational roots, which have to be factors of 420. Also because there's no quadratic term, the roots have to sum to 0.
DPatrick
2014-02-20 20:31:40
And we need two odd roots because the linear term is odd.
And we need two odd roots because the linear term is odd.
DPatrick
2014-02-20 20:31:52
And we're looking for the third side of a 3-10-$r$ triangle, where $r$ is the longest side, so $r$ is probably either 11 or 12, and only 12 is a factor of 420.
And we're looking for the third side of a 3-10-$r$ triangle, where $r$ is the longest side, so $r$ is probably either 11 or 12, and only 12 is a factor of 420.
ABCDE
2014-02-20 20:32:08
-5, -7, 12 work
-5, -7, 12 work
matholympiad25
2014-02-20 20:32:08
12 works
12 works
DPatrick
2014-02-20 20:32:14
Indeed, a little experimentation shows that the cubic factors as \[(r-12)(r+7)(r+5) = 0.\]
Indeed, a little experimentation shows that the cubic factors as \[(r-12)(r+7)(r+5) = 0.\]
DPatrick
2014-02-20 20:32:29
The only positive root is $r=12.$
The only positive root is $r=12.$
crastybow
2014-02-20 20:32:48
plug these into the equations for b and g
plug these into the equations for b and g
Tommy2000
2014-02-20 20:32:48
plug in to the equations for b and g
plug in to the equations for b and g
DPatrick
2014-02-20 20:33:00
Right, from here, we can find $b$ and $g$ using our previous equations for them:
\begin{align*}
g &= 10 + \frac{42}{r} = 10 + \frac{42}{12} = 10 + \frac72 = \frac{27}{2}, \\
b &= 3 + \frac{140}{r} = 3 + \frac{140}{12} = 3 + \frac{35}{3} = \frac{44}{3}.
\end{align*}
Right, from here, we can find $b$ and $g$ using our previous equations for them:
\begin{align*}
g &= 10 + \frac{42}{r} = 10 + \frac{42}{12} = 10 + \frac72 = \frac{27}{2}, \\
b &= 3 + \frac{140}{r} = 3 + \frac{140}{12} = 3 + \frac{35}{3} = \frac{44}{3}.
\end{align*}
Rogman
2014-02-20 20:33:16
add add add
add add add
geogirl08
2014-02-20 20:33:18
3r+g+b = ?
3r+g+b = ?
DPatrick
2014-02-20 20:33:24
And to finish, our sum is \[3(12) + \frac{27}{2} + \frac{44}{3} = \frac{6(36)+3(27)+2(44)}{6} = \frac{216+81+88}{6} = \frac{385}{6}.\]
And to finish, our sum is \[3(12) + \frac{27}{2} + \frac{44}{3} = \frac{6(36)+3(27)+2(44)}{6} = \frac{216+81+88}{6} = \frac{385}{6}.\]
DPatrick
2014-02-20 20:33:31
This is in lowest terms, so our answer is $385+6=391.$ Answer (D).
This is in lowest terms, so our answer is $385+6=391.$ Answer (D).
DPatrick
2014-02-20 20:33:50
While this was a fine solution, it requires knowledge of Ptolemy's Theorem, which is a bit of a technical result. It's mildly unreasonable (in my opinion) to expect all contest takers to know this result.
While this was a fine solution, it requires knowledge of Ptolemy's Theorem, which is a bit of a technical result. It's mildly unreasonable (in my opinion) to expect all contest takers to know this result.
DPatrick
2014-02-20 20:34:00
So, let me show you a solution where you don't need Ptolemy's Theorem at all.
So, let me show you a solution where you don't need Ptolemy's Theorem at all.
DPatrick
2014-02-20 20:34:21
The picture is still up top, but let me post it down below again:
The picture is still up top, but let me post it down below again:
DPatrick
2014-02-20 20:34:30
Tommy2000
2014-02-20 20:34:41
would a law of cosines bash work as well?
would a law of cosines bash work as well?
DivideBy0
2014-02-20 20:34:41
law of cosines?
law of cosines?
DPatrick
2014-02-20 20:35:10
We've got lots of lengths, so a Law of Cosines attack might work.
We've got lots of lengths, so a Law of Cosines attack might work.
DPatrick
2014-02-20 20:35:33
We need a convenient triangle to get a cosine from, though.
We need a convenient triangle to get a cosine from, though.
dli00105
2014-02-20 20:35:55
ACE
ACE
Larklight
2014-02-20 20:35:55
CEA!
CEA!
Allan Z
2014-02-20 20:36:00
ACE?
ACE?
DPatrick
2014-02-20 20:36:13
Good idea. Triangle $ACE$ is isosceles with base 14 and two legs $r.$
Good idea. Triangle $ACE$ is isosceles with base 14 and two legs $r.$
DPatrick
2014-02-20 20:36:32
So if we let $\theta = \angle CAE$, what is $\cos\theta$?
So if we let $\theta = \angle CAE$, what is $\cos\theta$?
DrMath
2014-02-20 20:37:04
7/AC
7/AC
Tommy2000
2014-02-20 20:37:04
7/r
7/r
joshxiong
2014-02-20 20:37:04
7/r
7/r
DPatrick
2014-02-20 20:37:19
Right: $\cos\theta = \dfrac{7}{r}.$
Right: $\cos\theta = \dfrac{7}{r}.$
DPatrick
2014-02-20 20:37:42
(Drop the perpendicular from $C$ to $\overline{AE}$ to get a right triangle, then $7$ is the "adjacent" side to $A$ and $r$ is the hypotenuse.)
(Drop the perpendicular from $C$ to $\overline{AE}$ to get a right triangle, then $7$ is the "adjacent" side to $A$ and $r$ is the hypotenuse.)
DPatrick
2014-02-20 20:37:54
So that's helpful...because?
So that's helpful...because?
DPatrick
2014-02-20 20:38:12
Is there another angle that has a related cosine?
Is there another angle that has a related cosine?
danzhi
2014-02-20 20:38:46
EDC
EDC
DPatrick
2014-02-20 20:39:00
Right! I would use angle $CDE$ on the opposite side of the circle.
Right! I would use angle $CDE$ on the opposite side of the circle.
DPatrick
2014-02-20 20:39:15
(We've got to use the fact that we're inside a circle somewhere.)
(We've got to use the fact that we're inside a circle somewhere.)
DPatrick
2014-02-20 20:39:44
Because $\angle CAE$ and $\angle CDE$ intercept opposite arcs that make up the whole circle, the angles are supplementary (sum to $180^\circ$.)
Because $\angle CAE$ and $\angle CDE$ intercept opposite arcs that make up the whole circle, the angles are supplementary (sum to $180^\circ$.)
DPatrick
2014-02-20 20:39:54
So what is $\cos(\angle CDE)?$
So what is $\cos(\angle CDE)?$
joshxiong
2014-02-20 20:40:07
$\cos CDE=-\frac{7}{r}$
$\cos CDE=-\frac{7}{r}$
ingridzhang97
2014-02-20 20:40:07
cos(180-theta)
cos(180-theta)
mathmaster2012
2014-02-20 20:40:07
-7/r
-7/r
sparkles257
2014-02-20 20:40:07
-7/r
-7/r
mathmaster2012
2014-02-20 20:40:15
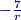
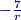
blueferret
2014-02-20 20:40:15
-7/r
-7/r
DPatrick
2014-02-20 20:40:25
Right: $\cos(\angle CDE) = -\cos(180^\circ - \theta) = -\cos\theta = -\frac{7}{r}.$
Right: $\cos(\angle CDE) = -\cos(180^\circ - \theta) = -\cos\theta = -\frac{7}{r}.$
DrMath
2014-02-20 20:40:36
now LOC to find CE?
now LOC to find CE?
sparkles257
2014-02-20 20:40:36
now we can do cosine bash
now we can do cosine bash
DPatrick
2014-02-20 20:40:54
Right, now we can use the Law of Cosine on triangle $CDE$: \[(CE)^2 = (CD)^2 + (DE)^2 - 2\cos(\angle CDE)(CD)(CE).\]
Right, now we can use the Law of Cosine on triangle $CDE$: \[(CE)^2 = (CD)^2 + (DE)^2 - 2\cos(\angle CDE)(CD)(CE).\]
DPatrick
2014-02-20 20:41:09
Plugging in our values, we get \[r^2 = 3^2 + 10^2 + 2\left(\frac{7}{r}\right)(3)(10).\]
Plugging in our values, we get \[r^2 = 3^2 + 10^2 + 2\left(\frac{7}{r}\right)(3)(10).\]
mathtastic
2014-02-20 20:41:22
not so ugly anymore
not so ugly anymore
ABCDE
2014-02-20 20:41:26
same cubic
same cubic
DPatrick
2014-02-20 20:41:36
Right, when we simplify, we get $r^3 = 109r + 420,$ or $r^3 - 109r - 420 = 0.$
Right, when we simplify, we get $r^3 = 109r + 420,$ or $r^3 - 109r - 420 = 0.$
guilt
2014-02-20 20:41:43
same cubic so r = 12
same cubic so r = 12
Tommy2000
2014-02-20 20:41:43
Its the same cubic!!!!!!!!!!1
Its the same cubic!!!!!!!!!!1
DrMath
2014-02-20 20:41:43
wait a minute- this gives the same cubic woth ptolemy!
wait a minute- this gives the same cubic woth ptolemy!
DPatrick
2014-02-20 20:41:48
This is the same cubic as we had in the previous solution, so $r=12$ is the positive root.
This is the same cubic as we had in the previous solution, so $r=12$ is the positive root.
DPatrick
2014-02-20 20:42:01
The fact that it's the same cubic is of course not a coincidence!
The fact that it's the same cubic is of course not a coincidence!
DPatrick
2014-02-20 20:42:16
Now how do we find the green and blue lengths? (Again without using Ptolemy?)
Now how do we find the green and blue lengths? (Again without using Ptolemy?)
guilt
2014-02-20 20:42:59
more trig using LOC
more trig using LOC
mathtastic
2014-02-20 20:42:59
or more law of cosigns
or more law of cosigns
DPatrick
2014-02-20 20:43:19
We could keep bashing with Law of Cosines, but we could also use some of the isosceles trapezoids in the picture.
We could keep bashing with Law of Cosines, but we could also use some of the isosceles trapezoids in the picture.
DPatrick
2014-02-20 20:43:31
For example, consider $ABCD$:
For example, consider $ABCD$:
DPatrick
2014-02-20 20:43:37
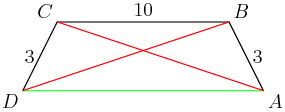
DPatrick
2014-02-20 20:43:47
The red diagonals have length 12. How do we find the length of the green base?
The red diagonals have length 12. How do we find the length of the green base?
Larklight
2014-02-20 20:44:08
drop altitudes
drop altitudes
elsw
2014-02-20 20:44:08
Right triangles?
Right triangles?
mathtastic
2014-02-20 20:44:08
pythag??
pythag??
DPatrick
2014-02-20 20:44:22
Right. We drop a perpendicular from $C$ down to $\overline{AD}$:
Right. We drop a perpendicular from $C$ down to $\overline{AD}$:
DPatrick
2014-02-20 20:44:28
mathtastic
2014-02-20 20:44:37
OH WAIT!! THIS IS LIKE AMC 10B #21!!!!
OH WAIT!! THIS IS LIKE AMC 10B #21!!!!
DPatrick
2014-02-20 20:44:44
Indeed it is.
Indeed it is.
DPatrick
2014-02-20 20:44:49
Using the Pythagorean Theorem, \[h^2 = 9-a^2 = 144-(10+a)^2.\]
Using the Pythagorean Theorem, \[h^2 = 9-a^2 = 144-(10+a)^2.\]
DPatrick
2014-02-20 20:44:58
This simplifies to $9-a^2 = 44-20a-a^2$, so $a = \frac{35}{20} = \frac{7}{4}.$
This simplifies to $9-a^2 = 44-20a-a^2$, so $a = \frac{35}{20} = \frac{7}{4}.$
DPatrick
2014-02-20 20:45:05
Thus the green side is $g = 10+2a = 10+\frac{7}{2}=\frac{27}{2},$ as before.
Thus the green side is $g = 10+2a = 10+\frac{7}{2}=\frac{27}{2},$ as before.
DPatrick
2014-02-20 20:45:21
A similar technique on trapezoid $BCDE$ can be used to find $b$. (I'll skip this -- you're probably sick of this problem by now.)
A similar technique on trapezoid $BCDE$ can be used to find $b$. (I'll skip this -- you're probably sick of this problem by now.)
DPatrick
2014-02-20 20:45:42
So the problem can be solved without knowing anything about Ptolemy's Theorem!
So the problem can be solved without knowing anything about Ptolemy's Theorem!
DPatrick
2014-02-20 20:45:57
OK, on to AMC 12B #25!
OK, on to AMC 12B #25!
DPatrick
2014-02-20 20:46:06
25. What is the sum of all positive real solutions $x$ to the equation\[2\cos(2x)\left(\cos(2x)-\cos\left(\frac{2014\pi^2}x\right)\right)=\cos(4x)-1\,?\]
$\phantom{12B:25}$
$\text{(A) } \pi \quad \text{(B) } 810\pi \quad \text{(C) } 1008\pi \quad \text{(D) } 1080\pi \quad \text{(E) } 1800\pi$
25. What is the sum of all positive real solutions $x$ to the equation\[2\cos(2x)\left(\cos(2x)-\cos\left(\frac{2014\pi^2}x\right)\right)=\cos(4x)-1\,?\]
$\phantom{12B:25}$
$\text{(A) } \pi \quad \text{(B) } 810\pi \quad \text{(C) } 1008\pi \quad \text{(D) } 1080\pi \quad \text{(E) } 1800\pi$
ompatel99
2014-02-20 20:46:36
2x=z?
2x=z?
DPatrick
2014-02-20 20:46:45
That's one idea, but I'd take it a step further.
That's one idea, but I'd take it a step further.
DPatrick
2014-02-20 20:46:53
Since $\cos(2x)$ appears in a couple of places, let's call it $y.$
Since $\cos(2x)$ appears in a couple of places, let's call it $y.$
DPatrick
2014-02-20 20:47:02
Can we also write the right side of the equation in terms of $y$?
Can we also write the right side of the equation in terms of $y$?
Larklight
2014-02-20 20:47:25
double angle identity on cos(4x)
double angle identity on cos(4x)
joshxiong
2014-02-20 20:47:25
Use the double angle formula on $\cos(4x)$
Use the double angle formula on $\cos(4x)$
Tinyyy
2014-02-20 20:47:25
Double angle formula for cos (4x)
Double angle formula for cos (4x)
mathwizard888
2014-02-20 20:47:25
yes, using double angle formula
yes, using double angle formula
DPatrick
2014-02-20 20:47:37
By the double-angle formula for cosine, \[\cos(4x) = 2\cos^2(2x)-1 = 2y^2 - 1.\]
By the double-angle formula for cosine, \[\cos(4x) = 2\cos^2(2x)-1 = 2y^2 - 1.\]
DPatrick
2014-02-20 20:47:53
So our equation has become \[2y\left(y - \cos\left(\frac{2014\pi^2}{x}\right)\right)=2y^2-2.\]
So our equation has become \[2y\left(y - \cos\left(\frac{2014\pi^2}{x}\right)\right)=2y^2-2.\]
DPatrick
2014-02-20 20:48:11
(Of course, you don't need to use $y$, but I find it easier to keep track of things.)
(Of course, you don't need to use $y$, but I find it easier to keep track of things.)
tanishq1
2014-02-20 20:48:17
encouraged because there's a 2y^2 on both sides.
encouraged because there's a 2y^2 on both sides.
Wickedestjr
2014-02-20 20:48:22
The 2y^2 cancels on both sides
The 2y^2 cancels on both sides
cheeptricks
2014-02-20 20:48:28
2y^2 cancel out
2y^2 cancel out
ahaanomegas
2014-02-20 20:48:35
Divide both sides by 2 because why-not.
Divide both sides by 2 because why-not.
hotstuffFTW
2014-02-20 20:48:35
divide by 2
divide by 2
jeffgreenfan8
2014-02-20 20:48:35
we can divide by 2
we can divide by 2
DPatrick
2014-02-20 20:48:41
Hurray, life is good. The $2y^2$ terms cancel, and after dividing by -2 this is just \[y\cos\left(\frac{2014\pi^2}{x}\right) = 1.\]
Hurray, life is good. The $2y^2$ terms cancel, and after dividing by -2 this is just \[y\cos\left(\frac{2014\pi^2}{x}\right) = 1.\]
DPatrick
2014-02-20 20:48:52
$y$ isn't really helping us anymore, so let's put everything back in terms of $x$: \[\cos(2x)\cos\left(\frac{2014\pi^2}{x}\right) = 1.\]
$y$ isn't really helping us anymore, so let's put everything back in terms of $x$: \[\cos(2x)\cos\left(\frac{2014\pi^2}{x}\right) = 1.\]
DPatrick
2014-02-20 20:49:06
So, now I ask myself: when is a product of two cosines equal to 1?
So, now I ask myself: when is a product of two cosines equal to 1?
mssmath
2014-02-20 20:49:30
both are +1 or -1
both are +1 or -1
ABCDE
2014-02-20 20:49:30
both 1 or -1
both 1 or -1
blueferret
2014-02-20 20:49:30
they are either both 1 or -1
they are either both 1 or -1
Allan Z
2014-02-20 20:49:30
both of them -1 or both of them 1
both of them -1 or both of them 1
joshxiong
2014-02-20 20:49:30
so they must both be -1 or 1
so they must both be -1 or 1
wehac
2014-02-20 20:49:30
when they are both 1 or both -1
when they are both 1 or both -1
ompatel99
2014-02-20 20:49:30
they are both 1 or -1
they are both 1 or -1
alex31415
2014-02-20 20:49:30
Both are +/-1
Both are +/-1
mathawesomeness777
2014-02-20 20:49:30
Both 1 or -1.
Both 1 or -1.
DPatrick
2014-02-20 20:49:39
Righto. The two cosines themselves must both be 1 or both be -1.
Righto. The two cosines themselves must both be 1 or both be -1.
DPatrick
2014-02-20 20:49:50
So it looks like we have two cases to consider.
So it looks like we have two cases to consider.
DPatrick
2014-02-20 20:50:11
We'll start with the $+1$ case. When do we have \[\cos(2x)=\cos\left(\frac{2014\pi^2}{x}\right) = 1\,?\]
We'll start with the $+1$ case. When do we have \[\cos(2x)=\cos\left(\frac{2014\pi^2}{x}\right) = 1\,?\]
DPatrick
2014-02-20 20:50:24
When is a cosine equal to 1?
When is a cosine equal to 1?
ompatel99
2014-02-20 20:50:57
2pi*n
2pi*n
alex31415
2014-02-20 20:50:57
2pi*n for an integer n
2pi*n for an integer n
joshualee2000
2014-02-20 20:50:57
when it is 2pin
when it is 2pin
dli00105
2014-02-20 20:50:57
when angle multiple of 2pi
when angle multiple of 2pi
blueferret
2014-02-20 20:50:57
the angle=2n*pi
the angle=2n*pi
Hydroxide
2014-02-20 20:50:57
multiple of 2pi
multiple of 2pi
DPatrick
2014-02-20 20:51:20
Right. $\cos(\theta)=1$ if and only if $\theta$ is an even integer multiple of $\pi.$ (Please, don't use degrees in this problem -- the presence of $\pi$ should tell you that that's a bad idea.)
Right. $\cos(\theta)=1$ if and only if $\theta$ is an even integer multiple of $\pi.$ (Please, don't use degrees in this problem -- the presence of $\pi$ should tell you that that's a bad idea.)
DPatrick
2014-02-20 20:51:35
So we must have $x = n\pi$ for some positive integer $n$ in order for $\cos(2x) = 1.$
So we must have $x = n\pi$ for some positive integer $n$ in order for $\cos(2x) = 1.$
DPatrick
2014-02-20 20:51:51
And for the other term, this leaves \[\cos\left(\frac{2014\pi^2}{x}\right) = \cos\left(\frac{2014\pi^2}{n\pi}\right) = \cos\left(\frac{2014}{n}\pi\right) = 1.\]
And for the other term, this leaves \[\cos\left(\frac{2014\pi^2}{x}\right) = \cos\left(\frac{2014\pi^2}{n\pi}\right) = \cos\left(\frac{2014}{n}\pi\right) = 1.\]
DPatrick
2014-02-20 20:51:58
When does this occur?
When does this occur?
blueferret
2014-02-20 20:52:16
when 2014/n is even
when 2014/n is even
joshxiong
2014-02-20 20:52:16
n is an odd factor of 2014
n is an odd factor of 2014
joshualee2000
2014-02-20 20:52:16
when n is a odd divisor of 2014
when n is a odd divisor of 2014
DPatrick
2014-02-20 20:52:25
Right. We need that $\dfrac{2014}{n}$ is an even positive integer.
Right. We need that $\dfrac{2014}{n}$ is an even positive integer.
DPatrick
2014-02-20 20:52:46
Now is a good time to note that $2014 = 2 \cdot 19 \cdot 53.$ (A common mistake here might be to factor $2014 = 2 \cdot 1007$, and assume that $1007$ is prime.)
Now is a good time to note that $2014 = 2 \cdot 19 \cdot 53.$ (A common mistake here might be to factor $2014 = 2 \cdot 1007$, and assume that $1007$ is prime.)
jeffgreenfan8
2014-02-20 20:53:15
always know the prime factors of the year you are taking the exam in
always know the prime factors of the year you are taking the exam in
DPatrick
2014-02-20 20:53:16
MathStudent2002
2014-02-20 20:53:24
4 odd factors!
4 odd factors!
Tommy2000
2014-02-20 20:53:24
4 n's, 1, 19, 53, 1007
4 n's, 1, 19, 53, 1007
DPatrick
2014-02-20 20:53:34
So $n$ must be one of $1,$ $19,$ $53,$ or $19 \cdot 53$ for us to have a solution. (If you mistakenly thought 1007 was prime, you'd only get the solution $n=1.$)
So $n$ must be one of $1,$ $19,$ $53,$ or $19 \cdot 53$ for us to have a solution. (If you mistakenly thought 1007 was prime, you'd only get the solution $n=1.$)
alex31415
2014-02-20 20:53:43
Sum of factors of 1007=(19+1)(53+1)=1080
Sum of factors of 1007=(19+1)(53+1)=1080
akshay9
2014-02-20 20:53:54
This gives us four possible values of x: pi, 19pi, 53pi, 1007pi
This gives us four possible values of x: pi, 19pi, 53pi, 1007pi
DPatrick
2014-02-20 20:54:05
Right: our solutions in this case are $\pi$, $19\pi$, $53\pi$, and $(19 \cdot 53)\pi.$
Right: our solutions in this case are $\pi$, $19\pi$, $53\pi$, and $(19 \cdot 53)\pi.$
DPatrick
2014-02-20 20:54:12
They sum to $(1+19+53+19\cdot53)\pi = (1+19)(1+53)\pi = (20)(54)\pi = 1080\pi.$ (Note the clever trick we used to add them!)
They sum to $(1+19+53+19\cdot53)\pi = (1+19)(1+53)\pi = (20)(54)\pi = 1080\pi.$ (Note the clever trick we used to add them!)
DPatrick
2014-02-20 20:54:34
This happens to be choice (D), and we've ruled out all but (D) or (E). If you're pressed for time, you can either guess that there are no solutions in the other case, or that there are.
This happens to be choice (D), and we've ruled out all but (D) or (E). If you're pressed for time, you can either guess that there are no solutions in the other case, or that there are.
DPatrick
2014-02-20 20:54:57
We're not pressed for time, so let's look.
We're not pressed for time, so let's look.
DPatrick
2014-02-20 20:55:02
When do we have \[\cos(2x)=\cos\left(\frac{2014\pi^2}{x}\right) = -1\,?\]
When do we have \[\cos(2x)=\cos\left(\frac{2014\pi^2}{x}\right) = -1\,?\]
joshxiong
2014-02-20 20:55:32
if both are an odd multiple of $\pi$
if both are an odd multiple of $\pi$
brandongeren
2014-02-20 20:55:32
odd multiples of pi
odd multiples of pi
ABCDE
2014-02-20 20:55:32
odd multiple of pi
odd multiple of pi
bli1999
2014-02-20 20:55:32
odd multiple of pi
odd multiple of pi
DPatrick
2014-02-20 20:55:38
Right. $\cos(\theta) = -1$ if and only if $\theta$ is an odd integer multiple of $\pi$.
Right. $\cos(\theta) = -1$ if and only if $\theta$ is an odd integer multiple of $\pi$.
DPatrick
2014-02-20 20:55:48
So we must have $x = \left(n + \frac12\right)\pi$ for some nonnegative integer $n$ in order for $\cos(2x) = -1.$
So we must have $x = \left(n + \frac12\right)\pi$ for some nonnegative integer $n$ in order for $\cos(2x) = -1.$
DPatrick
2014-02-20 20:56:01
(That is, $x$ must be a half-integer multiple of $\pi$.)
(That is, $x$ must be a half-integer multiple of $\pi$.)
DPatrick
2014-02-20 20:56:16
But this leaves \[\cos\left(\frac{2014\pi^2}{x}\right) = \cos\left(\frac{2014\pi^2}{\left(n+\frac12\right)\pi}\right) = \cos\left(\frac{2014}{n+\frac12}\pi\right) = -1.\]
But this leaves \[\cos\left(\frac{2014\pi^2}{x}\right) = \cos\left(\frac{2014\pi^2}{\left(n+\frac12\right)\pi}\right) = \cos\left(\frac{2014}{n+\frac12}\pi\right) = -1.\]
DPatrick
2014-02-20 20:56:35
So we must have $\dfrac{2014}{n+\frac12} = \dfrac{4028}{2n+1}$ be an odd positive integer.
So we must have $\dfrac{2014}{n+\frac12} = \dfrac{4028}{2n+1}$ be an odd positive integer.
Rogman
2014-02-20 20:56:57
nope
nope
Tommy2000
2014-02-20 20:56:57
impossible
impossible
DrMath
2014-02-20 20:56:57
i dont think thats possible!
i dont think thats possible!
BobaFett101
2014-02-20 20:56:57
not possible
not possible
lucylai
2014-02-20 20:56:57
impossible
impossible
DPatrick
2014-02-20 20:57:16
We can't divide 4028 by an odd integer and be left with an odd integer!
We can't divide 4028 by an odd integer and be left with an odd integer!
DPatrick
2014-02-20 20:57:39
So indeed there are no solutions in this case.
So indeed there are no solutions in this case.
joshxiong
2014-02-20 20:57:54
which means that the final answer is $1080\pi$
which means that the final answer is $1080\pi$
thiennguyen
2014-02-20 20:57:54
D 1080 $ \pi$
D 1080 $ \pi$
LightningX48
2014-02-20 20:57:54
so the ans is (d) 1080pi
so the ans is (d) 1080pi
DPatrick
2014-02-20 20:58:04
Our answer is our previous sum, $1080\pi$, answer (D).
Our answer is our previous sum, $1080\pi$, answer (D).
mathawesomeness777
2014-02-20 20:58:19
Wow, this was easier that #24! Pretty easy for a #25, but not saying that it was easy.
Wow, this was easier that #24! Pretty easy for a #25, but not saying that it was easy.
mssmath
2014-02-20 20:58:19
Easy #25 in your opinion??
Easy #25 in your opinion??
DPatrick
2014-02-20 20:58:36
It was fairly easy for a #25. Lots of people find trig scary, but this was pretty straightforwards.
It was fairly easy for a #25. Lots of people find trig scary, but this was pretty straightforwards.
DPatrick
2014-02-20 20:59:02
We zipped through these problems pretty quickly, so let's do one or two more from 16-20 on either test. Please vote for the one you want to see!
We zipped through these problems pretty quickly, so let's do one or two more from 16-20 on either test. Please vote for the one you want to see!
DPatrick
2014-02-20 20:59:22
(you need to say which contest when you vote!)
(you need to say which contest when you vote!)
DPatrick
2014-02-20 21:00:22
We had a lot of votes for 19 and 20 on the 10B and 20 on the 12B.
We had a lot of votes for 19 and 20 on the 10B and 20 on the 12B.
DPatrick
2014-02-20 21:00:29
They're all pretty quick so let's do 'em all!
They're all pretty quick so let's do 'em all!
DPatrick
2014-02-20 21:00:39
19. Two concentric circles have radii 1 and 2. Two points on the outer circle are chosen independently and uniformly at random. What is the probability that the chord joining the two points intersects the inner circle?
$\phantom{10b:19}$
(A) $\dfrac16$ (B) $\dfrac14$ (C) $\dfrac{2-\sqrt2}{2}$ (D) $\dfrac13$ (E) $\dfrac12$
19. Two concentric circles have radii 1 and 2. Two points on the outer circle are chosen independently and uniformly at random. What is the probability that the chord joining the two points intersects the inner circle?
$\phantom{10b:19}$
(A) $\dfrac16$ (B) $\dfrac14$ (C) $\dfrac{2-\sqrt2}{2}$ (D) $\dfrac13$ (E) $\dfrac12$
wehac
2014-02-20 21:01:03
draw a diagram
draw a diagram
summitwei
2014-02-20 21:01:03
DIAGRAM!!!
DIAGRAM!!!
AMN300
2014-02-20 21:01:03
diagram?
diagram?
fluffyanimal
2014-02-20 21:01:03
Draw a diagram?
Draw a diagram?
DPatrick
2014-02-20 21:01:09
This is basically the picture you need:
This is basically the picture you need:
DPatrick
2014-02-20 21:01:15
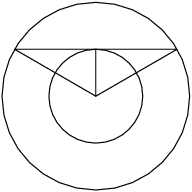
DPatrick
2014-02-20 21:01:40
That's the "border" case where the chord just touches the inner circle. What do we know about those triangles?
That's the "border" case where the chord just touches the inner circle. What do we know about those triangles?
joshualee2000
2014-02-20 21:01:57
its a 30-60-90 triangle
its a 30-60-90 triangle
distortedwalrus
2014-02-20 21:01:57
the right triangles are 30-60-90
the right triangles are 30-60-90
hotstuffFTW
2014-02-20 21:01:57
two 30-60-90 triangles
two 30-60-90 triangles
Dragon6point1
2014-02-20 21:01:57
30-60-90s
30-60-90s
alex31415
2014-02-20 21:01:57
30 60 90
30 60 90
elsw
2014-02-20 21:01:57
30-60-90
30-60-90
Allan Z
2014-02-20 21:01:57
30-60-90
30-60-90
DPatrick
2014-02-20 21:02:16
Indeed. The vertical leg is 1 (the radius of the small circle) and the hypotenuses are 2 (the radius of the big circle), so they're 30-60-90.
Indeed. The vertical leg is 1 (the radius of the small circle) and the hypotenuses are 2 (the radius of the big circle), so they're 30-60-90.
DPatrick
2014-02-20 21:02:25
And in particular the central angle is 120 degrees.
And in particular the central angle is 120 degrees.
DPatrick
2014-02-20 21:02:42
What does that tell us about the chord? How far about do the two points have to be to intersect the small circle?
What does that tell us about the chord? How far about do the two points have to be to intersect the small circle?
XxAndreixX
2014-02-20 21:03:08
more than 120 degrees
more than 120 degrees
joshualee2000
2014-02-20 21:03:08
they have to be more than 120 degrees apart
they have to be more than 120 degrees apart
sparkles257
2014-02-20 21:03:08
120 degrees
120 degrees
cheeptricks
2014-02-20 21:03:08
if the points are farther apart, they will intersect the circle
if the points are farther apart, they will intersect the circle
DPatrick
2014-02-20 21:03:28
Right: if the two points are more than 120 degrees apart along the outer circle, the line will intersect the inner circle.
Right: if the two points are more than 120 degrees apart along the outer circle, the line will intersect the inner circle.
DPatrick
2014-02-20 21:03:43
(That is, if they're farther apart than they are in the picture above).
(That is, if they're farther apart than they are in the picture above).
DivideBy0
2014-02-20 21:03:57
have to be on the opposite 120 degree arc
have to be on the opposite 120 degree arc
Tommy2000
2014-02-20 21:03:57
only 120/360 degrees work
only 120/360 degrees work
DPatrick
2014-02-20 21:04:17
Right. If we pick the first point arbitrarily, then the second point can't be within 120 degrees of the first point on either side.
Right. If we pick the first point arbitrarily, then the second point can't be within 120 degrees of the first point on either side.
DPatrick
2014-02-20 21:04:37
That means it has to be in the 120 degree arc that lies opposite the first point (or, you can think of 240 degrees worth of arc that "fail").
That means it has to be in the 120 degree arc that lies opposite the first point (or, you can think of 240 degrees worth of arc that "fail").
acegikmoqsuwy2000
2014-02-20 21:04:44
so thats 360-240 = 120 and 120/360 is 1/3
so thats 360-240 = 120 and 120/360 is 1/3
Larklight
2014-02-20 21:04:44
(d) 1/3
(d) 1/3
mathawesomeness777
2014-02-20 21:04:44
So it's just 1/3 D!
So it's just 1/3 D!
DPatrick
2014-02-20 21:04:57
Exactly. The probability is $\dfrac{120}{360} = \dfrac13.$ Answer (D).
Exactly. The probability is $\dfrac{120}{360} = \dfrac13.$ Answer (D).
DPatrick
2014-02-20 21:05:13
OK, on to 10B #20:
OK, on to 10B #20:
DPatrick
2014-02-20 21:05:18
20. For how many integers $x$ is the number $x^4 - 51x^2 + 50$ negative?
$\phantom{10b:20}$
(A) 8 (B) 10 (C) 12 (D) 14 (E) 16
20. For how many integers $x$ is the number $x^4 - 51x^2 + 50$ negative?
$\phantom{10b:20}$
(A) 8 (B) 10 (C) 12 (D) 14 (E) 16
ompatel99
2014-02-20 21:05:56
(x^2-50)(x^2-1)
(x^2-50)(x^2-1)
dli00105
2014-02-20 21:05:56
begging to be factored!!
begging to be factored!!
mathbeida
2014-02-20 21:05:56
let y = x^2
let y = x^2
mathtastic
2014-02-20 21:05:56
let y=x^2 then factor
let y=x^2 then factor
ahaanomegas
2014-02-20 21:05:56
Use y = x^2.
Use y = x^2.
distortedwalrus
2014-02-20 21:05:56
factor as (x^2 - 50)(x^2 - 1)
factor as (x^2 - 50)(x^2 - 1)
DPatrick
2014-02-20 21:06:14
Right. You might find it helpful to substitute $y = x^2$ to get it as a quadratic in $y$.
Right. You might find it helpful to substitute $y = x^2$ to get it as a quadratic in $y$.
DPatrick
2014-02-20 21:06:21
Or you could just factor it straight away.
Or you could just factor it straight away.
DPatrick
2014-02-20 21:06:29
We end up with $(x^2-50)(x^2-1) < 0.$
We end up with $(x^2-50)(x^2-1) < 0.$
DPatrick
2014-02-20 21:06:53
This is only negative when the smaller factor $(x^2-50)$ is negative and the larger factor $(x^2-1)$ is positive.
This is only negative when the smaller factor $(x^2-50)$ is negative and the larger factor $(x^2-1)$ is positive.
jk23541
2014-02-20 21:07:09
x^2 has to be less than 50 but greater than 1
x^2 has to be less than 50 but greater than 1
fluffyanimal
2014-02-20 21:07:09
1<x^2<50?
1<x^2<50?
wehac
2014-02-20 21:07:09
so 1 < x^2 < 50 *it's non inclusive*
so 1 < x^2 < 50 *it's non inclusive*
VD8M9
2014-02-20 21:07:09
1<x^2<50?
1<x^2<50?
DPatrick
2014-02-20 21:07:28
Exactly. We must have $x^2-50 < 0 < x^2-1$, or $1 < x^2 < 50$.
Exactly. We must have $x^2-50 < 0 < x^2-1$, or $1 < x^2 < 50$.
DPatrick
2014-02-20 21:07:41
But remember that we only want to count integer solutions to this.
But remember that we only want to count integer solutions to this.
mathtastic
2014-02-20 21:07:59
we can find -7,-6,-5,-4,-3,-2,2,3,4,5,6,7 work so 12 values which is c
we can find -7,-6,-5,-4,-3,-2,2,3,4,5,6,7 work so 12 values which is c
ompatel99
2014-02-20 21:07:59
2 to 7 and -2 to -7
2 to 7 and -2 to -7
Tommy2000
2014-02-20 21:07:59
12 solutions, 6 positive and 6 negative x's
12 solutions, 6 positive and 6 negative x's
distortedwalrus
2014-02-20 21:07:59
so there are 6 on either side of 0
so there are 6 on either side of 0
DPatrick
2014-02-20 21:08:20
Right: there are 6 perfect squares of integers between 1 and 50, from $2^2 = 4$ up through $7^2 = 49$.
Right: there are 6 perfect squares of integers between 1 and 50, from $2^2 = 4$ up through $7^2 = 49$.
DPatrick
2014-02-20 21:08:34
Each perfect square $x^2$ gives two solutions for $x$ (for example, $2$ and $-2$).
Each perfect square $x^2$ gives two solutions for $x$ (for example, $2$ and $-2$).
DPatrick
2014-02-20 21:08:45
So there are $6 \cdot 2 = 12$ solutions. Answer (C).
So there are $6 \cdot 2 = 12$ solutions. Answer (C).
DPatrick
2014-02-20 21:09:15
(I think the question would have been meaner if 6 was an answer choice.)
(I think the question would have been meaner if 6 was an answer choice.)
DPatrick
2014-02-20 21:09:26
And on to 12B #20:
And on to 12B #20:
DPatrick
2014-02-20 21:09:32
20. For how many positive integers $x$ is $\log_{10}(x-40)+\log_{10}(60-x) < 2$?
$\phantom{12b:20}$
(A) 10 (B) 18 (C) 19 (D) 20 (E) infinitely many
20. For how many positive integers $x$ is $\log_{10}(x-40)+\log_{10}(60-x) < 2$?
$\phantom{12b:20}$
(A) 10 (B) 18 (C) 19 (D) 20 (E) infinitely many
blueberry7
2014-02-20 21:10:00
use log laws...
use log laws...
crastybow
2014-02-20 21:10:00
use log identities
use log identities
distortedwalrus
2014-02-20 21:10:00
combine then using the log rule
combine then using the log rule
ingridzhang97
2014-02-20 21:10:00
use the log product sum rule thing
use the log product sum rule thing
akshay9
2014-02-20 21:10:00
Start by combining logs and then taking it out of logarithmic form!
Start by combining logs and then taking it out of logarithmic form!
DPatrick
2014-02-20 21:10:16
Right: we can use the identity $\log a + \log b = \log ab$.
Right: we can use the identity $\log a + \log b = \log ab$.
DPatrick
2014-02-20 21:10:41
So our inequality becomes $\log_{10}(x-40)(60-x) < 2$.
So our inequality becomes $\log_{10}(x-40)(60-x) < 2$.
elsw
2014-02-20 21:11:00
(x-40)(60-x)<100
(x-40)(60-x)<100
mathmaster2012
2014-02-20 21:11:00
(x-40)(60-x)<100
(x-40)(60-x)<100
ingridzhang97
2014-02-20 21:11:00
that menas (x-40)(60-x)<100
that menas (x-40)(60-x)<100
DPatrick
2014-02-20 21:11:30
Indeed, this gives $(x-40)(60-x) < 10^2 = 100.$
Indeed, this gives $(x-40)(60-x) < 10^2 = 100.$
DPatrick
2014-02-20 21:11:59
So we can now expand and simplify this quadratic inequality.
So we can now expand and simplify this quadratic inequality.
ompatel99
2014-02-20 21:12:08
x^2-100x+2500>0
x^2-100x+2500>0
DPatrick
2014-02-20 21:12:21
It simplifies to $x^2 - 100x + 2500 > 0$, or $(x-50)^2 > 0$.
It simplifies to $x^2 - 100x + 2500 > 0$, or $(x-50)^2 > 0$.
DPatrick
2014-02-20 21:12:32
So this seems true for all $x$ except for $x=50$, so is the answer (E)??
So this seems true for all $x$ except for $x=50$, so is the answer (E)??
BobaFett101
2014-02-20 21:12:47
x-40 or x-60 can't be negative
x-40 or x-60 can't be negative
XxAndreixX
2014-02-20 21:12:47
restrictions on x
restrictions on x
joshxiong
2014-02-20 21:12:47
the logarithm is not defined for negative numbers
the logarithm is not defined for negative numbers
joshualee2000
2014-02-20 21:12:47
the log cannot be negative
the log cannot be negative
Tuxianeer
2014-02-20 21:12:47
no log domain
no log domain
DPatrick
2014-02-20 21:12:54
Good catch!
Good catch!
DPatrick
2014-02-20 21:13:10
We can't take the log of a negative number, so we need the original values in the logs to be positive.
We can't take the log of a negative number, so we need the original values in the logs to be positive.
DPatrick
2014-02-20 21:13:17
That is, we need $x-40 > 0$ and $60-x > 0$.
That is, we need $x-40 > 0$ and $60-x > 0$.
DPatrick
2014-02-20 21:13:25
This restricts us to $40 < x < 60$.
This restricts us to $40 < x < 60$.
DPatrick
2014-02-20 21:13:39
And we ruled out $x = 50$ as well.
And we ruled out $x = 50$ as well.
ILoveYouMC
2014-02-20 21:13:58
18.
18.
cheeptricks
2014-02-20 21:13:58
18 b
18 b
sparkles257
2014-02-20 21:13:58
18
18
DPatrick
2014-02-20 21:14:16
There are 19 numbers between 40 and 60 (exclusive), and then we throw away $x=50$, so we have 18 solutions. Answer (B).
There are 19 numbers between 40 and 60 (exclusive), and then we throw away $x=50$, so we have 18 solutions. Answer (B).
DPatrick
2014-02-20 21:14:41
That's all for the 2014 AMC 10B/12B Math Jam!
That's all for the 2014 AMC 10B/12B Math Jam!
DPatrick
2014-02-20 21:14:47
Next up on the calendar for many of you is the 2014 AIME. The main date for the AIME is Thursday, March 13 (3 weeks from today), and the alternate date is Wednesday, March 26.
Next up on the calendar for many of you is the 2014 AIME. The main date for the AIME is Thursday, March 13 (3 weeks from today), and the alternate date is Wednesday, March 26.
DPatrick
2014-02-20 21:14:57
For each contest, we will have our AIME Math Jam two days after the contest:
- AIME I Math Jam on Saturday, March 15 at 7 PM ET / 4 PM PT
- AIME II Math Jam on Friday, March 28 at 7 PM ET / 4 PM PT
We will discuss all 15 problems on the contest during each Math Jam. We hope you'll be able to join us!
For each contest, we will have our AIME Math Jam two days after the contest:
- AIME I Math Jam on Saturday, March 15 at 7 PM ET / 4 PM PT
- AIME II Math Jam on Friday, March 28 at 7 PM ET / 4 PM PT
We will discuss all 15 problems on the contest during each Math Jam. We hope you'll be able to join us!
DPatrick
2014-02-20 21:15:08
Finally, AoPS offers a weekend Special AIME Problem Seminar for students preparing for the AIME. The seminar meets on Saturday, March 1 and Sunday, March 2, from 3:30-6:30 Eastern (12:30-3:30 Pacific) each day. The cost is $80 (which includes both days). Details at http://www.artofproblemsolving.com/School/courseinfo.php?course_id=maa:aime:special
Finally, AoPS offers a weekend Special AIME Problem Seminar for students preparing for the AIME. The seminar meets on Saturday, March 1 and Sunday, March 2, from 3:30-6:30 Eastern (12:30-3:30 Pacific) each day. The cost is $80 (which includes both days). Details at http://www.artofproblemsolving.com/School/courseinfo.php?course_id=maa:aime:special
DPatrick
2014-02-20 21:15:23
Thanks -- have a good night!
Thanks -- have a good night!
Copyright © 2024 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
