2014 AIME I Math Jam
Go back to the Math Jam ArchiveAoPS instructors discuss all 15 problems of the 2014 AIME I.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Dave Patrick
DPatrick
2014-03-15 19:00:19
Welcome to the 2014 AIME I Math Jam!
Welcome to the 2014 AIME I Math Jam!
DPatrick
2014-03-15 19:00:28
I'm Dave Patrick, and I'll be leading our discussion tonight.
I'm Dave Patrick, and I'll be leading our discussion tonight.
DPatrick
2014-03-15 19:00:36
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
DPatrick
2014-03-15 19:00:52
This classroom is moderated, meaning that you can type into the classroom, but these comments will not go directly into the room. These comments go to the moderators, who may choose to share your comments with the room.
This classroom is moderated, meaning that you can type into the classroom, but these comments will not go directly into the room. These comments go to the moderators, who may choose to share your comments with the room.
DPatrick
2014-03-15 19:01:02
This helps keep the session organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
This helps keep the session organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
DPatrick
2014-03-15 19:01:20
There are a lot of students here! As I said, only a relatively small fraction of the well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
There are a lot of students here! As I said, only a relatively small fraction of the well-written comments will be passed to the entire group. Please do not take it personally if your comments do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!!
DPatrick
2014-03-15 19:01:40
Also, we won't be going through all the math quite as thoroughly as we do in our classes -- I can't teach all the necessary material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We always to try do so in our regular online classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
Also, we won't be going through all the math quite as thoroughly as we do in our classes -- I can't teach all the necessary material for every problem as we go. Another difference between tonight and our regular online classes is that it is very unlikely that we'll be able to answer every single question you ask. We always to try do so in our regular online classes, but we have a large number of students tonight! So, please go ahead and ask questions, but also please understand if we aren't able to answer them all!
DPatrick
2014-03-15 19:02:15
We do have two teaching assistants with us tonight to help answer your questions: Elena (Anna Smith) and Alyssa (baozhale). (At least I expect to have two -- one is apparently running late.)
We do have two teaching assistants with us tonight to help answer your questions: Elena (Anna Smith) and Alyssa (baozhale). (At least I expect to have two -- one is apparently running late.)
DPatrick
2014-03-15 19:02:30
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
DPatrick
2014-03-15 19:03:06
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. Also on occasion we may stop to prove things that you wouldn't necessary need to prove while doing the contest. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, so please don't write comments that skip key steps or jump ahead in the problem.
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics. Also on occasion we may stop to prove things that you wouldn't necessary need to prove while doing the contest. So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, so please don't write comments that skip key steps or jump ahead in the problem.
DPatrick
2014-03-15 19:03:34
Let's get started! We're going to work through all 15 problems, in order.
Let's get started! We're going to work through all 15 problems, in order.
DPatrick
2014-03-15 19:03:42
1. The 8 eyelets for the lace of a sneaker all lie on a rectangle, four equally spaced on each of the longer sides. The rectangle has a width of 50 mm and a length of 80 mm. There is one eyelet at each vertex of the rectangle. The lace itself must pass between the vertex eyelets along a width side of the rectangle and then crisscross between successive eyelets until it reaches the two eyelets at the other width side of the rectangle as shown. After passing through these final eyelets, each of the ends of the lace must extend at least 200 mm farther to allow a knot to be tied. Find the minimum length of the lace in millimeters.
1. The 8 eyelets for the lace of a sneaker all lie on a rectangle, four equally spaced on each of the longer sides. The rectangle has a width of 50 mm and a length of 80 mm. There is one eyelet at each vertex of the rectangle. The lace itself must pass between the vertex eyelets along a width side of the rectangle and then crisscross between successive eyelets until it reaches the two eyelets at the other width side of the rectangle as shown. After passing through these final eyelets, each of the ends of the lace must extend at least 200 mm farther to allow a knot to be tied. Find the minimum length of the lace in millimeters.
DPatrick
2014-03-15 19:03:48
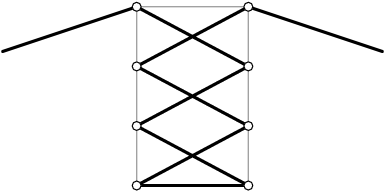

DPatrick
2014-03-15 19:03:59
(Note that I will always place the current problem under discussion at the top of the classroom window. You can resize the top area of the classroom by dragging the horizontal bar separating it from the rest of the classroom.)
(Note that I will always place the current problem under discussion at the top of the classroom window. You can resize the top area of the classroom by dragging the horizontal bar separating it from the rest of the classroom.)
DPatrick
2014-03-15 19:04:17
What is the total lace length that we have to count up?
What is the total lace length that we have to count up?
DPatrick
2014-03-15 19:04:25
How would you describe it, in words?
How would you describe it, in words?
poweroftwo
2014-03-15 19:04:58
ends, bottom, and diagonals
ends, bottom, and diagonals
minimario
2014-03-15 19:04:58
The 2 ends + the 6 crosses + the bottom line
The 2 ends + the 6 crosses + the bottom line
borntobeweild
2014-03-15 19:04:58
The 6 digs, the bottom, and the two trailing ends
The 6 digs, the bottom, and the two trailing ends
checkmate1021
2014-03-15 19:04:58
the six diagonal things, the bottom width, and the two ends
the six diagonal things, the bottom width, and the two ends
cellobix
2014-03-15 19:04:58
2 ends, 6 diagonals, and 1 horizontal piece
2 ends, 6 diagonals, and 1 horizontal piece
DuoCapital
2014-03-15 19:04:58
The bottom, plus the complementary diagonals, plus the two ends
The bottom, plus the complementary diagonals, plus the two ends
Quadratic64
2014-03-15 19:04:58
6 * diagonals + 2 * 200mm extensions + straight part on the bottom
6 * diagonals + 2 * 200mm extensions + straight part on the bottom
DPatrick
2014-03-15 19:05:07
Right. Simply put, we have:
2 * (the length of laces that extends to either side) +
6 * (the length of the diagonal segments) +
(the length of the bottom segment)
Right. Simply put, we have:
2 * (the length of laces that extends to either side) +
6 * (the length of the diagonal segments) +
(the length of the bottom segment)
DPatrick
2014-03-15 19:05:23
The first of these is easy: the laces extend for 200 mm on either side.
The first of these is easy: the laces extend for 200 mm on either side.
joshualee2000
2014-03-15 19:05:42
the bottom is just 50mm
the bottom is just 50mm
DPatrick
2014-03-15 19:05:51
The last (the bottom piece) is also easy: it's just the width of 50 mm.
The last (the bottom piece) is also easy: it's just the width of 50 mm.
DPatrick
2014-03-15 19:05:56
How about the diagonal lengths?
How about the diagonal lengths?
mathtastic
2014-03-15 19:06:23
You can use a well known theorem, known as the Pythagorean Theorem, to find the lengths of the diagonals.
You can use a well known theorem, known as the Pythagorean Theorem, to find the lengths of the diagonals.
aimingforimo
2014-03-15 19:06:23
draw right triangles
draw right triangles
ingridzhang97
2014-03-15 19:06:23
the diagonals are easy too. just use pythagorean
the diagonals are easy too. just use pythagorean
blizzard10
2014-03-15 19:06:23
pythagoream theorem
pythagoream theorem
vinayak-kumar
2014-03-15 19:06:23
Pythagorean Theorem
Pythagorean Theorem
hamup1
2014-03-15 19:06:23
each eyelet section is 80/3, and the width is 150/3 (pythag triples)
each eyelet section is 80/3, and the width is 150/3 (pythag triples)
DPatrick
2014-03-15 19:06:34
Right. We can zoom in on one of the diagonal segments.
Right. We can zoom in on one of the diagonal segments.
DPatrick
2014-03-15 19:06:40


DPatrick
2014-03-15 19:06:59
As you can see, it's a right triangle. The top side has length 50 mm, and the right side has length (80/3) mm.
As you can see, it's a right triangle. The top side has length 50 mm, and the right side has length (80/3) mm.
jeff10
2014-03-15 19:07:24
hypotenuse of the right triangle with legs 50 and 80/3, which is 150/3 and 80/3, so each of the 6 crosses has a length of 170/3
hypotenuse of the right triangle with legs 50 and 80/3, which is 150/3 and 80/3, so each of the 6 crosses has a length of 170/3
LightningX48
2014-03-15 19:07:24
so it's 170/3 (8, 15, 17)
so it's 170/3 (8, 15, 17)
Tommy2000
2014-03-15 19:07:24
use pythagorean theorem for 50, 80/3 to get the diagonal as 170/3
use pythagorean theorem for 50, 80/3 to get the diagonal as 170/3
sat113
2014-03-15 19:07:24
8-15-17
8-15-17
dli00105
2014-03-15 19:07:24
170/3
170/3
summitwei
2014-03-15 19:07:24
8-15-17
8-15-17
Rectangle_Square
2014-03-15 19:07:24
one side 80/3 other is 150/3 knowing 8-15-17 triple the diagonal is 170/3
one side 80/3 other is 150/3 knowing 8-15-17 triple the diagonal is 170/3
DPatrick
2014-03-15 19:07:38
Exactly. You could use the Pythagorean Theorem, but we know that the final answer is an integer, so we suspect that this triangle must be a multiple of a Pythagorean triple.
Exactly. You could use the Pythagorean Theorem, but we know that the final answer is an integer, so we suspect that this triangle must be a multiple of a Pythagorean triple.
DPatrick
2014-03-15 19:07:48
Indeed, the triangle is similar to an 8-15-17 triangle (with scale factor 10/3: 80/3 = (10/3)*8 and 50 = (10/3)*15).
Indeed, the triangle is similar to an 8-15-17 triangle (with scale factor 10/3: 80/3 = (10/3)*8 and 50 = (10/3)*15).
DPatrick
2014-03-15 19:08:08
So the hypotenuse has length 170/3 mm.
So the hypotenuse has length 170/3 mm.
ninjataco
2014-03-15 19:08:37
So the total is 2*200 + 50 + 6*170/3 = 790
So the total is 2*200 + 50 + 6*170/3 = 790
1915933
2014-03-15 19:08:37
2(200)+6(170/3)+1(50)=790
2(200)+6(170/3)+1(50)=790
Eudokia
2014-03-15 19:08:37
multiply by 6 to get 340 for the diagonals
multiply by 6 to get 340 for the diagonals
tRIG
2014-03-15 19:08:37
multiply that by 6?
multiply that by 6?
bunniesrcute
2014-03-15 19:08:37
so our final answer is 50 + 6*170/3 + 200*2 = 790
so our final answer is 50 + 6*170/3 + 200*2 = 790
DPatrick
2014-03-15 19:08:49
Right, summing up all these lengths, we get a total length of 2(200)+6(170/3)+50=400+340+50=790.
Right, summing up all these lengths, we get a total length of 2(200)+6(170/3)+50=400+340+50=790.
DPatrick
2014-03-15 19:09:23
That was the traditional AIME warmup question -- pretty straightforward but as always you have to be careful with the computation.
That was the traditional AIME warmup question -- pretty straightforward but as always you have to be careful with the computation.
DPatrick
2014-03-15 19:09:30
On to #2:
On to #2:
DPatrick
2014-03-15 19:09:34
2. An urn contains 4 green balls and 6 blue balls. A second urn contains 16 green balls and N blue balls. A single ball is drawn at random from each urn. The probability that both balls are of the same color is 0.58. Find N.
2. An urn contains 4 green balls and 6 blue balls. A second urn contains 16 green balls and N blue balls. A single ball is drawn at random from each urn. The probability that both balls are of the same color is 0.58. Find N.
DPatrick
2014-03-15 19:09:51
How can we approach this?
How can we approach this?
VietaFan
2014-03-15 19:10:28
Cases: Blue and blue or green and green
Cases: Blue and blue or green and green
bob2
2014-03-15 19:10:28
casework for 2 green balls and 2 blue balls
casework for 2 green balls and 2 blue balls
aimingforimo
2014-03-15 19:10:28
find probability of green, then add to blue
find probability of green, then add to blue
genesis2
2014-03-15 19:10:28
probability of green balls from both boxes + same for blue
probability of green balls from both boxes + same for blue
navygoat123
2014-03-15 19:10:28
find the probability for two green balls, and find the probability for two blue balls and add them up
find the probability for two green balls, and find the probability for two blue balls and add them up
DPatrick
2014-03-15 19:10:33
Right. There are two cases for us to "succeed" in drawing two balls of the same color: we can draw two green balls, or we can draw two blue balls.
Right. There are two cases for us to "succeed" in drawing two balls of the same color: we can draw two green balls, or we can draw two blue balls.
DPatrick
2014-03-15 19:10:43
These cases are exclusive (they don't overlap), so we can compute the probability separately of each case, and then add those probabilities to get the overall probability of success.
These cases are exclusive (they don't overlap), so we can compute the probability separately of each case, and then add those probabilities to get the overall probability of success.
DPatrick
2014-03-15 19:10:53
What's the probability of drawing 2 green balls?
What's the probability of drawing 2 green balls?
bellyflop
2014-03-15 19:11:21
both green=> (4/10)(16/16+N)
both green=> (4/10)(16/16+N)
brian22
2014-03-15 19:11:21
Green balls: (4/10)*(16/16+N)
Green balls: (4/10)*(16/16+N)
forthegreatergood
2014-03-15 19:11:21
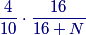
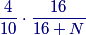
Zer0waltz
2014-03-15 19:11:21
2/5 times 16/16+n
2/5 times 16/16+n
raptorw
2014-03-15 19:11:21
4/10*16/(N+16)
4/10*16/(N+16)
DPatrick
2014-03-15 19:11:29
There's a 25 chance of drawing a green ball from the first urn.
There's a 25 chance of drawing a green ball from the first urn.
DPatrick
2014-03-15 19:11:36
There's a 16N+16 chance of drawing a green ball from the second urn.
There's a 16N+16 chance of drawing a green ball from the second urn.
DPatrick
2014-03-15 19:11:44
So there's a 325(N+16) of drawing green balls from both urns.
So there's a 325(N+16) of drawing green balls from both urns.
DPatrick
2014-03-15 19:11:51
What's the probability of drawing 2 blue balls?
What's the probability of drawing 2 blue balls?
sparkles257
2014-03-15 19:12:14
3/5 * N/16+N
3/5 * N/16+N
maxwellfl
2014-03-15 19:12:14
(6/10)*(N/16+N) for blues
(6/10)*(N/16+N) for blues
checkmate1021
2014-03-15 19:12:14
610×N16+N
610×N16+N
chezbgone2
2014-03-15 19:12:14
610⋅nn+16
610⋅nn+16
bgu
2014-03-15 19:12:14
both red => (3/5)(N/16+N)
both red => (3/5)(N/16+N)
borntobeweild
2014-03-15 19:12:14
3/5*N/(N+16)
3/5*N/(N+16)
samuelczhao
2014-03-15 19:12:14
3/5 * N/N+16
3/5 * N/N+16
1023ong
2014-03-15 19:12:14
6/10 * N/(N+16)
6/10 * N/(N+16)
DPatrick
2014-03-15 19:12:18
There's a 35 chance of drawing a blue ball from the first urn.
There's a 35 chance of drawing a blue ball from the first urn.
DPatrick
2014-03-15 19:12:24
There's a NN+16 chance of drawing a blue ball from the second urn.
There's a NN+16 chance of drawing a blue ball from the second urn.
DPatrick
2014-03-15 19:12:29
So there's a 3N5(N+16) of drawing blue balls from both urns.
So there's a 3N5(N+16) of drawing blue balls from both urns.
DPatrick
2014-03-15 19:12:40
So what is the probability of drawing balls of the same color?
So what is the probability of drawing balls of the same color?
niraekjs
2014-03-15 19:13:12
This is the equation we can write 410⋅1616+N+610⋅N16+N=2950.
This is the equation we can write 410⋅1616+N+610⋅N16+N=2950.
mathtastic
2014-03-15 19:13:12
sum of them=58/100
sum of them=58/100
shreshrej
2014-03-15 19:13:12
Add them up!
Add them up!
bluephoenix
2014-03-15 19:13:12
29/100
29/100
popcorn1
2014-03-15 19:13:12
0.58
0.58
Lightningwing
2014-03-15 19:13:12
(32+3n)/5(16+n)
(32+3n)/5(16+n)
Tarin57
2014-03-15 19:13:12
32 + 3N / 5n + 80
32 + 3N / 5n + 80
DPatrick
2014-03-15 19:13:26
Right, since these are exclusive cases. we add the above probabilities: 325(N+16)+3N5(N+16)=32+3N5(N+16).
Right, since these are exclusive cases. we add the above probabilities: 325(N+16)+3N5(N+16)=32+3N5(N+16).
DPatrick
2014-03-15 19:13:33
Thus we have the equation 32+3N5(N+16)=0.58=2950.
Thus we have the equation 32+3N5(N+16)=0.58=2950.
jigglypuff
2014-03-15 19:13:57
cross multiply
cross multiply
6stars
2014-03-15 19:13:57
Cross mulitply, get N = 144
Cross mulitply, get N = 144
ViolinNinja256
2014-03-15 19:13:57
so now we can cross multiply
so now we can cross multiply
cellobix
2014-03-15 19:13:57
Cross-multiply.
Cross-multiply.
picuberoot
2014-03-15 19:13:57
Solve for N!
Solve for N!
Rectangle_Square
2014-03-15 19:13:57
cross multiply and solve
cross multiply and solve
DPatrick
2014-03-15 19:14:02
Right, it's straightforward algebra from here.
Right, it's straightforward algebra from here.
DPatrick
2014-03-15 19:14:07
Multiply both sides by 5 to get 32+3NN+16=2910.
Multiply both sides by 5 to get 32+3NN+16=2910.
DPatrick
2014-03-15 19:14:14
Cross-multiply to get 320+30N=29N+464.
Cross-multiply to get 320+30N=29N+464.
MathStudent2002
2014-03-15 19:14:24


dli00105
2014-03-15 19:14:24
N=144
N=144
LightningX48
2014-03-15 19:14:24
n = 144!
n = 144!
Tommy2000
2014-03-15 19:14:24
answer = 144
answer = 144
vinayak-kumar
2014-03-15 19:14:24
N=144
N=144
DPatrick
2014-03-15 19:14:28
And yes, N=464−320=144.
And yes, N=464−320=144.
DPatrick
2014-03-15 19:15:11
Again, a reminder: there are nearly 200 students here! So please don't feel bad if your comments don't get posted -- I can only post a small portion of what you guys type in. But please keep participating!
Again, a reminder: there are nearly 200 students here! So please don't feel bad if your comments don't get posted -- I can only post a small portion of what you guys type in. But please keep participating!
DPatrick
2014-03-15 19:15:20
On to #3:
On to #3:
DPatrick
2014-03-15 19:15:25
3. Find the number of rational numbers r, 0<r<1, such that when r is written as a fraction in lowest terms, the numerator and denominator have a sum of 1000.
3. Find the number of rational numbers r, 0<r<1, such that when r is written as a fraction in lowest terms, the numerator and denominator have a sum of 1000.
DPatrick
2014-03-15 19:15:37
What do these fractions look like?
What do these fractions look like?
basketball8
2014-03-15 19:16:01
x/1000-x
x/1000-x
bob2
2014-03-15 19:16:01
r/(1000-r)
r/(1000-r)
chezbgone2
2014-03-15 19:16:01
n1000−n
n1000−n
tRIG
2014-03-15 19:16:01
a/(1000-a) where a<500
a/(1000-a) where a<500
Eudokia
2014-03-15 19:16:01
n/(1000-n)
n/(1000-n)
hwl0304
2014-03-15 19:16:01
n/(1000-n)
n/(1000-n)
TheEconomist
2014-03-15 19:16:01
n/1000-n
n/1000-n
allaoc
2014-03-15 19:16:01
n/(1000-n)
n/(1000-n)
DPatrick
2014-03-15 19:16:08
Right: they're of the form n1000−n where 0<n<500. (If n≥500, then the fraction is greater than 1.)
Right: they're of the form n1000−n where 0<n<500. (If n≥500, then the fraction is greater than 1.)
DPatrick
2014-03-15 19:16:25
What does it mean that it is in lowest terms?
What does it mean that it is in lowest terms?
alex31415
2014-03-15 19:16:49
gcd(n,1000-n)=1
gcd(n,1000-n)=1
ashgabat
2014-03-15 19:16:49
They have no common divisors
They have no common divisors
fz0718
2014-03-15 19:16:49
GCD(N,1000-N)=1
GCD(N,1000-N)=1
sat113
2014-03-15 19:16:49
n and 1000-n are relatively prime
n and 1000-n are relatively prime
mathman523
2014-03-15 19:16:49
gcf of n and 1000-n is 1
gcf of n and 1000-n is 1
Bluedevil98
2014-03-15 19:16:49
relatively prime
relatively prime
VCheep
2014-03-15 19:16:49
n and 1000-n are relatively prime
n and 1000-n are relatively prime
DPatrick
2014-03-15 19:16:55
Exactly. It means that n and 1000−n have no common factors.
Exactly. It means that n and 1000−n have no common factors.
DPatrick
2014-03-15 19:17:03
But what's equivalent to this, and simpler?
But what's equivalent to this, and simpler?
El_Ectric
2014-03-15 19:17:24
gcd(n,1000-n) => gcd(n,1000)=1 by euclidean algorihtm
gcd(n,1000-n) => gcd(n,1000)=1 by euclidean algorihtm
mentalgenius
2014-03-15 19:17:24
n and 1000 have no common factors
n and 1000 have no common factors
Quadratic64
2014-03-15 19:17:24
n and 1000 are relatively prime
n and 1000 are relatively prime
martian179
2014-03-15 19:17:24
n coprime with 1000
n coprime with 1000
DrMath
2014-03-15 19:17:24
Euclidean algorithm -----------> gcd(a,1000)=1
Euclidean algorithm -----------> gcd(a,1000)=1
sjain
2014-03-15 19:17:24
no common factors between 1000 and n
no common factors between 1000 and n
ingridzhang97
2014-03-15 19:17:24
n and 1000 are relatively prime
n and 1000 are relatively prime
DPatrick
2014-03-15 19:18:05
Right. Note that gcd(n,1000−n)=gcd(n,1000), so n and 1000 cannot have any common factors. (That's one step of the Euclidean Algorithm for finding greatest common divisor. Or, you can note that if n and 1000−n are both multiples of the some number, then so is their sum of 1000.)
Right. Note that gcd(n,1000−n)=gcd(n,1000), so n and 1000 cannot have any common factors. (That's one step of the Euclidean Algorithm for finding greatest common divisor. Or, you can note that if n and 1000−n are both multiples of the some number, then so is their sum of 1000.)
claudeaops
2014-03-15 19:18:20
n is not divisible by 2 or 5
n is not divisible by 2 or 5
Verjok
2014-03-15 19:18:20
n is not divisible by 2 or 5
n is not divisible by 2 or 5
bengals
2014-03-15 19:18:20
2 or 5 does not divide n
2 or 5 does not divide n
Tan
2014-03-15 19:18:20
n doesnt not have any prime factors of 2 and 5
n doesnt not have any prime factors of 2 and 5
DPatrick
2014-03-15 19:18:37
Right, going one step further, n is relatively prime to 1000 if and only if n has no prime factors of 2 or 5.
Right, going one step further, n is relatively prime to 1000 if and only if n has no prime factors of 2 or 5.
DPatrick
2014-03-15 19:18:47
So we need to count how many numbers in 0<n<500 have no factors of 2 or 5.
So we need to count how many numbers in 0<n<500 have no factors of 2 or 5.
DPatrick
2014-03-15 19:19:25
A lot of you are saying fancy things like "totient" or "Euler's Formula" or "inclusion-exclusion", but it's much simpler than that.
A lot of you are saying fancy things like "totient" or "Euler's Formula" or "inclusion-exclusion", but it's much simpler than that.
DPatrick
2014-03-15 19:19:31
How many odd numbers are between 0 and 500?
How many odd numbers are between 0 and 500?
ninjataco
2014-03-15 19:19:43
250
250
summitwei
2014-03-15 19:19:43
250
250
poweroftwo
2014-03-15 19:19:43
250
250
minimario
2014-03-15 19:19:43
250
250
navygoat123
2014-03-15 19:19:43
250
250
popcorn1
2014-03-15 19:19:43
250
250
CornSaltButter
2014-03-15 19:19:43
250.
250.
DPatrick
2014-03-15 19:19:47
There are 250 odd integers between 0 and 500.
There are 250 odd integers between 0 and 500.
DPatrick
2014-03-15 19:20:03
And how many of them do we have to throw away because they are (odd) multiples of 5?
And how many of them do we have to throw away because they are (odd) multiples of 5?
bellyflop
2014-03-15 19:20:21
1/5 aof them are div by 5
1/5 aof them are div by 5
ViolinNinja256
2014-03-15 19:20:21
1/5th are divisible by 5
1/5th are divisible by 5
forthegreatergood
2014-03-15 19:20:21
a fifth of these are multiples of 5 so 250-50=200 (ANSWER)
a fifth of these are multiples of 5 so 250-50=200 (ANSWER)
aimingforimo
2014-03-15 19:20:21
50
50
picuberoot
2014-03-15 19:20:21
50
50
kenneth102099
2014-03-15 19:20:21
50
50
darthvader1521
2014-03-15 19:20:21
50
50
joshualee2000
2014-03-15 19:20:21
50
50
samuelczhao
2014-03-15 19:20:21
50
50
raptorw
2014-03-15 19:20:21
50
50
DPatrick
2014-03-15 19:20:26
Exactly 50: 1*5, 3*5, 5*5, ..., up to 99*5.
Exactly 50: 1*5, 3*5, 5*5, ..., up to 99*5.
DPatrick
2014-03-15 19:20:31
So that leaves 250−50=200 values of n, and thus 200 such rational numbers.
So that leaves 250−50=200 values of n, and thus 200 such rational numbers.
DPatrick
2014-03-15 19:20:54
OK, on to #4:
OK, on to #4:
DPatrick
2014-03-15 19:20:58
4. Jon and Steve ride their bicycles along a path that parallels two side-by-side train tracks running in the east/west direction. Jon rides east at 20 miles per hour, and Steve rides west at 20 miles per hour. Two trains of equal lengths, traveling in opposite directions at constant but different speeds, each pass the two riders. Each train takes exactly 1 minute to go past Jon. The westbound train takes 10 times as long as the eastbound train to go past Steve. The length of each train is mn miles, where m and n are relatively prime positive integers. Find m+n.
4. Jon and Steve ride their bicycles along a path that parallels two side-by-side train tracks running in the east/west direction. Jon rides east at 20 miles per hour, and Steve rides west at 20 miles per hour. Two trains of equal lengths, traveling in opposite directions at constant but different speeds, each pass the two riders. Each train takes exactly 1 minute to go past Jon. The westbound train takes 10 times as long as the eastbound train to go past Steve. The length of each train is mn miles, where m and n are relatively prime positive integers. Find m+n.
DPatrick
2014-03-15 19:21:11
Yikes, that's a lot of words. With a wordy problem like this, be sure to read it carefully.
Yikes, that's a lot of words. With a wordy problem like this, be sure to read it carefully.
Bluedevil98
2014-03-15 19:21:24
d=rt
d=rt
sat113
2014-03-15 19:21:24
d=rt
d=rt
cellobix
2014-03-15 19:21:24
d=rt
d=rt
DPatrick
2014-03-15 19:21:40
Indeed, the equation (distance) = (rate)(time), or d=rt for short, is probably going to be our main tool in this problem.
Indeed, the equation (distance) = (rate)(time), or d=rt for short, is probably going to be our main tool in this problem.
DPatrick
2014-03-15 19:22:24
Some of you might find that drawing a picture is helpful to keep track of which train is which and which cyclist is which. If you want to do that, that's great. I didn't in fact draw one myself.
Some of you might find that drawing a picture is helpful to keep track of which train is which and which cyclist is which. If you want to do that, that's great. I didn't in fact draw one myself.
ninjataco
2014-03-15 19:22:29
I would like to define several variables.
I would like to define several variables.
Bluedevil98
2014-03-15 19:22:29
assign variables
assign variables
DPatrick
2014-03-15 19:22:39
Sure, let's start by assigning variables to the various unknown quantities.
Sure, let's start by assigning variables to the various unknown quantities.
DPatrick
2014-03-15 19:22:43
Let:
L be the length of each train in miles
vE be the speed of the eastbound train in miles per hour
vW be the speed of the westbound train in miles per hour
t be the time that it takes the eastbound train to pass Steve (in hours)
(The time that the westbound train takes to pass Steve is then 10t.)
Let:
L be the length of each train in miles
vE be the speed of the eastbound train in miles per hour
vW be the speed of the westbound train in miles per hour
t be the time that it takes the eastbound train to pass Steve (in hours)
(The time that the westbound train takes to pass Steve is then 10t.)
DPatrick
2014-03-15 19:23:03
This is everything that's unknown in the problem as far as I can tell. And remember that we're trying to find L.
This is everything that's unknown in the problem as far as I can tell. And remember that we're trying to find L.
DPatrick
2014-03-15 19:23:18
OK, now how can we use the data given in the problem?
OK, now how can we use the data given in the problem?
DPatrick
2014-03-15 19:23:56
I should mention that there are lots of different ways you could assign variables and set up equations...I'm just going to present the method that seemed most natural to me. (And it turned out to work nice in the end.)
I should mention that there are lots of different ways you could assign variables and set up equations...I'm just going to present the method that seemed most natural to me. (And it turned out to work nice in the end.)
DPatrick
2014-03-15 19:24:12
What equation(s) can we write for "Each train takes exactly 1 minute to go past Jon"?
What equation(s) can we write for "Each train takes exactly 1 minute to go past Jon"?
DPatrick
2014-03-15 19:24:51
Let's focus on the eastbound train first.
Let's focus on the eastbound train first.
LightningX48
2014-03-15 19:25:22
1 minute * v_e = 1/3 mile + L
1 minute * v_e = 1/3 mile + L
DPatrick
2014-03-15 19:25:43
That's right, but let's try to keep all our units in miles and hours.
That's right, but let's try to keep all our units in miles and hours.
DPatrick
2014-03-15 19:25:50
To pass Jon in 1 minute, how much distance does the eastbound train have to cover?
To pass Jon in 1 minute, how much distance does the eastbound train have to cover?
bellyflop
2014-03-15 19:26:15
1/3+L
1/3+L
mdlu
2014-03-15 19:26:15
L+1/3 mile
L+1/3 mile
danusv
2014-03-15 19:26:15
1/3+L
1/3+L
hamup1
2014-03-15 19:26:15
1/3+L miles
1/3+L miles
Tommy2000
2014-03-15 19:26:15
L+1/3
L+1/3
DPatrick
2014-03-15 19:26:39
Right. Jon bikes 13 mile in 1 minute, going in the same direction as the train. So the back end of the train to be even with Jon 1 minute after the front of the train is even with Jon. Thus it has to go L+13 miles in that 1 minute.
Right. Jon bikes 13 mile in 1 minute, going in the same direction as the train. So the back end of the train to be even with Jon 1 minute after the front of the train is even with Jon. Thus it has to go L+13 miles in that 1 minute.
claudeaops
2014-03-15 19:27:14
L+1/3=v_e*1/60
L+1/3=v_e*1/60
DPatrick
2014-03-15 19:27:31
Exactly, but let's get rid of the fraction. In an hour, the eastbound train travels 60L+20 miles. Thus its velocity is vE=60L+20.
Exactly, but let's get rid of the fraction. In an hour, the eastbound train travels 60L+20 miles. Thus its velocity is vE=60L+20.
shreshrej
2014-03-15 19:27:57
Now for the westbound train!
Now for the westbound train!
DPatrick
2014-03-15 19:28:19
Right. You can probably guess the answer by symmetry, but what's the velocity of the westbound train, given that it also takes 1 minute to pass Jon?
Right. You can probably guess the answer by symmetry, but what's the velocity of the westbound train, given that it also takes 1 minute to pass Jon?
hwl0304
2014-03-15 19:28:45
60L-20?
60L-20?
ninjataco
2014-03-15 19:28:45
L−1/3=160vW⟹60L−20=vW
L−1/3=160vW⟹60L−20=vW
othuum0149
2014-03-15 19:28:45
60L-20
60L-20
vinayak-kumar
2014-03-15 19:28:45
60L−20
60L−20
allaoc
2014-03-15 19:28:45
60L - 20
60L - 20
CornSaltButter
2014-03-15 19:28:45
60L-20?
60L-20?
mathwizard888
2014-03-15 19:28:45
60L-20
60L-20
dantx5
2014-03-15 19:28:45
60L-20
60L-20
Eudokia
2014-03-15 19:28:45
v_W=60L-20
v_W=60L-20
picuberoot
2014-03-15 19:28:45
v_w = 60L - 20
v_w = 60L - 20
DPatrick
2014-03-15 19:28:59
Right. Since Jon has moved 13 mile in the opposite direction, the westbound train only has to go L−13 miles in 1 minute.
Right. Since Jon has moved 13 mile in the opposite direction, the westbound train only has to go L−13 miles in 1 minute.
DPatrick
2014-03-15 19:29:12
So in an hour, it travels 60L−20 miles. Its velocity is thus vW=60L−20.
So in an hour, it travels 60L−20 miles. Its velocity is thus vW=60L−20.
DPatrick
2014-03-15 19:29:24
Let's recap. Now we have:
L is the length of each train in miles
The eastbound train is moving at a speed of 60L+20 miles per hour, and passes Steve in time t.
The westbound train is moving at a speed of 60L−20 miles per hour, and passes Steve in time 10t.
Let's recap. Now we have:
L is the length of each train in miles
The eastbound train is moving at a speed of 60L+20 miles per hour, and passes Steve in time t.
The westbound train is moving at a speed of 60L−20 miles per hour, and passes Steve in time 10t.
DPatrick
2014-03-15 19:29:50
So let's try to write the same equations for passing Steve for each train.
So let's try to write the same equations for passing Steve for each train.
DPatrick
2014-03-15 19:30:12
How far does the eastbound train have to travel to pass Steve?
How far does the eastbound train have to travel to pass Steve?
DPatrick
2014-03-15 19:30:52
Remember, it has to go a distance of L minus however long Steve has traveled in time t. (Steve is moving opposite the train, shortening the necessary distance.)
Remember, it has to go a distance of L minus however long Steve has traveled in time t. (Steve is moving opposite the train, shortening the necessary distance.)
othuum0149
2014-03-15 19:31:16
L-20t
L-20t
bellyflop
2014-03-15 19:31:20
L-20t
L-20t
hwl0304
2014-03-15 19:31:20
L-20t?
L-20t?
DPatrick
2014-03-15 19:31:26
Right. Steve has moved 20t miles in time t.
Right. Steve has moved 20t miles in time t.
DPatrick
2014-03-15 19:31:36
Thus the train has to travel L−20t miles in time t.
Thus the train has to travel L−20t miles in time t.
DPatrick
2014-03-15 19:31:42
What equation does that allow us to write?
What equation does that allow us to write?
mdlu
2014-03-15 19:32:22
L-20t=(60L+20)t
L-20t=(60L+20)t
Eudokia
2014-03-15 19:32:22
L-20t=(60L+20)t
L-20t=(60L+20)t
Tarin57
2014-03-15 19:32:22
L - 20t = (60L + 20)(t)
L - 20t = (60L + 20)(t)
navygoat123
2014-03-15 19:32:22
L-20t/t = 60L-20
L-20t/t = 60L-20
DPatrick
2014-03-15 19:32:30
We can use the usual d=rt equation to write
L−20t=(60L+20)(t).
We can use the usual d=rt equation to write
L−20t=(60L+20)(t).
DPatrick
2014-03-15 19:32:42
How about the westbound train?
How about the westbound train?
LightningX48
2014-03-15 19:33:03
And for the westbound train, it has to go L + 200t miles
And for the westbound train, it has to go L + 200t miles
DPatrick
2014-03-15 19:33:24
Right: for the westbound train, the signs are reversed, and t gets replaced by 10t.
Right: for the westbound train, the signs are reversed, and t gets replaced by 10t.
cellobix
2014-03-15 19:33:30
The train travels L+200t, so L+200t=(60t-20)(10t)
The train travels L+200t, so L+200t=(60t-20)(10t)
DPatrick
2014-03-15 19:34:01
Again, though, in words:
Again, though, in words:
DPatrick
2014-03-15 19:34:15
The westbound train takes 10t hours to pass Steve.
The westbound train takes 10t hours to pass Steve.
DPatrick
2014-03-15 19:34:35
It has to travel its length L plus the distance Steve has traveled. (Steve is moving in the same direction as the train, thus lengthening the distance necessary.)
It has to travel its length L plus the distance Steve has traveled. (Steve is moving in the same direction as the train, thus lengthening the distance necessary.)
DPatrick
2014-03-15 19:34:41
But Steve has moved 200t miles in time 10t.
But Steve has moved 200t miles in time 10t.
DPatrick
2014-03-15 19:34:49
Thus the train has to travel L+200t miles in time 10t.
Thus the train has to travel L+200t miles in time 10t.
DPatrick
2014-03-15 19:34:54
Again using d=rt, we have L+200t=(60L−20)(10t).
Again using d=rt, we have L+200t=(60L−20)(10t).
LightningX48
2014-03-15 19:35:01
yeay two equations two variables; let's solve!
yeay two equations two variables; let's solve!
popcorn1
2014-03-15 19:35:01
combine the two equations
combine the two equations
DPatrick
2014-03-15 19:35:09
Indeed, now we have a system of two equations in two variables:
L−20t=(60L+20)t,L+200t=(60L−20)(10t).
Indeed, now we have a system of two equations in two variables:
L−20t=(60L+20)t,L+200t=(60L−20)(10t).
DPatrick
2014-03-15 19:35:27
Remember: our goal is to solve for L. How do we continue?
Remember: our goal is to solve for L. How do we continue?
VietaFan
2014-03-15 19:35:47
isolate L on one side
isolate L on one side
DPatrick
2014-03-15 19:36:14
As usual, there are tons of ways to solve "two equations in two variables", but I think the most efficient is to isolate L in each of them, because something nice happens.
As usual, there are tons of ways to solve "two equations in two variables", but I think the most efficient is to isolate L in each of them, because something nice happens.
DPatrick
2014-03-15 19:36:22
We can rearrange slightly to get
L=t(60L+40),L=t(600L−400).
We can rearrange slightly to get
L=t(60L+40),L=t(600L−400).
swamih
2014-03-15 19:36:44
the t's cancel out
the t's cancel out
Quadratic64
2014-03-15 19:36:44
equate them and the t's cancel
equate them and the t's cancel
mathtastic
2014-03-15 19:36:44
set equal divide by t
set equal divide by t
room456
2014-03-15 19:36:47
60L+40=600L-400
60L+40=600L-400
ninjataco
2014-03-15 19:36:47
600L−400=60L+40
600L−400=60L+40
DPatrick
2014-03-15 19:37:09
Right: equating them and dividing by t just leaves 60L+40=600L−400.
Right: equating them and dividing by t just leaves 60L+40=600L−400.
shreshrej
2014-03-15 19:37:21
Simplify for L = 22/27, so 22+27= 49
Simplify for L = 22/27, so 22+27= 49
raptorw
2014-03-15 19:37:21
L=22/27
L=22/27
bellyflop
2014-03-15 19:37:21
22/27=L so our answer is 49.
22/27=L so our answer is 49.
joshxiong
2014-03-15 19:37:28
540L=440⟹L=2227
540L=440⟹L=2227
dli00105
2014-03-15 19:37:28
22/27 so 49
22/27 so 49
DPatrick
2014-03-15 19:37:34
Yes. This simplifies to 440=540L, so L=4454=2227. Hence the answer is 22+27=049.
Yes. This simplifies to 440=540L, so L=4454=2227. Hence the answer is 22+27=049.
DPatrick
2014-03-15 19:38:08
It wasn't super-hard if you defined your variables carefully and just applied d=rt consistently throughout.
It wasn't super-hard if you defined your variables carefully and just applied d=rt consistently throughout.
DPatrick
2014-03-15 19:38:15
It was a bit tedious, though.
It was a bit tedious, though.
DPatrick
2014-03-15 19:38:23
On to #5:
On to #5:
DPatrick
2014-03-15 19:38:27
5. Let the set S={P1,P2,…,P12} consist of the twelve vertices of a regular 12-gon. A subset Q of S is called communal if there is a circle such that all points of Q are inside the circle, and all the points of S not in Q are outside of the circle. How many communal subsets are there? (Note that the empty set is a communal subset.)
5. Let the set S={P1,P2,…,P12} consist of the twelve vertices of a regular 12-gon. A subset Q of S is called communal if there is a circle such that all points of Q are inside the circle, and all the points of S not in Q are outside of the circle. How many communal subsets are there? (Note that the empty set is a communal subset.)
DPatrick
2014-03-15 19:38:46
Here a picture that might help clarify things:
Here a picture that might help clarify things:
DPatrick
2014-03-15 19:38:50
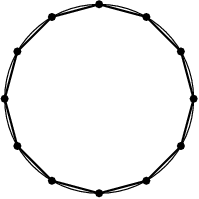

bellyflop
2014-03-15 19:39:11
only way to get a communal set is to have consecutive vertices
only way to get a communal set is to have consecutive vertices
DrMath
2014-03-15 19:39:11
after testing some communal subsets we have that the points must be consecutive
after testing some communal subsets we have that the points must be consecutive
mathtastic
2014-03-15 19:39:11
the word "communal" strongly implies that all verticies are next to each other
the word "communal" strongly implies that all verticies are next to each other
vinayak-kumar
2014-03-15 19:39:11
Aren't these just consecutive points
Aren't these just consecutive points
picuberoot
2014-03-15 19:39:11
For the circle to only contain points in Q, the points all have to be next to eachother. Casework!!
For the circle to only contain points in Q, the points all have to be next to eachother. Casework!!
DPatrick
2014-03-15 19:39:32
How do we know that? Why is it that the communal sets are exactly the sets of consecutive points around the 12-gon?
How do we know that? Why is it that the communal sets are exactly the sets of consecutive points around the 12-gon?
shreshrej
2014-03-15 19:39:52
Hmm, start drawing some circles?
Hmm, start drawing some circles?
Wolstenholme
2014-03-15 19:39:52
circles intersect at at most two points
circles intersect at at most two points
DPatrick
2014-03-15 19:40:09
Exactly: look at what happens if we draw a circle to carve out a communal subset:
Exactly: look at what happens if we draw a circle to carve out a communal subset:
DPatrick
2014-03-15 19:40:15


DPatrick
2014-03-15 19:40:30
The points that are inside the blue circle are consecutive -- it's a bunch of points from the 12-gon in a row, with none skipped.
The points that are inside the blue circle are consecutive -- it's a bunch of points from the 12-gon in a row, with none skipped.
DPatrick
2014-03-15 19:40:50
And we know that any intersecting circle (that's not tangent) intersects the circle of our 12-gon in exactly two points, and one of the two arcs between those two points will lie inside the new circle, and the other arc will lie outside the new circle.
And we know that any intersecting circle (that's not tangent) intersects the circle of our 12-gon in exactly two points, and one of the two arcs between those two points will lie inside the new circle, and the other arc will lie outside the new circle.
DPatrick
2014-03-15 19:41:23
So we can always only get an arc-full of points in our communal set. And we can get any arc we want if we take a big enough circle.
So we can always only get an arc-full of points in our communal set. And we can get any arc we want if we take a big enough circle.
DPatrick
2014-03-15 19:41:44
So we just need to count the subsets of consecutive points. How?
So we just need to count the subsets of consecutive points. How?
wangt
2014-03-15 19:42:20
so 12*11 (because subsets with 1-11 points all have 12) + 1 for all 12 + 1 for none?
so 12*11 (because subsets with 1-11 points all have 12) + 1 for all 12 + 1 for none?
bobthesmartypants
2014-03-15 19:42:20
casework on 0 points and 12 points, and 1->11 points
casework on 0 points and 12 points, and 1->11 points
poweroftwo
2014-03-15 19:42:20
there's 12 for each number of elements 1-11
there's 12 for each number of elements 1-11
danusv
2014-03-15 19:42:20
12*11 + 1 + 1
12*11 + 1 + 1
allaoc
2014-03-15 19:42:20
Define a starting point for sets from 1 to 11 elements, and there is just one for 12
Define a starting point for sets from 1 to 11 elements, and there is just one for 12
room456
2014-03-15 19:42:20
casework bash: 1 (empty) + 1 (full) + 11*12 (any other case)
casework bash: 1 (empty) + 1 (full) + 11*12 (any other case)
summitwei
2014-03-15 19:42:20
for 1-11 points there are 12 ways
for 1-11 points there are 12 ways
DPatrick
2014-03-15 19:42:27
Right!
Right!
checkmate1021
2014-03-15 19:42:36
there are 12 possible "starting" location for each length of consecutive points, and 11 possible lengths, so 11(12) = 132
there are 12 possible "starting" location for each length of consecutive points, and 11 possible lengths, so 11(12) = 132
DPatrick
2014-03-15 19:42:58
Exactly -- we can get a "nontrivial" subset (non-empty and not all 12 points) by picking the "first" point (say, counting counterclockwise) and then picking the number of additional number of points to add. This number of additional points can be from 0 to 10 inclusive.
Exactly -- we can get a "nontrivial" subset (non-empty and not all 12 points) by picking the "first" point (say, counting counterclockwise) and then picking the number of additional number of points to add. This number of additional points can be from 0 to 10 inclusive.
DPatrick
2014-03-15 19:43:12
So that gives us 12⋅11=132 consecutive subsets with a "start" point plus 0 through 10 additional points.
So that gives us 12⋅11=132 consecutive subsets with a "start" point plus 0 through 10 additional points.
mathwizard888
2014-03-15 19:43:30
adding the empty set and whole set gives 134 ans
adding the empty set and whole set gives 134 ans
ninjataco
2014-03-15 19:43:30
So it's just 1+1+12(11)=134.
So it's just 1+1+12(11)=134.
Tommy2000
2014-03-15 19:43:30
132+2 = 134
132+2 = 134
Satyaprakash2009rta
2014-03-15 19:43:30
132+2=134
132+2=134
ninjataco
2014-03-15 19:43:30
Then the empty set and full subset add two more
Then the empty set and full subset add two more
hjl00
2014-03-15 19:43:30
132+1+1=134
132+1+1=134
guilt
2014-03-15 19:43:30
and also the empty and full sets so 134
and also the empty and full sets so 134
raptorw
2014-03-15 19:43:30
two more cases of empty and full set
two more cases of empty and full set
claudeaops
2014-03-15 19:43:30
132+1(empty set) + 1 (full set)
132+1(empty set) + 1 (full set)
DPatrick
2014-03-15 19:43:51
Right: this doesn't yet include the empty set (if the blue circle is entirely inside the 12-gon) and the set of all 12 points (if the blue circle contains the entire 12-gon) that are also both communal.
Right: this doesn't yet include the empty set (if the blue circle is entirely inside the 12-gon) and the set of all 12 points (if the blue circle contains the entire 12-gon) that are also both communal.
DPatrick
2014-03-15 19:43:57
Adding the two trivial subsets (the empty set and the set of all 12 points) gives us a total of 132+2=134 subsets.
Adding the two trivial subsets (the empty set and the set of all 12 points) gives us a total of 132+2=134 subsets.
DPatrick
2014-03-15 19:44:22
OK, we're 1/3 of the way home! On to #6:
OK, we're 1/3 of the way home! On to #6:
DPatrick
2014-03-15 19:44:27
6. The graphs of y=3(x−h)2+j and y=2(x−h)2+k have y-intercepts of 2013 and 2014, respectively, and each graph has two positive integer x-intercepts. Find h.
6. The graphs of y=3(x−h)2+j and y=2(x−h)2+k have y-intercepts of 2013 and 2014, respectively, and each graph has two positive integer x-intercepts. Find h.
bengals
2014-03-15 19:45:00
expand first
expand first
mathtastic
2014-03-15 19:45:00
expand them both
expand them both
swamih
2014-03-15 19:45:00
expand the binomials
expand the binomials
DPatrick
2014-03-15 19:45:12
Perhaps we can use the equations in their current form, but we're probably more familiar with y=ax2+bx+c, so let's convert them into that form.
Perhaps we can use the equations in their current form, but we're probably more familiar with y=ax2+bx+c, so let's convert them into that form.
DPatrick
2014-03-15 19:45:18
The first equation becomes y=3x2−6hx+(3h2+j).
The first equation becomes y=3x2−6hx+(3h2+j).
DPatrick
2014-03-15 19:45:24
But what else do we know?
But what else do we know?
tRIG
2014-03-15 19:45:56
3h^2 + j = 2013 and 2h^2+k = 2014
3h^2 + j = 2013 and 2h^2+k = 2014
pedronr
2014-03-15 19:45:56
3h^2+j=2013, 2h^2+j=2014
3h^2+j=2013, 2h^2+j=2014
samuelczhao
2014-03-15 19:45:56
u know the y intercept
u know the y intercept
sat113
2014-03-15 19:45:56
3h^2+j=2013
3h^2+j=2013
cellobix
2014-03-15 19:45:56
3h^2 + j = 2013
3h^2 + j = 2013
DrMath
2014-03-15 19:45:56
the y intercept is 2013
the y intercept is 2013
blizzard10
2014-03-15 19:45:56
when y=2013, x=0
when y=2013, x=0
othuum0149
2014-03-15 19:45:56
y intercept of 2013, so 3h^2+j=2013
y intercept of 2013, so 3h^2+j=2013
sparkles257
2014-03-15 19:45:56
3h^2+j = 2013
3h^2+j = 2013
Ericaops
2014-03-15 19:45:56
when x-0, y is 2013
when x-0, y is 2013
DPatrick
2014-03-15 19:46:03
Right: when we plug in x=0 we need to get y=2013.
Right: when we plug in x=0 we need to get y=2013.
DPatrick
2014-03-15 19:46:13
Thus the first equation is just y=3x2−6hx+2013.
Thus the first equation is just y=3x2−6hx+2013.
DPatrick
2014-03-15 19:46:26
What about the second equation?
What about the second equation?
CornSaltButter
2014-03-15 19:46:50
it goes through (0,2014) so plug those values in
it goes through (0,2014) so plug those values in
raptorw
2014-03-15 19:46:50
likewise, 2h^2+k=2014
likewise, 2h^2+k=2014
vinayak-kumar
2014-03-15 19:46:50
we have the constant term to be 2014
we have the constant term to be 2014
shreshrej
2014-03-15 19:46:50
2x2−4hx+2014
2x2−4hx+2014
DPatrick
2014-03-15 19:46:56
By the same logic, the second equation is y=2x2−4hx+2014.
By the same logic, the second equation is y=2x2−4hx+2014.
DPatrick
2014-03-15 19:47:07
So to quickly recap, our equations are
y=3x2−6hx+2013,y=2x2−4hx+2014.
And we also have the data that each has two positive integer x-intercepts.
So to quickly recap, our equations are
y=3x2−6hx+2013,y=2x2−4hx+2014.
And we also have the data that each has two positive integer x-intercepts.
DPatrick
2014-03-15 19:47:14
What's a less-fancy way of saying that?
What's a less-fancy way of saying that?
vinayak-kumar
2014-03-15 19:47:42
they have positive integer roots
they have positive integer roots
MSTang
2014-03-15 19:47:42
Roots are pos ints
Roots are pos ints
VietaFan
2014-03-15 19:47:42
the roots are positive integer values of x
the roots are positive integer values of x
swamih
2014-03-15 19:47:42
the roots of the equation are integers
the roots of the equation are integers
sat113
2014-03-15 19:47:42
it has two positive integer roots
it has two positive integer roots
DPatrick
2014-03-15 19:47:57
Yes: "x-intercept" is just a fancy word for "root".
Yes: "x-intercept" is just a fancy word for "root".
DPatrick
2014-03-15 19:48:09
(The x-intercepts are the values of x that make y=0.)
(The x-intercepts are the values of x that make y=0.)
DPatrick
2014-03-15 19:48:15
So we are given that the solutions to the two quadratics
0=3x2−6hx+2013,0=2x2−4hx+2014,
are all positive integers.
So we are given that the solutions to the two quadratics
0=3x2−6hx+2013,0=2x2−4hx+2014,
are all positive integers.
ViolinNinja256
2014-03-15 19:48:28
simplify
simplify
mathtastic
2014-03-15 19:48:37
divide first by 3 and second by 2
divide first by 3 and second by 2
DPatrick
2014-03-15 19:48:46
Sure, we can simplify a little and divide by the quadratic coefficients of each and not change the roots:
0=x2−2hx+671,0=x2−2hx+1007.
Sure, we can simplify a little and divide by the quadratic coefficients of each and not change the roots:
0=x2−2hx+671,0=x2−2hx+1007.
DPatrick
2014-03-15 19:48:52
Now what?
Now what?
dli00105
2014-03-15 19:49:30
prime factor 671 and 1007
prime factor 671 and 1007
brian22
2014-03-15 19:49:30
Vieta: sums of the roots are the same
Vieta: sums of the roots are the same
joshxiong
2014-03-15 19:49:30
find the factors of 671 and 1007
find the factors of 671 and 1007
ninjataco
2014-03-15 19:49:30
The sums of the roots are the same, look for numbers that multiply to get 671 and 1007 and have same sum
The sums of the roots are the same, look for numbers that multiply to get 671 and 1007 and have same sum
Eudokia
2014-03-15 19:49:30
Factor 671 and 1007
Factor 671 and 1007
amudol
2014-03-15 19:49:30
prime factor 671 and/or 1007 to see what positive integer roots you can get
prime factor 671 and/or 1007 to see what positive integer roots you can get
DPatrick
2014-03-15 19:49:44
Right. To say all this another way, now we can use Vieta's Formulas to get information about the roots of the two equations.
Right. To say all this another way, now we can use Vieta's Formulas to get information about the roots of the two equations.
DPatrick
2014-03-15 19:49:52
In the first equation, the roots have product 671 and sum 2h.
In the second equation, the roots have product 1007 and sum 2h.
In the first equation, the roots have product 671 and sum 2h.
In the second equation, the roots have product 1007 and sum 2h.
DPatrick
2014-03-15 19:50:14
Happily, 671 and 1007 don't have a lot of positive integer factors, and we're looking for a pair for each that have the same sum.
Happily, 671 and 1007 don't have a lot of positive integer factors, and we're looking for a pair for each that have the same sum.
mathmaster2012
2014-03-15 19:50:35
671=61*11, 1007=19*53
671=61*11, 1007=19*53
room456
2014-03-15 19:50:35
671=61*11, 1007=19*53
671=61*11, 1007=19*53
cellobix
2014-03-15 19:50:35
671=11*61, 1007=19*53
671=11*61, 1007=19*53
mathwizard888
2014-03-15 19:50:35
11 and 61, 19 and 53
11 and 61, 19 and 53
DPatrick
2014-03-15 19:50:41
The prime factorization of 671 is 11⋅61, and the prime factorization of 1007 is 19⋅53.
The prime factorization of 671 is 11⋅61, and the prime factorization of 1007 is 19⋅53.
guilt
2014-03-15 19:50:54
11+61 = 19+53 = 72 = 2h ; so h = 36
11+61 = 19+53 = 72 = 2h ; so h = 36
adamz
2014-03-15 19:50:54
they both sum to 72
they both sum to 72
acegikmoqsuwy2000
2014-03-15 19:51:04
11+61=19+53
11+61=19+53
DPatrick
2014-03-15 19:51:13
What do you know, those pairs of factors have the same sum of 72!
What do you know, those pairs of factors have the same sum of 72!
LightningX48
2014-03-15 19:51:35
yeay 2h = 72 h = 36 | 036 is ans
yeay 2h = 72 h = 36 | 036 is ans
mdlu
2014-03-15 19:51:35
they both add up to 72 so h=36.
they both add up to 72 so h=36.
navygoat123
2014-03-15 19:51:35
h = 36
h = 36
kquittman
2014-03-15 19:51:35
so h=36.
so h=36.
willwin4sure
2014-03-15 19:51:35


DPatrick
2014-03-15 19:51:44
So the roots of the first quadratic are 11 and 61, and the roots of the second quadratic are 19 and 53. And thus 2h=11+61=19+53=72, and our answer is h=036.
So the roots of the first quadratic are 11 and 61, and the roots of the second quadratic are 19 and 53. And thus 2h=11+61=19+53=72, and our answer is h=036.
DPatrick
2014-03-15 19:52:08
That's all for page 1 of the contest. On to #7:
That's all for page 1 of the contest. On to #7:
DPatrick
2014-03-15 19:52:14
7. Let w and z be complex numbers such that |w|=1 and |z|=10. Let θ=arg(w−zz). The maximum possible value of tan2θ can be written as pq, where p and q are relatively prime positive integers. Find p+q. (Note that arg(w), for w≠0, denotes the measure of the angle that the ray from 0 to w makes with the positive real axis in the complex plane.)
7. Let w and z be complex numbers such that |w|=1 and |z|=10. Let θ=arg(w−zz). The maximum possible value of tan2θ can be written as pq, where p and q are relatively prime positive integers. Find p+q. (Note that arg(w), for w≠0, denotes the measure of the angle that the ray from 0 to w makes with the positive real axis in the complex plane.)
DPatrick
2014-03-15 19:52:35
The AIME always seems to have one of this sort of problem, that's fairly easy if you know how to use the geometry of the complex plane, and nearly impossible if you don't.
The AIME always seems to have one of this sort of problem, that's fairly easy if you know how to use the geometry of the complex plane, and nearly impossible if you don't.
DPatrick
2014-03-15 19:52:52
How can we get at the expression arg(w−zz)?
How can we get at the expression arg(w−zz)?
Wickedestjr
2014-03-15 19:52:55
Simplify (w-z)/z ?
Simplify (w-z)/z ?
DPatrick
2014-03-15 19:53:09
Yeah, w−zz is a bit hard to work with.
Yeah, w−zz is a bit hard to work with.
bobthesmartypants
2014-03-15 19:53:17
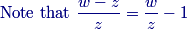
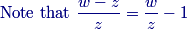
minimario
2014-03-15 19:53:17
wz−1
wz−1
PlatinumFalcon
2014-03-15 19:53:17
Split up into w/z-1
Split up into w/z-1
mdlu
2014-03-15 19:53:22
wz−1?
wz−1?
raptorw
2014-03-15 19:53:22
w/z-1
w/z-1
Ericaops
2014-03-15 19:53:22
w/z-1
w/z-1
hjl00
2014-03-15 19:53:22
w/z-1
w/z-1
DPatrick
2014-03-15 19:53:26
Let's rewrite it as w−zz=wz−1.
Let's rewrite it as w−zz=wz−1.
DPatrick
2014-03-15 19:53:31
What do we know about wz?
What do we know about wz?
claudeaops
2014-03-15 19:53:55
w/z has absolute value 1/10
w/z has absolute value 1/10
hi how are you doing toda
2014-03-15 19:53:55
magnitude is 1/10
magnitude is 1/10
Tommy2000
2014-03-15 19:53:55
magnitude is 1/10?
magnitude is 1/10?
othuum0149
2014-03-15 19:53:55
magnitude of 1/10
magnitude of 1/10
bunniesrcute
2014-03-15 19:53:55
norm is 1/10
norm is 1/10
DrMath
2014-03-15 19:53:55
has magnitude 1/10
has magnitude 1/10
TheStrangeCharm
2014-03-15 19:53:55
it has magnitude 110
it has magnitude 110
DPatrick
2014-03-15 19:54:03
Right. It's a point in the complex plane with magnitude |wz|=|w||z|=110.
Right. It's a point in the complex plane with magnitude |wz|=|w||z|=110.
DPatrick
2014-03-15 19:54:37
Where do these points live on the complex plane?
Where do these points live on the complex plane?
PlatinumFalcon
2014-03-15 19:54:58
So it's on the circle centered at the origin with radius 0.1.
So it's on the circle centered at the origin with radius 0.1.
Nitzuga
2014-03-15 19:54:58
That's a circle with radius 1/10
That's a circle with radius 1/10
MSTang
2014-03-15 19:54:58
It can be any such point
It can be any such point
csmath
2014-03-15 19:54:58
A circle radius 1/10
A circle radius 1/10
joshualee2000
2014-03-15 19:54:58
a circle of radius 1/10
a circle of radius 1/10
pedronr
2014-03-15 19:54:58
circle with r=1/10
circle with r=1/10
tiger21
2014-03-15 19:54:58
a circle with center at origin and radius 1/10
a circle with center at origin and radius 1/10
DPatrick
2014-03-15 19:55:03
Exactly. These points live on a circle of radius 110 around the origin.
Exactly. These points live on a circle of radius 110 around the origin.
DPatrick
2014-03-15 19:55:07
So where do the points wz−1 live on the complex plane?
So where do the points wz−1 live on the complex plane?
dli00105
2014-03-15 19:55:38
1/10 away freom -1
1/10 away freom -1
mathtastic
2014-03-15 19:55:38
that circle shifted 1 unit left
that circle shifted 1 unit left
joshxiong
2014-03-15 19:55:38
circle translated to the left by 1
circle translated to the left by 1
allaoc
2014-03-15 19:55:38
A circle of radius 1/10 centered at -1
A circle of radius 1/10 centered at -1
checkmate1021
2014-03-15 19:55:38
circle radius 1/10 centered at (-1, 0)
circle radius 1/10 centered at (-1, 0)
DPatrick
2014-03-15 19:55:47
They live on a circle of radius 110 centered at the real number −1 (on the negative real axis).
They live on a circle of radius 110 centered at the real number −1 (on the negative real axis).
DPatrick
2014-03-15 19:55:52


DPatrick
2014-03-15 19:56:02
(This picture is not to scale -- the actual circle should be much smaller. But a picture drawn to scale would be too hard to use!)
(This picture is not to scale -- the actual circle should be much smaller. But a picture drawn to scale would be too hard to use!)
DPatrick
2014-03-15 19:56:31
OK, so we're trying to maximize tan2θ where θ is the argument of some point on that circle. So what ray from the origin to the blue circle gives us an angle θ with the maximum possible tan2θ?
OK, so we're trying to maximize tan2θ where θ is the argument of some point on that circle. So what ray from the origin to the blue circle gives us an angle θ with the maximum possible tan2θ?
tanuagg13
2014-03-15 19:56:58
the tangent ray
the tangent ray
sat113
2014-03-15 19:56:58
the tangent line
the tangent line
guilt
2014-03-15 19:56:58
The tangent!
The tangent!
mentalgenius
2014-03-15 19:56:58
tan(gent) lol
tan(gent) lol
ingridzhang97
2014-03-15 19:56:58
the tangent line
the tangent line
vinayak-kumar
2014-03-15 19:56:58
A tangent!
A tangent!
DPatrick
2014-03-15 19:57:15
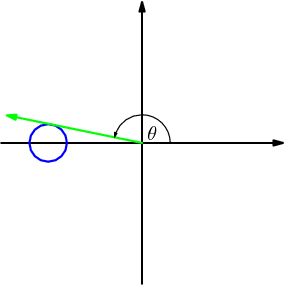
Right! Remember that tangent is slope. Thus, we want the ray to be as far as possible away from the real axis. How can we get it as far away as possible from the real axis, and yet still intersect the circle? We pick the tangent line.
Right! Remember that tangent is slope. Thus, we want the ray to be as far as possible away from the real axis. How can we get it as far away as possible from the real axis, and yet still intersect the circle? We pick the tangent line.
DPatrick
2014-03-15 19:57:22

DPatrick
2014-03-15 19:57:42
What is the tangent of that angle θ?
What is the tangent of that angle θ?
negativebplusorminus
2014-03-15 19:58:25
Well, its cosine is 1/10.
Well, its cosine is 1/10.
DPatrick
2014-03-15 19:59:03
Is that true? That angle looks pretty close to 180 degrees to me...
Is that true? That angle looks pretty close to 180 degrees to me...
hi how are you doing toda
2014-03-15 19:59:21
the sin is 1/10.
the sin is 1/10.
csmath
2014-03-15 19:59:21
Wait so sine=1/10
Wait so sine=1/10
ashgabat
2014-03-15 19:59:21
Its sin is 1/10 no?
Its sin is 1/10 no?
DPatrick
2014-03-15 19:59:45
Right, got it backwards. It's the sine that's 1/10: the sine is the ratio of the radius of the little circle to the distance to that circle's center.
Right, got it backwards. It's the sine that's 1/10: the sine is the ratio of the radius of the little circle to the distance to that circle's center.
DPatrick
2014-03-15 19:59:53
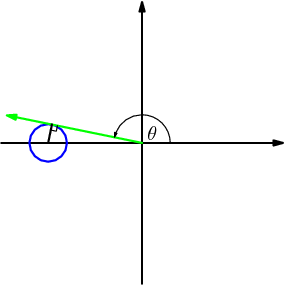
Drawing this little right triangle might help:
Drawing this little right triangle might help:
DPatrick
2014-03-15 19:59:58

dantx5
2014-03-15 20:00:19
cos = sqrt(99)/10
cos = sqrt(99)/10
csmath
2014-03-15 20:00:19
Therefore its cos=sqrt(99)/10
Therefore its cos=sqrt(99)/10
Tommy2000
2014-03-15 20:00:19
cosine is sqrt99/10
cosine is sqrt99/10
DPatrick
2014-03-15 20:00:56
Well, technically we have cosθ=−√9910 (the angle is between 90 and 180 degrees so the cosine is negative), but it doesn't matter since we're squaring later anyway.
Well, technically we have cosθ=−√9910 (the angle is between 90 and 180 degrees so the cosine is negative), but it doesn't matter since we're squaring later anyway.
pedronr
2014-03-15 20:01:12
and tan=-1/sqrt(99)
and tan=-1/sqrt(99)
DPatrick
2014-03-15 20:01:36
Right: tanθ=sinθcosθ=−1√99.
Right: tanθ=sinθcosθ=−1√99.
acegikmoqsuwy2000
2014-03-15 20:01:53
tan square is 1/99 then
tan square is 1/99 then
buzzyun
2014-03-15 20:01:53
tan^2=1/99, so 1+99=100
tan^2=1/99, so 1+99=100
mdlu
2014-03-15 20:01:53
199 so the answer is 100
199 so the answer is 100
claudeaops
2014-03-15 20:01:53
the answer is 1/99 -> 100
the answer is 1/99 -> 100
summitwei
2014-03-15 20:01:53
so its 1/99 so the answer is 100
so its 1/99 so the answer is 100
Eudokia
2014-03-15 20:02:01
so tan^2=1/99 => ans. is 100
so tan^2=1/99 => ans. is 100
DPatrick
2014-03-15 20:02:03
Right. Hence tan2θ=199, and our answer is 1+99=100.
Right. Hence tan2θ=199, and our answer is 1+99=100.
DPatrick
2014-03-15 20:02:50
Again, if you didn't know the geometry of complex numbers, you probably had little chance with this problem.
Again, if you didn't know the geometry of complex numbers, you probably had little chance with this problem.
DPatrick
2014-03-15 20:02:58
Anyway, on to #8:
Anyway, on to #8:
DPatrick
2014-03-15 20:03:02
8. The positive integers N and N2 both end in the same sequence of four digits abcd when written in base 10, where digit a is not zero. Find the three-digit number abc.
8. The positive integers N and N2 both end in the same sequence of four digits abcd when written in base 10, where digit a is not zero. Find the three-digit number abc.
DPatrick
2014-03-15 20:03:29
What does it mean that N and N2 end in the same four digits?
What does it mean that N and N2 end in the same four digits?
guilt
2014-03-15 20:04:16
we see that N^2 - N = 10000x
we see that N^2 - N = 10000x
tRIG
2014-03-15 20:04:16
n^2-n = 0 mod 10000
n^2-n = 0 mod 10000
joshxiong
2014-03-15 20:04:16
N^2-N must be divisible by 10000
N^2-N must be divisible by 10000
dli00105
2014-03-15 20:04:16
n==n^2 mod 10000
n==n^2 mod 10000
vinayak-kumar
2014-03-15 20:04:16
N^2\equiv N\pmod{10000}
N^2\equiv N\pmod{10000}
aimingforimo
2014-03-15 20:04:16
n=n^2(mod 10000)
n=n^2(mod 10000)
Wickedestjr
2014-03-15 20:04:16
They are equivalent mod 10,000
They are equivalent mod 10,000
cellobix
2014-03-15 20:04:16
They are the same modulo 10 000
They are the same modulo 10 000
adi12
2014-03-15 20:04:16
N(N-1)= some multiple of 10000
N(N-1)= some multiple of 10000
tiger21
2014-03-15 20:04:16
N^2-N=0 mod 10000
N^2-N=0 mod 10000
DPatrick
2014-03-15 20:04:25
Right. It means that N^2 - N is a multiple of 10000.
Right. It means that N^2 - N is a multiple of 10000.
DPatrick
2014-03-15 20:04:33
But this means that N(N-1) is a multiple of 10000.
But this means that N(N-1) is a multiple of 10000.
DPatrick
2014-03-15 20:04:38
How can this happen?
How can this happen?
henrikjb
2014-03-15 20:05:20
so either N or N-1 is a multiple of 16, and similarly for 625
so either N or N-1 is a multiple of 16, and similarly for 625
pedronr
2014-03-15 20:05:20
N and N-1 are consecutive multiples of 625 and 16
N and N-1 are consecutive multiples of 625 and 16
DrMath
2014-03-15 20:05:20
N and N-1 are relatively prime so one of them is a multiple of 2^4 other 5^4.
N and N-1 are relatively prime so one of them is a multiple of 2^4 other 5^4.
TheEconomist
2014-03-15 20:05:20
factors must have 5^4 and 2^4
factors must have 5^4 and 2^4
mathtastic
2014-03-15 20:05:20
one has to be a multiple of 5^4, other has to be multiple of 2^4
one has to be a multiple of 5^4, other has to be multiple of 2^4
hamup1
2014-03-15 20:05:20
either N or N-1 is a multiple of 625
either N or N-1 is a multiple of 625
TheStrangeCharm
2014-03-15 20:05:20
if one is divisible by 2^4, and the other is divisible by 5^4.
if one is divisible by 2^4, and the other is divisible by 5^4.
infiniteturtle
2014-03-15 20:05:20
one is a multiple of 16, the other of 625
one is a multiple of 16, the other of 625
DPatrick
2014-03-15 20:05:37
We're getting slightly ahead of ourselves, but yes. Let me fill in the missing steps.
We're getting slightly ahead of ourselves, but yes. Let me fill in the missing steps.
DPatrick
2014-03-15 20:05:52
One possibility, of course, is that N could be a multiple of 10000 itself. But then its thousands digit a would be 0.
One possibility, of course, is that N could be a multiple of 10000 itself. But then its thousands digit a would be 0.
DPatrick
2014-03-15 20:06:01
N could also be 1 more than a multiple of 10000, so that N-1 is a multiple of 10000. But then N would end in 0001 -- still not allowed.
N could also be 1 more than a multiple of 10000, so that N-1 is a multiple of 10000. But then N would end in 0001 -- still not allowed.
DPatrick
2014-03-15 20:06:38
So that leaves the possibility that N is a multiple of some factors of 10000, and N-1 is a multiple of the remaining factors of 10000.
So that leaves the possibility that N is a multiple of some factors of 10000, and N-1 is a multiple of the remaining factors of 10000.
DPatrick
2014-03-15 20:07:02
But we know that 10000 = 10^4 = 2^4 \cdot 5^4 = 16 \cdot 625. And we also know that N and N-1 don't have any factors in common.
But we know that 10000 = 10^4 = 2^4 \cdot 5^4 = 16 \cdot 625. And we also know that N and N-1 don't have any factors in common.
DPatrick
2014-03-15 20:07:13
So we must have either:
(I) N is a multiple of 16 and N-1 is a multiple of 625
or
(II) N is a multiple of 625 and N-1 is a multiple of 16
So we must have either:
(I) N is a multiple of 16 and N-1 is a multiple of 625
or
(II) N is a multiple of 625 and N-1 is a multiple of 16
DPatrick
2014-03-15 20:07:41
If you know the Chinese Remainder Theorem, then you know that there is a unique value of N (modulo 10000) that satisfies either of these conditions. (But it's not necessarily to know this to finish the problem.)
If you know the Chinese Remainder Theorem, then you know that there is a unique value of N (modulo 10000) that satisfies either of these conditions. (But it's not necessarily to know this to finish the problem.)
DPatrick
2014-03-15 20:08:03
Let's deal with case (II) first because it's easier. What value of N satisfies case (II)?
Let's deal with case (II) first because it's easier. What value of N satisfies case (II)?
othuum0149
2014-03-15 20:08:36
625
625
lovejj
2014-03-15 20:08:36
N=625
N=625
sat113
2014-03-15 20:08:36
625
625
Tommy2000
2014-03-15 20:08:36
625
625
firemike
2014-03-15 20:08:36
625?
625?
cheeptricks
2014-03-15 20:08:36
625
625
sat113
2014-03-15 20:08:36
625 lol
625 lol
checkmate1021
2014-03-15 20:08:36
N = 625
N = 625
DPatrick
2014-03-15 20:08:51
Right: N = 625 is already the solution for case (II)! (Because N-1 = 624 = 16 \cdot 39.)
Right: N = 625 is already the solution for case (II)! (Because N-1 = 624 = 16 \cdot 39.)
cellobix
2014-03-15 20:09:05
But this is 0625, which is not allowed
But this is 0625, which is not allowed
shreshrej
2014-03-15 20:09:05
but a is 0
but a is 0
ninjataco
2014-03-15 20:09:05
this doesn't work because a = 0
this doesn't work because a = 0
bookhunter7
2014-03-15 20:09:05
0625 isn't allowed though
0625 isn't allowed though
DPatrick
2014-03-15 20:09:14
Indeed, this means that all numbers that satisfy (II) end in the digits 0625 -- which is still not allowed!
Indeed, this means that all numbers that satisfy (II) end in the digits 0625 -- which is still not allowed!
DPatrick
2014-03-15 20:09:23
So we must be looking for an N with condition (I): N is a multiple of 16 and N-1 is a multiple of 625.
So we must be looking for an N with condition (I): N is a multiple of 16 and N-1 is a multiple of 625.
DPatrick
2014-03-15 20:09:30
How do we find it?
How do we find it?
bellyflop
2014-03-15 20:09:52
try multioles of 625 for n-1
try multioles of 625 for n-1
dantx5
2014-03-15 20:09:52
try each multiple of 625 less than 10000
try each multiple of 625 less than 10000
DPatrick
2014-03-15 20:10:15
That's a good strategy. There are lots of multiples of 16 to hunt through...what's easier is to look for M such that M+1 is a multiple of 16 and M is a multiple of 625. (So N = M+1 will be our answer.)
That's a good strategy. There are lots of multiples of 16 to hunt through...what's easier is to look for M such that M+1 is a multiple of 16 and M is a multiple of 625. (So N = M+1 will be our answer.)
CornSaltButter
2014-03-15 20:10:27
notice that 625 is congruent to 1 mod 16
notice that 625 is congruent to 1 mod 16
DPatrick
2014-03-15 20:10:34
Indeed, we already know that 625 itself is 1 more than a multiple of 16. How does that help?
Indeed, we already know that 625 itself is 1 more than a multiple of 16. How does that help?
dli00105
2014-03-15 20:11:01
try 15
try 15
shreshrej
2014-03-15 20:11:01
so if you multiply by 15, you will get 15 mod 16
so if you multiply by 15, you will get 15 mod 16
ashgabat
2014-03-15 20:11:01
We try 15*625
We try 15*625
MSTang
2014-03-15 20:11:01
15 * 625 + 1 is then 15 + 1 = 16 = 0 mod 16
15 * 625 + 1 is then 15 + 1 = 16 = 0 mod 16
negativebplusorminus
2014-03-15 20:11:01
15 of them will be -1 mod 16.
15 of them will be -1 mod 16.
joshxiong
2014-03-15 20:11:01
so 15 * 625 = 15 = -1 (mod 16)
so 15 * 625 = 15 = -1 (mod 16)
martian179
2014-03-15 20:11:01
15 * 625 + 1 = 0 mod 16
15 * 625 + 1 = 0 mod 16
DPatrick
2014-03-15 20:11:15
That's exactly right.
That's exactly right.
DPatrick
2014-03-15 20:11:33
Or, to say it with less-fancy language: we know that 15 \cdot 625 is 15 more than a multiple of 16. So 15 \cdot 625 + 1 is 16 more than a multiple of 16, which again is a multiple of 16.
Or, to say it with less-fancy language: we know that 15 \cdot 625 is 15 more than a multiple of 16. So 15 \cdot 625 + 1 is 16 more than a multiple of 16, which again is a multiple of 16.
csmath
2014-03-15 20:11:50
By doing that we get N=9376 so answer = 937
By doing that we get N=9376 so answer = 937
navygoat123
2014-03-15 20:11:50
N-1 is 9375 so N is 9376 so abc = 937
N-1 is 9375 so N is 9376 so abc = 937
adi12
2014-03-15 20:11:50
so its 9376 and 9375!
so its 9376 and 9375!
urmilla
2014-03-15 20:11:50
N-1 = 9375, so N = 9376
N-1 = 9375, so N = 9376
acegikmoqsuwy2000
2014-03-15 20:11:50
9376
9376
DPatrick
2014-03-15 20:11:59
Thus M = 15 \cdot 625 = 9375, and hence N = M+1 = 9376 is the number we're looking for.
Thus M = 15 \cdot 625 = 9375, and hence N = M+1 = 9376 is the number we're looking for.
DPatrick
2014-03-15 20:12:06
(You can check that 9376^2 = 87909376.)
(You can check that 9376^2 = 87909376.)
DPatrick
2014-03-15 20:12:19
So our answer is the first three digits of N, or \boxed{937}.
So our answer is the first three digits of N, or \boxed{937}.
DPatrick
2014-03-15 20:12:35
On to #9:
On to #9:
DPatrick
2014-03-15 20:12:39
9. Let x_1 < x_2 < x_3 be the three real roots of the equation \sqrt{2014}x^3 - 4029x^2 + 2 = 0.Find x_2(x_1+x_3).
9. Let x_1 < x_2 < x_3 be the three real roots of the equation \sqrt{2014}x^3 - 4029x^2 + 2 = 0.Find x_2(x_1+x_3).
checkmate1021
2014-03-15 20:13:10
vieta
vieta
LightningX48
2014-03-15 20:13:10
Vieta's!
Vieta's!
bellyflop
2014-03-15 20:13:10
vieta
vieta
minimario
2014-03-15 20:13:10
Vieta's Formulae
Vieta's Formulae
guilt
2014-03-15 20:13:10
Vieta's!
Vieta's!
hwl0304
2014-03-15 20:13:10
Vietas??
Vietas??
Tommy2000
2014-03-15 20:13:10
vieta's formula?
vieta's formula?
DPatrick
2014-03-15 20:13:21
Good idea. Since we want an expression that involves the roots, Vieta's Formulas are probably useful for this problem.
Good idea. Since we want an expression that involves the roots, Vieta's Formulas are probably useful for this problem.
DPatrick
2014-03-15 20:13:38
(If you don't know what Vieta's Formulas are, you can look them up after the Math Jam, or ask on the message board...or try to figure them out on your own!)
(If you don't know what Vieta's Formulas are, you can look them up after the Math Jam, or ask on the message board...or try to figure them out on your own!)
DPatrick
2014-03-15 20:13:45
Let's go ahead and list the Vieta's Formulas for this equation.
Let's go ahead and list the Vieta's Formulas for this equation.
DPatrick
2014-03-15 20:13:50
\begin{align*} x_1 + x_2 + x_3 &= \dfrac{4029}{\sqrt{2014}}, \\[2ex] x_1x_2 + x_2x_3 + x_3x_1 &= 0, \\[2ex] x_1x_2x_3 &= -\dfrac{2}{\sqrt{2014}}. \end{align*}
\begin{align*} x_1 + x_2 + x_3 &= \dfrac{4029}{\sqrt{2014}}, \\[2ex] x_1x_2 + x_2x_3 + x_3x_1 &= 0, \\[2ex] x_1x_2x_3 &= -\dfrac{2}{\sqrt{2014}}. \end{align*}
DPatrick
2014-03-15 20:14:03
That quantity that we're looking for...which does it resemble?
That quantity that we're looking for...which does it resemble?
mishai
2014-03-15 20:14:27
using the second we need to find -x3x1
using the second we need to find -x3x1
raptorw
2014-03-15 20:14:27
so what we're looking for is -x_3*x_1
so what we're looking for is -x_3*x_1
mentalgenius
2014-03-15 20:14:27
second
second
vinayak-kumar
2014-03-15 20:14:27
The second equations
The second equations
pedronr
2014-03-15 20:14:27
the second one
the second one
ViolinNinja256
2014-03-15 20:14:27
the 2nd equation
the 2nd equation
danusv
2014-03-15 20:14:27
so x2(x1+x3)=-x1x3
so x2(x1+x3)=-x1x3
kcui
2014-03-15 20:14:27
the second formula!
the second formula!
room456
2014-03-15 20:14:27
2nd one
2nd one
DPatrick
2014-03-15 20:14:35
What we want to find resembles the middle one quite a bit.
What we want to find resembles the middle one quite a bit.
DPatrick
2014-03-15 20:14:42
Indeed, x_2(x_1 + x_3) = -x_1x_3 by the middle formula.
Indeed, x_2(x_1 + x_3) = -x_1x_3 by the middle formula.
DPatrick
2014-03-15 20:14:54
And what does that resemble?
And what does that resemble?
Tuxianeer
2014-03-15 20:15:11
third one
third one
mathtastic
2014-03-15 20:15:11
third one!!
third one!!
tiger21
2014-03-15 20:15:11
the third
the third
samuelczhao
2014-03-15 20:15:11
last one
last one
mikechen
2014-03-15 20:15:11
the last equation
the last equation
Nitzuga
2014-03-15 20:15:11
the third
the third
firemike
2014-03-15 20:15:11
the third one!
the third one!
Acstar00
2014-03-15 20:15:11
the third equation
the third equation
niraekjs
2014-03-15 20:15:11
the third one!!!
the third one!!!
DPatrick
2014-03-15 20:15:22
Right! Then -x_1x_3 = \dfrac{2}{x_2\sqrt{2014}} by the third formula.
Right! Then -x_1x_3 = \dfrac{2}{x_2\sqrt{2014}} by the third formula.
DPatrick
2014-03-15 20:15:29
So the quantity we're looking for as our final answer is just \dfrac{2}{x_2\sqrt{2014}}.
So the quantity we're looking for as our final answer is just \dfrac{2}{x_2\sqrt{2014}}.
DPatrick
2014-03-15 20:15:43
Thus, if we can find the middle root of the cubic, we're done.
Thus, if we can find the middle root of the cubic, we're done.
DPatrick
2014-03-15 20:16:08
OK, that's probably as far as Vieta's Formulas will get us for now. Let's go back and look at our cubic.
OK, that's probably as far as Vieta's Formulas will get us for now. Let's go back and look at our cubic.
DPatrick
2014-03-15 20:16:26
What do you notice about it that looks notable?
What do you notice about it that looks notable?
raptorw
2014-03-15 20:16:44
4029 is really close to 2014*2
4029 is really close to 2014*2
bookhunter7
2014-03-15 20:16:44
4029=2*2014+1
4029=2*2014+1
Tuxianeer
2014-03-15 20:16:44
4029=2*2014+1
4029=2*2014+1
raptorw
2014-03-15 20:16:44
4029=2014*2+1
4029=2014*2+1
guilt
2014-03-15 20:16:44
4029 = 2*2014 + 1
4029 = 2*2014 + 1
joshxiong
2014-03-15 20:16:44
4029 = 2014 * 2 + 1
4029 = 2014 * 2 + 1
MSTang
2014-03-15 20:16:44
A bunch of 2014s
A bunch of 2014s
cellobix
2014-03-15 20:16:44
4029 is almost 2*2014
4029 is almost 2*2014
Eudokia
2014-03-15 20:16:44
4029=2014*2+1
4029=2014*2+1
DPatrick
2014-03-15 20:16:58
Yeah, you should notice the weird coefficients.
Yeah, you should notice the weird coefficients.
DPatrick
2014-03-15 20:17:02
And in particular, 4029 = 2(2014) + 1.
And in particular, 4029 = 2(2014) + 1.
henrikjb
2014-03-15 20:17:18
Substitute in \sqrt{2014}=a
Substitute in \sqrt{2014}=a
vinayak-kumar
2014-03-15 20:17:25
Make a substitution y=\sqrt{2014}
Make a substitution y=\sqrt{2014}
MSTang
2014-03-15 20:17:29
Let n = \sqrt{2014}
Let n = \sqrt{2014}
DPatrick
2014-03-15 20:17:36
That's a great idea. I don't like carrying these big numbers around: let's set a = \sqrt{2014}.
That's a great idea. I don't like carrying these big numbers around: let's set a = \sqrt{2014}.
DPatrick
2014-03-15 20:17:40
Then our cubic is ax^3 - (2a^2 + 1)x^2 + 2 = 0.
Then our cubic is ax^3 - (2a^2 + 1)x^2 + 2 = 0.
DPatrick
2014-03-15 20:17:53
Cubics are hard to solve in general -- but is there an "obvious" root?
Cubics are hard to solve in general -- but is there an "obvious" root?
DPatrick
2014-03-15 20:18:12
In particular...what would make that "+2" cancel out?
In particular...what would make that "+2" cancel out?
nickduensing
2014-03-15 20:18:38
-2
-2
navygoat123
2014-03-15 20:18:38
-2
-2
cheeptricks
2014-03-15 20:18:38
-2
-2
willwin4sure
2014-03-15 20:18:38
-2
-2
ChenthuranA
2014-03-15 20:18:38
-2
-2
DPatrick
2014-03-15 20:18:54
Indeed...and what value of x would produce a "-2" term to cancel with the "+2"?
Indeed...and what value of x would produce a "-2" term to cancel with the "+2"?
dli00105
2014-03-15 20:19:20
+-1/a
+-1/a
dantx5
2014-03-15 20:19:20
1/a
1/a
jimBriggs
2014-03-15 20:19:20
1/a
1/a
SuperSnivy
2014-03-15 20:19:20
x = 1/a
x = 1/a
negativebplusorminus
2014-03-15 20:19:20
1/a
1/a
danzhi
2014-03-15 20:19:20
1/a
1/a
minimario
2014-03-15 20:19:20
\frac{1}{a}
\frac{1}{a}
DPatrick
2014-03-15 20:19:31
Right. If x = \frac{1}{a}, then the 2's would cancel...
Right. If x = \frac{1}{a}, then the 2's would cancel...
Tuxianeer
2014-03-15 20:19:45
and so does everything
and so does everything
martian179
2014-03-15 20:19:49
and so does everything else
and so does everything else
DPatrick
2014-03-15 20:19:54
...and the other terms would cancel too!
...and the other terms would cancel too!
DPatrick
2014-03-15 20:20:03
Specifically,
a\left(\frac{1}{a}\right)^3 - (2a^2+1)\left(\frac{1}{a}\right)^2 + 2 = \frac{1}{a^2} - 2 - \frac{1}{a^2} + 2 = 0.
Specifically,
a\left(\frac{1}{a}\right)^3 - (2a^2+1)\left(\frac{1}{a}\right)^2 + 2 = \frac{1}{a^2} - 2 - \frac{1}{a^2} + 2 = 0.
samuelczhao
2014-03-15 20:20:19
so one solution is 1/ sqrt (2014)
so one solution is 1/ sqrt (2014)
kquittman
2014-03-15 20:20:19
so x=1/sqrt(2014)!
so x=1/sqrt(2014)!
DPatrick
2014-03-15 20:20:27
Indeed, we've checked that \dfrac{1}{a} = \dfrac{1}{\sqrt{2014}} is one of the three roots.
Indeed, we've checked that \dfrac{1}{a} = \dfrac{1}{\sqrt{2014}} is one of the three roots.
checkmate1021
2014-03-15 20:20:37
but how to prove that that is the middle root?
but how to prove that that is the middle root?
csmath
2014-03-15 20:20:37
So we can "guess" x2=1/sqrt(2014) however we don't know if this is actually the middle root but it does give us integer
So we can "guess" x2=1/sqrt(2014) however we don't know if this is actually the middle root but it does give us integer
DPatrick
2014-03-15 20:20:52
Good question! Since this cancels nicely with the radical in our final answer and leaves us with just 2, I'd be tempted to guess that this is the middle root. But the AIME writers are often tricky...
Good question! Since this cancels nicely with the radical in our final answer and leaves us with just 2, I'd be tempted to guess that this is the middle root. But the AIME writers are often tricky...
DPatrick
2014-03-15 20:21:10
Is this in fact the middle root? How can we be sure (or discover that it's not)?
Is this in fact the middle root? How can we be sure (or discover that it's not)?
Petaminx
2014-03-15 20:21:30
factor the original equation, then use quadratic formula to find the other 2 roots
factor the original equation, then use quadratic formula to find the other 2 roots
ksun48
2014-03-15 20:21:30
well, we can find the other roots with quadratic formula.
well, we can find the other roots with quadratic formula.
ashgabat
2014-03-15 20:21:30
Well we could long divide >.<
Well we could long divide >.<
vinayak-kumar
2014-03-15 20:21:30
Hmm, factor out the root?
Hmm, factor out the root?
Verjok
2014-03-15 20:21:30
use polynomial division
use polynomial division
DPatrick
2014-03-15 20:21:45
Ick. This might work, but I sure don't want to do it.
Ick. This might work, but I sure don't want to do it.
hi how are you doing toda
2014-03-15 20:21:53
we know the smallest root has to be negative
we know the smallest root has to be negative
DPatrick
2014-03-15 20:22:08
Aha...let's go back and talk to our friend Vieta again.
Aha...let's go back and talk to our friend Vieta again.
DPatrick
2014-03-15 20:22:38
The product of the three roots is negative, right? So since we've already found a positive root, we know that there's exactly one negative root and one other positive root.
The product of the three roots is negative, right? So since we've already found a positive root, we know that there's exactly one negative root and one other positive root.
DPatrick
2014-03-15 20:23:05
And can we tell if the root we've found is the larger or the smalller or the positive roots?
And can we tell if the root we've found is the larger or the smalller or the positive roots?
negativebplusorminus
2014-03-15 20:23:27
And the other two roots sum to 2Sqrt[2014] so the positive one has to be big.
And the other two roots sum to 2Sqrt[2014] so the positive one has to be big.
Tuxianeer
2014-03-15 20:23:27
use sum
use sum
room456
2014-03-15 20:23:37
first equation of vietas
first equation of vietas
allaoc
2014-03-15 20:23:37
And the other positive root is larger because of the sum of roots
And the other positive root is larger because of the sum of roots
adi12
2014-03-15 20:23:37
yes because of the sum
yes because of the sum
genesis2
2014-03-15 20:23:37
yes, by looking at the sum, we know that the sum is 2 sqrt 2014
yes, by looking at the sum, we know that the sum is 2 sqrt 2014
DPatrick
2014-03-15 20:23:56
Right! Using the first of Vieta's Formula, we see that the sum is about 2\sqrt{2014}, which is a big number.
Right! Using the first of Vieta's Formula, we see that the sum is about 2\sqrt{2014}, which is a big number.
DPatrick
2014-03-15 20:24:25
Since we have one negative root, and the root we found is pretty tiny, we know that the third root must be relatively big (at least 2\sqrt{2014} or so).
Since we have one negative root, and the root we found is pretty tiny, we know that the third root must be relatively big (at least 2\sqrt{2014} or so).
mondi
2014-03-15 20:24:35
so it must be the middle root
so it must be the middle root
csmath
2014-03-15 20:24:47
This means our answer is 002
This means our answer is 002
dantx5
2014-03-15 20:24:47
ans is 002
ans is 002
samuelczhao
2014-03-15 20:24:47
so 1/ sqrt 2014 must be in the middle ,so u can just plug it in to the earlier equation
so 1/ sqrt 2014 must be in the middle ,so u can just plug it in to the earlier equation
MSTang
2014-03-15 20:24:47
So the answer IS 2
So the answer IS 2
adi12
2014-03-15 20:24:47
therefore the answer of 2 is proven
therefore the answer of 2 is proven
DPatrick
2014-03-15 20:24:57
Yes. We've proved that indeed x_2 = \dfrac{1}{\sqrt{2014}}, and our answer is \dfrac{2}{\frac{1}{\sqrt{2014}}\cdot\sqrt{2014}} = \boxed{002}.
Yes. We've proved that indeed x_2 = \dfrac{1}{\sqrt{2014}}, and our answer is \dfrac{2}{\frac{1}{\sqrt{2014}}\cdot\sqrt{2014}} = \boxed{002}.
DPatrick
2014-03-15 20:25:41
OK, on to the double-digit problems!
OK, on to the double-digit problems!
DPatrick
2014-03-15 20:25:47
10. A disk with radius 1 is externally tangent to a disk with radius 5. Let A be the point where the disks are tangent, C be the center of the smaller disk, and E be the center of the larger disk. While the larger disk remains fixed, the smaller disk is allowed to roll along the outside of the larger disk until the smaller disk has turned through an angle of 360^\circ. That is, if the center of the smaller disk has moved to point D, and the point on the smaller disk that began at A has now moved to point B, then \overline{AC} is parallel to \overline{BD}. Then \sin^2(\angle BEA) = \frac{m}{n}, where m and n are relatively prime positive integers. Find m+n.
10. A disk with radius 1 is externally tangent to a disk with radius 5. Let A be the point where the disks are tangent, C be the center of the smaller disk, and E be the center of the larger disk. While the larger disk remains fixed, the smaller disk is allowed to roll along the outside of the larger disk until the smaller disk has turned through an angle of 360^\circ. That is, if the center of the smaller disk has moved to point D, and the point on the smaller disk that began at A has now moved to point B, then \overline{AC} is parallel to \overline{BD}. Then \sin^2(\angle BEA) = \frac{m}{n}, where m and n are relatively prime positive integers. Find m+n.
mathtastic
2014-03-15 20:26:08
draw draw draw
draw draw draw
bookhunter7
2014-03-15 20:26:08
DRAW IT
DRAW IT
vinayak-kumar
2014-03-15 20:26:08
Draw a picture!!
Draw a picture!!
bellyflop
2014-03-15 20:26:08
draw a picture
draw a picture
guilt
2014-03-15 20:26:11
Draw a diagram!
Draw a diagram!
mishai
2014-03-15 20:26:11
diagram?
diagram?
DPatrick
2014-03-15 20:26:17
Yeah, let's draw a picture with all this information:
Yeah, let's draw a picture with all this information:
DPatrick
2014-03-15 20:26:22

DPatrick
2014-03-15 20:26:40
What else would be helpful in this picture?
What else would be helpful in this picture?
DrMath
2014-03-15 20:27:04
radii
radii
Tommy2000
2014-03-15 20:27:04
draw EA and ED
draw EA and ED
Wickedestjr
2014-03-15 20:27:04
Lines connecting ED and AE
Lines connecting ED and AE
nickduensing
2014-03-15 20:27:04
Radius of larger circle
Radius of larger circle
kquittman
2014-03-15 20:27:04
the radii of the circles.
the radii of the circles.
pedronr
2014-03-15 20:27:04
connect CE, ED, and EB
connect CE, ED, and EB
minimario
2014-03-15 20:27:04
Drawing BE
Drawing BE
2kev111
2014-03-15 20:27:04
de and ce
de and ce
danzhi
2014-03-15 20:27:04
connect centers
connect centers
DPatrick
2014-03-15 20:27:12
We'll almost certainly want to connect E with C and D. We'll also need E connected with B (since we eventually want to investigate \angle BEA:
We'll almost certainly want to connect E with C and D. We'll also need E connected with B (since we eventually want to investigate \angle BEA:
DPatrick
2014-03-15 20:27:20

DPatrick
2014-03-15 20:27:34
What else do we know?
What else do we know?
DPatrick
2014-03-15 20:28:02
We know a lot of lengths -- but I won't put them in the diagram just yet, they're easy to add later.
We know a lot of lengths -- but I won't put them in the diagram just yet, they're easy to add later.
DPatrick
2014-03-15 20:28:09
What do we know about the angles in this diagram?
What do we know about the angles in this diagram?
Petaminx
2014-03-15 20:28:16
bd parallel to ac
bd parallel to ac
imak64
2014-03-15 20:28:16
ac parallel to bd
ac parallel to bd
raptorw
2014-03-15 20:28:22
<BDE=<CED
<BDE=<CED
Quadratic64
2014-03-15 20:28:22
BD // AC
BD // AC
joshxiong
2014-03-15 20:28:29
AC || BD so BDE = DEC
AC || BD so BDE = DEC
Deathranger999
2014-03-15 20:28:29
DEC and BDE are equal.
DEC and BDE are equal.
DPatrick
2014-03-15 20:28:53
Right. \overline{AC} and \overline{BD} are parallel, so the angles BDD and DEC are equal. Let's call them \theta:
Right. \overline{AC} and \overline{BD} are parallel, so the angles BDD and DEC are equal. Let's call them \theta:
DPatrick
2014-03-15 20:28:59

DPatrick
2014-03-15 20:29:21
Now what? How do we use the data about the rotation? Can we figure out \theta?
Now what? How do we use the data about the rotation? Can we figure out \theta?
vinayak-kumar
2014-03-15 20:29:56
We can compare arc lengths
We can compare arc lengths
kenneth102099
2014-03-15 20:29:56
by circumference
by circumference
sinani206
2014-03-15 20:29:56
from the arc length ratio
from the arc length ratio
DPatrick
2014-03-15 20:30:28
It can be a little unclear what's going on here, and some evidence of that is the number of you telling me that \theta is 72^\circ. It's not, so let's investigate more closely.
It can be a little unclear what's going on here, and some evidence of that is the number of you telling me that \theta is 72^\circ. It's not, so let's investigate more closely.
DPatrick
2014-03-15 20:30:50
The blue arc of the big circle shown below is the amount of arc of the big circle that the little circle rolled along.
The blue arc of the big circle shown below is the amount of arc of the big circle that the little circle rolled along.
DPatrick
2014-03-15 20:30:56


DPatrick
2014-03-15 20:31:10
How does that correspond to an arc on the little circle?
How does that correspond to an arc on the little circle?
DPatrick
2014-03-15 20:31:51
The little circle covers the arc shown in blue below: (Imagine the big circle is covered in blue paint, and the little circle picks up the paint as it rolls.)
The little circle covers the arc shown in blue below: (Imagine the big circle is covered in blue paint, and the little circle picks up the paint as it rolls.)
DPatrick
2014-03-15 20:32:00


DPatrick
2014-03-15 20:32:26
So those two blue arcs have to have the same length.
So those two blue arcs have to have the same length.
vinayak-kumar
2014-03-15 20:33:17
Now we have 5\theta=2\pi-\theta
Now we have 5\theta=2\pi-\theta
csmath
2014-03-15 20:33:17
So 5/6 on the little circle = 1/6 of the big circle so we get theta=60
So 5/6 on the little circle = 1/6 of the big circle so we get theta=60
mathtastic
2014-03-15 20:33:17
it goes 2pi/12pi=1/6=60 degrees around so theta=60^o
it goes 2pi/12pi=1/6=60 degrees around so theta=60^o
DPatrick
2014-03-15 20:33:35
Right -- now you can perhaps "eyeball" \theta from the picture, or we can set up an equation.
Right -- now you can perhaps "eyeball" \theta from the picture, or we can set up an equation.
DPatrick
2014-03-15 20:33:42
The blue arc length on the big circle is 5\theta (if \theta is in radians).
The blue arc length on the big circle is 5\theta (if \theta is in radians).
DPatrick
2014-03-15 20:33:58
The blue arc length on the little circle is 2\pi - \theta. (It's all but \theta of the little circle of radius 1.)
The blue arc length on the little circle is 2\pi - \theta. (It's all but \theta of the little circle of radius 1.)
DPatrick
2014-03-15 20:34:04
So 5\theta = 2\pi - \theta.
And thus \theta = \frac{2}{6}\pi = \frac{\pi}{3}. (Or, if you prefer, 60 degrees.)
So 5\theta = 2\pi - \theta.
And thus \theta = \frac{2}{6}\pi = \frac{\pi}{3}. (Or, if you prefer, 60 degrees.)
DPatrick
2014-03-15 20:34:39
So we know that angles BDE and DEA are 60^\circ. How do we finish from here?
So we know that angles BDE and DEA are 60^\circ. How do we finish from here?
tRIG
2014-03-15 20:35:00
find BE with law of cosines
find BE with law of cosines
claudeaops
2014-03-15 20:35:00
law of cosines
law of cosines
DPatrick
2014-03-15 20:35:14
Certainly, we could finish with some fancy trigonometry, but we don't need it.
Certainly, we could finish with some fancy trigonometry, but we don't need it.
DPatrick
2014-03-15 20:35:30
(Not that fancy I suppose: Law of Cosines is not exactly uncommon.)
(Not that fancy I suppose: Law of Cosines is not exactly uncommon.)
ninjataco
2014-03-15 20:35:56
find \sin BEA by dropping an perpendicular from B
find \sin BEA by dropping an perpendicular from B
ViolinNinja256
2014-03-15 20:35:56
would drawing a 30-60-90 triangle work?
would drawing a 30-60-90 triangle work?
DPatrick
2014-03-15 20:36:10
Right. Just drop a perpendicular from B down to \overline{AE}. Call the points it hits along the way X and Y.
Right. Just drop a perpendicular from B down to \overline{AE}. Call the points it hits along the way X and Y.
DPatrick
2014-03-15 20:36:17

DPatrick
2014-03-15 20:36:27
Now BDX and EXY are 30-60-90 triangles!
Now BDX and EXY are 30-60-90 triangles!
DPatrick
2014-03-15 20:36:54
And we can just chase the lengths we need to compute \sin(\angle BEA).
And we can just chase the lengths we need to compute \sin(\angle BEA).
DPatrick
2014-03-15 20:37:16
What are the lengths in triangle BDX?
What are the lengths in triangle BDX?
ChilledLemonade
2014-03-15 20:37:44
BD=1
BD=1
googol.plex
2014-03-15 20:37:44
1, sqrt3, 2
1, sqrt3, 2
cellobix
2014-03-15 20:37:44
1, 2, sqrt3
1, 2, sqrt3
claudeaops
2014-03-15 20:37:44
XD=2, BX=√3
XD=2, BX=√3
torquoiseworld
2014-03-15 20:37:44
bx= sqrt 3
bx= sqrt 3
tiger21
2014-03-15 20:37:44
1, sqrt3, 2
1, sqrt3, 2
ptes77
2014-03-15 20:37:44
BD=1, DX=2, BX=sqrt3
BD=1, DX=2, BX=sqrt3
Tommy2000
2014-03-15 20:37:44
1, sqrt3, 2
1, sqrt3, 2
raptorw
2014-03-15 20:37:44
1, 2, \sqrt3
1, 2, \sqrt3
DrMath
2014-03-15 20:37:44
1, root3, 2
1, root3, 2
DPatrick
2014-03-15 20:37:48
BD = 1, so BX = \sqrt3 and DX = 2.
BD = 1, so BX = \sqrt3 and DX = 2.
DPatrick
2014-03-15 20:37:58
Then what does EXY tell us?
Then what does EXY tell us?
MSTang
2014-03-15 20:38:10
EX = 4
EX = 4
room456
2014-03-15 20:38:10
ex is 4
ex is 4
mishai
2014-03-15 20:38:20
2, 2sqrt3, 4
2, 2sqrt3, 4
Tommy2000
2014-03-15 20:38:20
then 2, 2sqrt3, 4
then 2, 2sqrt3, 4
mathtastic
2014-03-15 20:38:20
xe=6-2=4 so xey has sides 2 4 and 2sqrt 3 mainly ey=2
xe=6-2=4 so xey has sides 2 4 and 2sqrt 3 mainly ey=2
Deathranger999
2014-03-15 20:38:25
The ratio from big to small is 2:1.
The ratio from big to small is 2:1.
DPatrick
2014-03-15 20:38:35
Right. Since ED = 5+1 = 6 and DX = 2, we have that EX = 4. Therefore EY = 2 and XY = 2\sqrt3.
Right. Since ED = 5+1 = 6 and DX = 2, we have that EX = 4. Therefore EY = 2 and XY = 2\sqrt3.
DPatrick
2014-03-15 20:38:55
So BE is the hypotenuse of right triangle BYE with sides BY = BX + XY = 3\sqrt3 and EY = 2.
So BE is the hypotenuse of right triangle BYE with sides BY = BX + XY = 3\sqrt3 and EY = 2.
summitwei
2014-03-15 20:39:05
BE=\sqrt{31}
BE=\sqrt{31}
csmath
2014-03-15 20:39:05
This means we have BYE as 2, 3sqrt(3), sqrt(31)
This means we have BYE as 2, 3sqrt(3), sqrt(31)
gamjawon
2014-03-15 20:39:05


DPatrick
2014-03-15 20:39:15
Right: BE = \sqrt{27 + 4} = \sqrt{31}.
Right: BE = \sqrt{27 + 4} = \sqrt{31}.
gamjawon
2014-03-15 20:39:41
So then \sin^2{\angle BEA}=\frac{27}{31} ?
So then \sin^2{\angle BEA}=\frac{27}{31} ?
joshxiong
2014-03-15 20:39:47
so \sin^2(\angle BEA) = \frac{27}{31}
so \sin^2(\angle BEA) = \frac{27}{31}
Deathranger999
2014-03-15 20:39:47
Which means sine squared is 27/31.
Which means sine squared is 27/31.
room456
2014-03-15 20:39:47
so sin^2(angle BEA) = 27/31
so sin^2(angle BEA) = 27/31
DPatrick
2014-03-15 20:39:59
Exactly: we have all the sides of BEY, so \sin\angle BEA = \sin\angle BEY = \frac{BY}{BE} = \frac{3\sqrt3}{\sqrt{31}}.
Exactly: we have all the sides of BEY, so \sin\angle BEA = \sin\angle BEY = \frac{BY}{BE} = \frac{3\sqrt3}{\sqrt{31}}.
DPatrick
2014-03-15 20:40:08
Thus \sin^2\angle BEA = \dfrac{27}{31}, and our answer is 27 + 31 = \boxed{058}.
Thus \sin^2\angle BEA = \dfrac{27}{31}, and our answer is 27 + 31 = \boxed{058}.
DPatrick
2014-03-15 20:40:39
On to the final third! Next is #11:
On to the final third! Next is #11:
DPatrick
2014-03-15 20:40:45
11. A token starts at the point (0,0) of an xy-coordinate grid and then makes a sequence of six moves. Each move is 1 unit in a direction parallel to one of the coordinate axes. Each move is selected randomly from the four possible directions and independently of the other moves. The probability the token ends at a point on the graph of |y| = |x| is \frac{m}{n}, where m and n are relatively prime positive integers. Find m+n.
11. A token starts at the point (0,0) of an xy-coordinate grid and then makes a sequence of six moves. Each move is 1 unit in a direction parallel to one of the coordinate axes. Each move is selected randomly from the four possible directions and independently of the other moves. The probability the token ends at a point on the graph of |y| = |x| is \frac{m}{n}, where m and n are relatively prime positive integers. Find m+n.
DPatrick
2014-03-15 20:41:09
There are a few different ways to approach this problem. But virtually all of them involve careful bookkeeping of the various paths.
There are a few different ways to approach this problem. But virtually all of them involve careful bookkeeping of the various paths.
DPatrick
2014-03-15 20:41:34
What does the graph of |y| = |x| look like?
What does the graph of |y| = |x| look like?
turkeybob777
2014-03-15 20:42:01
an X
an X
aimingforimo
2014-03-15 20:42:01
y=x and y=-x
y=x and y=-x
MSTang
2014-03-15 20:42:01
y=x and y=-x
y=x and y=-x
ashgabat
2014-03-15 20:42:01
It looks like a big X
It looks like a big X
CornSaltButter
2014-03-15 20:42:01
The graphs of y=x and y=-x
The graphs of y=x and y=-x
mikechen
2014-03-15 20:42:01
the lines y=x and y=-x combined
the lines y=x and y=-x combined
kquittman
2014-03-15 20:42:01
y=x and y=-x.
y=x and y=-x.
Rectangle_Square
2014-03-15 20:42:01
v and upside down v
v and upside down v
allaoc
2014-03-15 20:42:01
X
X
dasobson
2014-03-15 20:42:01
a big x
a big x
aprobs21
2014-03-15 20:42:01
X
X
DPatrick
2014-03-15 20:42:11
It's the union of the lines y=x and y=-x. If you drew it, it'd be a big "X" through the origin.
It's the union of the lines y=x and y=-x. If you drew it, it'd be a big "X" through the origin.
DPatrick
2014-03-15 20:42:24
So one strategy is that we can separately look at the number of 6-move paths that end on either line.
So one strategy is that we can separately look at the number of 6-move paths that end on either line.
DPatrick
2014-03-15 20:42:34
Of course, the origin (0,0) is on both lines, so it'll be double-counted and we'll have to correct for it later.
Of course, the origin (0,0) is on both lines, so it'll be double-counted and we'll have to correct for it later.
DPatrick
2014-03-15 20:42:41
Let's start with paths landing on y=x. What do we know about such paths?
Let's start with paths landing on y=x. What do we know about such paths?
MSTang
2014-03-15 20:42:57
y-x = 0
y-x = 0
mishai
2014-03-15 20:43:11
same number of up down and right left
same number of up down and right left
gamjawon
2014-03-15 20:43:11
y-x=0!
y-x=0!
sinani206
2014-03-15 20:43:11
number of moves up or left = number of moves down or right
number of moves up or left = number of moves down or right
DPatrick
2014-03-15 20:43:16
Exactly!
Exactly!
DPatrick
2014-03-15 20:43:28
We land on y=x if and only if 3 of the 6 moves are ups or lefts, and 3 of the 6 moves are downs or rights.
We land on y=x if and only if 3 of the 6 moves are ups or lefts, and 3 of the 6 moves are downs or rights.
DPatrick
2014-03-15 20:43:45
One way to see this is to keep track of the value of y-x as the point moves. Moving up or left increases y-x by 1, and moving down or right decreases y-x by 1. To land on y=x, it has to finish at y-x = 0.
One way to see this is to keep track of the value of y-x as the point moves. Moving up or left increases y-x by 1, and moving down or right decreases y-x by 1. To land on y=x, it has to finish at y-x = 0.
DPatrick
2014-03-15 20:44:24
Or more broadly, moving up or left moves "northwest" and moving down or right moves "southeast".
Or more broadly, moving up or left moves "northwest" and moving down or right moves "southeast".
DPatrick
2014-03-15 20:44:32
So we need to count the number of 6-move paths in which 3 of the moves are U or L and 3 of the moves are D or R.
So we need to count the number of 6-move paths in which 3 of the moves are U or L and 3 of the moves are D or R.
DPatrick
2014-03-15 20:44:43
How many are there? How can we count them?
How many are there? How can we count them?
MSTang
2014-03-15 20:45:19
\dbinom{6}{3} \cdot 2^6
\dbinom{6}{3} \cdot 2^6
torquoiseworld
2014-03-15 20:45:19
6choose 3 and each of the 6 moves have two options
6choose 3 and each of the 6 moves have two options
tiger21
2014-03-15 20:45:19
6 choose 3 times 2^6
6 choose 3 times 2^6
aprobs21
2014-03-15 20:45:19
6C3 2^6?
6C3 2^6?
mentalgenius
2014-03-15 20:45:27
choose 3 from 6 for which are DR, rest are UL. Then you have 2^3 for each, to get 2^6 * (6 choose 3)
choose 3 from 6 for which are DR, rest are UL. Then you have 2^3 for each, to get 2^6 * (6 choose 3)
DPatrick
2014-03-15 20:45:31
Good!
Good!
DPatrick
2014-03-15 20:45:54
First, we can decide which 3 of the 6 moves are U or L. We can choose 3 of the 6 moves to be U or L in \binom63 = 20 ways. (The other 3 will then be D or R.)
First, we can decide which 3 of the 6 moves are U or L. We can choose 3 of the 6 moves to be U or L in \binom63 = 20 ways. (The other 3 will then be D or R.)
DPatrick
2014-03-15 20:46:04
Now each move has two choices: if it's slotted as an "U or L" move, we must choose U or L, and if it's slotted as a "D or R" move, we must choose D or R.
Now each move has two choices: if it's slotted as an "U or L" move, we must choose U or L, and if it's slotted as a "D or R" move, we must choose D or R.
samuelczhao
2014-03-15 20:46:18
1280
1280
Deathranger999
2014-03-15 20:46:18
Which is 20 times 64=1280.
Which is 20 times 64=1280.
DPatrick
2014-03-15 20:46:35
Yes: calculating this out, there are \binom63 \cdot 2^6 = 20 \cdot 64 = 1280 paths ending on y=x.
Yes: calculating this out, there are \binom63 \cdot 2^6 = 20 \cdot 64 = 1280 paths ending on y=x.
sinani206
2014-03-15 20:46:52
and you get the same number for y = -x so now you just have to get rid of doubles
and you get the same number for y = -x so now you just have to get rid of doubles
cellobix
2014-03-15 20:46:52
And same thing for the line y=-x
And same thing for the line y=-x
summitwei
2014-03-15 20:46:52
same for y=-x
same for y=-x
mishai
2014-03-15 20:46:58
by symmetry, are there the same amount landing in y=-x?
by symmetry, are there the same amount landing in y=-x?
DPatrick
2014-03-15 20:47:13
Right! For paths landing on y=-x, we could do the same computation, or just note that by the symmetry of the problem, there are also 1280 such paths. (For example, take any path landing on y=x and rotate it 90 degrees.)
Right! For paths landing on y=-x, we could do the same computation, or just note that by the symmetry of the problem, there are also 1280 such paths. (For example, take any path landing on y=x and rotate it 90 degrees.)
DPatrick
2014-03-15 20:47:26
So that's 2(1280) = 2560 paths that land on y=x or y=-x...
So that's 2(1280) = 2560 paths that land on y=x or y=-x...
mathtastic
2014-03-15 20:47:40
then subtract for overcount of orgin
then subtract for overcount of orgin
pedronr
2014-03-15 20:47:40
but you're overcounting the origin
but you're overcounting the origin
ninjataco
2014-03-15 20:47:40
the only overcount is (0,0)
the only overcount is (0,0)
SockFoot
2014-03-15 20:47:40
but then subtract the ones where it ends on the origin
but then subtract the ones where it ends on the origin
mentalgenius
2014-03-15 20:47:40
but you doublecounted the origin
but you doublecounted the origin
shreshrej
2014-03-15 20:47:40
But we cannot overcount 0,0! That can be bad
But we cannot overcount 0,0! That can be bad
DPatrick
2014-03-15 20:47:49
...indeed, as mentioned earlier, we've double-counted paths that land on the origin. So we need to subtract these from our count.
...indeed, as mentioned earlier, we've double-counted paths that land on the origin. So we need to subtract these from our count.
DPatrick
2014-03-15 20:48:00
So let's count 6-move paths that end at (0,0). What can we say about such paths?
So let's count 6-move paths that end at (0,0). What can we say about such paths?
sinani206
2014-03-15 20:48:30
up = down and left = right
up = down and left = right
speck
2014-03-15 20:48:30
R=L, U=D
R=L, U=D
shreshrej
2014-03-15 20:48:30
The number of up is equal to down, the number of left is equal to right
The number of up is equal to down, the number of left is equal to right
allaoc
2014-03-15 20:48:30
Up = down, left = right
Up = down, left = right
sparkles257
2014-03-15 20:48:30
all cancel out L and R or D and U
all cancel out L and R or D and U
ChilledLemonade
2014-03-15 20:48:30
Number of up= down left = right
Number of up= down left = right
claudeaops
2014-03-15 20:48:30
# of Ups=# of Downs, # of Lefts= # of Rights
# of Ups=# of Downs, # of Lefts= # of Rights
MSTang
2014-03-15 20:48:30
numOfU = numOfD and numOfL = numOfR
numOfU = numOfD and numOfL = numOfR
LightningX48
2014-03-15 20:48:35
for every right, there is a left and for every up there is a down
for every right, there is a left and for every up there is a down
VietaFan
2014-03-15 20:48:35
ups = downs, lefts = rights
ups = downs, lefts = rights
DPatrick
2014-03-15 20:48:41
Yep. They must have an equal number of Us and Ds, and an equal number of Ls and Rs.
Yep. They must have an equal number of Us and Ds, and an equal number of Ls and Rs.
mentalgenius
2014-03-15 20:49:00
UUUDDD, UUDDRL, UDRRLL, or RRRLLL (permuatations of each of these)
UUUDDD, UUDDRL, UDRRLL, or RRRLLL (permuatations of each of these)
shreshrej
2014-03-15 20:49:05
RRRLLL, UUUDDD, RRLLUD, RLUUDD
RRRLLL, UUUDDD, RRLLUD, RLUUDD
DPatrick
2014-03-15 20:49:31
Right, all such paths must be UUUDDD, UUDDLR, UDLLRR, or LLLRRR in some order. So there's some simple casework to count the number of ordering of each of these. (I don't know a slick way to do them all at once.)
Right, all such paths must be UUUDDD, UUDDLR, UDLLRR, or LLLRRR in some order. So there's some simple casework to count the number of ordering of each of these. (I don't know a slick way to do them all at once.)
DPatrick
2014-03-15 20:49:43
How many with UUUDDD in some order?
How many with UUUDDD in some order?
ViolinNinja256
2014-03-15 20:50:17
2 * 6C3 + 2*6C4*4C2
2 * 6C3 + 2*6C4*4C2
Deathranger999
2014-03-15 20:50:17
6C3.
6C3.
sparkles257
2014-03-15 20:50:17
6C3
6C3
sophiazhi
2014-03-15 20:50:17
20
20
shreshrej
2014-03-15 20:50:17
6C3 or 20
6C3 or 20
guilt
2014-03-15 20:50:17
6C3 = 20
6C3 = 20
Descrip
2014-03-15 20:50:17
6 choose 3
6 choose 3
ninjataco
2014-03-15 20:50:17
20
20
aimingforimo
2014-03-15 20:50:17
20
20
lovejj
2014-03-15 20:50:17
20
20
tiger21
2014-03-15 20:50:17
6C3=20
6C3=20
othuum0149
2014-03-15 20:50:17
20
20
room456
2014-03-15 20:50:17
6C3
6C3
ViolinNinja256
2014-03-15 20:50:17
6C3
6C3
TheEconomist
2014-03-15 20:50:17
6!/(3!3!)
6!/(3!3!)
hjl00
2014-03-15 20:50:17
20
20
DPatrick
2014-03-15 20:50:24
We just need to choose 3 of the 6 positions in which to place a U (and the other 3 then becomes Ds). So there are \binom63 = 20 such paths.
We just need to choose 3 of the 6 positions in which to place a U (and the other 3 then becomes Ds). So there are \binom63 = 20 such paths.
DPatrick
2014-03-15 20:50:48
Or you can think of it as \dfrac{6!}{3!3!}, where we're arranging 6 letters, with two letters each repeated 3 times. (It's the same number!)
Or you can think of it as \dfrac{6!}{3!3!}, where we're arranging 6 letters, with two letters each repeated 3 times. (It's the same number!)
cellobix
2014-03-15 20:51:01
Same thing for LLLRRR
Same thing for LLLRRR
kgator
2014-03-15 20:51:01
RRRLLL is also 20
RRRLLL is also 20
mathtastic
2014-03-15 20:51:01
same for RRRLLL
same for RRRLLL
mishai
2014-03-15 20:51:01
same for RRRLLL
same for RRRLLL
ViolinNinja256
2014-03-15 20:51:01
same for RRRLLL
same for RRRLLL
allaoc
2014-03-15 20:51:01
LLLRRR is the same
LLLRRR is the same
DPatrick
2014-03-15 20:51:08
Indeed, by symmetry, there are also 20 paths with LLLRRR in some order.
Indeed, by symmetry, there are also 20 paths with LLLRRR in some order.
DPatrick
2014-03-15 20:51:13
How about paths with UUDDLR?
How about paths with UUDDLR?
sparkles257
2014-03-15 20:51:42
6!/4
6!/4
dli00105
2014-03-15 20:51:42
180
180
kquittman
2014-03-15 20:51:42
180
180
MSTang
2014-03-15 20:51:42
6 * 5 * (4 choose 2) = 180
6 * 5 * (4 choose 2) = 180
sharonmath
2014-03-15 20:51:42
180
180
bakugon321
2014-03-15 20:51:42
6!/(2*2)
6!/(2*2)
DrMath
2014-03-15 20:51:42
180
180
danusv
2014-03-15 20:51:42
6!/2!2!
6!/2!2!
firemike
2014-03-15 20:51:42
180
180
mathmaster2012
2014-03-15 20:51:42
6!/(2!2!)
6!/(2!2!)
joey8189681
2014-03-15 20:51:42
6!/2!2!
6!/2!2!
WalkerTesla
2014-03-15 20:51:42
180
180
DPatrick
2014-03-15 20:51:52
There are 6! ways to arrange 6 letters, but we divide by 2 \cdot 2 because there are 2 Us and 2Ds. Thus there are \dfrac{6!}{4} = 180 paths with UUDDLR in some order.
There are 6! ways to arrange 6 letters, but we divide by 2 \cdot 2 because there are 2 Us and 2Ds. Thus there are \dfrac{6!}{4} = 180 paths with UUDDLR in some order.
DPatrick
2014-03-15 20:52:13
You could also count this as 6 ways to slot the L, then 5 ways to slot to R, then \binom42 ways to pick 2 of the remaining slots for U.
You could also count this as 6 ways to slot the L, then 5 ways to slot to R, then \binom42 ways to pick 2 of the remaining slots for U.
kgator
2014-03-15 20:52:29
same with RRLLUD
same with RRLLUD
cellobix
2014-03-15 20:52:29
Same for UDLLRR
Same for UDLLRR
sinani206
2014-03-15 20:52:29
so 180 llrrud as well
so 180 llrrud as well
sparkles257
2014-03-15 20:52:29
same for the other one by symmetry
same for the other one by symmetry
firemike
2014-03-15 20:52:29
same for LLRRUD
same for LLRRUD
kunsun
2014-03-15 20:52:29
also 180 for UDLLRR
also 180 for UDLLRR
claudeaops
2014-03-15 20:52:29
same for UDLLRR
same for UDLLRR
dli00105
2014-03-15 20:52:29
same for RRLLUD
same for RRLLUD
bakugon321
2014-03-15 20:52:29
Same for udrrll
Same for udrrll
DPatrick
2014-03-15 20:52:33
By the same reasoning there are also 180 paths with UDLLRR in some order.
By the same reasoning there are also 180 paths with UDLLRR in some order.
DPatrick
2014-03-15 20:52:40
So that's a total of 20+180+180+20 = 400 paths that end at the origin.
So that's a total of 20+180+180+20 = 400 paths that end at the origin.
DPatrick
2014-03-15 20:52:48
Thus how many total paths that work for this problem?
Thus how many total paths that work for this problem?
sinani206
2014-03-15 20:53:06
2560-400 = 2160
2560-400 = 2160
sparkles257
2014-03-15 20:53:06
overcounted 400
overcounted 400
sparkles257
2014-03-15 20:53:06
2160
2160
sinani206
2014-03-15 20:53:06
2160
2160
MSTang
2014-03-15 20:53:06
2160
2160
DrMath
2014-03-15 20:53:06
2160
2160
ashgabat
2014-03-15 20:53:06
2160
2160
guilt
2014-03-15 20:53:06
2560-400 = 2160
2560-400 = 2160
WalkerTesla
2014-03-15 20:53:06
2160
2160
ninjataco
2014-03-15 20:53:06
2160
2160
DPatrick
2014-03-15 20:53:26
Right: we initially counted 2560 paths, but then discovered that we overcounted by 400. Thus there are 2560 - 400 = 2160 paths that work.
Right: we initially counted 2560 paths, but then discovered that we overcounted by 400. Thus there are 2560 - 400 = 2160 paths that work.
DPatrick
2014-03-15 20:53:46
And to finish we need to compute the probability of such a path randomly occurring.
And to finish we need to compute the probability of such a path randomly occurring.
mathtastic
2014-03-15 20:54:06
2160/4^6
2160/4^6
kgator
2014-03-15 20:54:06
in total there are 4096 cases
in total there are 4096 cases
aprobs21
2014-03-15 20:54:06
Out of 4^6 total
Out of 4^6 total
cellobix
2014-03-15 20:54:06
4^6 total paths (4 options for each move)
4^6 total paths (4 options for each move)
sophiazhi
2014-03-15 20:54:06
2160/4^6
2160/4^6
joey8189681
2014-03-15 20:54:06
2160/2^12
2160/2^12
Quadratic64
2014-03-15 20:54:06
The total number of paths is 4^6
The total number of paths is 4^6
mishai
2014-03-15 20:54:06
divided by 4^6=4096
divided by 4^6=4096
samuelczhao
2014-03-15 20:54:06
2160/4096 = 135 / 256
2160/4096 = 135 / 256
bob2
2014-03-15 20:54:06
4^6 TOTAL
4^6 TOTAL
Satyaprakash2009rta
2014-03-15 20:54:06
2160/4^6=135/256 so our answer is 135+256=391
2160/4^6=135/256 so our answer is 135+256=391
DPatrick
2014-03-15 20:54:11
Right. Each of the 6 moves has 4 possibilities, so there are 4^6 = 4096 total paths.
Right. Each of the 6 moves has 4 possibilities, so there are 4^6 = 4096 total paths.
DPatrick
2014-03-15 20:54:21
Thus our probability is \dfrac{2160}{4096}. This reduces to \dfrac{135}{256}, so our answer is 135 + 256 = \boxed{391}.
Thus our probability is \dfrac{2160}{4096}. This reduces to \dfrac{135}{256}, so our answer is 135 + 256 = \boxed{391}.
DPatrick
2014-03-15 20:54:42
I'm going to take a 2-minute break to get a glass of water -- brb!
I'm going to take a 2-minute break to get a glass of water -- brb!
DPatrick
2014-03-15 20:56:28
OK, I'm back and refreshed!
OK, I'm back and refreshed!
DPatrick
2014-03-15 20:56:37
We're about at the 2-hour mark, and just 4 problems to go!
We're about at the 2-hour mark, and just 4 problems to go!
DPatrick
2014-03-15 20:56:42
12. Let A = \{1,2,3,4\}, and let f and g be randomly chosen (not necessarily distinct) functions from A to A. The probability that the range of f and the range of g are disjoint is \frac{m}{n}, where m and n are relatively prime positive integers. Find m.
12. Let A = \{1,2,3,4\}, and let f and g be randomly chosen (not necessarily distinct) functions from A to A. The probability that the range of f and the range of g are disjoint is \frac{m}{n}, where m and n are relatively prime positive integers. Find m.
DPatrick
2014-03-15 20:57:15
I would have preferred it if #11 and #12 were spaced a bit apart -- this is two bookwork-y counting problems in a row.
I would have preferred it if #11 and #12 were spaced a bit apart -- this is two bookwork-y counting problems in a row.
DPatrick
2014-03-15 20:57:36
But we have to deal with it. As with #11, the trickiest part is just keeping careful track of stuff.
But we have to deal with it. As with #11, the trickiest part is just keeping careful track of stuff.
DPatrick
2014-03-15 20:57:58
By the way, since many of you are asking: "disjoint" means that the ranges have no numbers in common.
By the way, since many of you are asking: "disjoint" means that the ranges have no numbers in common.
firemike
2014-03-15 20:58:21
casework again!
casework again!
bengals
2014-03-15 20:58:21
casework
casework
claudeaops
2014-03-15 20:58:21
Split into cases based on the # of outputs f has
Split into cases based on the # of outputs f has
DPatrick
2014-03-15 20:58:32
That's what I did. We can do casework on the number of elements in the range of f.
That's what I did. We can do casework on the number of elements in the range of f.
joshxiong
2014-03-15 20:58:39
Note that |range f| cannot = 4
Note that |range f| cannot = 4
DPatrick
2014-03-15 20:58:57
Indeed, we can't use all 4 elements in the range for either function, because then there'd be none left for the other one.
Indeed, we can't use all 4 elements in the range for either function, because then there'd be none left for the other one.
DPatrick
2014-03-15 20:59:12
So there are 3 cases we have to work them. Let's just have at them.
So there are 3 cases we have to work them. Let's just have at them.
DPatrick
2014-03-15 20:59:18
Case 1: the range of f has 1 element.
Case 1: the range of f has 1 element.
DPatrick
2014-03-15 20:59:22
How many f's have just 1 element in the range?
How many f's have just 1 element in the range?
sparkles257
2014-03-15 20:59:40
4
4
checkmate1021
2014-03-15 20:59:40
4
4
Tommy2000
2014-03-15 20:59:40
4?
4?
guilt
2014-03-15 20:59:40
4
4
kquittman
2014-03-15 20:59:40
4
4
SockFoot
2014-03-15 20:59:40
4
4
buzzyun
2014-03-15 20:59:40
4
4
mathmaster2012
2014-03-15 20:59:40
4
4
inductor
2014-03-15 20:59:40
4
4
MSTang
2014-03-15 20:59:40
4: f(x) = 1, 2, 3, 4
4: f(x) = 1, 2, 3, 4
DPatrick
2014-03-15 20:59:44
Just 4: the four constant functions.
Just 4: the four constant functions.
DPatrick
2014-03-15 20:59:54
For each of these, how many g's are there with disjoint range?
For each of these, how many g's are there with disjoint range?
claudeaops
2014-03-15 21:00:22
3^4
3^4
alex31415
2014-03-15 21:00:22
3^4=81
3^4=81
apple.singer
2014-03-15 21:00:22
3^4
3^4
dli00105
2014-03-15 21:00:22
81
81
aprobs21
2014-03-15 21:00:22
3^4
3^4
TheStrangeCharm
2014-03-15 21:00:22
3^4 = 81
3^4 = 81
SuperSnivy
2014-03-15 21:00:22
3^4
3^4
jimBriggs
2014-03-15 21:00:22
3^4
3^4
joshxiong
2014-03-15 21:00:22
3^4 = 81
3^4 = 81
DPatrick
2014-03-15 21:00:43
Right. Each element in A can map via g to one of the three numbers not in the range of f.
Right. Each element in A can map via g to one of the three numbers not in the range of f.
DPatrick
2014-03-15 21:01:00
So since we have 3 choice for each of the 4 elements in the domain of g, we have 3^4 = 81 such g's.
So since we have 3 choice for each of the 4 elements in the domain of g, we have 3^4 = 81 such g's.
DPatrick
2014-03-15 21:01:06
So, how many pairs of functions in case 1?
So, how many pairs of functions in case 1?
sinani206
2014-03-15 21:01:28
324
324
aimingforimo
2014-03-15 21:01:28
324
324
aprobs21
2014-03-15 21:01:28
324
324
dli00105
2014-03-15 21:01:28
324
324
SockFoot
2014-03-15 21:01:28
81*4
81*4
kquittman
2014-03-15 21:01:28
324
324
mishai
2014-03-15 21:01:28
4*81=324
4*81=324
cellobix
2014-03-15 21:01:28
4*81=324
4*81=324
CornSaltButter
2014-03-15 21:01:28
81*4=324
81*4=324
summitwei
2014-03-15 21:01:28
4*81=324
4*81=324
ViolinNinja256
2014-03-15 21:01:28
4*81=324
4*81=324
DPatrick
2014-03-15 21:01:43
Right: there are 4 f's and each f has 81 possible g's. Hence, there are 4 \cdot 81 = 324 pairs of functions in case 1.
Right: there are 4 f's and each f has 81 possible g's. Hence, there are 4 \cdot 81 = 324 pairs of functions in case 1.
DPatrick
2014-03-15 21:01:53
Case 2: the range of f has 2 elements.
Case 2: the range of f has 2 elements.
DPatrick
2014-03-15 21:01:58
How many such f are there?
How many such f are there?
Wolstenholme
2014-03-15 21:02:38
14*6 = 84
14*6 = 84
othuum0149
2014-03-15 21:02:38
84
84
DPatrick
2014-03-15 21:02:46
84 is correct -- let's see how we get it.
84 is correct -- let's see how we get it.
DPatrick
2014-03-15 21:03:07
An easier question is: how many choices for a 2-element range of f?
An easier question is: how many choices for a 2-element range of f?
DPatrick
2014-03-15 21:03:22
(Without worrying yet about which elements map to which.)
(Without worrying yet about which elements map to which.)
VietaFan
2014-03-15 21:03:39
4C2= 6
4C2= 6
firemike
2014-03-15 21:03:39
4 choose 2?
4 choose 2?
allaoc
2014-03-15 21:03:39
4C2 = 6
4C2 = 6
ChilledLemonade
2014-03-15 21:03:39
4C2=6
4C2=6
ninjataco
2014-03-15 21:03:39
6
6
bengals
2014-03-15 21:03:39
6
6
ashgabat
2014-03-15 21:03:39
6
6
Quadratic64
2014-03-15 21:03:39
4 choose 2 = 6
4 choose 2 = 6
martian179
2014-03-15 21:03:39
4 choose 2 = 6
4 choose 2 = 6
DPatrick
2014-03-15 21:03:57
Right: there are \binom42 = 6 choices for the range of f. (We just have to choose the 2 elements out of the 4 that we want in the range.)
Right: there are \binom42 = 6 choices for the range of f. (We just have to choose the 2 elements out of the 4 that we want in the range.)
DPatrick
2014-03-15 21:04:11
And then for each of these choices, how many functions are there that have this range?
And then for each of these choices, how many functions are there that have this range?
Petaminx
2014-03-15 21:04:38
2^4-2
2^4-2
joshxiong
2014-03-15 21:04:38
2^4 but we have to subtract 2 since we do not want |range f| = 1 so 14 in total
2^4 but we have to subtract 2 since we do not want |range f| = 1 so 14 in total
tiger21
2014-03-15 21:04:38
4C1+4C2+4C3=4+6+4=14
4C1+4C2+4C3=4+6+4=14
raptorw
2014-03-15 21:04:38
2^4?
2^4?
aimingforimo
2014-03-15 21:04:38
2^4-2=14
2^4-2=14
martian179
2014-03-15 21:04:38
2^4 - 2 (to remove the two constant functions)
2^4 - 2 (to remove the two constant functions)
DPatrick
2014-03-15 21:05:03
Right. There are 2^4 = 16 functions total that map from A to 2-elements, but we don't want to count the 2 constant functions -- we already dealt with those in Case 1!
Right. There are 2^4 = 16 functions total that map from A to 2-elements, but we don't want to count the 2 constant functions -- we already dealt with those in Case 1!
DPatrick
2014-03-15 21:05:15
So there are 16 - 2 = 14 functions f with a given 2-element range.
So there are 16 - 2 = 14 functions f with a given 2-element range.
DPatrick
2014-03-15 21:05:56
Therefore, since there were 6 choices for a possible range, and then 14 functions with that particular range, we conclude that there are 6 \cdot 14 = 84 possible f's in Case 2.
Therefore, since there were 6 choices for a possible range, and then 14 functions with that particular range, we conclude that there are 6 \cdot 14 = 84 possible f's in Case 2.
DPatrick
2014-03-15 21:06:03
And for each f, how many functions g are there with disjoint range?
And for each f, how many functions g are there with disjoint range?
claudeaops
2014-03-15 21:06:37
2^4=16
2^4=16
MSTang
2014-03-15 21:06:37
16
16
larry333
2014-03-15 21:06:37
16
16
Petaminx
2014-03-15 21:06:37
2^4
2^4
Tommy2000
2014-03-15 21:06:37
2^4?
2^4?
DPatrick
2014-03-15 21:07:00
Right, each element of A has 2 choices of where it can map to under g (because it has to miss the range of f), so there are 2^4 = 16 such g (for each f).
Right, each element of A has 2 choices of where it can map to under g (because it has to miss the range of f), so there are 2^4 = 16 such g (for each f).
DPatrick
2014-03-15 21:07:28
Therefore, how many pairs of functions in Case 2?
Therefore, how many pairs of functions in Case 2?
Satyaprakash2009rta
2014-03-15 21:07:57
16*84=1344
16*84=1344
mishai
2014-03-15 21:07:57
1344
1344
Tommy2000
2014-03-15 21:07:57
16*84 = 1344
16*84 = 1344
ChilledLemonade
2014-03-15 21:07:57
84*16=1344
84*16=1344
sparkles257
2014-03-15 21:07:57
84*16
84*16
hwl0304
2014-03-15 21:07:57
84*16
84*16
cellobix
2014-03-15 21:07:57
So 84*16 pairs!
So 84*16 pairs!
kgator
2014-03-15 21:07:57
and 84 * 16 = 1334
and 84 * 16 = 1334
vinayak-kumar
2014-03-15 21:07:57
84*16
84*16
guilt
2014-03-15 21:07:57
16*84 = 1344
16*84 = 1344
DPatrick
2014-03-15 21:08:17
Yep: 84 possible f's and then 16 possible g's for each f, so 84 \cdot 16 = 1344 pairs total in case 2.
Yep: 84 possible f's and then 16 possible g's for each f, so 84 \cdot 16 = 1344 pairs total in case 2.
DPatrick
2014-03-15 21:08:33
Case 3: the range of f has 3 elements.
Case 3: the range of f has 3 elements.
DPatrick
2014-03-15 21:08:39
How many such f are there?
How many such f are there?
raptorw
2014-03-15 21:09:36
144
144
claudeaops
2014-03-15 21:09:36
4*3*12=144
4*3*12=144
nsun48
2014-03-15 21:09:36
4*4C2*6=144
4*4C2*6=144
joshxiong
2014-03-15 21:09:36
(4 choose 3) * (3^4-3*2^4+3*1^4) = 144
(4 choose 3) * (3^4-3*2^4+3*1^4) = 144
DPatrick
2014-03-15 21:09:55
Indeed there are 144, and there are a few different ways to count them.
Indeed there are 144, and there are a few different ways to count them.
DPatrick
2014-03-15 21:10:17
There's are ugly casework ways, but there's a simpler way too.
There's are ugly casework ways, but there's a simpler way too.
DPatrick
2014-03-15 21:10:31
How many TOTAL functions from A to A are there, with no restrictions?
How many TOTAL functions from A to A are there, with no restrictions?
dli00105
2014-03-15 21:10:55
256
256
negativebplusorminus
2014-03-15 21:10:55
4^4
4^4
jilynne1992
2014-03-15 21:10:55
256
256
shreshrej
2014-03-15 21:10:55
4^4
4^4
othuum0149
2014-03-15 21:10:55
4^4=256
4^4=256
apple.singer
2014-03-15 21:10:55
4^4=256
4^4=256
VietaFan
2014-03-15 21:10:55
4^4 = 256
4^4 = 256
aprobs21
2014-03-15 21:10:55
4^4
4^4
DPatrick
2014-03-15 21:11:10
Right: each of the four elements of A can map to any of 4 elements, so there are 4^4 = 256 total functions.
Right: each of the four elements of A can map to any of 4 elements, so there are 4^4 = 256 total functions.
DPatrick
2014-03-15 21:11:17
How many functions are there that have a 4-element range?
How many functions are there that have a 4-element range?
joshxiong
2014-03-15 21:11:53
4! = 24
4! = 24
othuum0149
2014-03-15 21:11:53
24
24
ashgabat
2014-03-15 21:11:53
4! = 24
4! = 24
mathtastic
2014-03-15 21:11:53
4!=24
4!=24
Quadratic64
2014-03-15 21:11:53
4!=24
4!=24
phil9047
2014-03-15 21:11:53
24
24
DPatrick
2014-03-15 21:12:11
Right: a map from A to A with a 4-element range is just a permutation of A, and we know there are 4! = 24 of those.
Right: a map from A to A with a 4-element range is just a permutation of A, and we know there are 4! = 24 of those.
ashgabat
2014-03-15 21:12:36
So we know that the number of functions with a 3-element range is 256 - 84 - 24 - 4 = 144.
So we know that the number of functions with a 3-element range is 256 - 84 - 24 - 4 = 144.
DPatrick
2014-03-15 21:12:48
So since we've already counted the 1-element and 2-element range functions and now we've counted the 4-element range functions, what's leftover are the 3-element range functions!
So since we've already counted the 1-element and 2-element range functions and now we've counted the 4-element range functions, what's leftover are the 3-element range functions!
DPatrick
2014-03-15 21:12:58
So there are 256 - 4 - 84 - 24 = 144 of them.
So there are 256 - 4 - 84 - 24 = 144 of them.
DPatrick
2014-03-15 21:13:15
And how many functions g for each such f?
And how many functions g for each such f?
kquittman
2014-03-15 21:13:41
1
1
firemike
2014-03-15 21:13:41
1
1
summitwei
2014-03-15 21:13:41
1
1
ruiqiu2000
2014-03-15 21:13:41
one
one
danzhi
2014-03-15 21:13:41
1
1
allaoc
2014-03-15 21:13:41
1
1
DPatrick
2014-03-15 21:14:02
Just 1: our g must map all four elements of A to the fourth element that's not in the range of f.
Just 1: our g must map all four elements of A to the fourth element that's not in the range of f.
DPatrick
2014-03-15 21:14:11
So there are 144 pairs of functions in case 3.
So there are 144 pairs of functions in case 3.
DPatrick
2014-03-15 21:14:38
Phew! That's all of the cases, so we've counted all of the pairs.
Phew! That's all of the cases, so we've counted all of the pairs.
DPatrick
2014-03-15 21:14:46
Adding the cases, there are 324 + 1344 + 144 = 1812 pairs of functions total.
Adding the cases, there are 324 + 1344 + 144 = 1812 pairs of functions total.
allaoc
2014-03-15 21:14:58
So (324+1244+144)/(256^2)
So (324+1244+144)/(256^2)
shreshrej
2014-03-15 21:15:05
We add all of them, and divide by 256^2
We add all of them, and divide by 256^2
firemike
2014-03-15 21:15:12
so 144+324+1344/256^2 = 453/2^14 and our answer is 453
so 144+324+1344/256^2 = 453/2^14 and our answer is 453
DPatrick
2014-03-15 21:15:35
Right. To finish, note that there are 256 functions, so there are 256^2 = 2^{16} pairs of functions possible.
Right. To finish, note that there are 256 functions, so there are 256^2 = 2^{16} pairs of functions possible.
DPatrick
2014-03-15 21:15:44
Thus the probability of picking a pair with disjoint ranges is \dfrac{1812}{2^{16}}.
Thus the probability of picking a pair with disjoint ranges is \dfrac{1812}{2^{16}}.
DPatrick
2014-03-15 21:15:55
This simplifies down to \dfrac{453}{2^{14}}, so the answer is \boxed{453}.
This simplifies down to \dfrac{453}{2^{14}}, so the answer is \boxed{453}.
DPatrick
2014-03-15 21:16:30
On to the final page! #13:
On to the final page! #13:
DPatrick
2014-03-15 21:16:37
13. On square ABCD, points E, F, G, and H lie on sides \overline{AB}, \overline{BC}, \overline{CD}, and \overline{DA}, respectively, so that \overline{EG} \perp \overline{FH} and EG = FH = 34. Segments \overline{EG} and \overline{FH} intersect at a point P, and the areas of quadrilaterals AEPH, BFPE, CGPF, and DHPG are in the ratio 269:275:405:411. Find the area of square ABCD.
13. On square ABCD, points E, F, G, and H lie on sides \overline{AB}, \overline{BC}, \overline{CD}, and \overline{DA}, respectively, so that \overline{EG} \perp \overline{FH} and EG = FH = 34. Segments \overline{EG} and \overline{FH} intersect at a point P, and the areas of quadrilaterals AEPH, BFPE, CGPF, and DHPG are in the ratio 269:275:405:411. Find the area of square ABCD.
DPatrick
2014-03-15 21:16:53
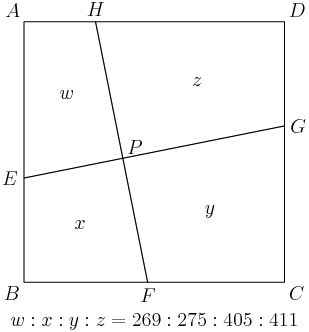

DPatrick
2014-03-15 21:17:07
They were kind enough to provide the picture on the contest.
They were kind enough to provide the picture on the contest.
DPatrick
2014-03-15 21:17:24
But this diagram is a bit silly -- let's put the numbers from the ratio into the diagram. But remember -- they're just ratios! They're not the actual areas! So let's call them 269k, 275k, etc. where k is some constant that we want to determine later.
But this diagram is a bit silly -- let's put the numbers from the ratio into the diagram. But remember -- they're just ratios! They're not the actual areas! So let's call them 269k, 275k, etc. where k is some constant that we want to determine later.
DPatrick
2014-03-15 21:17:34

room456
2014-03-15 21:17:50
the picture is not to scale
the picture is not to scale
DPatrick
2014-03-15 21:18:06
Indeed, it is so not to scale. I hope no one tried to measure from this picture.
Indeed, it is so not to scale. I hope no one tried to measure from this picture.
othuum0149
2014-03-15 21:18:15
total area of 1360k
total area of 1360k
j2002
2014-03-15 21:18:26
isnt the area 1360k
isnt the area 1360k
DPatrick
2014-03-15 21:18:39
Indeed, the total area is 1360k. So if we can find k, then we're done.
Indeed, the total area is 1360k. So if we can find k, then we're done.
DPatrick
2014-03-15 21:18:57
Let's also let s be the side length of the square just so we have it around as a variable. So s^2 = 1360k. (This will probably come in handy later.)
Let's also let s be the side length of the square just so we have it around as a variable. So s^2 = 1360k. (This will probably come in handy later.)
DPatrick
2014-03-15 21:19:12
Those numbers are very strange. Any patterns among them?
Those numbers are very strange. Any patterns among them?
vinayak-kumar
2014-03-15 21:19:28
269k+411k=275k+405k
269k+411k=275k+405k
guilt
2014-03-15 21:19:28
note that 269+ 411 = 275+405
note that 269+ 411 = 275+405
shreshrej
2014-03-15 21:19:28
the first thing i saw was 269+411=275+405
the first thing i saw was 269+411=275+405
csmath
2014-03-15 21:19:28
275+405=269+411 so EG cuts this square in half
275+405=269+411 so EG cuts this square in half
VietaFan
2014-03-15 21:19:28
k(269+411) = k(275+405)
k(269+411) = k(275+405)
guilt
2014-03-15 21:19:28
269+411 = 275+405
269+411 = 275+405
sojourner1
2014-03-15 21:19:38
680k, 680k
680k, 680k
DPatrick
2014-03-15 21:19:47
Aha -- the area of ADGE is 269k+411k = 680k and the area of BCGE is 275k+405k = 680k too! So \overline{EG} splits the square in half!
Aha -- the area of ADGE is 269k+411k = 680k and the area of BCGE is 275k+405k = 680k too! So \overline{EG} splits the square in half!
raptorw
2014-03-15 21:20:02
EG goes through center of square?
EG goes through center of square?
sojourner1
2014-03-15 21:20:02
EG passes through the center of ABCD
EG passes through the center of ABCD
DPatrick
2014-03-15 21:20:13
Yes: for one thing, this means that \overline{EG} passes through the center of the square. Let's call it O and add it to the diagram:
Yes: for one thing, this means that \overline{EG} passes through the center of the square. Let's call it O and add it to the diagram:
DPatrick
2014-03-15 21:20:23

DPatrick
2014-03-15 21:20:37
That was fruitful, so let's look at the other segment now. How does \overline{FH} spilt the square?
That was fruitful, so let's look at the other segment now. How does \overline{FH} spilt the square?
mssmath
2014-03-15 21:21:08
3(269+275)=2(405+411)
3(269+275)=2(405+411)
guilt
2014-03-15 21:21:08
also note (411+405)/(269+275) = 3/2
also note (411+405)/(269+275) = 3/2
martian179
2014-03-15 21:21:08
ratio of 2 : 3
ratio of 2 : 3
sparkles257
2014-03-15 21:21:08
2/3!
2/3!
LightningX48
2014-03-15 21:21:08
2:3?
2:3?
raptorw
2014-03-15 21:21:08
2:3
2:3
negativebplusorminus
2014-03-15 21:21:08
2 : 3
2 : 3
minimario
2014-03-15 21:21:08
2:3
2:3
DPatrick
2014-03-15 21:21:20
The area of ABFH is 269k + 275k = 544k and the area of CDHF is 411k+405k = 816k.
The area of ABFH is 269k + 275k = 544k and the area of CDHF is 411k+405k = 816k.
DPatrick
2014-03-15 21:21:28
And \dfrac{544k}{816k} = \dfrac{544}{816} = \dfrac23.
And \dfrac{544k}{816k} = \dfrac{544}{816} = \dfrac23.
DPatrick
2014-03-15 21:21:35
So \overline{FH} splits the square in a 2:3 ratio.
So \overline{FH} splits the square in a 2:3 ratio.
DPatrick
2014-03-15 21:21:40
How do we use that information?
How do we use that information?
martian179
2014-03-15 21:22:22
draw line through O parallel to BC
draw line through O parallel to BC
joshxiong
2014-03-15 21:22:22
consider the midpoint of FH
consider the midpoint of FH
guilt
2014-03-15 21:22:22
draw line through oh parallel to bc. fh splits it into 2:3 ratio
draw line through oh parallel to bc. fh splits it into 2:3 ratio
DPatrick
2014-03-15 21:22:51
Right. We now know that the midpoint of \overline{FH} is a point that is \frac25ths of the way from \overline{AB} to \overline{CD}.
(One way to think of this is that the median of the trapezoid AHFB has length \frac25 the side of the square.)
Right. We now know that the midpoint of \overline{FH} is a point that is \frac25ths of the way from \overline{AB} to \overline{CD}.
(One way to think of this is that the median of the trapezoid AHFB has length \frac25 the side of the square.)
DPatrick
2014-03-15 21:22:59
So let's add that point and call it Q. We get Q by drawing the segment from O that's parallel to \overline{AD} and \overline{BC}.
So let's add that point and call it Q. We get Q by drawing the segment from O that's parallel to \overline{AD} and \overline{BC}.
DPatrick
2014-03-15 21:23:08

DPatrick
2014-03-15 21:23:27
And what do we know about OQ?
And what do we know about OQ?
guilt
2014-03-15 21:23:48
note oq = s/10
note oq = s/10
ashgabat
2014-03-15 21:23:48
QO=1/10*s
QO=1/10*s
martian179
2014-03-15 21:23:48
OQ = 1/10 s
OQ = 1/10 s
guilt
2014-03-15 21:23:48
oq = s/10
oq = s/10
apple.singer
2014-03-15 21:23:48
s/10?
s/10?
Tommy2000
2014-03-15 21:23:48
1/10s?
1/10s?
othuum0149
2014-03-15 21:23:48
s/10
s/10
DrMath
2014-03-15 21:23:48
1/10 side length
1/10 side length
DPatrick
2014-03-15 21:23:59
Right. Q is \frac25 of the way from the left to the right, and O is exactly halfway. So OQ = \dfrac{s}{2} - \dfrac{2s}{5} = \dfrac{s}{10}.
Right. Q is \frac25 of the way from the left to the right, and O is exactly halfway. So OQ = \dfrac{s}{2} - \dfrac{2s}{5} = \dfrac{s}{10}.
DPatrick
2014-03-15 21:24:12
Hmmm...we've got a tiny right triangle OPQ in the middle, and we now know that its hypotenuse is \dfrac{s}{10}.
Hmmm...we've got a tiny right triangle OPQ in the middle, and we now know that its hypotenuse is \dfrac{s}{10}.
DPatrick
2014-03-15 21:24:18
What else can we learn about it?
What else can we learn about it?
DPatrick
2014-03-15 21:24:53
What other segment might be useful in this picture? (At least one person suggested it earlier but I lost it.)
What other segment might be useful in this picture? (At least one person suggested it earlier but I lost it.)
mathtastic
2014-03-15 21:25:17
line through o parallel to HF
line through o parallel to HF
summitwei
2014-03-15 21:25:17
the line through O parallel to HF
the line through O parallel to HF
DPatrick
2014-03-15 21:25:29
Yes -- I'd want to draw \overline{F'H'}, which is \overline{FH} slid over to pass through O:
Yes -- I'd want to draw \overline{F'H'}, which is \overline{FH} slid over to pass through O:
DPatrick
2014-03-15 21:25:35

DPatrick
2014-03-15 21:25:50
Why is that segment really really useful?
Why is that segment really really useful?
ptes77
2014-03-15 21:26:16
Now AH'F'B is equal to half the square
Now AH'F'B is equal to half the square
summitwei
2014-03-15 21:26:16
cuts it into four equal parts
cuts it into four equal parts
sinani206
2014-03-15 21:26:16
it splits square in half
it splits square in half
shreshrej
2014-03-15 21:26:16
It splits ABCD In half as well?
It splits ABCD In half as well?
Deathranger999
2014-03-15 21:26:16
The lines are perpendicular, it divides the square equally.
The lines are perpendicular, it divides the square equally.
ashgabat
2014-03-15 21:26:16
Splits ABCD in half
Splits ABCD in half
tennis1729
2014-03-15 21:26:16
goes through the center o
goes through the center o
CornSaltButter
2014-03-15 21:26:16
it means that the parallelogram is 1/10 the area of the square
it means that the parallelogram is 1/10 the area of the square
DPatrick
2014-03-15 21:26:46
Yeah, that new line really helps us keep track of the areas, because now \overline{EG} and \overline{F'H'} split the square into quarters!
Yeah, that new line really helps us keep track of the areas, because now \overline{EG} and \overline{F'H'} split the square into quarters!
DPatrick
2014-03-15 21:27:04
The picture is deceptive now because, for example, 411k is the area of HDGP, not of H'DGO, and similarly 405k is deceptive. So let's adjust the area labels for our new regions.
The picture is deceptive now because, for example, 411k is the area of HDGP, not of H'DGO, and similarly 405k is deceptive. So let's adjust the area labels for our new regions.
sinani206
2014-03-15 21:27:17
340k
340k
gamjawon
2014-03-15 21:28:06
340k!
340k!
firemike
2014-03-15 21:28:06
340k
340k
kgator
2014-03-15 21:28:06
If you eliminate the original HF then the resulting sectors have equal area of 340
If you eliminate the original HF then the resulting sectors have equal area of 340
vinayak-kumar
2014-03-15 21:28:06
we have 1/4 of the area now
we have 1/4 of the area now
kquittman
2014-03-15 21:28:06
340k
340k
kgator
2014-03-15 21:28:06
340k
340k
ptes77
2014-03-15 21:28:11
So HH'OP=71k and OPFF'=65k
So HH'OP=71k and OPFF'=65k
DPatrick
2014-03-15 21:28:13
Right, our big upper-right hunk H'DGO and our lower-right hunk OGCF' are each exactly one-quarter of the entire square, so they're each \frac14(1360k) = 340k.
Right, our big upper-right hunk H'DGO and our lower-right hunk OGCF' are each exactly one-quarter of the entire square, so they're each \frac14(1360k) = 340k.
DPatrick
2014-03-15 21:28:36
That makes HH'OP the remaining 71k from the upper-right, and FF'OP the remaining 65k from the lower-right:
That makes HH'OP the remaining 71k from the upper-right, and FF'OP the remaining 65k from the lower-right:
DPatrick
2014-03-15 21:28:49

DPatrick
2014-03-15 21:29:02
Now what does this tell us about the area of the little triangle OPQ?
Now what does this tell us about the area of the little triangle OPQ?
ashgabat
2014-03-15 21:29:22
Still kinda a little deceptive
Still kinda a little deceptive
DPatrick
2014-03-15 21:29:41
Right...just to clarify, it's OP that divides the skinny parallelogram into 71k and 65k.
Right...just to clarify, it's OP that divides the skinny parallelogram into 71k and 65k.
tiger21
2014-03-15 21:30:04
it's 3k!
it's 3k!
pickten
2014-03-15 21:30:04
area 3k
area 3k
negativebplusorminus
2014-03-15 21:30:04
3k
3k
Tommy2000
2014-03-15 21:30:04
it is area 3k.
it is area 3k.
room456
2014-03-15 21:30:04
3k is area
3k is area
summitwei
2014-03-15 21:30:04
3k
3k
joshxiong
2014-03-15 21:30:04
3k
3k
ViolinNinja256
2014-03-15 21:30:04
its 3k
its 3k
ptes77
2014-03-15 21:30:04
it's 3k
it's 3k
DPatrick
2014-03-15 21:30:45
Right! Because we know that OQ divides that parallelogram in half exactly, with 68k on each side.
Right! Because we know that OQ divides that parallelogram in half exactly, with 68k on each side.
DPatrick
2014-03-15 21:31:07
So OPQ has area 3k: it's the "extra" 3k of area on the top side of OP and the "missing" 3k of area from the bottom side of OP.
So OPQ has area 3k: it's the "extra" 3k of area on the top side of OP and the "missing" 3k of area from the bottom side of OP.
DPatrick
2014-03-15 21:31:18
Getting closer...we've got right triangle OPQ with area 3k and hypotenuse \dfrac{s}{10}. But we still need more data.
Getting closer...we've got right triangle OPQ with area 3k and hypotenuse \dfrac{s}{10}. But we still need more data.
tennis1729
2014-03-15 21:31:35
FH is 34
FH is 34
guilt
2014-03-15 21:31:43
use the data about 34
use the data about 34
mishai
2014-03-15 21:31:43
we haven't used 34 yet
we haven't used 34 yet
DPatrick
2014-03-15 21:31:54
Indeed, now is a good time to ask: What haven't we used yet?
Indeed, now is a good time to ask: What haven't we used yet?
DPatrick
2014-03-15 21:31:59
We haven't used at all the fact that EG = FH = 34. How does that help?
We haven't used at all the fact that EG = FH = 34. How does that help?
DPatrick
2014-03-15 21:32:10
Here's the pic again:
Here's the pic again:
DPatrick
2014-03-15 21:32:23


cxiong
2014-03-15 21:32:38
area of FF'H'H
area of FF'H'H
DPatrick
2014-03-15 21:32:58
Good! In particular, the area of parallelogram FF'H'H is 136k, and FH = 34. What can you conclude?
Good! In particular, the area of parallelogram FF'H'H is 136k, and FH = 34. What can you conclude?
CornSaltButter
2014-03-15 21:33:31
34(OP)=136k, so OP=4k!
34(OP)=136k, so OP=4k!
LightningX48
2014-03-15 21:33:31
height is 4k of ff'h'h
height is 4k of ff'h'h
sojourner1
2014-03-15 21:33:31
OP=4k
OP=4k
room456
2014-03-15 21:33:31
op is 4k
op is 4k
MSTang
2014-03-15 21:33:31
PO = 4k
PO = 4k
Tommy2000
2014-03-15 21:33:31
op = 4k
op = 4k
Quadratic64
2014-03-15 21:33:31
OP = 136k/34
OP = 136k/34
SuperSnivy
2014-03-15 21:33:31
OP=4k
OP=4k
sirknightingfail
2014-03-15 21:33:31
OP=4k
OP=4k
DPatrick
2014-03-15 21:33:39
OP is the height of that parallelogram! So we have OP = \frac{136k}{34} = 4k.
OP is the height of that parallelogram! So we have OP = \frac{136k}{34} = 4k.
DPatrick
2014-03-15 21:33:54
Aha...now we have right triangle OPQ with area 3k, hypotenuse \dfrac{s}{10}, and one leg 4k.
Aha...now we have right triangle OPQ with area 3k, hypotenuse \dfrac{s}{10}, and one leg 4k.
SockFoot
2014-03-15 21:34:27
other leg is 3/2
other leg is 3/2
mentalgenius
2014-03-15 21:34:27
the other leg is 1.5
the other leg is 1.5
VietaFan
2014-03-15 21:34:27
other leg is 3/2
other leg is 3/2
othuum0149
2014-03-15 21:34:27
other leg is then 3/2
other leg is then 3/2
DrMath
2014-03-15 21:34:27
so one leg is 3/2
so one leg is 3/2
MSTang
2014-03-15 21:34:27
The other leg is 3/2
The other leg is 3/2
pickten
2014-03-15 21:34:27
other leg has length 3/2
other leg has length 3/2
DPatrick
2014-03-15 21:34:39
If the area is 3k and one leg is 4k, then the other leg must be \frac32.
If the area is 3k and one leg is 4k, then the other leg must be \frac32.
DPatrick
2014-03-15 21:34:47
So now our right triangle has legs \frac32 and 4k and hypotenuse \dfrac{s}{10}.
So now our right triangle has legs \frac32 and 4k and hypotenuse \dfrac{s}{10}.
firemike
2014-03-15 21:34:55
pythagorean theorem
pythagorean theorem
Tommy2000
2014-03-15 21:34:55
pythagorean theorem
pythagorean theorem
hwl0304
2014-03-15 21:34:55
pyth theorem
pyth theorem
DPatrick
2014-03-15 21:35:02
Pythagorean Theorem time!
Pythagorean Theorem time!
DPatrick
2014-03-15 21:35:09
We have the equation \left(\frac32\right)^2 + (4k)^2 = \left(\frac{s}{10}\right)^2.
We have the equation \left(\frac32\right)^2 + (4k)^2 = \left(\frac{s}{10}\right)^2.
DPatrick
2014-03-15 21:35:18
This simplifies to \dfrac94 + 16k^2 = \dfrac{s^2}{100}.
This simplifies to \dfrac94 + 16k^2 = \dfrac{s^2}{100}.
raptorw
2014-03-15 21:35:38
use s^2=1360k
use s^2=1360k
sparkles257
2014-03-15 21:35:38
now s^2 = 1360 k comes in handy
now s^2 = 1360 k comes in handy
dli00105
2014-03-15 21:35:38
s^2=1360k
s^2=1360k
guilt
2014-03-15 21:35:38
aslo s^2 = 1360k
aslo s^2 = 1360k
Deathranger999
2014-03-15 21:35:38
s squared equals 1360k.
s squared equals 1360k.
DPatrick
2014-03-15 21:35:45
I knew that would come in handy later!
I knew that would come in handy later!
DPatrick
2014-03-15 21:35:51
Remember that s^2 = 1360k.
Remember that s^2 = 1360k.
DPatrick
2014-03-15 21:35:58
So we have \dfrac94 + 16k^2 = \dfrac{136k}{10}. That's a quadratic in k so we can solve it!
So we have \dfrac94 + 16k^2 = \dfrac{136k}{10}. That's a quadratic in k so we can solve it!
DPatrick
2014-03-15 21:36:14
Multiply through by 20 to clear denominators, and move all the terms to one side:
320k^2 - 272k + 45 = 0.
Multiply through by 20 to clear denominators, and move all the terms to one side:
320k^2 - 272k + 45 = 0.
DPatrick
2014-03-15 21:36:44
You can use the quadratic formula to solve this, but 45 doesn't have a ton of factors (and we know we want a rational solution) so you might find factoring easier.
You can use the quadratic formula to solve this, but 45 doesn't have a ton of factors (and we know we want a rational solution) so you might find factoring easier.
SuperSnivy
2014-03-15 21:36:55
(8k-5)(40k-9)=0
(8k-5)(40k-9)=0
DPatrick
2014-03-15 21:37:04
It factors as (40k-9)(8k-5) = 0.
It factors as (40k-9)(8k-5) = 0.
DPatrick
2014-03-15 21:37:11
So the solutions are k=\dfrac{9}{40} and k=\dfrac{5}{8}.
So the solutions are k=\dfrac{9}{40} and k=\dfrac{5}{8}.
ws5188
2014-03-15 21:37:32
how do we know which root to use?
how do we know which root to use?
raptorw
2014-03-15 21:37:32
oh there's another positive sol...
oh there's another positive sol...
mathtastic
2014-03-15 21:37:32
oh no
oh no
DPatrick
2014-03-15 21:37:38
Since the area of the square is 1360k, this gives possible areas of 1360\left(\frac{9}{40}\right) = 34 \cdot 9 = 306 and 1360\left(\frac58\right) = 170 \cdot 5 = 850.
Since the area of the square is 1360k, this gives possible areas of 1360\left(\frac{9}{40}\right) = 34 \cdot 9 = 306 and 1360\left(\frac58\right) = 170 \cdot 5 = 850.
DPatrick
2014-03-15 21:37:48
I didn't come all this way just to guess which of these is correct. Which one do we want?
I didn't come all this way just to guess which of these is correct. Which one do we want?
ViolinNinja256
2014-03-15 21:38:10
oh it has be bigger than 578
oh it has be bigger than 578
ashgabat
2014-03-15 21:38:10
We know the area is greater than (34)^2/2 = 578
We know the area is greater than (34)^2/2 = 578
negativebplusorminus
2014-03-15 21:38:10
Must be greater than half of 34^2.
Must be greater than half of 34^2.
DPatrick
2014-03-15 21:38:19
Right. There's one part of the area of the entire square that we definitely know, and that's the area of EFGH -- it's a quadrilateral with perpendicular diagonals of length 34, so its area is \frac12(34)^2 = 578.
Right. There's one part of the area of the entire square that we definitely know, and that's the area of EFGH -- it's a quadrilateral with perpendicular diagonals of length 34, so its area is \frac12(34)^2 = 578.
DPatrick
2014-03-15 21:38:33
Thus the area of ABCD is at least 578.
Thus the area of ABCD is at least 578.
DPatrick
2014-03-15 21:38:41
And happily, only one of our two solutions is bigger than 578 -- that's \boxed{850}.
And happily, only one of our two solutions is bigger than 578 -- that's \boxed{850}.
mssmath
2014-03-15 21:39:06
Hardest problem?
Hardest problem?
DPatrick
2014-03-15 21:39:28
For us here at AoPS, it definitely was. We got a lot of messy solutions but it took a while for us to come up with this fairly nice solution.
For us here at AoPS, it definitely was. We got a lot of messy solutions but it took a while for us to come up with this fairly nice solution.
DPatrick
2014-03-15 21:39:34
Anyway, only 2 more to go!
Anyway, only 2 more to go!
DPatrick
2014-03-15 21:39:40
14. Let m be the largest real solution to the equation
\frac{3}{x-3} + \frac{5}{x-5} + \frac{17}{x-17} + \frac{19}{x-19} = x^2 - 11x - 4. There are positive integers a, b, and c such that m = a + \sqrt{b+\sqrt{c}}. Find a+b+c.
14. Let m be the largest real solution to the equation
\frac{3}{x-3} + \frac{5}{x-5} + \frac{17}{x-17} + \frac{19}{x-19} = x^2 - 11x - 4. There are positive integers a, b, and c such that m = a + \sqrt{b+\sqrt{c}}. Find a+b+c.
qwertyu
2014-03-15 21:40:12
Add four to both sides
Add four to both sides
ws5188
2014-03-15 21:40:12
add 4 to both sides
add 4 to both sides
liuh008
2014-03-15 21:40:12
Add 4 to both sides.
Add 4 to both sides.
SockFoot
2014-03-15 21:40:12
+4 to all sides
+4 to all sides
mssmath
2014-03-15 21:40:12
Add 4 to both sides
Add 4 to both sides
theinfinite
2014-03-15 21:40:12
add 4 to both sides
add 4 to both sides
dli00105
2014-03-15 21:40:15
4 terms on LHS and -4 on RHS
4 terms on LHS and -4 on RHS
DPatrick
2014-03-15 21:40:32
Yeah, that -4 looks weird on the right side. And there happens to be 4 terms on the left side.
Yeah, that -4 looks weird on the right side. And there happens to be 4 terms on the left side.
DPatrick
2014-03-15 21:40:38
What if we add 4 to both sides, by adding 1 to each of the fractions on the left?
What if we add 4 to both sides, by adding 1 to each of the fractions on the left?
DPatrick
2014-03-15 21:40:45
\left(\frac{3}{x-3} + 1\right) +\left(\frac{5}{x-5} + 1\right) +\left(\frac{17}{x-17} + 1\right) +\left(\frac{19}{x-19} + 1\right) = x^2 - 11x.
\left(\frac{3}{x-3} + 1\right) +\left(\frac{5}{x-5} + 1\right) +\left(\frac{17}{x-17} + 1\right) +\left(\frac{19}{x-19} + 1\right) = x^2 - 11x.
gamjawon
2014-03-15 21:41:06
then simplify!
then simplify!
vinayak-kumar
2014-03-15 21:41:06
the numerators turn into an x !
the numerators turn into an x !
aprobs21
2014-03-15 21:41:06
Well then all the numerators have x's!
Well then all the numerators have x's!
brian22
2014-03-15 21:41:06
x/(x-3)+x/(x-5)+x/(x-17)+x/(x-19)=x(x-11)
x/(x-3)+x/(x-5)+x/(x-17)+x/(x-19)=x(x-11)
cxiong
2014-03-15 21:41:06
that simplifies a lot
that simplifies a lot
DPatrick
2014-03-15 21:41:19
Ooh, those parentheses simplify nicely!
Ooh, those parentheses simplify nicely!
DPatrick
2014-03-15 21:41:25
\frac{x}{x-3} + \frac{x}{x-5} + \frac{x}{x-17} + \frac{x}{x-19} = x^2 - 11x.
\frac{x}{x-3} + \frac{x}{x-5} + \frac{x}{x-17} + \frac{x}{x-19} = x^2 - 11x.
theinfinite
2014-03-15 21:41:44
divide out x
divide out x
summitwei
2014-03-15 21:41:44
and then divide out an x
and then divide out an x
mishai
2014-03-15 21:41:44
divide by x
divide by x
hjl00
2014-03-15 21:41:44
divide by x
divide by x
VietaFan
2014-03-15 21:41:44
divide by x
divide by x
othuum0149
2014-03-15 21:41:44
divide both sides by x
divide both sides by x
DPatrick
2014-03-15 21:41:49
The number we're looking for is clearly not x=0, so let's divide by x.
The number we're looking for is clearly not x=0, so let's divide by x.
DPatrick
2014-03-15 21:41:58
\frac{1}{x-3} + \frac{1}{x-5} + \frac{1}{x-17} + \frac{1}{x-19} = x - 11.
\frac{1}{x-3} + \frac{1}{x-5} + \frac{1}{x-17} + \frac{1}{x-19} = x - 11.
DPatrick
2014-03-15 21:42:08
Now what?
Now what?
vinayak-kumar
2014-03-15 21:42:20
hmm, lots of symmetry
hmm, lots of symmetry
aprobs21
2014-03-15 21:42:20
symmetry about 11
symmetry about 11
othuum0149
2014-03-15 21:42:36
substitute for x-11
substitute for x-11
MSTang
2014-03-15 21:42:36
y = x-11
y = x-11
aprobs21
2014-03-15 21:42:36
symmetry about 11
symmetry about 11
sparkles257
2014-03-15 21:42:36
let a = x-11
let a = x-11
cellobix
2014-03-15 21:42:36
sub y=x-11?
sub y=x-11?
DPatrick
2014-03-15 21:42:42
There's some symmetry here that we'd like to take advantage of. The x-11 on the right side is also a clue.
There's some symmetry here that we'd like to take advantage of. The x-11 on the right side is also a clue.
DPatrick
2014-03-15 21:42:48
Let's make the substitution y = x-11 to capture the symmetry.
Let's make the substitution y = x-11 to capture the symmetry.
DPatrick
2014-03-15 21:42:54
Now we have
\frac{1}{y+8} + \frac{1}{y+6} + \frac{1}{y-6} + \frac{1}{y-8} = y.
Now we have
\frac{1}{y+8} + \frac{1}{y+6} + \frac{1}{y-6} + \frac{1}{y-8} = y.
raptorw
2014-03-15 21:43:21
pair up the first and last terms in LHS
pair up the first and last terms in LHS
mathtastic
2014-03-15 21:43:21
DIFF OF SOME SQUARES YO
DIFF OF SOME SQUARES YO
dli00105
2014-03-15 21:43:21
pair them off!
pair them off!
raptorw
2014-03-15 21:43:21
Diff of squares
Diff of squares
SockFoot
2014-03-15 21:43:21
group pairs of fractions together
group pairs of fractions together
checkmate1021
2014-03-15 21:43:21
difference of squares?
difference of squares?
CornSaltButter
2014-03-15 21:43:21
Difference of squares yes
Difference of squares yes
buzzyun
2014-03-15 21:43:21
difference of squares
difference of squares
DPatrick
2014-03-15 21:43:28
It makes sense to try to combine the fractions on the left with y \pm 6 and y \pm 8 in the denominators.
It makes sense to try to combine the fractions on the left with y \pm 6 and y \pm 8 in the denominators.
DPatrick
2014-03-15 21:43:37
\frac{2y}{y^2 - 36} + \frac{2y}{y^2 - 64} = y.
\frac{2y}{y^2 - 36} + \frac{2y}{y^2 - 64} = y.
joshualee2000
2014-03-15 21:44:03
dvide by y
dvide by y
Rectangle_Square
2014-03-15 21:44:03
divide by y
divide by y
hwl0304
2014-03-15 21:44:03
divide by y
divide by y
sojourner1
2014-03-15 21:44:03
take out the y
take out the y
liuh008
2014-03-15 21:44:03
Divide out y - the answer is not 11.
Divide out y - the answer is not 11.
LightningX48
2014-03-15 21:44:03
divide by y
divide by y
DPatrick
2014-03-15 21:44:14
Now y=0 is also not the solution we want (it gives x=11, which is not the right format), so we can divide by y:
\frac{2}{y^2 - 36} + \frac{2}{y^2 - 64} = 1.
Now y=0 is also not the solution we want (it gives x=11, which is not the right format), so we can divide by y:
\frac{2}{y^2 - 36} + \frac{2}{y^2 - 64} = 1.
mentalgenius
2014-03-15 21:44:47
nice easy quadratic
nice easy quadratic
aprobs21
2014-03-15 21:44:47
Quadratic in y^2
Quadratic in y^2
DPatrick
2014-03-15 21:45:06
We could certainly make another substitution now, but at this point it's "simple" enough that I'd probably just plow through to the end from here.
We could certainly make another substitution now, but at this point it's "simple" enough that I'd probably just plow through to the end from here.
DPatrick
2014-03-15 21:45:17
We can expand this out by multiplying by (y^2-36)(y^2-64):
2(y^2-64) + 2(y^2-36) = (y^2-36)(y^2-64).
This simplifies to y^4 - 104y^2 + 2504 = 0.
We can expand this out by multiplying by (y^2-36)(y^2-64):
2(y^2-64) + 2(y^2-36) = (y^2-36)(y^2-64).
This simplifies to y^4 - 104y^2 + 2504 = 0.
googol.plex
2014-03-15 21:45:43
quadratic formula
quadratic formula
theinfinite
2014-03-15 21:45:43
quadratic
quadratic
gamjawon
2014-03-15 21:45:43
Quadratic formula?
Quadratic formula?
DPatrick
2014-03-15 21:45:46
This is a quadratic in y^2 so we can use the quadratic formula:
y^2 = \frac{104 \pm \sqrt{104^2 - 4 \cdot 2504}}{2} = 52 \pm \sqrt{52^2 - 2504} = 52 \pm \sqrt{200}.
This is a quadratic in y^2 so we can use the quadratic formula:
y^2 = \frac{104 \pm \sqrt{104^2 - 4 \cdot 2504}}{2} = 52 \pm \sqrt{52^2 - 2504} = 52 \pm \sqrt{200}.
DPatrick
2014-03-15 21:46:06
And now we just unwind our substitution.
And now we just unwind our substitution.
DPatrick
2014-03-15 21:46:13
Recall that x = y + 11, and we want the largest root.
Recall that x = y + 11, and we want the largest root.
danusv
2014-03-15 21:46:22
so x= 11 + root( 52 + root(200)
so x= 11 + root( 52 + root(200)
googol.plex
2014-03-15 21:46:26
a=11, b=52, c=200 so 263
a=11, b=52, c=200 so 263
csmath
2014-03-15 21:46:39
We need the LARGEST sol so we get 11+sqrt(52+sqrt(200))
We need the LARGEST sol so we get 11+sqrt(52+sqrt(200))
ashgabat
2014-03-15 21:46:39


DPatrick
2014-03-15 21:46:41
So x = 11 + \sqrt{52 + \sqrt{200}} is the largest root. Our answer is 11 + 52 + 200 = \boxed{263}.
So x = 11 + \sqrt{52 + \sqrt{200}} is the largest root. Our answer is 11 + 52 + 200 = \boxed{263}.
DPatrick
2014-03-15 21:46:58
On to the grand finale...
On to the grand finale...
DPatrick
2014-03-15 21:47:04
15. In \triangle ABC, AB = 3, BC = 4, CA = 5. Circle \omega intersects \overline{AB} and E and B, \overline{BC} at B and D, and \overline{AC} and F and G. Given that EF = DF and \frac{DG}{EG} = \frac34, length DE = \frac{a\sqrt{b}}{c}, where a and c are relatively prime positive integers, and b is a positive integer not divisible by the square of any prime. Find a+b+c.
15. In \triangle ABC, AB = 3, BC = 4, CA = 5. Circle \omega intersects \overline{AB} and E and B, \overline{BC} at B and D, and \overline{AC} and F and G. Given that EF = DF and \frac{DG}{EG} = \frac34, length DE = \frac{a\sqrt{b}}{c}, where a and c are relatively prime positive integers, and b is a positive integer not divisible by the square of any prime. Find a+b+c.
ptes77
2014-03-15 21:47:23
Draw
Draw
room456
2014-03-15 21:47:23
DIAGRAM!
DIAGRAM!
pedronr
2014-03-15 21:47:23
Draw a picture!!
Draw a picture!!
ChilledLemonade
2014-03-15 21:47:23
diagram!
diagram!
DPatrick
2014-03-15 21:47:29
Let's try to sketch a picture. It'll likely be out-of-whack at first, but we can refine it as we learn more.
Let's try to sketch a picture. It'll likely be out-of-whack at first, but we can refine it as we learn more.
DPatrick
2014-03-15 21:47:36


DPatrick
2014-03-15 21:47:55
We want the length DE, which I've drawn in blue. What do we know about the blue segment?
We want the length DE, which I've drawn in blue. What do we know about the blue segment?
joshxiong
2014-03-15 21:48:21
DE is a diameter
DE is a diameter
ninjataco
2014-03-15 21:48:21
diameter of circle
diameter of circle
MSTang
2014-03-15 21:48:21
A diameter of the circle
A diameter of the circle
Rectangle_Square
2014-03-15 21:48:21
diameter of circle
diameter of circle
Deathranger999
2014-03-15 21:48:21
It's the diamter.
It's the diamter.
ws5188
2014-03-15 21:48:21
it is the diameter of the circle
it is the diameter of the circle
shreshrej
2014-03-15 21:48:21
diameter because of right angle B
diameter because of right angle B
Deathranger999
2014-03-15 21:48:21
It's the diameter.
It's the diameter.
DPatrick
2014-03-15 21:48:28
Since \angle DBE is right, the blue segment \overline{DE} is a diameter of the circle.
Since \angle DBE is right, the blue segment \overline{DE} is a diameter of the circle.
DPatrick
2014-03-15 21:48:46
OK, let's next look at F. We have DF = EF -- what does that tell us?
OK, let's next look at F. We have DF = EF -- what does that tell us?
MSTang
2014-03-15 21:49:16
DEF is 45-45-90
DEF is 45-45-90
summitwei
2014-03-15 21:49:16
DEF is isoceles
DEF is isoceles
vinayak-kumar
2014-03-15 21:49:16
its a 45 45 90 triangle
its a 45 45 90 triangle
CornSaltButter
2014-03-15 21:49:16
DFE is 45-45-90 triangle
DFE is 45-45-90 triangle
cxiong
2014-03-15 21:49:16
DEF is isosceles right triangle
DEF is isosceles right triangle
othuum0149
2014-03-15 21:49:16
45-45-90 triangle
45-45-90 triangle
mishai
2014-03-15 21:49:16
iscosceles 90 45 45 triangle
iscosceles 90 45 45 triangle
larry333
2014-03-15 21:49:16
DEF is 45-45-90
DEF is 45-45-90
mdlu
2014-03-15 21:49:16
isosceles right triangle
isosceles right triangle
DPatrick
2014-03-15 21:49:27
Well, we can tell that I drew a pretty lousy picture, for one thing. F needs to be equidistant from D and E.
Well, we can tell that I drew a pretty lousy picture, for one thing. F needs to be equidistant from D and E.
DPatrick
2014-03-15 21:49:49
Indeed, we know that \angle DFE is a right angle too, since it intercepts a semicircle. (And \angle DGE is too -- let's file that away for later.) So DFE is a 45-45-90 isosceles right triangle. And in particular F is the midpoint of the arc from D to E.
Indeed, we know that \angle DFE is a right angle too, since it intercepts a semicircle. (And \angle DGE is too -- let's file that away for later.) So DFE is a 45-45-90 isosceles right triangle. And in particular F is the midpoint of the arc from D to E.
LightningX48
2014-03-15 21:50:06
NDP = New Diagram Plz
NDP = New Diagram Plz
DPatrick
2014-03-15 21:50:17
Yeah, let's try to make the picture more accurate in light of what we've got so far:
Yeah, let's try to make the picture more accurate in light of what we've got so far:
DPatrick
2014-03-15 21:50:24


DPatrick
2014-03-15 21:50:41
Notice anything else about F?
Notice anything else about F?
DPatrick
2014-03-15 21:51:06
Remember, we just learned that arcs DF and FE are each one-quarter of the circle. What does that tell us?
Remember, we just learned that arcs DF and FE are each one-quarter of the circle. What does that tell us?
SuperSnivy
2014-03-15 21:51:34
BF is angle bisector of <ABC
BF is angle bisector of <ABC
ABCDE
2014-03-15 21:51:34
BF is angle bisector
BF is angle bisector
DPatrick
2014-03-15 21:51:59
Exactly. BF bisects the arc DFE, so it bisects the inscribed angle \angle DBE too.
Exactly. BF bisects the arc DFE, so it bisects the inscribed angle \angle DBE too.
DPatrick
2014-03-15 21:52:17
Or, you can note that \angle DBF and \angle EBF are each 45^\circ, because they each intercept a 90^\circ arc.
Or, you can note that \angle DBF and \angle EBF are each 45^\circ, because they each intercept a 90^\circ arc.
DPatrick
2014-03-15 21:52:39
OK, on to G.
OK, on to G.
DPatrick
2014-03-15 21:52:48
We have \dfrac{DG}{EG} = \dfrac34. Hmmm...those numbers are familiar...and \angle DGE is a right angle from earlier.
We have \dfrac{DG}{EG} = \dfrac34. Hmmm...those numbers are familiar...and \angle DGE is a right angle from earlier.
mishai
2014-03-15 21:53:06
DG:EG=3/4, so DEG is similar to ACB
DG:EG=3/4, so DEG is similar to ACB
vinayak-kumar
2014-03-15 21:53:06
Draw triangle DGE
Draw triangle DGE
LightningX48
2014-03-15 21:53:06
yeay 3,4,5
yeay 3,4,5
othuum0149
2014-03-15 21:53:06
3-4-5 triangle
3-4-5 triangle
CornSaltButter
2014-03-15 21:53:06
HHMMMMM... 3-4-5??
HHMMMMM... 3-4-5??
ashgabat
2014-03-15 21:53:06
∆DGE ~ ∆ABC
∆DGE ~ ∆ABC
mentalgenius
2014-03-15 21:53:06
3-4-5 right triangle
3-4-5 right triangle
DPatrick
2014-03-15 21:53:15
Aha: triangle DGE is similar to a 3-4-5 triangle. Let me draw it in red and mark the equal angles:
Aha: triangle DGE is similar to a 3-4-5 triangle. Let me draw it in red and mark the equal angles:
DPatrick
2014-03-15 21:53:23

DPatrick
2014-03-15 21:54:01
Any other angles equal to those angles too? (Maybe I need to add another segment?)
Any other angles equal to those angles too? (Maybe I need to add another segment?)
joshxiong
2014-03-15 21:54:28
BG
BG
MSTang
2014-03-15 21:54:35
EBG
EBG
lovejj
2014-03-15 21:54:35
<DBG
<DBG
DPatrick
2014-03-15 21:54:52
Let's add \overline{BG}:
Let's add \overline{BG}:
DPatrick
2014-03-15 21:55:00

mdlu
2014-03-15 21:55:08
angles that intercept the same arcs
angles that intercept the same arcs
ashgabat
2014-03-15 21:55:08
Same arc.
Same arc.
DPatrick
2014-03-15 21:55:25
Right:
\angle DEG and \angle DBG intercept the same arc DG, so they're the same angle.
\angle EDG and \angle EBG intercept the same arc EG, so they're the same angle.
Right:
\angle DEG and \angle DBG intercept the same arc DG, so they're the same angle.
\angle EDG and \angle EBG intercept the same arc EG, so they're the same angle.
DPatrick
2014-03-15 21:55:35
So what?
So what?
mathwizard888
2014-03-15 21:55:45
CG=BG=AG
CG=BG=AG
ChilledLemonade
2014-03-15 21:55:45
Isoceles triangles!
Isoceles triangles!
joshualee2000
2014-03-15 21:55:45
we get two isoceles triangles
we get two isoceles triangles
cxiong
2014-03-15 21:55:54
G is the midpoint of AC
G is the midpoint of AC
dli00105
2014-03-15 21:55:54
G miodpoint of AC
G miodpoint of AC
checkmate1021
2014-03-15 21:55:54
BG = AG
BG = AG
MSTang
2014-03-15 21:55:54
GA = GB = GC
GA = GB = GC
DPatrick
2014-03-15 21:56:00
This means that CGB is isosceles (it has two green base angles), so CG = BG.
This means that CGB is isosceles (it has two green base angles), so CG = BG.
DPatrick
2014-03-15 21:56:10
Also that AGB is isosceles (with two pink base angles), so AG = BG.
Also that AGB is isosceles (with two pink base angles), so AG = BG.
DPatrick
2014-03-15 21:56:19
This means that AG = BG = CG. In other words, G is the midpoint of \overline{AC}!
This means that AG = BG = CG. In other words, G is the midpoint of \overline{AC}!
DPatrick
2014-03-15 21:56:35
So to summarize so far, we've concluded that:
(1) -- \overline{DE} is the diameter of the circle
(2) -- \overline{BF} is the angle bisector of right angle \angle ABC
(3) -- G is the midpoint of \overline{AC}.
So to summarize so far, we've concluded that:
(1) -- \overline{DE} is the diameter of the circle
(2) -- \overline{BF} is the angle bisector of right angle \angle ABC
(3) -- G is the midpoint of \overline{AC}.
DPatrick
2014-03-15 21:56:50
Here's the "clean" picture again:
Here's the "clean" picture again:
DPatrick
2014-03-15 21:56:56


DPatrick
2014-03-15 21:57:22
We have a lot of information now, and there are many ways to finish from here.
We have a lot of information now, and there are many ways to finish from here.
joshxiong
2014-03-15 21:57:43
Power of a point maybe
Power of a point maybe
mathtastic
2014-03-15 21:57:43
ANGLE BISECTOR THEOREM
ANGLE BISECTOR THEOREM
DPatrick
2014-03-15 21:58:33
I agree: I think that's probably the easiest way to finish. We know a lot of info about how F and G divide up the distances on \overline{AC}, so we should be able to use Power of a Point on points A and C.
I agree: I think that's probably the easiest way to finish. We know a lot of info about how F and G divide up the distances on \overline{AC}, so we should be able to use Power of a Point on points A and C.
DPatrick
2014-03-15 21:58:51
Let's look at Power of a Point on A: (AF)(AG) = (AE)(AB).
Let's look at Power of a Point on A: (AF)(AG) = (AE)(AB).
DPatrick
2014-03-15 21:59:06
Which of these quantities do we know?
Which of these quantities do we know?
mathawesomeness777
2014-03-15 21:59:19
AB = 3
AB = 3
Petaminx
2014-03-15 21:59:19
AB=3
AB=3
Tommy2000
2014-03-15 21:59:19
ag = 5/2
ag = 5/2
brian22
2014-03-15 21:59:26
AF=15/7, AG=5/2
AF=15/7, AG=5/2
MSTang
2014-03-15 21:59:26
all except AE
all except AE
DPatrick
2014-03-15 21:59:37
Yes, we know three of them!
Yes, we know three of them!
DPatrick
2014-03-15 21:59:45
AB = 3 (we were given that).
AB = 3 (we were given that).
DPatrick
2014-03-15 21:59:55
AG = \dfrac52 because G is the midpoint.
AG = \dfrac52 because G is the midpoint.
DPatrick
2014-03-15 22:00:21
And AF = \dfrac{15}{7} by the Angle Bisector Theorem: we know that AF:FC = 3:4 and AF + FC = 5.
And AF = \dfrac{15}{7} by the Angle Bisector Theorem: we know that AF:FC = 3:4 and AF + FC = 5.
brian22
2014-03-15 22:00:38
AE=25/14
AE=25/14
DPatrick
2014-03-15 22:01:04
Right: plugging these in we get \dfrac{15}{7} \cdot \dfrac{5}{2} = AE \cdot 3.
Right: plugging these in we get \dfrac{15}{7} \cdot \dfrac{5}{2} = AE \cdot 3.
DPatrick
2014-03-15 22:01:18
So AE = \dfrac{25}{14} when we solve this.
So AE = \dfrac{25}{14} when we solve this.
brian22
2014-03-15 22:01:31
->BE=17/14
->BE=17/14
cxiong
2014-03-15 22:01:31
BE = 17/14
BE = 17/14
summitwei
2014-03-15 22:01:31
So BE=17/14
So BE=17/14
DPatrick
2014-03-15 22:01:44
And more importantly, BE = 3 - \dfrac{25}{14} = \dfrac{17}{14}.
And more importantly, BE = 3 - \dfrac{25}{14} = \dfrac{17}{14}.
brian22
2014-03-15 22:01:54
Then do it again to C to get BD
Then do it again to C to get BD
cxiong
2014-03-15 22:02:07
Do the same for BD, then use Pythagorean Thereom
Do the same for BD, then use Pythagorean Thereom
othuum0149
2014-03-15 22:02:07
proceed similarly to find BD
proceed similarly to find BD
googol.plex
2014-03-15 22:02:07
power of a point on C, 4*CD=(5/2)(20/7)
power of a point on C, 4*CD=(5/2)(20/7)
DPatrick
2014-03-15 22:02:22
Exactly: we do the same computation of Power of a Point at point C.
Exactly: we do the same computation of Power of a Point at point C.
DPatrick
2014-03-15 22:02:50
I'll skip the details since the computation is exactly the same: we know CF = \frac{20}{7}, CG = \frac52, and CB = 4, so CD = \frac{25}{14} and hence BD = \frac{31}{14}.
I'll skip the details since the computation is exactly the same: we know CF = \frac{20}{7}, CG = \frac52, and CB = 4, so CD = \frac{25}{14} and hence BD = \frac{31}{14}.
DPatrick
2014-03-15 22:03:27
(Note that it came out that AE = CD -- there are other ways to see that too. As I said, once you identify F and G there are tons of ways to finish.)
(Note that it came out that AE = CD -- there are other ways to see that too. As I said, once you identify F and G there are tons of ways to finish.)
Galindon
2014-03-15 22:03:39
Pythagorean theorem done
Pythagorean theorem done
joshxiong
2014-03-15 22:03:39
pythagorean theorem to finish
pythagorean theorem to finish
LightningX48
2014-03-15 22:03:39
pythag gives us
pythag gives us
DPatrick
2014-03-15 22:04:09
Right, using the Pythagorean Theorem on triangle BDE, we get DE = \frac{1}{14}\sqrt{17^2 + 31^2} = \frac{\sqrt{1250}}{14} = \frac{25\sqrt2}{14}.
Right, using the Pythagorean Theorem on triangle BDE, we get DE = \frac{1}{14}\sqrt{17^2 + 31^2} = \frac{\sqrt{1250}}{14} = \frac{25\sqrt2}{14}.
DPatrick
2014-03-15 22:04:20
So our answer is 25 + 2 + 14 = \boxed{041}.
So our answer is 25 + 2 + 14 = \boxed{041}.
DPatrick
2014-03-15 22:04:35
That's it for the AIME I! Thanks for hanging out with me on a Saturday night.
That's it for the AIME I! Thanks for hanging out with me on a Saturday night.
DPatrick
2014-03-15 22:04:43
A full transcript of this Math Jam will be available on the website in the very near future. Go to the "Math Jams" link under the "School" menu.
A full transcript of this Math Jam will be available on the website in the very near future. Go to the "Math Jams" link under the "School" menu.
DPatrick
2014-03-15 22:04:52
And please join us again for the AIME II Math Jam on Friday, March 28, when we'll do all this again for the AIME II.
And please join us again for the AIME II Math Jam on Friday, March 28, when we'll do all this again for the AIME II.
DPatrick
2014-03-15 22:08:45
Bye!
Bye!
ksun48
2014-03-15 22:09:01
Bye!
Bye!
sojourner1
2014-03-15 22:09:12
Bye
Bye
joshxiong
2014-03-15 22:09:15
Bye!
Bye!
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.









