2014 AIME II Math Jam
Go back to the Math Jam ArchiveAoPS instructors discuss all 15 problems of the 2014 AIME II.
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.
Facilitator: Dave Patrick
DPatrick
2014-03-28 19:00:09
Welcome to the 2014 AIME II Math Jam!
Welcome to the 2014 AIME II Math Jam!
DPatrick
2014-03-28 19:00:15
I'm Dave Patrick, and I'll be leading our discussion tonight.
I'm Dave Patrick, and I'll be leading our discussion tonight.
DPatrick
2014-03-28 19:00:23
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
Before we get started I would like to take a moment to explain our virtual classroom to those who have not previously participated in a Math Jam or one of our online classes.
DPatrick
2014-03-28 19:00:38
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
The classroom is moderated, meaning that students can type into the classroom, but these comments will not go directly into the room. These comments go to the instructors, who may choose to share your comments with the room.
DPatrick
2014-03-28 19:00:46
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
This helps keep the class organized and on track. This also means that only well-written comments will be dropped into the classroom, so please take time writing responses that are complete and easy to read.
DPatrick
2014-03-28 19:01:01
There are a lot of students here! As I said, only a relatively small fraction of the well-written comments will be passed to the entire group. Please do not take it personally if your responses do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!
There are a lot of students here! As I said, only a relatively small fraction of the well-written comments will be passed to the entire group. Please do not take it personally if your responses do not get posted, and please do not complain about it. I expect this Math Jam to be much larger than our typical class, so please be patient with me---there are quite a few of you here tonight!
DPatrick
2014-03-28 19:01:10
We do have two teaching assistants with us tonight to help answer your questions: Luis (Duelist) and Jessie (numberdance).
We do have two teaching assistants with us tonight to help answer your questions: Luis (Duelist) and Jessie (numberdance).
DPatrick
2014-03-28 19:01:23
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
They can answer questions by whispering to you or by opening a window with you to chat 1-on-1. However, due to the large size of the session tonight, they may not be able to get to you right away (or at all). Repeating your question over and over is more likely to annoy us than to get it answered faster, so please, just ask your question once and be patient, and please understand that we may not be able to answer all the questions tonight.
DPatrick
2014-03-28 19:01:37
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics.
Please also remember that the purpose of this Math Jam is to work through the solutions to AIME problems, and not to merely present the answers. "Working through the solutions" includes discussing problem-solving tactics.
DPatrick
2014-03-28 19:01:42
Also on occasion we may stop to prove things that you wouldn't necessary need to prove while doing the contest.
Also on occasion we may stop to prove things that you wouldn't necessary need to prove while doing the contest.
DPatrick
2014-03-28 19:01:50
So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be acknowledged.
So please, when a question is posted, do not simply respond with the final answer. That's not why we're here. We're going to work through the problems step-by-step, and comments that skip key steps or jump ahead in the problem, without providing explanation or motivation, won't be acknowledged.
DPatrick
2014-03-28 19:02:01
Let's get started! We're going to work through all 15 problems from the 2014 AIME II, in order.
Let's get started! We're going to work through all 15 problems from the 2014 AIME II, in order.
DPatrick
2014-03-28 19:02:07
1. Abe can paint the room in 15 hours, Bea can paint 50 percent faster than Abe, and Coe can paint twice as fast as Abe. Abe begins to paint the room and works alone for the first hour and a half. Then Bea joins Abe, and they work together until half the room is painted. Then Coe joins Abe and Bea, and they work together until the entire room is painted. Find the number of minutes after Abe begins for the three of them to finish painting the room.
1. Abe can paint the room in 15 hours, Bea can paint 50 percent faster than Abe, and Coe can paint twice as fast as Abe. Abe begins to paint the room and works alone for the first hour and a half. Then Bea joins Abe, and they work together until half the room is painted. Then Coe joins Abe and Bea, and they work together until the entire room is painted. Find the number of minutes after Abe begins for the three of them to finish painting the room.
DPatrick
2014-03-28 19:02:24
You'll note that I'll always put the current problem under discussion in a window at the top of the classroom.
You'll note that I'll always put the current problem under discussion in a window at the top of the classroom.
DPatrick
2014-03-28 19:02:42
You can resize that top area by dragging on the horizontal bar between it and the main classroom panel.
You can resize that top area by dragging on the horizontal bar between it and the main classroom panel.
DPatrick
2014-03-28 19:02:46
What's the key to solving long wordy problems like this?
What's the key to solving long wordy problems like this?
ChilledLemonade
2014-03-28 19:03:08
Reading!
Reading!
antler
2014-03-28 19:03:08
translate the words into math
translate the words into math
IsabeltheCat
2014-03-28 19:03:08
turn words into math!
turn words into math!
AndrewK
2014-03-28 19:03:08
Read the question
Read the question
DPatrick
2014-03-28 19:03:16
First and most important: READ THE PROBLEM CAREFULLY!
First and most important: READ THE PROBLEM CAREFULLY!
DPatrick
2014-03-28 19:03:25
Then we want to translate the words into mathematical expressions.
Then we want to translate the words into mathematical expressions.
DPatrick
2014-03-28 19:03:38
What is a general technique for "work" problems like this?
What is a general technique for "work" problems like this?
NormanWho
2014-03-28 19:04:01
a rate problem
a rate problem
hotstuffFTW
2014-03-28 19:04:01
Finding rates
Finding rates
Mathgeek727
2014-03-28 19:04:01
rate?
rate?
AndrewK
2014-03-28 19:04:01
Find the rate of working for each worker
Find the rate of working for each worker
poweroftwo
2014-03-28 19:04:01
express each person as work/hr ratio
express each person as work/hr ratio
XxAndreixX
2014-03-28 19:04:01
Find expressions for the painting speed of each person.
Find expressions for the painting speed of each person.
DPatrick
2014-03-28 19:04:10
Yes, it's usually best if we express the work rates in fractions of a completed job per unit time.
Yes, it's usually best if we express the work rates in fractions of a completed job per unit time.
DPatrick
2014-03-28 19:04:24
For example, rather than say "Abe can paint the room in 15 hours," how would we describe Abe's work rate?
For example, rather than say "Abe can paint the room in 15 hours," how would we describe Abe's work rate?
hnkevin42
2014-03-28 19:04:47
1/15 room/hr
1/15 room/hr
Modest_Ked
2014-03-28 19:04:47
1/15 done in 1 hour
1/15 done in 1 hour
Mathgeek727
2014-03-28 19:04:47
1/15 rooms per hour
1/15 rooms per hour
joey8189681
2014-03-28 19:04:47
1/15 per hour
1/15 per hour
tluo5458
2014-03-28 19:04:47
r=1/15
r=1/15
speck
2014-03-28 19:04:47
He paints 115 of the room in an hour
He paints 115 of the room in an hour
chezbgone2
2014-03-28 19:04:47
Abe paints 1 per 15 hours, so 1/15
Abe paints 1 per 15 hours, so 1/15
Bomist0
2014-03-28 19:04:47
1/15 job per hour
1/15 job per hour
AndrewK
2014-03-28 19:04:47
115 room/hour
115 room/hour
DPatrick
2014-03-28 19:04:52
He paints the entire room in 15 hours, so he paints 115 rooms per hour.
He paints the entire room in 15 hours, so he paints 115 rooms per hour.
DPatrick
2014-03-28 19:04:58
How fast do the other two paint?
How fast do the other two paint?
tluo5458
2014-03-28 19:05:30
Bea: 1/10 Coe: 2/15
Bea: 1/10 Coe: 2/15
hotstuffFTW
2014-03-28 19:05:30
1/10 for Bea and 2/15 for Coe
1/10 for Bea and 2/15 for Coe
mjlove
2014-03-28 19:05:30
1/10 and 2/15
1/10 and 2/15
danusv
2014-03-28 19:05:30
1/10 room per hour and 2/15 room per hour
1/10 room per hour and 2/15 room per hour
UrInvalid
2014-03-28 19:05:30
1/10 for bea, 2/15 for coe
1/10 for bea, 2/15 for coe
ChilledLemonade
2014-03-28 19:05:30
Bea paints at 1/10 per hour and Coe at 2/15 per hour
Bea paints at 1/10 per hour and Coe at 2/15 per hour
DPatrick
2014-03-28 19:05:35
Bea paints 50% faster than Abe, so she paints (1.5)115=110 rooms per hour.
Bea paints 50% faster than Abe, so she paints (1.5)115=110 rooms per hour.
DPatrick
2014-03-28 19:05:44
Coe paints twice as fast as Abe, so he paints 215 rooms per hour.
Coe paints twice as fast as Abe, so he paints 215 rooms per hour.
DPatrick
2014-03-28 19:05:51
Now we can translate the rest of the problem.
Now we can translate the rest of the problem.
DPatrick
2014-03-28 19:05:58
"Abe begins to paint the room and works alone for the first hour and a half."
What does this tell us?
"Abe begins to paint the room and works alone for the first hour and a half."
What does this tell us?
poweroftwo
2014-03-28 19:06:30
he gets 1/10 done in 90 minutes
he gets 1/10 done in 90 minutes
mathwizard888
2014-03-28 19:06:30
he painted 1/10 of the room
he painted 1/10 of the room
hotstuffFTW
2014-03-28 19:06:30
He completes 1.5/15 = 1/10 of the job
He completes 1.5/15 = 1/10 of the job
simon1221
2014-03-28 19:06:30
he does 1/10 of the total work
he does 1/10 of the total work
CornSaltButter
2014-03-28 19:06:30
He paints 1/10 of the room in that time
He paints 1/10 of the room in that time
dmagician34
2014-03-28 19:06:30
He painted 1.5 x 1/15 = 1/10 of the house
He painted 1.5 x 1/15 = 1/10 of the house
peterdragonking
2014-03-28 19:06:33
He finished1/10 of it
He finished1/10 of it
DPatrick
2014-03-28 19:06:37
Right. After 1.5 hours, Abe has painted (1.5)115=110 of the room.
Right. After 1.5 hours, Abe has painted (1.5)115=110 of the room.
DPatrick
2014-03-28 19:06:44
Next: "Then Bea joins Abe, and they work together until half the room is painted."
Next: "Then Bea joins Abe, and they work together until half the room is painted."
DPatrick
2014-03-28 19:06:52
How fast do they work together?
How fast do they work together?
tluo5458
2014-03-28 19:07:25
1/10+1/15=1/6
1/10+1/15=1/6
summitwei
2014-03-28 19:07:25
1/15+1/10
1/15+1/10
Bomist0
2014-03-28 19:07:25
1/10 + 1/15 = 1/6
1/10 + 1/15 = 1/6
danusv
2014-03-28 19:07:25
Combined they work at the rate of 1/15+ 1/10= 1/6 room per hour
Combined they work at the rate of 1/15+ 1/10= 1/6 room per hour
speck
2014-03-28 19:07:25
They paint at 16 of the total per hour
They paint at 16 of the total per hour
jap23
2014-03-28 19:07:25
1/6 per hour
1/6 per hour
hwl0304
2014-03-28 19:07:25
1/6 rph
1/6 rph
CornSaltButter
2014-03-28 19:07:25
1/15+1/10=5/30= 1/6 of the room in 1 hour
1/15+1/10=5/30= 1/6 of the room in 1 hour
wu2481632
2014-03-28 19:07:25
they work 1/15+1/10 per hour which is 1/6 per hour
they work 1/15+1/10 per hour which is 1/6 per hour
simon1221
2014-03-28 19:07:25
1/6 room/hour (1/15 + 1/10)
1/6 room/hour (1/15 + 1/10)
DPatrick
2014-03-28 19:07:31
Yes: Together they paint 115+110=16 of the room per hour.
Yes: Together they paint 115+110=16 of the room per hour.
DPatrick
2014-03-28 19:07:42
And how much of the room do they have to paint together?
And how much of the room do they have to paint together?
wu2481632
2014-03-28 19:08:00
4/10 of the room
4/10 of the room
AndrewK
2014-03-28 19:08:00
4/10 of the room
4/10 of the room
mathwizard888
2014-03-28 19:08:00
1/2-1/10=2/5
1/2-1/10=2/5
joey8189681
2014-03-28 19:08:00
2/5 of the room
2/5 of the room
danusv
2014-03-28 19:08:00
1/2-1/10=2/5 of the room
1/2-1/10=2/5 of the room
ChilledLemonade
2014-03-28 19:08:00
1/2-1/10=2/5
1/2-1/10=2/5
DPatrick
2014-03-28 19:08:04
They continue until 12 the room is done, and Abe already did 110, so they have 12−110=25 of the room that they have to paint together.
They continue until 12 the room is done, and Abe already did 110, so they have 12−110=25 of the room that they have to paint together.
DPatrick
2014-03-28 19:08:09
So how long does it take them?
So how long does it take them?
speck
2014-03-28 19:08:45
So x6=25, x=2.4
So x6=25, x=2.4
hotstuffFTW
2014-03-28 19:08:45
12/5 or 2.4
12/5 or 2.4
jap23
2014-03-28 19:08:45
2.4 hours
2.4 hours
wu2481632
2014-03-28 19:08:45
2/5 / 1/6 which is 2/5*6 which is 12/5
2/5 / 1/6 which is 2/5*6 which is 12/5
poweroftwo
2014-03-28 19:08:45
2/5 divided by 1/6 is 12/5
2/5 divided by 1/6 is 12/5
DPatrick
2014-03-28 19:08:52
Right: To paint 25 of the room at a rate of 16 room per hour, it takes them
2516=125 hours.
Right: To paint 25 of the room at a rate of 16 room per hour, it takes them
2516=125 hours.
DPatrick
2014-03-28 19:09:03
Next: "Then Coe joins Abe and Bea, and they work together until the entire room is painted."
Next: "Then Coe joins Abe and Bea, and they work together until the entire room is painted."
DPatrick
2014-03-28 19:09:07
How fast do they all work together?
How fast do they all work together?
mathwizard888
2014-03-28 19:09:40
1/6+2/15=3/10
1/6+2/15=3/10
abishek99
2014-03-28 19:09:40
3/10 room per hour
3/10 room per hour
UrInvalid
2014-03-28 19:09:40
1/6 + 2/15 = 3/10
1/6 + 2/15 = 3/10
wu2481632
2014-03-28 19:09:40
they work at 1/15+1/10+2/15 which is 9/30 which is 3/10
they work at 1/15+1/10+2/15 which is 9/30 which is 3/10
SaladQ
2014-03-28 19:09:40
1/10 + 1/15 + 2/15 = 3/10
1/10 + 1/15 + 2/15 = 3/10
CornSaltButter
2014-03-28 19:09:40
1/15+1/10+2/15= 3/10 of the room per hour
1/15+1/10+2/15= 3/10 of the room per hour
hjl00
2014-03-28 19:09:40
3/10 of the room per hour
3/10 of the room per hour
DPatrick
2014-03-28 19:09:44
Together they work 115+110+215=930=310 rooms per hour.
Together they work 115+110+215=930=310 rooms per hour.
DPatrick
2014-03-28 19:09:49
So how long does it take them to finish?
So how long does it take them to finish?
hnkevin42
2014-03-28 19:10:12
5/3 hours?
5/3 hours?
wu2481632
2014-03-28 19:10:12
1/2 / 3/10 which is 10/6 = 5/3
1/2 / 3/10 which is 10/6 = 5/3
UrInvalid
2014-03-28 19:10:12
1/2 / 3/10 = 5/3
1/2 / 3/10 = 5/3
CornSaltButter
2014-03-28 19:10:12
1/2 divided by 3/10, which is 5/3 hours
1/2 divided by 3/10, which is 5/3 hours
Bomist0
2014-03-28 19:10:12
½ ÷ 3/10 = 5/3 hours
½ ÷ 3/10 = 5/3 hours
IsabeltheCat
2014-03-28 19:10:12
5/3 hr
5/3 hr
DPatrick
2014-03-28 19:10:16
To paint the remaining 12 room, it takes them
12310=53 hours.
To paint the remaining 12 room, it takes them
12310=53 hours.
DPatrick
2014-03-28 19:10:22
And to finish: "Find the number of minutes after Abe begins for the three of them to finish painting the room."
And to finish: "Find the number of minutes after Abe begins for the three of them to finish painting the room."
DPatrick
2014-03-28 19:10:41
Abe spends 1.5 hours, or 90 minutes.
Abe and Bea spend 125 hours, or 144 minutes.
All three spend 53 hours, or 100 minutes.
Abe spends 1.5 hours, or 90 minutes.
Abe and Bea spend 125 hours, or 144 minutes.
All three spend 53 hours, or 100 minutes.
hjl00
2014-03-28 19:11:00
334 minutes
334 minutes
hotstuffFTW
2014-03-28 19:11:00
This means 5/3+12/5+3/2= 5 17/30 or 334 min
This means 5/3+12/5+3/2= 5 17/30 or 334 min
mathwizard888
2014-03-28 19:11:00
total 334 ans
total 334 ans
ChilledLemonade
2014-03-28 19:11:00
90+100+144 = 334
90+100+144 = 334
dantx5
2014-03-28 19:11:00
334 minutes total
334 minutes total
poweroftwo
2014-03-28 19:11:00
add them you get 334!
add them you get 334!
tluo5458
2014-03-28 19:11:00
so it's 334!
so it's 334!
jmann123456789
2014-03-28 19:11:00
334 minutes
334 minutes
DPatrick
2014-03-28 19:11:06
Right: all told, they take 90+144+100=334 minutes.
Right: all told, they take 90+144+100=334 minutes.
DPatrick
2014-03-28 19:11:29
The AIME almost always has a work or rate problem like this among the first few problems.
The AIME almost always has a work or rate problem like this among the first few problems.
DPatrick
2014-03-28 19:11:47
It's worth practicing how to do them quickly for future contests.
It's worth practicing how to do them quickly for future contests.
DPatrick
2014-03-28 19:11:52
Onwards!
Onwards!
DPatrick
2014-03-28 19:11:56
2. Arnold is studying the prevalence of three health risk factors, denoted by A, B, and C, within a population of men. For each of the three factors, the probability that a randomly selected man in the population has only this risk factor (and none of the others) is 0.1. For any two of the three factors, the probability that a randomly selected man has exactly these two risk factors (but not the third) is 0.14. The probability that a randomly selected man has all three risk factors, given that he has A and B is 13. The probability that a man has none of the three risk factors given that he does not have risk factor A is pq, where p and q are relatively prime positive integers. Find p+q.
2. Arnold is studying the prevalence of three health risk factors, denoted by A, B, and C, within a population of men. For each of the three factors, the probability that a randomly selected man in the population has only this risk factor (and none of the others) is 0.1. For any two of the three factors, the probability that a randomly selected man has exactly these two risk factors (but not the third) is 0.14. The probability that a randomly selected man has all three risk factors, given that he has A and B is 13. The probability that a man has none of the three risk factors given that he does not have risk factor A is pq, where p and q are relatively prime positive integers. Find p+q.
DPatrick
2014-03-28 19:12:10
Yikes, two wordy problems in a row to start us off!
Yikes, two wordy problems in a row to start us off!
poweroftwo
2014-03-28 19:12:32
venn diagram!!
venn diagram!!
abishek99
2014-03-28 19:12:32
venn diagram
venn diagram
dantx5
2014-03-28 19:12:32
venn diagram
venn diagram
hnkevin42
2014-03-28 19:12:37
"Given problems..." A Venn diagram would really help.
"Given problems..." A Venn diagram would really help.
AndrewK
2014-03-28 19:12:37
Assume there are 100 men and then draw a Venn Diagram
Assume there are 100 men and then draw a Venn Diagram
DPatrick
2014-03-28 19:12:49
Good idea. Since we're trying to essentially count men with some of A, B, or C, a 3-circle Venn Diagram might help a lot.
Good idea. Since we're trying to essentially count men with some of A, B, or C, a 3-circle Venn Diagram might help a lot.
DPatrick
2014-03-28 19:12:55

DPatrick
2014-03-28 19:13:05
Let's fill these in with percentages. How can we start?
Let's fill these in with percentages. How can we start?
poweroftwo
2014-03-28 19:13:36
just A, just B, or just C is .1
just A, just B, or just C is .1
abishek99
2014-03-28 19:13:36
outer regions have 10 people each
outer regions have 10 people each
wu2481632
2014-03-28 19:13:36
only one risk factor is 0.1
only one risk factor is 0.1
AndrewK
2014-03-28 19:13:36
Fill in only A, only B, and only C
Fill in only A, only B, and only C
UrInvalid
2014-03-28 19:13:36
each of the parts in only one circle is 0.10
each of the parts in only one circle is 0.10
hnkevin42
2014-03-28 19:13:36
Fill the outsides with 0.1 since those people have no other risk factors
Fill the outsides with 0.1 since those people have no other risk factors
Bomist0
2014-03-28 19:13:36
Ones only in A,B,C are 0.1 or 10%
Ones only in A,B,C are 0.1 or 10%
want2learn
2014-03-28 19:13:36
"For each of the three factors, the probability that a randomly selected man in the population has only this risk factor (and none of the others) is 0.1."
"For each of the three factors, the probability that a randomly selected man in the population has only this risk factor (and none of the others) is 0.1."
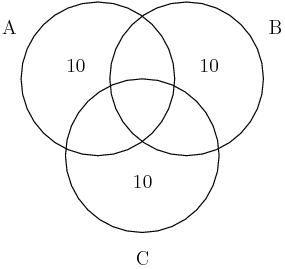
DPatrick
2014-03-28 19:13:43
Having exactly one risk factor is 10% (for each), so we'll put 10 inside of each of the 3 circles (but outside the overlap):
Having exactly one risk factor is 10% (for each), so we'll put 10 inside of each of the 3 circles (but outside the overlap):
DPatrick
2014-03-28 19:13:48

DPatrick
2014-03-28 19:14:16
I'm just going to put the numbers (without percent signs), but you should think of them as percentages. (Or you can think of there being exactly 100 men.) The numbers ought to total to 100 at the end.
I'm just going to put the numbers (without percent signs), but you should think of them as percentages. (Or you can think of there being exactly 100 men.) The numbers ought to total to 100 at the end.
DPatrick
2014-03-28 19:14:18
Now what?
Now what?
abishek99
2014-03-28 19:14:42
14% in intersections of only two circles
14% in intersections of only two circles
Vinni
2014-03-28 19:14:42
14 overlaps
14 overlaps
Mathgeek727
2014-03-28 19:14:42
in overlapping for 2 circles not 3, put 14??
in overlapping for 2 circles not 3, put 14??
joey8189681
2014-03-28 19:14:42
Put 14% on the two overlapping areas
Put 14% on the two overlapping areas
hwl0304
2014-03-28 19:14:42
do the same for 14
do the same for 14
wu2481632
2014-03-28 19:14:42
.14 for two of the risks
.14 for two of the risks
CornSaltButter
2014-03-28 19:14:42
Now look at the number of people with exactly two risk factors= 14 people for each region.
Now look at the number of people with exactly two risk factors= 14 people for each region.
danusv
2014-03-28 19:14:42
Put 14 in the union of A and B, A and C, and B and C
Put 14 in the union of A and B, A and C, and B and C
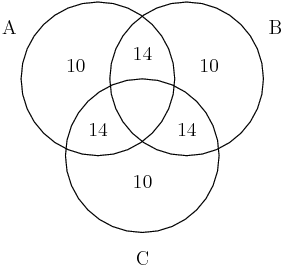
DPatrick
2014-03-28 19:14:49
Good -- having exactly two risk factors is 14% (for each pair), so we'll put 14 inside of each of the overlap regions of two circles:
Good -- having exactly two risk factors is 14% (for each pair), so we'll put 14 inside of each of the overlap regions of two circles:
DPatrick
2014-03-28 19:14:54

DPatrick
2014-03-28 19:15:05
Next -- How do we use this data:
"The probability that a randomly selected man has all three risk factors, given that he has A and B, is 13."
Next -- How do we use this data:
"The probability that a randomly selected man has all three risk factors, given that he has A and B, is 13."
DPatrick
2014-03-28 19:15:13
What region of the Venn Diagram corresponds to "given that he has A and B"?
What region of the Venn Diagram corresponds to "given that he has A and B"?
AndrewK
2014-03-28 19:15:31
The intersection of A and B
The intersection of A and B
dmagician34
2014-03-28 19:15:31
The intersection between A and B
The intersection between A and B
summitwei
2014-03-28 19:15:31
the intersection of A and B...
the intersection of A and B...
ChilledLemonade
2014-03-28 19:15:31
The intersection of all three and the intersection of A and B
The intersection of all three and the intersection of A and B
bengals
2014-03-28 19:15:31
the intersection of A and B
the intersection of A and B
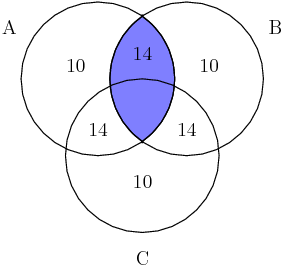
DPatrick
2014-03-28 19:15:35
It's the area inside both the A and B circles, shaded below:
It's the area inside both the A and B circles, shaded below:
DPatrick
2014-03-28 19:15:40

DPatrick
2014-03-28 19:15:52
So what does the quoted sentence from the problem tell us?
So what does the quoted sentence from the problem tell us?
DPatrick
2014-03-28 19:15:58
"The probability that a randomly selected man has all three risk factors, given that he has A and B, is 13."
"The probability that a randomly selected man has all three risk factors, given that he has A and B, is 13."
DPatrick
2014-03-28 19:15:59
?
?
poweroftwo
2014-03-28 19:16:39
1/3 of it is in the very center
1/3 of it is in the very center
AKAL3
2014-03-28 19:16:39
7 is the intersection of all 3
7 is the intersection of all 3
AndrewK
2014-03-28 19:16:39
It tells us the other 2/3 is 14 so the 1/3 with all 3 is 7
It tells us the other 2/3 is 14 so the 1/3 with all 3 is 7
jap23
2014-03-28 19:16:39
that there are 7 in the center!
that there are 7 in the center!
summitwei
2014-03-28 19:16:39
the intersection of everything is 7
the intersection of everything is 7
Readingrocks88
2014-03-28 19:16:39
middle section probability is .7
middle section probability is .7
AnneHahnlheem
2014-03-28 19:16:39
if x is the percentage in the middle area, x/x+14 should = 1/3
if x is the percentage in the middle area, x/x+14 should = 1/3
UrInvalid
2014-03-28 19:16:39
center/blue = 1/3
center/blue = 1/3
DPatrick
2014-03-28 19:16:51
Right. The part of that region with all three risk factors -- that is, the part in the center -- is 13 of the blue shaded region.
Right. The part of that region with all three risk factors -- that is, the part in the center -- is 13 of the blue shaded region.
DPatrick
2014-03-28 19:17:19
So if we let the number in the center be x, then we need to solve xx+14=13.
So if we let the number in the center be x, then we need to solve xx+14=13.
Allan Z
2014-03-28 19:17:27
so 14=2/3 of blue region
so 14=2/3 of blue region
DPatrick
2014-03-28 19:17:42
Or that's another good way to think about it: if the center is 1/3 of the blue region, then 14 is the other 2/3 of the blue regio.
Or that's another good way to think about it: if the center is 1/3 of the blue region, then 14 is the other 2/3 of the blue regio.
DPatrick
2014-03-28 19:17:49
...region,
...region,
DPatrick
2014-03-28 19:17:52
...region!
...region!
DPatrick
2014-03-28 19:18:05
So the blue region is 21 total, and what need to be in the center is 7.
So the blue region is 21 total, and what need to be in the center is 7.
DPatrick
2014-03-28 19:18:14
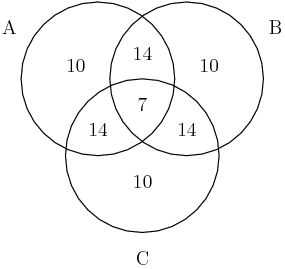

DPatrick
2014-03-28 19:18:21
And that leaves what?
And that leaves what?
mathwizard888
2014-03-28 19:18:41
21 have none
21 have none
tluo5458
2014-03-28 19:18:41
21 outside
21 outside
poweroftwo
2014-03-28 19:18:41
21 on the outside
21 on the outside
Bomist0
2014-03-28 19:18:41
outside, as 21%
outside, as 21%
Lemon123
2014-03-28 19:18:41
21 with none
21 with none
AnneHahnlheem
2014-03-28 19:18:41
21 with no risk factors
21 with no risk factors
Mathgeek727
2014-03-28 19:18:41
21 people with nothing
21 people with nothing
ChilledLemonade
2014-03-28 19:18:41
21 that dont have any risk factors
21 that dont have any risk factors
summitwei
2014-03-28 19:18:41
21 left
21 left
DPatrick
2014-03-28 19:18:47
We have 3(10) + 3(14) + 7 = 30 + 42 + 7 = 79 inside the circles, so that leaves 21 percent outside the circles:
We have 3(10) + 3(14) + 7 = 30 + 42 + 7 = 79 inside the circles, so that leaves 21 percent outside the circles:
DPatrick
2014-03-28 19:18:55
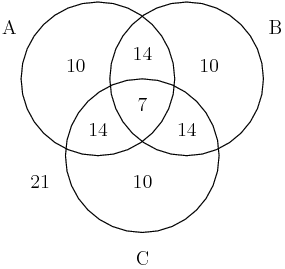

DPatrick
2014-03-28 19:19:00
And how do we finish?
And how do we finish?
DPatrick
2014-03-28 19:19:08
We want "the probability that a man has none of the three risk factors given that he does not have risk factor A".
We want "the probability that a man has none of the three risk factors given that he does not have risk factor A".
DPatrick
2014-03-28 19:19:11
What percentage of the men don't have risk factor A?
What percentage of the men don't have risk factor A?
poweroftwo
2014-03-28 19:19:31
55 don't have
55 don't have
AnneHahnlheem
2014-03-28 19:19:31
55
55
mathwizard888
2014-03-28 19:19:31
10+14+10+21=55
10+14+10+21=55
HYP135peppers
2014-03-28 19:19:31
55
55
poweroftwo
2014-03-28 19:19:31
55 don't have A
55 don't have A
IsabeltheCat
2014-03-28 19:19:31
55%
55%
Mathgeek727
2014-03-28 19:19:31
55?
55?
danusv
2014-03-28 19:19:31
55 percent
55 percent
DPatrick
2014-03-28 19:19:35
We add all the numbers outside of circle A, and get 21+10+14+10 = 55.
We add all the numbers outside of circle A, and get 21+10+14+10 = 55.
DPatrick
2014-03-28 19:19:44
So 55 don't have risk factor A.
So 55 don't have risk factor A.
DPatrick
2014-03-28 19:19:53
Hence, what is our probability?
Hence, what is our probability?
AndrewK
2014-03-28 19:20:12
2155!
2155!
AnneHahnlheem
2014-03-28 19:20:12
thus the probability is 21/55
thus the probability is 21/55
hnkevin42
2014-03-28 19:20:12
21/55
21/55
coldsummer
2014-03-28 19:20:12
21/55
21/55
hotstuffFTW
2014-03-28 19:20:12
21/55 or answer is 076
21/55 or answer is 076
Lemon123
2014-03-28 19:20:12
21/55
21/55
atmath2011
2014-03-28 19:20:12
21/55
21/55
jmann123456789
2014-03-28 19:20:12
21/55
21/55
DPatrick
2014-03-28 19:20:25
Right. Of these 55, only 21 don't have any of the three risk factors.
Right. Of these 55, only 21 don't have any of the three risk factors.
DPatrick
2014-03-28 19:20:31
Thus, our probability is 2155.
Thus, our probability is 2155.
DPatrick
2014-03-28 19:20:38
This is already in lowest terms, so our final answer is 21+55=076.
This is already in lowest terms, so our final answer is 21+55=076.
DPatrick
2014-03-28 19:21:06
This problem is an example of conditional probability. We'll come back to this topic in problem #6.
This problem is an example of conditional probability. We'll come back to this topic in problem #6.
DPatrick
2014-03-28 19:21:12
But in the meantime...
But in the meantime...
DPatrick
2014-03-28 19:21:15
3. A rectangle has sides of length a and 36. A hinge is installed at each vertex of the rectangle and at the midpoint of each side of length 36. The sides of length a can be pressed toward each other keeping those two sides parallel so the rectangle becomes a convex hexagon as shown. When the figure is a hexagon with the sides of length a parallel and separated by a distance of 24, the hexagon has the same area as the original rectangle. Find a2.
3. A rectangle has sides of length a and 36. A hinge is installed at each vertex of the rectangle and at the midpoint of each side of length 36. The sides of length a can be pressed toward each other keeping those two sides parallel so the rectangle becomes a convex hexagon as shown. When the figure is a hexagon with the sides of length a parallel and separated by a distance of 24, the hexagon has the same area as the original rectangle. Find a2.
DPatrick
2014-03-28 19:21:26
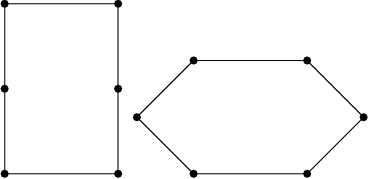

DPatrick
2014-03-28 19:21:43
We'll start easy: what's the area of the rectangle?
We'll start easy: what's the area of the rectangle?
abishek99
2014-03-28 19:21:57
36a
36a
antler
2014-03-28 19:21:57
36a
36a
wu2481632
2014-03-28 19:21:57
36a
36a
dantx5
2014-03-28 19:21:57
36a
36a
byunstephanie
2014-03-28 19:21:57
36a
36a
CornSaltButter
2014-03-28 19:21:57
36*a= 36a
36*a= 36a
dmagician34
2014-03-28 19:21:57
36a
36a
DPatrick
2014-03-28 19:22:13
...and about 30 others of you also correctly said 36a.
...and about 30 others of you also correctly said 36a.
DPatrick
2014-03-28 19:22:20
So we need to find a so that 36a is also the area of the hexagon.
So we need to find a so that 36a is also the area of the hexagon.
DPatrick
2014-03-28 19:22:30
Let's zoom in and label the known lengths of the hexagon:
Let's zoom in and label the known lengths of the hexagon:
DPatrick
2014-03-28 19:22:35
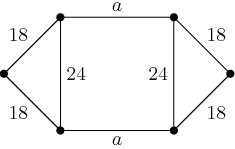

DPatrick
2014-03-28 19:22:45
Now what?
Now what?
byunstephanie
2014-03-28 19:23:14
drop altitudes for the triangles
drop altitudes for the triangles
ChilledLemonade
2014-03-28 19:23:14
Find area !
Find area !
ScottBusche
2014-03-28 19:23:14
Find the area of the triangles.
Find the area of the triangles.
want2learn
2014-03-28 19:23:14
Find the area of one of the side triangles.
Find the area of one of the side triangles.
hnkevin42
2014-03-28 19:23:14
finding the heights of the two triangles would help.
finding the heights of the two triangles would help.
Lemon123
2014-03-28 19:23:14
find height of the triangles
find height of the triangles
DPatrick
2014-03-28 19:23:23
We can draw heights of the two triangles on the left and right sides:
We can draw heights of the two triangles on the left and right sides:
DPatrick
2014-03-28 19:23:27
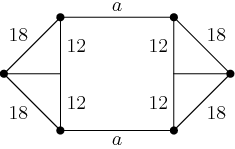

DPatrick
2014-03-28 19:23:47
Now we have 4 little right triangles with one side 12 and hypotenuse 18.
Now we have 4 little right triangles with one side 12 and hypotenuse 18.
DPatrick
2014-03-28 19:23:56
What's the third side of those little right triangles?
What's the third side of those little right triangles?
AKAL3
2014-03-28 19:24:16
6sqrt5 is height
6sqrt5 is height
HYP135peppers
2014-03-28 19:24:16
Therefore, the altitude is 6√5
Therefore, the altitude is 6√5
tluo5458
2014-03-28 19:24:16
so the altitude is 6√5!
so the altitude is 6√5!
AndrewK
2014-03-28 19:24:16
The height is 6√5
The height is 6√5
Awesome_1
2014-03-28 19:24:16
6sqrt5
6sqrt5
Readingrocks88
2014-03-28 19:24:16
6sqrt5
6sqrt5
simon1221
2014-03-28 19:24:16
6sqrt5
6sqrt5
UrInvalid
2014-03-28 19:24:16
use Pythagorean theorem: sqrt(18^2-12^2)=6sqrt5
use Pythagorean theorem: sqrt(18^2-12^2)=6sqrt5
rubberballs
2014-03-28 19:24:16
6sqrt5
6sqrt5
tfmtoto
2014-03-28 19:24:16
√182−122
√182−122
DPatrick
2014-03-28 19:24:23
By the Pythagorean Theorem, those sides have length √182−122=√324−144=√180=6√5.
By the Pythagorean Theorem, those sides have length √182−122=√324−144=√180=6√5.
DPatrick
2014-03-28 19:24:39
So what is the area of the hexagon?
So what is the area of the hexagon?
hwl0304
2014-03-28 19:25:12
24a+144sqrt5
24a+144sqrt5
AndrewK
2014-03-28 19:25:12
144√5+24a
144√5+24a
Bomist0
2014-03-28 19:25:12
6√5 * 24 + 24a
6√5 * 24 + 24a
danusv
2014-03-28 19:25:12
Area is 24 a + 144 root 5
Area is 24 a + 144 root 5
AnneHahnlheem
2014-03-28 19:25:12
24a+144sqrt5
24a+144sqrt5
tluo5458
2014-03-28 19:25:12
24a+144sqrt5
24a+144sqrt5
HYP135peppers
2014-03-28 19:25:12
144√5+24a
144√5+24a
DPatrick
2014-03-28 19:25:18
The rectangle in the center has area 24a, and the triangular areas sum to 144√5. (Each little triangle is a right triangle with legs 12 and 6√5, so each has area 36√5.)
The rectangle in the center has area 24a, and the triangular areas sum to 144√5. (Each little triangle is a right triangle with legs 12 and 6√5, so each has area 36√5.)
DPatrick
2014-03-28 19:25:27
So the total area is 24a+144√5.
And this must equal 36a.
So the total area is 24a+144√5.
And this must equal 36a.
IsabeltheCat
2014-03-28 19:25:54
a=12root5
a=12root5
abishek99
2014-03-28 19:25:54
a=12sqrt{5}
a=12sqrt{5}
Readingrocks88
2014-03-28 19:25:54
a=12sqrt5
a=12sqrt5
AndrewK
2014-03-28 19:25:54
a = 12√5
a = 12√5
poweroftwo
2014-03-28 19:25:54
12a=144sqrt5
12a=144sqrt5
jap23
2014-03-28 19:25:54
So a = 12sqrt5 because 12a = 144sqrt5
So a = 12sqrt5 because 12a = 144sqrt5
DPatrick
2014-03-28 19:26:06
Right. We get 12a=144√5, hence a=12√5, and thus our final answer is a2=144⋅5=720.
Right. We get 12a=144√5, hence a=12√5, and thus our final answer is a2=144⋅5=720.
DPatrick
2014-03-28 19:26:29
This might have been the easiest problem on the contest...or it might be the next one in fact:
This might have been the easiest problem on the contest...or it might be the next one in fact:
DPatrick
2014-03-28 19:26:34
4. The repeating decimals 0.abab¯ab and 0.abcabc¯abc satisfy 0.abab¯ab+0.abcabc¯abc=3337,where a, b, and c are (not necessarily distinct) digits. Find the three-digit number abc.
4. The repeating decimals 0.abab¯ab and 0.abcabc¯abc satisfy 0.abab¯ab+0.abcabc¯abc=3337,where a, b, and c are (not necessarily distinct) digits. Find the three-digit number abc.
DPatrick
2014-03-28 19:26:57
What can we do first?
What can we do first?
rubberballs
2014-03-28 19:27:14
ab/99+abc/999
ab/99+abc/999
summitwei
2014-03-28 19:27:14
ab/99+abc/999=33/37
ab/99+abc/999=33/37
math-rules
2014-03-28 19:27:14
write as fractions
write as fractions
hwl0304
2014-03-28 19:27:14
convert the repeating decimals to fractions
convert the repeating decimals to fractions
tluo5458
2014-03-28 19:27:14
ab/99+abc/999= 33/37
ab/99+abc/999= 33/37
joey8189681
2014-03-28 19:27:14
turn these to fractions
turn these to fractions
IIIIIII
2014-03-28 19:27:14
Expand the fraction
Expand the fraction
dmagician34
2014-03-28 19:27:14
Turn each into a fraction
Turn each into a fraction
tfmtoto
2014-03-28 19:27:14
Express as fractions.
Express as fractions.
DPatrick
2014-03-28 19:27:25
That's certainly one option, and that leads to an algebra problem.
That's certainly one option, and that leads to an algebra problem.
DPatrick
2014-03-28 19:27:30
But there's an even easier solution.
But there's an even easier solution.
hnkevin42
2014-03-28 19:27:38
Find 33/37 in decimal form, which is 0.891, with the 891 repeating
Find 33/37 in decimal form, which is 0.891, with the 891 repeating
nsun48
2014-03-28 19:27:38
Find the decimal representation of 33/37
Find the decimal representation of 33/37
danusv
2014-03-28 19:27:41
line them up so that ABABAB+ABCABC = 0.891891
line them up so that ABABAB+ABCABC = 0.891891
DPatrick
2014-03-28 19:27:45
Yeah. Since the left side is a repeating decimal, it might help if the right side is too.
Yeah. Since the left side is a repeating decimal, it might help if the right side is too.
DPatrick
2014-03-28 19:27:59
Since 37⋅27=999, we have 3337=33⋅2737⋅27=891999.
Since 37⋅27=999, we have 3337=33⋅2737⋅27=891999.
DPatrick
2014-03-28 19:28:07
Therefore, 3337=0.891891¯891.
Therefore, 3337=0.891891¯891.
DPatrick
2014-03-28 19:28:34
As an aside, the fact that 999 = 27 * 37 seems to come up a lot in these problems. It's a useful random fact to know.
As an aside, the fact that 999 = 27 * 37 seems to come up a lot in these problems. It's a useful random fact to know.
math-rules
2014-03-28 19:28:43
ababab + abcabc = 891891
ababab + abcabc = 891891
ChilledLemonade
2014-03-28 19:28:43
so ababab+abcabc=891
so ababab+abcabc=891
DPatrick
2014-03-28 19:28:49
Right, we have:
0.ababab…+0.abcabc…0.891891…
Right, we have:
0.ababab…+0.abcabc…0.891891…
DPatrick
2014-03-28 19:28:55
What does this tell us?
What does this tell us?
math-rules
2014-03-28 19:29:15
a=4
a=4
danusv
2014-03-28 19:29:15
A = 4
A = 4
lucylai
2014-03-28 19:29:15


Bomist0
2014-03-28 19:29:15
a=4
a=4
TheStrangeCharm
2014-03-28 19:29:15
a = 4
a = 4
tluo5458
2014-03-28 19:29:19
a=4 and b = 4?
a=4 and b = 4?
DPatrick
2014-03-28 19:29:23
Right! Just look at the first two digits to the right of the decimal point.
Right! Just look at the first two digits to the right of the decimal point.
DPatrick
2014-03-28 19:29:31
We can see that 0.ab is a little less than half of 0.89.
We can see that 0.ab is a little less than half of 0.89.
DPatrick
2014-03-28 19:30:01
In fact we must have 0.ab=0.44. (If 0.ab=0.43 then the sum is too small, and if 0.ab=0.45 then the sum is too big.) So a=b=4.
In fact we must have 0.ab=0.44. (If 0.ab=0.43 then the sum is too small, and if 0.ab=0.45 then the sum is too big.) So a=b=4.
rubberballs
2014-03-28 19:30:25
c=7?
c=7?
stani95
2014-03-28 19:30:25
c=7
c=7
firemike
2014-03-28 19:30:25
so c = 7
so c = 7
64138luc
2014-03-28 19:30:25
a=b=4, c=7
a=b=4, c=7
math-rules
2014-03-28 19:30:25
c=7 then
c=7 then
Mathgeek727
2014-03-28 19:30:25
then c is 7?
then c is 7?
jmann123456789
2014-03-28 19:30:25
c=7
c=7
DPatrick
2014-03-28 19:30:29
This must make c=7, so that (looking at the first three digits) aba+abc=444+447=891,and (looking at the next three digits) bab+abc=444+447=891.
This must make c=7, so that (looking at the first three digits) aba+abc=444+447=891,and (looking at the next three digits) bab+abc=444+447=891.
DPatrick
2014-03-28 19:30:44
Thus our answer is just 447.
Thus our answer is just 447.
DPatrick
2014-03-28 19:31:02
That problem should have been #1 in my opinion.
That problem should have been #1 in my opinion.
DPatrick
2014-03-28 19:31:18
Well, we've put it off long enough...
Well, we've put it off long enough...
DPatrick
2014-03-28 19:31:22
5. Real numbers r and s are roots of p(x)=x3+ax+b, and r+4 and s−3 are roots of q(x)=x3+ax+b+240. Find the sum of all possible values of |b|.
5. Real numbers r and s are roots of p(x)=x3+ax+b, and r+4 and s−3 are roots of q(x)=x3+ax+b+240. Find the sum of all possible values of |b|.
DPatrick
2014-03-28 19:31:40
I'm not going to lie: this problem is messy, and it seems (to me) too computationally-icky to be a #5.
I'm not going to lie: this problem is messy, and it seems (to me) too computationally-icky to be a #5.
DPatrick
2014-03-28 19:31:51
What's "hard" about it is getting from start to finish without making any algebraic mistakes.
What's "hard" about it is getting from start to finish without making any algebraic mistakes.
DPatrick
2014-03-28 19:31:56
What's going to be our main tool in this problem?
What's going to be our main tool in this problem?
coldsummer
2014-03-28 19:32:10
Vieta's Formulas
Vieta's Formulas
Nitzuga
2014-03-28 19:32:10
Vieta's
Vieta's
mathman500
2014-03-28 19:32:10
vieta's
vieta's
bestwillcui1
2014-03-28 19:32:10
Vieta's Formulae
Vieta's Formulae
HYP135peppers
2014-03-28 19:32:10
Vieta's!
Vieta's!
UrInvalid
2014-03-28 19:32:10
vieta's formulas
vieta's formulas
hjl00
2014-03-28 19:32:10
viettas
viettas
tapir1729
2014-03-28 19:32:10
vieta
vieta
DPatrick
2014-03-28 19:32:14
Vieta's Formulas!
Vieta's Formulas!
DPatrick
2014-03-28 19:32:33
In particular, one of the formulas gives us some strong information right off the bat. What do we notice about these cubics?
In particular, one of the formulas gives us some strong information right off the bat. What do we notice about these cubics?
math-rules
2014-03-28 19:32:55
sum of roots is 0
sum of roots is 0
simon1221
2014-03-28 19:32:55
no x^2
no x^2
lucylai
2014-03-28 19:32:55
the sum of roots is 0
the sum of roots is 0
UrInvalid
2014-03-28 19:32:55
no x^2 term
no x^2 term
IIIIIII
2014-03-28 19:32:55
they have no x^2
they have no x^2
XxAndreixX
2014-03-28 19:32:55
Sum of the roots is 0.
Sum of the roots is 0.
ChilledLemonade
2014-03-28 19:32:55
they have no x^2 term
they have no x^2 term
danusv
2014-03-28 19:32:55
The sum of roots is 0
The sum of roots is 0
hugzy2013
2014-03-28 19:32:55
they don't have a term that is to the second power
they don't have a term that is to the second power
TheStrangeCharm
2014-03-28 19:32:55
the roots sum to 0 because there is no x2 term.
the roots sum to 0 because there is no x2 term.
DPatrick
2014-03-28 19:33:02
There's no x2 term.
There's no x2 term.
DPatrick
2014-03-28 19:33:07
This means that the sum of the roots is 0.
This means that the sum of the roots is 0.
DPatrick
2014-03-28 19:33:16
So if we call the third root of p(x) to be t, then we know that r+s+t=0.
So if we call the third root of p(x) to be t, then we know that r+s+t=0.
DPatrick
2014-03-28 19:33:30
And what is the third root of q(x)?
And what is the third root of q(x)?
UrInvalid
2014-03-28 19:34:00
t-1
t-1
sojourner1
2014-03-28 19:34:00
t-1
t-1
dmagician34
2014-03-28 19:34:00
t-1
t-1
tluo5458
2014-03-28 19:34:00
t-1
t-1
lucylai
2014-03-28 19:34:00


AnneHahnlheem
2014-03-28 19:34:00
t-1
t-1
TheStrangeCharm
2014-03-28 19:34:00
−r−s−1.
−r−s−1.
hjl00
2014-03-28 19:34:00
-r-s-1
-r-s-1
atmath2011
2014-03-28 19:34:00
t-1
t-1
DPatrick
2014-03-28 19:34:06
Since they also have to sum to zero, the third root of q must be t−1, since (r+4)+(s−3)+(t−1)=r+s+t=0.
Since they also have to sum to zero, the third root of q must be t−1, since (r+4)+(s−3)+(t−1)=r+s+t=0.
DPatrick
2014-03-28 19:34:18
So p(x) has roots r,s,t, and q(x) has roots r+4,s−3,t−1.
So p(x) has roots r,s,t, and q(x) has roots r+4,s−3,t−1.
DPatrick
2014-03-28 19:34:27
Now what?
Now what?
math-rules
2014-03-28 19:34:44
use other 2 vieta formulas
use other 2 vieta formulas
bestwillcui1
2014-03-28 19:34:49
random vieta bash gg
random vieta bash gg
lucylai
2014-03-28 19:34:53
use a and b
use a and b
DPatrick
2014-03-28 19:35:02
Right, we've got two more Vieta's Formulas to use.
Right, we've got two more Vieta's Formulas to use.
DPatrick
2014-03-28 19:35:16
Let's just go left-to-right down the cubic, and look at the Vieta's Formula for the ax term in both p and q.
Let's just go left-to-right down the cubic, and look at the Vieta's Formula for the ax term in both p and q.
DPatrick
2014-03-28 19:35:25
From p, we get rs+rt+st=a.
From p, we get rs+rt+st=a.
DPatrick
2014-03-28 19:35:31
From q, we get (r+4)(s−3)+(r+4)(t−1)+(s−3)(t−1)=a.
From q, we get (r+4)(s−3)+(r+4)(t−1)+(s−3)(t−1)=a.
DPatrick
2014-03-28 19:35:48
(These are both the sum of products of pairs of roots.)
(These are both the sum of products of pairs of roots.)
DPatrick
2014-03-28 19:36:03
They're both a, so...?
They're both a, so...?
kevin38017
2014-03-28 19:36:15
set the two equal?
set the two equal?
hnkevin42
2014-03-28 19:36:15
set them equal
set them equal
Readingrocks88
2014-03-28 19:36:15
they equal each other!
they equal each other!
sojourner1
2014-03-28 19:36:15
set them equal to each other
set them equal to each other
mathwizard888
2014-03-28 19:36:15
set them equal
set them equal
antler
2014-03-28 19:36:15
put them equal to each other
put them equal to each other
DPatrick
2014-03-28 19:36:22
Sure, why not? Equating them, we get rs+rt+st=(r+4)(s−3)+(r+4)(t−1)+(s−3)(t−1).
Sure, why not? Equating them, we get rs+rt+st=(r+4)(s−3)+(r+4)(t−1)+(s−3)(t−1).
DPatrick
2014-03-28 19:36:31
Now comes the first of the messy parts...we need to simplify this.
Now comes the first of the messy parts...we need to simplify this.
DPatrick
2014-03-28 19:36:38
There's no point in us slogging through all the work now -- I'll just tell you that it simplifies to 0=−4r+3s+t−13.
There's no point in us slogging through all the work now -- I'll just tell you that it simplifies to 0=−4r+3s+t−13.
Bomist0
2014-03-28 19:36:50
t=-r-s
t=-r-s
DPatrick
2014-03-28 19:37:00
Right, we also know that r+s+t=0, so we can substitute t=−r−s.
Right, we also know that r+s+t=0, so we can substitute t=−r−s.
DPatrick
2014-03-28 19:37:08
This gives 0=−5r+2s−13.
This gives 0=−5r+2s−13.
DPatrick
2014-03-28 19:37:19
That's about as simple as we can get it for now.
That's about as simple as we can get it for now.
DPatrick
2014-03-28 19:37:40
Let's just leave it like that, and go to the third Vieta Formula, the one involving the product of all three roots.
Let's just leave it like that, and go to the third Vieta Formula, the one involving the product of all three roots.
math-rules
2014-03-28 19:37:54
now do the b terms
now do the b terms
danusv
2014-03-28 19:37:54
-b= rst and -b-240 = (r+4)(s-3)(-r-s-1)
-b= rst and -b-240 = (r+4)(s-3)(-r-s-1)
DPatrick
2014-03-28 19:37:57
From p, we get rst=−b.
From p, we get rst=−b.
DPatrick
2014-03-28 19:38:01
From q, we get (r+4)(s−3)(t−1)=−b−240.
From q, we get (r+4)(s−3)(t−1)=−b−240.
DPatrick
2014-03-28 19:38:18
Putting these together gives rst−240=(r+4)(s−3)(t−1).
Putting these together gives rst−240=(r+4)(s−3)(t−1).
CornSaltButter
2014-03-28 19:38:32
Expand again?!
Expand again?!
DPatrick
2014-03-28 19:38:37
Yes: again, we have to slog through expanding the right side. I'll save you the trouble.
Yes: again, we have to slog through expanding the right side. I'll save you the trouble.
DPatrick
2014-03-28 19:38:42
The rst term will cancel, and we'll end up with
0=−rs−3rt+4st+3r−4s−12t+252.
The rst term will cancel, and we'll end up with
0=−rs−3rt+4st+3r−4s−12t+252.
DPatrick
2014-03-28 19:38:54
Now what?
Now what?
kevin38017
2014-03-28 19:39:04
t=-r-s
t=-r-s
lucylai
2014-03-28 19:39:04


Bomist0
2014-03-28 19:39:04
sub t in again?!!!
sub t in again?!!!
hshiems
2014-03-28 19:39:04
t=-r-s
t=-r-s
pedronr
2014-03-28 19:39:04
substitute for t
substitute for t
UrInvalid
2014-03-28 19:39:04
t=-r-s
t=-r-s
DPatrick
2014-03-28 19:39:12
Sure, now we can again use t=−r−s. So we have
0=−rs−3r(−r−s)+4s(−r−s)+3r−4s−12(−r−s)+252.
Sure, now we can again use t=−r−s. So we have
0=−rs−3r(−r−s)+4s(−r−s)+3r−4s−12(−r−s)+252.
DPatrick
2014-03-28 19:39:21
This (after more simplifying!) becomes
0=3r2−4s2−2rs+15r+8s+252.
This (after more simplifying!) becomes
0=3r2−4s2−2rs+15r+8s+252.
DPatrick
2014-03-28 19:39:35
Now what?
Now what?
lucylai
2014-03-28 19:39:43


mathman500
2014-03-28 19:39:43
Substitute 2s=5r+13
Substitute 2s=5r+13
DPatrick
2014-03-28 19:39:53
Good choice. From earlier we know that 2s=5r+13, so we can substitute that in too:
0=3r2−(5r+13)2−r(5r+13)+15r+4(5r+13)+252.(Note that we're substituting for 2s, not just s.)
Good choice. From earlier we know that 2s=5r+13, so we can substitute that in too:
0=3r2−(5r+13)2−r(5r+13)+15r+4(5r+13)+252.(Note that we're substituting for 2s, not just s.)
DPatrick
2014-03-28 19:40:20
After yet more algebra(!), this simplifies down to 0=−27r2−108r+135.
After yet more algebra(!), this simplifies down to 0=−27r2−108r+135.
DPatrick
2014-03-28 19:40:31
Ooh, we can divide by -27 and have just 0=r2+4r−5.
Ooh, we can divide by -27 and have just 0=r2+4r−5.
hugzy2013
2014-03-28 19:40:43
factor?
factor?
joey8189681
2014-03-28 19:40:43
factor
factor
summitwei
2014-03-28 19:40:43
yay a quadratic!
yay a quadratic!
patl02
2014-03-28 19:40:43
Quadratics yay
Quadratics yay
summitwei
2014-03-28 19:40:48
(r-1)(r+5)
(r-1)(r+5)
math-rules
2014-03-28 19:40:48
(r+5)(r-1)=0
(r+5)(r-1)=0
DPatrick
2014-03-28 19:40:55
This factors as 0=(r+5)(r−1), so the solutions are r=−5 and r=1.
This factors as 0=(r+5)(r−1), so the solutions are r=−5 and r=1.
QuantumandMath
2014-03-28 19:41:15
substitute in
substitute in
HYP135peppers
2014-03-28 19:41:24
now we use 2s=5r−13
now we use 2s=5r−13
pedronr
2014-03-28 19:41:24
find s and t now
find s and t now
danusv
2014-03-28 19:41:24
Plug in the answers into s and t
Plug in the answers into s and t
DPatrick
2014-03-28 19:41:31
Right, going back and using 2s=5r+13 and r+s+t=0, we get the solutions
(r,s,t)=(−5,−6,11)and(r,s,t)=(1,9,−10).
Right, going back and using 2s=5r+13 and r+s+t=0, we get the solutions
(r,s,t)=(−5,−6,11)and(r,s,t)=(1,9,−10).
DPatrick
2014-03-28 19:41:48
We can double-check if these work if we want, but we've already spent enough time on this problem.
We can double-check if these work if we want, but we've already spent enough time on this problem.
LOTRFan123
2014-03-28 19:42:04
now find b
now find b
mathwizard888
2014-03-28 19:42:04
b is -330 or 90, so 330+90=420 ans
b is -330 or 90, so 330+90=420 ans
ChilledLemonade
2014-03-28 19:42:04
Find product of the roots
Find product of the roots
DPatrick
2014-03-28 19:42:17
Right. b=−rst, so the first triple gives b=−330 and the second triple gives b=90.
Right. b=−rst, so the first triple gives b=−330 and the second triple gives b=90.
DPatrick
2014-03-28 19:42:23
So our final answer is 330+90=420.
So our final answer is 330+90=420.
DPatrick
2014-03-28 19:42:53
I have to say that I HATED that problem. It was fairly uninteresting and just a lot of algebra-bashing. I had to do it 4 times until I got it right.
I have to say that I HATED that problem. It was fairly uninteresting and just a lot of algebra-bashing. I had to do it 4 times until I got it right.
DPatrick
2014-03-28 19:43:06
So on to better pastures...
So on to better pastures...
DPatrick
2014-03-28 19:43:11
6. Charles has two six-sided dice. One of the dice is fair, and the other die is biased so that it comes up six with probability 23, and each of the other five sides has probability 115. Charles chooses one of the two dice at random and rolls it three times. Given that the first two rolls are both sixes, the probability that the third roll will also be a six is pq, where p and q are relatively prime positive integers. Find p+q.
6. Charles has two six-sided dice. One of the dice is fair, and the other die is biased so that it comes up six with probability 23, and each of the other five sides has probability 115. Charles chooses one of the two dice at random and rolls it three times. Given that the first two rolls are both sixes, the probability that the third roll will also be a six is pq, where p and q are relatively prime positive integers. Find p+q.
Bomist0
2014-03-28 19:43:31
conditional probability
conditional probability
hwl0304
2014-03-28 19:43:31
Conditional probability??
Conditional probability??
UrInvalid
2014-03-28 19:43:31
conditional probability
conditional probability
DPatrick
2014-03-28 19:43:41
Indeed, this is another conditional probability problem.
Indeed, this is another conditional probability problem.
DPatrick
2014-03-28 19:44:04
There's a fancy formula called Bayes Theorem that you can use, but it's just as easy to reason it out.
There's a fancy formula called Bayes Theorem that you can use, but it's just as easy to reason it out.
bestwillcui1
2014-03-28 19:44:13
find probability that it used fair die and prob that biased die sa was used
find probability that it used fair die and prob that biased die sa was used
DPatrick
2014-03-28 19:44:39
Right: we first have to determine the probabilities that, after 2 rolls, we had the fair die or the biased die.
Right: we first have to determine the probabilities that, after 2 rolls, we had the fair die or the biased die.
DPatrick
2014-03-28 19:44:44
What's the probability that the fair die rolls two sixes?
What's the probability that the fair die rolls two sixes?
byunstephanie
2014-03-28 19:44:56
1/36
1/36
dmagician34
2014-03-28 19:44:56
1/36
1/36
bluebandit21
2014-03-28 19:44:56
1/36
1/36
tluo5458
2014-03-28 19:44:56
1/36
1/36
forthegreatergood
2014-03-28 19:44:56
(1/6)^2
(1/6)^2
firemike
2014-03-28 19:44:56
1/36
1/36
hjl00
2014-03-28 19:44:56
1/36
1/36
hnkevin42
2014-03-28 19:44:56
1/36
1/36
speck
2014-03-28 19:44:56
136
136
eswa2000
2014-03-28 19:44:56
1/36
1/36
DPatrick
2014-03-28 19:45:01
The fair die rolls 6-6 with probability 16⋅16=136.
The fair die rolls 6-6 with probability 16⋅16=136.
DPatrick
2014-03-28 19:45:06
What's the probability that the biased die rolls two sixes?
What's the probability that the biased die rolls two sixes?
LOTRFan123
2014-03-28 19:45:24
4/9 = 16/36
4/9 = 16/36
poweroftwo
2014-03-28 19:45:24
16/36=4/9
16/36=4/9
forthegreatergood
2014-03-28 19:45:24
(2/3)^2= 4/9 = 16/36
(2/3)^2= 4/9 = 16/36
CornSaltButter
2014-03-28 19:45:24
(2/3)^2=4/9
(2/3)^2=4/9
hnkevin42
2014-03-28 19:45:24
4/9 = 16/36
4/9 = 16/36
DivideBy0
2014-03-28 19:45:24
(2/3)^2
(2/3)^2
DPatrick
2014-03-28 19:45:27
The biased die rolls 6-6 with probability 46⋅46=1636. (Let's leave it over 36 because it's easier to compare the two dice that way.)
The biased die rolls 6-6 with probability 46⋅46=1636. (Let's leave it over 36 because it's easier to compare the two dice that way.)
DPatrick
2014-03-28 19:45:35
So if we roll two sixes, what's the likelihood that we have the fair die, and what's the likelihood that we have the biased die?
So if we roll two sixes, what's the likelihood that we have the fair die, and what's the likelihood that we have the biased die?
math-rules
2014-03-28 19:46:03
1/17 and 16/17
1/17 and 16/17
UrInvalid
2014-03-28 19:46:03
1/17 and 16/17
1/17 and 16/17
j2002
2014-03-28 19:46:03
1/17 and 16/17
1/17 and 16/17
poweroftwo
2014-03-28 19:46:03
16/17 biased, 1/17 fair
16/17 biased, 1/17 fair
alex31415
2014-03-28 19:46:03
1/17,16/17
1/17,16/17
hwl0304
2014-03-28 19:46:03
1/17, and 16/17
1/17, and 16/17
Readingrocks88
2014-03-28 19:46:03
1/17 and 16/17
1/17 and 16/17
hnkevin42
2014-03-28 19:46:03
1/17 for the fair, and 16/17 for the biased?
1/17 for the fair, and 16/17 for the biased?
AndrewK
2014-03-28 19:46:03
16/17 is the biased die and 1/17 the regular die
16/17 is the biased die and 1/17 the regular die
wu2481632
2014-03-28 19:46:03
1/17,m 16/17
1/17,m 16/17
speck
2014-03-28 19:46:03
Fair: 1/17, biased: 16/17
Fair: 1/17, biased: 16/17
IIIIIII
2014-03-28 19:46:06
1/17 and 16/17
1/17 and 16/17
DPatrick
2014-03-28 19:46:12
Right. We have the fair die with probability 136136+1636=117, and we have the biased die with probability 1636136+1636=1617.
Right. We have the fair die with probability 136136+1636=117, and we have the biased die with probability 1636136+1636=1617.
DPatrick
2014-03-28 19:46:27
(If you don't quite see this sort of conditional probability calculation, imagine that we list all 72 possibilities. In 36 of those, we'll pick the fair die, of which 1 time we'll get 6-6. In the other 36, we'll pick the biased die, of which 16 times we'll get 6-6. These are all equally likely. So of the 17 times we end up with 6-6, 1 of those comes from the fair die and 16 come from the biased die.)
(If you don't quite see this sort of conditional probability calculation, imagine that we list all 72 possibilities. In 36 of those, we'll pick the fair die, of which 1 time we'll get 6-6. In the other 36, we'll pick the biased die, of which 16 times we'll get 6-6. These are all equally likely. So of the 17 times we end up with 6-6, 1 of those comes from the fair die and 16 come from the biased die.)
DPatrick
2014-03-28 19:46:47
So how do we use this data to finish the problem?
So how do we use this data to finish the problem?
math-rules
2014-03-28 19:47:15
1/17 * 1/6 + 16/17 * 4/6
1/17 * 1/6 + 16/17 * 4/6
danusv
2014-03-28 19:47:15
So it is 16/17 * 2/3 + 1/17 * 1/6
So it is 16/17 * 2/3 + 1/17 * 1/6
urmilla
2014-03-28 19:47:15
(1/17)(1/6) + (16/17)(2/3) = 65/102
(1/17)(1/6) + (16/17)(2/3) = 65/102
byunstephanie
2014-03-28 19:47:15
1/17 * 1/6 + 16/17 * 2/3
1/17 * 1/6 + 16/17 * 2/3
Bomist0
2014-03-28 19:47:15
1/17*1/6 + 16/17 * 2/3
1/17*1/6 + 16/17 * 2/3
bluebandit21
2014-03-28 19:47:15
16/17*2/3 + 1/17*1/6
16/17*2/3 + 1/17*1/6
hnkevin42
2014-03-28 19:47:15
(1/17)(1/6) + (16/17)(2/3) = 65/102
(1/17)(1/6) + (16/17)(2/3) = 65/102
simon1221
2014-03-28 19:47:15
16/17*2/3 + 1/17*1/6
16/17*2/3 + 1/17*1/6
DPatrick
2014-03-28 19:47:23
In semi-English, its P(we have the fair die) * P(we roll a 6 on the fair die) + P(we have the biased die) * P(we roll a 6 on the biased die).
In semi-English, its P(we have the fair die) * P(we roll a 6 on the fair die) + P(we have the biased die) * P(we roll a 6 on the biased die).
DPatrick
2014-03-28 19:47:43
(This is basically casework in which the two cases are not equally likely.)
(This is basically casework in which the two cases are not equally likely.)
DPatrick
2014-03-28 19:47:50
So, we roll a third six with probability 117⋅16+1617⋅46.
So, we roll a third six with probability 117⋅16+1617⋅46.
DPatrick
2014-03-28 19:47:57
This simplifies to 65102, which is in lowest terms, so our answer is 65+102=167.
This simplifies to 65102, which is in lowest terms, so our answer is 65+102=167.
DPatrick
2014-03-28 19:48:18
Rolling on...
Rolling on...
DPatrick
2014-03-28 19:48:23
7. Let f(x)=(x2+3x+2)cos(πx). Find the sum of all positive integers n for which
|n∑k=1log10f(k)|=1.
7. Let f(x)=(x2+3x+2)cos(πx). Find the sum of all positive integers n for which
|n∑k=1log10f(k)|=1.
DPatrick
2014-03-28 19:48:43
It looks super-hard, but there's a lot of smoke and mirrors in this problem.
It looks super-hard, but there's a lot of smoke and mirrors in this problem.
DPatrick
2014-03-28 19:49:24
There are a lot of things that we can do to remove the smoke and the mirrors.
There are a lot of things that we can do to remove the smoke and the mirrors.
Bomist0
2014-03-28 19:49:40
cos(πx) = 1 when x is even, -1 when x is odd
cos(πx) = 1 when x is even, -1 when x is odd
UrInvalid
2014-03-28 19:49:40
cos(n*pi)=(-1)^n for int n
cos(n*pi)=(-1)^n for int n
CornSaltButter
2014-03-28 19:49:40
Wait cos(πx) is -1 or 1...
Wait cos(πx) is -1 or 1...
joey8189681
2014-03-28 19:49:40
cos(pi*x) is either equal to 1 or -1
cos(pi*x) is either equal to 1 or -1
atmath2011
2014-03-28 19:49:40
cos (pi x) = 1 when even
cos (pi x) = 1 when even
atmath2011
2014-03-28 19:49:40
-1 odd
-1 odd
QuantumandMath
2014-03-28 19:49:40
cos(pi x)is just 1 for even, -1 for odd
cos(pi x)is just 1 for even, -1 for odd
DPatrick
2014-03-28 19:49:57
Right: one thing to notice is that we only care about what this function looks like when x is an integer.
Right: one thing to notice is that we only care about what this function looks like when x is an integer.
DPatrick
2014-03-28 19:50:22
And cos(πk) is simple when k is an integer: It's 1 if k is even and -1 if k is odd.
And cos(πk) is simple when k is an integer: It's 1 if k is even and -1 if k is odd.
DPatrick
2014-03-28 19:50:31
Thus our function is f(k)=(k2+3k+2)(−1)k for positive integers k.
Thus our function is f(k)=(k2+3k+2)(−1)k for positive integers k.
TheStrangeCharm
2014-03-28 19:50:43
Factor as (x+1)(x+2)
Factor as (x+1)(x+2)
alex31415
2014-03-28 19:50:43
x^2+3x+2=(x+1)(x+2)
x^2+3x+2=(x+1)(x+2)
hugzy2013
2014-03-28 19:50:43
factor x^2+3x+2
factor x^2+3x+2
QuantumandMath
2014-03-28 19:50:43
x^2+3x+2=(x+1)(x+2)
x^2+3x+2=(x+1)(x+2)
DPatrick
2014-03-28 19:50:54
We also see that k2+3k+2=(k+1)(k+2).
We also see that k2+3k+2=(k+1)(k+2).
DPatrick
2014-03-28 19:51:03
So the function is just
f(k)={(k+1)(k+2)if k is even1(k+1)(k+2)if k is odd
So the function is just
f(k)={(k+1)(k+2)if k is even1(k+1)(k+2)if k is odd
DPatrick
2014-03-28 19:51:14
That is,
f(1)=12⋅3,f(2)=3⋅4,f(3)=14⋅5,f(4)=5⋅6,etc.
That is,
f(1)=12⋅3,f(2)=3⋅4,f(3)=14⋅5,f(4)=5⋅6,etc.
DPatrick
2014-03-28 19:51:28
Ok, let's look at our equation now:
|n∑k=1log10f(k)|=1.How can we simplify this?
Ok, let's look at our equation now:
|n∑k=1log10f(k)|=1.How can we simplify this?
DivideBy0
2014-03-28 19:51:58
take product sum log rule
take product sum log rule
UrInvalid
2014-03-28 19:51:58
sum of logs is log of product
sum of logs is log of product
colinhy
2014-03-28 19:51:58
log(a) + lob(b) = log(ab)
log(a) + lob(b) = log(ab)
XxAndreixX
2014-03-28 19:51:58
Use log sum to product identity.
Use log sum to product identity.
byunstephanie
2014-03-28 19:51:58
well sum for logs is multiplying the f(k)s
well sum for logs is multiplying the f(k)s
DPatrick
2014-03-28 19:52:07
Right: a sum of logs is just the log of the product!
Right: a sum of logs is just the log of the product!
DPatrick
2014-03-28 19:52:12
So
|n∑k=1log10f(k)|=|log10n∏k=1f(k)|=1.
So
|n∑k=1log10f(k)|=|log10n∏k=1f(k)|=1.
DPatrick
2014-03-28 19:52:23
And what does that tell us about the product?
And what does that tell us about the product?
ChilledLemonade
2014-03-28 19:52:47
f(k) must equal 0.1 or 10
f(k) must equal 0.1 or 10
IIIIIII
2014-03-28 19:52:47
log f1f2f3 fn equals 1 or 1/10
log f1f2f3 fn equals 1 or 1/10
fortenforge
2014-03-28 19:52:47
10 or 1/10
10 or 1/10
ChilledLemonade
2014-03-28 19:52:47
It is eqaul to 0.1 or 10
It is eqaul to 0.1 or 10
simon1221
2014-03-28 19:52:47
10 or 1/10?
10 or 1/10?
hnkevin42
2014-03-28 19:52:47
has to be 10 or 1/10?
has to be 10 or 1/10?
abishek99
2014-03-28 19:52:47
the product is 10 or 1/10
the product is 10 or 1/10
eswa2000
2014-03-28 19:52:47
it's 10 or 1/10
it's 10 or 1/10
DPatrick
2014-03-28 19:52:51
Right!
Right!
DPatrick
2014-03-28 19:52:55
If we have |log10y|=1, then either log10y=1 or log10y=−1.
If we have |log10y|=1, then either log10y=1 or log10y=−1.
DPatrick
2014-03-28 19:53:00
These respectively mean that y=10 or y=110.
These respectively mean that y=10 or y=110.
DPatrick
2014-03-28 19:53:22
(NOT -10! You can never take the log of a negative number.)
(NOT -10! You can never take the log of a negative number.)
DPatrick
2014-03-28 19:53:30
So we have
n∏k=1f(k)=10 or 110.
So we have
n∏k=1f(k)=10 or 110.
DPatrick
2014-03-28 19:53:37
But what does n∏k=1f(k) equal?
But what does n∏k=1f(k) equal?
DPatrick
2014-03-28 19:53:59
Listing a few might help.
Listing a few might help.
bestwillcui1
2014-03-28 19:54:13
1/(2*3) * 3*4 etc
1/(2*3) * 3*4 etc
eswa2000
2014-03-28 19:54:13
it telescopes
it telescopes
DPatrick
2014-03-28 19:54:17
If n=1, then the product is f(1)=12⋅3.
If n=1, then the product is f(1)=12⋅3.
DPatrick
2014-03-28 19:54:25
If n=2, then the product is 12⋅3⋅f(2)=12⋅3⋅(3⋅4)=42.
If n=2, then the product is 12⋅3⋅f(2)=12⋅3⋅(3⋅4)=42.
DPatrick
2014-03-28 19:54:34
If n=3, then the product is 42⋅f(3)=42⋅14⋅5=12⋅5.
If n=3, then the product is 42⋅f(3)=42⋅14⋅5=12⋅5.
DPatrick
2014-03-28 19:54:42
If n=4, then the product is 12⋅5⋅f(4)=12⋅5⋅(5⋅6)=62.
If n=4, then the product is 12⋅5⋅f(4)=12⋅5⋅(5⋅6)=62.
bestwillcui1
2014-03-28 19:54:52
n=3 works!!
n=3 works!!
Tan
2014-03-28 19:54:52
son=3 is a solution
son=3 is a solution
DPatrick
2014-03-28 19:55:13
Indeed, while doing this we saw that when n=3 we get a product of 1/10. So n=3 is one of our answers.
Indeed, while doing this we saw that when n=3 we get a product of 1/10. So n=3 is one of our answers.
DPatrick
2014-03-28 19:55:21
And do we see the general pattern?
And do we see the general pattern?
IIIIIII
2014-03-28 19:55:40
y=n/2+1 for y being even.
y=n/2+1 for y being even.
LOTRFan123
2014-03-28 19:55:40
It alternates between bigger than 1 and smaller than 1
It alternates between bigger than 1 and smaller than 1
tluo5458
2014-03-28 19:55:40
for evens it's just (n+2)/2
for evens it's just (n+2)/2
UrInvalid
2014-03-28 19:55:52
for even numbers product=(N+2)/2
for even numbers product=(N+2)/2
DPatrick
2014-03-28 19:56:03
Right: if n is even, then the product is n+22.
Right: if n is even, then the product is n+22.
IIIIIII
2014-03-28 19:56:20
the odd ones only go down.
the odd ones only go down.
DivideBy0
2014-03-28 19:56:29
(n+2)/2 or 1/(2n+4)
(n+2)/2 or 1/(2n+4)
DPatrick
2014-03-28 19:56:43
Indeed, if n is odd, then the product is 12(n+2). They decrease and we already found that n=3 gives us 1/10.
Indeed, if n is odd, then the product is 12(n+2). They decrease and we already found that n=3 gives us 1/10.
DPatrick
2014-03-28 19:56:48
What n gives us 10?
What n gives us 10?
joey8189681
2014-03-28 19:57:02
18 is the other answer
18 is the other answer
summitwei
2014-03-28 19:57:02
so n=18!
so n=18!
speck
2014-03-28 19:57:02
So n=18 is a solution as well
So n=18 is a solution as well
alex31415
2014-03-28 19:57:02
18
18
mathwizard888
2014-03-28 19:57:02
18
18
speck
2014-03-28 19:57:02
18
18
DPatrick
2014-03-28 19:57:20
We're looking for an even n such that n+22=10. Clearly we want n=18.
We're looking for an even n such that n+22=10. Clearly we want n=18.
Bomist0
2014-03-28 19:57:33
only solutions, so 18+3
only solutions, so 18+3
eswa2000
2014-03-28 19:57:33
so 3+18=21
so 3+18=21
DPatrick
2014-03-28 19:57:34
So n∈{3,18} are our solutions, and the final answer is 3+18=021.
So n∈{3,18} are our solutions, and the final answer is 3+18=021.
DPatrick
2014-03-28 19:57:54
Note that we could formally prove our formula for the product by induction if we wanted to, but I think the pattern is clear. It's a weird sort of telescoping product.
Note that we could formally prove our formula for the product by induction if we wanted to, but I think the pattern is clear. It's a weird sort of telescoping product.
DPatrick
2014-03-28 19:58:14
OK, on to the first of several harder geometry problems:
OK, on to the first of several harder geometry problems:
DPatrick
2014-03-28 19:58:20
8. Circle C with radius 2 has diameter ¯AB. Circle D is internally tangent to circle C at A. Circle E is internally tangent to circle C, externally tangent to circle D, and tangent to ¯AB. The radius of circle D is three times the radius of circle E and can be written in the form √m−n, where m and n are positive integers. Find m+n.
8. Circle C with radius 2 has diameter ¯AB. Circle D is internally tangent to circle C at A. Circle E is internally tangent to circle C, externally tangent to circle D, and tangent to ¯AB. The radius of circle D is three times the radius of circle E and can be written in the form √m−n, where m and n are positive integers. Find m+n.
hugzy2013
2014-03-28 19:58:33
diagram
diagram
ChilledLemonade
2014-03-28 19:58:33
Diagram please!
Diagram please!
tluo5458
2014-03-28 19:58:33
draw a diagram!
draw a diagram!
bestwillcui1
2014-03-28 19:58:33
Diagram!!! xD
Diagram!!! xD
kevin38017
2014-03-28 19:58:33
Draw a diagram!
Draw a diagram!
DPatrick
2014-03-28 19:58:39
Sure, let's sketch a picture.
Sure, let's sketch a picture.
DPatrick
2014-03-28 19:58:44

DPatrick
2014-03-28 19:58:55
The big outer circle is C, the larger circle inside is D, and the smaller circle is E.
The big outer circle is C, the larger circle inside is D, and the smaller circle is E.
DPatrick
2014-03-28 19:59:02
What else do we probably want to draw?
What else do we probably want to draw?
forthegreatergood
2014-03-28 19:59:12
connect some centers/points of tangency/etc
connect some centers/points of tangency/etc
eswa2000
2014-03-28 19:59:12
connect the centers
connect the centers
kevin38017
2014-03-28 19:59:12
centers of the circles
centers of the circles
math-rules
2014-03-28 19:59:12
radii!
radii!
hnkevin42
2014-03-28 19:59:12
the radii?
the radii?
hjl00
2014-03-28 19:59:12
the radii
the radii
alex31415
2014-03-28 19:59:12
Radii, points of tangency
Radii, points of tangency
DPatrick
2014-03-28 19:59:16
We probably want radii to all the points of tangency:
We probably want radii to all the points of tangency:
DPatrick
2014-03-28 19:59:23

DPatrick
2014-03-28 19:59:36
Note that it is not a straight line from the center of D to the center of E to the point of tangency with C! In fact, where does the segment from the center of E to its point of tangency with C go if we extend it in the other direction?
Note that it is not a straight line from the center of D to the center of E to the point of tangency with C! In fact, where does the segment from the center of E to its point of tangency with C go if we extend it in the other direction?
sillyd
2014-03-28 20:00:10
to the center of C
to the center of C
kevin38017
2014-03-28 20:00:10
cetner of C
cetner of C
math-rules
2014-03-28 20:00:10
center of c
center of c
sojourner1
2014-03-28 20:00:10
the center of C
the center of C
lucylai
2014-03-28 20:00:10
the center of C
the center of C
eswa2000
2014-03-28 20:00:10
center of C
center of C
Readingrocks88
2014-03-28 20:00:10
center of the circle
center of the circle
DPatrick
2014-03-28 20:00:16
It goes to the center of C. Let me add that too, and label some points. I'll label the centers of the circles to be C, D, and E, and a couple more points too:
It goes to the center of C. Let me add that too, and label some points. I'll label the centers of the circles to be C, D, and E, and a couple more points too:
DPatrick
2014-03-28 20:00:25

DPatrick
2014-03-28 20:00:36
Again, we note that C, E, and F are collinear.
Again, we note that C, E, and F are collinear.
DPatrick
2014-03-28 20:00:53
Now we can start chasing lengths.
Now we can start chasing lengths.
math-rules
2014-03-28 20:00:58
let radius of E be r, so radius of D is 3r.
let radius of E be r, so radius of D is 3r.
alex31415
2014-03-28 20:00:58
Let the radius of E be r and the radius of D be 3r
Let the radius of E be r and the radius of D be 3r
DPatrick
2014-03-28 20:01:04
Good call. Let's set the radius of circle E to be r, so that the radius of D is 3r. IMPORTANT TO NOT FORGET: our final answer will be 3r, NOT r. (But setting up the variables this way will avoid fractions.)
Good call. Let's set the radius of circle E to be r, so that the radius of D is 3r. IMPORTANT TO NOT FORGET: our final answer will be 3r, NOT r. (But setting up the variables this way will avoid fractions.)
DPatrick
2014-03-28 20:01:28
Can we chase lengths in a way that will let us set up an equation to solve for r?
Can we chase lengths in a way that will let us set up an equation to solve for r?
DPatrick
2014-03-28 20:01:31
How can we start?
How can we start?
math-rules
2014-03-28 20:02:03
use pythag on CEG and DEG
use pythag on CEG and DEG
HYP135peppers
2014-03-28 20:02:03
pythag on DEG
pythag on DEG
Bomist0
2014-03-28 20:02:03
pythagoras on DEG
pythagoras on DEG
DivideBy0
2014-03-28 20:02:03
Pythag!
Pythag!
bestwillcui1
2014-03-28 20:02:03
Pythagorean Theorem
Pythagorean Theorem
byunstephanie
2014-03-28 20:02:03
Pythagorean on the triangles?
Pythagorean on the triangles?
joey8189681
2014-03-28 20:02:03
right triangle with radii EG and DE
right triangle with radii EG and DE
DPatrick
2014-03-28 20:02:22
Right: certainly we've got a couple of right triangles that we'll be able to use the Pythagorean Theorem on.
Right: certainly we've got a couple of right triangles that we'll be able to use the Pythagorean Theorem on.
DPatrick
2014-03-28 20:02:54
For example, what sides of DEG do we know?
For example, what sides of DEG do we know?
danzhi
2014-03-28 20:03:19
EG=r, DE = 4r
EG=r, DE = 4r
Bomist0
2014-03-28 20:03:19
DE = 4r, EG = r, so DG = √15 r
DE = 4r, EG = r, so DG = √15 r
AndrewK
2014-03-28 20:03:19
DE = 4r and EG = r
DE = 4r and EG = r
dmagician34
2014-03-28 20:03:19
DE = 4r and EG = r
DE = 4r and EG = r
kevin38017
2014-03-28 20:03:19
we know DE=r+3r=4r and EG=r
we know DE=r+3r=4r and EG=r
vinayak-kumar
2014-03-28 20:03:19
All except DG
All except DG
twin77
2014-03-28 20:03:19
DE = 4r, EG = r
DE = 4r, EG = r
DPatrick
2014-03-28 20:03:29
Good. We know that DE=4r (the sum of the two radii) and EG=r.
Good. We know that DE=4r (the sum of the two radii) and EG=r.
DPatrick
2014-03-28 20:03:41
That gives us
DG=√(DE)2−(EG)2=√(4r)2−r2=r√15.
That gives us
DG=√(DE)2−(EG)2=√(4r)2−r2=r√15.
DPatrick
2014-03-28 20:03:52
How about CEG? What sides do we know?
How about CEG? What sides do we know?
byunstephanie
2014-03-28 20:04:19
We also know that CE is 2-r
We also know that CE is 2-r
mathwizard888
2014-03-28 20:04:19
CE=2-r, EG=r
CE=2-r, EG=r
tluo5458
2014-03-28 20:04:19
eg=r and ce=2-r
eg=r and ce=2-r
lucylai
2014-03-28 20:04:29
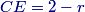
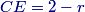
DPatrick
2014-03-28 20:04:41
Right. CF=2 and EF=r, so CE=2−r. And we already had EG=r.
Right. CF=2 and EF=r, so CE=2−r. And we already had EG=r.
DPatrick
2014-03-28 20:04:46
That makes
CG=√(CE)2−(EG)2=√(2−r)2−r2=√4−4r.
That makes
CG=√(CE)2−(EG)2=√(2−r)2−r2=√4−4r.
DPatrick
2014-03-28 20:05:03
So now we have DG and CG -- what does that give us?
So now we have DG and CG -- what does that give us?
twin77
2014-03-28 20:05:18
CD
CD
Bomist0
2014-03-28 20:05:18
DC?
DC?
TheStrangeCharm
2014-03-28 20:05:18
DC
DC
DaChickenInc
2014-03-28 20:05:24
CD
CD
ChilledLemonade
2014-03-28 20:05:24
DC
DC
DPatrick
2014-03-28 20:05:34
Right, we can subtract them to get
DC=DG−CG=r√15−√4−4r.
Right, we can subtract them to get
DC=DG−CG=r√15−√4−4r.
DPatrick
2014-03-28 20:05:39
Why is that helpful?
Why is that helpful?
eswa2000
2014-03-28 20:05:58
CD=2-3r
CD=2-3r
dmagician34
2014-03-28 20:05:58
and 2 - DC = radius of D
and 2 - DC = radius of D
Readingrocks88
2014-03-28 20:05:58
DC+3r=2
DC+3r=2
kevin38017
2014-03-28 20:05:58
because DC also equals 2-3r
because DC also equals 2-3r
TheStrangeCharm
2014-03-28 20:05:58
But that is also equal to 2 - 3r.
But that is also equal to 2 - 3r.
lucylai
2014-03-28 20:05:58
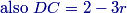
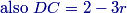
alex31415
2014-03-28 20:05:58
DC is also 2-3r; then we can solve for r.
DC is also 2-3r; then we can solve for r.
DPatrick
2014-03-28 20:06:16
Aha! We know AC=2 and AD=3r, so DC=2−3r.
Aha! We know AC=2 and AD=3r, so DC=2−3r.
DPatrick
2014-03-28 20:06:36
So now we have an equation equating our two calculations for DC:
r√15−√4−4r=2−3r.
So now we have an equation equating our two calculations for DC:
r√15−√4−4r=2−3r.
DPatrick
2014-03-28 20:06:46
How do we solve this for r?
How do we solve this for r?
Bomist0
2014-03-28 20:07:04
isolate the radical
isolate the radical
alex31415
2014-03-28 20:07:04
Move the r*sqrt15 to the other side, then square
Move the r*sqrt15 to the other side, then square
summitwei
2014-03-28 20:07:10
subtract rsqrt15 from both sides then square
subtract rsqrt15 from both sides then square
DPatrick
2014-03-28 20:07:15
Right, we want to isolate the term with the r inside the radical.
Right, we want to isolate the term with the r inside the radical.
DPatrick
2014-03-28 20:07:20
So we rewrite it as √4−4r=r√15+3r−2=(3+√15)r−2.
So we rewrite it as √4−4r=r√15+3r−2=(3+√15)r−2.
DPatrick
2014-03-28 20:07:33
Now we can square both sides:
4−4r=(3+√15)2r2−4(3+√15)r+4.
Now we can square both sides:
4−4r=(3+√15)2r2−4(3+√15)r+4.
DPatrick
2014-03-28 20:07:46
This simplifies to
−4r=(24+6√15)r2−(12+4√15)r.
This simplifies to
−4r=(24+6√15)r2−(12+4√15)r.
kevin38017
2014-03-28 20:08:03
divide both sides by r since r doesn't equal 0
divide both sides by r since r doesn't equal 0
bryanxqchen
2014-03-28 20:08:03
divide by r
divide by r
DPatrick
2014-03-28 20:08:18
It looks like a quadratic, but it's not. We can divide by r since we know r>0:
It looks like a quadratic, but it's not. We can divide by r since we know r>0:
DPatrick
2014-03-28 20:08:36
Doing this and then solving for r eventually gives:
r=4+2√1512+3√15.
Doing this and then solving for r eventually gives:
r=4+2√1512+3√15.
DPatrick
2014-03-28 20:08:51
We could simplify this now, or recall at this point that the quantity we really want is
3r=4+2√154+√15.
We could simplify this now, or recall at this point that the quantity we really want is
3r=4+2√154+√15.
summitwei
2014-03-28 20:09:01
rationalize the denominator...
rationalize the denominator...
Bomist0
2014-03-28 20:09:01
use conjugates
use conjugates
joey8189681
2014-03-28 20:09:01
rationalize the denominator
rationalize the denominator
bestwillcui1
2014-03-28 20:09:01
RATIONALISE THE DENOMInator yeah!!1
RATIONALISE THE DENOMInator yeah!!1
DPatrick
2014-03-28 20:09:16
Right. We multiply numerator and denominator by 4−√15 and notice that the denominator becomes 42−15=1! Therefore,
3r=(4+2√15)(4−√15)=16+4√15−30.
Right. We multiply numerator and denominator by 4−√15 and notice that the denominator becomes 42−15=1! Therefore,
3r=(4+2√15)(4−√15)=16+4√15−30.
alex31415
2014-03-28 20:09:34
this is sqrt240-14 so the answer is 254
this is sqrt240-14 so the answer is 254
Bomist0
2014-03-28 20:09:34
4√15 = √240
4√15 = √240
DPatrick
2014-03-28 20:09:36
This becomes 3r=√240−14 when written in the proper format, so our final answer is 240+14=254.
This becomes 3r=√240−14 when written in the proper format, so our final answer is 240+14=254.
DPatrick
2014-03-28 20:09:56
On to more counting:
On to more counting:
DPatrick
2014-03-28 20:10:01
9. Ten chairs are arranged in a circle. Find the number of subsets of this set of chairs that contain at least three adjacent chairs.
9. Ten chairs are arranged in a circle. Find the number of subsets of this set of chairs that contain at least three adjacent chairs.
DPatrick
2014-03-28 20:10:30
As with most counting problems, there are likely lots of ways to approach this, and not necessarily a single "best" approach.
As with most counting problems, there are likely lots of ways to approach this, and not necessarily a single "best" approach.
math-rules
2014-03-28 20:10:44
complementary casework
complementary casework
bestwillcui1
2014-03-28 20:10:44
Complementary counting
Complementary counting
hugzy2013
2014-03-28 20:10:44
complementary counting
complementary counting
DPatrick
2014-03-28 20:10:53
I thought it would be easier to count the complement: count subsets that do not contain three adjacent seats. (Although it is definitely also possible to solve by counting possible arrangements directly.)
I thought it would be easier to count the complement: count subsets that do not contain three adjacent seats. (Although it is definitely also possible to solve by counting possible arrangements directly.)
DPatrick
2014-03-28 20:11:02
The circularness of the table makes it a bit tricky. How do we account for the circularness?
The circularness of the table makes it a bit tricky. How do we account for the circularness?
hugzy2013
2014-03-28 20:11:23
fix one chair
fix one chair
CornSaltButter
2014-03-28 20:11:23
Set one chair at the top of the circle
Set one chair at the top of the circle
Bomist0
2014-03-28 20:11:23
fix a chair
fix a chair
DPatrick
2014-03-28 20:11:30
One way is to focus on a particular chair -- say the chair at the top of the table in the picture below:
One way is to focus on a particular chair -- say the chair at the top of the table in the picture below:
DPatrick
2014-03-28 20:11:37


DPatrick
2014-03-28 20:11:48
What are the possibilities involving that chair?
What are the possibilities involving that chair?
DPatrick
2014-03-28 20:11:53
(Remember that we're counting the complement -- subsets without 3 chairs in a row.)
(Remember that we're counting the complement -- subsets without 3 chairs in a row.)
tluo5458
2014-03-28 20:12:30
on or off
on or off
hnkevin42
2014-03-28 20:12:30
itself or one next to it
itself or one next to it
tluo5458
2014-03-28 20:12:30
that alone
that alone
Bomist0
2014-03-28 20:12:30
two in a row or 1 forever alone
two in a row or 1 forever alone
tluo5458
2014-03-28 20:12:30
that with left or right
that with left or right
kevin38017
2014-03-28 20:12:30
surrounded by one chair on left or right or no chairs at all
surrounded by one chair on left or right or no chairs at all
lucylai
2014-03-28 20:12:30
there is a person on the left or the right or neither
there is a person on the left or the right or neither
DPatrick
2014-03-28 20:12:44
That chair can be occupied (by "occupied" I mean "in the subset" -- I'm thinking of the subset as the set of chairs that people sit in)...
...and can have a single neighbor on either side, but not both. If there's a neighbor, then the chair beyond the neighbor must be empty.
That chair can be occupied (by "occupied" I mean "in the subset" -- I'm thinking of the subset as the set of chairs that people sit in)...
...and can have a single neighbor on either side, but not both. If there's a neighbor, then the chair beyond the neighbor must be empty.
DPatrick
2014-03-28 20:12:51
Or the chair can be unoccupied.
Or the chair can be unoccupied.
DPatrick
2014-03-28 20:12:59
So that makes 4 cases, as shown in the 4 pictures below. (An "X" indicates an occupied chair, the known empty chairs are shown, and a "?" indicates an unknown chair):
So that makes 4 cases, as shown in the 4 pictures below. (An "X" indicates an occupied chair, the known empty chairs are shown, and a "?" indicates an unknown chair):
DPatrick
2014-03-28 20:13:05


DPatrick
2014-03-28 20:13:11


DPatrick
2014-03-28 20:13:17


DPatrick
2014-03-28 20:13:24


DPatrick
2014-03-28 20:13:38
What's left to count in each of these cases?
What's left to count in each of these cases?
hugzy2013
2014-03-28 20:13:59
the question marks
the question marks
msinghal
2014-03-28 20:13:59
a line of chairs
a line of chairs
hjl00
2014-03-28 20:13:59
the ?'s
the ?'s
kevin38017
2014-03-28 20:13:59
the other chairs
the other chairs
Bomist0
2014-03-28 20:13:59
the ?
the ?
Awesome_1
2014-03-28 20:13:59
location of other occupants
location of other occupants
ChilledLemonade
2014-03-28 20:13:59
The possible arrangements of the other chairs
The possible arrangements of the other chairs
DPatrick
2014-03-28 20:14:05
Right.
Right.
DPatrick
2014-03-28 20:14:06
In the first two cases, we need to count ways to select from 6 chairs in a row with no 3 adjacent.
In the first two cases, we need to count ways to select from 6 chairs in a row with no 3 adjacent.
DPatrick
2014-03-28 20:14:13
In the third case, we need to count ways to select from 7 chairs in a row with no 3 adjacent.
In the third case, we need to count ways to select from 7 chairs in a row with no 3 adjacent.
DPatrick
2014-03-28 20:14:19
In the fourth case, we need to count ways to select from 9 chairs in a row with no 3 adjacent.
In the fourth case, we need to count ways to select from 9 chairs in a row with no 3 adjacent.
DPatrick
2014-03-28 20:14:29
This sounds like the same problem, but with different numbers of chairs.
This sounds like the same problem, but with different numbers of chairs.
msinghal
2014-03-28 20:14:41
recursion?
recursion?
lucylai
2014-03-28 20:14:41
recursion
recursion
vinayak-kumar
2014-03-28 20:14:41
recursion?
recursion?
sojourner1
2014-03-28 20:14:41
recursion type problem?
recursion type problem?
DPatrick
2014-03-28 20:14:49
Indeed, it does suggest trying to set up a recursion.
Indeed, it does suggest trying to set up a recursion.
DPatrick
2014-03-28 20:14:58
Let's call f(n) to be the number of ways to select from n chairs in a row with no 3 adjacent.
Let's call f(n) to be the number of ways to select from n chairs in a row with no 3 adjacent.
DPatrick
2014-03-28 20:15:13
So what we want to count for our complement is 2f(6)+f(7)+f(9).
So what we want to count for our complement is 2f(6)+f(7)+f(9).
QuantumandMath
2014-03-28 20:15:29
small cases
small cases
DPatrick
2014-03-28 20:15:35
f(1)=2 since either the chair is included or not.
f(1)=2 since either the chair is included or not.
DPatrick
2014-03-28 20:15:41
f(2)=4 since any subset of the 2 chairs is legal.
f(2)=4 since any subset of the 2 chairs is legal.
DPatrick
2014-03-28 20:15:46
What's f(3)?
What's f(3)?
tluo5458
2014-03-28 20:15:59
7
7
math-rules
2014-03-28 20:15:59
7
7
kevin38017
2014-03-28 20:15:59
8-1
8-1
bestwillcui1
2014-03-28 20:15:59
8-1
8-1
eswa2000
2014-03-28 20:15:59
7
7
DPatrick
2014-03-28 20:16:12
f(3)=7 since any subset except all 3 chairs is legal. So 23−1=7.
f(3)=7 since any subset except all 3 chairs is legal. So 23−1=7.
DPatrick
2014-03-28 20:16:19
How about f(n) for n≥4?
How about f(n) for n≥4?
Bomist0
2014-03-28 20:16:40
f(x) = f(x-1) + f(x-2) + f(x-3)
f(x) = f(x-1) + f(x-2) + f(x-3)
Allan Z
2014-03-28 20:16:40
fn-1+fn-2+fn-3
fn-1+fn-2+fn-3
DPatrick
2014-03-28 20:16:49
Exactly! Think of n chairs in a row.
Exactly! Think of n chairs in a row.
DPatrick
2014-03-28 20:16:54
If the first chair is not included, then there are f(n−1) ways to pick a subset from the remaining n−1 chairs.
If the first chair is not included, then there are f(n−1) ways to pick a subset from the remaining n−1 chairs.
DPatrick
2014-03-28 20:17:00
If the first chair is included but the second isn't, then there are f(n−2) ways to pick a subset from the remaining n−2 chairs.
If the first chair is included but the second isn't, then there are f(n−2) ways to pick a subset from the remaining n−2 chairs.
DPatrick
2014-03-28 20:17:07
If the first two chairs are included, then the third chair must be excluded. Then there are f(n−3) ways to pick a subset from the remaining n−3 chairs.
If the first two chairs are included, then the third chair must be excluded. Then there are f(n−3) ways to pick a subset from the remaining n−3 chairs.
DPatrick
2014-03-28 20:17:16
So f(n)=f(n−1)+f(n−2)+f(n−3) for all n≥4. (It's a tribonacci sequence!)
So f(n)=f(n−1)+f(n−2)+f(n−3) for all n≥4. (It's a tribonacci sequence!)
DPatrick
2014-03-28 20:17:34
So now we just turn the crank...
So now we just turn the crank...
DPatrick
2014-03-28 20:17:42
f(4)=2+4+7=13.
f(5)=4+7+13=24.
f(6)=7+13+24=44.
f(7)=13+24+44=81.
f(8)=24+44+81=149.
f(9)=44+81+149=274.
f(4)=2+4+7=13.
f(5)=4+7+13=24.
f(6)=7+13+24=44.
f(7)=13+24+44=81.
f(8)=24+44+81=149.
f(9)=44+81+149=274.
DPatrick
2014-03-28 20:17:59
And I helpfully stickied what we wanted to count up top...
And I helpfully stickied what we wanted to count up top...
bestwillcui1
2014-03-28 20:18:05
44*2+81+274
44*2+81+274
DPatrick
2014-03-28 20:18:12
2f(6)+f(7)+f(9)=88+81+274=443.
2f(6)+f(7)+f(9)=88+81+274=443.
bestwillcui1
2014-03-28 20:18:19
that's our complement however
that's our complement however
msinghal
2014-03-28 20:18:23
complement!
complement!
kevin38017
2014-03-28 20:18:23
but thats the complement
but thats the complement
msinghal
2014-03-28 20:18:34
subrtact from 1024
subrtact from 1024
mathwizard888
2014-03-28 20:18:34
1024-443=581 ans
1024-443=581 ans
alex31415
2014-03-28 20:18:34
The answer is 2^10-443=581
The answer is 2^10-443=581
atmath2011
2014-03-28 20:18:34
1024- 443
1024- 443
DPatrick
2014-03-28 20:18:36
Right! There are 210=1024 possible subsets, and 443 of them don't work, so 1024−443=581 do work.
Right! There are 210=1024 possible subsets, and 443 of them don't work, so 1024−443=581 do work.
DPatrick
2014-03-28 20:18:57
As I said, there are certainly other ways to set up the counting in this problem. I don't even claim what I did is best.
As I said, there are certainly other ways to set up the counting in this problem. I don't even claim what I did is best.
DPatrick
2014-03-28 20:19:11
But it's what came most naturally to me (for whatever reason) and it seemed pretty straightforward.
But it's what came most naturally to me (for whatever reason) and it seemed pretty straightforward.
DPatrick
2014-03-28 20:19:38
Let's do #10 (which is fairly quick), then I'm going to take a 5-min rest break before we go on to 11-15.
Let's do #10 (which is fairly quick), then I'm going to take a 5-min rest break before we go on to 11-15.
DPatrick
2014-03-28 20:19:43
10. Let z be a complex number with |z|=2014. Let P be the polygon in the complex plane whose vertices are z and every w such that 1z+w=1z+1w. Then the area enclosed by P can be written in the form n√3, where n is an integer. Find the remainder when n is divided by 1000.
10. Let z be a complex number with |z|=2014. Let P be the polygon in the complex plane whose vertices are z and every w such that 1z+w=1z+1w. Then the area enclosed by P can be written in the form n√3, where n is an integer. Find the remainder when n is divided by 1000.
DPatrick
2014-03-28 20:20:00
As I said on the first AIME Math Jam a couple of weeks ago: The AIME always seems to have one of this sort of problem, that's fairly easy if you know how to use the geometry of the complex plane, and nearly impossible if you don't.
As I said on the first AIME Math Jam a couple of weeks ago: The AIME always seems to have one of this sort of problem, that's fairly easy if you know how to use the geometry of the complex plane, and nearly impossible if you don't.
DPatrick
2014-03-28 20:20:21
How can we better write that equation?
How can we better write that equation?
msinghal
2014-03-28 20:20:40
multiply out
multiply out
math-rules
2014-03-28 20:20:45
(z^2 + zw + w^2) = 0
(z^2 + zw + w^2) = 0
DPatrick
2014-03-28 20:20:55
Sure, let's clear all the denominators by multiplying through by zw(z+w).
Sure, let's clear all the denominators by multiplying through by zw(z+w).
DPatrick
2014-03-28 20:21:01
Now our equation is zw=w(z+w)+z(z+w).
Now our equation is zw=w(z+w)+z(z+w).
DPatrick
2014-03-28 20:21:07
This simplifies further to z2+zw+w2=0.
This simplifies further to z2+zw+w2=0.
DPatrick
2014-03-28 20:21:13
Any further simplification?
Any further simplification?
math-rules
2014-03-28 20:21:29
multiply both sides by (z-w) to get (z-w)^3 = 0
multiply both sides by (z-w) to get (z-w)^3 = 0
lucylai
2014-03-28 20:21:29
multiply by z-w
multiply by z-w
bryanxqchen
2014-03-28 20:21:29
multiply by z-w
multiply by z-w
sojourner1
2014-03-28 20:21:32
we could multiply through by z-w for fun!
we could multiply through by z-w for fun!
DPatrick
2014-03-28 20:21:36
If we multiply both sides by z−w, then it's just z3−w3=0.
If we multiply both sides by z−w, then it's just z3−w3=0.
DPatrick
2014-03-28 20:21:47
Wow! What does that tell us about w?
Wow! What does that tell us about w?
LOTRFan123
2014-03-28 20:22:00
z^3=w^3
z^3=w^3
lucylai
2014-03-28 20:22:10
w is z rotated about origin by 120 or 240 degs
w is z rotated about origin by 120 or 240 degs
math-rules
2014-03-28 20:22:15
the polygon P is a triangle
the polygon P is a triangle
mathwizard888
2014-03-28 20:22:22
w=z*(a cube root of unity)
w=z*(a cube root of unity)
DPatrick
2014-03-28 20:22:34
Right. We see that w3=z3. So w must be a cube root of z3.
Right. We see that w3=z3. So w must be a cube root of z3.
DPatrick
2014-03-28 20:22:40
In other words, w=ζz, where ζ is a cube root of 1.
In other words, w=ζz, where ζ is a cube root of 1.
DPatrick
2014-03-28 20:23:04
So the possible w's are just z rotated 120 degrees (in either direction) about the origin.
So the possible w's are just z rotated 120 degrees (in either direction) about the origin.
DPatrick
2014-03-28 20:23:40
(Like I said: if you know complex number geometry, this is probably easy. If not, it's probably complete nonsense.)
(Like I said: if you know complex number geometry, this is probably easy. If not, it's probably complete nonsense.)
alex31415
2014-03-28 20:23:50
P is an equilateral triangle with side length 2014sqrt3
P is an equilateral triangle with side length 2014sqrt3
bestwillcui1
2014-03-28 20:23:50
we know that the magnitude of z is 2014
we know that the magnitude of z is 2014
DPatrick
2014-03-28 20:24:03
Exactly. We see that P is an equilateral triangle that's inscribed in a circle of radius 2014, with sides of length 2014√3.
Exactly. We see that P is an equilateral triangle that's inscribed in a circle of radius 2014, with sides of length 2014√3.
DPatrick
2014-03-28 20:24:27
So what's its area?
So what's its area?
kevin38017
2014-03-28 20:24:40
area of an equilateral triangle= s^2 * rt3 / 4
area of an equilateral triangle= s^2 * rt3 / 4
DPatrick
2014-03-28 20:24:53
The area is (2014√3)2√34=3(2014)2√34.
The area is (2014√3)2√34=3(2014)2√34.
DPatrick
2014-03-28 20:25:03
So we have n=3(2014)24=3(1007)2.
So we have n=3(2014)24=3(1007)2.
Bomist0
2014-03-28 20:25:21
-->3*7^2
-->3*7^2
alex31415
2014-03-28 20:25:21
1007=7mod 1000, so answer is 3*7^2=147
1007=7mod 1000, so answer is 3*7^2=147
kevin38017
2014-03-28 20:25:21
we only need mod 1000
we only need mod 1000
DPatrick
2014-03-28 20:25:29
Right. The last three digits of n are just 3⋅72=3⋅49=147.
Right. The last three digits of n are just 3⋅72=3⋅49=147.
DPatrick
2014-03-28 20:29:56
OK, ready to resume! 10 down, 5 to go.
OK, ready to resume! 10 down, 5 to go.
DPatrick
2014-03-28 20:30:01
On to more geometry:
On to more geometry:
DPatrick
2014-03-28 20:30:05
11. In △RED, RD=1, ∠DRE=75∘, and ∠RED=45∘. Let M be the midpoint of segment ¯RD. Point C lies on side ¯ED such that ¯RC⊥¯EM. Extend segment ¯DE through E to point A such that CA=AR. Then AE=a−√bc, where a and c are relatively prime positive integers, and b is a positive integer. Find a+b+c.
11. In △RED, RD=1, ∠DRE=75∘, and ∠RED=45∘. Let M be the midpoint of segment ¯RD. Point C lies on side ¯ED such that ¯RC⊥¯EM. Extend segment ¯DE through E to point A such that CA=AR. Then AE=a−√bc, where a and c are relatively prime positive integers, and b is a positive integer. Find a+b+c.
DPatrick
2014-03-28 20:30:19
Here's a picture:
Here's a picture:
DPatrick
2014-03-28 20:30:26

DPatrick
2014-03-28 20:30:36
There's one more line begging to be drawn...
There's one more line begging to be drawn...
Bomist0
2014-03-28 20:30:57
the altitude
the altitude
kevin38017
2014-03-28 20:30:57
perp from R to DA
perp from R to DA
math-rules
2014-03-28 20:30:57
altitude
altitude
DPatrick
2014-03-28 20:31:02
If we drop a perpendicular from R down to ¯DE, it splits triangle RED into a 30-60-90 triangle on the left (in blue) and a 45-45-90 triangle on the right (in red):
If we drop a perpendicular from R down to ¯DE, it splits triangle RED into a 30-60-90 triangle on the left (in blue) and a 45-45-90 triangle on the right (in red):
DPatrick
2014-03-28 20:31:12

DPatrick
2014-03-28 20:31:36
So let's chase lengths. What lengths do we quickly get, starting from RD=1?
So let's chase lengths. What lengths do we quickly get, starting from RD=1?
math-rules
2014-03-28 20:31:59
OD=1/2
OD=1/2
antler
2014-03-28 20:31:59
do=1/2, ro=sqrt3/2
do=1/2, ro=sqrt3/2
tluo5458
2014-03-28 20:31:59
do=1/2
do=1/2
bestwillcui1
2014-03-28 20:31:59
DO, RO, OE, RE
DO, RO, OE, RE
tluo5458
2014-03-28 20:31:59
ro=sqrt3/2
ro=sqrt3/2
math-rules
2014-03-28 20:31:59
RO = rt3/2
RO = rt3/2
tluo5458
2014-03-28 20:32:05
oe=sqrt3/2
oe=sqrt3/2
hwl0304
2014-03-28 20:32:05
RO=sqrt3/2
RO=sqrt3/2
twin77
2014-03-28 20:32:05
RO = sqrt3/2, DO = 1/2
RO = sqrt3/2, DO = 1/2
tluo5458
2014-03-28 20:32:11
re=sqrt6/2
re=sqrt6/2
math-rules
2014-03-28 20:32:11
OE=RO=rt3/2
OE=RO=rt3/2
Bomist0
2014-03-28 20:32:11
DO = ½, RO = √3/2
DO = ½, RO = √3/2
DPatrick
2014-03-28 20:32:15
RD=1, so that makes OD=12 and OR=√32.
RD=1, so that makes OD=12 and OR=√32.
DPatrick
2014-03-28 20:32:26
Then OE=√32 as well, and hence RE=√62.
Then OE=√32 as well, and hence RE=√62.
DPatrick
2014-03-28 20:32:52
So much for the easy lengths. And we still don't seem to know much about point A.
So much for the easy lengths. And we still don't seem to know much about point A.
DPatrick
2014-03-28 20:33:08
How do we get any info about point A?
How do we get any info about point A?
Bomist0
2014-03-28 20:33:23
CA = AR
CA = AR
bestwillcui1
2014-03-28 20:33:23
Well CA=AR
Well CA=AR
tluo5458
2014-03-28 20:33:23
ca=ar
ca=ar
Allan Z
2014-03-28 20:33:28
draw the perpendicular bisector of RC
draw the perpendicular bisector of RC
DPatrick
2014-03-28 20:33:42
Indeed, CAR is an isosceles triangle, so maybe drawing its median/altitude will help. Let's label the foot of the altitude from A to ¯CR as N, and note that N is also the midpoint of ¯CR.
Indeed, CAR is an isosceles triangle, so maybe drawing its median/altitude will help. Let's label the foot of the altitude from A to ¯CR as N, and note that N is also the midpoint of ¯CR.
DPatrick
2014-03-28 20:33:48

DPatrick
2014-03-28 20:33:58
Notice anything interesting?
Notice anything interesting?
kevin38017
2014-03-28 20:34:22
NA and ME are parallel
NA and ME are parallel
tanishq1
2014-03-28 20:34:22
AN parallel to ME...
AN parallel to ME...
tluo5458
2014-03-28 20:34:22
na and me
na and me
math-rules
2014-03-28 20:34:22
parallel lines!
parallel lines!
ashgabat
2014-03-28 20:34:26
AN || EM ??
AN || EM ??
DPatrick
2014-03-28 20:34:31
¯AN∥¯ME, because they're both perpendicular to ¯CR.
¯AN∥¯ME, because they're both perpendicular to ¯CR.
vinayak-kumar
2014-03-28 20:34:40
ME||AN
ME||AN
math-rules
2014-03-28 20:34:40
ME || NA ?!
ME || NA ?!
DaChickenInc
2014-03-28 20:34:40
MN∥AE, AN∥EM, AEMN is a parallelogram
MN∥AE, AN∥EM, AEMN is a parallelogram
DPatrick
2014-03-28 20:34:50
Why are MN and AE parallel?
Why are MN and AE parallel?
eswa2000
2014-03-28 20:35:22
M and N are midpoints
M and N are midpoints
DPatrick
2014-03-28 20:35:42
Right! ¯MN∥¯CD, because ¯MN is the segment connecting the midpoints of ¯RD and ¯RC. (Another way to say this is that RMN and RDC are similar triangles, in ratio 1:2.)
Right! ¯MN∥¯CD, because ¯MN is the segment connecting the midpoints of ¯RD and ¯RC. (Another way to say this is that RMN and RDC are similar triangles, in ratio 1:2.)
twin77
2014-03-28 20:35:59
so therefore MN = EA
so therefore MN = EA
DPatrick
2014-03-28 20:36:10
Exactly. So that means MNAE is a parallelogram!
Exactly. So that means MNAE is a parallelogram!
DPatrick
2014-03-28 20:36:17
In particular MN=AE, and as we just discussed, 2MN=CD.
In particular MN=AE, and as we just discussed, 2MN=CD.
Allan Z
2014-03-28 20:36:26
or AE=1/2DC!
or AE=1/2DC!
msinghal
2014-03-28 20:36:26
so AE = CD/2
so AE = CD/2
DPatrick
2014-03-28 20:36:36
Yes. The answer that we're looking for is just AE=MN=12CD.
Yes. The answer that we're looking for is just AE=MN=12CD.
DPatrick
2014-03-28 20:36:43
That's great, because now we don't need point A anymore! Let me remove it, as it just clutters the diagram:
That's great, because now we don't need point A anymore! Let me remove it, as it just clutters the diagram:
DPatrick
2014-03-28 20:36:53

DPatrick
2014-03-28 20:37:11
Our goal is to find 12CD. Now what?
Our goal is to find 12CD. Now what?
Allan Z
2014-03-28 20:37:44
find CO
find CO
antler
2014-03-28 20:37:44
use similar triangles?
use similar triangles?
DPatrick
2014-03-28 20:37:53
Certainly if we could find OC we'd be done, since CD=OD−OC and we know OD=12.
Certainly if we could find OC we'd be done, since CD=OD−OC and we know OD=12.
DPatrick
2014-03-28 20:38:15
So we might try to get at triangle ROC. Is there a triangle similar to ROC in the picture? Or can we make one?
So we might try to get at triangle ROC. Is there a triangle similar to ROC in the picture? Or can we make one?
Lord.of.AMC
2014-03-28 20:38:54
RC perpendicular to EM...
RC perpendicular to EM...
Bomist0
2014-03-28 20:38:54
EM perp to RC
EM perp to RC
Allan Z
2014-03-28 20:39:01
drop the altitude from M to DE
drop the altitude from M to DE
DPatrick
2014-03-28 20:39:46
Since EM is perpendicular to RC, it makes sense to look for a triangle similar to ROC that uses side ¯EM somehow.
Since EM is perpendicular to RC, it makes sense to look for a triangle similar to ROC that uses side ¯EM somehow.
DPatrick
2014-03-28 20:39:58
And it has to be a right triangle, of course.
And it has to be a right triangle, of course.
DPatrick
2014-03-28 20:40:18
So let's draw the perpendicular from M down to ¯DE, and call the foot of that perpendicular P:
So let's draw the perpendicular from M down to ¯DE, and call the foot of that perpendicular P:
DPatrick
2014-03-28 20:40:27

Lord.of.AMC
2014-03-28 20:40:42
RCO similar to EMP
RCO similar to EMP
DPatrick
2014-03-28 20:40:50
Now triangles MPE and COR are similar right triangles! I'll label them in green so that they're clearer:
Now triangles MPE and COR are similar right triangles! I'll label them in green so that they're clearer:
DPatrick
2014-03-28 20:40:57

DPatrick
2014-03-28 20:41:08
To see why they're similar, note that ¯ME, ¯MP, and ¯PE are each perpendicular, respectively, to ¯CR, ¯CO, and ¯OR. So in particular if we were to rotate MEP 90 degrees, its sides would all be parallel to the corresponding sides in CRO.
To see why they're similar, note that ¯ME, ¯MP, and ¯PE are each perpendicular, respectively, to ¯CR, ¯CO, and ¯OR. So in particular if we were to rotate MEP 90 degrees, its sides would all be parallel to the corresponding sides in CRO.
chessderek
2014-03-28 20:41:30
we know MP
we know MP
DPatrick
2014-03-28 20:41:47
Indeed we know a couple of the lengths in MEP!
Indeed we know a couple of the lengths in MEP!
Lord.of.AMC
2014-03-28 20:42:03
and DMP similar to DRO with factor 1/2
and DMP similar to DRO with factor 1/2
DPatrick
2014-03-28 20:42:12
Right, so in particular, MP=12RO=√34. (This is because triangle MPD is half of triangle ROD, since M and P are midpoints.)
Right, so in particular, MP=12RO=√34. (This is because triangle MPD is half of triangle ROD, since M and P are midpoints.)
DPatrick
2014-03-28 20:42:33
And EP=EO+12OD=√32+14=2√3+14.
And EP=EO+12OD=√32+14=2√3+14.
chessderek
2014-03-28 20:43:30
use ratios to solve for OC?
use ratios to solve for OC?
eswa2000
2014-03-28 20:43:30
side ratios to find CO
side ratios to find CO
kevin38017
2014-03-28 20:43:30
we have the stuff we need to find CO with similarity
we have the stuff we need to find CO with similarity
DPatrick
2014-03-28 20:43:47
Right, the side ratios of MPE∼COR give us OCOR=PMPE=√32√3+1.
Right, the side ratios of MPE∼COR give us OCOR=PMPE=√32√3+1.
DPatrick
2014-03-28 20:44:07
And we already know (from near the beginning -- it's still stickied up top) that OR=√32.
And we already know (from near the beginning -- it's still stickied up top) that OR=√32.
DPatrick
2014-03-28 20:44:23
So OC=OR⋅√32√3+1=√32⋅√32√3+1=34√3+2.
So OC=OR⋅√32√3+1=√32⋅√32√3+1=34√3+2.
DPatrick
2014-03-28 20:44:53
And this makes
CD=OD−OC=12−34√3+2.
And this makes
CD=OD−OC=12−34√3+2.
DPatrick
2014-03-28 20:45:02
(It's just algebra from here...)
(It's just algebra from here...)
DPatrick
2014-03-28 20:45:15
This simplifies to CD=2√3+1−34√3+2=2√3−24√3+2=√3−12√3+1.
This simplifies to CD=2√3+1−34√3+2=2√3−24√3+2=√3−12√3+1.
DPatrick
2014-03-28 20:45:31
And finally what we want is AE=12CD=√3−14√3+2.
And finally what we want is AE=12CD=√3−14√3+2.
QuantumandMath
2014-03-28 20:45:42
rationalize the denominator
rationalize the denominator
Bomist0
2014-03-28 20:45:42
rationalize denom
rationalize denom
ChilledLemonade
2014-03-28 20:45:42
Rationalize
Rationalize
DPatrick
2014-03-28 20:45:49
Right, we still need to rationalize the denominator to get it into the final form.
Right, we still need to rationalize the denominator to get it into the final form.
DPatrick
2014-03-28 20:45:57
AE=√3−14√3+2⋅4√3−24√3−2.
AE=√3−14√3+2⋅4√3−24√3−2.
DPatrick
2014-03-28 20:46:07
This simplifies to
AE=14−6√348−4=7−3√322=7−√2722.
This simplifies to
AE=14−6√348−4=7−3√322=7−√2722.
bestwillcui1
2014-03-28 20:46:25
7+27+22=56
7+27+22=56
twin77
2014-03-28 20:46:25
so 7 + 27 + 22 = 056
so 7 + 27 + 22 = 056
DPatrick
2014-03-28 20:46:29
Therefore, our final answer is 7+27+22=056.
Therefore, our final answer is 7+27+22=056.
DPatrick
2014-03-28 20:46:59
There are many other ways to do this problem. I just set up coordinates the first time and bashed through the calculations.
There are many other ways to do this problem. I just set up coordinates the first time and bashed through the calculations.
DPatrick
2014-03-28 20:47:27
Anyway, on to a different sort of geometry problem, one that's not really geometry at all:
Anyway, on to a different sort of geometry problem, one that's not really geometry at all:
DPatrick
2014-03-28 20:47:32
12. Suppose that the angles of △ABC satisfy cos(3A)+cos(3B)+cos(3C)=1. Two sides of the triangle have lengths 10 and 13. There is a positive integer m so that the maximum possible length for the remaining side of △ABC is √m. Find m.
12. Suppose that the angles of △ABC satisfy cos(3A)+cos(3B)+cos(3C)=1. Two sides of the triangle have lengths 10 and 13. There is a positive integer m so that the maximum possible length for the remaining side of △ABC is √m. Find m.
DPatrick
2014-03-28 20:47:47
Let's set a=3A and b=3B and c=3C so I don't have to keep writing "3" all the time.
Let's set a=3A and b=3B and c=3C so I don't have to keep writing "3" all the time.
DPatrick
2014-03-28 20:47:55
So we have a+b+c=3π and cosa+cosb+cosc=1.
So we have a+b+c=3π and cosa+cosb+cosc=1.
DPatrick
2014-03-28 20:48:08
What do we know?
What do we know?
Bomist0
2014-03-28 20:48:36
c = 3π -a-b
c = 3π -a-b
DPatrick
2014-03-28 20:49:03
Let's combine our equations by getting rid of c by substituting:
cosa+cosb+cos(3π−a−b)=1.
Let's combine our equations by getting rid of c by substituting:
cosa+cosb+cos(3π−a−b)=1.
DPatrick
2014-03-28 20:49:14
What does that third term simplify to?
What does that third term simplify to?
Allan Z
2014-03-28 20:49:39
cos(3pi-a-b)=-cos(a+b)
cos(3pi-a-b)=-cos(a+b)
kevin38017
2014-03-28 20:49:39
-cos(a+b)
-cos(a+b)
zhuangzhuang
2014-03-28 20:49:39
-cos(a+b)
-cos(a+b)
DPatrick
2014-03-28 20:50:02
3π inside a cosine is the same as π, and we use the identity cos(π−θ)=−cosθ. So now we have
cosa+cosb−cos(a+b)=1.
3π inside a cosine is the same as π, and we use the identity cos(π−θ)=−cosθ. So now we have
cosa+cosb−cos(a+b)=1.
DPatrick
2014-03-28 20:50:16
Let's write it without the minus sign: cosa+cosb=cos(a+b)+1.
Let's write it without the minus sign: cosa+cosb=cos(a+b)+1.
DPatrick
2014-03-28 20:50:27
Any ideas what we can do with this now?
Any ideas what we can do with this now?
DPatrick
2014-03-28 20:50:59
(Note: there are many ways to proceed, depending on how exotic a trig identity you want to use.)
(Note: there are many ways to proceed, depending on how exotic a trig identity you want to use.)
summitwei
2014-03-28 20:51:13
cos summation property
cos summation property
tluo5458
2014-03-28 20:51:13
sum of cosines
sum of cosines
zhuangzhuang
2014-03-28 20:51:34
sum to product
sum to product
DPatrick
2014-03-28 20:51:35
Well, I see a sum of cosines on both sides. (using cos0=1) so the cosine sum-to-product formula might be helpful:
cosx+cosy=2cos(x+y2)cos(x−y2).
Well, I see a sum of cosines on both sides. (using cos0=1) so the cosine sum-to-product formula might be helpful:
cosx+cosy=2cos(x+y2)cos(x−y2).
DPatrick
2014-03-28 20:51:57
When we apply that to our equation, we get
2cos(a+b2)cos(a−b2)=2cos(a+b2)cos(a+b2).
When we apply that to our equation, we get
2cos(a+b2)cos(a−b2)=2cos(a+b2)cos(a+b2).
DPatrick
2014-03-28 20:52:12
Aha! What does this tell us?
Aha! What does this tell us?
twin77
2014-03-28 20:52:33
so cos((a-b)/2) = cos((a+b)/2)
so cos((a-b)/2) = cos((a+b)/2)
Bomist0
2014-03-28 20:52:33
cos ((a-b)/2) = cos ((a+b)/2)
cos ((a-b)/2) = cos ((a+b)/2)
DPatrick
2014-03-28 20:52:38
Well...not so fast.
Well...not so fast.
zhuangzhuang
2014-03-28 20:52:44
cos(a-b/2)=cos(a+b/2) or cos(a+b/2)=0
cos(a-b/2)=cos(a+b/2) or cos(a+b/2)=0
DPatrick
2014-03-28 20:52:53
Yeah, that's a possibility too.
Yeah, that's a possibility too.
DPatrick
2014-03-28 20:52:58
Either cos(a+b2)=0, or we can divide by it (and 2) to get cos(a−b2)=cos(a+b2).
Either cos(a+b2)=0, or we can divide by it (and 2) to get cos(a−b2)=cos(a+b2).
DPatrick
2014-03-28 20:53:14
What happens in the first case, if cos(a+b2)=0?
What happens in the first case, if cos(a+b2)=0?
XxAndreixX
2014-03-28 20:53:47
a + b = pi
a + b = pi
DPatrick
2014-03-28 20:54:25
That's true, but it skips an important step. Initially all we know is that a+b2 must be a half-multiple of π.
That's true, but it skips an important step. Initially all we know is that a+b2 must be a half-multiple of π.
DPatrick
2014-03-28 20:54:37
But we know that 0<a+b<3π, so 0<a+b2<32π, and the only possibility is a+b2=π2.
But we know that 0<a+b<3π, so 0<a+b2<32π, and the only possibility is a+b2=π2.
DPatrick
2014-03-28 20:54:51
And indeed this means that a+b=π.
And indeed this means that a+b=π.
zhuangzhuang
2014-03-28 20:55:02
so C=120 degrees
so C=120 degrees
kevin38017
2014-03-28 20:55:10
this means the thrid angle of the triangle is 120
this means the thrid angle of the triangle is 120
DPatrick
2014-03-28 20:55:28
Right. This makes c=2π and C=23π. (Or if you prefer, C=120∘.)
Right. This makes c=2π and C=23π. (Or if you prefer, C=120∘.)
DPatrick
2014-03-28 20:55:39
What about the other case: cos(a−b2)=cos(a+b2)?
What about the other case: cos(a−b2)=cos(a+b2)?
DPatrick
2014-03-28 20:55:50
When do two angles have the same cosine?
When do two angles have the same cosine?
kevin38017
2014-03-28 20:56:37
b=0
b=0
Allan Z
2014-03-28 20:56:37
same or add up to 2pi
same or add up to 2pi
nalaxone44
2014-03-28 20:56:37
when they add to 360
when they add to 360
tluo5458
2014-03-28 20:56:37
when the sum to 360
when the sum to 360
nalaxone44
2014-03-28 20:56:37
when they add to 2pi
when they add to 2pi
bestwillcui1
2014-03-28 20:56:37
x and 360-x
x and 360-x
kevin38017
2014-03-28 20:56:46
when they differ by a multiple of 2pi, are the same angle, add up to 2pi
when they differ by a multiple of 2pi, are the same angle, add up to 2pi
DPatrick
2014-03-28 20:57:00
I think between you, you may have all the cases. More generally, their sum or difference has to be a multiple of 2π.
I think between you, you may have all the cases. More generally, their sum or difference has to be a multiple of 2π.
DPatrick
2014-03-28 20:57:44
But in our equation, the sum of the angles is a and their difference is b. The only way that one of these can be a multiple of 2π is if one of them itself is 2π. (We know they're not 0, and 4π is too big.)
But in our equation, the sum of the angles is a and their difference is b. The only way that one of these can be a multiple of 2π is if one of them itself is 2π. (We know they're not 0, and 4π is too big.)
tluo5458
2014-03-28 20:58:15
so one is 120 degrees
so one is 120 degrees
DPatrick
2014-03-28 20:58:16
So either a=2π or b=2π, and that means either A=23π=120∘ or B=23π=120∘.
So either a=2π or b=2π, and that means either A=23π=120∘ or B=23π=120∘.
kevin38017
2014-03-28 20:58:41
so either way our biggest angle is 120 degrees
so either way our biggest angle is 120 degrees
DPatrick
2014-03-28 20:58:49
Right. In summary, we've proved that our identity holds if and only if one of the angles in the triangle is 23π (or 120∘).
Right. In summary, we've proved that our identity holds if and only if one of the angles in the triangle is 23π (or 120∘).
DPatrick
2014-03-28 20:59:08
So what does that tell us about maximizing the length of the remaining side?
So what does that tell us about maximizing the length of the remaining side?
math-rules
2014-03-28 20:59:23
law of cosines
law of cosines
TheStrangeCharm
2014-03-28 20:59:23
it should be opposite the 120 degree angle
it should be opposite the 120 degree angle
kevin38017
2014-03-28 20:59:26
its opposite angle is 120 degrees
its opposite angle is 120 degrees
abishek99
2014-03-28 20:59:32
it has to be opposite the 120 degree angle
it has to be opposite the 120 degree angle
Bomist0
2014-03-28 20:59:32
use cos law, but the side is opposite 120 degrees
use cos law, but the side is opposite 120 degrees
zhuangzhuang
2014-03-28 20:59:32
let the 120 be between the 10, 13
let the 120 be between the 10, 13
DPatrick
2014-03-28 20:59:58
Right. We want to have a triangle with sides 10 and 13 and an angle of 2π3 between them. The side opposite the obtuse angle will be the longest side.
Right. We want to have a triangle with sides 10 and 13 and an angle of 2π3 between them. The side opposite the obtuse angle will be the longest side.
tanishq1
2014-03-28 21:00:10
now we jsut do law of cosines on 10 and 13
now we jsut do law of cosines on 10 and 13
simon1221
2014-03-28 21:00:10
law of cosines, get remaining side
law of cosines, get remaining side
Bomist0
2014-03-28 21:00:13
x^2 = 10^2 + 13^2 - 2*10*13*cos120
x^2 = 10^2 + 13^2 - 2*10*13*cos120
DPatrick
2014-03-28 21:00:32
By the Law of Cosines:
m=102+132−2(10)(13)(cos2π3).
By the Law of Cosines:
m=102+132−2(10)(13)(cos2π3).
DPatrick
2014-03-28 21:00:58
This simplifies to m=100+169−260(−0.5)=399.
This simplifies to m=100+169−260(−0.5)=399.
DPatrick
2014-03-28 21:01:31
Not too bad. On to #13:
Not too bad. On to #13:
DPatrick
2014-03-28 21:01:36
13. Ten adults enter a room, remove their shoes, and toss their shoes into a pile. Later, a child randomly pairs each left shoe with a right shoe without regard to which shoes belong together. The probability that for every positive integer k<5, no collection of k pairs made by the child contains the shoes from exactly k of the adults is mn, where m and n are relatively prime positive integers. Find m+n.
13. Ten adults enter a room, remove their shoes, and toss their shoes into a pile. Later, a child randomly pairs each left shoe with a right shoe without regard to which shoes belong together. The probability that for every positive integer k<5, no collection of k pairs made by the child contains the shoes from exactly k of the adults is mn, where m and n are relatively prime positive integers. Find m+n.
DPatrick
2014-03-28 21:01:53
Let's number the adults 1 through 10, and call their shoes L1, L2, ..., L10 and R1, R2, ..., R10 so that we can more easily discuss them.
Let's number the adults 1 through 10, and call their shoes L1, L2, ..., L10 and R1, R2, ..., R10 so that we can more easily discuss them.
DPatrick
2014-03-28 21:02:09
We can also denote the child's pairs as (Ln,Rf(n)) for some function f. (For example, if the child pairs L1 with R3, then f(1)=3 and (L1,R3) is one of our pairs.)
We can also denote the child's pairs as (Ln,Rf(n)) for some function f. (For example, if the child pairs L1 with R3, then f(1)=3 and (L1,R3) is one of our pairs.)
DPatrick
2014-03-28 21:02:25
First, we can count the denominator of our eventual probability. How many possible pairings can the child make?
First, we can count the denominator of our eventual probability. How many possible pairings can the child make?
Allan Z
2014-03-28 21:02:55
10!
10!
kevin38017
2014-03-28 21:02:55
10!
10!
mathwizard888
2014-03-28 21:02:55
10!
10!
math-rules
2014-03-28 21:02:55
10!
10!
DPatrick
2014-03-28 21:02:59
She has 10 choices for which right shoe to pair with L1.
She has 10 choices for which right shoe to pair with L1.
DPatrick
2014-03-28 21:03:05
Then she has 9 choices for which remaining right shoe to pair with L2.
Then she has 9 choices for which remaining right shoe to pair with L2.
DPatrick
2014-03-28 21:03:10
Then she has 8 choices for which remaining right shoe to pair with L3.
Then she has 8 choices for which remaining right shoe to pair with L3.
DPatrick
2014-03-28 21:03:16
And so on.
And so on.
DPatrick
2014-03-28 21:03:22
So there are 10! possible pairings.
So there are 10! possible pairings.
DPatrick
2014-03-28 21:04:00
(A fancy way to say this is that the function f that I described above gives us a permutation of the 10 right shoes, and there are 10! permutations of 10 objects.)
(A fancy way to say this is that the function f that I described above gives us a permutation of the 10 right shoes, and there are 10! permutations of 10 objects.)
DPatrick
2014-03-28 21:04:12
OK, on to the numerator.
OK, on to the numerator.
DPatrick
2014-03-28 21:04:26
Let's call a subset of the adults "good" if their shoes are all matched among each other. For example, if (L1,R8), (L8,R3), and (L3,R1) were all pairs, then the subset {1,3,8} would be good.
Let's call a subset of the adults "good" if their shoes are all matched among each other. For example, if (L1,R8), (L8,R3), and (L3,R1) were all pairs, then the subset {1,3,8} would be good.
DPatrick
2014-03-28 21:04:46
...because those 3 adults could grab those 3 pairs, and each retrieve their own shoes.
...because those 3 adults could grab those 3 pairs, and each retrieve their own shoes.
DPatrick
2014-03-28 21:04:53
So the problem is asking for the probability that there are no good subsets of size 1, 2, 3, or 4.
So the problem is asking for the probability that there are no good subsets of size 1, 2, 3, or 4.
DPatrick
2014-03-28 21:04:59
But if this is the case, what else do we know?
But if this is the case, what else do we know?
kevin38017
2014-03-28 21:05:27
we can have either 2 good subsets of 5 or 1 good subset of 10
we can have either 2 good subsets of 5 or 1 good subset of 10
msinghal
2014-03-28 21:05:31
it is 5-5 or 10
it is 5-5 or 10
DPatrick
2014-03-28 21:05:36
Why are those the only possibilities?
Why are those the only possibilities?
kevin38017
2014-03-28 21:05:41
because if we have a good subset of size 6,7,8,9 then we must have one of 1,2,3,4
because if we have a good subset of size 6,7,8,9 then we must have one of 1,2,3,4
DPatrick
2014-03-28 21:05:50
Right. There are no good subsets of size 6, 7, 8, or 9 either! Because if some of the adults form a good subset, then all the rest of the adults form a good subset too. (Continuing our example above, if {1,3,8} is good, then we know that {2,4,5,6,7,9,10} must have all their shoes paired among themselves as well, so it's a good subset too.)
Right. There are no good subsets of size 6, 7, 8, or 9 either! Because if some of the adults form a good subset, then all the rest of the adults form a good subset too. (Continuing our example above, if {1,3,8} is good, then we know that {2,4,5,6,7,9,10} must have all their shoes paired among themselves as well, so it's a good subset too.)
DPatrick
2014-03-28 21:06:32
So either there's a 5-person good subset, in which case the 10 people break up into two 5-person good subsets, or there isn't, in which case there are no proper good subsets other than the entire group of 10 people.
So either there's a 5-person good subset, in which case the 10 people break up into two 5-person good subsets, or there isn't, in which case there are no proper good subsets other than the entire group of 10 people.
DPatrick
2014-03-28 21:06:45
So let's count the possible pairings in these two cases.
So let's count the possible pairings in these two cases.
DPatrick
2014-03-28 21:06:56
How many pairings have a 5-person good subset? How can we construct one?
How many pairings have a 5-person good subset? How can we construct one?
tluo5458
2014-03-28 21:07:13
10c5
10c5
bestwillcui1
2014-03-28 21:07:13
Choose five people from 10
Choose five people from 10
DPatrick
2014-03-28 21:07:20
First, we have to choose 5 people to be our good subset. There are (105) ways to do this.
First, we have to choose 5 people to be our good subset. There are (105) ways to do this.
DPatrick
2014-03-28 21:07:28
Then how many ways can the child arrange the shoes?
Then how many ways can the child arrange the shoes?
DPatrick
2014-03-28 21:07:49
Let's think about how the child can construct a 5-person good pairing that doesn't have any 1,2,3,4-good subset.
Let's think about how the child can construct a 5-person good pairing that doesn't have any 1,2,3,4-good subset.
DPatrick
2014-03-28 21:07:58
She has 4 choices for which right to pair with the first left -- she can't pick the matching shoe.
She has 4 choices for which right to pair with the first left -- she can't pick the matching shoe.
DPatrick
2014-03-28 21:08:08
Then what should she do next?
Then what should she do next?
bestwillcui1
2014-03-28 21:08:29
Pick one of the other 4 shoes
Pick one of the other 4 shoes
kevin38017
2014-03-28 21:08:36
figure out how many choices the person whose right shoe she has's left shoe can be paired
figure out how many choices the person whose right shoe she has's left shoe can be paired
DPatrick
2014-03-28 21:08:48
Right: she tries to pair the left shoe that corresponds to the right shoe that she just picked. (For example, if she started by pairing L1 with R3, then she next tries to pair L3.)
Right: she tries to pair the left shoe that corresponds to the right shoe that she just picked. (For example, if she started by pairing L1 with R3, then she next tries to pair L3.)
DPatrick
2014-03-28 21:09:01
She then has 3 choices for which right to pair with the next left -- she can't pick the matching right shoe from the first pair, or otherwise she'd create a 2-person good subset. (For example, if the 5-person set was {1,2,3,4,5} and she paired L1 with R3, then she can't pair L3 with R1, because then {1,3} would be a 2-person good subset.)
She then has 3 choices for which right to pair with the next left -- she can't pick the matching right shoe from the first pair, or otherwise she'd create a 2-person good subset. (For example, if the 5-person set was {1,2,3,4,5} and she paired L1 with R3, then she can't pair L3 with R1, because then {1,3} would be a 2-person good subset.)
DPatrick
2014-03-28 21:09:26
Similarly, at each step she can choose any shoe except for the right shoe corresponding to the first left shoe -- because otherwise she'd make a smaller good set.
Similarly, at each step she can choose any shoe except for the right shoe corresponding to the first left shoe -- because otherwise she'd make a smaller good set.
DPatrick
2014-03-28 21:09:40
So she has 4⋅3⋅2⋅1⋅1=4! choices for pairing the shoes within the 5-person good subset.
So she has 4⋅3⋅2⋅1⋅1=4! choices for pairing the shoes within the 5-person good subset.
DPatrick
2014-03-28 21:10:05
Another way to think about it: imagine the 5 people sitting around a table, and each hands their right shoe to the person on their right. This creates a 5-good pairing of shoes.
Another way to think about it: imagine the 5 people sitting around a table, and each hands their right shoe to the person on their right. This creates a 5-good pairing of shoes.
DPatrick
2014-03-28 21:10:21
...and there are 4! ways to seat 5 people around a round table.
...and there are 4! ways to seat 5 people around a round table.
bestwillcui1
2014-03-28 21:10:30
the other five also have to have a 5-person good subset though
the other five also have to have a 5-person good subset though
DPatrick
2014-03-28 21:10:41
Right: the other 5 people also make a good subset, so there are 4! choices for pairing the shoes within that subset.
Right: the other 5 people also make a good subset, so there are 4! choices for pairing the shoes within that subset.
Doink
2014-03-28 21:10:57
Do we need to divide C(10, 5) by 2 because the order we chose the subsets does not matter?
Do we need to divide C(10, 5) by 2 because the order we chose the subsets does not matter?
Allan Z
2014-03-28 21:10:57
but wait, picking ABCDE is same as picking FGHIJ in 10C5, we overcounted by a multiple of 2
but wait, picking ABCDE is same as picking FGHIJ in 10C5, we overcounted by a multiple of 2
DPatrick
2014-03-28 21:11:16
You're right! We've double-counted!
You're right! We've double-counted!
DPatrick
2014-03-28 21:11:25
For example, we counted {1,2,3,4,5} as one of our (105) good subsets. But that leaves {6,7,8,9,10} as a good subset, which we also counted as one of our (105) good subsets.
For example, we counted {1,2,3,4,5} as one of our (105) good subsets. But that leaves {6,7,8,9,10} as a good subset, which we also counted as one of our (105) good subsets.
DPatrick
2014-03-28 21:11:37
So we have to divide by 2.
So we have to divide by 2.
DPatrick
2014-03-28 21:11:49
Therefore, collecting all our counts, there are 12(105)(4!)2 arrangements with two 5-person good subsets.
Therefore, collecting all our counts, there are 12(105)(4!)2 arrangements with two 5-person good subsets.
DPatrick
2014-03-28 21:12:13
And the other case: how many pairings with no proper good subsets at all?
And the other case: how many pairings with no proper good subsets at all?
math-rules
2014-03-28 21:12:32
9!?
9!?
TheStrangeCharm
2014-03-28 21:12:32
9!
9!
brzhang97
2014-03-28 21:12:32
9!
9!
bestwillcui1
2014-03-28 21:12:32
Same logic gives 9!
Same logic gives 9!
eswa2000
2014-03-28 21:12:32
9!
9!
XxAndreixX
2014-03-28 21:12:38
9!
9!
kevin38017
2014-03-28 21:12:38
9!
9!
morninglight
2014-03-28 21:12:38
9!
9!
QuantumandMath
2014-03-28 21:12:38
9!
9!
twin77
2014-03-28 21:12:38
9!
9!
DPatrick
2014-03-28 21:12:46
Right. We can count them just like we counted the arrangements of the 5-person good subsets.
Right. We can count them just like we counted the arrangements of the 5-person good subsets.
DPatrick
2014-03-28 21:12:52
The child can pair L1 with any of R2,...,R10, for 9 choices.
The child can pair L1 with any of R2,...,R10, for 9 choices.
DPatrick
2014-03-28 21:12:58
The child can pair the next left with any of 8 remaining right shoes (she can't pick L1 until the end, otherwise she creates a smaller good subset), for 8 choices.
The child can pair the next left with any of 8 remaining right shoes (she can't pick L1 until the end, otherwise she creates a smaller good subset), for 8 choices.
DPatrick
2014-03-28 21:13:06
The child can pair the next left with any of 7 remaining right shoes.
The child can pair the next left with any of 7 remaining right shoes.
DPatrick
2014-03-28 21:13:14
And so on. At the end, she'll pair the remaining left shoe with R1. So there are 9! pairings in this case.
And so on. At the end, she'll pair the remaining left shoe with R1. So there are 9! pairings in this case.
math-rules
2014-03-28 21:13:28
or just pass your right shoe around the table
or just pass your right shoe around the table
eswa2000
2014-03-28 21:13:28
or do the table sitting argument
or do the table sitting argument
DPatrick
2014-03-28 21:13:41
Right: the same analogy shows that there are 9! pairings.
Right: the same analogy shows that there are 9! pairings.
DPatrick
2014-03-28 21:13:48
Combining our two cases and dividing by the total number of pairings, we get that the probability is
12(105)(4!)2+9!10!.
Combining our two cases and dividing by the total number of pairings, we get that the probability is
12(105)(4!)2+9!10!.
DPatrick
2014-03-28 21:14:05
How do we efficiently simplify this?
How do we efficiently simplify this?
Bomist0
2014-03-28 21:14:21
divide into two parts
divide into two parts
kevin38017
2014-03-28 21:14:21
split the fraction
split the fraction
hjl00
2014-03-28 21:14:29
separate the 9! term
separate the 9! term
TheStrangeCharm
2014-03-28 21:14:29
break into two parts
break into two parts
DPatrick
2014-03-28 21:14:45
We could do that, since 9!10!=110 is easy.
We could do that, since 9!10!=110 is easy.
DPatrick
2014-03-28 21:15:19
That leaves 12(105)(4!)210!. How do we simplify this?
That leaves 12(105)(4!)210!. How do we simplify this?
Bomist0
2014-03-28 21:15:33
use definition of 10C5 = 10!/5!/5!
use definition of 10C5 = 10!/5!/5!
DPatrick
2014-03-28 21:15:48
The first step is to write out the binomial coefficient in terms of factorials:
10!4!4!2⋅5!5!10!.
The first step is to write out the binomial coefficient in terms of factorials:
10!4!4!2⋅5!5!10!.
antler
2014-03-28 21:16:08
cut off the five using the (4!)^2
cut off the five using the (4!)^2
DaChickenInc
2014-03-28 21:16:08
cancel the 10!
cancel the 10!
Bomist0
2014-03-28 21:16:08
10! cancels
10! cancels
DPatrick
2014-03-28 21:16:26
...and now most everything cancels. 10! cancels and 4!/5!=1/5 (twice).
...and now most everything cancels. 10! cancels and 4!/5!=1/5 (twice).
mssmath
2014-03-28 21:16:39
1/50
1/50
twin77
2014-03-28 21:16:39
(4!)^2/(2*(5!)^2) gives 1/50
(4!)^2/(2*(5!)^2) gives 1/50
DivideBy0
2014-03-28 21:16:39
1/50
1/50
DPatrick
2014-03-28 21:16:46
So it's just 150.
So it's just 150.
DPatrick
2014-03-28 21:17:05
So our final answer is 150+110=650=325, so our final answer is 3+25=028.
So our final answer is 150+110=650=325, so our final answer is 3+25=028.
DPatrick
2014-03-28 21:17:25
One more geometry:
One more geometry:
DPatrick
2014-03-28 21:17:31
14. In △ABC, AB=10, ∠A=30∘, and ∠C=45∘. Let H, D, and M be points on the line ¯BC such that ¯AH⊥¯BC, ∠BAD=∠CAD, and BM=CM. Point N is the midpoint of the segment ¯HM, and point P is on ray AD such that ¯PN⊥¯BC. Then AP2=mn, where m and n are relatively prime positive integers. Find m+n.
14. In △ABC, AB=10, ∠A=30∘, and ∠C=45∘. Let H, D, and M be points on the line ¯BC such that ¯AH⊥¯BC, ∠BAD=∠CAD, and BM=CM. Point N is the midpoint of the segment ¯HM, and point P is on ray AD such that ¯PN⊥¯BC. Then AP2=mn, where m and n are relatively prime positive integers. Find m+n.
DPatrick
2014-03-28 21:17:57
This should be a little reminiscent of #11. Again we've got a triangle that splits in 30-60-90 and 45-45-90.
This should be a little reminiscent of #11. Again we've got a triangle that splits in 30-60-90 and 45-45-90.
DPatrick
2014-03-28 21:18:05

DPatrick
2014-03-28 21:18:26
Note that M is the midpoint of ¯BC and N is the midpoint of ¯HM. (This is hard to label in the diagram.)
Note that M is the midpoint of ¯BC and N is the midpoint of ¯HM. (This is hard to label in the diagram.)
DPatrick
2014-03-28 21:18:34
What else do you notice?
What else do you notice?
Allan Z
2014-03-28 21:19:01
HAD is 30-60-90
HAD is 30-60-90
XxAndreixX
2014-03-28 21:19:06
<HAP = 30 degrees
<HAP = 30 degrees
Bomist0
2014-03-28 21:19:10
parallel lines
parallel lines
ashgabat
2014-03-28 21:19:15
AHC is a 45-45-90 Triangle
AHC is a 45-45-90 Triangle
Mathgeek727
2014-03-28 21:19:15
30 60 90 triangle
30 60 90 triangle
antler
2014-03-28 21:19:15
triangle ahc is 45 45 90
triangle ahc is 45 45 90
DPatrick
2014-03-28 21:19:19
Indeed, all these are good!
Indeed, all these are good!
DPatrick
2014-03-28 21:19:29
AHC is a 45-45-90 triangle, so ∠HAB=15∘.
AHC is a 45-45-90 triangle, so ∠HAB=15∘.
DPatrick
2014-03-28 21:19:42
That means that AHD is 30-60-90.
That means that AHD is 30-60-90.
DPatrick
2014-03-28 21:19:53
But we've also got parallel lines ¯AH and ¯PN.
But we've also got parallel lines ¯AH and ¯PN.
DPatrick
2014-03-28 21:20:08
So PND is 30-60-90 too!
So PND is 30-60-90 too!
DPatrick
2014-03-28 21:20:17
How does that help?
How does that help?
DPatrick
2014-03-28 21:20:49
Remember, keep your eye on the prize -- we're trying to find AP. Can we relate it to any lengths that are easier to find?
Remember, keep your eye on the prize -- we're trying to find AP. Can we relate it to any lengths that are easier to find?
DaChickenInc
2014-03-28 21:21:05
AP:HN=2
AP:HN=2
DPatrick
2014-03-28 21:21:18
Right: we know that AD=2HD and PD=2ND.
Right: we know that AD=2HD and PD=2ND.
DPatrick
2014-03-28 21:21:52
That means that the same ratio holds for their difference too AP=AD−PD=2HD−2ND=2HN.
That means that the same ratio holds for their difference too AP=AD−PD=2HD−2ND=2HN.
Allan Z
2014-03-28 21:22:10
AP=2HN=HM
AP=2HN=HM
DPatrick
2014-03-28 21:22:20
Right, even better: since N is the midpoint of ¯HM: it means that AP=2HN=HM.
Right, even better: since N is the midpoint of ¯HM: it means that AP=2HN=HM.
DPatrick
2014-03-28 21:22:32
So we can try to find HM instead of AP. That seems a lot easier.
So we can try to find HM instead of AP. That seems a lot easier.
DPatrick
2014-03-28 21:23:00
Any ideas?
Any ideas?
eswa2000
2014-03-28 21:23:08
HM=HB+1/2BC
HM=HB+1/2BC
DPatrick
2014-03-28 21:23:21
Right, we can use point B to split it up as HM=HB+BM. And both of those are easy to find!
Right, we can use point B to split it up as HM=HB+BM. And both of those are easy to find!
DPatrick
2014-03-28 21:24:00
We chase lengths around the original triangle (using the 30-60-90 and 45-45-90 split) to find BM, basically just like we did in problem #11: AB=10, so OB=5, so BC=5√2, so BM=12BC=5√22.
We chase lengths around the original triangle (using the 30-60-90 and 45-45-90 split) to find BM, basically just like we did in problem #11: AB=10, so OB=5, so BC=5√2, so BM=12BC=5√22.
DPatrick
2014-03-28 21:24:16
(I did it quick because we did the same thing three problems ago!)
(I did it quick because we did the same thing three problems ago!)
DPatrick
2014-03-28 21:24:24
And how do we find HB?
And how do we find HB?
Allan Z
2014-03-28 21:24:39
10sin15
10sin15
kevin38017
2014-03-28 21:24:39
10sin 15 degrees
10sin 15 degrees
Bomist0
2014-03-28 21:24:39
sin15?
sin15?
DPatrick
2014-03-28 21:24:47
Sure. Using right triangle AHB, we have HB=10sin15∘.
Sure. Using right triangle AHB, we have HB=10sin15∘.
DPatrick
2014-03-28 21:25:01
You might have sin15∘ memorized. (It seems to come up a lot.) I don't, so I just compute sin(45∘−30∘) using the sine subtraction formula. (I prefer this to the half-angle formula because I don't have to take a square root.)
You might have sin15∘ memorized. (It seems to come up a lot.) I don't, so I just compute sin(45∘−30∘) using the sine subtraction formula. (I prefer this to the half-angle formula because I don't have to take a square root.)
DPatrick
2014-03-28 21:25:14
sin15∘=sin45∘cos30∘−cos45∘sin30∘=√64−√24=√6−√24.
sin15∘=sin45∘cos30∘−cos45∘sin30∘=√64−√24=√6−√24.
DPatrick
2014-03-28 21:25:29
So HB=10sin15∘=5(√6−√2)2.
So HB=10sin15∘=5(√6−√2)2.
DPatrick
2014-03-28 21:25:51
How convenient when we add!
AP=HM=HB+BM=5(√6−√2)2+5√22=5√62.
How convenient when we add!
AP=HM=HB+BM=5(√6−√2)2+5√22=5√62.
DPatrick
2014-03-28 21:26:18
And to finish, we compute (AP)2=1504=752. So our final answer is 75+2=077.
And to finish, we compute (AP)2=1504=752. So our final answer is 75+2=077.
DPatrick
2014-03-28 21:26:44
And last but not least:
And last but not least:
DPatrick
2014-03-28 21:26:50
15. For any integer k≥1, let p(k) be the smallest prime which does not divide k. Define the integer function X(k) to be the product of all primes less than p(k) if p(k)>2, and X(k)=1 if p(k)=2. Let {xn} be the sequence defined by x0=1, and xn+1X(xn)=xnp(xn) for n≥0. Find the smallest positive integer t such that xt=2090.
15. For any integer k≥1, let p(k) be the smallest prime which does not divide k. Define the integer function X(k) to be the product of all primes less than p(k) if p(k)>2, and X(k)=1 if p(k)=2. Let {xn} be the sequence defined by x0=1, and xn+1X(xn)=xnp(xn) for n≥0. Find the smallest positive integer t such that xt=2090.
DPatrick
2014-03-28 21:27:22
How can we get started?
How can we get started?
Bomist0
2014-03-28 21:27:29
patterns, patterns, patterns
patterns, patterns, patterns
Bomist0
2014-03-28 21:27:34
List a few values?
List a few values?
Allan Z
2014-03-28 21:27:34
start with small cases
start with small cases
ashgabat
2014-03-28 21:27:34
Find le pattern
Find le pattern
DPatrick
2014-03-28 21:27:42
Absent any better ideas, we can try to compute the first few terms of the sequence, and try to find a pattern.
Absent any better ideas, we can try to compute the first few terms of the sequence, and try to find a pattern.
DPatrick
2014-03-28 21:27:52
We are given that x0=1.
We are given that x0=1.
DPatrick
2014-03-28 21:27:59
Let's rearrange the equation a little so that it looks more like a "formula" for the next term:
Let's rearrange the equation a little so that it looks more like a "formula" for the next term:
DPatrick
2014-03-28 21:28:04
xn+1=xnp(xn)X(xn)for all n≥0.
xn+1=xnp(xn)X(xn)for all n≥0.
DPatrick
2014-03-28 21:28:17
What is x1?
What is x1?
lucylai
2014-03-28 21:28:44
2
2
sillyd
2014-03-28 21:28:44
2
2
math-rules
2014-03-28 21:28:44
2
2
mathwizard888
2014-03-28 21:28:44
2
2
dantx5
2014-03-28 21:28:44
2
2
DPatrick
2014-03-28 21:28:54
From the given formula, x1=x0p(x0)X(x0)=1⋅p(1)X(1)=1⋅21=2.
From the given formula, x1=x0p(x0)X(x0)=1⋅p(1)X(1)=1⋅21=2.
DPatrick
2014-03-28 21:29:31
Note: p(1) is the smallest prime not dividing 1, which is 2, and X(1)=1 by the "exception" rule when p=2.
Note: p(1) is the smallest prime not dividing 1, which is 2, and X(1)=1 by the "exception" rule when p=2.
DPatrick
2014-03-28 21:29:42
What is x2?
What is x2?
mapletree14
2014-03-28 21:29:56
3
3
lucylai
2014-03-28 21:29:56
3
3
dantx5
2014-03-28 21:29:56
3
3
bengals
2014-03-28 21:29:56
3
3
DPatrick
2014-03-28 21:30:06
By the formula we have that x2=x1p(x1)X(x1)=2⋅p(2)X(2).
By the formula we have that x2=x1p(x1)X(x1)=2⋅p(2)X(2).
DPatrick
2014-03-28 21:30:21
We find that p(2)=3 and X(2)=2 is the product of all primes less than 3.
We find that p(2)=3 and X(2)=2 is the product of all primes less than 3.
DPatrick
2014-03-28 21:30:29
Thus we have x2=2p(2)X(2)=2⋅32=3.
Thus we have x2=2p(2)X(2)=2⋅32=3.
DPatrick
2014-03-28 21:30:39
What is x3?
What is x3?
lucylai
2014-03-28 21:30:53
6=2*3
6=2*3
math-rules
2014-03-28 21:30:53
6
6
dantx5
2014-03-28 21:30:53
6
6
eswa2000
2014-03-28 21:30:53
6
6
bengals
2014-03-28 21:30:53
6
6
tluo5458
2014-03-28 21:30:53
6
6
kevin38017
2014-03-28 21:30:53
6
6
DPatrick
2014-03-28 21:30:59
We have that x3=x2p(x2)X(x2)=3p(3)X(3).
We have that x3=x2p(x2)X(x2)=3p(3)X(3).
DPatrick
2014-03-28 21:31:08
Since p(3)=2 we get X(3)=1. Therefore x3=3p(3)X(3)=3⋅21=6.
Since p(3)=2 we get X(3)=1. Therefore x3=3p(3)X(3)=3⋅21=6.
DPatrick
2014-03-28 21:31:16
Let's do a couple more, but I'll speed it up a bit...
Let's do a couple more, but I'll speed it up a bit...
DPatrick
2014-03-28 21:31:22
We have x4=x3p(x3)X(x3)=6p(6)X(6)=6⋅56=5.
We have x4=x3p(x3)X(x3)=6p(6)X(6)=6⋅56=5.
DPatrick
2014-03-28 21:31:28
And we have that x5=x4p(x4)X(x4)=5p(5)X(5)=5⋅21=10.
And we have that x5=x4p(x4)X(x4)=5p(5)X(5)=5⋅21=10.
DPatrick
2014-03-28 21:31:43
In fact, here are the first few terms of the sequence:nxn0112233645510615730879141021
In fact, here are the first few terms of the sequence:nxn0112233645510615730879141021
DPatrick
2014-03-28 21:31:49
Do you notice any patterns?
Do you notice any patterns?
lucylai
2014-03-28 21:32:10
factorize them
factorize them
dantx5
2014-03-28 21:32:10
prime factorization
prime factorization
lucylai
2014-03-28 21:32:10
factorize the x_n
factorize the x_n
ABCDE
2014-03-28 21:32:10
prime factorize
prime factorize
DPatrick
2014-03-28 21:32:17
Since we are multiplying and dividing by primes to get to the next term, we can try finding the prime factorization of each term.
Since we are multiplying and dividing by primes to get to the next term, we can try finding the prime factorization of each term.
DPatrick
2014-03-28 21:32:25
nxn01122332⋅34552⋅563⋅572⋅3⋅58792⋅7103⋅7
nxn01122332⋅34552⋅563⋅572⋅3⋅58792⋅7103⋅7
DPatrick
2014-03-28 21:32:35
Now we really see some interesting things.
Now we really see some interesting things.
ABCDE
2014-03-28 21:32:56
binary
binary
Allan Z
2014-03-28 21:32:56
binary by index of prime
binary by index of prime
bengals
2014-03-28 21:32:56
sort of like binary
sort of like binary
DPatrick
2014-03-28 21:33:14
Yes! Redrawing my chart might make this a little clearer: 7532binarynxn001∙112∙1023∙∙1136∙10045∙∙101510∙∙110615∙∙∙111730∙100087∙∙1001914∙∙10101021
Yes! Redrawing my chart might make this a little clearer: 7532binarynxn001∙112∙1023∙∙1136∙10045∙∙101510∙∙110615∙∙∙111730∙100087∙∙1001914∙∙10101021
DPatrick
2014-03-28 21:33:28
All I did was put dots in the columns corresponding to the binary representation of n, and then multiplied the primes with dots in their column to get xn.
All I did was put dots in the columns corresponding to the binary representation of n, and then multiplied the primes with dots in their column to get xn.
DPatrick
2014-03-28 21:33:43
It looks like what's happening is that we're taking the binary representation of n, and then we're multiplying the primes that correspond to digits that are 1.
It looks like what's happening is that we're taking the binary representation of n, and then we're multiplying the primes that correspond to digits that are 1.
DPatrick
2014-03-28 21:33:55
For example, 6 is 110 in binary, so we multiply the 2nd the 3rd primes to get x6=3⋅5.
For example, 6 is 110 in binary, so we multiply the 2nd the 3rd primes to get x6=3⋅5.
DPatrick
2014-03-28 21:34:15
This is just a conjecture, but the evidence is pretty strong, so on a contest like the AIME I'd be tempted to assume that it's true and use it to finish the problem. Let's do that now, and then we can go back and try to prove it.
This is just a conjecture, but the evidence is pretty strong, so on a contest like the AIME I'd be tempted to assume that it's true and use it to finish the problem. Let's do that now, and then we can go back and try to prove it.
ashgabat
2014-03-28 21:34:24
2090=2*5*11*19
2090=2*5*11*19
math-rules
2014-03-28 21:34:24
2090=2*5*11*19
2090=2*5*11*19
DPatrick
2014-03-28 21:34:37
We want t such that xt=2090=2⋅5⋅11⋅19.
We want t such that xt=2090=2⋅5⋅11⋅19.
DPatrick
2014-03-28 21:34:44
Which primes are these?
Which primes are these?
math-rules
2014-03-28 21:35:09
19,17,13,11,7,5,3,2...............10010101
19,17,13,11,7,5,3,2...............10010101
ashgabat
2014-03-28 21:35:09
So we have 10010101
So we have 10010101
kevin38017
2014-03-28 21:35:17
2 is first 5 is 3rd 11 is 5th 19 is 8th
2 is first 5 is 3rd 11 is 5th 19 is 8th
tluo5458
2014-03-28 21:35:23
first, third, fifth, eighth
first, third, fifth, eighth
Allan Z
2014-03-28 21:35:23
1,3,5,8
1,3,5,8
tluo5458
2014-03-28 21:35:23
10010101
10010101
DPatrick
2014-03-28 21:35:31
The first few primes are 2, 3, 5, 7, 11, 13, 17, 19, ...
So 2090 is the product of the 1st, 3rd, 5th, and 8th primes.
The first few primes are 2, 3, 5, 7, 11, 13, 17, 19, ...
So 2090 is the product of the 1st, 3rd, 5th, and 8th primes.
DPatrick
2014-03-28 21:35:49
So assume that our conjecture is true, we want t to be the number whose binary representation is 10010101 -- that is, it has 1's in the first, third, fifth, and eighth digits (counting from the right).
So assume that our conjecture is true, we want t to be the number whose binary representation is 10010101 -- that is, it has 1's in the first, third, fifth, and eighth digits (counting from the right).
mathwizard888
2014-03-28 21:36:00
2090=2*5*11*19, which goes to 10010101 in binary, which is 149 ans
2090=2*5*11*19, which goes to 10010101 in binary, which is 149 ans
alex31415
2014-03-28 21:36:00
128+16+4+1=149 is our answer
128+16+4+1=149 is our answer
DPatrick
2014-03-28 21:36:07
So t=128+16+4+1=149 is the answer.
So t=128+16+4+1=149 is the answer.
DPatrick
2014-03-28 21:36:21
...we think. Is the conjecture actually true?
...we think. Is the conjecture actually true?
DPatrick
2014-03-28 21:36:33
(Note: I feel like this is somewhat flawed as an AIME problem, because you can observe the conjecture based on a few computations, and you don't need to prove it to answer the problem.)
(Note: I feel like this is somewhat flawed as an AIME problem, because you can observe the conjecture based on a few computations, and you don't need to prove it to answer the problem.)
Allan Z
2014-03-28 21:37:03
prove it by induction!
prove it by induction!
math-rules
2014-03-28 21:37:03
induction???
induction???
DPatrick
2014-03-28 21:37:05
We can try prove this using induction, since the sequence {xn} is defined recursively.
We can try prove this using induction, since the sequence {xn} is defined recursively.
DPatrick
2014-03-28 21:37:15
The result holds for the base case n=0, so let's assume that it holds for some xn. That is, xn is the product of the primes that correspond to digits of 1 in the binary representation of n.
The result holds for the base case n=0, so let's assume that it holds for some xn. That is, xn is the product of the primes that correspond to digits of 1 in the binary representation of n.
DPatrick
2014-03-28 21:37:34
Then what is p(xn), the smallest prime that does not divide xn?
Then what is p(xn), the smallest prime that does not divide xn?
XxAndreixX
2014-03-28 21:37:59
The last 0 in the binary representation.
The last 0 in the binary representation.
lucylai
2014-03-28 21:38:06
the rightmost 0
the rightmost 0
DPatrick
2014-03-28 21:38:39
Yes. The smallest prime that does not divide xn is the prime corresponding to the rightmost 0 in the binary representation of n. Let's call this prime P. (Note that if n has all 1's, then we might have to go to a leading zero: for example, if n=7, then the rightmost zero is the 0 in 0111, and P=7, the fourth prime.)
Yes. The smallest prime that does not divide xn is the prime corresponding to the rightmost 0 in the binary representation of n. Let's call this prime P. (Note that if n has all 1's, then we might have to go to a leading zero: for example, if n=7, then the rightmost zero is the 0 in 0111, and P=7, the fourth prime.)
DPatrick
2014-03-28 21:38:54
What is X(xn), the product of all the primes less than p(xn)?
What is X(xn), the product of all the primes less than p(xn)?
math-rules
2014-03-28 21:39:34
all the 1s to the right of the 0
all the 1s to the right of the 0
mathwizard888
2014-03-28 21:39:42
the 1s at the end
the 1s at the end
DPatrick
2014-03-28 21:40:08
It's the product of all the primes before P. Notice that these primes all correspond to all the 1's in the binary representation of n that are to the right of the rightmost zero.
It's the product of all the primes before P. Notice that these primes all correspond to all the 1's in the binary representation of n that are to the right of the rightmost zero.
DPatrick
2014-03-28 21:40:32
So n ends with something like 011....1. The 0 is corresponds to p(xn), and the 1's all correspond to X(xn).
So n ends with something like 011....1. The 0 is corresponds to p(xn), and the 1's all correspond to X(xn).
DPatrick
2014-03-28 21:40:38
And what happens when we go from n to n+1?
And what happens when we go from n to n+1?
math-rules
2014-03-28 21:41:07
so you are basically making the rightmost 0 a 1, and all of the 1s to the right of it 0, which is how you count up in binary
so you are basically making the rightmost 0 a 1, and all of the 1s to the right of it 0, which is how you count up in binary
mathwizard888
2014-03-28 21:41:07
011....1 goes to 100....0
011....1 goes to 100....0
lucylai
2014-03-28 21:41:07
the rightmost 0 changes to a 1 and the 1's to the right of it change to 0
the rightmost 0 changes to a 1 and the 1's to the right of it change to 0
DPatrick
2014-03-28 21:41:25
Right. Our 011....1 becomes 100....0
Right. Our 011....1 becomes 100....0
DPatrick
2014-03-28 21:42:18
So all the primes that make up X(xn) get taken out when we go from xn to xn+1 (since all those 1s changed to 0s), and the new prime that corresponds to p(xn) gets multiplied in when we go from xn to xn+1 (since the rightmost 0 changed to a 1).
So all the primes that make up X(xn) get taken out when we go from xn to xn+1 (since all those 1s changed to 0s), and the new prime that corresponds to p(xn) gets multiplied in when we go from xn to xn+1 (since the rightmost 0 changed to a 1).
DPatrick
2014-03-28 21:42:54
But that's exactly what our recursive formula tells us to do! We divide by X(xn) (getting rid of those primes) and we multiply by p(xn) (adding in that new prime).
But that's exactly what our recursive formula tells us to do! We divide by X(xn) (getting rid of those primes) and we multiply by p(xn) (adding in that new prime).
DPatrick
2014-03-28 21:43:08
Hence, the prime factorization of xn+1 corresponds to the binary representation of n+1.
Hence, the prime factorization of xn+1 corresponds to the binary representation of n+1.
DPatrick
2014-03-28 21:43:19
So the result holds for n+1, and by induction, it holds for all positive integers n.
So the result holds for n+1, and by induction, it holds for all positive integers n.
DPatrick
2014-03-28 21:43:40
That's all for the AIME II Math Jam! I hope you enjoyed it. Have a nice weekend!
That's all for the AIME II Math Jam! I hope you enjoyed it. Have a nice weekend!
Copyright © 2025 AoPS Incorporated. This page is copyrighted material. You can view and print this page for your own use, but you cannot share the contents of this file with others.









