Difference between revisions of "Talk:2021 USAMO Problems/Problem 1"
m (Formatting snafu) |
(Add Geogebra graph) |
||
| Line 10: | Line 10: | ||
Finally, since <math>A'</math> is on <math>AA_2</math> and <math>C'</math> is on <math>CC_2</math>, that gives <math>\angle A_2AC' = \angle A_2CC_1</math> - meaning <math>C'</math> is on the line <math>AC_1</math>. But <math>C'</math> is also on the line <math>CC_1</math> - so <math>C'=C1</math>. Similarly, <math>A'=A_2</math>. So the three diagonals <math>A_1C_2, B_1A_2, C_1B_2</math> intersect in <math>O</math>. | Finally, since <math>A'</math> is on <math>AA_2</math> and <math>C'</math> is on <math>CC_2</math>, that gives <math>\angle A_2AC' = \angle A_2CC_1</math> - meaning <math>C'</math> is on the line <math>AC_1</math>. But <math>C'</math> is also on the line <math>CC_1</math> - so <math>C'=C1</math>. Similarly, <math>A'=A_2</math>. So the three diagonals <math>A_1C_2, B_1A_2, C_1B_2</math> intersect in <math>O</math>. | ||
| + | |||
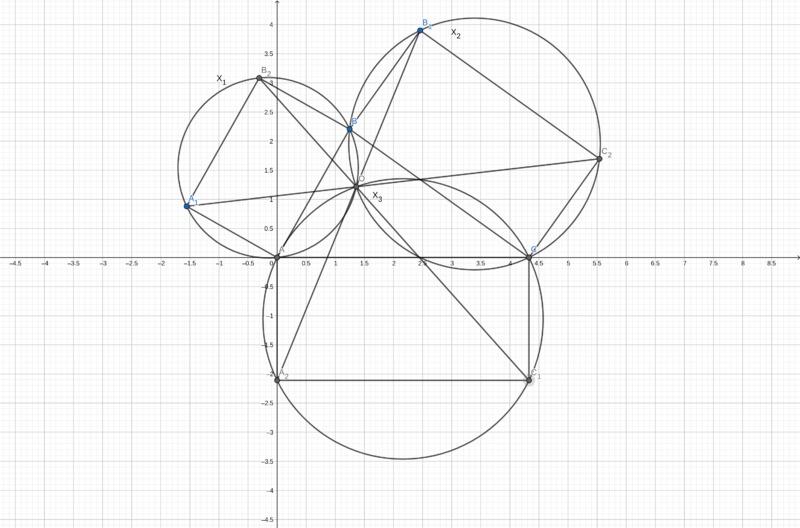
| + | [[File:USAMO_Q1.png|alt="USAMO Q1 graph"|800px|USAMO 2021 Q1 set-up]] | ||
Revision as of 15:09, 11 September 2021
We are given the acute triangle ![]() , rectangles
, rectangles ![]() such that
such that ![]() . Let's call
. Let's call ![]() .
.
Construct circumcircles ![]() around the rectangles
around the rectangles ![]() respectively.
respectively. ![]() intersect at two points:
intersect at two points: ![]() and a second point we will label
and a second point we will label ![]() . Now
. Now ![]() is a diameter of
is a diameter of ![]() , and
, and ![]() is a diameter of
is a diameter of ![]() , so
, so ![]() , and
, and ![]() , so
, so ![]() is on the diagonal
is on the diagonal ![]() .
.
![]() (angles standing on the same arc of the circle
(angles standing on the same arc of the circle ![]() ), and similarly,
), and similarly, ![]() . Therefore,
. Therefore, ![]() .
.
Construct another circumcircle ![]() around the triangle
around the triangle ![]() , which intersects
, which intersects ![]() in
in ![]() , and
, and ![]() in
in ![]() . We will prove that
. We will prove that ![]() . Note that
. Note that ![]() is a cyclic quadrilateral in
is a cyclic quadrilateral in ![]() , so since
, so since ![]() ,
, ![]() is a diameter of
is a diameter of ![]() and
and ![]() - so
- so ![]() is a rectangle.
is a rectangle.
Since ![]() ,
, ![]() is a diameter of
is a diameter of ![]() , and
, and ![]() . Similarly,
. Similarly, ![]() , so O is on
, so O is on ![]() , and by opposite angles,
, and by opposite angles, ![]() .
.
Finally, since ![]() is on
is on ![]() and
and ![]() is on
is on ![]() , that gives
, that gives ![]() - meaning
- meaning ![]() is on the line
is on the line ![]() . But
. But ![]() is also on the line
is also on the line ![]() - so
- so ![]() . Similarly,
. Similarly, ![]() . So the three diagonals
. So the three diagonals ![]() intersect in
intersect in ![]() .
.