Difference between revisions of "2007 AIME I Problems/Problem 15"
(→Solution 2) |
(→Solution 2) |
||
| Line 30: | Line 30: | ||
Now we have two equations with <math>m</math>, and <math>x</math> values for both equations must be the same, so we can solve for <math>x</math> in two equations. | Now we have two equations with <math>m</math>, and <math>x</math> values for both equations must be the same, so we can solve for <math>x</math> in two equations. | ||
<math>x=\frac{2m+1 \pm \sqrt{4m^2+4m+1-16m+336}}{4}; x=\frac{4+2m \pm \sqrt{4m^2+16m-144}}{4}</math>, then we can just use positive sign to solve, simplifies to <math>3+\sqrt{4m^2+16m-144}=\sqrt{4m^2-12m+337}</math>, getting <math>m=\frac{211-3\sqrt{989}}{10}</math>, since the triangle is equilateral, <math>AB=BC=2+m=\frac{251-3\sqrt{989}}{10}</math>, and the desired answer is <math>\boxed{989}</math> | <math>x=\frac{2m+1 \pm \sqrt{4m^2+4m+1-16m+336}}{4}; x=\frac{4+2m \pm \sqrt{4m^2+16m-144}}{4}</math>, then we can just use positive sign to solve, simplifies to <math>3+\sqrt{4m^2+16m-144}=\sqrt{4m^2-12m+337}</math>, getting <math>m=\frac{211-3\sqrt{989}}{10}</math>, since the triangle is equilateral, <math>AB=BC=2+m=\frac{251-3\sqrt{989}}{10}</math>, and the desired answer is <math>\boxed{989}</math> | ||
| + | |||
| + | ~bluesoul | ||
== See also == | == See also == | ||
Revision as of 01:03, 1 February 2022
Contents
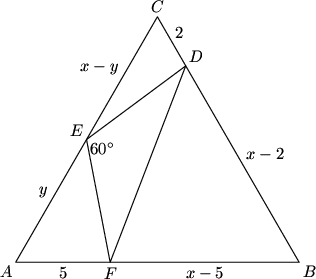
[hide]Problem
Let ![]() be an equilateral triangle, and let
be an equilateral triangle, and let ![]() and
and ![]() be points on sides
be points on sides ![]() and
and ![]() , respectively, with
, respectively, with ![]() and
and ![]() . Point
. Point ![]() lies on side
lies on side ![]() such that angle
such that angle ![]() . The area of triangle
. The area of triangle ![]() is
is ![]() . The two possible values of the length of side
. The two possible values of the length of side ![]() are
are ![]() , where
, where ![]() and
and ![]() are rational, and
are rational, and ![]() is an integer not divisible by the square of a prime. Find
is an integer not divisible by the square of a prime. Find ![]() .
.
Solution
Denote the length of a side of the triangle ![]() , and of
, and of ![]() as
as ![]() . The area of the entire equilateral triangle is
. The area of the entire equilateral triangle is ![]() . Add up the areas of the triangles using the
. Add up the areas of the triangles using the ![]() formula (notice that for the three outside triangles,
formula (notice that for the three outside triangles, ![]() ):
): ![]() . This simplifies to
. This simplifies to ![]() . Some terms will cancel out, leaving
. Some terms will cancel out, leaving ![]() .
.
![]() is an exterior angle to
is an exterior angle to ![]() , from which we find that
, from which we find that ![]() , so
, so ![]() . Similarly, we find that
. Similarly, we find that ![]() . Thus,
. Thus, ![]() . Setting up a ratio of sides, we get that
. Setting up a ratio of sides, we get that ![]() . Using the previous relationship between
. Using the previous relationship between ![]() and
and ![]() , we can solve for
, we can solve for ![]() .
.
![]()
![]()
![]()
![]()
Use the quadratic formula, though we only need the root of the discriminant. This is ![]()
![]() . The answer is
. The answer is ![]() .
.
Solution 2
First of all, assume ![]() , then we can find
, then we can find ![]() It is not hard to find
It is not hard to find ![]() , we apply LOC on
, we apply LOC on ![]() , getting that
, getting that ![]() , leads to
, leads to ![]() Apply LOC on
Apply LOC on ![]() separately, getting
separately, getting ![]() Add those terms together and use the inequality
Add those terms together and use the inequality ![]() , we can find:
, we can find:
![]()
According to basic angle chasing, ![]() , so
, so ![]() , the ratio makes
, the ratio makes ![]() , getting that
, getting that ![]() Now we have two equations with
Now we have two equations with ![]() , and
, and ![]() values for both equations must be the same, so we can solve for
values for both equations must be the same, so we can solve for ![]() in two equations.
in two equations.
![]() , then we can just use positive sign to solve, simplifies to
, then we can just use positive sign to solve, simplifies to ![]() , getting
, getting ![]() , since the triangle is equilateral,
, since the triangle is equilateral, ![]() , and the desired answer is
, and the desired answer is ![]()
~bluesoul
See also
| 2007 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.