Difference between revisions of "2014 AMC 10A Problems/Problem 22"
Isabelchen (talk | contribs) m |
Erics son07 (talk | contribs) (→Solution 7 (Pure Euclidian Geometry)) |
||
| Line 99: | Line 99: | ||
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen] | ~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen] | ||
| + | |||
| + | ==Solution 8 (Trigonometry)== | ||
| + | All trigonometric functions in this solution are in degrees. We know <cmath>\sin\left(a+b\right)=\sin\left(a\right)\cos\left(b\right)+\sin\left(b\right)\cos\left(a\right)</cmath> so <cmath>\sin\left(15\right)=\sin\left(45-30\right)=\sin\left(45\right)\cos\left(-30\right)+\sin\left(-30\right)\cos\left(45\right)</cmath> | ||
| + | <cmath>=\frac{\sqrt{2}}{2}\cdot\left(-\frac{\sqrt{3}}{2}\right)+\frac{1}{2}\cdot\frac{\sqrt{2}}{2}=\frac{-\sqrt{6}}{4}+\frac{\sqrt{2}}{4}=\frac{\sqrt{2}-\sqrt{6}}{4}</cmath> | ||
| + | <cmath>=\frac{\sqrt{2}-\sqrt{6}}{4}</cmath> | ||
| + | Let <math>EC=x</math>, then <math>BE=\sqrt{x^{2}+100}</math>. By the definition of sine, | ||
| + | <cmath>\frac{x}{\sqrt{x^{2}+100}}=\frac{\sqrt{2}-\sqrt{6}}{4}</cmath> | ||
| + | Squaring both sides, | ||
| + | <cmath>\frac{x^{2}}{x^{2}+100}=\frac{\left(\sqrt{2}-\sqrt{6}\right)^{2}}{16}=\frac{2-2\sqrt{12}+6}{16}=\frac{8-4\sqrt{3}}{16}=\frac{2-\sqrt{3}}{4}</cmath> | ||
| + | Cross-multiplying, | ||
| + | <cmath>4x^{2}=\left(2-\sqrt{3}\right)\left(x^{2}+100\right)=2x^{2}+200-\sqrt{3}x^{2}-100\sqrt{3}</cmath> | ||
| + | Simplifying, | ||
| + | <cmath>\left(2+\sqrt{3}\right)x^{2}=200-100\sqrt{3}</cmath> | ||
| + | <cmath>x^{2}=\frac{200-100\sqrt{3}}{2+\sqrt{3}}=\frac{100\left(2-\sqrt{3}\right)}{2+\sqrt{3}}=100\cdot\frac{2-\sqrt{3}}{2+\sqrt{3}}</cmath> | ||
| + | Let <math>\frac{2-\sqrt{3}}{2+\sqrt{3}}=x</math>. Notice that <math>\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)=2^{2}-\sqrt{3}^{2}=1</math> so <math>2-\sqrt{3}=\frac{1}{2+\sqrt{3}}</math>. <math>x</math> is then <cmath>\frac{2-\sqrt{3}}{2+\sqrt{3}}=\frac{\frac{1}{2+\sqrt{3}}}{2+\sqrt{3}}=\frac{1}{\left(2+\sqrt{3}\right)^{2}}</cmath> | ||
| + | Recall that | ||
| + | <cmath>x^{2}=100\cdot\frac{2-\sqrt{3}}{2+\sqrt{3}}</cmath> which we now know is <cmath>100\cdot\frac{1}{\left(2+\sqrt{3}\right)^{2}}=\frac{100}{\left(2+\sqrt{3}\right)^{2}}=\left(\frac{10}{2+\sqrt{3}}\right)^{2} | ||
| + | Therefore </cmath>x=\frac{10}{2+\sqrt{3}}<cmath> | ||
| + | Rationalizing the denominator, | ||
| + | </cmath>\frac{10}{2+\sqrt{3}}\cdot\frac{2-\sqrt{3}}{2-\sqrt{3}}=\frac{20-10\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}<cmath> | ||
| + | Which by difference of squares reduces to | ||
| + | </cmath>20-10\sqrt{3}<math></math> | ||
| + | so <math>EC=20-10\sqrt{3}</math>. <math>ED</math> is then <math>20-\left(20-10\sqrt{3}\right)=10\sqrt{3}</math> and since we know <math>AD=10</math>, by the Pythagorean theorem, <math>AE = 20</math>. The answer is <math>\boxed{\textbf{(E)}~20}</math> | ||
| + | |||
| + | An alternate way to finish: since we know the lengths of <math>AD</math> and <math>DE</math>, we can figure out that <math>m\angle AED=30^{\circ}</math> and therefore <math>m\angle BEA=75^{\circ}</math>. Hence <math>\triangle ABE</math> is isosceles and <math>AE=AB=\boxed{\textbf{(E)}~20}</math>. | ||
| + | |||
| + | ~JH. L | ||
== Video Solution by Richard Rusczyk == | == Video Solution by Richard Rusczyk == | ||
Revision as of 02:00, 20 June 2022
Contents
[hide]- 1 Problem
- 2 Solution 1 (Trigonometry)
- 3 Solution 2 (No Trigonometry)
- 4 Solution 3 Quick Construction (No Trigonometry)
- 5 Solution 4 (No Trigonometry)
- 6 Solution 5
- 7 Solution 6 (Pure Euclidian Geometry)
- 8 Solution 7 (Pure Euclidian Geometry)
- 9 Solution 8 (Trigonometry)
- 10 Video Solution by Richard Rusczyk
- 11 See Also
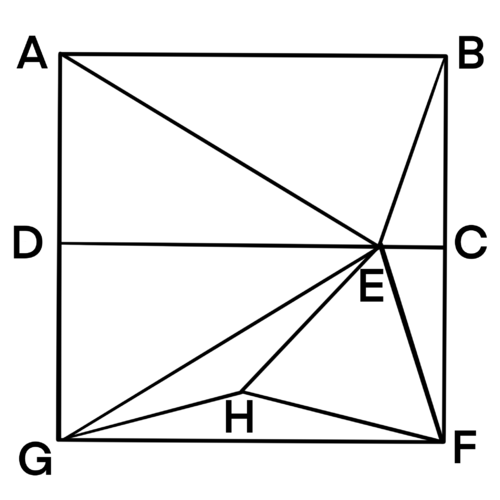
Problem
In rectangle ![]() ,
, ![]() and
and ![]() . Let
. Let ![]() be a point on
be a point on ![]() such that
such that ![]() . What is
. What is ![]() ?
?
![]()
Solution 1 (Trigonometry)
Note that ![]() . (It is important to memorize the sin, cos, and tan values of
. (It is important to memorize the sin, cos, and tan values of ![]() and
and ![]() .) Therefore, we have
.) Therefore, we have ![]() . Since
. Since ![]() is a
is a ![]() triangle,
triangle, ![]()
Solution 2 (No Trigonometry)
Let ![]() be a point on line
be a point on line ![]() such that points
such that points ![]() and
and ![]() are distinct and that
are distinct and that ![]() . By the angle bisector theorem,
. By the angle bisector theorem, ![]() . Since
. Since ![]() is a
is a ![]() right triangle,
right triangle, ![]() and
and ![]() . Additionally,
. Additionally, ![]() Now, substituting in the obtained values, we get
Now, substituting in the obtained values, we get  and
and ![]() . Substituting the first equation into the second yields
. Substituting the first equation into the second yields ![]() , so
, so ![]() . Because
. Because ![]() is a
is a ![]() triangle,
triangle, ![]() .
.
~edited by ripkobe_745
Solution 3 Quick Construction (No Trigonometry)
Reflect ![]() over line segment
over line segment ![]() . Let the point
. Let the point ![]() be the point where the right angle is of our newly reflected triangle. By subtracting
be the point where the right angle is of our newly reflected triangle. By subtracting ![]() to find
to find ![]() , we see that
, we see that ![]() is a
is a ![]() right triangle. By using complementary angles once more, we can see that
right triangle. By using complementary angles once more, we can see that ![]() is a
is a ![]() angle, and we've found that
angle, and we've found that ![]() is a
is a ![]() right triangle. From here, we can use the
right triangle. From here, we can use the ![]() properties of a
properties of a ![]() right triangle to see that
right triangle to see that ![]()
Solution 4 (No Trigonometry)
Let ![]() be a point on
be a point on ![]() such that
such that ![]() . Then
. Then ![]() Since
Since ![]() ,
, ![]() is isosceles.
is isosceles.
Let ![]() . Since
. Since ![]() is
is ![]() , we have
, we have ![]()
Since ![]() is isosceles, we have
is isosceles, we have ![]() . Since
. Since ![]() , we have
, we have ![]() Thus
Thus ![]() and
and ![]() .
.
Finally, by the Pythagorean Theorem, we have ![]()
~ Solution by Nafer
~ Edited by TheBeast5520
Note from williamgolly: When you find DE, note how ADE is congruent to a 30-60-90 triangle and you can easily find AE from there
Solution 5
First, divide all side lengths by ![]() to make things easier. We’ll multiply our answer by
to make things easier. We’ll multiply our answer by ![]() at the end.
Call side length
at the end.
Call side length ![]()
![]() . Using the Pythagorean Theorem, we can get side
. Using the Pythagorean Theorem, we can get side ![]() is
is ![]() .
.
The double angle identity for sine states that: ![]() So,
So, ![]() We know
We know ![]() . In triangle
. In triangle ![]() ,
, ![]() and
and ![]() . Substituting these in, we get our equation:
. Substituting these in, we get our equation: ![]() which simplifies to
which simplifies to ![]()
Now, using the quadratic formula to solve for ![]() .
. ![]() Because the length
Because the length ![]() must be close to one, the value of
must be close to one, the value of ![]() will be
will be ![]() .
We can now find
.
We can now find ![]() =
= ![]() and use it to find
and use it to find ![]() .
. ![]() .
To find
.
To find ![]() , we can use the Pythagorean Theorem with sides
, we can use the Pythagorean Theorem with sides ![]() and
and ![]() , OR we can notice that, based on the two side lengths we know,
, OR we can notice that, based on the two side lengths we know, ![]() is a
is a ![]() triangle. So
triangle. So ![]() .
.
Finally, we must multiply our answer by ![]() ,
, ![]() .
. ![]() .
.
~AWCHEN01
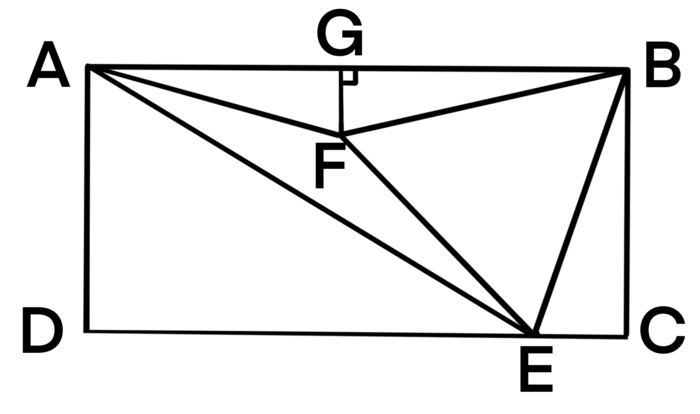
Solution 6 (Pure Euclidian Geometry)
We are going to use pure Euclidian geometry to prove ![]() .
.
Reflect rectangle ![]() along line
along line ![]() . Let the square be
. Let the square be ![]() as shown. Construct equilateral triangle
as shown. Construct equilateral triangle ![]() .
.
Because ![]() ,
, ![]() , and
, and ![]() ,
, ![]() by
by ![]() .
.
So, ![]() ,
, ![]() .
.
Because ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() by
by ![]() .
.
So, ![]() . By the reflection,
. By the reflection, ![]() .
. ![]()
This solution is inspired by AoPS "Introduction to Geometry" page 226 problem 8.22, and page 433 problem 16.42.
Solution 7 (Pure Euclidian Geometry)
We are going to use pure Euclidian geometry to prove ![]() .
.
Construct equilateral triangle ![]() , and let
, and let ![]() be the height of
be the height of ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() by
by ![]() .
.
![]() ,
, ![]() ,
, ![]() , by
, by ![]()
![]() .
.
So, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() by
by ![]() .
.
So, ![]()
Solution 8 (Trigonometry)
All trigonometric functions in this solution are in degrees. We know ![]() so
so ![]()
![\[=\frac{\sqrt{2}}{2}\cdot\left(-\frac{\sqrt{3}}{2}\right)+\frac{1}{2}\cdot\frac{\sqrt{2}}{2}=\frac{-\sqrt{6}}{4}+\frac{\sqrt{2}}{4}=\frac{\sqrt{2}-\sqrt{6}}{4}\]](http://latex.artofproblemsolving.com/6/d/d/6dd4ed713c1c2e26e3cd180a0cfc11c2ff411c81.png)
![]() Let
Let ![]() , then
, then ![]() . By the definition of sine,
. By the definition of sine,
![]() Squaring both sides,
Squaring both sides,
![\[\frac{x^{2}}{x^{2}+100}=\frac{\left(\sqrt{2}-\sqrt{6}\right)^{2}}{16}=\frac{2-2\sqrt{12}+6}{16}=\frac{8-4\sqrt{3}}{16}=\frac{2-\sqrt{3}}{4}\]](http://latex.artofproblemsolving.com/a/4/b/a4bce7a0ac3bbaa7c9bb9e5bf9c2d8a264a3c8a6.png) Cross-multiplying,
Cross-multiplying,
![]() Simplifying,
Simplifying,
![]()
![\[x^{2}=\frac{200-100\sqrt{3}}{2+\sqrt{3}}=\frac{100\left(2-\sqrt{3}\right)}{2+\sqrt{3}}=100\cdot\frac{2-\sqrt{3}}{2+\sqrt{3}}\]](http://latex.artofproblemsolving.com/f/2/a/f2ad342cb3bbeff8bc9b8cca8436f83e2fd935cd.png) Let
Let ![]() . Notice that
. Notice that ![]() so
so ![]() .
. ![]() is then
is then ![\[\frac{2-\sqrt{3}}{2+\sqrt{3}}=\frac{\frac{1}{2+\sqrt{3}}}{2+\sqrt{3}}=\frac{1}{\left(2+\sqrt{3}\right)^{2}}\]](http://latex.artofproblemsolving.com/b/0/2/b02415e89db9bc008dce6d58979ea6cb0e3dbd8a.png) Recall that
Recall that
![]() which we now know is
which we now know is ![\[100\cdot\frac{1}{\left(2+\sqrt{3}\right)^{2}}=\frac{100}{\left(2+\sqrt{3}\right)^{2}}=\left(\frac{10}{2+\sqrt{3}}\right)^{2} Therefore\]](http://latex.artofproblemsolving.com/f/f/5/ff51dbe34c01cadc3123139b128efa150bc1243e.png) x=\frac{10}{2+\sqrt{3}}
x=\frac{10}{2+\sqrt{3}}![]() \frac{10}{2+\sqrt{3}}\cdot\frac{2-\sqrt{3}}{2-\sqrt{3}}=\frac{20-10\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}
\frac{10}{2+\sqrt{3}}\cdot\frac{2-\sqrt{3}}{2-\sqrt{3}}=\frac{20-10\sqrt{3}}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}![]() 20-10\sqrt{3}$$ (Error compiling LaTeX. Unknown error_msg)
so
20-10\sqrt{3}$$ (Error compiling LaTeX. Unknown error_msg)
so ![]() .
. ![]() is then
is then ![]() and since we know
and since we know ![]() , by the Pythagorean theorem,
, by the Pythagorean theorem, ![]() . The answer is
. The answer is ![]()
An alternate way to finish: since we know the lengths of ![]() and
and ![]() , we can figure out that
, we can figure out that ![]() and therefore
and therefore ![]() . Hence
. Hence ![]() is isosceles and
is isosceles and ![]() .
.
~JH. L
Video Solution by Richard Rusczyk
https://www.youtube.com/watch?v=-GBvCLSfTuo
See Also
| 2014 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()