Difference between revisions of "2023 AMC 8 Problems/Problem 7"
(→Solution 2) |
MRENTHUSIASM (talk | contribs) m (→Solution 2) |
||
| Line 23: | Line 23: | ||
and | and | ||
<cmath> | <cmath> | ||
| − | Therefore, we can determine that the expression for line <math> AB </math> is <math> y=\frac{1}{3}x </math>. and the expression for line <math> CD </math> is <math> y=-\frac{1}{2}x + 10 </math>. When <math> x=15 </math>, the coordinates that line <math> AB </math> and line <math> CD </math> pass through are <math> (15, 5) </math> and <math> (15, \frac{5}{2}) </math>, and <math> (15, 5) </math> lies perfectly on one vertex of the rectangle while the <math> y </math> coordinate of <math> (15, \frac{5}{2}) </math> is out of the range <math> 3 \leq y \leq 5 </math> (lower than the bottom left corner of the rectangle <math> (15, 3) </math>). Considering that the <math> y </math> value of the line <math> CD </math> will only decrease, and the <math> y </math> value of the line <math> AB </math> will only increase, there will not be another point on the rectangle that lies on either of the two lines. Thus, we can conclude that the answer is <math>\boxed{\textbf{(B)}\ 1}</math> | + | Therefore, we can determine that the expression for line <math> AB </math> is <math> y=\frac{1}{3}x </math>. and the expression for line <math> CD </math> is <math> y=-\frac{1}{2}x + 10 </math>. When <math> x=15 </math>, the coordinates that line <math> AB </math> and line <math> CD </math> pass through are <math> (15, 5) </math> and <math> \left(15, \frac{5}{2}\right) </math>, and <math> (15, 5) </math> lies perfectly on one vertex of the rectangle while the <math> y </math> coordinate of <math> \left(15, \frac{5}{2}\right) </math> is out of the range <math> 3 \leq y \leq 5 </math> (lower than the bottom left corner of the rectangle <math> (15, 3) </math>). Considering that the <math> y </math> value of the line <math> CD </math> will only decrease, and the <math> y </math> value of the line <math> AB </math> will only increase, there will not be another point on the rectangle that lies on either of the two lines. Thus, we can conclude that the answer is <math>\boxed{\textbf{(B)}\ 1}</math> |
~Bloggish | ~Bloggish | ||
Revision as of 17:58, 26 January 2023
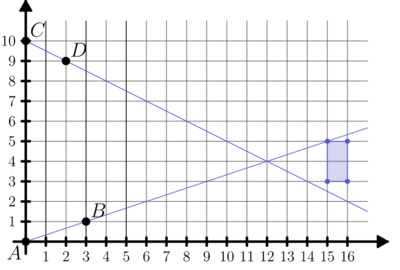
Problem
A rectangle, with sides parallel to the ![]() -axis and
-axis and ![]() -axis, has opposite vertices located at
-axis, has opposite vertices located at ![]() and
and ![]() . A line drawn through points
. A line drawn through points ![]() and
and ![]() . Another line is drawn through points
. Another line is drawn through points ![]() and
and ![]() . How many points on the rectangle lie on at least one of the two lines?
. How many points on the rectangle lie on at least one of the two lines?
![]()
Solution 1
If we extend the lines, we have
Hence, we see that the answer is ![]()
~MrThinker
Solution 2
If the analytic expression for line ![]() is
is ![]() , and the analytic expression for line
, and the analytic expression for line ![]() is
is ![]() , we have the systems of equations:
, we have the systems of equations:
![\[\begin{cases} b_{1} = 0 \\ 3k_{1} + b_{1} = 1 \end{cases}\]](http://latex.artofproblemsolving.com/6/7/1/67122988ab5c10edd133782a13298691b63c7db0.png) and
and
![\[\begin{cases} b_{2} = 10 \\ 2k_{2} + b_{2} = 9 \end{cases}\]](http://latex.artofproblemsolving.com/e/f/a/efa013783d9544a2494648b390d4c97f843fe85d.png) Solving the systems, we have:
Solving the systems, we have:
![\[\begin{cases} k_{1} = \frac{1}{3} \\ b_{1} = 0 \end{cases}\]](http://latex.artofproblemsolving.com/a/4/4/a4484711d6f7adfb727419edd7aa4ae9a8124892.png) and
and
![\[\begin{cases} k_{2} = -\frac{1}{2} \\ b_{2} = 10 \end{cases}\]](http://latex.artofproblemsolving.com/6/c/d/6cdfc7afad937ed249b1e1a939980b9db56b5d44.png) Therefore, we can determine that the expression for line
Therefore, we can determine that the expression for line ![]() is
is ![]() . and the expression for line
. and the expression for line ![]() is
is ![]() . When
. When ![]() , the coordinates that line
, the coordinates that line ![]() and line
and line ![]() pass through are
pass through are ![]() and
and ![]() , and
, and ![]() lies perfectly on one vertex of the rectangle while the
lies perfectly on one vertex of the rectangle while the ![]() coordinate of
coordinate of ![]() is out of the range
is out of the range ![]() (lower than the bottom left corner of the rectangle
(lower than the bottom left corner of the rectangle ![]() ). Considering that the
). Considering that the ![]() value of the line
value of the line ![]() will only decrease, and the
will only decrease, and the ![]() value of the line
value of the line ![]() will only increase, there will not be another point on the rectangle that lies on either of the two lines. Thus, we can conclude that the answer is
will only increase, there will not be another point on the rectangle that lies on either of the two lines. Thus, we can conclude that the answer is ![]()
~Bloggish
Video Solution by Magic Square
https://youtu.be/-N46BeEKaCQ?t=5151
See Also
| 2023 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 6 |
Followed by Problem 8 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.