Difference between revisions of "Symmetry"
(→Hidden symmetry) |
|||
| Line 2: | Line 2: | ||
==Hidden symmetry== | ==Hidden symmetry== | ||
[[File:Hidden S.png|200px|right]] | [[File:Hidden S.png|200px|right]] | ||
| + | [[File:Hidden Sy.png|200px|right]] | ||
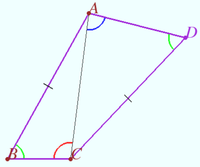
Let the convex quadrilateral <math>ABCD</math> be given. | Let the convex quadrilateral <math>ABCD</math> be given. | ||
<cmath>AC = DE, \angle CAD + \angle ACB = 180^\circ.</cmath> | <cmath>AC = DE, \angle CAD + \angle ACB = 180^\circ.</cmath> | ||
Revision as of 13:35, 28 August 2023
A proof utilizes symmetry if the steps to prove one thing is identical to those steps of another. For example, to prove that in triangle ABC with all three sides congruent to each other that all three angles are equal, you only need to prove that if ![]() then
then ![]() the other cases hold by symmetry because the steps are the same.
the other cases hold by symmetry because the steps are the same.
Hidden symmetry
Let the convex quadrilateral ![]() be given.
be given.
![]()
Prove that ![]()
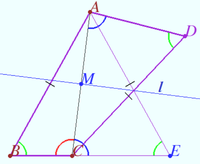
Proof
Let ![]() be bisector
be bisector ![]()
Let point ![]() be symmetric
be symmetric ![]() with respect
with respect ![]()
![]()
![]() is isosceles.
is isosceles.
Therefore ![]()