Difference between revisions of "2024 AIME II Problems/Problem 12"
(→Solution 7) |
(→Solution 7) |
||
| Line 253: | Line 253: | ||
Point <math>D = C</math> is a unique point on <math>AB</math> if the ellipse is tangent to the line <math>AB.</math> | Point <math>D = C</math> is a unique point on <math>AB</math> if the ellipse is tangent to the line <math>AB.</math> | ||
| − | In this case in point <math> | + | In this case in point <math>C</math> we get <math>\frac{dy}{dx} = \frac{dy}{d \alpha} : \frac{dx}{d \alpha} = - k \cot \alpha.</math> |
| − | The tangent of line <math>AB</math> is <math>- tan \alpha \implies k = \tan^2 \alpha.</math> | + | The tangent of the line <math>AB</math> is <math>- \tan \alpha \implies k = \tan^2 \alpha.</math> |
| + | |||
| + | For point <math>D</math> we get <math>k = \tan^2 \theta.</math> | ||
| + | |||
| + | <cmath>\tan \angle DOX = \tan \varphi = \frac {D_y}{D_x} = \frac{k \sin \theta}{k+1} : \frac{\cos \theta}{k+1} = k \cdot \tan \theta = \tan^3 \theta.</cmath> | ||
| + | |||
| + | For the line <math>AB \tan \theta = \frac {B_y}{A_x} = \sqrt{3} \implies k = 3 \implies</math> | ||
| + | <math>C = (\frac{\cos \alpha}{k+1}, \frac{k \sin \alpha}{k+1} = (\frac{1}{\sqrt{1+ \tan^2 \alpha} \cdot (k+1)}, \frac{k \tan \alpha}{\sqrt{1+ \tan^2 \alpha} \cdot (k+1)}) =</math> | ||
| + | <math> (\frac{1}{\sqrt{1+ k} \cdot (k+1)}, \frac{k \cdot k}{\sqrt{1+ k} \cdot (k+1)}) = \frac{1}{8}, \frac{3 \sqrt{3}}{8}.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
==Video Solution== | ==Video Solution== | ||
Revision as of 09:41, 1 September 2024
Contents
[hide]Problem
Let
Solution 1 (completely no calculus required)
Begin by finding the equation of the line ![]() :
: ![]() Now, consider the general equation of all lines that belong to
Now, consider the general equation of all lines that belong to ![]() . Let
. Let ![]() be located at
be located at ![]() and
and ![]() be located at
be located at ![]() . With these assumptions, we may arrive at the equation
. With these assumptions, we may arrive at the equation ![]() . However, a critical condition that must be satisfied by our parameters is that
. However, a critical condition that must be satisfied by our parameters is that ![]() , since the length of
, since the length of ![]() .
.
Here's the golden trick that resolves the problem: we wish to find some point ![]() along
along ![]() such that
such that ![]() passes through
passes through ![]() if
if ![]() . It's not hard to convince oneself of this, since the property
. It's not hard to convince oneself of this, since the property ![]() implies that if
implies that if ![]() , then
, then ![]() .
.
We should now try to relate the point ![]() to some value of
to some value of ![]() . This is accomplished by finding the intersection of two lines:
. This is accomplished by finding the intersection of two lines: ![]()
Where we have also used the fact that ![]() , which follows nicely from
, which follows nicely from ![]() .
. ![]()
Square both sides and go through some algebraic manipulations to arrive at
![]()
Note how ![]() is a solution to this polynomial, and it is logically so. If we found the set of intersections consisting of line segment
is a solution to this polynomial, and it is logically so. If we found the set of intersections consisting of line segment ![]() with an identical copy of itself, every single point on the line (all
with an identical copy of itself, every single point on the line (all ![]() values) should satisfy the equation. Thus, we can perform polynomial division to eliminate the extraneous solution
values) should satisfy the equation. Thus, we can perform polynomial division to eliminate the extraneous solution ![]() .
. ![]()
Remember our original goal. It was to find an ![]() value such that
value such that ![]() is the only valid solution. Therefore, we can actually plug in
is the only valid solution. Therefore, we can actually plug in ![]() back into the equation to look for values of
back into the equation to look for values of ![]() such that the relation is satisfied, then eliminate undesirable answers.
such that the relation is satisfied, then eliminate undesirable answers.
![]() This is easily factored, allowing us to determine that
This is easily factored, allowing us to determine that ![]() . The latter root is not our answer, since on line
. The latter root is not our answer, since on line ![]() ,
, ![]() , the horizontal line segment running from
, the horizontal line segment running from ![]() to
to ![]() covers that point. From this, we see that
covers that point. From this, we see that ![]() is the only possible candidate.
is the only possible candidate.
Going back to line ![]() , plugging in
, plugging in ![]() yields
yields ![]() . The distance from the origin is then given by
. The distance from the origin is then given by  . That number squared is
. That number squared is ![]() , so the answer is
, so the answer is ![]() .
.
~Installhelp_hex
Solution 2
![]()
Now, we want to find ![]() . By L'Hôpital's rule, we get
. By L'Hôpital's rule, we get ![]() . This means that
. This means that ![]() , so we get
, so we get ![]() .
.
~Bluesoul
Solution 3
The equation of line ![]() is
is ![]()
The position of line ![]() can be characterized by
can be characterized by ![]() , denoted as
, denoted as ![]() .
Thus, the equation of line
.
Thus, the equation of line ![]() is
is
![]()
Solving (1) and (2), the ![]() -coordinate of the intersecting point of lines
-coordinate of the intersecting point of lines ![]() and
and ![]() satisfies the following equation:
satisfies the following equation:
![]()
We denote the L.H.S. as ![]() .
.
We observe that ![]() for all
for all ![]() .
Therefore, the point
.
Therefore, the point ![]() that this problem asks us to find can be equivalently stated in the following way:
that this problem asks us to find can be equivalently stated in the following way:
We interpret Equation (1) as a parameterized equation that ![]() is a tuning parameter and
is a tuning parameter and ![]() is a variable that shall be solved and expressed in terms of
is a variable that shall be solved and expressed in terms of ![]() .
In Equation (1), there exists a unique
.
In Equation (1), there exists a unique ![]() , denoted as
, denoted as ![]() (
(![]() -coordinate of point
-coordinate of point ![]() ), such that the only solution is
), such that the only solution is ![]() . For all other
. For all other ![]() , there are more than one solutions with one solution
, there are more than one solutions with one solution ![]() and at least another solution.
and at least another solution.
Given that function ![]() is differentiable, the above condition is equivalent to the first-order-condition
is differentiable, the above condition is equivalent to the first-order-condition
![]()
Calculating derivatives in this equation, we get
![\[ - \left( \frac{\sqrt{3}}{2} - \sqrt{3} x_C \right) \frac{\cos 60^\circ}{\sin^2 60^\circ} + x_C \frac{\sin 60^\circ}{\cos^2 60^\circ} = 0. \]](http://latex.artofproblemsolving.com/4/3/a/43a5e2720c57d2a8c604b428074f9242206beb54.png)
By solving this equation, we get
![]()
Plugging this into Equation (1), we get the ![]() -coordinate of point
-coordinate of point ![]() :
:
![]()
Therefore,
Therefore, the answer is ![]() .
.
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Solution 4 (coordinate bash)
Let ![]() be a segment in
be a segment in ![]() with x-intercept
with x-intercept ![]() and y-intercept
and y-intercept ![]() . We can write
. We can write ![]() as
as
![]() lie on
lie on ![]() and no other segment in
and no other segment in ![]() . We can find
. We can find ![]() by solving
by solving
![]() and taking the limit as
and taking the limit as ![]() . Since
. Since ![]() has length
has length ![]() ,
, ![]() by the Pythagorean theorem. Solving this for
by the Pythagorean theorem. Solving this for ![]() , we get
, we get
![]() , the equation for
, the equation for ![]() becomes
becomes
![]()
In ![]() ,
, ![]() and
and ![]() . To find the x-coordinate of
. To find the x-coordinate of ![]() , we substitute these into the equation for
, we substitute these into the equation for ![]() and get
and get
![]() to get
to get
![]() We substitute
We substitute ![]() into the equation for
into the equation for ![]() to find the y-coordinate of
to find the y-coordinate of ![]() :
:
![]() The problem asks for
The problem asks for
![]() so
so ![]() .
.
Solution 5 (small perturb)
![[asy] pair O=(0,0); pair X=(1,0); pair Y=(0,1); pair A=(0.5,0); pair B=(0,sin(pi/3)); pair A1=(0.6,0); pair B1=(0,0.8); pair A2=(0.575,0.04); pair B2=(0.03,0.816); dot(O); dot(X); dot(Y); dot(A); dot(B); dot(A1); dot(B1); dot(A2); dot(B2); draw(X--O--Y); draw(A--B); draw(A1--B1); draw(A--A2); draw(B1--B2); label("$B$", B, W); label("$A$", A, S); label("$B_1$", B1, SW); label("$A_1$", A1, S); label("$B_2$", B2, E); label("$A_2$", A2, NE); label("$O$", O, SW); pair C=(0.18,0.56); label("$C$", C, E); dot(C); [/asy]](http://latex.artofproblemsolving.com/5/b/8/5b8b2170c51ddfe08233b19df590742415215e94.png)
Let's move a little bit from ![]() to
to ![]() , then
, then ![]() must move to
must move to ![]() to keep
to keep ![]() .
. ![]() intersects with
intersects with ![]() at
at ![]() . Pick points
. Pick points ![]() and
and ![]() on
on ![]() and
and ![]() such that
such that ![]() ,
, ![]() , we have
, we have ![]() . Since
. Since ![]() is very small,
is very small, ![]() ,
, ![]() , so
, so ![]() ,
, ![]() , by similarity,
, by similarity,  . So the coordinates of
. So the coordinates of ![]() is
is  .
.
so ![]() , the answer is
, the answer is ![]() .
.
Solution 6(trig identities and questionable rigidity)
Let's try to find the general form of a line that is in ![]() based on what angle it makes with the x-axis,
based on what angle it makes with the x-axis, ![]() , and
, and ![]() so its slope is
so its slope is ![]() and due to us knowing its y-intercept we know that our line has form
and due to us knowing its y-intercept we know that our line has form ![]()
Now we can analyze the system of equations made by ![]() and
and ![]() , this gives us that
, this gives us that ![]()
We can proceed to simplify our expression further:
![]()
![]()
![\[= \dfrac{2\sin{\dfrac{\theta - 60^\circ}{2}}\cos{\dfrac{\theta + 60^\circ}{2}}}{\dfrac{2\sin{\dfrac{\theta - 60^\circ}{2}}\cos{\dfrac{\theta - 60^\circ}{2}}}{\cos{\theta}\cos{60^\circ}}}\]](http://latex.artofproblemsolving.com/1/d/b/1dbb478649ada70d8d69ed54c549424536588f0d.png)
![\[= \dfrac{\sin{\dfrac{\theta - 60^\circ}{2}}}{\sin{\dfrac{\theta - 60^\circ}{2}}} \cdot \dfrac{\cos{\theta}\cos{60^\circ}\cos{\dfrac{\theta + 60^\circ}{2}}}{\cos{\dfrac{\theta - 60^\circ}{2}}}.\]](http://latex.artofproblemsolving.com/9/5/e/95ef1cb7bc18554776b76e4cfa61e3dfdd140899.png)
Seeing that there are only valid solutions when ![]() is acute(all that is allowed anyways) and when
is acute(all that is allowed anyways) and when ![]() since one of the expressions in our simplified solution will equal
since one of the expressions in our simplified solution will equal ![]() . Since there is only one intersection point for every
. Since there is only one intersection point for every ![]() and vice versa in the appropriate domain and range(we can easily prove this by contradiction), we know that the missing element of the range(the points) must correspond with the excluded value. The x-coordinate of which which can be evaluated by taking the limit of our expression as
and vice versa in the appropriate domain and range(we can easily prove this by contradiction), we know that the missing element of the range(the points) must correspond with the excluded value. The x-coordinate of which which can be evaluated by taking the limit of our expression as ![]() goes to
goes to ![]() which is
which is ![]() regardless of the direction we approach
regardless of the direction we approach ![]() from. The corresponding
from. The corresponding ![]() is
is ![]() and using the distance formula gives us
and using the distance formula gives us ![]() as our answer.
as our answer.
While this solution may seem long all of these steps come naturally.
~SailS
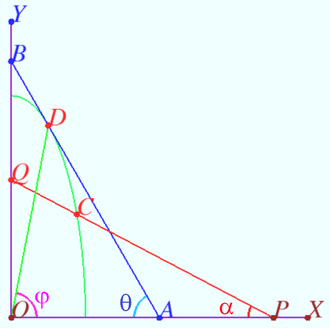
Solution 7
Denote ![]()
![]() Then
Then ![]()
Let ![]() be the point with property
be the point with property ![]()
![]()
So locus of points ![]() is the ellipse with semiaxes
is the ellipse with semiaxes ![]() and
and ![]()
Point ![]() is a unique point on
is a unique point on ![]() if the ellipse is tangent to the line
if the ellipse is tangent to the line ![]()
In this case in point ![]() we get
we get ![]()
The tangent of the line ![]() is
is ![]()
For point ![]() we get
we get ![]()
![]()
For the line ![]()
![]()

vladimir.shelomovskii@gmail.com, vvsss
Video Solution
https://youtu.be/914687Yv6SY?si=tc6XfoOIHu0gu6AL
(no calculus)
~MathProblemSolvingSkills.com
Video Solution
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Query
![[asy] pair O=(0,0); pair X=(1,0); pair Y=(0,1); pair A=(0.5,0); pair B=(0,sin(pi/3)); dot(O); dot(X); dot(Y); dot(A); dot(B); draw(X--O--Y); draw(A--B); label("$B$", B, W); pair P=(0.5, sin(pi/3)); dot(P); draw(A--P--B); label("$A$", A, S); label("$O$", O, SW); pair C=(1/8,3*sqrt(3)/8); dot(C); label("$C$", C, SW); draw(C--P); label("$P$", P, NE); [/asy]](http://latex.artofproblemsolving.com/8/1/2/8127f1ad0f774d25ffc13e4b52ee26adb0ca7b54.png) Let
Let ![]() be a fixed point in the first quadrant. Let
be a fixed point in the first quadrant. Let ![]() be a point on the positive
be a point on the positive ![]() -axis and
-axis and ![]() be a point on the positive
be a point on the positive ![]() -axis such that
-axis such that ![]() passes through
passes through ![]() and the length of
and the length of ![]() is minimal. Let
is minimal. Let ![]() be the point such that
be the point such that ![]() is a rectangle. Prove that
is a rectangle. Prove that ![]() . (One can solve this through algebra/calculus bash, but I'm trying to find a solution that mainly uses geometry. If you know such a solution, write it here on this wiki page.) ~Furaken
. (One can solve this through algebra/calculus bash, but I'm trying to find a solution that mainly uses geometry. If you know such a solution, write it here on this wiki page.) ~Furaken
I think there is such a geometry way:
Let ![]() pass through
pass through ![]() while point
while point ![]() is on the outside of line segment
is on the outside of line segment ![]() and point
and point ![]() is in between
is in between ![]() and
and ![]() . We aim to show
. We aim to show ![]() is longer than
is longer than ![]() . Now since
. Now since ![]() is the altitude of triangle
is the altitude of triangle ![]() yet just a cevian on the base
yet just a cevian on the base ![]() of triangle
of triangle ![]() (thus making the height shorter than
(thus making the height shorter than ![]() ), it suffices to show the area of triangle
), it suffices to show the area of triangle ![]() is bigger than that of triangle
is bigger than that of triangle ![]() . To do this, we compare these two triangles (let
. To do this, we compare these two triangles (let ![]() intersect
intersect ![]() at point
at point ![]() ), and we just want to show
), and we just want to show ![]() . This is trivial by similarity ratios. ~gougutheorem
. This is trivial by similarity ratios. ~gougutheorem
Thanks! Now we know that it's possible to solve the AIME problem with only geometry. ~Furaken
See also
| 2024 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.