Difference between revisions of "Pythagorean Theorem"
(remove nonexistent category) |
Michael5210 (talk | contribs) m (→Proofs) |
||
| (27 intermediate revisions by 13 users not shown) | |||
| Line 5: | Line 5: | ||
== Proofs == | == Proofs == | ||
| − | In these proofs, we will let <math>ABC </math> be any right triangle with a right angle at <math> | + | In these proofs, we will let <math>ABC </math> be any right triangle with a right angle at <math>\angle ACB</math>. |
=== Proof 1 === | === Proof 1 === | ||
| Line 32: | Line 32: | ||
</center> | </center> | ||
| − | Since <math>ABC, CBH, ACH</math> are similar right triangles, and the areas of similar triangles are | + | Since <math>ABC, CBH, ACH</math> are similar right triangles, and the areas of similar triangles are proportional to the squares of corresponding side lengths, |
<center> | <center> | ||
<math> \frac{[ABC]}{AB^2} = \frac{[CBH]}{CB^2} = \frac{[ACH]}{AC^2} </math>. | <math> \frac{[ABC]}{AB^2} = \frac{[CBH]}{CB^2} = \frac{[ACH]}{AC^2} </math>. | ||
| Line 44: | Line 44: | ||
<center>[[Image:Pyth2.png]]</center> | <center>[[Image:Pyth2.png]]</center> | ||
| − | Evidently, <math>AY = AB - BC </math> and <math>AX = AB + BC </math>. By considering the [[ | + | Evidently, <math>AY = AB - BC </math> and <math>AX = AB + BC </math>. By considering the [[Power of a Point | power of point]] <math>A </math> with respect to <math>\omega </math>, we see |
<center> | <center> | ||
<math>AC^2 = AY \cdot AX = (AB-BC)(AB+BC) = AB^2 - BC^2 </math>. {{Halmos}} | <math>AC^2 = AY \cdot AX = (AB-BC)(AB+BC) = AB^2 - BC^2 </math>. {{Halmos}} | ||
</center> | </center> | ||
| + | |||
| + | === Proof 3 === | ||
| + | |||
| + | <math>ABCD</math> and <math>EFGH</math> are squares. | ||
| + | <center> | ||
| + | <asy> | ||
| + | pair A, B,C,D; | ||
| + | A = (-10,10); | ||
| + | B = (10,10); | ||
| + | C = (10,-10); | ||
| + | D = (-10,-10); | ||
| + | |||
| + | pair E,F,G,H; | ||
| + | E = (7,10); | ||
| + | F = (10, -7); | ||
| + | G = (-7, -10); | ||
| + | H = (-10, 7); | ||
| + | |||
| + | draw(A--B--C--D--cycle); | ||
| + | label("$A$", A, NNW); | ||
| + | label("$B$", B, ENE); | ||
| + | label("$C$", C, ESE); | ||
| + | label("$D$", D, SSW); | ||
| + | |||
| + | draw(E--F--G--H--cycle); | ||
| + | label("$E$", E, N); | ||
| + | label("$F$", F,SE); | ||
| + | label("$G$", G, S); | ||
| + | label("$H$", H, W); | ||
| + | |||
| + | label("a", A--B,N); | ||
| + | label("a", B--F,SE); | ||
| + | label("a", C--G,S); | ||
| + | label("a", H--D,W); | ||
| + | label("b", E--B,N); | ||
| + | label("b", F--C,SE); | ||
| + | label("b", G--D,S); | ||
| + | label("b", A--H,W); | ||
| + | label("c", E--H,NW); | ||
| + | label("c", E--F); | ||
| + | label("c", F--G,SE); | ||
| + | label("c", G--H,SW); | ||
| + | </asy> | ||
| + | </center> | ||
| + | <math>(a+b)^2=c^2+4\left(\frac{1}{2}ab\right)\implies a^2+2ab+b^2=c^2+2ab\implies a^2 + b^2=c^2</math>. {{Halmos}} | ||
== Common Pythagorean Triples == | == Common Pythagorean Triples == | ||
| Line 55: | Line 100: | ||
<cmath>3-4-5</cmath> | <cmath>3-4-5</cmath> | ||
<cmath>5-12-13</cmath> | <cmath>5-12-13</cmath> | ||
| − | |||
<cmath>7-24-25</cmath> | <cmath>7-24-25</cmath> | ||
<cmath>8-15-17</cmath> | <cmath>8-15-17</cmath> | ||
| Line 61: | Line 105: | ||
<cmath>12-35-37</cmath> | <cmath>12-35-37</cmath> | ||
<cmath>20-21-29</cmath> | <cmath>20-21-29</cmath> | ||
| + | <cmath>11-60-61</cmath> | ||
| + | |||
| + | |||
| + | Also Pythagorean Triples can be created with the a Pythagorean triple by multiplying the lengths by any integer. | ||
| + | For example, | ||
| + | <cmath>6-8-10 = (3-4-5)*2</cmath> | ||
| + | <cmath>21-72-75 = (7-24-25)*3</cmath> | ||
| + | <cmath>10-24-26 = (5-12-13)*2</cmath> | ||
| + | Note that (-1,0,1) and (3,4,5) are the only pythagoren triplets that consist of consecutive integers. | ||
| + | |||
| + | Also, if (a,b,c) are a pythagorean triplet it follows that (ka,kb,kc) will also form a pythagorean triplet for any constant k. | ||
| + | |||
| + | k can also be imaginary. | ||
== Problems == | == Problems == | ||
| Line 66: | Line 123: | ||
* [[2006_AIME_I_Problems/Problem_1 | 2006 AIME I Problem 1]] | * [[2006_AIME_I_Problems/Problem_1 | 2006 AIME I Problem 1]] | ||
* [[2007 AMC 12A Problems/Problem 10 | 2007 AMC 12A Problem 10]] | * [[2007 AMC 12A Problems/Problem 10 | 2007 AMC 12A Problem 10]] | ||
| + | |||
| + | === Sample Problem === | ||
| + | Right triangle <math>ABC</math> has legs of length <math>333</math> and <math>444</math>. Find the hypotenuse of <math>ABC</math>. | ||
| + | ==== Solution 1 (Bash) ==== | ||
| + | <math>\sqrt{333^2 + 444^2} = 555</math>. | ||
| + | ==== Solution 2 (Using 3-4-5) ==== | ||
| + | We see <math>333-444</math> looks like the legs of a <math>3-4-5</math> right triangle with a multiplication factor of 111. Thus <math>5*111 = 555</math>. | ||
| + | |||
| + | === Another Problem === | ||
| + | Right triangle <math>ABC</math> has side lengths of <math>3</math> and <math>4</math>. Find the sum of all the possible hypotenuses. | ||
| + | ==== Solution (Casework) ==== | ||
| + | Case 1: | ||
| + | |||
| + | 3 and 4 are the legs. Then 5 is the hypotenuse. | ||
| + | |||
| + | Case 2: | ||
| + | |||
| + | 3 is a leg and 4 is the hypotenuse. | ||
| + | |||
| + | There are no more cases as the hypotenuse has to be greater than the leg. | ||
| + | |||
| + | This makes the sum <math>4+5=9</math>. | ||
== External links == | == External links == | ||
| − | *[http://www.cut-the-knot.org/pythagoras/index.shtml | + | *[http://www.cut-the-knot.org/pythagoras/index.shtml 122 proofs of the Pythagorean Theorem] |
[[Category:Geometry]] | [[Category:Geometry]] | ||
[[Category:Theorems]] | [[Category:Theorems]] | ||
| − | |||
| − | |||
Latest revision as of 22:03, 5 October 2024
The Pythagorean Theorem states that for a right triangle with legs of length ![]() and
and ![]() and hypotenuse of length
and hypotenuse of length ![]() we have the relationship
we have the relationship ![]() . This theorem has been know since antiquity and is a classic to prove; hundreds of proofs have been published and many can be demonstrated entirely visually(the book The Pythagorean Proposition alone consists of more than 370). The Pythagorean Theorem is one of the most frequently used theorems in geometry, and is one of the many tools in a good geometer's arsenal. A very large number of geometry problems can be solved by building right triangles and applying the Pythagorean Theorem.
. This theorem has been know since antiquity and is a classic to prove; hundreds of proofs have been published and many can be demonstrated entirely visually(the book The Pythagorean Proposition alone consists of more than 370). The Pythagorean Theorem is one of the most frequently used theorems in geometry, and is one of the many tools in a good geometer's arsenal. A very large number of geometry problems can be solved by building right triangles and applying the Pythagorean Theorem.
This is generalized by the Pythagorean Inequality and the Law of Cosines.
Contents
[hide]Proofs
In these proofs, we will let ![]() be any right triangle with a right angle at
be any right triangle with a right angle at ![]() .
.
Proof 1
We use ![]() to denote the area of triangle
to denote the area of triangle ![]() .
.
Let ![]() be the perpendicular to side
be the perpendicular to side ![]() from
from ![]() .
.
![[asy] pair A, B, C, H; A = (0, 0); B = (4, 3); C = (4, 0); H = foot(C, A, B); draw(A--B--C--cycle); draw(C--H); draw(rightanglemark(A, C, B)); draw(rightanglemark(C, H, B)); label("$A$", A, SSW); label("$B$", B, ENE); label("$C$", C, SE); label("$H$", H, NNW); [/asy]](http://latex.artofproblemsolving.com/a/1/9/a19bed9f5ac971139756a395da4e29366d45fc52.png)
Since ![]() are similar right triangles, and the areas of similar triangles are proportional to the squares of corresponding side lengths,
are similar right triangles, and the areas of similar triangles are proportional to the squares of corresponding side lengths,
![]() .
.
But since triangle ![]() is composed of triangles
is composed of triangles ![]() and
and ![]() ,
, ![]() , so
, so ![]() . ∎
. ∎
Proof 2
Consider a circle ![]() with center
with center ![]() and radius
and radius ![]() . Since
. Since ![]() and
and ![]() are perpendicular,
are perpendicular, ![]() is tangent to
is tangent to ![]() . Let the line
. Let the line ![]() meet
meet ![]() at
at ![]() and
and ![]() , as shown in the diagram:
, as shown in the diagram:
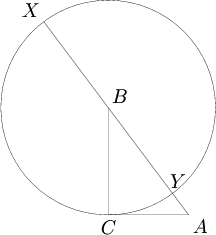
Evidently, ![]() and
and ![]() . By considering the power of point
. By considering the power of point ![]() with respect to
with respect to ![]() , we see
, we see
![]() . ∎
. ∎
Proof 3
![]() and
and ![]() are squares.
are squares.
![[asy] pair A, B,C,D; A = (-10,10); B = (10,10); C = (10,-10); D = (-10,-10); pair E,F,G,H; E = (7,10); F = (10, -7); G = (-7, -10); H = (-10, 7); draw(A--B--C--D--cycle); label("$A$", A, NNW); label("$B$", B, ENE); label("$C$", C, ESE); label("$D$", D, SSW); draw(E--F--G--H--cycle); label("$E$", E, N); label("$F$", F,SE); label("$G$", G, S); label("$H$", H, W); label("a", A--B,N); label("a", B--F,SE); label("a", C--G,S); label("a", H--D,W); label("b", E--B,N); label("b", F--C,SE); label("b", G--D,S); label("b", A--H,W); label("c", E--H,NW); label("c", E--F); label("c", F--G,SE); label("c", G--H,SW); [/asy]](http://latex.artofproblemsolving.com/2/e/7/2e79de6673cd591bf38bff3efa048140bda61e9f.png)
![]() . ∎
. ∎
Common Pythagorean Triples
A Pythagorean Triple is a set of 3 positive integers such that ![]() , i.e. the 3 numbers can be the lengths of the sides of a right triangle. Among these, the Primitive Pythagorean Triples, those in which the three numbers have no common divisor, are most interesting. A few of them are:
, i.e. the 3 numbers can be the lengths of the sides of a right triangle. Among these, the Primitive Pythagorean Triples, those in which the three numbers have no common divisor, are most interesting. A few of them are:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Also Pythagorean Triples can be created with the a Pythagorean triple by multiplying the lengths by any integer.
For example,
![]()
![]()
![]() Note that (-1,0,1) and (3,4,5) are the only pythagoren triplets that consist of consecutive integers.
Note that (-1,0,1) and (3,4,5) are the only pythagoren triplets that consist of consecutive integers.
Also, if (a,b,c) are a pythagorean triplet it follows that (ka,kb,kc) will also form a pythagorean triplet for any constant k.
k can also be imaginary.
Problems
Introductory
Sample Problem
Right triangle ![]() has legs of length
has legs of length ![]() and
and ![]() . Find the hypotenuse of
. Find the hypotenuse of ![]() .
.
Solution 1 (Bash)
![]() .
.
Solution 2 (Using 3-4-5)
We see ![]() looks like the legs of a
looks like the legs of a ![]() right triangle with a multiplication factor of 111. Thus
right triangle with a multiplication factor of 111. Thus ![]() .
.
Another Problem
Right triangle ![]() has side lengths of
has side lengths of ![]() and
and ![]() . Find the sum of all the possible hypotenuses.
. Find the sum of all the possible hypotenuses.
Solution (Casework)
Case 1:
3 and 4 are the legs. Then 5 is the hypotenuse.
Case 2:
3 is a leg and 4 is the hypotenuse.
There are no more cases as the hypotenuse has to be greater than the leg.
This makes the sum ![]() .
.









