Difference between revisions of "2015 AIME I Problems/Problem 15"
(→Problem) |
(→Solution 4 - Author : Shiva Kumar Kannan - In Progress) |
||
| (47 intermediate revisions by 15 users not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
| − | A block of wood has the shape of a right circular cylinder with radius <math>6</math> and height <math>8</math>, and its entire surface has been painted blue. Points <math>A</math> and <math>B</math> are chosen on the edge of one of the circular faces of the cylinder so that <math>\overarc{AB}</math> on that face measures <math>120^\ | + | A block of wood has the shape of a right circular cylinder with radius <math>6</math> and height <math>8</math>, and its entire surface has been painted blue. Points <math>A</math> and <math>B</math> are chosen on the edge of one of the circular faces of the cylinder so that <math>\overarc{AB}</math> on that face measures <math>120^\circ</math>. The block is then sliced in half along the plane that passes through point <math>A</math>, point <math>B</math>, and the center of the cylinder, revealing a flat, unpainted face on each half. The area of one of these unpainted faces is <math>a\cdot\pi + b\sqrt{c}</math>, where <math>a</math>, <math>b</math>, and <math>c</math> are integers and <math>c</math> is not divisible by the square of any prime. Find <math>a+b+c</math>. |
<asy> | <asy> | ||
| Line 36: | Line 36: | ||
add(rpic.fit(),(1,0)); </asy> | add(rpic.fit(),(1,0)); </asy> | ||
| − | Credit to Royalreter1 and chezbgone2 | + | --Credit to Royalreter1 and chezbgone2 For The Diagram-- |
| − | ==Solution== | + | ==Solution 1== |
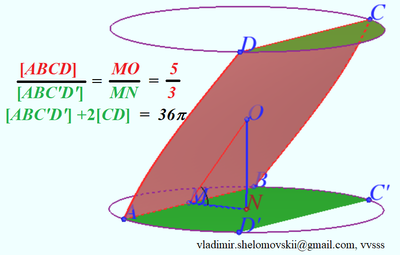
| − | Label the points where the plane intersects the top face of the cylinder as <math>C</math> and <math>D</math>, and the center of the cylinder as <math>O</math>, such that <math>C,O,</math> and <math>A</math> are collinear. Let <math> | + | [[File:2015 AIME I 15.png|400px|right]] |
| + | Label the points where the plane intersects the top face of the cylinder as <math>C</math> and <math>D</math>, and the center of the cylinder as <math>O</math>, such that <math>C,O,</math> and <math>A</math> are collinear. Let <math>N</math> be the center of the bottom face, and <math>M</math> the midpoint of <math>\overline{AB}</math>. Then <math>ON=4</math>, <math>MN=3</math> (because of the 120 degree angle), and so <math>OM=5</math>. | ||
| − | Project <math>C</math> and <math>D</math> onto the bottom face to get <math>X</math> and <math>Y</math>, respectively. Then the section <math>ABCD</math> (whose area we need to find), is a stretching of the section <math>ABXY</math> on the bottom face. The ratio of stretching is <math>\frac{OM}{ | + | Project <math>C</math> and <math>D</math> onto the bottom face to get <math>X</math> and <math>Y</math>, respectively. Then the section <math>ABCD</math> (whose area we need to find), is a stretching of the section <math>ABXY</math> on the bottom face. The ratio of stretching is <math>\frac{OM}{MN}=\frac{5}{3}</math>, and we do not square this value when finding the area because it is only stretching in one direction. Using 30-60-90 triangles and circular sectors, we find that the area of the section <math>ABXY</math> is <math>18\sqrt{3}\ + 12 \pi</math>. Thus, the area of section <math>ABCD</math> is <math>20\pi + 30\sqrt{3}</math>, and so our answer is <math>20+30+3=\boxed{053}</math>. |
| − | |||
| − | |||
==Solution 2== | ==Solution 2== | ||
| Line 51: | Line 50: | ||
Now, the use of simple calculus is required. Conceptualize an infinite number of lines perpendicular to <math>AE</math> intersecting both <math>AE</math> and <math>AD</math>. Consider the area between point <math>A</math> and the first vertical line. Label the point where the line intersects AE as E', and the point where the line intersects AD as D'. The area of the part of the initial unpainted face within these two positions approaches a rectangle with length AD' and width <math>w</math>. The area of the base within these two positions approaches a rectangle with length AE' and width <math>w</math>. The ratio of AD':AE' is 10:6, since the ratio of AD:AE is 10:6. This means that the area of the initial unpainted surface within these two positions to the area of the base within these two positions is equal to 10<math>w</math>:6<math>w</math> = 10:6. Through a similar argument, the areas between each set of vertical lines also maintains a ratio of 10:6. Therefore, the ratio of the area we wish to find to the area of the base between AB and CD (from the top perspective) is 10:6. Using 30-60-90 triangles and partial circles, the area of the base between AB and CD is calculated to be <math>18\sqrt{3}\ + 12 \pi</math>. The area of the unpainted surface therefore becomes <math>20\pi + 30\sqrt{3}</math>, and so our answer is <math>\boxed{053}</math>. | Now, the use of simple calculus is required. Conceptualize an infinite number of lines perpendicular to <math>AE</math> intersecting both <math>AE</math> and <math>AD</math>. Consider the area between point <math>A</math> and the first vertical line. Label the point where the line intersects AE as E', and the point where the line intersects AD as D'. The area of the part of the initial unpainted face within these two positions approaches a rectangle with length AD' and width <math>w</math>. The area of the base within these two positions approaches a rectangle with length AE' and width <math>w</math>. The ratio of AD':AE' is 10:6, since the ratio of AD:AE is 10:6. This means that the area of the initial unpainted surface within these two positions to the area of the base within these two positions is equal to 10<math>w</math>:6<math>w</math> = 10:6. Through a similar argument, the areas between each set of vertical lines also maintains a ratio of 10:6. Therefore, the ratio of the area we wish to find to the area of the base between AB and CD (from the top perspective) is 10:6. Using 30-60-90 triangles and partial circles, the area of the base between AB and CD is calculated to be <math>18\sqrt{3}\ + 12 \pi</math>. The area of the unpainted surface therefore becomes <math>20\pi + 30\sqrt{3}</math>, and so our answer is <math>\boxed{053}</math>. | ||
| + | |||
| + | ==Solution 3== | ||
| + | This problem can be calculus-bashed (for those like me who never noticed the surface was merely a stretch of its projection). Label points as in the first paragraph of Solution 1 (<math>A</math> and <math>B</math> as given, <math>M</math> the midpoint of <math>AB</math>, <math>O</math> the center of the cylinder, <math>T</math> the center of the bottom face of the cylinder). Because of the 120 degrees and right triangle calculations, we find <math>MT</math> = 3, <math>OT</math> = 4, <math>OM</math> = 5). We will be integrating with respect to the y-coordinate which we define as distance downwards from <math>O</math> (in this system, the <math>y</math>-coordinate of the bottom face would be 4). | ||
| + | |||
| + | We note that by similar triangles, we have that the length from <math>O</math> to the point on the unpainted surface of coordinate <math>y</math> is <math>\ell = \frac{5}{4} y</math>, and therefore <math>d\ell = \frac{5}{4} dy</math>. Define the segment <math>A'B'</math> to be the intersection of the painted surface with the circular cross section of the cylinder of coordinate <math>y</math>, with endpoints <math>A'</math> and <math>B'</math> and midpoint <math>M'</math>, with <math>T'</math> the center of this circular cross section. Then, by similar triangles, <math>T'M' = \frac{3}{4} y</math> and thus <cmath>A'B' = 2A' M' = 2 \sqrt{ 6^2 - \left( \frac{3}{4}y\right)^2 } = \frac{3}{2} \sqrt{ 64 - y^2 }</cmath>. We know that <math>A'B'</math> is perpendicular to <math>OM</math>. | ||
| + | |||
| + | Now we can set up our integral: we will integrate <math>y</math> from 0 to 4 and multiply by two because the total height is 8. | ||
| + | <cmath> A = 2\int_0^4 \left(\frac{3}{2}\sqrt{ 64 - y^2 }\right) \left( \frac{5}{4} dy\right) </cmath> | ||
| + | <cmath> A = \frac{15}{4} \int_0^4 \sqrt{ 64 - y^2 }dy </cmath> | ||
| + | |||
| + | Then we substitute <math>y = 8\sin \theta</math> with <math>dy = 8 \cos \theta d \theta</math>, changing the bounds to 0 to <math>\frac{\pi}{6}</math> as appropriate. | ||
| + | <cmath> A = \frac{15}{4} \int_0^\frac{\pi}{6} \sqrt{ 64 - 64\sin^2 \theta }\cdot 8\cos\theta d\theta </cmath> | ||
| + | <cmath> A = 240 \int_0^\frac{\pi}{6} \cos^2 \theta d\theta </cmath> | ||
| + | <cmath> A = 240 \left[ \frac{\theta}{2} + \frac{\sin 2\theta}{4} \right]_0^\frac{\pi}{6} = 240 \left[ \frac{\pi}{12} + \frac{\sqrt{3}}{8} \right] = 20{\pi} + 30\sqrt{3}</cmath> | ||
| + | |||
| + | Therefore, <math>a + b + c = 20 + 30 + 3 = \boxed{053}</math>. | ||
| + | |||
| + | |||
| + | == Solution 4 - Author : Shiva Kumar Kannan - In Progress == | ||
| + | |||
| + | |||
| + | Extend the cylinder such that the cylinder has a height of <math>16</math> and the same radius of <math>6</math>. Let <math>Q</math> be a point on the circumference of the top face of the cylinder. Let <math>R</math> be a point on the bottom face of the cylinder, and the farthest point from A on the cylinder. Let a plane <math>P</math> pass through points <math>Q</math> and <math>R</math>. The cross section formed by the intersection of the plane and this stretched cylinder, is an ellipse. Notice that the cross section area we want to find is a part the part of this ellipse contained in the original cylinder. | ||
| + | |||
| + | |||
| + | The semi-major axis length of the ellipse is <cmath> \sqrt{6^2 + 8^2} = 10</cmath>. | ||
| + | The semiminor axis length is just the radius of the cylinder, which is <math> 6 </math>. | ||
| + | |||
| + | |||
| + | If we take the plane of this ellipse to be the <math>2</math> dimensional Cartesian plane and take the center of this ellipse as <math>(0, 0)</math>, this ellipse has the equation : <cmath>\frac{x^2}{10^2} + \frac{y^2}{6^2} = 1</cmath>. | ||
| + | |||
| + | |||
| + | Notice that the cross section area we want to find is the area bounded by this ellipse from <math> x = -5 </math> to <math> x = 5 </math>. Thus we must integrate the equation of the ellipse from <math>-5</math> to <math>5</math>. That will give us the positive area bounded by the ellipse and the <math>x </math> axis. We want to double it, as we want both the positive and negative area as that is our cross section. | ||
| + | |||
| + | |||
| + | Rewrite the ellispe equation as <cmath>y = \frac{3}{5} \sqrt{100 - x^2}</cmath>. | ||
| + | We want to find <cmath>2\int_{-5}^{5} \left(\frac{3}{5}\sqrt{100 - x^2 }\right) \left( dx\right) </cmath>. | ||
| + | |||
| + | |||
| + | Evaluate this integral : It comes out to be <cmath> 20\pi + 30\sqrt{3}</cmath>. Finally, the answer we give, is <cmath>20 + 30 + 3 = \boxed{053}</cmath>. | ||
| + | |||
| + | Motivation : Notice that a cross section of any diagonal plane not going through the top or bottom face of the cylinder is an ellipse. When the plane does cross the bottom and top faces, the resulting cross section will be a portion of an ellipse. When the plane is perpendicular to its top and bottom faces, the resulting cross section is a rectangle. So, from the moment the cross section starts cutting both circular faces, to the moment it is perpendicular to the circular bases, it goes from a full ellipse, to a rectangle. Hence, the cross section we want is a part of the ellipse. | ||
== See also == | == See also == | ||
{{AIME box|year=2015|n=I|num-b=14|after=Last Problem}} | {{AIME box|year=2015|n=I|num-b=14|after=Last Problem}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
| − | [[Category: | + | |
| + | [[Category:Intermediate Geometry Problems]] | ||
| + | [[Category:3D Geometry Problems]] | ||
Revision as of 06:00, 10 October 2024
Contents
[hide]Problem
A block of wood has the shape of a right circular cylinder with radius ![]() and height
and height ![]() , and its entire surface has been painted blue. Points
, and its entire surface has been painted blue. Points ![]() and
and ![]() are chosen on the edge of one of the circular faces of the cylinder so that
are chosen on the edge of one of the circular faces of the cylinder so that ![]() on that face measures
on that face measures ![]() . The block is then sliced in half along the plane that passes through point
. The block is then sliced in half along the plane that passes through point ![]() , point
, point ![]() , and the center of the cylinder, revealing a flat, unpainted face on each half. The area of one of these unpainted faces is
, and the center of the cylinder, revealing a flat, unpainted face on each half. The area of one of these unpainted faces is ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are integers and
are integers and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
![[asy] import three; import solids; size(8cm); currentprojection=orthographic(-1,-5,3); picture lpic, rpic; size(lpic,5cm); draw(lpic,surface(revolution((0,0,0),(-3,3*sqrt(3),0)..(0,6,4)..(3,3*sqrt(3),8),Z,0,120)),gray(0.7),nolight); draw(lpic,surface(revolution((0,0,0),(-3*sqrt(3),-3,8)..(-6,0,4)..(-3*sqrt(3),3,0),Z,0,90)),gray(0.7),nolight); draw(lpic,surface((3,3*sqrt(3),8)..(-6,0,8)..(3,-3*sqrt(3),8)--cycle),gray(0.7),nolight); draw(lpic,(3,-3*sqrt(3),8)..(-6,0,8)..(3,3*sqrt(3),8)); draw(lpic,(-3,3*sqrt(3),0)--(-3,-3*sqrt(3),0),dashed); draw(lpic,(3,3*sqrt(3),8)..(0,6,4)..(-3,3*sqrt(3),0)--(-3,3*sqrt(3),0)..(-3*sqrt(3),3,0)..(-6,0,0),dashed); draw(lpic,(3,3*sqrt(3),8)--(3,-3*sqrt(3),8)..(0,-6,4)..(-3,-3*sqrt(3),0)--(-3,-3*sqrt(3),0)..(-3*sqrt(3),-3,0)..(-6,0,0)); draw(lpic,(6*cos(atan(-1/5)+3.14159),6*sin(atan(-1/5)+3.14159),0)--(6*cos(atan(-1/5)+3.14159),6*sin(atan(-1/5)+3.14159),8)); size(rpic,5cm); draw(rpic,surface(revolution((0,0,0),(3,3*sqrt(3),8)..(0,6,4)..(-3,3*sqrt(3),0),Z,230,360)),gray(0.7),nolight); draw(rpic,surface((-3,3*sqrt(3),0)..(6,0,0)..(-3,-3*sqrt(3),0)--cycle),gray(0.7),nolight); draw(rpic,surface((-3,3*sqrt(3),0)..(0,6,4)..(3,3*sqrt(3),8)--(3,3*sqrt(3),8)--(3,-3*sqrt(3),8)--(3,-3*sqrt(3),8)..(0,-6,4)..(-3,-3*sqrt(3),0)--cycle),white,nolight); draw(rpic,(-3,-3*sqrt(3),0)..(-6*cos(atan(-1/5)+3.14159),-6*sin(atan(-1/5)+3.14159),0)..(6,0,0)); draw(rpic,(-6*cos(atan(-1/5)+3.14159),-6*sin(atan(-1/5)+3.14159),0)..(6,0,0)..(-3,3*sqrt(3),0),dashed); draw(rpic,(3,3*sqrt(3),8)--(3,-3*sqrt(3),8)); draw(rpic,(-3,3*sqrt(3),0)..(0,6,4)..(3,3*sqrt(3),8)--(3,3*sqrt(3),8)..(3*sqrt(3),3,8)..(6,0,8)); draw(rpic,(-3,3*sqrt(3),0)--(-3,-3*sqrt(3),0)..(0,-6,4)..(3,-3*sqrt(3),8)--(3,-3*sqrt(3),8)..(3*sqrt(3),-3,8)..(6,0,8)); draw(rpic,(-6*cos(atan(-1/5)+3.14159),-6*sin(atan(-1/5)+3.14159),0)--(-6*cos(atan(-1/5)+3.14159),-6*sin(atan(-1/5)+3.14159),8)); label(rpic,"$A$",(-3,3*sqrt(3),0),W); label(rpic,"$B$",(-3,-3*sqrt(3),0),W); add(lpic.fit(),(0,0)); add(rpic.fit(),(1,0)); [/asy]](http://latex.artofproblemsolving.com/d/d/5/dd5c3cbbc67a161c6ba03a3e44f37b82076d83cd.png)
--Credit to Royalreter1 and chezbgone2 For The Diagram--
Solution 1
Label the points where the plane intersects the top face of the cylinder as ![]() and
and ![]() , and the center of the cylinder as
, and the center of the cylinder as ![]() , such that
, such that ![]() and
and ![]() are collinear. Let
are collinear. Let ![]() be the center of the bottom face, and
be the center of the bottom face, and ![]() the midpoint of
the midpoint of ![]() . Then
. Then ![]() ,
, ![]() (because of the 120 degree angle), and so
(because of the 120 degree angle), and so ![]() .
.
Project ![]() and
and ![]() onto the bottom face to get
onto the bottom face to get ![]() and
and ![]() , respectively. Then the section
, respectively. Then the section ![]() (whose area we need to find), is a stretching of the section
(whose area we need to find), is a stretching of the section ![]() on the bottom face. The ratio of stretching is
on the bottom face. The ratio of stretching is ![]() , and we do not square this value when finding the area because it is only stretching in one direction. Using 30-60-90 triangles and circular sectors, we find that the area of the section
, and we do not square this value when finding the area because it is only stretching in one direction. Using 30-60-90 triangles and circular sectors, we find that the area of the section ![]() is
is ![]() . Thus, the area of section
. Thus, the area of section ![]() is
is ![]() , and so our answer is
, and so our answer is ![]() .
.
Solution 2
Label the points same as in the first sentence above. Consider a view of the cylinder such that height is disregarded, i.e. a top view. From this view, note that Cylinder ![]() has become a circle with
has become a circle with ![]() =
= ![]() =
= ![]() . Using 30-60-90 triangles, we get rectangle
. Using 30-60-90 triangles, we get rectangle ![]() to have a horizontal component of
to have a horizontal component of ![]() . Now, consider a side view, such that
. Now, consider a side view, such that ![]() and
and ![]() coincide at the bottom of the diagram. From this view, consider the right triangle composed of hypotenuse
coincide at the bottom of the diagram. From this view, consider the right triangle composed of hypotenuse ![]() and a point along the base of the viewpoint, which will be labeled as
and a point along the base of the viewpoint, which will be labeled as ![]() . From the top view,
. From the top view, ![]() . Because of the height of the cylinder,
. Because of the height of the cylinder, ![]() is equal to
is equal to ![]() . This makes
. This makes ![]() equal to
equal to ![]() .
.
Now, the use of simple calculus is required. Conceptualize an infinite number of lines perpendicular to ![]() intersecting both
intersecting both ![]() and
and ![]() . Consider the area between point
. Consider the area between point ![]() and the first vertical line. Label the point where the line intersects AE as E', and the point where the line intersects AD as D'. The area of the part of the initial unpainted face within these two positions approaches a rectangle with length AD' and width
and the first vertical line. Label the point where the line intersects AE as E', and the point where the line intersects AD as D'. The area of the part of the initial unpainted face within these two positions approaches a rectangle with length AD' and width ![]() . The area of the base within these two positions approaches a rectangle with length AE' and width
. The area of the base within these two positions approaches a rectangle with length AE' and width ![]() . The ratio of AD':AE' is 10:6, since the ratio of AD:AE is 10:6. This means that the area of the initial unpainted surface within these two positions to the area of the base within these two positions is equal to 10
. The ratio of AD':AE' is 10:6, since the ratio of AD:AE is 10:6. This means that the area of the initial unpainted surface within these two positions to the area of the base within these two positions is equal to 10![]() :6
:6![]() = 10:6. Through a similar argument, the areas between each set of vertical lines also maintains a ratio of 10:6. Therefore, the ratio of the area we wish to find to the area of the base between AB and CD (from the top perspective) is 10:6. Using 30-60-90 triangles and partial circles, the area of the base between AB and CD is calculated to be
= 10:6. Through a similar argument, the areas between each set of vertical lines also maintains a ratio of 10:6. Therefore, the ratio of the area we wish to find to the area of the base between AB and CD (from the top perspective) is 10:6. Using 30-60-90 triangles and partial circles, the area of the base between AB and CD is calculated to be ![]() . The area of the unpainted surface therefore becomes
. The area of the unpainted surface therefore becomes ![]() , and so our answer is
, and so our answer is ![]() .
.
Solution 3
This problem can be calculus-bashed (for those like me who never noticed the surface was merely a stretch of its projection). Label points as in the first paragraph of Solution 1 (![]() and
and ![]() as given,
as given, ![]() the midpoint of
the midpoint of ![]() ,
, ![]() the center of the cylinder,
the center of the cylinder, ![]() the center of the bottom face of the cylinder). Because of the 120 degrees and right triangle calculations, we find
the center of the bottom face of the cylinder). Because of the 120 degrees and right triangle calculations, we find ![]() = 3,
= 3, ![]() = 4,
= 4, ![]() = 5). We will be integrating with respect to the y-coordinate which we define as distance downwards from
= 5). We will be integrating with respect to the y-coordinate which we define as distance downwards from ![]() (in this system, the
(in this system, the ![]() -coordinate of the bottom face would be 4).
-coordinate of the bottom face would be 4).
We note that by similar triangles, we have that the length from ![]() to the point on the unpainted surface of coordinate
to the point on the unpainted surface of coordinate ![]() is
is ![]() , and therefore
, and therefore ![]() . Define the segment
. Define the segment ![]() to be the intersection of the painted surface with the circular cross section of the cylinder of coordinate
to be the intersection of the painted surface with the circular cross section of the cylinder of coordinate ![]() , with endpoints
, with endpoints ![]() and
and ![]() and midpoint
and midpoint ![]() , with
, with ![]() the center of this circular cross section. Then, by similar triangles,
the center of this circular cross section. Then, by similar triangles, ![]() and thus
and thus ![\[A'B' = 2A' M' = 2 \sqrt{ 6^2 - \left( \frac{3}{4}y\right)^2 } = \frac{3}{2} \sqrt{ 64 - y^2 }\]](http://latex.artofproblemsolving.com/c/1/b/c1b4ca1b7953a52bd39d9ebeecdde67745d41c8e.png) . We know that
. We know that ![]() is perpendicular to
is perpendicular to ![]() .
.
Now we can set up our integral: we will integrate ![]() from 0 to 4 and multiply by two because the total height is 8.
from 0 to 4 and multiply by two because the total height is 8.
![]()
![]()
Then we substitute ![]() with
with ![]() , changing the bounds to 0 to
, changing the bounds to 0 to ![]() as appropriate.
as appropriate.
![]()
![]()
![\[A = 240 \left[ \frac{\theta}{2} + \frac{\sin 2\theta}{4} \right]_0^\frac{\pi}{6} = 240 \left[ \frac{\pi}{12} + \frac{\sqrt{3}}{8} \right] = 20{\pi} + 30\sqrt{3}\]](http://latex.artofproblemsolving.com/4/b/0/4b0372c4737561b2ea93e088c43eb3dce8cc22a4.png)
Therefore, ![]() .
.
Solution 4 - Author : Shiva Kumar Kannan - In Progress
Extend the cylinder such that the cylinder has a height of ![]() and the same radius of
and the same radius of ![]() . Let
. Let ![]() be a point on the circumference of the top face of the cylinder. Let
be a point on the circumference of the top face of the cylinder. Let ![]() be a point on the bottom face of the cylinder, and the farthest point from A on the cylinder. Let a plane
be a point on the bottom face of the cylinder, and the farthest point from A on the cylinder. Let a plane ![]() pass through points
pass through points ![]() and
and ![]() . The cross section formed by the intersection of the plane and this stretched cylinder, is an ellipse. Notice that the cross section area we want to find is a part the part of this ellipse contained in the original cylinder.
. The cross section formed by the intersection of the plane and this stretched cylinder, is an ellipse. Notice that the cross section area we want to find is a part the part of this ellipse contained in the original cylinder.
The semi-major axis length of the ellipse is ![]() .
The semiminor axis length is just the radius of the cylinder, which is
.
The semiminor axis length is just the radius of the cylinder, which is ![]() .
.
If we take the plane of this ellipse to be the ![]() dimensional Cartesian plane and take the center of this ellipse as
dimensional Cartesian plane and take the center of this ellipse as ![]() , this ellipse has the equation :
, this ellipse has the equation : ![]() .
.
Notice that the cross section area we want to find is the area bounded by this ellipse from ![]() to
to ![]() . Thus we must integrate the equation of the ellipse from
. Thus we must integrate the equation of the ellipse from ![]() to
to ![]() . That will give us the positive area bounded by the ellipse and the
. That will give us the positive area bounded by the ellipse and the ![]() axis. We want to double it, as we want both the positive and negative area as that is our cross section.
axis. We want to double it, as we want both the positive and negative area as that is our cross section.
Rewrite the ellispe equation as ![]() .
We want to find
.
We want to find ![]() .
.
Evaluate this integral : It comes out to be ![]() . Finally, the answer we give, is
. Finally, the answer we give, is ![]() .
.
Motivation : Notice that a cross section of any diagonal plane not going through the top or bottom face of the cylinder is an ellipse. When the plane does cross the bottom and top faces, the resulting cross section will be a portion of an ellipse. When the plane is perpendicular to its top and bottom faces, the resulting cross section is a rectangle. So, from the moment the cross section starts cutting both circular faces, to the moment it is perpendicular to the circular bases, it goes from a full ellipse, to a rectangle. Hence, the cross section we want is a part of the ellipse.
See also
| 2015 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.