Difference between revisions of "2021 Fall AMC 12B Problems/Problem 15"
Lopkiloinm (talk | contribs) (→Solution) |
Erringbubble (talk | contribs) m (added latex to previous edit) |
||
| (31 intermediate revisions by 9 users not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
Three identical square sheets of paper each with side length <math>6</math> are stacked on top of each other. The middle sheet is rotated clockwise <math>30^\circ</math> about its center and the top sheet is rotated clockwise <math>60^\circ</math> about its center, resulting in the <math>24</math>-sided polygon shown in the figure below. The area of this polygon can be expressed in the form <math>a-b\sqrt{c}</math>, where <math>a</math>, <math>b</math>, and <math>c</math> are positive integers, and <math>c</math> is not divisible by the square of any prime. What is <math>a+b+c</math>? | Three identical square sheets of paper each with side length <math>6</math> are stacked on top of each other. The middle sheet is rotated clockwise <math>30^\circ</math> about its center and the top sheet is rotated clockwise <math>60^\circ</math> about its center, resulting in the <math>24</math>-sided polygon shown in the figure below. The area of this polygon can be expressed in the form <math>a-b\sqrt{c}</math>, where <math>a</math>, <math>b</math>, and <math>c</math> are positive integers, and <math>c</math> is not divisible by the square of any prime. What is <math>a+b+c</math>? | ||
| − | + | <center><asy> | |
| − | + | defaultpen(fontsize(8)+0.8); size(150); | |
| − | + | pair O,A1,B1,C1,A2,B2,C2,A3,B3,C3,A4,B4,C4; | |
| + | real x=45, y=90, z=60; O=origin; | ||
| + | A1=dir(x); A2=dir(x+y); A3=dir(x+2y); A4=dir(x+3y); | ||
| + | B1=dir(x-z); B2=dir(x+y-z); B3=dir(x+2y-z); B4=dir(x+3y-z); | ||
| + | C1=dir(x-2z); C2=dir(x+y-2z); C3=dir(x+2y-2z); C4=dir(x+3y-2z); | ||
| + | draw(A1--A2--A3--A4--A1, gray+0.25+dashed); | ||
| + | filldraw(B1--B2--B3--B4--cycle, white, gray+dashed+linewidth(0.25)); | ||
| + | filldraw(C1--C2--C3--C4--cycle, white, gray+dashed+linewidth(0.25)); | ||
| + | dot(O); | ||
| + | pair P1,P2,P3,P4,Q1,Q2,Q3,Q4,R1,R2,R3,R4; | ||
| + | P1=extension(A1,A2,B1,B2); Q1=extension(A1,A2,C3,C4); | ||
| + | P2=extension(A2,A3,B2,B3); Q2=extension(A2,A3,C4,C1); | ||
| + | P3=extension(A3,A4,B3,B4); Q3=extension(A3,A4,C1,C2); | ||
| + | P4=extension(A4,A1,B4,B1); Q4=extension(A4,A1,C2,C3); | ||
| + | R1=extension(C2,C3,B2,B3); R2=extension(C3,C4,B3,B4); | ||
| + | R3=extension(C4,C1,B4,B1); R4=extension(C1,C2,B1,B2); | ||
| + | draw(A1--P1--B2--R1--C3--Q1--A2); | ||
| + | draw(A2--P2--B3--R2--C4--Q2--A3); | ||
| + | draw(A3--P3--B4--R3--C1--Q3--A4); | ||
| + | draw(A4--P4--B1--R4--C2--Q4--A1); | ||
| + | </asy></center> | ||
<math>(\textbf{A})\: 75\qquad(\textbf{B}) \: 93\qquad(\textbf{C}) \: 96\qquad(\textbf{D}) \: 129\qquad(\textbf{E}) \: 147</math> | <math>(\textbf{A})\: 75\qquad(\textbf{B}) \: 93\qquad(\textbf{C}) \: 96\qquad(\textbf{D}) \: 129\qquad(\textbf{E}) \: 147</math> | ||
| − | ==Solution== | + | ==Solution 1== |
<asy> | <asy> | ||
| + | defaultpen(fontsize(8)+0.8); size(100); | ||
pair A=(0,0); | pair A=(0,0); | ||
pair B=(1.732,3); | pair B=(1.732,3); | ||
pair C=(3,3); | pair C=(3,3); | ||
pair D=(3,1.732); | pair D=(3,1.732); | ||
| − | draw(A--B--C--D-- | + | draw(A--(0,3)--C--(3,0)--A, lightgray+dashed); |
| − | label("A",A,W); | + | draw(A--B--C--A); |
| − | label("B",B,N); | + | draw(A--D--C, gray); |
| − | label("C",C, | + | label("$A$",A,W); |
| − | label("D",D,E); | + | label("$B$",B,N); |
| + | label("$C$",C,NE); | ||
| + | label("$D$",D,E); | ||
| + | label("$E$",(0,3),NW); | ||
| + | label("$F$",(3,0),E); | ||
</asy> | </asy> | ||
| − | + | The <math>24</math>-sided polygon is made out of <math>24</math> shapes like <math>\triangle ABC</math>. Then <math>\angle BAC=360^\circ/24=15^\circ</math>, and <math>\angle EAC = 45^\circ</math>, so <math>\angle{EAB} = 30^{\circ}</math>. Then <math>EB=AE\tan 30^\circ = \sqrt{3}</math>; therefore <math>BC=EC-EB=3-\sqrt{3}</math>. Thus | |
| + | <cmath>[ABC] = \frac{BC}{EC}\cdot [ACE] = \frac{3-\sqrt{3}}{3}\cdot \frac 92 </cmath>and the required area is <math>24\cdot[ABC] =108-36\sqrt{3}</math>. Finally <math>108+36+3=\boxed{(\textbf{E})\ 147}</math>. | ||
| + | ~lopkiloinm | ||
| + | |||
| + | Note: Drop an altitude from <math>A</math> to <math>\overline{BC}</math> to construct point <math>E</math>. This creates right triangles. ~erringbubble | ||
| + | |||
| + | == Solution 2 == | ||
| + | As shown in [[:Image:2021_AMC_12B_(Nov)_Problem_15,_sol.png]], all 12 vertices of three squares form a regular dodecagon (12-gon). | ||
| + | Denote by <math>O</math> the center of this dodecagon. | ||
| + | |||
| + | Hence, <math>\angle AOB = \frac{360^\circ}{12} = 30^\circ</math>. | ||
| + | |||
| + | Because the length of a side of a square is 6, <math>AO = 3 \sqrt{2}</math>. | ||
| + | |||
| + | Hence, <math>AB = 2 AO \sin \frac{\angle AOB}{2} = 3 \left( \sqrt{3} - 1 \right)</math>. | ||
| + | |||
| + | We notice that <math>\angle MAB = \angle MBA = 30^\circ</math>. | ||
| + | Hence, <math>AM = \frac{AB}{2\cos \angle MAB} = 3 - \sqrt{3}</math>. | ||
| + | |||
| + | Therefore, the area of the region that three squares cover is | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | & {\rm Area} \ ABCDEFGHIJKL - 12 {\rm Area} \ \triangle MAB \ | ||
| + | & = 12 {\rm Area} \ \triangle OAB - 12 {\rm Area} \ \triangle MAB \ | ||
| + | & = 12 \cdot \frac{1}{2} OA \cdot OB \sin \angle AOB | ||
| + | - 12 \cdot \frac{1}{2} MA \cdot MB \sin \angle AMB \ | ||
| + | & = 6 OA^2 \sin \angle AOB - 6 MA^2 \sin \angle AMB \ | ||
| + | & = 108 - 36 \sqrt{3} . | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | |||
| + | Therefore, the answer is <math>\boxed{\textbf{(E) }147}</math>. | ||
| + | |||
| + | ~Steven Chen (www.professorchenedu.com) | ||
| + | |||
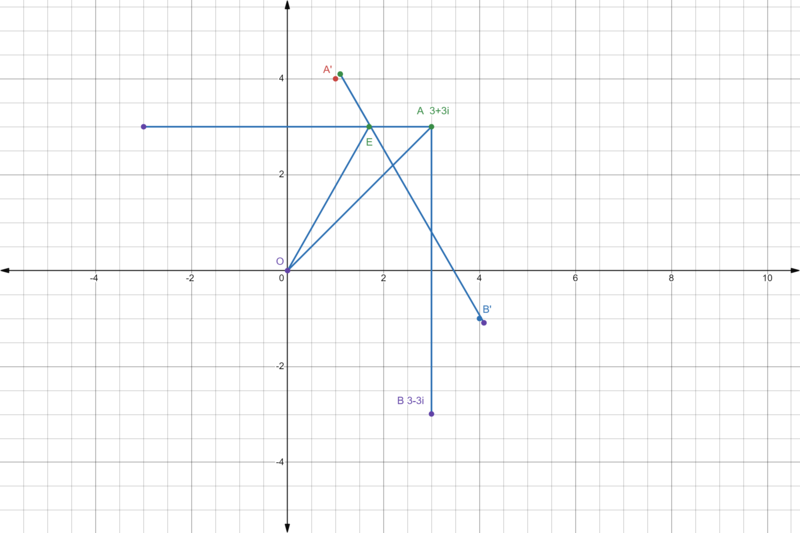
| + | == Solution 3 (complex number & coordinate geometry)== | ||
| + | |||
| + | [[Image:2021_amc_12b_fall_P15_S3.png|thumb|center|800px]] | ||
| + | |||
| + | set A = 3+3i , A' , B' rotate 30 degree from A, B | ||
| + | |||
| + | A'= A <math> \cdot e^i30^\circ = (3+3i)*(\sqrt{3}/2 + 1/2 i) =( \sqrt{3}/2 - 1/2) + (1/2 + \sqrt{3}/2) i </math> | ||
| + | |||
| + | line A'B' <math> \frac{y-(1/2 + \sqrt{3}/2)}{x - ( \sqrt{3}/2 - 1/2)} = Tan(90\circ+30\circ) = -\sqrt{3} </math> | ||
| + | |||
| + | intersect with line y=3 at point <math>E_{x} = \sqrt{3}</math> , then length <math> AE = A_{x} - E_{x} = 3- \sqrt{3}</math> , | ||
| + | |||
| + | use shoelace or <math>\triangle OAE </math> = 1/2 * AE * AB/2 = 1/2 * <math>(3- \sqrt{3})</math> * 3 | ||
| + | |||
| + | total area = 24 * <math>\triangle OAE </math> = = 108 - 36 <math>\sqrt{3}</math> the answer is <math>\boxed{\textbf{(E) }147}</math>. | ||
| + | |||
| + | ~[https://artofproblemsolving.com/wiki/index.php/User:Cyantist luckuso] | ||
| + | |||
| + | ==Video Solution (Just 4 min!)== | ||
| + | https://youtu.be/u_8EWGBErs8 | ||
| + | |||
| + | <i> ~Education, the Study of Everything </i> | ||
| + | |||
| + | ==Video Solution by TheBeautyofMath== | ||
| + | https://youtu.be/YD9J394zeig | ||
| + | |||
| + | ~IceMatrix | ||
| + | |||
| + | ==See Also== | ||
| + | {{AMC10 box|year=2021 Fall|ab=B|num-a=19|num-b=17}} | ||
| + | {{AMC12 box|year=2021 Fall|ab=B|num-a=16|num-b=14}} | ||
| + | {{MAA Notice}} | ||
Latest revision as of 20:41, 10 October 2024
Contents
[hide]Problem
Three identical square sheets of paper each with side length ![]() are stacked on top of each other. The middle sheet is rotated clockwise
are stacked on top of each other. The middle sheet is rotated clockwise ![]() about its center and the top sheet is rotated clockwise
about its center and the top sheet is rotated clockwise ![]() about its center, resulting in the
about its center, resulting in the ![]() -sided polygon shown in the figure below. The area of this polygon can be expressed in the form
-sided polygon shown in the figure below. The area of this polygon can be expressed in the form ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. What is
is not divisible by the square of any prime. What is ![]() ?
?
![[asy] defaultpen(fontsize(8)+0.8); size(150); pair O,A1,B1,C1,A2,B2,C2,A3,B3,C3,A4,B4,C4; real x=45, y=90, z=60; O=origin; A1=dir(x); A2=dir(x+y); A3=dir(x+2y); A4=dir(x+3y); B1=dir(x-z); B2=dir(x+y-z); B3=dir(x+2y-z); B4=dir(x+3y-z); C1=dir(x-2z); C2=dir(x+y-2z); C3=dir(x+2y-2z); C4=dir(x+3y-2z); draw(A1--A2--A3--A4--A1, gray+0.25+dashed); filldraw(B1--B2--B3--B4--cycle, white, gray+dashed+linewidth(0.25)); filldraw(C1--C2--C3--C4--cycle, white, gray+dashed+linewidth(0.25)); dot(O); pair P1,P2,P3,P4,Q1,Q2,Q3,Q4,R1,R2,R3,R4; P1=extension(A1,A2,B1,B2); Q1=extension(A1,A2,C3,C4); P2=extension(A2,A3,B2,B3); Q2=extension(A2,A3,C4,C1); P3=extension(A3,A4,B3,B4); Q3=extension(A3,A4,C1,C2); P4=extension(A4,A1,B4,B1); Q4=extension(A4,A1,C2,C3); R1=extension(C2,C3,B2,B3); R2=extension(C3,C4,B3,B4); R3=extension(C4,C1,B4,B1); R4=extension(C1,C2,B1,B2); draw(A1--P1--B2--R1--C3--Q1--A2); draw(A2--P2--B3--R2--C4--Q2--A3); draw(A3--P3--B4--R3--C1--Q3--A4); draw(A4--P4--B1--R4--C2--Q4--A1); [/asy]](http://latex.artofproblemsolving.com/7/e/b/7eb8841b95d6e1c451addf20403c4e540f176116.png)
![]()
Solution 1
![[asy] defaultpen(fontsize(8)+0.8); size(100); pair A=(0,0); pair B=(1.732,3); pair C=(3,3); pair D=(3,1.732); draw(A--(0,3)--C--(3,0)--A, lightgray+dashed); draw(A--B--C--A); draw(A--D--C, gray); label("$A$",A,W); label("$B$",B,N); label("$C$",C,NE); label("$D$",D,E); label("$E$",(0,3),NW); label("$F$",(3,0),E); [/asy]](http://latex.artofproblemsolving.com/6/4/f/64f3c31b5b88bfd1d71ed15cecc5de817a573f8e.png) The
The ![]() -sided polygon is made out of
-sided polygon is made out of ![]() shapes like
shapes like ![]() . Then
. Then ![]() , and
, and ![]() , so
, so ![]() . Then
. Then ![]() ; therefore
; therefore ![]() . Thus
. Thus
![]() and the required area is
and the required area is ![]() . Finally
. Finally ![]() .
~lopkiloinm
.
~lopkiloinm
Note: Drop an altitude from ![]() to
to ![]() to construct point
to construct point ![]() . This creates right triangles. ~erringbubble
. This creates right triangles. ~erringbubble
Solution 2
As shown in Image:2021_AMC_12B_(Nov)_Problem_15,_sol.png, all 12 vertices of three squares form a regular dodecagon (12-gon).
Denote by ![]() the center of this dodecagon.
the center of this dodecagon.
Hence, ![]() .
.
Because the length of a side of a square is 6, ![]() .
.
Hence, ![]() .
.
We notice that ![]() .
Hence,
.
Hence, ![]() .
.
Therefore, the area of the region that three squares cover is

Therefore, the answer is ![]() .
.
~Steven Chen (www.professorchenedu.com)
Solution 3 (complex number & coordinate geometry)
set A = 3+3i , A' , B' rotate 30 degree from A, B
A'= A ![]()
line A'B' 
intersect with line y=3 at point ![]() , then length
, then length ![]() ,
,
use shoelace or ![]() = 1/2 * AE * AB/2 = 1/2 *
= 1/2 * AE * AB/2 = 1/2 * ![]() * 3
* 3
total area = 24 * ![]() = = 108 - 36
= = 108 - 36 ![]() the answer is
the answer is ![]() .
.
Video Solution (Just 4 min!)
~Education, the Study of Everything
Video Solution by TheBeautyofMath
~IceMatrix
See Also
| 2021 Fall AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 17 |
Followed by Problem 19 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2021 Fall AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 14 |
Followed by Problem 16 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.