Difference between revisions of "2014 AIME II Problems/Problem 14"
m (→Solution 1) |
Mathkiddie (talk | contribs) |
||
| (6 intermediate revisions by 4 users not shown) | |||
| Line 20: | Line 20: | ||
Let us just drop the perpendicular from <math>B</math> to <math>AC</math> and label the point of intersection <math>O</math>. We will use this point later in the problem. | Let us just drop the perpendicular from <math>B</math> to <math>AC</math> and label the point of intersection <math>O</math>. We will use this point later in the problem. | ||
As we can see, | As we can see, | ||
| − | |||
| − | |||
<math>M</math> is the midpoint of <math>BC</math> and <math>N</math> is the midpoint of <math>HM</math> | <math>M</math> is the midpoint of <math>BC</math> and <math>N</math> is the midpoint of <math>HM</math> | ||
| − | |||
| − | |||
<math>AHC</math> is a <math>45-45-90</math> triangle, so <math>\angle{HAB}=15^\circ</math>. | <math>AHC</math> is a <math>45-45-90</math> triangle, so <math>\angle{HAB}=15^\circ</math>. | ||
| − | |||
| − | |||
<math>AHD</math> is <math>30-60-90</math> triangle. | <math>AHD</math> is <math>30-60-90</math> triangle. | ||
| − | |||
<math>AH</math> and <math>PN</math> are parallel lines so <math>PND</math> is <math>30-60-90</math> triangle also. | <math>AH</math> and <math>PN</math> are parallel lines so <math>PND</math> is <math>30-60-90</math> triangle also. | ||
| − | + | Then if we use those informations we get <math>AD=2HD</math> and <math>PD=2ND</math> and <math>AP=AD-PD=2HD-2ND=2HN</math> or <math>AP=2HN=HM</math>. | |
| − | |||
| − | Then if we use those informations we get <math>AD=2HD</math> and | ||
| − | |||
| − | |||
| − | <math>PD=2ND</math> and <math>AP=AD-PD=2HD-2ND=2HN</math> | ||
| − | |||
| − | |||
Now we know that <math>HM=AP</math>, we can find for <math>HM</math> which is simpler to find. | Now we know that <math>HM=AP</math>, we can find for <math>HM</math> which is simpler to find. | ||
| − | |||
| − | |||
We can use point <math>B</math> to split it up as <math>HM=HB+BM</math>, | We can use point <math>B</math> to split it up as <math>HM=HB+BM</math>, | ||
| − | + | We can chase those lengths and we would get <math>AB=10</math>, so <math>OB=5</math>, so <math>BC=5\sqrt{2}</math>, so <math>BM=\dfrac{1}{2} \cdot BC=\dfrac{5\sqrt{2}}{2}</math> | |
| − | |||
| − | We can chase those lengths and we would get | ||
| − | |||
| − | |||
| − | <math>AB=10</math>, so <math>OB=5</math>, so <math>BC=5\sqrt{2}</math>, so <math>BM=\dfrac{1}{2} \cdot BC=\dfrac{5\sqrt{2}}{2}</math> | ||
| − | |||
| − | |||
We can also use Law of Sines: | We can also use Law of Sines: | ||
| − | |||
<cmath>\frac{BC}{AB}=\frac{\sin\angle A}{\sin\angle C}</cmath> | <cmath>\frac{BC}{AB}=\frac{\sin\angle A}{\sin\angle C}</cmath> | ||
<cmath>\frac{BC}{10}=\frac{\frac{1}{2}}{\frac{\sqrt{2}}{2}}\implies BC=5\sqrt{2}</cmath> | <cmath>\frac{BC}{10}=\frac{\frac{1}{2}}{\frac{\sqrt{2}}{2}}\implies BC=5\sqrt{2}</cmath> | ||
| − | |||
Then using right triangle <math>AHB</math>, we have <math>HB=10 \sin 15^\circ</math> | Then using right triangle <math>AHB</math>, we have <math>HB=10 \sin 15^\circ</math> | ||
| − | |||
| − | |||
So <math>HB=10 \sin 15^\circ=\dfrac{5(\sqrt{6}-\sqrt{2})}{2}</math>. | So <math>HB=10 \sin 15^\circ=\dfrac{5(\sqrt{6}-\sqrt{2})}{2}</math>. | ||
| − | |||
| − | |||
And we know that <math>AP = HM = HB + BM = \frac{5(\sqrt6-\sqrt2)}{2} + \frac{5\sqrt2}{2} = \frac{5\sqrt6}{2}</math>. | And we know that <math>AP = HM = HB + BM = \frac{5(\sqrt6-\sqrt2)}{2} + \frac{5\sqrt2}{2} = \frac{5\sqrt6}{2}</math>. | ||
| − | |||
| − | |||
Finally if we calculate <math>(AP)^2</math>. | Finally if we calculate <math>(AP)^2</math>. | ||
| − | |||
| − | |||
<math>(AP)^2=\dfrac{150}{4}=\dfrac{75}{2}</math>. So our final answer is <math>75+2=77</math>. | <math>(AP)^2=\dfrac{150}{4}=\dfrac{75}{2}</math>. So our final answer is <math>75+2=77</math>. | ||
| − | |||
| − | |||
<math>m+n=\boxed{077}</math> | <math>m+n=\boxed{077}</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
-Gamjawon | -Gamjawon | ||
| Line 91: | Line 52: | ||
<cmath>HC=\frac{5\sqrt2+5\sqrt6}{2}</cmath> | <cmath>HC=\frac{5\sqrt2+5\sqrt6}{2}</cmath> | ||
| − | <math>MC=\frac{ | + | <math>MC=\frac{BC}{2},</math> |
<cmath>HM=\frac{5\sqrt6}{2}</cmath> | <cmath>HM=\frac{5\sqrt6}{2}</cmath> | ||
<cmath>HN=\frac{5\sqrt6}{4}</cmath> | <cmath>HN=\frac{5\sqrt6}{4}</cmath> | ||
| Line 158: | Line 119: | ||
</asy> | </asy> | ||
Draw the <math>45-45-90 \triangle AHC</math>. Now, take the perpendicular bisector of <math>BC</math> to intersect the circumcircle of <math>\triangle ABC</math> and <math>AC</math> at <math>F, L, G</math> as shown, and denote <math>O</math> to be the circumcenter of <math>\triangle ABC</math>. It is not difficult to see by angle chasing that <math>AHBGO</math> is cyclic, namely with diameter <math>AB</math>. Then, by symmetry, <math>EH = HB</math> and as <math>HB, OG</math> are both subtended by equal arcs they are equal. Hence, <math>EH = GO</math>. Now, draw line <math>HL</math> and intersect it at <math>AC</math> at point <math>K</math> in the diagram. It is not hard to use angle chase to arrive at <math>AEOL</math> a parallelogram, and from our length condition derived earlier, <math>AL \parallel HG</math>. From here, it is clear that <math>AK = KG</math>; that is, <math>P</math> is just the intersection of the perpendicular from <math>K</math> down to <math>BC</math> and <math>AD</math>! After this point, note that <math>AP = PF</math>. It is easily derived that the circumradius of <math>\triangle ABC</math> is <math>\frac{10}{\sqrt{2}}</math>. Now, <math>APO</math> is a <math>30-60-90</math> triangle, and from here it is easy to arrive at the final answer of <math>\boxed{077}</math>. ~awang11's sol | Draw the <math>45-45-90 \triangle AHC</math>. Now, take the perpendicular bisector of <math>BC</math> to intersect the circumcircle of <math>\triangle ABC</math> and <math>AC</math> at <math>F, L, G</math> as shown, and denote <math>O</math> to be the circumcenter of <math>\triangle ABC</math>. It is not difficult to see by angle chasing that <math>AHBGO</math> is cyclic, namely with diameter <math>AB</math>. Then, by symmetry, <math>EH = HB</math> and as <math>HB, OG</math> are both subtended by equal arcs they are equal. Hence, <math>EH = GO</math>. Now, draw line <math>HL</math> and intersect it at <math>AC</math> at point <math>K</math> in the diagram. It is not hard to use angle chase to arrive at <math>AEOL</math> a parallelogram, and from our length condition derived earlier, <math>AL \parallel HG</math>. From here, it is clear that <math>AK = KG</math>; that is, <math>P</math> is just the intersection of the perpendicular from <math>K</math> down to <math>BC</math> and <math>AD</math>! After this point, note that <math>AP = PF</math>. It is easily derived that the circumradius of <math>\triangle ABC</math> is <math>\frac{10}{\sqrt{2}}</math>. Now, <math>APO</math> is a <math>30-60-90</math> triangle, and from here it is easy to arrive at the final answer of <math>\boxed{077}</math>. ~awang11's sol | ||
| + | |||
| + | ==Solution 5== | ||
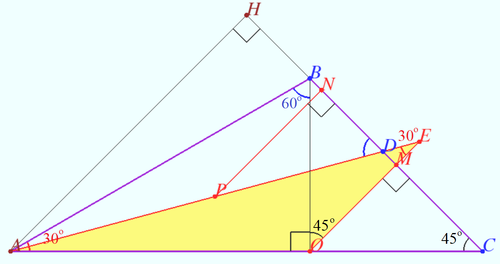
| + | [[File:2014 AIME II 14.png|500px|right]] | ||
| + | Let <math>BO \perp AC, O \in AC.</math> | ||
| + | |||
| + | Let <math>ME \perp BC, E \in AD.</math> | ||
| + | |||
| + | <math>MB = MC, \angle C = 45^\circ \implies</math> points <math>M, E, O</math> are collinear. | ||
| + | |||
| + | <math>HN = NM, AH||NP||ME \implies AP = PE.</math> | ||
| + | |||
| + | In <math>\triangle ABO \hspace{10mm} \angle A = 30^\circ \implies AO = AB \cos 60^\circ = 5 \sqrt{3}.</math> | ||
| + | |||
| + | In <math>\triangle AEO \hspace{10mm} \angle A = 15^\circ, \angle O = 90^\circ + 45^\circ = 135^\circ \implies</math> | ||
| + | <cmath>\angle AEO = 30^\circ \implies</cmath> | ||
| + | <cmath>AE = AO \frac {\sin 135^\circ}{\sin 30^\circ} = 5 \sqrt{3} \cdot \sqrt{2} = 5 \sqrt{6} \implies</cmath> | ||
| + | <cmath>AP = 5 \sqrt {\frac {3}{2}} \implies AP^2 = \frac {75}{2} \implies \boxed{\textbf{077}}.</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | |||
| + | ==Video solution== | ||
| + | |||
| + | https://www.youtube.com/watch?v=SvJ0wDJphdU | ||
| + | |||
== See also == | == See also == | ||
{{AIME box|year=2014|n=II|num-b=13|num-a=15}} | {{AIME box|year=2014|n=II|num-b=13|num-a=15}} | ||
Latest revision as of 19:40, 24 October 2024
Contents
[hide]Problem
In ![]() , and
, and ![]() . Let
. Let ![]() and
and ![]() be points on the line
be points on the line ![]() such that
such that ![]() ,
, ![]() , and
, and ![]() . Point
. Point ![]() is the midpoint of the segment
is the midpoint of the segment ![]() , and point
, and point ![]() is on ray
is on ray ![]() such that
such that ![]() . Then
. Then ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Diagram
![[asy] unitsize(20); pair A = MP("A",(-5sqrt(3),0)), B = MP("B",(0,5),N), C = MP("C",(5,0)), M = D(MP("M",0.5(B+C),NE)), D = MP("D",IP(L(A,incenter(A,B,C),0,2),B--C),N), H = MP("H",foot(A,B,C),N), N = MP("N",0.5(H+M),NE), P = MP("P",IP(A--D,L(N,N-(1,1),0,10))); D(A--B--C--cycle); D(B--H--A,blue+dashed); D(A--D); D(P--N); markscalefactor = 0.05; D(rightanglemark(A,H,B)); D(rightanglemark(P,N,D)); MP("10",0.5(A+B)-(-0.1,0.1),NW); [/asy]](http://latex.artofproblemsolving.com/5/f/e/5fea6b70f70aa37b2866f7629cd76c71151e666f.png)
Solution 1
Let us just drop the perpendicular from ![]() to
to ![]() and label the point of intersection
and label the point of intersection ![]() . We will use this point later in the problem.
As we can see,
. We will use this point later in the problem.
As we can see,
![]() is the midpoint of
is the midpoint of ![]() and
and ![]() is the midpoint of
is the midpoint of ![]()
![]() is a
is a ![]() triangle, so
triangle, so ![]() .
.
![]() is
is ![]() triangle.
triangle.
![]() and
and ![]() are parallel lines so
are parallel lines so ![]() is
is ![]() triangle also.
Then if we use those informations we get
triangle also.
Then if we use those informations we get ![]() and
and ![]() and
and ![]() or
or ![]() .
Now we know that
.
Now we know that ![]() , we can find for
, we can find for ![]() which is simpler to find.
We can use point
which is simpler to find.
We can use point ![]() to split it up as
to split it up as ![]() ,
We can chase those lengths and we would get
,
We can chase those lengths and we would get ![]() , so
, so ![]() , so
, so ![]() , so
, so ![]() We can also use Law of Sines:
We can also use Law of Sines:
![]()
![\[\frac{BC}{10}=\frac{\frac{1}{2}}{\frac{\sqrt{2}}{2}}\implies BC=5\sqrt{2}\]](http://latex.artofproblemsolving.com/9/b/0/9b0b5ead0c0c232875848ec246d471f494a4bc87.png) Then using right triangle
Then using right triangle ![]() , we have
, we have ![]() So
So ![]() .
And we know that
.
And we know that ![]() .
Finally if we calculate
.
Finally if we calculate ![]() .
.
![]() . So our final answer is
. So our final answer is ![]() .
.
![]()
-Gamjawon -edited by srisainandan6 to clarify and correct a small mistake
Solution 2
Here's a solution that doesn't need ![]() .
.
As above, get to ![]() . As in the figure, let
. As in the figure, let ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() . Then
. Then ![]() is a 45-45-90 triangle, and
is a 45-45-90 triangle, and ![]() is a 30-60-90 triangle. So
is a 30-60-90 triangle. So ![]() and
and ![]() ; also,
; also, ![]() ,
, ![]() , and
, and ![]() . But
. But ![]() and
and ![]() are parallel, both being orthogonal to
are parallel, both being orthogonal to ![]() . Therefore
. Therefore ![]() , or
, or ![]() , and we're done.
, and we're done.
Solution 3
Break our diagram into 2 special right triangle by dropping an altitude from ![]() to
to ![]() we then get that
we then get that ![]() Since
Since ![]() is a 45-45-90,
is a 45-45-90,
![]()
![]()
![]()
![]() We know that
We know that ![]() and are 30-60-90.
Thus,
and are 30-60-90.
Thus, ![]()
![]() . So our final answer is
. So our final answer is ![]() .
.
Solution 4
![[asy] /* Geogebra to Asymptote conversion, documentation at artofproblemsolving.com/Wiki go to User:Azjps/geogebra */ import graph; size(15cm); real labelscalefactor = 0.5; /* changes label-to-point distance */ pen dps = linewidth(0.7) + fontsize(10); defaultpen(dps); /* default pen style */ pen dotstyle = black; /* point style */ real xmin = -8.455641974276588, xmax = 26.731282460265, ymin = -10.92318356252699, ymax = 9.023689834456471; /* image dimensions */ pen wrwrwr = rgb(0.3803921568627451,0.3803921568627451,0.3803921568627451); pen rvwvcq = rgb(0.08235294117647059,0.396078431372549,0.7529411764705882); draw((-1.4934334172297545,2.6953043701763835)--(-1.459546107520503,-6.96389444957376)--(1.1286284157632023,-6.954814372303504)--(4.651736947776926,-3.406898607850789)--(4.642656870506668,-0.8187240845670819)--cycle, linewidth(2) + rvwvcq); /* draw figures */ draw((-1.4934334172297545,2.6953043701763835)--(1.1286284157632023,-6.954814372303504), linewidth(2) + wrwrwr); draw((xmin, -0.9930079421029264*xmin + 1.2123131258653241)--(xmax, -0.9930079421029264*xmax + 1.2123131258653241), linewidth(2) + wrwrwr); /* line */ draw((xmin, 0.0035082940460819836*xmin-6.958773932654766)--(xmax, 0.0035082940460819836*xmax-6.958773932654766), linewidth(2) + wrwrwr); /* line */ draw((xmin, -285.03882139434313*xmin-422.9911967079192)--(xmax, -285.03882139434313*xmax-422.9911967079192), linewidth(2) + wrwrwr); /* line */ draw((xmin, -1.7181023895538718*xmin + 0.12943284739433739)--(xmax, -1.7181023895538718*xmax + 0.12943284739433739), linewidth(2) + wrwrwr); /* line */ draw(circle((4.642656870506668,-0.8187240845670819), 7.071067811865476), linewidth(2) + wrwrwr); draw((xmin, -285.0388213943529*xmin + 1322.5187184230485)--(xmax, -285.0388213943529*xmax + 1322.5187184230485), linewidth(2) + wrwrwr); /* line */ draw((-1.4934334172297545,2.6953043701763835)--(4.617849638067675,6.252300211899359), linewidth(2) + wrwrwr); draw((4.617849638067675,6.252300211899359)--(-1.459546107520503,-6.96389444957376), linewidth(2) + wrwrwr); draw(circle((-0.18240250073327363,-2.12975500106356), 5), linewidth(2) + wrwrwr); draw((xmin, -285.0388213943432*xmin + 449.7637608575419)--(xmax, -285.0388213943432*xmax + 449.7637608575419), linewidth(2) + wrwrwr); /* line */ draw((1.1286284157632023,-6.954814372303504)--(4.651736947776926,-3.406898607850789), linewidth(2) + wrwrwr); draw((-1.4934334172297545,2.6953043701763835)--(4.642656870506668,-0.8187240845670819), linewidth(2) + wrwrwr); draw((-1.4934334172297545,2.6953043701763835)--(-1.459546107520503,-6.96389444957376), linewidth(2) + rvwvcq); draw((-1.459546107520503,-6.96389444957376)--(1.1286284157632023,-6.954814372303504), linewidth(2) + rvwvcq); draw((1.1286284157632023,-6.954814372303504)--(4.651736947776926,-3.406898607850789), linewidth(2) + rvwvcq); draw((4.651736947776926,-3.406898607850789)--(4.642656870506668,-0.8187240845670819), linewidth(2) + rvwvcq); draw((4.642656870506668,-0.8187240845670819)--(-1.4934334172297545,2.6953043701763835), linewidth(2) + rvwvcq); /* dots and labels */ dot((-1.4934334172297545,2.6953043701763835),dotstyle); label("$A$", (-1.3954084351380491,2.9230996889873015), NE * labelscalefactor); dot((1.1286284157632023,-6.954814372303504),dotstyle); label("$B$", (1.2093379191072373,-6.719031552166216), NE * labelscalefactor); dot((8.199652712229643,-6.930007139864511),linewidth(4pt) + dotstyle); label("$C$", (8.292420110475998,-6.741880204396438), NE * labelscalefactor); dot((-1.459546107520503,-6.96389444957376),linewidth(4pt) + dotstyle); label("$H$", (-1.3725597829078273,-6.787577508856881), NE * labelscalefactor); dot((-1.4686261847907602,-4.375719926290057),linewidth(4pt) + dotstyle); label("$E$", (-1.3725597829078273,-4.182831154611618), NE * labelscalefactor); dot((4.617849638067675,6.252300211899359),linewidth(4pt) + dotstyle); label("$L$", (4.705181710331174,6.441792132441429), NE * labelscalefactor); dot((4.642656870506668,-0.8187240845670819),linewidth(4pt) + dotstyle); label("$O$", (4.728030362561396,-0.6412900589272691), NE * labelscalefactor); dot((4.117194931218359,-6.944329602191013),linewidth(4pt) + dotstyle); label("$D$", (4.2025113612662945,-6.764728856626659), NE * labelscalefactor); dot((4.6674641029456625,-7.889748381033524),linewidth(4pt) + dotstyle); label("$F$", (4.750879014791618,-7.701523598065745), NE * labelscalefactor); dot((4.651736947776926,-3.406898607850789),linewidth(4pt) + dotstyle); label("$G$", (4.750879014791618,-3.2231877609423107), NE * labelscalefactor); dot((1.5791517652735851,-0.3557971188372022),linewidth(4pt) + dotstyle); label("$K$", (1.6663109637116735,-0.18431701432283698), NE * labelscalefactor); dot((1.5870153428579534,-2.5972220054285695),linewidth(4pt) + dotstyle); label("$P$", (1.6891596159418953,-2.4234849328845542), NE * labelscalefactor); clip((xmin,ymin)--(xmin,ymax)--(xmax,ymax)--(xmax,ymin)--cycle); /* end of picture */ [/asy]](http://latex.artofproblemsolving.com/d/2/9/d29efc8f524cbe013c8c1eb13100d2244e9e6c45.png) Draw the
Draw the ![]() . Now, take the perpendicular bisector of
. Now, take the perpendicular bisector of ![]() to intersect the circumcircle of
to intersect the circumcircle of ![]() and
and ![]() at
at ![]() as shown, and denote
as shown, and denote ![]() to be the circumcenter of
to be the circumcenter of ![]() . It is not difficult to see by angle chasing that
. It is not difficult to see by angle chasing that ![]() is cyclic, namely with diameter
is cyclic, namely with diameter ![]() . Then, by symmetry,
. Then, by symmetry, ![]() and as
and as ![]() are both subtended by equal arcs they are equal. Hence,
are both subtended by equal arcs they are equal. Hence, ![]() . Now, draw line
. Now, draw line ![]() and intersect it at
and intersect it at ![]() at point
at point ![]() in the diagram. It is not hard to use angle chase to arrive at
in the diagram. It is not hard to use angle chase to arrive at ![]() a parallelogram, and from our length condition derived earlier,
a parallelogram, and from our length condition derived earlier, ![]() . From here, it is clear that
. From here, it is clear that ![]() ; that is,
; that is, ![]() is just the intersection of the perpendicular from
is just the intersection of the perpendicular from ![]() down to
down to ![]() and
and ![]() ! After this point, note that
! After this point, note that ![]() . It is easily derived that the circumradius of
. It is easily derived that the circumradius of ![]() is
is ![]() . Now,
. Now, ![]() is a
is a ![]() triangle, and from here it is easy to arrive at the final answer of
triangle, and from here it is easy to arrive at the final answer of ![]() . ~awang11's sol
. ~awang11's sol
Solution 5
Let ![]()
Let ![]()
![]() points
points ![]() are collinear.
are collinear.
![]()
In ![]()
In ![]()
![]()
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Video solution
https://www.youtube.com/watch?v=SvJ0wDJphdU
See also
| 2014 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.