Difference between revisions of "2001 AIME II Problems/Problem 8"
(solution) |
(→Video Solution) |
||
| (15 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
| − | A certain [[function]] <math>f</math> has the properties that <math>f(3x) = 3f(x)</math> for all positive real values of <math>x</math>, and that <math>f(x) = 1 - | + | A certain [[function]] <math>f</math> has the properties that <math>f(3x) = 3f(x)</math> for all positive real values of <math>x</math>, and that <math>f(x) = 1-|x-2|</math> for <math>1\le x \le 3</math>. Find the smallest <math>x</math> for which <math>f(x) = f(2001)</math>. |
== Solution == | == Solution == | ||
| Line 7: | Line 7: | ||
<cmath>f(2001) = 729\left[1 - \left| \frac{2001}{729} - 2\right|\right] = 186.</cmath> | <cmath>f(2001) = 729\left[1 - \left| \frac{2001}{729} - 2\right|\right] = 186.</cmath> | ||
| − | We now need the smallest <math>x</math> such that <math>f(x) = 3^kf\left(\frac{x}{3^k}\right) = 186</math>. The [[range]] of <math>f(x),\ 1 \le x \le 3</math>, is <math>0 \le f(x) \le 1</math>. | + | We now need the smallest <math>x</math> such that <math>f(x) = 3^kf\left(\frac{x}{3^k}\right) = 186</math>. The [[range]] of <math>f(x),\ 1 \le x \le 3</math>, is <math>0 \le f(x) \le 1</math>. So when <math>1 \le \frac{x}{3^k} \le 3</math>, we have <math>0 \le f\left(\frac{x}{3^k}\right) = \frac{186}{3^k} \le 1</math>. Multiplying by <math>3^k</math>: <math>0 \le 186 \le 3^k</math>, so the smallest value of <math>k</math> is <math>k = 5</math>. Then, |
| − | <cmath>186 = 243\left[1 - \left| \frac{x}{243} - 2\right|\right] \Longrightarrow x = \pm 57 + 2 | + | <cmath>186 = {3^5}f\left(\frac{x}{3^5}\right).</cmath> |
| − | \cdot 243</cmath> | + | |
| + | Because we forced <math>1 \le \frac{x}{3^5} \le 3</math>, so | ||
| + | |||
| + | <cmath>186 = {3^5}f\left(\frac{x}{3^5}\right) = 243\left[1 - \left| \frac{x}{243} - 2\right|\right] \Longrightarrow x = \pm 57 + 2 | ||
| + | \cdot 243.</cmath> | ||
We want the smaller value of <math>x = \boxed{429}</math>. | We want the smaller value of <math>x = \boxed{429}</math>. | ||
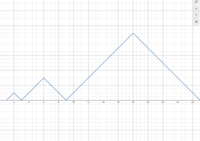
| − | An alternative approach is to consider the graph of <math>f(x)</math>, which | + | An alternative approach is to consider the graph of <math>f(x)</math>, which iterates every power of <math>3</math>, and resembles the section from <math>1 \le x \le 3</math> dilated by a factor of <math>3</math> at each iteration. |
| + | |||
| + | ==Solution 2 (Graphing)== | ||
| + | |||
| + | [[File:Screenshot 2023-06-14 194739.png|center|200px]] | ||
| + | |||
| + | First, we start by graphing the function when <math>1\leq{x}\leq3</math>, which consists of the lines <math>y=x-1</math> and <math>y=3-x</math> that intersect at <math>(2,1)</math>. Similarly, using <math>f(3x)=3f(x)</math>, we get a dilation of our initial figure by a factor of 3 for the next interval and so on. | ||
| + | Observe that the intersection of two lines always has coordinates <math>(2y,y)</math> where <math>y=3^a</math> for some <math>a</math>. First, we compute <math>f(2001)</math>. The nearest intersection point is <math>(1458,729)</math> when <math>a=7</math>. Therefore, we can safely assume that <math>f(2001)</math> is somewhere on the line with a slope of <math>-1</math> that intersects at that nearest point. Using the fact that the slope of the line is <math>-1</math>, we compute <math>f(2001)=729-543=186</math>. However, we want the minimum value such that <math>f(x)=186</math> and we see that there is another intersection point on the left which has a <math>y>186</math>, namely <math>(486,243)</math>. Therefore, we want the point that lies on the line with slope <math>1</math> that intersects this point. Once again, since the slope of the line is <math>1</math>, we get <math>x=486-57=\boxed{429}</math>. | ||
| + | |||
| + | ~[https://artofproblemsolving.com/wiki/index.php/User:Magnetoninja Magnetoninja] | ||
| + | |||
| + | ==Solution 3 (Complete Bash but FAST)== | ||
| + | |||
| + | We evaluate the first few terms of f(x) to try to find a pattern. | ||
| + | |||
| + | F(1)=0 | ||
| + | F(2)=1 | ||
| + | F(3)=0 | ||
| + | F(4)=1 | ||
| + | F(5) = 3(F(<math>\frac{5}{3}</math>)) = 2 | ||
| + | |||
| + | That doesn‘t seem to be getting us anywhere. | ||
| + | We notice what we did with f(5) will probably work with f(2001). | ||
| + | |||
| + | <math>F(2001) = 3f(667)=9f(\frac{667}{3}) = 27f(\frac{667}{9}) = 81f(\frac{667}{27})=243f(\frac{667}{81})=729f(\frac{667}{243})</math> | ||
| + | |||
| + | From here, we can evaluate f(2001) = <math>186</math> when we plug in <math>\frac{667}{243}</math> into <math>1 - |x - 2|</math>. So all we need to find is the least number, let‘s call it, say y such that f(y)=186. | ||
| + | |||
| + | Repeating the same process we did before with f(2001), | ||
| + | |||
| + | <math>188 = F(y)= 3f(\frac{y}{3}) = 9f(\frac{y}{9}) = 27f(\frac{y}{27})=81f(\frac{y}{81}) = 243f(\frac{y}{243})</math> | ||
| + | |||
| + | Notice that we stopped at <math>243f(\frac{y}{243})</math> because <math>\frac{186}{243}</math> is inside the range of <math>1-|x-2|</math>, which is [0,1]. Now, f(y/243) = 186/243. Setting <math>186/243 = 1-|x-2|</math>, we get 2 solutions for x: <math>\frac{543}{243}</math> and <math>\frac{429}{243}</math>. | ||
| + | |||
| + | Now, the problem asks for the smallest solution, so we obviously choose 429/243 as the solution for 243f(y/243) because it is smaller. | ||
| + | |||
| + | We found that <math>\frac{y}{243}=\frac{429}{243}</math>, and solving this equation gives our answer <math>\boxed{429}</math> | ||
| + | |||
| + | ~MathCosine | ||
| + | |||
| + | ==Video Solution== | ||
| + | |||
| + | https://www.youtube.com/watch?v=j3hj2yNga0w | ||
| + | |||
| + | by Coach Jay | ||
== See also == | == See also == | ||
| Line 20: | Line 68: | ||
[[Category:Intermediate Algebra Problems]] | [[Category:Intermediate Algebra Problems]] | ||
| + | {{MAA Notice}} | ||
Revision as of 14:53, 2 November 2024
Contents
[hide]Problem
A certain function ![]() has the properties that
has the properties that ![]() for all positive real values of
for all positive real values of ![]() , and that
, and that ![]() for
for ![]() . Find the smallest
. Find the smallest ![]() for which
for which ![]() .
.
Solution
Iterating the condition ![]() , we find that
, we find that ![]() for positive integers
for positive integers ![]() . We know the definition of
. We know the definition of ![]() from
from ![]() , so we would like to express
, so we would like to express ![]() . Indeed,
. Indeed,
![]()
We now need the smallest ![]() such that
such that ![]() . The range of
. The range of ![]() , is
, is ![]() . So when
. So when ![]() , we have
, we have ![]() . Multiplying by
. Multiplying by ![]() :
: ![]() , so the smallest value of
, so the smallest value of ![]() is
is ![]() . Then,
. Then,
![]()
Because we forced ![]() , so
, so
![]()
We want the smaller value of ![]() .
.
An alternative approach is to consider the graph of ![]() , which iterates every power of
, which iterates every power of ![]() , and resembles the section from
, and resembles the section from ![]() dilated by a factor of
dilated by a factor of ![]() at each iteration.
at each iteration.
Solution 2 (Graphing)
First, we start by graphing the function when ![]() , which consists of the lines
, which consists of the lines ![]() and
and ![]() that intersect at
that intersect at ![]() . Similarly, using
. Similarly, using ![]() , we get a dilation of our initial figure by a factor of 3 for the next interval and so on.
Observe that the intersection of two lines always has coordinates
, we get a dilation of our initial figure by a factor of 3 for the next interval and so on.
Observe that the intersection of two lines always has coordinates ![]() where
where ![]() for some
for some ![]() . First, we compute
. First, we compute ![]() . The nearest intersection point is
. The nearest intersection point is ![]() when
when ![]() . Therefore, we can safely assume that
. Therefore, we can safely assume that ![]() is somewhere on the line with a slope of
is somewhere on the line with a slope of ![]() that intersects at that nearest point. Using the fact that the slope of the line is
that intersects at that nearest point. Using the fact that the slope of the line is ![]() , we compute
, we compute ![]() . However, we want the minimum value such that
. However, we want the minimum value such that ![]() and we see that there is another intersection point on the left which has a
and we see that there is another intersection point on the left which has a ![]() , namely
, namely ![]() . Therefore, we want the point that lies on the line with slope
. Therefore, we want the point that lies on the line with slope ![]() that intersects this point. Once again, since the slope of the line is
that intersects this point. Once again, since the slope of the line is ![]() , we get
, we get ![]() .
.
Solution 3 (Complete Bash but FAST)
We evaluate the first few terms of f(x) to try to find a pattern.
F(1)=0
F(2)=1
F(3)=0
F(4)=1
F(5) = 3(F(![]() )) = 2
)) = 2
That doesn‘t seem to be getting us anywhere. We notice what we did with f(5) will probably work with f(2001).
![]()
From here, we can evaluate f(2001) = ![]() when we plug in
when we plug in ![]() into
into ![]() . So all we need to find is the least number, let‘s call it, say y such that f(y)=186.
. So all we need to find is the least number, let‘s call it, say y such that f(y)=186.
Repeating the same process we did before with f(2001),
![]()
Notice that we stopped at ![]() because
because ![]() is inside the range of
is inside the range of ![]() , which is [0,1]. Now, f(y/243) = 186/243. Setting
, which is [0,1]. Now, f(y/243) = 186/243. Setting ![]() , we get 2 solutions for x:
, we get 2 solutions for x: ![]() and
and ![]() .
.
Now, the problem asks for the smallest solution, so we obviously choose 429/243 as the solution for 243f(y/243) because it is smaller.
We found that ![]() , and solving this equation gives our answer
, and solving this equation gives our answer ![]()
~MathCosine
Video Solution
https://www.youtube.com/watch?v=j3hj2yNga0w
by Coach Jay
See also
| 2001 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 7 |
Followed by Problem 9 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()