Difference between revisions of "2024 AMC 12A Problems/Problem 19"
(→Solution 1) |
(→Solution 1) |
||
| Line 24: | Line 24: | ||
<cmath>8 \cdot 3+5 \cdot 3=7BD</cmath> | <cmath>8 \cdot 3+5 \cdot 3=7BD</cmath> | ||
<cmath>BD=\frac{39}{7}</cmath> | <cmath>BD=\frac{39}{7}</cmath> | ||
| − | Since <math>\frac{39}{7}< | + | Since <math>\frac{39}{7}<7</math>, |
The answer is <math>\boxed{\textbf{(D) }\frac{39}{7}}</math>. | The answer is <math>\boxed{\textbf{(D) }\frac{39}{7}}</math>. | ||
| − | ~lptoggled, formatting by eevee9406, image by ~[https://artofproblemsolving.com/wiki/index.php/User:Cyantist luckuso] | + | ~lptoggled, formatting by eevee9406, typo fixed by meh494, image by ~[https://artofproblemsolving.com/wiki/index.php/User:Cyantist luckuso] |
==Solution 2 (Law of Cosines + Law of Sines)== | ==Solution 2 (Law of Cosines + Law of Sines)== | ||
Revision as of 00:08, 9 November 2024
Problem
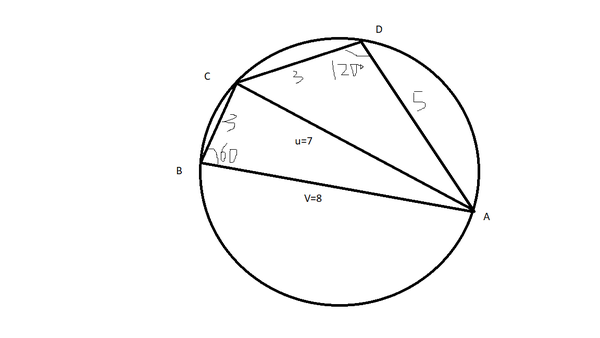
Cyclic quadrilateral ![]() has lengths
has lengths ![]() and
and ![]() with
with ![]() . What is the length of the shorter diagonal of
. What is the length of the shorter diagonal of ![]() ?
?
![]()
Solution 1
First, ![]() by properties of cyclic quadrilaterals.
by properties of cyclic quadrilaterals.
Let ![]() . Apply the Law of Cosines on
. Apply the Law of Cosines on ![]() :
:
![]()
![]()
Let ![]() . Apply the Law of Cosines on
. Apply the Law of Cosines on ![]() :
:
![]()
![]()
![]()
By Ptolemy’s Theorem,
![]()
![]()
![]() Since
Since ![]() ,
The answer is
,
The answer is ![]() .
.
~lptoggled, formatting by eevee9406, typo fixed by meh494, image by ~luckuso
Solution 2 (Law of Cosines + Law of Sines)
Draw diagonals ![]() and
and ![]() . By Law of Cosines,
. By Law of Cosines,
![]() is positive, taking the square root gives
is positive, taking the square root gives ![]() Let
Let ![]() . Since
. Since ![]() is isosceles, we have
is isosceles, we have ![]() . Notice we can eventually solve
. Notice we can eventually solve ![]() using the Extended Law of Sines:
using the Extended Law of Sines: ![]() where
where ![]() is the radius of the circumcircle
is the radius of the circumcircle ![]() . Since
. Since ![]() , we simply our equation:
, we simply our equation: ![]() Now we just have to find
Now we just have to find ![]() and
and ![]() . Since
. Since ![]() is cyclic, we have
is cyclic, we have ![]() . By Law of Cosines on
. By Law of Cosines on ![]() , we have
, we have ![]() Thus,
Thus, ![]() Similarly, by Law of Sines on
Similarly, by Law of Sines on ![]() , we have
, we have ![]() Hence,
Hence, ![]() . Now, using Law of Sines on
. Now, using Law of Sines on ![]() , we have
, we have ![]() so
so ![]() Therefore,
Therefore, ![\[\frac{BD}{2\left(\frac{3\sqrt3}{14}\right) \left(\frac{13}{14} \right)}=\frac{14\sqrt3}{3}.\]](http://latex.artofproblemsolving.com/e/e/f/eef351847fa46f866a609f18d090da4b96872e9c.png) Solving,
Solving, ![]() so the answer is
so the answer is ![]() .
.
~evanhliu2009
See also
| 2024 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 18 |
Followed by Problem 20 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()