Difference between revisions of "2024 AMC 12B Problems/Problem 13"
Numerophile (talk | contribs) (→Solution 3) |
m (→Solution 1 (Easy and Fast)) |
||
| Line 13: | Line 13: | ||
==Solution 1 (Easy and Fast)== | ==Solution 1 (Easy and Fast)== | ||
| − | Adding up the first and second | + | Adding up the first and second equation, we get: |
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | h + k &= 2x^2 + 2y^2 - 16x - 4y \ | ||
| + | &= 2(x^2 - 8x) + 2(y^2 - 2y) \ | ||
| + | &= 2(x^2 - 8x) + 2(y^2 - 2y) \ | ||
| + | &= 2(x^2 - 8x + 16) - (2)(16) + 2(y^2 - 2y + 1) - (2)(1) \ | ||
| + | &= 2(x - 4)^2 + 2(y - 1)^2 - 34 | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | All squared values must be greater than or equal to <math>0</math>. As we are aiming for the minimum value, we set the two squared terms to be <math>0</math>. | ||
| − | + | This leads to <math>\min(h + k) = 0 + 0 - 34 = \boxed{\textbf{(C)} -34}</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | This leads to (h+k) | ||
~mitsuihisashi14 | ~mitsuihisashi14 | ||
Revision as of 18:33, 14 November 2024
Contents
[hide]Problem 13
There are real numbers ![]() and
and ![]() that satisfy the system of equations
that satisfy the system of equations![]()
![]() What is the minimum possible value of
What is the minimum possible value of ![]() ?
?
![]()
Solution 1 (Easy and Fast)
Adding up the first and second equation, we get:
 All squared values must be greater than or equal to
All squared values must be greater than or equal to ![]() . As we are aiming for the minimum value, we set the two squared terms to be
. As we are aiming for the minimum value, we set the two squared terms to be ![]() .
.
This leads to ![]()
~mitsuihisashi14
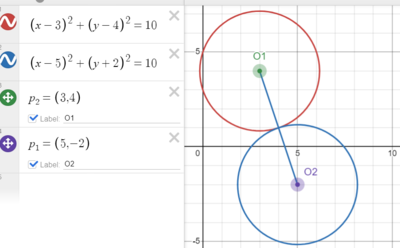
Solution 2 (Coordinate Geometry and HM-GM)
![]()
![]() distance between 2 circle centers is
distance between 2 circle centers is ![]()
![]()
![\[h + k + 54 = (h + 25) + (k + 29) =\sqrt{(h + 25)}^2 + \sqrt{(k + 29)}^2 \geq \frac{\left(\sqrt{h + 25} + \sqrt{k + 29}\right)^2}{2} = \frac{\left(2\sqrt{10}\right)^2}{2} = 20.\]](http://latex.artofproblemsolving.com/4/d/d/4dd6945ff3be5001554b4c445692bbcccb29a178.png) min( h + k ) =
min( h + k ) = ![]() .
.
Solution 3
~Kathan
See also
| 2024 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 12 |
Followed by Problem 14 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.