Difference between revisions of "2024 AMC 12B Problems/Problem 13"
m (→Solution 1 (Easy and Fast)) |
(→Solution 2 (Coordinate Geometry and HM-GM)) |
||
| Line 36: | Line 36: | ||
<cmath>(x-5)^2 + (y+2)^2 = k + 29 </cmath> | <cmath>(x-5)^2 + (y+2)^2 = k + 29 </cmath> | ||
distance between 2 circle centers is <cmath>d^2 = (5-3)^2 + (4 - (-2)) ^2 = 40 </cmath> | distance between 2 circle centers is <cmath>d^2 = (5-3)^2 + (4 - (-2)) ^2 = 40 </cmath> | ||
| − | <cmath>\sqrt{h+25} + \sqrt{k+29} = 2*\sqrt{10} </cmath> | + | the 2 circle must interact, so |
| + | <cmath>\sqrt{h+25} + \sqrt{k+29} >= 2*\sqrt{10} </cmath> | ||
| + | the min value will be reached when 2 circles are external tangent to each other | ||
<cmath> | <cmath> | ||
h + k + 54 = (h + 25) + (k + 29) =\sqrt{(h + 25)}^2 + \sqrt{(k + 29)}^2 \geq \frac{\left(\sqrt{h + 25} + \sqrt{k + 29}\right)^2}{2} | h + k + 54 = (h + 25) + (k + 29) =\sqrt{(h + 25)}^2 + \sqrt{(k + 29)}^2 \geq \frac{\left(\sqrt{h + 25} + \sqrt{k + 29}\right)^2}{2} | ||
| − | = \frac{\left(2\sqrt{10}\right)^2}{2} = 20. | + | >= \frac{\left(2\sqrt{10}\right)^2}{2} = 20. |
</cmath> | </cmath> | ||
min( h + k ) = <math>\boxed{C -34} </math>. | min( h + k ) = <math>\boxed{C -34} </math>. | ||
Revision as of 20:43, 14 November 2024
Contents
[hide]Problem 13
There are real numbers ![]() and
and ![]() that satisfy the system of equations
that satisfy the system of equations![]()
![]() What is the minimum possible value of
What is the minimum possible value of ![]() ?
?
![]()
Solution 1 (Easy and Fast)
Adding up the first and second equation, we get:
 All squared values must be greater than or equal to
All squared values must be greater than or equal to ![]() . As we are aiming for the minimum value, we set the two squared terms to be
. As we are aiming for the minimum value, we set the two squared terms to be ![]() .
.
This leads to ![]()
~mitsuihisashi14
Solution 2 (Coordinate Geometry and HM-GM)
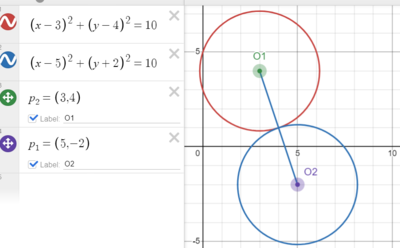
![]()
![]() distance between 2 circle centers is
distance between 2 circle centers is ![]() the 2 circle must interact, so
the 2 circle must interact, so
![]() the min value will be reached when 2 circles are external tangent to each other
the min value will be reached when 2 circles are external tangent to each other
![\[h + k + 54 = (h + 25) + (k + 29) =\sqrt{(h + 25)}^2 + \sqrt{(k + 29)}^2 \geq \frac{\left(\sqrt{h + 25} + \sqrt{k + 29}\right)^2}{2} >= \frac{\left(2\sqrt{10}\right)^2}{2} = 20.\]](http://latex.artofproblemsolving.com/f/1/b/f1b269bdbf7a178d41e86e90cca6a3febc5dded2.png) min( h + k ) =
min( h + k ) = ![]() .
.
Solution 3
~Kathan
See also
| 2024 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 12 |
Followed by Problem 14 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.