Difference between revisions of "2024 AMC 12B Problems/Problem 12"
(→Problem) |
|||
| (15 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
| − | + | Suppose <math>z</math> is a complex number with positive imaginary part, with real part greater than <math>1</math>, and with <math>|z| = 2</math>. In the complex plane, the four points <math>0</math>, <math>z</math>, <math>z^{2}</math>, and <math>z^{3}</math> are the vertices of a quadrilateral with area <math>15</math>. What is the imaginary part of <math>z</math>? | |
| − | <math>\textbf{(A) }\frac{3}{4}\qquad | + | <math>\textbf{(A) }\frac{3}{4}\qquad\textbf{(B) }1\qquad\textbf{(C) }\frac{4}{3}\qquad\textbf{(D) }\frac{3}{2}\qquad\textbf{(E) }\frac{5}{3}</math> |
| − | \textbf{(B) }1\qquad | ||
| − | \textbf{(C) }\frac{4} | ||
| − | \textbf{(D) }\frac{3}{2}\qquad | ||
| − | \textbf{(E) }\frac{5} | ||
==Diagram== | ==Diagram== | ||
| − | [[File:2024_12B_Q12.png| | + | [[File:2024_12B_Q12.png|600px]] |
| − | ==Solution 1 | + | ==Solution 1== |
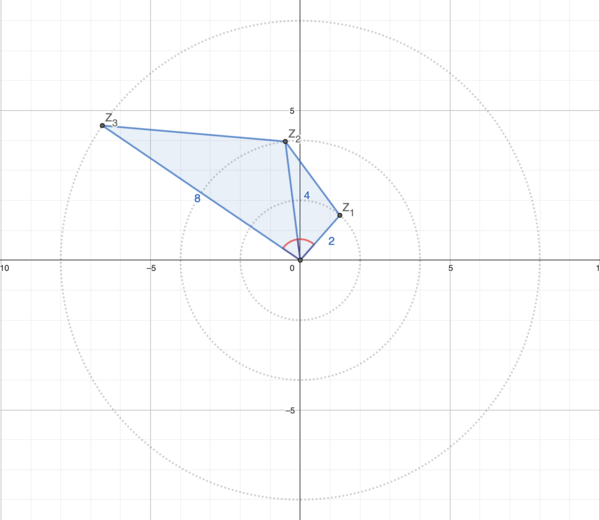
By making a rough estimate of where <math>z</math>, <math>z^2</math>, and <math>z^3</math> are on the complex plane, we can draw a pretty accurate diagram (like above.) | By making a rough estimate of where <math>z</math>, <math>z^2</math>, and <math>z^3</math> are on the complex plane, we can draw a pretty accurate diagram (like above.) | ||
| Line 22: | Line 18: | ||
Additionally, we know that <math>\angle{Z_1OZ_2}\cong\angle{Z_2OZ_3}</math> (since every power of <math>z</math> rotates around the origin by the same angle.) We set these angles equal to <math>\theta</math>. | Additionally, we know that <math>\angle{Z_1OZ_2}\cong\angle{Z_2OZ_3}</math> (since every power of <math>z</math> rotates around the origin by the same angle.) We set these angles equal to <math>\theta</math>. | ||
| − | + | We have that | |
| + | \begin{align*} | ||
| + | [OZ_1Z_2Z_3]&=[OZ_1Z_2]+[OZ_2Z_3] \ | ||
| + | &=\frac{1}{2}\cdot2\cdot4 \sin\theta+\frac{1}{2}\cdot4\cdot8 \sin\theta \ | ||
| + | &=4\sin\theta+16\sin\theta \ | ||
| + | &=20 \sin\theta | ||
| + | \end{align*} | ||
| − | + | Since this is equal to <math>15</math>, we have <math>20\sin\theta=15</math>, so <math>\sin\theta=\frac{3}{4}</math>. | |
| − | + | Thus, <math>\text{Im}(z)=|z|\sin(\theta)=2(\frac{3}{4})=\boxed{\textbf{(D) }\frac{3}{2}}</math>. | |
| − | + | ~nm1728 | |
| + | |||
| + | ==Solution 2 (Shoelace Theorem)== | ||
| + | We have the vertices: | ||
| + | |||
| + | <math> 0 </math> at<math>(0, 0)</math> , <math> z </math> at<math>(2\cos \theta, 2\sin \theta)</math> , <math> z^2 </math> at<math>(4\cos 2\theta, 4\sin 2\theta)</math> , <math> z^3 </math> at<math>(8\cos 3\theta, 8\sin 3\theta)</math> | ||
| + | |||
| + | The Shoelace formula for the area is: | ||
| + | <cmath> | ||
| + | = \frac{1}{2} \left| x_1 y_2 + x_2 y_3 + x_3 y_4 + x_4 y_1 - (y_1 x_2 + y_2 x_3 + y_3 x_4 + y_4 x_1) \right|. | ||
| + | </cmath> | ||
| + | <cmath> | ||
| + | = \frac{1}{2} \left| 0 + 2\cos \theta \cdot 4\sin 2\theta + 4\cos 2\theta \cdot 8\sin 3\theta - (2\sin \theta \cdot 4\cos 2\theta + 4\sin 2\theta \cdot 8\cos 3\theta) \right|. | ||
| + | </cmath> | ||
| + | <cmath> | ||
| + | = \frac{1}{2} \left| 8\cos \theta \sin 2\theta + 32\cos 2\theta \sin 3\theta - 8\sin \theta \cos 2\theta - 32\sin 2\theta \cos 3\theta \right| | ||
| + | </cmath> | ||
| + | <cmath> | ||
| + | = \frac{1}{2} \left|(8\cos \theta \sin 2\theta - 8\sin \theta \cos 2\theta) + (32\cos 2\theta \sin 3\theta - 32\sin 2\theta \cos 3\theta) \right|</cmath> | ||
| + | <cmath> | ||
| + | = \frac{1}{2} \left|8\sin(2\theta - \theta) + 32\sin(2\theta - \theta) \right| | ||
| + | </cmath> | ||
| + | <cmath> | ||
| + | = \frac{1}{2} \left| 8\sin \theta + 32\sin \theta \right| | ||
| + | </cmath> | ||
| + | <cmath>= \frac{1}{2} \left| 40\sin \theta \right| | ||
| + | </cmath> | ||
| + | Given that the area is 15: | ||
| + | <cmath> | ||
| + | \frac{1}{2} \left| 40\sin \theta \right| = 15. | ||
| + | </cmath> | ||
| + | <cmath> | ||
| + | 20|\sin \theta| = 15 \implies |\sin \theta| = \frac{3}{4}. | ||
| + | </cmath> | ||
| + | Since <math> \theta </math> corresponds to a complex number <math> z </math> with a positive imaginary part, we have: | ||
| + | |||
| + | <cmath> | ||
| + | \sin \theta = \frac{3}{4}. | ||
| + | </cmath> | ||
| + | <cmath> | ||
| + | \text{Imaginary part} = 2\sin \theta = 2 \times \frac{3}{4} = \boxed{\textbf{(D) }\frac{3}{2}}. | ||
| + | </cmath> | ||
| + | |||
| + | ~[https://artofproblemsolving.com/wiki/index.php/User:Cyantist luckuso] | ||
| + | |||
| + | ==Solution 3 (No Trig)== | ||
| + | |||
| + | Let <math>z = a + bi</math>, so <math>z^2 = a^2 + 2abi - b^2</math> and <math>z^3 = a^3 + 3a^2 bi - 3ab^2 - b^3 i</math>. Therefore, converting <math>0, z, z^2, z^3</math> from complex coordinates to Cartesian coordinates gives us the following. | ||
| + | |||
| + | <cmath>(0, 0)</cmath> | ||
| + | |||
| + | <cmath>(a, b)</cmath> | ||
| − | + | <cmath>(a^2 - b^2, 2ab)</cmath> | |
| − | + | <cmath>(a^3 - 3ab^2, 3a^2 b - b^3)</cmath> | |
| + | |||
| + | The Shoelace Theorem tells us that the area is | ||
| + | |||
| + | <cmath>\frac{1}{2} \Bigg| \Big[ (0)(b) + (a)(2ab) + (a^2 - b^2)(3a^2 b - b^3) + (a^3 - 3ab^2)(0) \Big] - \Big[ (0)(a) + (b)(a^2 - b^2) + (2ab)(a^3 - 3ab^2) + (3a^2 b - b^3)(0) \Big] \Bigg|</cmath> | ||
| + | |||
| + | <cmath>= \frac{1}{2} \Bigg| \Big[ (0) + (2a^2 b) + (3a^4 b - a^2 b^3 - 3a^2 b^3 + b^5) + (0) \Big] - \Big[ (0) + (a^2 b - b^3) + (2a^4 b - 6a^2 b^3) + (0) \Big] \Bigg|</cmath> | ||
| + | |||
| + | <cmath>= \frac{1}{2} \Big| [3a^4 b - 4a^2 b^3 + b^5 + 2a^2 b] - [2a^4 b - 6a^2 b^3 + a^2 b - b^3] \Big|</cmath> | ||
| + | |||
| + | <cmath>= \frac{1}{2} | a^4 b + 2a^2 b^3 + b^5 + a^2 b + b^3 |.</cmath> | ||
| + | |||
| + | We know that <math>|z| = |a + bi| = \sqrt{a^2 + b^2} = 2</math>, so <math>a^2 = 4 - b^2</math>. Substituting this gives us this: | ||
| + | |||
| + | <cmath>\frac{1}{2} \Big| (4 - b^2)^2 b + 2(4 - b^2)b^3 + b^5 + (4 - b^2)b + b^3 \Big|</cmath> | ||
| + | |||
| + | <cmath>= \frac{1}{2} \Big| (16b - 8b^3 + b^5) + (8b^3 - 2b^5) + b^5 + (4b - b^3) + b^3 \Big|</cmath> | ||
| + | |||
| + | <cmath>= \frac{1}{2} | 0b^5 + 0b^3 + 20b|</cmath> | ||
| + | |||
| + | <cmath>= 15.</cmath> | ||
| + | |||
| + | In other words, | ||
| + | |||
| + | <cmath>|10b| = 15</cmath> | ||
| + | |||
| + | <cmath>b = \textbf{(D) } \frac{3}{2}.</cmath> | ||
| + | |||
| + | ==Solution 4== | ||
| + | ==Video Solution 1 by SpreadTheMathLove== | ||
| + | https://www.youtube.com/watch?v=OMR5MYtu11s&t=0s | ||
| + | |||
| + | |||
| + | ==See also== | ||
| + | {{AMC12 box|year=2024|ab=B|num-b=11|num-a=13}} | ||
| + | {{MAA Notice}} | ||
Latest revision as of 00:15, 16 November 2024
Contents
[hide]Problem
Suppose ![]() is a complex number with positive imaginary part, with real part greater than
is a complex number with positive imaginary part, with real part greater than ![]() , and with
, and with ![]() . In the complex plane, the four points
. In the complex plane, the four points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are the vertices of a quadrilateral with area
are the vertices of a quadrilateral with area ![]() . What is the imaginary part of
. What is the imaginary part of ![]() ?
?
![]()
Diagram
Solution 1
By making a rough estimate of where ![]() ,
, ![]() , and
, and ![]() are on the complex plane, we can draw a pretty accurate diagram (like above.)
are on the complex plane, we can draw a pretty accurate diagram (like above.)
Here, points ![]() ,
, ![]() , and
, and ![]() lie at the coordinates of
lie at the coordinates of ![]() ,
, ![]() , and
, and ![]() respectively, and
respectively, and ![]() is the origin.
is the origin.
We're given ![]() , so
, so ![]() and
and ![]() . This gives us
. This gives us ![]() ,
, ![]() , and
, and ![]() .
.
Additionally, we know that ![]() (since every power of
(since every power of ![]() rotates around the origin by the same angle.) We set these angles equal to
rotates around the origin by the same angle.) We set these angles equal to ![]() .
.
We have that
Since this is equal to ![]() , we have
, we have ![]() , so
, so ![]() .
.
Thus, ![]() .
.
~nm1728
Solution 2 (Shoelace Theorem)
We have the vertices:
![]() at
at![]() ,
, ![]() at
at![]() ,
, ![]() at
at![]() ,
, ![]() at
at![]()
The Shoelace formula for the area is:
![]()
![]()
![]()
![]()
![]()
![]()
![]() Given that the area is 15:
Given that the area is 15:
![]()
![]() Since
Since ![]() corresponds to a complex number
corresponds to a complex number ![]() with a positive imaginary part, we have:
with a positive imaginary part, we have:
![]()
![]()
Solution 3 (No Trig)
Let ![]() , so
, so ![]() and
and ![]() . Therefore, converting
. Therefore, converting ![]() from complex coordinates to Cartesian coordinates gives us the following.
from complex coordinates to Cartesian coordinates gives us the following.
![]()
![]()
![]()
![]()
The Shoelace Theorem tells us that the area is
![\[\frac{1}{2} \Bigg| \Big[ (0)(b) + (a)(2ab) + (a^2 - b^2)(3a^2 b - b^3) + (a^3 - 3ab^2)(0) \Big] - \Big[ (0)(a) + (b)(a^2 - b^2) + (2ab)(a^3 - 3ab^2) + (3a^2 b - b^3)(0) \Big] \Bigg|\]](http://latex.artofproblemsolving.com/8/2/c/82c1d36f8218aff4120364dd9851abe42983eec5.png)
![\[= \frac{1}{2} \Bigg| \Big[ (0) + (2a^2 b) + (3a^4 b - a^2 b^3 - 3a^2 b^3 + b^5) + (0) \Big] - \Big[ (0) + (a^2 b - b^3) + (2a^4 b - 6a^2 b^3) + (0) \Big] \Bigg|\]](http://latex.artofproblemsolving.com/7/b/2/7b246ed5734bf5031f1762fcb56d5f6be59f30c8.png)
![]()
![]()
We know that ![]() , so
, so ![]() . Substituting this gives us this:
. Substituting this gives us this:
![]()
![]()
![]()
![]()
In other words,
![]()
![]()
Solution 4
Video Solution 1 by SpreadTheMathLove
https://www.youtube.com/watch?v=OMR5MYtu11s&t=0s
See also
| 2024 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 11 |
Followed by Problem 13 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.