Difference between revisions of "Sharygin Olympiads, the best"
(→2024, Problem 23) |
(→The problem from MGTU) |
||
| (53 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
The best problems of these Olympiads will be published. The numbering contains the year of the Olympiad and the serial number of the problem. Solutions are often different from the original ones. | The best problems of these Olympiads will be published. The numbering contains the year of the Olympiad and the serial number of the problem. Solutions are often different from the original ones. | ||
| + | |||
| + | ==2024 tur 2 klass 10 Problem 6== | ||
| + | [[File:2024 final 10 6.png|350px|right]] | ||
| + | A point <math>P</math> lies on one of medians of triangle <math>\triangle ABC</math> in such a way that <math>\angle PAB = \angle PBC = \angle PCA.</math> Prove that there exists a point <math>Q</math> on another median such that <math>\angle QBA = \angle QCB = \angle QAC.</math> (A.Zaslavsky) | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | 1. Denote <math>a = BC, b = AC, c = AB. </math> | ||
| + | It is known that barycentric coordinates are | ||
| + | <cmath>P = (a^2 b^2 : b^2 c^2 : c^2 a^2), P \in AD \implies b^2 c^2 = c^2 a^2 \implies AC = BC.</cmath> | ||
| + | |||
| + | 2. Denote <math>\omega = \odot APB, \Omega = \odot APC. </math> | ||
| + | |||
| + | <math>\angle ABP = \angle PAC \implies AC </math> is tangent to <math>\omega.</math> | ||
| + | |||
| + | <math>\angle PAC = \angle PCB \implies BC</math> is tangent <math>\Omega.</math> | ||
| + | |||
| + | <math>PC</math> is the radical axes of <math>\omega</math> and <math>\Omega,</math> the power of a point <math>D</math> with respect to a circle <math>\Omega</math> is <math>CD^2</math> so the power of a point <math>D</math> with respect to a circle <math>\omega</math> is <math>CD^2.</math> | ||
| + | |||
| + | <math>BD^2 = CD^2,</math> so <math>BD</math> is tangent to <math>\omega \implies \angle ABC = \angle CAB \implies AC = BC.</math> | ||
| + | |||
| + | <math>AC = BC,</math> so point <math>Q</math> symmetrical to <math>P</math> with respect to the <math>C-</math>median satisfies the conditions. <math>\blacksquare</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | |||
| + | ==2024 tur 2 klass 10 Problem 7== | ||
| + | [[File:2024 final 10 7.png|380px|right]] | ||
| + | Let <math>ABC</math> be a triangle with <math>\angle A = 60^\circ, AD, BE,</math> and <math>CF</math> be its bisectors, <math>P, Q</math> be the projections of <math>A</math> to <math>EF</math> and <math>BC</math> respectively, and <math>R</math> be the second common point of the circle <math>\omega = \odot DEF</math> with <math>AD.</math> | ||
| + | |||
| + | Prove that points <math>P, Q, R</math> are collinear. (K.Belsky) | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Denote <math>a = BC, b = AC, c = AB, I -</math> the incenter of <math>\triangle ABC,</math> | ||
| + | <math>L=FE \cap AD, R' -</math> the midpoint of <math>AI.</math> | ||
| + | |||
| + | It is known ([[Bisector | Division of bisector]]) that | ||
| + | <cmath>\frac {AI}{DI} = \frac {b+c}{a}, \frac {DI}{IL} = 1+ \frac {2a}{b+c} \implies \frac{1}{IL} = \frac{1}{DI} + \frac{2}{AI} \implies</cmath> <cmath>2 DI (\frac{AI}{2} - IL) =AI \cdot IL \implies 2 DI \cdot LR' = AI \cdot IL.</cmath> | ||
| + | |||
| + | <cmath>DL \cdot LR' = (DI + IL) \cdot LR' = \frac {AI \cdot IL}{2} + IL \cdot (\frac{AI}{2} - IL) = AI \cdot IL - IL^2 = AL \cdot IL.</cmath> | ||
| + | <math>\angle BAC = 60^\circ \implies \angle BIC = \angle FIE = 120^\circ \implies AEIF </math> is cyclic. | ||
| + | |||
| + | Therefore <math>AL \cdot IL = LE \cdot LF = DL \cdot LR' \implies EDFR'</math> is cyclic <math>\implies R = R'.</math> | ||
| + | [[File:2024 final 10 7a.png|430px|right]] | ||
| + | Let <math>AG \perp AD, G \in BC, H = AP \cap BC, Q' = RP \cap BC.</math> | ||
| + | |||
| + | It is known that points <math>F, E,</math> and <math>G</math> are collinear, | ||
| + | <cmath>\angle AGB = \frac{|\angle ACB - \angle ABC|}{2}, \angle AGE = \angle BGE.</cmath> | ||
| + | |||
| + | <math>AP \perp EF, AQ \perp BG \implies AG</math> is the diameter of <math>\odot APQG \implies</math> | ||
| + | <cmath>\overset{\Large\frown} {QP} = \overset{\Large\frown} {AP} \implies \angle DAP = \angle QAP, AP = PH.</cmath> | ||
| + | <cmath>AR = RI, AP = PH \implies RP || IH \implies \frac {DH}{HQ'} = \frac {DI}{IR} = \frac {2a}{b+c}.</cmath> | ||
| + | <math>AH</math> is the bisector of <math>\angle DAQ \implies \frac {DH}{HQ} = \frac {AD}{AQ}.</math> | ||
| + | |||
| + | Bisector <math>AD = \frac {2 b c \cos 30^\circ}{b+c}.</math> | ||
| + | |||
| + | Altitude <math>AQ = \frac {2[ABC]}{BC}= \frac {bc \sin 60^\circ}{a} \implies \frac {AD}{AQ} = \frac {2a}{b+c} = \frac {DH}{HQ} = \frac {DH}{HQ'} \implies Q = Q'. \blacksquare</math> | ||
| + | |||
| + | Note that the point <math>R</math> is a Feuerbach point of <math>\triangle ABC</math> since both the inscribed circle and the Euler circle pass through it. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==2024 tur 2 klass 9 Problem 7== | ||
| + | [[File:Incircle and secants.png|400px|right]] | ||
| + | Let triangle <math>\triangle ABC</math> and point <math>P</math> on the side <math>BC</math> be given. Let <math>P'</math> be such point on the side <math>BC</math> that <math>BP = P'C.</math> The cross points of segments <math>AP</math> and <math>AP'</math> with the incircle <math>\omega</math> of <math>\triangle ABC</math> form a convex quadrilateral <math>EFE'F'.</math> | ||
| + | |||
| + | Find the locus of crosspoints of diagonals <math>EFE'F'.</math> (D.Brodsky) | ||
| + | |||
| + | <i><b>Solution</b></i> | ||
| + | 1. Particular case of [[Projective geometry (simplest cases) | Fixed point]] . | ||
| + | |||
| + | 2. Denote <math>p_a = \frac{b+c-a}{2}, p_b = \frac{a-b+c}{2}, p_c = \frac{a+b-c}{2}, m = \frac {CP}{BP}, \mu = \frac {PF'}{AF'}.</math> | ||
| + | <cmath>PD = \frac {m p_b - p_c} {m+1}, AD' = p_a \implies</cmath> | ||
| + | <cmath>x(x+y) = p_a^2, z(z+y) = PD^2, x+y+z = AP, \mu = \frac {z}{x+y}.</cmath> | ||
| + | We perform simple transformations and get: | ||
| + | <cmath>\mu^2 p_a^2 - \mu (AP^2 - p_a^2 - PD^2) + PD^2 = 0.</cmath> | ||
| + | We use Stewart's theorem and get: | ||
| + | <cmath> AP^2 = \frac {AC^2}{1+m} + \frac {m AB^2}{1+m} - \frac {m BC^2}{(1+m)^2} \implies</cmath> | ||
| + | <cmath>(\mu p_a)^2 - 2 (\mu p_a) \frac {m p_b + p_c}{m+1} + \frac {(m p_b - p_c)^2} {(m+1)^2} = 0.</cmath> | ||
| + | <cmath>\mu = \frac {(\sqrt{m p_b} \pm \sqrt{p_c})^2}{(m+1) p_a}.</cmath> | ||
| + | Similarly <cmath>\nu = \frac {\eta + \zeta}{\xi}= \frac {(\sqrt{m p_c} \pm \sqrt{p_b})^2}{(m+1) p_a}.</cmath> | ||
| + | Therefore <math>\frac {\nu + \mu}{2} = \frac {a}{2 p_a}</math> not depends from <math>m.</math> | ||
| + | |||
| + | Let <math>M</math> be the midpoint of <math>BC, AM</math> is the median of <math>\triangle ABC</math> and <math>\triangle PAP'.</math> | ||
| + | |||
| + | The line <math>FF'</math> cross the median of <math>\triangle PAP'</math> at point <math>G'</math> such that <math>\frac {MG'}{G'A} = \frac {\nu + \mu}{2} = \frac {p_b + p_c}{2 p_a} = \frac {a}{2 p_a}.</math> | ||
| + | |||
| + | So point <math>G'</math> is fixed and this point lyes on <math>EE' \implies G = G'</math>. | ||
| + | |||
| + | Therefore the locus of crosspoints of diagonals <math>EFE'F'</math> is point <math>G.</math> | ||
| + | |||
| + | <i><b>Corollary</b></i> | ||
| + | |||
| + | Let line <math>MQ||D'D'', Q \in AC</math>. Then <math>\frac {D''Q}{AD''} = \frac {a}{2 p_a} \implies 2 D''Q = BC.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==2024 tur 2 klass 9 Problem 5== | ||
| + | [[File:2024 final 9 5.png|350px|right]] | ||
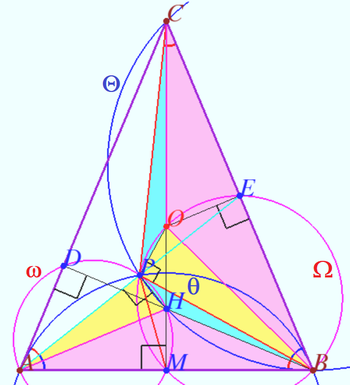
| + | Let <math>ABC</math> be an isosceles triangle <math>(AC = BC), O</math> be its circumcenter,<math>H</math> be the orthocenter, and <math>P</math> be a point inside the triangle such that <math>\angle APH = \angle BPO = 90^\circ.</math> | ||
| + | |||
| + | Prove that <math>\angle PAC = \angle PBA = \angle PCB.</math> (A.Zaslavsky) | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Denote <math>E -</math> the midpoint <math>BC, M-</math> the midpoint <math>AB, D -</math> the foot from <math>B</math> to <math>\overline{AC}, \alpha = \angle ABC, \omega = \odot ADHM, \Omega = \odot BEOM, \Theta = \odot BHC, \theta = \odot AB</math> tangent to <math>\overline{BC}.</math> | ||
| + | |||
| + | <math>AH = BH, BO = CO , \angle BAH = 90^\circ - \alpha = \angle BCO \implies \triangle ABH \sim \triangle BCO.</math> | ||
| + | There is a spiral similarity <math>T</math> centered at point <math>X</math> that maps <math>\triangle ABH</math> into <math>\triangle BCO.</math> | ||
| + | |||
| + | The coefficient of similarity <math>k = \frac {BC}{AB} = \frac {1}{2 \cos \alpha},</math> rotation angle equal <math>180^\circ - \alpha.</math> | ||
| + | <cmath>B = T(A), B = AB \cap BC \implies X \in \theta.</cmath> | ||
| + | <cmath>C = T(B), B = AB \cap BC \implies X \in \Theta</cmath> | ||
| + | <math>(\angle BCH = \angle ABH,</math> so <math>AB</math> is tangent to <math>\Theta).</math> [[Spiral similarity | Basic information]] | ||
| + | <cmath>E = T(M), B = AM \cap BE \implies X \in \Omega.</cmath> | ||
| + | <cmath>AB = T(CA), CO = T(BH), D = AC \cap BH, M = AB \cap CO \implies M = T(D).</cmath> | ||
| + | <cmath>A = AD \cap BM \implies X \in \omega.</cmath> | ||
| + | <cmath>P = \theta \cap \Theta \implies P = X.</cmath> | ||
| + | <cmath>P = T(P) \implies \triangle BPC = T(\triangle APB) \implies \triangle BPC \sim \triangle APB \implies \angle PAB = \angle PCB.</cmath> | ||
| + | <cmath>\triangle OBP = T(\triangle HAP) \implies \triangle OBP \sim \triangle HAP \implies \angle OBP = \angle HAP .</cmath> | ||
| + | <cmath>\angle PAC = \alpha - \angle HAP - \angle BAH = \alpha - \angle OBP - \angle OBC = \angle PBA.\blacksquare</cmath> | ||
| + | <cmath>\triangle ADM \sim \triangle ABC \implies \angle ADM = \alpha = \angle APM, \angle EPM = 180^\circ - \alpha \implies</cmath> | ||
| + | Points <math>A,P,</math> and <math>E</math> are collinear, so <math>P \in A-</math> median of <math>\triangle ABC.</math> | ||
| + | |||
| + | <math>\angle PAB = \angle PCB, \angle ABC = \angle BAC \implies PC</math> is <math>B-</math> symmedian of <math>\triangle ABC.</math> | ||
| + | |||
| + | <math>\angle APH = 90^\circ \implies P</math> is <math>A-</math> Humpty point. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==2024 tur 2 klass 9 Problem 4== | ||
| + | [[File:2024 final 9 4d.png|400px|right]] | ||
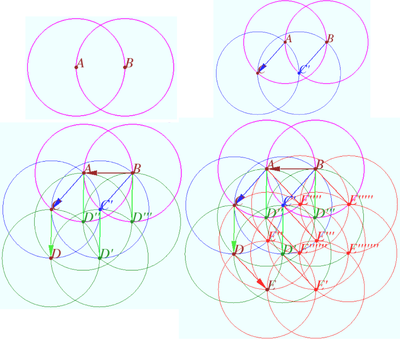
| + | For which <math>n > 0</math> it is possible to mark several different points and several different circles on the plane in such a way that: | ||
| + | |||
| + | - exactly <math>n</math> marked circles pass through each marked point; | ||
| + | |||
| + | - exactly <math>n</math> marked points lie on each marked circle; | ||
| + | |||
| + | - the center of each marked circle is marked? (P.Puchkov) | ||
| + | |||
| + | <i><b>Solution</b></i> | ||
| + | |||
| + | Case <math>n = 1.</math> Circles centered at <math>A</math> and <math>B</math> with radii <math>R = |\vec {AB}|.</math> | ||
| + | |||
| + | Case <math>n = 2, \vec {AC} = \vec {BC'}, |\vec {AB} = \vec {AC}|, \vec {AC}</math> is not paralel to <math>\vec {AB}.</math> | ||
| + | |||
| + | Four circles are centered at points <math>A, B, C,</math> and <math>C'.</math> Each radius is equal <math>R.</math> | ||
| + | |||
| + | Case <math>n = 3, \vec {CD} = \vec {AD''} = \vec {C'D'} = \vec {BD'''}, \vec {CD}</math> is not paralel to <math>\vec {AB}</math> or <math>\vec {AC}, |\vec {AB}| = \vec {CD}|</math> | ||
| + | |||
| + | Eight circles centered at <math>A, B, C, C', D, D',D''</math> and <math>D'''</math> have radii <math>R.</math> | ||
| + | |||
| + | Case <math>n = 4, \vec {DE} = \vec {D'E'} = ...,|\vec {DE}| = R,..</math> | ||
| + | |||
| + | <i><b>Answer </b></i> For all <math>n.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==2024 tur 2 klass 9 Problem 3== | ||
| + | [[File:2024 final 9 3.png|450px|right]] | ||
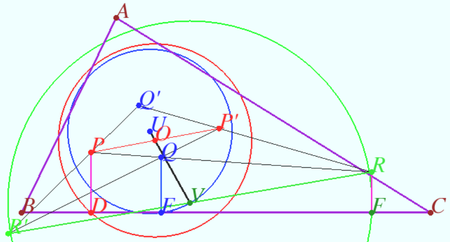
| + | Let <math>(P,P')</math> and <math>(Q,Q')</math> be two pairs of points isogonally conjugated with respect to a triangle <math>ABC,</math> and <math>R</math> be the common point of lines <math>PQ</math> and <math>P'Q'.</math> | ||
| + | Prove that the pedal circles of points <math>P,Q,</math> and <math>R</math> are coaxial. (L.Shatunov, V.Shelomovskii) | ||
| + | |||
| + | <i><b>Solution</b></i> | ||
| + | |||
| + | 1. Let <math>P'</math> be the isogonal conjugate of a point <math>P</math> with respect to a triangle <math>\triangle ABC.</math> Then circle centered at the midpoint <math>PP'</math> is the common pedal circle of points <math>P</math> and <math>P'.</math> ([[Isogonal conjugate | Circumcircle of pedal triangles]]) So center <math>O</math> is the midpoint <math>PP'</math> and center <math>U</math> is the midpoint <math>QQ'.</math> | ||
| + | |||
| + | 2. Denote <math>R' = PQ' \cap P'Q.</math> Then <math>R'</math> is the isogonal conjugate of a point <math>R</math> with respect to <math>\triangle ABC.</math> So center <math>V</math> is the midpoint <math>RR'.</math> ([[Isogonal conjugate | Two pares of isogonally conjugate points]]) | ||
| + | |||
| + | 3. The Gauss line (or Gauss–Newton line) is the line joining the midpoints of the three diagonals of a complete quadrilateral <math>PQ'P'Q</math> ([[Gauss line]]).So points <math>U,O,</math> and <math>V</math> are collinear as was to be proven. <math>\blacksquare</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | == 2024 tur 2 klass 8 Problem 4== | ||
| + | [[File:2024 final 8 4.png|300px|right]] | ||
| + | [[File:2024 final 8 4a.png|300px|right]] | ||
| + | A square with sidelength <math>1</math> is cut from the paper. Construct a segment with length <math>\frac{1}{2024}</math> using at most <math>13</math> folds. No instruments are available, it is allowed only to fold the paper and to mark the common points of folding lines. (M.Evdokimov) | ||
| + | |||
| + | <i><b>Solution</b></i> | ||
| + | |||
| + | Main idea: <math>\frac{1}{2024} = \frac{1}{4} \cdot \left [ \frac{1}{22} - \frac{1}{23} \right ].</math> | ||
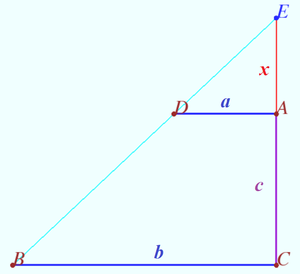
| + | <cmath>\frac {a}{b} = \frac{x}{x+c} \implies x = \frac {a \cdot c}{b - a}.</cmath> | ||
| + | <cmath>EG = EA - GA = c \cdot \left [ \frac {1}{b/a - 1} - \frac {1}{(b+FB)/a - 1} \right ].</cmath> | ||
| + | Let <math>c = \frac{1}{2}, a = \frac{1}{64}, b = \frac{45}{64}, FB = \frac{2}{64}.</math> | ||
| + | <cmath>EG = \frac{1}{2} \cdot \left [ \frac {1}{45 - 1} - \frac {1}{47 - 1} \right] = \frac{1}{2024}.</cmath> | ||
| + | We perform <math>1</math> horizontal fold of the sheet. We get line <math>AD (AC = \frac{1}{2}).</math> We perform | ||
| + | |||
| + | <math>6</math> vertical folds of the sheet. We get <math>62</math> vertical lines at a distance of <math>\frac{1}{64}</math> from each other. | ||
| + | |||
| + | Point <math>F</math> is the lower left corner of the sheet, point <math>B</math> is the lower point of the second vertical line, point <math>C</math> is the lower point of the <math>47^{th}</math> line, point <math>D</math> is the point at the intersection of the horizontal line and the <math>46^{th}</math> vertical line. | ||
| + | |||
| + | Points <math>E</math> and <math>G</math> are at the intersection of the lines <math>BD</math> and <math>FD</math> and the <math>47^{th}</math> vertical line. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | == 2024 tur 2 klass 8 Problem 2== | ||
| + | [[File:2024 final 8 2.png|450px|right]] | ||
| + | Let <math>M</math> be the midpoint of side <math>AB</math> of an acute-angled triangle <math>ABC,</math> and <math>P</math> be the projection of the orthocenter <math>H</math> to the bisector of angle <math>C.</math> | ||
| + | Prove that <math>MP</math> bisects the segment <math>CH.</math> (L.Emelyanov) | ||
| + | |||
| + | <i><b>Solution</b></i> | ||
| + | |||
| + | Denote <math>D</math> - the midpoint of <math>CH, A',B',</math> and <math>C'</math> the foots of the heights, <math>\angle A = 2 \alpha, \angle B = 2 \beta, \angle C = 2 \gamma, \omega</math> be the Euler circle <math>A'DB'C'M.</math> | ||
| + | |||
| + | <math>\Omega</math> is the circle <math>\odot CA'B'</math> with the diameter <math>CH.</math> | ||
| + | <cmath>HP \perp CP \implies P \in \Omega.</cmath> | ||
| + | <cmath>AA' \perp BA' \implies A'M = BM \implies \angle BA'M = 2 \beta.</cmath> | ||
| + | <cmath>\triangle ABC \sim \triangle A'BC' \implies \angle BA'C' = 2 \alpha \implies</cmath> | ||
| + | <cmath>\angle MA'C' = 2|\alpha - \beta| = \angle MDC'.</cmath> | ||
| + | <cmath>\angle ACC' = 90^\circ - 2 \alpha, \angle ACP = \gamma,</cmath> <cmath>\angle PCC' = |\angle ACC' - \angle ACP| = | ||
| + | |90^\circ - 2 \alpha - \gamma| = | \alpha + \beta + \gamma - 2 \alpha - \gamma| = | \alpha - \beta|.</cmath> | ||
| + | <cmath>PD = CD \implies \angle PDH = 2 \angle PCD = 2|\alpha - \beta|.</cmath> | ||
| + | <math>\angle PDH = \angle MDH \implies</math> points <math>M,P,</math> and <math>D</math> are collinear. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
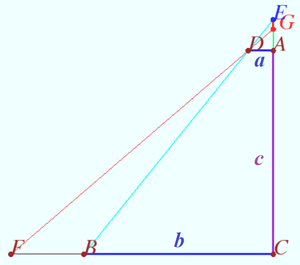
==2024, Problem 23== | ==2024, Problem 23== | ||
| Line 18: | Line 233: | ||
<math>O</math> is the circumcenter of <math>\triangle APC, O'</math> is the circumcenter of <math>\triangle BPC.</math> | <math>O</math> is the circumcenter of <math>\triangle APC, O'</math> is the circumcenter of <math>\triangle BPC.</math> | ||
| − | Let <math>K</math> and <math>L</math> be the midpoints of the arcs <math>\overset{\Large\frown}{CB'}</math> of <math>\theta.</math> | + | Let <math>K</math> and <math>L</math> be the midpoints of the arcs <math>\overset{\Large\frown}{CB'}</math> of <math>\theta,D = AL \cap \omega.</math> |
| − | Let <math>K'</math> and <math>L'</math> be the midpoints of the arcs <math>\overset{\Large\frown}{CA'}</math> of <math>\theta'.</math> | + | Let <math>K'</math> and <math>L'</math> be the midpoints of the arcs <math>\overset{\Large\frown}{CA'}</math> of <math>\theta', D' = BL' \cap \omega'.</math> |
These points not depends from position of point <math>P.</math> | These points not depends from position of point <math>P.</math> | ||
| Line 28: | Line 243: | ||
<cmath>O'D' = O'C, OC = OD \implies \triangle OCD \sim \triangle O'D'C \implies OC||O'D'.</cmath> | <cmath>O'D' = O'C, OC = OD \implies \triangle OCD \sim \triangle O'D'C \implies OC||O'D'.</cmath> | ||
Let <math>F= CD \cup OO' \implies \frac {FO}{FO'} = \frac {OC}{O'D'} \implies Q = F.</math> | Let <math>F= CD \cup OO' \implies \frac {FO}{FO'} = \frac {OC}{O'D'} \implies Q = F.</math> | ||
| + | [[File:2024 23 3.png|350px|right]] | ||
<cmath>\angle LCB' = \alpha = \angle B'BL' \implies LC || L'B.</cmath> | <cmath>\angle LCB' = \alpha = \angle B'BL' \implies LC || L'B.</cmath> | ||
Similarly, <math>AL || CL' \implies \triangle DLC \sim \triangle CL'D' \implies \frac {LC}{L'D'} = \frac {DC}{CD'} = \frac {OC}{O'D'}.</math> | Similarly, <math>AL || CL' \implies \triangle DLC \sim \triangle CL'D' \implies \frac {LC}{L'D'} = \frac {DC}{CD'} = \frac {OC}{O'D'}.</math> | ||
| Line 34: | Line 250: | ||
Therefore <math>Q \in LL'.</math> Similarly, if <math>P \in \overset{\Large\frown} {B'A'}</math> then <math>Q \in KK'.</math> | Therefore <math>Q \in LL'.</math> Similarly, if <math>P \in \overset{\Large\frown} {B'A'}</math> then <math>Q \in KK'.</math> | ||
| + | |||
| + | <i><b>Claim</b></i> | ||
| + | |||
| + | Points <math>D, C,</math> and <math>D'</math> are collinear. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | <math>S</math> is the midpoint of arc <math>\overset{\Large\frown}{A'B'} \implies \angle SAC = \angle SBC.</math> | ||
| + | Denote <math>\angle CAP = \alpha, \angle CBP = \beta, \angle SAC = \angle SBC = \varphi.</math> | ||
| + | <cmath>D \in \omega \implies \angle PDC = \alpha, \angle PCD = \pi - \alpha - \varphi.</cmath> | ||
| + | <cmath>D' \in \omega' \implies \angle PD'C = \beta, \angle PCD' = \pi - \beta - \varphi.</cmath> | ||
| + | <cmath>S \in \Omega \implies \angle SAP + \angle SBP = \alpha + \beta + 2 \varphi = \pi.</cmath> | ||
| + | Therefore <math>\angle PCD + \angle PCD' = \pi \implies </math> points <math>D, C,</math> and <math>D'</math> are collinear. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==One-to-one mapping of the circle== | ||
| + | [[File:2024 23 AA.png|350px|right]] | ||
| + | Let a circle <math>\Omega,</math> two fixed points <math>A</math> and <math>B</math> on it and a point <math>C</math> inside it be given. | ||
| + | Then there is a one-to-one mapping of the circle <math>\Omega</math> onto itself, based on the following two theorems. | ||
| + | |||
| + | 1. Let a circle <math>\Omega,</math> two fixed points <math>A</math> and <math>B</math> on <math>\Omega,</math> and a point <math>C</math> inside <math>\Omega</math> be given. | ||
| + | |||
| + | Let an arbitrary point <math>Q \in \Omega</math> be given. | ||
| + | |||
| + | Let <math>A' = AC \cap \Omega, A' \ne A, B' = BC \cap \Omega, B' \ne B. S</math> is the midpoint of the arc <math>A'B', D = A'Q \cap BS, E = B'Q \cap AS.</math> | ||
| + | |||
| + | Denote <math>\omega = \odot AEC, \omega' = \odot BCD, P = \omega \cap \omega'.</math> Prove that <math>P \in \Omega.</math> | ||
| + | |||
| + | 2. Let a circle <math>\Omega,</math> two fixed points <math>A</math> and <math>B</math> on <math>\Omega,</math> and a point <math>C</math> inside <math>\Omega</math> be given. | ||
| + | |||
| + | Let an arbitrary point <math>P \in \Omega</math> be given. | ||
| + | |||
| + | Let <math>A' = AC \cap \Omega, A' \ne A, B' = BC \cap \Omega, B' \ne B. S</math> is the midpoint of the arc <math>A'B'.</math> | ||
| + | |||
| + | Denote <math>\omega = \odot ACP, \omega' = \odot BCP, D = BS \cap \omega' , E = \omega \cap AS.</math> | ||
| + | |||
| + | Denote <math>Q = A'D \cap B'E.</math> Prove that <math>Q \in \Omega.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | <math>1. C = AA' \cap BB', D = A'Q \cap BS, E = B'Q \cap AS \implies </math> | ||
| + | |||
| + | Points <math>D,C,E </math> are collinear. | ||
| + | <cmath>\angle APC = \angle SEC, \angle BPC = \angle SDC.</cmath> | ||
| + | <cmath>\angle APC + \angle BPC + \angle ASC = \angle SEC + \angle SDC + \angle DSE = 180 ^\circ \implies P \in \Omega.</cmath> | ||
| + | |||
| + | 2. Points <math>D, C,</math> and <math>E</math> are collinear (see Claim in <i><b>2024, Problem 23</b></i>). | ||
| + | |||
| + | We use Pascal's theorem for points <math>A,B',S,A',B</math> and crosspoints <math>C,D,E</math> and get <math>Q \in \Omega.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==2024, Problem 22== | ||
| + | [[File:2023 22 2.png|350px|right]] | ||
| + | [[File:2024 22.png|350px|right]] | ||
| + | A segment <math>AB</math> is given. Let <math>C</math> be an arbitrary point of the perpendicular bisector to <math>AB,</math> | ||
| + | <math>O</math> be the point on the circumcircle of <math>\triangle ABC</math> opposite to <math>C,</math> and an ellipse centered at <math>O</math> touche <math>AB, BC, CA.</math> | ||
| + | |||
| + | Find the locus of touching points <math>P</math> of the ellipse with the line <math>BC.</math> | ||
| + | |||
| + | <i><b>Solution</b></i> | ||
| + | |||
| + | Denote <math>M</math> the midpoint <math>AB, D</math> the point on the line <math>CO, DO = MO, \alpha = \angle CBM, b = OM.</math> | ||
| + | |||
| + | <cmath>\angle CBO = 90^\circ \implies \angle COB = \alpha, MB = b \tan \alpha,</cmath> | ||
| + | <cmath>CB = \frac {b \sin \alpha}{\cos^2 \alpha}, CO = \frac {b} {\cos^2 \alpha}, CD = b \left (1 + \frac {1} {\cos^2 \alpha} \right ).</cmath> | ||
| + | In order to find the ordinate of point <math>P,</math> we perform an affine transformation (compression along axis <math>AB)</math> which will transform the ellipse <math>MPD</math> into a circle with diameter <math>MD.</math> The tangent of the <math>CP</math> maps into the tangent of the <math>CE, E = \odot CBO \cap \odot MD, PF \perp CO.</math> | ||
| + | <cmath>\angle OEF = \angle ECO \implies OF = OE \sin \angle OEF = OE \sin \angle ECO = b \cos^2 \alpha.</cmath> | ||
| + | <cmath>CP = \frac {CF}{\sin \alpha} = \frac {b}{\sin \alpha}\left ( \frac {1} {\cos^2 \alpha} - \cos^2 \alpha \right ) = b \sin \alpha \left ( \frac {1}{\cos^2 \alpha } + 1 \right).</cmath> | ||
| + | <cmath>\frac {CP}{CD} = \sin \alpha , \angle PCD = 90^\circ - \alpha \implies \angle CPD = 90^\circ.</cmath> | ||
| + | <cmath>BP = CP - CB = b \sin \alpha.</cmath> | ||
| + | Denote <math>Q = AB \cap DP \implies BQ = \frac {BP}{\cos \alpha} = b \tan \alpha = MB.</math> | ||
| + | |||
| + | So point <math>Q</math> is the fixed point (<math>P</math> not depends from angle <math>\alpha, \angle BPQ = 90^\circ ).</math> | ||
| + | |||
| + | Therefore point <math>P</math> lies on the circle with diameter <math>BQ</math> (except points <math>B</math> and <math>Q.)</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==2024, Problem 21== | ||
| + | [[File:2024 21 0.png|350px|right]] | ||
| + | [[File:2024 21 1.png|350px|right]] | ||
| + | A chord <math>PQ</math> of the circumcircle of a triangle <math>ABC</math> meets the sides <math>BC, AC</math> at points <math>A', B',</math> respectively. The tangents to the circumcircle at <math>A</math> and <math>B</math> meet at point <math>X,</math> and the tangents at points <math>P</math> and <math>Q</math> meets at point <math>Y.</math> The line <math>XY</math> meets <math>AB</math> at point <math>C'.</math> | ||
| + | |||
| + | Prove that the lines <math>AA', BB',</math> and <math>CC'</math> concur. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | WLOG, <math>P \in \overset{\Large\frown} {AC}.</math> | ||
| + | Denote <math>\Omega = \odot ABC, Z = BB' \cap AA', D = AQ \cap BP.</math> | ||
| + | |||
| + | Point <math>D</math> is inside <math>\Omega.</math> | ||
| + | |||
| + | We use Pascal’s theorem for quadrilateral <math>APQB</math> and get <math>D \in XY.</math> | ||
| + | |||
| + | We use projective transformation which maps <math>\Omega</math> to a circle and that maps the point <math>D</math> to its center. | ||
| + | |||
| + | From this point we use the same letters for the results of mapping. Therefore the segments <math>AQ</math> and <math>BP</math> are the diameters of <math>\Omega, C'D \in XY || AP \implies C'</math> is the midpoint <math>AB.</math> | ||
| + | |||
| + | <math>AB|| PQ \implies AB || B'A' \implies C' \in CZ \implies</math> | ||
| + | |||
| + | preimage <math>Z</math> lies on preimage <math>CC'.\blacksquare</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==2024, Problem 20== | ||
| + | [[File:2024 20.png|350px|right]] | ||
| + | Let a triangle <math>ABC,</math> points <math>D</math> and <math>E \in BD</math> be given, <math>F = AD \cap CE.</math> | ||
| + | Points <math>D', E'</math> and <math>F'</math> are the isogonal conjugate of the points <math>D, E,</math> and <math>F,</math> respectively, with respect to <math>\triangle ABC.</math> | ||
| + | |||
| + | Denote <math>R</math> and <math>R'</math> the circumradii of triangles <math>\triangle DEF</math> and <math>\triangle D'E'F',</math> respectively. | ||
| + | |||
| + | Prove that <math>\frac {[DEF]}{R} = \frac {[D'E'F']}{R'},</math> where <math>[DEF]</math> is the area of <math>\triangle DEF.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Denote <math>\angle BAC = \alpha, \angle ABC = \beta, \angle ACB = \gamma,</math> | ||
| + | <cmath>\angle EDF = \Theta, \angle E'D'F' = \theta, \angle DEF = \Psi, \angle D'E'F' = \psi,</cmath> | ||
| + | <cmath>\angle BAD' = \angle CAF = \varphi_A, \angle CBD' = \angle ABD = \varphi_B, \angle BCE' = \angle ACE = \varphi_C.</cmath> | ||
| + | It is easy to prove that | ||
| + | <math>\frac {[DEF]}{R} = \frac {[D'E'F']}{R'}</math> is equivalent to <math>DE \cdot \sin \Theta \cdot \sin \Psi = D'E' \cdot \sin \theta \cdot \sin \psi.</math> | ||
| + | <cmath>\Theta = \alpha - \varphi_A + \varphi_B, \theta = \beta - \varphi_B + \varphi_A, \Psi = \beta - \varphi_B + \varphi_C, \psi = \gamma - \varphi_C + \varphi_B \implies</cmath> | ||
| + | <cmath>\theta = 180^\circ - \gamma - \Theta, \psi = 180^\circ - \alpha - \Psi.</cmath> | ||
| + | By applying the law of sines, we get | ||
| + | <cmath>\frac {BE}{\sin \varphi_C} = \frac {BC}{\sin \Psi}, \frac {BD}{\sin (\alpha - \varphi_A)} = \frac {AB}{\sin \Theta}, \frac {BC}{\sin \alpha} = \frac {AB}{\sin \gamma}.</cmath> | ||
| + | <cmath>ED = BD - BE \implies DE \cdot \sin \Theta \cdot \sin \Psi = \frac {AB}{\sin \gamma} \left ( \sin \gamma \cdot \sin (\alpha - \varphi_A) \cdot \sin \Psi - \sin \alpha \cdot \sin \varphi_C \cdot \sin \Theta \right )</cmath> | ||
| + | |||
| + | <cmath>\frac {BE'}{\sin (\gamma - \varphi_C)} = \frac {BC}{\sin \psi}, \frac {BD'}{\sin \varphi_A} = \frac {AB}{\sin \theta}.</cmath> | ||
| + | <cmath>D'E' = BE' - BD' \implies D'E' \cdot \sin \theta \cdot \sin \psi = \frac {AB}{\sin \gamma} (\sin \alpha \cdot \sin (\gamma - \varphi_C) \cdot \sin \theta - \sin \gamma \cdot \sin \varphi_A \cdot \sin \psi ).</cmath> | ||
| + | We need to prove that | ||
| + | <cmath>\sin \gamma \cdot \sin (\alpha - \varphi_A) \cdot \sin \Psi - \sin \alpha \cdot \sin \varphi_C \cdot \sin \Theta = \sin \alpha \cdot \sin (\gamma - \varphi_C) \cdot \sin \theta - \sin \gamma \cdot \sin \varphi_A \cdot \sin \psi</cmath> | ||
| + | We make the transformations: | ||
| + | <cmath>\sin \alpha \left[ \sin \varphi_C \cdot \sin \Theta + \sin (\gamma - \varphi_C) \cdot \sin (\gamma + \Theta) \right] = \sin \gamma \left[ \sin (\alpha - \varphi_A) \cdot \sin \Psi + \sin \varphi_A \cdot \sin (\alpha + \Psi) \right]</cmath> | ||
| + | |||
| + | <cmath>\sin \alpha \left[ \sin \varphi_C \cdot \sin \Theta + (\sin \gamma \cos \varphi_C - \cos \gamma \sin \varphi_C) \cdot (\sin \gamma \cos \Theta + \cos \gamma \sin \Theta \right] =</cmath> | ||
| + | <cmath>= \sin \gamma \left[ \sin \alpha \cos \varphi_A \cdot \sin \Psi - \cos \alpha \sin \varphi_A \cdot \sin \Psi + \sin \varphi_A \cdot \sin \alpha \cos \Psi + \sin \varphi_A \cdot \cos \alpha \sin \Psi \right]</cmath> | ||
| + | <cmath>\sin \alpha \left[ \sin \varphi_C \cdot \sin \Theta + \sin^2 \gamma \cos \varphi_C \cos \Theta - \cos ^2 \gamma \sin \varphi_C \cdot \sin \Theta + \cos \gamma \sin \Theta + \sin \gamma \cos \gamma (\cos \varphi_C \sin \Theta - \sin \varphi_C \cos \Theta) \right] =</cmath> | ||
| + | <cmath>= \sin \gamma \cdot \sin \alpha \left[\cos \varphi_A \cdot \sin \Psi + \sin \varphi_A \cdot \cos \Psi \right]</cmath> | ||
| + | |||
| + | <cmath>\sin \alpha \left[ \sin^2 \gamma \cdot \cos (\Theta - \varphi_C) + \sin \gamma \cdot \cos \gamma \cdot \sin (\Theta - \varphi_C)\right] = \sin \gamma \cdot \sin \alpha \cdot \sin (\Psi + \varphi_A)</cmath> | ||
| + | |||
| + | <cmath>\sin \alpha \cdot \sin \gamma \cdot \sin (\gamma + \Theta - \varphi_C) = \sin \gamma \cdot \sin \alpha \cdot \sin (\beta + \varphi_A - \varphi_B + \varphi_C).</cmath> The last statement is obvious. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==2024, Problem 19== | ||
| + | [[File:2024 19 4.png|250px|right]] | ||
| + | [[File:2024 19 2.png|250px|right]] | ||
| + | [[File:2024 19 3.png|250px|right]] | ||
| + | A triangle <math>ABC,</math> its circumcircle <math>\Omega</math>, and its incenter <math>I</math> are drawn on the plane. | ||
| + | |||
| + | Construct the circumcenter <math>O</math> of <math>\triangle ABC</math> using only a ruler. | ||
| + | |||
| + | <i><b>Solution</b></i> | ||
| + | |||
| + | We successively construct: | ||
| + | |||
| + | - the midpoint <math>D = BI \cap \Omega</math> of the arc <math>AB,</math> | ||
| + | |||
| + | - the midpoint <math>E = CI \cap \Omega</math> of the arc <math>AC,</math> | ||
| + | |||
| + | - the polar <math>H'H''</math> of point <math>H \in DE,</math> | ||
| + | |||
| + | - the polar <math>G'G''</math> of point <math>G \in DE,</math> | ||
| + | |||
| + | - the polar <math>F = H'H'' \cap G'G''</math> of the line <math>DE,</math> | ||
| + | |||
| + | - the tangent <math>FD || AC</math> to <math>\Omega,</math> | ||
| + | |||
| + | - the tangent <math>FE || AB</math> to <math>\Omega,</math> | ||
| + | |||
| + | - the trapezium <math>ACDF,</math> | ||
| + | |||
| + | - the point <math>K = AF \cap CD,</math> | ||
| + | |||
| + | - the point <math>L = AD \cap CF,</math> | ||
| + | |||
| + | - the midpoint <math>M = AC \cap KL</math> of the segment <math>AB,</math> | ||
| + | |||
| + | - the midpoint <math>M'</math> of the segment <math>AC,</math> | ||
| + | |||
| + | - the diameter <math>DM</math> of <math>\Omega,</math> | ||
| + | |||
| + | - the diameter <math>EM'</math> of <math>\Omega,</math> | ||
| + | |||
| + | - the circumcenter <math>O = DM \cap EM'.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==2024, Problem 18== | ||
| + | [[File:2024 18 1.png|390px|right]] | ||
| + | Let <math>AH, BH', CH''</math> be the altitudes of an acute-angled triangle <math>ABC, I_A</math> be its excenter corresponding to <math>A, I'_A</math> be the reflection of <math>I_A</math> about the line <math>AH.</math> Points <math>I'_B, I'_C</math> are defined similarly. Prove that the lines <math>HI'_A, H'I'_B, H''I'_C</math> concur. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Denote <math>I</math> the incenter of <math>\triangle ABC.</math> Points <math>A, I, I_A</math> are collinear. | ||
| + | We will prove that <math>I \in HI'_A.</math> | ||
| + | Denote <math>D \in BC, ID \perp BC, D' \in I'_AI_A, ID' \perp BC, E = BC \cap AI_A,</math> | ||
| + | <math>F \in BC, I_AF \perp BC, AH = h_A, ID = r, I_AF = r_A, BC = a, s</math> - semiperimeter. | ||
| + | <cmath>\frac {HD}{HF} = \frac {AI}{AI_A} = \frac {h_A - r}{h_A + r}.</cmath> | ||
| + | The area <math>[ABC] = r \cdot s = r_A (s - a) = \frac {a h_A}{2} \implies</math> | ||
| + | <cmath>\frac {1}{r} = \frac {1}{r_A} + \frac {2}{h_A} \implies \frac {h_A - r}{h_A+ r} = \frac {r_A}{r}.</cmath> | ||
| + | <cmath>\frac {I'_AD'}{HD} = \frac {HD + HF}{HD} = 1 + \frac {HF}{HD} = 1 + \frac {r_A}{r}= \frac {r_A + r}{r} \implies</cmath> | ||
| + | Points <math>I, H, I'_a</math> are collinear, so the lines <math>HI'_A, H'I'_B, H''I'_C</math> concur at the point <math>I.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==2024, Problem 17== | ||
| + | [[File:2024 17 1.png|400px|right]] | ||
| + | Let <math>\triangle ABC</math> be not isosceles triangle, <math>\omega</math> be its incircle. | ||
| + | |||
| + | Let <math>D, E,</math> and <math>F</math> be the points at which the incircle of <math>\triangle ABC</math> touches the sides <math>BC, CA,</math> and <math>AB,</math> respectively. | ||
| + | |||
| + | Let <math>K</math> be the point on ray <math>EF</math> such that <math>EK = AB.</math> | ||
| + | |||
| + | Let <math>L</math> be the point on ray <math>FE</math> such that <math>FL = AC.</math> | ||
| + | |||
| + | The circumcircles of <math>\triangle BFK</math> and <math>\triangle CEL</math> intersect <math>\omega</math> again at <math>Q</math> and <math>P,</math> respectively. | ||
| + | |||
| + | Prove that <math>BQ, CP,</math> and <math>AD</math> are concurrent. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | <math>\frac {KE} {FL} = \frac {AB}{AC},</math> so points <math>Q,P,</math> and <math>G = FE \cap BC</math> are collinear (see [[Symmetry | Symmetry and incircle]] for details). | ||
| + | |||
| + | Therefore lines <math>BQ, CP,</math> and <math>AD</math> are concurrent (see [[ Symmetry | Symmetry and incircle A]] for details.) | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==2024, Problem 16== | ||
| + | [[File:2024 16 1.png|300px|right]] | ||
| + | Let <math>AA', BB',</math> and <math>CC'</math> be the bisectors of a triangle <math>\triangle ABC.</math> | ||
| + | |||
| + | The segments <math>BB'</math> and <math>A'C'</math> meet at point <math>D.</math> Let <math>E</math> be the projection of <math>D</math> to <math>AC.</math> | ||
| + | |||
| + | Points <math>P</math> and <math>Q</math> on the sides <math>AB</math> and <math>BC,</math> respectively, are such that <math>EP = PD, EQ = QD.</math> | ||
| + | |||
| + | Prove that <math>\angle PDB' = \angle EDQ.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | <math>\triangle PDQ = \triangle PEQ (DQ = EQ, DP = PF, PQ</math> is the common side) <math>\implies</math> | ||
| + | |||
| + | <math>PQ \perp DE, F = PQ \cap DE</math> is the midpoint <math>DE \implies</math> | ||
| + | |||
| + | <math>G = BB' \cap PQ</math> is the midpoint of <math>DB'.</math> | ||
| + | <cmath>\frac{BG}{BB'} =\frac {BQ}{BC} = \frac {BP}{BA} = \frac {BD}{BI}.</cmath> | ||
| + | (see [[Bisector | Division of bisector]] for details.) | ||
| + | |||
| + | So <math>DQ || CC', PD || AA'.</math> Denote <math>\angle ACC' = \angle BCC' = \gamma, \angle A'AC = \alpha, B'BC = \beta.</math> | ||
| + | <cmath>\angle PDB' = \angle AIB' = \angle BB'C - \angle IAC = 180^\circ - \beta - 2 \gamma - \alpha = 90^\circ - \gamma.</cmath> | ||
| + | <cmath>\angle QDE = 90^\circ - \angle DQP = 90^\circ - \gamma = \angle PDB'.</cmath> | ||
| + | |||
| + | Another solution see [[Isogonal_conjugate | 2024_Sharygin_olimpiad_Problem_16]] | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==2024, Problem 15== | ||
| + | [[File:2024 15.png|390px|right]] | ||
| + | The difference of two angles of a triangle is greater than <math>90^\circ.</math> Prove that the ratio of its circumradius and inradius is greater than <math>4.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Suppose, <math>\angle BAC = \alpha = \angle ACB + 90^\circ = \gamma + 90^\circ.</math> | ||
| + | |||
| + | Let <math>\Omega = \odot ABC, C'</math> be the point on <math>\Omega</math> opposite <math>C, B'</math> be the midpoint of arc <math>\overset{\Large\frown} {AC}.</math> | ||
| + | Then <cmath>\angle CAC' = 90^\circ \implies \angle BAC' = \angle ACB = \gamma = \angle BCC' \implies</cmath> | ||
| + | <cmath>\overset{\Large\frown} {AB} = \overset{\Large\frown} {BC'} \implies BB' || CC'.</cmath> | ||
| + | <cmath>BO = CO \implies \angle CBO = \angle OCB = \angle ACB = \gamma.</cmath> | ||
| + | <cmath>\angle ABC = \beta = 180^\circ - \gamma - \alpha = 90^\circ - 2 \gamma.</cmath> | ||
| + | <cmath>\angle OBB' = \frac {\beta}{2} + \gamma = 45^\circ.</cmath> | ||
| + | <cmath>BO = OB' = R \implies \angle BB'O = 45^\circ, \angle BOB' = 90^\circ.</cmath> | ||
| + | Incenter <math>I</math> triangle <math>\triangle ABC</math> lies on <math>BB',</math> therefore <math>OI \ge \frac {R}{\sqrt {2}}.</math> | ||
| + | |||
| + | We use the Euler law <math>OI^2 = R^2 - 2 Rr \implies \frac {2r}{R} = 1 - \frac {OI^2}{R^2} \le \frac{1}{2} \implies \frac{R}{r} \ge 4.</math> | ||
| + | |||
| + | If <math>R = 4r</math> then <math>OI \perp BB' \implies \frac {BI}{IB'} = 1 \implies \frac {BC + AB}{AC} = 2, BI = \frac{R}{\sqrt{2}}.</math> | ||
| + | <cmath>\sin CBI = \frac {r}{BI} = \frac{r \sqrt{2}}{R} = \frac{1}{2\sqrt{2}} \implies \sin \beta = \frac{\sqrt{7}}{4} \implies</cmath> | ||
| + | <cmath>AC = 2R \sin \beta = R \frac {\sqrt{7}}{2},AB = AC (1 - \frac{1}{\sqrt {7}}), BC = AC (1 + \frac{1}{\sqrt {7}}).</cmath> | ||
| + | |||
| + | If <math>\angle BAC' > \angle ACB \implies \frac {OI}{R}</math> increases so <math>\frac {r}{R}</math> decreases. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==2024, Problem 14== | ||
| + | [[File:2024 14 1.png|390px|right]] | ||
| + | The incircle <math>\omega</math> of a right-angled triangle <math>\triangle ABC</math> touches the circumcircle <math>\theta</math> of its medial triangle at point <math>F.</math> Let <math>OE</math> be the tangent to <math>\omega</math> from the midpoint <math>O</math> of the hypothenuse <math>AB</math> distinct from <math>AB.</math> Prove that <math>CE = CF.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let <math>\Omega</math> and <math>I</math> be the circumcircle and the incenter of <math>\triangle ABC, D = \omega \cap AB.</math> | ||
| + | |||
| + | Let <math>Q</math> be nine-point center of <math>\triangle ABC, G</math> be the point at <math>OB</math> such that <math>OG = DO, K \in DI, KQ ||AB.</math> | ||
| + | |||
| + | Denote <math>r = ID, R = AO,a = BC, b = AC,c= AB, \beta = \angle ABC.</math> | ||
| + | |||
| + | <math>\triangle ABC</math> is the right-angled triangle, so <math>Q</math> is the midpoint <math>CO,</math> | ||
| + | |||
| + | <cmath>2R = c, r = \frac {a+b-c}{2},FQ = \frac{R}{2}.</cmath> | ||
| + | Let <math>h(X)</math> be the result of the homothety of the point <math>X</math> centered in <math>C</math> with the coefficient <math>2.</math> Then | ||
| + | <cmath>h(\theta) = \Omega, F' = h(F) \in \Omega, O = h(Q) \implies FQ || F'O.</cmath> | ||
| + | <cmath>DO = EO = GO \implies \angle DEG = 90^\circ.</cmath> | ||
| + | <cmath>\angle DOE = 2 \angle DOI = 2 \angle EGD \implies \angle DOI = \angle EGD, IO || EG.</cmath> | ||
| + | WLOG, <math>a > b \implies DO = \frac {a-b}{2} = \tan IOD = \frac{r}{DO} = \frac{a+b-c}{a-b} = \frac{\cos\beta + \sin \beta -1}{\cos\beta - \sin \beta}.</math> | ||
| + | |||
| + | Let <math>H</math> be the foot from <math>C</math> to <math>\overline{AB}</math>. | ||
| + | <math>CH = a \sin \beta = c \sin \beta \cos \beta, BH = a \cos \beta, BG = AD = \frac{c+b-a}{2}.</math> | ||
| + | <cmath>\tan \angle CGH = \frac {CH}{BH - BG} = \frac{2 \sin \beta \cos \beta}{2 \cos^2 \beta +\cos \beta - \sin \beta -1} =</cmath> | ||
| + | <cmath>= \frac{(\sin \beta + \cos \beta -1)(\sin \beta + \cos \beta +1)}{(\cos \beta - \sin \beta)(\sin \beta + \cos \beta +1)} = \frac{\cos\beta + \sin \beta -1}{\cos\beta - \sin \beta} = \tan IOD.</cmath> | ||
| + | Therefore points <math>C,E,</math> and <math>G</math> are collinear. | ||
| + | <cmath>\psi = \angle BCG = \angle AGC - \angle ABC \implies</cmath> | ||
| + | <cmath>\tan \psi = \frac {\tan \angle AGC - \tan \angle ABC}{1 + \tan \angle AGC \cdot \tan \angle ABC} = \frac {c - a}{c-b}.</cmath> | ||
| + | <cmath>\sin 2\psi = \frac {2\tan \psi}{1 + \tan^2 \psi} = \frac {2(c-a)(c-b)}{c(3c - 2b - 2a)},</cmath> | ||
| + | <cmath>\angle AOF' = \angle KQI, \sin \angle KQI = \frac{CH/2 -r}{QF - r}.</cmath> | ||
| + | <cmath>4c(QF - r) = c(c -2a -2b +2c) = c(3c -2a -2b),</cmath> | ||
| + | <cmath>2c(CH - 2r) = 2(ab -ac -bc +c^2) = 2(c - a)(c - b),</cmath> | ||
| + | <cmath>\sin \angle KQI = \frac {2(c-a)(c-b)}{c(3c - 2b - 2a)}= \sin 2 \psi \implies \angle KQI = 2 \psi.</cmath> | ||
| + | <cmath>\angle ACF' = \frac {\angle AOF'}{2} = \frac {\angle KQI}{2} = \psi = \angle BCG \implies \angle FCI = \angle ECI \implies CF = CE.</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==2024, Problem 12== | ||
| + | [[File:2024 12.png|390px|right]] | ||
| + | The bisectors <math>AE, CD</math> of a <math>\triangle ABC</math> with <math>\angle B = 60^\circ</math> meet at point <math>I.</math> | ||
| + | |||
| + | The circumcircles of triangles <math>ABC, DIE</math> meet at point <math>P.</math> | ||
| + | |||
| + | Prove that the line <math>PI</math> bisects the side <math>AC.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Denote <math>M</math> the midpoint <math>AC, \omega = \odot DIE,</math> | ||
| + | <cmath>\varphi = \angle CIM, \phi = \angle DIP, f(x) = \frac {\sin x}{\sin(120^\circ -x)}.</cmath> | ||
| + | <cmath>\angle AIC = 90^\circ + \frac {\angle ABC}{2} = 120^\circ = 180^\circ - \angle ABC \implies B \in \omega.</cmath> | ||
| + | In triangles <math>\triangle CIM</math> and <math>\triangle AIM</math>, by applying the law of sines, we get | ||
| + | <cmath>\frac {IM}{\sin \angle ACI} = \frac {CM}{\sin \varphi}, \frac {IM}{\sin \angle CAI} = \frac {AM}{\sin (120^\circ -\varphi)} \implies f(\varphi) = \frac {\sin \varphi} {\sin (120^\circ -\varphi)} = \frac {\sin \angle ACI}{\sin \angle CAI}.</cmath> | ||
| + | |||
| + | We use the formulas for circle <math>\omega</math> and get <cmath>\frac {PD}{\sin \angle PID} = \frac {PE}{\sin \angle PIE} \implies f(\phi) = \frac {\sin \phi} {\sin (120^\circ -\phi)} = \frac {PD}{PE}.</cmath> | ||
| + | |||
| + | <cmath>\angle BDI = \angle AEC \implies \angle ADC = 180^\circ - \angle AEC.</cmath> | ||
| + | In triangles <math>\triangle ADC</math> and <math>\triangle AEC</math>, by applying the law of sines, we get | ||
| + | <cmath> \frac {AD}{\sin \angle ACD} = \frac {AC}{\sin \angle ADC} = \frac {AC}{\sin \angle AEC} \implies \frac {AD}{CE} = \frac {\sin \angle ACI}{\sin \angle CAI}.</cmath> | ||
| + | |||
| + | <cmath>\angle BEP = \angle BDP, \angle BCP = \angle BAP \implies \triangle APD \sim \triangle CPE \implies \frac {AD}{CE} = \frac {PD}{PE}.</cmath> | ||
| + | |||
| + | Therefore <math>f(\phi) = f(\varphi).</math> The function <math>f</math> increases monotonically on the interval <math>(0, \frac {2 \pi}{3}).</math> | ||
| + | |||
| + | This means <math>\phi = \varphi</math> and points <math>P,I,</math> and <math>M</math> are collinear. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==2024, Problem 9== | ||
| + | [[File:2024 9.png|370px|right]] | ||
| + | Let <math>ABCD (AD || BC</math> be a trapezoid circumscribed around a circle <math>\omega,</math> centered at <math>O</math> which touches the sides <math>AB, BC, CD,</math> and <math>AD</math> at points <math>P, Q, R, S,</math> respectively. | ||
| + | |||
| + | The line passing trough <math>P</math> and parallel to the bases of trapezoid meets <math>QR</math> at point <math>X.</math> | ||
| + | |||
| + | Prove that <math>AB, QS,</math> and <math>DX</math> concur. | ||
| + | |||
| + | <i><b>Solution</b></i> | ||
| + | |||
| + | Solution 1. <math>AP = AS \implies \angle AOS = \frac {\overset{\Large\frown} {PS}}{2} = \angle PQS \implies PQ||AO.</math> | ||
| + | |||
| + | <cmath>OD \perp OC, QR \perp OC \implies OD || QX. AD ||PX \implies</cmath> | ||
| + | |||
| + | <math>E = AP \cap QS</math> is the center of similarity of triangles <math>\triangle PQX</math> and <math>\triangle AOD.</math> | ||
| + | |||
| + | Solution 2. <math>\triangle ODS \sim \triangle QXG \implies \frac {SD}{GX} = \frac {SO}{GQ} = \frac {1}{2} \cdot \frac {SQ}{GQ} = \frac {1}{2} \cdot \frac {AB}{PB}.</math> | ||
| + | |||
| + | Denote <math>EA = x, AP = AS = y, BP = BQ = z.</math> | ||
| + | |||
| + | <cmath>\triangle AES \sim BEQ \implies \frac {x}{x+y+z}= \frac {y}{z} \implies xz = xy + y^2 + yz \implies | ||
| + | 2xz = xy + y^2 + yz + xz \implies</cmath> | ||
| + | |||
| + | <cmath>\frac {x}{x+y}= \frac {y+z}{2z} \implies \frac {AS}{AG} = \frac {1}{2} \cdot \frac {AB}{PB} \implies \triangle ESD \sim \triangle EGX \implies E \in DX.</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==2024, Problem 8== | ||
| + | [[File:2024 8.png|390px|right]] | ||
| + | Let <math>ABCD</math> be a quadrilateral with <math>\angle B = \angle D</math> and <math>AD = CD.</math> | ||
| + | |||
| + | The incircle of <math>\triangle ABC</math> touches the sides <math>BC</math> and <math>AB</math> at points <math>E</math> and <math>F</math> respectively. | ||
| + | |||
| + | The midpoints of segments <math>AC, BD, AE,</math> and <math>CF</math> are points <math>M,X,Y,Z.</math> | ||
| + | |||
| + | Prove that points <math>M,X,Y,Z.</math> are concyclic. | ||
| + | |||
| + | <i><b>Solution</b></i> | ||
| + | |||
| + | <cmath>ZM || AB, YM || BC \implies \angle YMZ = \angle ABC = \angle ADC = \alpha.</cmath> | ||
| + | <cmath>2 \vec {XY} = \vec {DA} + \vec {BE}, 2 \vec {XZ} = \vec {DC} + \vec {BF}.</cmath> | ||
| + | <math>\vec {DC}</math> is the rotation of <math>\vec {DA}</math> around a point <math>D</math> through an angle <math>\alpha.</math> | ||
| + | |||
| + | <math>\vec {BF}</math> is the rotation of <math>\vec {BE}</math> around a point <math>B</math> through an angle <math>\alpha.</math> | ||
| + | |||
| + | So <math>\vec {XZ}</math> is the rotation of <math>\vec {XE}</math> around a point <math>X</math> through an angle <math>\alpha.</math> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==2024, Problem 2== | ||
| + | [[File:2024 2.png|330px|right]] | ||
| + | [[File:2024 2a.png|330px|right]] | ||
| + | [[File:2024 2b.png|330px|right]] | ||
| + | Three distinct collinear points are given. Construct the isosceles triangles such that these points are their circumcenter, incenter and excenter (in some order). | ||
| + | |||
| + | <i><b>Solution</b></i> | ||
| + | |||
| + | Let <math>M</math> be the midpoint of the segment connecting the incenter and excenter. It is known that point <math>M</math> belong the circumcircle. | ||
| + | Construction is possible if a circle with diameter IE (incenter – excenter) intersects a circle with radius OM (circumcenter – M). Situation when <math>E</math> between <math>I</math> and <math>O</math> is impossible. | ||
| + | |||
| + | Denote points <math>A, B, C</math> such that <math>B \in AC</math> and <math>AB \le BC.</math> | ||
| + | |||
| + | Suppose point <math>A</math> is circumcenter, so <math>B</math> is incenter. <math>M</math> is midpoint BC. The vertices of the desired triangle are located at the intersection of a circle with center <math>A</math> and radius <math>AM</math> with <math>\omega</math> and a line <math>AB.</math> | ||
| + | |||
| + | Suppose point <math>C</math> is circumcenter, so <math>B</math> is incenter. <math>M</math> is midpoint <math>AB.</math> The vertices of the desired triangle are located at the intersection of a circle with center <math>A</math> and radius <math>AM</math> with <math>\omega</math> and a line <math>AB.</math> | ||
| + | |||
| + | Suppose point <math>B</math> is circumcenter, so <math>A</math> is incenter. <math>M</math> is midpoint <math>AB.</math> Suppose <math>3 AB < BC.</math> The vertices of the desired triangle are located at the intersection of a circle with center <math>B</math> and radius <math>BM</math> with <math>\omega</math> and a line <math>AB.</math> | ||
| + | |||
| + | If <math>3 AB \ge BC</math> there is not desired triangle. | ||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | ==The problem from MGTU== | ||
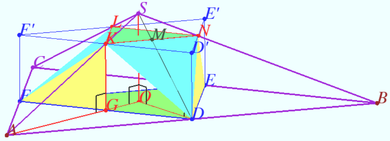
| + | [[File:2024 olimp november pr 9.png|390px|right]] | ||
| + | The lateral face of the regular triangular pyramid <math>SABC</math> is inclined to the plane of the base <math>ABC</math> at an angle of <math>\alpha = \arctan \frac{3}{4}.</math> Points <math>D, E, F</math> are the midpoints of the sides of the <math>\triangle ABC.</math> Triangle <math>\triangle DEF</math> is the lower base of a right prism. The edges of the upper base of the prism intersect the lateral edges of the pyramid <math>SABC</math> at points <math>K, L, N.</math> The area of the total surface of the polyhedron with vertices <math>D, E, F, K, L, N</math> is equal to <math>53 \sqrt{3}.</math> Find the side of <math>\triangle ABC.</math> | ||
| + | |||
| + | <i><b>Solution</b></i> | ||
| + | |||
| + | Denote <math>AB = BC = AC = a, O</math> is the center of <math>\triangle ABC, G = DF \cap AO, GK \perp ABC, K \in AS, M = SD \cap KN.</math> | ||
| + | <cmath>OD = \frac{ CD}{3} = \frac {a \sqrt {3}}{6}, SO = OD \cdot \tan \alpha = \frac {a \sqrt {3}}{8}.</cmath> | ||
| + | <cmath>AG = \frac {AE}{2}, AO = \frac{2AE}{3} \implies \frac {KG}{SO} = \frac{AG}{AO} = \frac{3}{4} \implies KG = \frac {3 a \sqrt{3}}{32} = h.</cmath> | ||
| + | <cmath>MD = \frac{KG}{\sin \alpha} = \frac{5}{3} KG = \frac{5h}{3}.</cmath> | ||
| + | The area of the total surface of the polyhedron with vertices <math>D, E, F, K, L, N</math> is | ||
| + | <cmath>Area = [DEF] + [KLN] + 3[DFK]+ 3[DKN].</cmath> | ||
| + | <cmath>[ABC] = \frac {a^2 \sqrt{3}}{4} = 4[DEF] =4 s \implies s = \frac {a^2 \sqrt{3}}{16}.</cmath> | ||
| + | <cmath>\frac{KN}{AB} = \frac {SK}{SA} = \frac{GO}{AO} = \frac {1}{4} \implies [KLN] =\frac{[ABC]}{16} = \frac {s}{4} \implies [DEF] + [KLN] = \frac {5s}{4}.</cmath> | ||
| + | <cmath>[DFK] = \frac{KG \cdot DF}{2} = \frac{ah}{4}, ah = \frac{3}{2} s.</cmath> | ||
| + | <cmath>[DKN] = \frac{MD \cdot KN}{2} = \frac{5ah}{24} \implies 3[DFK]+ 3[DKN] = \frac{11ah}{8} = \frac{33s}{16}.</cmath> | ||
| + | <cmath>Area = \frac {5s}{4} + \frac{33s}{16} = \frac{53s}{16} = 53 \sqrt{3} \implies s = 16 \sqrt {3} = \frac {a^2 \sqrt{3}}{16} \implies a = 16.</cmath> | ||
| + | ==The trapezoid problem from MGTU== | ||
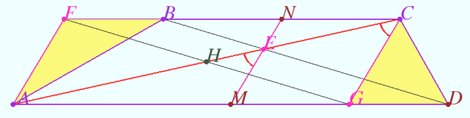
| + | [[File:2024 olimp november pr 7.png|470px|right]] | ||
| + | Points <math>M</math> and <math>N</math> are the midpoints of bases <math>AD</math> and <math>BC</math> of trapezoid <math>ABCD.</math> | ||
| + | |||
| + | Denote <math>\alpha</math> the angle between lines <math>MN</math> and <math>AC, \cos \alpha = \frac{11}{16}.</math> | ||
| + | |||
| + | Find the area of trapezoid <math>ABCD</math> if <math>MN = 2, BD = 6.</math> | ||
| + | |||
| + | <i><b>Solution</b></i> | ||
| + | |||
| + | <cmath>AF||MN||CG \implies AG = CF = AM+NC \implies FB=DG \implies</cmath> | ||
| + | <cmath>[ABCD] = [AFCG] = AC \cdot CG \cdot \sin \alpha = 2 CH \cdot CG \cdot \sin \alpha.</cmath> | ||
| + | By applying the Law of Cosines on <math>\triangle CHG, HG = \frac {BD}{2} = 3,</math> we get | ||
| + | <cmath>CH^2 + CG^2- 2 CH \cdot CG \cos \alpha = GH^2 \implies CH^2 - \frac {11}{4} CH - 5 = 0 \implies CH = 4.</cmath> | ||
| + | <cmath>\sin ^2 \alpha = 1 - \cos^2 \alpha = \frac {135}{16^2} \implies [ABCD] = 2 \cdot 4 \cdot 2 \frac {\sqrt{135}}{16} = \sqrt{135}.</cmath> | ||
Latest revision as of 14:29, 17 November 2024
Igor Fedorovich Sharygin (13/02/1937 - 12/03/2004, Moscow) - Soviet and Russian mathematician and teacher, specialist in elementary geometry, popularizer of science. He wrote many textbooks on geometry and created a number of beautiful problems. He headed the mathematics section of the Russian Soros Olympiads. After his death, Russia annually hosts the Geometry Olympiad for high school students. It consists of two rounds – correspondence and final. The correspondence round lasts 3 months.
The best problems of these Olympiads will be published. The numbering contains the year of the Olympiad and the serial number of the problem. Solutions are often different from the original ones.
Contents
[hide]- 1 2024 tur 2 klass 10 Problem 6
- 2 2024 tur 2 klass 10 Problem 7
- 3 2024 tur 2 klass 9 Problem 7
- 4 2024 tur 2 klass 9 Problem 5
- 5 2024 tur 2 klass 9 Problem 4
- 6 2024 tur 2 klass 9 Problem 3
- 7 2024 tur 2 klass 8 Problem 4
- 8 2024 tur 2 klass 8 Problem 2
- 9 2024, Problem 23
- 10 One-to-one mapping of the circle
- 11 2024, Problem 22
- 12 2024, Problem 21
- 13 2024, Problem 20
- 14 2024, Problem 19
- 15 2024, Problem 18
- 16 2024, Problem 17
- 17 2024, Problem 16
- 18 2024, Problem 15
- 19 2024, Problem 14
- 20 2024, Problem 12
- 21 2024, Problem 9
- 22 2024, Problem 8
- 23 2024, Problem 2
- 24 The problem from MGTU
- 25 The trapezoid problem from MGTU
2024 tur 2 klass 10 Problem 6
A point ![]() lies on one of medians of triangle
lies on one of medians of triangle ![]() in such a way that
in such a way that ![]() Prove that there exists a point
Prove that there exists a point ![]() on another median such that
on another median such that ![]() (A.Zaslavsky)
(A.Zaslavsky)
Proof
1. Denote ![]() It is known that barycentric coordinates are
It is known that barycentric coordinates are
![]()
2. Denote ![]()
![]() is tangent to
is tangent to ![]()
![]() is tangent
is tangent ![]()
![]() is the radical axes of
is the radical axes of ![]() and
and ![]() the power of a point
the power of a point ![]() with respect to a circle
with respect to a circle ![]() is
is ![]() so the power of a point
so the power of a point ![]() with respect to a circle
with respect to a circle ![]() is
is ![]()
![]() so
so ![]() is tangent to
is tangent to ![]()
![]() so point
so point ![]() symmetrical to
symmetrical to ![]() with respect to the
with respect to the ![]() median satisfies the conditions.
median satisfies the conditions. ![]()
vladimir.shelomovskii@gmail.com, vvsss
2024 tur 2 klass 10 Problem 7
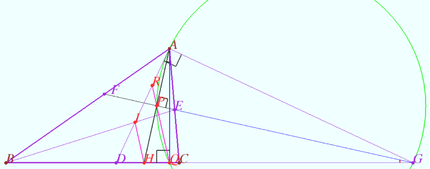
Let ![]() be a triangle with
be a triangle with ![]() and
and ![]() be its bisectors,
be its bisectors, ![]() be the projections of
be the projections of ![]() to
to ![]() and
and ![]() respectively, and
respectively, and ![]() be the second common point of the circle
be the second common point of the circle ![]() with
with ![]()
Prove that points ![]() are collinear. (K.Belsky)
are collinear. (K.Belsky)
Proof
Denote ![]() the incenter of
the incenter of ![]()
![]() the midpoint of
the midpoint of ![]()
It is known ( Division of bisector) that
![]()
![]()
![]()
![]() is cyclic.
is cyclic.
Therefore ![]() is cyclic
is cyclic ![]()
Let ![]()
It is known that points ![]() and
and ![]() are collinear,
are collinear,
![]()
![]() is the diameter of
is the diameter of ![]()
![]()
![]()
![]() is the bisector of
is the bisector of ![]()
Bisector ![]()
Altitude ![]()
Note that the point ![]() is a Feuerbach point of
is a Feuerbach point of ![]() since both the inscribed circle and the Euler circle pass through it.
since both the inscribed circle and the Euler circle pass through it.
vladimir.shelomovskii@gmail.com, vvsss
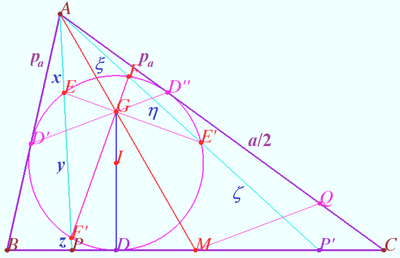
2024 tur 2 klass 9 Problem 7
Let triangle ![]() and point
and point ![]() on the side
on the side ![]() be given. Let
be given. Let ![]() be such point on the side
be such point on the side ![]() that
that ![]() The cross points of segments
The cross points of segments ![]() and
and ![]() with the incircle
with the incircle ![]() of
of ![]() form a convex quadrilateral
form a convex quadrilateral ![]()
Find the locus of crosspoints of diagonals ![]() (D.Brodsky)
(D.Brodsky)
Solution 1. Particular case of Fixed point .
2. Denote ![]()
![]()
![]() We perform simple transformations and get:
We perform simple transformations and get:
![]() We use Stewart's theorem and get:
We use Stewart's theorem and get:
![]()
![]()
![]() Similarly
Similarly ![]() Therefore
Therefore ![]() not depends from
not depends from ![]()
Let ![]() be the midpoint of
be the midpoint of ![]() is the median of
is the median of ![]() and
and ![]()
The line ![]() cross the median of
cross the median of ![]() at point
at point ![]() such that
such that ![]()
So point ![]() is fixed and this point lyes on
is fixed and this point lyes on ![]() .
.
Therefore the locus of crosspoints of diagonals ![]() is point
is point ![]()
Corollary
Let line ![]() . Then
. Then ![]()
vladimir.shelomovskii@gmail.com, vvsss
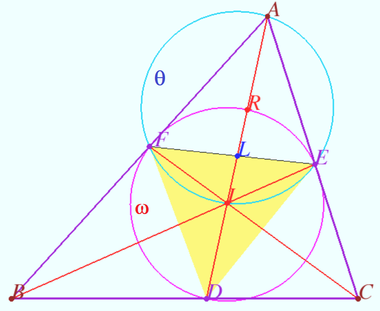
2024 tur 2 klass 9 Problem 5
Let ![]() be an isosceles triangle
be an isosceles triangle ![]() be its circumcenter,
be its circumcenter,![]() be the orthocenter, and
be the orthocenter, and ![]() be a point inside the triangle such that
be a point inside the triangle such that ![]()
Prove that ![]() (A.Zaslavsky)
(A.Zaslavsky)
Proof
Denote ![]() the midpoint
the midpoint ![]() the midpoint
the midpoint ![]() the foot from
the foot from ![]() to
to ![]() tangent to
tangent to ![]()
![]() There is a spiral similarity
There is a spiral similarity ![]() centered at point
centered at point ![]() that maps
that maps ![]() into
into ![]()
The coefficient of similarity ![]() rotation angle equal
rotation angle equal ![]()
![]()
![]()
![]() so
so ![]() is tangent to
is tangent to ![]() Basic information
Basic information
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Points
Points ![]() and
and ![]() are collinear, so
are collinear, so ![]() median of
median of ![]()
![]() is
is ![]() symmedian of
symmedian of ![]()
![]() is
is ![]() Humpty point.
Humpty point.
vladimir.shelomovskii@gmail.com, vvsss
2024 tur 2 klass 9 Problem 4
For which ![]() it is possible to mark several different points and several different circles on the plane in such a way that:
it is possible to mark several different points and several different circles on the plane in such a way that:
- exactly ![]() marked circles pass through each marked point;
marked circles pass through each marked point;
- exactly ![]() marked points lie on each marked circle;
marked points lie on each marked circle;
- the center of each marked circle is marked? (P.Puchkov)
Solution
Case ![]() Circles centered at
Circles centered at ![]() and
and ![]() with radii
with radii ![]()
Case ![]() is not paralel to
is not paralel to ![]()
Four circles are centered at points ![]() and
and ![]() Each radius is equal
Each radius is equal ![]()
Case ![]() is not paralel to
is not paralel to ![]() or
or ![]()
Eight circles centered at ![]() and
and ![]() have radii
have radii ![]()
Case ![]()
Answer For all ![]()
vladimir.shelomovskii@gmail.com, vvsss
2024 tur 2 klass 9 Problem 3
Let ![]() and
and ![]() be two pairs of points isogonally conjugated with respect to a triangle
be two pairs of points isogonally conjugated with respect to a triangle ![]() and
and ![]() be the common point of lines
be the common point of lines ![]() and
and ![]() Prove that the pedal circles of points
Prove that the pedal circles of points ![]() and
and ![]() are coaxial. (L.Shatunov, V.Shelomovskii)
are coaxial. (L.Shatunov, V.Shelomovskii)
Solution
1. Let ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]() Then circle centered at the midpoint
Then circle centered at the midpoint ![]() is the common pedal circle of points
is the common pedal circle of points ![]() and
and ![]() ( Circumcircle of pedal triangles) So center
( Circumcircle of pedal triangles) So center ![]() is the midpoint
is the midpoint ![]() and center
and center ![]() is the midpoint
is the midpoint ![]()
2. Denote ![]() Then
Then ![]() is the isogonal conjugate of a point
is the isogonal conjugate of a point ![]() with respect to
with respect to ![]() So center
So center ![]() is the midpoint
is the midpoint ![]() ( Two pares of isogonally conjugate points)
( Two pares of isogonally conjugate points)
3. The Gauss line (or Gauss–Newton line) is the line joining the midpoints of the three diagonals of a complete quadrilateral ![]() (Gauss line).So points
(Gauss line).So points ![]() and
and ![]() are collinear as was to be proven.
are collinear as was to be proven. ![]()
vladimir.shelomovskii@gmail.com, vvsss
2024 tur 2 klass 8 Problem 4
A square with sidelength ![]() is cut from the paper. Construct a segment with length
is cut from the paper. Construct a segment with length ![]() using at most
using at most ![]() folds. No instruments are available, it is allowed only to fold the paper and to mark the common points of folding lines. (M.Evdokimov)
folds. No instruments are available, it is allowed only to fold the paper and to mark the common points of folding lines. (M.Evdokimov)
Solution
Main idea: ![]()
![]()
![]() Let
Let ![]()
![]() We perform
We perform ![]() horizontal fold of the sheet. We get line
horizontal fold of the sheet. We get line ![]() We perform
We perform
![]() vertical folds of the sheet. We get
vertical folds of the sheet. We get ![]() vertical lines at a distance of
vertical lines at a distance of ![]() from each other.
from each other.
Point ![]() is the lower left corner of the sheet, point
is the lower left corner of the sheet, point ![]() is the lower point of the second vertical line, point
is the lower point of the second vertical line, point ![]() is the lower point of the
is the lower point of the ![]() line, point
line, point ![]() is the point at the intersection of the horizontal line and the
is the point at the intersection of the horizontal line and the ![]() vertical line.
vertical line.
Points ![]() and
and ![]() are at the intersection of the lines
are at the intersection of the lines ![]() and
and ![]() and the
and the ![]() vertical line.
vertical line.
vladimir.shelomovskii@gmail.com, vvsss
2024 tur 2 klass 8 Problem 2
Let ![]() be the midpoint of side
be the midpoint of side ![]() of an acute-angled triangle
of an acute-angled triangle ![]() and
and ![]() be the projection of the orthocenter
be the projection of the orthocenter ![]() to the bisector of angle
to the bisector of angle ![]() Prove that
Prove that ![]() bisects the segment
bisects the segment ![]() (L.Emelyanov)
(L.Emelyanov)
Solution
Denote ![]() - the midpoint of
- the midpoint of ![]() and
and ![]() the foots of the heights,
the foots of the heights, ![]() be the Euler circle
be the Euler circle ![]()
![]() is the circle
is the circle ![]() with the diameter
with the diameter ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() points
points ![]() and
and ![]() are collinear.
are collinear.
vladimir.shelomovskii@gmail.com, vvsss
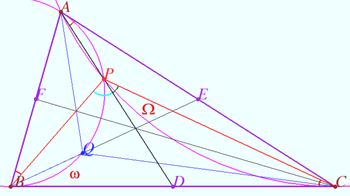
2024, Problem 23
A point ![]() moves along a circle
moves along a circle ![]() Let
Let ![]() and
and ![]() be fixed points of
be fixed points of ![]() and
and ![]() be an arbitrary point inside
be an arbitrary point inside ![]()
The common external tangents to the circumcircles of triangles ![]() and
and ![]() meet at point
meet at point ![]()
Prove that all points ![]() lie on two fixed lines.
lie on two fixed lines.
Solution
Denote ![]()
![]()
![]() is the circumcenter of
is the circumcenter of ![]() is the circumcenter of
is the circumcenter of ![]()
Let ![]() and
and ![]() be the midpoints of the arcs
be the midpoints of the arcs ![]() of
of ![]()
Let ![]() and
and ![]() be the midpoints of the arcs
be the midpoints of the arcs ![]() of
of ![]()
These points not depends from position of point ![]()
Suppose, ![]() see diagram).
see diagram).
![]()
![]() Let
Let ![]()
![]() Similarly,
Similarly, ![]()
Let ![]()
Therefore ![]() Similarly, if
Similarly, if ![]() then
then ![]()
Claim
Points ![]() and
and ![]() are collinear.
are collinear.
Proof
![]() is the midpoint of arc
is the midpoint of arc ![]() Denote
Denote ![]()
![]()
![]()
![]() Therefore
Therefore ![]() points
points ![]() and
and ![]() are collinear.
are collinear.
vladimir.shelomovskii@gmail.com, vvsss
One-to-one mapping of the circle
Let a circle ![]() two fixed points
two fixed points ![]() and
and ![]() on it and a point
on it and a point ![]() inside it be given.
Then there is a one-to-one mapping of the circle
inside it be given.
Then there is a one-to-one mapping of the circle ![]() onto itself, based on the following two theorems.
onto itself, based on the following two theorems.
1. Let a circle ![]() two fixed points
two fixed points ![]() and
and ![]() on
on ![]() and a point
and a point ![]() inside
inside ![]() be given.
be given.
Let an arbitrary point ![]() be given.
be given.
Let ![]() is the midpoint of the arc
is the midpoint of the arc ![]()
Denote ![]() Prove that
Prove that ![]()
2. Let a circle ![]() two fixed points
two fixed points ![]() and
and ![]() on
on ![]() and a point
and a point ![]() inside
inside ![]() be given.
be given.
Let an arbitrary point ![]() be given.
be given.
Let ![]() is the midpoint of the arc
is the midpoint of the arc ![]()
Denote ![]()
Denote ![]() Prove that
Prove that ![]()
Proof
![]()
Points ![]() are collinear.
are collinear.
![]()
![]()
2. Points ![]() and
and ![]() are collinear (see Claim in 2024, Problem 23).
are collinear (see Claim in 2024, Problem 23).
We use Pascal's theorem for points ![]() and crosspoints
and crosspoints ![]() and get
and get ![]()
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 22
A segment ![]() is given. Let
is given. Let ![]() be an arbitrary point of the perpendicular bisector to
be an arbitrary point of the perpendicular bisector to ![]()
![]() be the point on the circumcircle of
be the point on the circumcircle of ![]() opposite to
opposite to ![]() and an ellipse centered at
and an ellipse centered at ![]() touche
touche ![]()
Find the locus of touching points ![]() of the ellipse with the line
of the ellipse with the line ![]()
Solution
Denote ![]() the midpoint
the midpoint ![]() the point on the line
the point on the line ![]()
![]()
![]() In order to find the ordinate of point
In order to find the ordinate of point ![]() we perform an affine transformation (compression along axis
we perform an affine transformation (compression along axis ![]() which will transform the ellipse
which will transform the ellipse ![]() into a circle with diameter
into a circle with diameter ![]() The tangent of the
The tangent of the ![]() maps into the tangent of the
maps into the tangent of the ![]()
![]()
![]()
![]()
![]() Denote
Denote ![]()
So point ![]() is the fixed point (
is the fixed point (![]() not depends from angle
not depends from angle ![]()
Therefore point ![]() lies on the circle with diameter
lies on the circle with diameter ![]() (except points
(except points ![]() and
and ![]()
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 21
A chord ![]() of the circumcircle of a triangle
of the circumcircle of a triangle ![]() meets the sides
meets the sides ![]() at points
at points ![]() respectively. The tangents to the circumcircle at
respectively. The tangents to the circumcircle at ![]() and
and ![]() meet at point
meet at point ![]() and the tangents at points
and the tangents at points ![]() and
and ![]() meets at point
meets at point ![]() The line
The line ![]() meets
meets ![]() at point
at point ![]()
Prove that the lines ![]() and
and ![]() concur.
concur.
Proof
WLOG, ![]() Denote
Denote ![]()
Point ![]() is inside
is inside ![]()
We use Pascal’s theorem for quadrilateral ![]() and get
and get ![]()
We use projective transformation which maps ![]() to a circle and that maps the point
to a circle and that maps the point ![]() to its center.
to its center.
From this point we use the same letters for the results of mapping. Therefore the segments ![]() and
and ![]() are the diameters of
are the diameters of ![]() is the midpoint
is the midpoint ![]()
![]()
preimage ![]() lies on preimage
lies on preimage ![]()
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 20
Let a triangle ![]() points
points ![]() and
and ![]() be given,
be given, ![]() Points
Points ![]() and
and ![]() are the isogonal conjugate of the points
are the isogonal conjugate of the points ![]() and
and ![]() respectively, with respect to
respectively, with respect to ![]()
Denote ![]() and
and ![]() the circumradii of triangles
the circumradii of triangles ![]() and
and ![]() respectively.
respectively.
Prove that ![]() where
where ![]() is the area of
is the area of ![]()
Proof
Denote ![]()
![]()
![]() It is easy to prove that
It is easy to prove that
![]() is equivalent to
is equivalent to ![]()
![]()
![]() By applying the law of sines, we get
By applying the law of sines, we get
![]()
![]()
![]()
![]() We need to prove that
We need to prove that
![]() We make the transformations:
We make the transformations:
![]()
![]()
![]()
![]()
![]()
![]()
![]() The last statement is obvious.
The last statement is obvious.
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 19
A triangle ![]() its circumcircle
its circumcircle ![]() , and its incenter
, and its incenter ![]() are drawn on the plane.
are drawn on the plane.
Construct the circumcenter ![]() of
of ![]() using only a ruler.
using only a ruler.
Solution
We successively construct:
- the midpoint ![]() of the arc
of the arc ![]()
- the midpoint ![]() of the arc
of the arc ![]()
- the polar ![]() of point
of point ![]()
- the polar ![]() of point
of point ![]()
- the polar ![]() of the line
of the line ![]()
- the tangent ![]() to
to ![]()
- the tangent ![]() to
to ![]()
- the trapezium ![]()
- the point ![]()
- the point ![]()
- the midpoint ![]() of the segment
of the segment ![]()
- the midpoint ![]() of the segment
of the segment ![]()
- the diameter ![]() of
of ![]()
- the diameter ![]() of
of ![]()
- the circumcenter ![]()
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 18
Let ![]() be the altitudes of an acute-angled triangle
be the altitudes of an acute-angled triangle ![]() be its excenter corresponding to
be its excenter corresponding to ![]() be the reflection of
be the reflection of ![]() about the line
about the line ![]() Points
Points ![]() are defined similarly. Prove that the lines
are defined similarly. Prove that the lines ![]() concur.
concur.
Proof
Denote ![]() the incenter of
the incenter of ![]() Points
Points ![]() are collinear.
We will prove that
are collinear.
We will prove that ![]() Denote
Denote ![]()
![]() - semiperimeter.
- semiperimeter.
![]() The area
The area ![]()
![]()
![]() Points
Points ![]() are collinear, so the lines
are collinear, so the lines ![]() concur at the point
concur at the point ![]()
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 17
Let ![]() be not isosceles triangle,
be not isosceles triangle, ![]() be its incircle.
be its incircle.
Let ![]() and
and ![]() be the points at which the incircle of
be the points at which the incircle of ![]() touches the sides
touches the sides ![]() and
and ![]() respectively.
respectively.
Let ![]() be the point on ray
be the point on ray ![]() such that
such that ![]()
Let ![]() be the point on ray
be the point on ray ![]() such that
such that ![]()
The circumcircles of ![]() and
and ![]() intersect
intersect ![]() again at
again at ![]() and
and ![]() respectively.
respectively.
Prove that ![]() and
and ![]() are concurrent.
are concurrent.
Proof
![]() so points
so points ![]() and
and ![]() are collinear (see Symmetry and incircle for details).
are collinear (see Symmetry and incircle for details).
Therefore lines ![]() and
and ![]() are concurrent (see Symmetry and incircle A for details.)
are concurrent (see Symmetry and incircle A for details.)
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 16
Let ![]() and
and ![]() be the bisectors of a triangle
be the bisectors of a triangle ![]()
The segments ![]() and
and ![]() meet at point
meet at point ![]() Let
Let ![]() be the projection of
be the projection of ![]() to
to ![]()
Points ![]() and
and ![]() on the sides
on the sides ![]() and
and ![]() respectively, are such that
respectively, are such that ![]()
Prove that ![]()
Proof
![]() is the common side)
is the common side) ![]()
![]() is the midpoint
is the midpoint ![]()
![]() is the midpoint of
is the midpoint of ![]()
![]() (see Division of bisector for details.)
(see Division of bisector for details.)
So ![]() Denote
Denote ![]()
![]()
![]()
Another solution see 2024_Sharygin_olimpiad_Problem_16
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 15
The difference of two angles of a triangle is greater than ![]() Prove that the ratio of its circumradius and inradius is greater than
Prove that the ratio of its circumradius and inradius is greater than ![]()
Proof
Suppose, ![]()
Let ![]() be the point on
be the point on ![]() opposite
opposite ![]() be the midpoint of arc
be the midpoint of arc ![]() Then
Then ![]()
![]()
![]()
![]()
![]()
![]() Incenter
Incenter ![]() triangle
triangle ![]() lies on
lies on ![]() therefore
therefore ![]()
We use the Euler law ![]()
If ![]() then
then ![]()
![]()
![]()
If ![]() increases so
increases so ![]() decreases.
decreases.
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 14
The incircle ![]() of a right-angled triangle
of a right-angled triangle ![]() touches the circumcircle
touches the circumcircle ![]() of its medial triangle at point
of its medial triangle at point ![]() Let
Let ![]() be the tangent to
be the tangent to ![]() from the midpoint
from the midpoint ![]() of the hypothenuse
of the hypothenuse ![]() distinct from
distinct from ![]() Prove that
Prove that ![]()
Proof
Let ![]() and
and ![]() be the circumcircle and the incenter of
be the circumcircle and the incenter of ![]()
Let ![]() be nine-point center of
be nine-point center of ![]() be the point at
be the point at ![]() such that
such that ![]()
Denote ![]()
![]() is the right-angled triangle, so
is the right-angled triangle, so ![]() is the midpoint
is the midpoint ![]()
![]() Let
Let ![]() be the result of the homothety of the point
be the result of the homothety of the point ![]() centered in
centered in ![]() with the coefficient
with the coefficient ![]() Then
Then
![]()
![]()
![]() WLOG,
WLOG, ![]()
Let ![]() be the foot from
be the foot from ![]() to
to ![]() .
.
![]()
![]()
![]() Therefore points
Therefore points ![]() and
and ![]() are collinear.
are collinear.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 12
The bisectors ![]() of a
of a ![]() with
with ![]() meet at point
meet at point ![]()
The circumcircles of triangles ![]() meet at point
meet at point ![]()
Prove that the line ![]() bisects the side
bisects the side ![]()
Proof
Denote ![]() the midpoint
the midpoint ![]()
![]()
![]() In triangles
In triangles ![]() and
and ![]() , by applying the law of sines, we get
, by applying the law of sines, we get
![]()
We use the formulas for circle ![]() and get
and get ![]()
![]() In triangles
In triangles ![]() and
and ![]() , by applying the law of sines, we get
, by applying the law of sines, we get
![]()
![]()
Therefore ![]() The function
The function ![]() increases monotonically on the interval
increases monotonically on the interval ![]()
This means ![]() and points
and points ![]() and
and ![]() are collinear.
are collinear.
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 9
Let ![]() be a trapezoid circumscribed around a circle
be a trapezoid circumscribed around a circle ![]() centered at
centered at ![]() which touches the sides
which touches the sides ![]() and
and ![]() at points
at points ![]() respectively.
respectively.
The line passing trough ![]() and parallel to the bases of trapezoid meets
and parallel to the bases of trapezoid meets ![]() at point
at point ![]()
Prove that ![]() and
and ![]() concur.
concur.
Solution
Solution 1. ![]()
![]()
![]() is the center of similarity of triangles
is the center of similarity of triangles ![]() and
and ![]()
Solution 2. ![]()
Denote ![]()
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 8
Let ![]() be a quadrilateral with
be a quadrilateral with ![]() and
and ![]()
The incircle of ![]() touches the sides
touches the sides ![]() and
and ![]() at points
at points ![]() and
and ![]() respectively.
respectively.
The midpoints of segments ![]() and
and ![]() are points
are points ![]()
Prove that points ![]() are concyclic.
are concyclic.
Solution
![]()
![]()
![]() is the rotation of
is the rotation of ![]() around a point
around a point ![]() through an angle
through an angle ![]()
![]() is the rotation of
is the rotation of ![]() around a point
around a point ![]() through an angle
through an angle ![]()
So ![]() is the rotation of
is the rotation of ![]() around a point
around a point ![]() through an angle
through an angle ![]()
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 2
Three distinct collinear points are given. Construct the isosceles triangles such that these points are their circumcenter, incenter and excenter (in some order).
Solution
Let ![]() be the midpoint of the segment connecting the incenter and excenter. It is known that point
be the midpoint of the segment connecting the incenter and excenter. It is known that point ![]() belong the circumcircle.
Construction is possible if a circle with diameter IE (incenter – excenter) intersects a circle with radius OM (circumcenter – M). Situation when
belong the circumcircle.
Construction is possible if a circle with diameter IE (incenter – excenter) intersects a circle with radius OM (circumcenter – M). Situation when ![]() between
between ![]() and
and ![]() is impossible.
is impossible.
Denote points ![]() such that
such that ![]() and
and ![]()
Suppose point ![]() is circumcenter, so
is circumcenter, so ![]() is incenter.
is incenter. ![]() is midpoint BC. The vertices of the desired triangle are located at the intersection of a circle with center
is midpoint BC. The vertices of the desired triangle are located at the intersection of a circle with center ![]() and radius
and radius ![]() with
with ![]() and a line
and a line ![]()
Suppose point ![]() is circumcenter, so
is circumcenter, so ![]() is incenter.
is incenter. ![]() is midpoint
is midpoint ![]() The vertices of the desired triangle are located at the intersection of a circle with center
The vertices of the desired triangle are located at the intersection of a circle with center ![]() and radius
and radius ![]() with
with ![]() and a line
and a line ![]()
Suppose point ![]() is circumcenter, so
is circumcenter, so ![]() is incenter.
is incenter. ![]() is midpoint
is midpoint ![]() Suppose
Suppose ![]() The vertices of the desired triangle are located at the intersection of a circle with center
The vertices of the desired triangle are located at the intersection of a circle with center ![]() and radius
and radius ![]() with
with ![]() and a line
and a line ![]()
If ![]() there is not desired triangle.
there is not desired triangle.
vladimir.shelomovskii@gmail.com, vvsss
The problem from MGTU
The lateral face of the regular triangular pyramid ![]() is inclined to the plane of the base
is inclined to the plane of the base ![]() at an angle of
at an angle of ![]() Points
Points ![]() are the midpoints of the sides of the
are the midpoints of the sides of the ![]() Triangle
Triangle ![]() is the lower base of a right prism. The edges of the upper base of the prism intersect the lateral edges of the pyramid
is the lower base of a right prism. The edges of the upper base of the prism intersect the lateral edges of the pyramid ![]() at points
at points ![]() The area of the total surface of the polyhedron with vertices
The area of the total surface of the polyhedron with vertices ![]() is equal to
is equal to ![]() Find the side of
Find the side of ![]()
Solution
Denote ![]() is the center of
is the center of ![]()
![]()
![]()
![]() The area of the total surface of the polyhedron with vertices
The area of the total surface of the polyhedron with vertices ![]() is
is
![]()
![]()
![]()
![]()
![]()
![]()
The trapezoid problem from MGTU
Points ![]() and
and ![]() are the midpoints of bases
are the midpoints of bases ![]() and
and ![]() of trapezoid
of trapezoid ![]()
Denote ![]() the angle between lines
the angle between lines ![]() and
and ![]()
Find the area of trapezoid ![]() if
if ![]()
Solution
![]()
![]() By applying the Law of Cosines on
By applying the Law of Cosines on ![]() we get
we get
![]()
![]()