Difference between revisions of "2024 AIME II Problems/Problem 10"
(→Problem) |
(→Solution 10) |
||
| (104 intermediate revisions by 11 users not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
Let <math>\triangle ABC</math> have circumcenter <math>O</math> and incenter <math>I</math> with <math>\overline{IA}\perp\overline{OI}</math>, circumradius <math>13</math>, and inradius <math>6</math>. Find <math>AB\cdot AC</math>. | Let <math>\triangle ABC</math> have circumcenter <math>O</math> and incenter <math>I</math> with <math>\overline{IA}\perp\overline{OI}</math>, circumradius <math>13</math>, and inradius <math>6</math>. Find <math>AB\cdot AC</math>. | ||
| + | |||
| + | ==Solution 1 (Similar Triangles and PoP)== | ||
| + | |||
| + | Start off by (of course) drawing a diagram! Let <math>I</math> and <math>O</math> be the incenter and circumcenters of triangle <math>ABC</math>, respectively. Furthermore, extend <math>AI</math> to meet <math>BC</math> at <math>L</math> and the circumcircle of triangle <math>ABC</math> at <math>D</math>. | ||
<asy> | <asy> | ||
| Line 6: | Line 10: | ||
import olympiad; | import olympiad; | ||
real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; | real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; | ||
| − | pair | + | pair B=(0,0),C=(c,0), D = (c/2-0.01, -2.26); |
| − | pair | + | pair A = (c/3,8.65*c/10); |
draw(circumcircle(A,B,C)); | draw(circumcircle(A,B,C)); | ||
pair I=incenter(A,B,C); | pair I=incenter(A,B,C); | ||
pair O=circumcenter(A,B,C); | pair O=circumcenter(A,B,C); | ||
| − | pair L=extension( | + | pair L=extension(A,I,C,B); |
dot(I^^O^^A^^B^^C^^D^^L); | dot(I^^O^^A^^B^^C^^D^^L); | ||
| − | draw( | + | draw(A--L); |
| + | draw(A--D); | ||
path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} | path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} | ||
| − | draw( | + | draw(C--B--D--cycle); |
draw(A--C--B); | draw(A--C--B); | ||
| − | draw(A--I-- | + | draw(A--B); |
| + | draw(B--I--C^^A--I); | ||
draw(incircle(A,B,C)); | draw(incircle(A,B,C)); | ||
| − | label("$ | + | label("$B$",B,SW); |
| − | label("$ | + | label("$C$",C,SE); |
| − | label("$ | + | label("$A$",A,N); |
label("$D$",D,S); | label("$D$",D,S); | ||
| − | label("$I$",I, | + | label("$I$",I,NW); |
label("$L$",L,SW); | label("$L$",L,SW); | ||
label("$O$",O,E); | label("$O$",O,E); | ||
| − | label("$\alpha$", | + | label("$\alpha$",B,5*dir(midangle(A,B,I)),fontsize(8)); |
| − | label("$\alpha$", | + | label("$\alpha$",B,5*dir(midangle(I,B,C)),fontsize(8)); |
| − | label("$\beta$", | + | label("$\beta$",C,12*dir(midangle(B,C,I)),fontsize(8)); |
| − | label("$\beta$", | + | label("$\beta$",C,12*dir(midangle(I,C,A)),fontsize(8)); |
| − | label("$\gamma$", | + | label("$\gamma$",A,5*dir(midangle(B,A,I)),fontsize(8)); |
| − | label("$\gamma$", | + | label("$\gamma$",A,5*dir(midangle(I,A,C)),fontsize(8)); |
| + | |||
| + | draw(I--O); | ||
| + | draw(A--O); | ||
| + | draw(rightanglemark(A,I,O)); | ||
</asy> | </asy> | ||
| − | Solution in | + | |
| + | We'll tackle the initial steps of the problem in two different manners, both leading us to the same final calculations. | ||
| + | ==Solution 1.1== | ||
| + | Since <math>I</math> is the incenter, <math>\angle BAL \cong \angle DAC</math>. Furthermore, <math>\angle ABC</math> and <math>\angle ADC</math> are both subtended by the same arc <math>AC</math>, so <math>\angle ABC \cong \angle ADC.</math> Therefore by AA similarity, <math>\triangle ABL \sim \triangle ADC</math>. | ||
| + | From this we can say that <cmath>\frac{AB}{AD} = \frac{AL}{AC} \implies AB \cdot AC = AL \cdot AD </cmath> | ||
| + | |||
| + | Since <math>AD</math> is a chord of the circle and <math>OI</math> is a perpendicular from the center to that chord, <math>OI</math> must bisect <math>AD</math>. This can be seen by drawing <math>OD</math> and recognizing that this creates two congruent right triangles. Therefore, <cmath>AD = 2 \cdot ID \implies AB \cdot AC = 2 \cdot AL \cdot ID</cmath> | ||
| + | |||
| + | We have successfully represented <math>AB \cdot AC</math> in terms of <math>AL</math> and <math>ID</math>. Solution 1.2 will explain an alternate method to get a similar relationship, and then we'll rejoin and finish off the solution. | ||
| + | |||
| + | ==Solution 1.2== | ||
| + | |||
| + | <math>\angle ALB \cong \angle DLC</math> by vertical angles and <math>\angle LBA \cong \angle CDA</math> because both are subtended by arc <math>AC</math>. Thus <math>\triangle ABL \sim \triangle CDL</math>. | ||
| + | |||
| + | Thus <cmath>\frac{AB}{CD} = \frac{AL}{CL} \implies AB = CD \cdot \frac{AL}{CL}</cmath> | ||
| + | |||
| + | Symmetrically, we get <math>\triangle ALC \sim \triangle BLD</math>, so | ||
| + | <cmath>\frac{AC}{BD} = \frac{AL}{BL} \implies AC = BD \cdot \frac{AL}{BL}</cmath> | ||
| + | |||
| + | Substituting, we get <cmath>AB \cdot AC = CD \cdot \frac{AL}{CL} \cdot BD \cdot \frac{AL}{BL}</cmath> | ||
| + | |||
| + | Lemma 1: BD = CD = ID | ||
| + | |||
| + | Proof: | ||
| + | |||
| + | We commence angle chasing: we know <math>\angle DBC \cong DAC = \gamma</math>. Therefore <cmath>\angle IBD = \alpha + \gamma</cmath>. | ||
| + | Looking at triangle <math>ABI</math>, we see that <math>\angle IBA = \alpha</math>, and <math>\angle BAI = \gamma</math>. Therefore because the sum of the angles must be <math>180</math>, <math>\angle BIA = 180-\alpha - \gamma</math>. Now <math>AD</math> is a straight line, so <cmath>\angle BID = 180-\angle BIA = \alpha+\gamma</cmath>. | ||
| + | Since <math>\angle IBD = \angle BID</math>, triangle <math>IBD</math> is isosceles and thus <math>ID = BD</math>. | ||
| + | |||
| + | A similar argument should suffice to show <math>CD = ID</math> by symmetry, so thus <math>ID = BD = CD</math>. | ||
| + | |||
| + | Now we regroup and get <cmath>CD \cdot \frac{AL}{CL} \cdot BD \cdot \frac{AL}{BL} = ID^2 \cdot \frac{AL^2}{BL \cdot CL}</cmath> | ||
| + | |||
| + | Now note that <math>BL</math> and <math>CL</math> are part of the same chord in the circle, so we can use Power of a point to express their product differently. <cmath>BL \cdot CL = AL \cdot LD \implies AB \cdot AC = ID^2 \cdot \frac{AL}{LD}</cmath> | ||
| + | |||
| + | ==Solution 1 (Continued)== | ||
| + | Now we have some sort of expression for <math>AB \cdot AC</math> in terms of <math>ID</math> and <math>AL</math>. Let's try to find <math>AL</math> first. | ||
| + | |||
| + | Drop an altitude from <math>D</math> to <math>BC</math>, <math>I</math> to <math>AC</math>, and <math>I</math> to <math>BC</math>: | ||
| + | |||
| + | <asy> | ||
| + | size(300); | ||
| + | import olympiad; | ||
| + | real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; | ||
| + | pair B=(0,0),C=(c,0), D = (c/2-0.01, -2.26), E = (c/2-0.01,0); | ||
| + | pair A = (c/3,8.65*c/10); | ||
| + | pair F = (2*c/3-0.14, 4-0.29); | ||
| + | pair G = (c/2-0.68,0); | ||
| + | draw(circumcircle(A,B,C)); | ||
| + | pair I=incenter(A,B,C); | ||
| + | pair O=circumcenter(A,B,C); | ||
| + | pair L=extension(A,I,C,B); | ||
| + | dot(I^^O^^A^^B^^C^^D^^L^^E^^F^^G); | ||
| + | draw(A--L); | ||
| + | draw(A--D); | ||
| + | draw(D--E); | ||
| + | draw(I--F); | ||
| + | draw(I--G); | ||
| + | path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} | ||
| + | draw(C--B--D--cycle); | ||
| + | draw(A--C--B); | ||
| + | draw(A--B); | ||
| + | draw(B--I--C^^A--I); | ||
| + | draw(incircle(A,B,C)); | ||
| + | label("$B$",B,SW); | ||
| + | label("$C$",C,SE); | ||
| + | label("$A$",A,N); | ||
| + | label("$D$",D,S); | ||
| + | label("$I$",I,NW); | ||
| + | label("$L$",L,SW); | ||
| + | label("$O$",O,E); | ||
| + | label("$E$",E,N); | ||
| + | label("$F$",F,NE); | ||
| + | label("$G$",G,SW); | ||
| + | label("$\alpha$",B,5*dir(midangle(A,B,I)),fontsize(8)); | ||
| + | label("$\alpha$",B,5*dir(midangle(I,B,C)),fontsize(8)); | ||
| + | label("$\beta$",C,12*dir(midangle(B,C,I)),fontsize(8)); | ||
| + | label("$\beta$",C,12*dir(midangle(I,C,A)),fontsize(8)); | ||
| + | label("$\gamma$",A,5*dir(midangle(B,A,I)),fontsize(8)); | ||
| + | label("$\gamma$",A,5*dir(midangle(I,A,C)),fontsize(8)); | ||
| + | |||
| + | |||
| + | draw(I--O); | ||
| + | draw(A--O); | ||
| + | draw(rightanglemark(A,I,O)); | ||
| + | draw(rightanglemark(B,E,D)); | ||
| + | draw(rightanglemark(I,F,A)); | ||
| + | draw(rightanglemark(I,G,L)); | ||
| + | </asy> | ||
| + | |||
| + | Since <math>\angle DBE \cong \angle IAF</math> and <math>\angle BED \cong \angle IFA</math>, <math>\triangle BDE \sim \triangle AIF</math>. | ||
| + | |||
| + | Furthermore, we know <math>BD = ID</math> and <math>AI = ID</math>, so <math>BD = AI</math>. Since we have two right similar triangles and the corresponding sides are equal, these two triangles are actually congruent: this implies that <math>DE = IF = 6</math> since <math>IF</math> is the inradius. | ||
| + | |||
| + | Now notice that <math>\triangle IGL \sim \triangle DEL</math> because of equal vertical angles and right angles. Furthermore, <math>IG</math> is the inradius so it's length is <math>6</math>, which equals the length of <math>DE</math>. Therefore these two triangles are congruent, so <math>IL = DL</math>. | ||
| + | |||
| + | Since <math>IL+DL = ID</math>, <math>ID = 2 \cdot IL</math>. Furthermore, <math>AL = AI + IL = ID + IL = 3 \cdot IL</math>. | ||
| + | |||
| + | We can now plug back into our initial equations for <math>AB \cdot AC</math>: | ||
| + | |||
| + | From <math>1.1</math>, <math>AB \cdot AC = 2 \cdot AL \cdot ID = 2 \cdot 3 \cdot IL \cdot 2 \cdot IL</math> | ||
| + | |||
| + | <cmath>\implies AB \cdot AC = 3 \cdot (2 \cdot IL) \cdot (2 \cdot IL) = 3 \cdot ID^2</cmath> | ||
| + | |||
| + | Alternatively, from <math>1.2</math>, <math>AB \cdot AC = ID^2 \cdot \frac{AL}{DL}</math> | ||
| + | <cmath>\implies AB \cdot AC = ID^2 \cdot \frac{3 \cdot IL}{IL} = 3 \cdot ID^2</cmath> | ||
| + | |||
| + | Now all we need to do is find <math>ID</math>. | ||
| + | |||
| + | The problem now becomes very simple if one knows Euler's Formula for the distance between the incenter and the circumcenter of a triangle. This formula states that <math>OI^2 = R(R-2r)</math>, where <math>R</math> is the circumradius and <math>r</math> is the inradius. We will prove this formula first, but if you already know the proof, skip this part. | ||
| + | |||
| + | Theorem: in any triangle, let <math>d</math> be the distance from the circumcenter to the incenter of the triangle. Then <math>d^2 = R \cdot (R-2r)</math>, where <math>R</math> is the circumradius of the triangle and <math>r</math> is the inradius of the triangle. | ||
| + | |||
| + | Proof: | ||
| + | |||
| + | Construct the following diagram: | ||
| + | |||
| + | |||
| + | <asy> | ||
| + | size(300); | ||
| + | import olympiad; | ||
| + | real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; | ||
| + | pair B=(0,0),C=(c,0), D = (c/2-0.01, -2.26), E = (c/2-0.01,0); | ||
| + | pair A = (c/3,8.65*c/10); | ||
| + | pair F = (2*c/3-0.14, 4-0.29); | ||
| + | pair G = (c/2-0.68,0); | ||
| + | draw(circumcircle(A,B,C)); | ||
| + | pair I=incenter(A,B,C); | ||
| + | pair O=circumcenter(A,B,C); | ||
| + | pair L=extension(A,I,C,B); | ||
| + | dot(I^^O^^A^^B^^C^^D^^L^^F); | ||
| + | draw(A--L); | ||
| + | draw(A--D); | ||
| + | draw(I--F); | ||
| + | path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} | ||
| + | draw(C--B--D--cycle); | ||
| + | draw(A--C--B); | ||
| + | draw(A--B); | ||
| + | draw(A--I); | ||
| + | draw(incircle(A,B,C)); | ||
| + | label("$B$",B,SW); | ||
| + | label("$C$",C,SE); | ||
| + | label("$A$",A,N); | ||
| + | label("$D$",D,S); | ||
| + | label("$I$",I,NW); | ||
| + | label("$L$",L,SW); | ||
| + | label("$O$",O,S); | ||
| + | label("$F$",F,NE); | ||
| + | label("$\gamma$",A,5*dir(midangle(B,A,I)),fontsize(8)); | ||
| + | label("$\gamma$",A,5*dir(midangle(I,A,C)),fontsize(8)); | ||
| + | |||
| + | pair H = (10*c/8-1.46,2*c/3-1.85), J = (-0.55,1.4); | ||
| + | dot(H^^J); | ||
| + | label("$H$", H, E); | ||
| + | label("$J$", J, W); | ||
| + | |||
| + | |||
| + | draw(I--O); | ||
| + | draw(I--H); | ||
| + | draw(I--J); | ||
| + | draw(rightanglemark(I,F,A)); | ||
| + | </asy> | ||
| + | |||
| + | |||
| + | Let <math>OI = d</math>, <math>OH = R</math>, <math>IF = r</math>. By the Power of a Point, <math>IH \cdot IJ = AI \cdot ID</math>. | ||
| + | <math>IH = R+d</math> and <math>IJ = R-d</math>, so <cmath>(R+d) \cdot (R-d) = AI \cdot ID = AI \cdot CD</cmath> | ||
| + | |||
| + | Now consider <math>\triangle ACD</math>. Since all three points lie on the circumcircle of <math>\triangle ABC</math>, the two triangles have the same circumcircle. Thus we can apply law of sines and we get <math>\frac{CD}{\sin(\angle DAC)} = 2R</math>. This implies | ||
| + | |||
| + | <cmath>(R+d)\cdot (R-d) = AI \cdot 2R \cdot \sin(\angle DAC)</cmath> | ||
| + | |||
| + | Also, <math>\sin(\angle DAC)) = \sin(\angle IAF))</math>, and <math>\triangle IAF</math> is right. Therefore <cmath>\sin(\angle IAF) = \frac{IF}{AI} = \frac{r}{AI}</cmath> | ||
| + | |||
| + | Plugging in, we have | ||
| + | |||
| + | <cmath>(R+d)\cdot (R-d) = AI \cdot 2R \cdot \frac{r}{AI} = 2R \cdot r</cmath> | ||
| + | |||
| + | Thus <cmath>R^2-d^2 = 2R \cdot r \implies d^2 = R \cdot (R-2r)</cmath> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Now we can finish up our solution. We know that <math>AB \cdot AC = 3 \cdot ID^2</math>. Since <math>ID = AI</math>, <math>AB \cdot AC = 3 \cdot AI^2</math>. Since <math>\triangle AOI</math> is right, we can apply the pythagorean theorem: <math>AI^2 = AO^2-OI^2 = 13^2-OI^2</math>. | ||
| + | |||
| + | Plugging in from Euler's formula, <math>OI^2 = 13 \cdot (13 - 2 \cdot 6) = 13</math>. | ||
| + | |||
| + | Thus <math>AI^2 = 169-13 = 156</math>. | ||
| + | |||
| + | Finally <math>AB \cdot AC = 3 \cdot AI^2 = 3 \cdot 156 = \textbf{468}</math>. | ||
| + | |||
| + | |||
~KingRavi | ~KingRavi | ||
| − | ==Solution== | + | ==Solution 2 (Excenters)== |
By Euler's formula <math>OI^{2}=R(R-2r)</math>, we have <math>OI^{2}=13(13-12)=13</math>. Thus, by the Pythagorean theorem, <math>AI^{2}=13^{2}-13=156</math>. Let <math>AI\cap(ABC)=M</math>; notice <math>\triangle AOM</math> is isosceles and <math>\overline{OI}\perp\overline{AM}</math> which is enough to imply that <math>I</math> is the midpoint of <math>\overline{AM}</math>, and <math>M</math> itself is the midpoint of <math>II_{a}</math> where <math>I_{a}</math> is the <math>A</math>-excenter of <math>\triangle ABC</math>. Therefore, <math>AI=IM=MI_{a}=\sqrt{156}</math> and <cmath>AB\cdot AC=AI\cdot AI_{a}=3\cdot AI^{2}=\boxed{468}.</cmath> | By Euler's formula <math>OI^{2}=R(R-2r)</math>, we have <math>OI^{2}=13(13-12)=13</math>. Thus, by the Pythagorean theorem, <math>AI^{2}=13^{2}-13=156</math>. Let <math>AI\cap(ABC)=M</math>; notice <math>\triangle AOM</math> is isosceles and <math>\overline{OI}\perp\overline{AM}</math> which is enough to imply that <math>I</math> is the midpoint of <math>\overline{AM}</math>, and <math>M</math> itself is the midpoint of <math>II_{a}</math> where <math>I_{a}</math> is the <math>A</math>-excenter of <math>\triangle ABC</math>. Therefore, <math>AI=IM=MI_{a}=\sqrt{156}</math> and <cmath>AB\cdot AC=AI\cdot AI_{a}=3\cdot AI^{2}=\boxed{468}.</cmath> | ||
| Line 43: | Line 243: | ||
| − | ==Solution | + | ==Solution 3== |
Denote <math>AB=a, AC=b, BC=c</math>. By the given condition, <math>\frac{abc}{4A}=13; \frac{2A}{a+b+c}=6</math>, where <math>A</math> is the area of <math>\triangle{ABC}</math>. | Denote <math>AB=a, AC=b, BC=c</math>. By the given condition, <math>\frac{abc}{4A}=13; \frac{2A}{a+b+c}=6</math>, where <math>A</math> is the area of <math>\triangle{ABC}</math>. | ||
| − | Moreover, since <math>OI\bot AI</math>, the second intersection of the line <math>AI</math> and <math>(ABC)</math> is the reflection of <math>A</math> about <math>I</math>, denote that as <math>D</math>. By the incenter-excenter lemma, <math>DI=BD=CD=\frac{AD}{2}\implies BD(a+b)=2BD\cdot c\implies a+b=2c</math>. | + | Moreover, since <math>OI\bot AI</math>, the second intersection of the line <math>AI</math> and <math>(ABC)</math> is the reflection of <math>A</math> about <math>I</math>, denote that as <math>D</math>. By the incenter-excenter lemma with Ptolemy's Theorem, <math>DI=BD=CD=\frac{AD}{2}\implies BD(a+b)=2BD\cdot c\implies a+b=2c</math>. |
Thus, we have <math>\frac{2A}{a+b+c}=\frac{2A}{3c}=6, A=9c</math>. Now, we have <math>\frac{abc}{4A}=\frac{abc}{36c}=\frac{ab}{36}=13\implies ab=\boxed{468}</math> | Thus, we have <math>\frac{2A}{a+b+c}=\frac{2A}{3c}=6, A=9c</math>. Now, we have <math>\frac{abc}{4A}=\frac{abc}{36c}=\frac{ab}{36}=13\implies ab=\boxed{468}</math> | ||
| Line 53: | Line 253: | ||
~Bluesoul | ~Bluesoul | ||
| − | ==Solution | + | ==Solution 4 (Trig)== |
Denote by <math>R</math> and <math>r</math> the circumradius and inradius, respectively. | Denote by <math>R</math> and <math>r</math> the circumradius and inradius, respectively. | ||
First, we have | First, we have | ||
| − | \[ | + | <cmath>\[ |
r = 4 R \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2} \hspace{1cm} (1) | r = 4 R \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2} \hspace{1cm} (1) | ||
| − | \] | + | \]</cmath> |
Second, because <math>AI \perp IO</math>, | Second, because <math>AI \perp IO</math>, | ||
| Line 119: | Line 319: | ||
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com) | ~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com) | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Solution 5 (Trig)== | ||
| + | |||
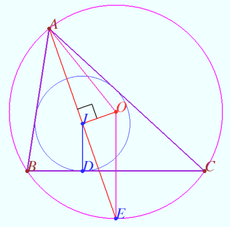
| + | [[File:2024AIMEIIProblem10.png|450px|center]] | ||
| + | |||
| + | |||
| + | Firstly, we can construct the triangle <math>\triangle ABC</math> by drawing the circumcirlce (centered at <math>O</math> with radius <math>R = OA = 13</math>) and incircle (centered at <math>I</math> with radius <math>r = 6</math>). Next, from <math>A</math>, construct tangent lines to the incircle meeting the circumcirlce at point <math>B</math> and <math>C</math>, say, as shown in the diagram. By Euler's theorem (relating the distance between <math>O</math> and <math>I</math> to the circumradius and inradius), we have | ||
| + | <cmath> | ||
| + | OI = \sqrt{R^2 - 2rR} = \sqrt{13}. | ||
| + | </cmath> | ||
| + | This leads to | ||
| + | <cmath> | ||
| + | AI = \sqrt{R^2 - OI^2} = \sqrt{156}. | ||
| + | </cmath> | ||
| + | Let <math>P</math> be the point of tangency where the incircle meets the side <math>\overline{AC}</math>. Now we denote | ||
| + | <cmath> | ||
| + | \theta \coloneqq \angle BAI = \angle IAP \qquad \text{and} \qquad \phi \coloneqq \angle OAI. | ||
| + | </cmath> | ||
| + | Notice that <math>\angle BAO = \angle BAI - \angle OAI = \theta - \phi</math>. Finally, the crux move is to recognize | ||
| + | <cmath> | ||
| + | AB = 2R \cos(\theta - \phi) \qquad \text{and} \qquad AC = 2R \cos(\theta + \phi) | ||
| + | </cmath> | ||
| + | since <math>O</math> is the circumcenter. Then multiply these two expressions and apply the compound-angle formula to get | ||
| + | \begin{aligned} | ||
| + | AB \cdot AC | ||
| + | &= 4R^2 \cos(\theta - \phi) \cos(\theta + \phi) \[0.3em] | ||
| + | &= 4R^2\left( | ||
| + | \cos^2\theta \cos^2\phi - \sin^2\theta \sin^2\phi | ||
| + | \right) \[0.3em] | ||
| + | &= 4\cos^2\theta(\underbrace{R\cos\phi}_{AI \, = \, \sqrt{156}})^2 - 4\sin^2\theta(\underbrace{R\sin\phi}_{OI \, = \, \sqrt{13}})^2 \[0.3em] | ||
| + | &= 52 (12\cos^2\theta - \sin^2 \theta) \[0.3em] | ||
| + | AB \cdot AC | ||
| + | &= 52 (12 - 13\sin^2\theta), | ||
| + | \end{aligned} | ||
| + | where in the last equality, we make use of the substitution <math>\cos^2\theta = 1 - \sin^2\theta</math>. Looking at <math>\triangle AIP</math>, we learn that <math>\sin \theta = \frac{r}{AI} = \frac{6}{\sqrt{156}}</math> which means <math>\sin^2 \theta = \frac{3}{13}</math>. Hence we have | ||
| + | <cmath> | ||
| + | AB \cdot AC = 52\left( 12 - 13 \cdot \tfrac{3}{13} \right) = 52 \cdot 9 = \boxed{468}. | ||
| + | </cmath> | ||
| + | This completes the solution | ||
| + | |||
| + | -- VensL. | ||
| + | |||
| + | ==Solution 6 (Close to Solution 3)== | ||
| + | [[File:2024 AIME II 10.png|230px|right]] | ||
| + | Denote <math>E = \odot ABC \cap AI, AB = c, AC = b, BC=a, r</math> is inradius. | ||
| + | <cmath>AO = EO = R \implies AI = EI.</cmath> | ||
| + | It is known that <math>\frac {AI}{EI} = \frac {b+c}{a} – 1 = 1 \implies b + c = 2a.</math> | ||
| + | *[[Barycentric_coordinates | Points on bisectors]] | ||
| + | <cmath>[ABC] =\frac{ (a+b+c) r}{2} = \frac {3ar}{2} = \frac {abc}{4R} \implies bc = 6Rr = \boxed{468}.</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Solution 7== | ||
| + | |||
| + | Call side <math>BC = a</math>, and similarly label the other sides. Note that <math>{OI}^2 = R^2 - 2Rr</math>. Also note that <math>AO = R</math>, so by the right angle, <math>AI = \sqrt{2Rr}</math>. However, we can double Angle Bisector theorem. The length of the angle bisector from A is <math>\sqrt{(bc)(1 - \frac{a^2}{(b+c)^2})}</math>. As a direct result, the length AI simplifies down to <math>\frac{\sqrt{(bc)(b+c-a)}}{\sqrt{{a+b+c}}}</math>. | ||
| + | |||
| + | Draw the incircle and call the tangent to side AB F. Then, <math>AF = \frac{b+c-a}{2}</math>. But this length, by Pythagorean, is <math>\sqrt{120}</math>, so <math>b+c-a = 2\sqrt{120}</math>. | ||
| + | |||
| + | Also note that the area of the triangle is <math>[ABC] = \frac{abc}{52}</math>, by <math>\frac{abc}{4S} = R</math>. By the incircle, we know that <math>\sin{\frac{A}{2}} = \frac{6}{\sqrt{156}}</math>, and similarly, <math>\cos{\frac{A}{2}} = \frac{\sqrt{120}}{\sqrt{156}}</math>. By double-angle, <math>\sin A = \frac{\sqrt{120}}{13}</math>. But the area of the triangle <math>[ABC]</math> is simply <math>\frac{1}{2}bc \sin A</math>, which is also <math>2\sqrt{120}bc</math>. But we know this is <math>abc</math> from above, so <math>a = 2\sqrt{120}</math>. As a direct result, <math>a+b+c = | ||
| + | 6\sqrt{120}</math>. | ||
| + | |||
| + | Apply this to the formula <math>\frac{\sqrt{(bc)(b+c-a)}}{\sqrt{a+b+c}}</math> listed above to get <math>2Rr = 156 = \frac{bc}{3}</math>, so <math>bc = 468</math>. We're done. - sepehr2010 | ||
| + | |||
| + | ==Solution 8== | ||
| + | |||
| + | Let the intersection of the <math>A</math>-angle bisector and the circumcircle be <math>M</math>, and denote the <math>A</math>-excenter as <math>I_A</math>. Denote the tangent to the incircle from <math>AC</math> as <math>E</math> and the tangent to the excircle from <math>AC</math> as <math>E_A</math>. | ||
| + | |||
| + | Notice that our perpendicular condition implies <math>AI = IM</math>, and Incenter-Excenter gives <math>IM = MI_A</math>. Thus we have <math>AI_A = 3AI</math>. From similar triangles we get <math>3(s-a) = 3AE = AE_A = s</math>. This implies <math>a = \frac23 S</math>. | ||
| + | |||
| + | Using areas we have that <math>\frac{abc}{4R} = rs</math>. Substituting gives <math>\frac{sbc}{6R} = rs \implies bc = 6Rr = \boxed{468}</math> and we're done. - thoom | ||
| + | |||
| + | ==Solution 9== | ||
| + | |||
| + | We know that the area of <math>\triangle{ABC}</math> is equal to <math>\frac{abc}{4R}</math>, but is also equal to <math>\frac{a+b+c}{2}r</math>, where R is the circumcircle and r is the incircle. So, <math>abc = 156(a+b+c)</math>. Let's extend <math>AI</math> so it intersects the circumcircle of <math>\triangle{ABC}</math> at <math>P</math>. Something that we see is that <math>\triangle{AIO}</math> is congruent to <math>\triangle{PIO}</math>. Something else that we notice that since <math>AI</math> is the angle bisector of <math>\angle{A}</math>, <math>P</math> is the midpoint of arc <math>BC</math>. Now, let's try calculating <math>AI</math>. By Euler's Theorem, <math>OI^{2} = R^{2} - 2Rr</math> where R is the circumcircle and r is the incircle, so <math>OI = \sqrt{13}</math>. Using Pythagorean Theorem on <math>\triangle{AOI}</math> gives us <math>AI = 3\sqrt{39}</math> as we know that <math>AO</math> is 13. | ||
| + | |||
| + | However, since <math>\triangle{AOI}</math> is congruent to <math>\triangle{POI}</math>, <math>PI = 3\sqrt{39}</math>. Since we know that <math>P</math> is the midpoint of arc <math>BC</math>, we can apply the Incenter-Excenter Lemma to get that <math>BP = 3\sqrt{39}</math> and <math>CP = 3\sqrt{39}</math>. Now, we can use Ptolemy's Theorem on quadrilateral ABPC: | ||
| + | |||
| + | <math>(b+c)(3\sqrt{39}) = a \times 6\sqrt{39}</math> | ||
| + | |||
| + | However, we know that <math>abc = 156(a+b+c)</math>, so we can solve for a! So, <math>abc - 156c = 156a + 156b</math>. Dividing gives us <math>a = \frac{156b + 156c}{bc - 156}</math>. Substituting and cancelling into our equation, | ||
| + | |||
| + | <math>b+c = 2\frac{156b+156c}{bc-156}</math>. | ||
| + | |||
| + | Multiplying, <math>(b+c)(bc-156) = 2 \times 156(b+c).</math> | ||
| + | |||
| + | So, <math>(bc-156)</math> = 312. Our answer is 312 + 156 = <math>\boxed{468}</math>. | ||
| + | |||
| + | ~aleyang | ||
| + | |||
| + | ==Solution 10== | ||
| + | We know by Euler's theorem <math>OI^2=R^2-2Rr.</math> Since <math>AO=R,</math> we have <math>AI=\sqrt{2Rr}.</math> Now, extend <math>AI</math> to meet <math>BC</math> at <math>A'</math> and the circumcircle of <math>\Delta ABC</math> at <math>L.</math> By the Incenter-Excenter lemma, <math>BL=CL=IL=r_a.</math> (Note that <math>OI \perp AL \rightarrow AI=IL=r_a\rightarrow r_a=\sqrt{2Rr}.</math>) Using Ptolemy in the cyclic quadrilateral <math>ABLC,</math> we have <math>c\cdot r_a+b\cdot r_a=2r_a\cdot a \iff \frac{b+c}{a}=2.</math> Also using the angle-bisector theorem we get, <math>\frac{c}{A'B}=\frac{b}{A'C}=\frac{b+c}{a}=2,</math> so call <math>c=2m, b=2n, A'B=m, A'C=n.</math> Since <math>\Delta AA'B \sim \Delta CA'L,</math> <math>\frac{AB}{r_a}=\frac{A'B}{A'L}\rightarrow LA'=\frac{r_a}{2}.</math> Thus, <math>AA'=\frac{3r_a}{2}</math> (as <math>AL=2r_a</math>), and <math>mn=AA'\cdot LA'=\frac{3r_a^2}{4}=\frac{3Rr}{2}.</math> In this problem, we want to find <math>4mn=6Rr,</math> yielding an answer of <math>\boxed{468}.</math> | ||
| + | |||
| + | ~anduran | ||
==Video Solution== | ==Video Solution== | ||
| Line 126: | Line 422: | ||
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com) | ~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com) | ||
| + | ==Video Solution== | ||
| + | |||
| + | https://www.youtube.com/watch?v=pPBPfpo12j4 | ||
| + | |||
| + | ~MathProblemSolvingSkills.com | ||
==See also== | ==See also== | ||
Revision as of 03:22, 1 December 2024
Contents
[hide]- 1 Problem
- 2 Solution 1 (Similar Triangles and PoP)
- 3 Solution 1.1
- 4 Solution 1.2
- 5 Solution 1 (Continued)
- 6 Solution 2 (Excenters)
- 7 Solution 3
- 8 Solution 4 (Trig)
- 9 Solution 5 (Trig)
- 10 Solution 6 (Close to Solution 3)
- 11 Solution 7
- 12 Solution 8
- 13 Solution 9
- 14 Solution 10
- 15 Video Solution
- 16 Video Solution
- 17 See also
Problem
Let ![]() have circumcenter
have circumcenter ![]() and incenter
and incenter ![]() with
with ![]() , circumradius
, circumradius ![]() , and inradius
, and inradius ![]() . Find
. Find ![]() .
.
Solution 1 (Similar Triangles and PoP)
Start off by (of course) drawing a diagram! Let ![]() and
and ![]() be the incenter and circumcenters of triangle
be the incenter and circumcenters of triangle ![]() , respectively. Furthermore, extend
, respectively. Furthermore, extend ![]() to meet
to meet ![]() at
at ![]() and the circumcircle of triangle
and the circumcircle of triangle ![]() at
at ![]() .
.
![[asy] size(300); import olympiad; real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; pair B=(0,0),C=(c,0), D = (c/2-0.01, -2.26); pair A = (c/3,8.65*c/10); draw(circumcircle(A,B,C)); pair I=incenter(A,B,C); pair O=circumcenter(A,B,C); pair L=extension(A,I,C,B); dot(I^^O^^A^^B^^C^^D^^L); draw(A--L); draw(A--D); path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} draw(C--B--D--cycle); draw(A--C--B); draw(A--B); draw(B--I--C^^A--I); draw(incircle(A,B,C)); label("$B$",B,SW); label("$C$",C,SE); label("$A$",A,N); label("$D$",D,S); label("$I$",I,NW); label("$L$",L,SW); label("$O$",O,E); label("$\alpha$",B,5*dir(midangle(A,B,I)),fontsize(8)); label("$\alpha$",B,5*dir(midangle(I,B,C)),fontsize(8)); label("$\beta$",C,12*dir(midangle(B,C,I)),fontsize(8)); label("$\beta$",C,12*dir(midangle(I,C,A)),fontsize(8)); label("$\gamma$",A,5*dir(midangle(B,A,I)),fontsize(8)); label("$\gamma$",A,5*dir(midangle(I,A,C)),fontsize(8)); draw(I--O); draw(A--O); draw(rightanglemark(A,I,O)); [/asy]](http://latex.artofproblemsolving.com/6/f/c/6fc13cdc5b8bc74ab49a662898b75f45eb6300bc.png)
We'll tackle the initial steps of the problem in two different manners, both leading us to the same final calculations.
Solution 1.1
Since ![]() is the incenter,
is the incenter, ![]() . Furthermore,
. Furthermore, ![]() and
and ![]() are both subtended by the same arc
are both subtended by the same arc ![]() , so
, so ![]() Therefore by AA similarity,
Therefore by AA similarity, ![]() .
From this we can say that
.
From this we can say that ![]()
Since ![]() is a chord of the circle and
is a chord of the circle and ![]() is a perpendicular from the center to that chord,
is a perpendicular from the center to that chord, ![]() must bisect
must bisect ![]() . This can be seen by drawing
. This can be seen by drawing ![]() and recognizing that this creates two congruent right triangles. Therefore,
and recognizing that this creates two congruent right triangles. Therefore, ![]()
We have successfully represented ![]() in terms of
in terms of ![]() and
and ![]() . Solution 1.2 will explain an alternate method to get a similar relationship, and then we'll rejoin and finish off the solution.
. Solution 1.2 will explain an alternate method to get a similar relationship, and then we'll rejoin and finish off the solution.
Solution 1.2
![]() by vertical angles and
by vertical angles and ![]() because both are subtended by arc
because both are subtended by arc ![]() . Thus
. Thus ![]() .
.
Thus ![]()
Symmetrically, we get ![]() , so
, so
![]()
Substituting, we get ![]()
Lemma 1: BD = CD = ID
Proof:
We commence angle chasing: we know ![]() . Therefore
. Therefore ![]() .
Looking at triangle
.
Looking at triangle ![]() , we see that
, we see that ![]() , and
, and ![]() . Therefore because the sum of the angles must be
. Therefore because the sum of the angles must be ![]() ,
, ![]() . Now
. Now ![]() is a straight line, so
is a straight line, so ![]() .
Since
.
Since ![]() , triangle
, triangle ![]() is isosceles and thus
is isosceles and thus ![]() .
.
A similar argument should suffice to show ![]() by symmetry, so thus
by symmetry, so thus ![]() .
.
Now we regroup and get ![]()
Now note that ![]() and
and ![]() are part of the same chord in the circle, so we can use Power of a point to express their product differently.
are part of the same chord in the circle, so we can use Power of a point to express their product differently. ![]()
Solution 1 (Continued)
Now we have some sort of expression for ![]() in terms of
in terms of ![]() and
and ![]() . Let's try to find
. Let's try to find ![]() first.
first.
Drop an altitude from ![]() to
to ![]() ,
, ![]() to
to ![]() , and
, and ![]() to
to ![]() :
:
![[asy] size(300); import olympiad; real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; pair B=(0,0),C=(c,0), D = (c/2-0.01, -2.26), E = (c/2-0.01,0); pair A = (c/3,8.65*c/10); pair F = (2*c/3-0.14, 4-0.29); pair G = (c/2-0.68,0); draw(circumcircle(A,B,C)); pair I=incenter(A,B,C); pair O=circumcenter(A,B,C); pair L=extension(A,I,C,B); dot(I^^O^^A^^B^^C^^D^^L^^E^^F^^G); draw(A--L); draw(A--D); draw(D--E); draw(I--F); draw(I--G); path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} draw(C--B--D--cycle); draw(A--C--B); draw(A--B); draw(B--I--C^^A--I); draw(incircle(A,B,C)); label("$B$",B,SW); label("$C$",C,SE); label("$A$",A,N); label("$D$",D,S); label("$I$",I,NW); label("$L$",L,SW); label("$O$",O,E); label("$E$",E,N); label("$F$",F,NE); label("$G$",G,SW); label("$\alpha$",B,5*dir(midangle(A,B,I)),fontsize(8)); label("$\alpha$",B,5*dir(midangle(I,B,C)),fontsize(8)); label("$\beta$",C,12*dir(midangle(B,C,I)),fontsize(8)); label("$\beta$",C,12*dir(midangle(I,C,A)),fontsize(8)); label("$\gamma$",A,5*dir(midangle(B,A,I)),fontsize(8)); label("$\gamma$",A,5*dir(midangle(I,A,C)),fontsize(8)); draw(I--O); draw(A--O); draw(rightanglemark(A,I,O)); draw(rightanglemark(B,E,D)); draw(rightanglemark(I,F,A)); draw(rightanglemark(I,G,L)); [/asy]](http://latex.artofproblemsolving.com/d/e/4/de4c8e3077d3dd4a3677912855a88f0dbfa8f631.png)
Since ![]() and
and ![]() ,
, ![]() .
.
Furthermore, we know ![]() and
and ![]() , so
, so ![]() . Since we have two right similar triangles and the corresponding sides are equal, these two triangles are actually congruent: this implies that
. Since we have two right similar triangles and the corresponding sides are equal, these two triangles are actually congruent: this implies that ![]() since
since ![]() is the inradius.
is the inradius.
Now notice that ![]() because of equal vertical angles and right angles. Furthermore,
because of equal vertical angles and right angles. Furthermore, ![]() is the inradius so it's length is
is the inradius so it's length is ![]() , which equals the length of
, which equals the length of ![]() . Therefore these two triangles are congruent, so
. Therefore these two triangles are congruent, so ![]() .
.
Since ![]() ,
, ![]() . Furthermore,
. Furthermore, ![]() .
.
We can now plug back into our initial equations for ![]() :
:
From ![]() ,
, ![]()
![]()
Alternatively, from ![]() ,
, ![]()
![]()
Now all we need to do is find ![]() .
.
The problem now becomes very simple if one knows Euler's Formula for the distance between the incenter and the circumcenter of a triangle. This formula states that ![]() , where
, where ![]() is the circumradius and
is the circumradius and ![]() is the inradius. We will prove this formula first, but if you already know the proof, skip this part.
is the inradius. We will prove this formula first, but if you already know the proof, skip this part.
Theorem: in any triangle, let ![]() be the distance from the circumcenter to the incenter of the triangle. Then
be the distance from the circumcenter to the incenter of the triangle. Then ![]() , where
, where ![]() is the circumradius of the triangle and
is the circumradius of the triangle and ![]() is the inradius of the triangle.
is the inradius of the triangle.
Proof:
Construct the following diagram:
![[asy] size(300); import olympiad; real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; pair B=(0,0),C=(c,0), D = (c/2-0.01, -2.26), E = (c/2-0.01,0); pair A = (c/3,8.65*c/10); pair F = (2*c/3-0.14, 4-0.29); pair G = (c/2-0.68,0); draw(circumcircle(A,B,C)); pair I=incenter(A,B,C); pair O=circumcenter(A,B,C); pair L=extension(A,I,C,B); dot(I^^O^^A^^B^^C^^D^^L^^F); draw(A--L); draw(A--D); draw(I--F); path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} draw(C--B--D--cycle); draw(A--C--B); draw(A--B); draw(A--I); draw(incircle(A,B,C)); label("$B$",B,SW); label("$C$",C,SE); label("$A$",A,N); label("$D$",D,S); label("$I$",I,NW); label("$L$",L,SW); label("$O$",O,S); label("$F$",F,NE); label("$\gamma$",A,5*dir(midangle(B,A,I)),fontsize(8)); label("$\gamma$",A,5*dir(midangle(I,A,C)),fontsize(8)); pair H = (10*c/8-1.46,2*c/3-1.85), J = (-0.55,1.4); dot(H^^J); label("$H$", H, E); label("$J$", J, W); draw(I--O); draw(I--H); draw(I--J); draw(rightanglemark(I,F,A)); [/asy]](http://latex.artofproblemsolving.com/e/3/3/e333afe640d20807f2730097d5f9683e031251fb.png)
Let ![]() ,
, ![]() ,
, ![]() . By the Power of a Point,
. By the Power of a Point, ![]() .
.
![]() and
and ![]() , so
, so ![]()
Now consider ![]() . Since all three points lie on the circumcircle of
. Since all three points lie on the circumcircle of ![]() , the two triangles have the same circumcircle. Thus we can apply law of sines and we get
, the two triangles have the same circumcircle. Thus we can apply law of sines and we get ![]() . This implies
. This implies
![]()
Also, ![]() , and
, and ![]() is right. Therefore
is right. Therefore ![]()
Plugging in, we have
![]()
Thus ![]()
Now we can finish up our solution. We know that ![]() . Since
. Since ![]() ,
, ![]() . Since
. Since ![]() is right, we can apply the pythagorean theorem:
is right, we can apply the pythagorean theorem: ![]() .
.
Plugging in from Euler's formula, ![]() .
.
Thus ![]() .
.
Finally ![]() .
.
~KingRavi
Solution 2 (Excenters)
By Euler's formula ![]() , we have
, we have ![]() . Thus, by the Pythagorean theorem,
. Thus, by the Pythagorean theorem, ![]() . Let
. Let ![]() ; notice
; notice ![]() is isosceles and
is isosceles and ![]() which is enough to imply that
which is enough to imply that ![]() is the midpoint of
is the midpoint of ![]() , and
, and ![]() itself is the midpoint of
itself is the midpoint of ![]() where
where ![]() is the
is the ![]() -excenter of
-excenter of ![]() . Therefore,
. Therefore, ![]() and
and ![]()
Note that this problem is extremely similar to 2019 CIME I/14.
Solution 3
Denote ![]() . By the given condition,
. By the given condition, ![]() , where
, where ![]() is the area of
is the area of ![]() .
.
Moreover, since ![]() , the second intersection of the line
, the second intersection of the line ![]() and
and ![]() is the reflection of
is the reflection of ![]() about
about ![]() , denote that as
, denote that as ![]() . By the incenter-excenter lemma with Ptolemy's Theorem,
. By the incenter-excenter lemma with Ptolemy's Theorem, ![]() .
.
Thus, we have ![]() . Now, we have
. Now, we have ![]()
~Bluesoul
Solution 4 (Trig)
Denote by ![]() and
and ![]() the circumradius and inradius, respectively.
the circumradius and inradius, respectively.
First, we have
![]()
Second, because ![]() ,
,
Thus,
Taking ![]() , we get
\[
4 \sin \frac{B}{2} \sin \frac{C}{2} = \cos \frac{B-C}{2} .
\]
, we get
\[
4 \sin \frac{B}{2} \sin \frac{C}{2} = \cos \frac{B-C}{2} .
\]
We have
Plugging this into the above equation, we get \[ \cos \frac{B-C}{2} = 2 \cos \frac{B+C}{2} . \hspace{1cm} (3) \]
Now, we analyze Equation (2). We have
Solving Equations (3) and (4), we get \[ \cos \frac{B+C}{2} = \sqrt{\frac{r}{2R}}, \hspace{1cm} \cos \frac{B-C}{2} = \sqrt{\frac{2r}{R}} . \hspace{1cm} (5) \]
Now, we compute ![]() . We have
. We have
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Solution 5 (Trig)
Firstly, we can construct the triangle ![]() by drawing the circumcirlce (centered at
by drawing the circumcirlce (centered at ![]() with radius
with radius ![]() ) and incircle (centered at
) and incircle (centered at ![]() with radius
with radius ![]() ). Next, from
). Next, from ![]() , construct tangent lines to the incircle meeting the circumcirlce at point
, construct tangent lines to the incircle meeting the circumcirlce at point ![]() and
and ![]() , say, as shown in the diagram. By Euler's theorem (relating the distance between
, say, as shown in the diagram. By Euler's theorem (relating the distance between ![]() and
and ![]() to the circumradius and inradius), we have
to the circumradius and inradius), we have
![]() This leads to
This leads to
![]() Let
Let ![]() be the point of tangency where the incircle meets the side
be the point of tangency where the incircle meets the side ![]() . Now we denote
. Now we denote
![]() Notice that
Notice that ![]() . Finally, the crux move is to recognize
. Finally, the crux move is to recognize
![]() since
since ![]() is the circumcenter. Then multiply these two expressions and apply the compound-angle formula to get
is the circumcenter. Then multiply these two expressions and apply the compound-angle formula to get
![]() . Looking at
. Looking at ![]() , we learn that
, we learn that ![]() which means
which means ![]() . Hence we have
. Hence we have
![]() This completes the solution
This completes the solution
-- VensL.
Solution 6 (Close to Solution 3)
Denote ![]() is inradius.
is inradius.
![]() It is known that
It is known that ![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Solution 7
Call side ![]() , and similarly label the other sides. Note that
, and similarly label the other sides. Note that ![]() . Also note that
. Also note that ![]() , so by the right angle,
, so by the right angle, ![]() . However, we can double Angle Bisector theorem. The length of the angle bisector from A is
. However, we can double Angle Bisector theorem. The length of the angle bisector from A is  . As a direct result, the length AI simplifies down to
. As a direct result, the length AI simplifies down to ![]() .
.
Draw the incircle and call the tangent to side AB F. Then, ![]() . But this length, by Pythagorean, is
. But this length, by Pythagorean, is ![]() , so
, so ![]() .
.
Also note that the area of the triangle is ![]() , by
, by ![]() . By the incircle, we know that
. By the incircle, we know that ![]() , and similarly,
, and similarly, ![]() . By double-angle,
. By double-angle, ![]() . But the area of the triangle
. But the area of the triangle ![]() is simply
is simply ![]() , which is also
, which is also ![]() . But we know this is
. But we know this is ![]() from above, so
from above, so ![]() . As a direct result,
. As a direct result, ![]() .
.
Apply this to the formula ![]() listed above to get
listed above to get ![]() , so
, so ![]() . We're done. - sepehr2010
. We're done. - sepehr2010
Solution 8
Let the intersection of the ![]() -angle bisector and the circumcircle be
-angle bisector and the circumcircle be ![]() , and denote the
, and denote the ![]() -excenter as
-excenter as ![]() . Denote the tangent to the incircle from
. Denote the tangent to the incircle from ![]() as
as ![]() and the tangent to the excircle from
and the tangent to the excircle from ![]() as
as ![]() .
.
Notice that our perpendicular condition implies ![]() , and Incenter-Excenter gives
, and Incenter-Excenter gives ![]() . Thus we have
. Thus we have ![]() . From similar triangles we get
. From similar triangles we get ![]() . This implies
. This implies ![]() .
.
Using areas we have that ![]() . Substituting gives
. Substituting gives ![]() and we're done. - thoom
and we're done. - thoom
Solution 9
We know that the area of ![]() is equal to
is equal to ![]() , but is also equal to
, but is also equal to ![]() , where R is the circumcircle and r is the incircle. So,
, where R is the circumcircle and r is the incircle. So, ![]() . Let's extend
. Let's extend ![]() so it intersects the circumcircle of
so it intersects the circumcircle of ![]() at
at ![]() . Something that we see is that
. Something that we see is that ![]() is congruent to
is congruent to ![]() . Something else that we notice that since
. Something else that we notice that since ![]() is the angle bisector of
is the angle bisector of ![]() ,
, ![]() is the midpoint of arc
is the midpoint of arc ![]() . Now, let's try calculating
. Now, let's try calculating ![]() . By Euler's Theorem,
. By Euler's Theorem, ![]() where R is the circumcircle and r is the incircle, so
where R is the circumcircle and r is the incircle, so ![]() . Using Pythagorean Theorem on
. Using Pythagorean Theorem on ![]() gives us
gives us ![]() as we know that
as we know that ![]() is 13.
is 13.
However, since ![]() is congruent to
is congruent to ![]() ,
, ![]() . Since we know that
. Since we know that ![]() is the midpoint of arc
is the midpoint of arc ![]() , we can apply the Incenter-Excenter Lemma to get that
, we can apply the Incenter-Excenter Lemma to get that ![]() and
and ![]() . Now, we can use Ptolemy's Theorem on quadrilateral ABPC:
. Now, we can use Ptolemy's Theorem on quadrilateral ABPC:
![]()
However, we know that ![]() , so we can solve for a! So,
, so we can solve for a! So, ![]() . Dividing gives us
. Dividing gives us ![]() . Substituting and cancelling into our equation,
. Substituting and cancelling into our equation,
![]() .
.
Multiplying, ![]()
So, ![]() = 312. Our answer is 312 + 156 =
= 312. Our answer is 312 + 156 = ![]() .
.
~aleyang
Solution 10
We know by Euler's theorem ![]() Since
Since ![]() we have
we have ![]() Now, extend
Now, extend ![]() to meet
to meet ![]() at
at ![]() and the circumcircle of
and the circumcircle of ![]() at
at ![]() By the Incenter-Excenter lemma,
By the Incenter-Excenter lemma, ![]() (Note that
(Note that ![]() ) Using Ptolemy in the cyclic quadrilateral
) Using Ptolemy in the cyclic quadrilateral ![]() we have
we have ![]() Also using the angle-bisector theorem we get,
Also using the angle-bisector theorem we get, ![]() so call
so call ![]() Since
Since ![]()
![]() Thus,
Thus, ![]() (as
(as ![]() ), and
), and ![]() In this problem, we want to find
In this problem, we want to find ![]() yielding an answer of
yielding an answer of ![]()
~anduran
Video Solution
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Video Solution
https://www.youtube.com/watch?v=pPBPfpo12j4
~MathProblemSolvingSkills.com
See also
| 2024 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()