Difference between revisions of "2003 AMC 10A Problems/Problem 22"
(→See Also) |
|||
| Line 7: | Line 7: | ||
== Solution == | == Solution == | ||
| + | === Solution 1 === | ||
Since <math>ABCD</math> is a rectangle, <math>CD=AB=8</math>. | Since <math>ABCD</math> is a rectangle, <math>CD=AB=8</math>. | ||
| Line 40: | Line 41: | ||
<math>GF=2 \cdot FD+8=2\cdot6+8=20 \Rightarrow B</math> | <math>GF=2 \cdot FD+8=2\cdot6+8=20 \Rightarrow B</math> | ||
| + | |||
| + | === Solution 2 === | ||
| + | Since <math>ABCD</math> is a rectangle, <math>CD=3</math>, <math>EA=5</math>, and <math>CD=8</math>. From the [[Pythagorean Theorem]], <math>CE^2=CD^2+DE^2=80\Rightarrow CE=4\sqrt{5}</math>. | ||
| + | ==== Lemma ==== | ||
| + | Statement: <math>GCH \approx GEA</math> | ||
| + | |||
| + | Proof: <math>\angle CGH=\angle EGA</math>, obviously. | ||
| + | |||
| + | <math>\begin{eqnarray} | ||
| + | \angle HCE=180^{\circ}-\angle CHG\ | ||
| + | \angle DCE=\angle CHG-90^{\circ}\ | ||
| + | \angle CEED=180-\angle CHG\ | ||
| + | \angle GEA=\angle GCH | ||
| + | \end{eqnarray}</math> | ||
| + | |||
| + | Since two angles of the triangles are equal, the third angles must equal each other. Therefore, the triangles are similar. | ||
| + | |||
| + | |||
| + | |||
| + | Let <math>GC=x</math>. | ||
| + | |||
| + | <cmath>\begin{eqnarray} | ||
| + | \dfrac{x}{3}=\dfrac{x+4\sqrt{5}}{5}\ | ||
| + | 5x=3x+12\sqrt{5}\ | ||
| + | 2x=12\sqrt{5}\ | ||
| + | x=6\sqrt{5} | ||
| + | \end{eqnarray}</cmath> | ||
| + | |||
| + | Also, <math>\triangle GFE\approx \triangle CDE</math>, therefore | ||
| + | |||
| + | <cmath>\dfrac{8}{4\sqrt{5}}=\dfrac{GF}{10\sqrt{5}}</cmath> | ||
| + | |||
| + | We can multiply both sides by <math>\sqrt{5}</math> to get that <math>GF is twice of 10, or </math>20\Rightarrow \mathrm{(B)}$ | ||
== See Also == | == See Also == | ||
Revision as of 09:58, 6 March 2008
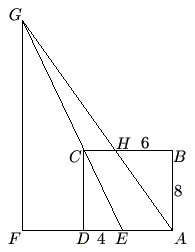
Problem
In rectangle ![]() , we have
, we have ![]() ,
, ![]() ,
, ![]() is on
is on ![]() with
with ![]() ,
, ![]() is on
is on ![]() with
with ![]() , line
, line ![]() intersects line
intersects line ![]() at
at ![]() , and
, and ![]() is on line
is on line ![]() with
with ![]() . Find the length of
. Find the length of ![]() .
.
![]()
Solution
Solution 1
Since ![]() is a rectangle,
is a rectangle, ![]() .
.
Since ![]() is a rectangle and
is a rectangle and ![]() ,
, ![]() .
.
Since ![]() is a rectangle,
is a rectangle, ![]() .
.
So, ![]() is a transversal, and
is a transversal, and ![]() .
.
This is sufficient to prove that ![]() and
and ![]() .
.
Using ratios:
![]()
![]()
![]()
![]()
![]()
![]()
Since ![]() can't have 2 different lengths, both expressions for
can't have 2 different lengths, both expressions for ![]() must be equal.
must be equal.
![]()
![]()
![]()
![]()
Solution 2
Since ![]() is a rectangle,
is a rectangle, ![]() ,
, ![]() , and
, and ![]() . From the Pythagorean Theorem,
. From the Pythagorean Theorem, ![]() .
.
Lemma
Statement: ![]()
Proof: ![]() , obviously.
, obviously.
$
Since two angles of the triangles are equal, the third angles must equal each other. Therefore, the triangles are similar.
Let ![]() .
.

Also, ![]() , therefore
, therefore
![]()
We can multiply both sides by ![]() to get that
to get that ![]() 20\Rightarrow \mathrm{(B)}$
20\Rightarrow \mathrm{(B)}$
See Also
| 2003 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||