Difference between revisions of "2007 AMC 10A Problems"
| Line 42: | Line 42: | ||
== Problem 7 == | == Problem 7 == | ||
| − | Last year Mr. Jon Q. Public received an inheritance. He paid <math>20\%</math> in federal taxes on the inheritance, and paid <math>10\%</math> of what he had left in state taxes. He paid a total of <math>$</ | + | Last year Mr. Jon Q. Public received an inheritance. He paid <math>20\%</math> in federal taxes on the inheritance, and paid <math>10\%</math> of what he had left in state taxes. He paid a total of <math>$10500</math> for both taxes. How many dollars was his inheritance? |
| − | < | + | <math>(\mathrm {A})\ 30000 \qquad (\mathrm {B})\ 32500 \qquad(\mathrm {C})\ 35000 \qquad(\mathrm {D})\ 37500 \qquad(\mathrm {E})\ 40000</math> |
[[2007 AMC 10A Problems/Problem 7|Solution]] | [[2007 AMC 10A Problems/Problem 7|Solution]] | ||
== Problem 8 == | == Problem 8 == | ||
| − | Triangles < | + | Triangles <math>ABC</math> and <math>ADC</math> are isosceles with <math>AB=BC</math> and <math>AD=DC</math>. Point <math>D</math> is inside triangle <math>ABC</math>, angle <math>ABC</math> measures 40 degrees, and angle <math>ADC</math> measures 140 degrees. What is the degree measure of angle <math>BAD</math>? |
| − | < | + | <math>\mathrm{(A)}\ 20\qquad \mathrm{(B)}\ 30\qquad \mathrm{(C)}\ 40\qquad \mathrm{(D)}\ 50\qquad \mathrm{(E)}\ 60</math> |
[[2007 AMC 10A Problems/Problem 8|Solution]] | [[2007 AMC 10A Problems/Problem 8|Solution]] | ||
== Problem 9 == | == Problem 9 == | ||
| − | Real numbers < | + | Real numbers <math>a</math> and <math>b</math> satisfy the equations <math>3^{a} = 81^{b + 2}</math> and <math>125^{b} = 5^{a - 3}</math>. What is <math>ab</math>? |
| − | < | + | <math>\text{(A)}\ -60 \qquad \text{(B)}\ -17 \qquad \text{(C)}\ 9 \qquad \text{(D)}\ 12 \qquad \text{(E)}\ 60</math> |
[[2007 AMC 10A Problems/Problem 9|Solution]] | [[2007 AMC 10A Problems/Problem 9|Solution]] | ||
== Problem 10 == | == Problem 10 == | ||
| − | The Dunbar family consists of a mother, a father, and some children. The average age of the members of the family is < | + | The Dunbar family consists of a mother, a father, and some children. The average age of the members of the family is <math>20</math>, the father is <math>48</math> years old, and the average age of the mother and children is <math>16</math>. How many children are in the family? |
| − | < | + | <math>\text{(A)}\ 2 \qquad \text{(B)}\ 3 \qquad \text{(C)}\ 4 \qquad \text{(D)}\ 5 \qquad \text{(E)}\ 6</math> |
[[2007 AMC 10A Problems/Problem 10|Solution]] | [[2007 AMC 10A Problems/Problem 10|Solution]] | ||
== Problem 11 == | == Problem 11 == | ||
| − | The numbers from < | + | The numbers from <math>1</math> to <math>8</math> are placed at the vertices of a cube in such a manner that the sum of the four numbers on each face is the same. What is this common sum? |
| − | < | + | <math>\text{(A)}\ 14 \qquad \text{(B)}\ 16 \qquad \text{(C)}\ 18 \qquad \text{(D)}\ 20 \qquad \text{(E)}\ 24</math> |
[[2007 AMC 10A Problems/Problem 11|Solution]] | [[2007 AMC 10A Problems/Problem 11|Solution]] | ||
| Line 79: | Line 79: | ||
Two tour guides are leading six tourists. The guides decide to split up. Each tourist must choose one of the guides, but with the stipulation that each guide must take at least one tourist. How many different groupings of guides and tourists are possible? | Two tour guides are leading six tourists. The guides decide to split up. Each tourist must choose one of the guides, but with the stipulation that each guide must take at least one tourist. How many different groupings of guides and tourists are possible? | ||
| − | < | + | <math>\text{(A)}\ 56 \qquad \text{(B)}\ 58 \qquad \text{(C)}\ 60 \qquad \text{(D)}\ 62 \qquad \text{(E)}\ 64</math> |
[[2007 AMC 10A Problems/Problem 12|Solution]] | [[2007 AMC 10A Problems/Problem 12|Solution]] | ||
| Line 86: | Line 86: | ||
Yan is somewhere between his home and the stadium. To get to the stadium he can walk directly to the stadium, or else he can walk home and then ride his bicycle to the stadium. He rides 7 times as fast as he walks, and both choices require the same amount of time. What is the [[ratio]] of Yan's distance from his home to his distance from the stadium? | Yan is somewhere between his home and the stadium. To get to the stadium he can walk directly to the stadium, or else he can walk home and then ride his bicycle to the stadium. He rides 7 times as fast as he walks, and both choices require the same amount of time. What is the [[ratio]] of Yan's distance from his home to his distance from the stadium? | ||
| − | < | + | <math>\mathrm{(A)}\ \frac 23\qquad \mathrm{(B)}\ \frac 34\qquad \mathrm{(C)}\ \frac 45\qquad \mathrm{(D)}\ \frac 56\qquad \mathrm{(E)}\ \frac 78</math> |
[[2007 AMC 10A Problems/Problem 13|Solution]] | [[2007 AMC 10A Problems/Problem 13|Solution]] | ||
== Problem 14 == | == Problem 14 == | ||
| − | A triangle with side lengths in the ratio < | + | A triangle with side lengths in the ratio <math>3 : 4 : 5</math> is inscribed in a circle with radius <math>3</math>. What is the area of the triangle? |
| − | < | + | <math>\mathrm{(A)}\ 8.64\qquad \mathrm{(B)}\ 12\qquad \mathrm{(C)}\ 5\pi\qquad \mathrm{(D)}\ 17.28\qquad \mathrm{(E)}\ 18</math> |
[[2007 AMC 10A Problems/Problem 14|Solution]] | [[2007 AMC 10A Problems/Problem 14|Solution]] | ||
== Problem 15 == | == Problem 15 == | ||
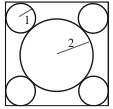
| − | Four circles of radius < | + | Four circles of radius <math>1</math> are each tangent to two sides of a square and externally tangent to a circle of radius <math>2</math>, as shown. What is the area of the square? |
<center> | <center> | ||
[[Image:2007 AMC 10A -15 for wiki.png]] | [[Image:2007 AMC 10A -15 for wiki.png]] | ||
</center> | </center> | ||
| − | < | + | <math>\text{(A)}\ 32 \qquad \text{(B)}\ 22 + 12\sqrt {2}\qquad \text{(C)}\ 16 + 16\sqrt {3}\qquad \text{(D)}\ 48 \qquad \text{(E)}\ 36 + 16\sqrt {2}</math> |
[[2007 AMC 10A Problems/Problem 15|Solution]] | [[2007 AMC 10A Problems/Problem 15|Solution]] | ||
== Problem 16 == | == Problem 16 == | ||
| − | Integers < | + | Integers <math>a, b, c,</math> and <math>d</math>, not necessarily distinct, are chosen independently and at random from 0 to 2007, inclusive. What is the probability that <math>ad-bc</math> is even? |
| − | < | + | <math>\mathrm{(A)}\ \frac 38\qquad \mathrm{(B)}\ \frac 7{16}\qquad \mathrm{(C)}\ \frac 12\qquad \mathrm{(D)}\ \frac 9{16}\qquad \mathrm{(E)}\ \frac 58</math> |
[[2007 AMC 10A Problems/Problem 16|Solution]] | [[2007 AMC 10A Problems/Problem 16|Solution]] | ||
== Problem 17 == | == Problem 17 == | ||
| − | Suppose that < | + | Suppose that <math>m</math> and <math>n</math> are positive integers such that <math>75m = n^{3}</math>. What is the minimum possible value of <math>m + n</math>? |
| − | < | + | <math>\text{(A)}\ 15 \qquad \text{(B)}\ 30 \qquad \text{(C)}\ 50 \qquad \text{(D)}\ 60 \qquad \text{(E)}\ 5700</math> |
[[2007 AMC 10A Problems/Problem 17|Solution]] | [[2007 AMC 10A Problems/Problem 17|Solution]] | ||
== Problem 18 == | == Problem 18 == | ||
| − | Consider the < | + | Consider the <math>12</math>-sided polygon <math>ABCDEFGHIJKL</math>, as shown. Each of its sides has length <math>4</math>, and each two consecutive sides form a right angle. Suppose that <math>\overline{AG}</math> and <math>\overline{CH}</math> meet at <math>M</math>. What is the area of quadrilateral <math>ABCM</math>? |
<center> | <center> | ||
[[Image:2007-AMC-10A--18.png]] | [[Image:2007-AMC-10A--18.png]] | ||
</center> | </center> | ||
| − | < | + | <math>\text{(A)}\ \frac {44}{3}\qquad \text{(B)}\ 16 \qquad \text{(C)}\ \frac {88}{5}\qquad \text{(D)}\ 20 \qquad \text{(E)}\ \frac {62}{3}</math> |
[[2007 AMC 10A Problems/Problem 18|Solution]] | [[2007 AMC 10A Problems/Problem 18|Solution]] | ||
| Line 134: | Line 134: | ||
[[Image:2007 AMC 10A Problems-Problem 19 Picture.png|120]] | [[Image:2007 AMC 10A Problems-Problem 19 Picture.png|120]] | ||
</center> | </center> | ||
| − | < | + | <math>\text{(A)}\ 2\sqrt {2} + 1 \qquad \text{(B)}\ 3\sqrt {2}\qquad \text{(C)}\ 2\sqrt {2} + 2 \qquad \text{(D)}\ 3\sqrt {2} + 1 \qquad \text{(E)}\ 3\sqrt {2} + 2</math> |
[[2007 AMC 10A Problems/Problem 19|Solution]] | [[2007 AMC 10A Problems/Problem 19|Solution]] | ||
== Problem 20 == | == Problem 20 == | ||
| − | Suppose that the number < | + | Suppose that the number <math>a</math> satisfies the equation <math>4 = a + a^{ - 1}</math>. What is the value of <math>a^{4} + a^{ - 4}</math>? |
| − | < | + | <math>\text{(A)}\ 164 \qquad \text{(B)}\ 172 \qquad \text{(C)}\ 192 \qquad \text{(D)}\ 194 \qquad \text{(E)}\ 212</math> |
[[2007 AMC 10A Problems/Problem 20|Solution]] | [[2007 AMC 10A Problems/Problem 20|Solution]] | ||
== Problem 21 == | == Problem 21 == | ||
| − | A sphere is inscribed in a cube that has a surface area of < | + | A sphere is inscribed in a cube that has a surface area of <math>24</math> square meters. A second cube is then inscribed within the sphere. What is the surface area in square meters of the inner cube? |
| − | < | + | <math>\text{(A)}\ 3 \qquad \text{(B)}\ 6 \qquad \text{(C)}\ 8 \qquad \text{(D)}\ 9 \qquad \text{(E)}\ 12</math> |
[[2007 AMC 10A Problems/Problem 21|Solution]] | [[2007 AMC 10A Problems/Problem 21|Solution]] | ||
== Problem 22 == | == Problem 22 == | ||
| − | A finite sequence of three-digit integers has the property that the tens and units digits of each term are, respectively, the hundreds and tens digits of the next term, and the tens and units digits of the last term are, respectively, the hundreds and tens digits of the first term. For example, such a sequence might begin with the terms 247, 475, and 756 and end with the term 824. Let < | + | A finite sequence of three-digit integers has the property that the tens and units digits of each term are, respectively, the hundreds and tens digits of the next term, and the tens and units digits of the last term are, respectively, the hundreds and tens digits of the first term. For example, such a sequence might begin with the terms 247, 475, and 756 and end with the term 824. Let <math>S</math> be the sum of all the terms in the sequence. What is the largest prime factor that always divides <math>S</math>? |
| − | < | + | <math>\mathrm{(A)}\ 3\qquad \mathrm{(B)}\ 7\qquad \mathrm{(C)}\ 13\qquad \mathrm{(D)}\ 37\qquad \mathrm{(E)}\ 43</math> |
[[2007 AMC 10A Problems/Problem 22|Solution]] | [[2007 AMC 10A Problems/Problem 22|Solution]] | ||
== Problem 23 == | == Problem 23 == | ||
| − | How many ordered pairs < | + | How many ordered pairs <math>(m,n)</math> of positive integers, with <math>m \ge n</math>, have the property that their squares differ by <math>96</math>? |
| − | < | + | <math>\text{(A)}\ 3 \qquad \text{(B)}\ 4 \qquad \text{(C)}\ 6 \qquad \text{(D)}\ 9 \qquad \text{(E)}\ 12</math> |
[[2007 AMC 10A Problems/Problem 23|Solution]] | [[2007 AMC 10A Problems/Problem 23|Solution]] | ||
== Problem 24 == | == Problem 24 == | ||
| − | Circles centered at < | + | Circles centered at <math>A</math> and <math>B</math> each have radius <math>2</math>, as shown. Point <math>O</math> is the midpoint of <math>\overline{AB}</math>, and <math>OA = 2\sqrt {2}</math>. Segments <math>OC</math> and <math>OD</math> are tangent to the circles centered at <math>A</math> and <math>B</math>, respectively, and <math>EF</math> is a common tangent. What is the area of the shaded region <math>ECODF</math>? |
<center> | <center> | ||
[[Image:2007 AMC 10A problem 24.png]] | [[Image:2007 AMC 10A problem 24.png]] | ||
</center> | </center> | ||
| − | < | + | <math>\text{(A)}\ \frac {8\sqrt {2}}{3} \qquad \text{(B)}\ 8\sqrt {2} - 4 - \pi \qquad \text{(C)}\ 4\sqrt {2} \qquad \text{(D)}\ 4\sqrt {2} + \frac {\pi}{8} \qquad \text{(E)}\ 8\sqrt {2} - 2 - \frac {\pi}{2}</math> |
[[2007 AMC 10A Problems/Problem 24|Solution]] | [[2007 AMC 10A Problems/Problem 24|Solution]] | ||
== Problem 25 == | == Problem 25 == | ||
| − | For each positive integer < | + | For each positive integer <math>n</math>, let <math>S(n)</math> denote the sum of the digits of <math>n.</math> For how many values of <math>n</math> is <math>n + S(n) + S(S(n)) = 2007?</math> |
| − | < | + | <math>\mathrm{(A)}\ 1 \qquad \mathrm{(B)}\ 2 \qquad \mathrm{(C)}\ 3 \qquad \mathrm{(D)}\ 4 \qquad \mathrm{(E)}\ 5</math> |
[[2007 AMC 10A Problems/Problem 25|Solution]] | [[2007 AMC 10A Problems/Problem 25|Solution]] | ||
Revision as of 10:45, 4 July 2013
Contents
[hide]Problem 1
One ticket to a show costs ![]() 20$at full price. Susan buys 4 tickets using a coupon that gives her a 25% discount. Pam buys 5 tickets using a coupon that gives her a 30% discount. How many more dollars does Pam pay than Susan?$ (Error compiling LaTeX. Unknown error_msg)\mathrm{(A)}\ 2\qquad \mathrm{(B)}\ 5\qquad \mathrm{(C)}\ 10\qquad \mathrm{(D)}\ 15\qquad \mathrm{(E)}\ 20$[[2007 AMC 10A Problems/Problem 1|Solution]]
20$at full price. Susan buys 4 tickets using a coupon that gives her a 25% discount. Pam buys 5 tickets using a coupon that gives her a 30% discount. How many more dollars does Pam pay than Susan?$ (Error compiling LaTeX. Unknown error_msg)\mathrm{(A)}\ 2\qquad \mathrm{(B)}\ 5\qquad \mathrm{(C)}\ 10\qquad \mathrm{(D)}\ 15\qquad \mathrm{(E)}\ 20$[[2007 AMC 10A Problems/Problem 1|Solution]]
== Problem 2 ==
Define$ (Error compiling LaTeX. Unknown error_msg)a@b = ab - b^{2}![]() a\#b = a + b - ab^{2}
a\#b = a + b - ab^{2}![]() \frac {6@2}{6\#2}
\frac {6@2}{6\#2}![]() \text{(A)}\ - \frac {1}{2}\qquad \text{(B)}\ - \frac {1}{4}\qquad \text{(C)}\ \frac {1}{8}\qquad \text{(D)}\ \frac {1}{4}\qquad \text{(E)}\ \frac {1}{2}$[[2007 AMC 10A Problems/Problem 2|Solution]]
\text{(A)}\ - \frac {1}{2}\qquad \text{(B)}\ - \frac {1}{4}\qquad \text{(C)}\ \frac {1}{8}\qquad \text{(D)}\ \frac {1}{4}\qquad \text{(E)}\ \frac {1}{2}$[[2007 AMC 10A Problems/Problem 2|Solution]]
== Problem 3 == An aquarium has a rectangular base that measures 100 cm by 40 cm and has a height of 50 cm. It is filled with water to a height of 40 cm. A brick with a rectangular base that measures 40 cm by 20 cm and a height of 10 cm is placed in the aquarium. By how many centimeters does the water rise?$ (Error compiling LaTeX. Unknown error_msg)\text{(A)}\ 0.5 \qquad \text{(B)}\ 1 \qquad \text{(C)}\ 1.5 \qquad \text{(D)}\ 2 \qquad \text{(E)}\ 2.5$[[2007 AMC 10A Problems/Problem 3|Solution]]
== Problem 4 == The larger of two consecutive odd integers is three times the smaller. What is their sum?$ (Error compiling LaTeX. Unknown error_msg)\text{(A)}\ 4 \qquad \text{(B)}\ 8 \qquad \text{(C)}\ 12 \qquad \text{(D)}\ 16 \qquad \text{(E)}\ 20$[[2007 AMC 10A Problems/Problem 4|Solution]]
== Problem 5 ==
A school store sells 7 pencils and 8 notebooks for$ (Error compiling LaTeX. Unknown error_msg)$ ![]() . It also sells 5 pencils and 3 notebooks for
. It also sells 5 pencils and 3 notebooks for ![]() 1.77
1.77![]() \text{(A)}\ $
\text{(A)}\ $ ![]() 5.84 \qquad \text{(C)}\ $
5.84 \qquad \text{(C)}\ $ ![]() 6.16 \qquad \text{(E)}\ $
6.16 \qquad \text{(E)}\ $ ![]()
Problem 6
At Euclid High School, the number of students taking the AMC 10 was ![]() in 2002,
in 2002, ![]() in 2003,
in 2003, ![]() in 2004,
in 2004, ![]() in 2005,
in 2005, ![]() and 2006, and is
and 2006, and is ![]() in 2007. Between what two consecutive years was there the largest percentage increase?
in 2007. Between what two consecutive years was there the largest percentage increase?
![]()
Problem 7
Last year Mr. Jon Q. Public received an inheritance. He paid ![]() in federal taxes on the inheritance, and paid
in federal taxes on the inheritance, and paid ![]() of what he had left in state taxes. He paid a total of
of what he had left in state taxes. He paid a total of ![]() for both taxes. How many dollars was his inheritance?
for both taxes. How many dollars was his inheritance?
![]()
Problem 8
Triangles ![]() and
and ![]() are isosceles with
are isosceles with ![]() and
and ![]() . Point
. Point ![]() is inside triangle
is inside triangle ![]() , angle
, angle ![]() measures 40 degrees, and angle
measures 40 degrees, and angle ![]() measures 140 degrees. What is the degree measure of angle
measures 140 degrees. What is the degree measure of angle ![]() ?
?
![]()
Problem 9
Real numbers ![]() and
and ![]() satisfy the equations
satisfy the equations ![]() and
and ![]() . What is
. What is ![]() ?
?
![]()
Problem 10
The Dunbar family consists of a mother, a father, and some children. The average age of the members of the family is ![]() , the father is
, the father is ![]() years old, and the average age of the mother and children is
years old, and the average age of the mother and children is ![]() . How many children are in the family?
. How many children are in the family?
![]()
Problem 11
The numbers from ![]() to
to ![]() are placed at the vertices of a cube in such a manner that the sum of the four numbers on each face is the same. What is this common sum?
are placed at the vertices of a cube in such a manner that the sum of the four numbers on each face is the same. What is this common sum?
![]()
Problem 12
Two tour guides are leading six tourists. The guides decide to split up. Each tourist must choose one of the guides, but with the stipulation that each guide must take at least one tourist. How many different groupings of guides and tourists are possible?
![]()
Problem 13
Yan is somewhere between his home and the stadium. To get to the stadium he can walk directly to the stadium, or else he can walk home and then ride his bicycle to the stadium. He rides 7 times as fast as he walks, and both choices require the same amount of time. What is the ratio of Yan's distance from his home to his distance from the stadium?
![]()
Problem 14
A triangle with side lengths in the ratio ![]() is inscribed in a circle with radius
is inscribed in a circle with radius ![]() . What is the area of the triangle?
. What is the area of the triangle?
![]()
Problem 15
Four circles of radius ![]() are each tangent to two sides of a square and externally tangent to a circle of radius
are each tangent to two sides of a square and externally tangent to a circle of radius ![]() , as shown. What is the area of the square?
, as shown. What is the area of the square?
![]()
Problem 16
Integers ![]() and
and ![]() , not necessarily distinct, are chosen independently and at random from 0 to 2007, inclusive. What is the probability that
, not necessarily distinct, are chosen independently and at random from 0 to 2007, inclusive. What is the probability that ![]() is even?
is even?
![]()
Problem 17
Suppose that ![]() and
and ![]() are positive integers such that
are positive integers such that ![]() . What is the minimum possible value of
. What is the minimum possible value of ![]() ?
?
![]()
Problem 18
Consider the ![]() -sided polygon
-sided polygon ![]() , as shown. Each of its sides has length
, as shown. Each of its sides has length ![]() , and each two consecutive sides form a right angle. Suppose that
, and each two consecutive sides form a right angle. Suppose that ![]() and
and ![]() meet at
meet at ![]() . What is the area of quadrilateral
. What is the area of quadrilateral ![]() ?
?
![]()
Problem 19
A paint brush is swept along both diagonals of a square to produce the symmetric painted area, as shown. Half the area of the square is painted. What is the ratio of the side length of the square to the brush width?
![]()
Problem 20
Suppose that the number ![]() satisfies the equation
satisfies the equation ![]() . What is the value of
. What is the value of ![]() ?
?
![]()
Problem 21
A sphere is inscribed in a cube that has a surface area of ![]() square meters. A second cube is then inscribed within the sphere. What is the surface area in square meters of the inner cube?
square meters. A second cube is then inscribed within the sphere. What is the surface area in square meters of the inner cube?
![]()
Problem 22
A finite sequence of three-digit integers has the property that the tens and units digits of each term are, respectively, the hundreds and tens digits of the next term, and the tens and units digits of the last term are, respectively, the hundreds and tens digits of the first term. For example, such a sequence might begin with the terms 247, 475, and 756 and end with the term 824. Let ![]() be the sum of all the terms in the sequence. What is the largest prime factor that always divides
be the sum of all the terms in the sequence. What is the largest prime factor that always divides ![]() ?
?
![]()
Problem 23
How many ordered pairs ![]() of positive integers, with
of positive integers, with ![]() , have the property that their squares differ by
, have the property that their squares differ by ![]() ?
?
![]()
Problem 24
Circles centered at ![]() and
and ![]() each have radius
each have radius ![]() , as shown. Point
, as shown. Point ![]() is the midpoint of
is the midpoint of ![]() , and
, and ![]() . Segments
. Segments ![]() and
and ![]() are tangent to the circles centered at
are tangent to the circles centered at ![]() and
and ![]() , respectively, and
, respectively, and ![]() is a common tangent. What is the area of the shaded region
is a common tangent. What is the area of the shaded region ![]() ?
?
![]()
Problem 25
For each positive integer ![]() , let
, let ![]() denote the sum of the digits of
denote the sum of the digits of ![]() For how many values of
For how many values of ![]() is
is ![]()
![]()
See also
- AMC 10
- AMC 10 Problems and Solutions
- 2007 AMC 10A
- 2007 AMC A Math Jam Transcript
- Mathematics competition resources
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()