Difference between revisions of "Power of a Point Theorem"
I like pie (talk | contribs) (Categories; minor edits) |
(Formatting) (Tag: Undo) |
||
| (42 intermediate revisions by 29 users not shown) | |||
| Line 1: | Line 1: | ||
| − | The '''Power of a Point Theorem''' | + | The '''Power of a Point Theorem''' is a relationship that holds between the lengths of the [[line segment]]s formed when two [[line]]s [[intersect]] a [[circle]] and each other. |
| − | == | + | == Statement == |
| − | |||
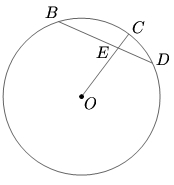
| − | # The two lines are [[ | + | There are three possibilities as displayed in the figures below: |
| − | # One of the lines is [[tangent line|tangent]] to the circle while the other is a [[secant line|secant]] (middle figure). | + | # The two lines are [[chord]]s of the circle and intersect inside the circle (figure on the left). In this case, we have <math>AE\cdot CE = BE\cdot DE</math>. |
| − | # Both lines are [[secant line|secants]] of the circle and intersect outside of it (figure on the right). In this case, we have <math> CB\cdot CA = CD\cdot CE. </math> | + | # One of the lines is [[tangent line|tangent]] to the circle while the other is a [[secant line|secant]] (middle figure). In this case, we have <math>AB^2 = BC\cdot BD</math>. |
| + | # Both lines are [[secant line|secants]] of the circle and intersect outside of it (figure on the right). In this case, we have <math>CB\cdot CA = CD\cdot CE.</math> | ||
[[Image:Pop.PNG|center]] | [[Image:Pop.PNG|center]] | ||
=== Alternate Formulation === | === Alternate Formulation === | ||
| + | |||
This alternate formulation is much more compact, convenient, and general. | This alternate formulation is much more compact, convenient, and general. | ||
| − | Consider a circle O and a point P in the plane where P is not on the circle. | + | Consider a circle <math>O</math> and a point <math>P</math> in the plane where <math>P</math> is not on the circle. Now draw a line through <math>P</math> that intersects the circle in two places. The power of a point theorem says that the product of the length from <math>P</math> to the first point of intersection and the length from <math>P</math> to the second point of intersection is constant for any choice of a line through <math>P</math> that intersects the circle. This constant is called the power of point <math>P</math>. For example, in the figure below |
| − | <cmath> | + | <cmath>PX^2=PA_1\cdot PB_1=PA_2\cdot PB_2=\cdots=PA_i\cdot PB_i</cmath> |
| − | PX^2=PA_1\cdot PB_1=PA_2\cdot PB_2=\cdots=PA_i\cdot PB_i | ||
| − | </cmath> | ||
[[Image:Popalt.PNG|center]] | [[Image:Popalt.PNG|center]] | ||
| − | Notice how this definition still works if <math>A_k</math> and <math>B_k</math> coincide (as is the case with X). | + | === Hint for Proof=== |
| + | |||
| + | Draw extra lines to create similar triangles (Draw <math>AD</math> on all three figures. Draw another line as well.) | ||
| + | |||
| + | Notice how this definition still works if <math>A_k</math> and <math>B_k</math> coincide (as is the case with <math>X</math>). Consider also when <math>P</math> is inside the circle. The definition still holds in this case. | ||
| + | |||
| + | == Notes == | ||
| − | + | One important result of this theorem is that both tangents from any point <math>P</math> outside of a circle to that circle are equal in length. | |
| − | One important result of this theorem is that both tangents from | ||
The theorem generalizes to higher dimensions, as follows. | The theorem generalizes to higher dimensions, as follows. | ||
| − | Let <math>P</math> be a point, and let <math>S</math> be an <math>n</math>-sphere. Let two arbitrary lines passing through <math>P </math> intersect <math>S </math> at <math>A_1 , B_1 ; A_2 , B_2 </math>, respectively. Then | + | Let <math>P</math> be a point, and let <math>S</math> be an <math>n</math>-sphere. Let two arbitrary lines passing through <math>P</math> intersect <math>S</math> at <math>A_1,B_1;A_2,B_2</math>, respectively. Then |
| − | <cmath> | + | <cmath>PA_1\cdot PB_1=PA_2\cdot PB_2</cmath> |
| − | PA_1 \cdot PB_1 = PA_2 \cdot PB_2 | ||
| − | </cmath> | ||
| − | ''Proof.'' | + | ''Proof.'' We have already proven the theorem for a <math>1</math>-sphere (a circle), so it only remains to prove the theorem for more dimensions. Consider the [[plane]] <math>p</math> containing both of the lines passing through <math>P</math>. The intersection of <math>P</math> and <math>S</math> must be a circle. If we consider the lines and <math>P</math> with respect simply to that circle, then we have reduced our claim to the case of two dimensions, in which we know the theorem holds. |
== Problems == | == Problems == | ||
| − | |||
=== Introductory === | === Introductory === | ||
| − | |||
| − | |||
| − | [[Image:popprob1.PNG|center]] | + | * Find the value of <math>x</math> in the following diagram: [[Image:popprob1.PNG|center]] |
| + | :[[Power of a Point Theorem/Introductory_Problem_1|Solution]] | ||
| − | [[Power of a Point Theorem/ | + | * Find the value of <math>x</math> in the following diagram: [[Image:popprob2.PNG|center]] |
| + | :[[Power of a Point Theorem/Introductory_Problem_2|Solution]] | ||
| − | == | + | * ([[ARML]]) In a circle, chords <math>AB</math> and <math>CD</math> intersect at <math>R</math>. If <math>AR:BR=1:4</math> and <math>CR:DR=4:9</math>, find the ratio <math>AB:CD</math> . |
| − | + | [[Image:popprob3.PNG|center]] | |
| + | :[[Power of a Point Theorem/Introductory_Problem_3|Solution]] | ||
| − | [[ | + | * ([[ARML]]) Chords <math>AB</math> and <math>CD</math> of a given circle are [[perpendicular]] to each other and intersect at a right angle at point <math>E</math>. Given that <math>BE=16</math>, <math>DE=4</math>, and <math>AD=5</math>, find <math>CE</math>. |
| + | :[[Power of a Point Theorem/Introductory_Problem_4|Solution]] | ||
| − | + | === Intermediate === | |
| − | + | * Two tangents from an external point <math>P</math> are drawn to a circle and intersect it at <math>A</math> and <math>B</math>. A third tangent meets the circle at <math>T</math>, and the tangents <math>\overrightarrow{PA}</math> and <math>\overrightarrow{PB}</math> at points <math>Q</math> and <math>R</math>, respectively (this means that T is on the minor arc <math>AB</math>). If <math>AP = 20</math>, find the perimeter of <math>\triangle PQR</math>. ([[1961_AHSME_Problems/Problem_11|Source]]) | |
| − | |||
| − | [[ | + | * Square <math>ABCD</math> of side length <math>10</math> has a circle inscribed in it. Let <math>M</math> be the midpoint of <math>\overline{AB}</math>. Find the length of that portion of the segment <math>\overline{MC}</math> that lies outside of the circle. ([[2020 AMC 12B Problems/Problem 10|Source]]) |
| − | [[ | + | * <math>DEB</math> is a chord of a circle such that <math>DE=3</math> and <math>EB=5 .</math> Let <math>O</math> be the center of the circle. Join <math>OE</math> and extend <math>OE</math> to cut the circle at <math>C.</math> Given <math>EC=1,</math> find the radius of the circle. ([[1971_Canadian_MO_Problems/Problem_1|Source]]) |
| + | [[Image:CanadianMO_1971-1.jpg]] | ||
| − | = | + | * Triangle <math>ABC</math> has <math>BC=20.</math> The incircle of the triangle evenly trisects the median <math>AD.</math> If the area of the triangle is <math>m \sqrt{n}</math> where <math>m</math> and <math>n</math> are integers and <math>n</math> is not divisible by the square of a prime, find <math>m+n.</math> ([[2005 AIME I Problems/Problem 15|Source]]) |
| − | |||
| − | + | === Olympiad === | |
| − | + | * {{problem}} | |
| − | |||
| − | |||
| − | ==== | + | == See Also == |
| − | |||
| − | |||
* [[Geometry]] | * [[Geometry]] | ||
* [[Planar figures]] | * [[Planar figures]] | ||
| + | * [{{SERVER}}/community/c6h2513977 Kagebaka's Handout] | ||
[[Category:Geometry]] | [[Category:Geometry]] | ||
[[Category:Theorems]] | [[Category:Theorems]] | ||
| + | {{stub}} | ||
Latest revision as of 17:04, 21 February 2025
The Power of a Point Theorem is a relationship that holds between the lengths of the line segments formed when two lines intersect a circle and each other.
Contents
[hide]Statement
There are three possibilities as displayed in the figures below:
- The two lines are chords of the circle and intersect inside the circle (figure on the left). In this case, we have
 .
. - One of the lines is tangent to the circle while the other is a secant (middle figure). In this case, we have
 .
. - Both lines are secants of the circle and intersect outside of it (figure on the right). In this case, we have

Alternate Formulation
This alternate formulation is much more compact, convenient, and general.
Consider a circle ![]() and a point
and a point ![]() in the plane where
in the plane where ![]() is not on the circle. Now draw a line through
is not on the circle. Now draw a line through ![]() that intersects the circle in two places. The power of a point theorem says that the product of the length from
that intersects the circle in two places. The power of a point theorem says that the product of the length from ![]() to the first point of intersection and the length from
to the first point of intersection and the length from ![]() to the second point of intersection is constant for any choice of a line through
to the second point of intersection is constant for any choice of a line through ![]() that intersects the circle. This constant is called the power of point
that intersects the circle. This constant is called the power of point ![]() . For example, in the figure below
. For example, in the figure below
![]()
Hint for Proof
Draw extra lines to create similar triangles (Draw ![]() on all three figures. Draw another line as well.)
on all three figures. Draw another line as well.)
Notice how this definition still works if ![]() and
and ![]() coincide (as is the case with
coincide (as is the case with ![]() ). Consider also when
). Consider also when ![]() is inside the circle. The definition still holds in this case.
is inside the circle. The definition still holds in this case.
Notes
One important result of this theorem is that both tangents from any point ![]() outside of a circle to that circle are equal in length.
outside of a circle to that circle are equal in length.
The theorem generalizes to higher dimensions, as follows.
Let ![]() be a point, and let
be a point, and let ![]() be an
be an ![]() -sphere. Let two arbitrary lines passing through
-sphere. Let two arbitrary lines passing through ![]() intersect
intersect ![]() at
at ![]() , respectively. Then
, respectively. Then
![]()
Proof. We have already proven the theorem for a ![]() -sphere (a circle), so it only remains to prove the theorem for more dimensions. Consider the plane
-sphere (a circle), so it only remains to prove the theorem for more dimensions. Consider the plane ![]() containing both of the lines passing through
containing both of the lines passing through ![]() . The intersection of
. The intersection of ![]() and
and ![]() must be a circle. If we consider the lines and
must be a circle. If we consider the lines and ![]() with respect simply to that circle, then we have reduced our claim to the case of two dimensions, in which we know the theorem holds.
with respect simply to that circle, then we have reduced our claim to the case of two dimensions, in which we know the theorem holds.
Problems
Introductory
- Find the value of
 in the following diagram:
in the following diagram:
- Find the value of
 in the following diagram:
in the following diagram:
- (ARML) In a circle, chords
 and
and  intersect at
intersect at  . If
. If  and
and  , find the ratio
, find the ratio  .
.
- (ARML) Chords
 and
and  of a given circle are perpendicular to each other and intersect at a right angle at point
of a given circle are perpendicular to each other and intersect at a right angle at point  . Given that
. Given that  ,
,  , and
, and  , find
, find  .
.
Intermediate
- Two tangents from an external point
 are drawn to a circle and intersect it at
are drawn to a circle and intersect it at  and
and  . A third tangent meets the circle at
. A third tangent meets the circle at  , and the tangents
, and the tangents  and
and  at points
at points  and
and  , respectively (this means that T is on the minor arc
, respectively (this means that T is on the minor arc  ). If
). If  , find the perimeter of
, find the perimeter of  . (Source)
. (Source)
- Square
 of side length
of side length  has a circle inscribed in it. Let
has a circle inscribed in it. Let  be the midpoint of
be the midpoint of  . Find the length of that portion of the segment
. Find the length of that portion of the segment  that lies outside of the circle. (Source)
that lies outside of the circle. (Source)
 is a chord of a circle such that
is a chord of a circle such that  and
and  Let
Let  be the center of the circle. Join
be the center of the circle. Join  and extend
and extend  to cut the circle at
to cut the circle at  Given
Given  find the radius of the circle. (Source)
find the radius of the circle. (Source)
- Triangle
 has
has  The incircle of the triangle evenly trisects the median
The incircle of the triangle evenly trisects the median  If the area of the triangle is
If the area of the triangle is  where
where  and
and  are integers and
are integers and  is not divisible by the square of a prime, find
is not divisible by the square of a prime, find  (Source)
(Source)
Olympiad
- This problem has not been edited in. Help us out by adding it.
See Also
This article is a stub. Help us out by expanding it.