Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2007 AMC 12A Problems/Problem 20"

(add solution)
 
(→‎Solution)
Line 5: Line 5:
  
 
== Solution ==
 
== Solution ==
−
{{image}}
+
[[Image:2007_AMC_12A_Problem_20.png]]
  
 
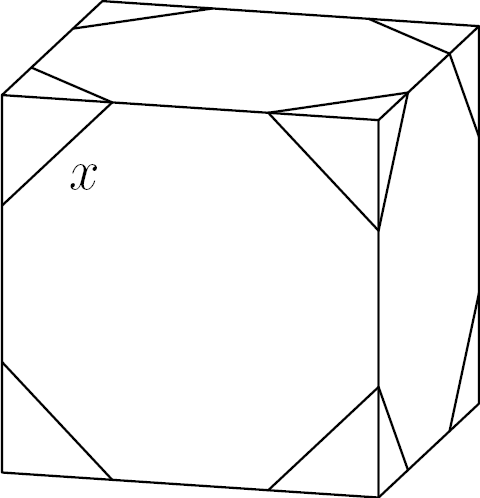
Since the sides of a [[regular polygon]] are equal in length, we can call each side <math>x</math>. Examine one edge of the unit cube: each contains two slanted diagonal edges of an octagon and one straight edge. The diagonal edges form <math>45-45-90 \triangle</math> [[right triangle]]s, making the distance on the edge of the cube <math>\frac{x}{\sqrt{2}}</math>. Thus, <math>2 \cdot \frac{x}{\sqrt{2}} + x = 1</math>, and <math>x = \frac{1}{\sqrt{2} + 1} \cdot \left(\frac{\sqrt{2} - 1}{\sqrt{2} - 1}\right) = \sqrt{2} - 1</math>.  
 
Since the sides of a [[regular polygon]] are equal in length, we can call each side <math>x</math>. Examine one edge of the unit cube: each contains two slanted diagonal edges of an octagon and one straight edge. The diagonal edges form <math>45-45-90 \triangle</math> [[right triangle]]s, making the distance on the edge of the cube <math>\frac{x}{\sqrt{2}}</math>. Thus, <math>2 \cdot \frac{x}{\sqrt{2}} + x = 1</math>, and <math>x = \frac{1}{\sqrt{2} + 1} \cdot \left(\frac{\sqrt{2} - 1}{\sqrt{2} - 1}\right) = \sqrt{2} - 1</math>.  

Revision as of 17:19, 18 July 2007

Problem

Corners are sliced off a unit cube so that the six faces each become regular octagons. What is the total volume of the removed tetrahedra?

$\mathrm{(A)}\ \frac{5\sqrt{2}-7}{3}\qquad \mathrm{(B)}\ \frac{10-7\sqrt{2}}{3}\qquad \mathrm{(C)}\ \frac{3-2\sqrt{2}}{3}\qquad \mathrm{(D)}\ \frac{8\sqrt{2}-11}{3}\qquad \mathrm{(E)}\ \frac{6-4\sqrt{2}}{3}$

Solution

2007 AMC 12A Problem 20.png

Since the sides of a regular polygon are equal in length, we can call each side $x$. Examine one edge of the unit cube: each contains two slanted diagonal edges of an octagon and one straight edge. The diagonal edges form $45-45-90 \triangle$ right triangles, making the distance on the edge of the cube $\frac{x}{\sqrt{2}}$. Thus, $2 \cdot \frac{x}{\sqrt{2}} + x = 1$, and $x = \frac{1}{\sqrt{2} + 1} \cdot \left(\frac{\sqrt{2} - 1}{\sqrt{2} - 1}\right) = \sqrt{2} - 1$.

Each of the cut off corners is a pyramid, whose volume can be calculated by $V = \frac 13 Bh$. Use the base as one of the three congruent isosceles triangles, with the height being one of the edges of the pyramid that sits on the edges of the cube. The height is $\frac x{\sqrt{2}} = 1 - \frac{1}{\sqrt{2}}$. The base is a $45-45-90 \triangle$ with leg of length $1 - \frac{1}{\sqrt{2}}$, making its area $\frac 12\left(1 - \frac 1{\sqrt{2}}\right)^2 = \frac{3 - 2\sqrt{2}}4$. Plugging this in, we get that the area of one of the tetrahedra is $\frac 13 \left(1 - \frac{1}{\sqrt{2}}\right)\left(\frac{3 - 2\sqrt{2}}4\right) = \frac{10 - 7\sqrt{2}}{24}$. Since there are 8 removed corners, we get an answer of $\frac{10 - 7\sqrt{2}}{3} \Longrightarrow \mathrm{B}$

See also

2007 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 19 		Followed by
Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2007_AMC_12A_Problems/Problem_20&oldid=15724"