Difference between revisions of "2024 AMC 10B Problems/Problem 10"
m (→Problem) |
(→Solution 2) |
||
| Line 16: | Line 16: | ||
==Solution 2== | ==Solution 2== | ||
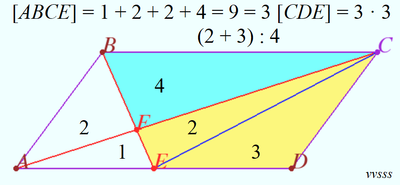
Let <math>[AFE]=1</math>. Since <math>\triangle AFE\sim\triangle CFB</math> with a scale factor of <math>2</math>, <math>[CFB]=4</math>. The scale factor of <math>2</math> also means that <math>\dfrac{AF}{FC}=\dfrac{1}{2}</math>, therefore since <math>\triangle BCF</math> and <math>\triangle BFA</math> have the same height, <math>[BFA]=2</math>. Since <math>ABCD</math> is a parallelogram, <cmath>[BCA]=[DAC]\implies4+2=1+[CDEF]\implies [CDEF]=5\implies\boxed{\text{(A) }5:4}</cmath> ~Tacos_are_yummy_1 | Let <math>[AFE]=1</math>. Since <math>\triangle AFE\sim\triangle CFB</math> with a scale factor of <math>2</math>, <math>[CFB]=4</math>. The scale factor of <math>2</math> also means that <math>\dfrac{AF}{FC}=\dfrac{1}{2}</math>, therefore since <math>\triangle BCF</math> and <math>\triangle BFA</math> have the same height, <math>[BFA]=2</math>. Since <math>ABCD</math> is a parallelogram, <cmath>[BCA]=[DAC]\implies4+2=1+[CDEF]\implies [CDEF]=5\implies\boxed{\text{(A) }5:4}</cmath> ~Tacos_are_yummy_1 | ||
| + | [[File:2024 AMC 10B 10.png|400px|left]] | ||
==Video Solution 1 by Pi Academy (Fast and Easy ⚡🚀)== | ==Video Solution 1 by Pi Academy (Fast and Easy ⚡🚀)== | ||
Revision as of 08:57, 15 November 2024
Contents
[hide]Problem
Quadrilateral ![]() is a parallelogram, and
is a parallelogram, and ![]() is the midpoint of the side
is the midpoint of the side ![]() . Let
. Let ![]() be the intersection of lines
be the intersection of lines ![]() and
and ![]() . What is the ratio of the area of
quadrilateral
. What is the ratio of the area of
quadrilateral ![]() to the area of
to the area of ![]() ?
?
![]()
Solution 1
Let ![]() have length
have length ![]() and let the altitude of the parallelogram perpendicular to
and let the altitude of the parallelogram perpendicular to ![]() have length
have length ![]() .
.
The area of the parallelogram is ![]() and the area of
and the area of ![]() equals
equals ![]() . Thus, the area of quadrilateral
. Thus, the area of quadrilateral ![]() is
is ![]() .
.
We have from ![]() that
that ![]() . Also,
. Also, ![]() , so the length of the altitude of
, so the length of the altitude of ![]() from
from ![]() is twice that of
is twice that of ![]() . This means that the altitude of
. This means that the altitude of ![]() is
is ![]() , so the area of
, so the area of ![]() is
is ![]() .
.
Then, the area of quadrilateral ![]() equals the area of
equals the area of ![]() minus that of
minus that of ![]() , which is
, which is ![]() . Finally, the ratio of the area of
. Finally, the ratio of the area of ![]() to the area of triangle
to the area of triangle ![]() is
is  , so the answer is
, so the answer is ![]() .
.
Solution 2
Let ![]() . Since
. Since ![]() with a scale factor of
with a scale factor of ![]() ,
, ![]() . The scale factor of
. The scale factor of ![]() also means that
also means that ![]() , therefore since
, therefore since ![]() and
and ![]() have the same height,
have the same height, ![]() . Since
. Since ![]() is a parallelogram,
is a parallelogram, ![]() ~Tacos_are_yummy_1
~Tacos_are_yummy_1
Video Solution 1 by Pi Academy (Fast and Easy ⚡🚀)
https://youtu.be/QLziG_2e7CY?feature=shared
~ Pi Academy
Video Solution 2 by SpreadTheMathLove
https://www.youtube.com/watch?v=24EZaeAThuE
See also
| 2024 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()