1986 AIME Problems/Problem 14
Problem
The shortest distances between an interior diagonal of a rectangular parallelepiped, ![]() , and the edges it does not meet are
, and the edges it does not meet are ![]() ,
, ![]() , and
, and ![]() . Determine the volume of
. Determine the volume of ![]() .
.
Solution
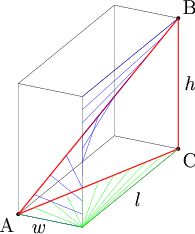
In the above diagram, we focus on the line that appears closest and is parallel to ![]() . All the blue lines are perpendicular lines to
. All the blue lines are perpendicular lines to ![]() and their other points are on
and their other points are on ![]() , the main diagonal. The green lines are projections of the blue lines onto the bottom face; all of the green lines originate in the corner and reach out to
, the main diagonal. The green lines are projections of the blue lines onto the bottom face; all of the green lines originate in the corner and reach out to ![]() , and have the same lengths as their corresponding blue lines. So we want to find the shortest distance between
, and have the same lengths as their corresponding blue lines. So we want to find the shortest distance between ![]() and that corner, which is
and that corner, which is ![]() .
.
So we have:
![]()
![]()
![]()
Notice the familiar roots: ![]() ,
, ![]() ,
, ![]() , which are
, which are ![]() ,
, ![]() ,
, ![]() , respectively. (This would give us the guess that the sides are of the ratio 1:2:3, but let's provide the complete solution.)
, respectively. (This would give us the guess that the sides are of the ratio 1:2:3, but let's provide the complete solution.)
![]()
![]()
![]()
We invert the above equations to get a system of linear equations in ![]() ,
, ![]() , and
, and ![]() :
:
![]()
![]()
![]()
We see that ![]() ,
, ![]() ,
, ![]() . Therefore
. Therefore ![]() .
.
See also
| 1986 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()









