Projective geometry (simplest cases)
Projective geometry contains a number of intuitively obvious statements that can be effectively used to solve some Olympiad mathematical problems.
Useful simplified information
Let two planes ![]() and
and ![]() and a point
and a point ![]() not lying in them be defined in space. To each point
not lying in them be defined in space. To each point ![]() of plane
of plane ![]() we assign the point
we assign the point ![]() of plane
of plane ![]() at which the line
at which the line ![]() intersects this plane. We want to find a one-to-one mapping of plane
intersects this plane. We want to find a one-to-one mapping of plane ![]() onto plane
onto plane ![]() using such a projection.
using such a projection.
We are faced with the following problem. Let us construct a plane containing a point ![]() and parallel to the plane
and parallel to the plane ![]() Let us denote the line along which it intersects the plane
Let us denote the line along which it intersects the plane ![]() as
as ![]() No point of the line
No point of the line ![]() has an image in the plane
has an image in the plane ![]() Such new points are called points at infinity.
Such new points are called points at infinity.
To solve it, we turn the ordinary Euclidean plane into a projective plane. We consider that the set of all points at infinity of each plane forms a line. This line is called the line at infinity. The plane supplemented by such line is called the projective plane, and the line for which the central projection is not defined is called (in Russian tradition) the exceptional line of the transformation. We define the central projection as follows.
Let us define two projective planes ![]() and
and ![]() and a point
and a point ![]()
For each point ![]() of plane
of plane ![]() we assign either:
we assign either:
- the point ![]() of plane
of plane ![]() at which line
at which line ![]() intersects
intersects ![]()
- or a point at infinity if line ![]() does not intersect plane
does not intersect plane ![]()
We define the inverse transformation similarly.
A mapping of a plane onto a plane is called a projective transformation if it is a composition of central projections and affine transformations.
Properties of a projective transformation
1. A projective transformation is a one-to-one mapping of a set of points of a projective plane, and is also a one-to-one mapping of a set of lines.
2. The inverse of a projective transformation is projective transformation. The composition of projective transformations is a projective transformation.
3. Let two quadruples of points ![]() and
and ![]() be given. In each quadruple no three points lie on the same line: Then there exists a unique projective transformation that maps
be given. In each quadruple no three points lie on the same line: Then there exists a unique projective transformation that maps ![]() to
to ![]()
![]() to
to ![]() to
to ![]() to
to ![]()
4. There is a central projection that maps any quadrilateral to a square. A square can be obtained as a central projection of any quadrilateral.
5. There is a central projection that maps a circle to a circle, and a chosen interior point of the first circle to the center of the second circle. This central projection maps the polar of the chosen point to the line at infinity.
6. The relationships of segments belonging to lines parallel to the exceptional line are the same for images and preimages.
Contents
[hide]- 1 Projection of a circle into a circle
- 2 Butterfly theorem
- 3 Sharygin’s Butterfly theorem
- 4 Semi-inscribed circle
- 5 Fixed point
- 6 Sphere and two points
- 7 Projecting non-convex quadrilateral into rectangle
- 8 Projecting convex quadrilateral into square
- 9 Medians crosspoint
- 10 Six segments
- 11 Sines of the angles of a quadrilateral
Projection of a circle into a circle
Let a circle ![]() with diameter
with diameter ![]() and a point
and a point ![]() on this diameter
on this diameter ![]() be given.
be given.
Find the prospector of the central projection that maps the circle ![]() into the circle
into the circle ![]() and the point
and the point ![]() into point
into point ![]() - the center of
- the center of ![]()
Solution
Let ![]() be the center of transformation (perspector) which is located on the perpendicular through the point
be the center of transformation (perspector) which is located on the perpendicular through the point ![]() to the plane containing
to the plane containing ![]() Let
Let ![]() be the diameter of
be the diameter of ![]() and plane
and plane ![]() is perpendicular to
is perpendicular to ![]()
Spheres with diameter ![]() and with diameter
and with diameter ![]() contain a point
contain a point ![]() , so they intersect along a circle
, so they intersect along a circle ![]()
Therefore the circle ![]() is a stereographic projection of the circle
is a stereographic projection of the circle ![]() from the point
from the point ![]()
That is, if the point ![]() lies on
lies on ![]() , there is a point
, there is a point ![]() on the circle
on the circle ![]() along which the line
along which the line ![]() intersects
intersects ![]()
It means that ![]() is projected into
is projected into ![]() under central projection from the point
under central projection from the point ![]()
![]() is antiparallel
is antiparallel ![]() in
in ![]()
![]() is the symmedian.
is the symmedian.
![\[\frac {AQ}{AP} = \frac {SQ^2}{SP^2} \implies \frac {QP - AP}{AP} = \frac {SP^2 + PQ^2}{SP^2} \implies SP = \frac {QP}{\sqrt{\frac {QP}{AP}-2}}.\]](http://latex.artofproblemsolving.com/9/3/e/93e85031af1d0e616afd74d171e74007bae2ec32.png)
Corollary
Let ![]()
![]() The inverse of a point
The inverse of a point ![]() with respect to a reference circle
with respect to a reference circle ![]() is
is ![]()
The line throught ![]() in plane of circle
in plane of circle ![]() perpendicular to
perpendicular to ![]() is polar of point
is polar of point ![]()
The central projection of this line to the plane of circle ![]() from point
from point ![]() is the line at infinity.
is the line at infinity.
vladimir.shelomovskii@gmail.com, vvsss
Butterfly theorem
Let ![]() be the midpoint of a chord
be the midpoint of a chord ![]() of a circle
of a circle ![]() through which two other chords
through which two other chords ![]() and
and ![]() are drawn;
are drawn; ![]() and
and ![]() intersect chord
intersect chord ![]() at
at ![]() and
and ![]() correspondingly.
correspondingly.
Prove that ![]() is the midpoint of
is the midpoint of ![]()
Proof
Let point ![]() be the center of
be the center of ![]()
We make the central projection that maps the circle ![]() into the circle
into the circle ![]() and the point
and the point ![]() into the center of
into the center of ![]()
Let's designate the images points with the same letters as the preimages points.
Chords ![]() and
and ![]() maps into diameters, so
maps into diameters, so ![]() maps into rectangle and in this plane
maps into rectangle and in this plane ![]() is the midpoint of
is the midpoint of ![]()
The exceptional line of the transformation is perpendicular to ![]() so parallel to
so parallel to ![]()
The relationships of segments belonging to lines parallel to the exceptional line are the same for images and preimages. We're done! ![]() .
.
vladimir.shelomovskii@gmail.com, vvsss
Sharygin’s Butterfly theorem
Let a circle ![]() and a chord
and a chord ![]() be given. Points
be given. Points ![]() and
and ![]() lyes on
lyes on ![]() such that
such that ![]() Chords
Chords ![]() and
and ![]() are drawn through points
are drawn through points ![]() and
and ![]() respectively such that quadrilateral
respectively such that quadrilateral ![]() is convex.
is convex.
Lines ![]() and
and ![]() intersect the chord
intersect the chord ![]() at points
at points ![]() and
and ![]()
Prove that ![]()
Proof
Let us perform a projective transformation that maps the midpoint of the chord ![]() to the center of the circle
to the center of the circle ![]() . The image
. The image ![]() will become the diameter, the equality
will become the diameter, the equality ![]() will be preserved.
will be preserved.
Let ![]() and
and ![]() be the points symmetrical to the points
be the points symmetrical to the points ![]() and
and ![]() with respect to line
with respect to line ![]() the bisector
the bisector ![]()
Denote ![]() (Sharygin’s idea.)
(Sharygin’s idea.)
![]() is cyclic
is cyclic ![]()
![]() is cyclic
is cyclic ![]()
![]() points
points ![]() and
and ![]() are collinear.
are collinear.
Similarly points ![]() and
and ![]() are collinear.
are collinear.
We use the symmetry lines ![]() and
and ![]() with respect
with respect ![]() and get in series
and get in series
![]() symmetry
symmetry ![]() and
and ![]() with respect
with respect ![]()
![]() symmetry
symmetry ![]() and CB with respect
and CB with respect ![]()
![]() symmetry
symmetry ![]() and
and ![]() with respect
with respect ![]()
vladimir.shelomovskii@gmail.com, vvsss
Semi-inscribed circle
Let triangle ![]() and circle
and circle ![]() centered at point
centered at point ![]() and touches sides
and touches sides ![]() and
and ![]() at points
at points ![]() and
and ![]() be given.
be given.
Point ![]() is located on chord
is located on chord ![]() so that
so that ![]()
Prove that points ![]() and
and ![]() (the midpoint
(the midpoint ![]() are collinear.
are collinear.
Proof
Denote ![]() point on line
point on line ![]() such that
such that ![]()
![]()
Therefore line ![]() is the polar of
is the polar of ![]()
Let us perform a projective transformation that maps point ![]() to the center of
to the center of ![]()
Image ![]() is the point at infinity, so images
is the point at infinity, so images ![]() and
and ![]() are parallel.
are parallel.
Image ![]() is diameter, so image
is diameter, so image ![]() is midpoint of image
is midpoint of image ![]() and image
and image ![]() is midpoint of image
is midpoint of image ![]()
![]() so image
so image ![]() is parallel to the line at infinity and the ratio
is parallel to the line at infinity and the ratio ![]() is the same as ratio of images.
is the same as ratio of images.
vladimir.shelomovskii@gmail.com, vvsss
Fixed point
Let triangle ![]() and circle
and circle ![]() centered at point
centered at point ![]() and touches sides
and touches sides ![]() and
and ![]() at points
at points ![]() and
and ![]() be given.
be given.
The points ![]() and
and ![]() on the side
on the side ![]() are such that
are such that ![]()
The cross points of segments ![]() and
and ![]() with
with ![]() form a convex quadrilateral
form a convex quadrilateral ![]()
Point ![]() lies at
lies at ![]() and satisfies the condition
and satisfies the condition ![]()
Prove that ![]()
Proof
Let us perform a projective transformation that maps point ![]() to the center of
to the center of ![]()
Image ![]() is the point at infinity, so images
is the point at infinity, so images ![]() and
and ![]() are parallel. The plane of images is shown, notation is the same as for preimages.
are parallel. The plane of images is shown, notation is the same as for preimages.
Image ![]() is diameter
is diameter ![]() image
image ![]() is parallel to the line at infinity, so in image plane
is parallel to the line at infinity, so in image plane
![]()
Denote ![]()
![]()
![]()
![]() is rectangle, so
is rectangle, so ![]()
vladimir.shelomovskii@gmail.com, vvsss
Sphere and two points
Let a sphere ![]() and points
and points ![]() and
and ![]() be given in space. The line
be given in space. The line ![]() does not has the common points with the sphere. The sphere is inscribed in tetrahedron
does not has the common points with the sphere. The sphere is inscribed in tetrahedron ![]()
Prove that the sum of the angles of the spatial quadrilateral ![]() (i.e. the sum
(i.e. the sum ![]() does not depend on the choice of points
does not depend on the choice of points ![]() and
and ![]()
Proof
Denote ![]() points of tangency
points of tangency ![]() and faces of
and faces of ![]() (see diagram),
(see diagram), ![]()
![]()
It is known that ![]()
![]()
![]() Similarly,
Similarly, ![]()
![]()
![]() The sum not depend on the choice of points
The sum not depend on the choice of points ![]() and
and ![]()
vladimir.shelomovskii@gmail.com, vvsss
Projecting non-convex quadrilateral into rectangle
Let a non-convex quadrilateral ![]() be given. Find a projective transformation of points
be given. Find a projective transformation of points ![]() into the vertices of rectangle.
into the vertices of rectangle.
Solution
WLOG, point ![]() is inside the
is inside the ![]()
![]()
Let ![]() and
and ![]() be the rays,
be the rays, ![]() be any point on segment
be any point on segment ![]()
![]() Planes
Planes ![]() and
and ![]() are perpendicular, planes
are perpendicular, planes ![]() and
and ![]() are parallel, so image
are parallel, so image ![]() is line at infinity and
is line at infinity and ![]() is rectangle.
is rectangle.
Let's paint the parts of the planes ![]() and
and ![]() that maps into each other with the same color.
that maps into each other with the same color.
![]() maps into
maps into ![]() (yellow).
(yellow).
Green infinite triangle between ![]() and
and ![]() maps into
maps into ![]() where plane
where plane ![]() is parallel to plane
is parallel to plane ![]()
Blue infinite quadrilateral between ![]() and
and ![]() with side
with side ![]() maps into quadrilateral
maps into quadrilateral ![]()
Therefore inner part of quadrilateral ![]() maps into external part of rectangle
maps into external part of rectangle ![]() For example
For example ![]() maps into
maps into ![]() where
where ![]() is the intersection of planes
is the intersection of planes ![]() and
and ![]()
vladimir.shelomovskii@gmail.com, vvsss
Projecting convex quadrilateral into square
Let ![]() be a convex quadrilateral with no parallel sides.
be a convex quadrilateral with no parallel sides.
Find the projective transformation of ![]() into the square
into the square ![]() if the angle between the planes
if the angle between the planes ![]() and
and ![]() is given. This angle is not equal to
is given. This angle is not equal to ![]() or
or ![]()
Solution
Denote ![]()
Let ![]() be the point satisfying the conditions
be the point satisfying the conditions ![]()
The locus of such points is the intersection circle of spheres with diameters ![]() and
and ![]()
Let ![]() be the perspector and the image plane be parallel to plane
be the perspector and the image plane be parallel to plane ![]() We use the plane contains
We use the plane contains ![]() so image
so image ![]()
Then image ![]() is the line at infinity, point
is the line at infinity, point ![]() is point at infinity, so images
is point at infinity, so images ![]() (line
(line ![]() ) and
) and ![]() (line
(line ![]() ) are parallel to
) are parallel to ![]()
Similarly point ![]() is the point at infinity, so images
is the point at infinity, so images ![]() is the rectangle.
is the rectangle.
Point ![]() is the point at infinity, so
is the point at infinity, so ![]() Point
Point ![]() is the point at infinity, so
is the point at infinity, so ![]()
![]() is the square.
is the square.
Let ![]() be such point that
be such point that ![]()
The angle between ![]() and plane
and plane ![]() is the angle we can choose. It is equal to the angle between planes
is the angle we can choose. It is equal to the angle between planes ![]() and
and ![]()
vladimir.shelomovskii@gmail.com, vvsss
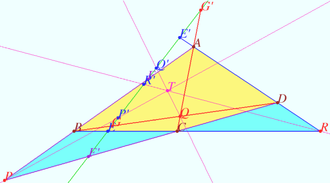
Medians crosspoint
Let a convex quadrilateral ![]() and line
and line ![]() in common position be given (points
in common position be given (points ![]() and
and ![]() not belong
not belong ![]() sides and diagonals are not parallel to
sides and diagonals are not parallel to ![]() Denote
Denote ![]()
![]() Denote
Denote ![]() and
and ![]() midpoints of
midpoints of ![]() and
and ![]() respectively.
Prove that lines
respectively.
Prove that lines ![]() and
and ![]() are collinear.
Proof
are collinear.
Proof
Six segments
Let a convex quadrilateral ![]() and line
and line ![]() in common position be given (points
in common position be given (points ![]() and
and ![]() not belong
not belong ![]() sides and diagonals are not parallel to
sides and diagonals are not parallel to ![]() Denote
Denote ![]() Prove that
Prove that ![]()
Proof
By applying the law of sines, we get:
![]()
![]()
![]()
![]()
![]() (see Sines of the angles of a quadrilateral)
(see Sines of the angles of a quadrilateral)
vladimir.shelomovskii@gmail.com, vvsss
Sines of the angles of a quadrilateral
Let a convex quadrilateral ![]() be given. Prove that
be given. Prove that
![]()
Proof
By applying the law of sines, we get:
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss