Barycentric coordinates
This can be used in mass points. http://mathworld.wolfram.com/BarycentricCoordinates.html This article is a stub. Help us out by expanding it.
Barycentric coordinates are triples of numbers ![]() corresponding to masses placed at the vertices of a reference triangle
corresponding to masses placed at the vertices of a reference triangle ![]() . These masses then determine a point
. These masses then determine a point ![]() , which is the geometric centroid of the three masses and is identified with coordinates
, which is the geometric centroid of the three masses and is identified with coordinates ![]() . The vertices of the triangle are given by
. The vertices of the triangle are given by ![]() ,
, ![]() , and
, and ![]() . Barycentric coordinates were discovered by Möbius in 1827 (Coxeter 1969, p. 217; Fauvel et al. 1993).
. Barycentric coordinates were discovered by Möbius in 1827 (Coxeter 1969, p. 217; Fauvel et al. 1993).
The Central NC Math Group published a lecture concerning this topic at https://www.youtube.com/watch?v=KQim7-wrwL0 if you would like to view it.
Contents
[hide]- 1 Useful formulas
- 2 Product of isogonal segments
- 3 Ratio of isogonal segments
- 4 Point on incircle
- 5 Crossing point
- 6 Fixed point on circumcircle
- 7 Two pare isogonal points
- 8 Collinearity for two pares of isogonal points
- 9 Points on bisectors
- 10 Crosspoint of median and set of secants
- 11 Set of lines in triangle
- 12 Set of parallel lines
- 13 Feuerbach point of a scalene triangle
- 14 Small Pascal's theorem
Useful formulas
Notation
Let the triangle ![]() be a given triangle,
be a given triangle, ![]() be the lengths of
be the lengths of ![]()
We use the following Conway symbols:
![]() is semiperimeter,
is semiperimeter, ![]() is twice the area of
is twice the area of ![]()
![]() where
where ![]() is the inradius,
is the inradius, ![]() is the circumradius,
is the circumradius,
![]() is the cosine of the Brocard angle,
is the cosine of the Brocard angle,
![]()
Main
For any point in the plane ![]() there are barycentric coordinates(BC):
there are barycentric coordinates(BC): ![]()
![]()
![]() The normalized (absolute) barycentric coordinates NBC satisfy the condition
The normalized (absolute) barycentric coordinates NBC satisfy the condition ![]() they are uniquely determined:
they are uniquely determined:
![]()
![]() Triangle vertices
Triangle vertices ![]()
The barycentric coordinates of a point do not change under an affine transformation.
Lines
The straight line in barycentric coordinates (BC) is given by the equation ![]()
The lines given in the BC by the equations ![]() and
and ![]() intersect at the point
intersect at the point
![]()
These lines are parallel iff ![]()
The sideline ![]() contains the points
contains the points ![]() its equation is
its equation is ![]()
The line ![]() has equation
has equation ![]() it intersects the sideline
it intersects the sideline ![]() at the point
at the point ![]()
Iff ![]() then
then ![]()
Let NBC of points ![]() and
and ![]() be
be ![]()
Then the square of distance ![]()
![]() The equation of bisector of
The equation of bisector of ![]() is:
is:
![]() Nagel line :
Nagel line : ![]()
Circles
Any circle is given by an equation of the form ![]()
Circumcircle contains the points ![]() the equation of this circle:
the equation of this circle: ![]()
The incircle contains the tangent points of the incircle with the sides:
![]()
The equation of the incircle is
![]() where
where ![]()
The radical axis of two circles given by equations of this form is:
![]() Conjugate
Conjugate
The point ![]() is isotomically conjugate with respect to
is isotomically conjugate with respect to ![]() with the point
with the point ![]()
The point ![]() is isogonally conjugate with respect to
is isogonally conjugate with respect to ![]() with the point
with the point ![]()
The point ![]() is isocircular conjugate with respect to
is isocircular conjugate with respect to ![]() with the point
with the point ![]()
Triangle centers
The median ![]() centroid is
centroid is ![]()
The simmedian point ![]() is isogonally conjugate with respect to
is isogonally conjugate with respect to ![]() with the point
with the point ![]()
The bisector ![]() the incenter is
the incenter is ![]()
The excenters are ![]()
The circumcenter ![]() lies at the intersection of the bisectors
lies at the intersection of the bisectors ![]() and
and ![]() its BC coordinates
its BC coordinates ![]()
The orthocenter ![]() is isogonally conjugate with respect to
is isogonally conjugate with respect to ![]() with the point
with the point ![]()
Let Nagel point ![]() lies at line
lies at line ![]()
The Gergonne point is the isotomic conjugate of the Nagel point, so ![]()
vladimir.shelomovskii@gmail.com, vvsss
Product of isogonal segments
Let triangle ![]() the circumcircle
the circumcircle ![]() and isogonals
and isogonals ![]() and
and ![]() of the
of the ![]() be given.
Let point
be given.
Let point ![]() and
and ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() and
and ![]() with respect to
with respect to ![]() Prove that
Prove that ![]()
Proof
We fixed ![]() and the point
and the point ![]() So isogonal
So isogonal ![]() is fixed.
is fixed.
Denote ![]()
We need to prove that ![]() do not depends from
do not depends from ![]()
Line ![]() has the equation
has the equation ![]()
To find the point ![]() we solve the equation:
we solve the equation: ![]()
![]() We use the formula for isogonal cobnjugate point and get
We use the formula for isogonal cobnjugate point and get
![]() and then
and then ![]()
To find the point ![]() we solve the equation:
we solve the equation: ![]()
![]() We calculate distances (using NBC) and get:
We calculate distances (using NBC) and get:
![]()
![]() where
where ![]() has sufficiently big formula.
has sufficiently big formula.
Therefore ![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Ratio of isogonal segments
Let triangle ![]() and point
and point ![]() be given.
Denote
be given.
Denote ![]() the isogonal conjugate of a point
the isogonal conjugate of a point ![]() with respect to
with respect to ![]()
![]() Prove that
Prove that ![]()
Proof
We use the formula for isogonal conjugate point and get ![]()
![]()
![]()
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
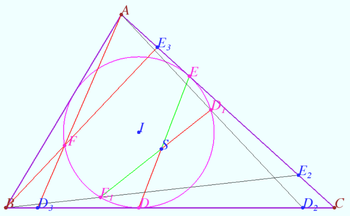
Point on incircle
Let triangle ![]() be given. Denote the incircle
be given. Denote the incircle ![]() the incenter
the incenter ![]() , the Spieker center
, the Spieker center ![]()
Let ![]() be the point corresponding to the condition
be the point corresponding to the condition ![]() is symmetric
is symmetric ![]() with respect midpoint
with respect midpoint ![]()
Symilarly denote ![]()
Prove that point ![]() lies on
lies on ![]()
Proof
![]()
![]() We calculate distances (using NBC) and solve the system of equations:
We calculate distances (using NBC) and solve the system of equations:
![]()
We know one solution of this system (point D), so we get linear equation and get:
![]()
![]()
![]() Similarly
Similarly ![]() Therefore
Therefore ![]() We calculate the length of the segment
We calculate the length of the segment ![]() and get
and get ![]()
The author learned about the existence of such a point from Leonid Shatunov in August 2023.
vladimir.shelomovskii@gmail.com, vvsss
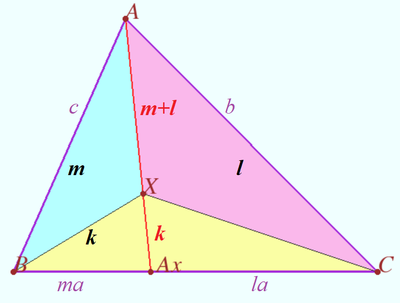
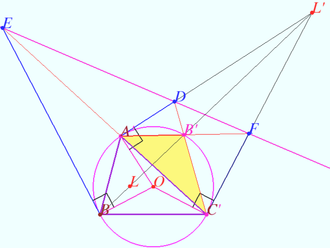
Crossing point
Let triangle ![]() and points
and points ![]() and
and ![]() be given. Let point
be given. Let point ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]() Let
Let ![]() be an arbitrary point at
be an arbitrary point at ![]()
![]() Prove that
Prove that ![]() lies on
lies on ![]()
This configuration can be used as a straight-line mechanism since it allows to create a mechanism that converts the rotational motion of a point Z to perfect straight-line motion of the X point or vice versa. Of course, we need to use the prismatic joint at the points ![]() and
and ![]()
Proof
We use the barycentric coordinates: ![]()
![]() We get the equations for some lines:
We get the equations for some lines:
Line ![]() is
is ![]()
line ![]() is
is ![]()
line ![]() is
is ![]()
line ![]() is
is ![]()
line ![]() is
is ![]()
We get the equations for some points:
point ![]() is
is ![]()
point ![]() is
is ![]()
point ![]() is
is ![]()
Any circle is given by an equation of the form ![]() We find the coefficients for the circles (these formulas are big), but can be used for calculations of the crossing points:
We find the coefficients for the circles (these formulas are big), but can be used for calculations of the crossing points:
![]()
![]() We get the equations for some lines
We get the equations for some lines ![]() and
and ![]() :
:
![]()
![]() We get the equation for the point
We get the equation for the point ![]()
![]() Let point
Let point ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
![]() The sum of coordinates is equal zero, so
The sum of coordinates is equal zero, so ![]() is in infinity, therefore the point
is in infinity, therefore the point ![]() lies on
lies on ![]()
vladimir.shelomovskii@gmail.com, vvsss
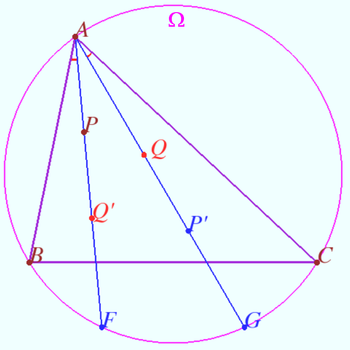
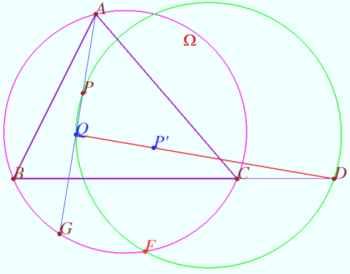
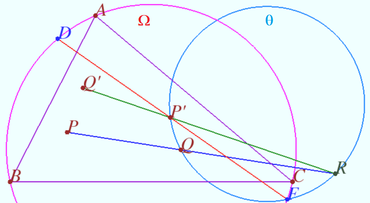
Fixed point on circumcircle
Let triangle ![]() point
point ![]() on circumcircle
on circumcircle ![]() and point
and point ![]() be given.
Point
be given.
Point ![]() lies on
lies on ![]() point
point ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() with respect to a triangle
with respect to a triangle ![]()
Prove that ![]() is fixed point and not depends from position of
is fixed point and not depends from position of ![]()
Proof
Denote the coordinates of the points ![]()
![]()
![]()
![]() The line
The line ![]() is
is ![]()
The line ![]() is
is ![]()
![]() We find the circle
We find the circle ![]() and get the point
and get the point
![\[F =\left( \frac {a^2}{\frac {c^2}{z_D \cdot z_G} - \frac{b^2}{y_D \cdot y_G}} : y_G \cdot y_D : - z_G \cdot z_D \right).\]](http://latex.artofproblemsolving.com/a/5/d/a5d259e35346d42f2d09081f526a415652f99cbe.png)
![]() depends only from points
depends only from points ![]() and
and ![]()
vladimir.shelomovskii@gmail.com, vvsss
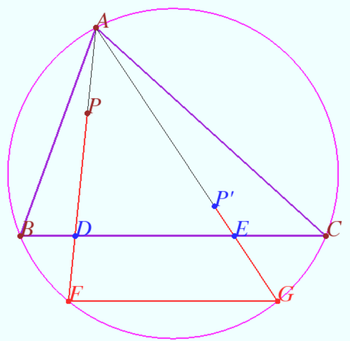
Two pare isogonal points
Let triangle ![]() and points
and points ![]() and
and ![]() (points do not lie on sidelines) be given.
(points do not lie on sidelines) be given.
Let point ![]() and
and ![]() be the isogonal conjugate of a point
be the isogonal conjugate of a point ![]() and
and ![]() with respect to a triangle
with respect to a triangle ![]()
Denote ![]()
Prove that ![]() and
and ![]() lies on
lies on ![]()
Proof
The line ![]() is
is
![]() The line
The line ![]() is
is
![]()
![]()
![]()
![]()
![]() Denote
Denote ![]() is the isogonal conjugate of a point
is the isogonal conjugate of a point ![]() with respect to
with respect to ![]()
![]()
![]() If we use NBC, we get
If we use NBC, we get ![]()
![\[L = EP \cap FQ = \left( \frac {1}{\frac {b^2} {x_Q y_P} - \frac {b^2} {x_P y_Q}+ \frac {c^2} {x_Q z_P}- \frac {c^2} {x_Q z_P}} : \frac {1}{\frac {a^2} {x_Q y_P} - \frac {a^2} {x_P y_Q}+ \frac {c^2} {z_Q y_P}- \frac {c^2} {y_Q z_P}} : \frac {1}{\frac {a^2} {x_Q z_P} - \frac {a^2} {x_P z_Q}+ \frac {b^2} {y_Q z_P}- \frac {b^2} {y_P z_Q}} \right).\]](http://latex.artofproblemsolving.com/b/a/f/baf8817822cfb7f7378ad045edd3c3ee8c5658a3.png)
![]() If we use NBC, we get
If we use NBC, we get ![]()
vladimir.shelomovskii@gmail.com, vvsss
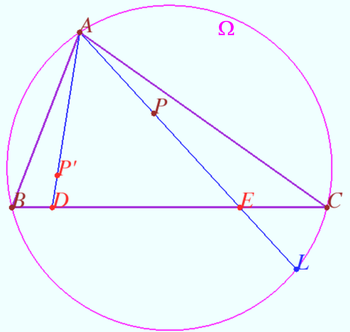
Collinearity for two pares of isogonal points
Let triangle ![]() and points
and points ![]() and
and ![]() be given. Let point
be given. Let point ![]() and
and ![]() be the isogonal conjugate of the points
be the isogonal conjugate of the points ![]() and
and ![]() with respect to a triangle
with respect to a triangle ![]()
Denote ![]() is the point isogonal conjugate to line
is the point isogonal conjugate to line ![]() with respect
with respect ![]() Isogonal_bijection_lines_and_points
Isogonal_bijection_lines_and_points
Prove that points ![]() and
and ![]() are collinear.
are collinear.
Proof
![]() After the simple calculations one can get:
After the simple calculations one can get:
![]()
![]()
![]() We use the normalized barycentric coordinates NBC and get line
We use the normalized barycentric coordinates NBC and get line ![]() in the form of:
in the form of:
![]()
![]()
![]() We check the condition of collinearity for points
We check the condition of collinearity for points ![]() and
and ![]() and finishing the proof.
and finishing the proof. ![]()
vladimir.shelomovskii@gmail.com, vvsss
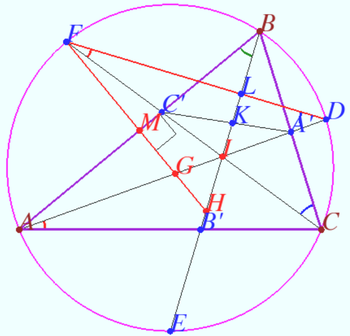
Points on bisectors
Let a triangle ![]() be given.
be given.
Let segments ![]() and
and ![]() be the bisectors of
be the bisectors of ![]()
The lines ![]() and
and ![]() meet circumcircle
meet circumcircle ![]() ) at points
) at points ![]() respectively.
respectively. ![]() is the midpoint
is the midpoint ![]() Denote
Denote ![]()
We will find barycentric coordinates of the points and length of the segments.
![]()
![]() Line
Line ![]() is
is ![]() line
line ![]() is
is ![]() line
line ![]() is
is ![]()
Circle ![]() is
is ![]()
![]()
![]()
Line ![]() is
is ![]()
Point ![]()
Line ![]() is
is ![]()
Point ![]()
Point ![]()
Some simple formulas:
![]()
![]()
![]()
![]() Circumcenter
Circumcenter ![]()
Tangent ![]() is
is ![]()
Line ![]() is
is ![]()
![]()
![]()
![]()
![]() is the midpoint
is the midpoint ![]()
![]()
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
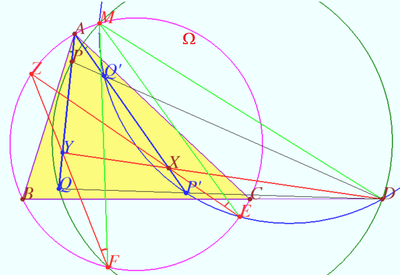
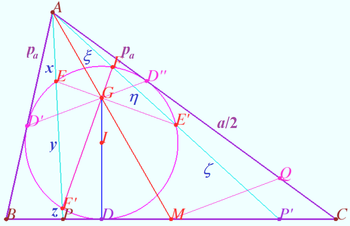
Crosspoint of median and set of secants
Triangle ![]() and point
and point ![]() be given. The incircle
be given. The incircle ![]() of
of ![]() touches side
touches side ![]() at point
at point ![]() Point
Point ![]() is symmetrical to point
is symmetrical to point ![]() with respect midpoint
with respect midpoint ![]() of
of ![]() The common points of segments
The common points of segments ![]() and
and ![]() with
with ![]() form a convex quadrilateral
form a convex quadrilateral ![]()
Prove that point ![]() lies on
lies on ![]()
Proof
Denote ![]()
![]()
![]() Line
Line ![]() line
line ![]()
We solve the system of these equations and get:
![\[E = \left( \left(\sqrt{\frac {p_c}{m}} + \sqrt {p_b \cdot m} \right)^2 : mp_a : \frac {p_a}{m} \right),\]](http://latex.artofproblemsolving.com/b/9/8/b980a5d9d2d9a837d9feabc9e64ee610f34aa780.png)
![\[F' = \left( \left(\sqrt{\frac {p_c}{m}} - \sqrt {p_b \cdot m} \right)^2 : mp_a : \frac {p_a}{m} \right),\]](http://latex.artofproblemsolving.com/4/9/7/497cc0bf7fcbfa02ae5e15d051d0fe5af55ae2b0.png)
![\[F = \left( \left(\sqrt{p_c \cdot m} + \sqrt {\frac {p_b}{m}} \right)^2 : \frac {p_a}{m} : mp_a \right),\]](http://latex.artofproblemsolving.com/a/f/f/affca988932bfb00eb209f2da36058cd4b977787.png)
![\[E' = \left( \left(\sqrt{p_c \cdot m} - \sqrt {\frac {p_b}{m}} \right)^2 : \frac {p_a}{m} : mp_a \right).\]](http://latex.artofproblemsolving.com/3/4/8/3489667fe2f62071569247e466eb1535f682eca3.png) We find the lines
We find the lines ![]() and
and ![]() we solve the system of equations for this lines and get:
we solve the system of equations for this lines and get:
![]() This point lies at the line
This point lies at the line ![]() Point
Point ![]() lies at line
lies at line ![]() and
and ![]()
Corollary
Denote ![]() Then
Then ![]()
vladimir.shelomovskii@gmail.com, vvsss
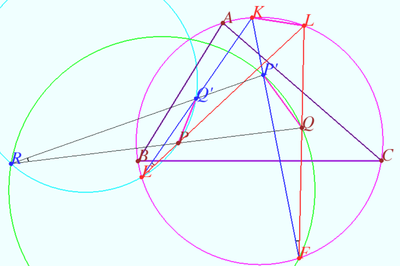
Set of lines in triangle
Let triangle ![]() and points
and points ![]() at the line
at the line ![]() be given.
be given.
Denote ![]() point in
point in ![]() such that
such that ![]() Similarly,
Similarly, ![]()
![]()
![]()
Prove that lines ![]() and
and ![]() are concurrent.
are concurrent.
Proof
Let ![]()
Then ![]()
![]()
![]()
Point ![]() lies at lines
lies at lines ![]() and
and ![]()
vladimir.shelomovskii@gmail.com, vvsss
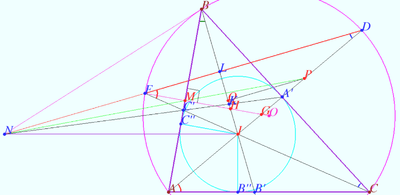
Set of parallel lines
Let triangle ![]() and points
and points ![]() at the line
at the line ![]() be given.
be given.
Denote ![]()
Let ![]() be the point such that
be the point such that ![]()
Similarly, ![]()
Prove that lines ![]() and
and ![]() are concurrent.
are concurrent.
Find the condition that ![]()
Proof
One can get ![]()
![]()
![]() If
If ![]() then
then ![]()
Corollary
Let points ![]() and
and ![]() lie at the lines
lie at the lines ![]() and
and ![]()
Denote circle ![]()
![]()
Let ![]()
![]()
Then lines ![]() and
and ![]() are concurrent.
are concurrent.
WLOG, situation is shown on diagram.
The proof contain calculations started from ![]() and finished at
and finished at ![]()
vladimir.shelomovskii@gmail.com, vvsss
Feuerbach point of a scalene triangle
The Feuerbach point of a scalene triangle lies on one of its bisectors. Prove that the angle corresponding to this bisector is ![]()
Proof
Denote ![]() given triangle,
given triangle, ![]() the incenter,
the incenter, ![]() - the Feuerbach point.
- the Feuerbach point.
The barycentric coordinates of point
![]()
![]()
![]()
![]() Another proof Scalene triangle with angle 60^\circ .
Another proof Scalene triangle with angle 60^\circ .
vladimir.shelomovskii@gmail.com, vvsss
Small Pascal's theorem
Let ![]() and point
and point ![]() be given. Let
be given. Let ![]() be the circumcircle of
be the circumcircle of ![]()
![]() Let the tangent line to
Let the tangent line to ![]() at point
at point ![]() cross line
cross line ![]() at point
at point ![]() Similarly denote points
Similarly denote points ![]() and
and ![]()
Prove that the points ![]() and
and ![]() are collinear.
are collinear.
Proof
1. Simplest case, ![]() is the Lemoine point,
is the Lemoine point, ![]()
The equation of ![]() is
is ![]()
Line ![]() is
is ![]()
![]() The line
The line ![]() is
is ![]()
Similarly, ![]()
The line ![]() is
is ![]()
2. Simple case, ![]() is one of the external Lemoine point,
is one of the external Lemoine point, ![]()
This point is the crosspoint of the tangent lines to ![]() in points
in points ![]() and
and ![]() so
so
![]() The line
The line ![]() is
is ![]()
Similarly, ![]()
The line ![]() is
is ![]()
Similarly, if ![]() then the line
then the line ![]() is
is ![]()
If ![]() then the line
then the line ![]() is
is ![]()
These three lines intersect in pairs at points ![]() and
and ![]() of the line of case 1.
of the line of case 1.
3. Common case. Denote the coordinates of the point ![]() The equation of
The equation of ![]() is
is ![]()
Line ![]() is
is ![]()
Similarly, ![]()
The tangent line ![]() to
to ![]() at
at ![]() is
is ![]()
The line ![]() is
is ![]()
![]()
Similarly, ![]()
![]() The line
The line ![]() is
is ![]()
vladimir.shelomovskii@gmail.com, vvsss