2003 AMC 12A Problems/Problem 17
Contents
[hide]Problem
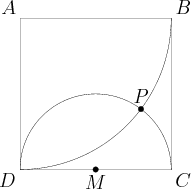
Square ![]() has sides of length
has sides of length ![]() , and
, and ![]() is the midpoint of
is the midpoint of ![]() . A circle with radius
. A circle with radius ![]() and center
and center ![]() intersects a circle with radius
intersects a circle with radius ![]() and center
and center ![]() at points
at points ![]() and
and ![]() . What is the distance from
. What is the distance from ![]() to
to ![]() ?
?
![]()
Solution
Let ![]() be the origin.
be the origin. ![]() is the point
is the point ![]() and
and ![]() is the point
is the point ![]() . We are given the radius of the quarter circle and semicircle as
. We are given the radius of the quarter circle and semicircle as ![]() and
and ![]() , respectively, so their equations, respectively, are:
, respectively, so their equations, respectively, are:
![]()
![]()
Algebraically manipulating the second equation gives:
![]()
![]()
![]()
![]()
Substituting this back into the first equation:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Solving each factor for 0 yields ![]() . The first value of
. The first value of ![]() is obviously referring to the x-coordinate of the point where the circles intersect at the origin,
is obviously referring to the x-coordinate of the point where the circles intersect at the origin, ![]() , so the second value must be referring to the x coordinate of
, so the second value must be referring to the x coordinate of ![]() . Since
. Since ![]() is the y-axis, the distance to it from
is the y-axis, the distance to it from ![]() is the same as the x-value of the coordinate of
is the same as the x-value of the coordinate of ![]() , so the distance from
, so the distance from ![]() to
to ![]() is
is ![]()
Solution 2
Note that ![]() is merely a reflection of
is merely a reflection of ![]() over
over ![]() . Call the intersection of
. Call the intersection of ![]() and
and ![]()
![]() . Drop perpendiculars from
. Drop perpendiculars from ![]() and
and ![]() to
to ![]() , and denote their respective points of intersection by
, and denote their respective points of intersection by ![]() and
and ![]() . We then have
. We then have ![]() , with a scale factor of 2. Thus, we can find
, with a scale factor of 2. Thus, we can find ![]() and double it to get our answer. With some analytical geometry, we find that
and double it to get our answer. With some analytical geometry, we find that ![]() , implying that
, implying that ![]() .
.