Difference between revisions of "1963 AHSME Problems/Problem 27"
Rockmanex3 (talk | contribs) m (→Solutions) |
Omicrongamma (talk | contribs) (→Solutions) |
||
| Line 22: | Line 22: | ||
With careful drawing, one can draw all six lines and count the regions. There are <math>22</math> regions in total, which is answer choice <math>\boxed{\textbf{(C)}}</math>. | With careful drawing, one can draw all six lines and count the regions. There are <math>22</math> regions in total, which is answer choice <math>\boxed{\textbf{(C)}}</math>. | ||
| + | |||
| + | ===Solution 3 === | ||
| + | |||
| + | We can use the fact that the number of regions that <math>n</math> lines divide a plane is given by the equation <math>L_n = \frac{n^2 + n +2}{2}</math>, and in this problems, <math>n=6</math>, from which the answer is <math>\boxed{22}</math>. | ||
| + | |||
| + | The formula is proved in Engel's Extremal Principles chapter or https://www.cut-the-knot.org/proofs/LinesDividePlane.shtml gives two proofs for it. | ||
==See Also== | ==See Also== | ||
Revision as of 19:57, 13 January 2019
Problem
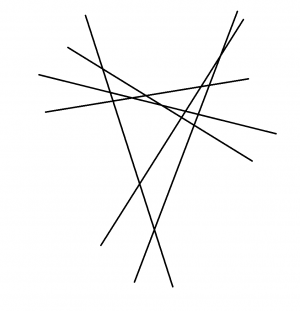
Six straight lines are drawn in a plane with no two parallel and no three concurrent. The number of regions into which they divide the plane is:
![]()
Solutions
Solution 1
The first line divides the plane into two regions. The second line intersects one line, creating two regions. The third line intersects two lines, creating three regions. Similarly, the fourth line intersects three lines and creates four regions, the fifth line intersects four lines and creates five regions, and the sixth line intersects five lines and creates six regions.
Totaling the regions created results in ![]() regions, which is answer choice
regions, which is answer choice ![]() .
.
Solution 2
With careful drawing, one can draw all six lines and count the regions. There are ![]() regions in total, which is answer choice
regions in total, which is answer choice ![]() .
.
Solution 3
We can use the fact that the number of regions that ![]() lines divide a plane is given by the equation
lines divide a plane is given by the equation ![]() , and in this problems,
, and in this problems, ![]() , from which the answer is
, from which the answer is ![]() .
.
The formula is proved in Engel's Extremal Principles chapter or https://www.cut-the-knot.org/proofs/LinesDividePlane.shtml gives two proofs for it.
See Also
| 1963 AHSC (Problems • Answer Key • Resources) | ||
| Preceded by Problem 26 |
Followed by Problem 28 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 • 31 • 32 • 33 • 34 • 35 • 36 • 37 • 38 • 39 • 40 | ||
| All AHSME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.