1971 Canadian MO Problems/Problem 1
Problem
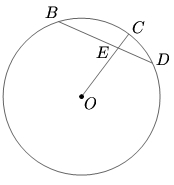
![]() is a chord of a circle such that
is a chord of a circle such that ![]() and
and ![]() Let
Let ![]() be the center of the circle. Join
be the center of the circle. Join ![]() and extend
and extend ![]() to cut the circle at
to cut the circle at ![]() Given
Given ![]() find the radius of the circle
find the radius of the circle
Solution
First, extend ![]() to meet the circle at
to meet the circle at ![]() Let the radius be
Let the radius be ![]() Applying Power of a Point,
Applying Power of a Point,
![]() and
and ![]() Hence,
Hence, ![]()