1977 Canadian MO Problems

The seven problems were all on the same day.

Problem 1

If $\displaystyle f(x)=x^2+x,$ prove that the equation $\displaystyle 4f(a)=f(b)$ has no solutions in positive integers $\displaystyle a$ and $\displaystyle b.$

Solution

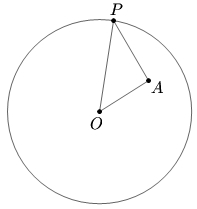
Problem 2

Let $\displaystyle O$ be the center of a circle and $\displaystyle A$ be a fixed interior point of the circle different from $\displaystyle O.$ Determine all points $\displaystyle P$ on the circumference of the circle such that the angle $\displaystyle OPA$ is a maximum.

Solution

Problem 3

$\displaystyle N$ is an integer whose representation in base $\displaystyle b$ is $\displaystyle 777.$ Find the smallest positive integer $\displaystyle b$ for which $\displaystyle N$ is the fourth power of an integer.

Solution

Problem 4

Let $p(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0$ and $q(x)=b_mx^m+b_{m-1}x^{m-1}+\cdots +b_1x+b_0$ be two polynomials with integer coefficients. Suppose that all of the coefficients of the product $p(x)\cdot q(x)$ are even, but not all of them are divisible by 4. Show that one of $p(x)$ and $q(x)$ has all even coefficients and the other has at least one odd coefficient.

Solution

Problem 5

Solution

Problem 6

Let $0<u<1$ and define $u_1=1+u\quad ,\quad u_2=\frac{1}{u_1}+u\quad \ldots\quad u_{n+1}=\frac{1}{u_n}+u\quad ,\quad n\ge 1$ Show that $u_n>1$ for all values of $n=1,2,3\ldots$ .

Solution

Problem 7

Solution

Page

Toolbox

Search

1977 Canadian MO Problems

Contents

Problem 1

Problem 2

Problem 3

Problem 4

Problem 5

Problem 6

Problem 7

Resources