1983 AHSME Problems
| 1983 AHSME (Answer Key) Printable versions: • AoPS Resources • PDF | ||
|
Instructions
| ||
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
Contents
- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 Problem 26
- 27 Problem 27
- 28 Problem 28
- 29 Problem 29
- 30 Problem 30
- 31 See also
Problem 1
If ![]() and
and ![]() , then
, then ![]() equals
equals
![]()
Problem 2
Point ![]() is outside circle
is outside circle ![]() on the plane. At most how many points on
on the plane. At most how many points on ![]() are
are ![]() cm from P?
cm from P?
![]()
Problem 3
Three primes ![]() and
and ![]() satisfy
satisfy ![]() and
and ![]() . Then
. Then ![]() equals
equals
![]()
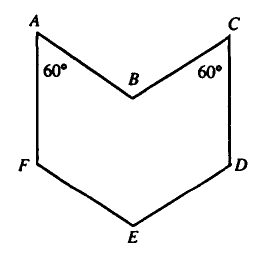
Problem 4
In the adjoining plane figure, sides ![]() and
and ![]() are parallel, as are sides
are parallel, as are sides ![]() and
and ![]() ,
and sides
,
and sides ![]() and
and ![]() . Each side has length
. Each side has length ![]() . Also,
. Also, ![]() .
The area of the figure is
.
The area of the figure is
![]()
Problem 5
Triangle ![]() has a right angle at
has a right angle at ![]() . If
. If ![]() , then
, then ![]() is
is
![]()
Problem 6
When ![]() and
and ![]() are multiplied, the product is a polynomial of degree
are multiplied, the product is a polynomial of degree
![]()
Problem 7
Alice sells an item at ![]() less than the list price and receives
less than the list price and receives ![]() of her selling price as her commission.
Bob sells the same item at
of her selling price as her commission.
Bob sells the same item at ![]() less than the list price and receives
less than the list price and receives ![]() of his selling price as his commission.
If they both get the same commission, then the list price is
of his selling price as his commission.
If they both get the same commission, then the list price is
![]()
Problem 8
Let ![]() . Then for
. Then for ![]() is
is
![]()
Problem 9
In a certain population the ratio of the number of women to the number of men is ![]() to
to ![]() .
If the average (arithmetic mean) age of the women is
.
If the average (arithmetic mean) age of the women is ![]() and the average age of the men is
and the average age of the men is ![]() ,
then the average age of the population is
,
then the average age of the population is
![]()
Problem 10
Segment ![]() is both a diameter of a circle of radius
is both a diameter of a circle of radius ![]() and a side of an equilateral triangle
and a side of an equilateral triangle ![]() .
The circle also intersects
.
The circle also intersects ![]() and
and ![]() at points
at points ![]() and
and ![]() , respectively. The length of
, respectively. The length of ![]() is
is
![]()
Problem 11
Simplify ![]() .
.
![]()
Problem 12
If ![]() , then
, then ![]() equals
equals
![]()
Problem 13
If ![]() and
and ![]() , and none of these quantities is
, and none of these quantities is ![]() , then
, then ![]() equals
equals
![]()
Problem 14
The units digit of ![]() is
is
![]()
Problem 15
Three balls marked ![]() and
and ![]() are placed in an urn. One ball is drawn, its number is recorded, and then the ball is returned to the urn. This process is repeated and then repeated once more, and each ball is equally likely to be drawn on each occasion. If the sum of the numbers recorded is
are placed in an urn. One ball is drawn, its number is recorded, and then the ball is returned to the urn. This process is repeated and then repeated once more, and each ball is equally likely to be drawn on each occasion. If the sum of the numbers recorded is ![]() , what is the probability that the ball numbered
, what is the probability that the ball numbered ![]() was drawn all three times?
was drawn all three times?
![]()
Problem 16
Let ![]() , where the digits are obtained by writing the integers
, where the digits are obtained by writing the integers ![]() through
through ![]() in order.
The
in order.
The ![]() rd digit to the right of the decimal point is
rd digit to the right of the decimal point is
![]()
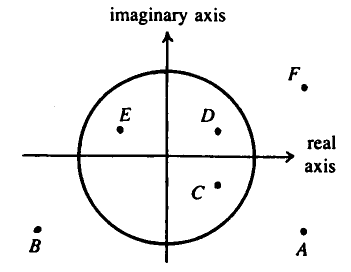
Problem 17
The diagram above shows several numbers in the complex plane. The circle is the unit circle centered at the origin.
One of these numbers is the reciprocal of ![]() . Which one?
. Which one?
![]()
Problem 18
Let ![]() be a polynomial function such that, for all real
be a polynomial function such that, for all real ![]() ,
,
![]() .
For all real
.
For all real ![]() is
is
![]()
Problem 19
Point ![]() is on side
is on side ![]() of triangle
of triangle ![]() . If
. If
![]() ,
then the length of
,
then the length of ![]() is
is
![]()
Problem 20
If ![]() and
and ![]() are the roots of
are the roots of ![]() , and
, and ![]() and
and ![]() are the roots of
are the roots of ![]() , then
, then ![]() is necessarily
is necessarily
![]()
Problem 21
Find the smallest positive number from the numbers below.
![]()
Problem 22
Consider the two functions ![]() and
and ![]() , where the variable
, where the variable ![]() and the constants
and the constants ![]() and
and ![]() are real numbers.
Each such pair of constants
are real numbers.
Each such pair of constants ![]() and
and ![]() may be considered as a point
may be considered as a point ![]() in an
in an ![]() -plane.
Let
-plane.
Let ![]() be the set of such points
be the set of such points ![]() for which the graphs of
for which the graphs of ![]() and
and ![]() do not intersect (in the
do not intersect (in the ![]() -plane). The area of
-plane). The area of ![]() is
is
![]()
Problem 23
In the adjoining figure the five circles are tangent to one another consecutively and to the lines
![]() and
and ![]() .
If the radius of the largest circle is
.
If the radius of the largest circle is ![]() and that of the smallest one is
and that of the smallest one is ![]() , then the radius of the middle circle is
, then the radius of the middle circle is
![[asy] size(250);defaultpen(linewidth(0.7)); real alpha=5.797939254, x=71.191836; int i; for(i=0; i<5; i=i+1) { real r=8*(sqrt(6)/2)^i; draw(Circle((x+r)*dir(alpha), r)); x=x+2r; } real x=71.191836+40+20*sqrt(6), r=18; pair A=tangent(origin, (x+r)*dir(alpha), r, 1), B=tangent(origin, (x+r)*dir(alpha), r, 2); pair A1=300*dir(origin--A), B1=300*dir(origin--B); draw(B1--origin--A1); pair X=(69,-5), X1=reflect(origin, (x+r)*dir(alpha))*X, Y=(200,-5), Y1=reflect(origin, (x+r)*dir(alpha))*Y, Z=(130,0), Z1=reflect(origin, (x+r)*dir(alpha))*Z; clip(X--Y--Y1--X1--cycle); label("$L_2$", Z, S); label("$L_1$", Z1, dir(2*alpha)*dir(90));[/asy]](http://latex.artofproblemsolving.com/a/a/a/aaa7232e66c0c4c548469d800da4877f6661951f.png)
![]()
Problem 24
How many non-congruent right triangles are there such that the perimeter in ![]() and the area in
and the area in ![]() are numerically equal?
are numerically equal?
![]()
Problem 25
If ![]() and
and ![]() , then
, then ![]() is
is
![]()
Problem 26
The probability that event ![]() occurs is
occurs is ![]() ; the probability that event B occurs is
; the probability that event B occurs is ![]() .
Let
.
Let ![]() be the probability that both
be the probability that both ![]() and
and ![]() occur. The smallest interval necessarily containing
occur. The smallest interval necessarily containing ![]() is the interval
is the interval
![]()
Problem 27
A large sphere is on a horizontal field on a sunny day. At a certain time the shadow of the sphere reaches out a distance
of ![]() m from the point where the sphere touches the ground. At the same instant a meter stick
(held vertically with one end on the ground) casts a shadow of length
m from the point where the sphere touches the ground. At the same instant a meter stick
(held vertically with one end on the ground) casts a shadow of length ![]() m. What is the radius of the sphere in meters?
(Assume the sun's rays are parallel and the meter stick is a line segment.)
m. What is the radius of the sphere in meters?
(Assume the sun's rays are parallel and the meter stick is a line segment.)
![]()
Problem 28
Triangle ![]() in the figure has area
in the figure has area ![]() . Points
. Points ![]() and
and ![]() , all distinct from
, all distinct from ![]() and
and ![]() ,
are on sides
,
are on sides ![]() and
and ![]() respectively, and
respectively, and ![]() . If triangle
. If triangle ![]() and quadrilateral
and quadrilateral ![]() have equal areas, then that area is
have equal areas, then that area is
![[asy] defaultpen(linewidth(0.7)+fontsize(10)); pair A=origin, B=(10,0), C=(8,7), F=7*dir(A--C), E=(10,0)+4*dir(B--C), D=4*dir(A--B); draw(A--B--C--A--E--F--D); pair point=incenter(A,B,C); label("$A$", A, dir(point--A)); label("$B$", B, dir(point--B)); label("$C$", C, dir(point--C)); label("$D$", D, dir(point--D)); label("$E$", E, dir(point--E)); label("$F$", F, dir(point--F)); label("$2$", (2,0), S); label("$3$", (7,0), S);[/asy]](http://latex.artofproblemsolving.com/6/4/f/64fdde55003bf41e0208ea11eb611aadc3c8bbea.png)
![]()
Problem 29
A point ![]() lies in the same plane as a given square of side
lies in the same plane as a given square of side ![]() . Let the vertices of the square,
taken counterclockwise, be
. Let the vertices of the square,
taken counterclockwise, be ![]() and
and ![]() . Also, let the distances from
. Also, let the distances from ![]() to
to ![]() and
and ![]() , respectively, be
, respectively, be ![]() and
and ![]() .
What is the greatest distance that
.
What is the greatest distance that ![]() can be from
can be from ![]() if
if ![]() ?
?
![]()
Problem 30
Distinct points ![]() and
and ![]() are on a semicircle with diameter
are on a semicircle with diameter ![]() and center
and center ![]() .
The point
.
The point ![]() is on
is on ![]() and
and ![]() . If
. If ![]() , then
, then ![]() equals
equals
![]()
See also
| 1983 AHSME (Problems • Answer Key • Resources) | ||
| Preceded by 1982 AHSME |
Followed by 1984 AHSME | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
| All AHSME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.