Difference between revisions of "1985 AIME Problems"
(→Problem 9) |
Megahertz13 (talk | contribs) (→Problem 1) |
||
| (8 intermediate revisions by 6 users not shown) | |||
| Line 2: | Line 2: | ||
==Problem 1== | ==Problem 1== | ||
| − | Let <math>x_1=97</math>, and for <math>n>1</math> let <math>x_n=\frac{n}{x_{n-1}}</math>. Calculate the product <math> | + | Let <math>x_1=97</math>, and for <math>n>1</math> let <math>x_n=\frac{n}{x_{n-1}}</math>. Calculate the product <math>x_1x_2 \ldots x_8</math>. |
[[1985 AIME Problems/Problem 1 | Solution]] | [[1985 AIME Problems/Problem 1 | Solution]] | ||
| + | |||
==Problem 2== | ==Problem 2== | ||
When a right triangle is rotated about one leg, the volume of the cone produced is <math>800\pi \;\textrm{cm}^3</math>. When the triangle is rotated about the other leg, the volume of the cone produced is <math>1920\pi \;\textrm{cm}^3</math>. What is the length (in cm) of the hypotenuse of the triangle? | When a right triangle is rotated about one leg, the volume of the cone produced is <math>800\pi \;\textrm{cm}^3</math>. When the triangle is rotated about the other leg, the volume of the cone produced is <math>1920\pi \;\textrm{cm}^3</math>. What is the length (in cm) of the hypotenuse of the triangle? | ||
| Line 15: | Line 16: | ||
==Problem 4== | ==Problem 4== | ||
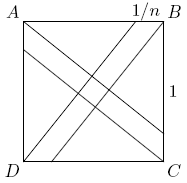
| − | A small square is constructed inside a square of area 1 by dividing each side of the unit square into <math>n</math> equal parts, and then connecting the vertices to the division points closest to the opposite vertices. Find the value of <math>n</math> if the the area of the small square is exactly <math>\frac1{1985}</math>. | + | A small square is constructed inside a square of area <math>1</math> by dividing each side of the unit square into <math>n</math> equal parts, and then connecting the vertices to the division points closest to the opposite vertices, as shown in the figure. Find the value of <math>n</math> if the the area of the small square is exactly <math>\frac1{1985}</math>. |
[[Image:AIME 1985 Problem 4.png]] | [[Image:AIME 1985 Problem 4.png]] | ||
| Line 22: | Line 23: | ||
==Problem 5== | ==Problem 5== | ||
| − | A sequence of integers <math>a_1, a_2, a_3, \ldots</math> is chosen so that <math>a_n = a_{n - 1} - a_{n - 2}</math> for each <math>n \ge 3</math>. What is the sum of the first 2001 terms of this sequence if the sum of the first 1492 terms is 1985, and the sum of the first 1985 terms is 1492? | + | A sequence of integers <math>a_1, a_2, a_3, \ldots</math> is chosen so that <math>a_n = a_{n - 1} - a_{n - 2}</math> for each <math>n \ge 3</math>. What is the sum of the first <math>2001</math> terms of this sequence if the sum of the first <math>1492</math> terms is <math>1985</math>, and the sum of the first <math>1985</math> terms is <math>1492</math>? |
[[1985 AIME Problems/Problem 5 | Solution]] | [[1985 AIME Problems/Problem 5 | Solution]] | ||
==Problem 6== | ==Problem 6== | ||
| − | As shown in the figure, | + | As shown in the figure, <math>\triangle ABC</math> is divided into six smaller triangles by lines drawn from the vertices through a common interior point. The areas of four of these triangles are as indicated. Find the area of <math>\triangle ABC</math>. |
[[Image:AIME 1985 Problem 6.png]] | [[Image:AIME 1985 Problem 6.png]] | ||
| Line 34: | Line 35: | ||
==Problem 7== | ==Problem 7== | ||
| − | Assume that <math>a</math>, <math>b</math>, <math>c</math> | + | Assume that <math>a</math>, <math>b</math>, <math>c</math> and <math>d</math> are positive integers such that <math>a^5 = b^4</math>, <math>c^3 = d^2</math> and <math>c - a = 19</math>. Determine <math>d - b</math>. |
[[1985 AIME Problems/Problem 7 | Solution]] | [[1985 AIME Problems/Problem 7 | Solution]] | ||
==Problem 8== | ==Problem 8== | ||
| − | The sum of the following seven numbers is exactly 19: <math>a_1 = 2.56</math>, <math>a_2 = 2.61</math>, <math>a_3 = 2.65</math>, <math>a_4 = 2.71</math>, <math>a_5 = 2.79</math>, <math>a_6 = 2. | + | The sum of the following seven numbers is exactly 19: <math>a_1 = 2.56</math>, <math>a_2 = 2.61</math>, <math>a_3 = 2.65</math>, <math>a_4 = 2.71</math>, <math>a_5 = 2.79</math>, <math>a_6 = 2.82</math>, <math>a_7 = 2.86</math>. It is desired to replace each <math>a_i</math> by an integer approximation <math>A_i</math>, <math>1\le i \le 7</math>, so that the sum of the <math>A_i</math>'s is also <math>19</math> and so that <math>M</math>, the maximum of the "errors" <math>\lvert A_i-a_i \rvert</math>, is as small as possible. For this minimum <math>M</math>, what is <math>100M</math>? |
[[1985 AIME Problems/Problem 8 | Solution]] | [[1985 AIME Problems/Problem 8 | Solution]] | ||
==Problem 9== | ==Problem 9== | ||
| − | In a circle, parallel chords of lengths 2, 3, and 4 determine central angles of <math>\alpha</math>, <math>\beta</math>, and <math>\alpha + \beta </math> radians, respectively, where <math>\alpha + \beta < \pi</math>. If <math>\cos \alpha</math>, which is a positive rational number, is expressed as a fraction in lowest terms, what is the sum of its numerator and denominator? | + | In a circle, parallel chords of lengths <math>2</math>, <math>3</math>, and <math>4</math> determine central angles of <math>\alpha</math>, <math>\beta</math>, and <math>\alpha + \beta </math> radians, respectively, where <math>\alpha + \beta < \pi</math>. If <math>\cos \alpha</math>, which is a positive rational number, is expressed as a fraction in lowest terms, what is the sum of its numerator and denominator? |
[[1985 AIME Problems/Problem 9 | Solution]] | [[1985 AIME Problems/Problem 9 | Solution]] | ||
==Problem 10== | ==Problem 10== | ||
| − | How many of the first 1000 positive integers can be expressed in the form | + | How many of the first <math>1000</math> positive integers can be expressed in the form |
<math>\lfloor 2x \rfloor + \lfloor 4x \rfloor + \lfloor 6x \rfloor + \lfloor 8x \rfloor</math>, | <math>\lfloor 2x \rfloor + \lfloor 4x \rfloor + \lfloor 6x \rfloor + \lfloor 8x \rfloor</math>, | ||
| Line 63: | Line 64: | ||
==Problem 12== | ==Problem 12== | ||
| − | Let <math>A</math>, <math>B</math>, <math>C</math> and <math>D</math> be the | + | Let <math>A</math>, <math>B</math>, <math>C</math> and <math>D</math> be the vertices of a regular tetrahedron, each of whose edges measures <math>1</math> meter. A bug, starting from vertex <math>A</math>, observes the following rule: at each vertex it chooses one of the three edges meeting at that vertex, each edge being equally likely to be chosen, and crawls along that edge to the vertex at its opposite end. Let <math>p = \frac{n}{729}</math> be the probability that the bug is at vertex <math>A</math> when it has crawled exactly <math>7</math> meters. Find the value of <math>n</math>. |
[[1985 AIME Problems/Problem 12 | Solution]] | [[1985 AIME Problems/Problem 12 | Solution]] | ||
==Problem 13== | ==Problem 13== | ||
| − | The numbers in the [[sequence]] <math>101</math>, <math>104</math>, <math>109</math>, <math>116</math>,<math>\ldots</math> are of the form <math>a_n=100+n^2</math>, where <math>n=1,2,3,\ldots</math> For each <math>n</math>, let <math>d_n</math> be the greatest common divisor of <math>a_n</math> and <math>a_{n+1}</math>. Find the maximum value of <math>d_n</math> as <math>n</math> ranges through the [[positive integer]]s. | + | The numbers in the [[sequence]] <math>101</math>, <math>104</math>, <math>109</math>, <math>116</math>,<math>\ldots</math> are of the form <math>a_n=100+n^2</math>, where <math>n=1,2,3,\ldots</math>. For each <math>n</math>, let <math>d_n</math> be the greatest common divisor of <math>a_n</math> and <math>a_{n+1}</math>. Find the maximum value of <math>d_n</math> as <math>n</math> ranges through the [[positive integer]]s. |
[[1985 AIME Problems/Problem 13 | Solution]] | [[1985 AIME Problems/Problem 13 | Solution]] | ||
==Problem 14== | ==Problem 14== | ||
| − | In a tournament each player played exactly one game against each of the other players. In each game the winner was awarded 1 point, the loser got 0 points, and each of the two players earned 1/ | + | In a tournament each player played exactly one game against each of the other players. In each game the winner was awarded 1 point, the loser got 0 points, and each of the two players earned <math>\frac{1}{2}</math> point if the game was a tie. After the completion of the tournament, it was found that exactly half of the points earned by each player were earned in games against the ten players with the least number of points. (In particular, each of the ten lowest scoring players earned half of her/his points against the other nine of the ten). What was the total number of players in the tournament? |
[[1985 AIME Problems/Problem 14 | Solution]] | [[1985 AIME Problems/Problem 14 | Solution]] | ||
==Problem 15== | ==Problem 15== | ||
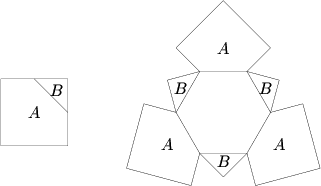
| − | Three 12 cm <math>\times</math> | + | Three <math>12</math> cm <math>\times 12</math> cm [[square (geometry) | squares]] are each cut into two pieces <math>A</math> and <math>B</math>, as shown in the first figure below, by joining the [[midpoint]]s of two adjacent sides. These six pieces are then attached to a [[regular polygon | regular]] [[hexagon]], as shown in the second figure, so as to fold into a [[polyhedron]]. What is the [[volume]] (in <math>\mathrm{cm}^3</math>) of this polyhedron? |
[[Image:AIME 1985 Problem 15.png]] | [[Image:AIME 1985 Problem 15.png]] | ||
| Line 85: | Line 86: | ||
==See also== | ==See also== | ||
| + | |||
| + | {{AIME box|year=1985|before=[[1984 AIME Problems]]|after=[[1986 AIME Problems]]}} | ||
| + | |||
* [[1985 AIME]] | * [[1985 AIME]] | ||
* [[American Invitational Mathematics Examination]] | * [[American Invitational Mathematics Examination]] | ||
| Line 90: | Line 94: | ||
* [[Mathematics competition resources]] | * [[Mathematics competition resources]] | ||
| + | {{MAA Notice}} | ||
[[Category:AIME Problems]] | [[Category:AIME Problems]] | ||
Latest revision as of 19:24, 23 February 2024
| 1985 AIME (Answer Key) | AoPS Contest Collections • PDF | ||
|
Instructions
| ||
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
Contents
Problem 1
Let ![]() , and for
, and for ![]() let
let ![]() . Calculate the product
. Calculate the product ![]() .
.
Problem 2
When a right triangle is rotated about one leg, the volume of the cone produced is ![]() . When the triangle is rotated about the other leg, the volume of the cone produced is
. When the triangle is rotated about the other leg, the volume of the cone produced is ![]() . What is the length (in cm) of the hypotenuse of the triangle?
. What is the length (in cm) of the hypotenuse of the triangle?
Problem 3
Find ![]() if
if ![]() ,
, ![]() , and
, and ![]() are positive integers which satisfy
are positive integers which satisfy ![]() , where
, where ![]() .
.
Problem 4
A small square is constructed inside a square of area ![]() by dividing each side of the unit square into
by dividing each side of the unit square into ![]() equal parts, and then connecting the vertices to the division points closest to the opposite vertices, as shown in the figure. Find the value of
equal parts, and then connecting the vertices to the division points closest to the opposite vertices, as shown in the figure. Find the value of ![]() if the the area of the small square is exactly
if the the area of the small square is exactly ![]() .
.
Problem 5
A sequence of integers ![]() is chosen so that
is chosen so that ![]() for each
for each ![]() . What is the sum of the first
. What is the sum of the first ![]() terms of this sequence if the sum of the first
terms of this sequence if the sum of the first ![]() terms is
terms is ![]() , and the sum of the first
, and the sum of the first ![]() terms is
terms is ![]() ?
?
Problem 6
As shown in the figure, ![]() is divided into six smaller triangles by lines drawn from the vertices through a common interior point. The areas of four of these triangles are as indicated. Find the area of
is divided into six smaller triangles by lines drawn from the vertices through a common interior point. The areas of four of these triangles are as indicated. Find the area of ![]() .
.
Problem 7
Assume that ![]() ,
, ![]() ,
, ![]() and
and ![]() are positive integers such that
are positive integers such that ![]() ,
, ![]() and
and ![]() . Determine
. Determine ![]() .
.
Problem 8
The sum of the following seven numbers is exactly 19: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . It is desired to replace each
. It is desired to replace each ![]() by an integer approximation
by an integer approximation ![]() ,
, ![]() , so that the sum of the
, so that the sum of the ![]() 's is also
's is also ![]() and so that
and so that ![]() , the maximum of the "errors"
, the maximum of the "errors" ![]() , is as small as possible. For this minimum
, is as small as possible. For this minimum ![]() , what is
, what is ![]() ?
?
Problem 9
In a circle, parallel chords of lengths ![]() ,
, ![]() , and
, and ![]() determine central angles of
determine central angles of ![]() ,
, ![]() , and
, and ![]() radians, respectively, where
radians, respectively, where ![]() . If
. If ![]() , which is a positive rational number, is expressed as a fraction in lowest terms, what is the sum of its numerator and denominator?
, which is a positive rational number, is expressed as a fraction in lowest terms, what is the sum of its numerator and denominator?
Problem 10
How many of the first ![]() positive integers can be expressed in the form
positive integers can be expressed in the form
![]() ,
,
where ![]() is a real number, and
is a real number, and ![]() denotes the greatest integer less than or equal to
denotes the greatest integer less than or equal to ![]() ?
?
Problem 11
An ellipse has foci at ![]() and
and ![]() in the
in the ![]() -plane and is tangent to the
-plane and is tangent to the ![]() -axis. What is the length of its major axis?
-axis. What is the length of its major axis?
Problem 12
Let ![]() ,
, ![]() ,
, ![]() and
and ![]() be the vertices of a regular tetrahedron, each of whose edges measures
be the vertices of a regular tetrahedron, each of whose edges measures ![]() meter. A bug, starting from vertex
meter. A bug, starting from vertex ![]() , observes the following rule: at each vertex it chooses one of the three edges meeting at that vertex, each edge being equally likely to be chosen, and crawls along that edge to the vertex at its opposite end. Let
, observes the following rule: at each vertex it chooses one of the three edges meeting at that vertex, each edge being equally likely to be chosen, and crawls along that edge to the vertex at its opposite end. Let ![]() be the probability that the bug is at vertex
be the probability that the bug is at vertex ![]() when it has crawled exactly
when it has crawled exactly ![]() meters. Find the value of
meters. Find the value of ![]() .
.
Problem 13
The numbers in the sequence ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() are of the form
are of the form ![]() , where
, where ![]() . For each
. For each ![]() , let
, let ![]() be the greatest common divisor of
be the greatest common divisor of ![]() and
and ![]() . Find the maximum value of
. Find the maximum value of ![]() as
as ![]() ranges through the positive integers.
ranges through the positive integers.
Problem 14
In a tournament each player played exactly one game against each of the other players. In each game the winner was awarded 1 point, the loser got 0 points, and each of the two players earned ![]() point if the game was a tie. After the completion of the tournament, it was found that exactly half of the points earned by each player were earned in games against the ten players with the least number of points. (In particular, each of the ten lowest scoring players earned half of her/his points against the other nine of the ten). What was the total number of players in the tournament?
point if the game was a tie. After the completion of the tournament, it was found that exactly half of the points earned by each player were earned in games against the ten players with the least number of points. (In particular, each of the ten lowest scoring players earned half of her/his points against the other nine of the ten). What was the total number of players in the tournament?
Problem 15
Three ![]() cm
cm ![]() cm squares are each cut into two pieces
cm squares are each cut into two pieces ![]() and
and ![]() , as shown in the first figure below, by joining the midpoints of two adjacent sides. These six pieces are then attached to a regular hexagon, as shown in the second figure, so as to fold into a polyhedron. What is the volume (in
, as shown in the first figure below, by joining the midpoints of two adjacent sides. These six pieces are then attached to a regular hexagon, as shown in the second figure, so as to fold into a polyhedron. What is the volume (in ![]() ) of this polyhedron?
) of this polyhedron?
See also
| 1985 AIME (Problems • Answer Key • Resources) | ||
| Preceded by 1984 AIME Problems |
Followed by 1986 AIME Problems | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
- 1985 AIME
- American Invitational Mathematics Examination
- AIME Problems and Solutions
- Mathematics competition resources
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.