Difference between revisions of "1985 AIME Problems/Problem 15"
(→See also) |
Gougutheorem (talk | contribs) m (→Solution) |
||
| (7 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
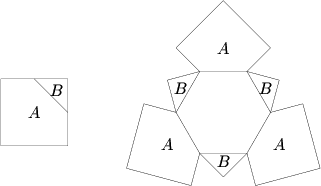
| + | Three 12 cm <math>\times</math>12 cm [[square (geometry) | squares]] are each cut into two pieces <math>A</math> and <math>B</math>, as shown in the first figure below, by joining the [[midpoint]]s of two adjacent sides. These six pieces are then attached to a [[regular polygon | regular]] [[hexagon]], as shown in the second figure, so as to fold into a [[polyhedron]]. What is the [[volume]] (in <math>\mathrm{cm}^3</math>) of this polyhedron? | ||
| + | |||
| + | [[Image:AIME 1985 Problem 15.png]] | ||
== Solution == | == Solution == | ||
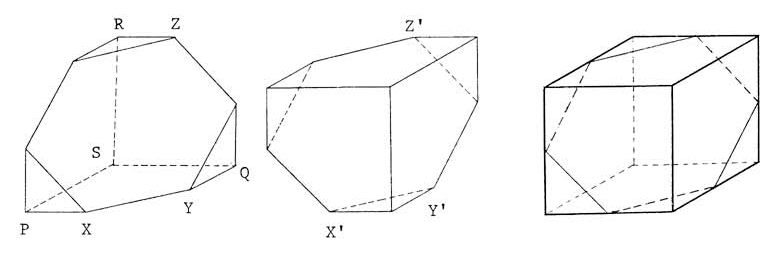
| + | Note that gluing two of the given polyhedra together along a hexagonal face (rotated <math>60^\circ</math> from each other) yields a [[cube (geometry) | cube]], so the volume is <math>\frac12 \cdot 12^3 = 864</math>, so our answer is <math>\boxed{864}</math>. | ||
| + | |||
| + | Image: [[Image:AoPS_AIME_1985.png]] | ||
| + | |||
| + | Sidenote: What if this simple and beautiful way was not realized? | ||
| + | Taking a reference to the above left diagram, obviously SP, SQ and SR are perpendicular to each other. Thus expanding plane SPQ, SQR and SRP to intersect with the plane XYZ that contains the regular hexagon, we form a pyramid with S the top vertex and the base being an equilateral triangle with side length of 18 <math>\sqrt{2}</math> . This pyramid has a volume of 972, because it is also 1/6 of the volume of a cube with side length of 18. Then subtracting 3 congruent pyramids with volume of 36 each, we get <math>864</math>. | ||
== See also == | == See also == | ||
| − | * [[ | + | {{AIME box|year=1985|num-b=14|after=Last Question}} |
| + | * [[AIME Problems and Solutions]] | ||
| + | * [[American Invitational Mathematics Examination]] | ||
| + | * [[Mathematics competition resources]] | ||
| + | |||
| + | [[Category:Intermediate Geometry Problems]] | ||
Revision as of 11:05, 14 April 2021
Problem
Three 12 cm 
12 cm squares are each cut into two pieces 
and 
, as shown in the first figure below, by joining the midpoints of two adjacent sides. These six pieces are then attached to a regular hexagon, as shown in the second figure, so as to fold into a polyhedron. What is the volume (in 
) of this polyhedron?
Solution
Note that gluing two of the given polyhedra together along a hexagonal face (rotated 
from each other) yields a cube, so the volume is 
, so our answer is 
.
Image: 
Sidenote: What if this simple and beautiful way was not realized?
Taking a reference to the above left diagram, obviously SP, SQ and SR are perpendicular to each other. Thus expanding plane SPQ, SQR and SRP to intersect with the plane XYZ that contains the regular hexagon, we form a pyramid with S the top vertex and the base being an equilateral triangle with side length of 18 
. This pyramid has a volume of 972, because it is also 1/6 of the volume of a cube with side length of 18. Then subtracting 3 congruent pyramids with volume of 36 each, we get 
.
See also
| 1985 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
