Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1987 AIME Problems/Problem 4"
m (→‎Solution 2)
Line 28: Line 28:
 
By simple sketching, we see the shape that looks like the image in Solution 1 (graph it out and you'll see). We see that the partial area we seek in this part is the triangle with the vertices <math>(60,15)</math>, <math>(48,0)</math>, <math>(80,0)</math>. This triangle has an area of <math>(80-48)*15*0.5=240</math>.  
 
By simple sketching, we see the shape that looks like the image in Solution 1 (graph it out and you'll see). We see that the partial area we seek in this part is the triangle with the vertices <math>(60,15)</math>, <math>(48,0)</math>, <math>(80,0)</math>. This triangle has an area of <math>(80-48)*15*0.5=240</math>.  
  
−
Simply double the area and we get 480 as our final answer. I can't box the answer for some reason. Please let me know what's wrong.  
+
Simply double the area and we get <math>\boxed{480}</math> as our final answer. I can't box the answer for some reason. Please let me know what's wrong.  
  
 
~hastapasta
 
~hastapasta

Revision as of 12:27, 6 February 2022

Problem

Find the area of the region enclosed by the graph of $|x-60|+|y|=\left|\frac{x}{4}\right|.$

Solution 1

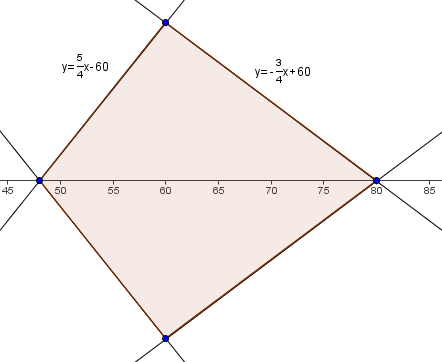
1987 AIME-4.png

Since $|y|$ is nonnegative, $\left|\frac{x}{4}\right| \ge |x - 60|$. Solving this gives us two equations: $\frac{x}{4} \ge x - 60\ \mathrm{and} \ -\frac{x}{4} \le x - 60$. Thus, $48 \le x \le 80$. The maximum and minimum y value is when $|x - 60| = 0$, which is when $x = 60$ and $y = \pm 15$. Since the graph is symmetric about the y-axis, we just need casework upon $x$. $\frac{x}{4} > 0$, so we break up the condition $|x-60|$:

  • $x - 60 > 0$. Then $y = -\frac{3}{4}x+60$.
  • $x - 60 < 0$. Then $y = \frac{5}{4}x-60$.

The area of the region enclosed by the graph is that of the quadrilateral defined by the points $(48,0),\ (60,15),\ (80,0), \ (60,-15)$. Breaking it up into triangles and solving or using shoelace, we get $2 \cdot \frac{1}{2}(80 - 48)(15) = \boxed{480}$.

Solution 2

Since $|y|$ is the only present $y$ "term" in this equation, we know that the area must be symmetrical about the x-axis.

We'll consider the area when $y>0$ and we only consider the portion enclosed with $y=0$. Then, we'll double that area since the graph is symmetrical.

Now, let us remove the absolute values:

When $x>60$ or $x=60$: $x-60+y=0.25x$. This rearranges to $y=-0.75x+60$.

When $0<=x<60$: $60-x+y=0.25$. So $y=1.25x-60$.

When $x<0$: $60-x+y=-0.25x$. So $y=0.75x-60$.

By simple sketching, we see the shape that looks like the image in Solution 1 (graph it out and you'll see). We see that the partial area we seek in this part is the triangle with the vertices $(60,15)$, $(48,0)$, $(80,0)$. This triangle has an area of $(80-48)*15*0.5=240$.

Simply double the area and we get $\boxed{480}$ as our final answer. I can't box the answer for some reason. Please let me know what's wrong.

~hastapasta

See also

1987 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 3 		Followed by
Problem 5
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1987_AIME_Problems/Problem_4&oldid=171040"