Difference between revisions of "1987 AIME Problems/Problem 9"
(→Note) |
Phoenixfire (talk | contribs) (→Note) |
||
| Line 16: | Line 16: | ||
<cmath>4x = 132 \Longrightarrow x = \boxed{033}.</cmath> | <cmath>4x = 132 \Longrightarrow x = \boxed{033}.</cmath> | ||
=== Note === | === Note === | ||
| − | This is the Fermat point of the triangle. | + | This is the [[Fermat point]] of the triangle. |
== See also == | == See also == | ||
Revision as of 07:52, 4 March 2021
Contents
Problem
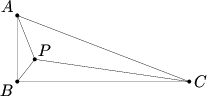
Triangle ![]() has right angle at
has right angle at ![]() , and contains a point
, and contains a point ![]() for which
for which ![]() ,
, ![]() , and
, and ![]() . Find
. Find ![]() .
.
Solution
Let ![]() . Since
. Since ![]() , each of them is equal to
, each of them is equal to ![]() . By the Law of Cosines applied to triangles
. By the Law of Cosines applied to triangles ![]() ,
, ![]() and
and ![]() at their respective angles
at their respective angles ![]() , remembering that
, remembering that ![]() , we have
, we have
![]()
Then by the Pythagorean Theorem, ![]() , so
, so
![]()
and
![]()
Note
This is the Fermat point of the triangle.
See also
| 1987 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 8 |
Followed by Problem 10 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.